Computers, Materials & Continua DOI:10.32604/cmc.2022.028830
Article

A Hybrid Particle Swarm Optimization to Forecast Implied Volatility Risk

Kais Tissaoui1,2,*, Sahbi Boubaker3,4, Waleed Saud Alghassab1, Taha Zaghdoudi1,5 and Jamel Azibi6

1University of Ha’il, Applied College, Hail City, Saudi Arabia
2University of Tunis El Manar, Faculty of Economic Sciences and Management of Tunis, the International Finance Group, Tunis, Tunisia
3Department of Computer and Network Engineering, College of Computer Science and Engineering, University of Jeddah, Jeddah, 21959, Saudi Arabia
4Research Unit on Study of Systems and Renewable Energy, National College of Engineering of Monastir, University of Monastir, Monastir, Tunisia
5LAREQUAD & FSEGT, University of Tunis El Manar, Tunis, Tunisia
6University of Jendouba, Law Faculty, Management and Economic Sciences of Jendouba, Tunisia
*Corresponding Author: Kais Tissaoui. Email: k.tissaoui@yahoo.com
Received: 19 February 2022; Accepted: 06 May 2022

Abstract: The application of optimization methods to prediction issues is a continually exploring field. In line with this, this paper investigates the connectedness between the infected cases of COVID-19 and US fear index from a forecasting perspective. The complex characteristics of implied volatility risk index such as non-linearity structure, time-varying and non-stationarity motivate us to apply a nonlinear polynomial Hammerstein model with known structure and unknown parameters. We use the Hybrid Particle Swarm Optimization (HPSO) tool to identify the model parameters of nonlinear polynomial Hammerstein model. Findings indicate that, following a nonlinear polynomial behaviour cascaded to an autoregressive with exogenous input (ARX) behaviour, the fear index in US financial market is significantly affected by COVID-19-infected cases in the US, COVID-19-infected cases in the world and COVID-19-infected cases in China, respectively. Statistical performance indicators provided by the developed models show that COVID-19-infected cases in the US are particularly powerful in predicting the Cboe volatility index compared to COVID-19-infected cases in the world and China (MAPE (2.1013%); R2 (91.78%) and RMSE (0.6363 percentage points)). The proposed approaches have also shown good convergence characteristics and accurate fits of the data.

Keywords: Forecasting; Cboe’s volatility index; COVID-19 pandemic; nonlinear polynomial hammerstein model; hybrid particle swarm optimization

1  Introduction

From the Chinese city of Wuhan, the world is going through difficult conditions these days caused by the rapidly spreading COVID-19 pandemic, which has strangled the worldwide economy, the financial markets, the oil market, the banking and insurance industries [1–3]. As of 18 June 2020, more than 8 million confirmed cases and over 450,000 deaths have been recorded (https://www.worldometers.info/coronavirus/). The authors in [4] argue that the influence of the coronavirus on the financial markets is negative, i.e., more cases lead to a more negative impact and vice versa. Similarly, the authors in [5] added that this crisis is particularly marked in contrast to all previous crises, in which traders were concerned not only about the value of their assets and investments, but also about their individual health, safety, personal security, well-being and that of their families. This creates great uncertainty about financial stability for even the most sophisticated traders. Moreover, it is historically unique that an influenza epidemic has triggered crises and spread dynamic volatility in the stock and oil markets.

In this paper, we focus on the financial market in the United States of America (USA), which has suffered historic losses in the first three months of 2020. Daily FT [6] reinforced this view by claiming that, “The Dow Jones, and S&P both of which take into account the share prices of a variety of companies in the US have dropped by over 20%”. The authors of [7] also mentioned that the value of the S&P 500 index fell by more than $5 trillion in one week between 24 March and 28 March, while the 10 largest companies lost more than $1.4 trillion in that period. Reference [8] have pointed out that the unexpected outbreak of the COVID-19 pandemic caused fatal distress in the US financial market, leading to higher levels of equity volatility than those observed in the financial crises of October 1987, December 2008 and the 1929 crash. Based on the above discussion, our study will focus on the US financial market for two reasons: First, the US financial market is the largest stock market in the world. Second, it is considered one of the main sources of spreading volatility and uncertainty to other markets [7–9]. Accordingly, with the increase in COVID-19 cases around the world and in the US, the US financial market is now still in a state of exhaustion and seesawing, despite procedures that would have previously supported the markets, have been interpreted as a source of confusion and an indication of dangerous market conditions.

This leads investors into a vicious cycle of random selling and further declines in stock prices. The team in [10] supports this reality by stating that the COVID-19 pandemic forces stock traders to react to unprecedented volatility. Reference [11] confirmed this by providing evidence that the durability of COVID-19 leads to increased market uncertainty and volatility as well as financial stability. Furthermore, [12] added that the dominance of the COVID-19 crisis in the US financial market remains significant during the second phase of the epidemic, even after the practice of quarantine precautions. This uncertainty about the stability and performance of the US financial market forces investors to take short positions in risky assets. This financial market panic in the US can be reflected by the rise in the Cboe Volatility Index (known as the VIX), which has jumped to 82.69 percentage points. This value is higher than those recorded during the 2008 global financial crisis Fig. 1. In fact, the Cboe Fear Index or Volatility Index has been used as a proxy for market expectations of short-term fluctuations in stock index option prices [13]. The author of [9] pointed out that when the VIX is falling, traders take a long position by buying puts on individual stocks. Thus, low-cost portfolio protection is taken. On the other hand, if the VIX rises, traders find themselves in short position and under pressure. So, more expensive portfolio protection was undertaken.

Given these circumstances that are caused by COVID-19, traders find themselves in a state of blurred vision about the future and more specifically regarding the expected cash flows that can affect the value of a company. Indeed, forecasting the fear index in the US market has become a necessity for traders and other market participants. Thus, many studies in financial economics have examined the forecasting of the implied volatility risk index. The authors in [14] and [9] proved that it is important to make an accurate forecast of the fear index for investors. This contributes to having correct expectations in the financial markets with regard to performance and stock price formation.

The objective of this paper is to study the predictive power of COVID-19 cases worldwide, in the United States of America and in China for the US financial market fear index. This is done using the Hammerstein-ARX approach estimated by a hybrid particle swarm optimization (HPSO). Many reasons have been put forward in the literature to justify the use of HPSO to estimate the Hammerstein-ARX approach. The authors in [15,16] reported many contributions behind using the HPSO to optimally tune the model parameters: (i) both the polynomial part and the ARX part have two types of parameters; namely integer orders and real coefficients. (ii) The HPSO is characterized by global search ability which may allow finding global solutions instead of local solutions that are probably provided by gradient-based optimization algorithms and (iii) the proposed approach has an ability to combine the local and global searches abilities. Moreover, the random initialization of the candidate solutions allows covering the overall integer-real-valued search spaces.

The author in [9] provided evidence that the application of HPSO to estimate Hammerstein-ARX is appropriate for predicting the fear index which has a non-linear pattern. The authors in [17,18] showed that the transmission of information to equity market and the anticipation by investors of future market movements represent a major source of non-linearity in the implied volatility process. This stylized effect prompts us to use effective complex tools such as the Hammerstein discrete-time model. The authors of [19] indicated that this approach does not require stationarity of the original data to perform the forecasting operation. They pointed out that the implementation of HPSO is not affected by the number of observations in the sample. The authors in [16] also showed that the Hammerstein-ARX approach is very challenging and outperforms linear models in terms of accuracy and convergence because it is constructed in two blocks: a static non-linear and a linear dynamic blocks respectively.

Our research is based on the literature dealing with the response of financial markets to several disasters and crises. First, we refer to [20], which studied the response of financial markets and the evolution of stock prices to Hurricane Katrina during 2005. Second, many authors in [21–25] considered the response of financial markets to the global financial crisis of 2007–2009. Third, other authors, such as [26], examined the link between air disasters and stock markets. We also mention other authors who have studied the “spillover effects” of terrorist attacks, such as those of September 11, on financial markets [27,28]. Fourth, the team in [29] also considered the impact of the political crisis in South and North Korea on the financial markets. Finally, the authors in [30] discuss the response of stock market to the mine disasters. Similarly, [31] reported that the analysis of many pandemics in the past shows that none of them affected stock market performance to the same extent as COVID-19. Many authors have demonstrated the enormous effect of official announcements of new COVID-19 cases and mortality rates on US stock market volatility [32]. This indicates that the COVID-19 epidemic represents a significant source of fear for investors compared to previous pandemics. As observed, implied volatility reached its highest value in the last decade, in parallel with the spread of the Corona epidemic, exceeding the value of 65 percentage points. Thus, implied volatility can be used by investors to make predictions about future market behaviour. In addition, the accuracy of volatility forecasting can help investors understand the changes in returns to be expected during the pandemic. This has been the subject of much discussion in academic and industry circles. Clear information on how stock prices will fluctuate is essential to make better investment decisions, especially during a pandemic [33].

This study contributes to the previous studies in several ways. First, to the best of our knowledge, no studies have investigated the effect of COVID-19 outbreak on the fear index of U.S. Financial market. This study is the first to explore the forecasting power of the infected cases of COVID-19 in USA, in World and in China for the Cboe’s volatility index. Second, the complex pricing of Cboe’s volatility index caused by the spillover effect of different disasters and pandemics on financial markets prompts us to apply the Artificial Intelligence (AI) Techniques. Driven by their minor complexity and costs, greater accuracy, and fast processing times, this study is the pioneer to use the Hammerstein models tuned by a particle swarm optimization (PSO) algorithm to forecast Cboe’s volatility index during the COVID-19 outbreak. Third, our estimated findings provide important implications for policymakers and investors when considering the forecasting power of useful information’s about infected cases COVID-19 for the uncertainty in US financial market to better respectively tacking measures to ensure satisfactory level of stability and confidence in US financial market and formulating optimal investment strategies and efficient use of hedging instruments.

The rest of this article is organized as follows. Section 2 describes the research methodology. The data and preliminary results is presented and analyzed in Section 3. Section 4 summarizes the empirical findings, while Section 5 provides conclusion and implications.

2  Materials and Methods

The main objective of this paper is to predict the fear index in the US financial market using the COVID-19 infected cases in the world, in the US and in China. This is achieved by developing a Hammerstein-ARX model. The parameters of the model were identified and estimated using hybrid particle swarm optimization (HPSO). The Hammerstein nonlinear part will be modelled using a polynomial function.

2.1 The Hammerstein Models with Known Nonlinearity Pattern

In this study, we first estimate the parameters of a relevant model reflecting the effect of the COVID-19 infected cases on the Cboe’s volatility index from a forecasting perspective. Fig. 1 plots the discrete-time Hammerstein-ARX model. In fact, it is divided into two blocks: A nonlinear static part and a linear dynamic part described as an autoregressive with exogenous input (ARX).

Figure 1: The discrete-time Hammerstein model block-diagram

From a dynamical systems perspective, the input of the present system is the infected cases of Covid-19, u(t) and the output is the Cboe’s volatility index, y(t). The parametric structure of the Hammerstein model is the most widely used by researchers [15–19]. The intermediate variable, x(t)  is non-accessible for measurement and represents the output of the nonlinear component f(.). The proposed system works as follows: First, u(t) is supplied to the static non-linear structure f(.) which generates the intermediate signal. Second, the intermediate signal is delayed by a block comprising delay operator units. The proposed model is then described by the following equations:

y(t) =z−dF−1(z−1)B(z−1)[∑i=1r⁡ciui(t)](1)

with

B(z−1)=1+a1z−1+a2z−2+…+apz−p(2)

F(z−1)=b0+b1z−1+b2z−2+…+bqz−q(3)

where z−1 represent the unit delay operator and d is the global pure lag, which have values inside the discrete-valued set {0, 1, 2}. u(t) and y(t) represents respectively the input and the output. d, r, p, and q constitute the constant integer orders of the model, with p and q which considered as the orders of polynomials B(z−1)    and   F−1(z−1) and r represents the order of the static polynomial part. The parameters ci, aj, bl constitute the real coefficients of the model. In this paper, the deterministic case where the noise block is excluded is considered without loss of generality.

2.2 Hammerstein ARX Model Identification Using HPSO

Let Xi be the Hammerstein parameter vector to be identified:

Xi=[di,ri, pi, qi,c1i,c2i, …,cRmaxi,a1i, a2i,…, aPmaxi, b0i,b1i,…,bqmaxi](4)

In the proposed HPSO algorithm [34–36], each particle (ith particle) represents a candidate solution for the identification problem defined as an optimization framework aiming to minimize the quadratic error between the forecasted and the observed Cboe’s volatility index.

Each particle represents an element in D-dimensional vector. The ith particle position is defined as:

Xi=(X1i , X2i…………XDi)(5)

We consider the prior best position of any particle in the swarm as follows:

Pi=(P1i , P2i…………PDi)(6)

The velocity of any particle in the swarm i as follows:

Vi=(V1i , V2i…………VDi)(7)

The position visited on previous occasion by the ith particle is defined as Pi and a velocity operator expressing the position change is defined as Vi. Both the two vectors have the same dimensions and components’ nature as in Xi.

The principle of the HPSO search for the optimal solution is based on the combination of three trends: (i) Following the current search direction, (ii) following the local search during which the particle records the best previous position; and (iii) the global search ability in which each particle in the swarm try to follow the leader current realization.

Accordingly, the particles evolve following the move equations:

Vk+1i=wkVki+c1r1(Pi−Xi)+c2r2 (Gi−Xi) (8)

 Xk+1i=Xki+Vk+1i (9)

Since the Hammerstein-ARX model parameters include integers, the corresponding dimensions (d, p, q and r) are updated according to:

Xk+1i=round(Xki+Vk+1i)(10)

We consider  Gi as the global best solution of the swarm, C1  and  C2      represent the acceleration coefficients where   set  between 0  and 2. r1, and r2 are random values having values between 0 and 1. wk is linearly decreasing with the iterative generations. It represents the inertial coefficient (inertia weight). It is computed by the following formula:

wk=wmax−wmax−wminkmax∗k(11)

where kmax   represents the maximum number of iterations (which will be used as the stopping criterion of the optimization algorithm); k  indicates the indice of the actual iteration during the identification process.

In addition, the optimization of the fitness function will be achieved through the minimization of the total of the squared residuals between the observed values and the predicted values of the Cboe’s volatility index defined as follows:

J(X)= Min∑t=1NT(yf(t)−yr(t))2(12)

where NT  represents the sub-sample served for running the training model. We consider  yf(t) and yr(t) as the forecasted values and the real value at time t, respectively.

To achieve this, the PSO identification algorithm is run in three steps [34–36]: (i). Evaluate the ability of each particle; 2. Update the global and individual top performers; 3. Refresh the position and velocity of each particle. Algorithm stages are completed after a certain number of iterations, and the particle fitness values are achieved. To judge the accuracy of the forecasted values, four metrics have been used in literature [9], namely:

Mean  Absolute  Percentage  Error (MAPE)=100Ny∑t=1Ny|yt^−yt|y¯(13)

Root  Mean  Squared  Error (RMSE)=1Ny∑t=1Ny(yt−y^t)2(14)

Coefficient  of  Determination (R2)=1−1Ny∑t=1Ny⁡(y−y^t)21Ny∑t=1Ny⁡(y−y¯)2 (15)

where  y^t is the forecasted Cboe’s volatility index, yt is the tth actual Cboe’s volatility index, y¯ is the mean Cboe’s volatility index, and Ny is the size of sub-sample employed for the validation model. Therefore, to have a best forecast, all metrics must be minimized (except of R2 which is better to be near of 1).

2.3 Robustness Check

For robustness reasons, we compare our proposed Hammerstein ARX model with the two classical time series models such as the heterogeneous autoregressive model (HARX) and the fractionally integrated autoregressive moving average models (ARFIMAX (p, d, q)). This is very essential to show the advantage of the complex machine learning models over the classical and traditional approaches. First, the ARFIMAX (p, d, q) model is a time series model that generalizes ARIMAX (p, d, q) by allowing non-integer values of the differentiation parameter d. It can be defined as follows:

Δdyt=δ+∑i=1pφiyt−i+∑i=0qσiεt−i +∑i=1kωiut−i+d+e(16)

where y(t) is the output (the VIX index) ; y(t−i) are the previous values of the output (the VIX index).  δ is a constant and d is the order of integration. φi, σi and ωi  denote the coefficient parameters, p, q and k, are the maximum time lag related to output sequence and residuals respectively. e(t) is an error term. To find the best fit of ARFIMAX (p, d, q), we use the Box and Jenkins method to find the autoregressive (AR) and moving average (MA) parts based on the partial autoregressive functions (PACF) and autoregressive functions (ACF). The AIC is used to select the best models among the different possible ARFIMAX (p, d, q) models.

Second, it is the heterogeneous autoregressive model (HAR) that [37] develops. This is a hierarchical model with three parts consisting of time horizons of one day, one week and one month. These three parts are identified as the results of the heterogeneity of traders in the financial market. In particular, [37] adds three volatility parts respectively to three types of traders: Short-term traders with a daily or higher trading frequency, medium-term traders intervening in the financial markets so as to readjust their positions every week and long-term investors with a characteristic time of one or more months. Following [9], we use the HAR model adapted to the implied volatility risk index. The final HAR process with exogenous input used for forecasting is defined as:

log⁡(yt)=w0+w1log⁡(yt−1)+w2(5−1∑j=15log(yt−j ))+w3(22−1∑j=122log(yt−j))+w4log⁡(ut−1)+ w5(5−1∑j=15log(ut−j ))+w6(22−1∑j=122log(ut−j))+εt(17)

where log⁡(yt) is the output (VIX index). log⁡(yt−1), 5−1∑j=15⁡log(yt−j ) and 22−1∑j=122⁡log(yt−j) are respectively daily, weekly and monthly observed outputs (VIX index); whereas, log⁡(ut−1), 5−1∑j=15⁡log(ut−j ) and 22−1∑j=122⁡log(ut−j) indicate respectively daily, weekly and monthly observed exogenous inputs(the infected cases of COVID -19 around the world, in USA and in China index).

2.4 Model Illustration

The procedure has been implemented for 3 case studies. In what follows, details about case 1 related to the USA covid-19 data and their effect on the implied volatility will be detailed. Five steps have been followed including data collection, model calibration, parameters estimation and model validation. The first step consists of collecting the data from from 31 December 2019 to 05 June 2020. The data has been divided into 80% for the model development and 20% for the model validation.

In this paper, we have proposed Hammerstein model since it includes two blocks: A linear and nonlinear in order to capture the complex dynamics of the implied volatility as affected by the number of covid-19 cases.

The proposed model has the structure as in Fig. 1 and Eqs. (1) to (12).

The main contribution of the present paper is to optimally estimate the model parameters that fit as accurately as possible the estimated infections (by the model) and the real infections (recorded by the health authorities). The problem is posed as an optimization problem solved in this study using a hybrid PSO algorithm combining discrte parameters (model orders) and real parameters (model coefficients). After running the algorithm, the results of case 1 are provided in Tab. 2. Moreover, the convergence features of the proposed method are illustrated in Figs 6 and 7.

3  Data and Preliminary Analysis

Our data sample consists of daily series of two variables: (i) We collect the US fear index from the Chicago Board Options Exchange (Cboe) Global Markets. (ii) Covid-19 infected cases obtained from the European Union Open Data Portal (EU ODP). The study period is from 31 December 2019 to 05 June 2020. We essentially have 158 observations divided into 2 series: The first set consists of 128 observations (NT = 128) which will be used for training the model. The second subsample is used for model validation. It contains 30 observations (NV = 30). The choice of this period is mainly motivated by the fact that it witnessed the peak of the spread of the Corona epidemic, as the World Health Organization confirmed that it was an epidemic. This is considered a huge shock to most countries in the world and has forced them to take many precautionary and proactive measures to limit its spread.

Descriptive statistics about all series of Cboe’s volatility index and the Covid-19 infected cases are presented in Tab. 1. We indicate the non-normal distribution of different series of our sample. All Jarque–Bera values appear statistically significant at 1% level. Results show the distributions of observations are asymmetric for all variables (Skewness values are greater than zero). We can deduce from kurtosis values than all values are inferior to 3 in all cases: Cboe’s volatility index, Covid-19 infected cases in USA and in the World. This reveals that the distributions of all series are Mesokurtic. Then, the distributions of this data are light-tailed. However, the distribution of Covid-19 infected cases in China is leptokurtic. The data have a heavy tail compared to the normal distribution.

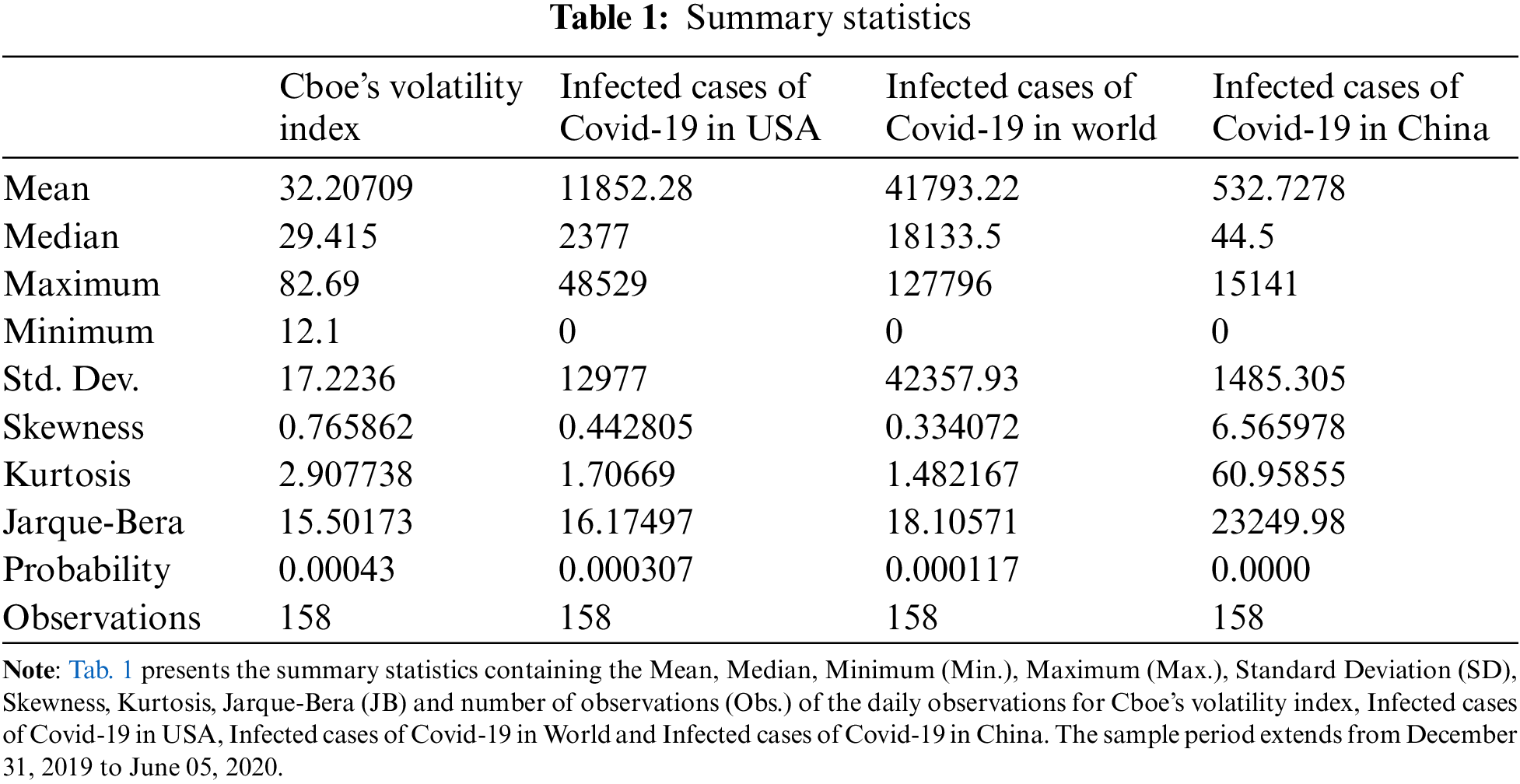
Fig. 2 shows the evolution of the Cboe volatility index between 2007 and 2020. It can be seen that in the event of a crisis, the United States (US) financial market experiences strong fluctuations in the fear index (VIX). In detail, we observed that the VIX peaked during the global financial crisis (GFC) in 2008 and especially in the first quarter of 2020 due to fears about the new coronavirus (COVID-19 pandemic). What is even more remarkable is that the fear index, which represents investor sentiment, is more affected by the pandemic than by the financial crisis. This suggests that once the COVID-19 pandemic is underway, there is uncertainty as to when the fear index in the US stock market should return to the mean.

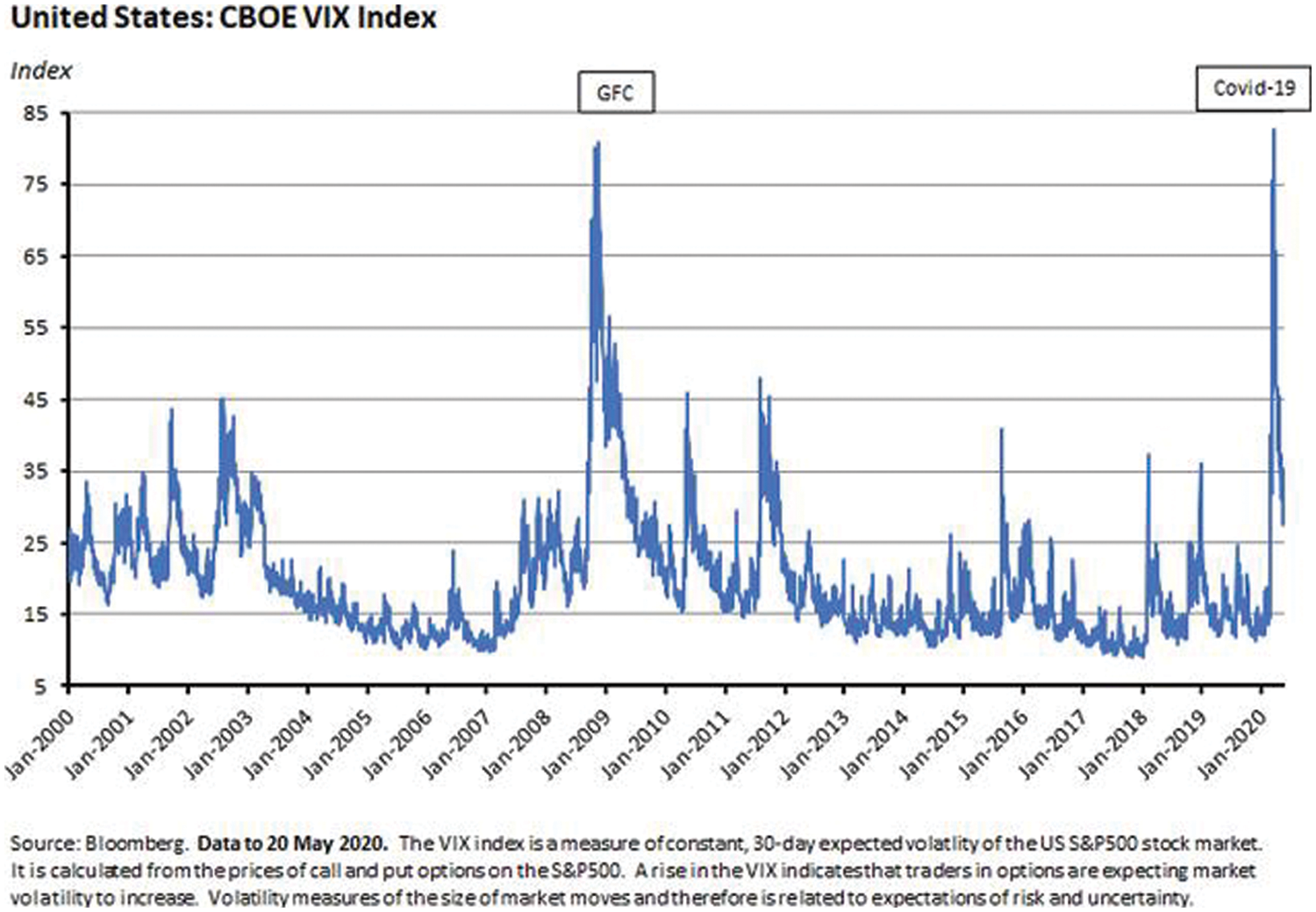
Figure 2: Evolution of Cboe’s volatility index between 2000 and 2020

Fig. 3 shows the evolution of the Cboe volatility index in relation to the Covid-19 infected cases in the US, the world and China respectively. First, as shown in the graph grouping the Cboe volatility index and the Covid-19 infected cases in the US, the curve of the fear index has almost the same trend as the Covid-19 infected cases during the whole period and especially during the period between 31 March 2020 and 5 June 2020. However, we observe an opposite evolution between the two series during the period from 17 March 2020 to 31 March 2020. Second, the figure illustrating the Cboe volatility index and the international COVID-19 cases shows that the fear index has almost similar movements to the international COVID-19 cases until 17 March 2020. Then, contradictory behaviour is identified in the period between 17 March 2020 and 31 March 2020. After 31 March 2020, we can see that when the global COVID-19 cases increase, the Cboe volatility index shows a decrease. Third the figure showing the Cboe volatility index and the Chinese COVID-19 cases provides evidence that it is extremely difficult to identify variability in the data in the Chinese case. To address this problem, we apply an appropriate normalization of the data using the z-score approach. This allows us to show that the pattern of the two series is completely different throughout the sample period, except for the period from 31 December 2019 to 28 January 2020, where a similar trend was found. In conclusion, we report evidence that there is similarity between the pattern of Cboe’s volatility index and the Covid-19 infected cases in the US. However, we highlight that this correspondence in movement is less pronounced in the International and Chinese cases.

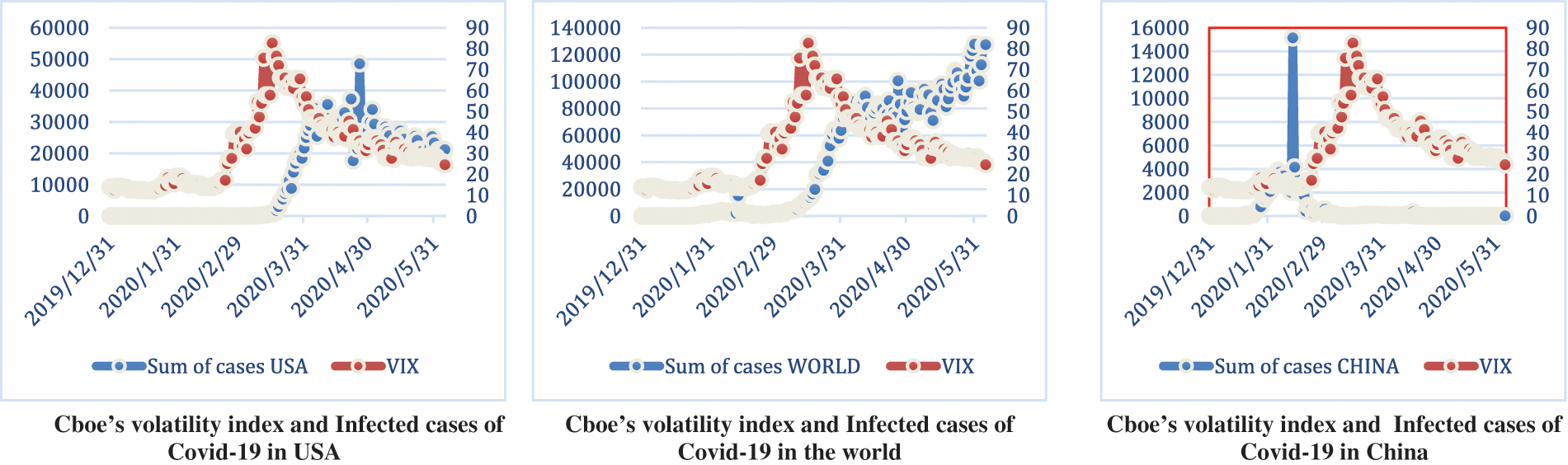
Figure 3: The dynamic of Cboe’s volatility index, infected cases of Covid-19 in USA, in World and in China

4  Empirical Analysis

We now analyze the empirical evidence of the application of HPSO used to determine the parameters of the Hammerstein-ARX model. Referring to Tab. 2, we indicate that the HPSO technique succeeds to identify all optimal parameters of the model. This highlights that the fear index in the US responds to COVID-19 infected cases both linearly and non-linearly. Fig. 4 confirms this finding and proves that the Hammerstein-ARX model generates reliable forecasts. Based on the predicted and observed series of the US fear index, we provide evidence that all curves of the US fear index forecasted by the COVID-19 infected cases in the US, in World and in China respectively have the same trend (Note that the green curve of the current values of Cboe’s volatility index). More particularly, we highlight that the blue curve of the Cboe’s volatility index predicted by COVID-19 infected cases in the US are very near to green curve of current values compared to other curves of International and Chinese cases. This indicates that the domestic COVID-19 cases in the US outperform the global and Chinese cases in forecasting the fear index. This evidence also means that the discrete-time Hammerstein model proves an effective follow-up behaviour during the validation phase.

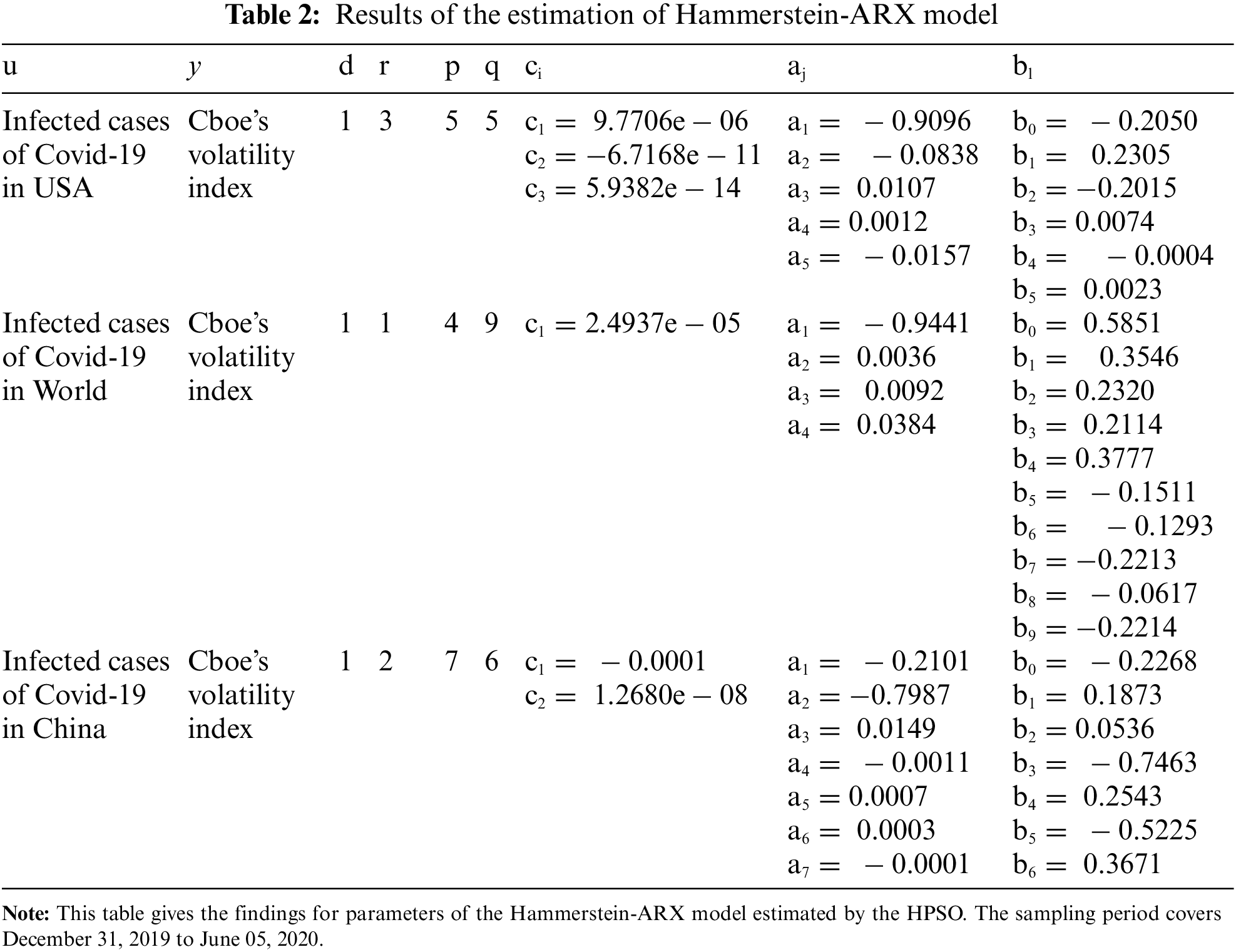
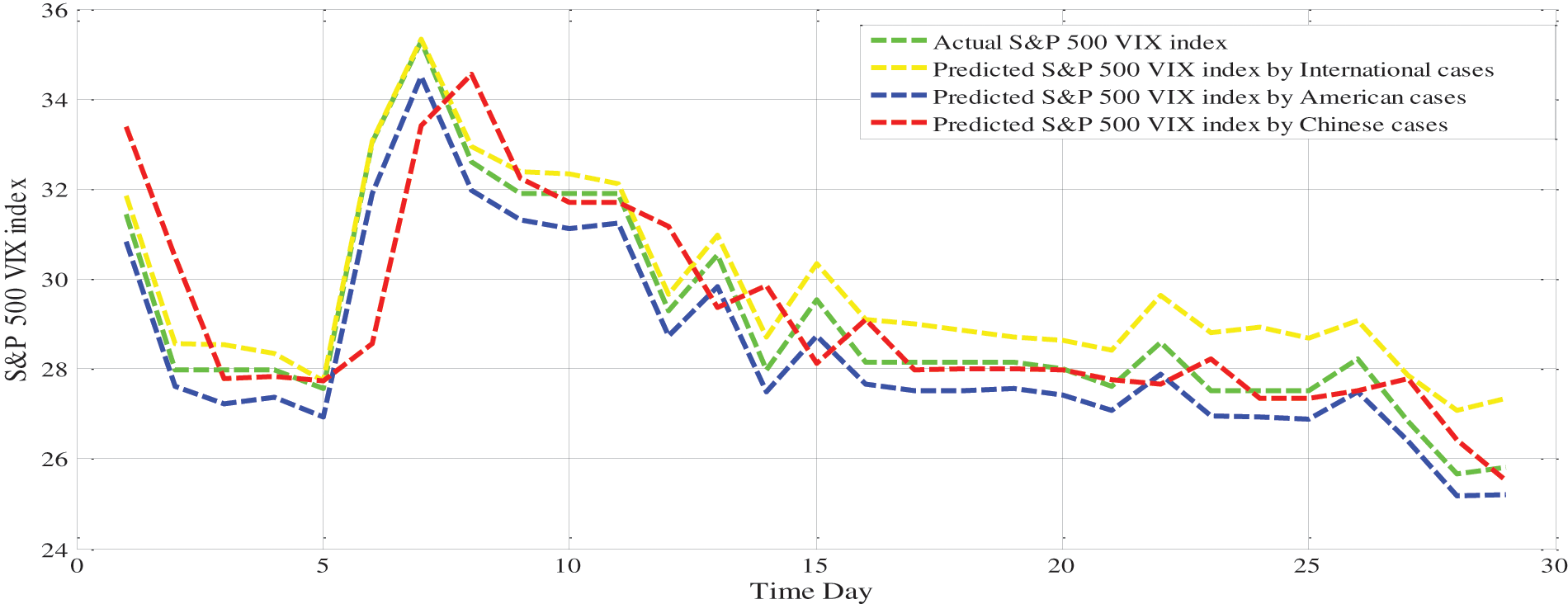
Figure 4: Plot of actual and predicted Cboe’s volatility index

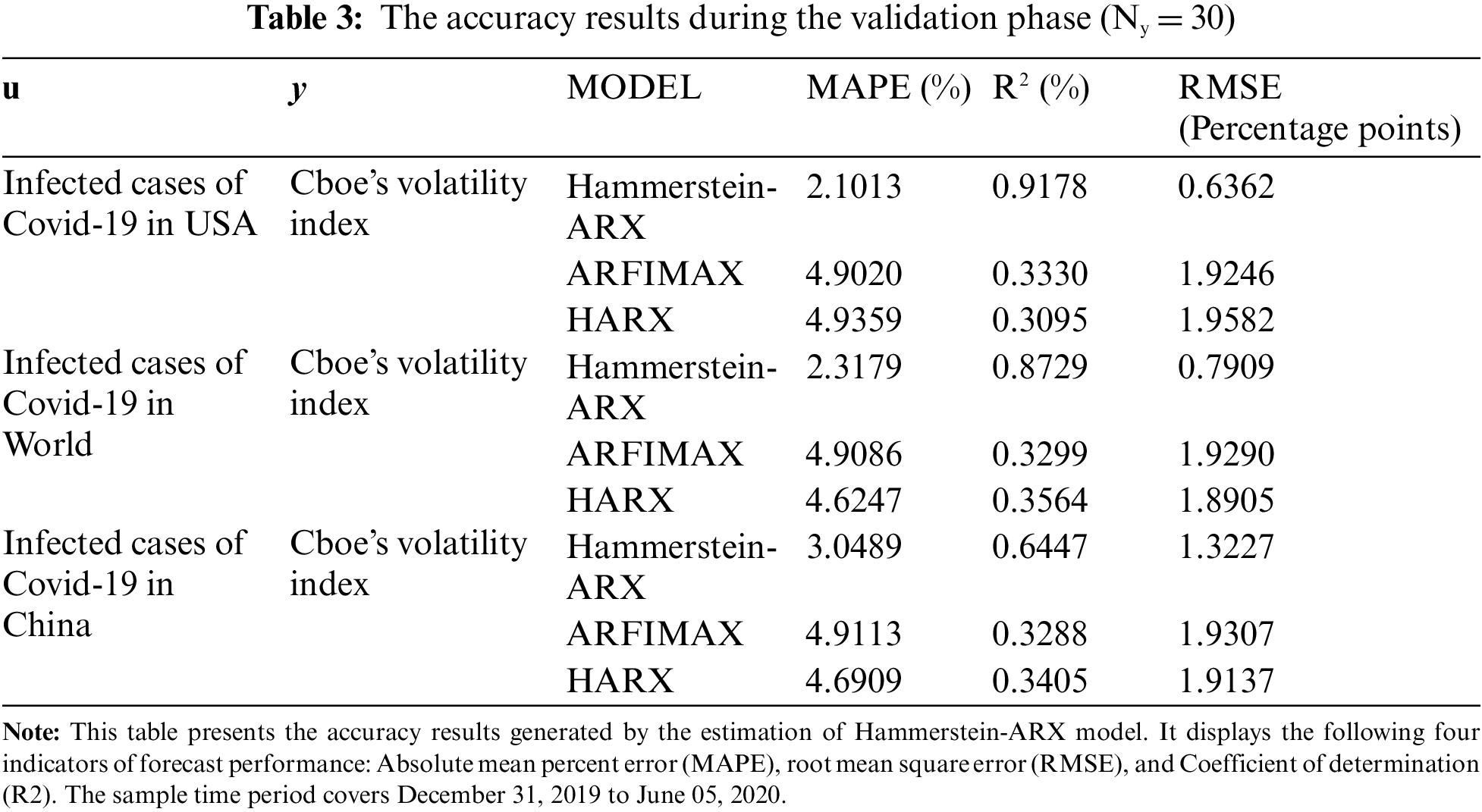
Tab. 3 shows the results of the performance indicators generated by the best execution of the HammersteinARX model. First, the results show a perfect fit of the predicted values in all cases. Empirically, all performance indicators support the use of the Hammerstein-ARX model. It performed well with lower MAPE and RMSE as well as R2 values close to 1 compared to the ARFIMAX and HARX models in US, CHINA and world cases. We also report that the Hammerstein-ARX model appears superior in predicting the VIX index compared to the ARFIMAX and HARX models during the COVID-19 pandemic period. The potential reason for this result is that the Hammerstein-ARX model is able to take into account complex features related to non-linearity and long memory [9].

Furthermore, we observe that the Hammerstein-ARX model run using the US COVID-19 infected cases as input provides better performance than that obtained by the international and Chinese COVID -19 infected cases. This highlight the superiority of domestic COVID-19 cases in predicting the fear index of the United States of America compared to international and Chinese COVID-19 cases. In addition, we note that the Cboe volatility index responds to the COVID-19 cases in both linear and non-linear ways. In summary, Fig. 4 and Tab. 3 show that the Hammerstein-ARX model estimated by the HPSO technique provides good forecast accuracy and better performance.

This becomes even more evident when we look at Fig. 5, which represents the scatter plot of the predicted values of the US fear index. The bisector curve as a straight line indicates ideally effective forecasts. First, there is a better match between the forecasted and observed values of Cboe’s volatility index in the American case. This means that the points of correspondence available in yellow colour are very close to the bisector and have the same tendency. Second, such correspondence does not exist to the same degree in the international and Chinese cases. We notice that the points of correspondence are close to the bisector, but randomly scattered. They are located once below, once on and once above the bisector curve. Overall, the results of scatter graph corroborate our previous results that the HPSO applied to the Hammerstein-ARX model provides a good forecast fit of in all cases.

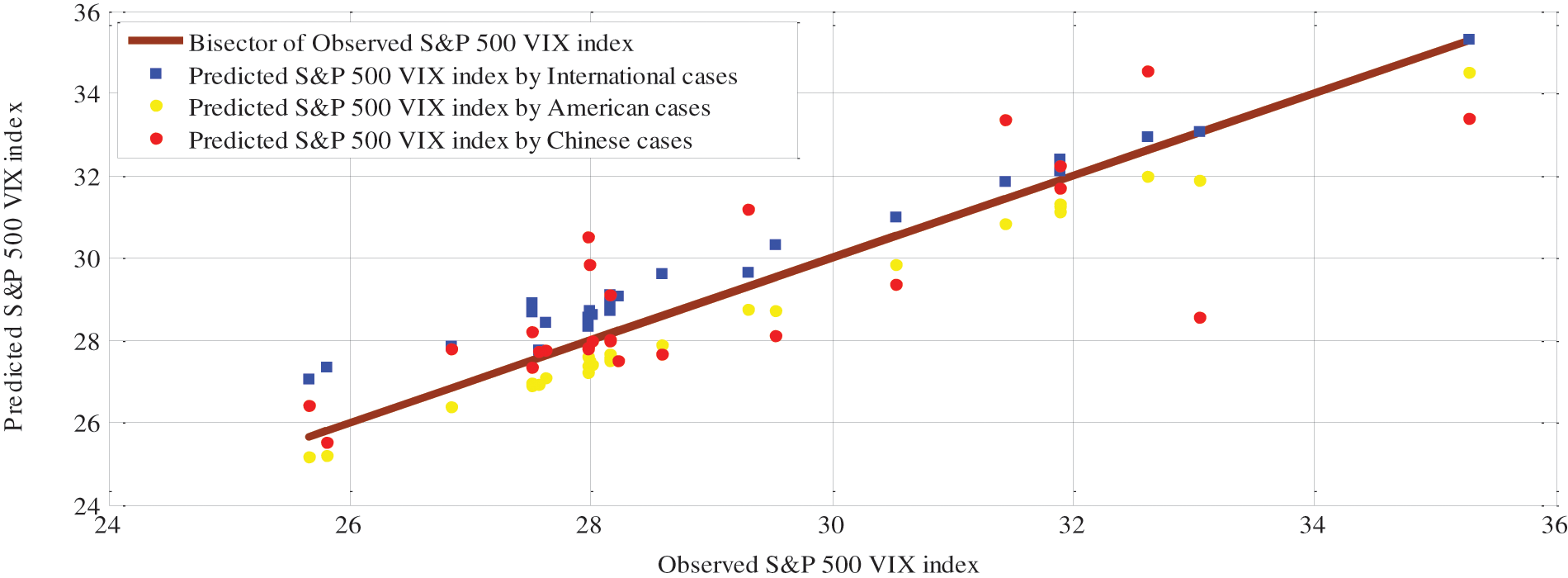
Figure 5: Scatter graph of predicted Cboe’s volatility index

A further aspect consists to examine the convergence of the HPSO technique that is already well served to forecast the Cboe’s volatility index by COVID-19 cases. Fig. 6 exhibit the convergence of the best RMSE (named also the cost function) for a number of 100 iterations for all cases. Hybrid PSO technique provides evidence that the RMSE converges perfectly. Results indicates that the cost function converges too quickly to optimal solution in all cases. Regarding the nexus between the Cboe volatility index and the Covid-19 infected cases in the US, the cost function is stable from iteration 27 at a constant value (0.00 × 1010 percentage points). However, the RMSE appears stable from iteration 37 to a constant value (0.00 × 1010 percentage points) when we use the international Covid-19 infected cases as a predictor for the Cboe volatility index. When considering the causality between the volatility index of Cboe and the Covid-19 infected cases in China, the result is different from the two previous cases. The cost function converges to the optimal solution from iteration 42 at a constant value (0.0003 × 107 percentage points). Not surprisingly, the convergence of cost function is more pronounced in the US cases than in the international and Chinese cases. We focus now on the convergence of the orders (r, p, and q). Fig. 7 displays the convergence of orders. We see that the convergence of the orders is very fast, reaching the optimal solution before 50 iterations. This indicates the good fitting and accuracy of HPSO technique used in our research.

Figure 6: Convergence of the cost function to optimal solutions

Figure 7: Convergence of the orders (r, p, q) to optimal solutions

5  Analysis and Concluding Remarks

Since the announcement by the World Health Organization on 11 March 2020 that COVID-19 represents a global influenza pandemic, fears have spread around the world to affect all aspects. The financial markets have taken a lion’s share of these fears, with trading volumes falling sharply in most countries. On this basis, the US financial markets are at the forefront of the trading decline and prices collapse until the end of March 2020. This fear has quickly spread to investors who are concerned about the short and long term effects of the crisis. As outlined above, many authors have attempted to study the nexus between the COVID-19 pandemic and financial markets. In response to this, our paper examines the prediction of the fear index in the US financial market using the COVID-19 infection cases in the US, the world, and China. Indeed, a non-linear Hammerstein polynomial model combined with an artificial intelligence technique was used to identify and estimate the model parameters.

Our research reveals several key findings. First, the use of HPSO as a parameter identification tool for the Hammerstein-ARX model parameters shows that the fear index in US financial market responds linearly and nonlinearly to Covid-19 infected cases in the US, Covid-19 infected cases in the world and Covid-19 infected cases in China. Performance indicators such as MAPE, RMSE and R2 provide evidence that Covid-19 infected cases are particularly dominant in forecasting the US fear index compared to global and Chinese COVID-19 cases. Second, our study showed that the Hammerstein-ARX model is the best-fitting model, which underlines its superiority over classical time series models such as ARFIMAX and HARX. Third, the combination of Hammerstein-ARX with the HPSO tool produces good convergence and better performance indicators. This further confirms the fitness and the accuracy of the proposed approach.

From a financial perspective, many practical implications arise from our results. Useful information on Covid-19 infected cases can be used by investors to forecast uncertainty in the US financial market. Similarly, the predictive power of the Covid-19 infected cases in the US for the Cboe volatility index can help individual investors to better formulate their investment strategies and effective use of hedging instruments. Thus, detecting the fear index with good accuracy allows investors to protect their portfolio at a lower cost. This will enable them to know how to manipulate the realized volatility market and the systematic risk associated with the COVID-19 pandemic.

For the US financial authorities, our study provides an opportunity to learn that the COVID-19 cases contribute to increased instability and uncertainty in the US financial market in the short term. Thus, policy makers will be obliged to intervene to limit this danger by taking measures to ensure a satisfactory level of stability and confidence in the financial market. However, these policies are likely to raise doubts among investors about market conditions, and increase questions about the ability of government interventions to limit the crisis and lead to a faster restoration of market stability in the short term [9]. Consistent with [8], we indicate that, despite this uncertainty in the short-term, the investors can become stable in the long term with the additional financial measures taken by the government. In addition, this crisis also proves that institutional investors, whose portfolios are based on these sectors (Hospitality, real estate, tourism, transport and non-essential retail), have been the most affected by COVID-19 pandemic. In the face of this situation, asset managers seem to have a leading role to play in navigating and steering the danger. This is done through effective communication and support by providing technological leverage to communicate and strategic views on how to optimally inject more funds into their portfolios with a COVID-19 pandemic still in progress. Furthermore, the combination of Hammerstein-ARX with the HPSO tool appears to have a greater ability to effectively capture the complex structure in the relationship between COVID-19 data and the US fear index. This allows policy makers to use this hybrid tool to forecast the implied volatility risk index even in times of crisis. Considering that our study has shown important financial implications when using a non-linear polynomial structure in the data, leading to evidence that Covid-19 infected cases are a good predictor for the US fear index, this attractive question may merit further future work by extending the time period and using other types of block-oriented models such as Hammerstein-Wiener models.

Acknowledgement: This research has been funded by Scientific Research Deanship at University of Ha’il, Saudi Arabia through project number RG-20 210.

Funding Statement: This research has been funded by Scientific Research Deanship at University of Ha’il, Saudi Arabia through Project number RG-20 210.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.