DOI:10.32604/cmc.2022.029609

| Computers, Materials & Continua DOI:10.32604/cmc.2022.029609 |  |
| Article |
Encryption Algorithm for Securing Non-Disclosure Agreements in Outsourcing Offshore Software Maintenance
1Faculty of Ocean Engineering Technology and Informatics, University Malaysia Terengganu, Kuala Terengganu, Malaysia
2Department of Computer Science & Information Technology, Faculty of Information Technology, The University of Lahore, Lahore, 54000, Pakistan
3Department of Software Engineering, Faculty of Information Technology, The University of Lahore, Lahore, 54000, Pakistan
4Advanced Informatics Department, Razak Faculty of Technology and Informatics, Universiti Teknologi Malaysia, 54100, Kuala Lumpur, Malaysia
5Computer Science and Information Systems Department, College of Business Studies Public Authority for Applied Education and Training, (PAAET), Adailiya, Kuwait
*Corresponding Author: Atif Ikram. Email: atif.ikram@cs.uol.ed.pk
Received: 08 March 2022; Accepted: 07 May 2022
Abstract: Properly created and securely communicated, non-disclosure agreement (NDA) can resolve most of the common disputes related to outsourcing of offshore software maintenance (OSMO). Occasionally, these NDAs are in the form of images. Since the work is done offshore, these agreements or images must be shared through the Internet or stored over the cloud. The breach of privacy, on the other hand, is a potential threat for the image owners as both the Internet and cloud servers are not void of danger. This article proposes a novel algorithm for securing the NDAs in the form of images. As an agreement is signed between the two parties, it will be encrypted before sending to the cloud server or travelling through the public network, the Internet. As the image is input to the algorithm, its pixels would be scrambled through the set of randomly generated rectangles for an arbitrary amount of time. The confusion effects have been realized through an XOR operation between the confused image, and chaotic data. Besides, 5D multi-wing hyperchaotic system has been employed to spawn the chaotic vectors due to good properties of chaoticity it has. The machine experimentation and the security analysis through a comprehensive set of validation metric vividly demonstrate the robustness, defiance to the multifarious threats and the prospects for some real-world application of the proposed encryption algorithm for the NDA images.
Keywords: Non-disclosure agreement; encryption; decryption; secret key; chaoticmap; confusion; diffusion
The globalization of the resources has dramatically increased cross-border business cooperation. Be-sides, international software development and maintenance outsourcing industry has gained exponential growth. Onshore software outsourcing technology is commonly practiced by offshore providers to localize different companies in the client countries. This strategy can be further divided to sub-categories as per client’s requirements. Near-shore software outsourcing points to the closeness or nearness of the offshore country location to the country of origin. This nearness helps to moderate certain problems like coordination, time and cultural differences that are characteristically linked with offshore outsourcing. In pure offshore outsourcing, the client and vendor are situated on different offshore countries. The vendor’s main services providing strengths exist in its own country which is different than client’s country [1]. Offshore software outsourcing includes different models as per client’s need, ownership and control as shown in the Fig. 1.
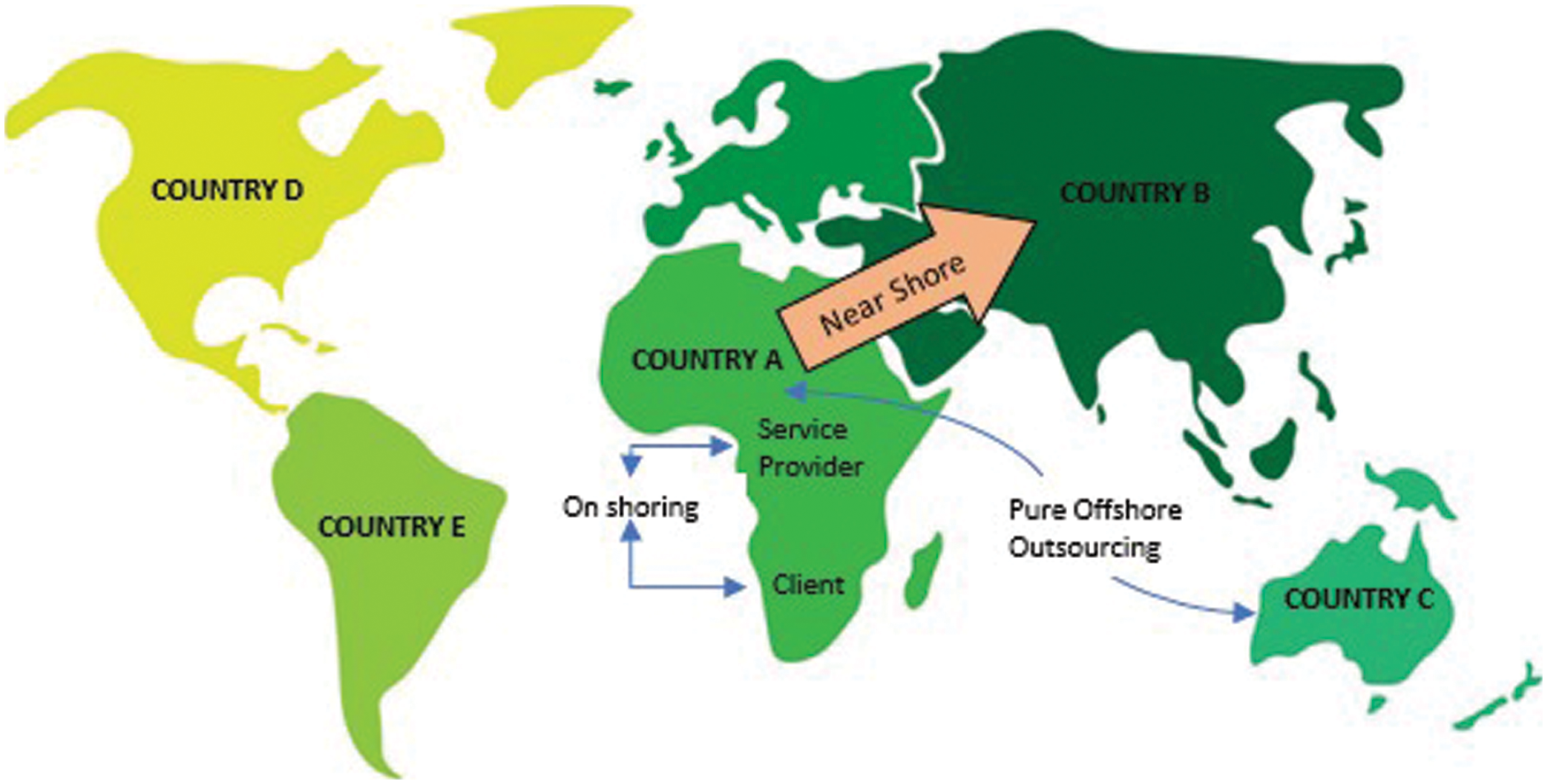
Figure 1: Offshore outsourcing models
Organizations around the globe are progressively adopting offshore software maintenance outsourcing (OSMO) to gain different strategic and economic advantages. This offshore outsourcing has become an emerging trend for both the developing and the developed countries. In OSMO, client outsources all or a portion of the software related services to a vendor in a second country [2,3]. The success of this outsourcing process depends upon different factors. Well written and well communicated non-disclosure agreements (NDAs) are one of the most important indicators of the success of the OSMO process [4], for instance. Both client and vendor must share this NDA and other important legal documents through the Internet or must store it on the cloud. At this stage, protection and privacy may become a big challenge for both legal documents owners as sharing medium is semi-trusted [5]. Despite the benefits the Internet and cloud services render, the public disclosure of sensitive information such as corporate financial data, personal information and service level agreement (SLA) related documents poses a major threat to the stakeholders. Outsourcing sensitive data and personal documents through Internet without addressing the potential security threats is a major challenge. A very intuitive approach for the addressal of this challenge is to first encrypt the document and then outsource it over the Internet or the cloud [6]. In this research endeavor, we have devised a novel algorithm for the security of the NDAs. Although, this work would encrypt a single NDA but many NDAs can also be encrypted in one go by developing the algorithms for multiple images [7,8].
Diffusion and confusion are two main processes which are normally carried out while developing any security product. Confusion refers to permuting or re-ordering the letters or pixels for the given text document or the image respectively. While in the diffusion operation, the value of the data is changed. To realize the effects of diffusion, we have generated the rectangles of arbitrary dimensions for several times in the given input image. Then, the length of the parallel sides is swapping with each other. For the diffusion effects, an XOR operation between the stream of random numbers and the confused image has been carried out. For random numbers, 5D multi-wing hyperchaotic map has been selected. This map enjoys the excellent properties of ergodicity, mixing, arbitrariness randomness etc. Hackers also sometimes launch a differential attack on the ciphers. To frustrate this attack, we have not resorted to the time consuming and complex hash codes, rather, the mean value of the given input image has been utilized to spawn the random data. In this way, the feature of plaintext sensitivity has been added in the proposed image encryption algorithm. Having said that, nonetheless, the bullet points described below highlight essential properties of this proposed image cipher.
i) First time any image encryption algorithm has been written to ensure the security of the non-disclosure agreements as they are stored on the cloud servers or they are travelled through some open network like the internet.
ii) Effects of confusion has been achieved through the dynamic generation of rectangles in the given input image.
iii) Plaintext sensitivity has been injected without resorting to the time consuming and complicated methods to enhance the computational complexity. This act would foil the potential differential attacks.
iv) Both the security analysis and the machine simulation vividly exhibit the do-ability of the idea.
Remaining part of the paper has been fashioned like this. Section 2 describes chaotic systems in general and the 5D multi-wing hyperchaotic system. Proposed image encryption scheme has been elaborated in the Section 3. Sections 4 and 5 are for the machine experimentation and the performance analyses. The paper wraps up along with the necessary concluding remarks in the last Section 6.
Here the two building blocks will be discussed upon which our work stands. These are the chaotic systems and the randomly generated rectangles.
2.1 Theory of Chaos and Chaotic Systems
Theory of chaos investigates the behavior of dynamical systems. These systems are highly dependent over the initial values and the system parameters. The faintest change in either of the initial values or the system parameters causes to end up with a radical change in the output. These characteristic are very much in harmony with the business of cryptography. After complying with this notion, scientists have invented many chaotic systems and maps. These systems enjoy the excellent characteristics of ergodicity, aperiodicity, mixing, randomness and unpredictability [9]. These maps can be compartmentalized into one-dimensional, two-dimensional and higher dimensional. These systems have been employed extensively in the niche of image encryption to get the random numbers. This random data is used to carry out the operations of confusion and diffusion.
According to algorithmic requirements of current study, we have selected the 5D hyper-chaotic system [10]. The following set of Eq. (1) defines this map in the mathematical terms.
The list of system parameters and the state variables in the above chaotic map are x, y, z, w, v and a, b, c, d, e, f, g, h respectively. Apart from that, yz, xy and x2y constitute the nonlinear of the map. Additionally, [10] sheds light on the different facets of the chaotic behavior of this map like periodic orbit etc.
2.1.1 5D Multi-Wing Hyperchaotic System’s Attractors and Lyapunov Exponents
To draw the attractors of the 5D multi-wing hyperchaotic system, step of time for system’s solution is 0.001. Moreover, system’s behavior of chaoticity (1) can be seen in the Fig. 2.
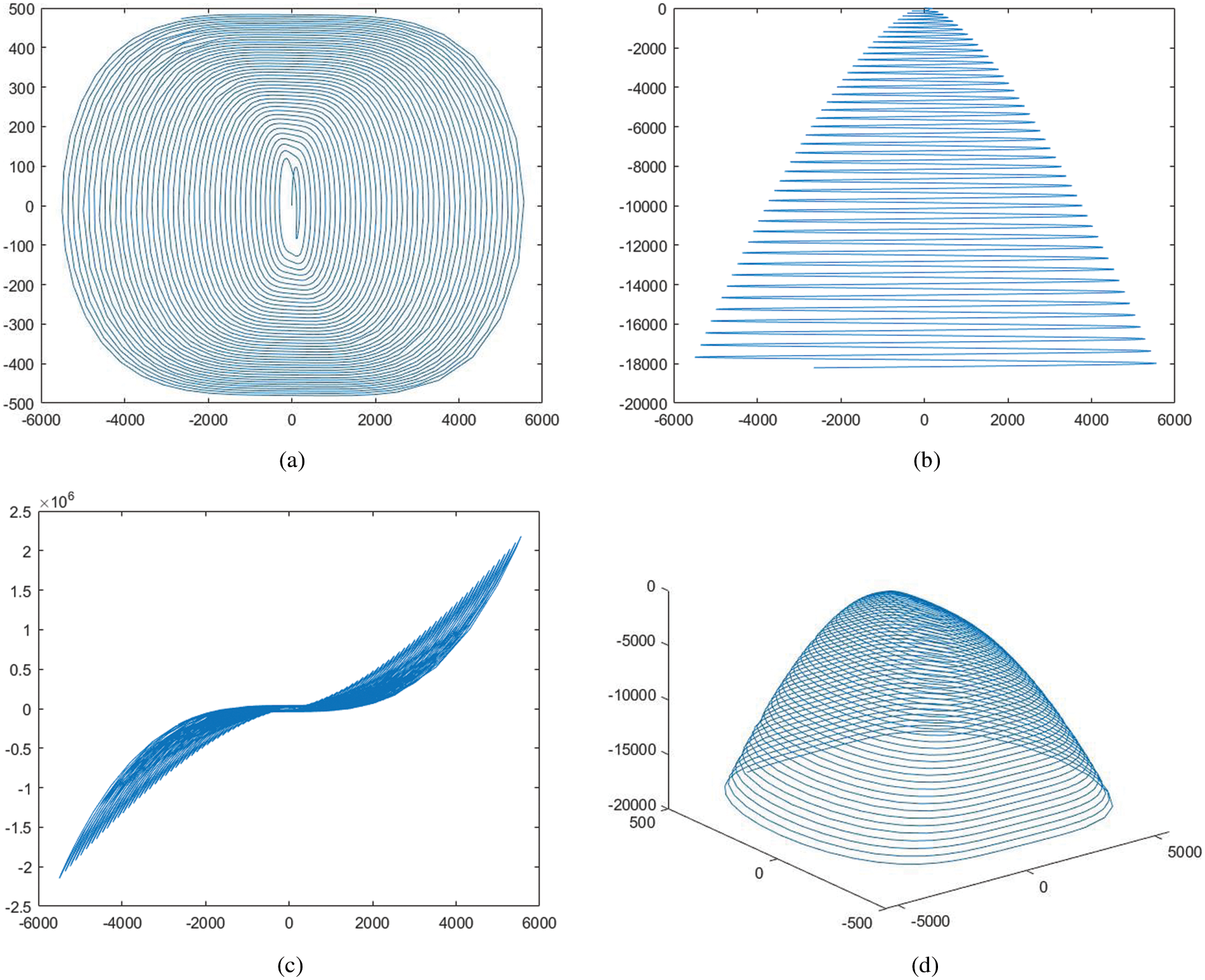
Figure 2: Different attractors of the system (1): (a) Projection on xy plane; (b) Projection on xw plane; (c) Projection on xv plane; (d) 3D view in the xyz space
Apart from that, Lyapunov exponents are L1 = 9.979, L2 = 1.96. L3 = 0.005362. L4 = −19.13. L5 = −27.82 shown in the Fig. 3.
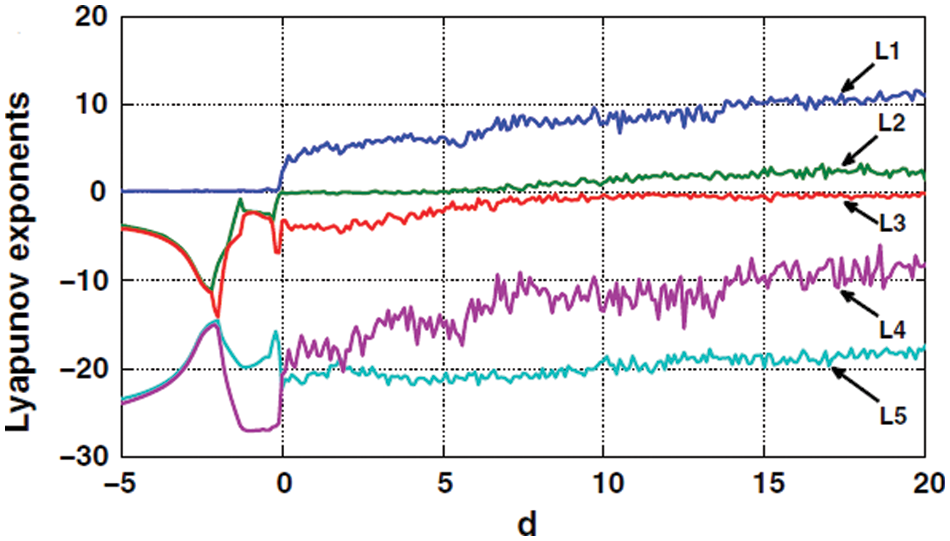
Figure 3: System 1’s Lyapunov exponents
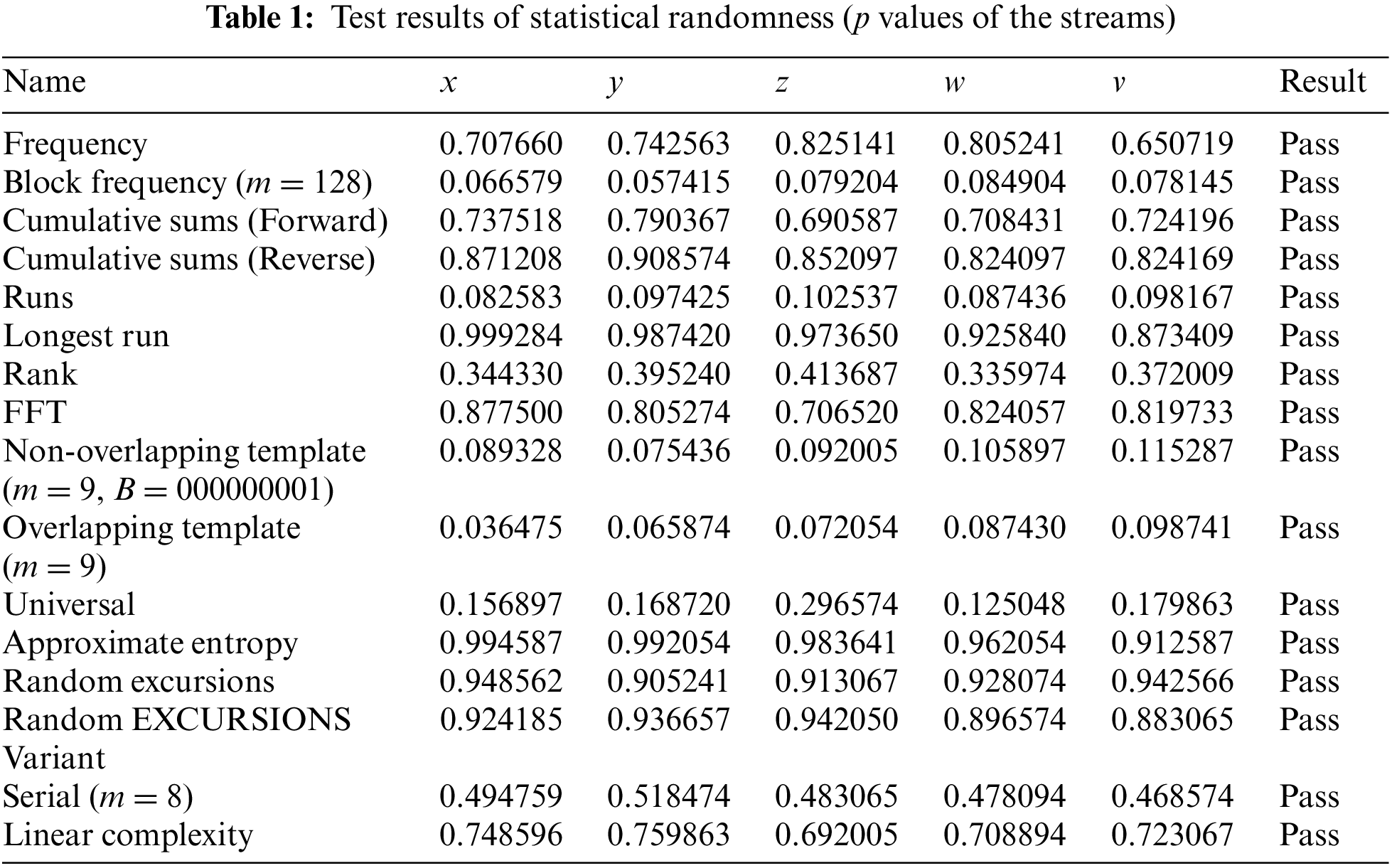
NIST Test Suite [11] provides a vast array of parameters to verify the extent with which the given numbers are random. According to this suite, the value of p, i.e., the level of significance, ought to be above the threshold value of 0.01 to be accepted as the requisite standard of randomness for the given bit of sequences [12]. Tab. 1 shows the results of test after five-bit streams are provided to the system (1).
2.2 Dynamically Generated Rectangles
Dynamically generated rectangles are the second building block upon which our work rests. As a modus operandi of our algorithm, we randomly create these rectangles with arbitrary sizes for the purpose of con-fusion. Once a rectangle is created, its horizontal lines are swapped with each other and its vertical lines are swapped with each other. Here, we have given a toy example on an image of the size of 10 × 10 to better understand the working shown in Fig. 4.
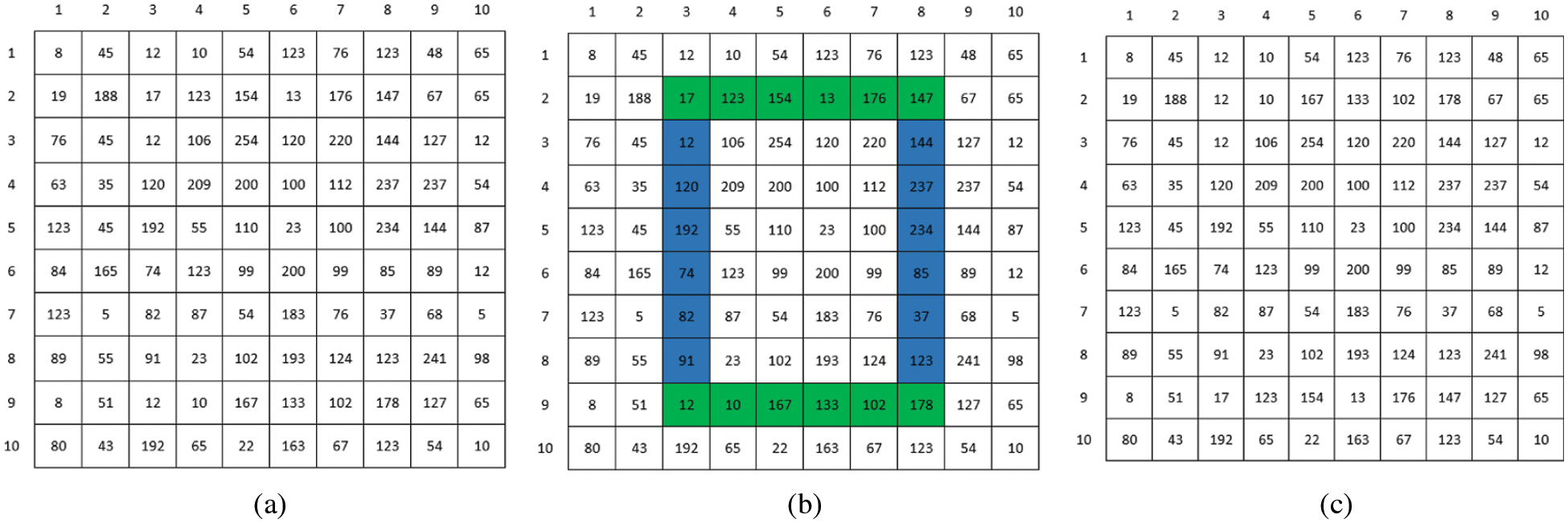
Figure 4: A demonstration of swapping operation on a 10 × 10 sized image: (a) A 10 × 10 sized image; (b) Selection of rectangle with top left corner (2, 3) and bottom right corner (9, 8); (c) Image after the swapping of horizontal lines with each other and the swapping of vertical lines with each other
3 Proposed Encryption Scheme for Non-Disclosure Agreement
As described earlier, this work has been carried out to secure the non-disclosure agreement struck between the two parties. Further, we have assumed that this agreement is in the form of gray scale images with dimension m × n. Fig. 5 shows the way this scheme has been implemented. As the client signs a contract, before sending it on the cloud document storage, it is encrypted through some encryption algorithm using the secret key. Vendor accesses this document from the cloud storage. Further, he decrypts it to get the actual contract in a readable format.
The encryption algorithm works like this. Plaintext sensitivity is a very essential feature for crypto-graphic products. This feature helps in curbing the potential threats of differential attack. This study has not resorted to the complicated and time-consuming hash codes for this purpose. Rather, we have tempered only one parameter x0 of the given chaotic system through the mean value of all the pixels of the given image. Through this way, for each input image, different streams of random numbers would be spawned which, in turn, bear ample promise to thwart the threats of future attacks. The set of secret keys along with one tempered initial variable has been fed to our chosen chaotic map which gave the five chaotic vectors namely x, y, z, w and v. These five chaotic vectors have been further translated into another vectors tlcx, tlcy, brcx, brcy and diff. The first four vectors facilitate in realizing the effects of confusion while the last one is for injecting the diffusion effects in the new cipher. The confusion effects have been created through dynamically generating the rectangles with the top left coordinates of (tlcx, tlcy) and bottom right coordinates of (brcx, brcy).
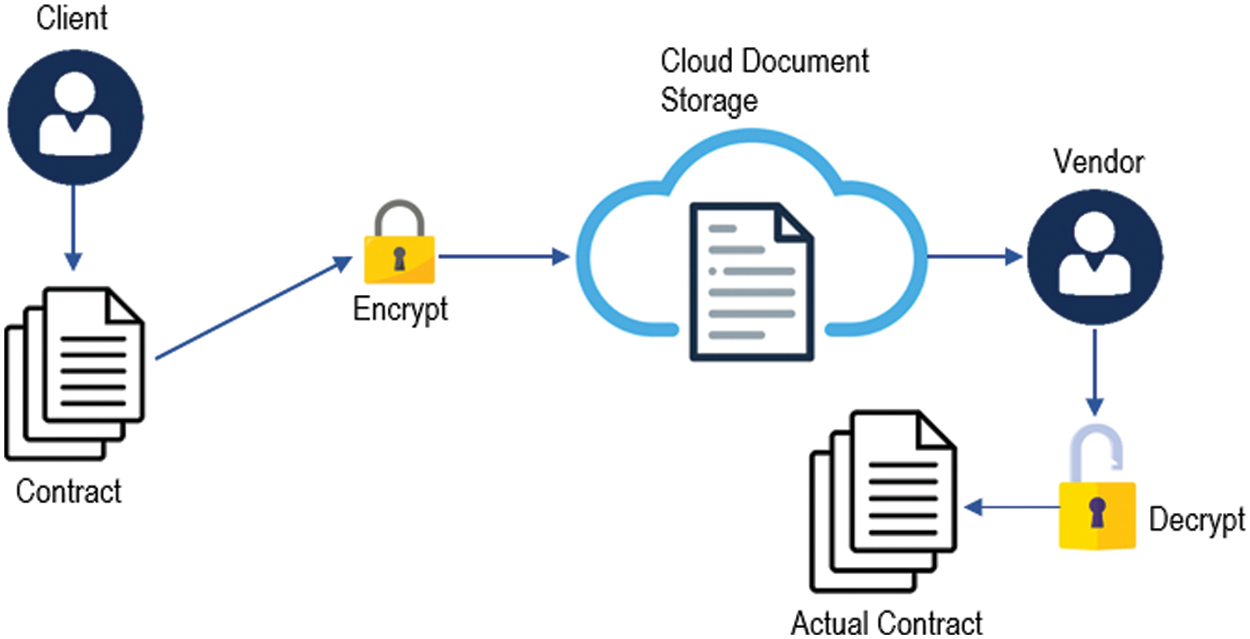
Figure 5: Encryption scheme
3.1 Key Stream Generation Procedure
Before sparking the chaotic system for the generation of random numbers, we have embedded the plain-text sensitivity in the proposed image encryption algorithm. Through following steps, we have generated random numbers’ streams.
Step 1: We have taken the average value of all the pixels of the given input image as avg. This average value tempers the initial value x0 of the chaotic map as follows.
In Eq. (2),
Step 2: This tempered initial value along with the other values have been given to the chaotic map (1) in or-der to generate the stream of chaotic vectors as x = [x1, x2, …xm+n0 ], y = [y1, y2, …yn+n0 ], z = [z1, z2, …zm+n0 ], w = [w1, w2, …wn+n0 ] and v = [v1, v2, …vmn+n0 ]. It is to be noted that (m, n) is the size of input image. Apart from that, n0 ≥500. Usually, n0 values are ignored to neutralize the transient effects of the used map.
Step 3: The above set of equations is not useful for the algorithmic logic we have conceived. So, the following Eq. (3) customize them and provide the new sequences tlcx, tlcy, brcx, brcy and diff which are in line with our potential algorithm.
Here mod is the remainder operator. Further, 1 ≤ i ≤ m, 1 ≤ j ≤ n and 1 ≤ k ≤ mn. Besides, the streams tlcx, tlcy, brcx and brcy correspond to coordinates for top left and bottom right corners of the randomly generated rectangles in the given input image. Moreover, the stream diff would be used to inject the diffusion effects after the input image gets scrambled.
3.2 Algorithm for Encryption of Non-Disclosure Agreements
Fig. 6 explains the encryption scheme which consists of some phases. Initially, the non-disclosure document plain image has been given to it. To create the plaintext sensitivity, the average value for all the pixels intensities has been calculated which tempered the initial value of the chaotic map, i.e., x0. Now the chaotic map has been sparked by providing it the secret key consisting of x0, y0, z0, w0, v0, a0, b, c, d, e, f, g and h. This map spawned five key streams. Four were used for the scrambling purpose whereas the fifth and last one facilitated in realizing the confusion effects. Lastly, we get the non-disclosure document cipher image.
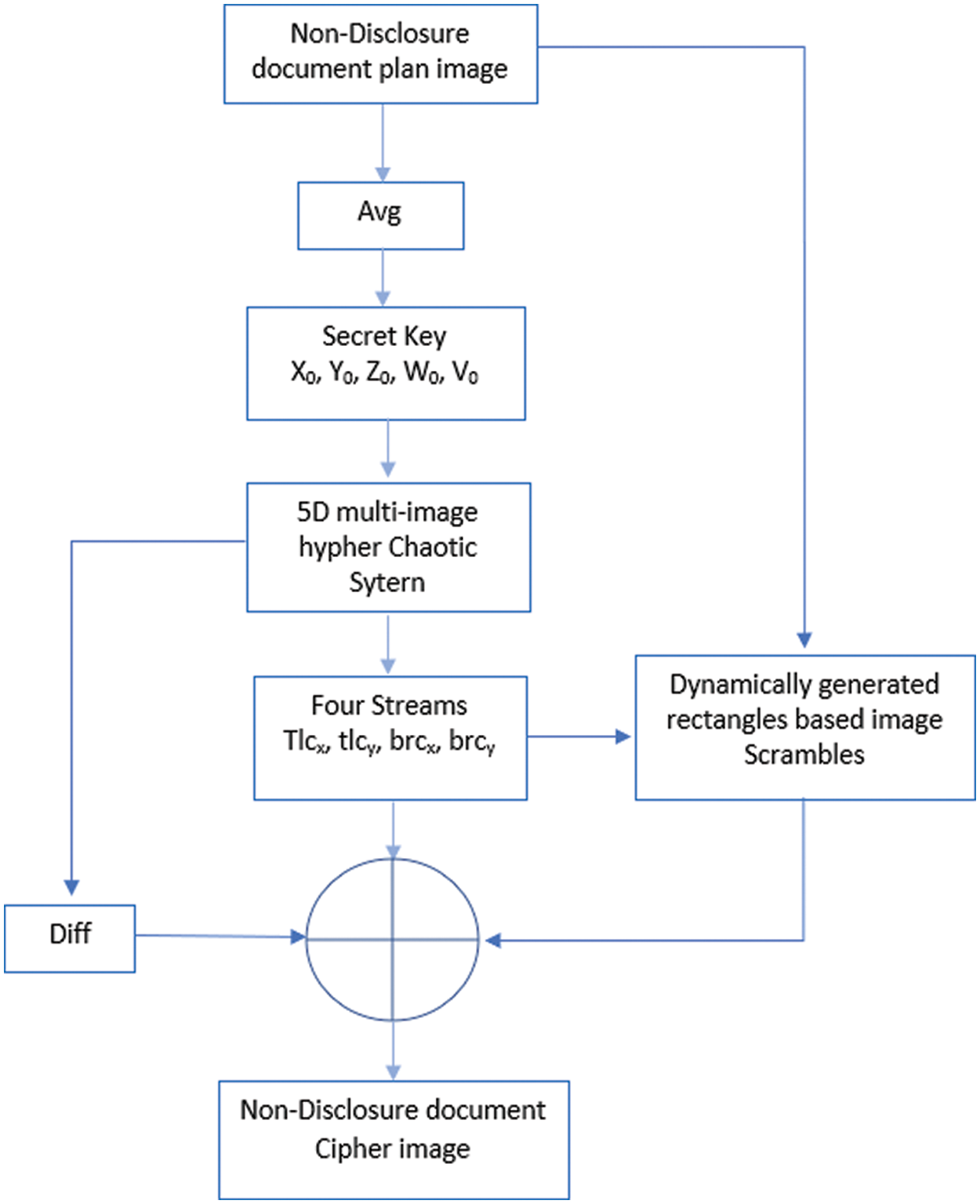
Figure 6: Encryption scheme
Now we formally explain the Algorithm 1 which takes the non-disclosure document as a grayscale plain image img with size m × n. Besides, this algorithm also takes the parameters tlcx, tlcy, brcx, brcy, m, n. Mandate of the scheme under consideration is to confuse pixels of given input image img and to return the confused image img′. Algorithm 1 contains the four if conditions. These conditions ensure that the x-and y-coordinates of the top left corner of the rectangle so formed should be less than those of their bottom right corner counterparts. In case, this does not happen, then all the four cases have been dealt with accordingly. Further, since the end points of the horizontal and vertical lines are common for each formed rectangle, so we have excluded the end points for the vertical lines as shown in the lines 4, 7, 10 and 13 of the algorithm. The line 14 assigns the confused image to img′. In order to embed the diffusion effects in the confused image, reshape the image img′ to 1 × mn and carry out the XOR operation between img′ and the fifth and last stream of the chaotic map, i.e., diff shown in Eq. (4).
Here, 1 ≤ i ≤ mn. Finally change the size of image img′′ to m × n for getting the final cipher image.

Since the proposed encryption scheme is complying with the idea of symmetric/ private key cryptography, therefore, decryption algorithm steps would be very simple, i.e., these steps are the reverse of the steps of the encryption algorithm.
In this Section, we will demonstrate practically the theoretical framework we have developed in the previous Section. In this regard, we have taken four images. These images are Agreement 1, Agreement 2, Lena and Couple. The size of first two images is 960 × 743 and that of the last two images is 256 × 256. The last two images were taken from USC-SIPI. It is to be noted that USC-SIPI is a large repository for the image datasets. These images have been chosen to do a comparative analysis with the other published works in the literature. Additionally, for experiment purpose, MATLAB tool 2016 has been used. Moreover, according to the IEEE [13] standard 754, it is 64-bit double-precision. The initial values and the system parameters taken for the generation of random data are x0 = 1, y0 = 1, z0 = 1, w0 = 1, v0 = 1, a = 10, b = 60, c = 20, d = 15, e = 40, f = 1, g = 50, and h = 10. Figs. 7–9 depict the selected plain gray scale images, cipher/encrypted images and decrypted/restored images respectively. One can check that the proposed image encryption algorithm has successfully converted the four plain images into the cloudy and unrecognizable format. Apart from that, these cipher images have been successfully converted back into their plain versions. This signals towards the successful implementation of both the encryption and decryption machineries of our framework.

Figure 7: The images (gray scale): (a) Agreement 1; (b) Agreement 2; (c) Lena; (d) Couple
5 Performance and Security Analyses
In such analyses, the cryptographic products are validated based on the different security parameters, the cryptographers have invented over the years. These security parameters shed light on the various facets of the products. Besides, we have chosen the following published works from the literature to carry out comparison [14–17].
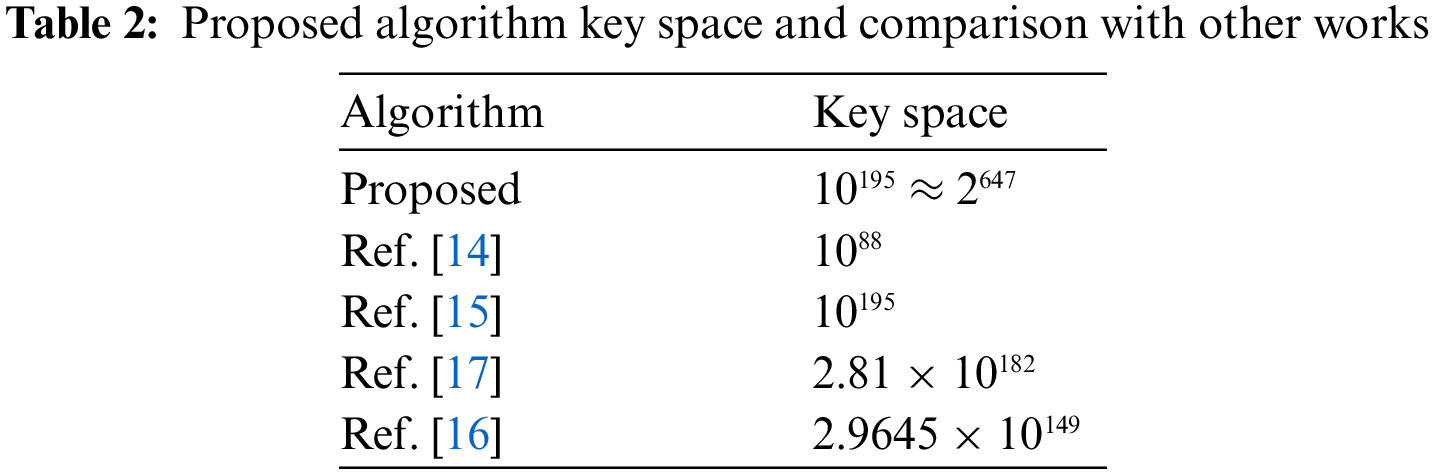
Brute force attack is one of the frequently launched attacks by the cryptanalysts. In this attack, they systematically generate all the possible keys for the cipher. This attack can be countered if the minimum key space of the cipher is 2100 [18]. The set of initial values and system parameters of chaotic map being employed constitutes the secret key of proposed cipher. If we take the computer precision of 10−15, then the key space comes out to be 10195 & 2647 for the variables a, b, c, d, e, f, g, h, x0, y0, z0, w0, v0. Hence, it has sufficient capability to thwart the potential brute-force threat since 2647 >> 2100. Additionally, Tab. 2 draws a comparison of this important metric between the other research and the proposed one. One can observe that the schemes given in [14–16] have been beaten by this new algorithm based on the metric of key space. So, the proposed cipher is better.

Figure 8: The cipher images:(a) Agreement 1; (b); Agreement 2; (c) Lena; (d) Couple

Figure 9: Decrypted images:(a) Agreement 1; (b); Agreement 2; (c) Lena; (d) Couple
Under this analysis, two parameters are covered. These parameters are correlation coefficient and histogram.
It is a frequently used instrument in image processing to depict the pixels frequency distribution of the given image. Histograms of the plain images normally have a slanting and bouncing upward and downward bars over them. This slanting bar is a great source of information for the potential hackers to reach to the original image. As the plain image is encrypted, the histogram made after it has a smooth and uniform bar over it. This uniformity and smoothness of histogram’s bar acts as a great barricade in reaching to some useful information. Hence, smoother bar of histogram of resultant cipher image is, the better it is. Agreement 1’s and Lena’s histograms have been shown in the Fig. 10 for both cipher and plain versions. According to Fig. 10, the bar is bouncing up and down for the plain image. But after it is encrypted, this bar has become smooth and uniform which implies the good effects of security.
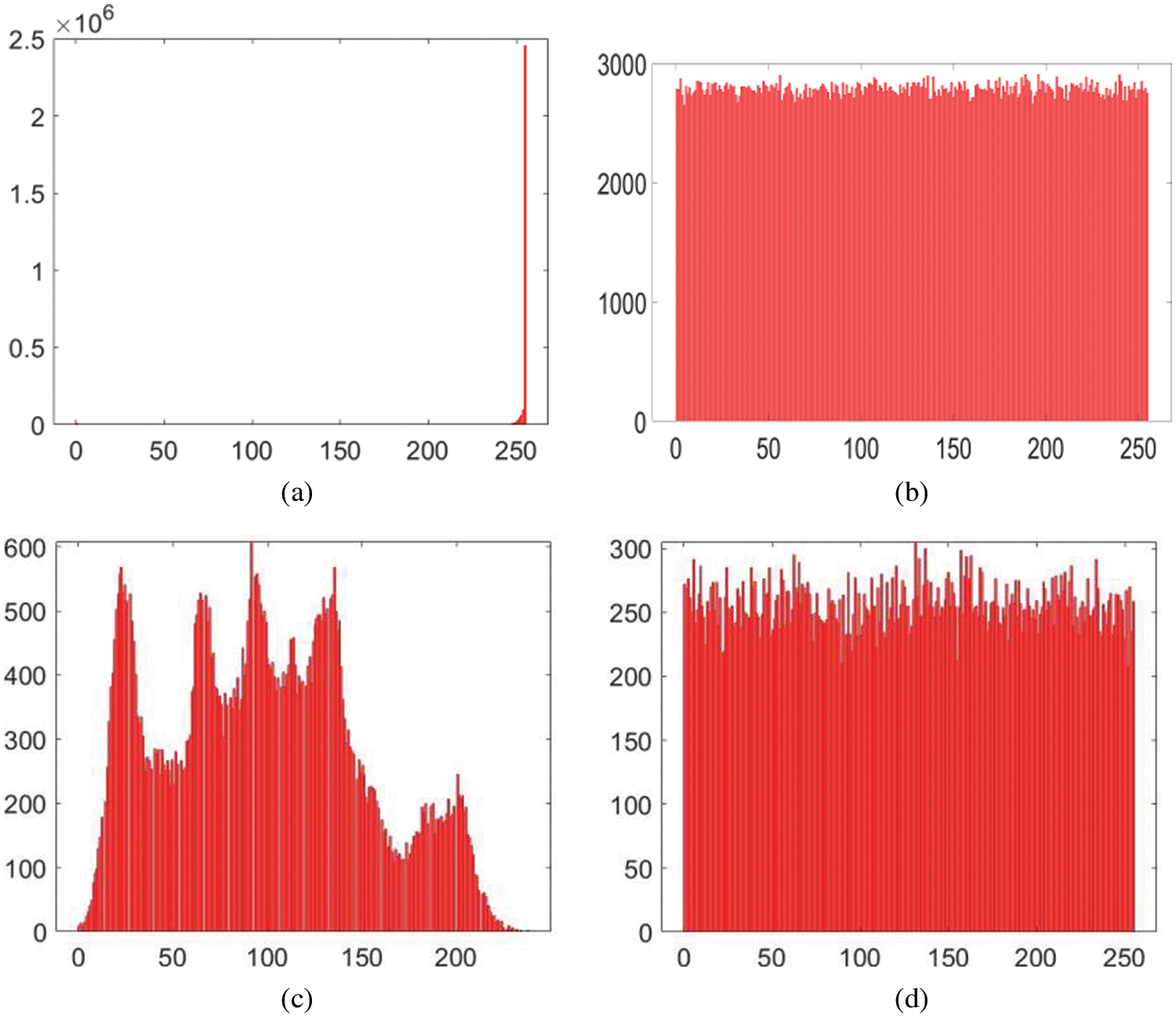
Figure 10: Histogram analysis (a) Plain agreement 1 image; (b) Encrypted agreement 1 image; (a) Plain Lena image; (a) Encrypted Lena image
5.2.2 Correlation Coefficient Analysis
Any normal image’s neighboring pixels are intensely correlated with each other. Further, there are three orientations for the consecutive/neighboring pixels. These include horizontal, vertical and diagonal. As the image encryption algorithm gets applied over normal image, this strong correlation/nexus gets broken and hence the correlation between the adjacent pixels drops steeply. If some image is encrypted to an idealistic proportion, the correlation between the pixels becomes zero. To demonstrate this metric, we have taken 5,000 pairs of the pixels both from the plain and cipher images. Further, they have been taken in the three orientations as stated above. Following mathematical formula is utilized to test this metric [19].
z and w refer to pixels’ intensity values in the above equation. Besides, P is representing the total number of pixels. Fig. 11 shows the Agreement 1’s plain and cipher images pixels distribution in the vertical, horizontal and diagonal directions. Besides, Tab. 3 provides the values of this metric. This metric denotes the values of CC for the consecutive pixels of both cipher and plain images of Agreement 1.
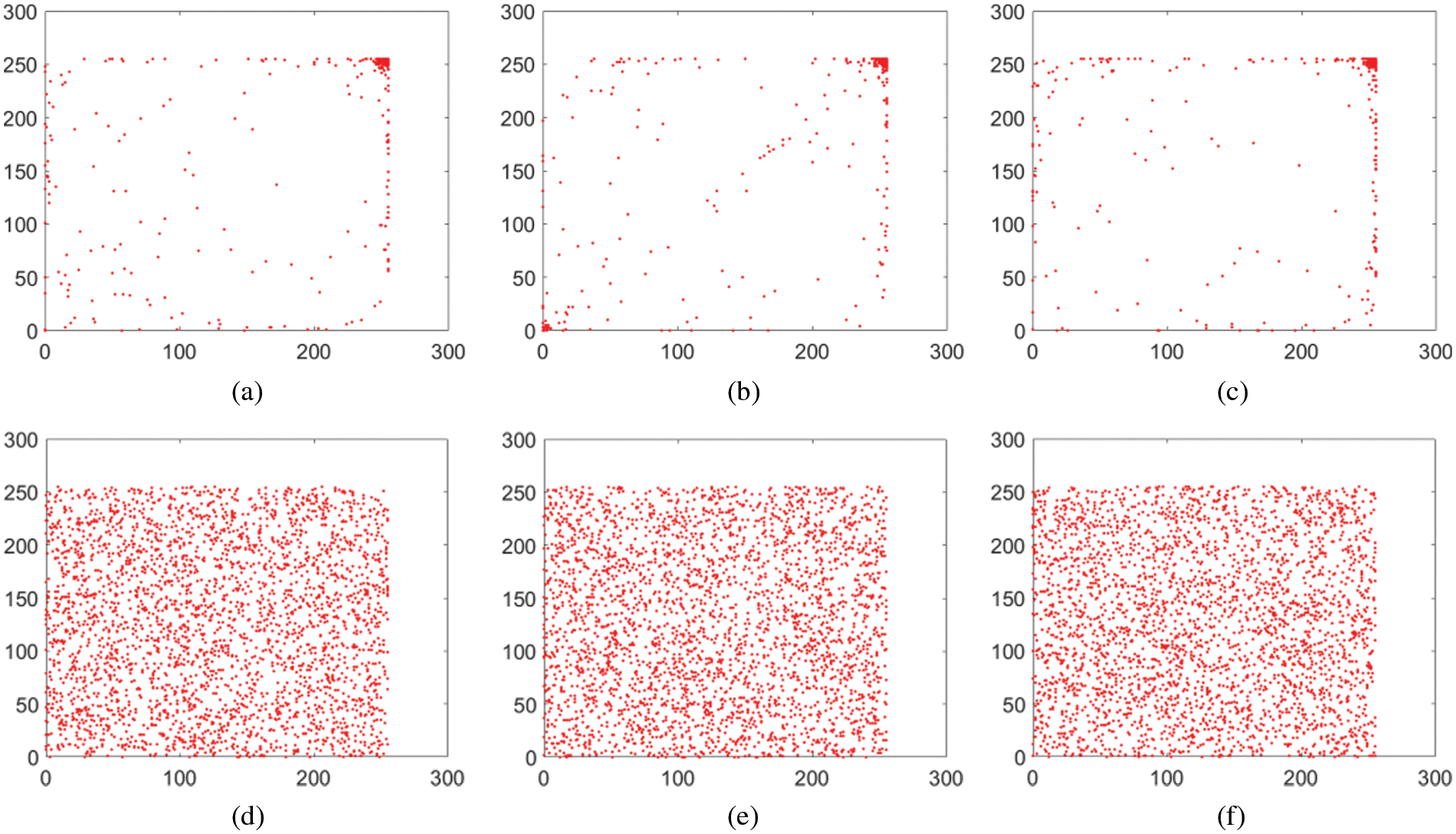
Figure 11: Correlation distribution for agreement 1 image (Image type, Direction): (a) (Plain, horizontal); (b) (Plain, vertical); (c) (Plain, diagonal); (d) (Cipher, horizontal); (e) (Cipher, vertical); (f) (Cipher, diagonal)
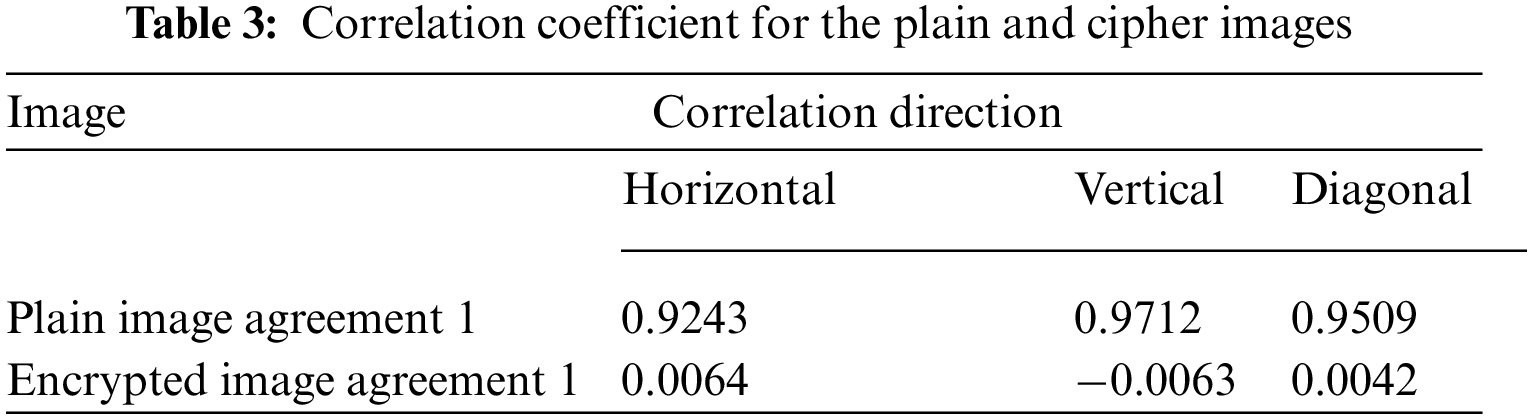
As one can see from this Tab.3, the value of this metric was nearly equal to 1 when encryption scheme was not applied over the document. But as the algorithm got applied, the value of this metric becomes nearly equal to zero. Tab. 3 and Fig. 11 demonstrate that the relationship between cipher and plain images dropped steeply as soon as the encryption scheme was applied.
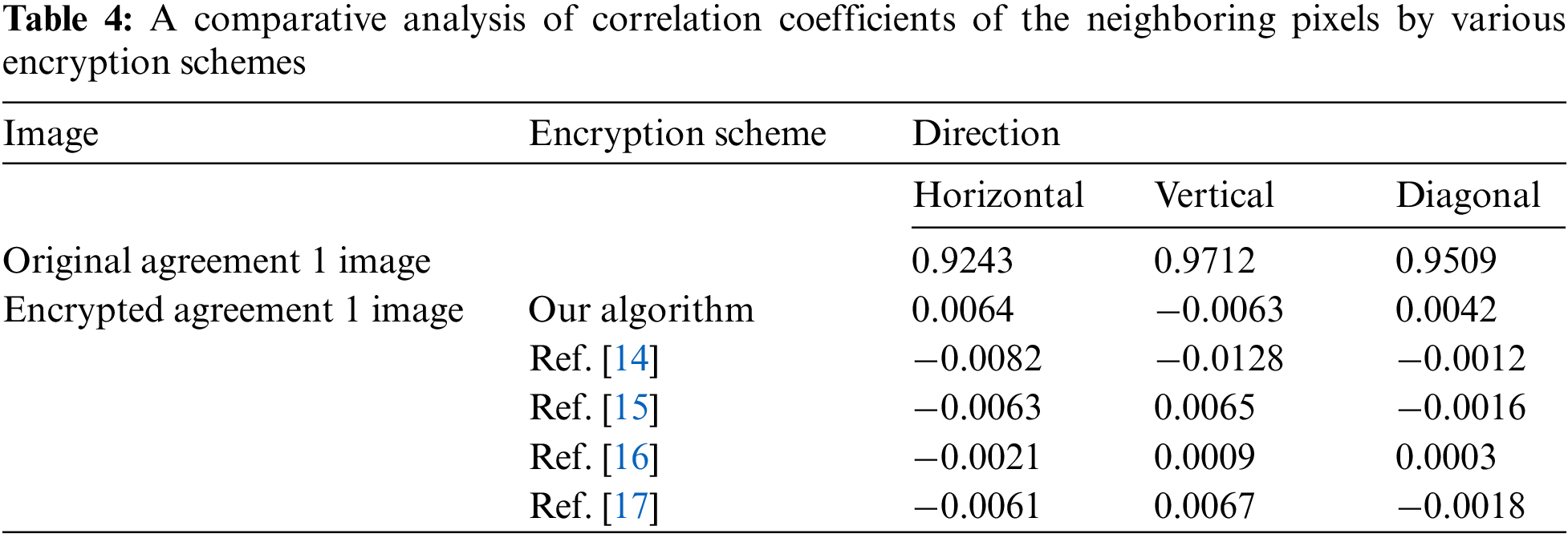
Apart from that, Tab. 4 made a comparison analysis with other image encryption schemes available in the literature. We can see that the stats of suggested algorithm are comparable to our selected research [14–17].
5.3 Information Entropy Analysis
It is a yet another powerful security parameter to judge effectiveness of the encryption algorithms. Fact of the matter is that as given image pixels are disturbed through the confusion and diffusion operations by the algorithm, we need to check this dispersion through some yardstick. The theory of information entropy is what we require. Through it, we can find the disturbance, arbitrariness of the pixels of the given image. It was information theorist Shannon who came up with its mathematical formula in 1949 [20].
In this formula, information entropy is being referred to by Z (r) for any signal r. Besides, p (rc) denotes probability of rc. Naturally, this value boosts after disturbance happens in the pixels of the given image. For an ideally confused and diffused image, its value becomes equal to exactly 8 for the images with 256 gray values. The values of the entropies can be seen in the accompanying Tab. 5 against our chosen images. Values of entropy for Agreement 1 and Agreement 2 images are 7.9996 and 7.9995. These two values are very close to the ideal value 8.
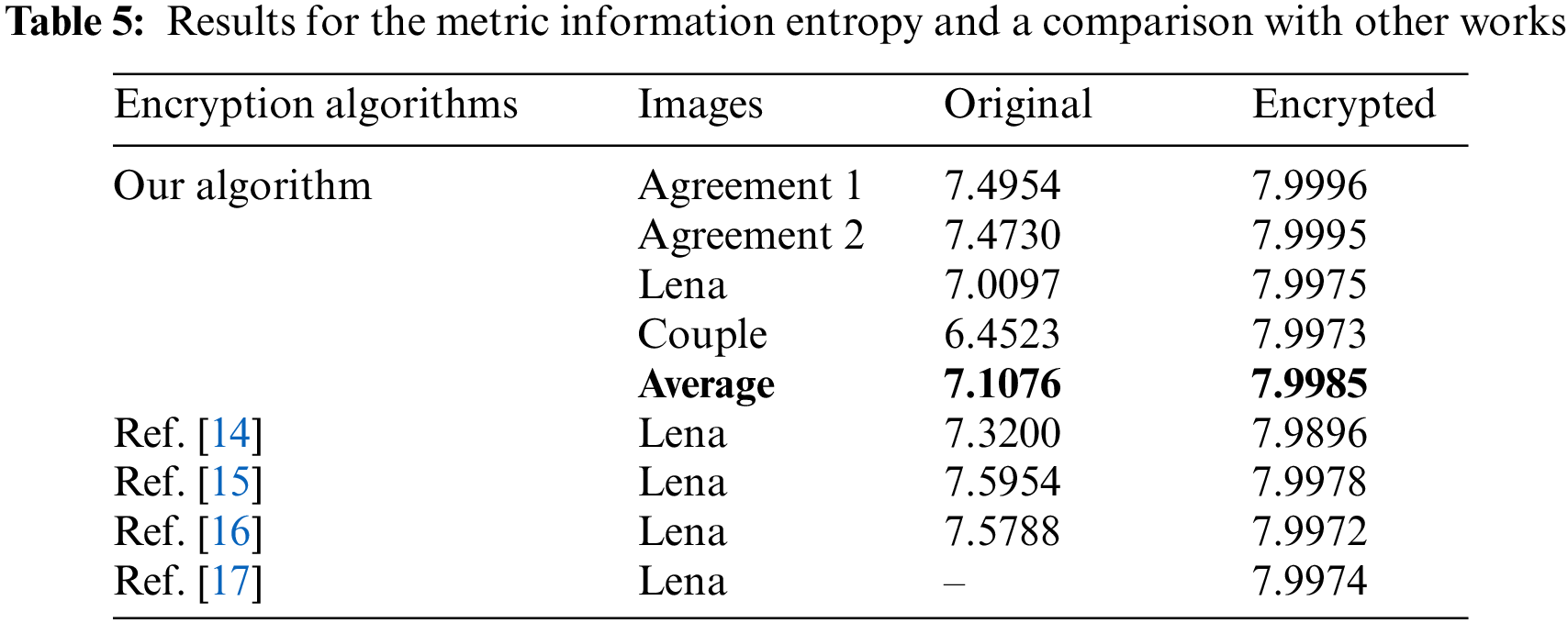
Hence, we can imply that the suggested cipher enjoys good effects of security. Additionally, 7.9985 is mean value for all the images, which is once again very close to 8. Hence, it can be asserted that the proposed cipher can avert the attacks of entropy over it. Apart from that, a comparison has been made between this new work and other research articles in Tab. 5. As the Tab.5 shows that this new image encryption scheme works better than [14,15,16,17] for the images of Agreement 1 and Agreement 2. Further, the images of Lena and Couple beat the works of [14,16,17] and [14,16] regarding this metric.
Our world is full of dangers and uncertainties. Sometimes, as the cipher image is got stored or transferred through the Internet, it comes under the assault of different noises. A nice encryption scheme is expected to withstand such kind of future noise attacks. To exhibit this characteristic of the proposed im-age cipher, we have artificially added the Pepper & Salt noise in the encrypted images of Agreement 1 and Agreement 2. The amount of densities are 0.05, 0.1 in a respective way. Figs. 12a and 12c show these images with noise attacks. The restored/decrypted images have been drawn in the Figs. 12b and 12d after the application of decryption algorithm over these images. These images can be clearly recognized which signals to the fact that the proposed encryption scheme for the non-disclosure documents can retrieve the polluted images with noise.


Figure 12: Noise attack (Pepper & Salt) on cipher images along with density of noise: (a) Agreement 1 image, 0.05; (b) Restored image agreement 1 from (a); (c) Agreement 2 image, 0.1; (d) Restored image Agreement 2 from (c)
5.5 Computational Time Analysis
For writing this image encryption scheme, we have selected Intel® CoreTM i7-3740QM Lenovo ThinkPad with CPU @ 2.70 GHz, 8 GB RAM and 500 GB Hard drive with Windows 10 Education operating system. As the cryptographers build different products, their thrust is ensuring their security. Apart from that, the cryptographic software taking lesser amount of time for their execution bear brighter prospects for their applications for the solution of real-world problems. The amount of time taken by the suggested scheme has been depicted in Tab. 6. Besides, our cipher has been compared with other published works in the literature. The suggested scheme beats these works [14–17] vis-à-vis time.

Safety of non-disclosure documents on the cloud servers and the Internet is a hot area of research. Normally, these documents are converted to the images before sending them. This work has proposed a novel encryption algorithm for images based on the set of dynamically generated rectangles within the given input image. As the plain image is given to the algorithm, the rectangles of different sizes are generated by the random numbers. The opposite sides of the rectangles have been swapped with each other for both the length and width of the rectangles. In this way, the confusion effects have been achieved. The diffusion effects were embedded through an XOR operation. 5D multi-wing hyperchaotic system has been used for the generation of the random data. Performance analyses and the computer simulation expressly indicate the robustness, aversion towards the various attacks and the bright prospects for some real-world application for the proposed image cipher. As far as the future work is concerned, the proposed idea can be easily tailored for the multiple images. Normally non-disclosure agreement consists of more than one documents. So, to address this need, we would write multiple image ciphers in the future.
Acknowledgement: The authors would like to thank and acknowledge to Universiti Malaysia Terengganu (UMT) Malaysia and every individual who has been a source of information, support and encouragement on successful completion of this manuscript.
Funding Statement: This research is fully funded by Universiti Teknologi Malaysia under the UTM Fundamental Research Grant (UTMFR) with Cost Center No Q.K130000.2556.21H14.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Yalaho, “Managing offshore outsourcing of software development using the ict-supported unified process model: A cross-case analysis,” Jyväskylä Studies in Computing, vol. 103, pp. 1–94, 2009. [Google Scholar]
2. H. U. Rahman, M. Raza, P. Afsar, A. Alharbi and S. Ahmad, “Multi-criteria decision-making model for application maintenance offshoring using analytic hierarchy process,” Applied Sciences, vol. 11, no. 18, pp. 8550, 2021. [Google Scholar]
3. A. Ikram, M. A. Jalil, A. B. Ngah and A. S. Khan, “Towards offshore software maintenance outsourcing process model,” International Journal of Computer Science and Network Security, vol. 20, no. 4, pp. 6–14, 2020. [Google Scholar]
4. M. Almutairi and S. Riddle, “State of the art of it outsourcing and future needs for managing its security risks,” in Int. Conf. on Information Management and Processing (ICIMP), London, UK, pp. 42–48, 2018. [Google Scholar]
5. H. Wang, Z. Xia, J. Fei and F. Xiao, “An aes-based secure image retrieval scheme using random mapping and bow in cloud computing,” IEEE Access, vol. 8, pp. 61138–61147, 2020. [Google Scholar]
6. N. Wang, J. Fu, K. B. Bhargava and J. Zeng, “Efficient retrieval over documents encrypted by attributes in cloud computing,” IEEE Transactions on Information Forensics and Security, vol. 13, no. 10, pp. 2653–2667, 2018. [Google Scholar]
7. M. Hanif, A. R. Naqvi, S. Abbas, M. A. Khan and N. Iqbal, “A novel and efficient 3d multiple images encryption scheme based on chaotic systems and swapping operations,” IEEE Access, vol. 8, pp. 123536–123555, 2020. [Google Scholar]
8. M. Hanif, S. Abbas, M. A. Khan, N. Iqbal and U. Z. Rehman, “A novel and efficient multiple rgb images cipher based on chaotic system and circular shift operations,” IEEE Access, vol. 8, pp. 146408–146427, 2020. [Google Scholar]
9. N. Iqbal, M. Hanif, S. Abbas, M. A. Khan and U. Z. Rehman, “Dynamic 3D scrambled image based rgb image encryption scheme using hyperchaotic system and dna encoding,” Journal of Information Security and Applications, vol. 58, no. 102809, pp. 102809, 2021. [Google Scholar]
10. Y. Li, C. Wang and H. Chen, “A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation,” Optics and Lasers in Engineering, vol. 90, pp. 238–246, 2017. [Google Scholar]
11. J. Zaman and R. Ghosh, “Review on fifteen statistical tests proposed by nist,” Journal of Theoretical Physics and Cryptography, vol. 1, pp. 18–31, 2012. [Google Scholar]
12. E. Yavuz, R. Yazıcı, M. C. Kasapbasi and E. Yamaç, “A chaos-based image encryption algorithm with simple logical functions,” Computers & Electrical Engineering, vol. 54, no. 3, pp. 471–483, 2016. [Google Scholar]
13. W. F. P. Group, “Standard for binary floating-point arithmetic–unicamp, IEEE computer society,” 1985. [Online]. Available: https://www.ime.unicamp.br/~biloti/download/ieee_754-1985.pdf. [Google Scholar]
14. X. Wu, K. Wang, X. Wang, H. Kan and J. Kurths, “Color image dna encryption using nca map-based cml and one-time keys,” Signal Processing, vol. 148, no. 9, pp. 272–287, 2018. [Google Scholar]
15. Z. Bashir, N. Iqbal and M. Hanif, “A novel gray scale image encryption scheme based on pixels swapping operations,” Multimedia Tools and Applications, vol. 80, no. 1, pp. 1029–1054, 2021. [Google Scholar]
16. X. Wang, Y. Wang, X. Zhu and C. Luo, “A novel chaotic algorithm for image encryption utilizing one-time pad based on pixel level and dna level,” Optics and Lasers in Engineering, vol. 125, pp. 105851, 2020. [Google Scholar]
17. N. Iqbal, A. R. Naqvi, M. Atif, M. A. Khan and M. Hanif, “On the image encryption algorithm based on the chaotic system, dna encoding, and castle,” IEEE Access, vol. 9, pp. 118253–118270, 2021. [Google Scholar]
18. N. Iqbal, M. Hanif, S. Abbas, M. A. Khan and S. H. Almotiri, “Dna strands level scrambling-based color image encryption scheme,” IEEE Access, vol. 8, pp. 178167–178182, 2020. [Google Scholar]
19. N. Iqbal, S. Abbas, M. A. Khan, T. Alyas and A. Fatima, “A rgb image cipher using chaotic systems, 15-puzzle problem and dna computing,” IEEE Access, vol. 7, pp. 174051–174071, 2019. [Google Scholar]
20. C. E. Shannon, “Communication theory of secrecy systems,” The Bell System Technical Journal, vol. 28, no. 4, pp. 656–715, 1949. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |