[BACK]
images Computer Modeling in Engineering & Sciences images

DOI: 10.32604/cmes.2021.011782

ARTICLE

New Computation of Unified Bounds via a More General Fractional Operator Using Generalized Mittag–Leffler Function in the Kernel

Saima Rashid1, Zakia Hammouch2, Rehana Ashraf3 and Yu-Ming Chu4,*

1Department of Mathematics, Government College University, Faisalabad, Pakistan
2Division of Applied mathematics, Thu Dau Mot University, Thu Dau Mot City, Vietnam
3Department of Mathematics, Lahore College Women University, Jhangh Campus, Lahore, Pakistan
4Department of Mathematics, Huzhou University, Huzhou, China
*Corresponding Author: Yu-Ming Chu. Email: chuyuming@zjh.edu.cn
Received: 29 May 2020; Accepted: 08 September 2020

Abstract: In the present case, we propose the novel generalized fractional integral operator describing Mittag–Leffler function in their kernel with respect to another function Φ. The proposed technique is to use graceful amalgamations of the Riemann–Liouville (RL) fractional integral operator and several other fractional operators. Meanwhile, several generalizations are considered in order to demonstrate the novel variants involving a family of positive functions 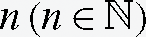images for the proposed fractional operator. In order to confirm and demonstrate the proficiency of the characterized strategy, we analyze existing fractional integral operators in terms of classical fractional order. Meanwhile, some special cases are apprehended and the new outcomes are also illustrated. The obtained consequences illuminate that future research is easy to implement, profoundly efficient, viable, and exceptionally precise in its investigation of the behavior of non-linear differential equations of fractional order that emerge in the associated areas of science and engineering.

Keywords: Integral inequality; generalized fractional integral with respect to another function; increasing and decreasing functions; Mittag–Leffler function

1  Introduction

A study was initiated in Newton’s time, but, lately, it has captivated the consideration of numerous researchers due to its intriguing nature, known as the fractional calculus. For the previous three decades, the most charming bounds in modelling and simulation have been discovered in the frame of fractional calculus. The idea of the fractional operators has been mechanized because of the complexities related to a heterogeneous phenomenon. The fractional differential operators are equipped for catching the conduct of multidimensional media as they have diffusion processes. It was considered to be an essential device, and numerous issues can be demonstrated more appropriately and more precisely with differential equations having an arbitrary order. Calculus with fractional order is related to concrete adventures and is widely utilized in nanotechnology, optics, diseases, chaos theory and different other fields [1–8]. The fractional derivatives for various sorts of equations, describe that these models have a significant job in depicting the idea of mathematical problems that are linked with science and technology, see the references [9–11].

In the present scenario, numerous significant fractional derivative and integral operators are systematically and successfully analyzed with the assistance of fractional calculus, see [10,11]. Several assorted operators that have been recommended by numerous senior researchers like, Riemann, Hadamard, Antagana–Baleanu, Caputo and Fabrizio. Nevertheless, these operators have their own repressions. Recently, Abdeljawad [1] reported fractional operators are known as fractional conformable derivatives and integrals. The exponential and Mittag–Leffler functions are used as kernels by several researchers for developing new fractional techniques that provide assistance to many researchers consult the derivative to model and integrals in order to analyze the nonlocal dynamics due to the presence of nonsingular kernels and helps to find the solution for diverse classes of non-linear complex problems. Kilbas et al. [11] and Almeida [9] introduced the generalized RL and Caputo derivative operators in the sense of another function. Rashid et al. [12] proposed another novel fractional approach which comes into existence in the theory of fractional calculus, which is known as generalized proportional fractional operators with respect to another function 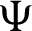images.

Adopting the aforementioned trend, we delineate the significance of the novel fractional operator and future plan, we, in the present the framework, consider the Mittag–Leffler function, which assumes a dynamic job in portraying the idea of porous media just as establishing the several generalizations by employing more generalized fractional operator with Mittag–Leffler in their kernels.

Mathematical inequalities considered to be a significant tool in diverse areas of science and technology, among others; especially we point out the initial value problem, the stability of linear transformation, integral differential equations, and impulse equations [13–15]. Variants regarding fractional integral operators are the use of noteworthy significant strategies and are also highly implemented in natural and social sciences to portray real-world problems.

Briefly, inequalities involve solid and rich communication among analysis, geometry and technology. In [16], Agarwal explored some new inequalities for Hadamard fractional integral operators. Also, Rashid et al. [17] established Hermite-Hadamard inequalities for exponentially m-convex functions via extended Mittag Leffler function. In [18], researchers have been focused their attention in order to find the distinguished version of the reverse Minkowski inequality for quantum Hahn fractional integral operators. Set et al. [19] derived Chebyshev type inequalities by employing fractional integral operator having Mittag–Leffler function in the kernel. For more details, see [20–38] and the reference cited therein. The diverse utilities of fractional integral operators compelled us to show the speculations by using a family of n positive functions involving generalized fractional integrals operators with respect to another function images as well-known special function in their kernel.

The principal objective of this article is that we demonstrate the notations of our newly introduced operator generalized fractional integral with respect to another function 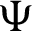images by introducing Mittag–Leffler function in their kernel. Also, we present the results concerning for a class of family of n 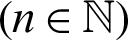images continuous positive decreasing functions on 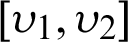images by employing generalized fractional integral operator proposed by Andric [39], Salim et al. [40], Rahman et al. [41], Srivastava et al. [42], Prabhakar [43] and Riemann-Liouville fractional integral operators [44]. The idea is quite new and seems to have opened new doors of investigation towards various scientific fields of research including engineering, fluid dynamics, bio-sciences, chaos, meteorology, vibration analysis, bio-chemistry, aerodynamics and many more. The authors argued that the generalized fractional integral in Hilfer sense can capture a limited number of complex problems on one hand and on the other hands it can also capture different types of complexities, thus putting these two concepts together can help us to understand the complexities of existing nature in a much better way.

2  Prelude

Here, we define the basic notion of the more generalized fractional integral operator as Mittag–Leffler function introduced in their kernel.

We begin with fractional integral operators defined by Salim and Faraj in [40] containing generalized Mittag–Leffler function in their kernels as follows:

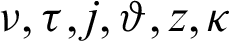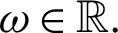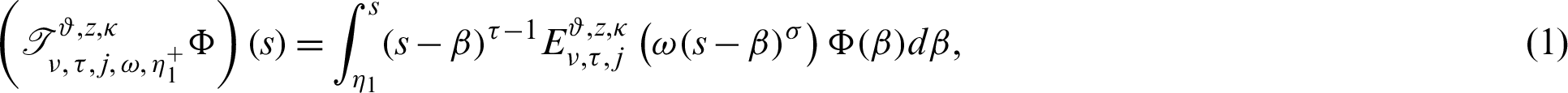
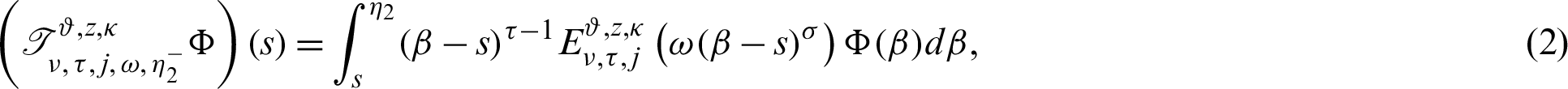
Definition 2.1. ([40]) Let images be positive real numbers and images Then the generalized fractional integral operators containing Mittag–Leffler function for a real-valued continuous function images are defined by

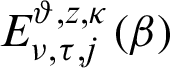images

images

where images is the generalized Mittag–Leffler function defined as

images

Andric et al. [39], defined the following fractional integral operators containing an extended generalized Mittag–Leffler function in their kernels:

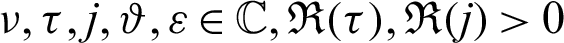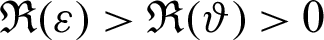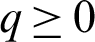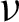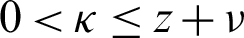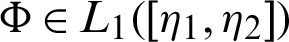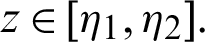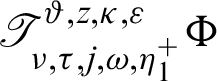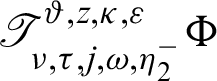Definition 2.2. ([39]) Let images, images, with images, images, z > 0 and images. Let images and images Then the generalized fractional integral operators images and images are defined by

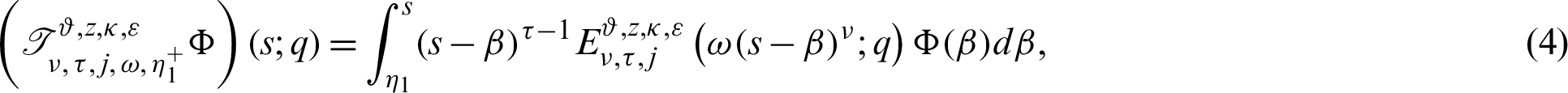
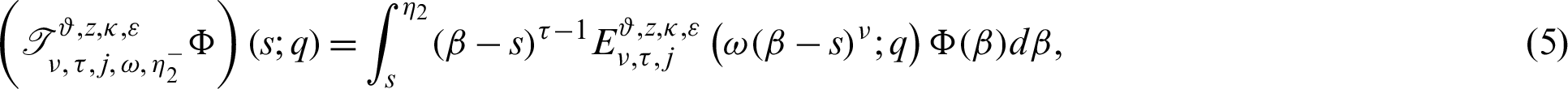
images

images

where 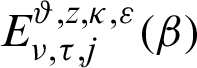images is the generalized Mittag–Leffler function defined as

images

is the extended generalized Mittag–Leffler function.

Now we present the concept of the generalized fractional integral operator in the Hilfer sense having Mittag–Leffler function in the kernel as follows:

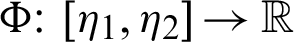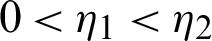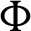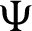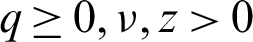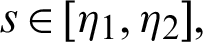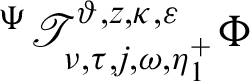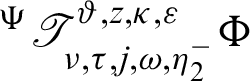Definition 2.3. Let images, images be a function such that images be a positive and integrable and images be a differentiable and strictly increasing. Also, let images with images and images Then for images the integral operators images and images are stated as:

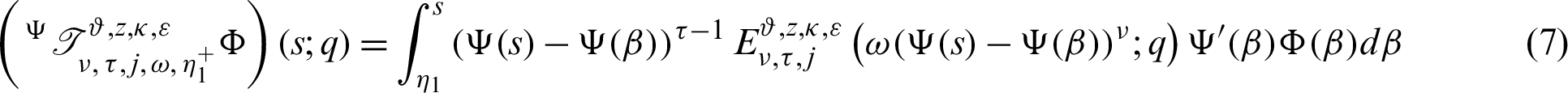
images

and

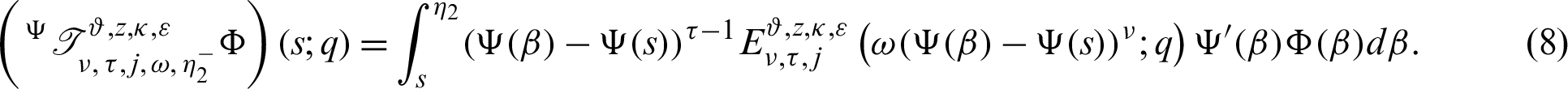
images

Remark 2.1. Definition 2.3 is the generalizations of the several noteworthy exisiting integrals are stated as follows:

1.    Letting 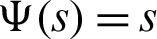images and q = 0, then the fractional integral operator (7) and (8) leads to the operators defined by Salim et al. [40].

2.    Letting images and j = z = 1, then the fractional integral operator (7) and (8) leads to the operators defined by Rahman et al. [41].

3.    Letting 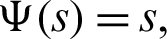images q = 0 and j = z = 1, then the fractional integral operator (7) and (8) leads to the operators defined by Srivastava et al. [42].

4.    Letting 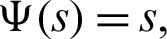images q = 0 and 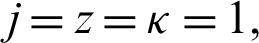images then the fractional integral operator (7) and (8) leads to the operators defined by Prabhakar [43].

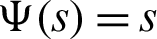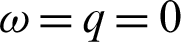5.    Letting images and images then the fractional integral operator (7) and (8) leads to the Riemann-Liouville fractional integral operators [44].

3  Main Results

In this section, we present the novel generalizations pertaining to the more generalized fractional integral operator using the Mittag–Leffler function in the kernel.

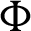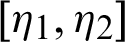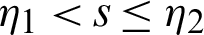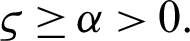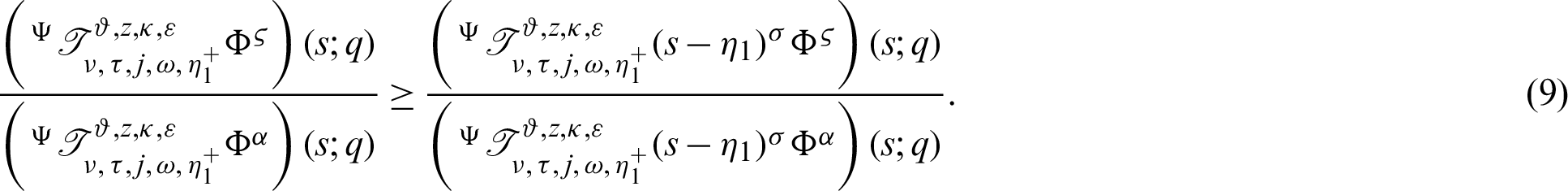
Theorem 3.1. Suppose images be a continuous positive decreasing function on images with images, images and images Suppose images be a differentiable and strictly increasing. Then the more generalized fractional integral operator defined in (7), we have

images

Proof. Using the hypothesis given in Theorem 3.1, we have

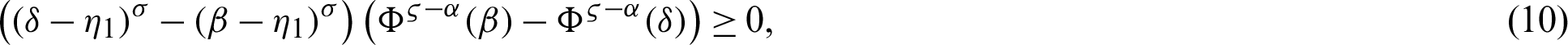
images

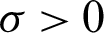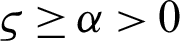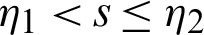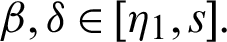
where images, images, images and images

By (10), we have

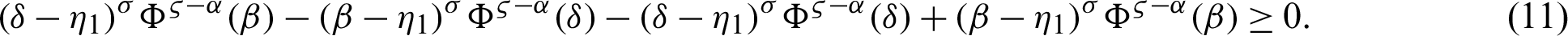
images

Let us define a function

images

Accordingly, the function 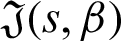images is positive for all 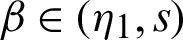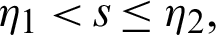images, images as every term of the supposed function is positive and explained in Theorem 3.1. Therefore, multiplying both sides of (11) with

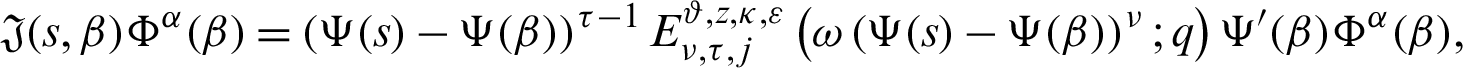
images

we have

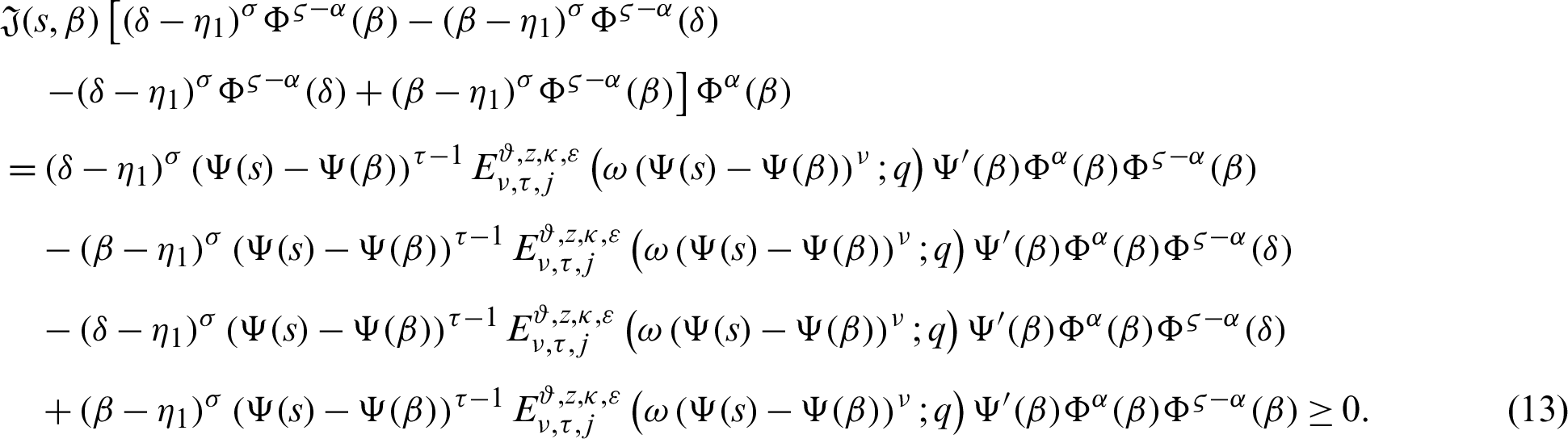
images

Integrating on both sides with respect to images from images to s, we have

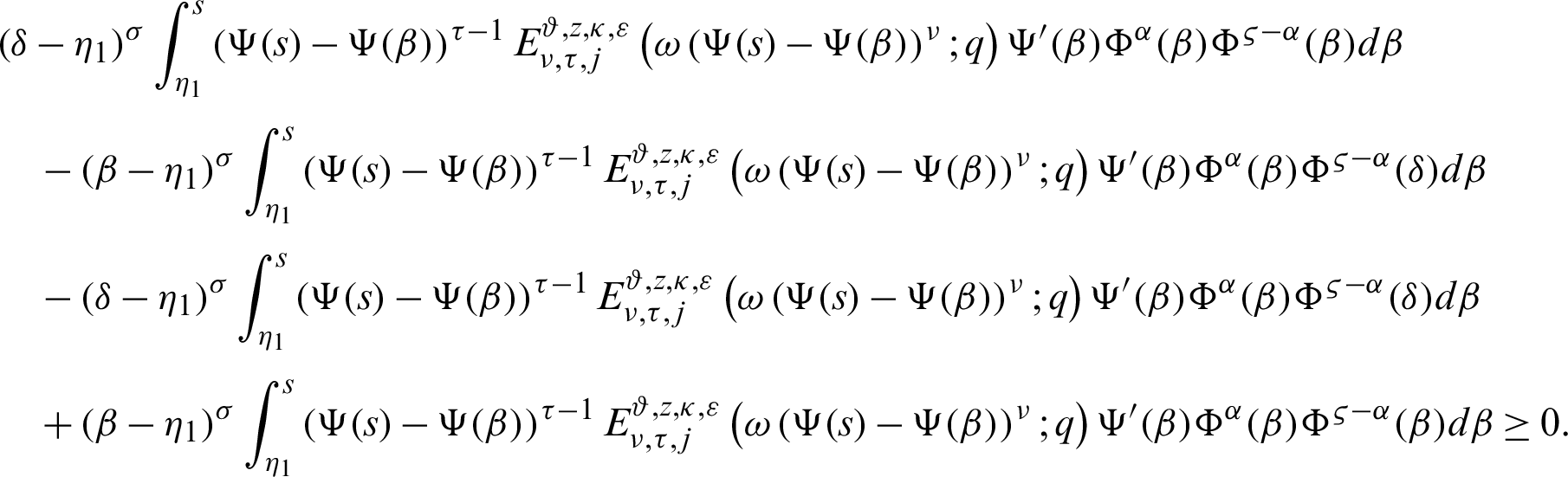
images

It follows that

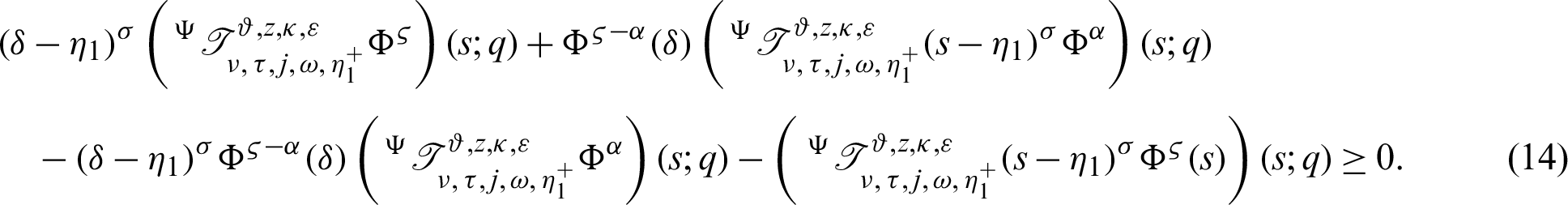
images

Multiplying (14) by

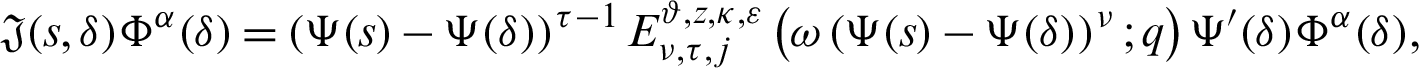
images

for 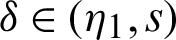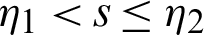images, images, and integrating the subsequent identity w.r.t 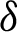images from images to s shows

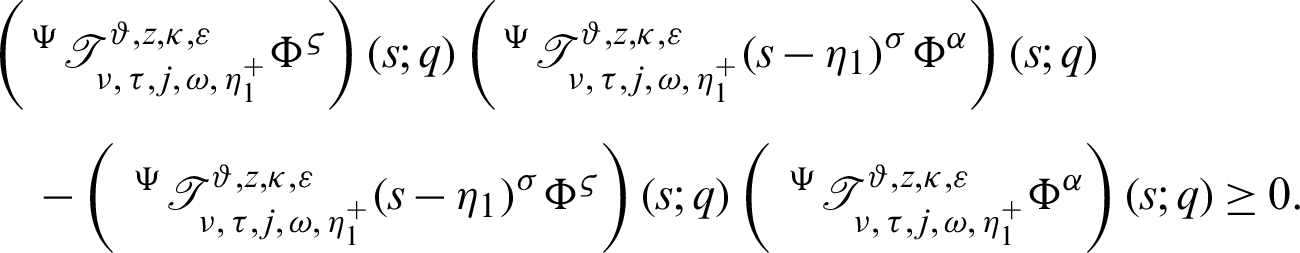
images

Dividing the above inequality by 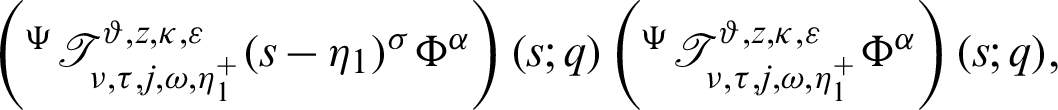images we get the desired inequality (9).

Some special remarkable cases of Theorem 3.1 are stated as follows:

Remark 3.1. In Theorem 3.1:

     I)  Take 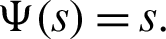images Then we get a new result for generalized fractional integral operator having Mittag–Leffler in the kernel as follows:

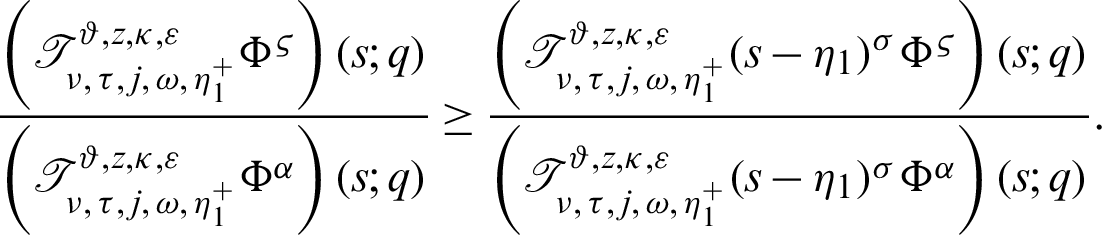
images

    II)  Take 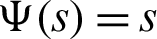images along with q = 0 Then we have a new result

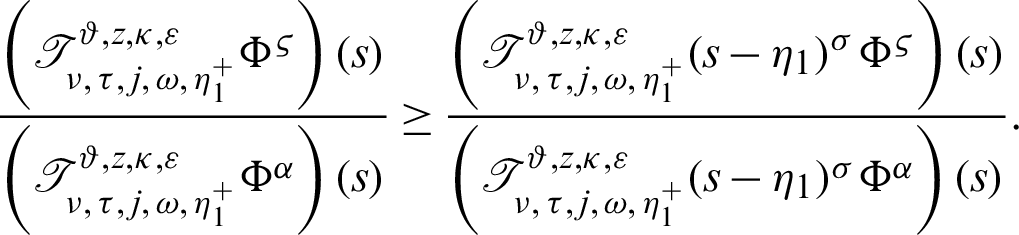
images

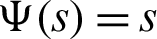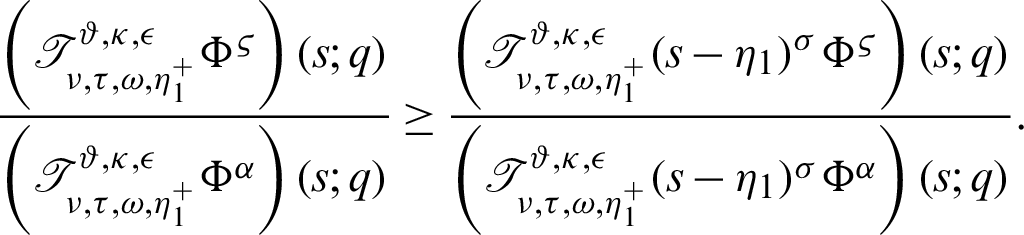
   III)  Take images along with j = z = 1 Then we have a new result

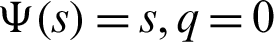images

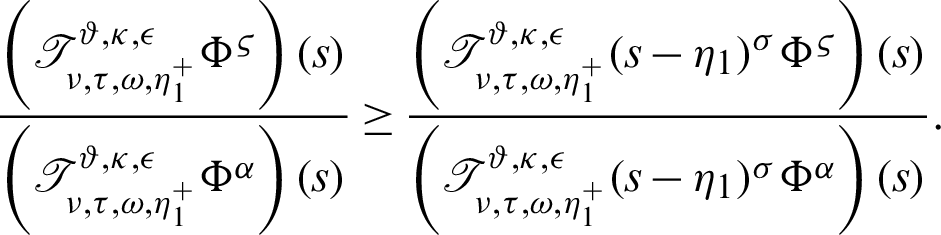
    IV)  Take images along with j = z = 1 Then we have a new result

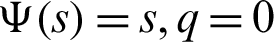images

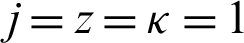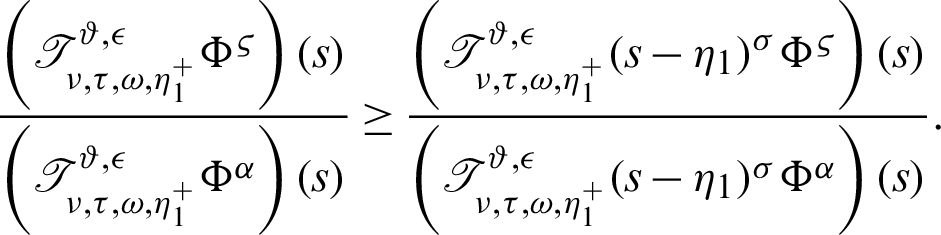
     V)  Take images along with images Then we have a new result

images

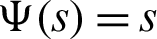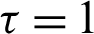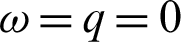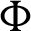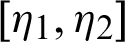Remark 3.2. If images, images and images, then Theorem 3.1 reduces to Theorem 3 of [45]. Moreover, the inequality (15) will reverse if images is an increasing function on images.

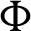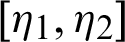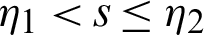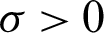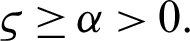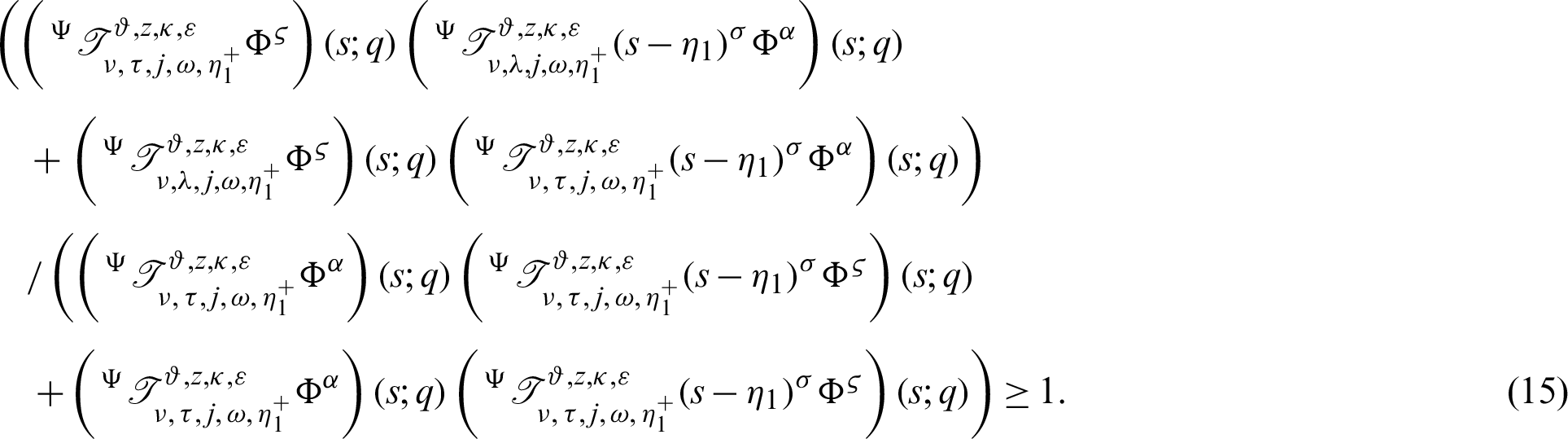
Theorem 3.2. Suppose images be a continuous positive decreasing function on images with images, images and images Suppose images be a differentiable and strictly increasing. Then the more generalized fractional integral operator defined in (7), we have

images

Proof. Taking product on both sides of (14) by

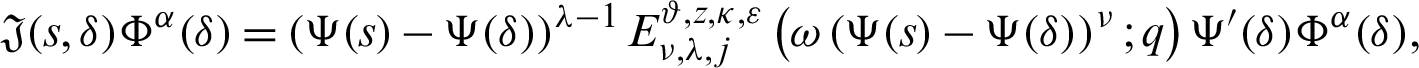
images

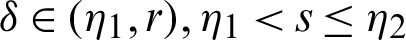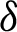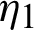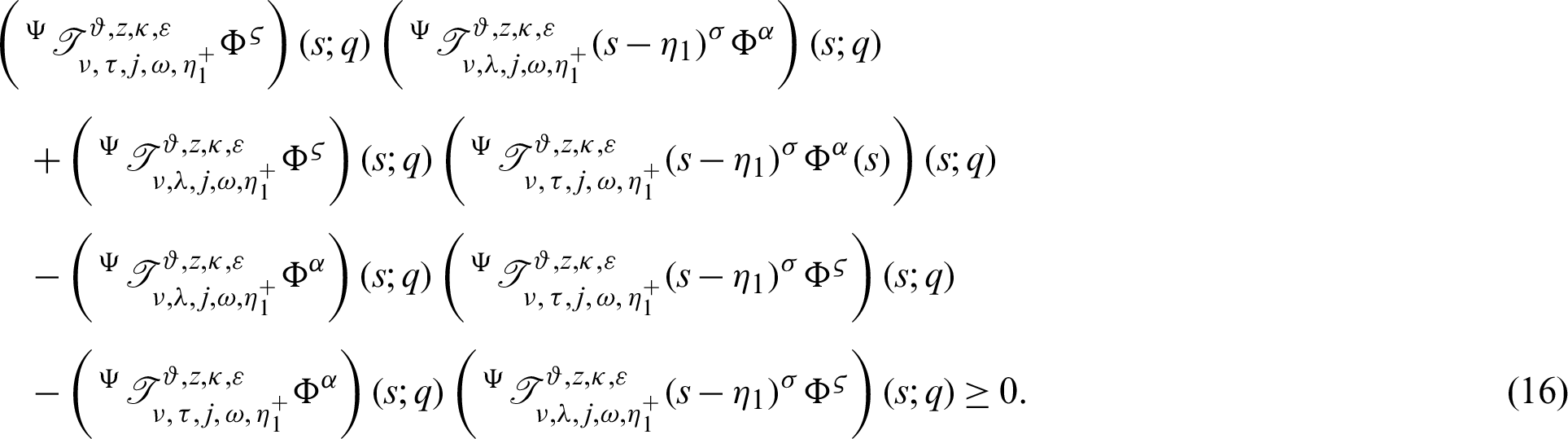
for images and integrating the subsequent identity w.r.t images from images to s shows

images

Hence, dividing (16) by

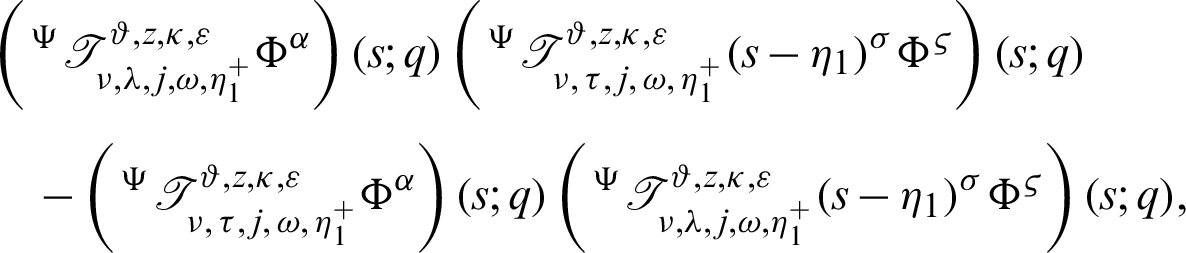
images

the proof of (15) is complete.

Remark 3.3. Letting 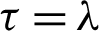images in inequality (15), then we attain the inequality (9).

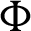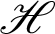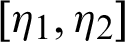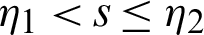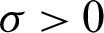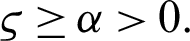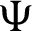Theorem 3.3 Let images be a continuous positive decreasing function on images and images be a continuous positive increasing function on images with images, images, and images Suppose images be a differentiable and strictly increasing. Then the more generalized fractional integral operator defined in (7), we have

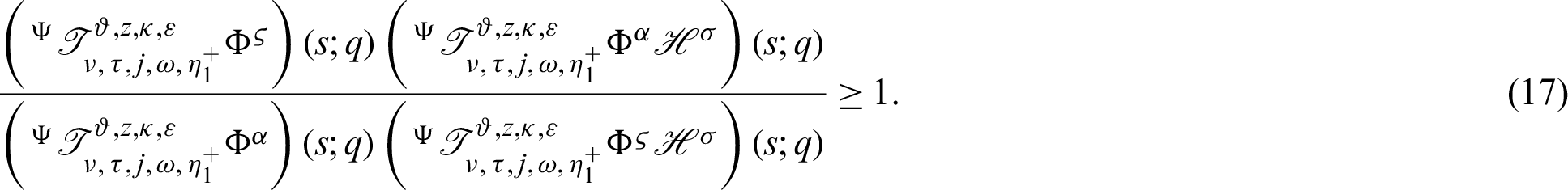
images

Proof. Using the hypothesis given in Theorem 3.3, we have

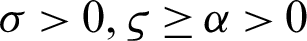images

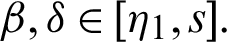where images and images From (18), we have

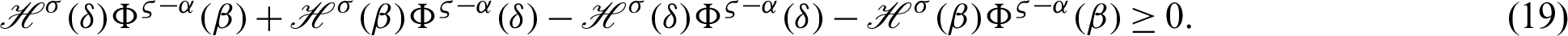
images

Taking product of (19) by

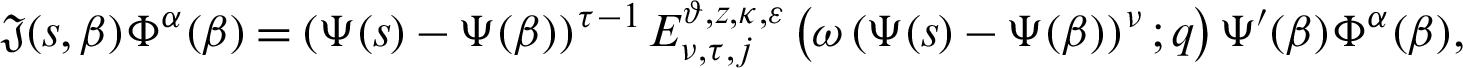
images

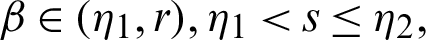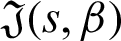for images where images is defined by (12), we have

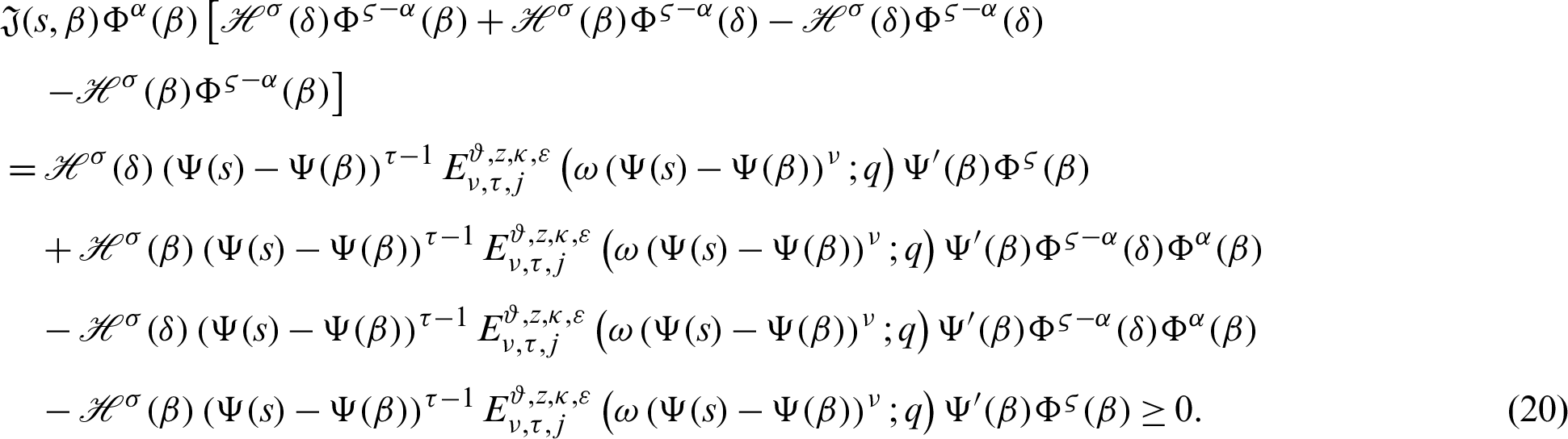
images

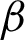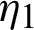Integrating (20) with respect to images from images to s, we have

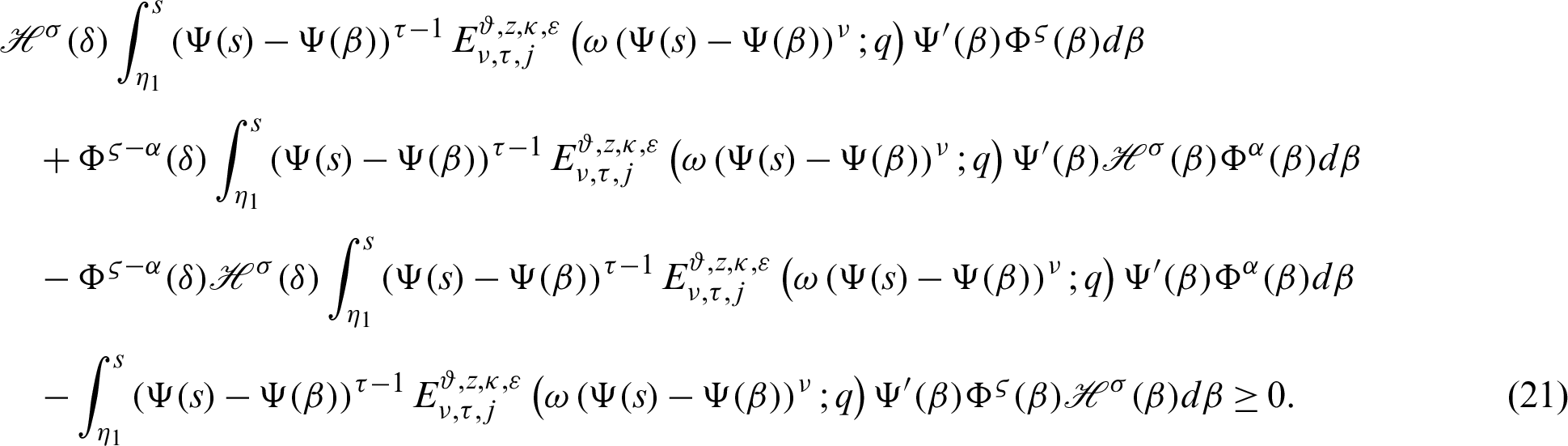
images

From (21), it follows that

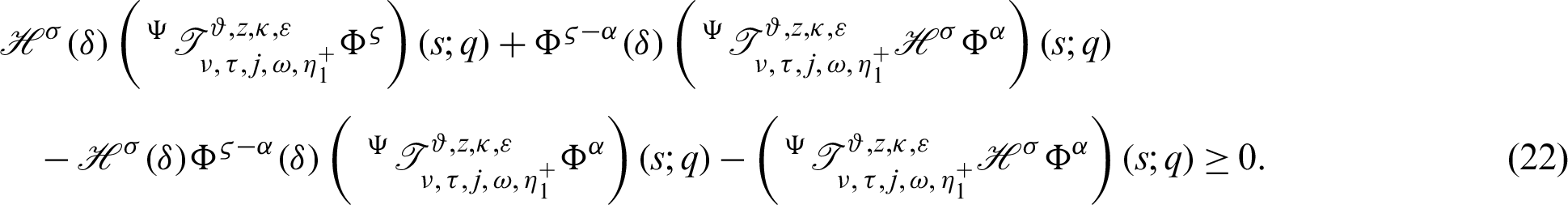
images

Again, taking product (14) by

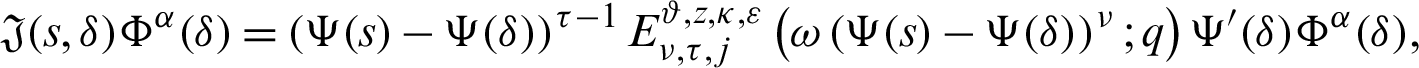
images

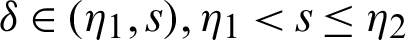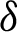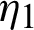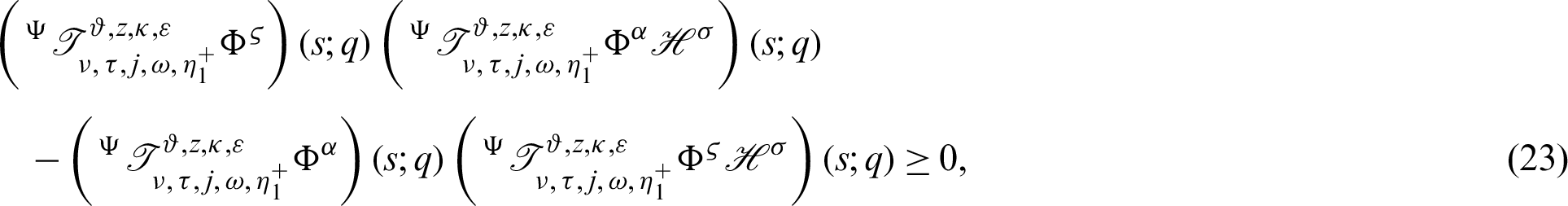
for images and integrating the subsequent identity w.r.t images from images to s shows

images

which completes the desired inequality (17) of Theorem 3.3.

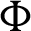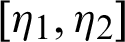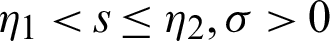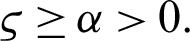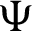Theorem 3.4. Let images be a continuous positive decreasing function on images and images be a continuous positive increasing function on images with images and images Suppose images be a differentiable and strictly increasing. Then the more generalized fractional integral operator defined in (7), we have

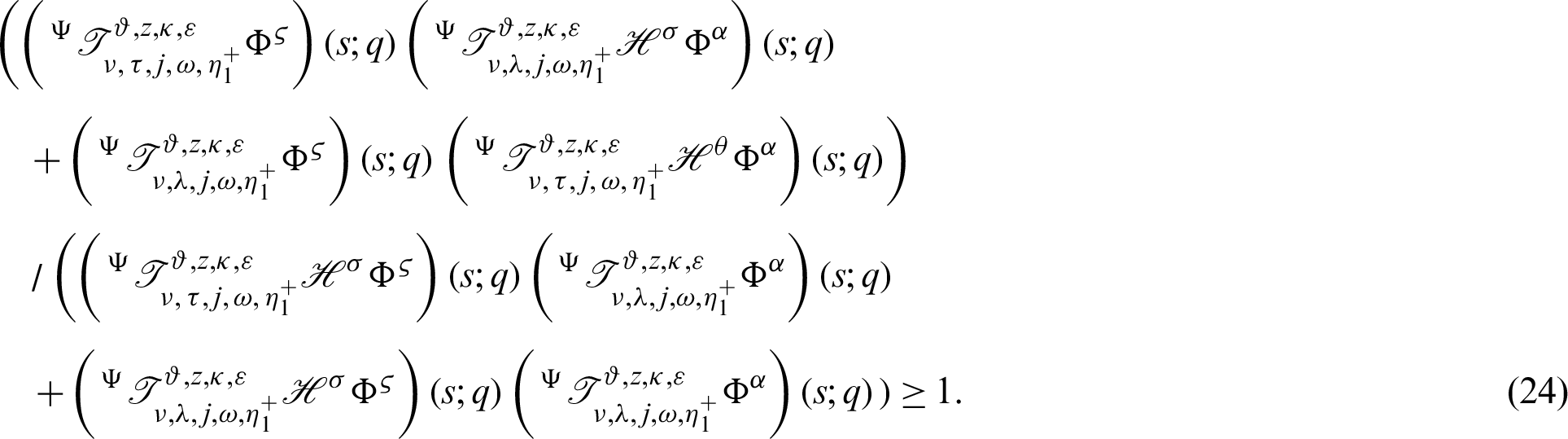
images

Proof. Taking product on both sides of (22) by

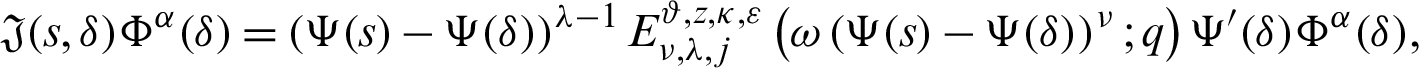
images

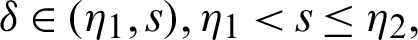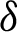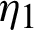for images and integrating the subsequent identity w.r.t images from images to s shows

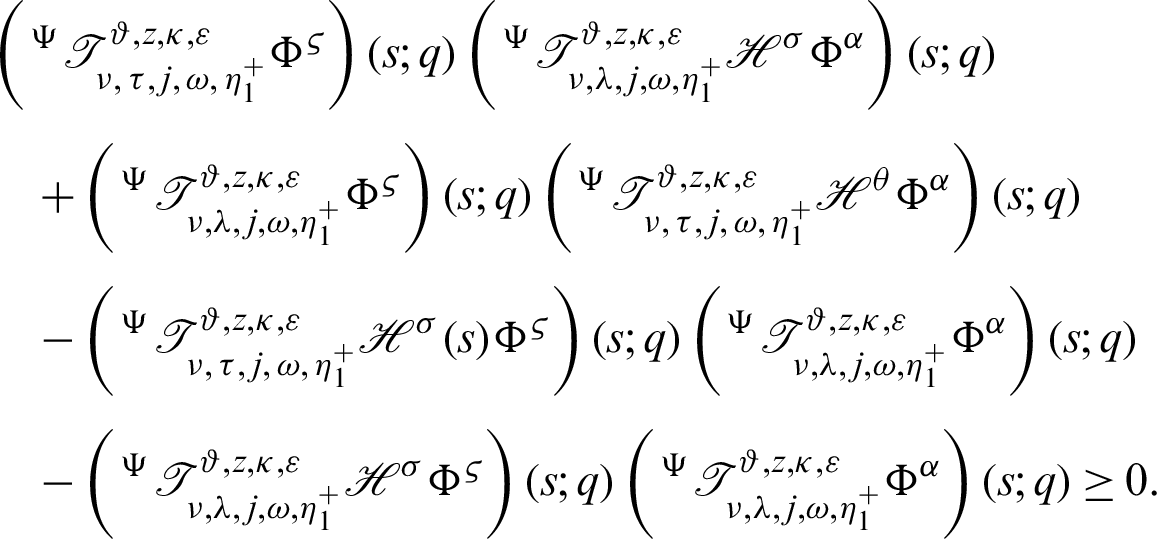
images

It follows that

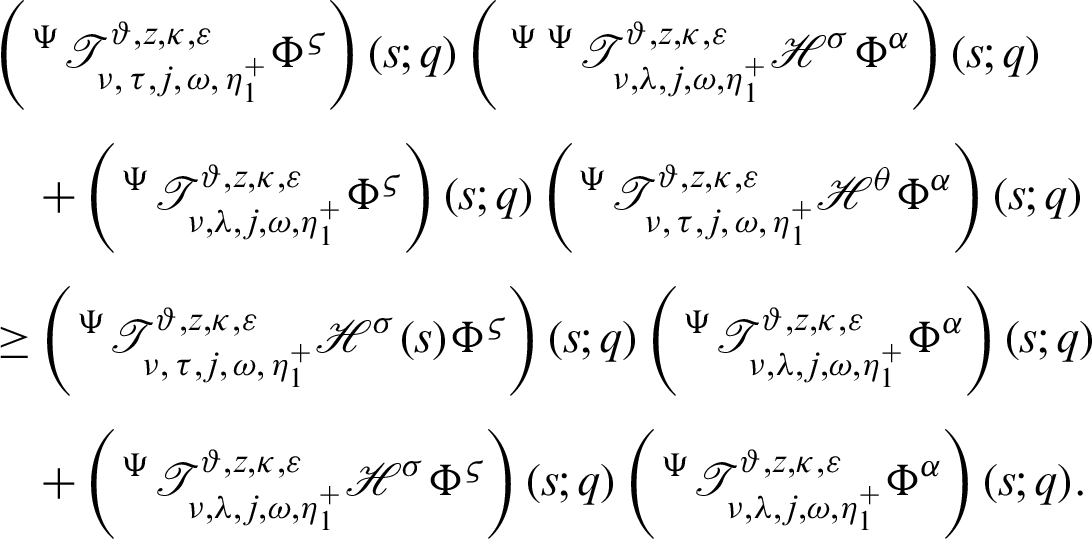
images

Dividing the above inequality by

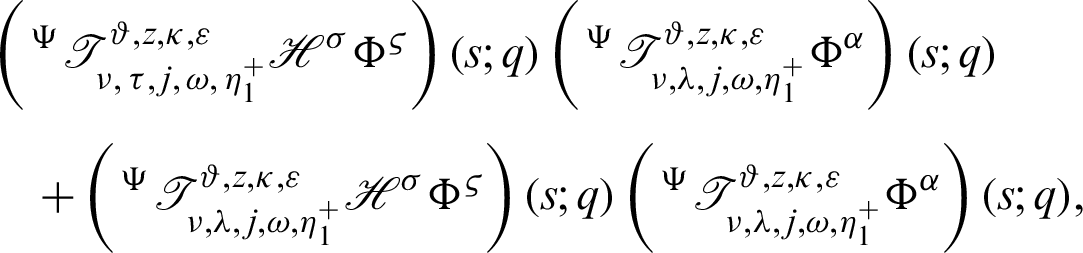
images

acquires the desired inequality (24).

Remark 3.4. Letting 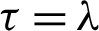images in inequality (24), then we attain the inequality (17).

Now, we demonstrate the following generalizations for more generalized fractional to derive some novel inequalities for a class of n-decreasing positive functions.

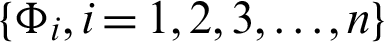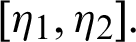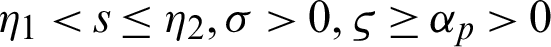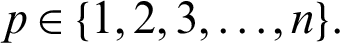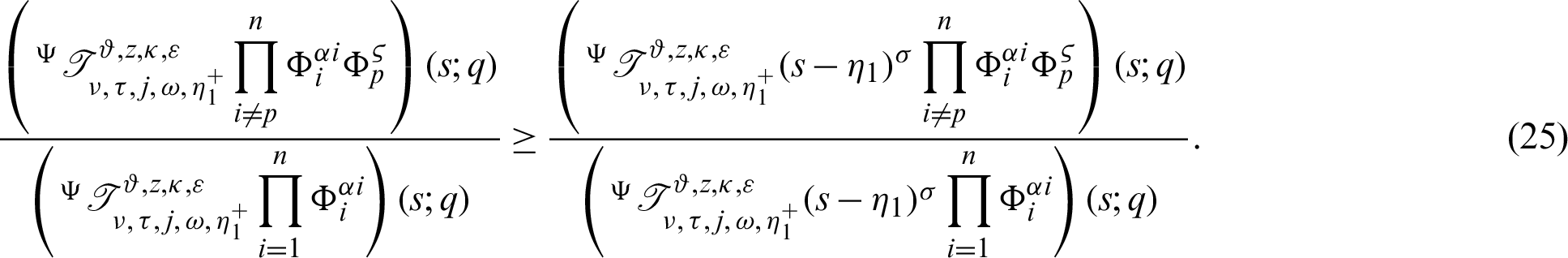
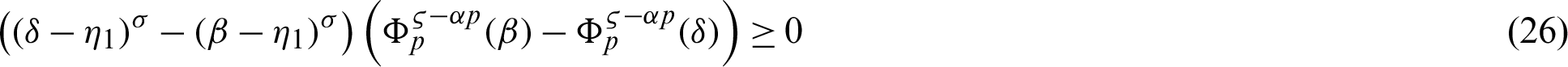
Theorem 3.5. Let images be a sequence of continuous positive decreasing functions on images Let images for any fixed images Suppose images be a differentiable and strictly increasing. Then the more generalized fractional integral operator defined in (7), we have

images

Proof. Let images be a sequence of continuous positive decreasing functions on images we have

images

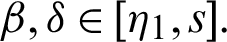
for any fixed images and images

By (26), we have

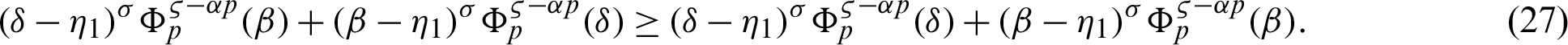
images

Taking product of (27) by

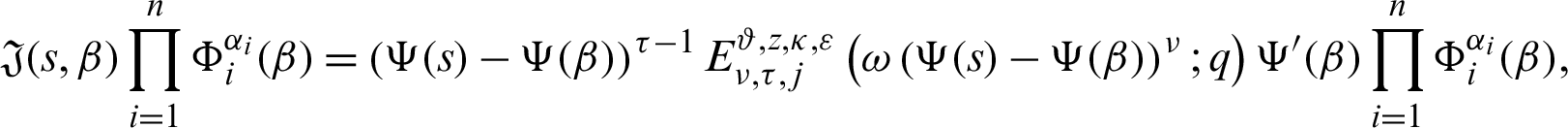
images

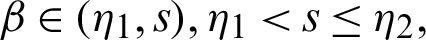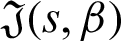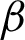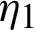for images where images is defined by (12), and integrating the subsequent identity w.r.t images from images to s we have

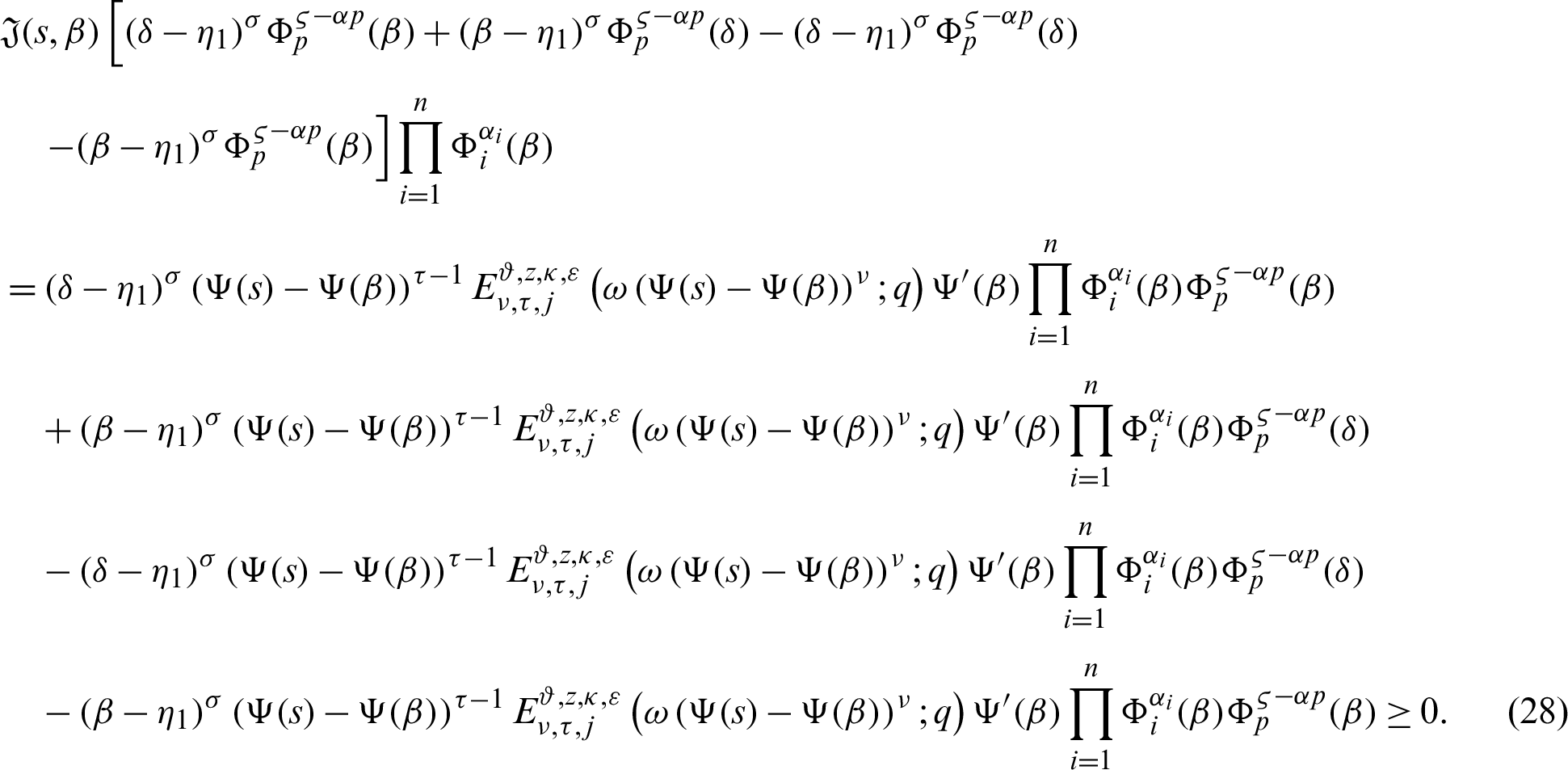
images

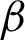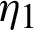Integrating (28) with respect to images from images to s, we have

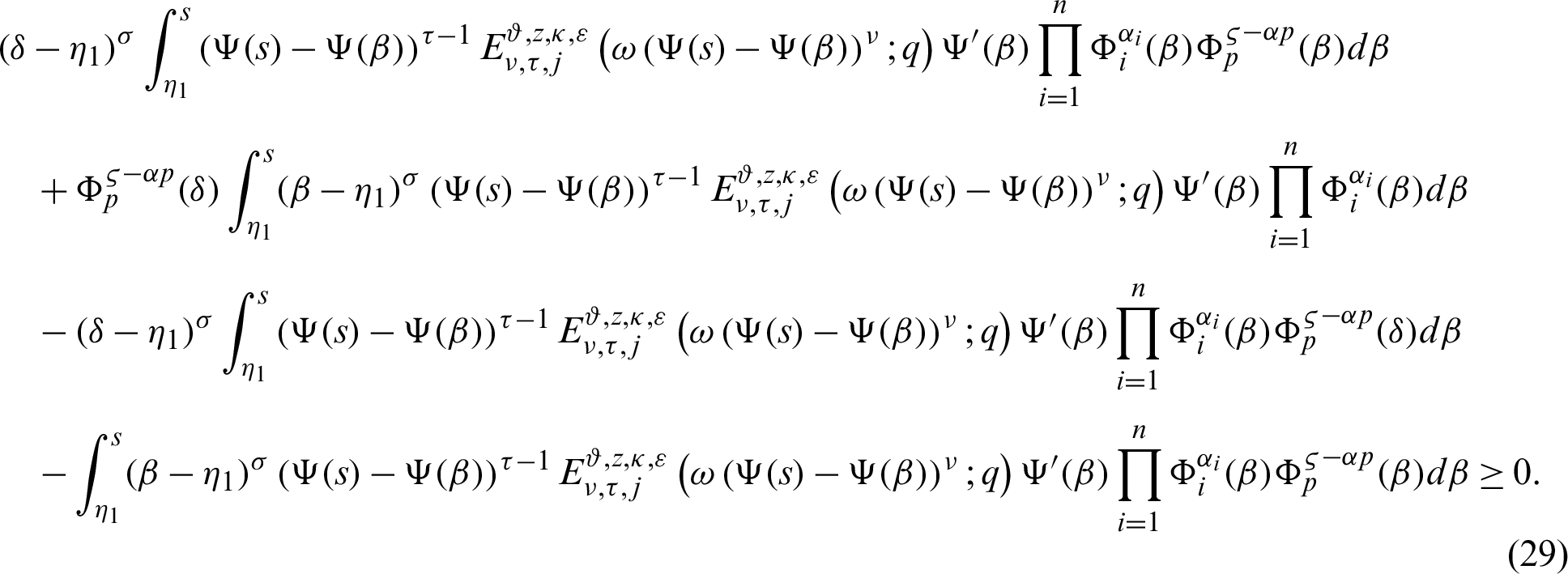
images

From (29), it follows that

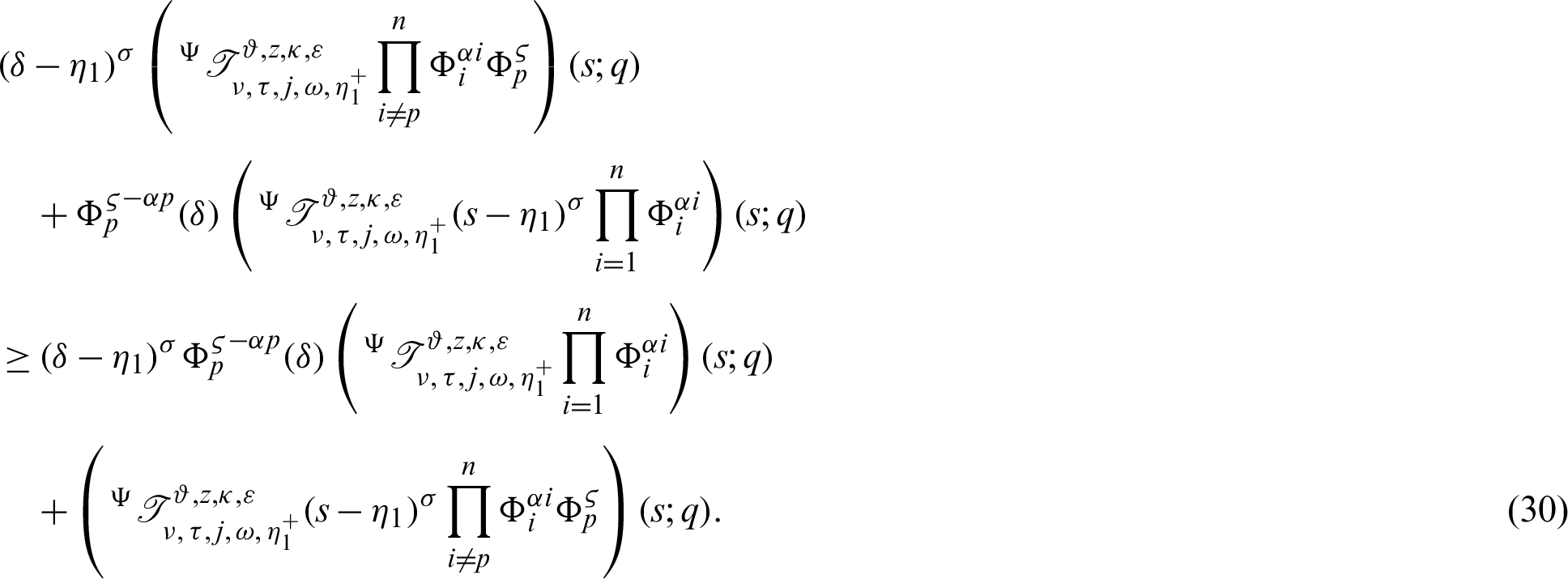
images

Again, taking product of (30) by

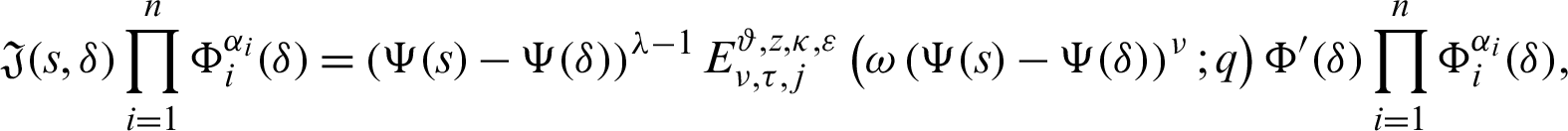
images

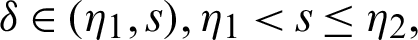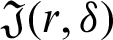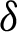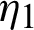for images where images is defined by (12), and integrating the subsequent identity w.r.t images from images to s, we have

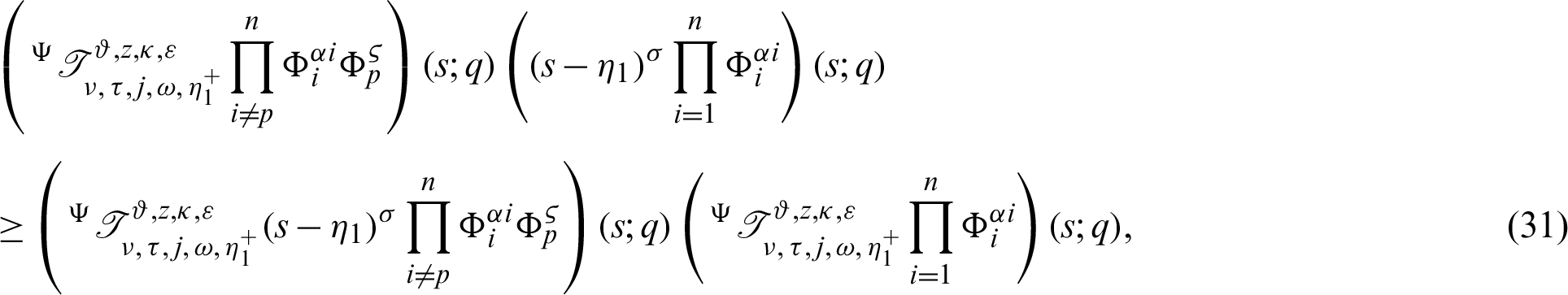
images

which gives the desired inequality (25).

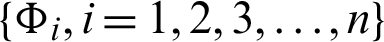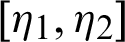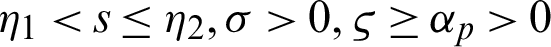Theorem 3.6. Let images be a sequence of continuous positive decreasing functions on images. Let images for any fixed 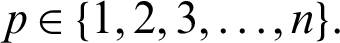images Suppose 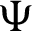images be a differentiable and strictly increasing. Then the more generalized fractional integral operator defined in (7), we have

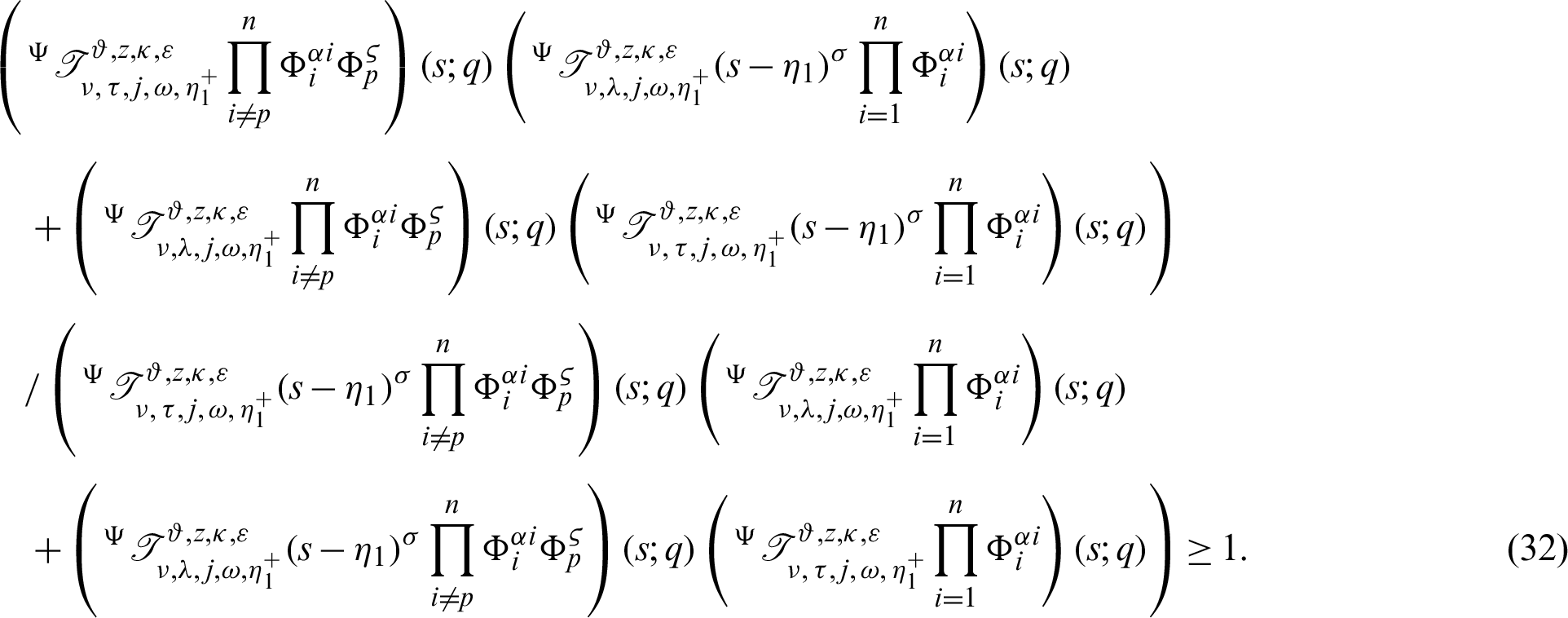
images

Proof. Taking product on both sides of (30) by

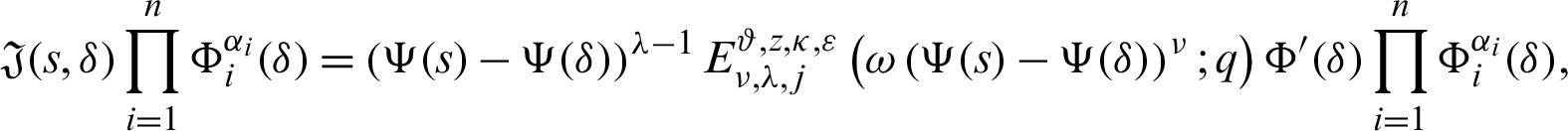
images

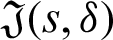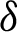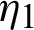for images where images is defined by (12) and integrating the subsequent identity w.r.t images from images to s, we have

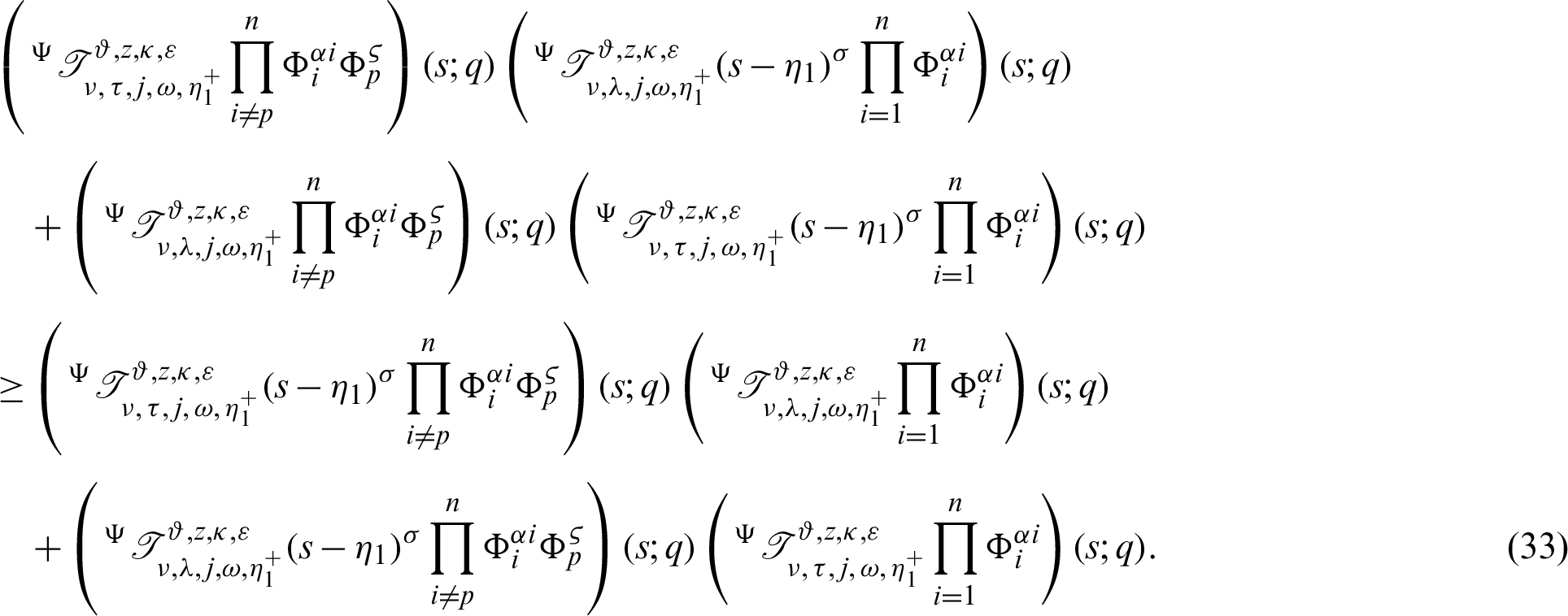
images

Dividing the above inequality by

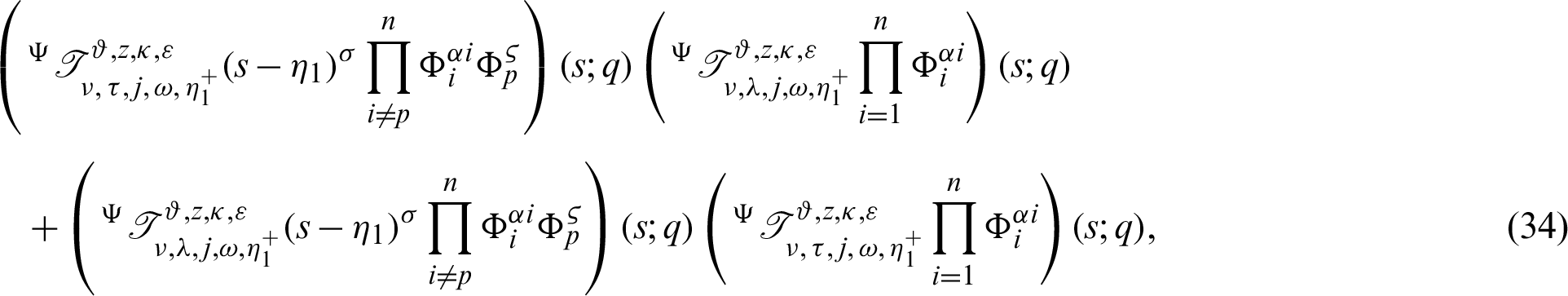
images

which gives the desired inequality (32).

Remark 3.5. Letting 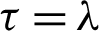images in inequality (32), then we attain the inequality (25).

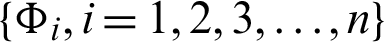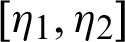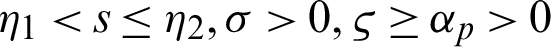Theorem 3.7. Let images be a continuous positive increasing functions and images be a sequence of continuous positive decreasing functions on images. Let images for any fixed 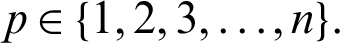images Suppose 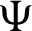images be a differentiable and strictly increasing. Then the more generalized fractional integral operator defined in (7), we have

images

Proof. Under the given hypothesis, we have

images

for any fixed images and images

From (41), we have

images

Taking product on both sides of (39) by

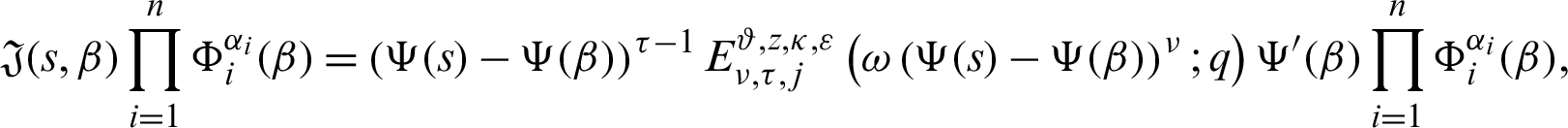
images

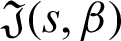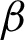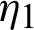for images, where images is defined by (12), and integrating the subsequent identity w.r.t images from images to s, we have

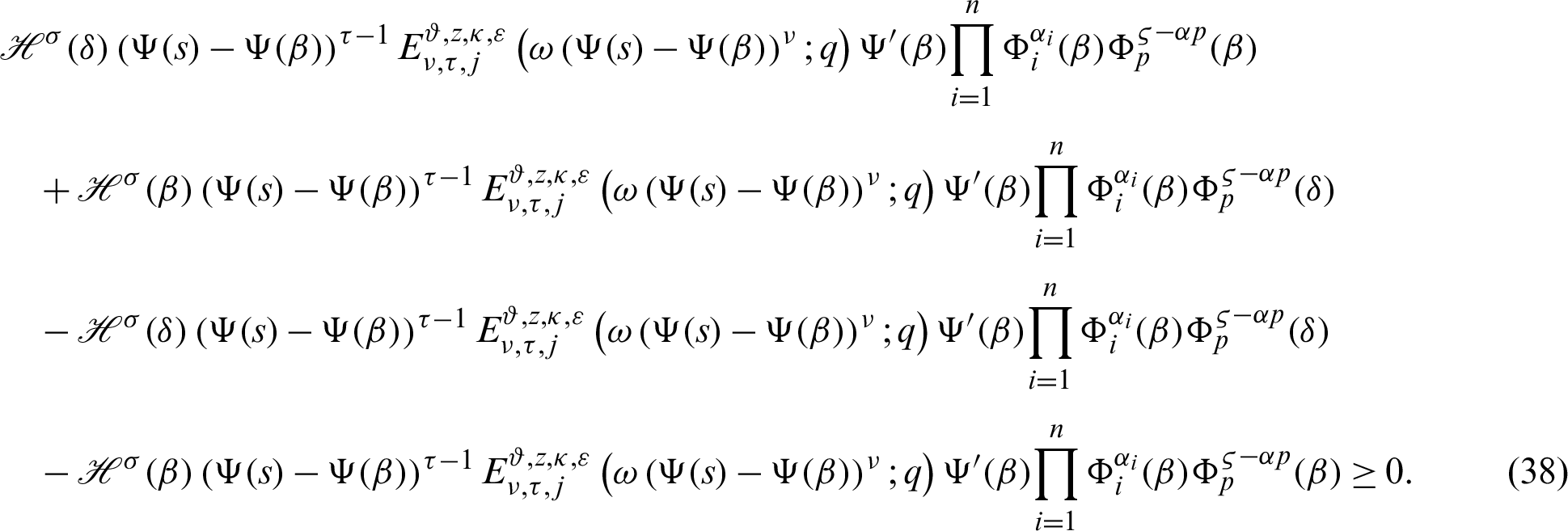
images

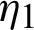Integrating (41) with respect to images from images to s, we have

images

From (39), it follows that

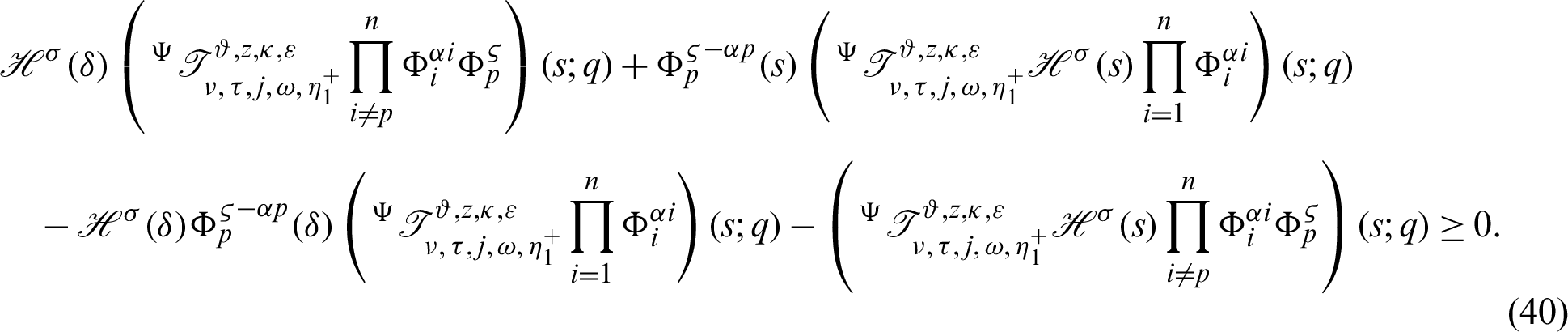
images

Again, taking product on both sides of (40) by

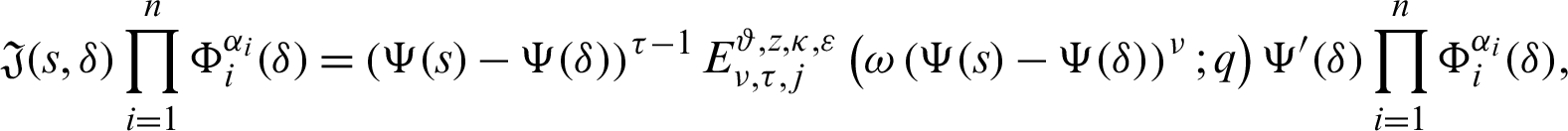
images

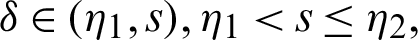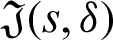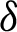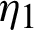for images where images is defined by (12), and integrating the subsequent identity w.r.t images from images to s, we have

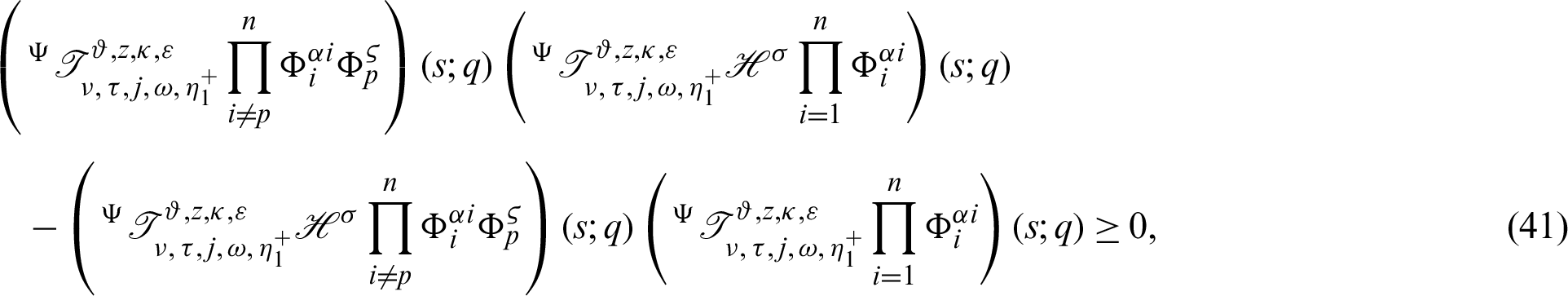
images

which establishes the desired inequality (35).

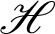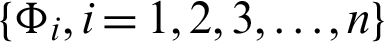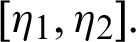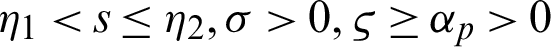Theorem 3.8. Let images be a continuous positive increasing functions and images be a sequence of continuous positive decreasing functions on images Let images for any fixed 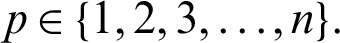images Then the more generalized fractional integral operator defined in (7), we have

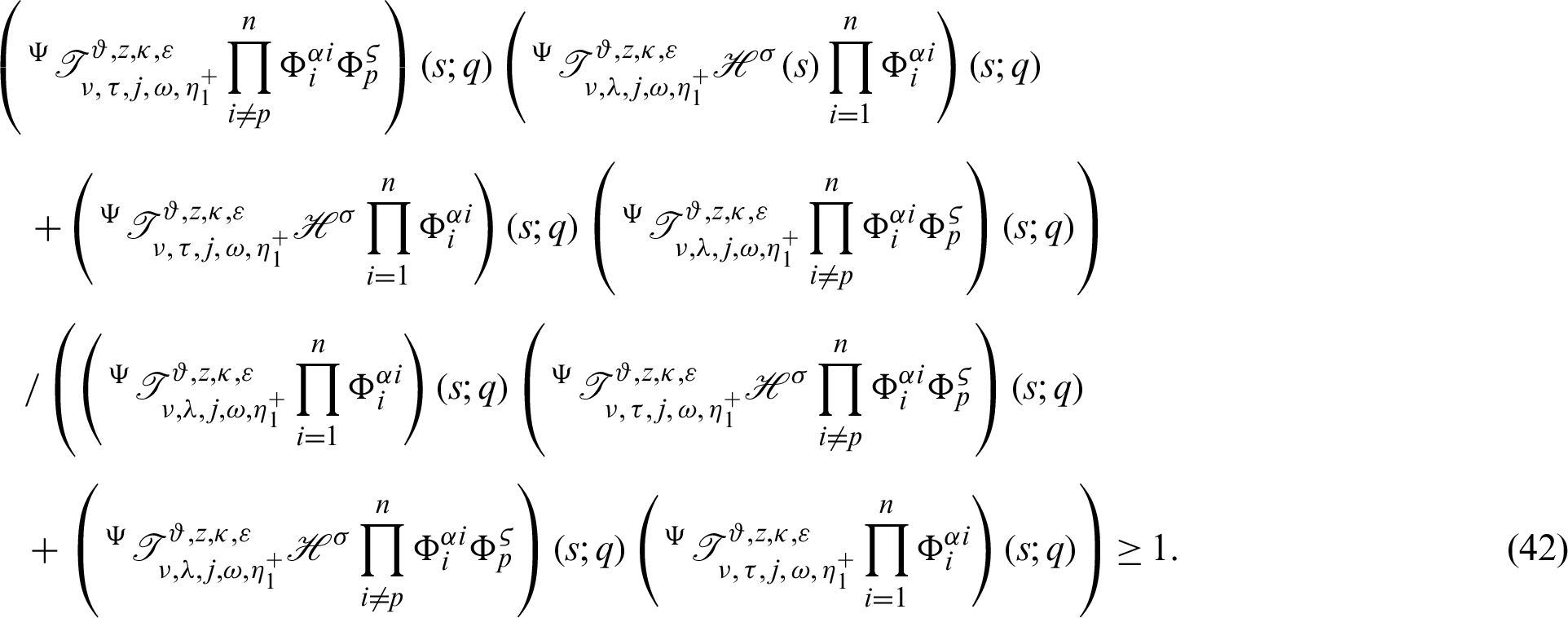
images

Proof. Taking product on both sides of (40) by

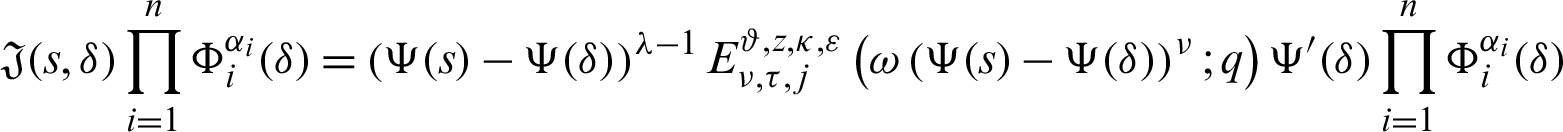
images

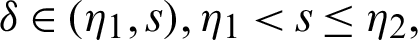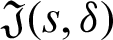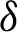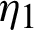for images where images is defined by (12) and integrating the subsequent identity w.r.t images from images to s, we have

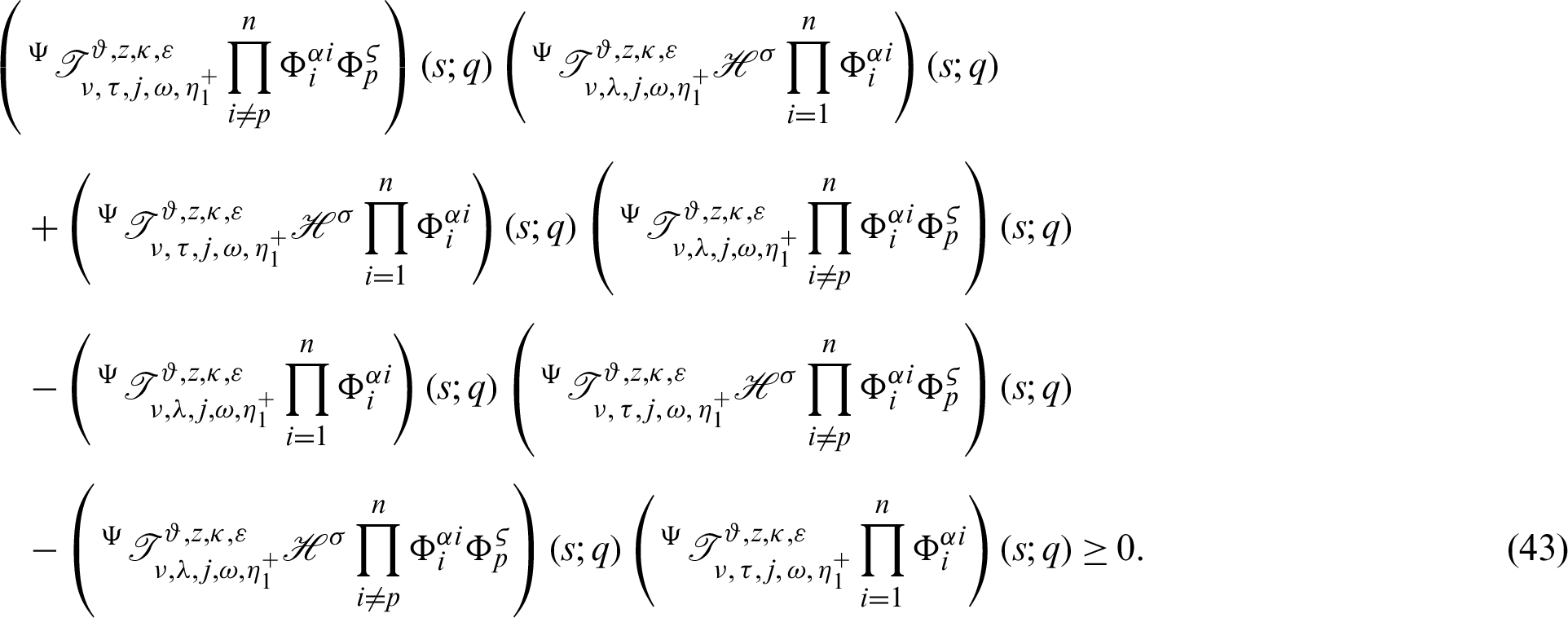
images

It follows that

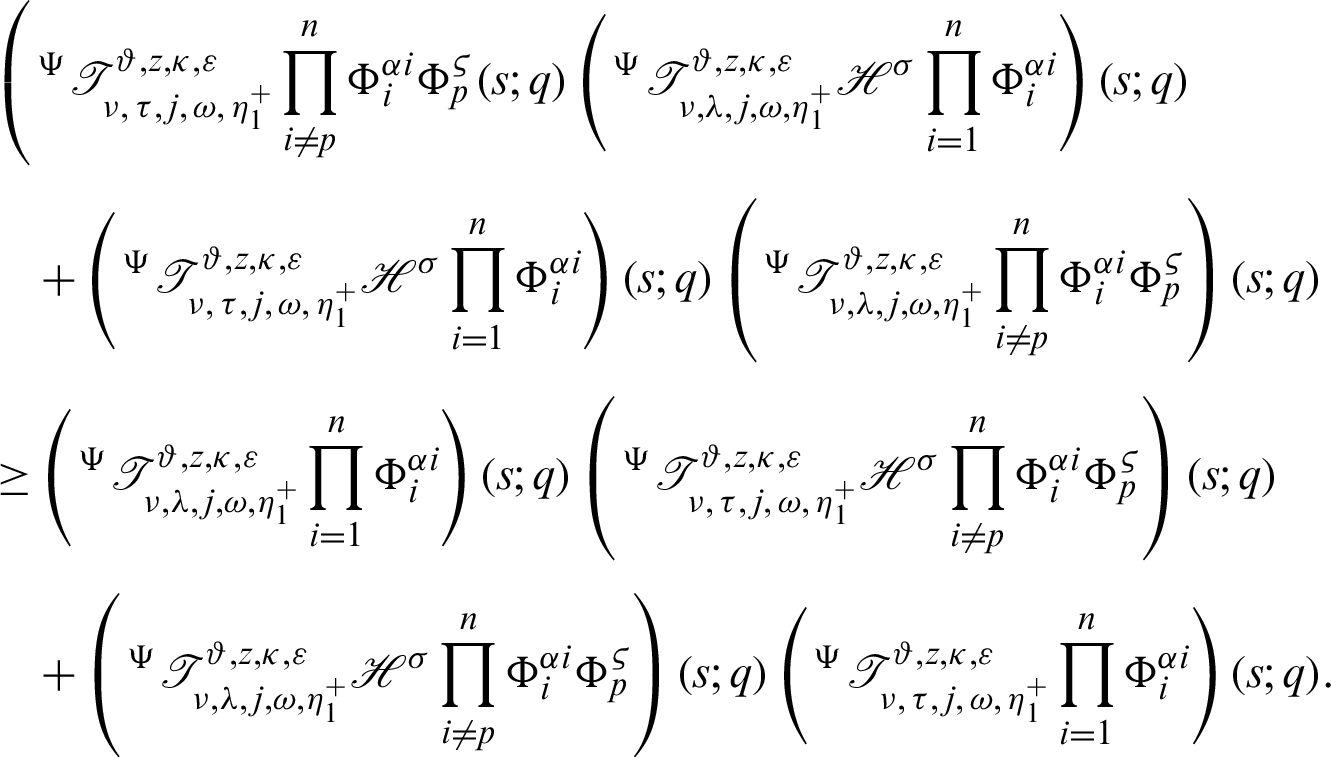
images

Dividing both sides by

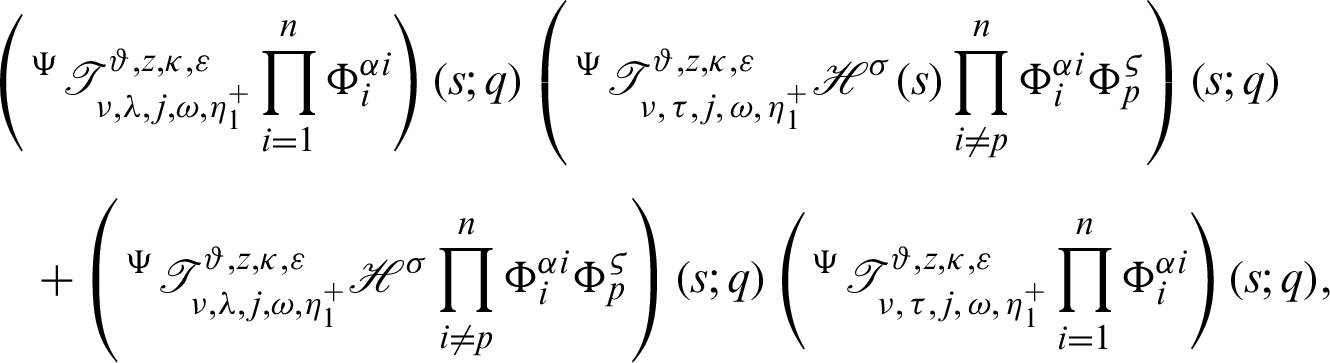
images

acquire the desired inequality (42).

Remark 3.6. Letting 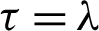images in inequality (42), then we attain the inequality (35).

4  Conclusion

A new concept of integration is introduced in this paper is known as the generalized fractional integral operator in the Hilfer sense having Mittag–Leffler function in the kernel. This new formulation admits as particular cases of the well-known fractional integrals, introduced by Andric et al. [39], Salim et al. [40], Rahman et al. [41], Srivastava et al. [42], Prabhakar [43] and RL-fractional integral operators. The new integration is combining of Mittag–Leffler function and fractional integration. New features are presented and some new theorems established for a class of n positive continuous and decreasing functions on the interval 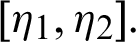images The derived consequences are the generalizations of the results presented in [45,46]. In addition to this, the established outcomes for the new fractional integral concedes as specific cases the notable fractional integrals of Hilfer, Hilfer–Hadamard, Riemann–Liouville, Hadamard, Weyl and Liouville. The newly introduced scheme will be used to solve a couple of equations at the Darcy scale describing flow in a dual medium, the solution of the non-linear problem without considering any discretization, perturbation or transformations. Finally, we can obtain the analytical solutions, using the method of successive approximations, to some fractional differential equations by the proposed study. This new scheme will be opening new doors of investigation toward fractional and fractal differentiations.

Availability of Supporting Data: No data were used to support this study.

Author Contributions: All authors read and approved the final manuscript.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant No. 61673169).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

  1. Abdeljawad, T. (2015). On conformable fractional calculus. Journal of Computational and Applied Mathematics, 279, 57-66. [Google Scholar] [CrossRef]
  2. Abdeljawad, T., & Baleanu, D. (2017). On fractional derivatives with exponential kernel and their discrete versions. Reports on Mathematical Physics, 80(1), 11-27. [Google Scholar] [CrossRef]
  3. Sene, N. (2020). SIR epidemic model with Mittag–Leffler fractional derivative. Chaos Solitons & Fractals, 137, 109833. [Google Scholar] [CrossRef]
  4. Sene, N., & Abdelmalek, K. (2019). Analysis of the fractional diffusion equations described by Atangana–Baleanu–Caputo fractional derivative. Chaos, Solitons & Fractals, 127, 158-164. [Google Scholar] [CrossRef]
  5. Sene, N. (2020). Fractional diffusion equation with new fractional operator. Alexandria Engineering Journal, 59, 2921-2926. [Google Scholar] [CrossRef]
  6. Panda, S. K., Abdeljawad, T., & Ravichandran, C. (2020). Novel fixed point approach to Atangana–Baleanu fractional and -Fredholm integral equations. Alexandria Engineering Journal, 59, 1959-1970. [Google Scholar]
  7. Panda, S. K., Abdeljawad, T., & Ravichandran, C. (2020). A complex valued approach to the solutions of Riemann–Liouville integral, Atangana–Baleanu integral operator and non-linear telegraph equation via fixed point method. Chaos Solitons & Fractals, 130, 109439. [Google Scholar] [CrossRef]
  8. Atangana, A. (2020). Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination?. Chaos, Solitons & Fractals, 136, 109860. [Google Scholar] [CrossRef]
  9. Almeida, R. (2017). A Caputo fractional derivative of a function with respect to another function. Communications in Nonlinear Science and Numerical Simulation, 44, 460-481. [Google Scholar] [CrossRef]
  10. Hilfer, R. (2000). Applications of Fractional Calculus in Physics. Singapore: World Scientific.
  11. Kilbas, A. A., Srivastava, H. M., Trujillo, J. J. (2006). Theory and applications of fractional differential equations, Amsterdam: Elsevier Science B.V.
  12. Rashid, S., Jarad, F., Noor, M. A., Kalsoom, H., & Chu, Y. M. (2020). Inequalities by means of generalized proportional fractional integral operators with respect to another function. Mathematics, 7(12), 1225. [Google Scholar] [CrossRef]
  13. Losada, J., & Nieto, J. J. (2015). Properties of a new fractional derivative without singular kernel. Progress in Fractional Differentiation and Applications, 1(2), 87-92. [Google Scholar]
  14. Magin, R. L. (2006). Fractional calculus in bioengineering. Redding: Begell House.
  15. Miller, K. S., Ross, B. (1993). An introduction to the fractional calculus and fractional differential equations. New York: John Wiley and Sons.
  16. Agarwal, P. (2017). Some inequalities involving Hadamard-type k-fractional integral operators. Mathematical Methods in the Applied Sciences, 40(11), 3882-3891. [Google Scholar]
  17. Rashid, S., Safdar, F., Akdemir, A. O., Noor, M. A., & Noor, K. I. (2019). Some new fractional integral inequalities for exponentially m-convex functions via extended generalized Mittag-Leffler function. Journal of Inequalities and Applications, 2019, 1-17. [Google Scholar] [CrossRef]
  18. Khan, H., Tunc, C., Alkhazan, A., Ameen, B., & Khan, A. (2018). A generalization of Minkowski’s inequality by Hahn integral operator. Journal of Taibah University for Science, 12(5), 506-513. [Google Scholar] [CrossRef]
  19. Set, E., Özdemir, M. E., & Demirbaş, S. (2020). Chebyshev type inequalities involving extended generalized fractional integral operators. AIMS Mathematics, 5(4), 3573-3583. [Google Scholar] [CrossRef]
  20. Rashid, S., Hammouch, Z., Kalsoom, H., Ashraf, R., & Chu, Y. M. (2020). New investigation on the generalized K-fractional integral operators. Frontier in Physics, 25(8), 563. [Google Scholar] [CrossRef]
  21. Rashid, S., Jarad, F., & Noor, M. A. (2020). Grüss-type integrals inequalities via generalized proportional fractional operators. RACSAM, 114(93), 165. [Google Scholar] [CrossRef]
  22. Rashid, S., Latif, M. A., Hammouch, Z., & Chu, Y. M. (2019). Fractional integral inequalities for strongly -preinvex functions for a kth order differentiable functions. Symmetry, 1448(11), 1-18. [Google Scholar] [CrossRef]
  23. JiLe, H. G., Rashid, S., Noor, M. A., Suhail, A., & Chu, Y. M. (2020). Some unified bounds for exponentially -convex functions governed by conformable fractional operators. AIMS Mathematics, 5(6), 6108-6123. [Google Scholar]
  24. Abdeljawad, T., Rashid, S., Khan, H., Chu, Y. M. (2020). On new fractional integral inequalities for p-convexity within interval-valued functions. Advances in Difference Equations.
  25. Abdeljawad, T., Rashid, S., Hammouch, Z., Chu, Y. M. (2020). Some new local fractional inequalities associated with generalized (s, m)-convex functions and applications. Advances in Difference Equations.
  26. Zhou, S. S., Rashid, S., & Jarad, F. (2020). New estimates considering the generalized proportional Hadamard fractional integral operators. Advances in Difference Equations, 2020, 1-15. [Google Scholar]
  27. Rashid, S., İşcan, İ., Baleanu, D., Chu, Y. M. (2020). Generation of new fractional inequalities via n-polynomials s-type convexity with applications. Advances in Difference Equations.
  28. Rashid, S., Jarad, F., Kalsoom, H., Chu, Y. M. (2020). On PólyaSzegö and Čebyšev type inequalities via generalized k-fractional integrals. Advances in Difference Equations.
  29. Rashid, S., Hammouch, Z., Ashraf, R., Nisar, K. S., Baleanu, D. (2020). New quantum estimates in the setting of fractional calculus theory. Advances in Difference Equations.
  30. Shen, J. M., Rashid , S., Noor, M. A., Ashraf, R., & Chu, Y. M. (2020). Certain novel estimates within fractional calculus theory on time scales. AIMS Mathematics, 5(6), 6073-6086. [Google Scholar] [CrossRef]
  31. Xu, L., Chu, Y. M., Rashid, S., Deeb, Al., & Nisar, K. S. (2020). On new unified bounds for a family of functions via fractional -calculus theory. Journal of Function Spaces, 4984612, 9. [Google Scholar]
  32. Rashid, S., Khalid, A., Rahman, G., Nisar, K. S., Chu, Y. M. (2020). On new modifications governed by quantum Hahn’s integral operator pertaining to fractional calculus. Journal of Function Spaces, 12.
  33. Chu, H. H., Rashid, S., Hammouch, Z., & Chu, Y. M. (2020). New fractional estimates for Hermite–Hadamard–Mercer’s type inequalities.. Alexandria Engineering Journal, 59, 3079-3089. [Google Scholar]
  34. Rashid, S., Noor, M. A., Nisar, K. S., & Baleanu, D. (2020). A new dynamic scheme via fractional operators on time scale. Frontiers in Physics, 8, 165. [Google Scholar] [CrossRef]
  35. Rashid, S., Jarad, F., & Chu, Y. M. (2020). A note on reverse Minkowski inequality via generalized proportional fractional integral operator with respect to another function. Mathematical Problems in Engineering, 2020, 1-12. [Google Scholar]
  36. Rashid, S., Ashraf, R., & Noor, M. A. (2020). New weighted generalizations for differentiable exponentially convex mapping with application. AIMS Mathematics, 5(4), 3525-3546. [Google Scholar] [CrossRef]
  37. Rashid, S., Noor, M. A., Noor, K. I., & Chu, Y. M. (2020). Ostrowski type inequalities in the sense of generalized K-fractional integral operator for exponentially convex functions. AIMS Mathematics, 5(3), 2629-2645. [Google Scholar] [CrossRef]
  38. Rashid, R., Noor, M. A., Noor, K. I., Safdar, F., & Chu, Y. (2019). Hermite-Hadamard type iInequalities for the class of convex functions on time scale. Mathematics, 7(10), 1-10. [Google Scholar]
  39. Andric, M., Farid, G., & Pecaric, J. (2018). A further extension of Mittag–Leffler function. Fractional Calculus and Applied Analysis, 21(5), 1377-1395. [Google Scholar] [CrossRef]
  40. Salim, T. O., & Faraj, A. W. (2012). A generalization of Mittag–Leffler function and integral operator associated with integral calculus. Journal of Fractional Calculus and Applications, 3(5), 1-13. [Google Scholar]
  41. Rahman, G., Baleanu, D., Qurashi, M. A., Purohit, S. D., Mubeen, S. et al. (2017). The extended Mittag–Leffler function via fractional calculus. Journal of Nonlinear Sciences and Applications, 10(8), 4244–4253. DOI 10.22436/jnsa.010.08.19. [CrossRef]
  42. Srivastava, H. M., & Tomovski, Z. (2009). Fractional calculus with an integral operator containing generalized Mittag–Leffler function in the kernal. Applied Mathematics and Computation, 211(1), 198-210. [Google Scholar]
  43. Prabhakar, T. R. (1971). A singular integral equation with a generalized Mittag–Leffler function in the kernel. Yokohama Mathematical Journal, 19, 7-15. [Google Scholar]
  44. Samko, G., Kilbas, A. A., Marichev, I. (1993). Fractional integrals and derivatives, theory and applications. Yverdon: Gordon and Breach.
  45. Liu, W. J., Ngo, Q. A., & Huy, V. N. (2009). Several interesting integral inequalities. Journal of Mathematical Inequalities, 3(2), 201-212. [Google Scholar] [CrossRef]
  46. Dahmani, Z. (2011). New classes of integral inequalities of fractional order. Le Matematiche, LXIX(2014), 237-247. [Google Scholar]
images This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.