| Computer Modeling in Engineering & Sciences | |
DOI: 10.32604/cmes.2021.012383
ARTICLE
Lemniscate of Leaf Function
Department of Mechanical Systems Engineering, Daido University, 10-3 Takiharu-cho, Minami-ku, Nagoya, 457-8530, Japan
*Corresponding Author: Kazunori Shinohara. Email: shinohara@06.alumni.u-tokyo.ac.jp
Received: 28 June 2020; Accepted: 14 September 2020
Abstract: A lemniscate is a curve defined by two foci, F1 and F2. If the distance between the focal points of F1 − F2 is 2a (a: constant), then any point P on the lemniscate curve satisfy the equation PF1.PF2 = a2. Jacob Bernoulli first described the lemniscate in 1694. The Fagnano discovered the double angle formula of the lemniscate (1718). The Euler extended the Fagnano’s formula to a more general addition theorem (1751). The lemniscate function was subsequently proposed by Gauss around the year 1800. These insights were summarized by Jacobi as the theory of elliptic functions. A leaf function is an extended lemniscate function. Some formulas of leaf functions have been presented in previous papers; these included the addition theorem of this function and its application to nonlinear equations. In this paper, the geometrical properties of leaf functions at n = 2 and the geometric relation between the angle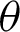 
and lemniscate arc length l are presented using the lemniscate curve. The relationship between the leaf functions sleaf2 (l) and cleaf2 (l) is derived using the geometrical properties of the lemniscate, similarity of triangles, and the Pythagorean theorem. In the literature, the relation equation for sleaf2 (l) and cleaf2 (l) (or the lemniscate functions, sl (l) and cl (l)) has been derived analytically; however, it is not derived geometrically.
Keywords: Geometry; lemniscate of Bernoulli; leaf functions; lemniscate functions; Pythagorean theorem; triangle similarity
An ordinary differential equation (ODE) comprises a function raised to the 2n −1 power and the second derivative of this function. Further, the initial conditions of the ODE are defined.
Another ODE and its initial conditions are given below:
The ODE comprises a function r(l)(or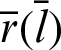 
) of one independent variable l(or 
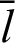) and the derivatives of this function. The variable n represents a natural number (
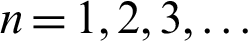). The above equation and the initial conditions constitute a very simple ODE. However, when this differential equation is numerically analyzed, mysterious waves are generated for all natural numbers. These mysterious waves are regular waves with some periodicity and amplitude. If these waves can be explained, they have the potential to solve various problems of nonlinear ODEs.
No elementary functions satisfy Eqs. (1)–(3). Therefore, in this paper, the function that satisfies Eqs. (1)–(3) is defined as cleafn(l). Function r(l) is abbreviated as r. By multiplying the derivative dr/dl with respect to Eq. (1), the following equation is obtained.
The following equation is obtained by integrating both sides of Eq. (7).
Using the initial conditions in Eqs. (2) and (3), the constant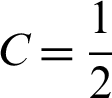 
is determined. The following equation is obtained by solving the derivative dr/dl in Eq. (8).
We can create a graph with the horizontal axis as the variable l and the vertical axis as the function r. Because function r is a wave with a period, the gradient dr/dl has positive and negative values, and it depends on domain l. In the domain,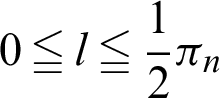 
(See Appendix A for the constant 
), the above gradient dr/dl becomes negative.
The following equation is obtained by integrating the above equation from 1 to r.
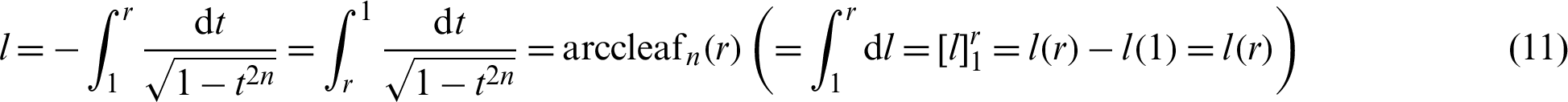
For integrating the left side of the above equation, the initial condition (Eq. (2), (l, r) = (0, 1)) is applied. The above equation represents the inverse function of the leaf function: cleafn(t) [1]. Therefore, the above equation is described as
Similarly, the function that satisfies Eqs. (4)–(6) is defined as sleaf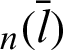
. In the domain, 
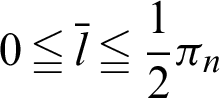(See Appendix A for constant 
), the gradient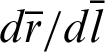 
becomes positive.
The following equation is obtained by integrating the above equation from 0 to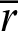 
.
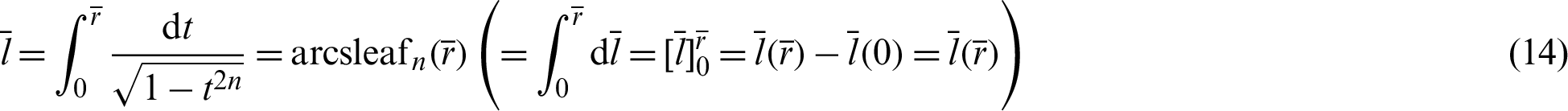
For integrating the left side of the above equation, the initial condition (Eq. (5), (l, r) = (0, 0)) is applied. The above equation represents the inverse function of the leaf function: sleaf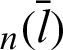
[2]. Therefore, the above equation is described as
Inverse leaf functions based on the basis n = 1 represent inverse trigonometric functions.
In 1796, Carl Friedrich Gauss presented the lemniscate function [3]. The inverse leaf functions based on the basis n = 2 represents inverse functions of the sin and cos lemniscates [4].
In 1827, Jacobi [5] presented the Jacobi elliptic functions. Compared to Eq. (18), the term t2 is added to the root of the integrand denominator.
Eq. (20) represents the inverse Jacobi elliptic function sn, where k is a constant; there are 12 Jacobi elliptic functions, including cn and dn, etc. In Eq. (20), variable t is raised to the fourth power in the denominator. Jacobi did not discuss variable t raised to higher powers as indicated below.
Thus, historically, the inverse functions have not been discussed in the case of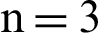 
or higher [6–14].
A lemniscate is a curve defined by two foci F1 and F2. If the distance between the focal points of F1 − F2 is 2a (a: constant), then any point P on the lemniscate curve satisfies the equation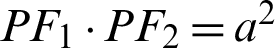 
. Jacob Bernoulli first described the lemniscate in 1694 [15,16]. Based on the lemniscate curve, its arc length can be bisected and trisected using a classical ruler and compass [17]. Based on this lemniscate, a lemniscate function was proposed by Gauss around the year 1800 [3,18]. Nishimura proposed a relationship between the product formula for the lemniscate function and Carson’s algorithm; it is known as the variant of the arithmetic–geometric mean of Gauss [19,20]. The Wilker and Huygens-type inequalities have been obtained for Gauss lemniscate functions [21]. Deng et al. [22] established some Shafer–Fink type inequalities for the Gauss lemniscate function. The geometrical characteristics of the lemniscate have been described [23,24]. Mendiratta et al. [25] investigated the geometric properties of functions. Levin [26] developed analogs of sine and cosine for the curve to prove the formula. Langer et al. [27] presented the lemniscate octahedral groups of projective symmetries. As a kinematic control problem, a five body choreography on an algebraic lemniscate was shown as the potential problem for two values of elliptic moduli [28]. The trajectory generation algorithm was applied by using the shape of the Bernoulli lemmiscate [29].
Leaf functions are extended lemniscate functions. Various formulas for leaf functions such as the addition theorem of the leaf functions and its application to nonlinear equations have been presented [30–32].
In this paper, the geometrical properties of leaf functions for n = 2, and the geometric relationship between the angle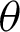 
and lemniscate arc length l are presented using the lemniscate curve. The relations between leaf functions 
and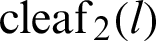 
are derived using the geometrical properties of the lemniscate curve, similarity of triangles, and the Pythagorean theorem. In the literature, the relationship equation of 
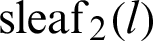and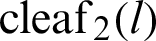 
is analytically derived; however, it is yet to be derived geometrically [33]. The relation between 
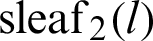and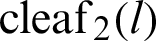 
can be expressed as
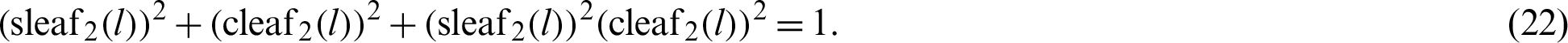
The Eq. (22) was analytically derived. However, it cannot be geometrically derived using the lemniscate curve because it is not possible to show the geometric relationship of the lemniscate functions sl (l) and cl (l) on a single lemniscate curve. In contrast, phase l of the lemniscate function and angle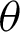 
can be visualized geometrically on a single lemniscate curve. Therefore, in the literature, Eq. (22) is derived using an analytical method without requiring the geometric relationship.
In this paper, the angle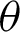 
, phase l, and leaf functions 
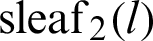and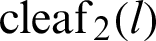 
(or lemniscate functions sl(l) and cl(l)) are visualized geometrically on a single lemniscate curve. Eq. (22) is derived based on the geometrical interpretation, similarity of triangles, and Pythagorean theorem.
2 Geometric Relationship with the Leaf Function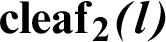 
Fig. 1 shows the geometric relationship between the lemniscate curve and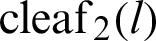 
. The y and x axes represent the vertical and horizontal axes, respectively. The equation of the curve is
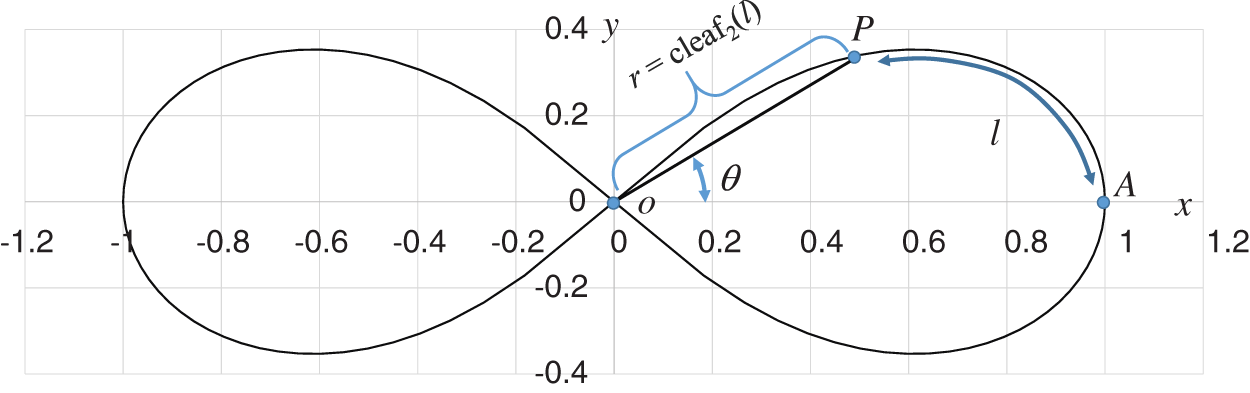
Figure 1: Geometric relationship between angle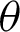 
and phase l of the leaf function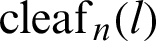 
If P is an arbitrary point on the lemniscate curve, then the following geometric relation exists.
When point P is circled along the contour of one leaf, the contour length corresponds to the half cycle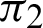 
(See Appendix A for the definition of the constant 
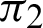). As shown in Fig. 1, with respect to an arbitrary phase l, angle 
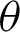must satisfy the following inequality.
Here, k is an integer.
3 Geometric Relationship between the Trigonometric Function and Leaf Function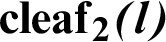 
Fig. 2 shows the foci F and F
of the lemniscate curve. The length of a straight line connecting an arbitrary point 
and one focal point 
is denoted by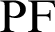 
. Similarly, 
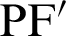denotes the length of the line connecting an arbitrary point 
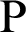and a second focal point 
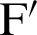. On the curve, the product of 
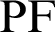and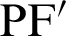 
is constant. The relationship equation is described as [34]
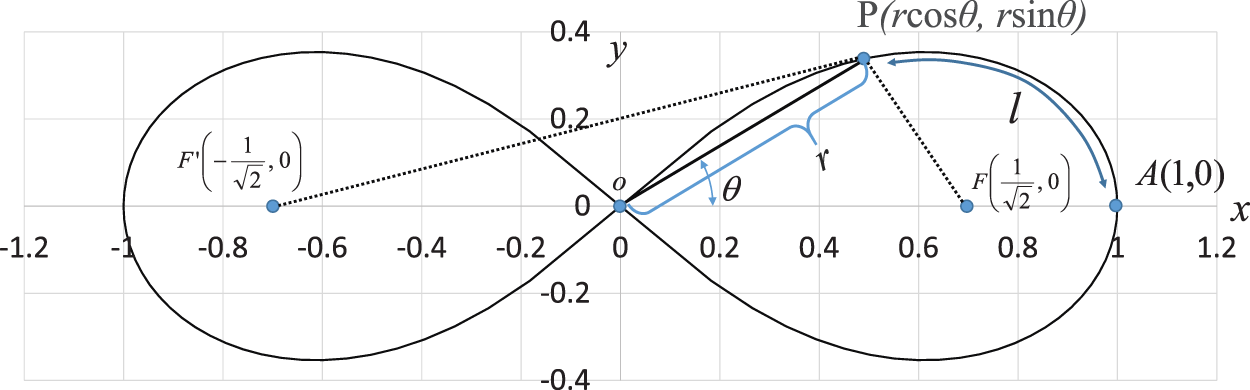
Figure 2: Lemniscate focus
The coordinates of point P are
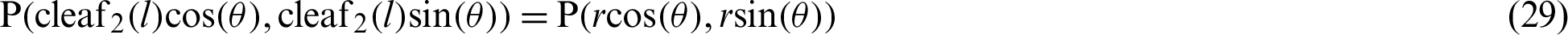
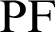and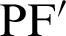 
are given by
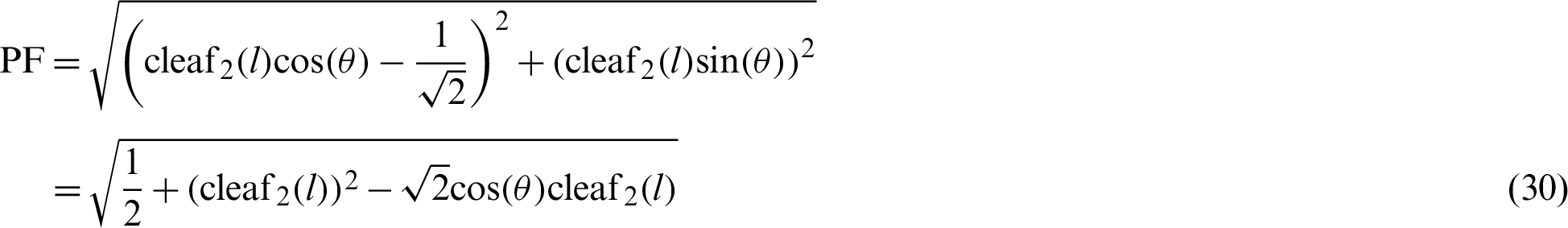
and
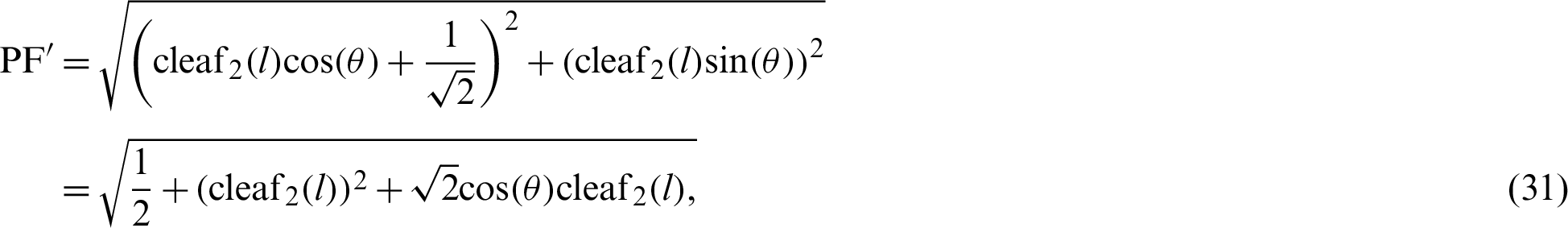
respectively.
By substituting Eqs. (30) and (31) into Eq. (28), the relationship equation between the leaf function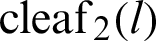 
and trigonometric function 
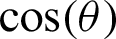can be derived as
After differentiating Eq. (32) with respect to l,
The following equation is obtained by combining Eqs. (32) and (33).
The differential equation can be integrated using variable l. Parameter t in the integrand is introduced to distinguish it from l. The integration of Eq. (34) in the region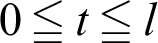 
yields the following equation (See Appendix C for details).
Therefore, the following equation holds.
Eq. (32) can only be described by variable l as
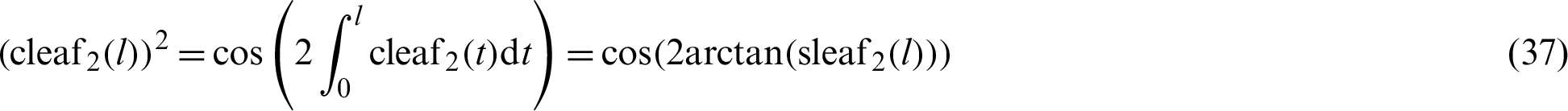
The phase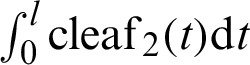 
of the cos function is plotted in Fig. 3 through numerical analysis. The horizontal and vertical axes represent variables l and 
, respectively. As shown in Fig. 3, angle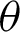 
satisfies the inequality
Figure 3: Curves of leaf functions (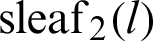
and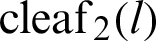 
) and the integrated leaf functions (
and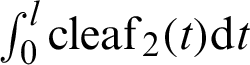 
)
Eq. (38) satisfies the inequality of Eq. (27) under the condition k = 0.
Fig. 4 shows the geometric relationship between functions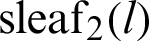 
and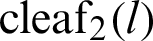 
. The geometric relation in Eq. (36) is illustrated in Fig. 4.
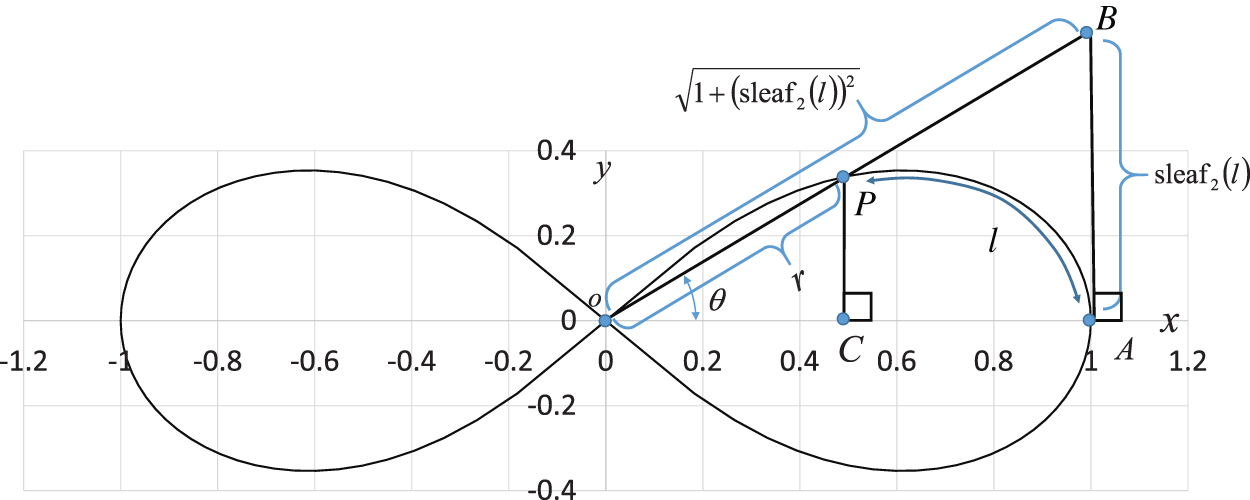
Figure 4: Geometric relationship between leaf functions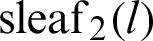 
and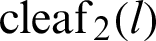 
Draw a perpendicular line from the point P on the lemniscate to the x-axis. This perpendicular is parallel to the y-axis. Let C be the intersection of this perpendicular and the x-axis. Therefore, the angle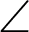 
OCP is 90
. Next, draw a line perpendicular to the x-axis from the intersection A(1,0) of the lemniscate and the x-axis. Let B be the intersection of this perpendicular and the extension of the straight line OP. Here,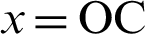 
and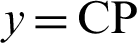 
. Substituting these into Eq. (23) gives
and
P and B are moving points, and point A is fixed. When angle 
is zero, both P and B are at A. The geometric relationship is then expressed as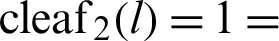 
OA and sleaf2(l) = 0 = AB. As 
increases, P moves away from A, and it moves along the lemniscate curve. Here, phase l of cleaf2(l) and sleaf2(l) corresponds to the length of the arc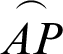 
. The length of the straight line OP is equal to the value of cleaf2(l). Point B is the intersection point of the straight lines OP and x = 1. In other words, P is the intersection point of the straight line OB and lemniscate curve. As 
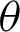increases, B moves away from A and onto the straight line x = 1. That is, it moves in the direction perpendicular to the x axis. The length of straight line AB is equal to the value of sleaf2(l). When 
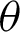reaches 
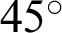, P moves to origin O and 
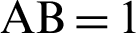. The length of arc 
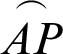(or phase l) is 
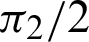. Moreover, cleaf2(l) = 0 = OP and sleaf2(l) = 1 = AB.
The relationship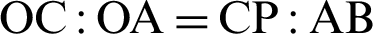 
is derived by the similarity of triangles 
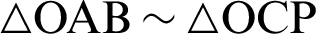, as shown in Fig. 4. Thus, the following equation holds.
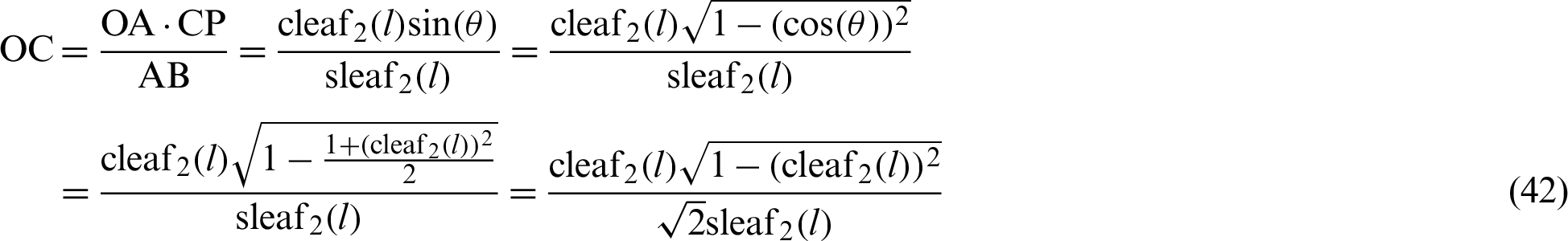
Eq. (32) is applied in the transformation process. Similarly, the relationship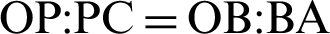 
is derived by the similarity of triangles 
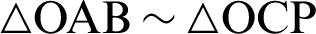, as shown in Fig. 4. Therefore, the following equation holds.
By substituting Eqs. (42) and (43) into Eq. (39), the following equation is obtained.
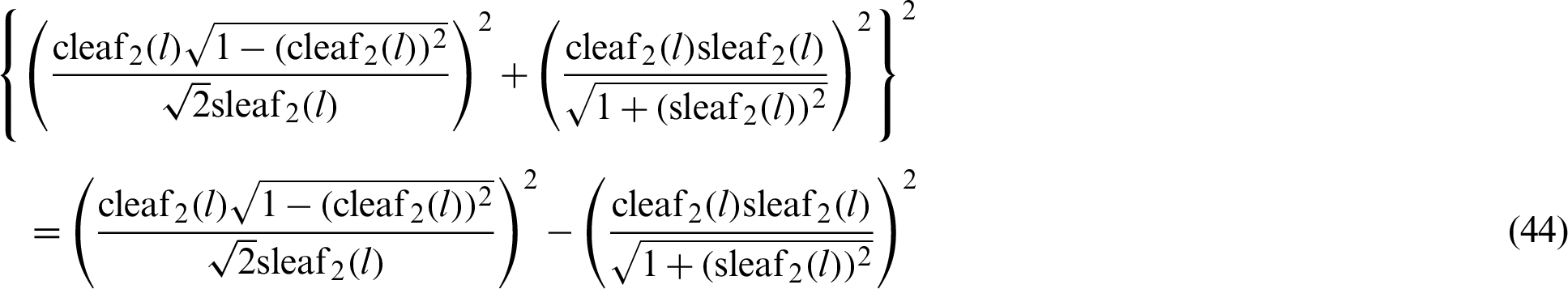
By rearranging Eq. (44), the following equation is obtained.
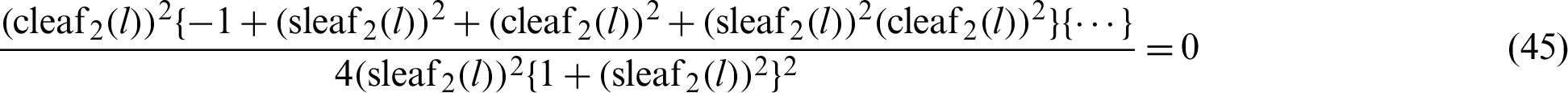
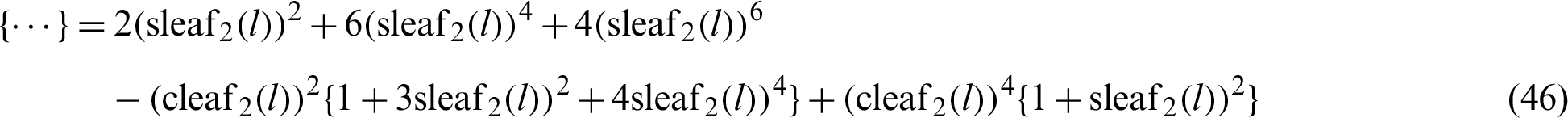
For arbitrary l,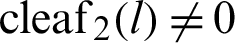 
and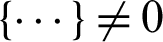 
. The relationship between 
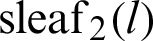and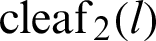 
can then be obtained as Eq. (22).
4 Geometric Relationship of the Leaf Function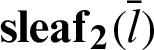 
Fig. 5 shows the geometric relationship between length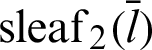 
and lemniscate curve inclined at 
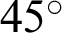. In Fig. 5, the y and x axes represent the vertical and horizontal axes, respectively. The equation of this curve is given as
Figure 5: Geometric relationship between angle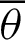 
and phase 
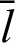of leaf function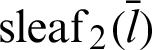 
If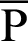 
is an arbitrary point on the lemniscate curve, the following geometric relation exists.
(See Appendix D)
In Fig. 5, for an arbitrary variable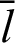 
, the range of angle 
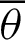is given by
Here, k is an integer.
5 Geometric Relationship between Trigonometric Function and Leaf Function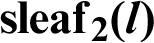 
Fig. 6 shows foci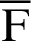 
and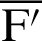 
of the lemniscate curve inclined at an angle of 
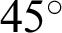. This curve has the same relation equation as shown in Fig. 2.
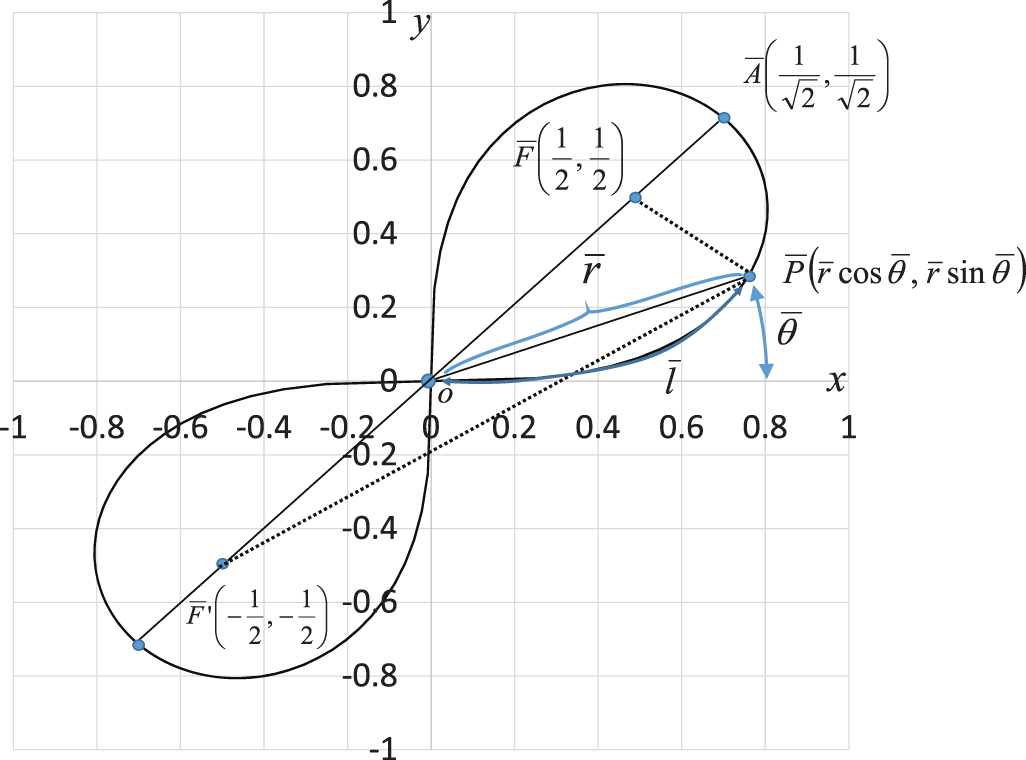
Figure 6: Lemniscate curve inclined at 
The coordinates of point 
on the lemniscate curve inclined at an angle of 
are given as
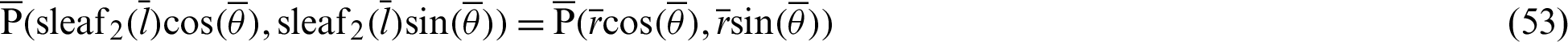
Lengths 
and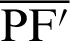 
are expressed by
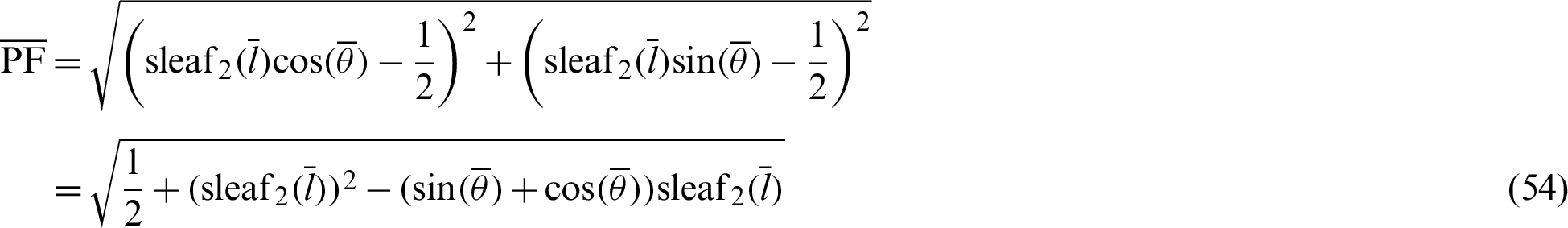
and
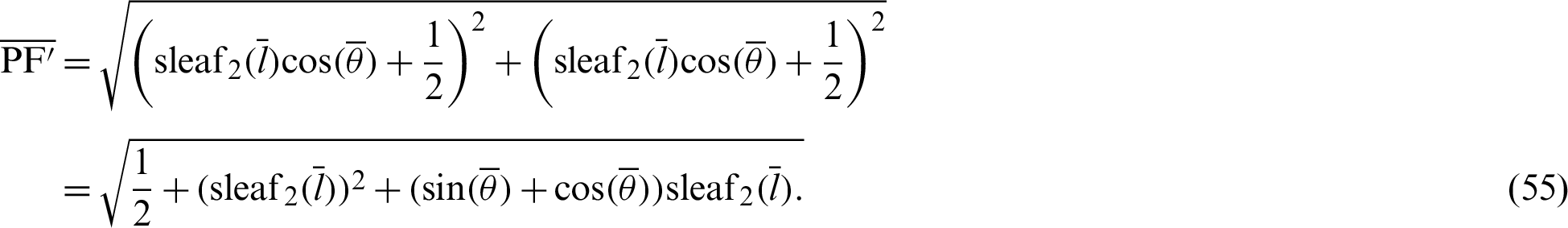
By substituting Eqs. (54) and (55) into Eq. (52), the relationship equation between the leaf function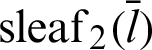 
and the trigonometric function 
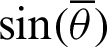can be derived as
The following equation is obtained by differentiating Eq. (56) with respect to the variable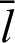 
.
After applying Eq. (56), the equation is transformed as
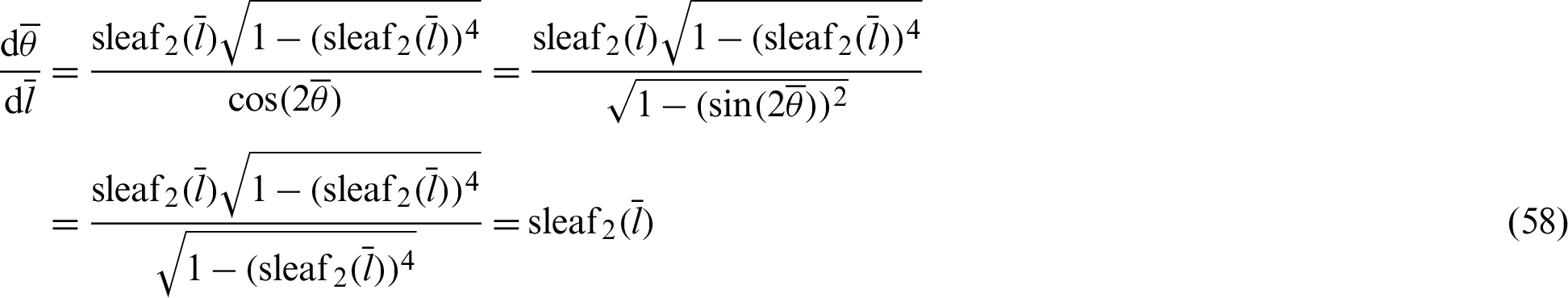
The differential equation is integrated by variable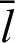 
. Parameter t is introduced to distinguish the parameter from variable 
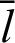in the integration region. The integration of Eq. (58) in region 
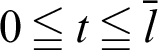(See Appendix C) yields
and the following equation holds.
Using Eq. (59), Eq. (56) can be described by variable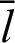 
as
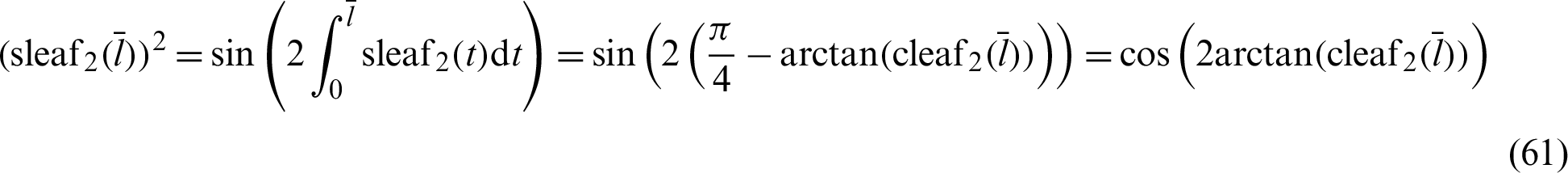
The curve of phase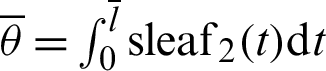 
is plotted in Fig. 3 through numerical analysis. The horizontal and vertical axes represent variables 
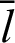and 
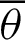, respectively. As shown in Fig. 3, angle 
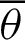satisfies the following range.
Eq. (62) satisfies the range of Eq. (51) under the condition k = 0. Fig. 7 shows the lemniscate curve inclined at 
. The geometric relation of Eq. (60) is added to Fig. 7.
Figure 7: Geometric relationship based on the lemniscate curve inclined at 
Let 
be the coordinates on line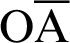 
, as shown in Fig. 7. Points 
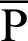and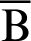 
are moving points, and point 
is fixed. When angle 
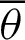is zero, 
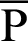is at origin O, and 
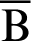is on the x-axis at 
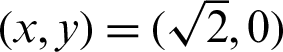. The geometric relationship is described as 
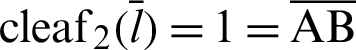and sleaf
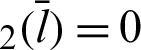. As 
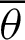increases, 
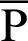moves away from origin O and along the lemniscate curve. The phase 
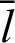of both cleaf
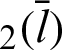and sleaf
corresponds to the length of arc 
. The length of the straight line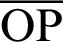 
is equal to the value of sleaf
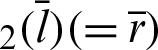. Point 
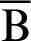is the intersection point of straight lines 
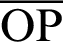and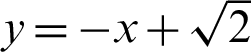 
. In other words, 
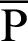is the intersection point of the straight line 
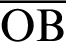and the lemniscate curve. As 
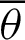increases, 
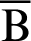moves away from point 
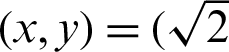,0) on a straight line 
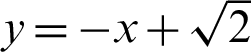. Here, the length of the straight line 
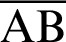is equal to the value of cleaf
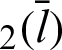. When 
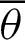reaches 
, 
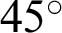moves to point 
. The length of arc 
(or phase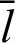 
) becomes 
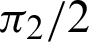. Furthermore, cleaf
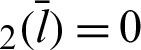and sleaf
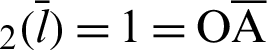. The linear equation 
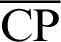is given by
By substituting Eq. (65) into Eq. (47) and solving for variable x, four solutions can be obtained as
As Eqs. (66) and (67) include imaginary numbers, the solutions for x using both Eqs. (68) and (69) are determined by the intersection points of line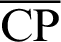 
and the lemniscate curve, as shown in Fig. 7. The larger x value is given by Eq. (69). That is, the coordinates of point 
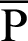can be expressed as
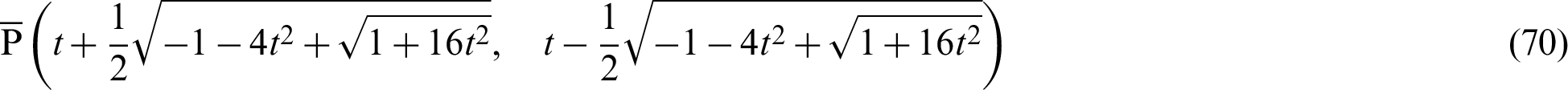
Therefore, the length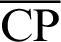 
is expressed as
The following equation is obtained from the Pythagorean theorem of the triangle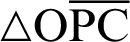 
.
Substitution of Eqs. (48) and (71) into Eq. (72) yields
The length ratio is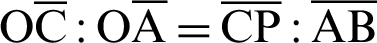 
owing to the similarity of triangles 
.
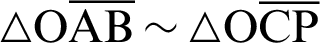The elimination of variable t from Eqs. (73) and (74) yields the relation equation, Eq. (22).
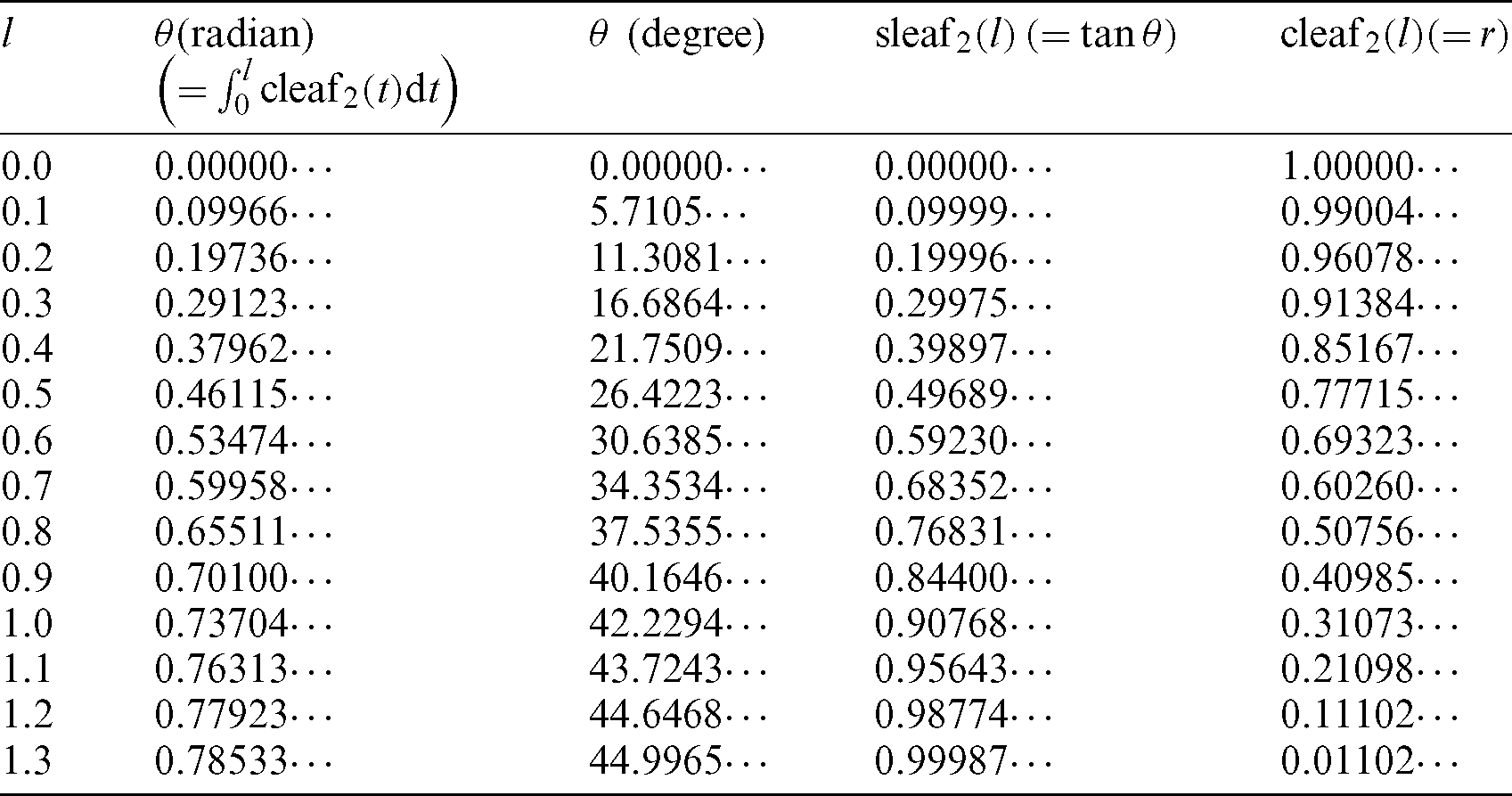
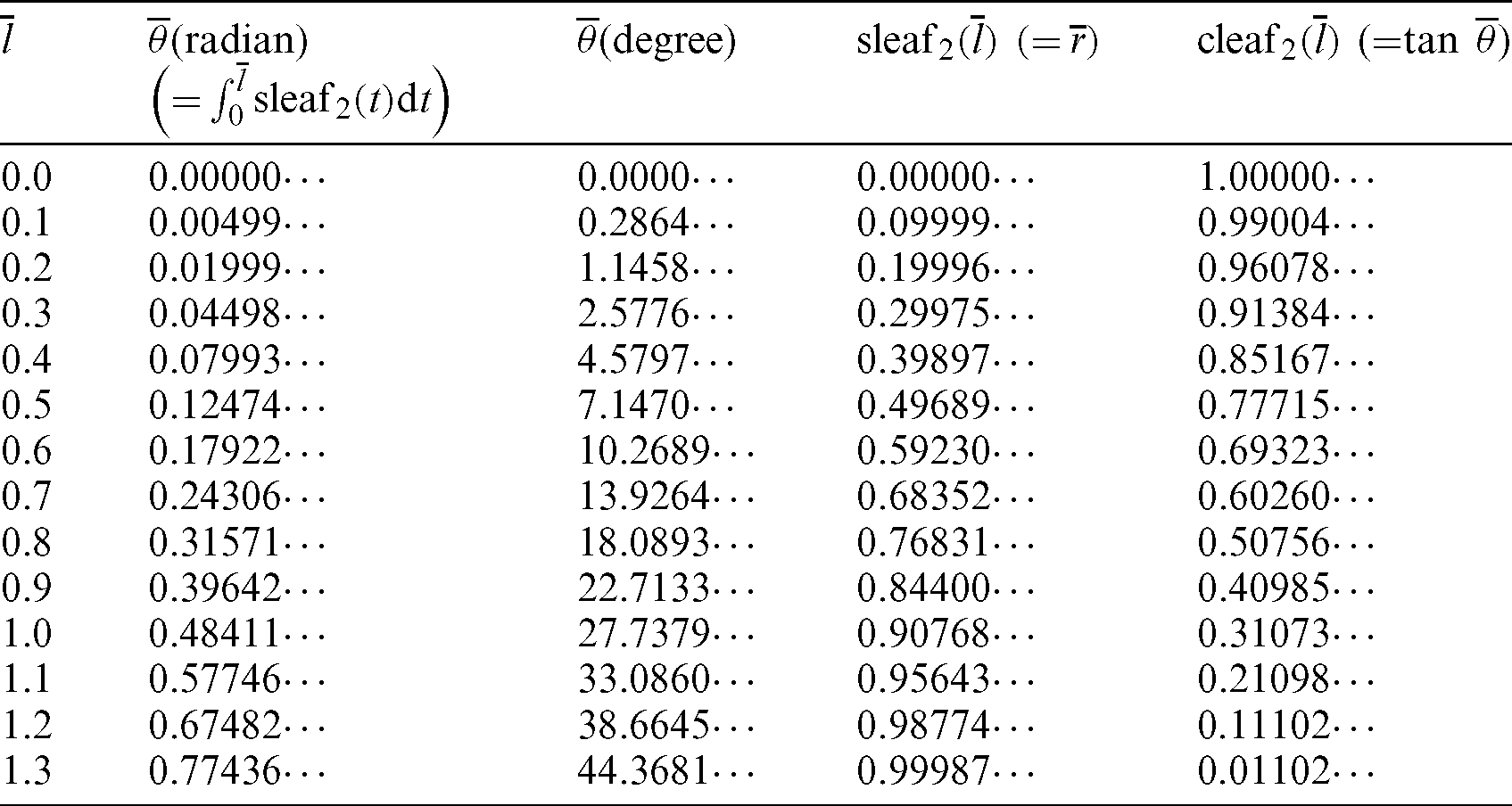
Tab. 1 lists the numerical values for Fig. 4. The angle 
and values of the leaf function (sleaf2(l) and cleaf2(l)) are calculated along the arc length l. The values of leaf functions cleaf2(l) are calculated by Eqs. (1)–(3). The values of leaf functions sleaf2(l) are calculated by Eqs. (4)–(6). Based on these data, the numerical data of functions sleaf2(l) and cleaf2(l) can be confirmed using Eq. (22). The function cleaf2(l) (= r) can also be confirmed by using Eq. (82). Angle 
can be calculated by using Eq. (35).
Table 1: Numerical data of arc length l, angle 
, and leaf functions sleaf2(l) and cleaf2(l) for Fig. 4
Tab. 2 shows the numerical values for Fig. 7. The angle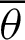 
and the values of leaf function (sleaf
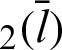and cleaf
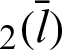) are calculated along the arc length 
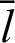. Based on these data, the function sleaf
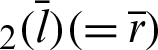can also be confirmed using Eq. (90). The angle 
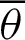can be calculated using Eq. (59).
Table 2: Numerical data of arc length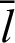 
, angle 
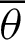, and leaf functions sleaf
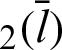and cleaf
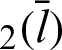for Fig. 7
Based on the geometric properties of the lemniscate curve, the geometric relationship among angle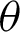 
, lemniscate length l, and leaf functions 
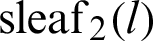and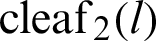 
were shown on the lemniscate curve. Using the similarity of triangles and the Pythagorean theorem, the relationship equation of leaf functions 
and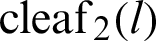 
was derived.
Acknowledgement: The author gratefully acknowledges the helpful comments and suggestions of the reviewers that have improved the presentation of this paper.
Funding Statement: This research is supported by Daido University research Grants (2020).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
Appendix A
The symbols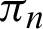 
are a constant given by
The numerical data of the symbol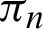 
are summarized in the Tab. 3.
Appendix B
The Eq. (23) of Cartesian coordinate system is transformed to the following equation of polar coordinates [1,3].
The variable r and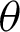 
represents OP and 
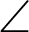AOP in Fig. 1. The arc length in the cartesian and polar coordinates is given by
The arc length l of the lemniscate with polar coordinates is given by
By differentiating Eq. (76) with respect to variable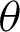 
,
Then, by applying Eq. (79),
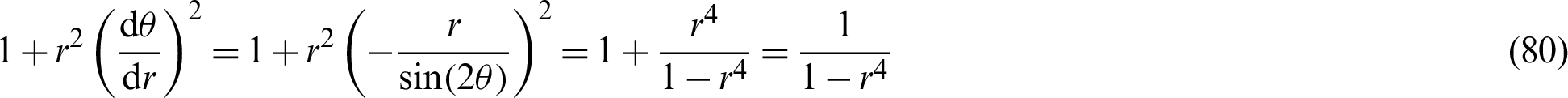
The following equation is applied to Eq. (80).
Hence, the arc length l becomes
Appendix C
The following function is differentiated.
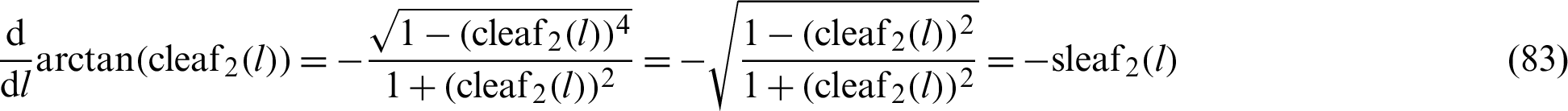
Integration of the above mentioned equation with respect to l yields
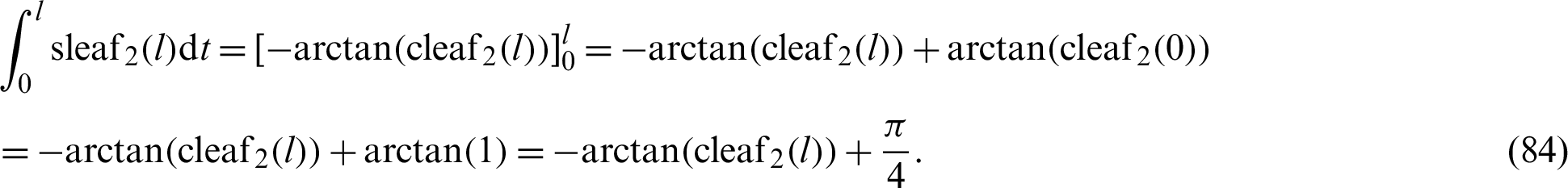
Similarly, the following function is differentiated with respect to variable l.
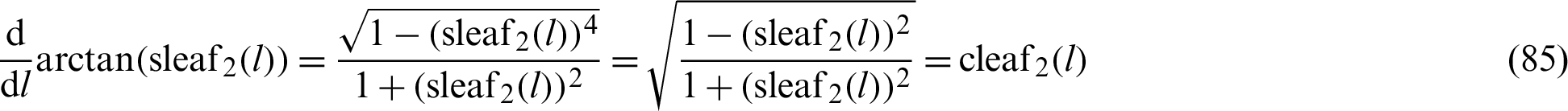
The following equation is obtained by integrating Eq. (85) with respect to l.
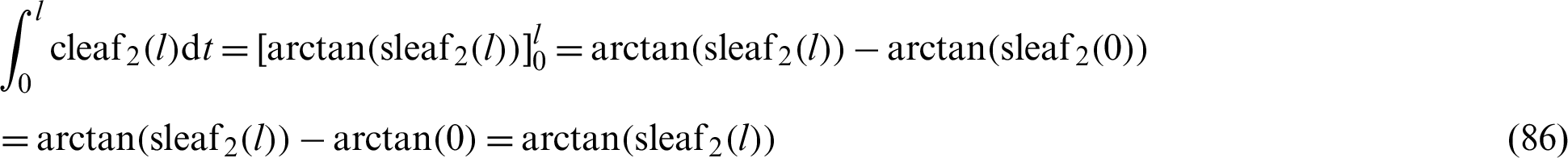
Appendix D
Eq. (47) of the Cartesian coordinate system is transformed to the following equation in the polar coordinates [2,35].
By differentiating Eq. (87) with respect to the variable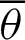 
,
Then, applying Eq. (88),
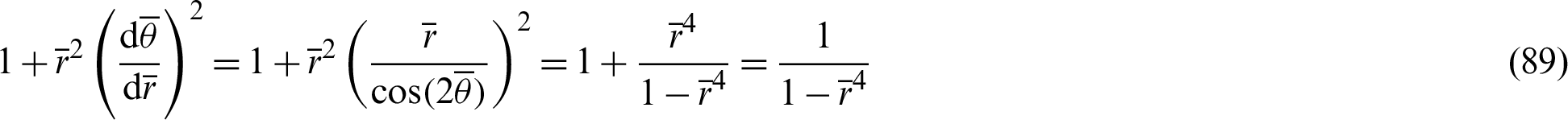
Hence, the arc length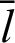 
becomes
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |