Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.013368

ARTICLE

Multiple Response Optimization of Dimensional Accuracy of Nimonic Alloy Miniature Gear Machined on Wire Edm Using Entropy Topsis Andpareto Anova

Tina Chaudhary1,*, Arshad Noor Siddiquee2, Arindam Kumar Chanda3, Shafi Ahmad2, Irfan Anjum Badruddin4,* and Zahid A. Khan2

1Department of Mechanical and Automation Engineering, Indira Gandhi Delhi Technical University for Women, Kashmere Gate, 110006, India
2Department of Mechanical Engineering, Jamia Millia Islamia (A Central University), New Delhi, 110025, India
3Department of Mechanical and Automation Engineering, G.B. Pant Engineering College, New Delhi, 110020, India
4Mechanical Engineering Department, College of Engineering, King Khalid University, Abha-61421, Asir, Saudi Arabia
*Corresponding Authors: Tina Chaudhary. Email: tina.mech.auto@gmail.com; Irfan Anjum Badruddin. Email: magami.irfan@gmail.com
Received: 04 August 2020; Accepted: 28 September 2020

1  Introduction

Among various micro parts, micro gear is the extensively used components in MEMS and NEMS technology, watches, turbines, pumps, harmonic drives, dental and medical devices, micro-motors, precision measuring instruments, and electronic home appliances, etc. [1]. Use of the miniature gears is continuously rising. Gears of less than 10 mm diameter is considered as miniature gears and subdivided into meso gear with outer diameter between 1–10 mm and micro gear with outer diameter less than 1 mm [2]. Fabrication of miniature gears were initially done by traditional processes like hobbing, gear rolling, stamping, die casting, and powder metallurgy etc. There are several limitations of traditional processes such as dimensional inaccuracy, tool wear, requirement of post finishing operation, and more time for setup etc. [2–4]. Non-traditional methods such as electric discharge machining (EDM), Wire EDM, wire electric grinding, etc. are in trend now a days. These nonconventional processes are preferred due to high accuracy, repeatability, good surface integrity, less time for setup and less stresses, etc. [5–7]. In WEDM, the material removal rate (MRR) is driven by electro-thermal mechanism. Wire feeds from upper spool using a wire guide; the spark formation takes place between wire and work due to high thermal flux density as the electrode wire crosses near workpiece, which results material removal through erosion and evaporation. Due to its distinct characteristics enable is suitable to use for high end applications in automotive and aerospace industries [8]. Wire-EDM is the variant of EDM and is most suited for the miniature gear manufacturing. It has ability to machines electrically conductive material with ease irrespective of its high hardness and toughness which make is difficult to machine via conventional methods. Furthermore, gears fabricated by Wire-EDM process are marked with good surface finishing, high accuracy, debris free surfaces and as well cost effective in comparison to other processes [9].

Mainly, miniature products including mini gears are made from a variety of materials like aluminium, bronze, brass, nickel, steels, and titanium based alloys, etc. [10]. Wide varieties of materials have been machined by WEDM and machining performance has been evaluated and reported. Many difficult to cut materials like nickel, in conel alloys, tungsten and titanium can be machined by WEDM machining [11,12]. Experiment based investigation on micromachining of titanium alloys have been conducted widely [13–16]. Titanium alloys show excellent properties corrosion resistance and high specific strength, etc. [17]. Nimonic alloys show excellent high temperature properties but are difficult to machines and the work on micro manufacturing are less reported [18–20].

Dimensional accuracy (DA) plays crucial role in deciding the quality of die manufactured using Wire EDM [21]. During machining by Wire EDM, material removal mechanism is based on melting and vaporization from micro-sized local affected volume on the workpiece surface. Thermal energy during WEDM is evolved due to spark generation and thermally affects upper layers of machined surface. These layers have different properties from original material [22]. Therefore, DA is a major issue in WEDM which needs considerable research attention. Good DA enhances the fatigue strength, wear resistance, and corrosion resistance [23–26]. The wire-EDM parameters, like cutting speed, current, pulse on time (PON) and pulse off time (POFF), wire tension (WT) on DA have been studied [27–32]. Another issue during WEDM is overcut due to spark generation from the lateral surface and bottom surface of the wire electrode. This causes concerns of dimensional inaccuracy of WEDM manufactured component. Peak current and PON time are identified as major parameters to affect the dimensional overcut [33–35].

It is important to note that more than one output responses are always involved when defining the quality of surfaces machined by WEDM. At times the effects of a single parameter on different output response are often contracting. This makes the multiple response optimization important in WEDM research. In recent researches, fuzzy logic multiple response decision making technique has become popular to optimize various manufacturing processes. Fuzzy-TOPSIS was applied to get the optimum responses like machining time, electrode wire wear rate, and dielectric fluid consumption during WEDM machining of steel [36]. Grey-fuzzy logic oriented technique was performed to optimize MRR, and SR while machining Al–4.5%Cu–TiC MMCs [37]. Principal component analysis (PCA) and fuzzy with Taguchi technique was applied to get the optimum values of WEDM parameters [38,39]. Combined approach of TOPSIS and fuzzy TOPSIS was conducted to optimize the multiple responses characteristics of the turning operation on the pure titanium grade 2 super alloys [40,41]. Taguchi and TOPSIS combined approach was applied to check the impact of EDM process parameters on SR of the machined components [42]. The importance of multi-response optimization and selections of new yet important process parameters which are not extensively investigated and affect the responses will prove useful to micromachining of gears. Based on the literature survey, it has been observed that TOPSIS methodology may prove to be effective to perform optimization on multi responses of WEDM process by using important process parameters and by addition dielectric fluid as one of them [43].

Dielectric fluid helps to remove material and debris from surface after machining. It acts as an insulating medium between the wire and workpiece and generates required energy. Mostly traditional dielectric fluid such as Deionized water, kerosene, white spirit has been used as a dielectric but researchers have identified new additive mixed dielectric fluids as well. Mixture of Aluminum and SiC in Kerosene improves the surface finishing by enlarging the space between wire electrode and workpiece which scattered the spark energy. Researchers have demonstrated that the mixture of aluminium powder with kerosene is better than mixture of silicon carbide with kerosene [44]. Graphite mixed dielectric reduces the surface tension of itself which results in improving the MRR. The study also revealed that the graphite percentage in dielectric directly affected SR and recast layer thickness. The high graphite percentage in dielectric fluid increased the recast layer thickness [16]. Oxygen has also been mixed with dielectric to enhance the sparking by oxidation process and improve the MRR, DA and cutting speed [45]. Oxygen gas improves cutting speed due to reduction in the inner electrode gap [46]. Nitrogen has also been used as a dielectric medium but its cutting speed is lower comparing with other gaseous medium. Air is a good dielectric medium with high cutting speed because of presence of oxygen [47]. The studies on WEDM have been reported in which investigations on specific hybrid dielectric have been performed but the use of dielectric as a process parameter is not used. Further, the constituents in powder, gas and liquid form have distinct effect but a hybridization of each of these is done separately. When the constituent in liquid/gas/powder form are mixed and hybrid dielectric is prepared a synergy among constituent may be advantageous. Further, by making different dielectric fluids as process parameter and analyzing their effect on responses simultaneously will prove greatly useful.

In the maiden present work hybridization of dielectric by mixing additive such as metals and ceramic powder, gas and liquid form in basic dielectric “DM water” have not been investigated. The hybridization by mixing additives in all three physical phases solid, liquid, gas (such as alumina ceramic powder, ethylene glycol and oxygen) in the basic dielectric DM water has been carried out. A hybridization of such as kind is also one of the novelty characteristics of this work.

The purpose of the study is to find out the optimum cutting parameters to achieve improved DA. Deviation in inner diameter (DID), Deviation in outer diameter (DOD), Deviation in land (DLAND), and Deviation in tooth width (DTW) are the parameters to investigate the DA. The scheme for the final experiments was chosen and the final experiments were performed to analyze the influence of process parameters and different dielectric fluids on the DA. Entropy TOPSIS and Pareto ANOVA were applied for multiple optimization of cutting parameters.

2  Experiments

2.1 Materials and Methods

Nimonic alloy is used to manufacture miniature gear of inner diameter of 5 mm, outer diameter of 7 mm and land of 0.5 mm. At present, Nimonic alloy is extensively used in many fields such as aerospace, transportation, and medical, etc. Main reason for extensive use of Nimonic alloys is its high temperature properties like wear resistance, strength and hardness, however it is difficult to cut. Further, little literature is available machining on Nimonic alloy for miniature gear. The chemical constituents of Nimonic alloy is shown in Tab. 1.

Table 1: Chemical composition of Nimonic alloy (wt.%)

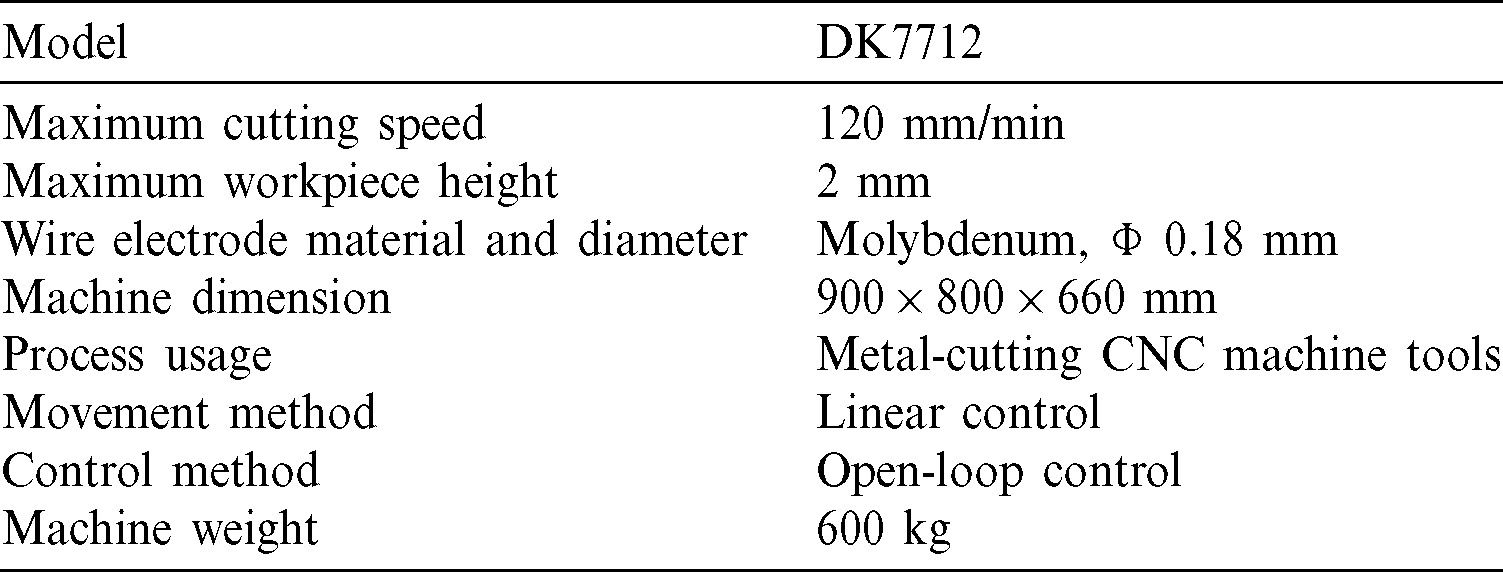
Wire EDM machine DK7712 CNC of Steer Corporation was used in experimentation. Schematic diagram of Wire EDM is represented in Fig. 1. The specifications of the Wire EDM employed in the work are given in Tab. 2. Molybdenum wire of 0.18 mm diameter was employed as electrode due to its high tensile strength and good conductivity. Special arrangements to provide measured variation to the wire tension were made by installing a push pull gauge which produced tension in electrode wire and were used as one of the process parameters.

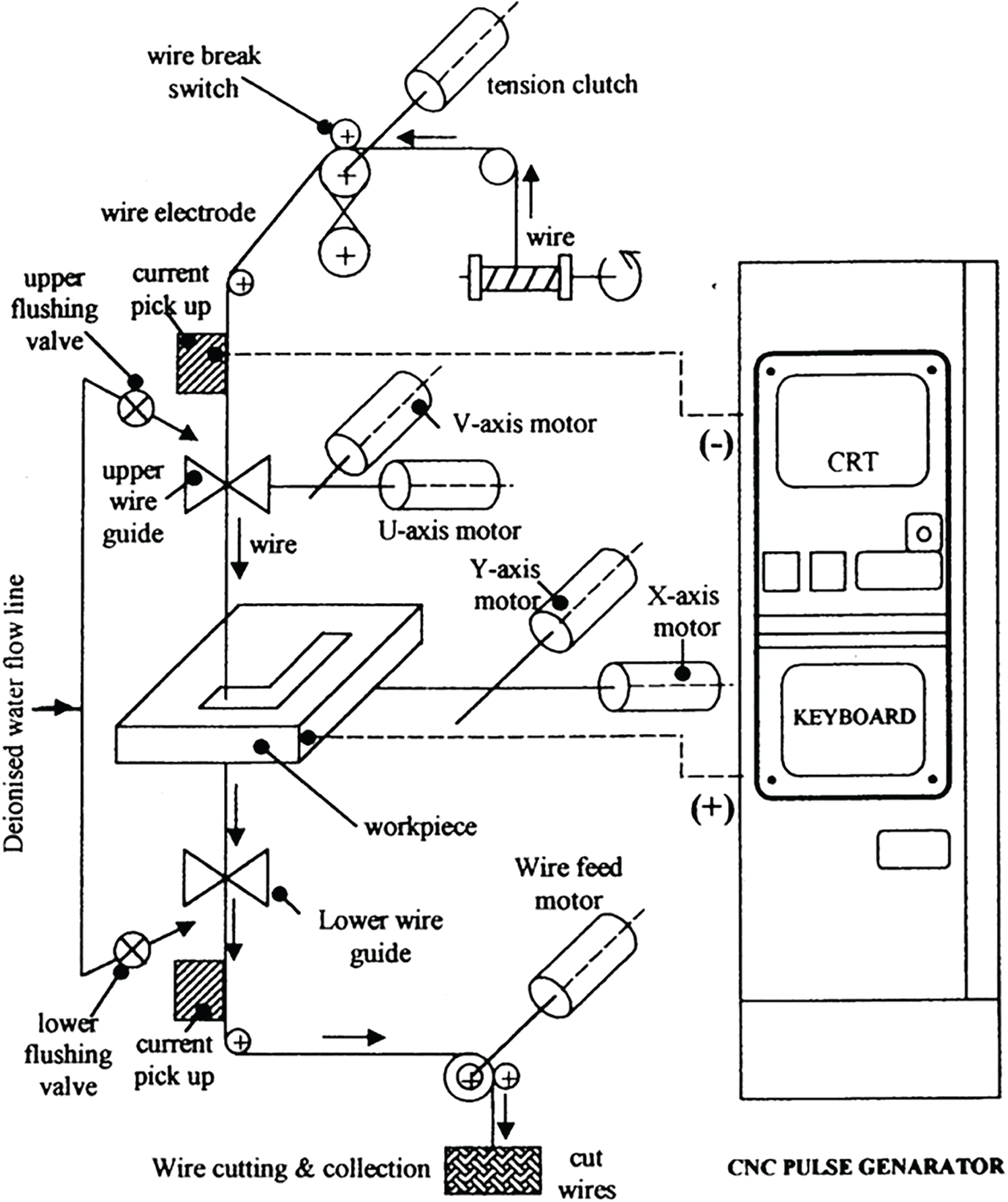
Figure 1: Schematic of wire EDM system

Table 2: Wire EDM specifications

The dielectric fluid is one of the most important factors in WEDM which affects all the response factors. Usually WEDM employs demineralized water (DM) as dielectric. In the present work the dielectric fluid was used as a base-dielectric. Constituents such as, Ethylene Glycol (EG, an organic liquid) Al2O3 (alumina nanopowder) and oxygen gas were blended in the base-dielectric and four different blends of dielectric fluids were prepared as per the details given in Tab. 3. The constituents and their concentrations were selected based on literature, dielectric strengths and trial experiments. The process parameters “dielectric fluid” was considered as a process parameter and four blends of dielectric fluid were used as its four levels.

Table 3: Range and levels of machining parameters

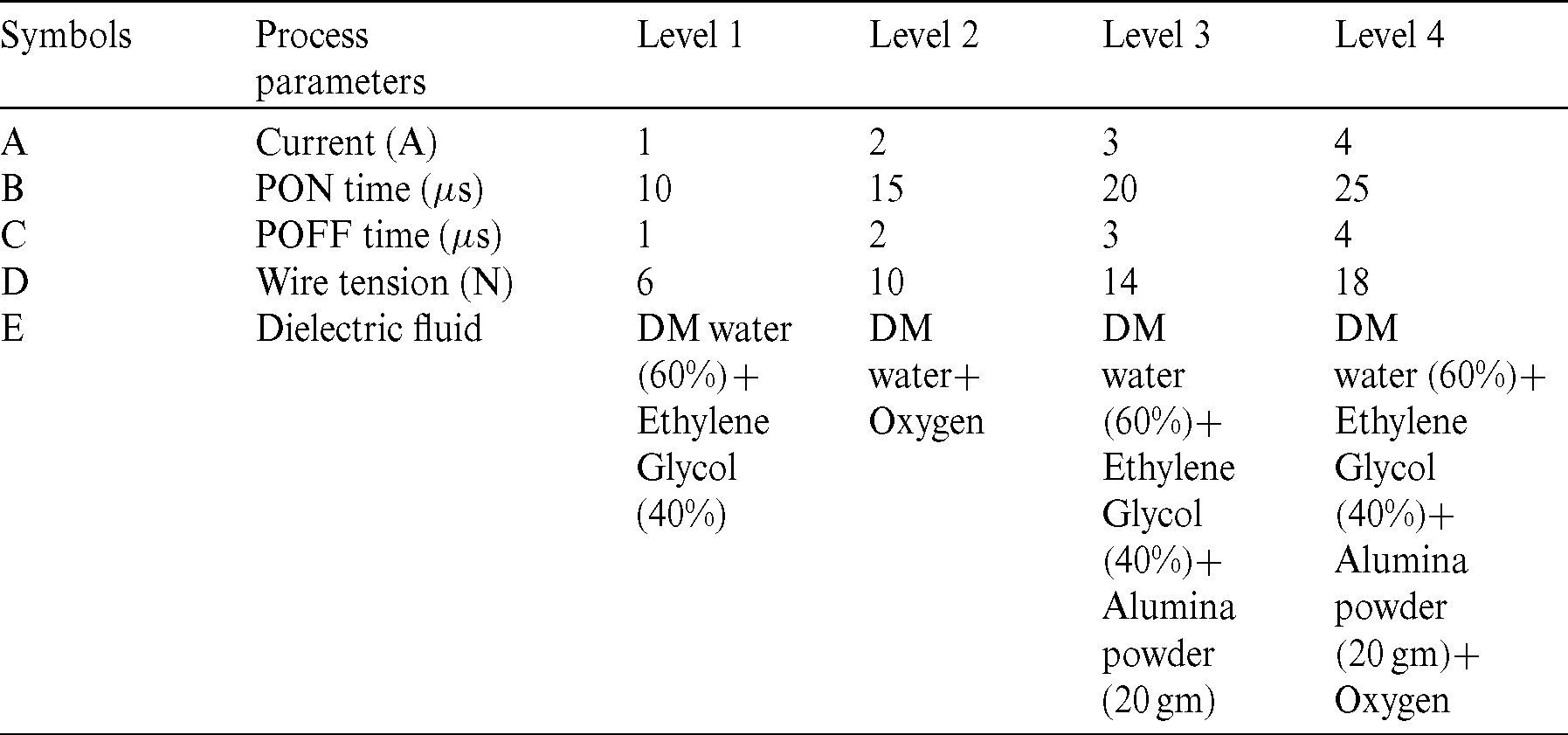
All the hybrid dielectric fluids hold different dielectric strength and play significant role in spark gap and discharge energy. The dielectric strengths of DM water, oxygen, alumina nano powder and ethylene glycol are 70 kV/mm, 0.92 kV/mm, 15 kV/mm and 35 kV/mm respectively. Dielectric fluid which has high strength delivers high spark energy and the one with low strength deliver slow spark energy. After machining dimensions of the machined miniature gear were measured using optical projectors (diameter 300 mm) of Banbros, JT series as shown in Fig. 2. The parameters and their values were chosen on the basis of literature and exhaustive trial experiments and they are given in Tab. 3.

Figure 2: Optical profile projector

The WEDM process works melting evaporation and erosion by electro-thermal energy which removes the material by distinct sparks between the workpiece and electrode wire. The sparking takes place with a present periodicity controlled by spark on and spark off time. During spark on the dielectric breaks down and releases the energy resulting in material removal. During spark off the dielectric fluid flushes out the debris from the gap and also cools down the workpiece. Dielectric is an insulating medium which avoids electrolysis effect on the wire electrode during machining. For every pulse, discharge takes place at single point where wire electrode material releases the energy which melts and vaporizes the material. Thus, small crater forms on electrode and workpiece surface [48]. The eroded particles form the debris which are removed by dielectric flow.

2.2 Entropy TOPSIS Method

There are various methods to access the weight of decision making processes like eigenvectors method, entropy method, weighted least square method, and linear programming method for multiple dimensional analyses of preferences (LINMAP) [49]. However, LINMAP and entropy methods are highly recommended when the decision matrix data is known. Entropy methodology provides faster results compared to LINMAP [50]. The entropy technique is mostly preferable to analyze the discrepancy between the set of information. In the entropy methodology, if identical values are obtained for some attributes for the dissimilar alternatives, attributes has to be removed.

The basic approach of TOPSIS methodology is the perfect alternative having minimum distance from positive ideal solutions (PIS) and maximum distance from negative ideal solutions (NIS) [51]. The benefit of TOPSIS technique is that it indicates the rational of human choice including both good and bad attributes of the alternatives concurrently, and the clarity on presentation and computation [52]. Number of steps is not affected by number of attributes thus it provides a quick solution [53]. In present scenario, TOPSIS method is used successfully as a decision-making tool into different areas such as water management [54–56], human resource [52], transportation planning [50], mechanical engineering [57], policies development [56], and manufacturing engineering [51].

Entropy TOPSIS method is used in this work to obtain the optimum cutting parameters for improved DA. Since, DA is defined in terms of DID, DOD, DLAND and DTW. Entropy TOPSIS method transforms multiple DA measures viz. DID, DOD, DLAND and DTW into a single parameter Pi. Entropy method is used to determine the weights of the responses. Whereas, TOPSIS method is employed to compute the single replicated parameter Pi for DA. The computational steps involved in Entropy TOPSIS method are as follows:

Step 1:  Formulate a decision matrix by arranging the alternatives in rows and attributes in columns as shown in Eq. (1). For better understanding of the computations steps, number of alternatives and attributes are denoted as “n” and “J” respectively.

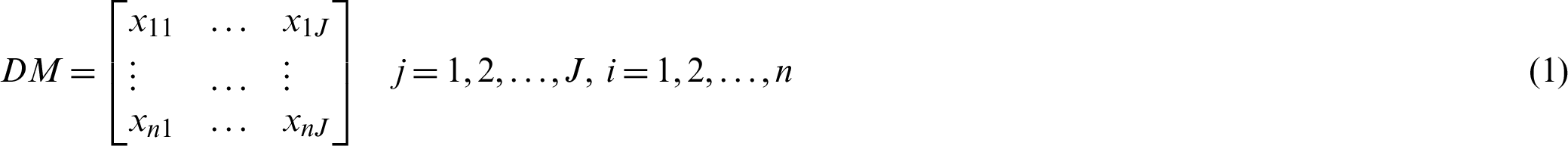
Step 2:  Normalize the decision matrix using Eq. (2):

Step 3:  Compute entropy of the attributes using Eq. (3).

where, 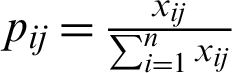and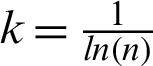

Step 4:  Compute weight of the attributes using Eq. (4).

where, dj = 1 − Ej

Step 5:  Calculate weighted normalized decision matrix as per Eq. (5).

where, wj is weight of jth attribute and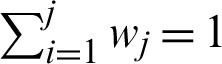

Step 6:  Determine Positive and negative ideal solutions by using Eqs. (6) and (7):

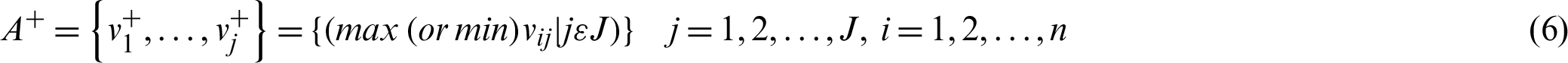
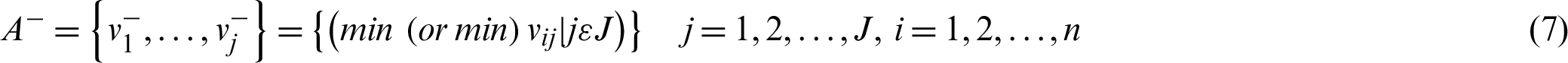
Step 7:  Calculate separation measures by using Eqs. (8) and (9). Ideal solution for separation of alternative is given as:

Step 8:  Calculate relative closeness from the ideal solutions as per Eq. (10).

Hence, 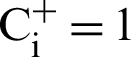when and when 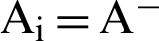, therefore recommended option is that one which is nearer to 1.

Step 9:  Ranking the order on the basis of descending order of . 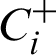is further defined as an index which indicates the combined performance values of the alternatives. It is to be noted that for better performance of the attributes, higher values of 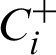is required.

2.3 Pareto ANOVA Optimization Technique

Pareto ANOVA is mostly used to examine the data for process optimization [58]. Pareto method is depended on Pareto principles which explain that 80% output is obtained by 20% input and it is comparatively easier than the statistical or classical ANOVA developed by Fisher. Therefore, ANOVA table and F-ratio are not required in this technique. Hence, this method is recommended when there is lack of sufficient knowledge of statistical/classical ANOVA approach. The advantage of this technique is that it provides simplified technique to analyze the results and this is the reason it is highly useful for the industrial practitioners.

3  Results and Discussions

The experiments were accomplished using L16 orthogonal array (OA) of the Taguchi’s design of experiment. Three replicates of each experiment were performed and average values of DID, DOD, DLAND, and DTW were recorded. The experimental data for deviation in inner diameter, outer diameter, and tooth width are shown in Tab. 4. One of the miniature gears which were machined is shown in Fig. 3.

Table 4: Experimental data for deviation in inner diameter, outer diameter, land and tooth width

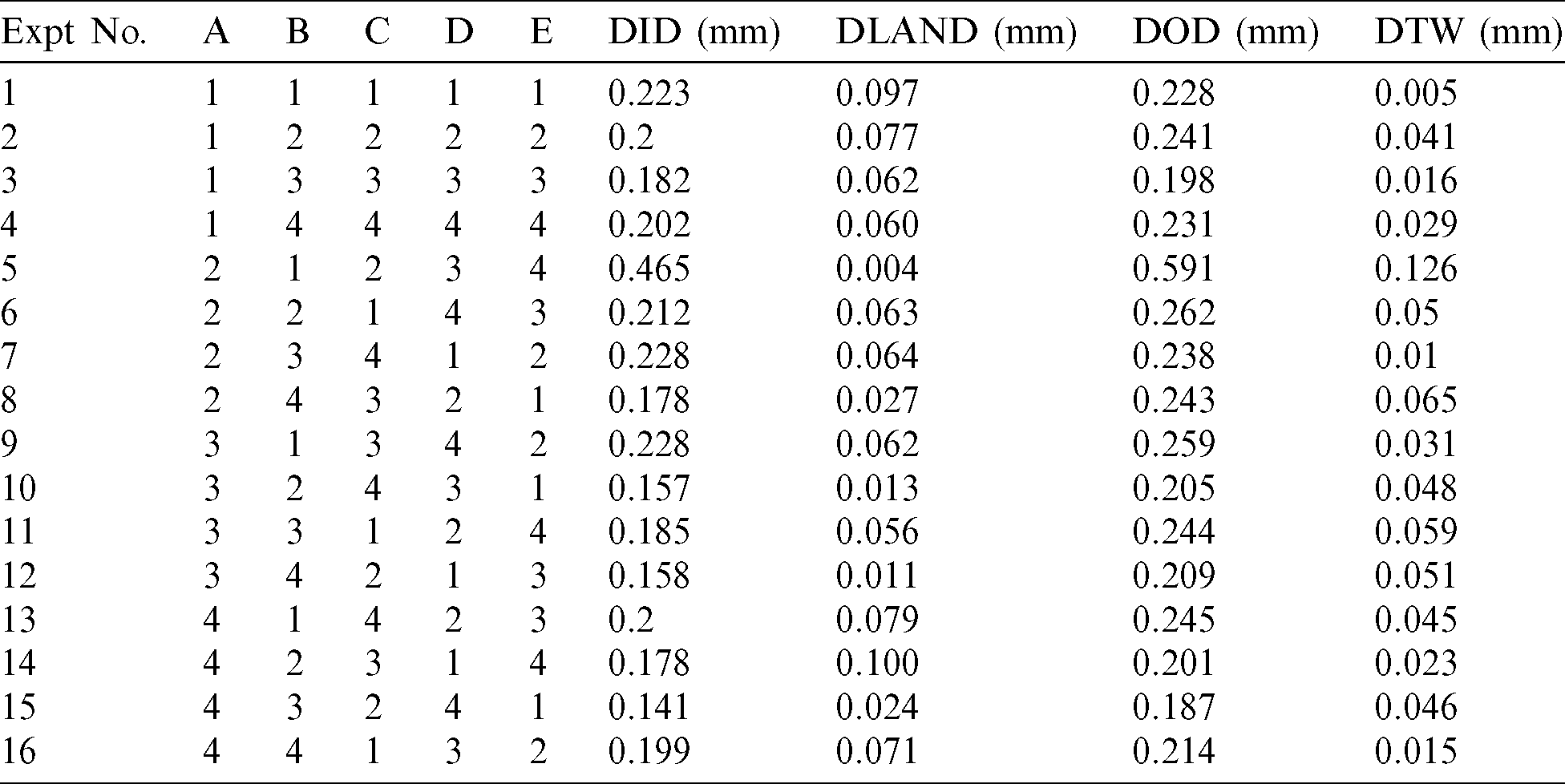
Figure 3: Nimonic alloy miniature gear

Deviations in the inner diameter, land, outer diameter and tooth width are the factors that were taken into account to define the dimensional accuracy of the miniature gear. A single multi-response comprising of all key elements of miniature-gear geometry are investigated in this maiden work. Hence, Entropy-TOPSIS multiple response characteristics was applied to assess the deviation of gear and Pareto ANOVA analysis was conducted to obtain the optimum combination of parameters shown from Tab. 5 to Tab. 11.

Table 5: rij matrix for DA

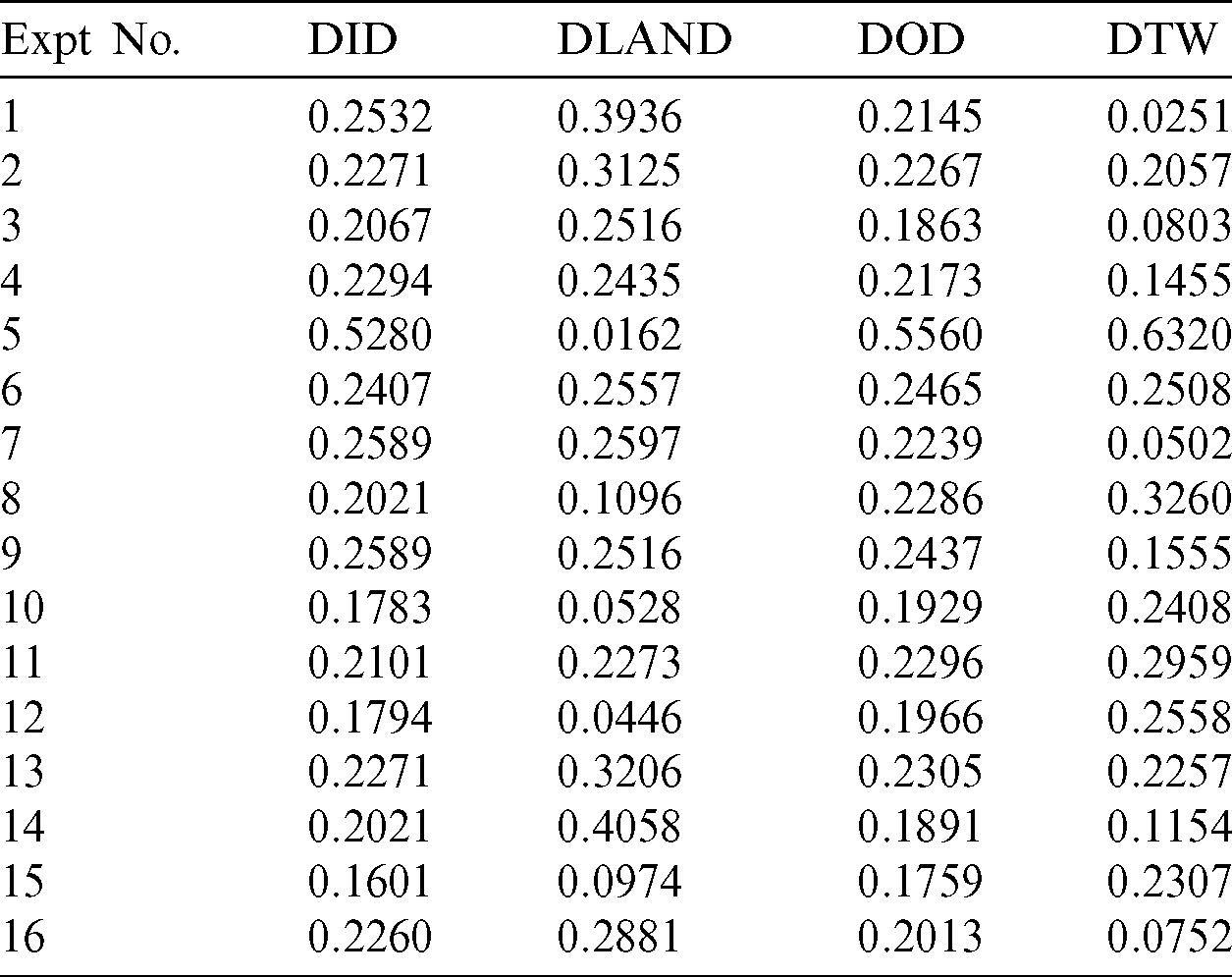
Table 6: Weights of the response variable for DA

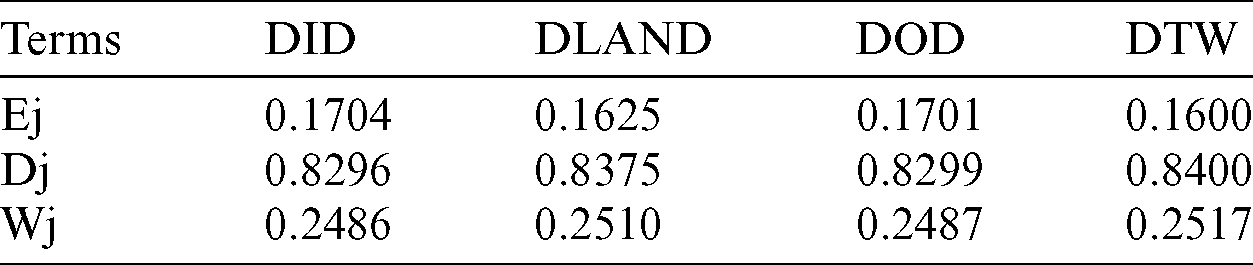
Table 7: Positive and negative ideal solutions for DA

Table 8: Closeness coefficient

Table 9: S/N ratios for Pi

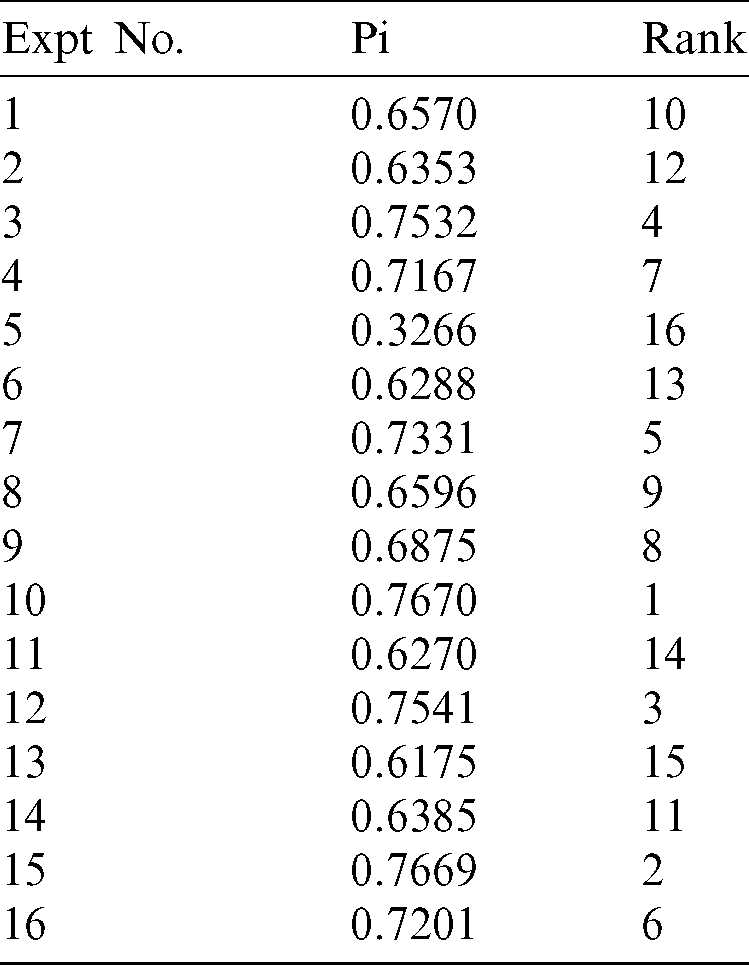
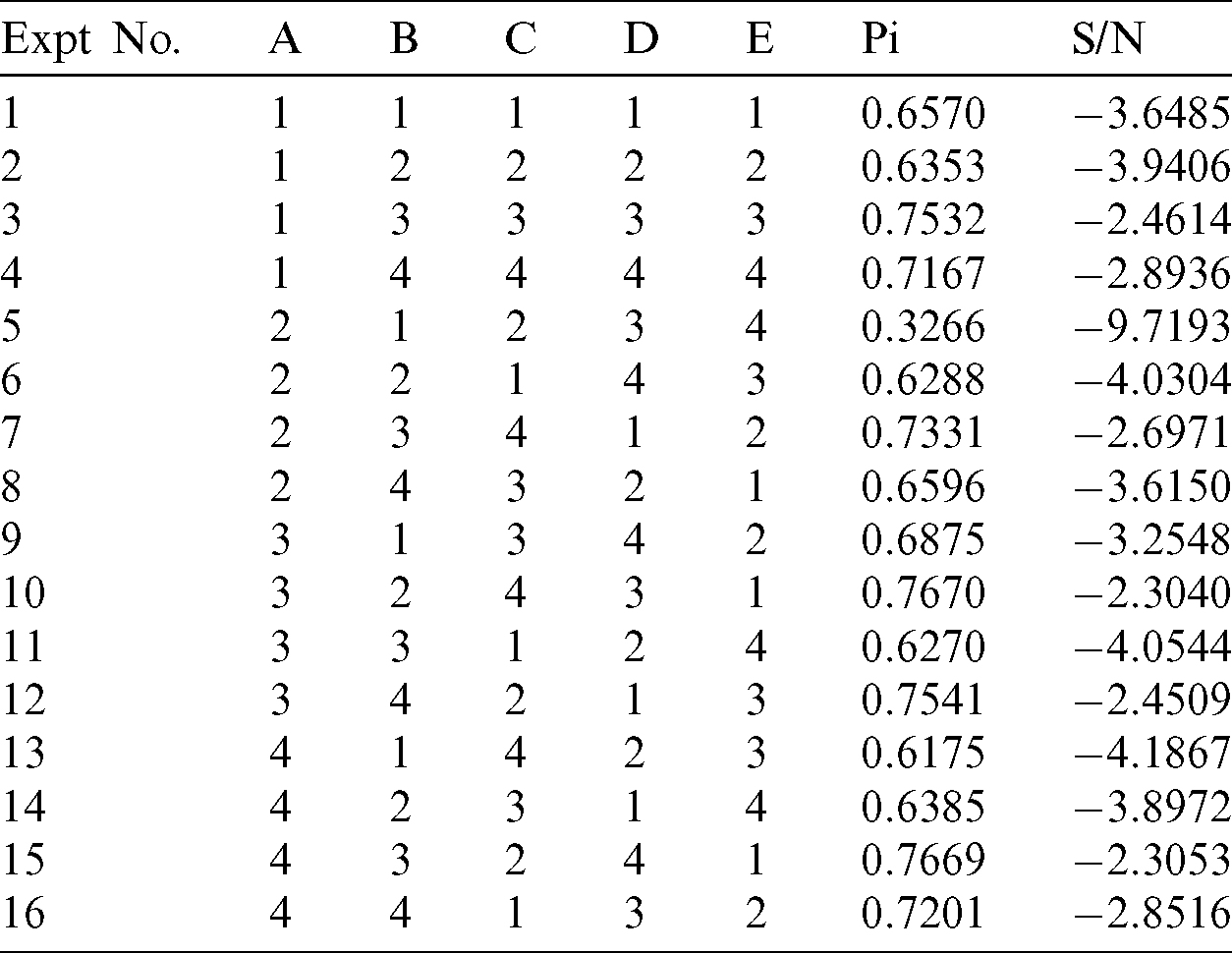
Table 10: Response Table for S/N ratio for Pi

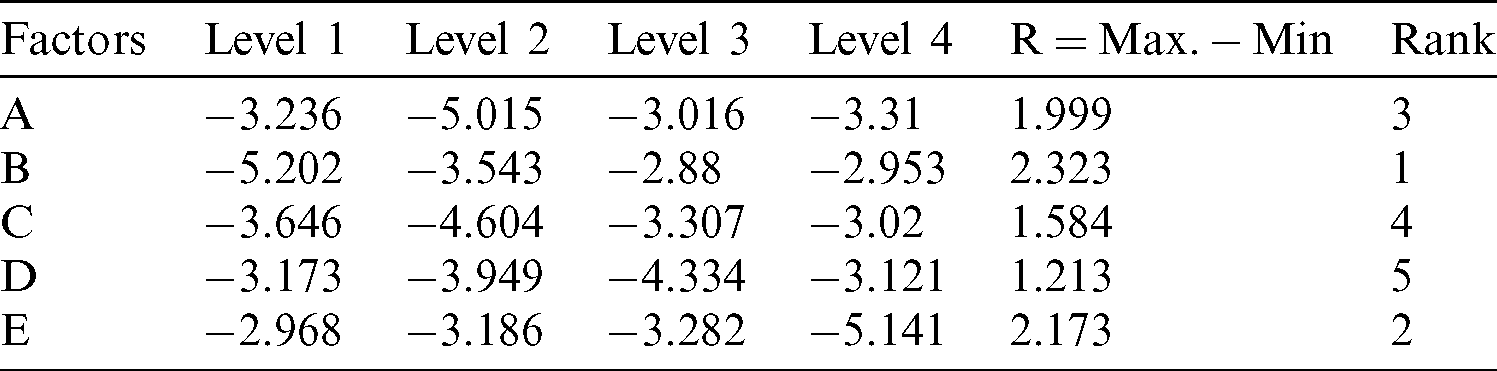
Table 11: Parto ANOVA analysis for Pi

Normalized decision matrix and rij normalized values were determined. Decision matrix was converted into dimensionless matrix by using rij matrix. rij matrix for multiple responses is shown in Tab. 5.

Weighted dimensionless matrix was obtained by the entropy methodology. Response variable weight for multiple responses is shown in Tab. 6.

Then positive and negative ideal solutions were identified. Values of the distances from PIS and NIS have been obtained as shown in Tab. 7. Closeness coefficient (Pi) was calculated after calculating PIS and NIS as shown in Tab. 8. The closeness coefficient represents a single index for simultaneous optimization of the multiple responses of DA considered in the present study.

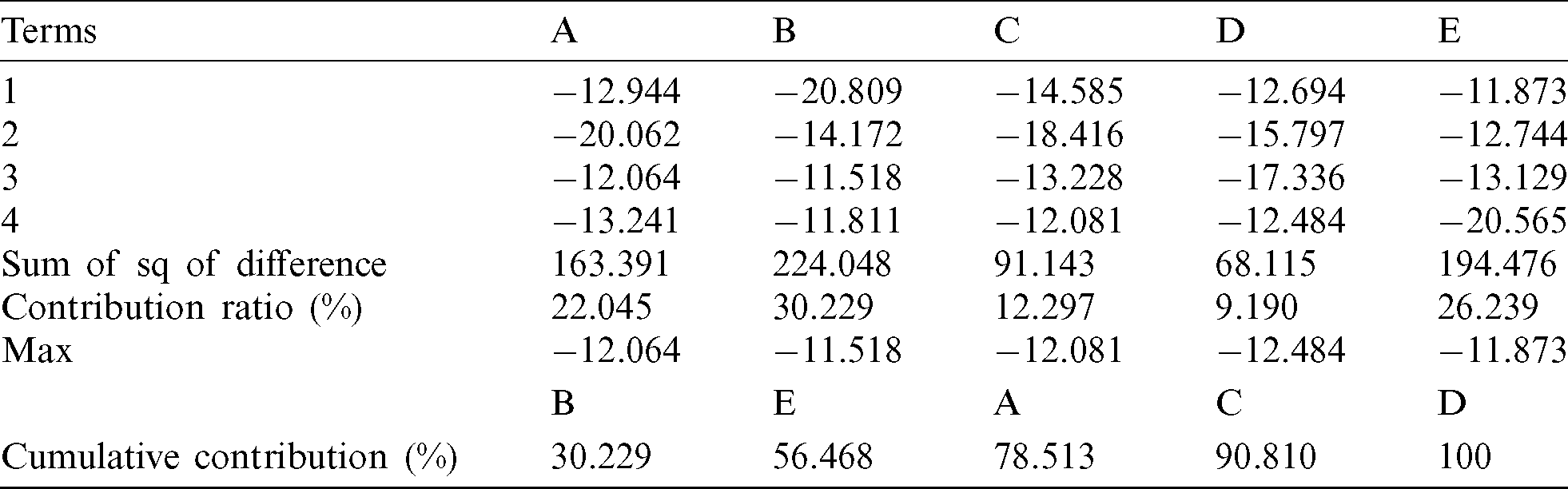
It can be seen from Tab. 8 that based on the closeness coefficient (Pi) value, experiment number 10 is the top ranked experiment (rank 1) which implies that the combination of machining parameters of this experiment, i.e., A3B2C4D3E1 is the best one for multiple responses but it cannot be inferred that whether it is optimum or not. Consequently, optimum combination of the machining parameters for multiple responses was obtained through further analysis of closeness coefficient (Pi) including computation of S/N ratios, analysis of mean (ANOM) in terms of response table, and Pareto ANOVA as suggested in the literature [59]. S/N ratio was calculated by considering higher-the-better characteristic for Pi as the objective is always to achieve its maximum value. The results of S/N ratio are shown in Tab. 9. In ANOM, mean value of the S/N ratio at each level of each machining parameter was computed and the results are presented in the response table, i.e., Tab. 10. The results of Pareto ANOVA are given in Tab. 11 and its plot is shown in Fig. 4 which reveals that the most important machining parameter is PON time (B) with the contribution ratio of 30.229%, second most significant parameter is dielectric fluid (E) with contribution ratio of 26.239%, third important parameter is current (A) with contribution ration of 22.045%. The least significant parameters are POFF time (C) and wire tension (D) with contribution ratio of 12.297% and 9.190% respectively. The levels of these parameters that yield optimum Pi value are selected from Tab. 10 which shows significance of the response table.

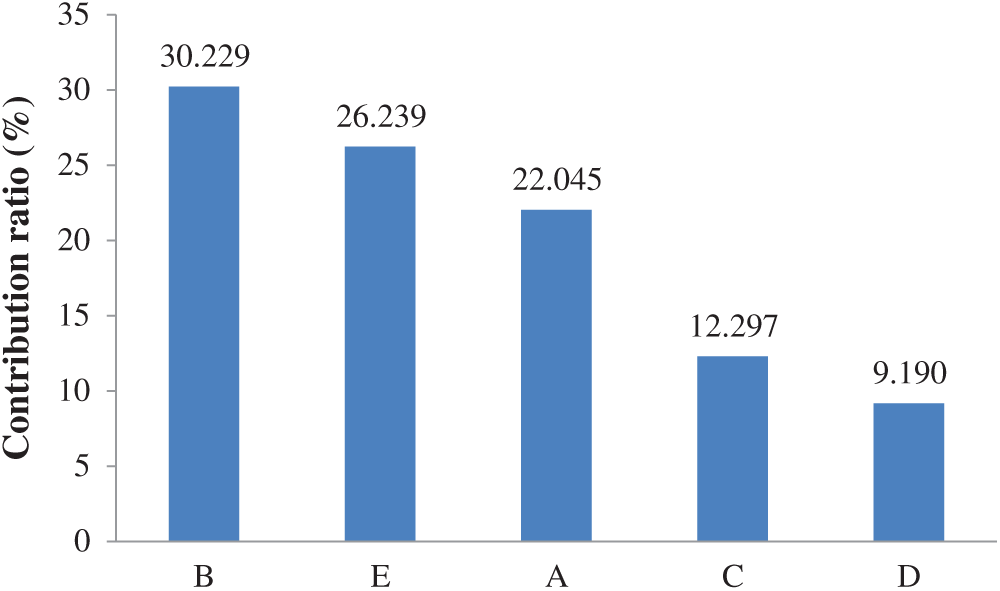
Figure 4: Pareto ANOVA plot represents contribution ratio of parameters for Pi

It may be noted that relationship formula of S/N ratio calculates its values which makes it independent of the characteristic type, i.e., whether it is lower-the-better or higher-the-better or nominal-the-better, maximum value of S/N ratio becomes the representative of desired performance. Consequently, it is evident from the results shown in Tabs. 10 and 11 that the optimum combination of machining parameters for DA is B3E1A3C4D4. Thus, current at third level (3 A), PON time at third level (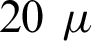s), POFF time at fourth level (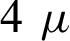s), WT at fourth level (18 N) and dielectric fluid represented at first level [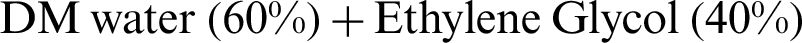] is the optimum combination for DA.

Fig. 4 shows that the most significant factor for dimensional deviation is PON time. The values of PON is the indicator for the duration of time for which the sparking will be on. This factor is therefore the sole factor responsible for the pulse energy dissipation in the machining zone and consequently is the most important factor for WEDM. The pulse on time at level 3 produced best condition for lowest DA and optimum accuracy. While during PON time period sustained machining takes place, but it is not paused, flushing-out of the debris will suffer and it will have detrimental effect on the machining accuracy and erosion of electrode wire. Thus, the PON time at level 3 optimum situation leading to better DA.

The dielectric fluid is the battery of electric power which is discharged as pulse energy during spark. In case of hybrid the nature of constituents such as oxygen and Al2O3 nanoparticles in the present case will alter the manner, this energy is dissipated. The presence of oxygen involves surface oxidation and adjustment of thermal expansions of constituents. The presence of oxygen, thus, creates the violent dissipation of energy and may increase the dimensional deviations. Similarly, the nanoparticles being solid insulating particles alter the average spark gap during travel of spark plasma between the electric poles. In the present case the pure DM water could be able to create a moderate spark and limit the deviation and enhanced the DA.

The current creates an effect of third largest contribution. The effect that a parameter creates on a response mainly depends on: (a) The range of parameters values and (b) The types of selected response. Further, the current is a factor which is responsible for the intensity of energy which is discharged in the spark gap. Under the range of parameters selected in this study the current at level 3, i.e., 3 A created optimum deviation which gave the best over accuracy of the multi-performance characteristics.

The fourth most significant parameter for dimensional deviation turns out to be POFF time. The DA is poor at low POFF time. As the POFF time increases, the dimensional deviation is lower because the pause of spark dictated by higher POFF the available time for the flushing-out of the debris is sufficient and the spark gap is properly cleared. The trapped debris being bad conductor also makes the spark erratic and leading to reduced accuracy. Thus, POFF time at level 4 gave best dimensional accuracy.

Among all the parameters chosen for the investigation in this work, WT is the only electrically neutral parameter. But is produces an indirect effect on the quality of machined surface. WT should be at optimum value to achieve better accuracy. Forces due to sparking act in the transverse direction on wire electrode, and this affects the dimensional inaccuracy in the manufacturing parts. The wire experiences transverse force every times the spark occurs. Under transverse forces, the wire vibrates and the frequency of vibration is proportional to the square root of wire tension. Here lies the main reason, that the wire vibrates following a wave-form, and at low tension the amplitude of vibrations is large. Large amplitude results in greater change in spark gap. Thus, every wire tension value results in a path-change of the spark front. This issue becomes compounded by all factors which influence the transverse force on the wire (e.g., peak current, type of dielectric, PON and POFF time, etc.). The wire tension at low level results in amplitude of vibration of wire to increase and significantly reduces the accuracy. As WT increases, deflection in wire reduce and frequency increases which consequently makes the path of spark front stabilized and results in improvement the DA.

3.1 Validation of Results

The correctness of the obtained results is ensured by comparing the experimental value of the Pi with that of its corresponding predicted value at optimum combination. In order to estimate the predicted value of the Pi, Eq. (11) was used [60].

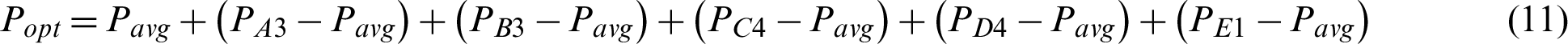
where, (PA3, 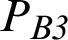, , 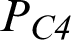, 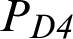PE1) represents the optimum level average values of Pi. Pavg state the average of all the Pi values obtained from the experimental study. As a result of the calculations, it was estimated that Popt = 0.8779.

To calculate the experimental value of Pi, it was required to perform the experiment for these settings. However, Pi value cannot be determined by performing only one experiment. Therefore, to determine the experimental values of Pi at optimum combination, regression analysis was performed [61]. Regression equation thus obtained for Pi is given in Eq. (12). The value of the coefficient of determination (R2) for Eq. (12) was found to be 0.9803 i.e., 98.03 % which shows a very strong relation between Pi and the various deviations (DID, DLAND, DOD and DTW).

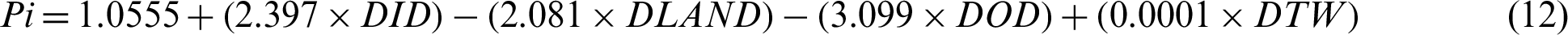
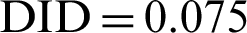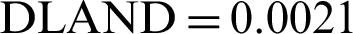Further, a confirmatory experiment was performed by setting input parameters at the optimum combination and the values of the DA were obtained which were as follows: mm, mm, 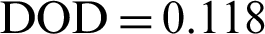mm and 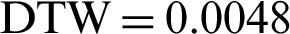mm. Subsequently, Eq. (11) was employed to obtain the experimental value of Pi which was found to be 0.8652. Since, the predicted (0.8779) and experimental (0.8652) values of Pi are in close agreement and thus, it validates the optimal result obtained in this study.

4  Conclusion

Multiple response optimization for Wire EDM Nimonic alloy miniature gear was performed in this research. Taguchi L16 orthogonal array was applied for design of experiments and Entropy TOPSIS was performed for multiple optimization of parameters. Pareto plot was employed to indicate the cumulative percentage contribution of the parameters to improve dimensional accuracy. The cutting parameters included in this research were current, pulse on time, pulse off time, wire tension and dielectric fluids while deviation in inner diameter, deviation in outer diameter, deviation in land and deviation in tooth width were main responses. Results indicated that pulse on time was the highly significant parameter for dimensional accuracy followed by dielectric fluid, current, pulse off time and wire tension. The PON time supplies time for the steady discharge of pulse energy and is the most significant parameter. The PON time at level 3 provided sufficient pulse energy discharge time to develop optimum accuracy. The dielectric fluid was next higher parameter to affect dimensional accuracy significantly. The pure DM water created conditions favorable for the optimum accuracy with the selected range all the parameters. The current which is responsible for the intensity of energy discharge in the gap was the third most significant parameter and the current at level 3 (3 A) created condition for minimum deviation and highest accuracy. The pulse OFF time provides essential pause in the discharge and makes way for the cooling and flushing-out of debris and increase the accuracy. The POFF time at level 4 produced conditions for the best dimensional accuracy. The only non-electric parameters, i.e., wire tension affected the machining performance mainly because of the deflections caused by the transverse forces generated due to spark. At lower tensions the magnitude of deflections are large and cause greater variation in the dimensions of machined part. The wire tension at level 4 created minimum deviation and best accuracy. Based on the study, the optimum machining parameters are pulse on time at 20 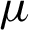s, current at 3 A, pulse off time at 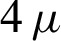s, wire tension at 18 N, and dielectric fluid at first level, i.e., .

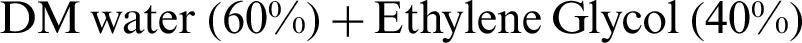Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, for funding this work through research groups program under Grant No. (R.G.P. 1/197/41).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Shichun, D., Ruining, H., Guanxin, C. (2006). Multiple attribute decision making: Methods and applications a state-of-the-art survey. Proceedings of the 1st IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Zhuhai, China. [Google Scholar]

 2.  Gupta, K., Laubscher, R. F., Davim, J. P., Jain, N. K. (2016). Recent developments in sustainable manufacturing of gears: A review. Journal of Cleaner Production, 112(4), 3320–3330. DOI 10.1016/j.jclepro.2015.09.133. [Google Scholar] [CrossRef]

 3.  Neugebauer, R., Hellfritzsch, U., Lahl, M., Milbrandt, M., Schiller, S. et al. (2013). Gear rolling process. In: Denkena, B., Hollmann, F. (Eds.Process machine interactions, lecture notes in production engineering, pp. 475–490. Berlin, Heidelberg: Springer.

 4.  Neugebauer, R., Putz, M., Hellfritzsch, U. (2007). Improved process design and quality for gear manufacturing with flat and round rolling. CIRP Annals, 56(1), 307–312. DOI 10.1016/j.cirp.2007.05.071. [Google Scholar] [CrossRef]

 5.  Gupta, K., Jain, N. K. (2014). Comparative study of wire-EDM and hobbing for manufacturing high-quality miniature gears. Materials and Manufacturing Processes, 29(11), 1470–1476. DOI 10.1080/10426914.2014.941865. [Google Scholar] [CrossRef]

 6.  Davim, J. P. (2013). Nontraditional machining processes: Research advances. London: Springer-Verlag.

 7.  Rahman, M., Asad, A. B. M. A., Wong, Y. S. (2014). Introduction to advanced machining technologies. Comprehensive materials processing. Amsterdam: Elsevier. [Google Scholar]

 8.  Singh, R., Pratap Singh, R., Tyagi, M., Kataria, R. (2020). Investigation of dimensional deviation in wire EDM of M42 HSS using cryogenically treated brass wire. Materials Today: Proceedings, 25, 679–685. DOI 10.1016/j.matpr.2019.08.028. [Google Scholar] [CrossRef]

 9.  Puri, A. B. (2017). Advancements in micro wire-cut electrical discharge machining. Non-Traditional micromachining processes, pp. 145–178. Cham, Switzerland: Springer International Publishing. [Google Scholar]

10. Davis, J. R. (2005). Gear materials, properties, and manufacture, Materials Park: ASM International. [Google Scholar]

11. Kuriakose, S., Shunmugam, M. S. (2005). Multi-objective optimization of wire-electro discharge machining process by non-dominated sorting genetic algorithm. Journal of Materials Processing Technology, 170(1–2), 133–141. DOI 10.1016/j.jmatprotec.2005.04.105. [Google Scholar] [CrossRef]

12. Chen, H. C., Lin, J. C., Yang, Y. K., Tsai, C. H. (2010). Optimization of wire electrical discharge machining for pure tungsten using a neural network integrated simulated annealing approach. Expert Systems with Applications, 37(10), 7147–7153. DOI 10.1016/j.eswa.2010.04.020. [Google Scholar] [CrossRef]

13. Alias, A., Abdullah, B., Abbas, N. M. (2012). Influence of machine feed rate in WEDM of titanium Ti–6Al–4 V with constant current (6A) using brass wire. Procedia Engineering, 41, 1806–1811. DOI 10.1016/j.proeng.2012.07.387. [Google Scholar] [CrossRef]

14. Chalisgaonkar, R., Kumar, J. (2015). Multi-response optimization and modeling of trim cut WEDM operation of commercially pure titanium (CPTi) considering multiple user’s preferences. Engineering Science and Technology, An International Journal, 18(2), 125–134. DOI 10.1016/j.jestch.2014.10.006.

15. Raj, D. A., Senthilvelan, T. (2015). Empirical modelling and optimization of process parameters of machining titanium alloy by wire-EDM using RSM. Materials Today: Proceedings, 2(5), 1682–1690. DOI 10.1016/j.matpr.2015.07.096.

16. Kolli, M., Kumar, A. (2015). Effect of dielectric fluid with surfactant and graphite powder on electrical discharge machining of titanium alloy using Taguchi method. Engineering Science and Technology, An International Journal, 18(4), 524–535. DOI 10.1016/j.jestch.2015.03.009. [Google Scholar] [CrossRef]

17. Sarkar, S., Mitra, S., Bhattacharyya, B. (2006). Parametric optimisation of wire electrical discharge machining of titanium aluminide alloy through an artificial neural network model. International Journal of Advanced Manufacturing Technology, 27(5–6), 501–508. DOI 10.1007/s00170-004-2203-7. [Google Scholar] [CrossRef]

18. Sreenivasa Rao, M., Venkaiah, N. (2015). Parametric optimization in machining of Nimonic-263 alloy using RSM and particle swarm optimization. 2nd International Conference on Nanomaterials and Technologies, Procedia Materials Science, 10, 70–79. [Google Scholar]

19. Goswami, A., Kumar, J. (2014). Optimization in wire-cut EDM of Nimonic-80A using Taguchi’s approach and utility concept. Engineering Science and Technology, An International Journal, 17(4), 236–246. DOI 10.1016/j.jestch.2014.07.001.

20. Choudhary, R., Gupta, V. K., Batra, Y., Singh, A. (2015). Performance and surface integrity of Nimonic75 alloy machined by electrical discharge machining. Materials Today: Proceedings, 2(4–5), 3481–3490. DOI 10.1016/j.matpr.2015.07.324. [Google Scholar] [CrossRef]

21. Lee, P. H., Chung, H., Lee, S. W., Yoo, J., Ko, J. (2014). Dimensional accuracy in additive manufacturing processes. International Manufacturing Science and Engineering Conference, 45806. [Google Scholar]

22. Bhattacharyya, B., Gangopadhyay, S., Sarkar, B. R. (2007). Modelling and analysis of EDMED job surface integrity. Journal of Materials Processing Technology, 189(1–3), 169–177. DOI 10.1016/j.jmatprotec.2007.01.018. [Google Scholar] [CrossRef]

23. Guu, Y. H., Hocheng, H. (2001). Improvement of fatigue life of electrical discharge machined AISI D2 tool steel by TiN coating. Materials Science and Engineering: A, 318(1–2), 155–162. DOI 10.1016/S0921-5093(01)01268-0. [Google Scholar] [CrossRef]

24. Jeelani, S., Collins, M. (1988). Effect of electric discharge machining on the fatigue life of Inconel 718. International Journal of Fatigue, 10(2), 121–125. DOI 10.1016/0142-1123(88)90040-0.

25. Abu Zeid, O. A. (1997). On the effect of electrodischarge machining parameters on the fatigue life of AISI D6 tool steel. Journal of Materials Processing Technology, 68(1), 27–32. DOI 10.1016/S0924-0136(96)02523-X.

26. Ramulu, M., Paul, G., Patel, J. (2001). EDM surface effects on the fatigue strength of a 15 vol% SiCp/Al metal matrix composite material. Composite Structures, 54(1), 79–86. DOI 10.1016/S0263-8223(01)00072-1. [Google Scholar] [CrossRef]

27. Luo, Y. F. (1995). An energy-distribution strategy in fast-cutting wire EDM. Journal of Materials Processing Technology, 55(4), 380–390. DOI 10.1016/0924-0136(95)02032-2. [Google Scholar] [CrossRef]

28. Huang, J. T., Liao, Y. S., Hsue, W. J. (1999). Determination of finish-cutting operation number and machining-parameters setting in wire electrical discharge machining. Journal of Materials Processing Technology, 87(3), 69–81. DOI 10.1016/S0924-0136(98)00334-3.

29. Sarkar, S., Mitra, S., Bhattacharyya, B. (2005). Parametric analysis and optimization of wire electrical discharge machining of -titanium aluminide alloy. Journal of Materials Processing Technology, 159(3), 286–294. DOI 10.1016/j.jmatprotec.2004.10.009.

30. Yan, M. T., Lai, Y. P. (2007). Surface quality improvement of wire-EDM using a fine-finish power supply. International Journal of Machine Tools and Manufacture, 47(11), 1686–1694. DOI 10.1016/j.ijmachtools.2007.01.006.

31. Sanchez, J. A., Rodil, J. L., Herrero, A., de Lacalle, L. N. L., Lamikiz, A. (2007). On the influence of cutting speed limitation on the accuracy of wire-EDM corner-cutting. Journal of Materials Processing Technology, 182(1–3), 574–579. DOI 10.1016/j.jmatprotec.2006.09.030.

32. Kanlayasiri, K., Boonmung, S. (2007). An investigation on effects of wire-EDM machining parameters on surface roughness of newly developed DC53 die steel. Journal of Materials Processing Technology, 187–188, 26–29. DOI 10.1016/j.jmatprotec.2006.11.220. [Google Scholar] [CrossRef]

33. Dhar, S., Purohit, R., Saini, N., Sharma, A., Kumar, G. H. (2007). Mathematical modeling of electric discharge machining of cast Al–4Cu–6Si alloy–10wt.% SiCP composites. Journal of Materials Processing Technology, 194(1–3), 24–29. DOI 10.1016/j.jmatprotec.2007.03.121. [Google Scholar] [CrossRef]

34. Lin, M. Y., Tsao, C. C., Huang, H. H., Wu, C. Y., Hsu, C. Y. (2014). Use of the grey-Taguchi method to optimise the micro-electrical discharge machining (micro-EDM) of Ti–6Al–4V alloy. International Journal of Computer Integrated Manufacturing, 28(6), 569–576. DOI 10.1080/0951192X.2014.880946.

35. Natarajan, N., Arunachalam, R. M., Thanigaivelan, R. (2013). Experimental study and analysis of micro holes machining in EDM of SS 304. International Journal of Machining and Machinability of Materials, 13(1), 1–16. DOI 10.1504/IJMMM.2013.051905. [Google Scholar] [CrossRef]

36. Sivapirakasam, S. P., Mathew, J., Surianarayanan, M. (2011). Multi-attribute decision making for green electrical discharge machining. Expert Systems with Applications, 38(7), 8370–8374. DOI 10.1016/j.eswa.2011.01.026. [Google Scholar] [CrossRef]

37. Das, B., Roy, S., Rai, R. N., Saha, S. C. (2016). Application of grey fuzzy logic for the optimization of CNC milling parameters for Al–4.5%Cu–TiC MMCs with multi-performance characteristics. Engineering Science and Technology, An International Journal, 19(2), 857–865. DOI 10.1016/j.jestch.2015.12.002. [Google Scholar] [CrossRef]

38. Puhan, D., Mahapatra, S. S., Sahu, J., Das, L. (2013). A hybrid approach for multi-response optimization of non-conventional machining on AlSiCp MMC. Measurement, 46(9), 3581–3592. DOI 10.1016/j.measurement.2013.06.007. [Google Scholar] [CrossRef]

39. Dewangan, S., Gangopadhyay, S., Biswas, C. K. (2015). Study of surface integrity and dimensional accuracy in EDM using Fuzzy TOPSIS and sensitivity analysis. Measurement, 63, 364–376. DOI 10.1016/j.measurement.2014.11.025. [Google Scholar] [CrossRef]

40. Khan, A., Maity, K. (2019). Application potential of combined fuzzy-TOPSIS approach in minimization of surface roughness, cutting force and tool wear during machining of CP-Ti grade II. Soft Computing, 23(15), 6667–6678. DOI 10.1007/s00500-018-3322-7. [Google Scholar] [CrossRef]

41. Khan, A., Maity, K. (2017). Application of MCDM-based TOPSIS method for the selection of optimal process parameter in turning of pure titanium. Benchmarking: An International Journal, 24(7), 2009–2021. DOI 10.1108/BIJ-01-2016-0004. [Google Scholar] [CrossRef]

42. Nguyen, H. P., Pham, V. D., Ngo, N. V. (2018). Application of TOPSIS to Taguchi method for multi-characteristic optimization of electrical discharge machining with titanium powder mixed into dielectric fluid. International Journal of Advanced Manufacturing Technology, 98(5–8), 1179–1198. DOI 10.1007/s00170-018-2321-2. [Google Scholar] [CrossRef]

43. Raj, S. O. N., Prabhu, S. (2017). Analysis of multi objective optimisation using TOPSIS method in EDM process with CNT infused copper electrode. International Journal of Machining and Machinability of Materials, 19(1), 76–94. DOI 10.1504/IJMMM.2017.081190. [Google Scholar] [CrossRef]

44. Chow, H. M., Yan, B. H., Huang, F. Y., Hung, J. C. (2000). Study of added powder in kerosene for the micro-slit machining of titanium alloy using electro-discharge machining. Journal of Materials Processing Technology, 101(1), 95–103. DOI 10.1016/S0924-0136(99)00458-6. [Google Scholar] [CrossRef]

45. Niamat, M., Sarfraz, S., Aziz, H., Jahanzaib, M., Shehab, E. et al. (2017). Effect of different dielectrics on material removal rate, electrode wear rate and microstructures in EDM. Procedia CIRP, Complex Systems Engineering and Development Proceedings of the 27th CIRP Design Conference Cranfield University, 60, 2–7. [Google Scholar]

46. Chiang, K. T., Chang, F. P. (2006). Optimization of the WEDM process of particle-reinforced material with multiple performance characteristics using grey relational analysis. Journal of Materials Processing Technology, 180(1–3), 96–101. DOI 10.1016/j.jmatprotec.2006.05.008. [Google Scholar] [CrossRef]

47. Shayan, A. V., Afza, R. A., Teimouri, R. (2013). Parametric study along with selection of optimal solutions in dry wire cut machining of cemented tungsten carbide (WC-Co). Journal of Manufacturing Processes, 15(4), 644–658. DOI 10.1016/j.jmapro.2013.05.001. [Google Scholar] [CrossRef]

48. Arunkumar, N. E., Ganesh, M., Vivekanandan, N. (2020). Optimization of machining parameters in WEDM of Monel 400 using Taguchi technique. Materials Today: Proceedings, 2nd International Conference on Materials Manufacturing and Modelling, 22, 2199–2206. [Google Scholar]

49. Hwang, C. L., Yoon, K. (1981). Multiple attribute decision making: Methods and applications a state-of-the-art survey. Lecture notes in economics and mathematical systems. Berlin, Heidelberg: Springer-Verlag. [Google Scholar]

50. Janic, M. (2003). Multicriteria evaluation of high-speed rail, transrapid maglev and air passenger transport in Europe. Transportation Planning and Technology, 26(6), 491–512. DOI 10.1080/0308106032000167373. [Google Scholar] [CrossRef]

51. Kwong, C. K., Tam, S. M. (2002). Case-based reasoning approach to concurrent design of low power transformers. Journal of Materials Processing Technology, 128(1–3), 136–141. DOI 10.1016/S0924-0136(02)00440-5. [Google Scholar] [CrossRef]

52. Shih, H. S., Shyur, H. J., Lee, E. S. (2007). An extension of TOPSIS for group decision making. Mathematical and Computer Modelling, 45(7–8), 801–813. DOI 10.1016/j.mcm.2006.03.023. [Google Scholar] [CrossRef]

53. İç, Y. T. (2012). An experimental design approach using TOPSIS method for the selection of computer-integrated manufacturing technologies. Robotics and Computer-Integrated Manufacturing, 28(2), 245–256. DOI 10.1016/j.rcim.2011.09.005. [Google Scholar] [CrossRef]

54. Lai, Y. J., Liu, T. Y., Hwang, C. L. (1994). TOPSIS for MODM. European Journal of Operational Research, Facility Location Models for Distribution Planning, 76(3), 486–500. [Google Scholar]

55. Srdjevic, B., Medeiros, Y. D. P., Faria, A. S. (2004). An objective multi-criteria evaluation of water management scenarios. Water Resources Management, 18(1), 35–54. DOI 10.1023/B:WARM.0000015348.88832.52.

56. Qin, X. S., Huang, G. H., Chakma, A., Nie, X. H., Lin, Q. G. (2008). A MCDM-based expert system for climate-change impact assessment and adaptation planning–-A case study for the Georgia Basin, Canada. Expert Systems with Applications, 34(3), 2164–2179. DOI 10.1016/j.eswa.2007.02.024. [Google Scholar] [CrossRef]

57. Milani, A. S., Shanian, A., Madoliat, R., Nemes, J. A. (2005). The effect of normalization norms in multiple attribute decision making models: A case study in gear material selection. Structural and Multidisciplinary Optimization, 29(4), 312–318. DOI 10.1007/s00158-004-0473-1. [Google Scholar] [CrossRef]

58. Rajesh, A., Venkatesh, J. (2014). Taguchi method and PARETO ANOVA: An approach for process parameter optimization in micro-EDM drilling. International Journal of Science & Engineering Research, 10(5), 38–42. [Google Scholar]

59. Ghani, J. A., Choudhury, I. A., Hassan, H. H. (2004). Application of Taguchi method in the optimization of end milling parameters. Journal of Materials Processing Technology, 145(1), 84–92. DOI 10.1016/S0924-0136(03)00865-3. [Google Scholar] [CrossRef]

60. Kıvak, T. (2014). Optimization of surface roughness and flank wear using the Taguchi method in milling of hadfield steel with PVD and CVD coated inserts. Measurement, 50, 19–28. DOI 10.1016/j.measurement.2013.12.017. [Google Scholar] [CrossRef]

61. Muqeem, M., Sherwani, A. F., Ahmad, M., Khan, Z. A. (2019). Application of the Taguchi based entropy weighted TOPSIS method for optimisation of diesel engine performance and emission parameters. International Journal of Heavy Vehicle Systems, 26(1), 69–94. DOI 10.1504/IJHVS.2019.097111. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.