Computer Modeling in Engineering & Sciences
| Computer Modeling in Engineering & Sciences | |
DOI: 10.32604/cmes.2021.014393
Article
Power Aggregation Operators and Similarity Measures Based on Improved Intuitionistic Hesitant Fuzzy Sets and their Applications to Multiple Attribute Decision Making
1Department of Mathematics and Statistics, International Islamic University, Islamabad, Pakistan
2Algebra and Applications Research Unit, Division of Computational Science, Faculty of Science, Prince of Songkla University, Hat Yai, Songkhla, Thailand
*Corresponding Author: Ronnason Chinram. Email: ronnason.c@psu.ac.th
Received: 23 September 2020; Accepted: 11 November 2020
Abstract: Intuitionistic hesitant fuzzy set (IHFS) is a mixture of two separated notions called intuitionistic fuzzy set (IFS) and hesitant fuzzy set (HFS), as an important technique to cope with uncertain and awkward information in realistic decision issues. IHFS contains the grades of truth and falsity in the form of the subset of the unit interval. The notion of IHFS was defined by many scholars with different conditions, which contain several weaknesses. Here, keeping in view the problems of already defined IHFSs, we will define IHFS in another way so that it becomes compatible with other existing notions. To examine the interrelationship between any numbers of IHFSs, we combined the notions of power averaging (PA) operators and power geometric (PG) operators with IHFSs to present the idea of intuitionistic hesitant fuzzy PA (IHFPA) operators, intuitionistic hesitant fuzzy PG (IHFPG) operators, intuitionistic hesitant fuzzy power weighted average (IHFPWA) operators, intuitionistic hesitant fuzzy power ordered weighted average (IHFPOWA) operators, intuitionistic hesitant fuzzy power ordered weighted geometric (IHFPOWG) operators, intuitionistic hesitant fuzzy power hybrid average (IHFPHA) operators, intuitionistic hesitant fuzzy power hybrid geometric (IHFPHG) operators and examined as well their fundamental properties. Some special cases of the explored work are also discovered. Additionally, the similarity measures based on IHFSs are presented and their advantages are discussed along examples. Furthermore, we initiated a new approach to multiple attribute decision making (MADM) problem applying suggested operators and a mathematical model is solved to develop an approach and to establish its common sense and adequacy. Advantages, comparative analysis, and graphical representation of the presented work are elaborated to show the reliability and effectiveness of the presented works.
Keywords: Intuitionistic fuzzy sets; intuitionistic hesitant fuzzy sets; power aggregation operators; similarity measures; multiple attribute decision making
In modern decision science, multi-attribute decision making (MADM) is a vital investigation area on how to choose the correct option corresponding to many prominent attributes [1–3]. Usually, the decision-makers (DMs) utilize crisp figures to express the favorites regarding the alternative in conventional multi-attribute decision making difficulties. But, because of shortage of data, lack of time, deficiency of information and quality values, particularly, for subjective attribute values, usually may not be shown by real numbers, and few of them are simpler to be stated by fuzzy data. Since Zadeh [4] introduced the notion of fuzzy set, several expansions of fuzzy sets (FS) were presented by scholars [5–7]. A FS contains an ordered pair of an element and a membership (MS) function, which gives grade of MS to every component of universal set X in the closed interval from 0 to 1. The model of fuzzy set is applied in many areas, mainly wherever traditional numerical methods restrict effectiveness, involving organic and social sciences, linguistics, psychology and mostly soft sciences. In these areas, variables are hard to evaluate and conditions among variables are so ill-defined. Further, Atanassov [8,9] gave the idea of intuitionistic fuzzy set IFS in 1986. IFS is an expansion of FS to cope with doubtful and complicated data. In IFS every object is indicated by an ordered pair set where every ordered pair set described a grade of MS as well as a grade of NMS.
The total of the grade of MS and the grade of NMS of each ordered pair set is smaller than or equivalent to 1 and greater than or equivalent to 0. The IFS has been receiving more consideration since its arrival [10–20]. Intuitionistic fuzzy set is extra influential in managing with vagueness than fuzzy set which only provides a grade of MS to every component. Undoubtedly, IF data aggregation performs a crucial part in intuitionistic fuzzy set, that is an attractive study direction. Zhao et al. [21] established few elementary arithmetic aggregation operators, whereas IF weighted averaging operator, IF ordered weighted averaging operator and IF hybrid averaging operator for aggregating IFSs. Xu et al. [22] established few basic geometric aggregation operators whereas IF weighted geometric operator, IF ordered weighted geometric operator, and IF hybrid geometric operator and enforced them to MADM established on IFS. Furthermore, Torra et al. [23,24] presented the hesitant fuzzy set HFS. An HFS is a direct simplification of FS. The theory of hesitant fuzzy set is extensively utilized in many problems. Many researchers gave a serious analysis on HF information aggregation methods and their implications in decision making [25–32].
An HFS allows the MS taking a set of conceivable values for example, in order to obtain a sensible decision outcome, a decision association, containing many DMs, which is approved to assess the grade that an alternative should fulfill a criterion. Consider there are three situations, few DMs offer 0.2, few offer 0.4, and the rest offer 0.9, and these units may not convince one another, thus the grade that the alternative should fulfill the criterion can be signified by an HF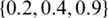 
. It is observed that the HF 
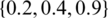may define the above condition more quantitatively than the interval-valued FS 
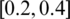, due to grades that alternatives fulfil the condition out of the convex of 0.2 and 0.9 or the interval between 0.2 and 0.9. Thereafter, several multi attribute decision making techniques [33–38] and procedures containing relationship, distance, and similarity have offered for hesitant fuzzy set by various investigators. Liao et al. [39,40] introduced the subtraction and division operations, hybrid arithmetical averaging for hesitant fuzzy sets, and hybrid arithmetical geometric for HFSs. Zhang [41] introduced power aggregation operators for HFS. In everyday life, DMs would think ranking among unlike conditions. To manage this type of position, Yager [42] established PA operator and implements it to multi-attribute decision making difficulties. Liu et al. [43] introduced POWA operator to manage the fuzzy data.
Mostly, this is noted that one fuzzy framework is not enough to deal with practical problems. There is a common trend of combining two or more fuzzy frameworks. Therefore, by mixing IFS and HFS established the theory of IHFS. IHFS is also described by the grade of MS and the grade of NMS, whose summation is smaller than or equivalent to 1 and greater than or equal to 0. IHFS has emerged as a powerful instrument for illustrating vagueness of the MADM difficulties. The determination of the article is to present the idea of power aggregation operators based on IHFS by combining the theory IFS and HFS. We found that two different definitions of IHFS which were proposed by Beg et al. [44] and Geetha et al. [45] are not compatible with the other existing notions. So, to make the IHFS compatible with the other existing notions we have defined IHFS in another way. In some situations the theories of HFS and IFS cannot deal effectively, for instance, when a decision maker gives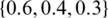 
for the grade of truth and 
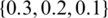for the grade of falsity then the condition of proposed improved IHFS is an important technique to cope with uncertain and unreliable information in realistic decision issues. The conditions of Beg et al. [44] and Geetha et al. [45] are that the sum of maximum (also for minimum) of the truth grade and the minimum (also for maximum) of the falsity grade cannot exceed from unit interval and the sum of the maximum of the truth grade and the maximum of the falsity exceeds from unit interval. To resolve such kinds of issues, we redefined the theory of IHFS with the new condition that the sum of the maximum of the truth grade and the maximum of the falsity grade cannot exceed from unit interval. Additionally, we have established the sequence of IHF power aggregation operators, which has weighting vectors varing by input reasons as well as permit data being aggregated to assist everyone and examine the required characteristics. Motivation and achievements of the article are shown as follows:
1. Enlarge several PA operators, as IHFPA operator, IHFPWA operator, IHFPOWA operator, IHFPHA operator, IHFPG operator, IHFPWG operator, IHFPOWG operator, IHFPHG operator and check their characteristics.
2. Explore the similarity measures based on IHFSs and justified with the help of numerical example.
3. Describe a new DM method consists over the proposal operations.
4. Provide some numerical to demonstrate the reliability and supremacy of described techniques.
The making of article is followed as in portion 2, it gives few fundamental notions as well as in this section we reviewed the definition of IHFS which are established by Beg et al. [44] and Geetha et al. [45]. In Section 3, we established few IHF power aggregation operators and calculated their suitable characteristics. In Section 4, we explored the similarity measures based on IHFSs. In Section 5, we utilized these operators to establish few forms for multi attribute decision making challenges founded by IHFPWA operator and IHFPWG operator with intuitionistic hesitant fuzzy data. Additionally, we mentioned a practical problem for examining efficiency of the suggested operators. In Section 6, we summarized this article and wrote few comments.
2 Another View of Intuitionistic Hesitant Fuzzy Sets
In this study, we review the idea of IHFS which was established by Beg et al. [44] and established by Geetha et al. [45]. Then we redefine IHFS to make it compatible with other existing notions [46].
Definition 1: [44] An IHFS on X are functions 
and v that when applied to X return the subsets of [0, 1], which can be represented as the following:
where 
and v(x) are sets of some values in [0, 1], denoting the possible membership degrees and non-membership degrees of the element 
to the set P with the conditions: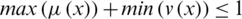 
and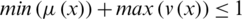 
. For convenience, 
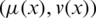is an intuitionistic hesitant fuzzy element (IHFE).
Definition 2: [45] An intuitionistic hesitant fuzzy set P on X is represented by using the two functions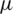 
and v. Mathematically, it is represented by following expression:
where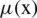 
and v(x) are sets of some values in [0, 1], denoting the possible membership degrees and non-membership degrees of the element 
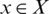to the set P with the condition that 
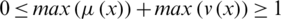. For convenience, 
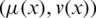is an intuitionistic hesitant fuzzy element (IHFE).
Definition 3: An intuitionistic hesitant fuzzy set P on X is represented by using the two functions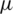 
and v. Mathematically, it is represented by following expression:
where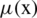 
and v(x) are sets of some values in [0, 1], denoting the possible membership degrees and non-membership degrees of the element 
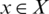to the set E with the condition that 
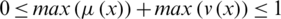. For convenience, 
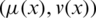an intuitionistic hesitant fuzzy element (IHFE). In this manuscript we will follow throughout the IHFS:
satisfying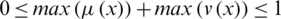 
.
Definition 4: For any IHFE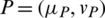 
, the score function and accuracy function are stated by:
where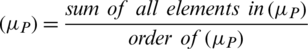 
, 
, 
, 
.
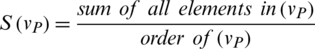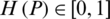Definition 5: For any two IHFEs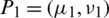 
and 
, then
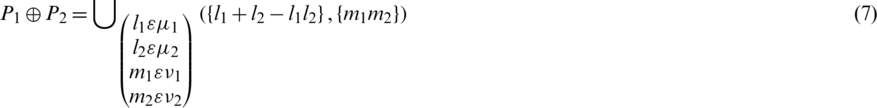
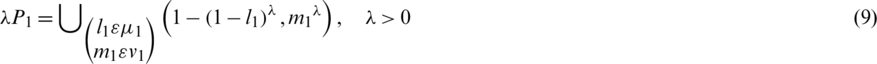
Definition 6: Power aggregation (PA) operator is defined as:
where
and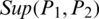 
is the 
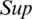for P1 from P2, which meets the given properties:
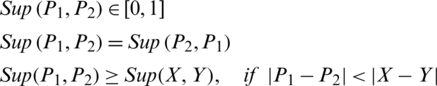
The support (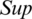
) amount is basically a similarity indicator.
Definition 7: Power geometric (PG) operator is defined as:
Based upon intuitionistic hesitant fuzzy PA operators and PG, we will describe few IHFPG aggregation operators. Next, we will establish few intuitionistic hesitant fuzzy power arithmetic aggregation operators.
3 Intuitionistic Hesitant Fuzzy Power Aggregation Operators
The purpose of this section is to establish few novel aggregation operators for IHFSs which are IHFPA, IHFPG, IHFPWA, IHFPWG, IHFPOWA, IHFPOWG, IHFPHA, IHFPHG operators and verify their fundamental properties. The mentioned operators are not only developed in this section but also their characteristics have been studied and their fitness is established using induction phenomenon.
Definition 8: Suppose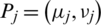 
is a gathering of IHFSs, then we describe the IHFPA operator as follow:
where
and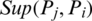 
is the support for Pj from Pi, with the conditions:
1. 
;
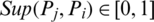2. 
;
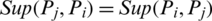3. 
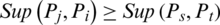if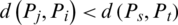 
, wherever d be a distance measure.
If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (15) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade is zero then the Eq. (15) will be converted for hesitant fuzzy sets.
Theorem 1: The aggregated objects by utilizing intuitionistic hesitant fuzzy power average (IHFPA) operator is as well an IHFS, wherever
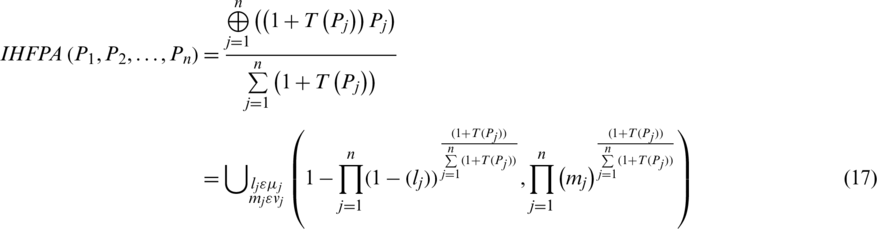
where
If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (17) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade is zero then the Eq. (17) will be converted for hesitant fuzzy sets.
Definition 9: Let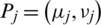 
be a group of IHFS and 
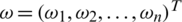is weight vector of Pj, 
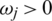and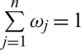 
, 
The IHFPWA operator is a function IHFPWA: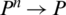 
where
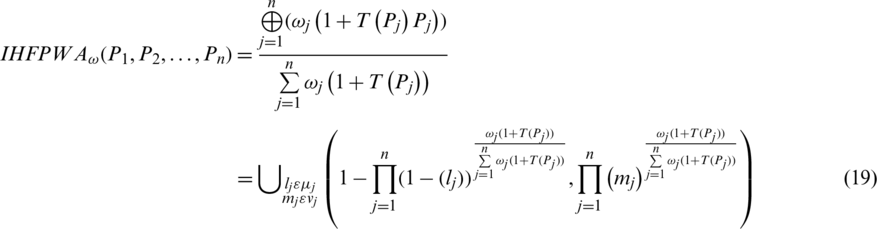
where
If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (19) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade to be zero then the Eq. (19) will be converted for hesitant fuzzy sets.
Property 1: (Idempotency) When Pj are equivalent, Pj = P for every 
, then
Property 2: (Boundedness) Let Pj be a family of IHFSs, and allows
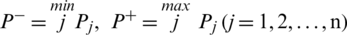
then
Property 3: (Monotonicity) Let Pj and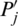 
be two sets of intuitionistic hesitant fuzzy sets (IHFSs), if 
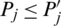for all j, then
Further, we give an IHFPOWA operator as follows:
Definition 10: Suppose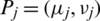 
is family of IHFSs, the IHFPOWA operator of dimension n a function IHFPOWA: 
, associated with weight vector 
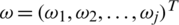such that 
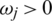and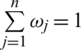 
. Furthermore
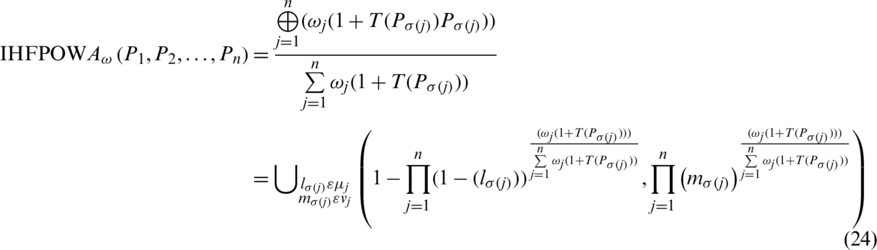
where 
indicates permutation of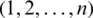 
, where 
, 
(
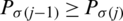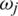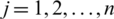) is family of weights in such a way that
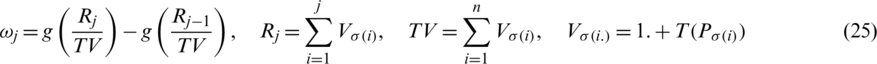
where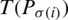 
implies the 
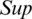of jth main IHFS 
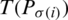by all the other (IHFSs), that is,
where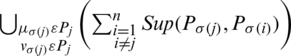 
shows the 
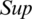of jth is the biggest intuitionistic hesitant fuzzy set (IHFS) 
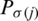, for the ith largest intuitionistic hesitant fuzzy set (IHFS) 
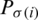. If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (24) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade is zero then the Eq. (24) will be converted for hesitant fuzzy sets. Some characteristics of IHFPOWA operator are as follow:
Property 4: (Idempotency) when each Pj is equivalent, which is, Pj = P for every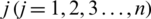 
, so
Property 5: (Boundedness) Suppose Pj is family of IHFSs, suppose
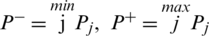
then
Property 6: (Monotonicity) Let Pj and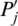 
be IHFSs, if 
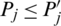for all j. Then
Property 7: (Commutativity) Let Pj and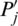 
be IHFSs, if 
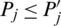for all j. Then
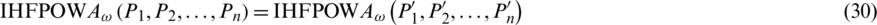
where 
be a permutation of Pj.
Definition 11: Let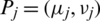 
be family of IHFSs, the intuitionistic hesitant fuzzy power hybrid averaging (IHFPHA) operator of elements n a function IHFPHA: 
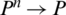, such that
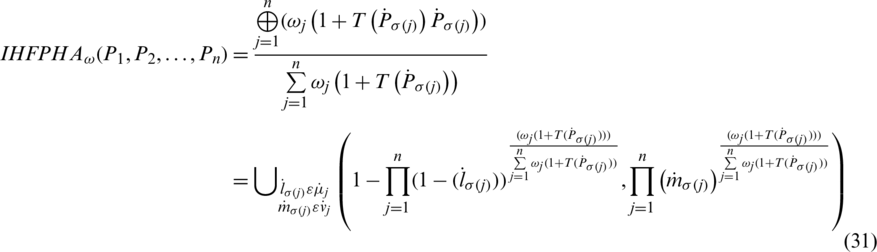
where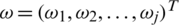 
is a mapped weight vector, such that 
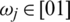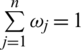and 
and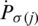 
is the jth biggest element in intuitionistic hesitant fuzzy arguments 
, 
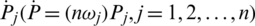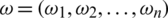be the weighting vector of IHF arguments 
, 
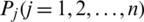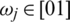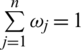and 
. And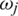 
be a family such that
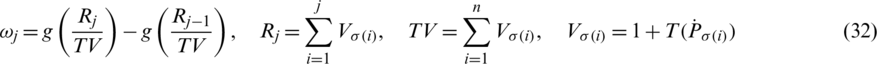
where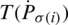 
is the 
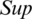of jth biggest IHFSs 
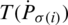by all the other (IHFSs), that is,
where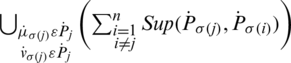 
shows the 
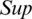of jth biggest IHFS 
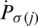, for the ith biggest IHFS 
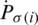. Particularly, IHFPHA is decreased to IHFPWA operator if 
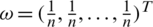and IHFPHA is decreased to IHFPOWA operator if 
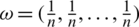. If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (31) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade is zero then the Eq. (31) will be converted for hesitant fuzzy sets.
Definition 12: Suppose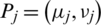 
is family of IHFSs, intuitionistic hesitant fuzzy power geometric (IHFPG) operator defined as a function IHFPG: 
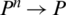where
where
where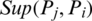 
is the support for Pj from Pi, with the conditions
1. 
;
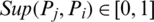2. 
;
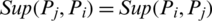3. 
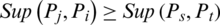if d(Pj, Pi) < d(Ps, Pt), such that d is a distance measure.
If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (34) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade is zero then the Eq. (34) will be converted for hesitant fuzzy sets.
Theorem 2: The aggregated elements by utilizing IHFPG operator define an IHFS, wherever
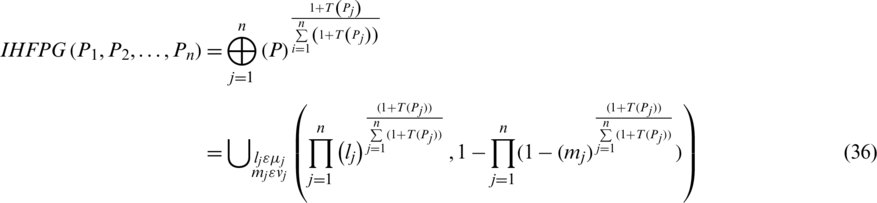
where
Definition 13: Let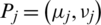 
(
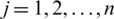) be family of IHFSs, 
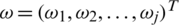is weight vector of Pj, 
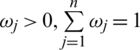. The IHFPWG operator defined as mapping IHFPWG: 
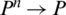where
where
If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (36) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade is zero then the Eq. (36) will be converted for hesitant fuzzy sets. IHFPWG operator has following characteristics.
Property 8: (Idempotency) when every Pj (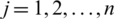
) is equivalent, such that Pj = P for every j, then
Property 9: (Boundedness) Suppose Pj is family of IHFSs, also suppose
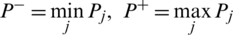
then
Property 10: (Monotonicity) Let Pj (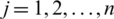
) and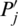 
be IHFSs, if 
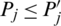for all j, then
Further, we give an IHFPOWG operator below:
Definition 14: Suppose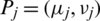 
is family of IHFSs, IHFPOWG operator of dimension n is mapping IHFPOWG: 
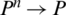, with an associated weight vector 
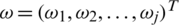such that 
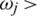0 and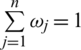 
. Furthermore
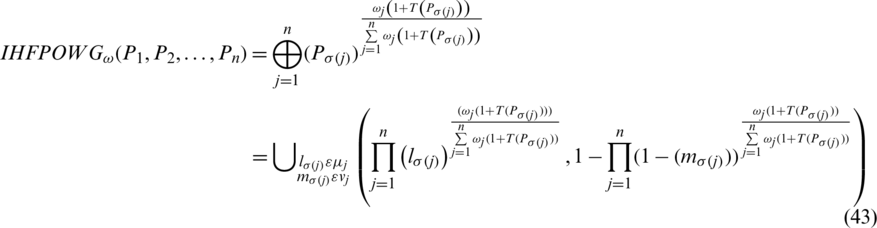
Such that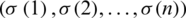 
be permutation of 
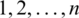, where 
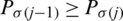for every 
, 
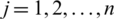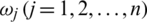is family of weights where
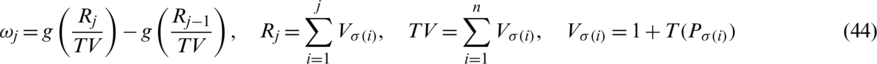
where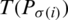 
indicates the sup of jth biggest intuitionistic hesitant fuzzy sets (IHFSs) 
by all the other (IHFSs), that is,
where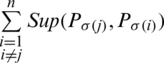 
shows the sup of jth biggest IHFS 
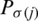,for the ith biggest IHFS 
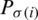. If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (43) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade is zero then the Eq. (43) will be converted for hesitant fuzzy sets. IHFPOWG operator provides the following characteristics.
Property 11: (Idempotency) when every Pj (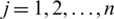
) is equivalent, such that, Pj = P for every j, so
Property 12: (Boundedness) Suppose Pj is family of IHFSs, suppose
then
Property 13: (Monotonicity) Let Pj and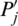 
be of intuitionistic hesitant fuzzy sets (IHFSs), if 
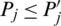for all j, then
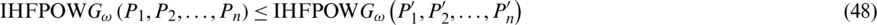
Property 14: (Commutativity) Let Pj and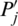 
be two intuitionistic hesitant fuzzy sets (IHFSs), if 
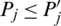for all j, then
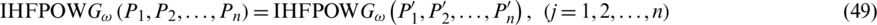
where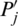 
be permutation of Pj.
Definition 15: Let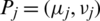 
be family of IHFSs, the IHFPHG operator of elements n is the function IHFPHG: 
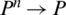, where
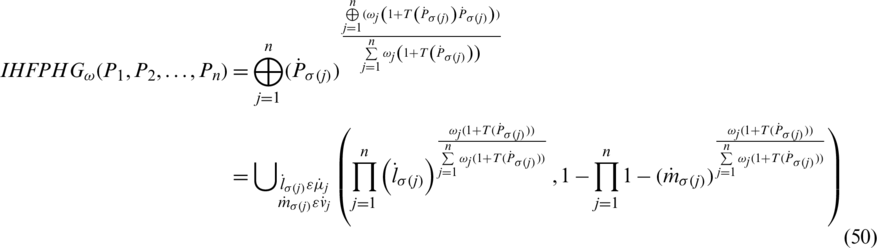
where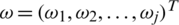 
is a related weight vector, where 
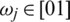and 
. 
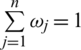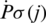is the jth biggest element of the intuitionistic hesitant fuzzy arguments 
(
, 
), 
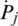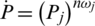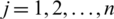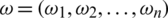is weighting vector of IHF arguments Pj where 
, 
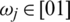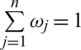and n is a matching factor, and 
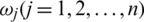is the collection of weights such that
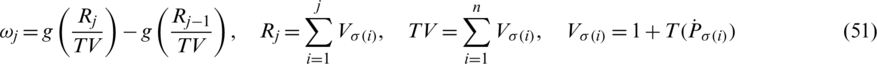
where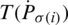 
indicates the 
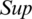of jth biggest IHFSs 
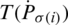by all the other (IHFSs), that is,
where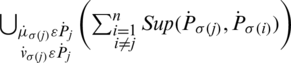 
shows the 
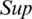of jth biggest IHFS 
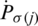and the ith biggest IHFS 
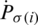. Particularly, IHFPHA is decreased to the IHFPWA operator when 
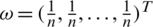IHFPHA is decreased to the IHFPOWA operator when 
. If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (50) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade to be zero then the Eq. (50) will be converted for hesitant fuzzy sets.
4 Similarity Measures Based on Intuitionistic Hesitant Fuzzy Sets
The VSM is one of the important tools for the similarity degree between objects. We straightforwardly utilized Jaccard, Dice and Cosine SM. Presently in this segment we characterize VSMs and weighted VSMs (WVSMs) for IHFSs.
Definition 16: Suppose that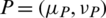 
and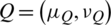 
are two IHFSs on X, then the Jaccard similarity measure (JSM) between P and Q is denoted and defined as follows:
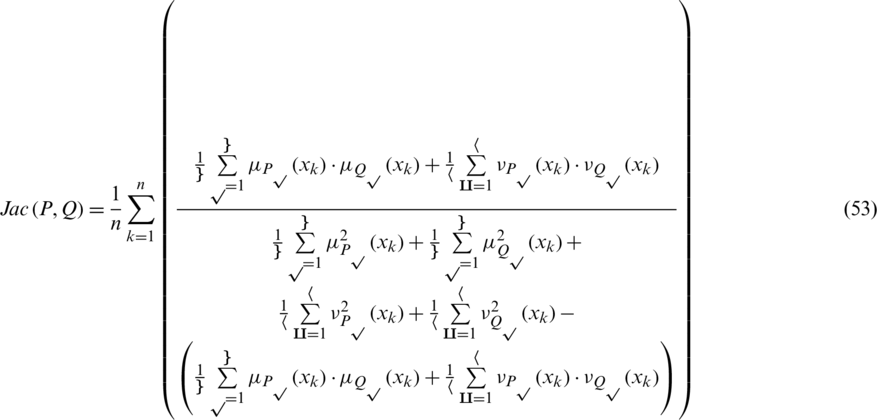
JSMs fulfill the following axioms:
1. 
;
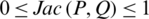2. 
;
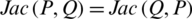3. 
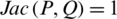, if P = Q.
If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (53) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade to be zero then the Eq. (53) will be converted for hesitant fuzzy sets.
Definition 17: Suppose that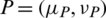 
and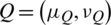 
are two IHFSs on X, then the weighted JSM (WJSM) between P and Q is denoted and defined as follows:
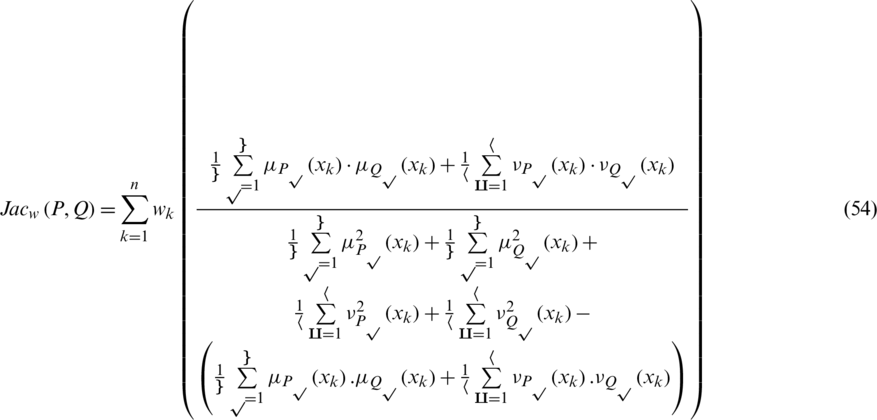
WJSMs fulfill the following axioms:
1. 
;
2. 
;
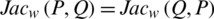3. 
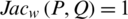, if P = Q.
where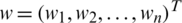 
speaks to the weight vector of every component 
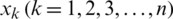contained in IHFS and the weight vector fulfills 
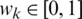for each 
, 
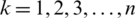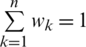. When we assume the weight vector be 
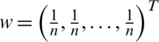, at that point the WJSM will change into JSM. Otherwise speaking w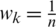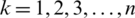hen 
, 
then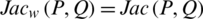 
. If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (54) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade to be zero then the Eq. (54) will be converted for hesitant fuzzy sets.
Definition 18: Suppose that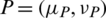 
and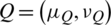 
are two IHFSs on X, then the Dice similarity measure (DSM) between P and Q is denoted and defined as follows:
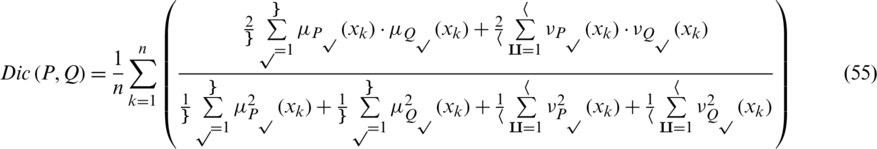
DSMs fulfills the following axioms:
1. 
;
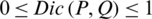2. 
;
3. 
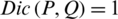, if P = Q.
If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (55) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade to be zero then the Eq. (55) will be converted for hesitant fuzzy sets.
Definition 19: Suppose that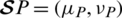 
and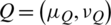 
are two IHFSs on X, then the weighted DSM (WDSM) between P and Q is denoted and defined as follows
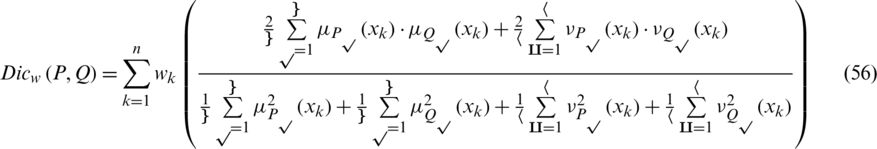
WDSMs fulfills the following axioms
1. 
;
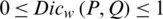2. 
;
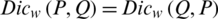3. 
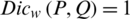, if P = Q.
where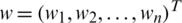 
speaks to the weight vector of every component 
contained in IHFS and the weight vector fulfills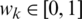 
for each 
, 
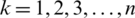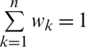. When we assume the weight vector be 
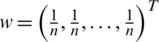, at that point the WDSM will change into DSM. Otherwise speaking w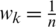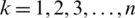hen 
, 
then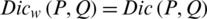 
. If we will choose the grade of truth and falsity in the form of singleton sets then the Eq. (56) will be converted for intuitionistic fuzzy sets. Similarly, if we choose the values of falsity grade to be zero then the Eq. (56) will be converted for hesitant fuzzy sets.
5 Multiple Attribute Decision Making Technique Based on Intuitionistic Hesitant Fuzzy Sets
In the portion, we use IHF power aggregation operators to multiple attribute DM through intuitionistic hesitant fuzzy data. Following hypotheses or concepts are utilized to signify the multiple attribute DM difficulties for possible calculation of developing technology commercialization with intuitionistic hesitant fuzzy data. Consider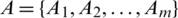 
is distinct set of alternatives, 
is the set of attributes. Consider 
(
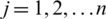) is weight vector of attributes, such that 
, 
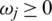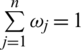. Then we will be going to apply the IHFPWA or PFPWG operator to the multiple attribute DM difficulties for possible calculation of developing technology commercialization by IHF data.
Step 1. Compute the supports:
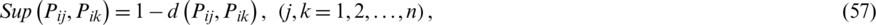
where justify 
terms (1)–(3) in portion 3. Here, with no loss of generalization, we compute d(Pij, Pik) with the normalized Hamming distance
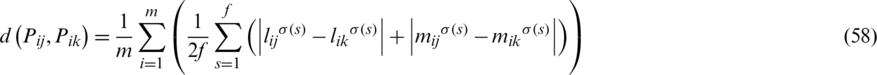
where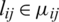 
, 
, 
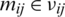and 
.
Step 2. Using the weights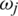 
of attribute Gj to compute weighted sup T(Pij) of the IHFS Pij by other IHFS Pik (j, 
, 
)
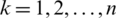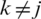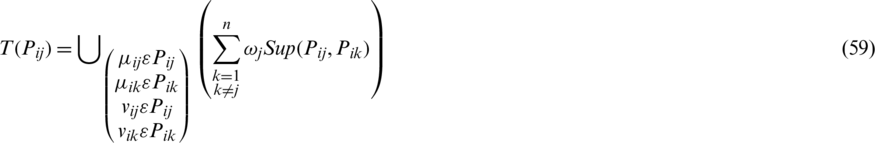
where calculated weight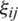 
is connected with the IHPFS Pij, (
, 
)
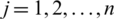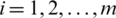where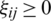 
, 
.
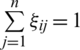Step 3. Use decision data provided in Tab. 1, IHFPWA operator
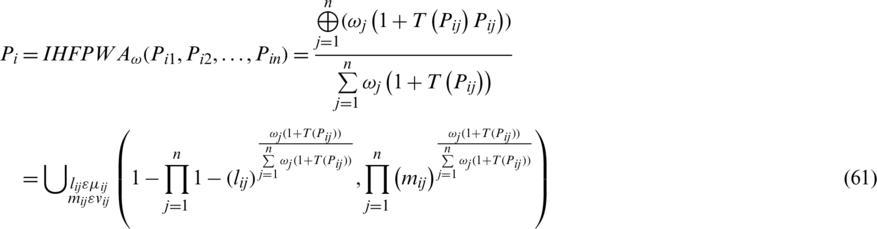
or
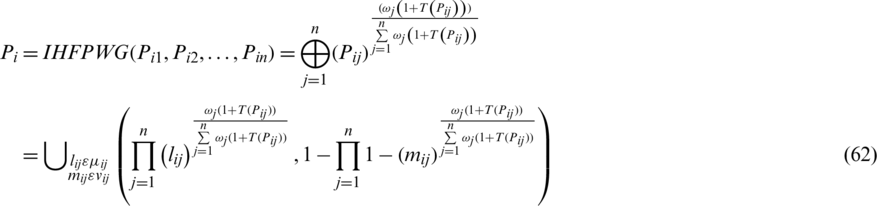
to receive the total preference objects Pi of the alternative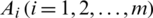 
.
Step 4. Compute scores S(Pi) of the whole IHFSs Pi to rank each the Ai then to select the top one(s). If two scores S(Pi) and S(Pj) have no difference then we want to compute the accuracy grades H(Pi), H(Pj) of the whole IHFSs Pi, Pj, respectively, classify the alternatives Ai, Aj consistent with accuracy grades H(Pi) and H(Pj).
Step 5. Ranking whole alternatives Ai and choose the greatest one(s) in accord by (Pi)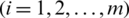 
.
Step 6. The end.
Example 1: Therefore, in the portion we give a mathematical model to illustrate the possible estimation of developing technology commercialization by intuition hesitant fuzzy data illustrating the technique recommended in this article. There is the board with five possible developing technologies enterprises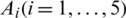 
to choose. Specialists choose four attributes to calculate the five possible developing technology enterprises: (i) G1 is the technical development (ii) G2 is the potential market and market risk; (iii) G3 is the industrialized structure, human resource management, and economic circumstances (iv) G4 is the job creation and the development of science and technology. The five possible developing technology enterprises Ai(i = 1, 2, 3, 4, 5) are to be estimated utilizing the IHF data by the decision maker in accordance with proposed attributes and weighting vector 
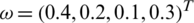shown in Tab. 1.
Table 1: Original decision matrix
Next, we use the method established to indicate potential evaluation of developing technology commercialization of four possible developing technology enterprises, see Tab. 2.
Table 2: Aggregated values by using the formulas of IHFPWA and IHFPWG
Step 1. Compute the weight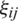 
(
, 
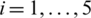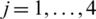) that is related by IHFN 
(
, 
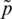), that included 
Step 2. Corresponding to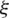 
and IHFN 
(
, 
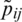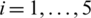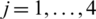), compute the whole IHFNs 
(i = 1, 2, 3, 4, 5, j = 1, 2, 3, 4) by utilizing the IHFPWA (IHFPWG) operator to get the whole IHFNs 
(i = 1, 2, 3, 4, 5) of the developing technology enterprise Ai. The aggregating values are reflected in Tab. 1.
By using the formula of score value, we examine the score values of the aggregated values of Tab. 2, see Tab. 3.
Step 1. In accordance with the aggregating values presented in Tab. 2 and the score functions of the developing technology enterprises are presented in Tab. 3.
Table 3: Score values of the aggregated values
Further, we examine ranking results of the score values.
Step 2. Approve the score functions presented in the Tab. 3, and compare the formula of score functions, the ranking of the developing technology enterprises as presented in Tab. 4. Remember this the greater than sign “ > ” implies “preference.”
From above analysis, we get as best option alternative 
.
Example 2: The amount from developments by an organization is legitimately corresponding to the standard of building substances they use. Appropriate review of building substance before development is the confirmation of good building measures. The building substances to be utilized ought to be carefully checked before applying. The best possible check and equalization arrangement of investigation approves the manufacturers to utilize the correct substances for developments to improve the standard of their task. Let five known building substances 
be as given in the IHFSs structure as follows:
and
By using the Eq. (56), we get the following values, which are summarized based on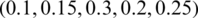 
:
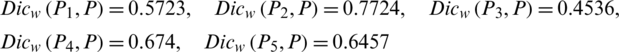
Ranking values of the above measures are summarized as follows:
Table 5: Comparative analysis of the explored and existing measures
The best option is P2. Additionally, if we choose the intuitionistic hesitant fuzzy types of information’s with existing conditions that are the sum of the maximum (also for minimum) of the truth grade and minimum (also for maximum) of the falsity grade cannot exceed from unit interval, and the sum of the maximum of the truth grade and falsity grade exceeds the unit interval, then it is very difficult to cope with such types of issues. But, when we choose the condition as in this explorative study then the sum of the maximum of the truth grade and falsity grade cannot exceed from the unit interval. The theories of intuitionistic fuzzy set and hesitant fuzzy set describe the foundation of the intuitionistic hesitant fuzzy set. When we choose the intuitionistic fuzzy types of information’s or hesitant fuzzy types of information then the explored approach easily copes with it. But, if we choose the intuitionistic hesitant fuzzy types of information’s, then the existing types of theories are cannot able to cope with it.
The comparative analysis of the explored measures with selected existing measures are summarized in Tab. 5.
From above analysis, the three different measures above share the same ranking values and the best option is P2. The graphical representation for the information of Tab. 5, we explained with the help of Fig. 1.
Figure 1: Graphical representation of the explored and existing measures
Fig. 1 represents the family of proposed and existing ideas and contains five types of values for each operator showing the family of alternatives. The alternative two provides the best values for all operators. For simplicity we have drawn the Fig. 1.
From the above analysis, the explored measures and operators based on IHFSs are more perfect and more proficient then existing methods and measures.
We explored the improved intuitionistic hesitant fuzzy set with a new condition that is the sum of the maximum of the truth grade and maximum of the falsity grade which cannot exceed from the unit interval. Additionally, we examine the multi-attribute decision making challenge built upon power aggregating operators with IHF data. So, inspired from the model of power aggregating operators, we established few power aggregation operators for aggregating IHF information: IHFPA operator, IHFPG operator, IHFPWA operator, IHFPWG operator, IHFPOWA operator, IHFPOWG operator, IHFPHA operator, and IHFPHG operator. Additionally, some similarity measures based on IHFSs are also explored and their special cases discussed. Outstanding feature of these recommended operators are examined. So, we used operators to establish few methods to resolve the IHF multi attribute DM difficulties. A helpful example is presented to confirm the established methodology and to determine its practicability and efficiency. The advantages, comparative analysis, and geometrical representation of the presented works are also discussed in detailed.
Notably, that the article results of the article can be expanded to the IvIHF situation and further fuzzy situations. In superior study, it is enough to get the implementation of these operators to resolve the actual DM drawbacks as fuzzy investigation, unsure programming and image recognition, etc. We must also deal with few new operators for the foundation of PHFNs for example, modify them to complex q-rung fuzzy aggregation operators [48–50], complex Pythagorean fuzzy set [51], spherical fuzzy operators [52].
Data Availability: The data used in this article are artificial and hypothetical, and anyone can use these data before prior permission by just citing this article.
Funding Statement: This paper is supported by “Algebra and Applications Research Unit, Division of Computational Science, Faculty of Science, Prince of Songkla University”.
Conflicts of Interest: The authors declare that they have no conflicts of interest.
1. Pamučar, D., Janković, A. (2020). The application of the hybrid interval rough weighted power-heronian operator in multi-criteria decision making. Operational Research in Engineering Sciences: Theory and Applications, 3(2), 54–73. DOI 10.31181/oresta2003049p. [Google Scholar] [CrossRef]
2. Sinani, F., Erceg, Z., Vasiljević, M. (2020). An evaluation of a third-party logistics provider: The application of the rough Dombi–Hamy mean operator. Decision Making: Applications in Management and Engineering, 3(1), 92–107. DOI 10.31181/dmame2003080f. [Google Scholar] [CrossRef]
3. Ullah, K., Ali, Z., Jan, N., Mahmood, T., Maqsood, S. (2018). Multi-attribute decision making based on averaging aggregation operators for picture hesitant fuzzy sets. Technical Journal, 23(4), 84–95. [Google Scholar]
4. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(2), 338–356. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
5. Jamkhaneh, E. B., Garg, H. (2018). Some new operations over the generalized intuitionistic fuzzy sets and their application to decision-making process. Granular Computing, 3(2), 111–122. DOI 10.1007/s41066-017-0059-0. [Google Scholar] [CrossRef]
6. Petrovic, I., Kankaras, M. (2020). A hybridized IT2FS-DEMATEL-AHP-TOPSIS multicriteria decision making approach: Case study of selection and evaluation of criteria for determination of air traffic control radar position. Decision Making: Applications in Management and Engineering, 3(1), 146–164. DOI 10.31181/dmame2003134p. [Google Scholar] [CrossRef]
7. Mizumoto, M., Tanaka, K. (1976). Some properties of fuzzy sets of type 2. Information and Control, 31(4), 312–340. DOI 10.1016/S0019-9958(76)80011-3. [Google Scholar] [CrossRef]
8. Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
9. Atanassov, K. T. (2012). On the concept of intuitionistic fuzzy sets. In: On intuitionistic fuzzy sets theory (1–16). Berlin, Heidelberg: Springer. [Google Scholar]
10. Garg, H., Arora, R. (2018). A nonlinear-programming methodology for multi-attribute decision-making problem with interval-valued intuitionistic fuzzy soft sets information. Applied Intelligence, 48(8), 2031–2046. DOI 10.1007/s10489-017-1035-8. [Google Scholar] [CrossRef]
11. Zeng, S., Su, W., Zhang, C. (2016). Intuitionistic fuzzy generalized probabilistic ordered weighted averaging operator and its application to group decision making. Technological and Economic Development of Economy, 22(2), 177–193. DOI 10.3846/20294913.2014.984253. [Google Scholar] [CrossRef]
12. Stanujkić, D., Karabašević, D. (2018). An extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: A case of website evaluation. Operational Research in Engineering Sciences: Theory and Applications, 1(1), 29–39. DOI 10.31181/ORESTA19012010129S. [Google Scholar] [CrossRef]
13. Sotirova, E., Atanassov, K., Shannon, A., Kim, T., Krawczak, M. et al. (2016). Intuitionistic fuzzy evaluations for analysis of a student’s knowledge of mathematics in university e-learning courses. 2016 IEEE 8th International Conference on Intelligent System, pp. 535–537, Sofia, Bulgaria, UK, IEEE. [Google Scholar]
14. Bustince, H., Burillo, P. (1996). Vague sets are intuitionistic fuzzy sets. Fuzzy Sets and Systems, 79(3), 403–405. DOI 10.1016/0165-0114(95)00154-9. [Google Scholar] [CrossRef]
15. Bustince, H., Burillo, P. (1995). Correlation of interval-valued intuitionistic fuzzy sets. Fuzzy Sets and Systems, 74(2), 237–244. DOI 10.1016/0165-0114(94)00343-6. [Google Scholar] [CrossRef]
16. Dubois, D., Gottwald, S., Hajek, P., Kacprzyk, J., Prade, H. (2005). Terminological difficulties in fuzzy set theory–-The case of “intuitionistic fuzzy sets. Infinite Study. [Google Scholar]
17. Ye, J. (2009). Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Expert Systems with Applications, 36(3), 6899– 6902. DOI 10.1016/j.eswa.2008.08.042. [Google Scholar] [CrossRef]
18. Wei, G. W. (2011). Gray relational analysis method for intuitionistic fuzzy multiple attribute decision making. Expert systems with Applications, 38(9), 11671–11677. DOI 10.1016/j.eswa.2011.03.048. [Google Scholar] [CrossRef]
19. Park, D. G., Kwun, Y. C., Park, J. H., Park, I. Y. (2009). Correlation coefficient of interval-valued intuitionistic fuzzy sets and its application to multiple attribute group decision making problems. Mathematical and Computer Modelling, 50(9–10), 1279–1293. DOI 10.1016/j.mcm.2009.06.010. [Google Scholar] [CrossRef]
20. Wei, G., Zhao, X., Lin, R. (2010). Some induced aggregating operators with fuzzy number intuitionistic fuzzy information and their applications to group decision making. International Journal of Computational Intelligence Systems, 3(1), 84–95. DOI 10.1080/18756891.2010.9727679. [Google Scholar] [CrossRef]
21. Zhao, H., Xu, Z., Ni, M., Liu, S. (2010). Generalized aggregation operators for intuitionistic fuzzy sets. International Journal of Intelligent Systems, 25(1), 1–30. DOI 10.1002/int.20386. [Google Scholar] [CrossRef]
22. Xu, Z., Yager, R. R. (2006). Some geometric aggregation operators based on intuitionistic fuzzy sets. International Journal of General Systems, 35(4), 417–433. DOI 10.1080/03081070600574353. [Google Scholar] [CrossRef]
23. Torra, V. (2010). Hesitant fuzzy sets. International Journal of Intelligent Systems, 25(6), 529–539. DOI 10.1002/int.20418. [Google Scholar] [CrossRef]
24. Torra, V., Narukawa, Y. (2009). On hesitant fuzzy sets and decision. IEEE International Conference on Fuzzy Systems, pp. 1378–1382, Jeju Island, Korea, IEEE. [Google Scholar]
25. Mahmood, T., Ullah, K., Jan, N., Deli, I., Khan, Q. (2017). Some aggregation operators for bipolar-valued hesitant fuzzy information based on Einstein operational laws. Journal of Engineering and Applied Sciences, 36(2), 63–72. DOI 10.4314/jfas.v10i4s.85. [Google Scholar] [CrossRef]
26. Mahmood, T., Mehmood, F., Khan, Q. (2017). Some generalized aggregation operators for cubic hesitant fuzzy sets and their applications to multi criteria decision making. Punjab University Journal of Mathematics, 49, 31–49. [Google Scholar]
27. Ullah, K., Mahmood, T., Jan, N., Broumi, S., Khan, Q. (2018). On bipolar-valued hesitant fuzzy sets and their applications in multi-attribute decision making. Nucleus, 55(2), 85–93. [Google Scholar]
28. Xia, M., Xu, Z., Chen, N. (2013). Some hesitant fuzzy aggregation operators with their application in group decision making. Group Decision and Negotiation, 22(2), 259–279. DOI 10.1007/s10726-011-9261-7. [Google Scholar] [CrossRef]
29. Xu, Z., Zhang, X. (2013). Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowledge-Based Systems, 52, 53–64. DOI 10.1016/j.knosys.2013.05.011. [Google Scholar] [CrossRef]
30. Sun, Q., Ouyang, J. (2015). Hesitant fuzzy multi-attribute decision making based on TOPSIS with entropy-weighted method. Management Science and Engineering, 9(3), 1–6. [Google Scholar]
31. Yu, D., Wu, Y., Zhou, W. (2011). Multi-criteria decision making based on Choquet integral under hesitant fuzzy environment. Journal of Computational Information Systems, 7(12), 4506–4513. [Google Scholar]
32. Liu, J., Sun, M. (2013). Generalized power average operator of hesitant fuzzy numbers and its application in multiple attribute decision making. Journal of Computational Information Systems, 9(8), 3051–3058. [Google Scholar]
33. Chen, J., Huang, X., Tang, J. (2018). Distance measures for higher order dual hesitant fuzzy sets. Computational and Applied Mathematics, 37(2), 1784–1806. DOI 10.1007/s40314-017-0423-3. [Google Scholar] [CrossRef]
34. Kumar, K., Garg, H. (2018). TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment. Computational and Applied Mathematics, 37(2), 1319–1329. DOI 10.1007/s40314-016-0402-0. [Google Scholar] [CrossRef]
35. Wei, G., Zhang, N. (2014). A multiple criteria hesitant fuzzy decision making with Shapley value based VIKOR method. Journal of Intelligent & Fuzzy Systems, 26(2), 1065–1075. DOI 10.3233/IFS-130798. [Google Scholar] [CrossRef]
36. Xu, G. L., Wan, S. P., Dong, J. Y. (2016). A hesitant fuzzy programming method for hybrid MADM with incomplete attribute weight information. Informatica, 27(4), 863–892. DOI 10.15388/Informatica.2016.115. [Google Scholar] [CrossRef]
37. Yu, D., Zhang, W., Huang, G. (2016). Dual hesitant fuzzy aggregation operators. Technological and Economic Development of Economy, 22(2), 194–209. DOI 10.3846/20294913.2015.1012657. [Google Scholar] [CrossRef]
38. Singh, P. (2014). A new method for solving dual hesitant fuzzy assignment problems with restrictions based on similarity measure. Applied Soft Computing, 24, 559–571. DOI 10.1016/j.asoc.2014.08.008. [Google Scholar] [CrossRef]
39. Liao, H., Xu, Z. (2014). Subtraction and division operations over hesitant fuzzy sets. Journal of Intelligent & Fuzzy Systems, 27(1), 65– 72. DOI 10.3233/IFS-130978. [Google Scholar] [CrossRef]
40. Liao, H., Xu, Z. (2014). Some new hybrid weighted aggregation operators under hesitant fuzzy multi-criteria decision-making environment. Journal of Intelligent & Fuzzy Systems, 26(4), 1601–1617. DOI 10.3233/IFS-130841. [Google Scholar] [CrossRef]
41. Zhang, Z. (2013). Hesitant fuzzy power aggregation operators and their application to multiple attribute group decision making. Information Sciences, 234, 150–181. DOI 10.1016/j.ins.2013.01.002. [Google Scholar] [CrossRef]
42. Yager, R. R. (2001). The power average operator. IEEE Transactions on Systems, Man, and Cybernetics–-Part A: Systems and Humans, 31(6), 724–731. DOI 10.1109/3468.983429. [Google Scholar] [CrossRef]
43. Liu, P., Li, Y., Antuchevičienė, J. (2016). Multi-criteria decision-making method based on intuitionistic trapezoidal fuzzy prioritised OWA operator. Technological and Economic Development of Economy, 22(3), 453–469. DOI 10.3846/20294913.2016.1171262. [Google Scholar] [CrossRef]
44. Beg, I., Rashid, T. (2014). Group decision making using intuitionistic hesitant fuzzy sets. International Journal of Fuzzy Logic and Intelligent Systems, 14(3), 181–187. DOI 10.5391/IJFIS.2014.14.3.181. [Google Scholar] [CrossRef]
45. Geetha, S., Narayanamoorthy, S., Kang, D., Kureethara, J. V. (2019). A novel assessment of healthcare waste disposal methods: Intuitionistic hesitant fuzzy MULTIMOORA decision making approach. IEEE Access, 7, 130283–130299. DOI 10.1109/ACCESS.2019.2940540. [Google Scholar] [CrossRef]
46. Wang, R., Li, Y. (2018). Picture hesitant fuzzy set and its application to multiple criteria decision-making. Symmetry, 10(7), 295. DOI 10.3390/sym10070295. [Google Scholar] [CrossRef]
47. Peng, J. J., Wang, J. Q., Wu, X. H., Zhang, H. Y., Chen, X. H. (2015). The fuzzy cross-entropy for intuitionistic hesitant fuzzy sets and their application in multi-criteria decision-making. International Journal of Systems Science, 46(13), 2335–2350. DOI 10.1080/00207721.2014.993744. [Google Scholar] [CrossRef]
48. Liu, P., Mahmood, T., Ali, Z. (2020). Complex q-Rung orthopair fuzzy aggregation operators and their applications in multi-attribute group decision making. Information–-An International Interdisciplinary Journal, 11(1), 5. DOI 10.3390/info11010005. [Google Scholar] [CrossRef]
49. Jan, N., Zedam, L., Mahmood, T., Ullah, K., Ali, Z. (2019). Multiple attribute decision making method under linguistic cubic information. Journal of Intelligent & Fuzzy Systems, 36(1), 253–269. DOI 10.3233/JIFS-181253. [Google Scholar] [CrossRef]
50. Liu, P., Ali, Z., Mahmood, T. (2019). A method to multi-attribute group decision-making problem with complex q-Rung orthopair linguistic information based on heronian mean operators. International Journal of Computational Intelligence Systems, 12(2), 1465–1496. DOI 10.2991/ijcis.d.191030.002. [Google Scholar] [CrossRef]
51. Ullah, K., Mahmood, T., Ali, Z., Jan, N. (2019). On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex & Intelligent Systems, 6(1), 15–27. DOI 10.1007/s40747-019-0103-6. [Google Scholar] [CrossRef]
52. Ullah, K., Mahmood, T., Jan, N., Ali, Z. (2019). A note on geometric aggregation operators in spherical fuzzy environment and its application in multi-attribute decision making. Journal of Engineering and Applied Sciences, 37(2), 77–98. DOI 10.25211/jeas.v37i2.2871. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |