 Computer Modeling in Engineering & Sciences
Computer Modeling in Engineering & Sciences
 Computer Modeling in Engineering & Sciences Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2021.013699
ARTICLE
Spherical Linear Diophantine Fuzzy Sets with Modeling Uncertainties in MCDM
1Department of Mathematics, University of the Punjab, Lahore, 54590, Pakistan
2Department of Logistics, Military academy, University of Defence, Belgrade, 11000, Serbia
3Department of Mathematics, Huzhou University, Huzhou, 313000, China
4Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering, Changsha University of Science & Technology, Changsha, 410114, China
*Corresponding Author: Yu-Ming Chu. Email: chuyuming@zjhu.edu.cn
Received: 17 August 2020; Accepted: 30 September 2020
Abstract: The existing concepts of picture fuzzy sets (PFS), spherical fuzzy sets (SFSs), T-spherical fuzzy sets (T-SFSs) and neutrosophic sets (NSs) have numerous applications in decision-making problems, but they have various strict limitations for their satisfaction, dissatisfaction, abstain or refusal grades. To relax these strict constraints, we introduce the concept of spherical linear Diophantine fuzzy sets (SLDFSs) with the inclusion of reference or control parameters. A SLDFS with parameterizations process is very helpful for modeling uncertainties in the multi-criteria decision making (MCDM) process. SLDFSs can classify a physical system with the help of reference parameters. We discuss various real-life applications of SLDFSs towards digital image processing, network systems, vote casting, electrical engineering, medication, and selection of optimal choice. We show some drawbacks of operations of picture fuzzy sets and their corresponding aggregation operators. Some new operations on picture fuzzy sets are also introduced. Some fundamental operations on SLDFSs and different types of score functions of spherical linear Diophantine fuzzy numbers (SLDFNs) are proposed. New aggregation operators named spherical linear Diophantine fuzzy weighted geometric aggregation (SLDFWGA) and spherical linear Diophantine fuzzy weighted average aggregation (SLDFWAA) operators are developed for a robust MCDM approach. An application of the proposed methodology with SLDF information is illustrated. The comparison analysis of the final ranking is also given to demonstrate the validity, feasibility, and efficiency of the proposed MCDM approach.
Keywords: Spherical linear Diophantine fuzzy set; new operations of picture fuzzy sets; spherical linear Diophantine fuzzy weighted geometric aggregation operator; spherical linear Diophantine fuzzy weighted average aggregation operator; MCDM
Classical mathematics is not necessarily useful when solving real-world issues because of the complexities and vagueness inherent in such questions. Zadeh [1] developed the fuzzy set concept by awarding the grades from [0, 1] to alternatives. Since Zadeh’s approach to the fuzzy collection and fuzzy logic has been utilized in numerous domains to describe imprecision, ambiguity, and obscureness. Zadeh [2] developed the definition of the linguistic component to linking real-life conditions to mathematical models. However according to Zadeh [2] linguistic index is a variable, whose meanings are statements or phrases in imaginary or real expression. When such terms are represented by fuzzy sets specified over a reference set, then the variable is said to be the fuzzy linguistic variable. Atanassov [3–5] established the notion of intuitionistic fuzzy sets (IFSs) as an extension of fuzzy sets by adding the notions of satisfaction degree and dissatisfaction degree including the constraint that the addition of such two classes would not surpass unity. Atanassov [6] described the geometrical viewpoint of the IF-objects. In 1998 the concept of the neutrosophic system was proposed by Smarandache [7] as an annexed form of IFSs and fuzzy sets. This structure contains satisfaction, indeterminacy, and dissatisfaction grades for every alternative of the reference set. All the grades are independent of each other and can be taken from [0, 1].
There exist various real situations in which we cannot tackle the input data by using fuzzy sets, IFSs and neutrosophic sets and human opinion cannot be always between yes or no. For example, in the last few decades there exists some real-life applications in medical image analysis and diagnosis [8–14], radar image processing [15–18], biometric and iris recognition [19,20], human detection [21,22]. Akbarizadeh [10,11] introduced a new statistical-based kurtosis wavelet energy feature for texture recognition of SAR images and Segmentation of SAR satellite images using cellular learning automata and adaptive chains. Akbarizadeh et al. [12,15] presented a new ensemble clustering method for PolSAR image segmentation. Akbarizadeh et al. [13] a new curvelet-based texture classification approach for land cover recognition of SAR satellite images. Akbarizadeh et al. [14] introduced the idea of a segmentation parameter estimation algorithm based on curvelet transform coefficients energy for feature extraction and texture description of SAR images. Gong et al. [23] defined the change detection in synthetic aperture radar images based on image fusion and fuzzy clustering. Modava et al. [21,22] introduced the coastline extraction from SAR images using spatial fuzzy clustering and the active contour method. Rahmani et al. [24] presented the unsupervised feature learning based on sparse coding and spectral clustering for segmentation of synthetic aperture radar images. Shanmugan et al. [25] introduced the textural features for radar image analysis. Tirandaz et al. [26] proposed a two-phased algorithm based on kurtosis curvelet energy and unsupervised spectral regression for segmentation for SAR images.
In many complex real-life circumstances, the knowledge can not necessarily be restricted to yes or no, although it may be yes, abstain, no, and denial. To deal with these types of situations Cuong [27–29] introduced the picture fuzzy set (PFS) in 2013. Elements in this system reflect degrees of happiness, abstinence, and dissatisfaction under the restriction
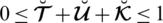 and with the refusal degree
and with the refusal degree
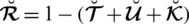 . This method is similar to human existence and also addresses uncertainty about decision-making difficulties.
. This method is similar to human existence and also addresses uncertainty about decision-making difficulties.
According to the constraint of the picture fuzzy set, all the grades are dependent on each other and make us unable to assign the values of these grades independently from [0, 1]. Considering these limitations Andekah et al. [30] presented the new idea of a spherical fuzzy set (SFS) with the constraint
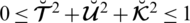 . To remove the restrictions of SFS, they established another structure named as T-spherical fuzzy set (T-SFS) satisfying the constraint
. To remove the restrictions of SFS, they established another structure named as T-spherical fuzzy set (T-SFS) satisfying the constraint
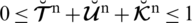 . As we know Pythagorean fuzzy sets (PyFSs) [31–34] and q-rung orthopair fuzzy sets (q-ROFSs) [35–37] are generalized models of IFSs. On the same pattern SFS and T-SFS are generalizations of picture fuzzy set. SFSs and T-SFSs enlarge the space of grades and easily handle ambiguities in decision-making problems. Si et al. [38] an approach to rank picture fuzzy numbers for decision-making problems. Stanujkić et al. [39] proposed an extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: A case of website evaluation. Sharma et al. [40] a rough set theory application in forecasting models.
. As we know Pythagorean fuzzy sets (PyFSs) [31–34] and q-rung orthopair fuzzy sets (q-ROFSs) [35–37] are generalized models of IFSs. On the same pattern SFS and T-SFS are generalizations of picture fuzzy set. SFSs and T-SFSs enlarge the space of grades and easily handle ambiguities in decision-making problems. Si et al. [38] an approach to rank picture fuzzy numbers for decision-making problems. Stanujkić et al. [39] proposed an extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: A case of website evaluation. Sharma et al. [40] a rough set theory application in forecasting models.
There exist some limitations in SFSs and T-SFSs corresponding to the satisfaction, abstinence, and dissatisfaction grades. Both constraints show that there exists some dependency between the grades. To remove these limitations, a novel model of spherical linear Diophantine fuzzy set (SLDFS) is introduced with the constraints
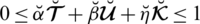 and
and
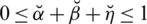 , where
, where
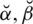 and
and
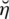 are reference parameters corresponding to the satisfaction, abstinence, and dissatisfaction grades respectively, and taken from the interval [0, 1]. The beauty of this new idea is that we can take all the grades independently from [0, 1] and reference parameters categorize the structure and handle uncertainties in a parametric manner. In the neutrosophic set, we can take all the grades independently but it does not contain parameterizations. So SLDFS is more efficient and effective as compared to picture fuzzy set, SFS, T-SFS, and neutrosophic set.
are reference parameters corresponding to the satisfaction, abstinence, and dissatisfaction grades respectively, and taken from the interval [0, 1]. The beauty of this new idea is that we can take all the grades independently from [0, 1] and reference parameters categorize the structure and handle uncertainties in a parametric manner. In the neutrosophic set, we can take all the grades independently but it does not contain parameterizations. So SLDFS is more efficient and effective as compared to picture fuzzy set, SFS, T-SFS, and neutrosophic set.
1.1 Decision-Making Based Hypothetical Data Interpretation
Molodtsov [41] emerged as a statistical paradigm for working out complexities of the sentiment of a different category of sets conventionally regarded as soft sets. Numerous mathematicians have worked on various hybrid structures of fuzzy and soft sets in the last few decades. Agarwal et al. [42] introduced different findings and their implementations on simplified intuitionistic fuzzy soft sets. Çağman et al. [43] developed the philosophy of fuzzy soft sets (FSSs) and its decision-making implementations. The notion of fuzzy topological spaces was developed by Chang [44]. Coker [45] developed the idea of IF-topological space.
Garg [46–48] described generalized aggregation of “Pythagorean fuzzy information” utilizing Einstein operations, generalized “intuitionstic fuzzy informational” geometric interaction operators utilizing Einstein t-conorm and t-norm, accuracy mapping under “interval-valued Pythagorean fuzzy environment” and their implementations in selecting optimal solution in different issues. Chen et al. [49] constructed the methodology of MCDM based on vague set theory. Tversky et al. [50] provided several developments on the collective representation of ambiguity in the prospect theory. With the addition of t-conorm and t-norm, Dombi [51] presented the definition of the Dombi operators. Feng et al. [52,53] established an adaptive solution to fuzzy soft sets decision-making obstacles. Using empirical examples they offered a novel perspective on “generalized intuitionistic fuzzy soft sets” (GIFSSs). Jose et al. [54] analyzed various operators, score with accuracy functions, and MCDM based on IF-numbers (IFNs). Kaur et al. [55] developed aggregation algorithms on “cubic intuitionistic fuzzy numbers” (CIFNs), and proposed a decision-making framework.
Mahmood et al. [56] developed cubic hesitant fuzzy numbers (CHFNs) generalized aggregation operators and introduced an algorithm for combinatorial optimization problems. Chen et al. [57] presented an annex of a bipolar fuzzy set titled an m-polar fuzzy set. Wang et al. [58] continued to work on single-valued neutrosophic structures and established their applications. Riaz et al. [59–62] investigated multiple-criteria group agribusiness decision-making utilizing distinct “cubic m-polar fuzzy aggregation operators.” They created the idea of a “linear Diophantine fuzzy set” (LDFSs) as an annex of IFSs, PyFSs, and q-ROFSs. They addressed the shortcomings of current systems and built a new model through the use of comparison parameters to tackle uncertainties. For the correct variety of material handling appliances the defined “linear Diophantine fuzzy soft rough sets” (LDFSRSs). Riaz et al. [63] established some results on “cubic bipolar fuzzy ordered weighted” aggregation operators with its implementations. Zhan et al. [64,65] introduced the principles of rough soft hemirings, soft rough cover, and their contributions to MCGDM obstacles. In emergency decision-taking based on WDBA and CODAS, Peng et al. [66] built several algorithms for interval-valued fuzzy soft sets utilizing new knowledge calculation.
Xu [67] presented the intuitionistic fuzzy aggregation operators. Xu et al. [68] introduced the principle and implementations of intuitionistic processing of fuzzy knowledge in their book. Xu [69] presented hesitant fuzzy sets theory and different forms of hesitant fuzzy aggregation operators in his book. Ye [70] implemented prioritized weighted operators with a valued interval hesitant fuzzy information and their implementation in MADM. Ye [71] implemented linguistic neutrosophic cubic numbers and their use in decision-making on various attributes. Guo [72] proposed the amount of information and attitudinal-based method for ranking Atanassov’s intuitionistic fuzzy values. Hong et al. [73] presented the multi-criteria fuzzy decision-making problems based on vague set theory.
Throughout contemporary science of decision-making, the theory of MCDM plays a significant part in addressing the challenges of our everyday lives. It is commonly used in a variety of fields, including industry, economics, human sciences, and engineering technologies include performance evaluation, mission appraisal, business decision-making, and many more. He et al. [74] set up a project to strengthen the method of the emergency rescue of fatal gas explosion incidents in Chinese coal mines. Zhang et al. [75,76] proposed a decision-making method focused on a consensus, multi-attribute community. In a linguistic sense, they presented the style of loss and the impact study. They also conducted a detailed empirical analysis of the efficiency of consensus in community decision-making. Yu et al. [77] implemented unbalanced hesitant linguistic word sets and proposed an expanded TODIM for community decision-making with multi-parameters. For incomplete preference relations on hesitant fuzzy information, Zhang et al. [78,79] and Kushwaha et al. [80] set priority weights and associated consistency. Under collective decision-making, they extracted priority weights from intuitionistic multiplicative choice relationships. They also developed an innovative method for handling multi-granular measurements of the linguistic continuum in large-scale MAGDM. Zolfani et al. [81] have implemented an automated framework to help reach consensus. They used techniques of group decision-making for heterogeneous choice systems.
Some mathematicians have developed several operations in recent years and have implemented various aggregations operators on fuzzy picture sets. Pamucar et al. [82] photographed the aggregation operators of Dombi and their MADM implementations. Using Muirhead mean operators, Xu et al. [83] developed a system for MADM with picture fuzzy knowledge. Wang et al. [84] have developed different approaches for picture fuzzy Muirhead means operators to address challenges in decision-making. Ramakrishnan and Chakraborty [85] implemented a picture fuzzy hesitant set and addressed their implementations in combinatorial optimization problems. Khan et al. [86,87] presented MADM obstacles utilizing logarithmic aggregation operators for PFNs. They set up picture fuzzy aggregation operators with their implementations focused on Einstein operations. Zhang et al. [88] have developed certain fuzzy Dombi Heronian mean operators with their MADM implementations.
1.2 Studies Inspiration, Highlights, and Emphasis
In the above-cited articles depends upon picture fuzzy sets and their aggregation operators, we found that various operations are not closed. If we input information data by using picture fuzzy numbers, then the output may be picture fuzzy numbers (PFNs), spherical fuzzy numbers (SFNs), T-spherical fuzzy numbers (T-SFNs), or neutrosophic numbers. As we know that all the defined operators have been constructed by using the operations of picture fuzzy numbers, so these aggregation operators were not closed. We present counterexamples to show these results and construct some new operations by using the idea of Wang et al. [89]. He constructed some new operations on a picture fuzzy set by using the idea of probability. We use the same idea and constructed some other operations of picture fuzzy numbers. By using the novel idea and new aggregation operators we observe that all the operations and operators are closed (see Tab. 4).
Due to the usage of reference or comparison parameters, the new SLDFS model is more effective and robust, rather than current methods. By modifying the physical meaning of reference parameters, SLDFS often classifies the data into MCDM issues. This collection encompasses the spaces of current systems and, with the aid of reference or control parameters, enlarges the space for reality, abstinence, and falsification classes. The inspiration of the developed model is provided in the entire paper, step by step. Now we are discussing some of the essential priorities of this article.
1. In certain real-life complexities, the amount of grade of truthness, grade of abstinence, and grade of falsity for an object fulfilling criteria given by the decision-maker (DM) can surpass 1 (e.g., 0.8+0.7+0.4 > 1) and their sum of squares can also surpass 1 (e.g., 0.82+0.72+0.42 > 1). For these cases, the PFS and the SFSs fails. To resolve such problems, the constraints on grades of reality/truthness, abstinence, and falsity/falsification are modified to
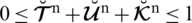 in case of T-SFSs. We can accommodate certain ratings independently except with very broad “n” values. In certain functional difficulties, when all classes are equivalent to 1 (i.e.,
in case of T-SFSs. We can accommodate certain ratings independently except with very broad “n” values. In certain functional difficulties, when all classes are equivalent to 1 (i.e.,
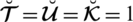 ), we get
), we get
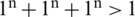 That violates the T-SFS constraint. In these cases, MCDM with T-SFS ends in a debacle. It affects the MCDM process and optimal judgment. Spherical linear Diophantine Fuzzy set (SLDFS) is more efficient and capable of grappling with such conditions. SLDFS presents a robust MCDM approach with a wide variety of feasible solutions for modern world issues.
That violates the T-SFS constraint. In these cases, MCDM with T-SFS ends in a debacle. It affects the MCDM process and optimal judgment. Spherical linear Diophantine Fuzzy set (SLDFS) is more efficient and capable of grappling with such conditions. SLDFS presents a robust MCDM approach with a wide variety of feasible solutions for modern world issues.
2. Our first goal is to address this research with an innovative framework of SLDFSs. Using this model, under the influence of control parameters, we will discuss the fuzzy, spherical fuzzy, T-spherical fuzzy, and neutrosophic existence of attributes. (For example for ( 0.6+0.9+0.7 > 1), reference or control parameters should be added so that (0.6)(0.3)+(0.9)(0.2)+(0.7)(0.1) < 1, where
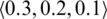 can be used as comparison parameters for grades of reality, abstinence and falsification). As the suggested framework appears identical to the well-known “linear Diophantine equation”
can be used as comparison parameters for grades of reality, abstinence and falsification). As the suggested framework appears identical to the well-known “linear Diophantine equation”
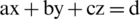 of three variables in pure mathematics, the most appropriate term for the suggested model is the spherical linear Diophantine fuzzy set (SLDFS).
of three variables in pure mathematics, the most appropriate term for the suggested model is the spherical linear Diophantine fuzzy set (SLDFS).
3. The second objective is to incorporate the reference or control parameters in SLDFSs and these parameterizations can not be considered by existing models like PFS, SFSs, T-SFSs, and NSs. SLDFS model enhances the current methodologies in the sense that DMs can select the degrees freely without any limitations. This definition often classifies the difficulty by modifying the parameters of the actual frame of reference. Additionally, the grades can be freely chosen in [0, 1] and their associated reference parameters may express the merits and demerits of these grades. One can consider the reference parameters as weights of these grades. The weight vector determined by reference parameters is a key feature of SLDFSs to deal with uncertainties in MCDM problems.
4. Our third aim is to show some drawbacks of operations of picture fuzzy sets and their corresponding aggregation operators. We introduced some new operations on picture fuzzy sets. We discuss various illustrations to support our results.
5. Our fourth aim is to develop a close relationship between this theoretical model and the challenges of decision-making under multiple criteria. We develop novel aggregation operators to manage data uncertainty in a parametric framework. We introduce various score functions and accuracy functions in the ranking of feasible alternatives in the MCDM approach.
This paper’s structure is formulated as follows: Section 2 presents certain primary principles of PFS, SFSs, T-SFSs, and NSs. In Section 3, we present the innovative definition of SLDFSs. We discuss the supremacy of the new model and contrast it with current systems. We provide different examples to link our system to issues in the actual world. In Section 4, we establish a contrast with the suggested structure by utilizing graphical descriptions of current systems. We are addressing the limitations of current operations and aggregation operators, and we are developing several new operations on picture fuzzy numbers. On SLDFNs we describe certain operations. The concept of spherical linear Diophantine fuzzy weighted geometric aggregation (SLDFWGA) and spherical linear Diophantine fuzzy weighted average aggregation (SLDFWAA) operators is set out in Section 5. For the contrast of SLDFNs with specific orders, we provide numerous score and accuracy functions. In Section 6, we suggest the concept of MCDM to pick an appropriate emergency strategy in a gas explosion incident, with the aid of identified operators. We provide a quick contrast between the new framework and the current models and demonstrate in the aggregated outcomes the effect of score functions on the final decision. Finally, Section 7 summarizes the result of the study.
Throughout this segment, we will explore several essential terms like neutrosophic sets, picture fuzzy sets (PFS), spherical fuzzy sets (SFSs), and T-spherical fuzzy sets (T-SFSs). For the creation of a hybrid structure called spherical linear Diophantine fuzzy set (SLDFS), we use these essential components.
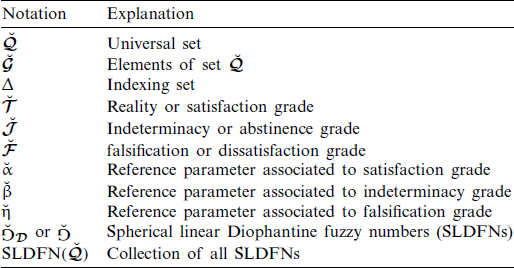
Tab. 1 describes the notations included in the entire paper.
Table 1: Overview of notations used throughout the paper
Definition 2.1 [7] For reference set
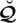 , the neutrosophic set (NS)
, the neutrosophic set (NS)
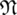 is portrayed by reality degree
is portrayed by reality degree
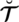 , an indeterminacy function
, an indeterminacy function
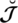 and a falsification part
and a falsification part
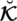 .
.
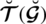 ,
,
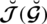 and
and
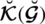 are real standard or non-standard objects of ]0−, 1+[. We portrayed it as:
are real standard or non-standard objects of ]0−, 1+[. We portrayed it as:
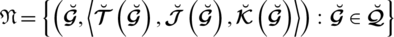
satisfying the constraint
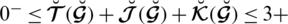 .
.
Afterward, other mathematicians focused on more hybrid fuzzy and IFSs such as neutrosophic collection, PyFSs, q-ROFSs, SFSs, and T-SFSs. Fuzzy systems and IFSs cannot be extended to decision-making difficulties in certain cases. The notion of picture fuzzy sets (PFS) was suggested by Cuong et al. [29], Andekah et al. [30] and Perić et al. [31] to eliminate this downside. Similar to prior ones this system is similar to human existence and addresses real-life scenarios.
Definition 2.2 [27–29]. For the universal set
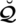 the picture fuzzy set (PFS) can be portrayed as
the picture fuzzy set (PFS) can be portrayed as
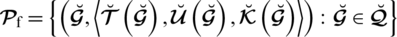
where,
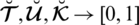 represents the satisfaction, uncertainty or abstinence and dissatisfaction degrees respectively, satisfying the constraint
represents the satisfaction, uncertainty or abstinence and dissatisfaction degrees respectively, satisfying the constraint
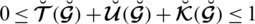 . The value
. The value
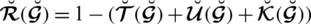 is known as a grade of refusal for
is known as a grade of refusal for
 in
in
 . The triplet
. The triplet
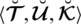 is called picture fuzzy number (PFN).
is called picture fuzzy number (PFN).
To deal with the limitations of PFS a novel idea of SFSs and T-SFSs was developed by Mahmood et al. [32] in 2018. Their phenomenon was similar to IFSs, Pythagorean fuzzy sets, and q-ROFSs, yet the planes are 2-dimensional in those situations. But Mahmood et al. [32] established extensions of PFS as SFSs and T-SFSs in 3-dimensional space.
Definition 2.3 [32]. For the universal set
 the spherical fuzzy set (SFS) can be portrayed as
the spherical fuzzy set (SFS) can be portrayed as
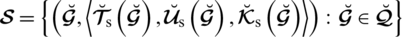
where,
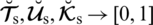 represents the real part, uncertainty or abstinence, and falsification grades respectively, with the constraint
represents the real part, uncertainty or abstinence, and falsification grades respectively, with the constraint
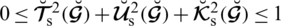 . The value
. The value
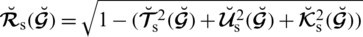 is known as a grade of refusal for
is known as a grade of refusal for
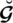 in
in
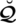 . The triplet
. The triplet
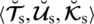 is called spherical fuzzy number (SFN).
is called spherical fuzzy number (SFN).
Definition 2.4 [32]. For
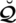 the T-spherical fuzzy set (T-SFS) can be portrayed as:
the T-spherical fuzzy set (T-SFS) can be portrayed as:
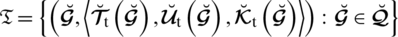
where,
 represents the satisfaction, uncertainty or abstinence and dissatisfaction grades respectively, with the constraint
represents the satisfaction, uncertainty or abstinence and dissatisfaction grades respectively, with the constraint
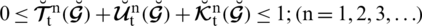 .
.
The value
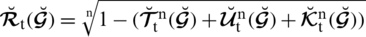 is known as a grade of refusal for
is known as a grade of refusal for
 in
in
 . The triplet
. The triplet
 is called a T-spherical fuzzy number (T-SFN).
is called a T-spherical fuzzy number (T-SFN).
3 Spherical Linear Diophantine Fuzzy Sets
Throughout this section, we illustrate an innovative definition of a spherical linear Diophantine fuzzy set (SLDFS). The suggested framework matches well known linear Diophantine equation in pure mathematics for three independent variables
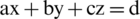 . Since, there are certain restrictions on participation, abstinence, and dissatisfaction categories in NSs, PFSs, SFSs, and T-SFSs. With the introduction of reference or control parameters, we proposed the idea of SLDFSs to get rid of certain restrictions. This principle eliminates the limitations on grades (satisfaction, abstinence, and dissatisfaction), and the decision-maker (DM) can select the grades equally without constraint. This framework often classifies the issue by picking various kinds of reference or control parameters. We address the framework of SLDFSs, its graphical depiction, and use diagrams to illustrate certain principles.
. Since, there are certain restrictions on participation, abstinence, and dissatisfaction categories in NSs, PFSs, SFSs, and T-SFSs. With the introduction of reference or control parameters, we proposed the idea of SLDFSs to get rid of certain restrictions. This principle eliminates the limitations on grades (satisfaction, abstinence, and dissatisfaction), and the decision-maker (DM) can select the grades equally without constraint. This framework often classifies the issue by picking various kinds of reference or control parameters. We address the framework of SLDFSs, its graphical depiction, and use diagrams to illustrate certain principles.
Definition 3.1. A spherical linear Diophantine fuzzy set (SLDFS)
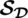 over
over
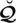 can be portrayed as
can be portrayed as

where,
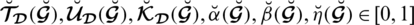 are a reality, uncertainty/abstinence, falsification grades, and reference/control parameters associated with the grades respectively. These grades fulfill the constraint
are a reality, uncertainty/abstinence, falsification grades, and reference/control parameters associated with the grades respectively. These grades fulfill the constraint
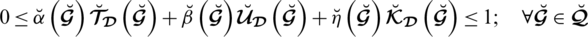
with
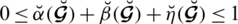 . These comparison parameters may assist to describe or identify a given system. By modifying the particular interpretation of certain parameters, we may classify the system. They raise the valuation portion of degrees used in SLDFSs and eliminate constraints on them. The portion of rejection (refusal part) may be measured as
. These comparison parameters may assist to describe or identify a given system. By modifying the particular interpretation of certain parameters, we may classify the system. They raise the valuation portion of degrees used in SLDFSs and eliminate constraints on them. The portion of rejection (refusal part) may be measured as
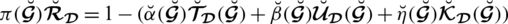 , where
, where
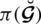 is the control parameter related to refusal degree. Simply
is the control parameter related to refusal degree. Simply
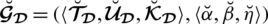 is called spherical linear Diophantine fuzzy number (SLDFN) with
is called spherical linear Diophantine fuzzy number (SLDFN) with
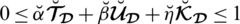 and
and
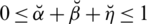 . The structure of SLDFSs can be shown visually as Fig. 1.
. The structure of SLDFSs can be shown visually as Fig. 1.
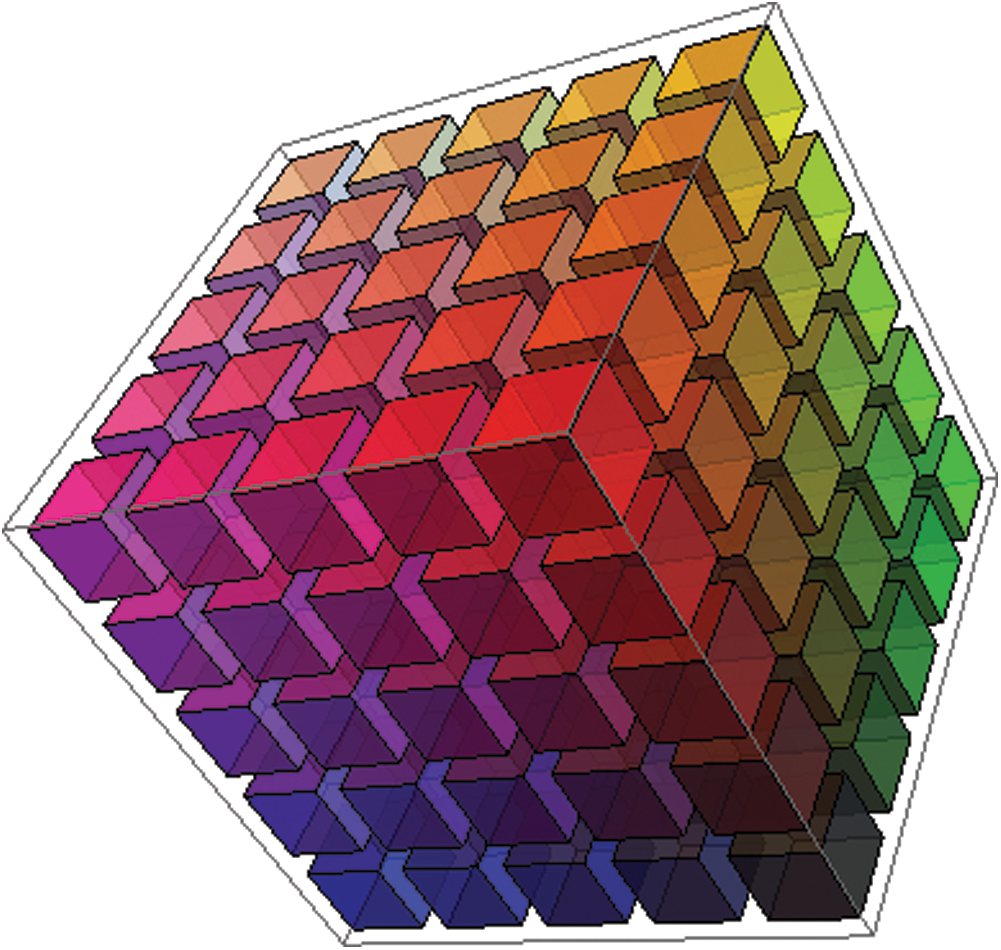
Figure 1: Visual representation for satisfaction, abstinence and dissatisfaction grades of Spherical linear Diophantine fuzzy set
Definition 3.2 A SLDFS
 is said to be absolute SLDFS and
is said to be absolute SLDFS and
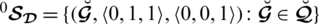 is said to be empty or null SLDFS.
is said to be empty or null SLDFS.
3.1 Superiority and Comparison of the Proposed Set with Other Approaches
Spherical linear Diophantine fuzzy set (SLDFS) is very important in different situations when we have opinions about the yes, no, abstinence, and refusal. A question emerges here: Why are we adopting SLDFS? And what are the drawbacks of preceding methodologies? In this part, we discuss the facts and needs of SLDFSs and compare our model with the existing approaches.
1. The main drawback of PFSs is due to its constraint, i.e.,
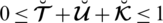 . A decision-maker (DM) cannot assign the values of his own choice to these grades. Due to this restriction we can choose these grades independently (e.g., 0.5+0.3+0.4 > 1). So this model cannot work for various decision-making problems.
. A decision-maker (DM) cannot assign the values of his own choice to these grades. Due to this restriction we can choose these grades independently (e.g., 0.5+0.3+0.4 > 1). So this model cannot work for various decision-making problems.
2. To remove the restrictions and to increase the space of PFS Mahmood at al. [32] introduced the concept of SFSs with the constraint
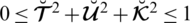 . By using this idea we can easily deal with various problems that arise in PFSs (e.g., 0.52+0.32+0.42 < 1). This constraint also increases the space of PFS and increases the domain of grades.
. By using this idea we can easily deal with various problems that arise in PFSs (e.g., 0.52+0.32+0.42 < 1). This constraint also increases the space of PFS and increases the domain of grades.
3. There exist many real-life situations for which SFS does not work (e.g., 0.72+0.82+0.62 > 1). To increase the space and to remove these limitations, they established the idea of T-SFSs in the same manuscript by using the constraint
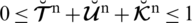 , (“n” is a non-zero positive integer). By using this novel idea one can easily deal with the problems that arise in SFSs (e.g., 0.74+0.84+0.64 < 1).
, (“n” is a non-zero positive integer). By using this novel idea one can easily deal with the problems that arise in SFSs (e.g., 0.74+0.84+0.64 < 1).
4. Mahmood et al. [32] presented the applications of SFS and T-SFS in medical and decision-making. But still the all three grades are dependent on each other (e.g., 1+1+1 > 1). We cannot deal with them independently in decision-making and real-life problems.
5. In the neutrosophic set all three grades are independent of each other with the constraint
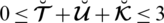 . The main deficiency in this model is that it cannot deal with parameterizations. We can only deal with the reality, uncertainty, and falsification grades of alternatives. As we can see that all the above models cannot deal with parameterizations of attributes of the universal set.
. The main deficiency in this model is that it cannot deal with parameterizations. We can only deal with the reality, uncertainty, and falsification grades of alternatives. As we can see that all the above models cannot deal with parameterizations of attributes of the universal set.
6. To remove all the above limitations in PFSs, SFSs, T-SFSs, and NSs, we introduced the idea of spherical linear Diophantine fuzzy sets (SLDFSs). The beauty of this structure is that it creates independence between all the grades and covers the space of PFSs, SFSs, and T-SFSs. All the decision-making difficulties, which cannot be tackled by using the existing approaches, can be easily handled by using SLDFSs.
7. Another main difference between existing structures and SLDFSs is its parameterizations. PFSs, SFSs, T-SFSs and neutrosophic sets do not deal with parameterizations. In SLDFSs the constraint is
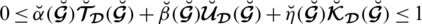 , where
, where
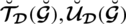 and
and
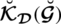 are membership, abstinence, and degree of non-membership, respectively. In this proposed model all, the grades are independent of each other. We can also find the grade of refusal in this model, which cannot be tackled in the neutrosophic set. In SLDFSs the triplet
are membership, abstinence, and degree of non-membership, respectively. In this proposed model all, the grades are independent of each other. We can also find the grade of refusal in this model, which cannot be tackled in the neutrosophic set. In SLDFSs the triplet
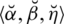 are reference and control parameters, which do not exist in any other model. Such comparison parameters fulfill the constraint
are reference and control parameters, which do not exist in any other model. Such comparison parameters fulfill the constraint
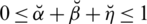 and will help to describe the classification of a defined framework. By modifying the particular interpretation of certain parameters, we can classify the challenge. That raises grade space and reduces its limitations (e.g., (0.2)(1)+(0.8)(1)+(0.1)(1) < 1, where
and will help to describe the classification of a defined framework. By modifying the particular interpretation of certain parameters, we can classify the challenge. That raises grade space and reduces its limitations (e.g., (0.2)(1)+(0.8)(1)+(0.1)(1) < 1, where
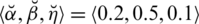 ). Tabs. 2 and 3 provide an overview of the SLDFSs compared with current methods.
). Tabs. 2 and 3 provide an overview of the SLDFSs compared with current methods.
Table 2: Comparative study of SLDFSs to existing methodologies

Table 3: Comparative study of SLDFSs to existing methodologies

LDFS has multiple practical uses in the areas of electronics, medical sciences, artificial intelligence, and MADM. Within this manuscript, one can observe a broad range of these implementations.
The analysis of photographs may be defined as both analog and optical image processing. In image enhancement, image reconstruction, image compression, and image detection, optical image processing may be very helpful. Researchers who have worked on various image recognition systems include medical imaging [8,9], radar image analysis [16–18], biometric and iris recognition [19,20], human detection [30,31].
The three image analysis levels are provided below as:
Low-Level Mechanisms: “At this level, the quality of an image is improved by reducing the noise and contrast is also enhanced.”
Medium-Level Mechanisms: “This level includes the extracting of attributes from image and segmentation of image.”
High-Level Mechanisms: “In this step, objects are recognized in an image for analysis.”
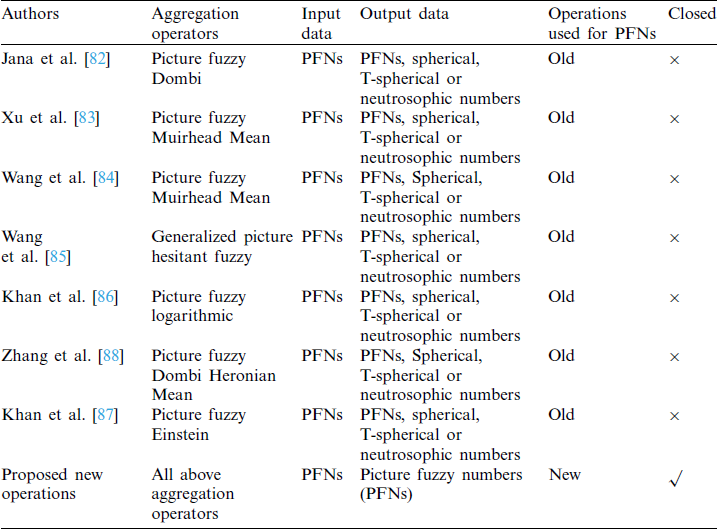
These three levels correspond with the membership, abstinence, and dissatisfaction grades of SLDFSs. The addition of control parameters increases the quality of the procedure and also includes the details to deal with these corresponding grades (Tab. 4).
Table 4: Characteristics of operations used for picture fuzzy numbers (PFNs)
In network systems, the important factor is the signal strength. Let
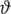 be a static threshold value for wi-fi signals which link a computer to a router. If the signal intensity exceeds
be a static threshold value for wi-fi signals which link a computer to a router. If the signal intensity exceeds
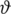 , the machine connects. If it is below
, the machine connects. If it is below
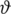 , then the device is not connected. There exists another possibility when signal strength fluctuates about
, then the device is not connected. There exists another possibility when signal strength fluctuates about
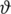 . Device switches from linked to disconnected in these cases and vice versa (within a limited time interval) (see Tab. 5). This phenomenon relates to this real-life situation with SLDFS. The addition of control parameters control measures and changes the theoretical sense of these three categories, and increases the domain of a decision maker’s (DM) grade.
. Device switches from linked to disconnected in these cases and vice versa (within a limited time interval) (see Tab. 5). This phenomenon relates to this real-life situation with SLDFS. The addition of control parameters control measures and changes the theoretical sense of these three categories, and increases the domain of a decision maker’s (DM) grade.

There are four types of voters in the process of voting. One who votes in favor, others who not against, others who refuse to vote, and last who abstain. We cannot deal with these real-life situations by using existing methodologies. Some existing approaches do not contain refusal grades and some of them do not deal with reference parameters (See Tabs. 6 and 7). These situations can be easily handled by using the proposed model of SLDFS. This structure combines all grade information and also classifies the difficulty using the control parameters (see Tab. 6).
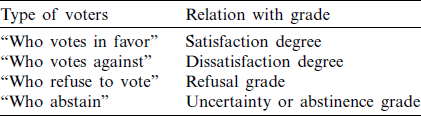
Table 7: Electrical engineering
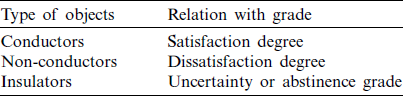
In Physics and electronic engineering, a conductor is a substance or material type that facilitates charging (electric current) to flow. There also exists some substances that do not conduct electricity called non-conductors. But there are other compounds in the presence of conductors and non-conductors whose internal electrical charges do not circulate freely. Under the power of an electrical field, a tiny volume of electric current passes into it. These are what are called insulators. So these types of problems can be handled by SLDFSs in the presence of reference parameters (see Tab. 7).
Several practical implementations of SLDFSs arise in the area of medicine and MADM issues. Medical diagnosis is the screening method and process, the prognosis, therapies, and the avoidance of diseases. Growing medicine has some physicochemical properties and some are used to treat several diseases. Let
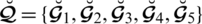 be a collection of some appropriate medicines dealing with multiple diseases, such as sinus infections, influenza, ear allergic reaction, chest infections, and skin diseases. We can conveniently categorize such drugs with good or bad results according to the disease chosen or any physical properties. When we find the parameters listed as:
be a collection of some appropriate medicines dealing with multiple diseases, such as sinus infections, influenza, ear allergic reaction, chest infections, and skin diseases. We can conveniently categorize such drugs with good or bad results according to the disease chosen or any physical properties. When we find the parameters listed as:
 =“Best effect chest infections”
=“Best effect chest infections”
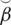 =“Not highly effected to chest infections (uneffected or neutral)”
=“Not highly effected to chest infections (uneffected or neutral)”
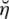 =“Bad effects or some side effects against chest infections”
=“Bad effects or some side effects against chest infections”
Then its SLDFS is given in Tab. 8.
Table 8: Spherical linear Diophantine fuzzy set

Every drug has diverse combinations of salt and chemicals in it. And we should give them different statistics of parameters due to their consistency and under the patient’s evaluation of the consequences. Such parameters indicate how many components we require from the specific drug and its grade values measures how much the specific element they include. When we adjust the parameter
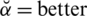 result against ear allergic reaction,
result against ear allergic reaction,
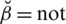 strongly influenced or favorable to ear allergic reaction and
strongly influenced or favorable to ear allergic reaction and
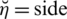 effects against ear allergic reaction or
effects against ear allergic reaction or
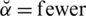 or minimal side effects,
or minimal side effects,
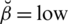 side effects and
side effects and
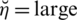 side effects, etc. We can then create further SLDFSs on the same collection of alternatives. Such guidelines allow a physician to prescribe the patient the correct and most suitable treatment for his disease. On the built SLDFSs, the final judgment can be conveniently tested using the appropriate algorithm. Through the inclusion of comparison criteria, this method expands the room for acceptable, abstinent, and unsatisfactory classes.
side effects, etc. We can then create further SLDFSs on the same collection of alternatives. Such guidelines allow a physician to prescribe the patient the correct and most suitable treatment for his disease. On the built SLDFSs, the final judgment can be conveniently tested using the appropriate algorithm. Through the inclusion of comparison criteria, this method expands the room for acceptable, abstinent, and unsatisfactory classes.
3.7 Selection of Optimal Choice
In the field of decision-making difficulties, when a DM wants to select an optimal object among the listed objects then he keeps his requirements in his mind. For the selection of the best “mobile phone,” best “air conditioner” or best “car,” one can choose the objects according to their own criteria. They can choose the objects on the basis of these reference parameters given as:
 =cheap or low cost
=cheap or low cost
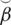 =Affordable cost
=Affordable cost
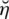 = Expansive or high cost
= Expansive or high cost
Suppose someone decides to purchase a cell phone. He wants to choose the latest smartphone that has multiple applications and a low price. Let
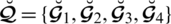 be the collection of certain well-known cell phones. The SLDFSs is provided in Tab. 9.
be the collection of certain well-known cell phones. The SLDFSs is provided in Tab. 9.

When we alter the physical definition of the comparison parameters then in another way we may classify the data in the context of SLDFSs. We can use the control parameters for the second SLDFS, as:
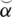 high battery timing
high battery timing
 =average battery timing
=average battery timing
 =low battery timing
=low battery timing
The SLDF-information can be taken as Tab. 10 for these reference or control parameters.
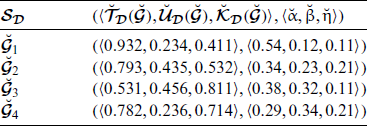
The reference parameters play a significant role here. They reflect any particular specific property whether it’s inexpensive, reasonable, costly, large, medium, or low battery scheduling, simple to learn, medium to learn or hard to learn, and so on. The ratings
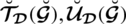 and
and
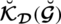 reflects the degrees of phone
reflects the degrees of phone
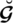 , which demonstrates how cheap, affordable, or expensive a phone is, while the parameters demonstrate how cheap, affordable, or expensive a machine should be. Such criteria are chosen according to the decision-makers’ preference, while alternative ratings are determined from the actual data. The major benefit of the comparison criteria is that the categories of alternatives are easily picked. These parameters parameterize the calculation and allow more space for our mathematical model. Thus we may describe specific SLDFSs for a specific collection of parameters on the same
, which demonstrates how cheap, affordable, or expensive a phone is, while the parameters demonstrate how cheap, affordable, or expensive a machine should be. Such criteria are chosen according to the decision-makers’ preference, while alternative ratings are determined from the actual data. The major benefit of the comparison criteria is that the categories of alternatives are easily picked. These parameters parameterize the calculation and allow more space for our mathematical model. Thus we may describe specific SLDFSs for a specific collection of parameters on the same
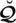 reference set. The values selected for the input information derived from the space of PFSs, SFSs, T-SFSs, and NSs.
reference set. The values selected for the input information derived from the space of PFSs, SFSs, T-SFSs, and NSs.
4 Graphical Interpretation of SLDFSs
Throughout this section, we present SLDFS’s graphical representation with comparison parameters and analyze how its space exceeds the space of PFSs, SFSs, and T-SFSs. Figs. 2–4 provide us the geometrical interpretation of PFSs, SFSs, and SLDFSs. Figs. 5–12 represent the graphical view of PFS, SFS, T-SFS with different values of “n” and SLDFS with a different selection of reference parameters.
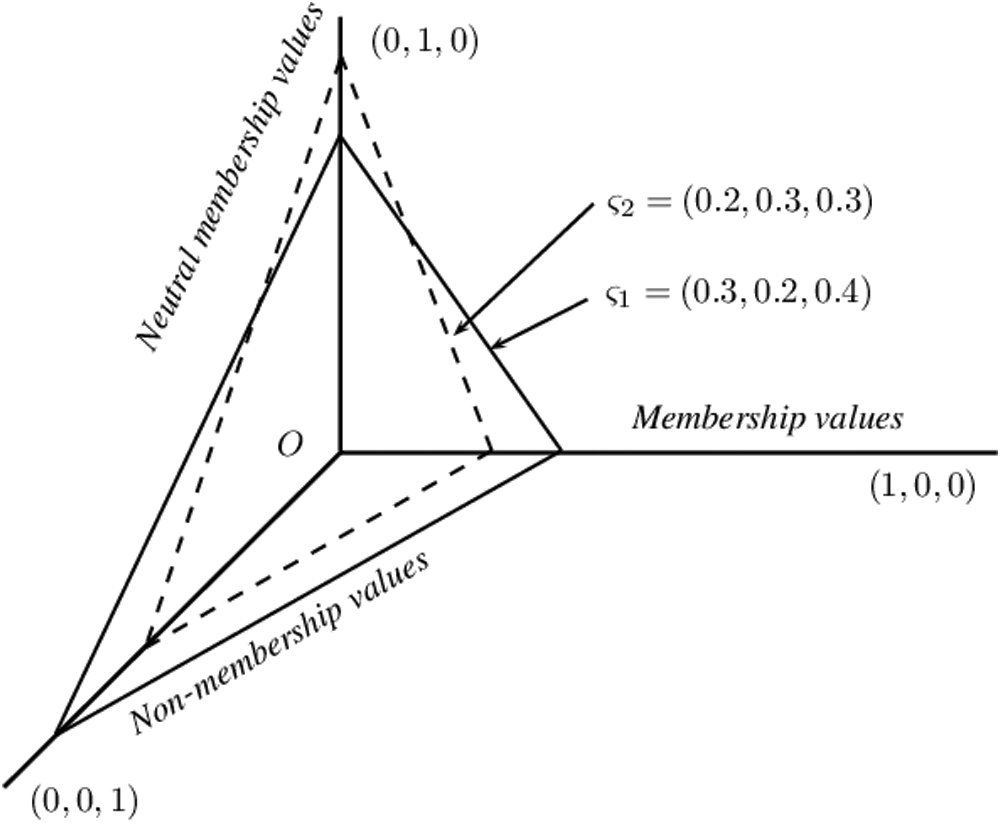
Figure 2: Geometrical representation for satisfaction, abstinence, and dissatisfaction grades of picture fuzzy set
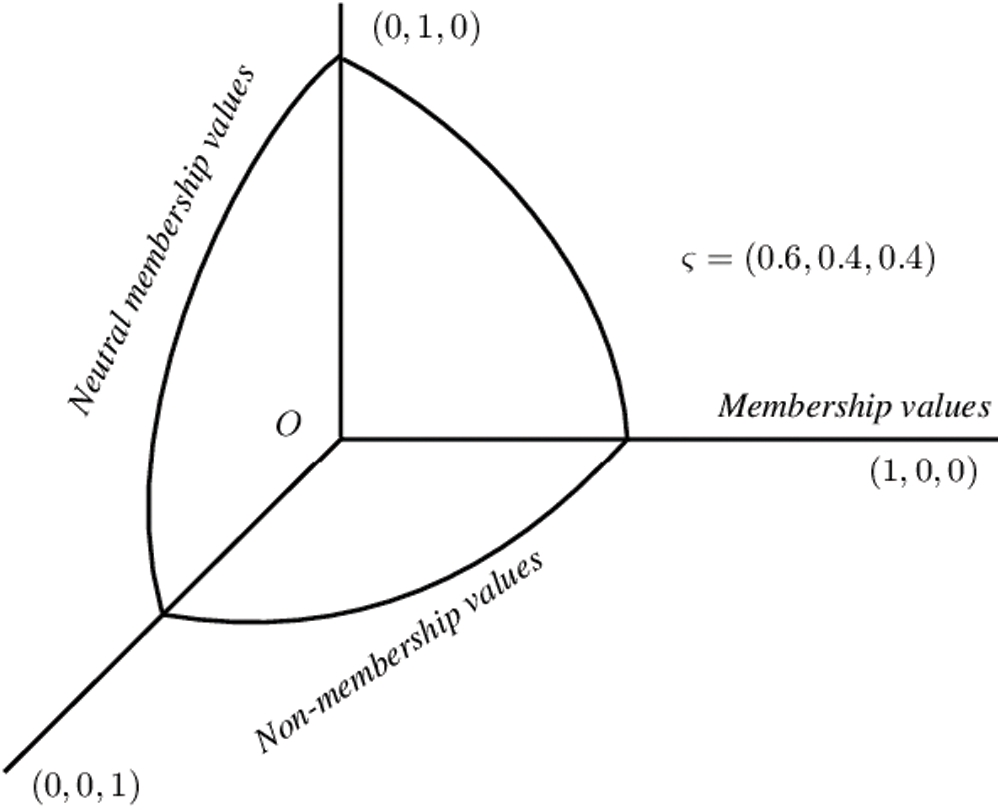
Figure 3: Geometrical representation for satisfaction, abstinence, and dissatisfaction grades of spherical fuzzy set
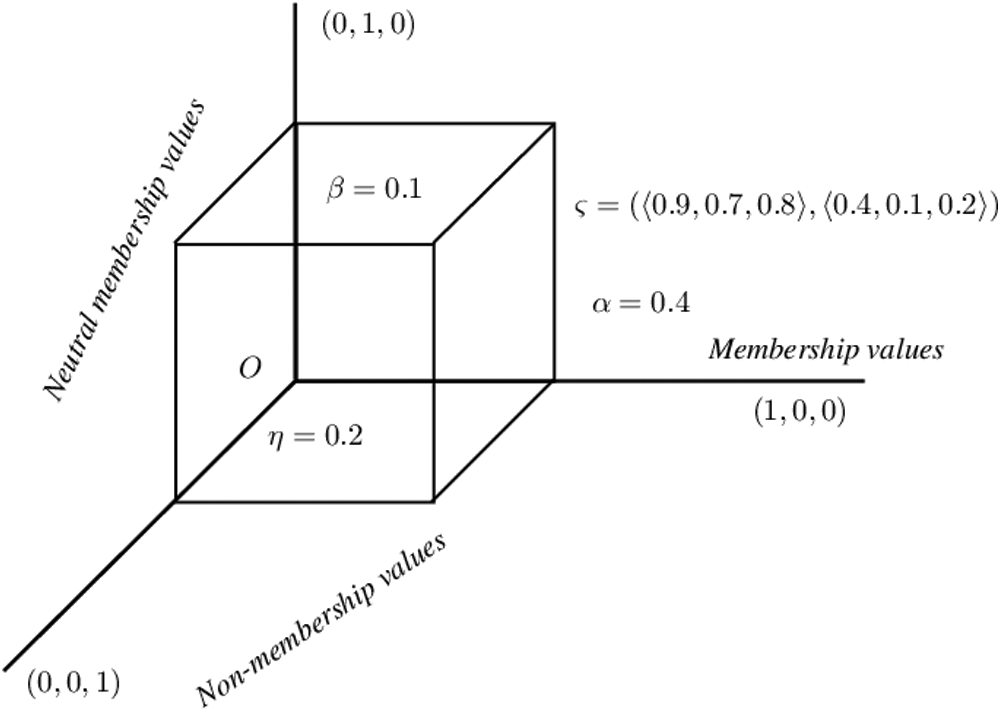
Figure 4: Geometrical representation for satisfaction, abstinence, and dissatisfaction grades of spherical linear Diophantine fuzzy set
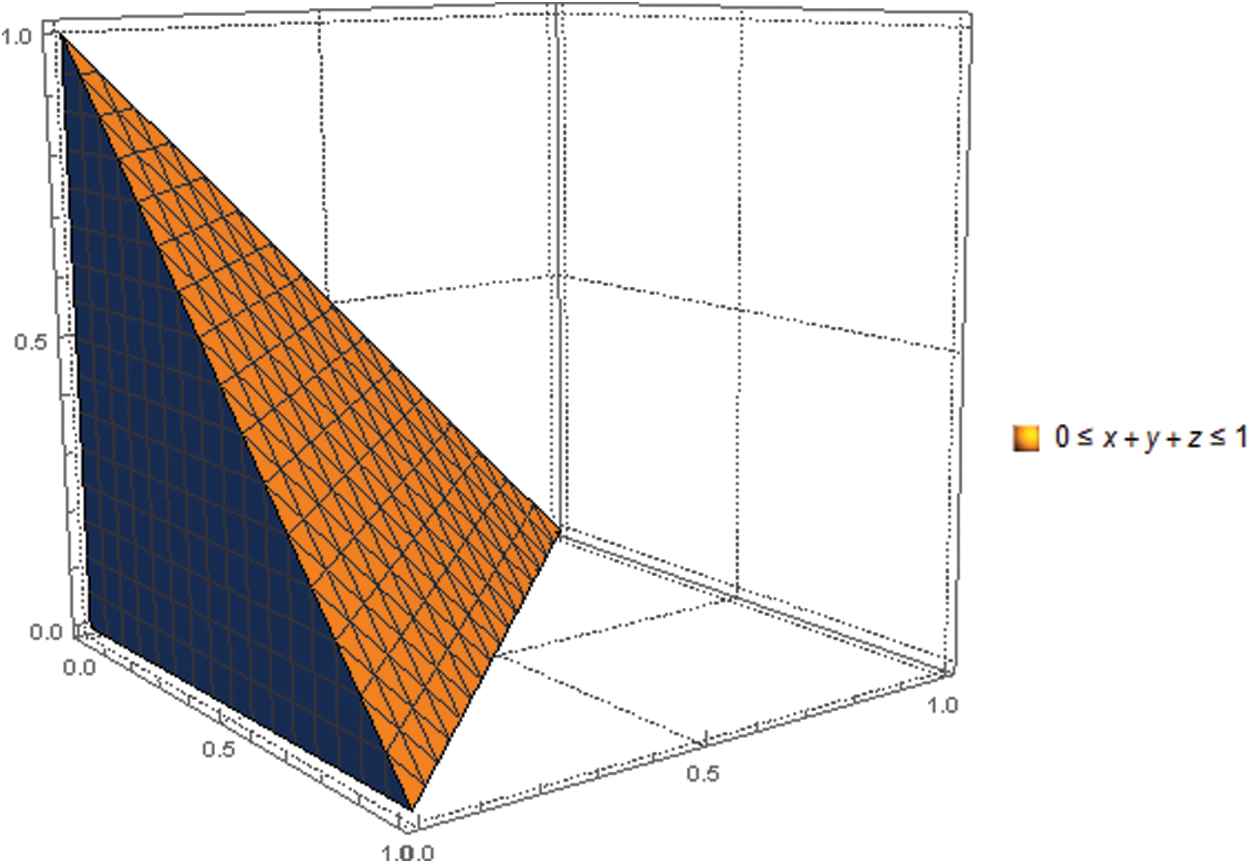
Figure 5: Graphical representation for satisfaction, abstinence, and dissatisfaction grades of picture fuzzy set
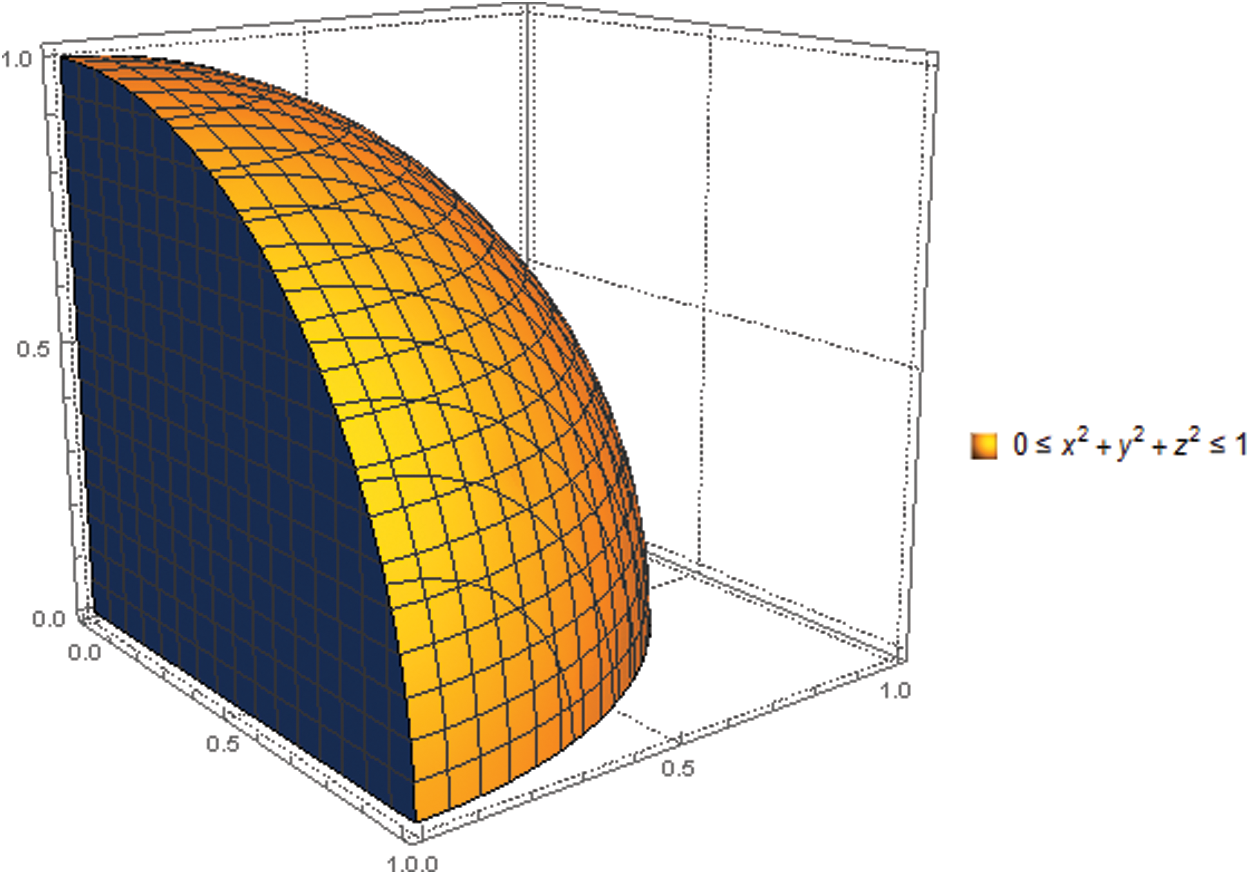
Figure 6: Graphical representation for satisfaction, abstinence, and dissatisfaction grades of spherical fuzzy set
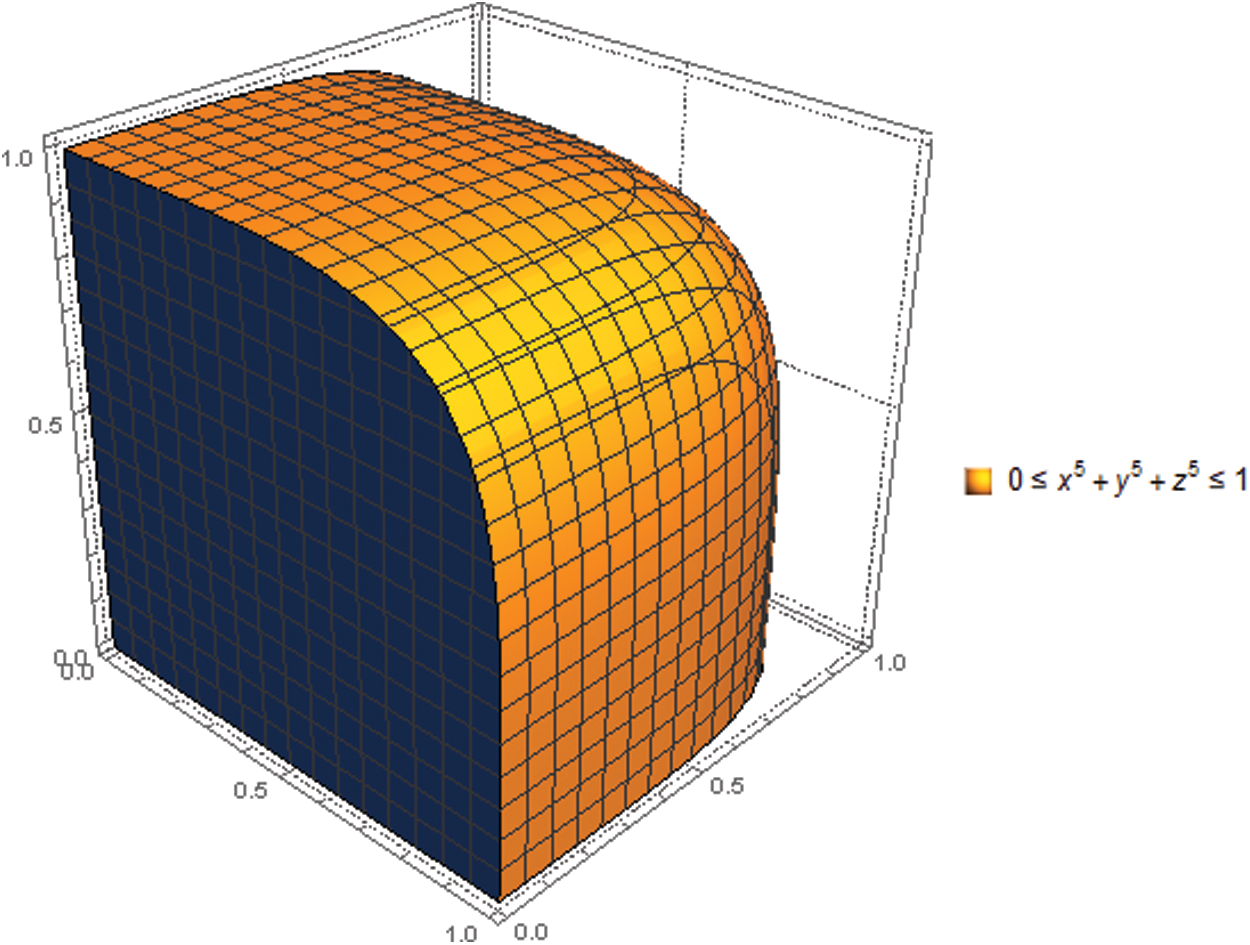
Figure 7: Graphical representation for satisfaction, abstinence, and dissatisfaction grades of T-spherical fuzzy set with
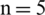
Figure 8: Graphical representation for satisfaction, abstinence, and dissatisfaction grades of T-spherical fuzzy set with
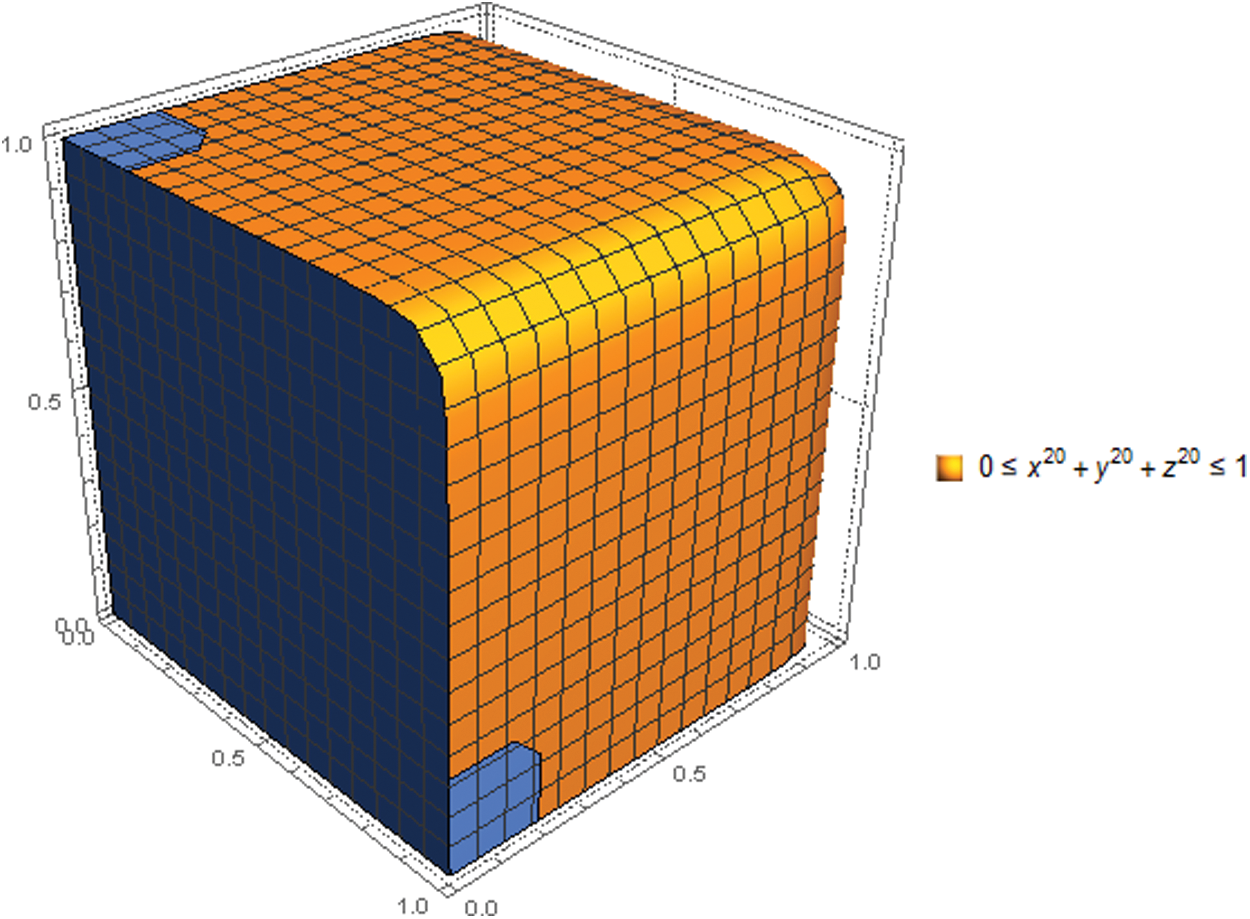
Figure 9: Graphical representation for satisfaction, abstinence, and dissatisfaction grades of T-spherical fuzzy set with
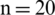
Figure 10: Graphical representation for satisfaction, abstinence, and dissatisfaction grades of T-spherical fuzzy set with

Figure 11: Graphical representation for satisfaction, abstinence, and dissatisfaction grades of T-spherical fuzzy set with
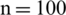

Figure 12: Graphical representation for satisfaction, abstinence, and dissatisfaction grades of spherical linear Diophantine fuzzy set for reference parameters
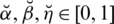
Theorem 4.1 The space of spherical linear Diophantine fuzzy number (SLDFN) is larger than the space of PFN, SFN, and T-SFN.
Proof. (1) Each PFN is also an SLDFN. Let
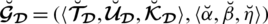 be an SLDFN with the constraints
be an SLDFN with the constraints
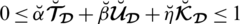 and
and
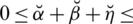 1, where
1, where
 ,
,
 ,
,
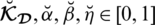 . The above disparity exists for both PFN and SFN for an unspecified set of comparison parameters.
. The above disparity exists for both PFN and SFN for an unspecified set of comparison parameters.
(2) A PFN or SFN can not automatically be an SLDFN. For example, if
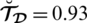 ,
,
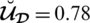 and
and
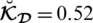 then
then
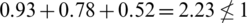 and
and
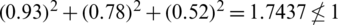 but for an arbitrary choice of reference parameters
but for an arbitrary choice of reference parameters
 ,
,
 ,
,
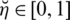 with the constraint
with the constraint
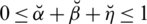 we have
we have
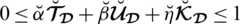 . As for
. As for
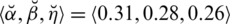 we have
we have
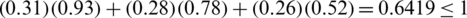 . So we effectively create a space that is greater than the space of PFSs, SFSs and T-SFSs. We have more choices for incorporating the values
. So we effectively create a space that is greater than the space of PFSs, SFSs and T-SFSs. We have more choices for incorporating the values
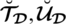 and
and
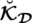 , which is unlikely in PFSs and SFSs.
, which is unlikely in PFSs and SFSs.
(3) As for
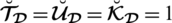 in T-SFS the constraint
in T-SFS the constraint
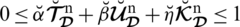 do not hold for any value of “n”.
do not hold for any value of “n”.
From all the above arguments it is clear that the space of SLDFS is greater than the space of PFS, SFS, and T-SFS. We can also choose different values of reference parameters to deal with the grades and to categorize the problem.
4.1 Some New Operations on Picture Fuzzy Sets (PFSs)
In this part, we define some new operations on picture fuzzy sets (PFSs) which are also applicable for PFNs. Many mathematicians worked on PFSs its operations and aggregation operators. We establish some contradictory illustrations to their definitions and introduce some new ideas.
1. For the PFS
 many mathematicians [82–88] used complement of PFS as
many mathematicians [82–88] used complement of PFS as

But they did not define the null and absolute PFSs. We define the null and absolute PFSs as
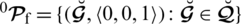 and
and
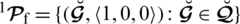 respectively. Now by following the defined null and absolute PFSs the existing definition implies;
respectively. Now by following the defined null and absolute PFSs the existing definition implies;


If we change the definitions of null and absolute PFSs then (2) and (3) fails to hold for (1).
2. In the field of MCDM obstacles aggregation operators plays an immense role. Many mathematicians [82–88] have worked on aggregation operators for PFSs and PFNs. In order to define the mathematical formula of aggregation operators, we need some operations of PFNs. The operations used by [82–88] for PFNs
 and
and
 are given as
are given as

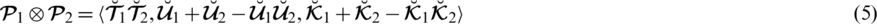

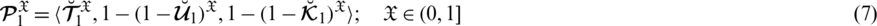
All cited mathematicians claim that these operations produce PFNs and their constructed aggregation operators produce results for PFNs. No, we check these operations for arbitrary PFNs. Let
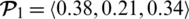 and
and
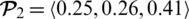 be two PFNs then
be two PFNs then

As we can see that for
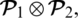 “0.095+0.415+0.610 > 1” and for
“0.095+0.415+0.610 > 1” and for
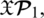 “0.091+0.731+0.805 > 1”. This implies that defined operations do not produce PFNs again by contradicting the constraint
“0.091+0.731+0.805 > 1”. This implies that defined operations do not produce PFNs again by contradicting the constraint
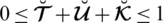 . So these operations are not closed. These values go in the sense of neutrosophic numbers with the constraint
. So these operations are not closed. These values go in the sense of neutrosophic numbers with the constraint
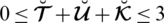 . Clearly, we can see that the input data is based on the PFNs and defined operations give neutrosophic numbers (i.e., operations are not closed). Cited mathematicians used these operations for Einstein [87], Dombi Heronian mean [88], Logarithmic [86], generalized picture hesitant fuzzy [85], Muirhead mean [83,84], picture fuzzy Dombi [82] aggregation operators in the context of PFNs. Results produced by their decision-making algorithms were not closed. Due to the defined operations, all these aggregation operators produce picture fuzzy numbers (PFNs) or sometimes spherical fuzzy numbers (SFNs), T-spherical fuzzy numbers (T-SFNs), or neutrosophic numbers.
. Clearly, we can see that the input data is based on the PFNs and defined operations give neutrosophic numbers (i.e., operations are not closed). Cited mathematicians used these operations for Einstein [87], Dombi Heronian mean [88], Logarithmic [86], generalized picture hesitant fuzzy [85], Muirhead mean [83,84], picture fuzzy Dombi [82] aggregation operators in the context of PFNs. Results produced by their decision-making algorithms were not closed. Due to the defined operations, all these aggregation operators produce picture fuzzy numbers (PFNs) or sometimes spherical fuzzy numbers (SFNs), T-spherical fuzzy numbers (T-SFNs), or neutrosophic numbers.
3. To remove this drawback Wang et al. [89] introduced certain novel operations on PFSs and they explained these operations from the point of view of probability. In the real-life example of voting, the intuitionistic fuzzy number (IFN)
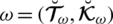 represents the ratio of those who vote for
represents the ratio of those who vote for
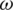 as
as
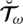 and ratio who vote against
and ratio who vote against
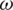 as
as
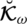 . For the two IFNs
. For the two IFNs
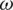 and
and
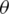 , the formula
, the formula
 is the ratio of those who vote for
is the ratio of those who vote for
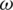 and
and
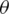 . This formula is constructed by using the multiplication formula of probability given as
. This formula is constructed by using the multiplication formula of probability given as
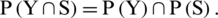
Then by the complementary formula of probability and
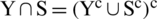 , we can get the ratio of those who vote against
, we can get the ratio of those who vote against
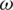 or vote against
or vote against
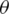 as;
as;
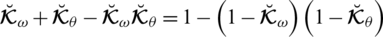
From this we can construct the
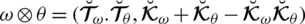 for IFNs (see Tab. 11).
for IFNs (see Tab. 11).
Next by explaining
 , we can obtain
, we can obtain
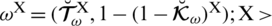 0 (see Tab. 11).
0 (see Tab. 11).
4. For picture fuzzy set (PFS), voters are divided into four categories”: vote for (it is ratio denoted as
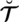 ), abstain (it is ratio denoted as
), abstain (it is ratio denoted as
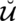 ), vote against (it is ratio denoted as
), vote against (it is ratio denoted as
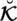 ) and refusal (it is ratio denoted as
) and refusal (it is ratio denoted as
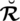 ). For two PFNs
). For two PFNs
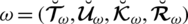 and
and
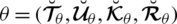 , we can construct the joint probability as in Tab. 12.
, we can construct the joint probability as in Tab. 12.
To compute
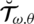 , we choose those who vote for both
, we choose those who vote for both
 and
and
 . So by using Tab. 12 we can write that
. So by using Tab. 12 we can write that
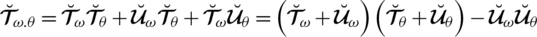
Those who are abstaining for
 and abstain for
and abstain for
 can be computed as
can be computed as
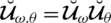
Similarly, we can compute other values as
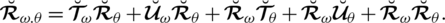
Next by explaining
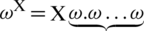 , we can obtain that
, we can obtain that
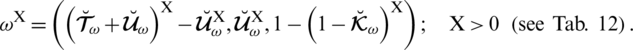
Based on the above theory and by using Wang et al. [89] idea, we can define some new operations on PFSs given below.
 and
and
 for IFNs from the point of view of the joint probability
for IFNs from the point of view of the joint probability

 and
and
 for PFNs from the point of view of the joint probability
for PFNs from the point of view of the joint probability
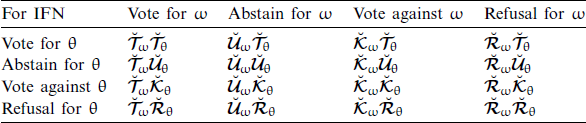
Definition 4.2 Let
 and
and
 be two PFNs and
be two PFNs and
 , then
, then

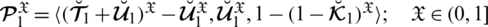
Remark When
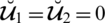 in Definition 4.2, then all the defined operations are reduced to the operations of intuitionistic fuzzy numbers.
in Definition 4.2, then all the defined operations are reduced to the operations of intuitionistic fuzzy numbers.
Theorem 4.3 Let
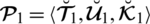 and
and
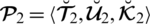 be two PFNs and
be two PFNs and
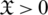 , then
, then
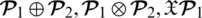 and
and
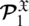 are also PFNs. (Note: Operations of Definition 4.2 will be used for this proof).
are also PFNs. (Note: Operations of Definition 4.2 will be used for this proof).
Proof. The proof is apparent and can be achieved conveniently using Definition 4.2.
Remark The operations of picture fuzzy numbers (PFNs) used by various mathematicians [82–88] as given in Eqs. (4)–(7) were not closed. They established various aggregation operators on PFNs by using old operations (Eqs. (4)–(7)) and get a result in the form of PFNs, SFNs, T-SFNs, and neutrosophic numbers. But by using the new operations on PFNs defined in Definition 4.2, we can reconstruct all the aggregation operators and they are closed. (i.e., if the input is a PFN then the output will also be a PFN). To observe this phenomenon one can see Tab. 12.
4.2 Fundamental Operations on Spherical Linear Diophantine Fuzzy Numbers
We define a few operations in this subsection on spherical linear Diophantine fuzzy numbers (SLDFNs). For the analysis of SLDFNs, we describe various score and accuracy functions.
Definition 4.4 Let
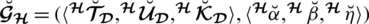 for
for
 (indexing set) be an assembling of SLDFNs over
(indexing set) be an assembling of SLDFNs over
 and
and
 then
then
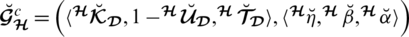 ,
,
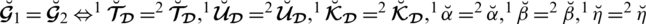 ,
,
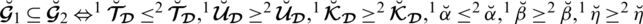 ,
,
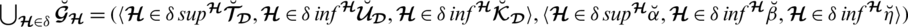 ,
,
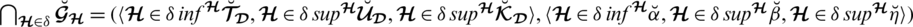 ,
,
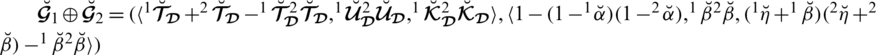 ,
,
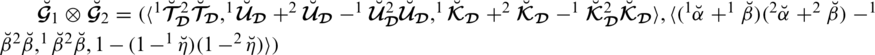 ,
,
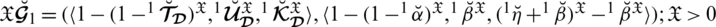 ,
,
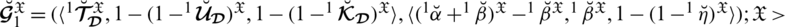 0.
0.
Remark If
 , then all above operations reduces to the operations for linear Diophantine fuzzy numbers [57].
, then all above operations reduces to the operations for linear Diophantine fuzzy numbers [57].
Proposition 4.5 Let
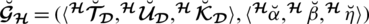 for
for
 (indexing set) be an assembling of SLDFNs over
(indexing set) be an assembling of SLDFNs over
 and
and
 0 then
0 then
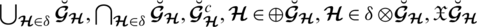 and
and
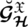 are also SLDFNs.
are also SLDFNs.
Proof. The proof is apparent and can be achieved conveniently using Definition 4.4.
Example 4.6 Let
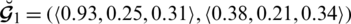 and
and
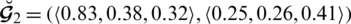 be two SLDFNs, then
be two SLDFNs, then
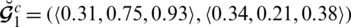
Obviously by Definition 4.4
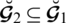
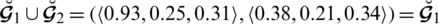


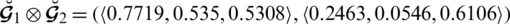
If
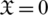 .1 then
.1 then
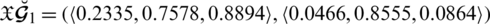
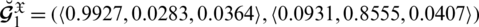
Proposition 4.7 Let
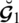 and
and
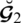 be two SLDFNs with
be two SLDFNs with
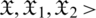 0 then the listed are satisfied
0 then the listed are satisfied
1.
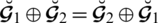
2.
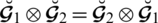
3.
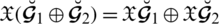
4.
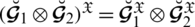
5.
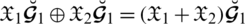
6.
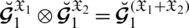
7.
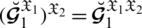
Proof. The proof is straightforward.
5 Spherical Linear Diophantine Fuzzy Weighted Aggregation Operators
We define certain score and accuracy functions for the comparative study of SLDFNs in MADM models. Chen et al. [49] invented the idea of the score feature on IFSs. Tversky et al. [50] suggested a related definition. The definition can be generalized for fuzzy hybrid versions and SLDFNs. According to specific techniques of multiple operators used in the algorithm, there are many more mappings for finding the value. In this manuscript, we specify various score functions to evaluate SLDFN’s behavior under the effect of these score functions, and after then relate their performance.
Definition 5.1 Let
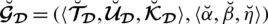 be an SLDFN, then mapping
be an SLDFN, then mapping
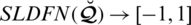 is called score function (SF) on
is called score function (SF) on
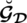 and portrayed as:
and portrayed as:
where
 be the collection of SLDFNs over
be the collection of SLDFNs over
 .
.
Definition 5.2 The mapping
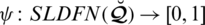 displays the accuracy function (AF) and depicted as:
displays the accuracy function (AF) and depicted as:
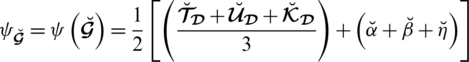
Definition 5.3 Let
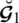 and
and
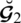 be two SLDFNs so we can conveniently equate these two SLDFNs using the SF and AF as:
be two SLDFNs so we can conveniently equate these two SLDFNs using the SF and AF as:
(i):For
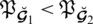 we have
we have
 ,
,
(ii):For
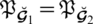 we have,
we have,
(a):For
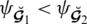 we have
we have
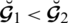 ,
,
(b):For
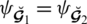 we have
we have
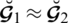 .
.
Further, we can displays it as a relation
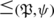 on
on
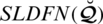 given as:
given as:
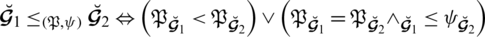
Definition 5.4 The mapping
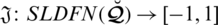 displays the quadratic score function (QSF) for SLDFN
displays the quadratic score function (QSF) for SLDFN
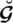 and portrayed as:
and portrayed as:
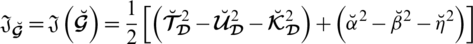
Definition 5.5 The mapping
 depicts the quadratic accuracy function (QAF) for SLDFN
depicts the quadratic accuracy function (QAF) for SLDFN
 which can be displayed as:
which can be displayed as:
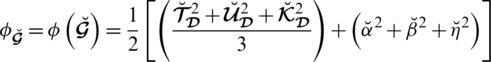
Definition 5.6 Let
 and
and
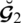 be two SLDFNs so we can conveniently equate these two SLDFNs using QSF and QAF as:
be two SLDFNs so we can conveniently equate these two SLDFNs using QSF and QAF as:
(i):For
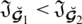 we have
we have
 ,
,
(ii):For
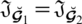 we have,
we have,
(a):For
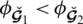 we have
we have
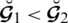 ,
,
(b):For
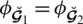 we have
we have
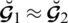 .
.
Further, we can display it as a relation
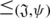 on
on
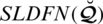 given as:
given as:
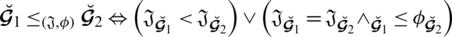
Definition 5.7 The expectation score function (ESF) on
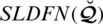 is depicted by the mapping
is depicted by the mapping
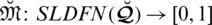 and defined as
and defined as
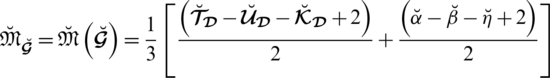
The ESF is a generalized form of SF. The ESF values are bounded in
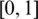 rather than
rather than
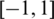 . ESF satisfies several of the properties described below.
. ESF satisfies several of the properties described below.
Definition 5.8 Let
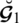 and
and
 be SLDFNs. The binary relation
be SLDFNs. The binary relation
 on
on
 can be defined as:
can be defined as:
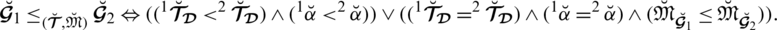
Definition 5.9 Let
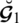 and
and
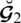 be SLDFNs. The binary relation
be SLDFNs. The binary relation
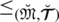 on
on
 can be defined as
can be defined as
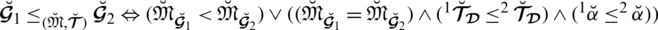 .
.
Now we define some aggregation operators based on spherical linear Diophantine fuzzy numbers (SLDFNs).
Theorem 5.10 For the assembling of SLDFNs
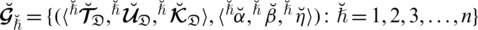 over
over
 with weight vector
with weight vector
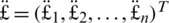 satisfying
satisfying
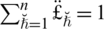 , we have
, we have
 , which is said to be “spherical linear Diophantine fuzzy weighted geometric aggregation” (SLDFWGA) operator and portrayed as:
, which is said to be “spherical linear Diophantine fuzzy weighted geometric aggregation” (SLDFWGA) operator and portrayed as:
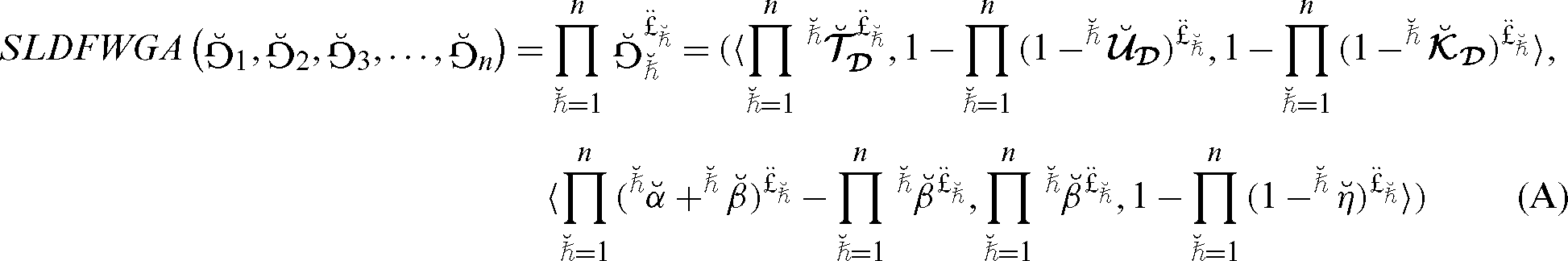
(A):
In SLDFWGA operator, we use
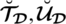 and
and
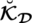 as satisfaction, abstinence, and dissatisfaction degrees respectively.
as satisfaction, abstinence, and dissatisfaction degrees respectively.
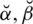 and
and
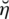 are control parameters for
are control parameters for
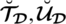 and
and
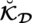 respectively and
respectively and
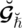 are the SLDFNs, where
are the SLDFNs, where
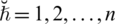 .
.
 be the assembling of all LDFNs.
be the assembling of all LDFNs.
Proof. Through utilizing the SLDFS operations and mathematical induction as described in [67] through Xu and [89] by Wang et al. we can easily prove this result.
Properties:
1. (Idempotency). Let
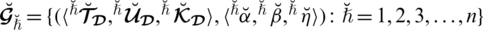 be a collection of SLDFNs over
be a collection of SLDFNs over
 . If
. If
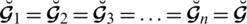 , then
, then
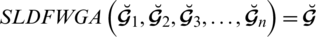
2. (Boundedness). Let
 be a collection of SLDFNs over
be a collection of SLDFNs over
 .
.
 is the grade of refusal for all
is the grade of refusal for all
 . If
. If
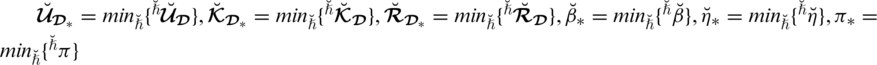 with
with
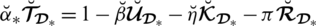 and
and
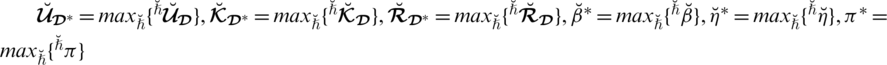 with
with
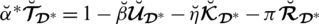 , then
, then
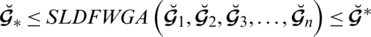
where
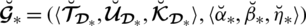 and
and
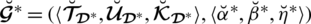 .
.
3. (Monotonicity). Let
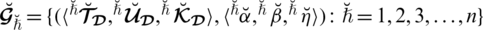 and
and
 be assemblings of SLDFNs over
be assemblings of SLDFNs over
 . If
. If
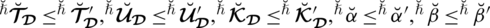 and
and
 , then
, then
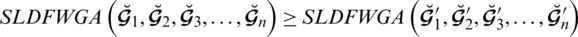
We can check all the properties by using basic operations defined on SLDFNs.
Theorem 5.11 For SLDFNs
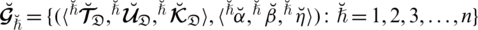 over
over
 with weight vector
with weight vector
 satisfying
satisfying
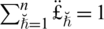 , the mapping
, the mapping
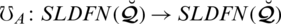 is said to be a “spherical linear Diophantine fuzzy weighted average aggregation” (SLDFWAA) operator and portrayed as
is said to be a “spherical linear Diophantine fuzzy weighted average aggregation” (SLDFWAA) operator and portrayed as
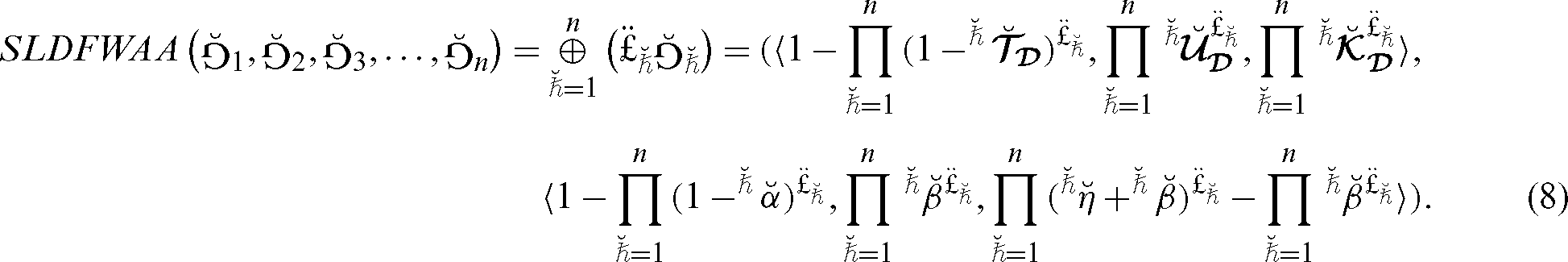
(8):
Proof. We can prove this on the same pattern as Theorem 5.10.
Properties:
1. (Idempotency). Let
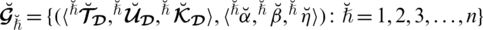 be a collection of SLDFNs over
be a collection of SLDFNs over
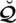 . If
. If
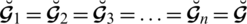 , then
, then
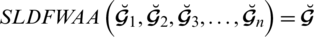
2. (Boundedness). Let
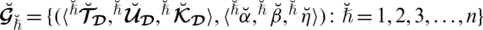 be a collection of SLDFNs over
be a collection of SLDFNs over
 .
.
 is the grade of refusal for all
is the grade of refusal for all
 . If
. If
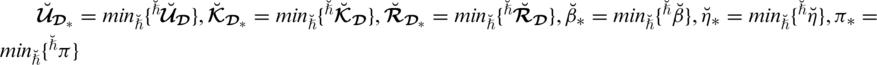 with
with
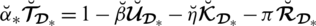 and
and
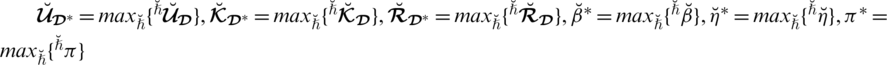 with
with
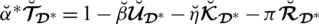 , then
, then
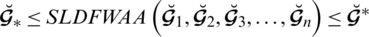
where
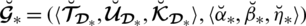 and
and
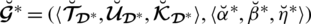 .
.
3. (Monotonicity). Let
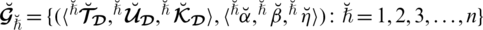 and
and
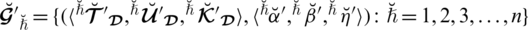 be assemblings of SLDFNs over
be assemblings of SLDFNs over
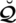 . If
. If
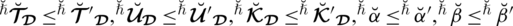 and
and
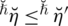 , then
, then
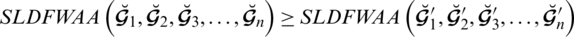
We can check all the properties by using basic operations defined on SLDFNs.
6 An Innovative Approach to MCDM Focused on Spherical Linear Diophantine Fuzzy Operators
Throughout this segment we propose, a novel framework to MCDM focused on SLDFWGA and SLDFWAA operators. For the same numerical case, we use two novel operators, and, use specific score function forms, we get separate ordering for the final judgment.
6.1 Case Study and Numerical Example
A gas explosion has historically been one of the serious disasters in coal mines and an effective emergency evacuation mechanism is one of the main safeguards for reducing accident damages. For emergency decision-making difficulties of mine injuries jobs, we would call the suggested MCDM algorithms focused on SLDFWGA and SLDFWAA operators, under the influence of various score functions. The mine accident risks job and life protection tremendously and imperils mine safety growth. As the events of the explosion frequently arise spontaneously and instantly, it is not possible to foresee the incident to a crumb and to have adequate plans and rescue measures in advance. Hence the emergency management strategies and incident scenarios are the required solution in crisis preparedness and effective responses. The great quality and effectiveness of the emergency decisions will directly affect the subsequent emergency motives and effect disaster development. Most mathematicians served with various conditions on emergency scenarios (see [66,74]). Fig. 13 reflects the procedure of a large coal mine’s condensed Gas Explosion Accident (GEA) emergency rescue.
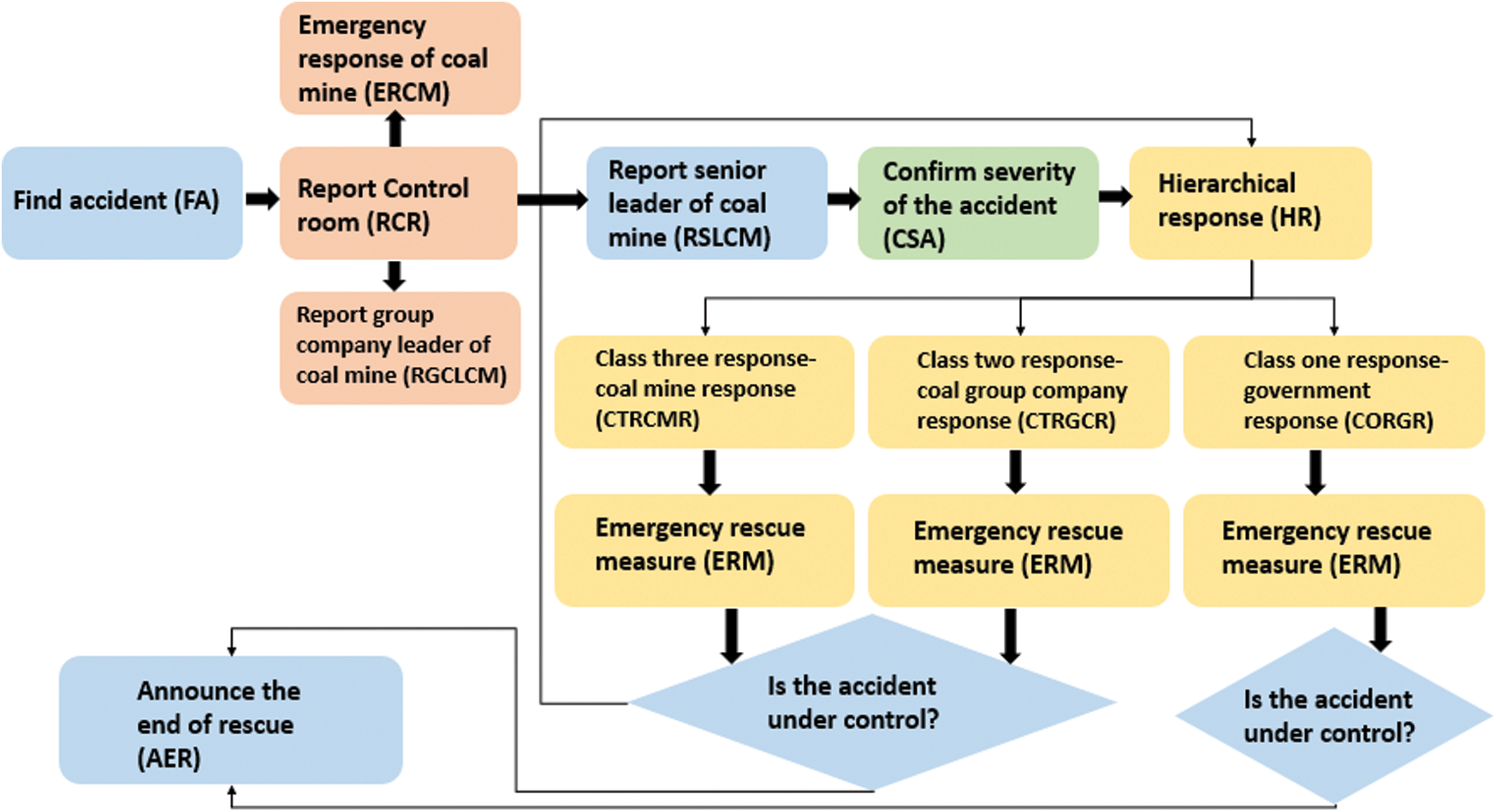
Figure 13: Simplified gas explosion accidents (GEA) emergency rescue workflow of a large coal mine
In this portion, we create an optimization technique on SLDFWGA and SLDFWAA operators. The scores are calculated using distinct score functions and finally, we correlate the outcomes achieved from both operators. The explanation for presenting two separate operators is that the definition of SLDFSs and its versatility to be used in various scenarios are expanded. Flowchart diagrams of the suggested algorithm can be seen in Fig. 14.

:
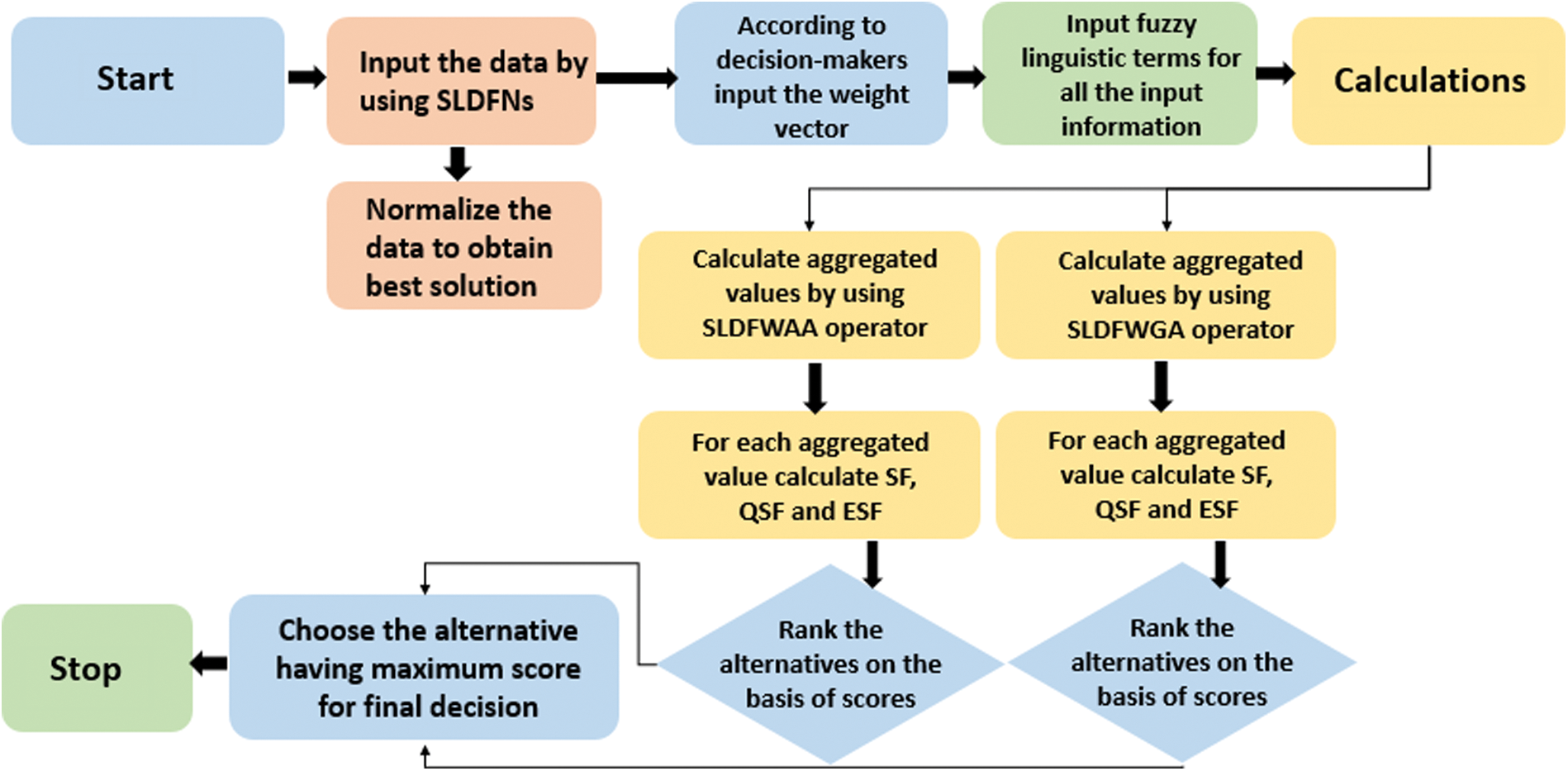
Figure 14: Diagram of the flow map of planned algorithm
Suppose that
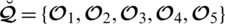 be an assembling of emergency plans, that is regarded by specialists in the coal mine for an explosion disaster. The specialists select the variables for the decision given as
be an assembling of emergency plans, that is regarded by specialists in the coal mine for an explosion disaster. The specialists select the variables for the decision given as
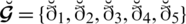 , where
, where

:
We should decide whether all the parameters are sufficient parameters based on the general changing theory and all the features of the mine incidents. We use other ambiguous linguistic concepts to describe the vector of weight according to specialists. Some values are provided in Tab. 13.
Table 13: Fuzzy linguistic values

The weight vector according to experts’ opinion and experiences is given as
 . We can write it as
. We can write it as
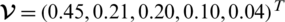 , with the condition
, with the condition
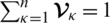 .
.
The assessments for emergency plans are according to experts and given in the form of SLDF-data in Tab. 14. Tab. 14 is constructed by using the information given in Tab. 13.
Table 14: SLDF-input information

By using spherical linear Diophantine fuzzy weighted geometric aggregation (SLDFWGA) operator given in Equation (A) over the input Tab. 14, we get aggregated values of alternatives given as

Now we evaluate the score values by using Definition 5.1 given as
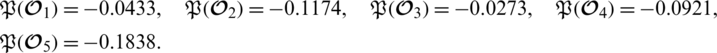
From Definition 5.3 we conclude that the preference order is
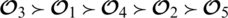 .
.
Now we evaluate the quadratic score values by using Definition 5.4 given as
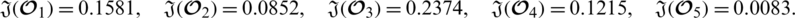
From Definition 5.6 we conclude that the preference order is
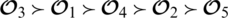 .
.
Now we evaluate the expectation score values by using Definition 5.7 given as
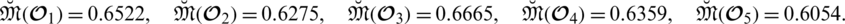
From Definition 5.9 we conclude that the preference order is
 .
.
The comparison between the ranking of all alternatives by using different score functions corresponding to the SLDFWGA operator is given in Fig. 15.
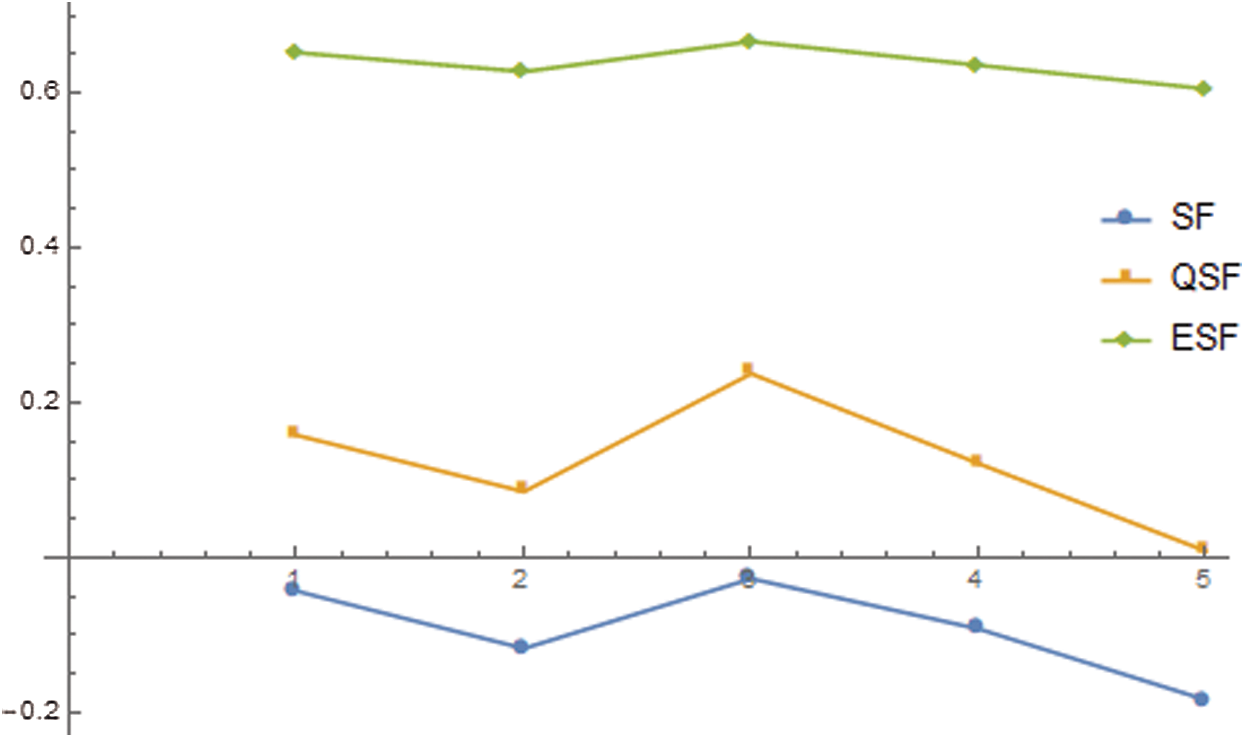
Figure 15: The comparison of “score function” (SF), “quadratic score function” (QSF), and “expectation score function” (ESF) for SLDFWGA operator
By using spherical linear Diophantine fuzzy weighted average aggregation (SLDFWAA) operator given in Eq. (8) over the input Tab. 14, we get aggregated values of alternatives given as

Now we evaluate the score values by using Definition 5.1 given as
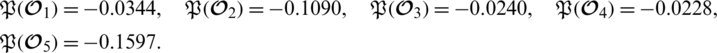
From Definition 5.3 we conclude that the preference order is
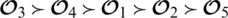 .
.
Now we evaluate the quadratic score values by using Definition 5.4 given as
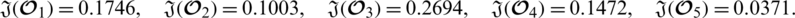
From Definition 5.6 we conclude that the preference order is
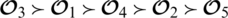 .
.
Now we evaluate the expectation score values by using Definition 5.7 given as
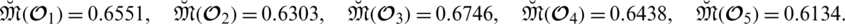
From Definition 5.9 we conclude that the preference order is
 . The comparison between the ranking of all alternatives by using different score functions corresponding to the SLDFWAA operator is given in Fig. 16.
. The comparison between the ranking of all alternatives by using different score functions corresponding to the SLDFWAA operator is given in Fig. 16.
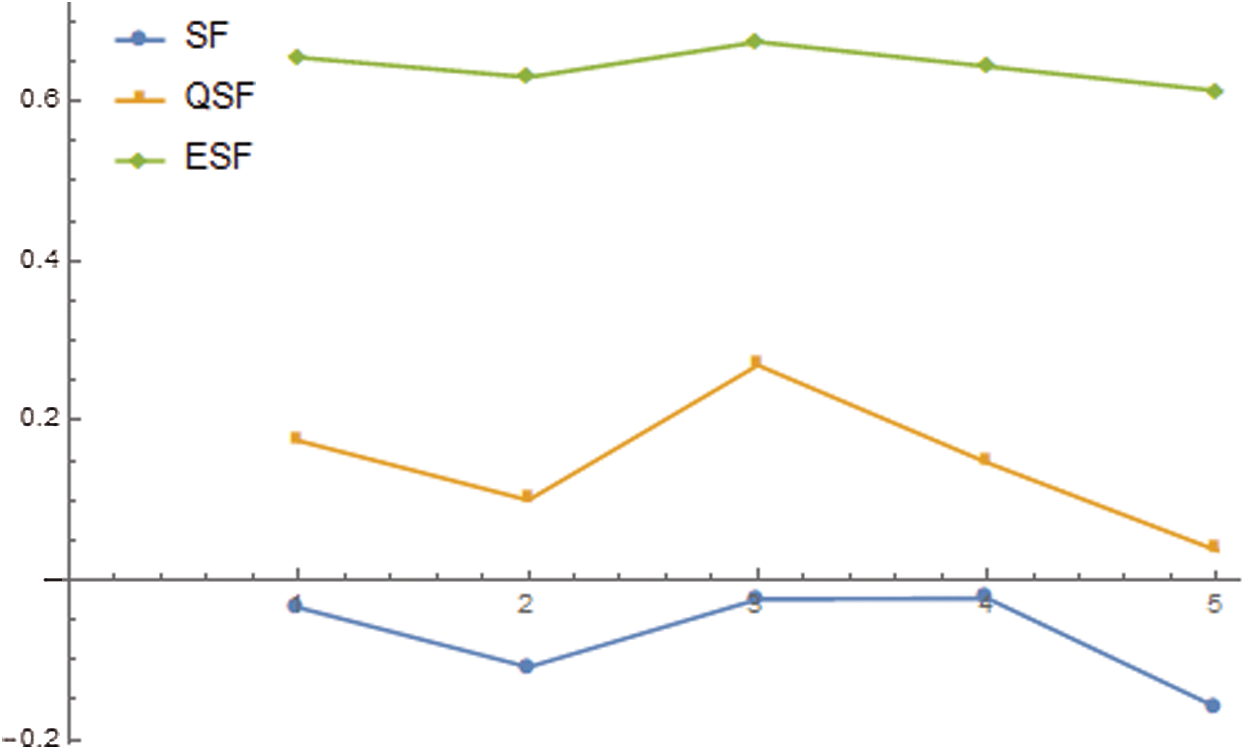
Figure 16: The comparison of “score function” (SF), “quadratic score function” (QSF), and “expectation score function” (ESF) for SLDFWAA operator
6.3 Study of the Discussions and Comparative Analysis
Throughout this subsection, we address the feasibility of the proposed process, it’s aggregation versatility to work with specific inputs and outputs, the effect of score functions, sensitivity analysis, supremacy, and finally the contrast of the presented methodology with current techniques.
Reliability of method and its consistency:
The recommended technique is accurate and appropriate for input data of all types. The developed framework is suitable for addressing uncertainties. Using control parameters it contains the space of PFSs, SFSs, T-SFSs, and NSs. Such parameters expand the space between satisfaction and dissatisfaction classes so we can utilize our model efficiently in various contexts by adjusting the practical meaning of certain parameters. We experience a variety of factors and input parameters according to the appropriate circumstances in certain MADM difficulties. The suggested SLDFS is straightforward and quick to grasp and can be readily extended to different alternatives and attributes.
Aggregation versatility, for specific inputs and outputs:
The recommended algorithms are robust and can be conveniently utilized for multiple inputs and output scenarios. Since the diverse score functions, there is no distinction in the classification of the suggested algorithms. This methodology is more robust than others as comparison parameters raise grade space and can differ based on the MADM system circumstances.
The impact of score function:
Feng et al. [53] provides different score functions for IFSs and addresses their relation. We add three forms of functions called score (SF), quadratic score (QSF), and expectation value (ESF) respectively. For the comparison of SLDFNs, we also define the associated accuracy functions. Every score method requires its estimation and specific ordering methods such that the slightly different result is accessible. From Tabs. 15 and 16, we can observe that there are identical scores for SF and ESF, but for QSF it is distinct from the others. Although it is essential to note that for all score functions, the outcome from both algorithms is nearly equivalent (Figs. 17 and 18).
Table 15: Ranking order of alternatives for SLDFWGA operator under different score functions

Table 16: Ranking order of alternatives for SLDFWAA operator under different score functions

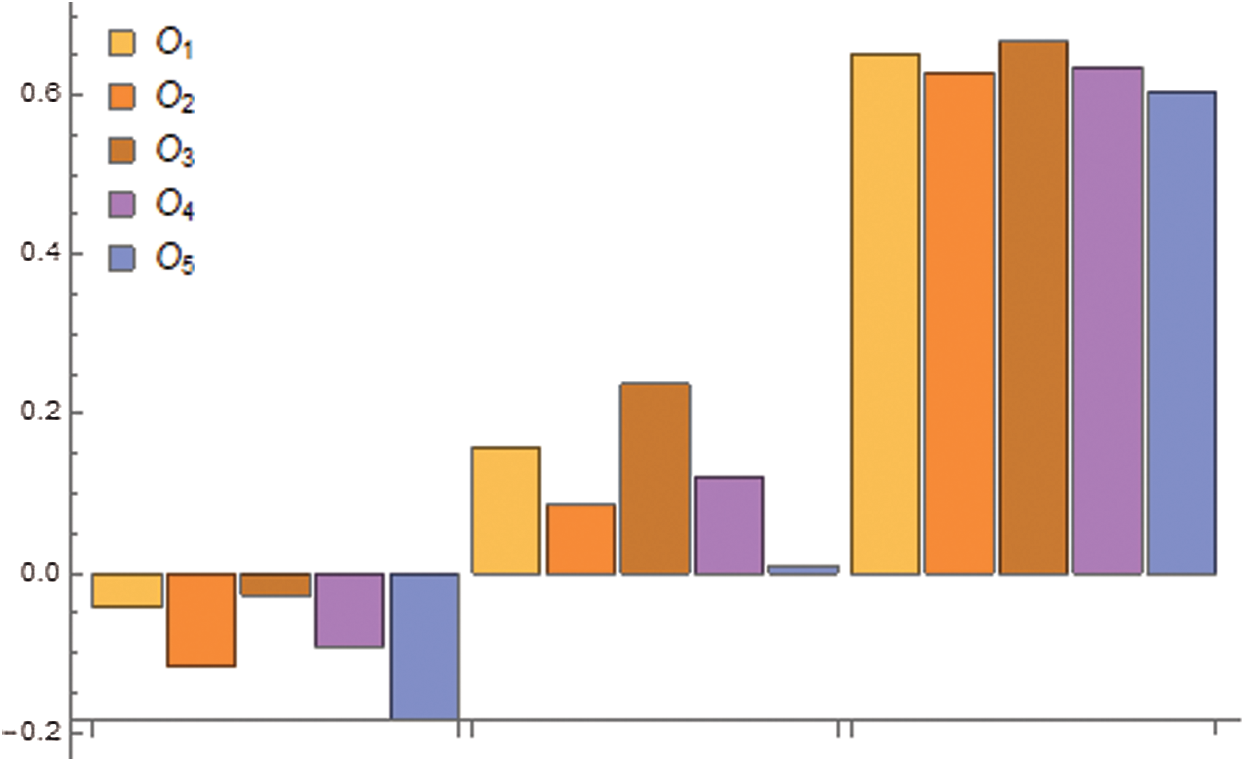
Figure 17: The comparison of 5 alternatives under SF, QSF, and ESF for SLDFWGA operator
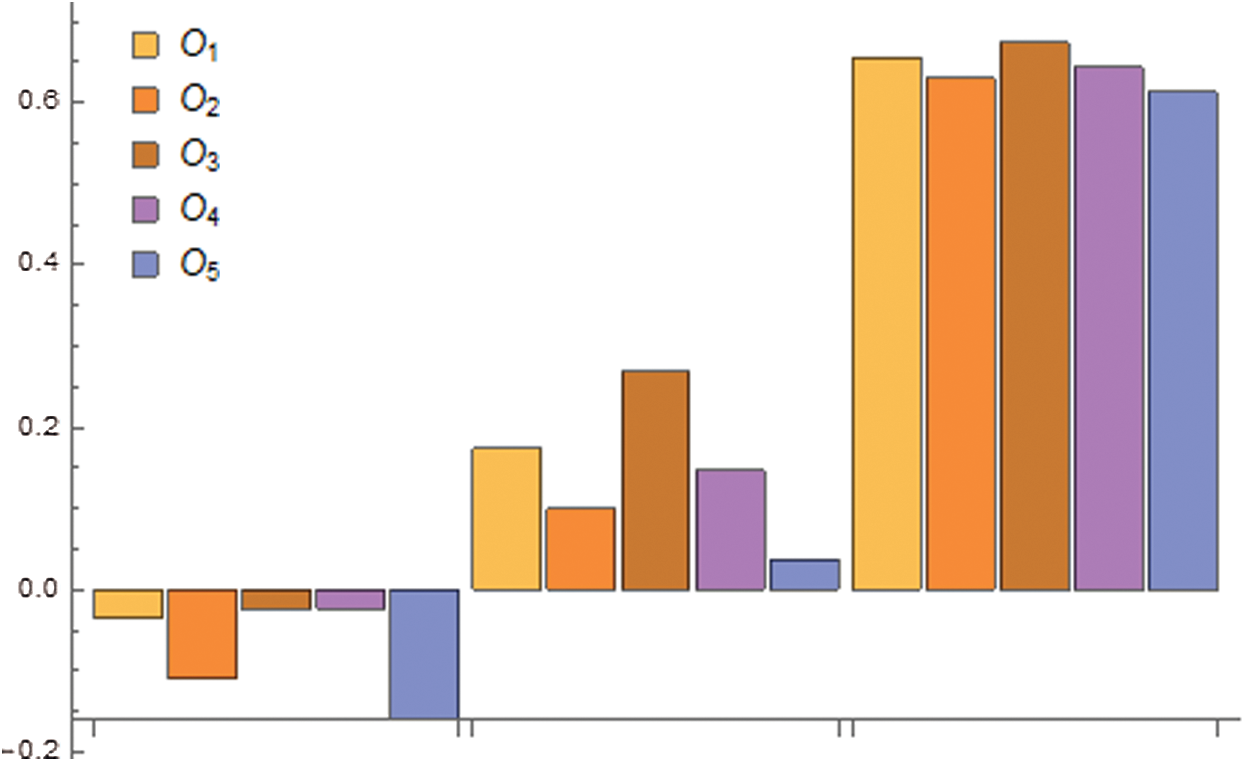
Figure 18: The comparison of 5 alternatives under SF, QSF, and ESF for SLDFWAA operator
The existing fuzzy models like picture fuzzy sets (PFSs), spherical fuzzy sets (SFSs), T-spherical fuzzy sets (T-SFSs), and neutrosophic sets (NSs) have had various strict limitations for their satisfaction, dissatisfaction, abstain or refusal grades. To relax these restrictions, we proposed a new extension of fuzzy sets named the spherical linear Diophantine Fuzzy set (SLDFS) which is more efficient to address various uncertainties in a parametric way. Spherical linear Diophantine fuzzy information includes additional features of the reference or control parameters denoted by
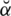 ,
,
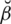 and
and
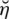 . We described the graphical analysis of SLDFSs to compare it with other fuzzy sets. For the selection of grades in MCDM, SLDFSs provide a broader space than PFSs, SFSs, T-SFSs, and NSs. To overcome the drawbacks of operations of picture fuzzy numbers and their corresponding aggregation operators, we defined novel operations on picture fuzzy numbers and their smooth aggregation operators. We introduced numerous score and accuracy functions for the analysis of spherical linear Diophantine fuzzy numbers (SLDFNs). We defined new aggregation operators named spherical linear Diophantine fuzzy geometric weighted aggregation (SLDFWGA) and spherical linear Diophantine fuzzy weighted average aggregation (SLDFWAA). We developed a new MCDM process focused on the suggested operators. We elaborated the distinction of suggested operators and practiced the influence of proposed score functions in the information aggregation.
. We described the graphical analysis of SLDFSs to compare it with other fuzzy sets. For the selection of grades in MCDM, SLDFSs provide a broader space than PFSs, SFSs, T-SFSs, and NSs. To overcome the drawbacks of operations of picture fuzzy numbers and their corresponding aggregation operators, we defined novel operations on picture fuzzy numbers and their smooth aggregation operators. We introduced numerous score and accuracy functions for the analysis of spherical linear Diophantine fuzzy numbers (SLDFNs). We defined new aggregation operators named spherical linear Diophantine fuzzy geometric weighted aggregation (SLDFWGA) and spherical linear Diophantine fuzzy weighted average aggregation (SLDFWAA). We developed a new MCDM process focused on the suggested operators. We elaborated the distinction of suggested operators and practiced the influence of proposed score functions in the information aggregation.
Our future work will be focused on solving other real-life problems with “spherical linear Diophantine fuzzy rough set” (SLDFRS), “spherical linear Diophantine Hesitant fuzzy set” (SLDHFS), “spherical linear Diophantine fuzzy graphs” (SLDF-graphs), and “interval-valued spherical linear Diophantine fuzzy set” (IVSLDFS). SLDFSs may be extended to any other aggregation operators, such as prioritized AOs, power mean AOs, Dombi’s AOs, Bonferroni mean AOs, Heronian mean AOs, and so on. We hope that our research results will be successful for researchers working in the fields of information aggregation, information fusion, robotics, pattern recognition, artificial intelligence, machine learning, neural networks, and medical diagnosis.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
2. Zadeh, L. A. (1975). The concept of a linguistic variable and its application to approximate reasoning–-I. Information Sciences, 8(3), 199–249. DOI 10.1016/0020-0255(75)90036-5. [Google Scholar] [CrossRef]
3. Atanassov, K. T. (1984). Intuitionistic fuzzy sets. In: Sgurev, V., (ed.) VII ITKRs Session. Sofia: Central Science and Technology Library, Bulgarian Academy of Sciences. [Google Scholar]
4. Atanassov, K. T., Stoeva, S. (1983). Intuitionistic fuzzy sets. Polish Symposium on Interval & Fuzzy Mathematics, pp. 23–26, Poznan. [Google Scholar]
5. Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
6. Atanassov, K. T. (2016). Geometrical interpretation of the elemets of the intuitionistic fuzzy objects. International Journal of Bio-Automation, 20(S1), S27–S42. [Google Scholar]
7. Smarandache, F. (1998). Neutrosophy neutrosophic probability, set and logic. American Research Press, Rehoboth. [Google Scholar]
8. Akbarizadeh, G., Moghaddam, A. E. (2016). Detection of lung nodes in CT scans based on unsupervised feature learning and fuzzy inference. Journal of Medical Imaging and Health Informatics, 6(2), 477–483. DOI 10.1166/jmihi.2016.1720. [Google Scholar] [CrossRef]
9. Suapang, P., Dejhan, K., Yimmun, S. (2010). Medical image processing and analysis for nuclear medicine diagnosis. International Conference on Control Automation and Systems (ICCASGyeonggi-do, South Korea. [Google Scholar]
10. Akbarizadeh, G. (2012). A new statistical-based kurtosis wavelet energy feature for texture recognition of SAR images. IEEE Transections on Geoscience and Remote Sensing, 50(11), 4358–4368. DOI 10.1109/TGRS.2012.2194787. [Google Scholar] [CrossRef]
11. Akbarizadeh, G. (2013). Segmentation of SAR satellite images unsing cellular learning automata and adaptive chains. Journal of Remote Sensing Technology, 1(2), 44–51. DOI 10.18005/JRST0102003. [Google Scholar] [CrossRef]
12. Akbarizadeh, G., Rahmani, M. (2015). A new ensemble clustering method for PolSAR image segmentation. 7th Conference on Information Knowledge and Technology, Urmia University, Urmia, Iran. [Google Scholar]
13. Akbarizadeh, G., Tirandaz, Z., Kooshesh, M. (2014). A new curvelet-based texture classification approach for land cover recognition of SAR satellite images. Malaysian Journal of Computer Science, 27(3), 218–239. [Google Scholar]
14. Akbarizadeh, G., Tirandaz, Z. (2015). Segmentation parameter estimation algorithm based on curvelet transform coefficients energy for feature extraction and texture description of SAR images. 7th Conference on Information and Knowledge Technology, Urmia University, Urmia, Iran. [Google Scholar]
15. Akbarizadeh, G., Rahmani, M. (2017). Efficient combination of texture and color features in a new spectral clustering method for PolSAR image segmentation. National Accademy Science Letters, 40(2), 117–120. DOI 10.1007/s40009-016-0513-6. [Google Scholar] [CrossRef]
16. Benz, U. C., Hofmann, P., Willhauck, G., Lingenfelder, I., Heynen, M. (2004). Multi-resolution object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS Journal of Photogrammetry and Remote Sensing, 58(3–4), 239–258. DOI 10.1016/j.isprsjprs.2003.10.002. [Google Scholar] [CrossRef]
17. Chanussot, J., Mauris, G., Lambert, P. (1999). Fuzzy fusion techniques for linear features detection in multitemporal SAR images. IEEE Transections on Geoscience and Remote Sensing, 37(3), 1292–1305. DOI 10.1109/36.763290. [Google Scholar] [CrossRef]
18. Faraji, Z., Akbarizadeh, G. (2015). A new computer vision algorithm for classification of POLSAR images. 7th Conference on Information and Knowledge Technology, Urmia University, Urmia, Iran. [Google Scholar]
19. Ahmadi, N., Akbarizadeh, G. (2017). Hybrid robust iris recognition approach using iris image pre-processing, two-dimensional gabor features and multi-layer perceptron neural network/PSO. IET Biometrics, 7(2), 153–162. DOI 10.1049/iet-bmt.2017.0041. [Google Scholar] [CrossRef]
20. Duagman, J. (2009). How iris recognition works. Essential Guide to Image Processing, 1(1), 715–739. DOI 10.1016/B978-0-12-374457-9.00025-1. [Google Scholar] [CrossRef]
21. Modava, M., Akbarizadeh, G. (2017). Coastline extraction from SAR images using spatial fuzzy clustering and the active contour method. International Journal of Remote Sensing, 38(2), 355–370. DOI 10.1080/01431161.2016.1266104. [Google Scholar] [CrossRef]
22. Modava, M., Akbarizadeh, G. (2017). A level set based method for coastline detection of SAR images. 3rd International Conference on Patteren Recognition and Image Analysis, Islamic Republic of Shahrekord, Iran. [Google Scholar]
23. Gong, M., Zhou, Z., Ma, J. (2012). Change detection in synthetic aperture radar images based on image fusion and fuzzy clustering. IEEE Transections on Image Processing, 21(4), 2141–2151. DOI 10.1109/TIP.2011.2170702. [Google Scholar] [CrossRef]
24. Rahmani, M., Akbarizadeh, G. (2015). Unsupervised feature learning based on sparse coding and spectral clustering for segmentation of synthetic aperture radar images. IET Computer Vision, 9(5), 629–638. DOI 10.1049/iet-cvi.2014.0295. [Google Scholar] [CrossRef]
25. Shanmugan, K. S., Narayanan, V., Frost, V. S., Stiles, J. A., Holtzman, J. C. (1981). Textural features for radar image analysis. IEEE Transections on Geoscience and Remote Sensing, 3(3), 153–156. DOI 10.1109/TGRS.1981.350344. [Google Scholar] [CrossRef]
26. Tirandaz, Z., Akbarizadeh, G. (2016). A two-phased algorithm based on kurtosis curvelet energy and unsupervised spectral regression for segmentation for SAR images. IEEE Journal of Selected Topics in Applied Earth and Observations and Remote Sensing, 9(3), 1244–1264. DOI 10.1109/JSTARS.2015.2492552. [Google Scholar] [CrossRef]
27. Cuong, B. C. (2013). Picture fuzzy sets-first results, part 1. In: Preprint of Seminar on Neuro-Fuzzy Systems with Applications. Institute of Mathematics, Hanoi. [Google Scholar]
28. Cuong, B. C. (2013). Picture fuzzy sets-first results, part 2. In: Preprint of Seminar on Neuro-Fuzzy Systems with Applications. Institute of Mathematics, Hanoi. [Google Scholar]
29. Cuong, B. C., Kreinovich, V. (2013). Picture fuzzy sets–-A new concept for computational intelligence problems. 3rd World Congress on Information and Communication Technologies, Hanoi, Vietnam. [Google Scholar]
30. Andekah, Z. A., Naderan, M., Akbarizadeh, G. (2017). Semi-supervised Hyperspectral image classification using spatial-spectral features and superpixel-based sparse codes. Iranian Conference of Electrical Engineering, pp. 2229–2234, Tehran, Iran. [Google Scholar]
31. Perić, N. (2015). Fuzzy logic and fuzzy set theory based edge detection algorithm. Serbian Journal of Electrical Engineering, 12(1), 109–116. DOI 10.2298/SJEE1501109P. [Google Scholar] [CrossRef]
32. Mahmood, T., Ullah, K., Khan, Q., Jan, N. (2018). An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Computing and Applications, 31(11), 7041–7053. DOI 10.1007/s00521-018-3521-2. [Google Scholar] [CrossRef]
33. Yager, R. P. (2013). Pythagorean fuzzy subsets. Proceedings of the IFSA World Congress and NAFIPS Annual Meeting, pp. 57–61, Edmonton, AB, Canada. [Google Scholar]
34. Yager, R. P. (2014). Pythagorean membership grades in multi criteria decision-making. IEEE Transections on Fuzzy Sytems, 22(4), 958–965. DOI 10.1109/TFUZZ.2013.2278989. [Google Scholar] [CrossRef]
35. Ali, M. I. (2018). Another view on q-rung orthopair fuzzy sets. International Journal of Intelligent Systems, 33(11), 2139–2153. DOI 10.1002/int.22007. [Google Scholar] [CrossRef]
36. Liu, P., Wang, P. (1983). Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision-making. International Journal of Intelligent Systems, 33(2), 259–280. DOI 10.1002/int.21927. [Google Scholar] [CrossRef]
37. Yager, R. P. (2017). Generalized orthopair fuzzy sets. IEEE Transections on Fuzzy Systems, 25(5), 1222–1230. DOI 10.1109/TFUZZ.2016.2604005. [Google Scholar] [CrossRef]
38. Si, A., Das, S., Kar, S. (2019). An approach to rank picture fuzzy numbers for decision-making problems. Decision Making: Applications in Management and Engineering, 2(2), 54–64. DOI 10.31181/dmame1902049s. [Google Scholar] [CrossRef]
39. Stanujkić, D., Karabašević, D. (2018). An extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: A case of website evaluation. Operational Research in Engineering Sciences: Theory and Applications, 1(1), 29–39. DOI 10.31181/oresta19012010129s. [Google Scholar] [CrossRef]
40. Sharma, H. K., Kumari, K., Kar, S. (2020). A rough set theory application in forecasting models. Decision Making: Applications in Management and Engineering, 3(1), 1–21. DOI 10.31181/dmame2003001s. [Google Scholar] [CrossRef]
41. Molodtsov, D. (1999). Soft set theory-first results. Computers and Mathematics with Applications, 37(4–5), 19–31. DOI 10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]
42. Agarwal, M., Biswas, K. K., Hanmandlu, M. (2013). Generalized intuitionitic fuzzy soft sets with applications in decision-making. Applied Soft Computing, 20(8), 3552–3566. DOI 10.1016/j.asoc.2013.03.015. [Google Scholar] [CrossRef]
43. Çağman, N., Enginoglu, S., Çitak, F. (2011). Fuzzy soft set theory and its applications. Iranian Journal of Fuzzy Systems, 8(8), 137–147. DOI 10.22111/ijfs.2011.292. [Google Scholar] [CrossRef]
44. Chang, C. L. (1968). Fuzzy topological spaces. Journal of Mathematical Analysis and Applications, 24(1), 182–190. DOI 10.1016/0022-247X(68)90057-7. [Google Scholar] [CrossRef]
45. Coker, D. (1997). An introduction to intuitionistic fuzzy topological spaces. Fuzzy Sets and Systems, 88(1), 81–89. DOI 10.1016/S0165-0114(96)00076-0. [Google Scholar] [CrossRef]
46. Garg, H. (2016). A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision-making. International Journal of Intelligent Systems, 31(9), 886–920. DOI 10.1002/int.21809. [Google Scholar] [CrossRef]
47. Garg, H. (2016). Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision-making. Computers & Industrial Engineering, 101, 53–69. DOI 10.1016/j.cie.2016.08.017. [Google Scholar] [CrossRef]
48. Garg, H. (2016). A novel accuracy function under interval-valued Pythagorean fuzzy environment for solving multi-criteria decision-making problem. Journal of Intelligent and Fuzzy Systems, 31(1), 529–540. DOI 10.3233/IFS-162165. [Google Scholar] [CrossRef]
49. Chen, S. M., Tan, M. J. (1994). Handling multicriteria fuzzy decision-makling problems based on vague set theory. Fuzzy Sets and Systems, 67(2), 163–172. DOI 10.1016/0165-0114(94)90084-1. [Google Scholar] [CrossRef]
50. Tversky, A., Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainity. Journal of Risk and Uncertainty, 5(4), 297–323. DOI 10.1007/BF00122574. [Google Scholar] [CrossRef]
51. Dombi, J. (1982). A general class of fuzzy operators, the demorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets and Systems, 8(2), 149–163. DOI 10.1016/0165-0114(82)90005-7. [Google Scholar] [CrossRef]
52. Feng, F., Jun, Y. B., Liu, X., Li, L. (2010). An adjustable approach to fuzzy soft set based decision-making. Journal of Computational and Applied Mathematics, 234(1), 10–20. DOI 10.1016/j.cam.2009.11.055. [Google Scholar] [CrossRef]
53. Feng, F., Fujita, H., Ali, M. I., Yager, R. R., Liu, X. (2019). Another view on generalized intuitionistic fuzzy soft sets and related multi-attribute decision-making methods. IEEE Transections on Fuzzy Systems, 27(3), 474–488. DOI 10.1109/TFUZZ.2018.2860967. [Google Scholar] [CrossRef]
54. Jose, S., Kuriaskose, S. (2014). Aggregation operators, score function and accuracy function for multi-criteria decision-making in intuitionistic fuzzy context. Notes on Intuitionistic Fuzzy Sets, 20(1), 40–44. [Google Scholar]
55. Kaur, G., Garg, H. (2018). Cubic intuitionistic fuzzy aggregation operators. International Journal of Uncertainity Quantification, 8(5), 405–427. DOI 10.1615/Int.J.UncertaintyQuantification.2018020471. [Google Scholar] [CrossRef]
56. Mahmood, T., Mehmood, F., Khan, Q. (2017). Some generalized aggregation operators for cubic hesitant fuzzy sets and their application to multi-criteria decision-making. Punjab University Journal of Mathematics, 49(1), 31–49. [Google Scholar]
57. Chen, J., Li, S., Ma, S., Wang, X. (2014). m-Polar fuzzy sets: An extension of bipolar fuzzy sets. Scientific World Journal, 2014(3), 1–8. DOI 10.1155/2014/416530. [Google Scholar] [CrossRef]
58. Wang, H., Smarandache, F., Zhang, Y. Q., Sunderraman, R. (2010). Single valued neutrosophic sets. Multispace and Multistructure, 4, 410–413. DOI 10.1007/s00357-017-9225-y. [Google Scholar] [CrossRef]
59. Riaz, M., Hashmi, M. R. (2019). MAGDM for agribusiness in the environment of various cubic m-polar fuzzy averaging aggregation operators. Journal of Intelligent & Fuzzy Systems, 37(3), 3671–3691. DOI 10.3233/JIFS-182809. [Google Scholar] [CrossRef]
60. Riaz, M., Hashmi, M. R. (2019). Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems. Journal of Intelligent & Fuzzy Systems, 37(4), 5417–5439. DOI 10.3233/JIFS-190550. [Google Scholar] [CrossRef]
61. Riaz, M., Hashmi, M. R. (2020). Soft rough Pythagorean m-polar fuzzy sets and Pythagorean m-polar fuzzy soft rough sets with application to decision-making. Computational and Applied Mathematics, 39(1), 1–36. DOI 10.1007/s40314-019-0989-z. [Google Scholar] [CrossRef]
62. Riaz, M., Hashmi, M. R., Kalsoom, H., Pamucar, D., Chu, Y. M. (2020). Linear Diophantine fuzzy soft rough sets for the selection of sustainable material handling equipment. Symmetry, 12(1215), 1–39. DOI 10.3390/sym12081215. [Google Scholar] [CrossRef]
63. Riaz, M., Tehrim, S. T. (2019). Cubic bipolar fuzzy ordered weighted geometric aggregation operators and their application using internal and external cubic bipolar fuzzy data. Computational & Applied Mathematics, 38(87), 1–25. DOI 10.1007/s40314-019-0767-y. [Google Scholar] [CrossRef]
64. Zhan, J., Liu, Q., Davvaz, B. (2015). A new rough set theory: Rough soft hemirings. Journal of Intelligent and Fuzzy Systems, 28(4), 1687–1697. DOI 10.3233/IFS-141455. [Google Scholar] [CrossRef]
65. Zhan, J., Alcantud, J. C. R. (2018). A novel type of soft rough covering and its application to multi-criteria group decision-making. Artificial Intelligence Review, 52(4), 2381–2410. DOI 10.1007/s10462-018-9617-3. [Google Scholar] [CrossRef]
66. Peng, X., Garg, H. (2018). Algorithms for interval-valued fuzzy soft sets in emergency decision-making based on WDBA and CODAS with new information measure. Computers and Industrial Engineering, 119, 439–452. DOI 10.1016/j.cie.2018.04.001. [Google Scholar] [CrossRef]
67. Xu, Z. S. (2007). Intuitionistic fuzzy aggregation operators. IEEE Transection on Fuzzy Systems, 15(6), 1179–1187. DOI 10.1109/TFUZZ.2006.890678. [Google Scholar] [CrossRef]
68. Xu, Z., Cai, X. (2012). Intuitionistic fuzzy information aggregation: Theory and applications. Berlin, Heidelberg: Science Press Beijing and Springer-Verlag. [Google Scholar]
69. Xu, Z. (2014). Studies in fuzziness and soft computing: Hesitant fuzzy sets theory. Springer International Publishing, Switzerland. [Google Scholar]
70. Ye, J. (2013). Interval-valued hesitant fuzzy prioritized weighted aggregation operators for multi-attribute decision-making. Journal of Algorithms & Computational Technology, 8(2), 179–192. DOI 10.1260/1748-3018.8.2.179. [Google Scholar] [CrossRef]
71. Ye, J. (2017). Linguistic neutrosophic cubic numbers and their multiple attribute decision-making method. Information-An International Interdisciplinary Journal, 8, 1–11. DOI 10.3390/info8030110. [Google Scholar] [CrossRef]
72. Guo, K. (2014). Amount of information and attitudinal-based method for ranking Atanassov’s intuitionistic fuzzy values. IEEE Transections on Fuzzy Systems, 22(1), 177–188. DOI 10.1109/TFUZZ.2013.2249586. [Google Scholar] [CrossRef]
73. Hong, D. H., Choi, C. H. (2000). Multi-criteria fuzzy decision-making problems based on vauge set theory. Fuzzy Sets and Systems, 114(1), 103–113. DOI 10.1016/S0165-0114(98)00271-1. [Google Scholar] [CrossRef]
74. He, Z., Wu, Q., Wen, L., Fu, G. (2019). A process mining approach to improve emergency rescue processes of fatal gas explosion accidents in Chinese coal mines. Safety Sciences, 111, 154–166. DOI 10.1016/j.ssci.2018.07.006. [Google Scholar] [CrossRef]
75. Zhang, H., Dong, Y., Carrascosa, I. P., Zhou, H. (2019). Failure mode and effect analysis in a linguistic context: A consensus-based multi-attribute group decision-making approach. IEEE Transection on Reliability, 68(2), 566–582. DOI 10.1109/TR.2018.2869787. [Google Scholar] [CrossRef]
76. Zhang, H., Dong, Y., Chiclana, F., Yu, S. (2019). Consensus efficiency in group decision making: A comprehensive comparative study and its optimal design. European Journal of Operational Research, 275(2), 580–598. DOI 10.1016/j.ejor.2018.11.052. [Google Scholar] [CrossRef]
77. Yu, W., Zhang, Z., Zhong, Q., Sun, L. (2017). Extended TODIM for multi-criteria group decision making based on unbalanced hesitant fuzzy linguistic term sets. Computers & Industrial Engineering, 114, 316–328. DOI 10.1016/j.cie.2017.10.029. [Google Scholar] [CrossRef]
78. Zhang, Z., Kou, X., Yu, W., Guo, C. (2018). On priority weights and consistency for incomplete hesitant fuzzy preference relations. Knowledge Based Systems, 143, 115–126. DOI 10.1016/j.knosys.2017.12.010. [Google Scholar] [CrossRef]
79. Zhang, Z., Guo, C. (2017). Deriving priority weights from intuitionistic multiplicative preference relations under group decision-making settings. Journal of the Operational Research Society, 68(12), 1582–1599. DOI 10.1057/s41274-016-0171-6. [Google Scholar] [CrossRef]
80. Kushwaha, D. K., Panchal, D., Sachdeva, A. (2020). Risk analysis of cutting system under intuitionistic fuzzy environment. Reports in Mechanical Engineering, 1(1), 162–173. DOI 10.31181/rme200101162k. [Google Scholar] [CrossRef]
81. Zolfani, S. H., Yazdani, M., Pamucar, D., Zarate, P. (2020). A VIKOR and TOPSIS focused reanalysis of the MADM methods based on logarithmic normalization. Facta universitatis series: Mechanical Engineering, 18(3), 341–355. DOI 10.22190/FUME191129016Z. [Google Scholar] [CrossRef]
82. Pamucar, D. (2020). Normalized weighted geometric dombi bonferoni mean operator with interval grey numbers: Application in multicriteria decision making. Reports in Mechanical Engineering, 1(1), 44–52. DOI 10.31181/rme200101044p. [Google Scholar] [CrossRef]
83. Xu, Y., Shang, X., Wang, J., Zhang, R., Li, W. et al. (2018). A method to multi-attribute decision-making with picture fuzzy information based on Muirhead mean. Journal of Intelligent and Fuzzy Systems, 36(4), 1–17. DOI 10.3233/JIFS-171531. [Google Scholar] [CrossRef]
84. Wang, R., Wang, J., Gao, H., Wei, G. (2019). Methods for MADM with picture fuzzy Muirhead mean operators and their applications for evaluating the financial investment risk. Symmetry, 11(6), 1–20. DOI 10.3390/sym11010006. [Google Scholar] [CrossRef]
85. Ramakrishnan, K. R., Chakraborty, S. (2020). A cloud TOPSIS model for green supplier selection. Facta Universitatis, Series: Mechanical Engineering, 18(3), 375–397. DOI 10.22190/FUME200307036R. [Google Scholar] [CrossRef]
86. Khan, S., Abdullah, S., Abdullah, L., Ashraf, S. (2019). Logarithmic aggregation operators of picture fuzzy numbers for multi-attribute decision-making problems. Mathematics, 7(608), 1–19. DOI 10.3390/math7070608. [Google Scholar] [CrossRef]
87. Khan, S., Abdullah, S., Ashraf, S. (2019). Picture fuzzy aggregation information based on Einstein operations and their application in decision-making. Mathematical Sciences, 13(3), 213–229. DOI 10.1007/s40096-019-0291-7. [Google Scholar] [CrossRef]
88. Pamucar, D., Jankovic, A. (2020). The application of the hybrid interval rough weighted Power-Heronian operator in multi-criteria decision making. Operational Research in Engineering Sciences: Theory and Applications, 3(2), 54–73. DOI 10.31181/oresta2003049p. [Google Scholar] [CrossRef]
89. Wang, C., Zhou, X., Tu, H., Tao, S. (2017). Some geometric aggregation operators based on picture fuzzy sets and their applications in multiple-attribute decision-making. Italian Journal of Pure and Applied Mathematics, 37, 477–492. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |