Engineering & Sciences
| Computer Modeling in Engineering & Sciences | |
DOI: 10.32604/cmes.2021.015685
ARTICLE
Robust Topology Optimization of Periodic Multi-Material Functionally Graded Structures under Loading Uncertainties
1College of Mechanical and Electrical Engineering, Qingdao University, Qingdao, 266071, China
2Power Integration and Energy Storage System Engineering Technology Center, Qingdao University, Qingdao, 266071, China
*Corresponding Author: Qinghai Zhao. Email: zqhbit@163.com
Received: 04 January 2021; Accepted: 24 February 2021
Abstract: This paper presents a robust topology optimization design approach for multi-material functional graded structures under periodic constraint with load uncertainties. To characterize the random-field uncertainties with a reduced set of random variables, the Karhunen-Loève (K-L) expansion is adopted. The sparse grid numerical integration method is employed to transform the robust topology optimization into a weighted summation of series of deterministic topology optimization. Under dividing the design domain, the volume fraction of each preset gradient layer is extracted. Based on the ordered solid isotropic microstructure with penalization (Ordered-SIMP), a functionally graded multi-material interpolation model is formulated by individually optimizing each preset gradient layer. The periodic constraint setting of the gradient layer is achieved by redistributing the average element compliance in sub-regions. Then, the method of moving asymptotes (MMA) is introduced to iteratively update the design variables. Several numerical examples are presented to verify the validity and applicability of the proposed method. The results demonstrate that the periodic functionally graded multi-material topology can be obtained under different numbers of sub-regions, and robust design structures are more stable than that indicated by the deterministic results.
Keywords: Multi-material; topology optimization; robust design; periodic functional gradient; sparse grid method
Functionally graded structure, known as non-uniform structure, has extensive application prospects in the fields of aerospace, aircraft design, communication and electronics, etc., due to excellent performances such as vibration absorption, heat insulation and noise reduction.
In recent years, there is a trend to optimize the design of functionally graded structures using topology optimization methods [1,2] to achieve specific performances. Paulino et al. [3] firstly discussed the effectiveness of the functionally graded structure topology optimization design using the criterion method. Since then, great achievements have been made in the study of topology optimization for functionally graded structures design. Xia et al. [4] achieved the parallel optimization design of material properties and material distribution of functionally graded structures. Huang et al. [5] employed the bi-directional evolutionary structural optimization (BESO) approach to obtain various anisotropic microstructures of porous materials and composite materials. Recently, a systematic multi-phase infill design method [6] is proposed to generate graded multi-material infill structures. According to the above introduction, existing topological optimization methods of functionally gradient structures generally ignore the influence of uncertain factors such as material uncertainty [7,8], load uncertainty [9,10], geometric size and boundary uncertainty [11,12], resulting in structural instability and unreliability after optimization. In this context, structural topology optimization considering uncertainties tends to make optimized topologies more stable and reliable [13,14].
Currently, topology optimization under loading uncertainties is generally classified into two categories, namely reliability-based topology optimization (RBTO) [15,16] and robust topology optimization (RTO) [17,18]. RBTO focuses on safety and aims to accurately provide structural safety measures, while RTO attaches importance to structural stability, which reduces the sensitivity of structural performance. Ben-Tal et al. [19] firstly employed the semidefinite programming to solve the RTO problem of truss structures. Compared with the discrete structure, the RTO problem of continuum structure is more practical and has become one of the research hotspots. Amir et al. [20] proposed a reanalysis method to solve RTO problem, aiming to improve the computational efficiency of RTO algorithm. Wu et al. [21] explored the RTO method for uncertainties of external load direction based on interval variables. Moreover, Zhang et al. [22] investigated a robust topology optimization method for designing the microstructures of PnCs by considering random field material properties. However, the above researches mainly focus on RTO of single material structures. The emergence of 3D additive printing technology makes the manufacturing and processing of multi-material structure possible. Recently, Kang et al. [23] proposed a robust shape and topology optimization method considering the uncertainties with the interface of multi-material structures. Chan et al. [24] presented a density-based RTO for meso- or macroscale multi-material lattice structures under any combination of material and load uncertainties. Zheng et al. [25] proposed an effective method for designing multi-material robust structures, aiming at minimizing the compliance of linear elastic structures. Romero et al. [26] performed the multi-material robust topology optimization problem by minimizing the topology derivative constructor of the functional to achieve the nucleation and evolution of the level set.
This paper optimizes the topology of the gradient layer with the mean and standard deviation weights of the structural compliance as the objective function and the volume fraction as the constraint to identify the optimal multi-material layout scheme. Meanwhile, considering the application in practical engineering, periodic constraints are applied in the macrostructure topology optimization model for easy manufacturing and assembly. A robust topology optimization design method for multi-material functionally graded structures with periodic constraints is proposed, which applies the Ordered-SIMP method to characterize the multi-material interpolation model. In terms of load random field distribution, the K-L expansion is employed to transform the random field into a finite number of unrelated load random variables, and the sparse grid numerical integration method is adopted to transform the RTO into a set of multi-weighted deterministic topology optimization (DTO).
The rest of the paper is organized as follows. Section 2 introduces the periodic multi-material functionally graded structure. Section 3 gives a brief introduction of multi-material structure interpolation model. The uncertainties in the characterization of the loading uncertainty with random fields are described in Section 4. Section 5 presents the establishment development and solution procedure of the proposed RTO formulation. Several numerical examples are given in Section 6 to verify the proposed method. Section 7 summarizes the remarkable conclusions.
2 Multi-Material Functionally Graded Structure
The macro design domain of a periodic multi-material functionally graded structure is divided into multiple gradient layers (
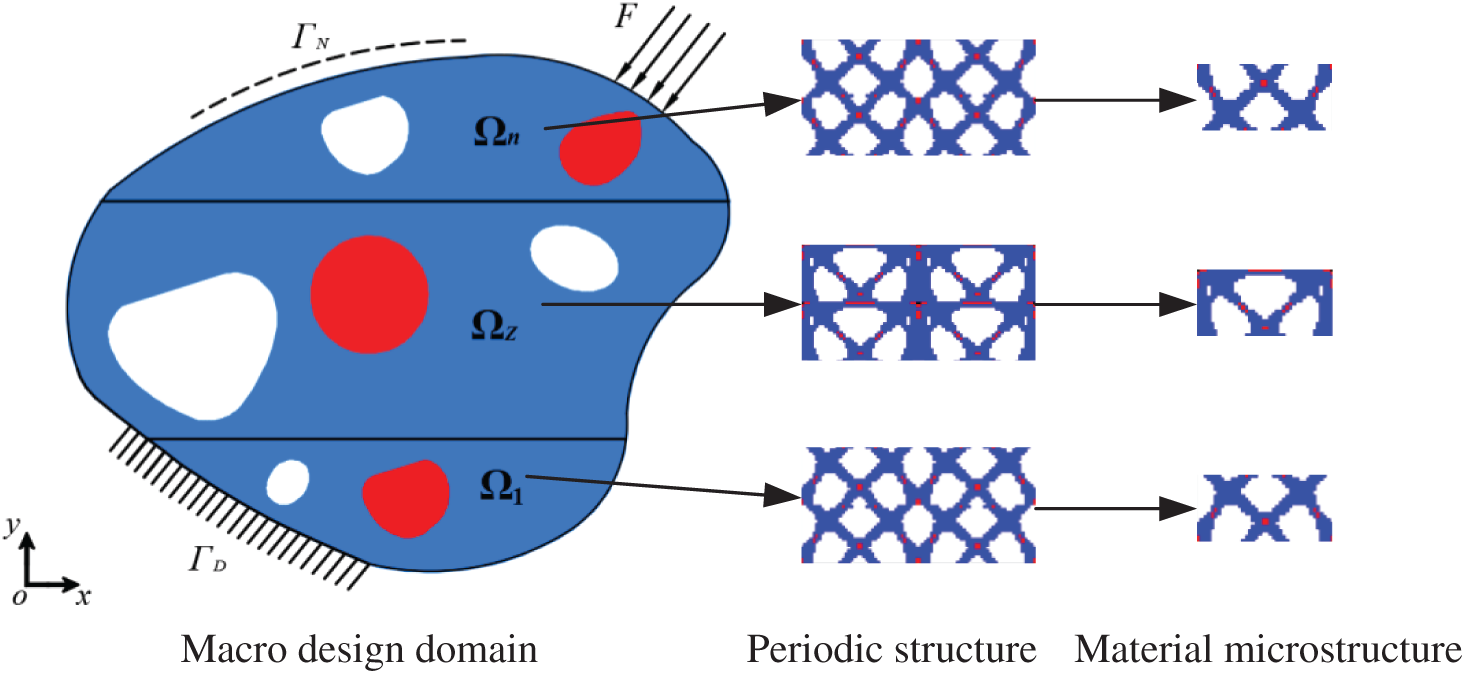
Figure 1: Periodic multi-material functionally graded structure
3 Multi-Material Interpolation Model Based on Ordered-SIMP
The SIMP method introduces cell design variables that vary continuously in the interval of 0–1 [27–29] to establish a nonlinear functional relationship between material properties and design variables.
In terms of the design of multiple materials structure, the elastic modulus and density of each material are firstly normalized, and the material properties are transformed into dimensionless relative values
where
The multiple material interpolation model based on the ordered-SIMP method [30] can be expressed as
where xe denotes the relative density of element e, which is the design variable,
where
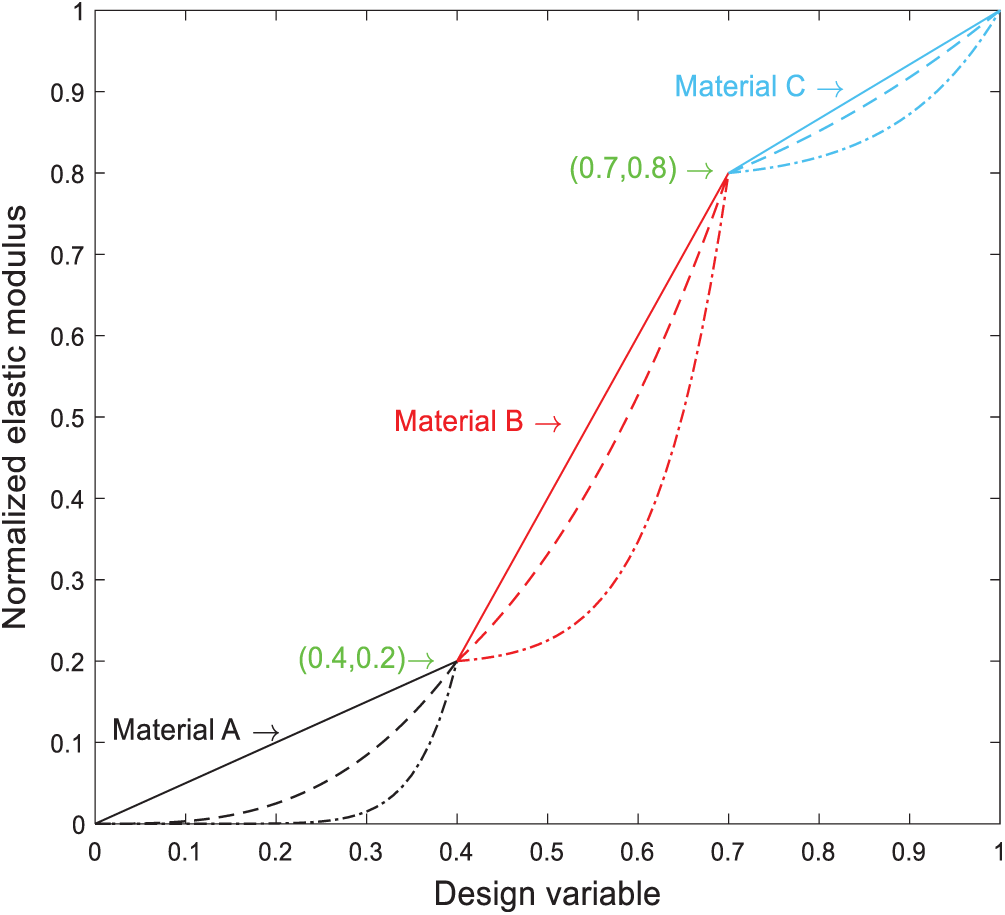
Figure 2: Three materials interpolation model based on Ordered-SIMP
4 Discretization of Random Field under Load Uncertainties
The load uncertainties can be characterized by random field or random variable. For distributed loads with spatial correlation, the commonly used discrete and simulation methods include the extended optimal linear estimation method [31] and the K-L expansion [32,33]. This paper uses the K-L expansion to transform the random field into the cumulative sum of a finite number of uncorrelated random variables under corresponding weights [34]. The K-L expansion of the random field can be described as
where
where
where
When the K-L expansion is applied to the discretization of random field
where e is the mean value of the random field at d observation points;
where the correlation matrix C is defined as
In practical problems, the main probability characteristics of a stochastic process are usually approximated by the random variables corresponding to the first few eigenvalues descending from the maximum eigenvalue. Taking the first M items and letting it as
when s is close enough to 1, the random field can be effectively characterized by dimensionality reduction K-L expansion [36,37].
5 Robust Topology Optimization Model of Multi-Material Functionally Graded Structure
5.1 Robust Topology Optimization Model
The purpose of robust topology optimization design is to reduce the sensitivity of performance function to uncertain random variables while optimizing the objective function, so as to minimize the variance of performance index fluctuation [38]. The difference between the deterministic optimal solution and the robust optimal solution is depicted in Fig. 3. It can be seen that the optimal performance of the robust design is worse than the former, but its performance index is less volatile and more superior to a certain extent. Therefore, robust topology optimization design, as a typical multi-objective optimization design problem, is usually achieved by weighting the expectation and standard deviation of the performance function into the objective function.
According to the mathematical description of uncertain variables, robust topology optimization design can be divided into non-probabilistic and probabilistic models [39]. Probabilistic models can be used to describe the characteristics of most uncertain factors. Based on probability theory and mathematical statistics, typical indicators for measuring the robustness of structural performance are termed as mean and standard deviation. The mathematical model for robust topology optimization of multi-material structures is established as follows:
where J is the objective function, w and
where
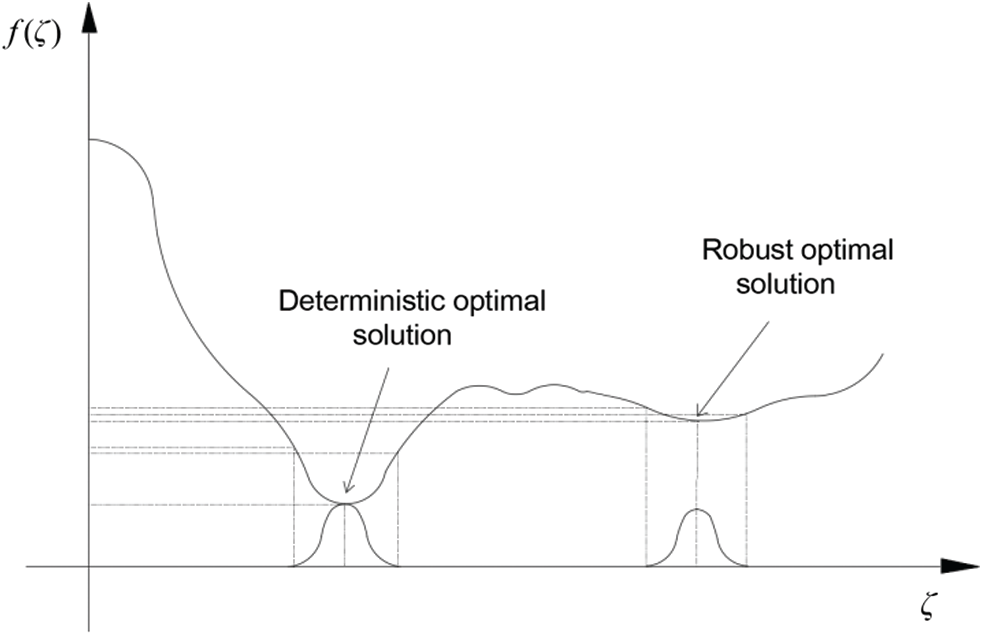
Figure 3: Deterministic optimal solution and robust optimal solution
5.2 Robust Topology Optimization Model of Functionally Graded Structure
In order to calculate the overall layout of a functionally graded structure [41,42] under volume constraints. The volume fraction of each preset gradient layer in the optimal topological configuration is extracted from the multi-material structure topology optimization model. The two-dimensional rectangular design domain is divided into n gradient layers: Layer
Then, each gradient layer is individually designed for optimization. The topology optimization model of the functionally graded structure design can be defined as
where N represents the number of element in the gradient layer,
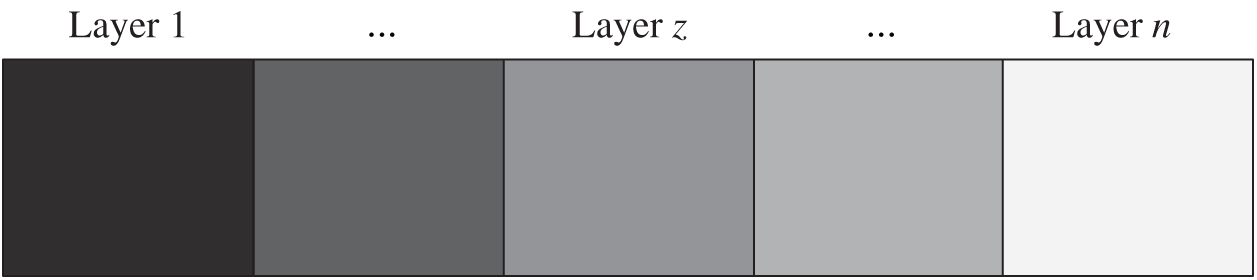
Figure 4: Layer-wise design
The optimization goal of this paper is the weighted sum of the mean and standard deviation of structural compliance. Among them, the sensitivity of the mean and standard deviation relative to the design variable
5.3 Sparse Grid Numerical Integration Method
In order to solve the objective function of the robust topology optimization design, a sparse grid method based on the Smolyak criterion [43] is employed. A basic idea is to construct a multidimensional product formulation using a special tensor product operation of one-dimensional configuration points as a linear combination. The advantage of this method is that the number of configuration points is limited, and the nodes that contribute less to the calculation accuracy are automatically deleted, so the sparse grid is applied to the robust design of statistical moment estimation. Based on the nested hierarchy principle, the one-dimensional interlayer difference is defined as
where k represents the dimension, when k = 0,
where
where
The corresponding weights are determined as
Thus, the configuration points are given as
By adjusting the level accuracy l value, the sparse grid integration accuracy is improved. Based on the Newton-Cotes integration rule, the Causs–Chebyshev [44] sparse grid
The sequence of figuration points is
Then, the corresponding weights are expressed as follows:
The sparse grid numerical integration method is employed to solve the mean and the standard deviation of the robust topology optimization design. The expression of mean and standard deviation can be modified as
According to Eqs. (17) and (18), the derivative of the optimization target J with respect to the density
The commonly used optimization solution algorithms include mathematical programming method and optimization criterion method. In the iterative process, MMA [45] has better applicability for problems with complex objectives and multi-constrained topology optimization. In this paper, MMA method is introduced to solve the topology optimization problem of multi-material functional graded structure. And the PDE filtering method based on Helmholts equation is adopted.
In order to obtain the periodic functionally graded structure, the elements of the different substructures of each gradient layer at the same position have the same material properties. The periodic layer-wise design is shown in Fig. 5. Each gradient layer is divided into
By reallocating the average element compliance in sub-regions, the periodic constraint setting of the gradient layer is achieved.
At this point, the sensitivity of elements at the same position is equal to that of different substructures to achieve periodic geometric constraints.
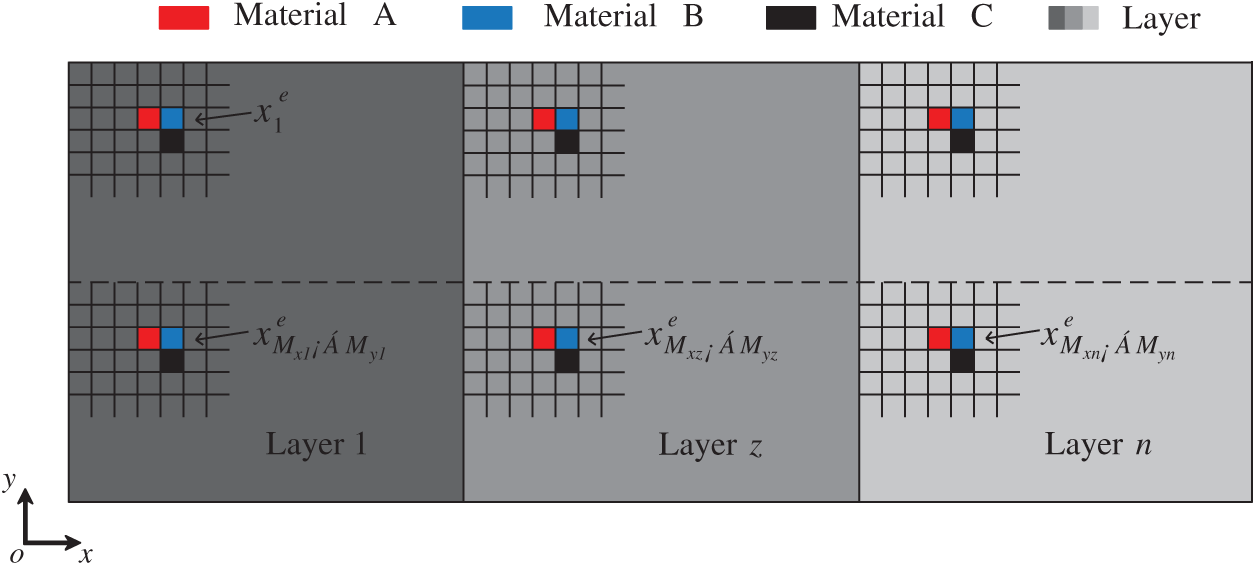
Figure 5: Periodic layer-wise design
This paper proposes three numerical examples to illustrate the difference between the optimal topologies under loading uncertainties and deterministic loading conditions. For comparison, the settings in the DTO are the same as those in the RTO examples. In the calculation examples, the design domain is discretized by square elements, and the weight coefficients of mean value and standard deviation are set to 0.5, respectively. In order to prove the effectiveness of the proposed method, gradient layers of 2, 3, 4 and 6 are preset for different design domains in this paper, and for more intuitive comparison of DTO and RTO,
The double-sided fixed beam is shown in Fig. 6. The design domain is a
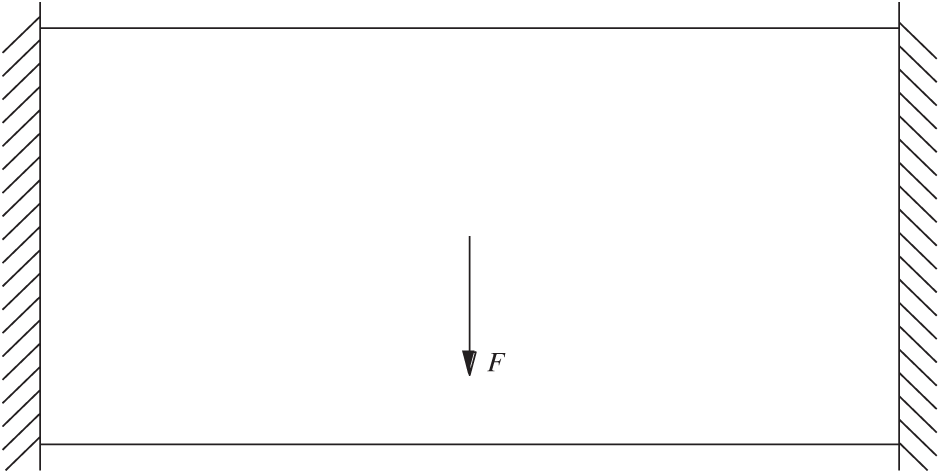
Figure 6: Design domain of double-sided fixed beam structure
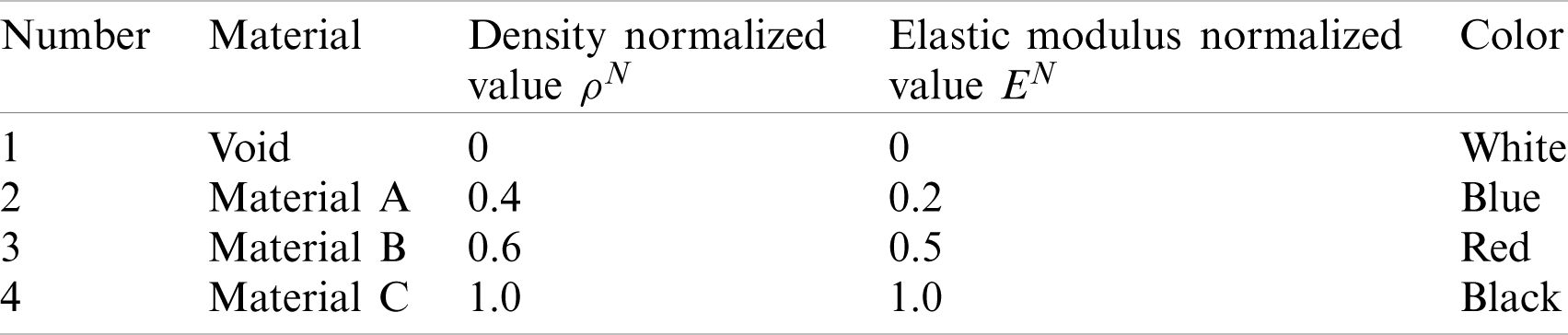
Table 1: Implementation of three materials parameters
The design domain is discretized into 12800 (
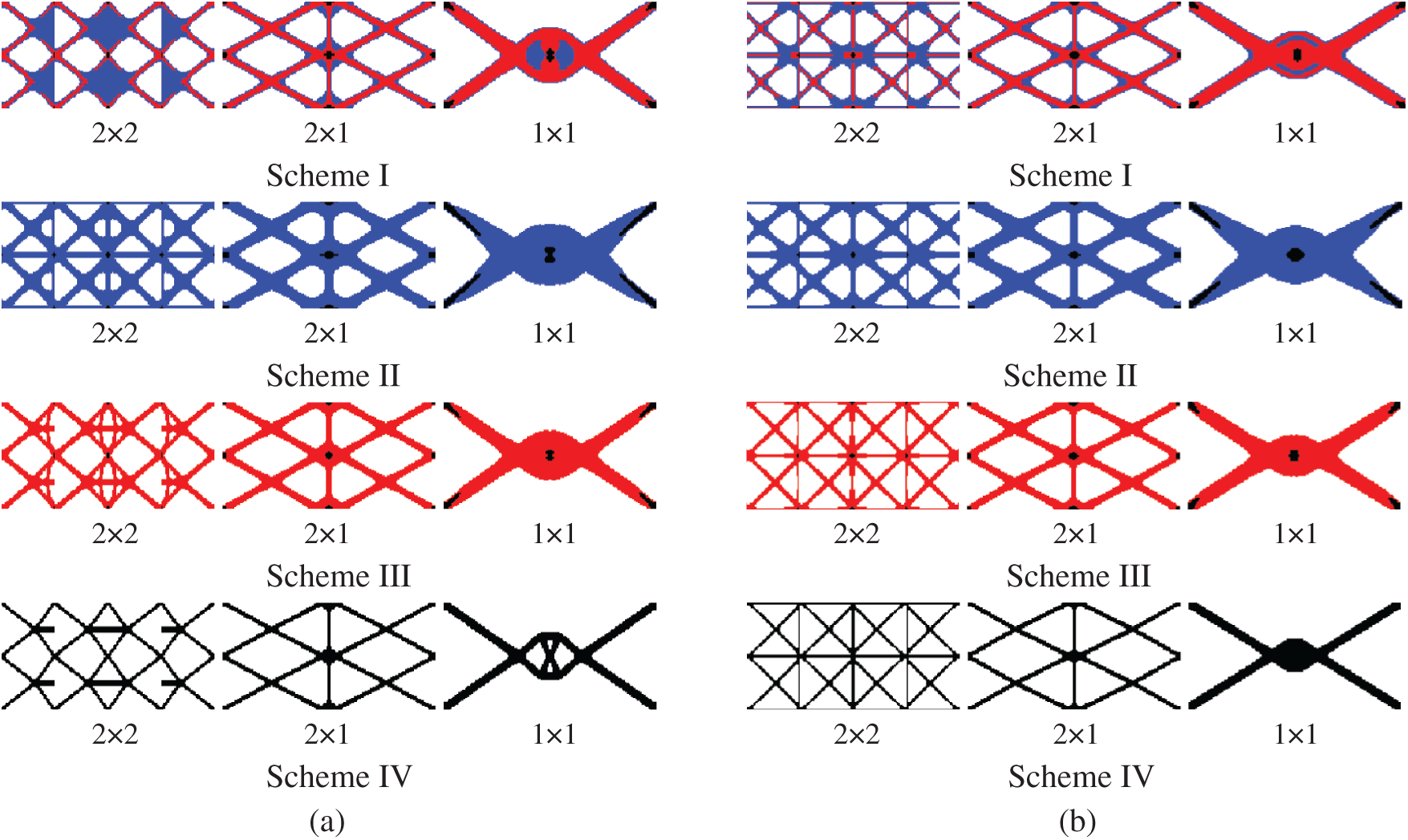
Figure 7: Comparison of optimized topologies of multi-material DTO and RTO under two gradient layers. (a) Deterministic design (b) robust design
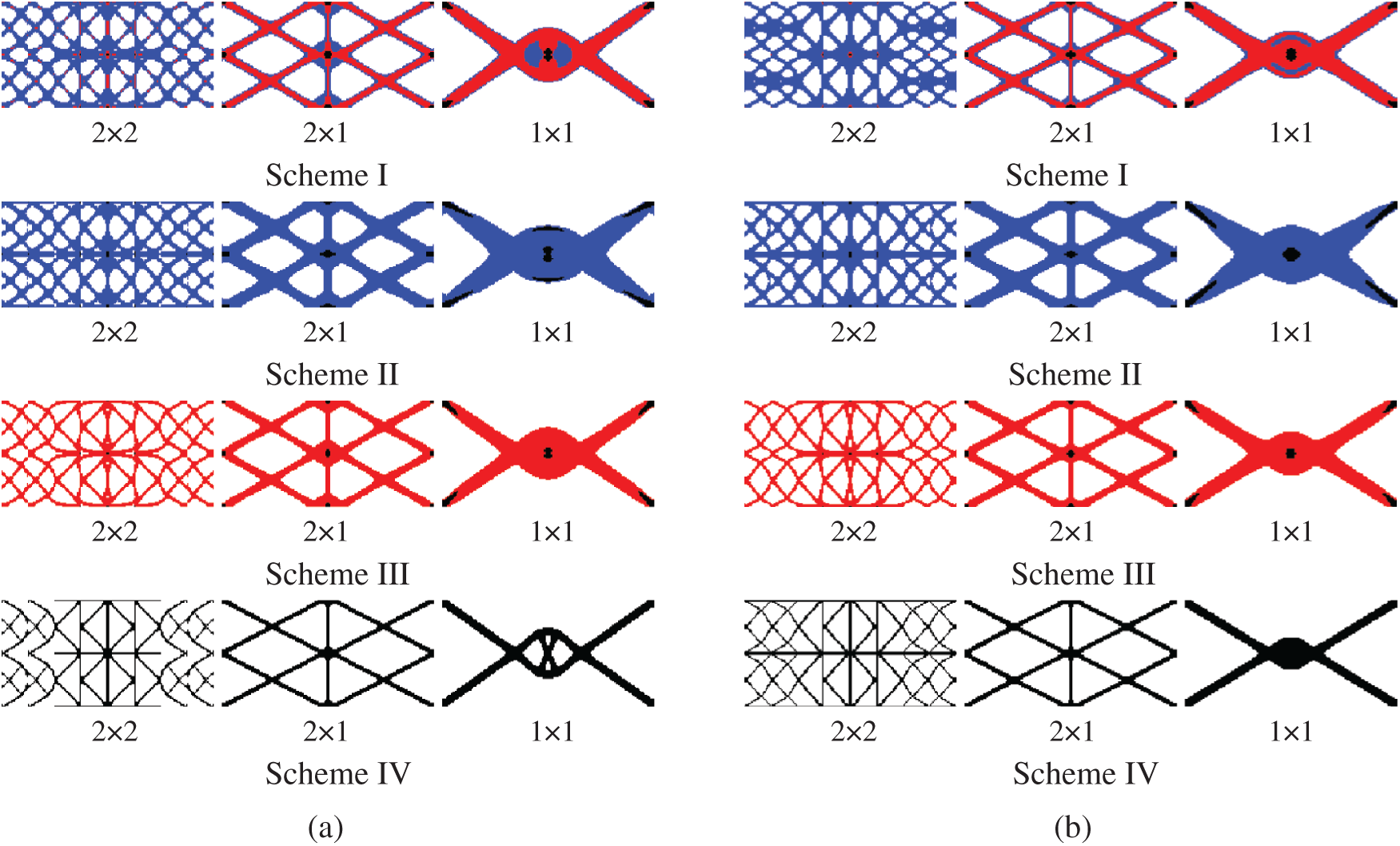
Figure 8: Comparison of optimized topologies of multi-material DTO and RTO under four gradient layers. (a) Deterministic design (b) robust design
Table 2: Volume fraction of gradient layer
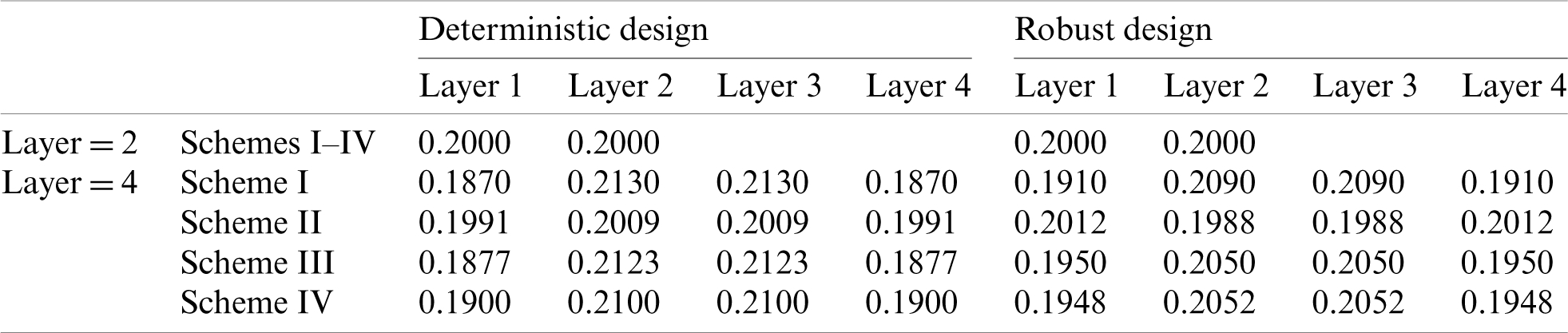
The optimization results show that the proposed method can effectively obtain the periodic functionally gradient structure under different gradient layers, periodic division and material combination schemes, and determine the reasonable material distribution, which shows the effectiveness of the proposed method. Compared with the DTO, the materials of the robust optimization structure are more concentrated on the horizontal force transmission route, thus improving the horizontal load capacity of the structure. It can be seen from Tab. 3 that the mean, standard deviation and objective function of the structural compliance obtained from the deterministic design are all higher than those obtained from the robust design. Therefore, the results of RTO have better stability under load uncertainty.
Table 3: The topology design result of double-sided fixed beam
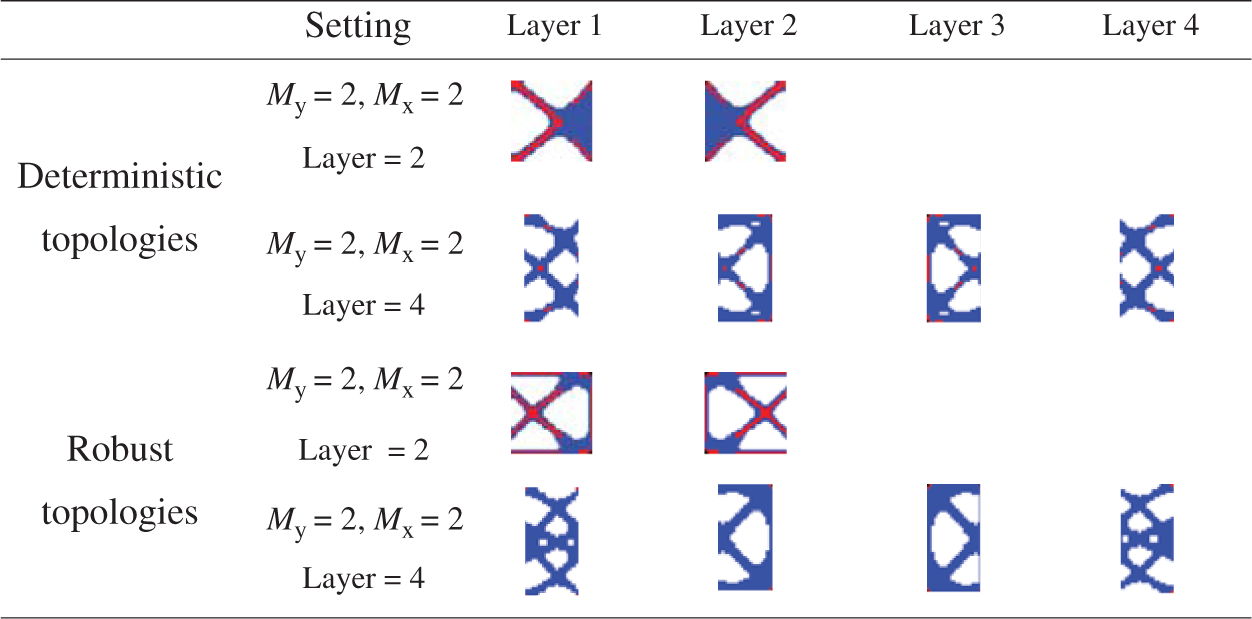
For the periodic functionally graded structure under the layered setting, the optimal periodic structure of each gradient layer can be obtained. According to the
Table 4: Substructure of gradient layer
The design domain of cantilever beam is a
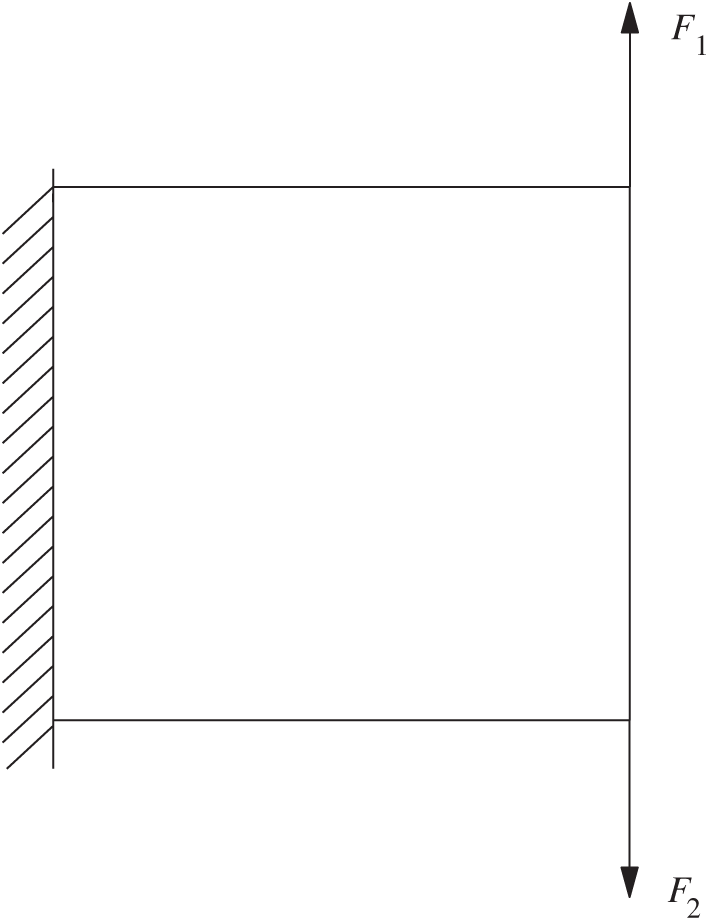
Figure 9: Design domain for a cantilever beam
The design domain is discretized into 14400 (
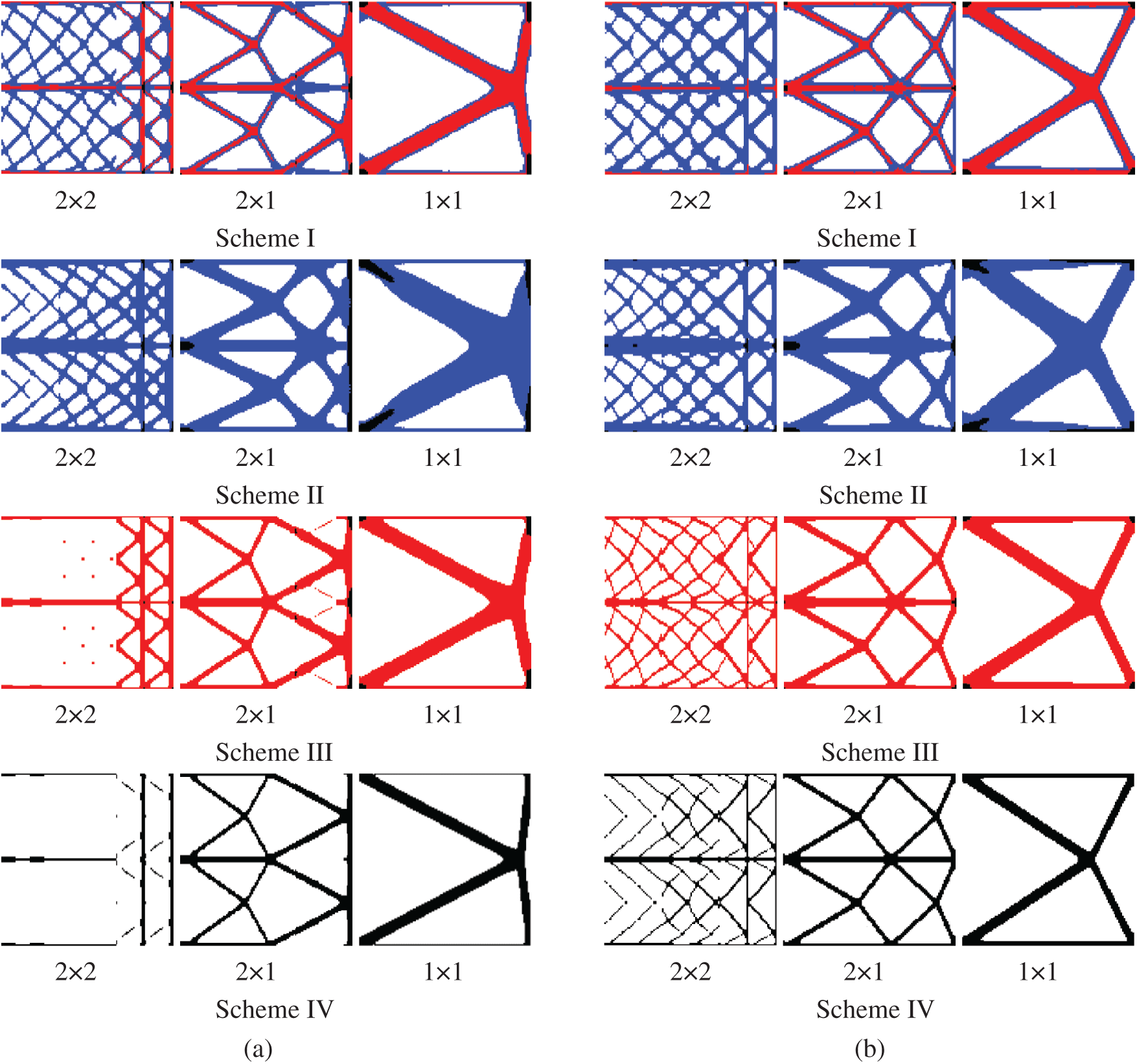
Figure 10: Comparison of optimized topologies of multi-material DTO and RTO under three gradient layers. (a) Deterministic design (b) robust design
The optimization results show that the optimized structures are symmetrical because the design domain, boundary conditions, and load effects of the two working conditions are all symmetrical. Compared with the deterministic design, the optimized results of the robust design have thicker upper and lower edges and better horizontal load bearing capacity due to the uncertain loads that generates horizontal partitioning. Although such a structure has a reduced vertical load bearing capacity, the horizontal load bearing capacity is enhanced and the overall structure becomes more stable.
Meanwhile, considering the influence of periodic functional gradient constraints, we observed that the material distribution of the fixed edge of the DTO was not obvious, and the load bearing capacity was weak. On the contrary, the overall material distribution of the RTO results is reasonable, which further proves that it exhibits better stability.
The convergence process is rapid and stable, indicating the stability of the algorithm. According to the
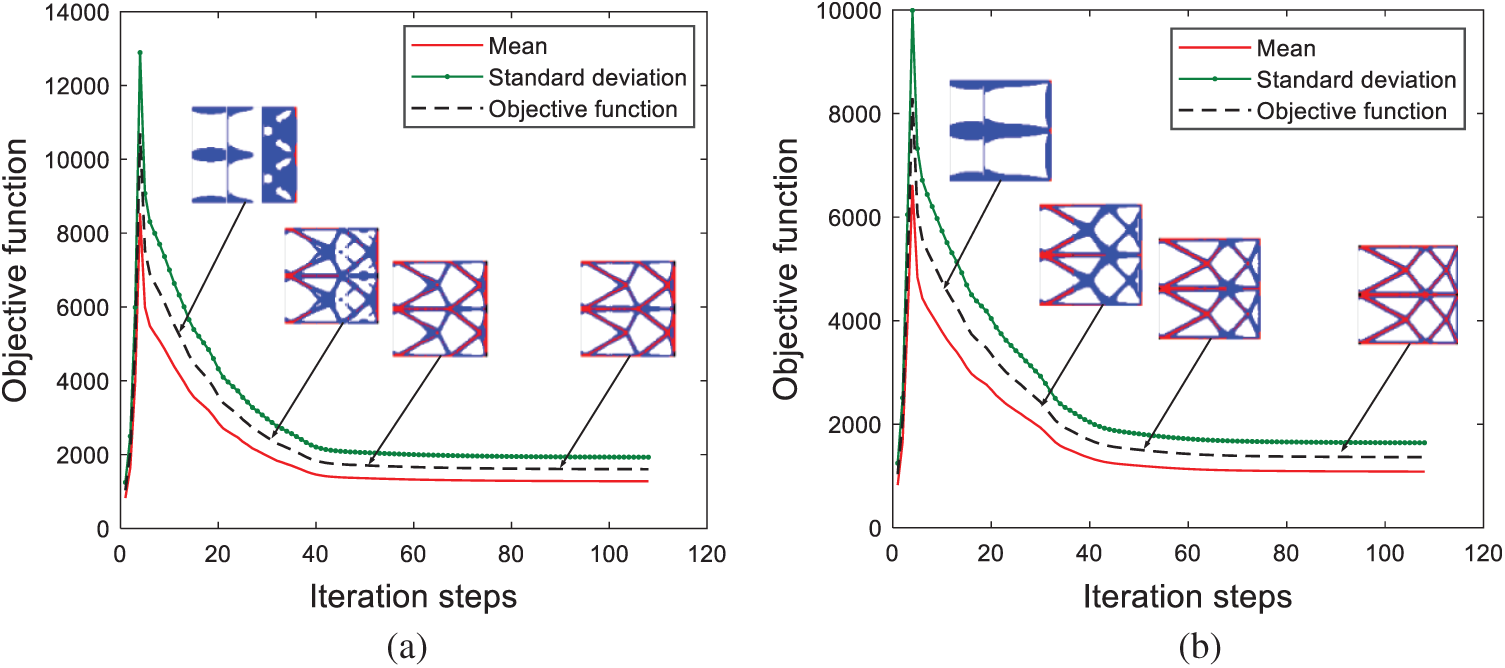
Figure 11: Variation curve of mean, standard deviation and objective function of compliance with the number of iterations. (a) Deterministic design (b) robust design
Table 5: The topology design result of cantilever beam
The simply supported beam structure is shown in Fig. 12. The design domain is a
where
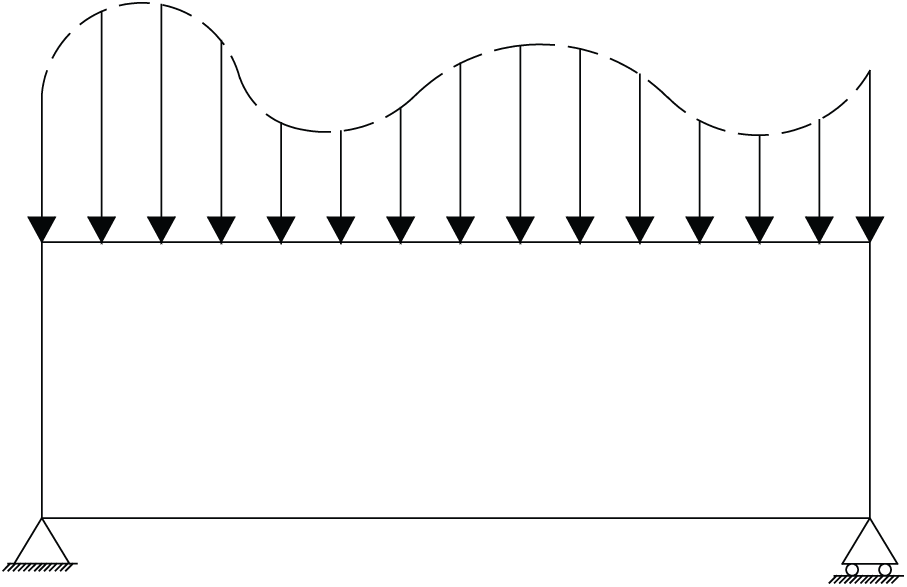
Figure 12: Simple beam design space
The design domain is discretized into 10800 (
where
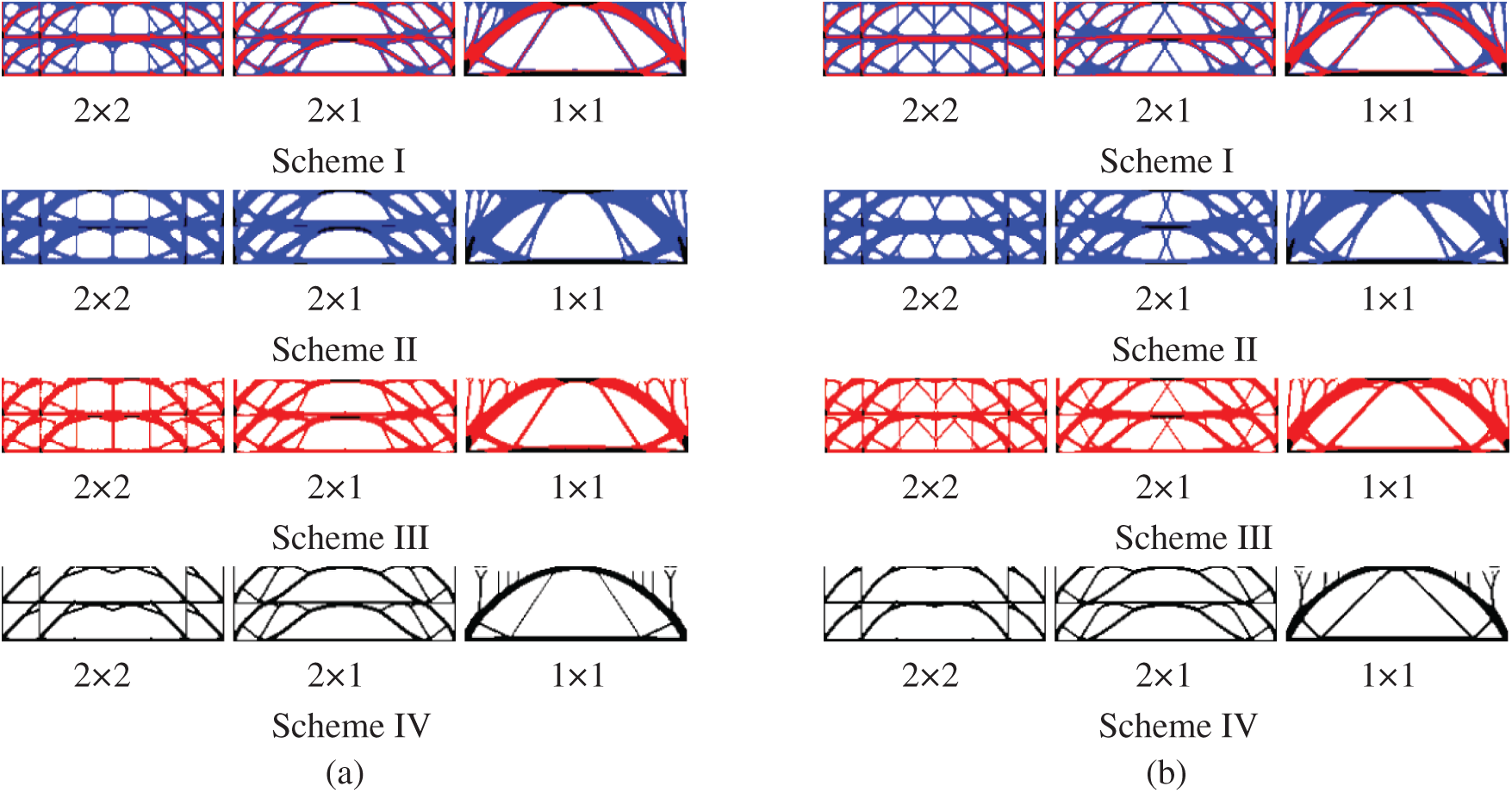
Figure 13: Comparison of optimized topologies of multi-material DTO and RTO under three gradient layers. (a) Deterministic design (b) robust design
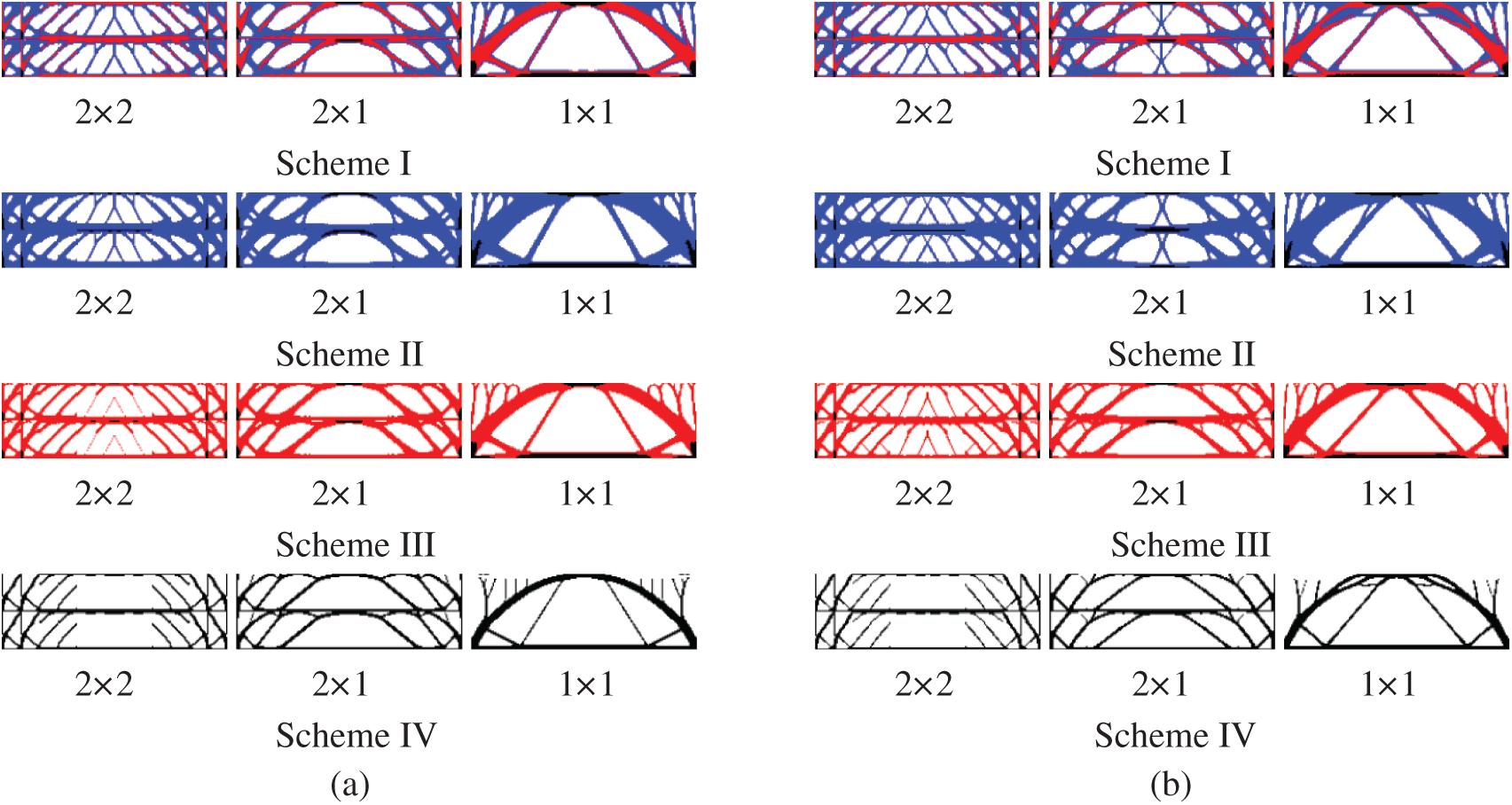
Figure 14: Comparison of optimized topologies of multi-material DTO and RTO under six gradient layers. (a) Deterministic design (b) robust design
It can be seen from the Figs. 13 and 14 that the boundary of the optimization result is clear, and that the periodic setting in the gradient layer clearly demonstrates the effectiveness of this method. Due to the superposition of multiple loads under the influence of different amplitudes, the configuration change of RTO was significantly different from that of DTO, which was mainly reflected in the obvious supporting effect of filling the rod-shaped materials in the middle of the structure, thus improving the stability of the structure. Meanwhile, the model has excellent applicability to different material combination schemes.
According to the
Table 6: The topology design result of simply supported beam
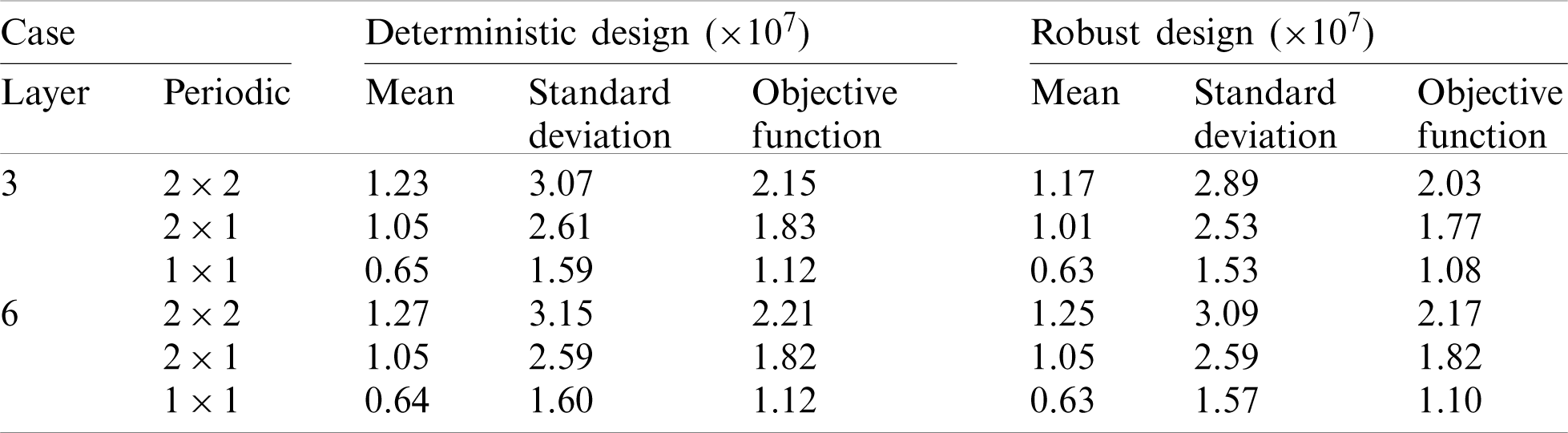
Figure 15: Variation curve of objective function of compliance with the number of iterations. (a) Three layer gradient, (b) six layer gradient
This paper presents a robust topology optimization design method for multi-material functional gradients considering periodic constraints. In order to optimize the topology of the multi-material functionally graded structure and minimize the structural compliance under the volume constraint, an ordered-SIMP interpolation is proposed. Meanwhile, the structure is set periodically considering the practical engineering applications. Then, the sparse grid numerical integration method is introduced to calculate the objective function, the mean and standard deviation solutions for the robust topological optimization design. The design is explored in terms of both deterministic and robust design for different load conditions. By three arithmetic examples, the effectiveness of the design method is demonstrated. From the results, it can be seen that the robust design provides a more reliable and effective design solution compared with the corresponding deterministic topology optimization design. In addition, the proposed approach yields better design results for different functional gradient settings and material combination schemes, further demonstrating the practicality of the design solution.
Acknowledgement: The authors are thankful for Professor Krister Svanberg for MMA program made freely available for research purposes and the anonymous reviewers for their helpful and constructive comments.
Funding Statement: This work is supported by the Natural Science Foundation of China (Grant 51705268) and China Postdoctoral Science Foundation Funded Project (Grant 2017M612191).
Conflicts of Interest: The authors declare that we have no conflicts of interest to report regarding the present study.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |