Engineering & Sciences

 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2021.014662
ARTICLE
Method for Collision Avoidance in Spacecraft Rendezvous Problems with Space Objects in a Phasing Orbit
1Nanjing University of Science and Technology, Nanjing, 210094, China
2Keldysh Institute of Applied Mathematics, Russian Academy of Sciences, Moscow, Russia
3Peoples’ Friendship University of Russia (RUDN University), Moscow, Russia
*Corresponding Author: Danhe Chen. Email: juliachen@njust.edu.cn
Received: 18 October 2020; Accepted: 13 January 2021
Abstract: As the number of space objects (SO) increases, collision avoidance problem in the rendezvous tasks or re-constellation of satellites with SO has been paid more attention, and the dangerous area of a possible collision should be derived. In this paper, a maneuvering method is proposed for avoiding collision with a space debris object in the phasing orbit of the initial optimal solution. Accordingly, based on the plane of eccentricity vector components, relevant dangerous area which is bounded by two parallel lines is formulated. The axises of eccentricity vector system pass through the end of eccentricity vector of phasing orbit in the optimal solution, and orientation of axis depends on the latitude argument where a collision will occur. The dangerous area is represented especially with the graphical dialogue, and it allows to find a compromise between the SO avoiding and the fuel consumption reduction. The proposed method to solve the collision avoidance problem provides simplicity to calculate rendezvous maneuvers, and possibility to avoid collisions from several collisions or from “slow” collisions in a phasing orbit, when the protected spacecraft and the object fly dangerously close to each other for a long period.
Keywords: Spacecraft; collision avoidance; rendezvous problem; space objects; phasing orbit
Currently, Spacecraft rendezvous has been considered as one of the key technologies for on-orbit service, including space debris removing, on-orbit assembly, spacecraft repairing, and on-orbit refueling [1–3]. Several on-orbit service missions have been carried out as technology demonstration for a cooperative spacecraft, XSS of Air Force Research Laboratory [4], Demonstration for Autonomous Rendezvous Technology (DART) program of NASA [5], ETS-VII project of JAXA [6] and etc. Meanwhile, several satellite systems consisting of hundreds of objects are created. For each satellite system, it is necessary to solve the problem of its transfer to a given position, and as the significantly increasing number of space debris objects, the task to ensure flight safety appears. Due to the importance of the collision avoidance, numerous papers are devoted to solve the problem of possible collision between spacecraft with space debris(SD). Research on rendezvous techniques for non-cooperative targets is also conducted, in the vast majority of these work, the fact of a possible collision is determined. A much smaller research focus on the calculation methods of the avoidance maneuvers of spacecraft. In [7], model predictive control strategy is used to realize the docking of rotating targets in space.
Also, sliding mode control is widely used in spacecraft rendezvous considering the collision avoidance. Kasaeian et al. [8] utilized a robust guidance algorithm based on sliding mode method for a chaser to rendezvous with a target in space. Meanwhile, the terminal sliding mode control method is applied to tracking control problem for autonomous underwater vehicles (AUVs) [9,10], and a fixed-time terminal sliding mode control strategy introduced to produce an artificial gravity environment by spinning tether system in high eccentricity transfer orbit [11]; an adaptive fuzzy sliding mode control is proposed to solve the problem of spacecraft attitude tracking for space debris removal [12]. A novel sliding mode control strategy is developed to avoid entering dangerous areas during the implementation of the rendezvous procedure [13], and new neural sliding mode guidance is studies for maneuvering target in [14].
Considering the optimal problem of fuel consumption, Cao et al. [15] proposed an optimal artificial potential function sliding mode control with obstacle avoidance in mind, which effectively reduced fuel consumption. Similarly, model predictive control has been extensively applied to spacecraft rendezvous under various constraints, including obstacle constraints, velocity constraints. The control problem of spacecraft autonomous rendezvous in an elliptical orbit is studied in reference [16]. Christopher Jewison et al. used model predictive control to compute an optimal control strategy for a chaser attempting to rendezvous with obstacle avoidance constraints and in which obstacles are approximated to ellipsoids [17]. The computational load of model predictive control is enormous, but the on-board computational capacity is limited. A real-time nonlinear model predictive control (MPC) toolbox named MATMPC is utilized to solve this problem in work [18]. Impulse and continuous thrust are the most recommended maneuvers [19], under the constant thrust model, Qi et al. [20] designed a new constant thrust switch control law for the active collision avoidance maneuver of the chiller along a specific trajectory.
Since the calculation of special single impulse maneuver which thrust the protected spacecraft out of the dangerous area is quite simple, the main attention in these work is paid to determining the size of the dangerous area in which could be a collision [21,22]. Thus, this group of researches can be attributed to the first class study, in which the possibility of a collision is determined. This is due to the fact that in most of the work, whenever possible, a collision in one way or another uses the size of the protected area, and special avoidance maneuvers are considered in a relatively lack of research.
The difference of this work is that it does not consider special avoidance maneuvers, but seeks such a solution to the rendezvous problem in order to evade a possible collision in a phasing orbit if a danger exists. The second difference is that the hazardous area (the position of which are considered known, since that they can be determined by the algorithms given in the above papers) is considered not in the traditional coordinate space, but on the plane of the components of the eccentricity vector. In addition, the proposed method to solve the problem makes it easy to calculate rendezvous maneuvers that provide avoidance from several collisions or from “slow” collisions in a phasing orbit, when the protected spacecraft and the SD object fly dangerously close to each other for a long time.
The need seeking for such a solution to the rendezvous problem can be explained by several reasons. For example, at the spacecraft “Soyuz” and “Progress”, after performing the first two maneuvers (in 2–3 orbits) from a series of four connected maneuvers with a two-day rendezvous scheme, beginning from deaf turns where it is impossible to conduct maneuvers. If the phasing orbit formed by the first two maneuvers is dangerous in terms of collision with SD objects on it, then changing it with a special velocity and thereby avoiding the collision is no longer possible. Considering that, the only way out for solving this problem can be described as follows: firstly, the orbit after applied the first two impulses should be predicted under the optimal scheme, if in this orbit there is a possibility of a collision with SD, constraints should be added to find a solution to the rendezvous that the spacecraft will not pass through the danger zone after the first two impulses.
Moreover, even if it is predicted that no collision will occur, recalculation for rendezvous maneuvers in order to form a safe phasing orbit allows to reduce both the number of maneuvers performed and the total fuel costs.
The paper is organized as follows: In Section 2, mathematical description of the problem to be solved is introduced. The specific methodology and solution is presented in Section 3, which provide the optimal solutions in plane of eccentricity vector in different maneuvers. Conclusions are summarized in the end of the paper.
2 Mathematical Description of the Problem
Assume that the chasing spacecraft and the target spacecraft are located in close near-circular orbits (or the target spacecraft as a given point in the final orbit to which the chasing spacecraft should be transferred during the formation of satellite systems or groups). Then we can use the linearized equations to calculate the parameters of maneuvers, influence of earth’s non-spherical perturbation and atmospheric drag on the spacecraft here are not considered, and instant change in spacecraft velocity is assumed. Using the famous iterative method [23], the solution of the problem that satisfies the terminal condition of a given precision with all disturbance factors considered can be obtained. The motion equation of flight reaches a given target orbit as a result of N velocity impulses can be written in the following dimensionless form:
where
Here, “f”, “0” are the index indicating the final and initial orbits; ef, e0 are the eccentricities of the final orbit and initial orbit; af, a0 are the semi-major axis of orbits;
A multi-turn flight scheme is also assumed in this paper. This scheme has several advantages as shown below: Firstly, when the total characteristic velocity (TCV) of the rendezvous problem is equal to the TCV of the solution to transition problem (there is no restriction on flight time.), in this case a fairly wide range of the initial phase can be considered (phase is the difference in the latitude argument
where F1,
For ensuring rendezvous problems of spacecraft by maneuvers, it is necessary to determine the parameters of impulses
Under the constraints defined by Eqs. (1), (6) and (7).
In this process, the protected area ranges are also determined. Since the rendezvous problem is solved and it is impossible to avoid collisions by changing position along the orbit, the minimum required deviation along the radius
Here it is advisable to choose a four-impulses scheme to solve this problem, two impulses are applied at the first maneuvering interval, and two impulses are applied at the second maneuvering interval. The proposed approach is described in detail in the following section.
3 Results and Discussion Methodology
The magnitude of semi-major axis of the phasing orbit, which should be formed by the impulses of the first maneuvering interval, is uniquely determined from Eq. (4) (determined by the initial phase difference
where
Thus, since the semi-major axis of phasing orbit is fixed, it is possible to obtain a safe orbit only by deliberately changing the eccentricity of phasing orbit.
On the ex, ey plane, region boundaries can be determined from which the eccentricity vector of phasing orbit derived in order to avoid a collision with SD. Assume that the phasing orbit has eccentricity e0, argument of the orbit pericenter is
In order to avoid collision with SD on the latitude argument u0, the radius of orbit at this moment should be increased to
Outer and inner boundary of the prohibited region can be built by Eqs. (12), (13), respectively. The derivation of eccentricity vector of the phasing orbit, formed by the maneuvers of first interval from the prohibited region allows avoiding a collision.
In Fig. 1 an example of a prohibited region for a phasing orbit with semi-major axis a0 = 10,000 km, eccentricity e0 = 0.3, and latitude argument
As is shown in Fig. 1, dashed line denotes symmetry line of the prohibited region; and the angle between this line and axis ex is u0. A solid line indicates the internal boundary of the prohibited region and a line of dots indicates its external boundary, point X corresponds to the phasing orbit (e0,
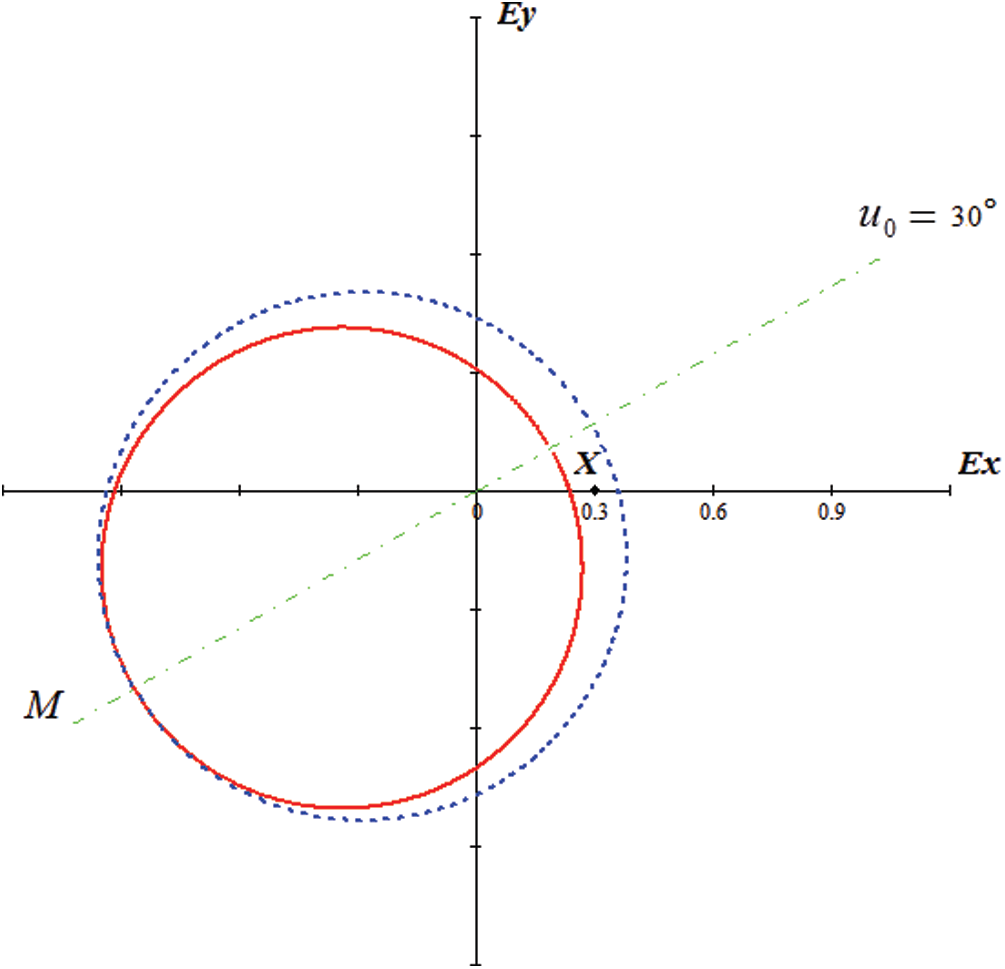
Figure 1: The prohibited area for rendezvous of spacecraft
Fig. 2 shows the prohibited regions if a dangerous approach occurs at angles u0 = 100
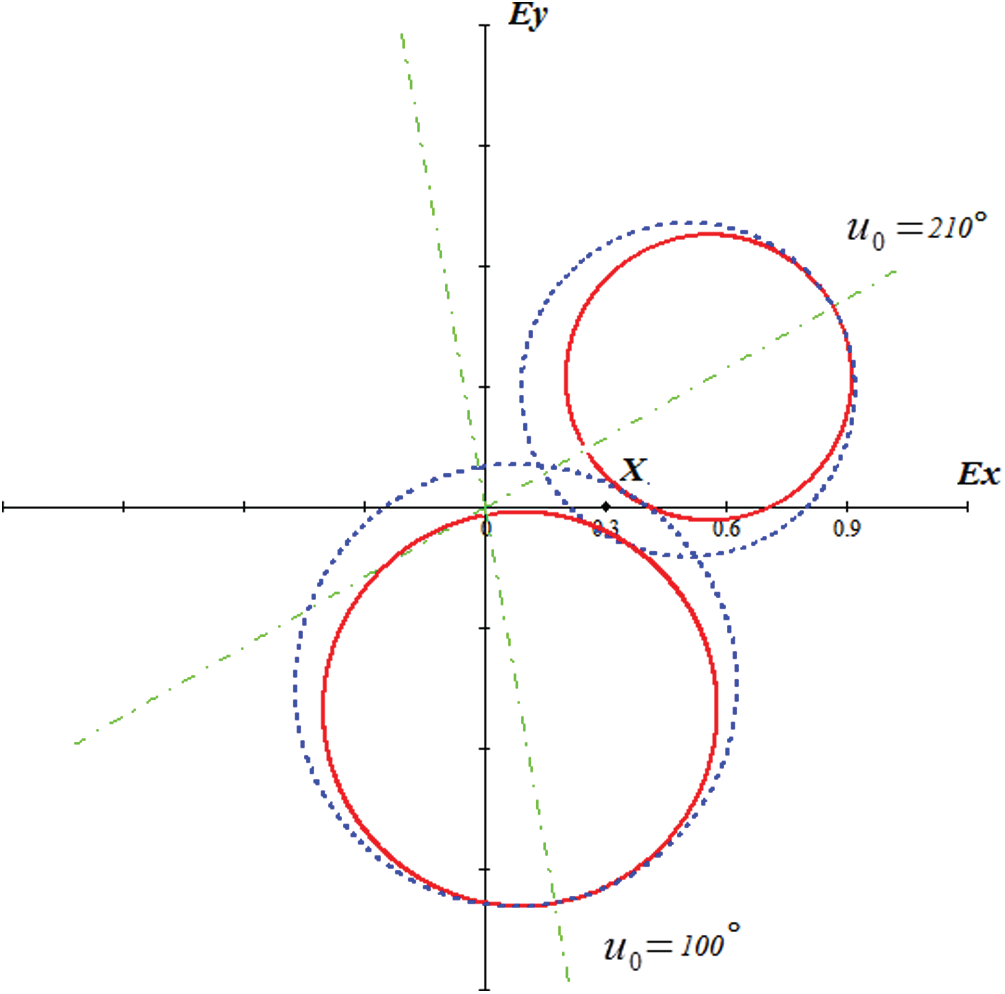
Figure 2: The position of prohibited regions for angles
As noted above, the actual value of
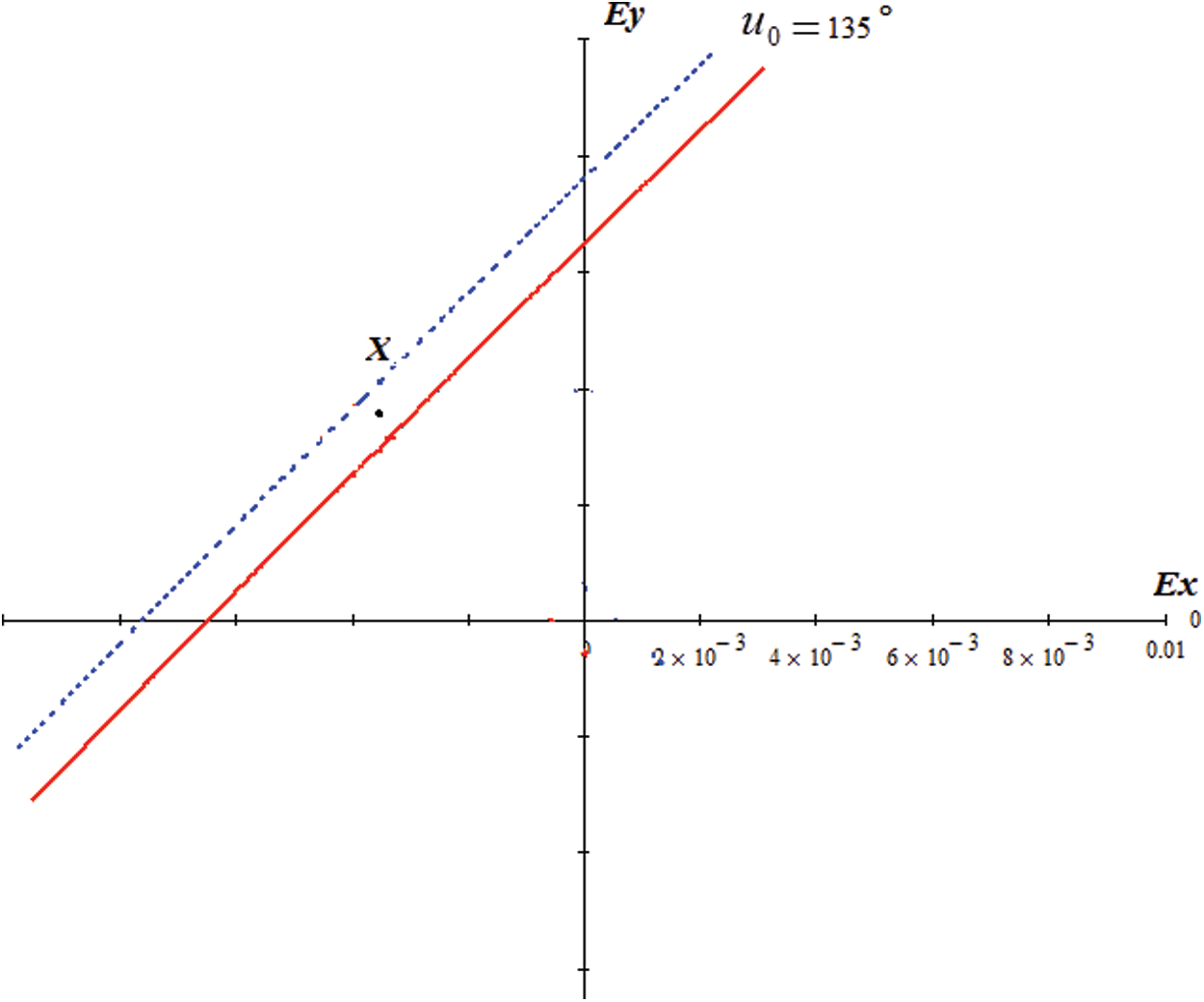
Figure 3: Position of the real prohibited region for angle u0 = 135
Based on this scheme, analyses about the position of prohibited region depending on the argument of latitude at which collision occurs can be carried out. In the same coordinate plane, several regions under study that correspond to the possibility of collisions at angles u0 = 0
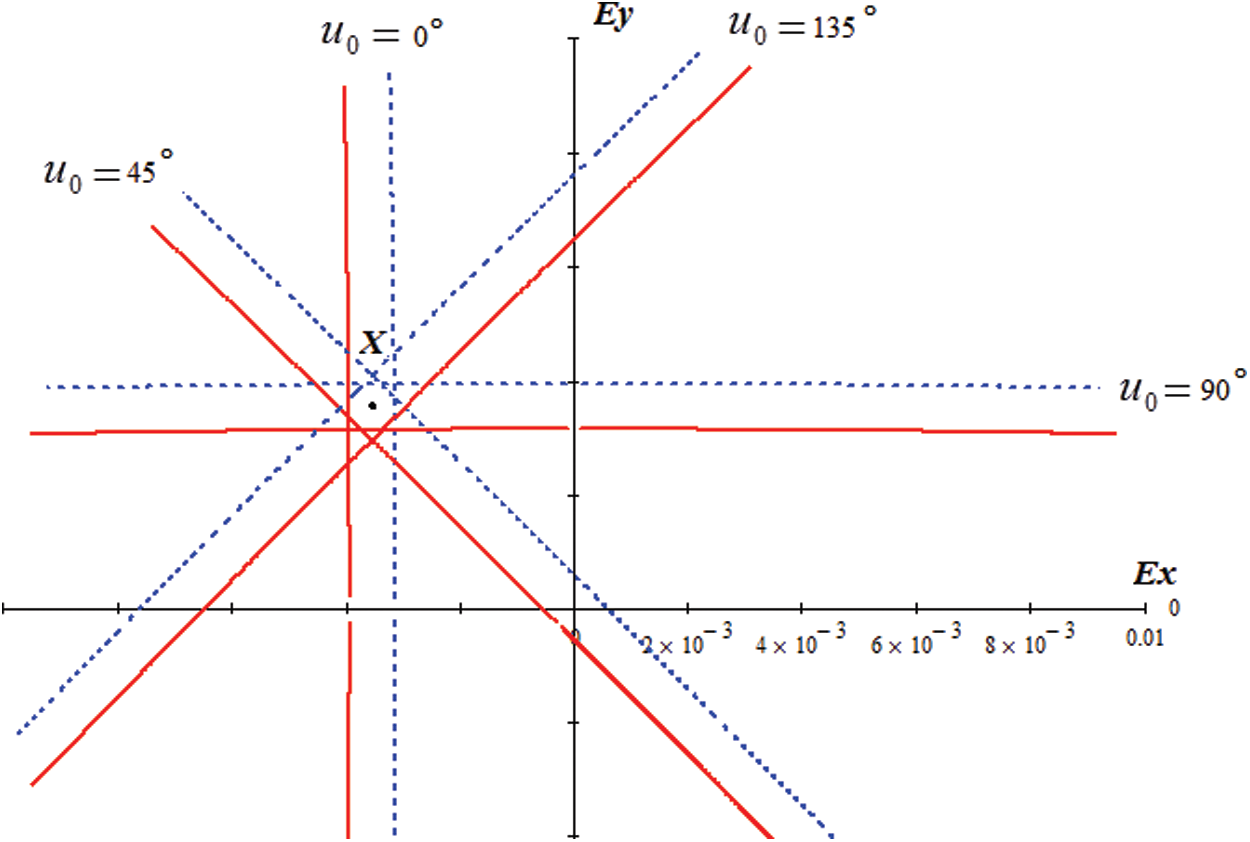
Figure 4: The prohibited region with different angle of u0
Consider an example for the Russian spacecraft “Soyuz” and orbit station “Progress” based on the results obtained previously. In order to ensure a flight to the station vicinity for these spacecraft, a four impulses rendezvous problem is initially solved. All the impulses have transversal components, and lateral components are performed in the first two impulses.
For near circular orbit motion, as described follows from Eqs. (1), (2), a change in the orbit eccentricity vector as a result of the application of transversal component Vti of the i-th velocity impulse on the ex, ey plane can be represented by the vector AB (see Fig. 5). The length of the vector is −2Vti, and forms an angle
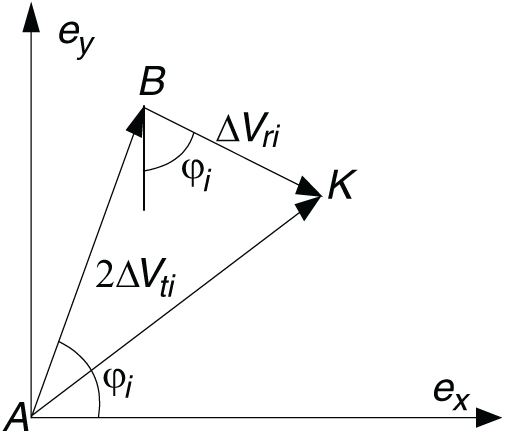
Figure 5: The eccentricity vector change of a velocity impulse
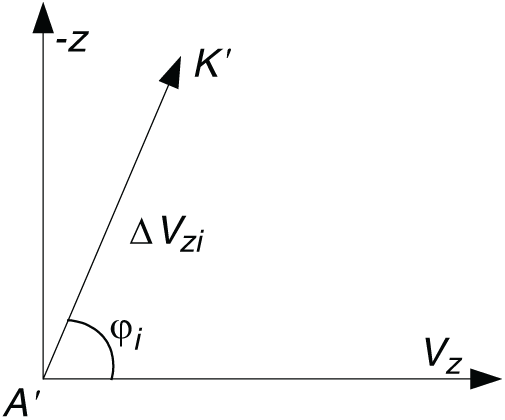
Figure 6: Orbit plane deviation of a normal impulse
From Eqs. (5), (6) it follows that on the plane (Vz, − z) of the normal component of the i-th impulse, which corresponds a vector A
Thus, in multi-impulse solution of the problem in coordinates ex, ey and Vz, − z are expressed as multiple polylines. Similarly, such polylines for a two-impulse solution with zero radial components are shown in Figs. 7 and 8. In this solution, Vt1, Vy2 , Vz1 are positive, Vz2 is negative.
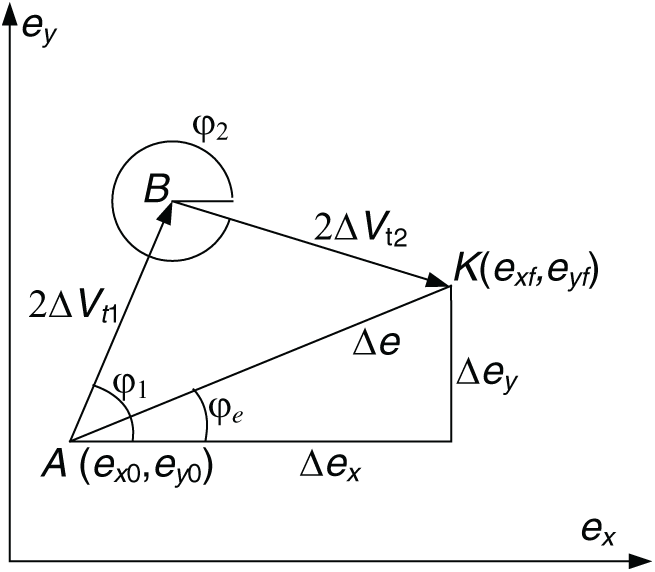
Figure 7: The two-impulses changes of eccentricity vector
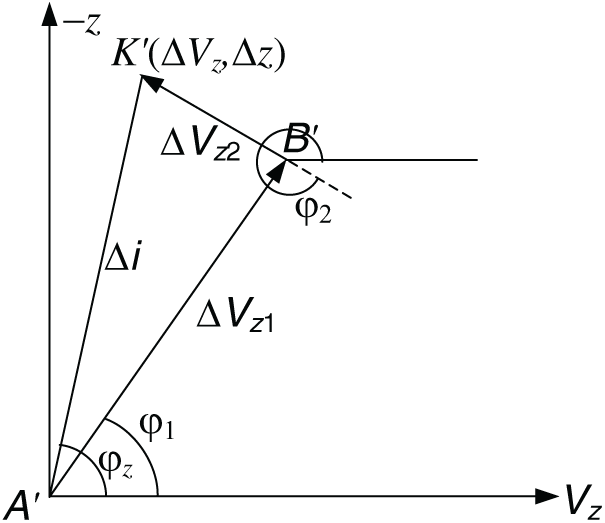
Figure 8: The two-impulses changes for orbit plane
The angle of impulse application is optimal for correcting the deviation of eccentricity vector. The angle of application of the lateral impulse component is optimal for correcting the deviation in the orientation of orbit plane (the impulse is applied on the line of nodes). These angles are calculated by the following formulas:
A four-impulse solution corresponds to a four-link broken line starting in point A and ending in point K. At the optimal initial phase for the transfer flight between non-intersected orbits, the optimal solution should have the same sign for the transversal components of impulse in each of the two maneuvering intervals. Two impulses of the first maneuvering interval correspond to a two-link broken line ABC of length 2VtI, from point A to B. The angles of application of the velocity impulses can be selected arbitrarily, this indicates that point C, corresponding to the eccentricity vector of the waiting orbit formed by maneuvers of the first interval, should belong to a circle of radius R1 = 2|VtI| with a center point A (see Fig. 7). Similarly, for the second maneuvering interval, point B should belong to a circle of radius R2 = 2|VtII| centered at K (see Fig. 8), since a broken CDK with a length of 2VtII corresponds to the second interval maneuvers for a flight from the waiting orbit (AB eccentricity vector) to a given orbit (BK eccentricity vector).
At the optimal initial phase for the optimal transfer flight between non-intersected orbits with radius R1 = 2|VtI| and R2 = 2|VtII|, intersected and have the same sign of VtI, VtII. In this case, there are many solutions with the same dimensionless total characteristic of velocity maneuvers |
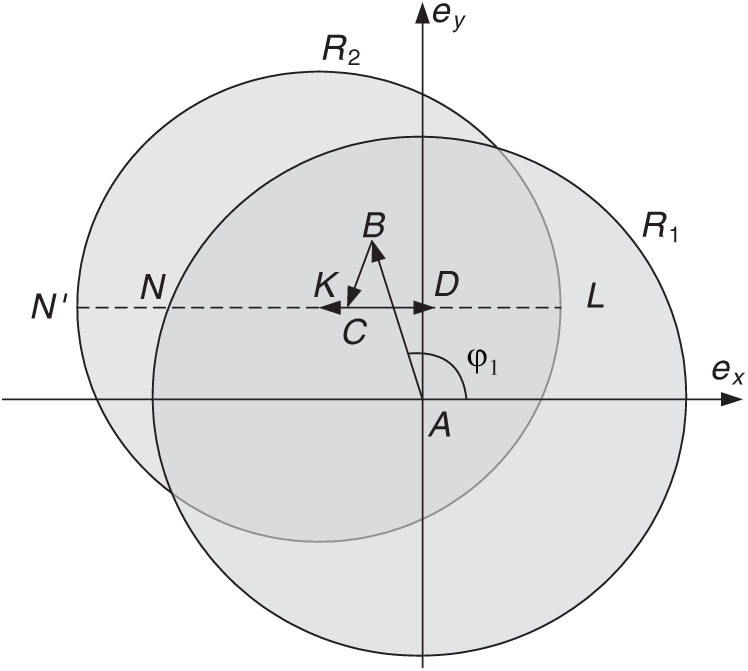
Figure 9: Four impulses solution for rendezvous mission
Solution set with the same V allows to introduce additional restrictions. When calculate the maneuvers of Soyuz spacecraft and Progress, angles of the last two velocity impulses are fixed per revolution and half to the meeting point. Thus, with the impulses of the first maneuvering interval, it is necessary to go to the segment LN which is parallel to the axis ex. The third impulse corresponds to the segment CD, the fourth segment DK. In order to reduce the fuel cost for necessary rotation of orbit plane, angles of velocity impulses in the first maneuvering interval, should be as close as possible to the line of nodes and lie on different sides of it.
With the adopted maneuvering scheme, it is possible to effectively avoid collision if the approaching point is close to the ascending or descending node of the orbit (u0 = 0
In order to obtain a safe solution, the eccentricity vector of the phasing orbit must be derived from the prohibited region, which is easy to realize by changing the angles of application of the first two impulses; and in order to obtain a solution in which TCV is close to the one of optimal solution, the eccentricity vector of phasing orbit should belong to the intersection region of circles with radius R1 and R2. A solution that satisfies both requirements is shown in Fig. 11.
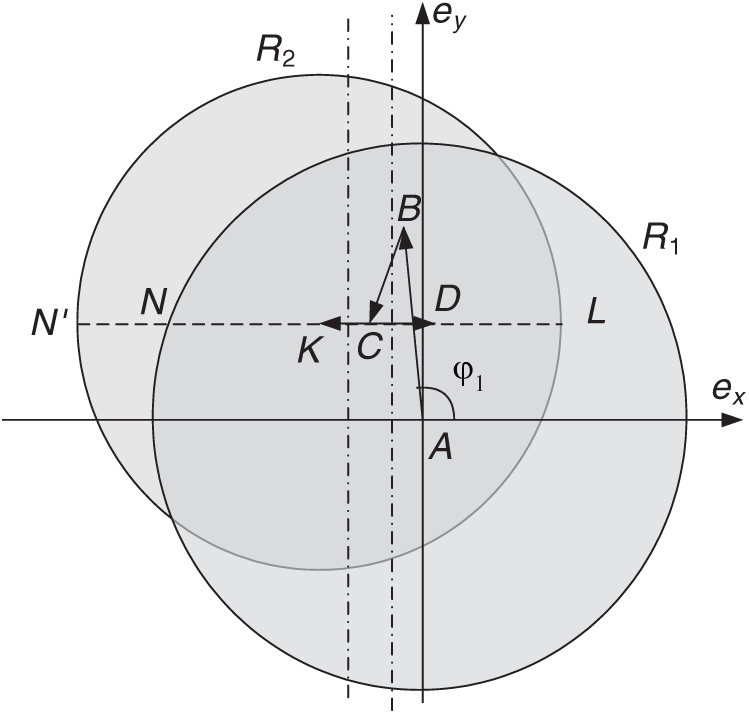
Figure 10: A collision solution with SD in the ascending node of the phasing orbit
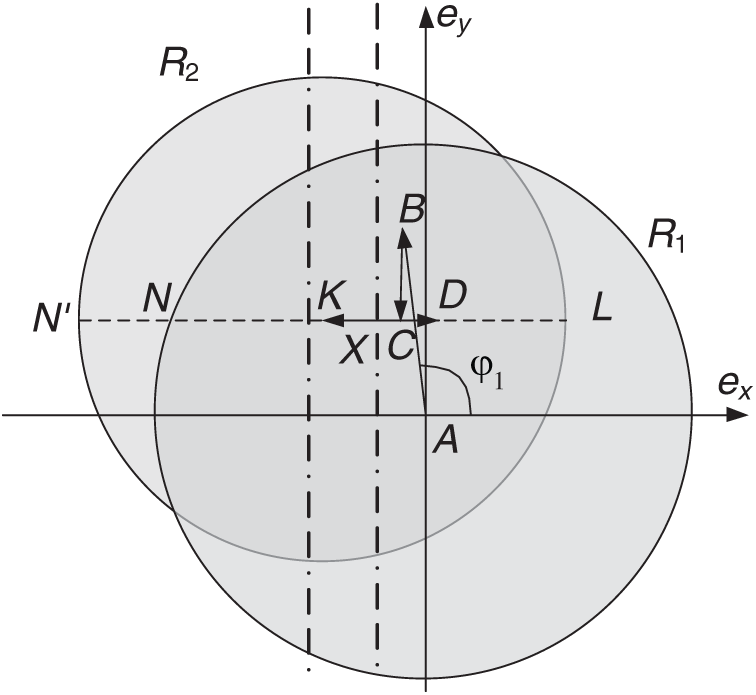
Figure 11: A solution to avoid collision without changing the scheme of maneuvering
Consider a more complicated case, when the point of possible collision is as far from the equator as possible (u0 = 90
Without changing the maneuvering scheme (changing the angle of application of the third or fourth pulses), it is impossible to avoid a collision, because the end of the eccentricity vector of the phasing orbit (
As shown in Fig. 13, a collision can be avoided by changing the angle at which one pulse in the second maneuvering interval is applied, and the effect would be better if the application angles of the two impulses in the second maneuvering interval are changed simultaneously. In this way, the eccentricity vector of the phasing orbit will be removed from the danger region.
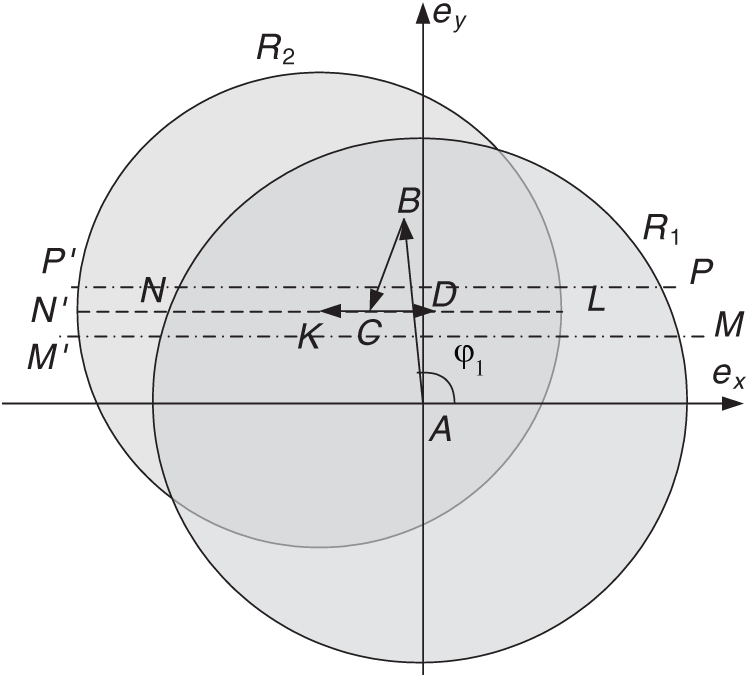
Figure 12: A solution in which a collision with a CM occurs in a phasing orbit
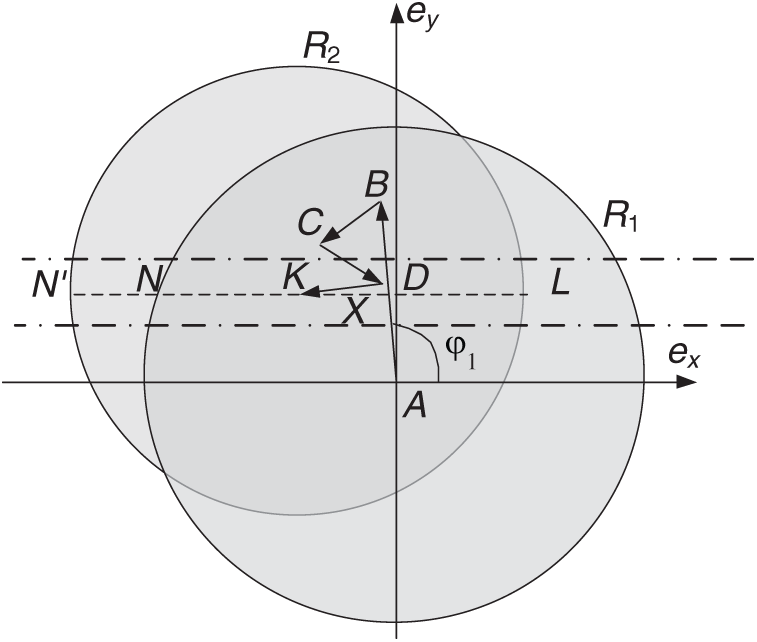
Figure 13: A solution to avoid collision after changing the maneuvering pattern
The area corresponding to collisions at different latitude arguments can also be considered as an option, when in a phasing orbit a collision with several SD objects at different points of the orbit. In slow collisions, the possibility of a collision does not exist at a point, but in a significant range of latitude arguments. The prohibited zone will be restricted to the boundaries line between the two extreme points.
In the slow rendezvous situation, the possibility of collision does not exist at a point, but over a wide range of latitude arguments. The prohibited lane will be limited by straight lines which are the areas boundaries for the two extreme points of the range of possible collisions. An approximate view of the danger area for such a case when a dangerous approach is possible in the latitude range from 60
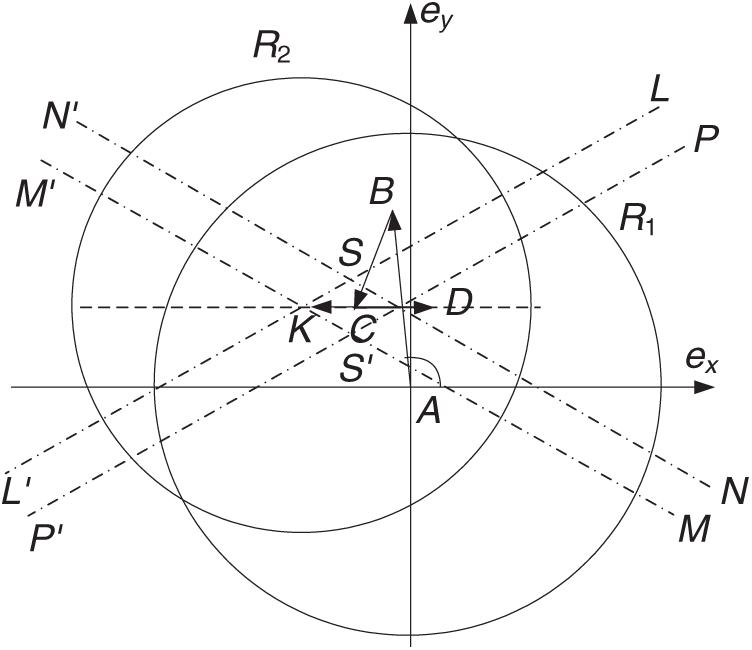
Figure 14: Prohibited area when collision is possible in the range of 60
It should be noted that if the eccentricity vector is derived from this area, then the risk of collision in the area from 240
The solution to the multi-impulse rendezvous problem for a given class of orbits is usually sought using the simplex method. We can offer two other methods for solving this problem, which have shown their effectiveness [24–27]. The first algorithm [25,26] is also numerical, but rather simple.
The angles of application of the first two impulses of velocity
It is most efficient to obtain the desired solution using a graphical dialogue with a problem. In this scheme, based on the analysis of the above presented, angles of application of any of the velocity impulses can be changed, and thus a compromise solution that displays the eccentricity vector of phasing orbit from the danger area can be obtained. Thus, a compromise solution can be obtained that removes the eccentricity vector of the phasing orbit from the dangerous region, but leaves it in the region of optimal solutions. A solution can be found in which point C will be sufficiently far from the danger area without a significant increase in
In this paper a fundamentally new approach to calculate maneuvers for avoiding a collision with space debris is proposed, an effective algorithm is proposed for solution changes to the rendezvous problem, which avoids the collision in phasing orbit of the initial optimal solution. It is demonstrated that the protected area from object must be derived is built on the plane of eccentricity vector components. The prohibited region is bounded by two parallel lines, the axis of this region passes through the end of the eccentricity vector of the phasing orbit of the optimal solution. The orientation of the axis depends on the latitude argument at which the collision may occur. The sizes of this region are determined, depending on
The prohibited region and the region of optimal solutions are depicted on the same plane, which allows using a graphical dialogue when solving the rendezvous problem to find a compromise between the desire to avoid the dangerous object as far as possible and to reduce the delta costs that grow with distance from the optimal solution. The proposed approach to solving the problem also makes it quite simple to calculate rendezvous maneuvers, which also provide evasion from several collisions or from “slow” collisions in a phasing orbit, when the protected spacecraft and the SD object fly dangerously close to each other for a long time. The use of the constructed area will allow solving the problem of collision avoidance of a satellite group (Satellite Formation Flying) with a group of space objects.
Data Availability: Both the methodology and simulation data used to support the findings of this study are available from the corresponding author upon request.
Funding Statement: This work is supported and funded by NSFC (Natural Science Foundation of China) [No. 51905272]. The authors would like to thank the editors and the anonymous reviewers for their valuable comments and constructive suggestions.
Conflicts of Interest: The authors declare that there is no conflict of interest regarding the publication of this paper.
1. Flores-Abad, A., Ma, O., Pham, K. (2014). A review of space robotics technologies for on-orbit servicing. Progress in Aerospace Sciences, 68(5), 1–26. DOI 10.1016/j.paerosci.2014.03.002. [Google Scholar] [CrossRef]
2. Long, A. M., Richards, M. G., Hastings, D. E. (2007). On-orbit servicing: A new value proposition for satellite design and operation. Journal of Spacecraft and Rockets, 44(4), 964–976. DOI 10.2514/1.27117. [Google Scholar] [CrossRef]
3. Lillie, C. F. (2006). On-orbit assembly and servicing of future space observatories. Proceedings of SPIE-The International Society for Optical Engineering, 62652D. DOI 10.1117/12.672528. [Google Scholar] [CrossRef]
4. Davis, T. M., Melanson, D. (2004). XSS-10 microsatellite flight demonstration program results, spacecraft platforms and infrastructure. International Society for Optics and Photonics, 5419, 16–25. DOI 10.1117/12.544316. [Google Scholar] [CrossRef]
5. Board, D. M. I. (2006). Overview of the dart mishap investigation results. http://www.nasa.gov/pdf/148072main_DART_mishap_overview. [Google Scholar]
6. Kawano, I., Mokuno, M., Kasai, T. (2001). Result of autonomous rendezvous docking experiment of engineering test satellite-VII. Journal of Spacecraft and Rockets, 38(1), 105–111. DOI 10.2514/2.3661. [Google Scholar] [CrossRef]
7. Li, Q., Yuan, J., Zhang, B. (2017). Model predictive control for autonomous rendezvous and docking with a tumbling target. Aerospace Science and Technology, 69(9), 700–711. DOI 10.1016/j.ast.2017.07.022. [Google Scholar] [CrossRef]
8. Kasaeian, S. A., Assadian, N., Ebrahimi, M. (2017). Sliding mode predictive guidance for terminal rendezvous in eccentric orbits. Acta Astronautica, 140(1), 142–155. DOI 10.1016/j.actaastro.2017.08.012. [Google Scholar] [CrossRef]
9. Liu, X., Zhang, M. J., Chen, J. W., Yin, B. J. (2020). Trajectory tracking with quaternion-based attitude representation for autonomous underwater vehicle based on terminal sliding mode control. Applied Ocean Research, 104, 102342. DOI 10.1016/j.apor.2020.102342. [Google Scholar] [CrossRef]
10. Ali, N., Tawiah, I., Zhang, W. D. (2020). Finite-time extended state observer based nonsingular fast terminal sliding mode control of autonomous underwater vehicles. Ocean Engineering, 218(2), 108179. DOI 10.1016/j.oceaneng.2020.108179. [Google Scholar] [CrossRef]
11. Li, A. J., Tian, H. H., Wang, W. Q. (2020). Fixed-time terminal sliding mode control of spinning tether system for artificial gravity environment in high eccentricity orbit. Acta Astronautica, 177, 834–841. DOI 10.1016/j.actaastro.2020.03.013. [Google Scholar] [CrossRef]
12. Liu, E. J., Yang, Y. N., Yan, Y. (2020). Spacecraft attitude tracking for space debris removal using adaptive fuzzy sliding mode control. Aerospace Science and Technology, 107(A6), 106310. DOI 10.1016/j.ast.2020.106310. [Google Scholar] [CrossRef]
13. Li, Q., Yuan, J., Wang, H. (2018). Sliding mode control for autonomous spacecraft rendezvous with collision avoidance. Acta Astronautica, 151, 743–751. DOI 10.1016/j.actaastro.2018.07.006. [Google Scholar] [CrossRef]
14. Wang, X., Qiu, X., Agarwal, P. (2020). Study on fuzzy neural sliding mode guidance law with terminal angle constraint for maneuvering target. Mathematical Problems in Engineering, 2020(3), 4597937. DOI 10.1155/2020/4597937. [Google Scholar] [CrossRef]
15. Cao, L., Qiao, D., Xu, J. (2018). Suboptimal artificial potential function sliding mode control for spacecraft rendezvous with obstacle avoidance. Acta Astronautica, 143(3), 133–146. DOI 10.1016/j.actaastro.2017.11.022. [Google Scholar] [CrossRef]
16. Li, P., Zhu, Z. H. (2018). Model predictive control for spacecraft rendezvous in elliptical orbit. Acta Astronautica, 146, 339–348. DOI 10.1016/j.actaastro.2018.03.025. [Google Scholar] [CrossRef]
17. Jewison, C., Erwin, R. S., Saenz-Otero, A. (2015). Model predictive control with ellipsoid obstacle constraints for spacecraft rendezvous. IFAC–PapersOnLine, 48(9), 257–262. DOI 10.1016/j.ifacol.2015.08.093. [Google Scholar] [CrossRef]
18. Larsén, A. K., Chen, Y., Bruschetta, M. (2019). A computationally efficient model predictive control scheme for space debris rendezvous. IFAC–PapersOnLine, 52(12), 103–110. DOI 10.1016/j.ifacol.2019.11.077. [Google Scholar] [CrossRef]
19. Zhu, Y. H., Wang, H., Zhang, J. (2015). Spacecraft multiple-impulse trajectory optimization using differential evolution algorithm with combined mutation strategies and boundary-handling schemes. Mathematical Problems in Engineering, 2015(1), 1–13. DOI 10.1155/2015/949480. [Google Scholar] [CrossRef]
20. Qi, Y., Jia, Y. (2011). Active collision avoidance maneuver under constant thrust. Advances in Space Research, 48(2), 349–361. DOI 10.1016/j.asr.2011.03.030. [Google Scholar] [CrossRef]
21. Shirazi, A., Ceberio, J., Lozano, J. A. (2019). An evolutionary discretized Lambert approach for optimal long-range rendezvous considering impulse limit. Aerospace Science and Technology, 94(11), 105400. DOI 10.1016/j.ast.2019.105400. [Google Scholar] [CrossRef]
22. Yang, X., Cao, X. (2015). A new approach to autonomous rendezvous for spacecraft with limited impulsive thrust: Based on switching control strategy. Aerospace Science and Technology, 43(4), 454–462. DOI 10.1016/j.ast.2015.04.007. [Google Scholar] [CrossRef]
23. Baranov, A. A. (2016). The maneuvering of the spacecraft in the vicinity of a circular orbit, pp. 512. Moscow: Sputnik Pub. [Google Scholar]
24. Baranov, A. A., Roldugin, D. S. (2012). Six-impulse maneuvers for rendezvous of spacecraft in near-circular noncoplanar orbits. Cosmic Research, 50(6), 441–448. DOI 10.1134/S0010952512050012. [Google Scholar] [CrossRef]
25. Baranov, A. A. (1986). Algorithm for calculating the parameters of four-impulse transitions between close almost-circular orbits. Cosmic Research, 24(3), 324–327. [Google Scholar]
26. Labourdette, P., Carbonne, D., Julien, E. (2009). Maneuver plans for the first ATV mission. AAS/AIAA Astrodynamics Specialist Conference, pp. 9–172. Preprint AAS. [Google Scholar]
27. Baranov, A. A. (1990). An algorithm for calculating parameters of multi-orbit maneuvers in remote guidance. Cosmic Research, 28(1), 61–67. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |