Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.015210

ARTICLE

Attribute-Based Keyword Search over the Encrypted Blockchain

Zhen Yang1, Hongao Zhang1, Haiyang Yu1,*, Zheng Li1, Bocheng Zhu1 and Richard O. Sinnott2

1Faculty of Information Technology, Beijing University of Technology, Beijing, 100124, China
2School of Computing and Information Systems, The University of Melbourne, Victoria, 3010, Australia
*Corresponding Author: Haiyang Yu. Email: yuhaiyang@bjut.edu.cn
Received: 02 December 2020; Accepted: 15 March 2021

1  Introduction

As an emerging decentralized technology, blockchain has gained attention worldwide over the past decade, which can be applied to many scenarios such as IoT, 5G networks [1], etc. Among the many appealing features of blockchain, highly redundant storage enables each user to possess a full copy of the blockchain, which means users can share their data with anyone in the blockchain network directly for many data driven applications [2]. This feature makes the blockchain a perfect technique for constructing data sharing schemes. However, since data is public to all users, it can be accessed by both data users and external (undesirable) users in the blockchain network, thus giving rise to privacy issues and malicious attacks [3]. To achieve confidentiality, data owners usually opt to encrypt their data before submitting it to the blockchain. Although encryption protects the data from being deciphered and understood by anyone in the network, the encrypted files hinder data users from conducting search operations on the blockchain. A search mechanism over the encrypted blockchain is thus desirable to achieve both data confidentiality and usability.

Several works [4–8] have focused on keyword search over the encrypted blockchain. However, existing schemes mostly adopted symmetric encryption and thereby have several major drawbacks. Firstly, since data users have to interact with each data owner before searching the data, these schemes cannot support efficient data retrieval over the whole blockchain. Secondly, interactions require data owners and users to share either the secret key or keyword, which can give rise to privacy erosion. Thirdly, since the authorization is entirely dependent on data owners, access control [9] in searching the blockchain is not supported. As an example of these issues, consider the following situation. There are a lot of users in the blockchain network belonging to the same university or company who have similar features or attributes and want to search shared data within the group (and only within the group). Contacting data owners individually to get the search permission makes the data sharing process highly inflexible and inefficient.

Traditional symmetric encryption schemes cannot address these issues well. Therefore, we propose an attribute-based keyword search scheme on blockchain. Data users can get the secret key from a trusted third party and use it to search on the blockchain without any interactions from the data owner, which avoids the possible privacy leakage of users. By improving the structure of the encrypted index, we achieved fine-grained access control and efficient search, which allows users to search encrypted files over the blockchain based on their attributes efficiently and accurately.

In summary, our contributions include:

1.    We proposed an attribute-based keyword search scheme enabling the searching of encrypted data over blockchains. By introducing Attribute-Based Encryption (ABE), the proposed scheme can achieve data retrieval over the whole blockchain with support for fine-grained access control.

2.    Motivated by the blockchain data structure, we design a data structure that is comprised of chained files with the same keyword to address the efficiency of encrypted data retrieval over blockchains.

3.    We analyze the security of our design and further implement a prototype of the proposed scheme on the Hyperledger Fabric platform. Theoretical analysis and experimental evaluation show the efficiency and feasibility of the proposed scheme.

2  Related Work

The concept of searchable encryption was first proposed by Song et al. [10] in 2000. This scheme could search encrypted data stored in remote servers by leveraging symmetric encryption methods. In 2004, Boneh et al. [11] first proposed a public-key encryption scheme with keyword search. However, the keyword privacy was not protected by this scheme. Subsequently, extensive research has been carried out on both symmetric [12–15] and asymmetric searchable encryption [16–19].

Searchable encryption has been well studied in cloud environments, however, limited research has been conducted on searching keywords on blockchains. Li et al. [20] presented a searchable encryption scheme using blockchain, which utilized blockchain techniques to ensure transaction security during the process of outsourced data retrieval. Cai et al. [21] designed an encrypted and distributed search protocol. This scheme considered submitted the retrieval results to the blockchain to achieve verifiability. Zhang et al. [22] proposed a trustworthy keyword search scheme over encrypted data based on blockchain. They adopted blockchains to ensure the security and fairness of payment for data retrieval. However, all these schemes did not search encrypted data over the blockchain, rather they only enhanced the reliability of transaction and payment occurrences during data retrieval over encrypted blockchains. Jiang et al. [7] proposed a stealth authorization scheme on blockchains to achieve private authorization delivery between data users and data owners, but the data user still had to inform the data owner of the search keywords. Tian et al. [23] designed a storage framework based on blockchain to protect digital data, which ensures the integrity and validity of evidence and better balances privacy and traceability. Yang et al. [8] proposed a blockchain based multi-keyword ranked search system, which realized the top-k ranked ciphertext retrieval on blockchain and used smart contracts to only return the most relevant encrypted files to data users. However, this scheme limited the structure of the index and therefore limited its scalability; it also increased the size of the index. Tahir et al. [24] proposed a privacy preserving searchable encryption framework to achieve data retrieval over encrypted blockchains. By introducing a probabilistic trapdoor, this scheme was able to protect the privacy of keywords. Unfortunately, this scheme only supported data retrieval by the data owner. Hu et al. [4] considered the use of smart contracts to support data retrieval. However, this scheme required the data user to send keywords to the data owner and the data owner would then search the dataset on behalf of the data user due to the adoption of symmetric searchable encryption. When considering searching over blockchains, the data user even needed to send keywords to all data owners, which is neither efficient nor privacy-preserving. Therefore, none of the above schemes meet the needs of data owners who want to share their data and achieve fine-grained access control while users who want to search independently on the blockchain without relying on the data owner.

3  Preliminaries

3.1 Bilinear Pairing

Let G1 and GT be two multiplicative cyclic groups of large prime order q. Denote g and gT as the generators of G1 and GT, respectively. A bilinear map is a map e: G1 × G1 → GT which satisfies the following three properties:

1) Bilinearity:

for u,v∈G1 and a,b∈Zp∗, e(ua,vb)=e(u,v)ab;

2) Non-degeneracy:

∃g∈G1 such that e(g,g)≠1;

3) Computability:

there exists an efficient algorithm to compute the map e.

3.2 System Model

The system model of the proposed scheme consists of three entities, as illustrated in Fig. 1: the attribute authority (AA), the data owner and the data user. An AA is a trusted third party responsible for distributing secret keys to users in the blockchain based on their attributes. Data owners possess files that can be shared within a group of data users with similar attributes. A data owner generates encrypted indexes and submits them to the blockchain. The data user encrypts the searching keyword and sends an encrypted token to the blockchain to retrieve the files it wants. The blockchain system is maintained and shared by all data owners and data users. A smart contract in the blockchain retrieves files and returns the search results to the data user.

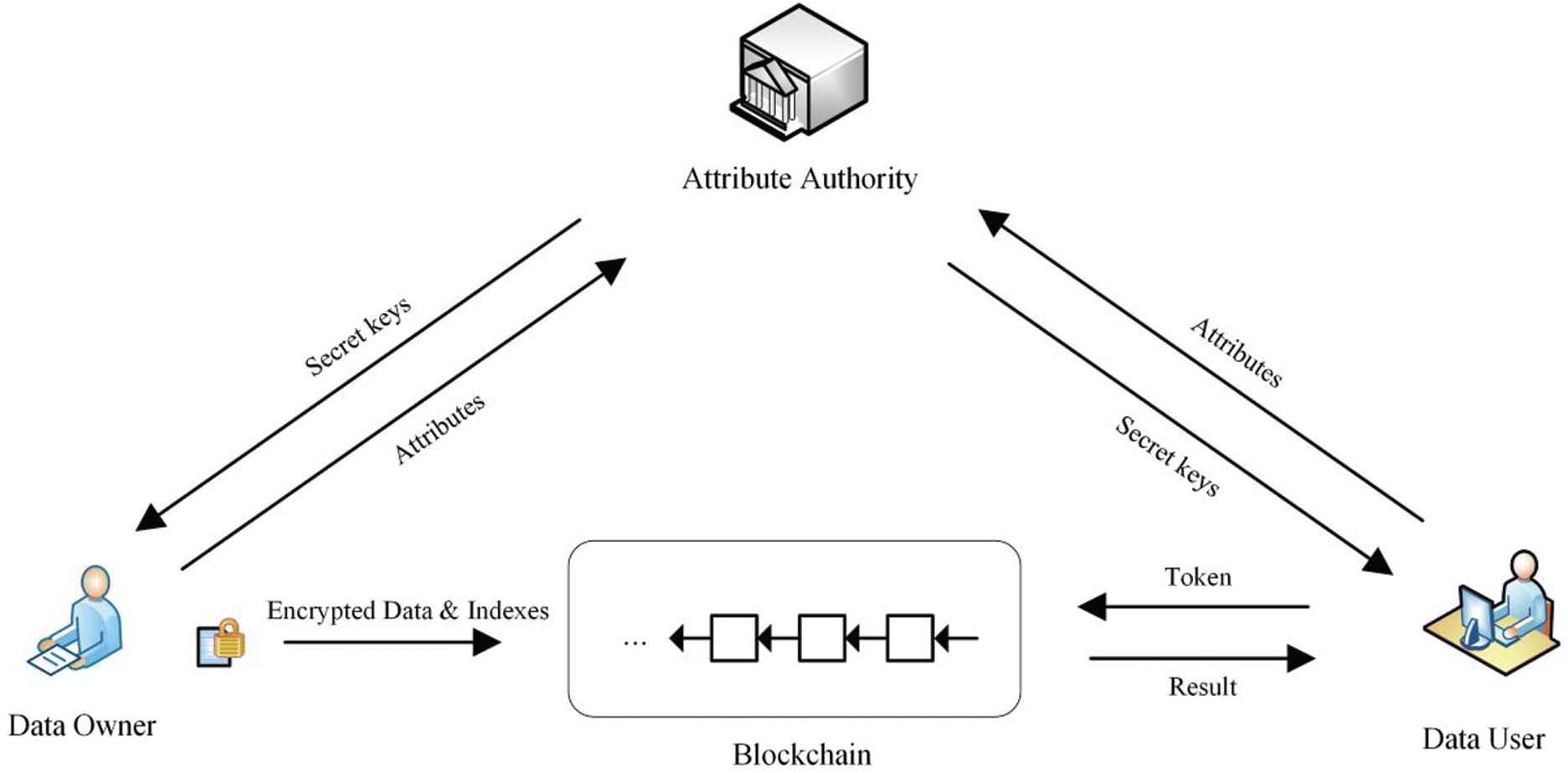
Figure 1: The system model of the proposed scheme including three entities: the attribute authority (AA), the data owner and the data user

3.3 Design Goals

The design goals of the proposed scheme are as follows:

1) Flexibility:

The data user can search files of all data owners in the blockchain without interacting individually with each data owner.

2) Attributed-Based Retrieval:

The encrypted files can only be retrieved and decrypted by data users with specific security attributes.

3) Reliability:

The search should return all matched results to the data user and the results should be the same each time the same query is executed.

4) Efficiency:

The retrieval performance should be higher than traditional traversal search in the blockchain.

3.4 Definition of the Proposed Scheme

Definition 1. The proposed scheme is comprised of six polynomial time algorithms including Setup, KeyGen, IndexGen, TokenGen, Search and Decrypt.

Setup(1k)→(msk,pm). The Setup algorithm takes a security parameter k as the input and returns the master key msk and the public parameters pm.

KeyGen(msk,As)→sk. The KeyGen algorithm takes the master key msk and the attributes As as inputs and outputs the secret key sk.

IndexGen(kw,T,F)→(cph,F~). The IndexGen algorithm requires the keyword kw, the access tree T, and the file F as inputs and returns the encrypted index cph and the encrypted file F~.

TokenGen(sk,kw)→tk. The TokenGen algorithm takes the secret key sk and the search keyword kw as inputs, and outputs the search token tk.

Search(tk,cph)→rst. The Search algorithm takes the search token tk and encrypted index cph as inputs and returns the search result rst.

Decrypt(rst)→{F}. The Decrypt algorithm takes the search result rst as the input and returns the file F.

3.5 Security Model

In this paper, the Selective-Set Security Game [25,26] is introduced to prove the security of the proposed scheme. The detailed game between a challenger C and an adversary A is defined as follows:

Init. An adversary A sends a challenge access policy with a set of attributes S to the challenger C.

Setup. The challenger C runs the Setup algorithm to generate the public parameters that are forwarded to the adversary A.

Phase 1. By submitting any access trees with attribute set As′ to the challenger C, the adversary A is allowed to request the secret key based on the attributes. The restriction is that As⊈As′.

Challenge. The adversary A forwards two different keywords kw1, kw2 to the challenger C. The challenger C randomly flips a coin μ ∈ {0, 1} and calculates the encrypted index cphμ. The challenger C returns cphμ to the adversary A.

Phase 2. Same as Phase 1.

Guess. Based on the forementioned steps, the adversary A outputs the guess μ′ of μ.

We say that the proposed scheme is secure if for any probabilistic polynomial time adversary A, the advantage of winning the Selective-Set Security Games is negligible.

4  Attribute-Based Keyword Search over Encrypted Blockchain

4.1 File Chain Structure

In a lot of cases, there may be several files with the same keyword when searching files in the blockchain. For instance, a stock analyst in a security company may submit several reports related to the company Apple to his boss. Thus, all these files may have the same keyword ‘Apple.’ A data owner can build a structure in advance to address this issue and improve the overall retrieval performance. Motivated by the data structure of chained blocks in blockchain, we designed a File Chain Structure (FCS) as shown in Fig. 2. An FCS is a chain structure links all files with the same keyword in the blockchain. Each node in the FCS contains the address of previous file and an encrypted file. All nodes linked end to end comprise the FCS.

The FCS can simplify the retrieval process. When users search on any file with certain keywords in the FCS, the smart contract only needs to search an index table and then traverse the FCS to retrieve all files with the same keyword instead of searching for other files by different tokens.

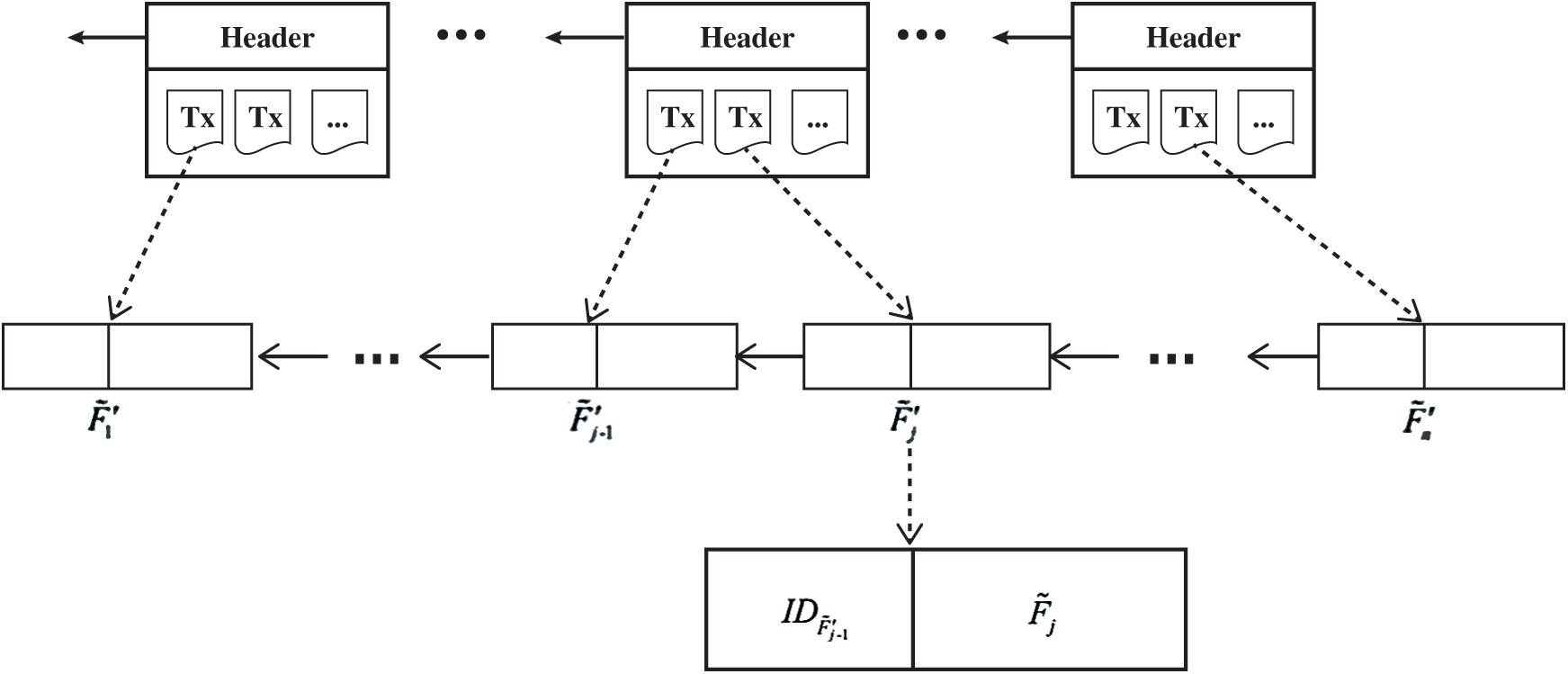
Figure 2: Example of the file chain structure, each node in the FCS contains the address of the previous file and an encrypted file

4.2 The Detailed Construction

As noted, the proposed scheme consists of six algorithms: Setup, KeyGen, IndexGen, TokenGen, Search, Decrypt.

Setup. k denotes the security parameter. Let G1 and GT be two multiplicative cyclic groups of prime order q. Let g be the generator of group G1. H:{0,1}∗→G1 and h:{0,1}∗→Zp∗ denotes two hash functions. AA randomly chooses a,b,c,x∈G1, sets the master secret key as msk=(a,b,c,x), and computes Ex=e(g,g)x. Finally, AA publishes the public parameters and keeps the master secret key msk private.

KeyGen. AA generates a random value r∈Zp∗, computes A=g(ac−r)/b and B=e(g,g)x+r. Let As be the attribute set of a data owner or user. For each attribute atti∈As, AA chooses a random value ri∈Zp∗, computes Mi=grH(atti)ri and Ni=gri. AA generates the keyword search key sk={As,A,B,{Mi,Ni∣atti∈As}} and returns it to the corresponding data owner or data user.

IndexGen. The data owner first generates a keyword kwj for each file Fj and then creates the secret key ck for symmetric encryption and encrypts the file Fj to generate F~j. Let {F~j}j∈[1,n] be a set of files containing the same keyword, where n is the number of files. For j = 1, it sets F1′~=null∣∣F~1, where IDFn′~=h(F~n) is the address of Fn′~. For j=2,…,n, the data owner calculates Fj′~=IDF~j−1∣∣F~j.

The data owner then chooses random values r1,r2∈Zp∗, calculates W0=gcr1, W1=ga(r1+r2)gbh(kw)r1, W2=gbr2,C0=ck⋅Exr2, C1=Br2. It constructs the access tree T based on the access policy. The access tree includes a set of attributes Ts where each leaf node represents an attribute. att(v) denotes the attribute of the leaf node v in the access tree T. By using the access tree T, the data owner shares the secret value r2 into the leaf nodes. The secret value of each leaf node v is qv(0), where qv(x) is the polynomial used in the access tree T. For each leaf node v∈T, it computes Wv=gqv(0) and Dv=H(att(v))qv(0). Finally, the data owner gets a ciphertext keyword cph={T,W0,W1,W2,C0,C1,{(Wv,Dv)∣att(v)∈Ts}} and submits the transaction Tx={cph,F~} to the blockchain.

TokenGen. The data user randomly chooses s∈Zp∗ and calculates tk1=(gagbh(kw))s,tk2=gcs,tk3=As. For each attribute atti∈As, the data user computes Mi′=Mis and Ni′=Nis. Finally, the data user generates search token tk={tk1,tk2,tk3,As,{(Mi′,Ni′)∣atti∈As}}.

Search. The data user invokes the search smart contract Sc with the search token tk. The smart contract Sc will search over each ciphertext keyword cph based on the search token tk. The smart contract Sc first checks if there exists a subset of attribute set As satisfying the access tree T in ciphertext keyword cph. If not, it will return an empty set. Otherwise, for each attribute atti=att(v)∈Ts, it computes Ev=e(Mi′,Wv)/e(Ni′,Dv)=e(g,g)rsqv(0). The smart contract Sc then calculates the secret values of the nodes of the access tree T from bottom to top, until recovering the secret value of root node Er=e(g,g)rsqr(0)=e(g,g)rsr2. It then checks if

e(W0,tk1)Ere(tk3,W2)=e(W1,tk2) (1)

If the equation holds, it splits the file Fj′~ to get the address IDF~j−1 and the encrypted file F~j. If null←IDF~j−1′, it stops. If F~j−1′←IDF~j−1′, it stores IDF~j−1′ and continues traversing the files in the FCS. Finally, the smart contract Sc returns the search results rst={{IDF~j′},Er,C0,C1}.

Decrypt. The data user invokes the smart contract Sc to read the rst. It then computes C0/(C1⋅Er(1/s))=ck to get the symmetric encryption key ck. Finally, it decrypts the files included in rst and gets the plaintext files {F}.

The algorithms in our scheme are described in Fig. 3.

Figure 3: Construction of our search scheme

4.3 Correctness

In this section, we illustrate the proof of correctness of Eq. (1) as follows:

e(W0,tk1)=e(gcr1,(gagbh(kw))s)

=e(g,g)scr1(a+bh(kw)) (2)

Er=e(g,g)rsr2 (3)

e(tk3,W2)=e(As,gbr2)

=e(gs(ac−r)/b,gbr2)

=e(g,g)r2s(ac−r) (4)

thus, we get

e(W0,tk1)Ere(tk3,W2)=e(g,g)sacr2+sacr1+scr1bh(kw)

=e(g,g)sc(a(r2+r1)+r1bh(kw))

=e(g(a(r2+r1)+r1bh(kw)),gsc)

=e(g(a(r1+r2))g(r1bh(kw)),gcs)

=e(W1,tk2) (5)

5  Security Analysis

In this paper, the AA and the blockchain infrastructure are assumed to be reliable. Thus, we focus on the secure search related privacy requirements of the proposed scheme, which mainly involves the keyword semantic security and token unlinkability.

Definition 2. (The DBDH Assumption). Let u,v,w,z∈Zp∗ be the random values and g be the generator of G1. The DBDH (Decisional Bilinear Diffie-Hellman) Assumption is that given a polynomial-time adversary A, it cannot distinguish the tuple (U=gu,V=gv,W=gw,e(g,g)uvw) from the tuple (U=gu,V=gv,W=gw,e(g,g)z) with non-negligible probability ε.

Theorem 1. Keyword semantic security. If there exists a probabilistic polynomial time adversary that can win the Selective-Set Security Game with non-negligible probability ɛ, then we can construct a simulator S to solve the DBDH problem with non-negligible probability ε2.

Proof. The DBDH challenger C first selects random values g,u,v,w,z∈Zq∗ and a bilinear map e. Then it flips a fair coin k and if k = 0 it sets U=gu,V=gv,W=gw,Z=e(g,g)uvw. Otherwise, it sets U=gu,V=gv,W=gw,Z=e(g,g)z. The challenger C sends g,U,V,W,Z to the simulator B. The simulator B executes the game by interacting with the adversary A as follows:

Init. The adversary A submits an attribute set S to the simulator B.

Setup. The simulator B sets x=x′+uv, where x′ is a random value in Zq∗ and then calculates Ex=e(g,g)x′+uv=e(U,V)e(g,g)x′. Finally, the public parameters are sent to the adversary A.

Phase 1. The adversary A queries B for the secret key sk of any access structure T with an attribute set As′. The simulator B computes B=e(g,g)x′+uv+r=e(U,V)e(g,g)x′+r.

Challenge. The adversary A provides two keywords kw1 and kw2 with equal length to B. The simulator B flips a fair coin μ∈{0,1} and encrypts kwμ with the access policy T and the secret keys. The simulator B chooses a random number r2′ and sets r2=r2′+w. It then computes W2=Wbgr2′b. Finally, it sets C0=ck⋅Z⋅e(U,V)r2′⋅e(g,g)x′(w+r2′) and C1=Z⋅e(U,V)r2′⋅e(g,g)(x′+r)(w+r2′).

Phase 2. The same as Phase 1.

Guess. The adversary A outputs a guess μ′ of μ. At the same time, the simulator B makes a guess k′ of k based on the output of the adversary A. If μ′≠μ, the simulator B guesses k′ = 1. Otherwise, it guesses k′ = 0.

If k = 1, Z=e(g,g)z, which means the adversary A cannot get any advantage of the game but a random guess. Therefore, Pr[μ′≠μ∣v=1]=12. When μ′≠μ, the simulator B outputs k′ = 1 such that Pr[k′=k∣k=1]=12.

If k = 0, Z=e(g,g)uvw, which means the adversary A will get a valid cph. Therefore, Pr[μ′=μ∣v=1]=12+ε. When μ′=μ, the simulator B outputs k′ = 0 such that Pr[k′=k∣k=0]=12+ε.

Finally, the overall advantage of the simulator B for winning this game can be calculated as Pr[k′=k]−12=12Pr[k′=k∣k=1]+12Pr[k′=k∣k=0]−12=12⋅12+12⋅(12+ε)−12=ε2.

Theorem 2. Token Unlinkability. Data users are unable to directly distinguish two or more search tokens even those containing the same keyword.

Proof. The search information submitted to the blockchain should be encrypted before submitting since it can be accessed by all users. The data user encrypts the keyword kw into tk1 with a random value s. In this way, other users cannot directly distinguish different search tokens because they are obfuscated by the random value s. Therefore, the proposed scheme can achieve token unlinkability.

6  Performance Evaluation

We implement a prototype of the proposed scheme using almost 3760 lines of code. We develop the blockchain system based on the Hyperledger Fabric blockchain platform. Both the data owner and the service peers were deployed on a machine with 8 GB of RAM, 2 Intel cores i5-8300H, running Ubuntu 20.04 LTS. The smart contract was implemented using chaincode in the Hyperledger Fabric platform. We implemented the pseudo-random function using the secure hash algorithm (SHA1).

The database of this experiment was randomly generated, each record consisted of a keyword and a file corresponding to the keyword. Furthermore, we generated two similar-sized databases with different numbers of keywords and of the same size to study the performance of our scheme on different datasets. The database DB1 consists of 3 K keyword-file pairs, 600 keywords where each keyword matched 5 files on average and the database DB2 also consisted of 3 K keyword-file pairs but had 300 keywords where each keyword matched 10 files on average. We ran each execution 20 times and averaged the results. The performance of our scheme for the different phases was recorded.

6.1 Index Generation

During this phase, the data owner encrypts keywords and corresponding files into encrypted indexes and associated encrypted files. Fig. 4 shows the index generation time varying with the number of keyword- file pairs. It can be observed that the time cost increases with the number of keyword-file pairs linearly. The time for generating indexes of 600 keyword-file pairs averages to 21.2 s.

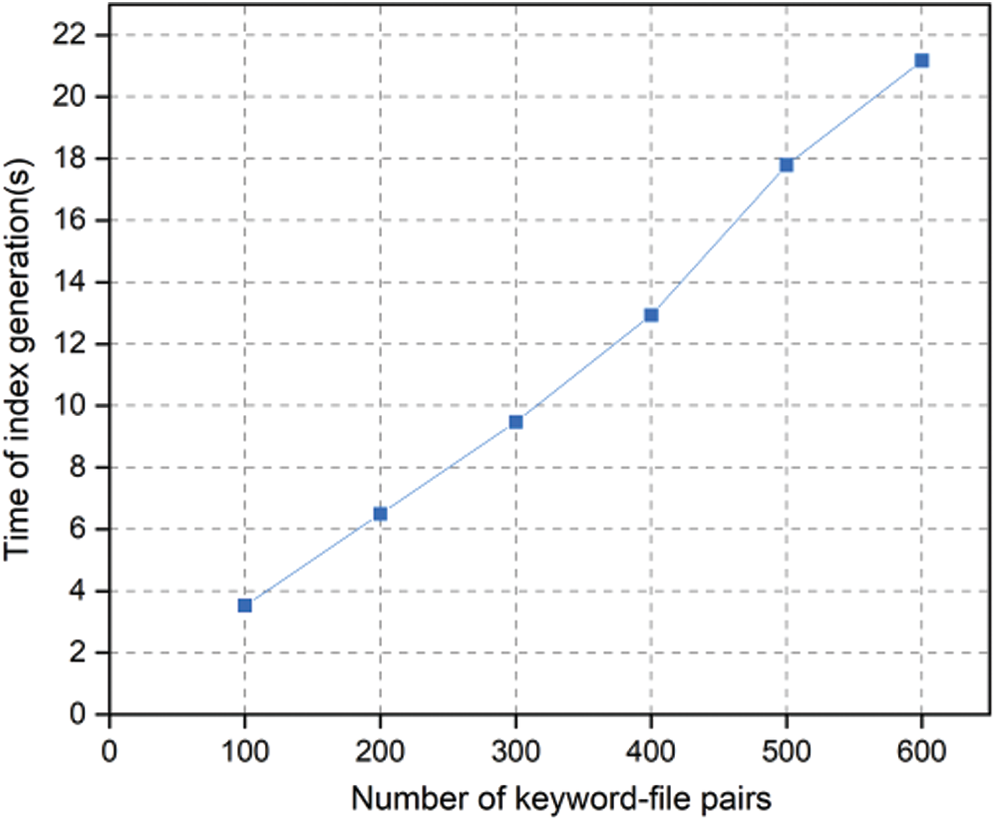
Figure 4: Time of index generation vs. the number of keyword-file pairs

6.2 Search

To search the blockchain, the data owner first needs to generate a search token. The time cost of token generation is shown in Fig. 5. It is obvious that the time cost increases with the number of keywords linearly because the data owner generates a search token for each keyword. The time for generating tokens of 600 keywords was 10.3 s on average.

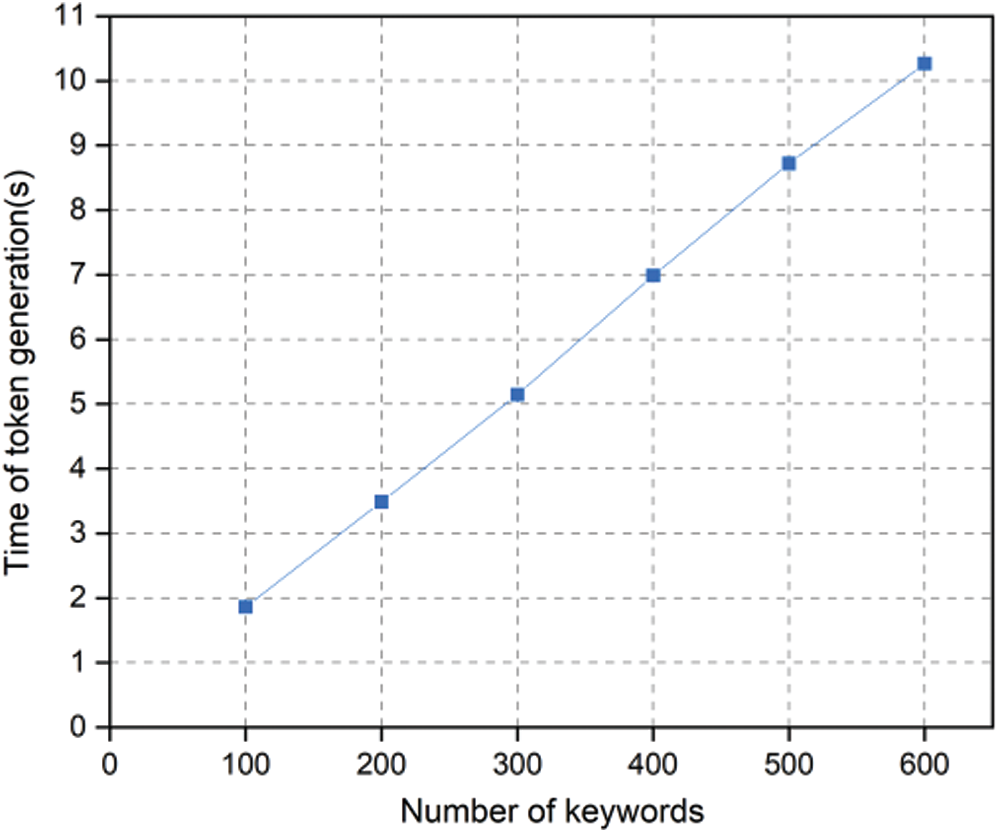
Figure 5: Time of token generation vs. the number of keyword-file pairs

On the service side, the smart contract accepts the search request from the data owner/data user and executes the query operation. We execute the query operation with DB1 and DB2 separately. We do not implement FCS here, which helps us focus on the performance of our scheme without additional optimization considerations. The experimental results are shown in Fig. 6. We can see that the time costs for both DB1 and DB2 increase linearly with the number of matching files. In addition, the search time for DB1 takes about twice as long as that of DB2, since the smart contract needs to traverse all the ciphertext keywords (cph) in this phase. The time for each traversal of DB1 is the same as DB2 because DB1 and DB2 are the same size. Each query on DB2 returns 10 results while DB1 returns 5 results, resulting in the time to be half of that for DB2.

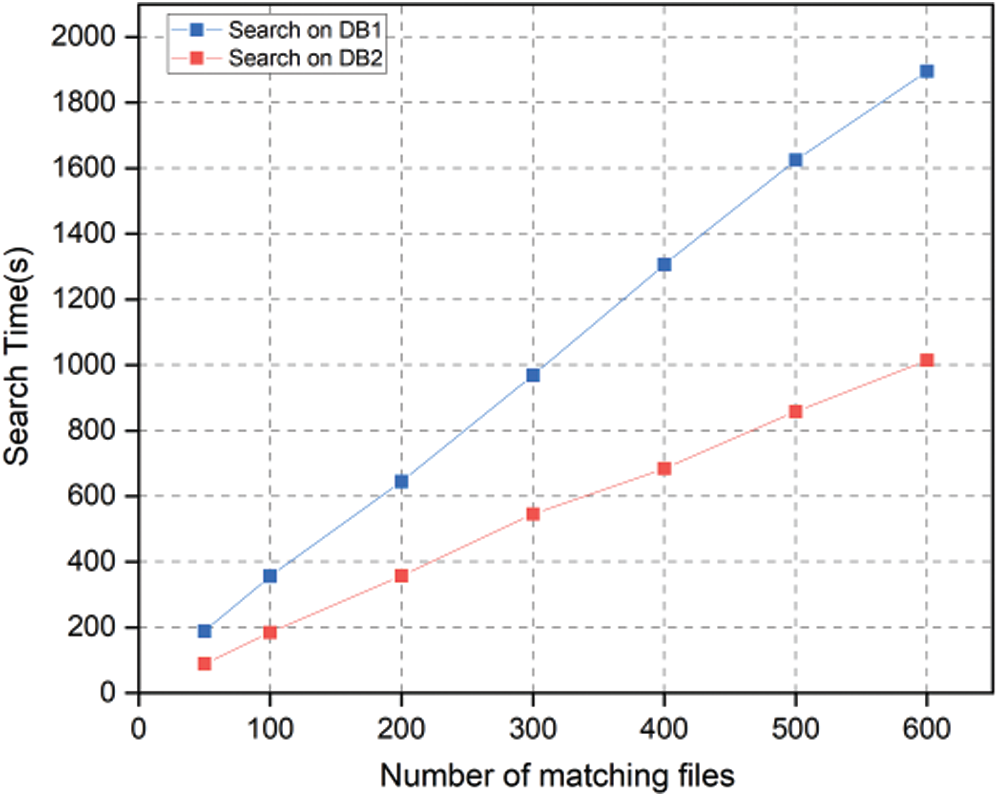
Figure 6: Comparing the search time of our scheme on DB1 and DB2 for various result set sizes

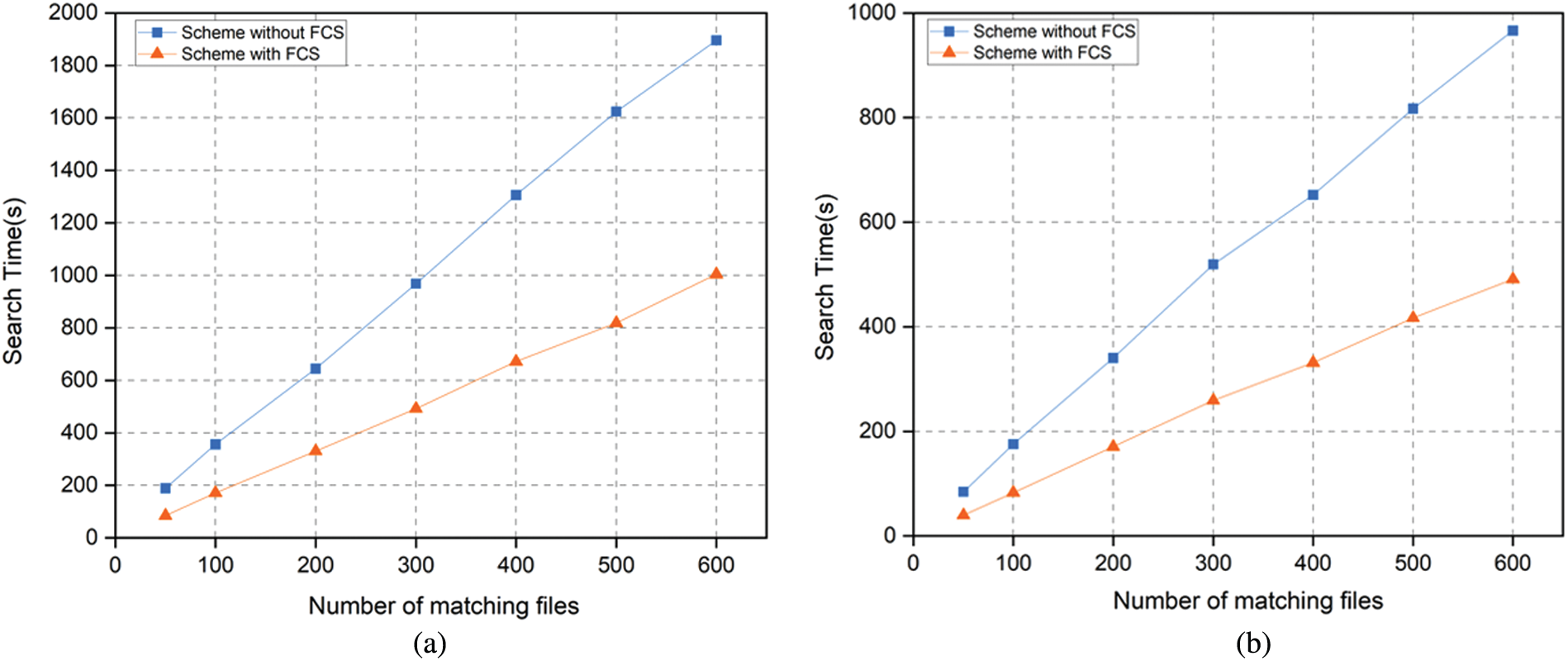
Figure 7: Comparing the search time of our scheme on DB1 and DB2 for various result set sizes, the time cost of scheme with and without FCS are compared on each database (a) Search time cost of our scheme on DB1 (b) Search time cost of our scheme on DB2

To demonstrate the efficiency of FCS, we present the search time cost with and without FCS respectively. Experimental results on DB1 are shown in Fig. 7a and those on DB2 are shown in Fig. 7b. It is obvious that the efficiency of the scheme with FCS is much higher than that without FCS for both DB1 and DB2. This shows the superiority of our FCS scheme. Besides, itis easy to see that both the time costs with and without FCS linearly increase with the number of matching files. This is because each query is independent of the other.

7  Conclusion

In this paper, we consider a scenario of encrypted data retrieval where data users could search over encrypted blockchains based on their attributes. Using attribute-based encryption, we designed an attribute-based encrypted keyword search scheme for blockchains, which allows a data user to search encrypted data across the blockchain. A novel File Chain Structure was proposed to improve the retrieval efficiency when searching files with the same keywords. The security analysis proves that our scheme can provide keyword semantic security and token unlinkability. The performance evaluation shows the feasibility and efficiency of the proposed scheme.

Funding Statement: This work was supported by the National Natural Science Foundation of China (61671030), Industrial Internet Innovation Development Project, China Postdoctoral Science Foundation (2019M660377), and National Key Research and Development Program of China (2020YFB2009501). It was also supported by Engineering Research Center of Intelligent Perception and Autonomous Control, Ministry of Education.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.