[BACK]
images Computer Modeling in Engineering & Sciences images

DOI: 10.32604/cmes.2021.016736

ARTICLE

Decision Making Algorithmic Approaches Based on Parameterization of Neutrosophic Set under Hypersoft Set Environment with Fuzzy, Intuitionistic Fuzzy and Neutrosophic Settings

Atiqe Ur Rahman*,1,*, Muhammad Saeed1, Sultan S. Alodhaibi2 and Hamiden Abd El-Wahed Khalifa3,4

1Department of Mathematics, University of Management and Technology, Lahore, 54000, Pakistan
2Department of Mathematics, College of Science and Arts, Qassim University, Al-Rass, 51921, Saudi Arabia
3Department of Operations Research, Faculty of Graduate Studies for Statistical Research, Cairo University, Giza, 12613, Egypt
4Department of Mathematics, College of Science and Arts, Qassim University, Al-Badaya, 51951, Saudi Arabia
*Corresponding Author: Atiqe Ur Rahman. Email: aurkhb@gmail.com
Received: 23 March 2021; Accepted: 07 May 2021

Abstract: Hypersoft set is an extension of soft set as it further partitions each attribute into its corresponding attribute-valued set. This structure is more flexible and useful as it addresses the limitation of soft set for dealing with the scenarios having disjoint attribute-valued sets corresponding to distinct attributes. The main purpose of this study is to make the existing literature regarding neutrosophic parameterized soft set in line with the need of multi-attribute approximate function. Firstly, we conceptualize the neutrosophic parameterized hypersoft sets under the settings of fuzzy set, intuitionistic fuzzy set and neutrosophic set along with some of their elementary properties and set theoretic operations. Secondly, we propose decision-making-based algorithms with the help of these theories. Moreover, illustrative examples are presented which depict the structural validity for successful application to the problems involving vagueness and uncertainties. Lastly, the generalization of the proposed structure is discussed.

Keywords: Neutrosophic set; hypersoft set; neutrosophic hypersoft set; parameterized soft set; parameterized hypersoft set

1  Introduction

Fuzzy sets theory (FST) [1] and intuitionistic fuzzy set theory (IFST) [2] are considered apt mathematical modes to tackle many intricate problems involving various uncertainties, in different mathematical disciplines. The former one emphasizes on the degree of true belongingness of a certain object from the initial sample space whereas the later one accentuates on degree of true membership and degree of non-membership with condition of their dependency on each other. These theories depict some kind of inadequacy regarding the provision of due status to degree of indeterminacy. Such impediment is addressed with the introduction of neutrosophic set theory (NST) [3,4] which not only considers the due status of degree of indeterminacy but also waives off the condition of dependency. This theory is more flexible and appropriate to deal with uncertainty and vagueness. NST has attracted the keen concentration of many researchers [5–19] to further utilization in statistics, topological spaces as well as in the development of certain neutrosophic-like blended structures with other existing models for useful applications in decision making. Edalatpanah [20] studied a system of neutrosophic linear equations (SNLE) based on the embedding approach. He used (α,β,γ)-cut for transformation of SNLE into a crisp linear system. Kumar et al. [21] exhibited a novel linear programming approach for finding the neutrosophic shortest path problem (NSSPP) considering Gaussian valued neutrosophic number.

FST, IFST and NST have some kind of complexities which restrain them to solve problems involving uncertainty professionally. The reason for these hurdles is, possibly, the inadequacy of the parametrization tool. It demands a mathematical tool free of all such impediments to tackle such issues. This scantiness is resolved with the development of soft set theory (SST) [22] which is a new parameterized family of subsets of the universe of discourse. The researchers [23–34] studied and investigated some elementary properties, operations, laws and hybrids of SST with applications in decision making. The gluing concept of NST and SST, is studied in [35,36] to make the NST adequate with parameterized tool. In many real life situations, distinct attributes are further partitioned in disjoint attribute-valued sets but existing SST is insufficient for dealing with such kind of attribute-valued sets. Hypersoft set theory (HST) [37] is developed to make the SST in line with attribute-valued sets to tackle real life scenarios. HST is an extension of SST as it transforms the single argument approximate function into a multi-argument approximate function. Certain elementary properties, aggregation operations, laws, relations and functions of HST, are investigated by [38–40] for proper understanding and further utilization in different fields. The applications of HST in decision making is studied by [41–44] and the intermingling study of HST with complex sets, convex and concave sets is studied by [45,46]. Deli [47] characterized hybrid set structures under uncertainly parameterized hypersoft sets with theory and applications. Gayen et al. [48] analyzed some essential aspects of plithogenic hypersoft algebraic structures. They also investigated the notions and basic properties of plithogenic hypersoft subgroups, i.e., plithogenic fuzzy hypersoft subgroup, plithogenic intuitionistic fuzzy hypersoft subgroup, plithogenic neutrosophic hypersoft subgroup.

1.1 Motivation

In miscellany of real-life applications, the attributes are required to be further partitioned into attribute values for more vivid understanding. Hypersoft set as a generalization of soft set, accomplishes this limitation and accentuates the disjoint attribute-valued sets for distinct attributes. This generalization reveals that the hypersoft set with neutrosophic, intuitionistic, and fuzzy set theory will be very helpful to construct a connection between alternatives and attributes. It is interesting that the hypersoft theory can be applied on any decision-making problem without the limitations of the selection of the values by the decision-makers. This theory can successfully be applied to Multi-criteria decision making (MCDM), Multi-criteria group decision making (MCGDM), shortest path selection, employee selection, e-learning, graph theory, medical diagnosis, probability theory, topology, and many others. It is pertinent that the existing literature regarding soft set should be adequate with the existence and the consideration of attribute-valued sets, therefore, this study aims to develop novel theories of embedding structures of parameterized neutrosophic set and hypersoft set with the setting of fuzzy, intuitionistic fuzzy and neutrosophic sets through the extension of concept investigated in [49–54]. Moreover, decision-making based algorithms are proposed for each setting to solve a real life problem relating to the purchase of most suitable and appropriate product with the help of some essential operations of these presented theories.

1.2 Organization of Paper

The rest of the paper is systemized as:

images

2  Preliminaries

Here some basic terms are recalled from existing literature to support the proposed work. Throughout the paper, X, ℙ(X) and I will denote the universe of discourse, power set of X and closed unit interval respectively. In this work, algorithmic approaches are followed from decision making methods stated in [49–54].

Definition 2.1. [1]

A fuzzy set F defined as F={(â,AF(â))∣â∈X} such that AF:X→I where AF(â) denotes the belonging value of â∈F.

Definition 2.2. [2]

An intuitionistic fuzzy set Y defined as Y={(b^,<AY(b^),BY(b^)>)∣b^∈X} such that AY:X→I and BY:X→I, where AY(b^) and BY(b^) denote the belonging value and not-belonging value of b^∈Y with condition of 0≤AY(b^)+BY(b^)≤1.

Definition 2.3. [3]

A neutrosophic set Z defined as Z={(ĉ,<AZ(ĉ),BZ(ĉ),CZ(ĉ)>)∣ĉ∈X} such that AZ(ĉ),BZ(ĉ),CZ(ĉ):X→(-0,1+), where AZ(ĉ),BZ(ĉ) and CZ(ĉ) denote the degrees of membership, indeterminacy and non-membership of ĉ∈Z with condition of -0≤AZ(ĉ)+BZ(ĉ)+CZ(ĉ)≤3+.

Definition 2.4. [22]

A pair (FS,Λ) is called a soft set over X, where FS:Λ→ℙ(X) and Λ be a subset of a set of attributes E.

For more detail on soft set, see [23–32].

Definition 2.5. [37]

The pair (W,G) is called a hypersoft set over X, where G is the cartesian product of n disjoint sets G1,G2,G3,…,Gn having attribute values of n distinct attributes ĝ1,ĝ2,ĝ3,…,ĝn respectively and W:G→ℙ(X).

For more definitions and operations of hypersoft set, see [38–40].

3  Neutrosophic Parameterized Fuzzy Hypersoft Set (npfhs-Set) with Application

In this section, npfhs-set theory is conceptualized and a decision making application is discussed.

Definition 3.1. Let X={X1,X2,X3,…,Xn} be a collection of disjoint attribute-valued sets corresponding to n distinct attributes α1,α2,α3,…,αn, respectively. A npfhs-set ΨA over X is defined as ΨA={(<PA(g),QA(g),RA(g)>/g,ψA(g)):g∈G,ψA(g)∈F(X)} where

     i)  F(X) is a collection of all fuzzy sets over X

    ii)  G=X1×X2×X3×…×Xn

   iii)  A is a neutrosophic set over G with PA,QA,RA:G→I as membership function, indeterminacy function and nonmembership function of npfhs-set.

    iv)  ψA(g) is a fuzzy set for all g∈G with ψA:G→F(X) and is called approximate function of npfhs-set.

Note that collection of all npfhs-sets is represented by ΩNPFHS(X).

Definition 3.2. Let ΨA∈ΩNPFHS(X). If ψA(g)=ϕ,PA(g)=0,QA(g)=1,RA(g)=1 for all g∈G, then ΨA is called A-empty npfhs-set, denoted by ΨΦA. If A=ϕ, then A-empty npfhs-set is called an empty npfhs-set, denoted by ΨΦ.

Definition 3.3. Let ΨA∈ΩNPFHS(X). If ψA(g)=X,PA(g)=1,QA(g)=0,RA(g)=0 for all g∈G, then ΨA is called A-universal npfhs-set, denoted by ΨÃ. If A=G, then the A-universal npfhs-set is called universal npfhs-set, denoted by ΨG̃.

Example 3.1. Consider X={u1,u2,u3,u4,u5} and X={X1,X2,X3} with X1={x^11,x^12},

X2={x^21,x^22},X3={x^31}, then G=X1×X2×X3 G={(x^11,x^21,x^31),(x^11,x^22,x^31),(x^12,x^21,x^31),(x^12,x^22,x^31)}={g1,g2,g3,g4}.

Case 1.

If A1={<0.2,0.3,0.4>/g2,<0,1,1>/g3,<1,0,0>/g4} and

ψA1(g2)={0.4/u2,0.6/u4},ψA1(g3)=∅, and ψA1(g4)=X, thenΨA1={(<0.2,0.3,0.4>/g2,{0.4/u2,0.6/u4}),(<0,1,1>/g3,∅),(<1,0,0>/g4,X)}.

Case 2.

If A2={<0,1,1>/g2,<0,1,1>/g3},ψA2(g2)=∅ and ψA2(g3)=∅, then ΨA2=ΨΦA2.

Case 3.

If A3=∅ corresponding to all elements of G, then ΨA3=ΨΦ.

Case 4.

If A4={<1,0,0>/g1,<1,0,0>/g2},ψA4(g1)=X, and ψA4(g2)=X, then ΨA4=ΨA4̃.

Case 5.

If A5=X with respect to all elements of G, then ΨA5=ΨG̃.

Definition 3.4. Let ΨA1, ΨA2∈ΩNPFHS(X) then ΨA1 is an npfhs-subset of ΨA2, denoted by ΨA1⊆̃fΨA2 if

PA1(g)≤PA2(g),QA1(g)≥QA2(g),RA1(g)≥RA2(g) and ψA1(g)⊆fψA2(g)<transpanc/><d>:ltl:italic:gtl:for:ltl:/italic:gtl::ltl:italic:gtl:all:ltl:/italic:gtl:</d><transpanop/>g∈G.

Definition 3.5. Let ΨA1,ΨA2∈ΩNPFHS(X) then, ΨA1 and ΨA2 are npfhs-equal, represented as ΨA1=ΨA2, if and only if PA1(g)=PA2(g),QA1(g)=QA2(g),RA1(g)=RA2(g) and ψA1(g)=fψA2(g) for all g∈G.

Definition 3.6. Let ΨA∈ΩNPFHS(X) then, complement of ΨA (i.e., ΨAc̃) is an npfhs-set given as PAc̃(g)=1-PA(g),QAc̃(g)=1-QA(g),RAc̃(g)=1-RA(g) and ψAc̃(g)=X\fψA(g).

Proposition 3.1. Let ΨA∈ΩNPFHS(X) then,

1.    (ΨAc̃)c̃=ΨA.

2.    Ψϕc̃=ΨG̃.

Definition 3.7. Let ΨA1,ΨA2∈ΩNPFHS(X) then, union of ΨA1 and ΨA2, denoted by ΨA1∪̃fΨA2, is an npfhs-set defined by

     i)  PA1∪̃A2(g)=max{PA1(x),PA2(g)},

    ii)  QA1∪̃A2(g)=min{QA1(x),QA2(g)},

   iii)  RA1∪̃A2(g)=min{RA1(x),RA2(g)},

    iv)  ψA1∪̃A2(g)=ψA1(g)∪̃fψA2(g), for all g∈G.

Definition 3.8. Let ΨA1,ΨA2∈ΩNPFHS(X) then intersection of ΨA1 and ΨA2, denoted by ΨA1∩̃fΨA2, is an npfhs-set defined by

     i)  PA1∩̃A2(g)=min{PA1(x),PA2(g)},

    ii)  QA1∩̃A2(g)=max{QA1(x),QA2(g)},

   iii)  RA1∩̃A2(g)=max{RA1(x),RA2(g)},

    iv)  ψA1∩̃A2(g)=ψA1(g)∩̃fψA2(g), for all g∈G.

Remark 3.1. Let ΨA∈ΩNPFHS(X). If ΨA≠fΨG̃, then ΨA∪̃fΨAc̃≠fΨG̃ and ΨA∩̃fΨAc̃≠fΨΦ

Proposition 3.2. Let ΨA1,ΨA2∈ΩNPFHS(X) D. Morgan laws are valid

1.    (ΨA1∪̃fΨA2)c̃=ΨA1c̃∩̃fΨA2c̃.

2.    (ΨA1∩̃fΨA2)c̃=ΨA1c̃∪̃fΨA2c̃.

Proof. For all g∈G,

(1).Since(PA1∪̃A2)c̃(g)=1-PA1∪̃A2(g)=1-max{PA1(g),PA2(g)}=min{1-PA1(g),1-PA2(g)}=min{PA1c̃(g),PA2c̃(g)}=PA1∩̃A2c̃(g)

also (QA1∪̃A2)c̃(g)=1-QA1∪̃A2(g)=1-min{QA1(g),QA2(g)}=max{1-QA1(g),1-QA2(g)}=max{QA1c̃(g),QA2c̃(g)}=QA1∩̃A2c̃(g) and (RA1∪̃A2)c̃(g)=1-RA1∪̃A2(g)=1-min{RA1(g),RA2(g)}=max{1-RA1(g),1-RA2(g)}=max{RA1c̃(g),RA2c̃(g)}=RA1∩̃A2c̃(g) and (ψA1∪̃A2)c̃(g)=X\fψA1∪̃A2(g)=X\f(ψA1(g)∪̃fψA2(g))=(X\fψA1(g))∩̃f(X\fψA2(g))=ψA1c̃(g)∩̃fψA2c̃(g)=ψA1∩̃A2c̃(g). similarly (2) can be proved easily.

Proposition 3.3. Let ΨA1, ΨA2, ΨA3∈ΩNPFHS(X) then

1.    ΨA1∪̃f(ΨA2∩̃fΨA3)=(ΨA1∪̃fΨA2)∩̃f(ΨA1∪̃fΨA3).

2.    ΨA1∩̃f(ΨA2∪̃fΨA3)=(ΨA1∩̃fΨA2)∪̃f(ΨA1∩̃fΨA3).

Proof. For all g∈G,

(1).SincePA1∪̃(A2∩̃A3)(g)=max{PA1(g),PA2∩̃A3(g)}=max{PA1(g),min{PA2(g),PA3(g)}}=min{max{PA1(g),PA2(g)},max{PA1(g),PA3(g)}}=min{PA1∪̃A2(g),PA1∪̃A3(g)}=P(A1∪̃A2)∩̃(A1∪̃A3)(g) and QA1∪̃(A2∩̃A3)(g)=min{QA1(g),QA2∩̃A3(g)}=min{QA1(g),max{QA2(g),QA3(g)}}=max{min{QA1(g),QA2(g)},min{QA1(g),QA3(g)}}=max{QA1∪̃A2(g),QA1∪̃A3(g)}=Q(A1∪̃A2)∩̃(A1∪̃A3)(g) and RA1∪̃(A2∩̃A3)(g)=min{RA1(g),RA2∩̃A3(g)}=min{RA1(g),max{RA2(g),RA3(g)}}=max{min{RA1(g),RA2(g)},min{RA1(g),RA3(g)}}=max{RA1∪̃A2(g),RA1∪̃A3(g)}=R(A1∪̃A2)∩̃(A1∪̃A3)(g) and ψA1∪̃(A2∩̃A3)(g)=ψA1(g)∪fψA2∩̃A3(g)=ψA1(g)∪f(ψA2(g)∩fψA3(g))=(ψA1(g)∪fψA2(g))∩f(ψA1(g)∪fψA3(g))=ψA1∪̃A2(g)∩fψA1ŨA3(g)=ψ(A1∪̃A2)∩̃(A1∪̃A3)(g)

In the same way, (2) can be proved.

Definition 3.9. Let ΨA1,ΨA2∈ΩNPFHS(X) then OR-operation of ΨA1 and ΨA2, denoted by ΨA1⋓̃ΨA2, is an npfhs-set defined by

     i)  PA1⋓̃A2(g1,g2)=max{PA1(g1),PA2(g2)},

    ii)  QA1⋓̃A2(g1,g2)=min{QA1(g1),QA2(g2)},

   iii)  RA1⋓̃A2(g1,g2)=min{RA1(g1),RA2(g2)},

    iv)  ψA1⋓̃A2(g1,g2)=ψA1(g1)∪fψA2(g2), for all (g1,g2)∈A1×A2.

Definition 3.10. Let ΨA1,ΨA2∈ΩNPFHS(X) then AND-operation of ΨA1 and ΨA2, denoted by ΨA1⋒̃ΨA2, is an npfhs-set defined by

     i)  PA1⋒̃A2(g1,g2)=min{PA1(g1),PA2(g2)},

    ii)  QA1⋒̃A2(g1,g2)=max{QA1(g1),QA2(g2)},

   iii)  RA1⋒̃A2(g1,g2)=max{RA1(g1),RA2(g2)},

    iv)  ψA1⋒̃A2(g1,g2)=ψA1(g1)∩fψA2(g2), for all (g1,g2)∈A1×A2.

Proposition 3.4. Let ΨA1,ΨA2,ΨA3∈ΩNPFHS(X) then

1.    ΨA1⋒̃ΨΦ=ΨΦ.

2.    (ΨA1⋒̃ΨA2)⋒̃ΨA3=ΨA1⋒̃(ΨA2⋒̃ΨA3).

3.    (ΨA1⋓̃ΨA2)⋓̃ΨA3=ΨA1⋓̃(ΨA2⋓̃ΨA3).

3.1 Neutrosophic Decision Set of npfhs-Set

An algorithm is presented with the help of characterization of neutrosophic decision set on npfhs-set which based on decision making technique and is explained with example.

Definition 3.11. Let ΨA∈ΩNPFHS(X) then a neutrosophic decision set of ΨA (i.e., ΨAD) is represented as

ΨAD={<TAD(u),IAD(u),FAD(u)>/u:u∈X} where TAD, IAD, FAD:X→I and TAD(u)=1|X|∑v∈S(A)TA(v)ΓψA(v)(u)IAD(u)=1|X|∑v∈S(A)IA(v)ΓψA(v)(u)FAD(u)=1|X|∑v∈S(A)FA(v)ΓψA(v)(u) where |∙| denotes set cardinality with ΓψA(v)(u)={ψA(v);u∈ΓψA(v)0;u∉ΓψA(v)

Definition 3.12. If ΨA∈ΩNPFHS(X) with neutrosophic decision set ΨAD then reduced fuzzy set of ΨAD is a fuzzy set represented as ℝ(ΨAD)={ζΨAD(u)/u:u∈X} where ζΨAD:X→I with ζΨAD(u)=TAD(u)+IAD(u)-FAD(u)

Algorithm 3.1. Once ΨAD has been established, it may be indispensable to select the best single substitute from the options. Therefore, decision can be set up with the help of following algorithm.

Step 1 Determine A={<TA(g),IA(g),FA(g)>/g:TA(g),IA(g),FA(g)∈I,g∈G},

Step 2 Find ψA(g)

Step 3 Construct ΨA over X,

Step 4 Compute ΨAD,

Step 5 Choose the maximum of ζΨAD(u).

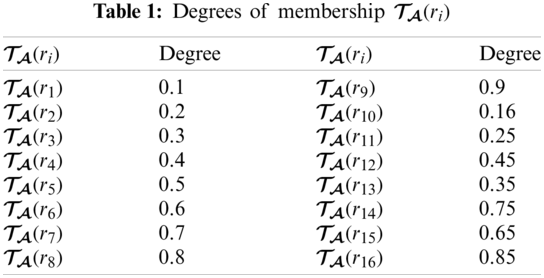
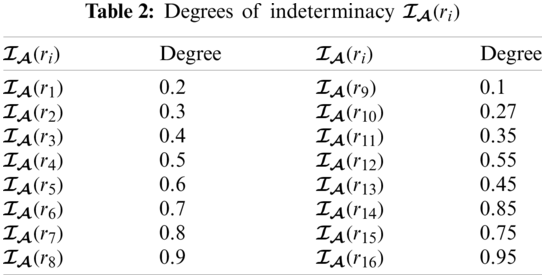
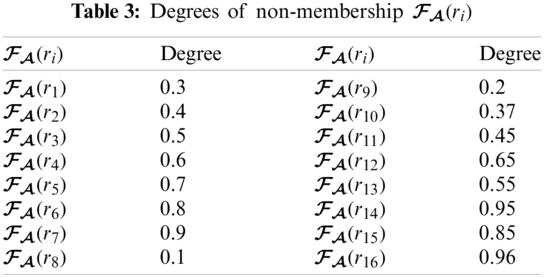
Example 3.2. Suppose that Mr. James Peter wants to buy a mobile tablet from a mobile market. There are eight kinds of tablets (options) which form the set of discourse X={T^1,T^2,T^3,T^4,T^5,T^6,T^7,T^8}. The best selection may be evaluated by observing the attributes, i.e., a1 = Storage (GB), a2 = Camera Resolution (mega pixels), a3 = Size (inches), a4 = RAM (GB), and a5 = Battery power (mAh). The attribute-valued sets corresponding to these attributes are:

A1={a11=64,a12=128}A2={a21=8,a22=16}A3={a31=10,a32=11}A4={a41=2,a42=4}A5={a51=5000} then ℝ=A1×A2×A3×A4×A5 ℝ={r1,r2,r3,r4,…,r16} where each ri,i=1,2,…,16, is a 5-tuples element.

Step 1:

From Tabs. 1–3, we can construct A as

A={<0.1,0.2,0.3>/r1,<0.2,0.3,0.4>/r2,<0.3,0.4,0.5>/r3,<0.4,0.5,0.6>/r4,<0.5,0.6,0.7>/r5,<0.6,0.7,0.8>/r6,<0.7,0.8,0.9>/r7,<0.8,0.9,0.1>/r8,<0.9,0.1,0.2>/r9,<0.16,0.27,0.37>/r10,<0.25,0.35,0.45>/r11,<0.45,0.55,0.65>/r12,<0.35,0.45,0.55>/r13,<0.75,0.85,0.95>/r14,<0.65,0.75,0.85>/r15,<0.85,0.95,0.96>/r16}.

Step 2:

Tab. 4 presents ψA(ri) corresponding to each element of G.

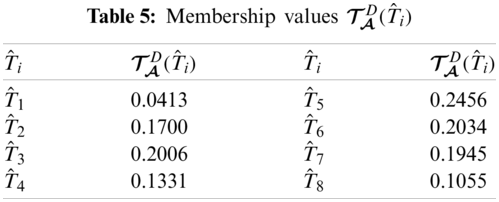
images

images

images

images

Step 3:

With the help of Step 1 and Step 2, we can construct ΨA as

ΨA={(<0.1,0.2,0.3>/r1,{0.2/T^1,0.3/T^2}),(<0.2,0.3,0.4>/r2,{0.1/T^1,0.5/T^2,0.1T^3}),(<0.3,0.4,0.5>/r3,{0.4/T^2,0.5/T^3,0.6/T^4}),(<0.4,0.5,0.6>/r4,{0.6/T^4,0.7/T^5,0.8/T^6}),(<0.5,0.6,0.7>/r5,{0.2/T^6,0.1/T^7,0.4/T^8}),(<0.6,0.7,0.8>/r6,{0.4/T^2,0.3/T^3,0.4/T^4}),(<0.7,0.8,0.9>/r7,{0.2/T^1,0.3/T^3,0.4/T^5}),(<0.8,0.9,0.1>/r8,{0.1/T^2,0.3/T^3,0.5/T^7}),(<0.9,0.1,0.2>/r9,{0.4/T^2,0.6/T^7,0.5/T^8}),(<0.16,0.27,0.37>/r10,{0.2/T^6,0.6/T^7,0.4/T^8}),(<0.25,0.35,0.45>/r11,{0.5/T^2,0.6/T^4,0.7/T^6}),(<0.45,0.55,0.65>/r12,{0.7/T^2,0.8/T^3,0.9/T^6}),(<0.35,0.45,0.55>/r13,{0.2/T^3,0.4/T^5,0.6/T^7}),(<0.75,0.85,0.95>/r14,{0.2/T^1,0.5/T^3,0.6/T^5}),(<0.65,0.75,0.85>/r15,{0.6/T^5,0.4/T^7,0.2/T^8}),(<0.85,0.95,0.96>/r16,{0.3/T^4,0.5/T^5,0.7/T^6})}

Step 4:

From Tabs. 5–8, we can construct ℝ(ΨAD) as

ℝ(ΨAD)={0.0325/T^1,0.1412/T^2,0.1968/T^3,0.1052/T^4,0.2112/T^5,0.1675/T^6,0.2158/T^7,0.0867/T^8}

The graphical representation of this decision system is presented in Fig. 1.

Step 5:

Since maximum of ζΨAD(T^i) is 0.2158 so the tablet T^7 is selected.

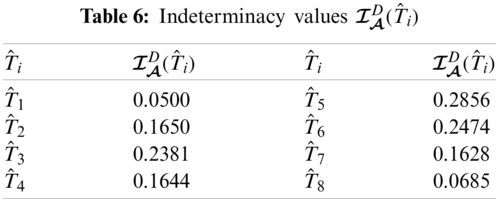
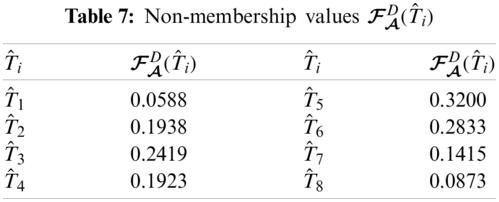
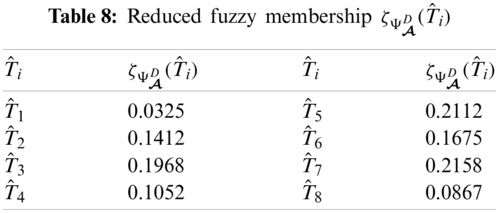
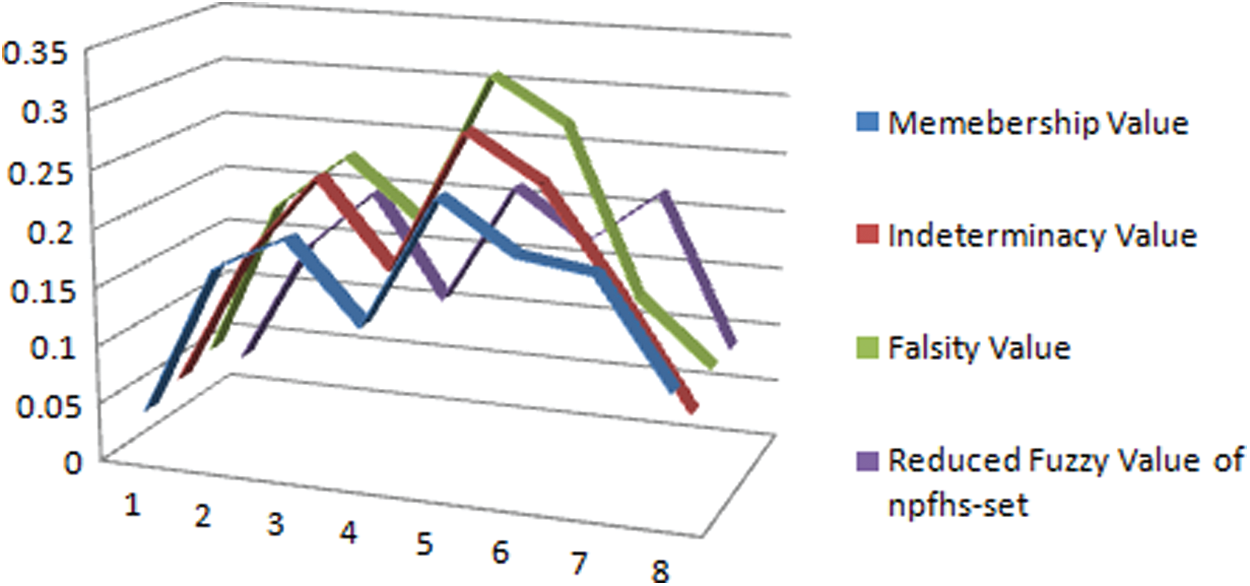
images

images

images

images

images

Figure 1: Neutrosophic decision system on npfhs-set

4  Neutrosophic Parameterized Intuitionistic Fuzzy Hypersoft Set (npifhs-set) with Application

In this section, npifhs-set theory is developed and decision making based application is presented.

Definition 4.1. Let Y={Y1,Y2,Y3,…,Yn} be a collection of disjoint attribute-valued sets corresponding to n distinct attributes α1,α2,α3,…,αn, respectively. A npifhs-set ΨB over X is defined as ΨB={(<LB(g),MB(g),NB(g)>/g,ψB(g)):g∈G,ψA(g)∈IF(X)} where

     i)  IF(U) is a collection of all intuitionistic fuzzy sets over X

    ii)  G=Y1×Y2×Y3×…×Yn

   iii)  B is a neutrosophic set over G with LB,MB,NB:G→I as membership function, indeterminacy function and nonmembership function of npifhs-set.

    iv)  ψB(g) is a fuzzy set for all g∈G with ψB:G→IF(X) and is called approximate function of npifhs-set.

Note that collection of all npifhs-sets is represented by ΩNPIFHS(X).

Definition 4.2. Let ΨB∈ΩNPIFHS(X). If ψB(g)=∅,LB(g)=0,MB(g)=1,NB(g)=1 for all g∈G, then ΨB is called B-empty npifhs-set, denoted by ΨΦB. If B=∅, then B-empty npifhs-set is called an empty npifhs-set, denoted by ΨΦ.

Definition 4.3. Let ΨB∈ΩNPIFHS(X). If ψB(g)=X,LB(g)=1,MB(g)=0,NB(g)=0 for all g∈G, then ΨB is called B-universal npifhs-set, denoted by ΨB̃. If B=G, then the B-universal npifhs-set is called universal npifhs-set, denoted by ΨG̃.

Example 4.1. Consider X={u1,u2,u3,u4,u5} and Y={Y1,Y2,Y3} with

Y1={ŷ11,ŷ12},Y2={ŷ21,ŷ22},Y3={ŷ31}, thenG=Y1×Y2×Y3G={(ŷ11,ŷ21,ŷ31),(ŷ11,ŷ22,ŷ31),(ŷ12,ŷ21,ŷ31),(ŷ12,ŷ22,ŷ31)}={g1,g2,g3,g4}.

Case 1.

If B1={<0.2,0.3,0.4>/g2,<0,1,1>/g3,<1,0,0>/g4} and

ψB1(g2)={<0.2,0.4>/u2,<0.3,0.5>/u4},ψB1(g3)=ϕ, and ψB1(g4)=X, thenΨB1={(<0.2,0.3,0.4>/g2,{<0.2,0.4>/u2,<0.3,0.5>/u4}),(<0,1,1>/g3,ϕ),(<1,0,0>/g4,X)}.

Case 2.

If B2={<0,1,1>/g2,<0,1,1>/g3},ψB2(g2)=ϕ and ψB2(g3)=ϕ, then ΨB2=ΨΦB2.

Case 3.

If B3=ϕ corresponding to all elements of G, then ΨB3=ΨΦ.

Case 4.

If B4={<1,0,0>/g1,<1,0,0>/g2},ψB4(g1)=X, and ψB4(g2)=X, then ΨB4=ΨB4̃.

Case 5.

If B5=X with respect to all elements of G, then ΨB5=ΨG̃.

Definition 4.4. Let ΨB1, ΨB2∈ΩNPIFHS(X) then ΨB1 is an npifhs-subset of ΨB2, denoted by ΨB1⊆̃ifΨB2 if

LB1(g)≤LB2(g),MB1(g)≥MB2(g),NB1(g)≥NB2(g) and ψB1(g)⊆ifψB2(g) for all g∈G.

Definition 4.5. Let ΨB1,ΨB2∈ΩNPIFHS(X) then, ΨB1 and ΨB2 are npifhs-equal, represented as ΨB1=ΨB2, if and only if LB1(g)=LB2(g),MB1(g)=MB2(g),NB1(g)=NB2(g) and ψB1(g)=ψB2(g) for all g∈G.

Definition 4.6. Let ΨB∈ΩNPIFHS(X) then, complement of ΨB (i.e., ΨBc̃) is an npifhs-set given as PBc̃(g)=1-LB(g),QBc̃(g)=1-MB(g),RBc̃(g)=1-NB(g) and ψBc̃(g)=X\ψB(g)

Proposition 4.1. Let ΨB∈ΩNPIFHS(X) then,

1.    (ΨBc̃)c̃=ΨB.

2.    Ψϕc̃=ΨG̃.

Definition 4.7. Let ΨB1,ΨB2∈ΩNPIFHS(X) then, union of ΨB1 and ΨB2, denoted by ΨB1∪̃ifΨB2, is an npifhs-set defined by

     i)  LB1∪̃B2(g)=max{LB1(x),LB2(g)},

    ii)  MB1∪̃B2(g)=min{MB1(x),MB2(g)},

   iii)  NB1∪̃B2(g)=min{NB1(x),NB2(g)},

    iv)  ψB1∪̃B2(g)=ψB1(g)∪̃ifψB2(g), for all g∈G.

Definition 4.8. Let ΨB1,ΨB2∈ΩNPIFHS(X) then intersection of ΨB1 and ΨB2, denoted by ΨB1∩̃ifΨB2, is an npifhs-set defined by

     i)  LB1∩̃B2(g)=min{LB1(x),LB2(g)},

    ii)  MB1∩̃B2(g)=max{MB1(x),MB2(g)},

   iii)  NB1∩̃B2(g)=max{NB1(x),NB2(g)},

    iv)  ψB1∩̃B2(g)=ψB1(g)∩̃ifψB2(g), for all g∈G.

Remark 4.1. Let ΨB∈ΩNPIFHS(X). If ΨB≠ifΨG̃, then ΨB∪̃ifΨBc̃≠ifΨG̃ and ΨB∩̃if ΨBc̃≠ifΨΦ

Proposition 4.2. Let ΨB1,ΨB2∈ΩNPIFHS(X) then following D. Morgan laws are valid:

1.    (ΨB1∪̃ifΨB2)c̃=ΨB1c̃∩̃ifΨB2c̃.

2.    (ΨB1∩̃ifΨB2)c̃=ΨB1c̃∪̃ifΨB2c̃.

Proof. For all g∈G, (1).Since (LB1∪̃B2)c̃(g)=1-LB1∪̃B2(g)=1-max{LB1(g),LB2(g)}=min{1-LB1(g),1-LB2(g)}=min{PB1c̃(g),PB2c̃(g)}=PB1∩̃B2c̃(g) also (MB1∪̃B2)c̃(g)=1-MB1∪̃B2(g)=1-min{MB1(g),MB2(g)}=max{1-MB1(g),1-MB2(g)}=max{QB1c̃(g),QB2c̃(g)}=QB1∩̃B2c̃(g) and (NB1∪̃B2)c̃(g)=1-NB1∪̃B2(g)=1-min{NB1(g),NB2(g)}=max{1-NB1(g),1-NB2(g)}=max{RB1c̃(g),RB2c̃(g)}=RB1∩̃B2c̃(g) and (ψB1∪̃B2)c̃(g)=X\ifψB1∪̃B2(g)=X\if(ψB1(g)∪̃ifψB2(g))=(X\ifψB1(g))∩̃if(X\ifψB2(g))=ψB1c̃(g)∩̃ifψB2c̃(g)=ψB1∩̃B2c̃(g). similarly (2) can be proved easily.

Proposition 4.3. Let ΨB1,ΨB2,ΨB3∈ΩNPIFHS(X) then

1.    ΨB1∪̃if(ΨB2∩̃ifΨB3)=(ΨB1∪̃ifΨB2)∩̃if(ΨB1∪̃ifΨB3).

2.    ΨB1∩̃if(ΨB2∪̃ifΨB3)=(ΨB1∩̃ifΨB2)∪̃if(ΨB1∩̃ifΨB3).

Proof. For all g∈G,

(1).Since LB1∪̃(B2∩̃B3)(g)=max{LB1(g),LB2∩̃B3(g)}=max{LB1(g),min{LB2(g),LB3(g)}}=min{max{LB1(g),LB2(g)},max{LB1(g),LB3(g)}}=min{LB1∪̃B2(g),LB1∪̃B3(g)}=L(B1∪̃B2)∩̃(B1∪̃B3)(g) and MB1∪̃(B2∩̃B3)(g)=min{MB1(g),MB2∩̃B3(g)}=min{MB1(g),max{MB2(g),MB3(g)}}=max{min{MB1(g),MB2(g)},min{MB1(g),MB3(g)}}=max{MB1∪̃B2(g),MB1∪̃B3(g)}=M(B1∪̃B2)∩̃(B1∪̃B3)(g) and NB1∪̃(B2∩̃B3)(g)=min{NB1(g),NB2∩̃B3(g)}=min{NB1(g),max{NB2(g),NB3(g)}}=max{min{NB1(g),NB2(g)},min{NB1(g),NB3(g)}}=max{NB1∪̃B2(g),NB1∪̃B3(g)}=N(B1∪̃B2)∩̃(B1∪̃B3)(g) and ψB1∪̃(B2∩̃B3)(g)=ψB1(g)∪̃ifψB2∩̃B3(g)=ψB1(g)∪̃if(ψB2(g)∩̃ifψB3(g))=(ψB1(g)∪̃ifψB2(g))∩̃if(ψB1(g)∪̃ifψB3(g))=ψB1∪̃B2(g)∩̃ifψB1ŨB3(g)=ψ(B1∪̃B2)∩̃(B1∪̃B3)(g)

In the same way, (2) can be proved.

Definition 4.9. Let ΨB1,ΨB2∈ΩNPIFHS(X) then OR-operation of ΨB1 and ΨB2, denoted by ΨB1⊻̃ΨB2, is an npifhs-set defined by

     i)  LB1⊻̃B2(g1,g2)=max{LB1(g1),LB2(g2)},

    ii)  MB1⊻̃B2(g1,g2)=min{MB1(g1),MB2(g2)},

   iii)  NB1⊻̃B2(g1,g2)=min{NB1(g1),NB2(g2)},

    iv)  ψB1⊻̃B2(g1,g2)=ψB1(g1)∪ψB2(g2), for all (g1,g2)∈B1×B2.

Definition 4.10. Let ΨB1,ΨB2∈ΩNPIFHS(X) then AND-operation of ΨB1 and ΨB2, denoted by ΨB1⊼̃ΨB2, is an npifhs-set defined by

     i)  LB1⊼̃B2(g1,g2)=min{LB1(g1),LB2(g2)},

    ii)  MB1⊼̃B2(g1,g2)=max{MB1(g1),MB2(g2)},

   iii)  NB1⊼̃B2(g1,g2)=max{NB1(g1),NB2(g2)},

    iv)  ψB1⊼̃B2(g1,g2)=ψB1(g1)∩ψB2(g2), for all (g1,g2)∈B1×B2.

Proposition 4.4. Let ΨB1,ΨB2,ΨB3∈ΩNPIFHS(X) then

1.    ΨB1⊼̃ΨΦ=ΨΦ.

2.    (ΨB1⊼̃ΨB2)⊼̃ΨB3=ΨB1⊼̃(ΨB2⊼̃ΨB3).

3.    (ΨB1⊻̃ΨB2)⊻̃ΨB3=ΨB1⊻̃(ΨB2⊻̃ΨB3).

4.1 Neutrosophic Decision Set of npifhs-Set

Here an algorithm is presented with the help of characterization of neutrosophic decision set on npifhs-set which based on decision making technique and is explained with example.

Definition 4.11. Let ΨB∈ΩNPIFHS(X) then a neutrosophic decision set of ΨB (i.e., ΨBD) is represented as

ΨBD={<TBD(u),IBD(u),FBD(u)>/u:u∈X} where TBD,IBD,FBD:X→I and TBD(u)=1|X|∑v∈S(B)TB(v)ΓψB(v)(u)IBD(u)=1|X|∑v∈S(B)IB(v)ΓψB(v)(u)FBD(u)=1|X|∑v∈S(B)FB(v)ΓψB(v)(u) where |∙| denotes set cardinality with ΓψB(v)(u)={|TψB(u)-FψB(u)|;u∈ΓψB(v)0;u∉ΓψB(v)

Definition 4.12. If ΨB∈ΩNPIFHS(X) with neutrosophic decision set ΨBD then reduced fuzzy set of ΨBD is a fuzzy set represented as ℝ(ΨBD)={ζΨBD(u)/u:u∈X} where ζΨBD:X→I with ζΨBD(u)=TBD(u)+IBD(u)-FBD(u)

4.2 Proposed Algorithm

Once ΨBD has been established, it may be indispensable to select the best single substitute from the options. Therefore, decision can be set up with the help of following algorithm:

Step 1 Determine B={<TB(g),IB(g),FB(g)>/g:TB(g),IB(g),FB(g)∈I,g∈G},

Step 2 Find ψB(g)

Step 3 Construct ΨB over X,

Step 4 Compute ΨBD,

Step 5 Choose the maximum of ζΨBD(u).

Example 4.2. Suppose that Mrs. Andrew wants to buy a washing machine from market. There are eight kinds of washing machines (options) which form the set of discourse X={Ŵ1,Ŵ2,Ŵ3,Ŵ4,Ŵ5,Ŵ6,Ŵ7,Ŵ8}. The best selection may be evaluated by observing the attributes i.e., b1 = Company, b2 = Power in Watts, b3 = Voltage, b4 = Capacity in kg, and b5 = Color. The attribute-valued sets corresponding to these attributes are:

B1={b11=National,b12=Hier}B2={b21=400,b22=500}B3={b31=220,b32=240}B4={b41=7,b42=10}B5={b51=White} then ℚ=B1×B2×B3×B4×B5 ℚ={q1,q2,q3,q4,…,q16} where each qi,i=1,2,…,16, is a 5-tuples element.

Step 1:

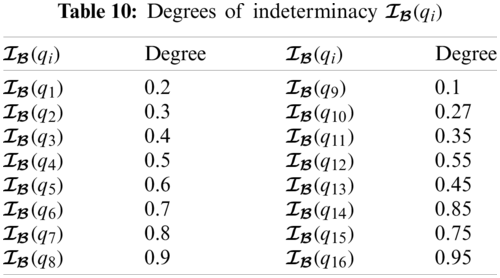
From Tabs. 9–11, we can construct B as

B={<0.1,0.2,0.3>/q1,<0.2,0.3,0.4>/q2,<0.3,0.4,0.5>/q3,<0.4,0.5,0.6>/q4,<0.5,0.6,0.7>/q5,<0.6,0.7,0.8>/q6,<0.7,0.8,0.9>/q7,<0.8,0.9,0.1>/q8,<0.9,0.1,0.2>/q9,<0.16,0.27,0.37>/q10,<0.25,0.35,0.45>/q11,<0.45,0.55,0.65>/q12,<0.35,0.45,0.55>/q13,<0.75,0.85,0.95>/q14,<0.65,0.75,0.85>/q15,<0.85,0.95,0.96>/q16}

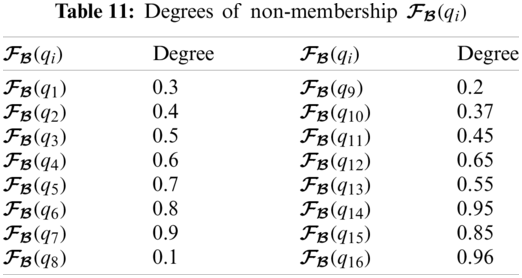
images

images

images

Step 2:

Tab. 12 presents ψB(qi) corresponding to each element of G.

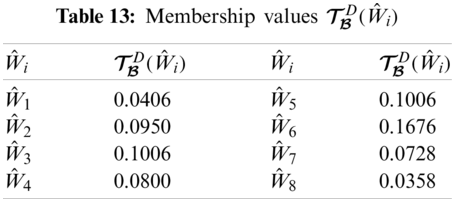
images

Step 3: With the help of Step 1 and Step 2, we can construct ΨB as performed in step of Section 3.

Step 4:

From Tabs. 13–16, we can construct ℝ(ΨBD) as

ℝ(ΨBD)={0.0331/Ŵ1,0.1100/Ŵ2,0.1019/Ŵ3,0.0659/Ŵ4,0.0855/Ŵ5,0.1394/Ŵ6,0.0690/Ŵ7,0.0296/Ŵ8}

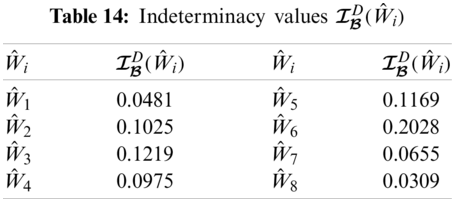
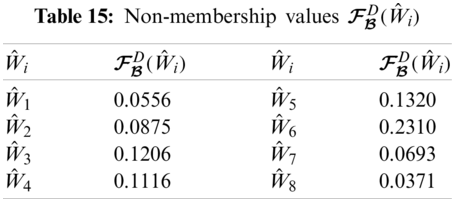
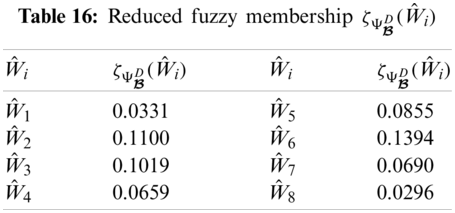
images

images

images

images

The graphical representation of this decision system is presented in Fig. 2.

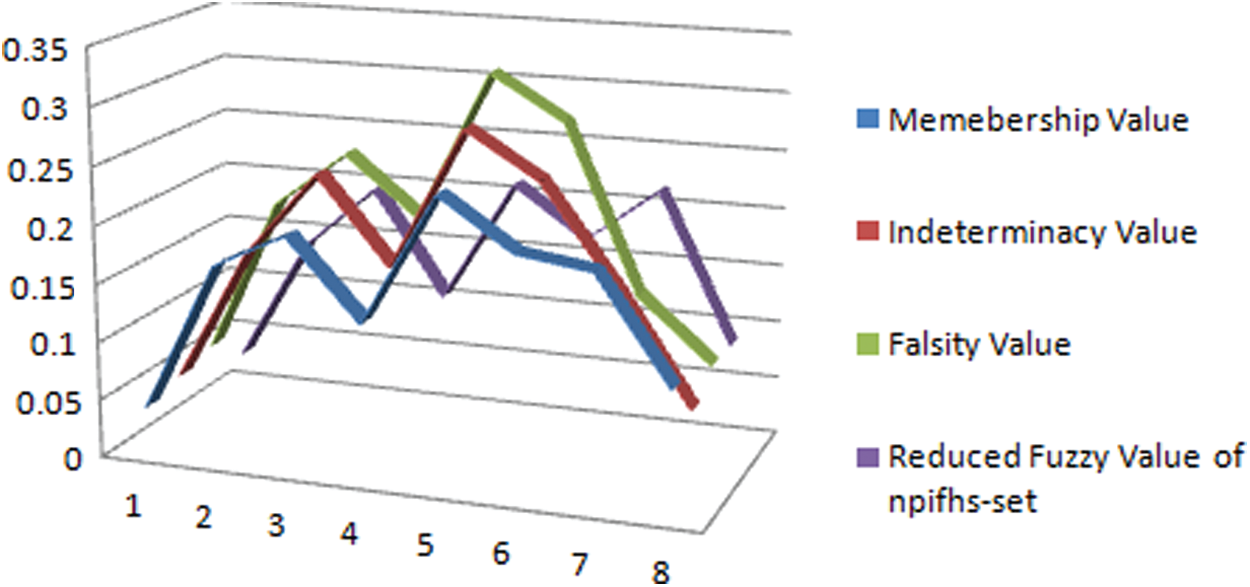
images

Figure 2: Neutrosophic decision system on npifhs-set

Step 5:

Since maximum of ζΨBD(Ŵi) is 0.5313 so the washing machine Ŵ3 is selected.

5  Neutrosophic Parameterized Neutrosophic Hypersoft Set (npnhs-Set) with Application

In this section, neutrosophic parameterized hypersoft set is conceptualized and some of its fundamentals are discussed.

Definition 5.1. Let Z={Z1,Z2,Z3,…,Zn} be a collection of disjoint attribute-valued sets corresponding to n distinct attributes α1,α2,α3,…,αn, respectively. A npnhs-set ΨD over X is defined as ΨD={(<AD(g),BD(g),CD(g)>/g,ψD(g)):g∈G,ψD(g)∈N(X)} where

     i)  N(X) is a collection of all neutrosophic sets over X

    ii)  G=Z1×Z2×Z3×…×Zn

   iii)  D is a neutrosophic set over G with AD,BD,CD:G→I as membership function, indeterminacy function and nonmembership function of npnhs-set.

    iv)  ψD(g) is a neutrosophic set for all g∈G with ψD:G→N(X) and is called approximate function of npnhs-set.

Note that collection of all npnhs-sets is represented by ΩNPNHS(X).

Definition 5.2. Let ΨD∈ΩNPNHS(X). If ψD(g)=∅,AD(g)=0,BD(g)=1,CD(g)=1 for all g∈G, then ΨD is called D-empty npnhs-set, denoted by ΨΦD. If D=∅, then D-empty npnhs-set is called an empty npnhs-set, denoted by ΨΦ.

Definition 5.3. Let ΨD∈ΩNPNHS(X). If ψD(g)=X,AD(g)=1,BD(g)=0,CD(g)=0 for all g∈G, then ΨD is called D-universal npnhs-set, denoted by ΨD̃. If D=G, then the D-universal npnhs-set is called universal npnhs-set, denoted by ΨG̃.

Example 5.1. Consider X={u1,u2,u3,u4,u5} and Z={Z1,Z2,Z3} with Z1={ẑ11,ẑ12}, Z2={ẑ21,ẑ22},Z3={ẑ31}, then

G=Z1×Z2×Z3G={(ẑ11,ẑ21,ẑ31),(ẑ11,ẑ22,ẑ31),(ẑ12,ẑ21,ẑ31),(ẑ12,ẑ22,ẑ31)}={g1,g2,g3,g4}.

Case 1.

If D1={<0.2,0.3,0.4>/g2,<0,1,1>/g3,<1,0,0>/g4} and

ψD1(g2)={<0.2,0.4,0.6>/u2,<0.3,0.5,0.7>/u4},ψD1(g3)=∅, and ψD1(g4)=X, thenΨD1={(<0.2,0.3,0.4>/g2,{<0.2,0.4,0.6>/u2,0.3,0.5,0.7>/u4}),(<0,1,1>/g3,∅),(<1,0,0>/g4,X)}.

Case 2.

If D2={<0,1,1>/g2,<0,1,1>/g3},ψD2(g2)=∅ and ψD2(g3)=∅, then ΨD2=ΨΦD2.

Case 3.

If D3=∅ corresponding to all elements of G, then ΨD3=ΨΦ.

Case 4.

If D4={<1,0,0>/g1,<1,0,0>/g2},ψD4(g1)=X, and ψD4(g2)=X, then ΨD4=ΨD4̃.

Case 5.

If D5=X with respect to all elements of G, then ΨD5=ΨG̃.

Definition 5.4. Let ΨD1, ΨD2∈ΩNPNHS(X) then ΨD1 is an npnhs-subset of ΨD2, denoted by ΨD1⊆̃ΨD2 if AD1(g)≤AD2(g),BD1(g)≥BD2(g),CD1(g)≥CD2(g) and ψD1(g)⊆nψD2(g) for all g∈G.

Proposition 5.1. Let ΨD1,ΨD2,ΨD3∈ΩNPNHS(X) then

1.    ΨD1⊆̃ΨG̃.

2.    ΨΦ⊆̃ΨD1.

3.    ΨD1⊆̃ΨD1.

4.    if ΨD1⊆̃ΨD2 and ΨD2⊆̃ΨD3 then ΨD1⊆̃ΨD3.

Definition 5.5. Let ΨD1,ΨD2∈ΩNPNHS(X) then, ΨD1 and ΨD2 are npnhs-equal, represented as ΨD1=ΨD2, if and only if AD1(g)=AD2(g),BD1(g)=BD2(g),CD1(g)=CD2(g) and ψD1(g)=nψD2(g) for all g∈G.

Proposition 5.2. Let ΨD1,ΨD2,ΨD3∈ΩNPNHS(X) then,

1.    if ΨD1=ΨD2 and ΨD2=ΨD3 then ΨD1=ΨD3.

2.    if ΨD1⊆̃ΨD2 and ΨD2⊆̃ΨD1⇔ΨD1=ΨD2.

Definition 5.6. Let ΨD∈ΩNPNHS(X) then, complement of ΨD (i.e., ΨDc̃) is a npnhs-set given as PDc̃(g)=1-AD(g),QDc̃(g)=1-BD(g),RDc̃(g)=1-CD(g) and ψDc̃(g)=X\nψD(g).

Proposition 5.3. Let ΨD∈ΩNPNHS(X) then,

1.    (ΨDc̃)c̃=ΨD.

2.    Ψϕc̃=ΨG̃.

Definition 5.7. Let ΨD1,ΨD2∈ΩNPNHS(X) then, union of ΨD1 and ΨD2, denoted by ΨD1∪̃ΨD2, is an npnhs-set defined by

     i)  AD1∪̃D2(g)=max{AD1(x),AD2(g)},

    ii)  BD1∪̃D2(g)=min{BD1(x),BD2(g)},

   iii)  CD1∪̃D2(g)=min{CD1(x),CD2(g)},

    iv)  ψD1∪̃D2(g)=ψD1(g)∪nψD2(g), for all g∈G.

Proposition 5.4. Let ΨD1,ΨD2,ΨD3∈ΩNPNHS(X) then,

1.    ΨD1∪̃ΨD1=ΨD1,

2.    ΨD1∪̃ΨΦ=ΨD1,

3.    ΨD1∪̃ΨG̃=ΨG̃,

4.    ΨD1∪̃ΨD2=ΨD2∪̃ΨD1,

5.    (ΨD1∪̃ΨD2)∪̃ΨD3=ΨD1∪̃(ΨD2∪̃ΨD3).

Definition 5.8. Let ΨD1,ΨD2∈ΩNPNHS(X) then intersection of ΨD1 and ΨD2, denoted by ΨD1∩̃ΨD2, is an npnhs-set defined by

     i)  AD1∩̃D2(g)=min{AD1(x),AD2(g)},

    ii)  BD1∩̃D2(g)=max{BD1(x),BD2(g)},

   iii)  CD1∩̃D2(g)=max{CD1(x),CD2(g)},

    iv)  ψD1∩̃D2(g)=ψD1(g)∩nψD2(g), for all g∈G.

Proposition 5.5. Let ΨD1,ΨD2,ΨD3∈ΩNPNHS(X) then

1.    ΨD1∩̃ΨD1=ΨD1.

2.    ΨD1∩̃ΨΦ=ΨΦ.

3.    ΨD1∩̃ΨG̃=ΨD1̃.

4.    ΨD1∩̃ΨD2=ΨD2∩̃ΨD1.

5.    (ΨD1∩̃ΨD2)∩̃ΨΨD3=ΨD1∩̃(ΨD2∩̃ΨΨD3).

Note: It is pertinent to mention here that Propositions 5.1, 5.2, 5.4 and 5.5 are also valid for elements of ΩNPFHS(X) and ΩNPIFHS(X).

Remark 5.1. Let ΨD∈ΩNPNHS(X). If ΨD≠ΨG̃, then ΨD∪̃ΨDc̃≠ΨG̃ and ΨD∩̃ΨDc̃≠ΨΦ

Proposition 5.6. Let ΨD1,ΨD2∈ΩNPNHS(X) then following D. Morgan laws are valid:

1.    (ΨD1∪̃ΨD2)c̃=ΨD1c̃∩̃ΨD2c̃.

2.    (ΨD1∩̃ΨD2)c̃=ΨD1c̃∪̃ΨD2c̃.

Proof. For all g∈G, (1).Since (AD1∪̃D2)c̃(g)=1-AD1∪̃D2(g)=1-max{AD1(g),AD2(g)}=min{1-AD1(g),1-AD2(g)}=min{PD1c̃(g),PD2c̃(g)}=PD1∩̃D2c̃(g) also (BD1∪̃D2)c̃(g)=1-BD1∪̃D2(g)=1-min{BD1(g),BD2(g)}=max{1-BD1(g),1-BD2(g)}=max{QD1c̃(g),QD2c̃(g)}=QD1∩̃D2c̃(g) and (CD1∪̃D2)c̃(g)=1-CD1∪̃D2(g)=1-min{CD1(g),CD2(g)}=max{1-CD1(g),1-CD2(g)}=max{RD1c̃(g),RD2c̃(g)}=RD1∩̃D2c̃(g) and (ψD1∪̃D2)c̃(g)=X\nψD1∪̃D2(g)=X\n(ψD1(g)∪nψD2(g))=(X\nψD1(g))∩n(X\nψD2(g))=ψD1c̃(g)∩ñψD2c̃(g)=ψD1∩̃D2c̃(g). similarly (2) can be proved easily.

Proposition 5.7. Let ΨD1,ΨD2,ΨD3∈ΩNPNHS(X) then

1.    ΨD1∪̃(ΨD2∩̃ΨD3)=(ΨD1∪̃ΨD2)∩̃(ΨD1∪̃ΨD3).

2.    ΨD1∩̃(ΨD2∪̃ΨD3)=(ΨD1∩̃ΨD2)∪̃(ΨD1∩̃ΨD3).

Proof. For all g∈G,

(1).Since AD1∪̃(D2∩̃D3)(g)=max{AD1(g),AD2∩̃D3(g)}=max{AD1(g),min{AD2(g),AD3(g)}}=min{max{AD1(g),AD2(g)},max{AD1(g),AD3(g)}}=min{AD1∪̃D2(g),AD1∪̃D3(g)}=A(D1∪̃D2)∩̃(D1∪̃D3)(g) and BD1∪̃(D2∩̃D3)(g)=min{BD1(g),BD2∩̃D3(g)}=min{BD1(g),max{BD2(g),BD3(g)}}=max{min{BD1(g),BD2(g)},min{BD1(g),BD3(g)}}=max{BD1∪̃D2(g),BD1∪̃D3(g)}=B(D1∪̃D2)∩̃(D1∪̃D3)(g) and CD1∪̃(D2∩̃D3)(g)=min{CD1(g),CD2∩̃D3(g)}=min{CD1(g),max{CD2(g),CD3(g)}}=max{min{CD1(g),CD2(g)},min{CD1(g),CD3(g)}}=max{CD1∪̃D2(g),CD1∪̃D3(g)}=C(D1∪̃D2)∩̃(D1∪̃D3)(g) and ψD1∪̃n(D2∪̃nD3)(g)=ψD1(g)∪nψD2∩̃nD3(g)=ψD1(g)∪n(ψD2(g)∩nψD3(g))=(ψD1(g)∪nψD2(g))∩n(ψD1(g)∪nψD3(g))=ψD1∪̃D2(g)∩nψD1∪̃D3(g)=ψ(D1∪̃D2)∩̃(D1∪̃D3)(g)

In the same way, (2) can be proved.

Definition 5.9. Let ΨD1,ΨD2∈ΩNPNHS(X) then OR-operation of ΨD1 and ΨD2, denoted by ΨD1⊕̃ΨD2, is an npnhs-set defined by

     i)  AD1⊕̃D2(g1,g2)=max{AD1(g1),AD2(g2)},

    ii)  BD1⊕̃D2(g1,g2)=min{BD1(g1),BD2(g2)},

   iii)  CD1⊕̃D2(g1,g2)=min{CD1(g1),CD2(g2)},

    iv)  ψD1⊕̃D2(g1,g2)=ψD1(g1)∪ψD2(g2), for all (g1,g2)∈D1×D2.

Definition 5.10. Let ΨD1,ΨD2∈ΩNPNHS(X) then AND-operation of ΨD1 and ΨD2, denoted by ΨD1⊗̃ΨD2, is an npnhs-set defined by

     i)  AD1⊗̃D2(g1,g2)=min{AD1(g1),AD2(g2)},

    ii)  BD1⊗̃D2(g1,g2)=max{BD1(g1),BD2(g2)},

   iii)  CD1⊗̃D2(g1,g2)=max{CD1(g1),CD2(g2)},

    iv)  ψD1⊗̃D2(g1,g2)=ψD1(g1)∩ψD2(g2), for all (g1,g2)∈D1×D2.

Proposition 5.8. Let ΨD1,ΨD2,ΨD3∈ΩNPNHS(X) then

1.    ΨD1⊗̃ΨΦ=ΨΦ.

2.    (ΨD1⊗̃ΨD2)⊗̃ΨD3=ΨD1⊗̃(ΨD2⊗̃ΨD3).

3.    (ΨD1⊕̃ΨD2)⊕̃ΨD3=ΨD1⊕̃(ΨD2⊕̃ΨD3).

5.1 Neutrosophic Decision Set of npnhs-Set

Here an algorithm is presented with the help of characterization of neutrosophic decision set on npnhs-set which based on decision making technique and is explained with example.

Definition 5.11. Let ΨD∈ΩNPNHS(X) then a neutrosophic decision set of ΨD (i.e., ΨDD) is represented as

ΨDD={<TDD(u),IDD(u),FDD(u)>/u:u∈X} where TDD,IDD,FDD:X→I and TDD(u)=1|X|∑v∈S(D)TD(v)ΓψD(v)(u)IDD(u)=1|X|∑v∈S(D)ID(v)ΓψD(v)(u)FDD(u)=1|X|∑v∈S(D)FD(v)ΓψD(v)(u) where |∙| denotes set cardinality with ΓψD(v)(u)={|TψD(u)+IψD(u)-FψD(u)|;u∈ΓψD(v)0;u∉ΓψD(v)

Definition 5.12. If ΨD∈ΩNPNHS(X) with neutrosophic decision set ΨDD then reduced fuzzy set of ΨDD is a fuzzy set represented as ℝ(ΨDD)={ζΨDD(u)/u:u∈X} where ζΨDD:X→I with ζΨDD(u)=TDD(u)+IDD(u)-FDD(u).

5.2 Proposed Algorithm

Once ΨDD has been established, it may be indispensable to select the best single substitute from the options. Therefore, decision can be set up with the help of following algorithm:

Step 1 Determine D={<TD(g),ID(g),FD(g)>/g:TD(g),ID(g),FD(g)∈I,g∈G},

Step 2 Find ψD(g)

Step 3 Construct ΨD over X,

Step 4 Compute ΨDD,

Step 5 Choose the maximum of ζΨDD(u).

Hand sanitizer is a liquid or gel mostly used to diminish infectious agents on the hands. According to the World Health Organization (WHO), in current epidemic circumstances of COVID-19, high-quality sanitation and physical distancing are the best ways to protect ourselves and everyone around us from this virus. This virus spreads by touching an ailing person. We cannot detach ourselves totally being cautious from this virus. So, high-quality sanitation can be the ultimate blockade between us and the virus. Alcohol-based hand sanitizers are recommended by WHO to remove the novel corona virus. Alcohol-based hand sanitizers avert the proteins of germs including bacteria and some viruses from functioning normally. Demand of a hand sanitizer has been increased terrifically in such serious condition of COVID-19. Therefore, it is tricky to have good and effectual hand sanitizers in local markets. Low quality hand sanitizers have also been introduced due to its increasing demand. The core motivation of this application is to select an effectual sanitizer to alleviate the spread of corona virus by applying the NPNHS-set theory.

Example 5.2. Suppose that Mr. William wants to purchase an effective hand sanitizer from the local market. There are eight kinds of Hand Sanitizer (options) which form the set of discourse

X={H1,H2,H3,H4,H5,H6,H7,H8}.

The best selection may be evaluated by observing the attributes i.e., k1 = Manufacturer, k2 = Quantity of Ethanol (percentage), k3 = Quantity of Distilled Water (percentage), k4 = Quantity of Glycerol (percentage), and k5 = Quantity of Hydrogen peroxide (percentage). The attribute-valued sets corresponding to these attributes are:

K1={k11=ProcterandGamble,k12=Unilever}K2={k21=75.15,k22=80}K3={k31=23.425,k32=18.425}K4={k41=1.30,k42=1.45}K5={k51=0.125} then ℙ=K1×K2×K3×K4×K5 ℙ={p1,p2,p3,p4,…,p16} where each pi,i=1,2,…,16,is a 5-tuples element.

Step 1:

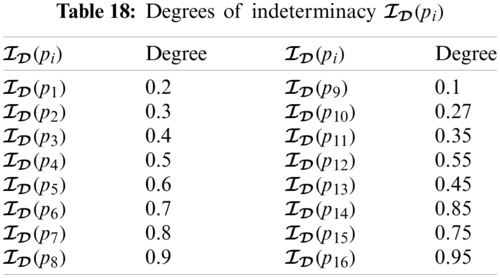
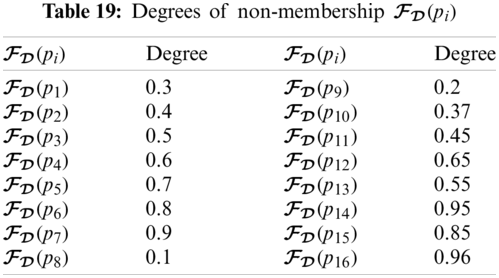
From Tabs. 17–19, we can construct D as

D={<0.1,0.2,0.3>/p1,<0.2,0.3,0.4>/p2,<0.3,0.4,0.5>/p3,<0.4,0.5,0.6>/p4,<0.5,0.6,0.7>/p5,<0.6,0.7,0.8>/p6,<0.7,0.8,0.9>/p7,<0.8,0.9,0.1>/p8,<0.9,0.1,0.2>/p9,<0.16,0.27,0.37>/p10,<0.25,0.35,0.45>/p11,<0.45,0.55,0.65>/p12,<0.35,0.45,0.55>/p13,<0.75,0.85,0.95>/p14,<0.65,0.75,0.85>/p15,<0.85,0.95,0.96>/p16}.

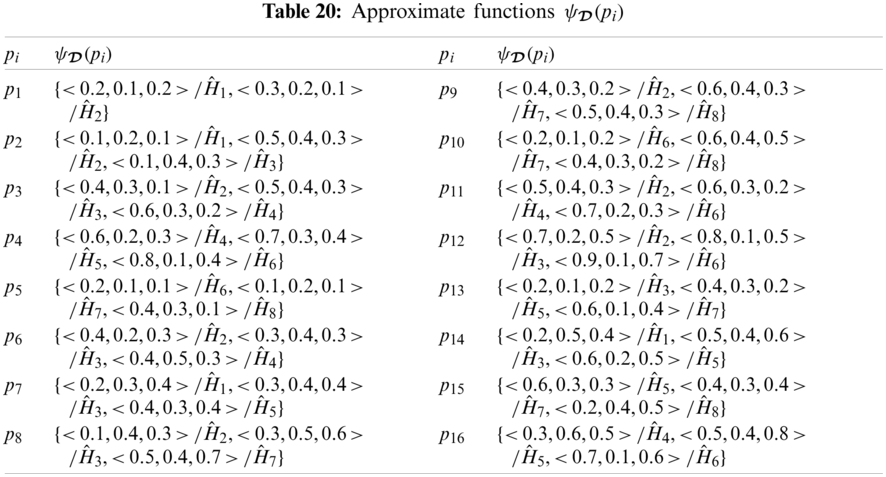
images

images

images

Step 2:

Tab. 20 presents ψD(pi) corresponding to each element of G.

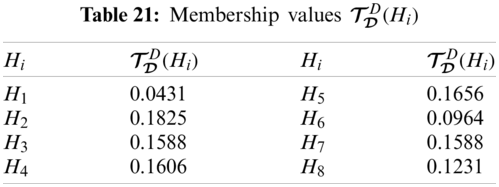
images

Step 3:

ΨD can be constructed with the help of Step 1 and Step 2 same as done in Step 3 of Section 3.

Step 4:

From Tabs. 21–24, we can construct ℝ(ΨDD) as

ℝ(ΨDD)={0.0344/H1,0.1600/H2,0.1500/H3,0.1289/H4,0.1367/H5,0.0749/H6,0.1538/H7,0.1006/H8}.

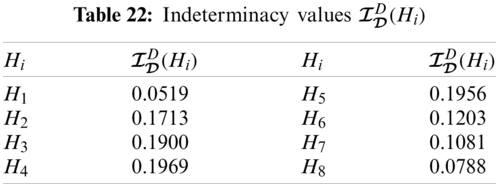
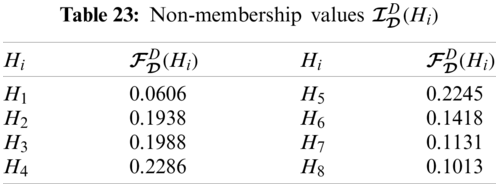
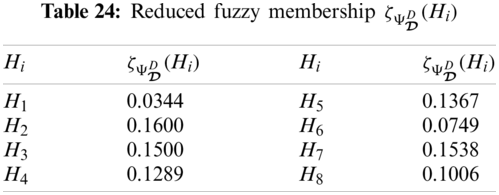
images

images

images

The graphical representation of this decision system is presented in Fig. 3.

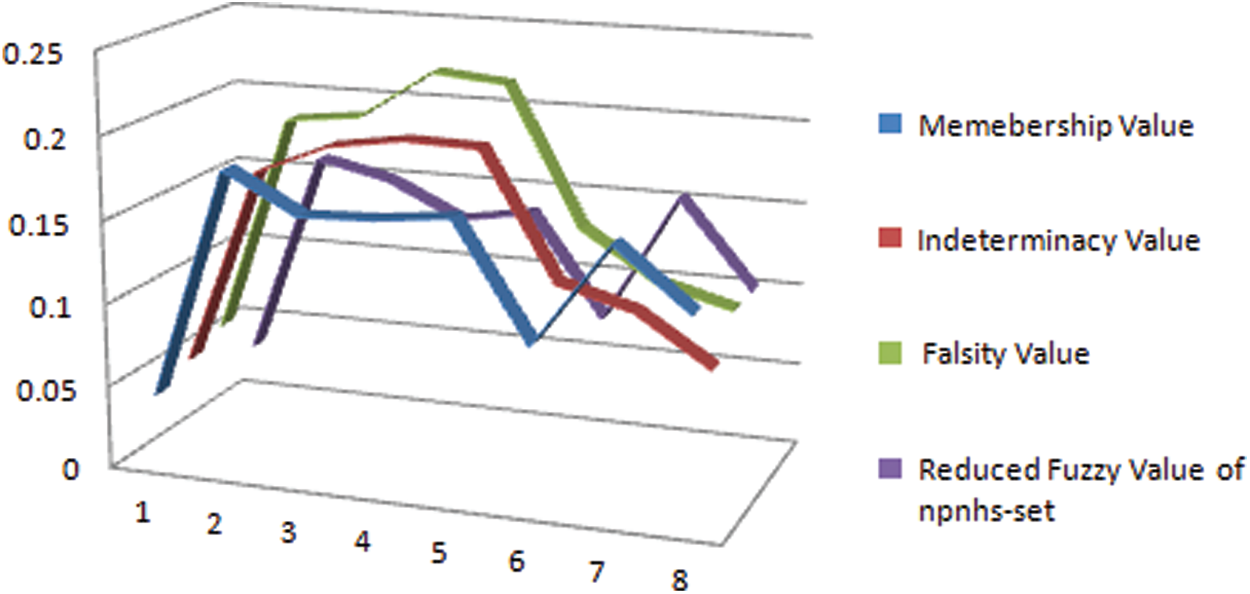
images

Figure 3: Neutrosophic decision system on npnhs-set

Step 5:

Since maximum of ζΨDD(Hi) is 0.1600 so the Hand Sanitizer H2 is selected.

6  Discussion

The development and stability of any society depends on its justice system and the judges, lawyers and plaintiffs play a key role in its basic components. The lawyer prepares the writ petition at the request of the plaintiff but when filing the case in the Court of Justice, he/she is in a state of uncertainty for its success. This uncertain condition can be of fuzzy, intuitionistic fuzzy or even neutrosophic. And after the case is submitted, the judge concerned writes his/her decision in the light of the facts, but usually all facts have some kind of uncertainty. Such factual vagueness again may be of fuzzy, intuitionistic fuzzy or neutrosophic nature. So when initial stage (submission stage) and final stage (decisive stage) are neutrosophic valued and the process is executed with the help of parameterized data (collections of parametric values) then we say that we are tackling such problem with the help of neutrosophic parameterized neutrosophic hypersoft set (npnhs-set). Since decision makers always face some sort of uncertainties and any decision taken by ignoring uncertainty may have some extent of inclination. Indeterminacy and uncertainty are both interconnected. In this study, it has been shown (i.e., see Fig. 4) that how results are affected when indeterminacy is ignored or considered. Our proposed structure npnhs-set is very useful in dealing with many decisive systems and it is the generalization of:

i)  Neutrosophic Parameterized Intuitionistic Fuzzy Hypersoft Set (npifhs-set) if indeterminacy is ignored and remaining two are made interdependent within closed unit interval in approximate function of npnhs-set,

ii)  Neutrosophic Parameterized Fuzzy Hypersoft Set (npfhs-set) if indeterminacy and falsity are ignored and remaining be restricted within closed unit interval in approximate function of npnhs-set,

iii)  Neutrosophic Parameterized Hypersoft Set (nphs-set) if all uncertain components are ignored and approximate function of npnhs-set is a subset of universe of discourse,

iv)  Neutrosophic Parameterized Neutrosophic Soft Set (npns-set) if attribute-valued sets are replaced with only attributes in npnhs-set,

v)  Neutrosophic Parameterized Intuitionistic Fuzzy Soft Set (npifs-set) if attribute-valued sets are replaced with only attributes and indeterminacy is ignored and remaining two are made interdependent within closed unit interval in approximate function of npnhs-set,

vi)  Neutrosophic Parameterized Fuzzy Soft Set (npfs-set) if attribute-valued sets are replaced with only attributes and indeterminacy, falsity are ignored and remaining be restricted within closed unit interval in approximate function of npnhs-set,

vii)  Neutrosophic Parameterized Soft Set (nps-set) if attribute-valued sets are replaced with only attributes and all uncertain components are ignored with approximate function of npnhs-set as a subset of universe of discourse.

Fig. 5 presents the pictorial view of the generalization of the proposed structure.

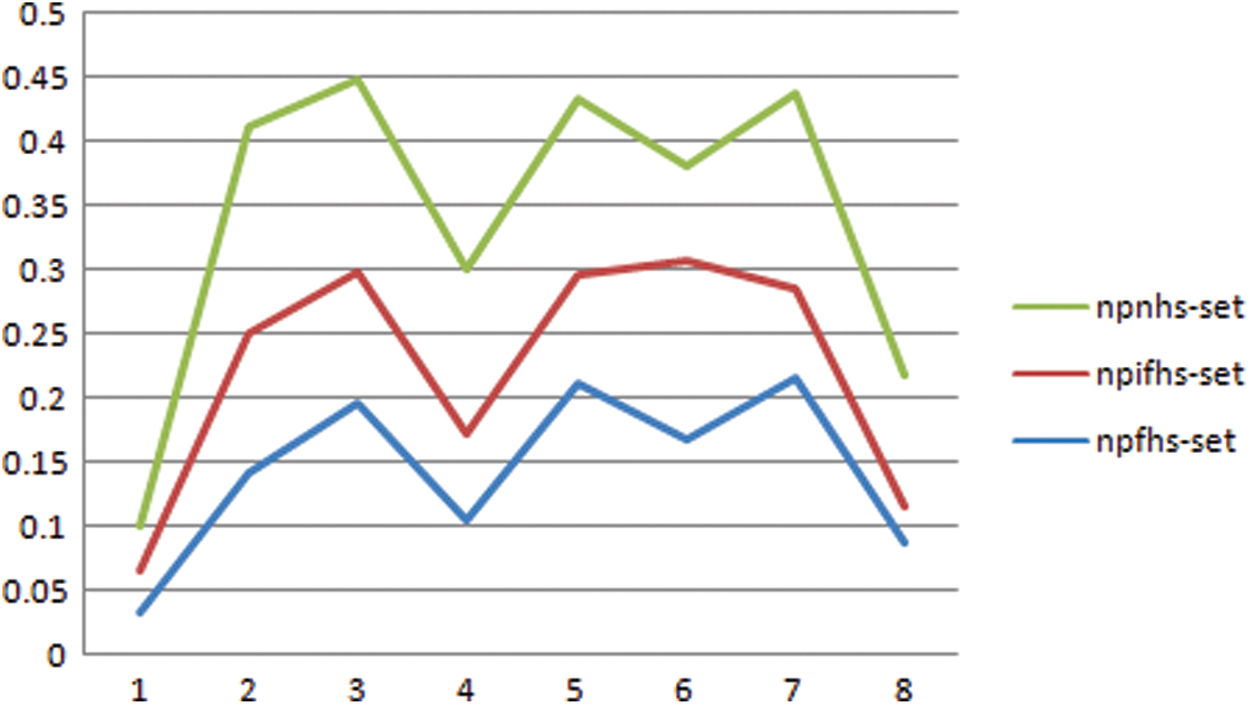
images

Figure 4: Comparison of neutrosophic decision system on npfhs-set, npifhs-set and npnhs-set

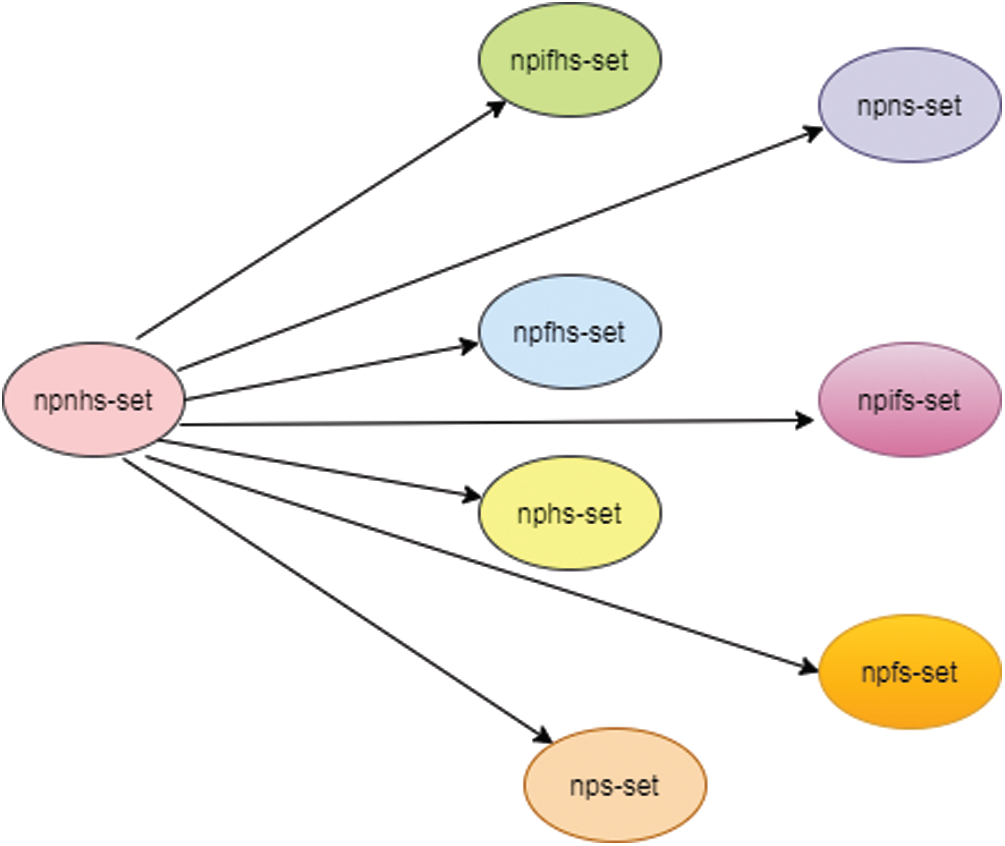
images

Figure 5: Generalization of npnhs-set

7  Conclusion

In this study, neutrosophic parameterized hypersoft set is conceptualized for the environments of fuzzy set, intuitionistic fuzzy set and neutrosophic set along with some of their elementary properties and theoretic operations. Novel algorithms are proposed for decision making and are validated with the help of illustrative examples for appropriate purchasing of suitable products i.e., Mobile Tablet, Washing Machines and Hand Sanitizers, from the local market. Future work may include the extension of this work for:

•   The development of algebraic structures i.e., topological spaces, vector spaces, etc.,

•   The development of hybrid structures with fuzzy-like environments,

•   Dealing with decision making problems with multi-criteria decision making techniques,

•   Applying in medical diagnosis and optimization for agricultural yield,

•   Investigating and determining similarity, distance, dissimilarity measures and entropies between the proposed structures.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Zadeh, L. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]

 2.  Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]

 3.  Smarandache, F. (1998). Neutrosophy: Neutrosophic probability, set, and logic: Analytic synthesis and synthetic analysis. Rehoboth: American Research Press. [Google Scholar]

 4.  Smarandache, F. (1999). A Unifying field in logics. Neutrosophy: Neutrosophic probability, set and logic. Rehoboth: American Research Press. [Google Scholar]

 5.  Smarandache, F. (2005). Neutrosophic set, a generalization of intuitionistic fuzzy sets. International Journal of Pure and Applied Mathematics, 24(3), 287–297. [Google Scholar]

 6.  Smarandache, F. (2006). Neutrosophic set—A generalization of intuitionistic fuzzy set. International Conference on Granular Computing, pp. 38–42. Atlanta, Georgia, USA, IEEE. [Google Scholar]

 7.  Wang, H., Rogatko, A., Smarandache, F., Sunderraman, R. (2006). A Neutrosophic description logic. International Conference on Granular Computing, pp. 305–308. Atlanta, Georgia, USA, IEEE. DOI 10.1109/GRC.2006.1635801. [Google Scholar] [CrossRef]

 8.  Smarandache, F. (2013). n-Valued refined neutrosophic logic and its applications in physics. Progress in Physics, 4, 143–146. DOI 10.5281/zenodo.49149. [Google Scholar] [CrossRef]

 9.  Smarandache, F. (2016a). Operators on single valued neutrosophic sets, neutrosophic undersets, and neutrosophic offsets. Journal of Mathematics and Informatics, 5, 63–67. DOI 10.5281/zenodo.57412. [Google Scholar] [CrossRef]

10. Smarandache, F. (2016b). Neutrosophic overset, neutrosophic underset, neutrosophic offset, similarly for neutrosophicover-/under-/offlogic, probability, and statistic. Brussels: Pons Editions. DOI 10.5281/zenodo.57410. [Google Scholar] [CrossRef]

11. Broumi, S., Bakali, A., Talea, M., Smarandache, F., Karaaslan, F. (2016). Interval valued neutrosophic soft graphs. New Trends in Neutrosophic Theory and Applications, 2, 214–251. DOI 10.5281/zenodo.1410271. [Google Scholar] [CrossRef]

12. Alhabib, R., Ranna, M. M., Farah, H., Salama, A. A. (2018). Some neutrosophic probability distributions. Neutrosophic Sets and Systems, 22, 30–38. DOI 10.5281/zenodo.2160479. [Google Scholar] [CrossRef]

13. Pramanik, S., Dey, P. P., Smarandache, F. (2018). Correlation coefficient measures of interval bipolar neutrosophic sets for solving multi-attribute decision making problems. Neutrosophic Sets and Systems, 19, 70–79. DOI 10.5281/zenodo.1235151. [Google Scholar] [CrossRef]

14. Broumi, S., Smarandache, F. (2013). Intuitionistic neutrosophic soft set. Journal of Information and Computing Science, 8(2), 130–140. DOI 10.5281/zenodo.2861554. [Google Scholar] [CrossRef]

15. Broumi, S., Smarandache, F. (2013). More on intuitionistic neutrosophic soft set. Computer Science and Information Technology, 1(4), 257–268. DOI 10.13189/csit.2013.010404. [Google Scholar] [CrossRef]

16. Broumi, S. (2013). Generalized neutrosophic soft set. International Journal of Computer Science, Engineering and Information Technology, 3(2), 17–30. DOI 10.5121/ijcseit.2013.3202. [Google Scholar] [CrossRef]

17. Broumi, S., Deli, I., Smarandache, F. (2014). Relations on interval valued neutrosophic soft sets. Journal of New Results in Science, 5, 1–20. DOI 10.5281/zenodo.30306. [Google Scholar] [CrossRef]

18. Deli, I. (2017). Interval-valued neutrosophic soft sets and its decision making. International Journal of Machine Learning and Cybernetics, 8(2), 665–676. DOI 10.1007/s13042-015-0461-3. [Google Scholar] [CrossRef]

19. Kharal, A. (2013). A neutrosophic multicriteria decision making method. New Mathematics and Natural Computation, 10(2), 143–162. DOI 10.1142/S1793005714500070. [Google Scholar] [CrossRef]

20. Edalatpanah, S. A. (2020). Systems of neutrosophic linear equations. Neutrosophic Sets and Systems, 33, 92–104. DOI 10.5281/zenodo.3782826. [Google Scholar] [CrossRef]

21. Kumar, R., Edalatpanah, S. A., Jha, S., Singh, R. (2019). A novel approach to solve gaussian valued neutrosophic shortest path problems. International Journal of Engineering and Advanced Technology, 8(3), 347–353. DOI 10.35940/ijeat.E1049.0585C19. [Google Scholar] [CrossRef]

22. Molodtsov, D. (1999). Soft set theory—First results. Computers and Mathematics with Applications, 37, 19–31. DOI 10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]

23. Maji, P. K., Biswas, R., Roy, A. R. (2003). Soft set theory. Computers and Mathematics with Applications, 45, 555–562. DOI 10.1016/S0898-1221(03)00016-6. [Google Scholar] [CrossRef]

24. Maji, P. K., Biswas, R., Roy, A. R. (2001). Fuzzy soft sets. Journal of Fuzzy Mathematics, 9(3), 589–602. [Google Scholar]

25. Pei, D., Miao, D. (2005). From soft set to information system. International Conference of Granular Computing, vol. 2, pp. 617–621. IEEE, DOI 10.1109/GRC.2005.1547365. [Google Scholar] [CrossRef]

26. Ali, M. I., Feng, F., Liu, X., Min, W. K., Sabir, M. (2009). On some new operations in soft set theory. Computers and Mathematics with Applications, 57, 1547–1553. DOI 10.1016/j.camwa.2008.11.009. [Google Scholar] [CrossRef]

27. Babitha, K. V., Sunil, J. J. (2010). Soft set relations and functions. Computers and Mathematics with Applications, 60, 1840–1849. DOI 10.1016/j.camwa.2010.07.014. [Google Scholar] [CrossRef]

28. Babitha, K. V., Sunil, J. J. (2011). Transitive closure and ordering in soft set. Computers and Mathematics with Applications, 61, 2235–2239. DOI 10.1016/j.camwa.2011.07.010. [Google Scholar] [CrossRef]

29. Sezgin, A., Atagün, A. O. (2011). On operations of soft sets. Computers and Mathematics with Applications, 61(5), 1457–1467. DOI 10.1016/j.camwa.2011.01.018. [Google Scholar] [CrossRef]

30. Ge, X., Yang, S. (2011). Investigations on some operations of soft sets. International Journal of Mathematical and Computational Sciences, 5(3), 370–373. [Google Scholar]

31. Li, F. (2011). Notes on soft set operations. ARPN Journal of Systems and Softwares, 1(6), 205–208. [Google Scholar]

32. Maji, P. K., Biswas, R., Roy, A. R. (2001). Intuitionistic fuzzy soft sets. Journal of Fuzzy Mathematics, 9(3), 677–692. [Google Scholar]

33. Çağman, N., Enginoğlu, S., Çitak, F. (2011). Fuzzy soft set theory and its applications. Iranian Journal of Fuzzy System, 8(3), 137–147. DOI 10.22111/IJFS.2011.292. [Google Scholar] [CrossRef]

34. Çağman, N., Karataş, S. (2013). Intuitionistic fuzzy soft set theory and its decision making. Journal of Intelligent and Fuzzy Systems, 24(4), 829–836. DOI 10.3233/IFS-2012-0601. [Google Scholar] [CrossRef]

35. Maji, P. K. (2013). Neutrosophic soft set. Annals of Fuzzy Mathematics and Informatics, 5(1), 157–168. [Google Scholar]

36. Mandal, D. (2015). Comparative study of intuitionistic and generalized neutrosophic soft sets. International Journal of Mathematical, Computational, Natural and Physical Engineering, 9(2), 111–114. DOI 10.5281/zenodo.1100511. [Google Scholar] [CrossRef]

37. Smarandache, F. (2018). Extension of soft set of hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets and Systems, 22, 168–170. DOI 10.5281/zenodo.2159755. [Google Scholar] [CrossRef]

38. Saeed, M., Ahsan, M., Siddique, M. K., Ahmad, M. R. (2020). A study of the fundamentals of hypersoft set theory. International Journal of Scientific and Engineering Research, 11(1), 320–329. [Google Scholar]

39. Saeed, M., Rahman, A. U., Ahsan, M., Smarandache, F. (2021). An inclusive study on fundamentals of hypersoft set. Theory and application of hypersoft set, pp. 1–23. Brussels: Pons Publishing House. [Google Scholar]

40. Abbas, F., Murtaza, G., Smarandache, F. (2020). Basic operations on hypersoft sets and hypersoft points. Neutrosophic Sets and Systems, 35, 407–421. DOI 10.5281/zenodo.3951694. [Google Scholar] [CrossRef]

41. Saqlain, M., Jafar, N., Moin, S., Saeed, M., Broumi, S. (2020). Single and multi-valued neutrosophic hypersoft set and tangent similarity measure of single valued neutrosophic hypersoft sets. Neutrosophic Sets and Systems, 32, 317–329. DOI 10.5281/zenodo.3723165. [Google Scholar] [CrossRef]

42. Saqlain, M., Moin, S., Jafar, N., Saeed, M., Smarandache, F. (2020). Aggregate operators of neutrosophic hypersoft sets. Neutrosophic Sets and Systems, 32, 294–306. DOI 10.5281/zenodo.3723155. [Google Scholar] [CrossRef]

43. Saqlain, M., Saeed, M., Ahmad, M. R., Smarandache, F. (2020). Generalization of TOPSIS for neutrosophic hypersoft sets using accuracy function and its application. Neutrosophic Sets and Systems, 27, 131–137. DOI 10.5281/zenodo.3275533. [Google Scholar] [CrossRef]

44. Martin, N., Smarandache, F. (2020). Concentric plithogenic hypergraph based on plithogenic hypersoft sets a novel outlook. Neutrosophic Sets and Systems, 33, 78–91. DOI 10.5281/zenodo.3782824. [Google Scholar] [CrossRef]

45. Rahman, A. U., Saeed, M., Smarandache, F., Ahmad, M. R. (2020). Development of hybrids of hypersoft set with complex fuzzy set, complex intuitionistic fuzzy set and complex neutrosophic set. Neutrosophic Sets and Systems, 38, 335–354. DOI 10.5281/zenodo.4300520. [Google Scholar] [CrossRef]

46. Rahman, A. U., Saeed, M., Smarandache, F. (2020). Convex and concave hypersoft sets with some properties. Neutrosophic Sets and Systems, 38, 497–508. DOI 10.5281/zenodo.4300580. [Google Scholar] [CrossRef]

47. Deli, I. (2020). Hybrid set structures under uncertainly parameterized hypersoft sets: Theory and applications. Theory and application of hypersoft set, pp. 24–49. Brussels: Pons Publishing House. [Google Scholar]

48. Gayen, S., Smarandache, F., Jha, S., Singh, M. K., Broumi, S. et al. (2020). Introduction to plithogenic hypersoft subgroup. Neutrosophic Sets and Systems, 33(1), 14. DOI 10.5281/zenodo.3782897. [Google Scholar] [CrossRef]

49. Çağman, N., Çitak, F., Enginoğlu, S. (2010). Fuzzy parameterized fuzzy soft set theory and its applications. Turkish Journal of Fuzzy System, 1(1), 21–35. [Google Scholar]

50. Deli, I., Çağman, N. (2015). Intuitionistic fuzzy parameterized soft set theory and its decision making. Applied Soft Computing, 28, 109–113. DOI 10.1016/j.asoc.2014.11.053. [Google Scholar] [CrossRef]

51. Karaaslan, F., Karataş, S. (2013). OR and AND-products of ifp-intuitionistic fuzzy soft sets and their applications in decision making. Journal of Intelligent and Fuzzy Systems, 31(3), 1427–1434. DOI 10.3233/IFS-162209. [Google Scholar] [CrossRef]

52. Çağman, N., Deli, I. (2012). Products of FP-soft sets and their applications. Hacettepe Journal of Mathematics and Statistics, 41(3), 365–374. [Google Scholar]

53. Çağman, N., Deli, I. (2012). Means of FP-soft sets and their applications. Hacettepe Journal of Mathematics and Statistics, 41(5), 615–625. [Google Scholar]

54. Broumi, S., Deli, I., Smarandache, F. (2014). Neutrosophic parametrized soft set theory and its decision making. International Frontier Science Letters, 1, 1–10. DOI 10.18052/www.scipress.com/IFSL.1.1. [Google Scholar] [CrossRef]

images This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.