Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.016356

ARTICLE

Medical Waste Treatment Station Selection Based on Linguistic q-Rung Orthopair Fuzzy Numbers

Jie Ling1,2, Xinmei Li1,2 and Mingwei Lin1,2,*

1College of Mathematics and Informatics, Fujian Normal University, Fuzhou, 350117, China
2Digital Fujian Internet-of-Things Laboratory of Environmental Monitoring, Fujian Normal University, Fuzhou, 350117, China
*Corresponding Author: Mingwei Lin. Email: linmwcs@163.com
Received: 28 February 2021; Accepted: 18 June 2021

1  Introduction

The current global public health emergency is the spread of COVID-19 and it has become a serious threat to human health. The rapid increase in the number of infections, coupled with the lack of initial attention by leaders in many countries, has led to COVID-19 becoming a global epidemic. As of mid-February 2021, COVID-19 has affected 185 countries. The cumulative number of confirmed cases of COVID-19 exceeds 100 million and active cases exceed 20 million [1]. The number of active cases in each country is shown in Fig. 1.

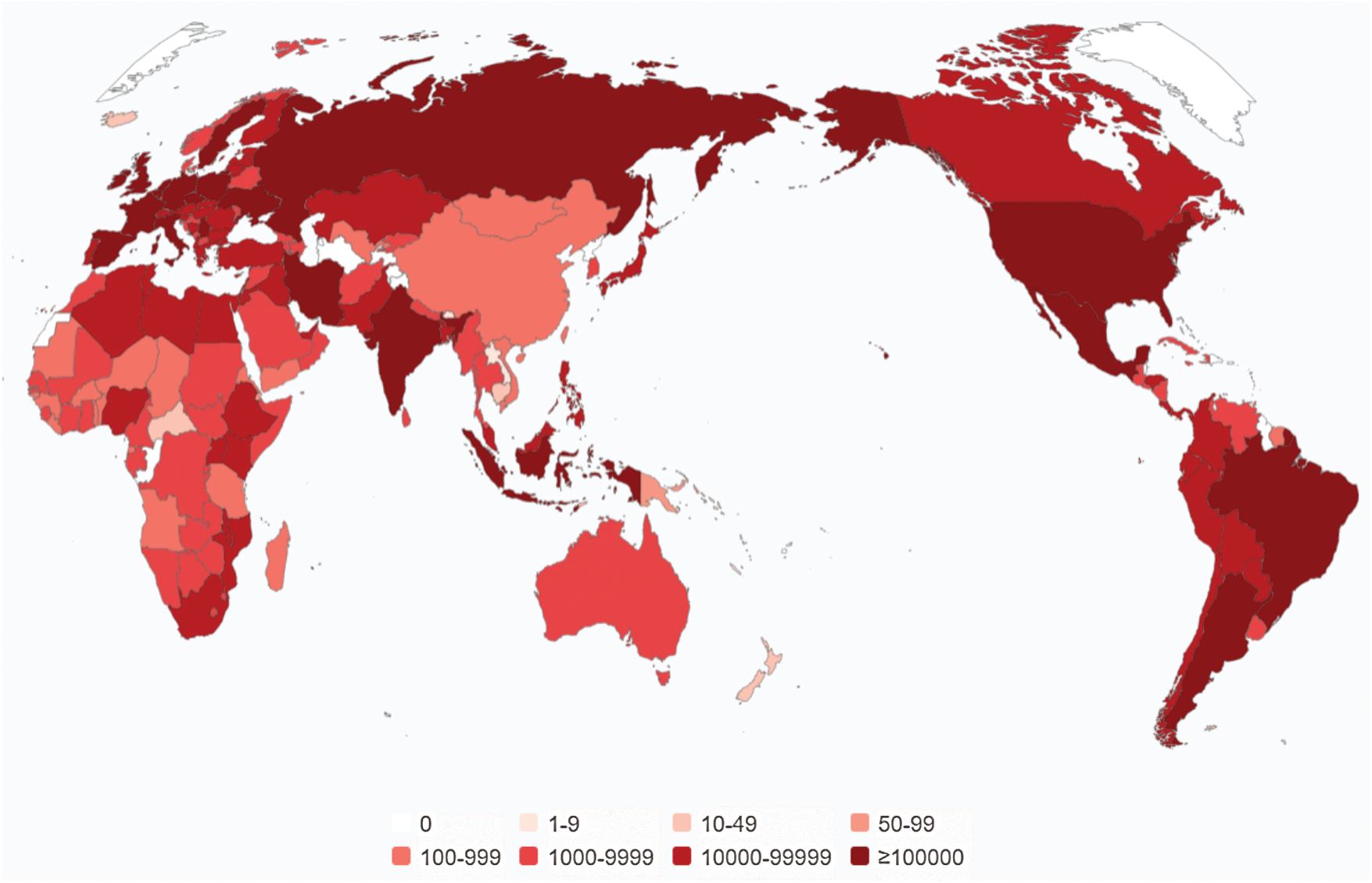
Figure 1: Active cases of COVID-19 in various countries

There are big challenges in controlling and preventing COVID-19 because of its rapid transmission, high infectiousness, and long incubation period. One of the key issues is how to handle medical waste in a rational manner. The reason for this is that with the rapid rise in the number of infections, the generation of medical waste has increased dramatically. Proper disposal of massive medical waste is an important way of preventing secondary transmission of COVID-19 [2]. In addition, most medical wastes are the plastic products, which can also cause environmental pollution if not handled properly. In order to solve the above problems, medical wastes need to be recycled and treated. The location of medical waste treatment stations is one of the key aspects [3,4].

Siting a suitable medical waste treatment station requires multiple considerations of economic, social, and environmental factors. Determining the best site is a challenge, as each station has its own advantages and disadvantages. Improper siting of the medical waste treatment stations will have the long-term negative impacts on environmental development and economic growth. Therefore, multi-attribute decision-making (MADM) can be used to solve the above siting problem [5,6]. The general process of the MADM method is to analyze the selection attributes and determine the weights of their importance. Then, an evaluation matrix is generated, and the score of each alternative is calculated and ranked.

To solve the medical waste station selection problem, this paper proposes a novel MADM method based on the partitioned Maclaurin symmetric mean (PMSM) operator. Because of the complexity of the medical waste station selection problem, in this paper, we evaluate the alternatives of medical waste stations in the form of linguistic q-rung orthopair fuzzy numbers (Lq-ROFNs), which are capable of handling the complex and fuzzy information [7,8]. Through analyzing the considered attributes of medical waste stations, we can find that attributes in the same clusters are closely related, while attributes in different clusters did not have the relationship. Therefore, in this paper, we use the PMSM operator to aggregate the evaluation information. It can capture the correlation among attributes in the same clusters and can reflect the independence among attributes in different clusters [9,10]. Meanwhile, the evaluation information provided by the decision-makers may contain unreasonable values. We further use the partitioned dual MSM (PDMSM) operator to process the evaluation information. It can reduce the influence of unreasonable evaluation values on the aggregation results.

The other sections of this paper are briefly described as follows. Section 2 is a literature review, which reviews the knowledge of fuzzy sets and MADM methods. Section 3 gives a brief introduction to relevant basic concepts, including the definition and properties of the Lq-ROFSs and the PMSM operators. Section 4 gives the definitions of the Lq-ROFPMSM and Lq-ROFWPMSM operators, and analyzes their relevant properties and typical examples. In Section 5, we define the Lq-ROFPDMSM and Lq-ROFWPDMSM operators and analyze their related features. A novel MADM method using the Lq-ROFWPMSM and Lq-ROFWPDMSM operators is proposed in Section 6. Section 7 verifies the reliability and superiority of the model in this paper by an application example. The last section is an analysis and conclusion of this paper.

2  Literature Review

As an important part of modern decision theory, MADM has been widely applied in various fields of engineering, business activities, and government actions. The purpose of MADM is to evaluate alternatives based on the evaluation information provided by the decision makers. The optimal solution is then selected based on the ranking results. Early decision-making problems usually use crisp numbers to evaluate objects. However, evaluation information can be fuzzy and uncertain as the complexity of the decision problems increases. It is difficult to accurately represent evaluation information with only crisp numbers. Therefore, Zadeh [11] proposed the fuzzy sets (FSs) theory, which uses the membership degree (MD) to describe the support degree of the decision makers. By extending the classical FSs theory, Atanassov [12] proposed the intuitionistic fuzzy sets (IFSs). It describes the degree of opposition of decision makers through the non-membership degree (NMD). The sum of MD α and NMD β is not greater than one [12,13]. IFSs can describe the degree of support, opposition, and hesitation for evaluating objects [14]. Thus, it has attracted a large number of scholars [15–19]. However, the MD α and the NMD β of IFSs must satisfy the constraint condition of α+β≤1, which makes the representation of evaluation information narrow. Therefore, Yager extended the IFSs and proposed the theory of Pythagorean fuzzy sets (PFSs) [20,21]. PFSs also use the MD and NMD to represent evaluation information. However, the sum of the square of MD α and the square of NMD β is not greater than one, i.e., α2+β2≤1. Therefore, PFSs are more capable of handling fuzzy problems [22–24]. Further, Yager proposed the theory of q-rung orthopair fuzzy sets (q-ROFSs) [25]. The sum of qth power of MD α and qth power of NMD β is not greater than one, i.e., αq+βq≤1. Thus, IFSs and PFSs are special forms of q-ROFSs.

In daily life, decision-makers usually use linguistic terms to describe evaluation information [26]. For instance, when describing the price of a product, decision-makers often use words such as “high”, “low”, “very high” or “very low”. To model this kind of evaluation information, the fuzzy linguistic methods that are more in line with the grammatical habits of decision makers are proposed by Zadeh [27]. Based on the intuitionistic fuzzy sets and linguistic term sets [28], Zhang proposed the concept of linguistic intuitionistic fuzzy set (LIFS) [29]. Then, Garg provided the definition of linguistic Pythagorean fuzzy set (LPFS) [30]. Linguistic q-rung orthopir fuzzy set (Lq-ROFS) is an extended form of LIFS and LPFS [31].

In the multi-attribute decision making activities, it is a challenge to aggregate the cluttered evaluation information into relatively intuitive data. The aggregation operator is an effective tool to solve the above problem. At present, many research results have been achieved in the aggregation operators. For example, Bonferroni mean (BM) operator [32], power average (PA) operator [33], Hamacher aggregation operator [34], Heronian mean (HM) operator [35], and so on. The Maclaurin symmetric mean (MSM) operator was first introduced by Maclaurin in 1729 [36] and then extended by Detemple et al. [37]. The MSM operator can capture the correlation among the evaluated information. It can reflect the risk preference of decision-makers during the evaluation. The MSM operator has been concerned by many scholars since it was proposed, and many achievements have been made in both theory and applications [38–40]. However, in practical decision problems, the attributes in the evaluation information are not always interrelated. There may be divisions among attributes, which cannot be handled by the MSM operator. To solve this problem, the partitioned MSM (PMSM) operator [41] has been proposed. The PMSM operator can handle the case where there are partitions among attributes.

As the complexity of the decision problem increases, the following situations may occur: 1) decision makers may use the linguistic terms to describe the evaluation object; 2) due to lack of experience, decision makers may give some evaluation values that are too high or too low. To deal with the above problems, we extend the PMSM operator and the partitioned dual PMSM operator to process Lq-ROFS. Then, we propose the linguistic q-rung orthopair fuzzy partitioned Maclaurin symmetric mean (Lq-ROFPMSM) operator, linguistic q-rung orthopair fuzzy partitioned dual Maclaurin symmetric mean (Lq-ROFPDMSM) operator, and their weighted form (Lq-ROFWPMSM and Lq-ROFWPDMSM). The Lq-ROFPMSM and Lq-ROFPDMSM operators can solve the decision-making problems that the attributes in the same clusters are closely related and the attributes in the different clusters have no relationship. The negative impact of unreasonable values in the evaluation information on the ranking results is also significantly reduced.

3  Preliminaries

In this chapter, will briefly review the definition and characteristics of the linguistic q-round orthopair fuzzy sets (Lq-ROFSs) and the partitioned Maclaurin symmetric mean (PMSM) operators.

3.1 Lq-ROFSs

Definition 1. [31]. Suppose X is the collection of discourse, S={sα∣α∈[0,t]} is a continuous linguistic term set, where t is a positive integer. An Lq-ROFS L is expressed as

L={(x,sa(x),sb(x))∣x∈X},(1)

where sa(x) and sb(x) respectively represent the MD and NMD of parameter x in Lq-ROFS L. We call the pair (sa(x),sb(x)) an Lq-ROFN. To express it conveniently, we assign (sa,sb) to represent it, which meets 0≤a≤t, 0≤b≤t, 0≤aq+bq≤tq and q≥1. Let sπ(x)=stq−aq−bqq, then sπ(x) represents the indeterminacy degree of the parameter x in Lq-ROFS L.

Definition 2. [31]. Let S={sα∣α∈[0,t]} be a linguistic term set and α=(sa,sb) be an Lq-ROFN, where sa,sb∈S, then we can express the score function of the Lq-ROFN α as follows:

D(α)=s(tq+aq−bq/2)1q.(2)

The accuracy function is expressed as:

J(α)=s(aq+bq)1q.(3)

Then, we can compare any two Lq-ROFN α and β in the following way:

(1)   If D(α)>D(β), then α≻β;

(2)   If D(α)=D(β), then

   If J(α)>J(β), then α≻β,

   If J(α)=J(β), then α=β.

Definition 3. [31]. Suppose λ is a positive real number and γ=(sa,sb), γ1=(sa1,sb1) and γ2=(sa2,sb2) are three arbitrary Lq-ROFNs. The operations among the Lq-ROFNs γ, γ1 and γ2 are shown as below:

γ1⊕γ2=(sa1,sb1)⊕(sa2,sb2)=(st(1−∏i=12(1−aiqtq))1q,st(b1b2t2)),(4)

γ1⊗γ2=(sa1,sb1)⊗(sa2,sb2)=(st(a1a2t2),st(1−∏i=12(1−biqtq))1q),(5)

λγ=λ(sa,sb)=(st(1−(1−aqtq)λ)1q,st(bt)λ),(6)

γλ=(sa,sb)λ=(st(at)λ,st(1−(1−bqtq)λ)1q).(7)

3.2 The PMSM Operator

Definition 4. [41]. Suppose ai is a set of real numbers not less than zero, where i=1,2,…,n, and separate them into d partitions P1,P2,…,Pd. k1,k2,…,kd are the parameters of the PMSM operator, and kr=1,2,…,|Pr|, where |Pr| represents the number of evaluation information in the partition Pr (r=1,2,…,d). Then, the formula of the partitioned MSM (PMSM) operator is shown below:

PMSM(k1,k2,…,kd)(α1,α2,…,αn)=1d∑r=1d(∑i1,i2,…ikr∈Pri1<i2⋯<ikr∏j=1krαijC|pr|kr)1kr,(8)

where {i1,i2,…ikr} is a collection of kr integers derived from the collection {1,2,…,|Pr|}, and 1≤i1<i2<⋯<ik≤|Pr|, C|pr|krdenotes the binomial coefficient and C|pr|kr=|pr|!kr!(|pr|−kr)!.

4  The Proposed Lq-ROFPMSM Operator and Lq-ROFWPMSM Operator

4.1 The Lq-ROFPMSM Operator

Definition 5. Let αi=(sai,sbi) be Lq-ROFNs, where i=1,2,…,n, which can be partitioned into d partitions Pr (r=1,2,…,d). k1,k2,…,kd are the parameters and kr=1,2,…,|Pr|, where |Pr| represents the number of evaluation information in the group Pr. Then, the Lq-ROFPMSM is shown as follows:

Lq−ROFPMSM(k1,k2,…,kd)(α1,α2,…,αn)=1d⊕r=1d⁡(⊕i1,i2,…ikr∈Pri1<i2⋯<ikr⁡(⊗j=1krαij)C|pr|kr)1kr,(9)

where {i1,i2,…ikr} is a collection of kr integers derived from the collection {1,2,…,|Pr|}, and 1≤i1<i2<⋯<ik≤|Pr|. C|pr|krdenotes the binomial coefficient and C|pr|kr=|pr|!kr!(|pr|−kr)!.

Theorem 1. Let αi=(sai,sbi) be Lq-ROFNs, where i=1,2,…,n, which can be partitioned into d partitions Pr (r=1,2,…,d). k1,k2,…,kd are the parameters and kr=1,2,…,|Pr|, where |Pr| represents the number of evaluation information in the partition Pr (r=1,2,…,d). Then we aggregate all the Lq-ROFNs using the above Lq-ROFPMSM operator and the result is still an Lq-ROFN, shown as below:

Lq−ROFPMSM(k1,k2,…,kd)(α1,α2,…,αn)=(st(1−(∏r=1d(1−(1−(∏i1,i2,…ikr∈Pri1<i2⋯<ikr(1−∏j=1kraijqtq))1C|pr|kr)1kr))1d)1qst(∏r=1d(1−(1−(∏i1,i2,…ikr∈Pri1<i2⋯<ikr(1−∏j=1kr(1−bijqtq)))1C|pr|kr)1kr)1q)1d).(10)

Proof. According to Definition 3, we have

and

Then we can get

Then

Therefore,

According to the above derivation process, the proof of Theorem 1 is completed. In the next part, some features of the Lq-ROFPMSM operator are analyzed.

(1) Idempotency. Suppose that αi=(sai,sbi)=α=(sa,sb), where i=1,2,…,n. We have

Lq−ROFPMSM(k1,k2,…,kd)(α1,α2,…,αn)=α.(11)

Proof. Due to αi=(sai,sbi)=α=(sa,sb), we have

Lq−ROFPMSM(k1,k2,…,kd)(α,α,…,α)=(st(1−(∏r=1d(1−(1−(∏i1,i2,…ikr∈Pri1<i2⋯<ikr(1−∏j=1kraqtq))1C|pr|kr)1kr))1d)1q,st(∏r=1d(1−(1−(∏i1,i2,…ikr∈Pri1<i2⋯<ikr(1−∏j=1kr(1−bqtq)))1C|pr|kr)1kr)1q)1d),

=(st(1−(∏r=1d(1−(1−((1−(aqtq)kr)C|pr|kr)1C|pr|kr)1kr))1d)1q,st(∏r=1d(1−(1−((1−(1−bijqtq)kr)C|pr|kr)1C|pr|kr)1kr)1q)1d),

=(st(1−(∏r=1d(1−(1−((1−(aqtq)kr)C|pr|kr)1C|pr|kr)1kr))1d)1q,st(∏r=1d(1−(1−((1−(1−bijqtq)kr)C|pr|kr)1C|pr|kr)1kr)1q)1d),

=(st(1−(∏r=1d(1−(1−(1−(aqtq)kr))1kr))1d)1q,st(∏r=1d(1−(1−(1−(1−bijqtq)kr))1kr)1q)1d)=(st(1−(∏r=1d(1−((aqtq)kr)1kr))1d)1q,st(∏r=1d(1−((1−bijqtq)kr)1kr)1q)1d),

=(st(1−(∏r=1d(1−aqtq))1d)1q,st(∏r=1d(1−(1−bijqtq))1q)1d)=(st(1−((1−aqtq)d)1d)1q,st(((bijqtq)1q)d)1d)=(st(1−(1−aqtq))1q,st(bt))=(st(aqtq)1q,st(bt))=(sa,sb).

According to the above derivation process, we have completed the proof of idempotency.

(2) Commutativity. Suppose αi=(sai,sbi) and αi′=(s′ai,s′bi) are two arbitrary sets of Lq-ROFNs, where i=1,2,…,n. If αi′ is an arbitrary permutation of αi, then

Lq−ROFPMSM(k1,k2,…,kd)(α1,α2,…,αn)=Lq−ROFPMSM(k1,k2,…,kd)(α′1,α′2,…,α′).(12)

Proof. As αi′ is an arbitrary permutation of αi, we can get

According to the above derivation process, we have completed the proof of commutativity.

(3) Monotonicity. Suppose αi=(sai,sbi) and αi′=(s′ai,s′bi) are two arbitrary sets of Lq-ROFNs, where i=1,2,…,n. If there is sai≥sai′ and sbi≤sbi′ for arbitrary i. We have

Lq−ROFPMSM(k1,k2,…,kd)(α1,α2,…,αn)≥Lq−ROFPMSM(k1,k2,…,kd)(α′1,α′2,…,α′n).(13)

Proof. As ai≥ai′≥0 and 0≤bi≤bi′, then we can get aij≥aij′≥0 and 0≤bij≤bij′. Thus