Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.016772

ARTICLE

The New Neutrosophic Double and Triple Exponentially Weighted Moving Average Control Charts

Ambreen Shafqat1,2, Muhammad Aslam3,*, Muhammad Saleem4 and Zameer Abbas5

1Department of Statistics and Financial Mathematics, School of Science, Nanjing University of Science and Technology, Nanjing, 210094, China
2Department of Statistics, University of Sargodha, Sargodha, 40100, Pakistan
3Department of Statistics, Faculty of Science, King Abdulaziz University, Jeddah, 21551, Saudi Arabia
4Department of Industrial Engineering, Faculty of Engineering-Rabigh, King Abdulaziz University, Jeddah, 21589, Saudi Arabia
5Goverment Ambala Muslim Graduate College, Sargodha, 40100, Pakistan
*Corresponding Author: Muhammad Aslam. Email: aslam_ravia@hotmail.com
Received: 25 March 2021; Accepted: 23 June 2021

Nomenclature

1  Introduction

Control charts play a vital role in monitoring processes and are used to remove assignable causes that are responsible for substandard products (or services), wastes, reworks, and high production or manufacturing costs. Shewhart [1] introduced control charting techniques in the 1920 and showed that these can be applied in different industries. Shewhart-type control charts are very famous for monitoring processes in different areas of productions due to their easy implementation and high speed in detecting large shifts. They are usually referred to as memoryless charts because they only use the current information. Since Shewhart-type charts are efficient in detecting large shifts, researchers have designed new control charting techniques to efficiently detect small-to-moderate process shifts as quickly as possible, including large shifts. These are referred to as memory-type control charts as they use the current and past information to compute the charting statistics, which makes them more sensitive in identifying small–to-moderate shifts. More specifically, Page [2] and Roberts [3] designed the cumulative sum (CUSUM) and the exponentially weighted moving average (EWMA) control charts, respectively. The properties of EWMA control chart have been studied by many researchers in the statistical process control (SPC) area. A lot of modifications to the EWMA chart have been introduced in the literature to enhance its performance in detecting small-to-moderate shifts. References [4,5] proposed the double EWMA (DEWMA) chart with asymptotic control limits. Later on, a lot of researchers worked on DEWMA control with different techniques. Shafqat et al. [6] proposed the DEWMA chart with asymptotic control limits based on linear prediction. Capizzi et al. [7] presented the adaptive EWMA control chart to detect instantaneously small-to-large magnitudes of shifts. Zhang et al. [8] studied DEWMA under time-varying control limits with different values for the smoothing parameters. More basic information about the control charts can be found in [9–12].

The traditional Shewhart control charts cannot be implemented when uncertainty is expected in the data, for more details on this, readers are referred to Aslam et al. [13] introduced the neutrosophic EWMA (NEWMA) X¯ chart (i.e., the EWMA chart using neutrosophic logic). The fuzzy-based control charts are the best alternative to monitor the process when observations or the parameters are under uncertainty scenario, thus, numerous authors paid attention to work on this; related literature can be seen in [14–20]. The fuzzy logic is a special case of neutrosophic logic. The classical statistical methods are applied under the assumption that all inspections in data are indomitable, certain, and particular. So, in the manufacturing process, it may not be possible to have documentation of all determined observations or parameters of the data. In this condition, the neutrosophic statistics can be more practical (or relevant) for the analysis of the data. Smarandache [21] introduced neutrosophic statistics which is a generalization of classical statistics. Neutrosophic statistics is more efficient when applied in the analysis of indefinite data than classical statistics. Chen et al. [22,23] demonstrated the efficiency of the neutrosophic statistics-based analysis. Aslam [24] introduced a new area of neutrosophic quality control monitoring. Thereafter, Aslam et al. [25,26] proposed attributes and variables charts under neutrosophic logic.

Recently, Alevizakos et al. [27,28] introduced a triple EWMA (TEWMA) control chart for normally and exponentially distributed data to enhance the performance of the EWMA chart with asymptotic and time-varying control limits. Letshedi et al. [29] proposed a distribution-free TEWMA control chart using Wilcoxon rank-sum statistics to improve the detection ability in the process location parameter with fast initial response features.

After exploring the literature, there is no work on the DEWMA and TEWMA control charts under neutrosophic statistics for normally distributed data (or, for any other distribution). In this study, the neutrosophic DEWMA, and TEWMA (labeled as; NDEWMA and NTEWMA) charts are proposed. In this paper, asymptotic control limits are used to examine the neutrosophic statistical performance of the NDEWMA and NTEWMA charts. The NDEWMA and NTEWMA control charts are compared with the classical and neutrosophic EWMA charts as well as the classical DEWMA and TEWMA control charts.

The rest of the manuscript is as follows: In the next Section, the design structures of the proposed control charts are discussed. In Section 3, the run-length characteristics via neutrosophic Monte Carlo simulations are theoretical and empirically provided. A comprehensive comparison of the proposed studies has been made with existing control charts in Section 3. In Section 4, two illustrative examples of the practical application of the proposed charts are given using simulation and real-life datasets. Concluding remarks are provided in Section 5.

2  The Design Structure of the Neutrosophic Control Charts Structure

In this section, the neutrosophic-based memory-type control charts (DEWMA and TEWMA) structures are presented. These are used for monitoring the process with small-to-moderate and moderate-to-large shifts under the neutrosophic environment. Neutrosophic environment is the environment when we have indeterminacy interval in the random variable.

2.1 The Design Structure of the Proposed NDEWMA Chart

Let Xi be a quality characteristic of a process whose distribution is normal with mean μN∈[μL,μU] and variance (σN2∈[σL2,σU2] and XNi,i=1,2,3…,XNi∈[XLi,XUi] be a sequence of independent and identically distributed (iid) observations from the process, where XLi and XUi are the minimum and maximum values of indeterminacy interval. When the process is in-control (IC), then μN=μN0; otherwise, μN=μN1 or μN≠μN0.

In this study, we are interested in the detection of shifts in the process mean from its IC value μ0 to an out-of-control (OOC) value μN1=μN0+δσN for δ≠0, assuming that the process variance is IC and remains unchanged. The NDEWMA chart is based on current and past observations with the NEWMA plotting statistic applied as an input in another NEWMA statistic. The charting statistics of the NEWMA can be expressed as:

YNi=λNX¯Ni+(1-λN)YN(i-1)(1)

where YN,i∈{YL,i,YU,i},λN∈[λL,λU], and thus, the NDEWMA charting statistic is given by:

ZNi=λNYNi+(1-λN)ZN(i-1)(2)

ZN,i∈{ZL,i,ZU,i} and λN∈[λL,λU]. Note that [0,0]<λN≤[1,1] denotes the neutrosophic smoothing constant. The starting values are typically defined as YN0=ZN0=μN0. Hence, the asymptotic mean and variance of the NDEWMA chart for large values of i can be written as:

E(ZN)=μ0(3)

and

Var(ZN)=λ(2-2λ+λ2)(2-λ)3σN2nN(4)

Therefore, the asymptotic control limits become:

UCLN/LCLN=μ0±kNVar(ZN)(5)

where UCLN∈[UCLL,UCLU],LCLN∈[LCLL,LCLU],ZN∈[ZL,ZU],kN∈[kL,kU]. Here kN is control limits coefficient which is customarily taken corresponding to the desired value of IC ARL.

2.2 The Design Structure of the Proposed NTEWMA Chart

The NTEWMA chart is based on current and past observations with the NEWMA smoothing procedure utilizes sampled information three times which can be mathematically defined as:

WNi=λNZNi+(1-λN)WN(i-1)(6)

where WNi∈{WLi,WUi},λN∈[λL,λU] and ZNi is as defined in Eq. (2). Note that [0,0]<λN≤[1,1] denotes the neutrosophic smoothing constant and the starting values of YN0=ZN0=WN0=μN0. Hence, the asymptotic mean and variance of the NTEWMA chart for large values of i can be written as:

E(WN)=μ0(7)

and

Var(WN)=(6(1-λ)6λ(2-λ)5+12(1-λ)4λ2(2-λ)4+7(1-λ)2λ3(2-λ)3+λ4(2-λ)2)σN2nN(8)

The asymptotic control limits become:

UCLN/LCLN=μ0±kNvar(WN)(9)

where UCLN∈[UCLL,UCLU],LCLN∈[LCLL,LCLU],WN∈[WL,WU] and kN∈[kL,kU]. The control limits of the NTEWMA control chart were obtained using individual measurements. Note though, if subgroups of nN > 1 are collected, then simply substitute XNi with the sample mean X¯N∈{X¯L,X¯U} and σN2 with σN2nN.

3  Neutrosophic Run-Length Performance of the Proposed Charts

Equations and mathematical expressions must be inserted into the main text. Two different types of styles can be used for equations and mathematical expressions. They are: in-line style, and display style.

3.1 Run-Length Distribution of the Proposed Neutrosophic Charts

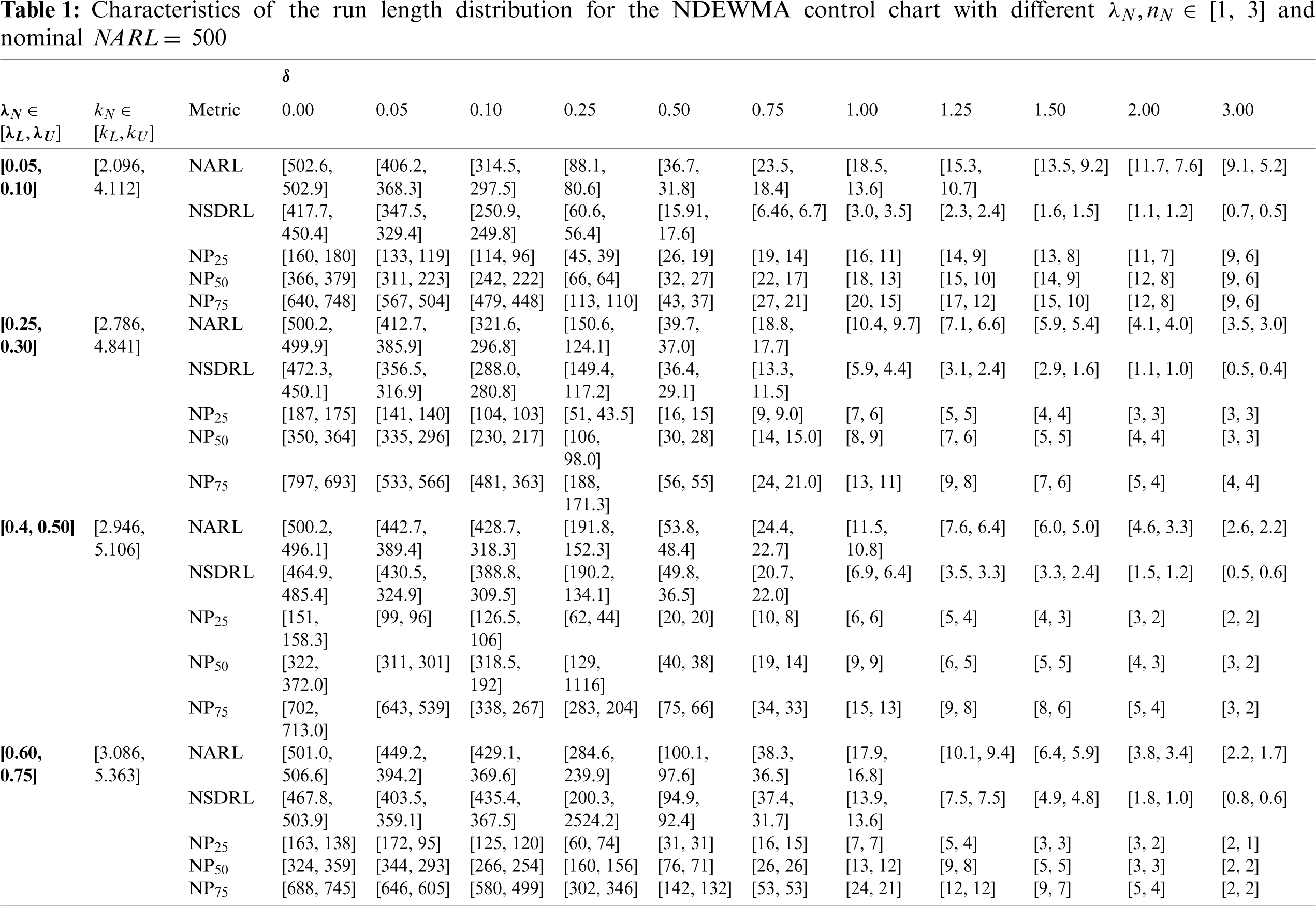
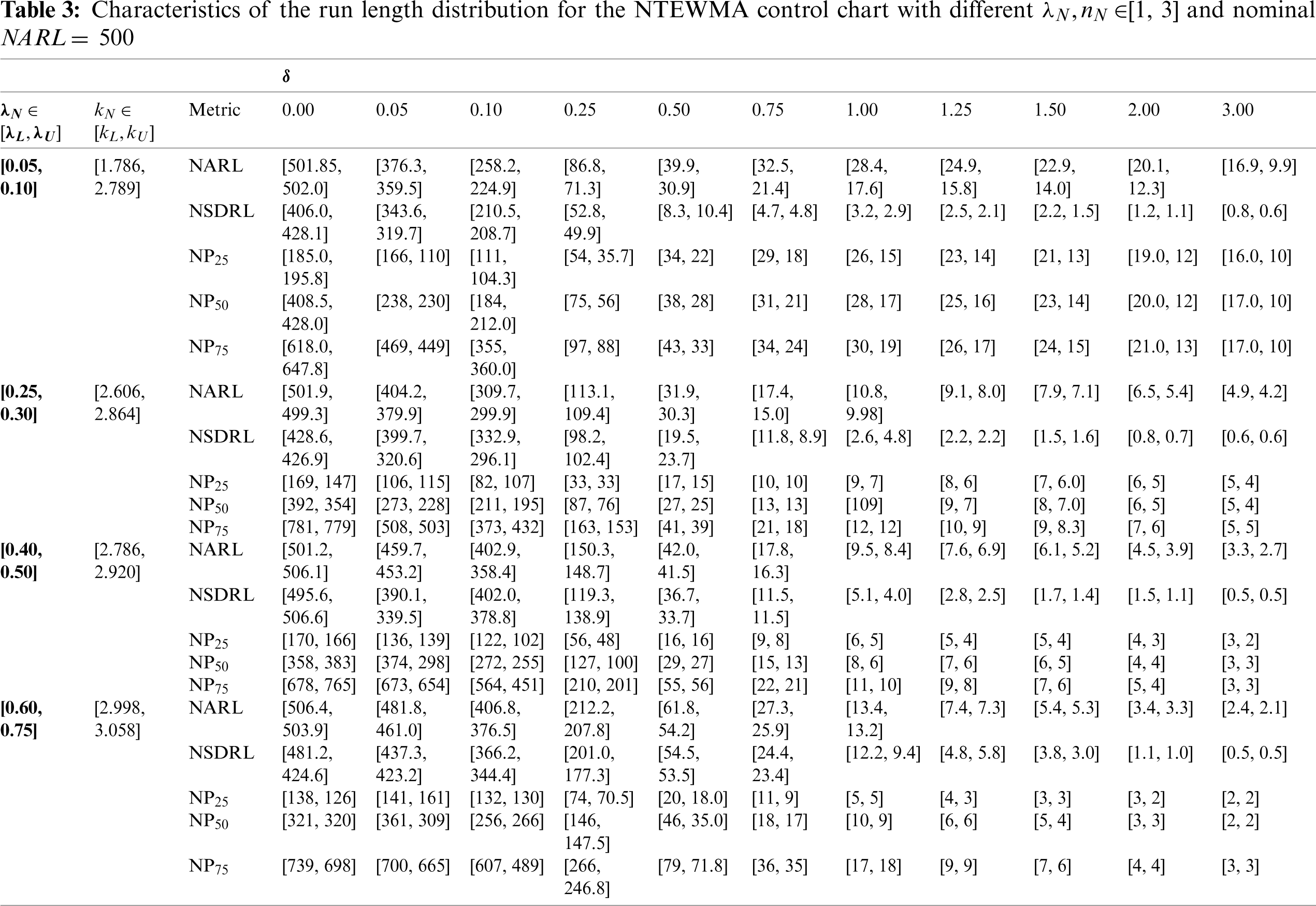
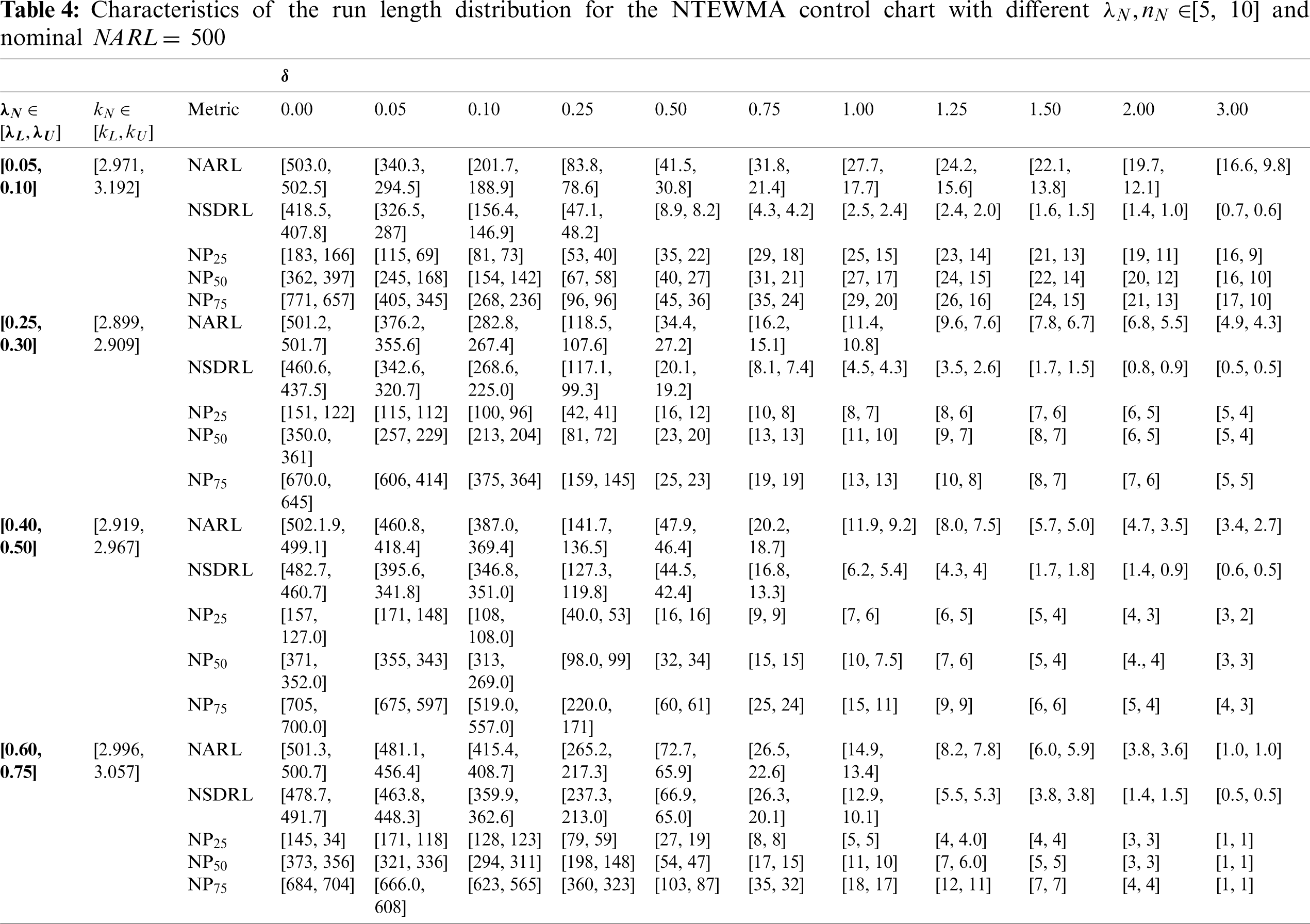
Generally, the performance of a control chart is determined using average run length (ARL) that is a characteristic of the run length use for measuring the superiority of the proposed chart. The IC process performance under ARL is denoted by ARL0 and the OOC process performance is denoted by ARL1. The comparative performance of the proposed charts is made under the neutrosophic simple random sampling scheme based on out-of-control values of run-length characteristics to detect shifts in a process. The neutrosophic run-length characteristics used in this paper are neutrosophic ARL (NARL), the neutrosophic standard deviation of the run-length (NSDRL), and neutrosophic percentile run-length (i.e., the 25th, 50th,  and 75th percentiles which are denoted as NP25, NP50,  and NP75). These neutrosophic characteristics are used for checking the novelty of the new work when we have uncertainty based data set or uncertainty environments. The IC ARL0 is the run length characteristic that shows the IC values and OOC neutrosophic ARL1 is the run length characteristic that used for checking the OOC signal at different values of shifts. Moreover, if the OOC neutrosophic ARL1 (NARL1) values are smaller than the attained IC neutrosophic ARL0 (NARL0) value, then a control chart is considered ARL-unbiased. The small the NARL1 value for a specific shift, the more efficient the control chart. The neutrosophic Monte Carlo simulations are utilized to calculate the run-length properties of the NDEWMA and NTEWMA control charts using the R programming language with different values of designed parameters. The run-length characteristics (like NARLs, NSDRLs, NP25, NP50,  and NP75) of the NDEWMA and NTEWMA charts are calculated through neutrosophic Monte Carlo simulations using the following algorithm:

1.    Specify the values of the smoothing parameter and parameters of the distribution (say, μN0=0 and σN=1). Generate random samples with μN0=0 and σN=1 from a normal distribution that is XNi~N(μN0+δσN,1),i=1,2,3,……100. Initially, if δ=0 the process is IC.

2.    Calculate the variance of plotting statistics using Eqs. (4) and (8), then calculate the control limits (LCLN∈[LCLL,LCLU],UCLN∈[UCLL,UCLU]) by adjusting the control limits coefficient (i.e., LN∈[LL,LU],kN∈[kL,kU])) such that the attained NARL0 is equal to the specified NARL0.

3.    Calculate the plotting statistics ZNi and WNi for each random sample using Eqs. (2) and (6).

4.    Compare the plotting statistics calculated in Step 3 to their respective control limits found in Step 2. Proceed until a point plots for the first time beyond the control limits and record the number of rational subgroups as one value of run length.

5.    Steps 1 to 4 are repeated N times (say, N = 104) to obtain the IC run-length characteristics in each instance.

6.    Calculate the neutrosophic mean, the standard deviation of the run-length (RL) and the percentiles of the RL obtained in Step 5 to get the NARL, NSDRL, NP25, NP50,  and NP75. If the attained NARL0 is equal to the specified NARL0, record the control limits and design parameters (these are considered as optimal design parameters and control limits). Otherwise, adjust the value of kN and repeat Steps 1 to 6 until NARL0 is equal to the specified NARL0 value.

7.    Next, generate random samples and use the optimal design parameters and control limits to evaluate the OOC characteristics of the run-length using Steps 3 to 6 by introducing a shift (δ≠0) in the process location and calculate the NARL, NSDRL, NP25, NP50 and NP75.

Note that the design parameters (kN,λN) of the NDEWMA and NTEWMA charts are selected in such a way that the target (or desired) NARL0 value is obtained.

3.2 Performance Evaluation of the NDEWMA and NTEWMA Charts

The control chart is the fundamental method of the SPC for checking the technical analysis of any industrial process monitoring. The performance of the control chart is evaluated using the run-length distribution, which is the most famous method used to check the control chart’s ability to identify the exact value of the run-length characteristics at each δ value. In this paper, we have used the nominal NARL equal to 500 to compute the run-length characteristics under the standard normal distribution, i.e., N(0, 1). To evaluate the OOC run-length distributions, the shift in the process is expressed in terms of the standard deviation, i.e., μN1=μN0+δσN, where δ denotes the scale of shift. The values of NARL1using the Monte Carlo simulations algorithm in Subsection 3.1 are presented in Tabs. 1 and 2 for the NDEWMA chart and Tabs. 3 and 4 for the NTEWMA chart. More specifically, the first row of each cell shows the NARL values, second row of each cell shows the NSDRL and 3rd to 5th rows of each cell show the percentile points (NP25, NP50 and NP75) of the run-length distribution. Tabs. 1 and 2 present the results of proposed NDEWMA control chart when nN∈[1,3] and nN∈[5,10], respectively, for the same values of λN. Tabs. 3 and 4 present the results of proposed NTEWMA control chart when nN∈[1,3] and nN∈[5,10], respectively, for the same values of λN. From Tabs. 1–4, it can be seen that for the same design parameters, there is an increasing trend in the values of NARL1 when λN increase, for small shifts; however, there is a decreasing trend in the values of NARL1 when λN increase, for large shifts. Moreover, small values of λN are preferred over larger values when the detection of small shifts are of interest; however, moderate to large values of λN are more effective in detecting moderate to large shifts. In other words, when shifts increase, the NARL1 shows a decreasing trend when the smoothing constant is large. The NARL1 decrease as the values of nN∈[nL,nU] increase, which implies that an increase in the neutrosophic sample size has a positive effect on the performance of the proposed control charts.

3.3 Comparison of the Proposed Control Charts with the Existing Control Charts

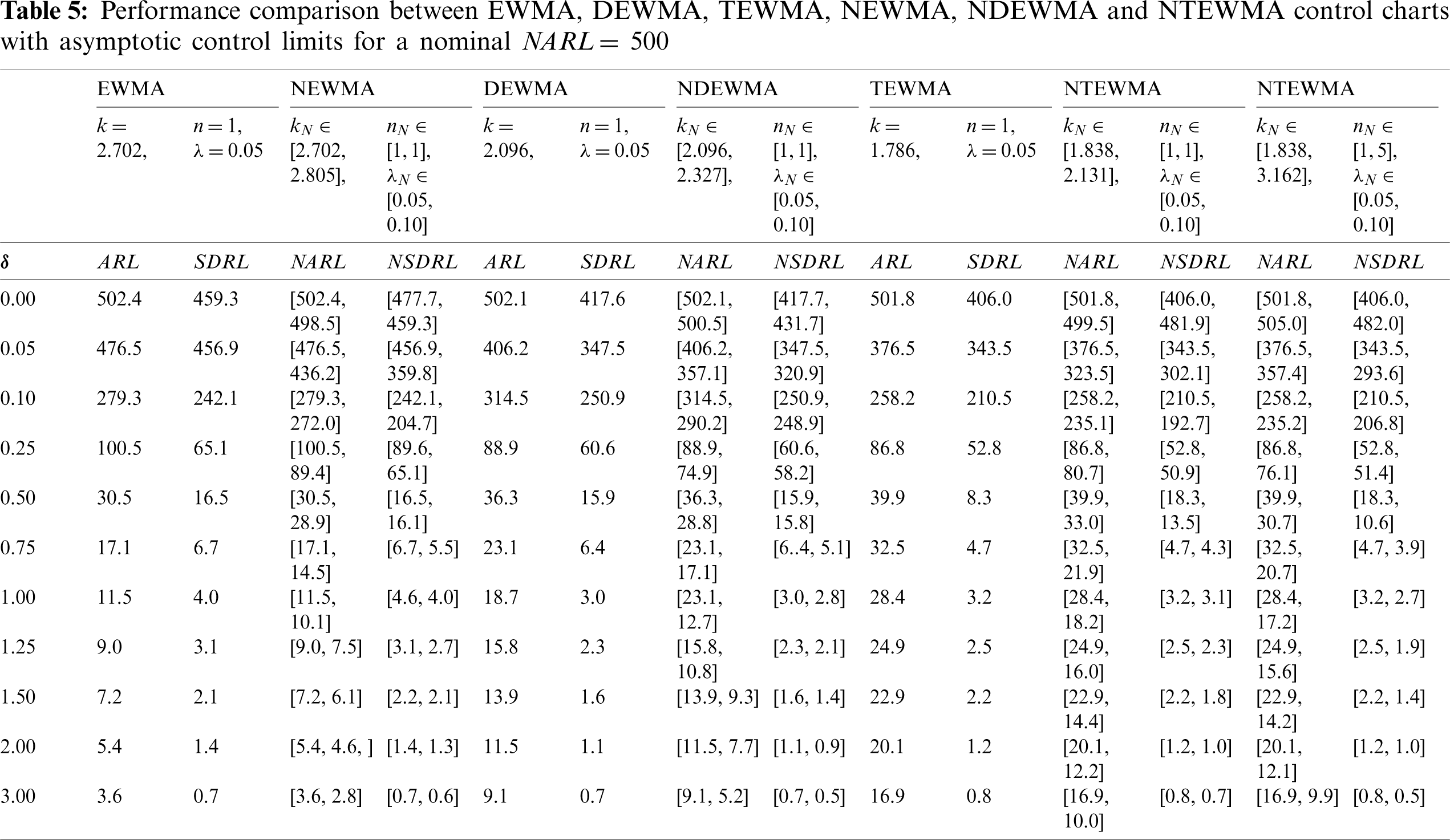
In this section, the comparisons between the two proposed control charts (i.e., NDEWMA and NTEWMA) and the existing NEWMA chart (presented by Aslam et al. [30]) are presented. In addition, the traditional EWMA, DEWMA and TEWMA control charts under classical statistics are also compared with their neutrosophic counterparts. In classical statistics, it is known that a control chart having smaller determined run-length values is said to be efficient in detecting the shift in the process. In neutrosophic theory, a method is said to be efficient if it provides the parameter in the indeterminacy interval rather than the determined values in uncertainty. A chart under the neutrosophic statistics is said to be more efficient if it has smaller values of neutrosophic run-length values than the competing charts. The comparison of the abovementioned control charts are presented in Tab. 5 when n = 1, with λ=0.05 for the classical control charts (with nominal ARL = 500) and λN∈[0.05,0.10] for the neutrosophic control charts (with nominal NARL = 500).

3.3.1 Comparison Performance between NTEWMA and DEWMA Control Charts

In this section, we show the comparison between the implementation of the NTEWMA control chart over the proposed NDEWMA control chart. For the neutrosophic value of λN∈[0.05,0.10] and n=1 the proposed NTEWMA control chart has smeller values at every value of the shift in contrast of NDEWMA control chart. Tab. 5 shows the NARL values of the control charts when sample size n = 1 and neutrosophic λN∈[0.05,0.10], while the NARL values of the control charts when neutrosophic nN∈[1,5] and λN∈[0.05,0.10]. We note that the proposed NTEWMA has smaller values of NARL as compared to the NDEWMA. For example, when n = 1, NARL0N∈[500,500],δ= 0.25, and λN∈[0.05,0.10] the NTEWMA control chart’s NARL and NSDRL are NARL1∈ [71.1, 90.4] and NSDRL1∈ [47.8, 51.2]. Note though, when sample size is nN∈[1,5] with the same λN, the NARL1∈ [80.3, 90.4] and NSDRL1∈ [47.8, 57.3]. The NARL and NSDRL values of the NDEWMA chart are NARL1∈ [82.5, 96.9],NSDRL1∈ [66.0,69.7]. The NTEWMA control chart has the best small shifts performance; however, the NDEWMA control chart has better large shifts performance.

3.3.2 Comparison Performance between NTEWMA, NDEWMA and NEWMA Control Charts

The proposed NTEWMA and NDEWMA control charts seem to have the better performance for small to moderate shifts; however, the existing NEWMA chart (by Aslam et al. [13]) has the better large shift performance, see Tab. 5. From Tab. 5, when λN∈[0.05,0.10],δ=0.25 and n = 1, the NTEWMA chart yields NARL1∈ [71.1, 90.4] and NSDRL1∈ [47.8, 51.2], while the NDEWMA chart yield NARL1∈ [82.5, 96.9] and NSDRL1∈ [69.74, 66.01] [66.0, 69.7] and the NEWMA chart yields NARL1∈ [89.4, 100.5] and NSDRL1∈ [65.1, 89.6]. Thus, it follows that the NTEWMA and NDEWMA charts.

Perform better than the NEWMA chart for small to moderate shifts. Note though, the NEWMA chart has the best performance for large shifts as compared to the NDEWMA and NTEWMA charts.

3.3.3 Comparison Performance between Neutrosophic Charts and Classical Control Charts

It is observed from Tab. 5 that the NEWMA, NDEWMA and NTEWMA charts under neutrosophic statistics have smaller NARL values as compared to the existing EWMA, DEWMA and TEWMA charts under classical statistics, respectively. For example, when δ=0.25, the EWMA and NEWMA charts yield ARL and NARL equal to 100.5 and [89.4, 100.5], respectively. Similarly, the DEWMA and NDEWMA charts yield 96.9 and [82.5, 96.9], respectively. Finally, the TEWMA and NTEWMA charts yield 90.4 and [71.1, 90.4], respectively. The comparisons of the proposed control charts under neutrosophic statistics show their superiority as compared to the existing control charts under classical statistics. Finally, it is worth noting that the neutrosophic charts reduces to their corresponding classical statistics chart when there is no indeterminacy.

4  Illustrative Examples

4.1 Simulated Data

For the simulated data, we suppose that nN∈[1,3],NARL0=500 and λN∈[0.05,0.10]. Note that 200 observations of the process mean from the normal distribution are generated, the first 100 observations were generated assuming that the process is IC, with μ0N=0 and σN=1 and the next 100 observations are generated assuming that the process has shifted with δ=0.5. The simulated data along with XNi∈[XL,XU] as well as the EWMA,DEWMA,DEWMAN,TEWMA, and TEWMAN charting statistics are shown in Figs. 1–6. From Tabs. 1 and 3, the calculated NARL for NDEWMA chart is NARL1∈ [31.3, 37.3] and the one for the NTEWMA chart is NARL1∈ [29.9, 40.9]; thus, it is expected that the shift in the simulated data of the NDEWMA and NTEWMA charts should be detected OOC between samples 31 and 37 and between samples 29 and 40, respectively. Using the asymptotic control limits, we select λN∈[0.05,0.10] and the control limits coefficients for the NEWMA chart are kN∈[2.702,2.805], while those of the NDEWMA chart are kN∈[2.096,4.112] and for the NTEWMA chart, kN∈[1.839,2.870]. From Alevizakos et al. [27], the control limits coefficients of the EWMA, DEWMA and TEWMA charts are given by k = 2.702, 2.055 and 1.838, respectively.

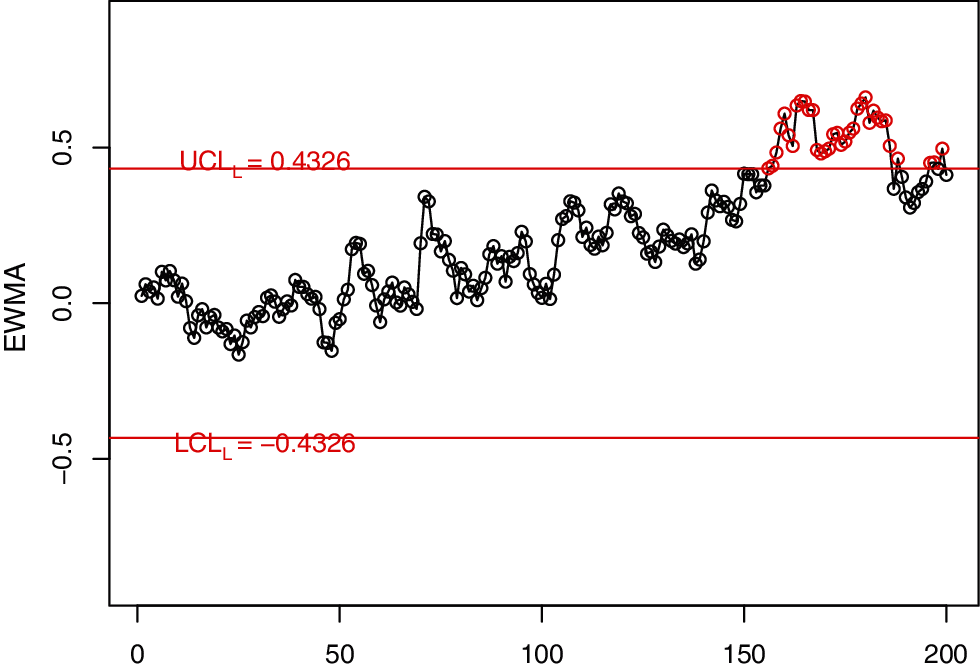
Figure 1: The EWMA control charts for simulated data

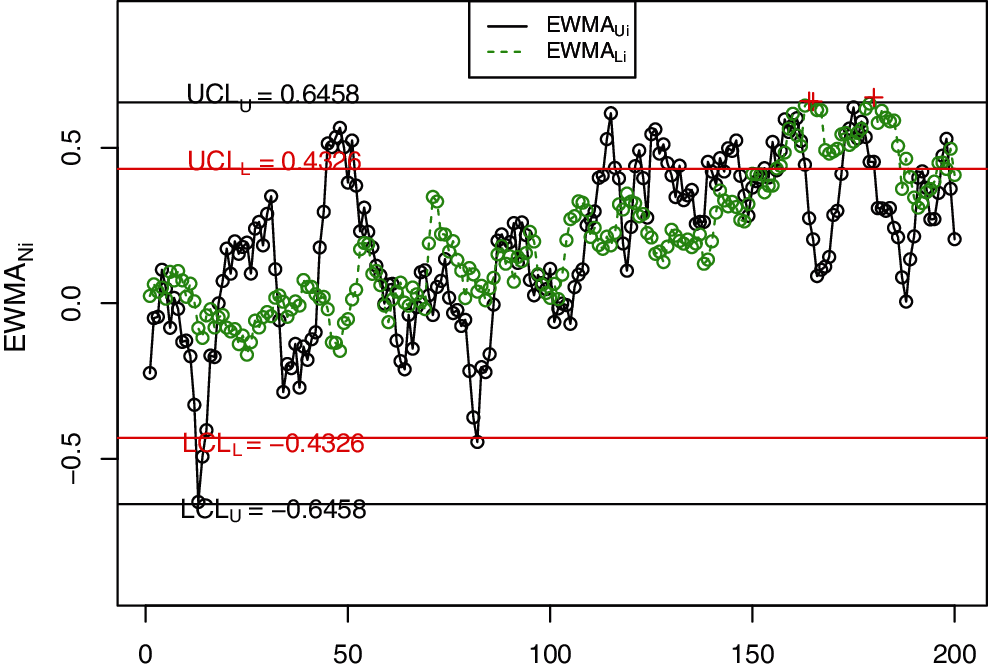
Figure 2: The NEWMA control charts for simulated data

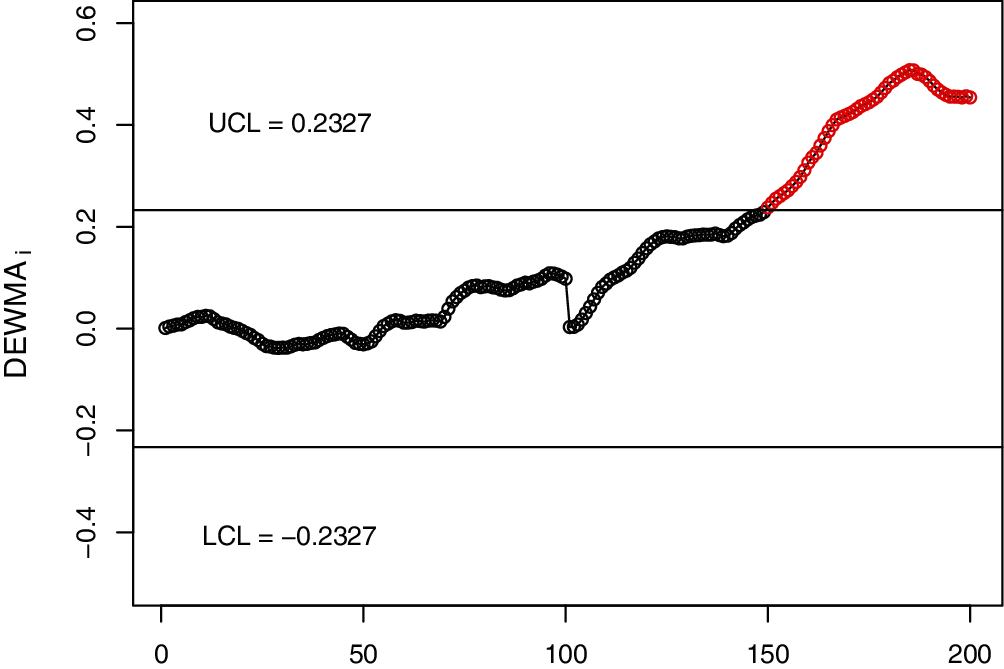
Figure 3: The DEWMA control charts for simulated data

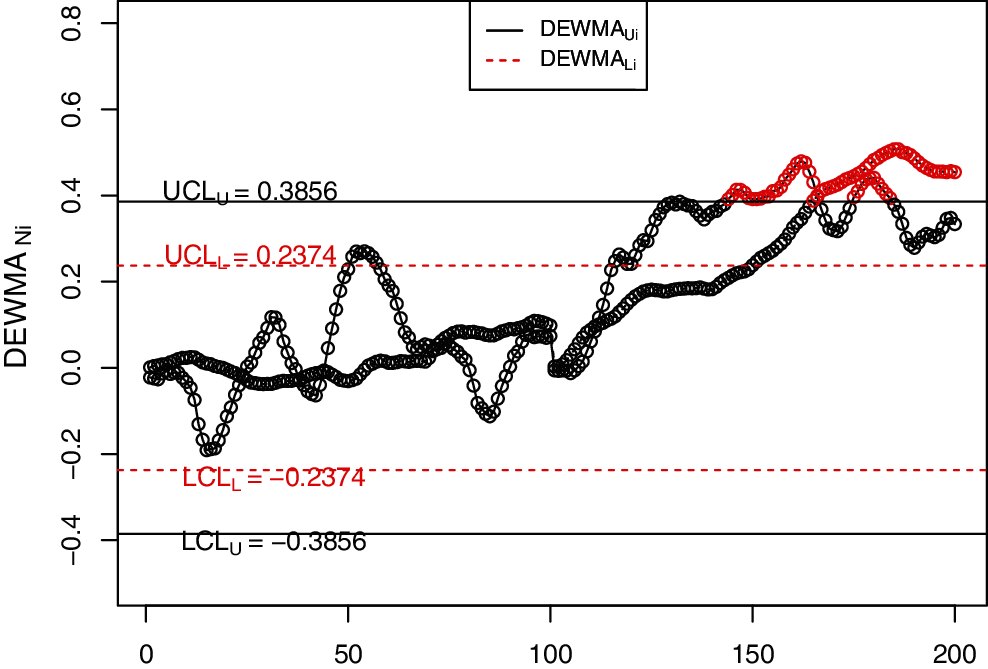
Figure 4: The NDEWMA control charts for simulated data

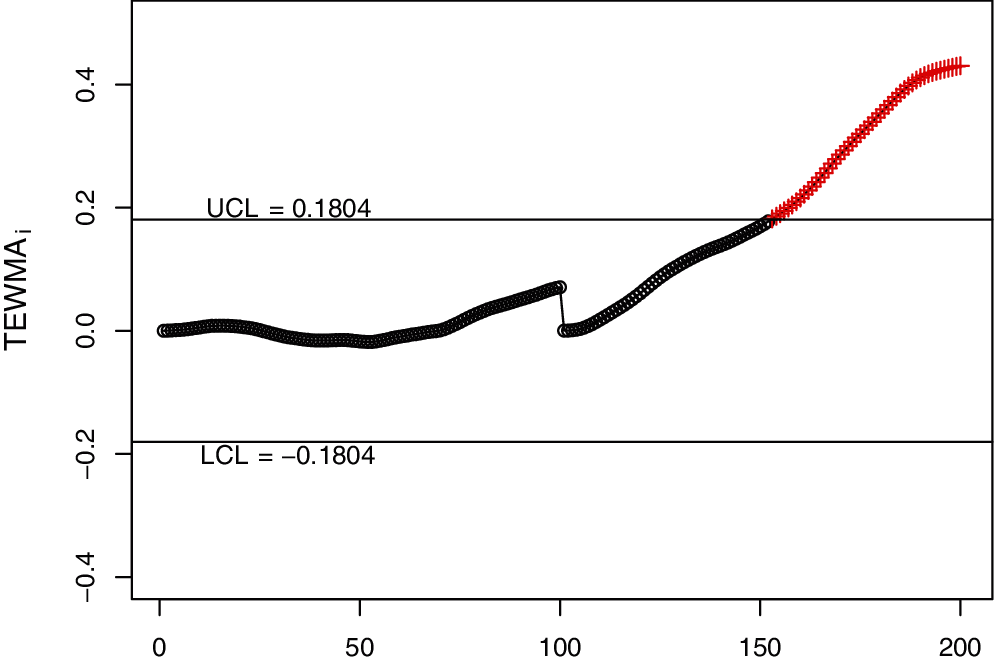
Figure 5: The TEWMA control charts for simulated data

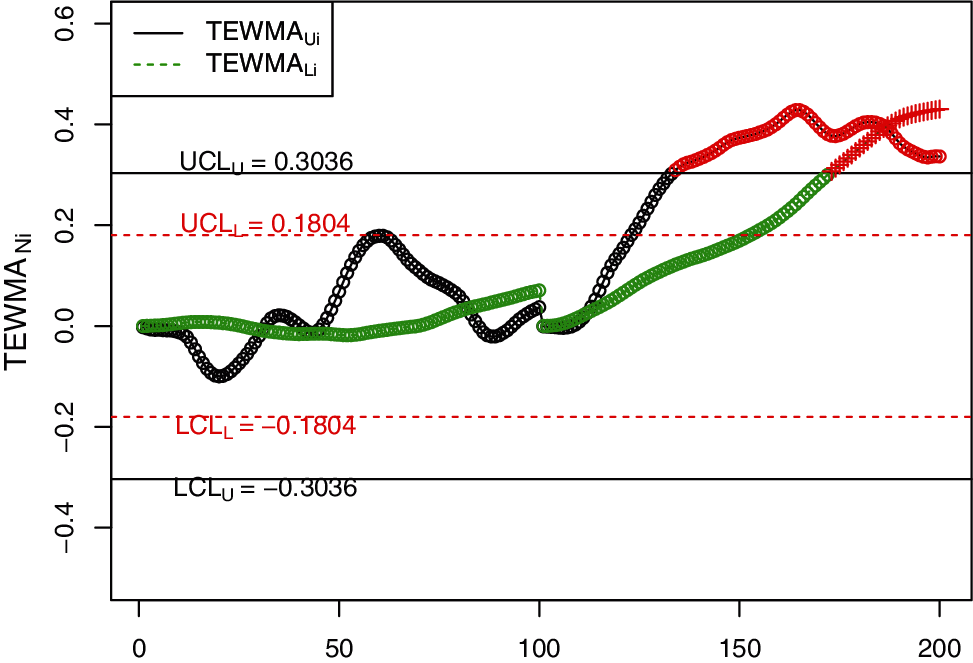
Figure 6: The proposed NTEWMA control charts for simulated data

In order to visually display the implementation of the NDEWMA and NTEWMA charts against the existing EWMA, DEWMA and TEWMA charts, Figs. 1–6 is constructed. The proposed NTEWMA chart detects the shift after the 130th observation while the NDEWMA chart detects the shift after the 144th observation but the existing NEWMA control chart (by Aslam et al. [30]) does not detect any shift. The existing classical EWMA, DEWMA and TEWMA control charts detect shifts after the 155th observation. This indicates the superiority of the NTEWMA chart over the NDEWMA and NEWMA charts as well as the classical EWMA, DEWMA and TEWMA charts in quickly detecting small shifts.

4.2 A Real Data Application

In this section, we use a real-life application discussed by Faisal et al. [31] to illustrate the application of the NDEWMA and NTEWMA charts. The dataset (i.e., The real life application example results dataset can be obtained from authors on request) is based on the voltage on the fixed capacitance level and contains 200 observations. The first 100 observations are obtained by applying a capacitance (C) of 200μF and are considered as IC observations. The dataset is found to follow a normal process model and the IC values of mean and variance are μ0=396.9804 V and σ02= 1.9887 V, respectively. The next 100 observations are obtained by applying a capacitance of 150μF and represent the OOC observations. The voltage and capacitance have an inverse relationship, i.e., when capacitance decrease then voltage increases. So, an electrical engineer decides to implement the NTEWMA chart with steady-state (or asymptotic) control limits to detect a shift of δ=1.5. Assuming that the nominal NARL0 = 500, the optimal neutrosophic design parameters are λN∈[0.55,0.60] and kN∈[2.941,2.989] for NTEWMA and the coefficient of the control limits for the NDEWMA chart are kN∈[3.073,3.086]. The proposed NTEWMA chart is displayed in Fig. 7, where the shift in the voltage mean is detected after the 111th observation. The NDEWMA chart is displayed in Fig. 8, where the shift in the voltage mean is detected after the 113th observation. The classical EWMA, NEWMA, classical DEWMA and classical TEWMA charts detect the shift after the 158th, 121st, 119th, and 120th observations, respectively (see Figs. 9–12). This indicates that the proposed NTEWMA control chart works more efficiently as compared to the competing charts under the uncertainty environment. It is worth mentioning that the proposed NDEWMA control chart also performs better than the existing NEWMA chart in an uncertain environment. More importantly, it is observed that the neutrosophic charts tend to outperform their classical counterparts.

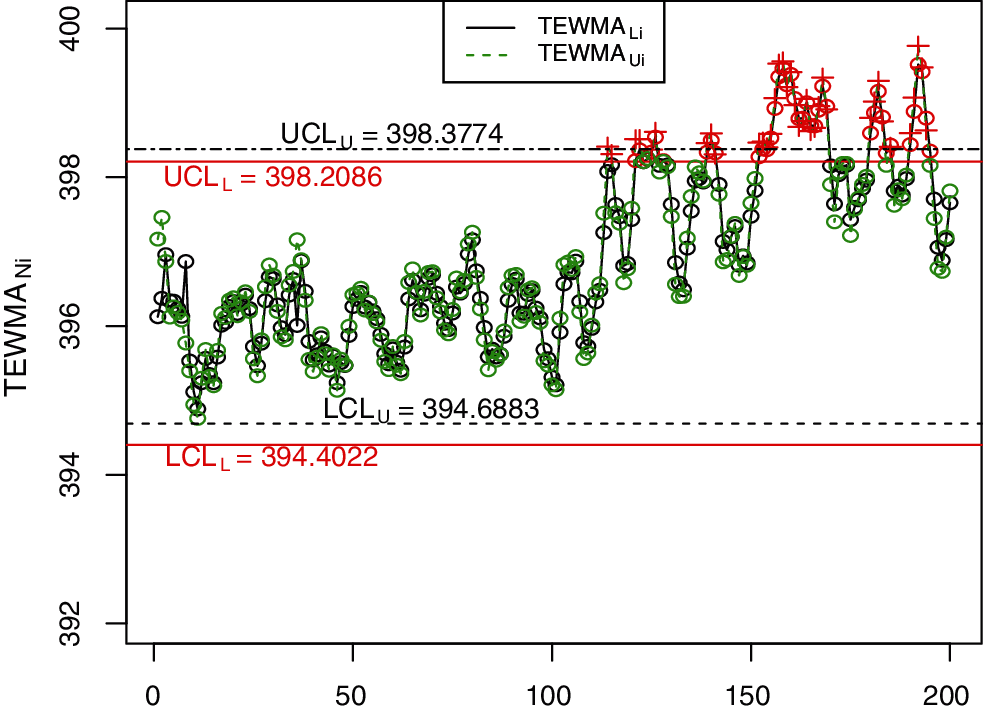
Figure 7: The proposed NTEWMA control chart for real life data

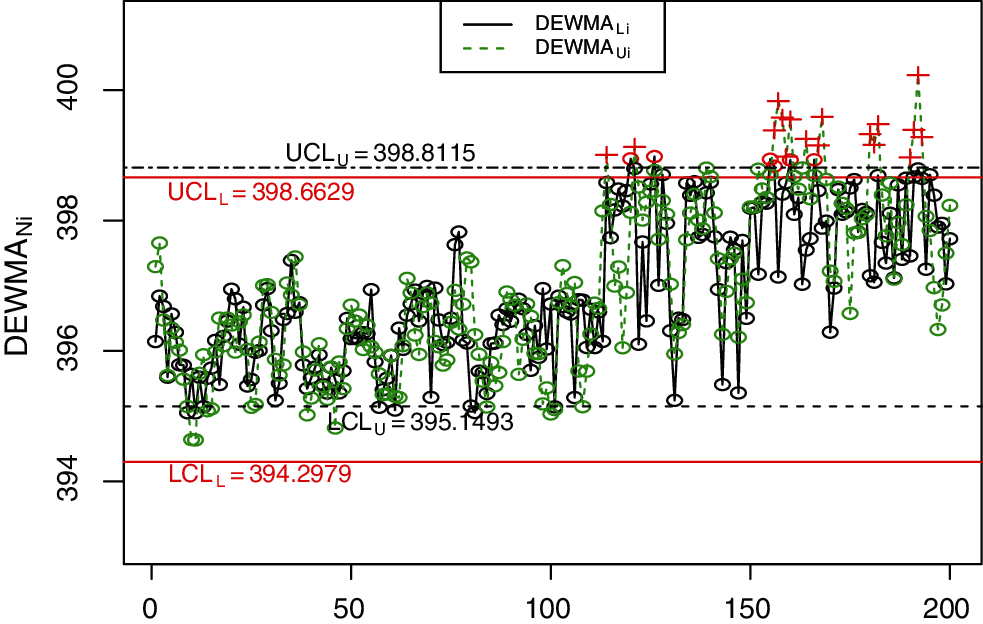
Figure 8: The proposed NDEWMA control chart for real-life data

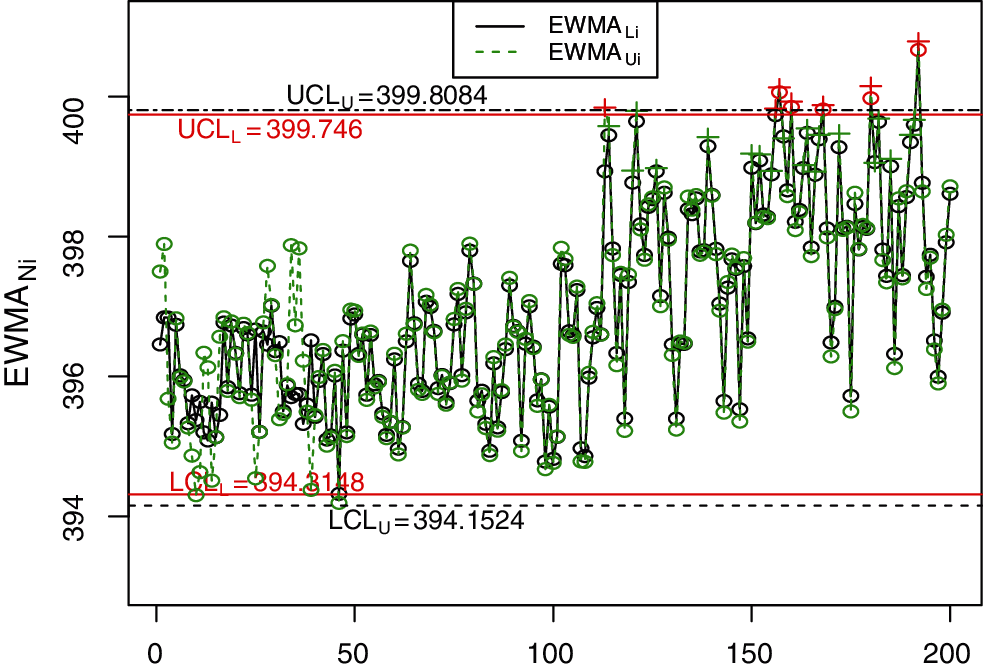
Figure 9: The NEWMA control chart for real-life data

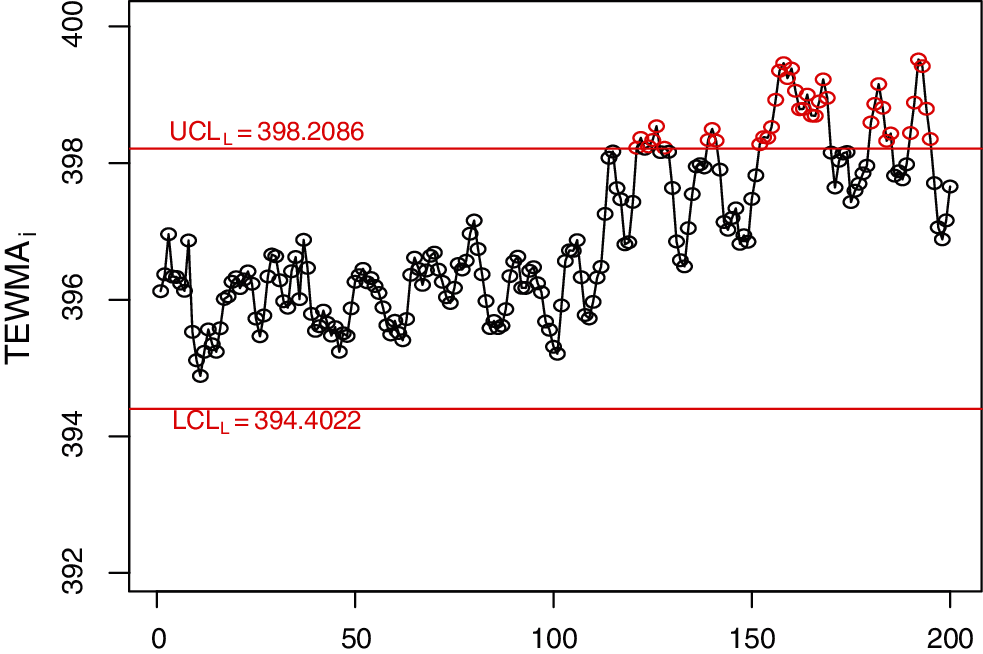
Figure 10: The classical TEWMA control chart for real-life data

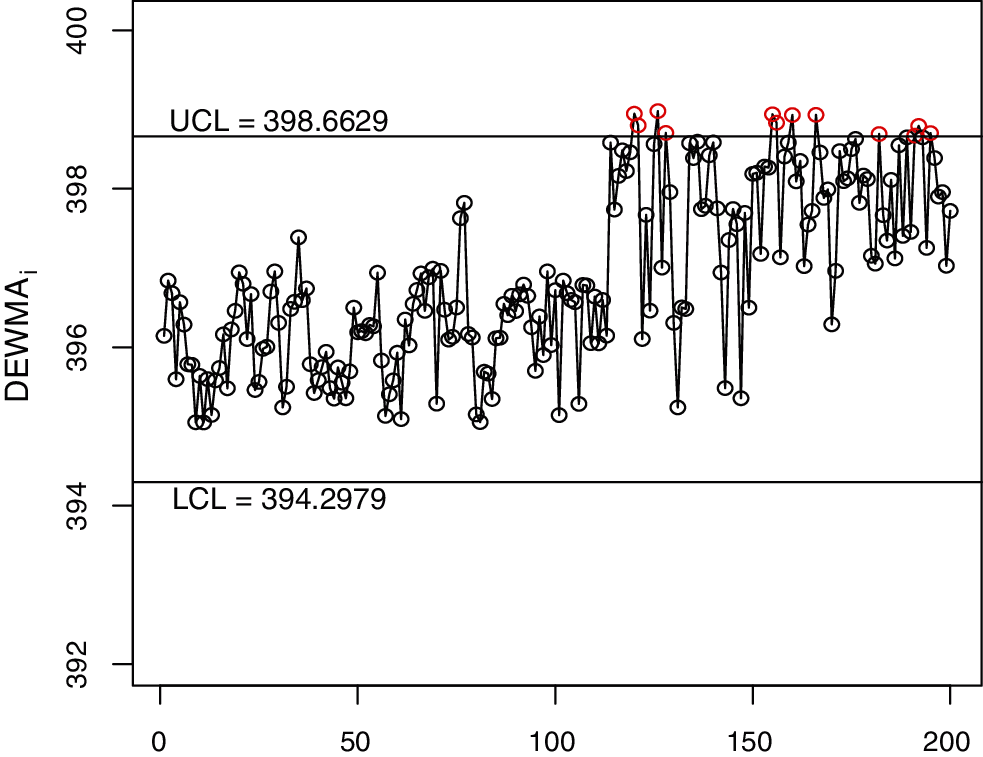
Figure 11: The classical DEWMA control chart for real-life data

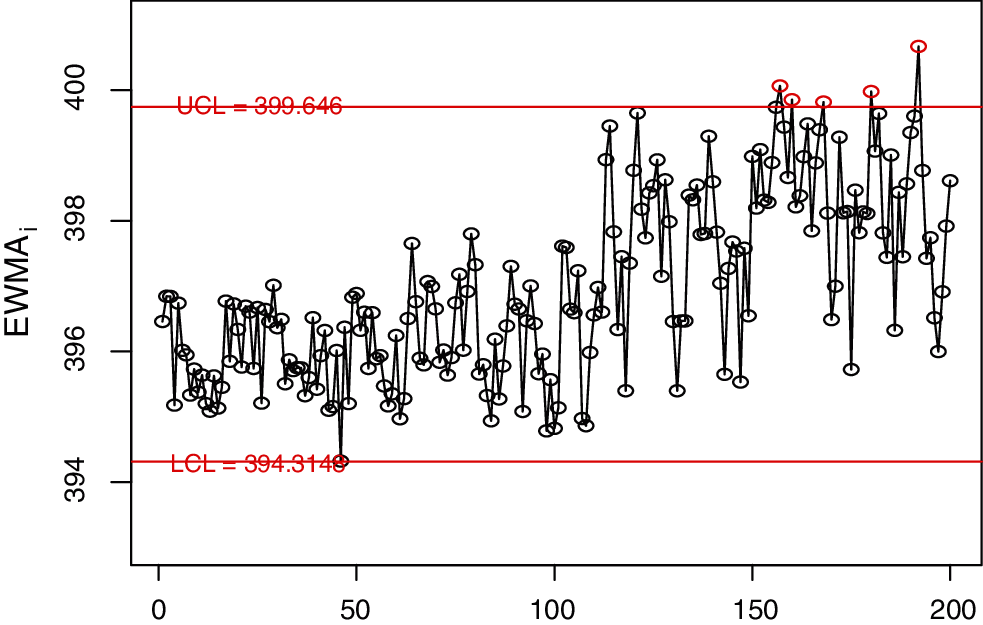
Figure 12: The classical EWMA control chart for real-life data

5  Concluding Remarks

The traditional Shewhart chart is the most preferred monitoring scheme in detecting large shifts more quickly; however, for small-to-moderate shift detection, the EWMA, DEWMA, and TEWMA control charts have been shown to have better performance. In this paper, we proposed new NDEWMA and NTEWMA control charts under an uncertainty environment, and these are shown to outperform the existing NEWMA chart for small shifts detection. We studied its run-length performance using the asymptotic control limits under neutrosophic environments with neutrosophic Monte Carlo simulations in R software. The NTEWMA chart is more efficient in a wider range of shifts as the value of the smoothing parameter increases. The results showed that the NTEWMA chart is very efficient in small shift detection when the smoothing constants are small. Finally, we applied the NTEWMA and NDEWMA charts as well as the EWMA, NEWMA, DEWMA, and TEWMA charts to simulated data and data from an electrical engineering process, where the results confirmed the findings.

The proposed charts using other sampling schemes can be studied as future research. The proposed control charts can be extended as future research to monitor process dispersion and joint monitoring for univariate and multivariate setup under a complex system or under an uncertainty. Moreover, the proposed charts using some non-normal distribution can be considered as future research.

Funding Statement: This work was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah. The authors, therefore, gratefully acknowledge the DSR technical and financial support.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Shewhart, W. A. (1926). Quality control charts. The Bell System Technical Journal, 5(4), 593–603. DOI 10.1002/j.1538-7305.1926.tb00125.x. [Google Scholar] [CrossRef]

 2.  Page, E. S. (1954). Continuous inspection schemes. Biometrika, 41(1/2), 100–115. DOI 10.2307/2333009. [Google Scholar] [CrossRef]

 3.  Roberts, S. W. (2000). Control chart tests based on geometric moving averages. Technometrics, 42(1), 97–101. DOI 10.1080/00401706.2000.10485986. [Google Scholar] [CrossRef]

 4.  Shamma, S. E., Amin, R. W., Shamma, A. K. (1991). A double exponentially weigiited moving average control procedure with variable sampling intervals. Communications in Statistics-Simulation and Computation, 20(2–3), 511–528. DOI 10.1080/03610919108812969. [Google Scholar] [CrossRef]

 5.  Shamma, S. E., Shamma, A. K. (1992). Development and evaluation of control charts using double exponentially weighted moving averages. International Journal of Quality & Reliability Management, 9(6), 18–25. DOI 10.1108/02656719210018570. [Google Scholar] [CrossRef]

 6.  Shafqat, A., Huang, Z., Aslam, M., Nawaz, M. S. (2020). A nonparametric repetitive sampling DEWMA control chart based on linear prediction. IEEE Access, 8, 74977–74990. DOI 10.1109/ACCESS.2020.2989132. [Google Scholar] [CrossRef]

 7.  Capizzi, G., Masarotto, G. (2003). An adaptive exponentially weighted moving average control chart. Technometrics, 45(3), 199–207. DOI 10.1198/004017003000000023. [Google Scholar] [CrossRef]

 8.  Zhang, L., Chen, G. (2005). An extended EWMA mean chart. Quality Technology and Quantitative Management, 2(1), 39–52. DOI 10.1080/16843703.2005.11673088. [Google Scholar] [CrossRef]

 9.  Hunter, J. S. (1986). The exponentially weighted moving average. Journal of Quality Technology, 18(4), 203–210. DOI 10.1080/00224065.1986.11979014. [Google Scholar] [CrossRef]

10. Lucas, J. M., Saccucci, M. S. (1990). Exponentially weighted moving average control schemes: Properties and enhancements. Technometrics, 32(1), 1–12. DOI 10.1080/00401706.1990.10484583. [Google Scholar] [CrossRef]

11. Zaman, B., Lee, M. H., Riaz, M., Abujiya, M. A. R. (2017). An adaptive EWMA scheme-based CUSUM accumulation error for efficient monitoring of process location. Quality and Reliability Engineering International, 33(8), 2463–2482. DOI 10.1002/qre.2203. [Google Scholar] [CrossRef]

12. Reynolds Jr, M. R., Stoumbos, Z. G. (2006). Comparisons of some exponentially weighted moving average control charts for monitoring the process mean and variance. Technometrics, 48(4), 550–567. DOI 10.1198/004017006000000255. [Google Scholar] [CrossRef]

13. Aslam, M., Khan, N., Jun, C. H. (2015). A new S2 control chart using repetitive sampling. Journal of Applied Statistics, 42(11), 2485–2496. DOI 10.1080/02664763.2015.1043861. [Google Scholar] [CrossRef]

14. Faraz, A., Moghadam, M. B. (2007). Fuzzy control chart a better alternative for Shewhart average chart. Quality & Quantity, 41(3), 375–385. DOI 10.1007/s11135-006-9007-9. [Google Scholar] [CrossRef]

15. FazalZarandi, M. H., Alaeddini, A., Turksen, I. B. (2008). A hybrid fuzzy adaptive sampling–-Run rules for Shewhart control chart. Information Sciences, 178(4), 1152–1170. DOI 10.1016/j.ins.2007.09.028. [Google Scholar] [CrossRef]

16. Faraz, A., Kazemzadeh, R. B., Moghadam, M. B., Bazdar, A. (2010). Constructing a fuzzy Shewhart control chart for variables when uncertainty and randomness are combined. Quality & Quantity, 44(5), 905–914. DOI 10.1007/s11135-009-9244-9. [Google Scholar] [CrossRef]

17. Wang, D., Hryniewicz, O. (2015). A fuzzy nonparametric Shewhart chart based on the bootstrap approach. International Journal of Applied Mathematics and Computer Science, 25(2), 389–401. DOI 10.1515/amcs-2015-0030. [Google Scholar] [CrossRef]

18. Kahraman, C., Gülbay, M., Boltürk, E. (2016). Fuzzy shewhart control charts. Cham: Springer. [Google Scholar]

19. Khan, M. Z., Khan, M. F., Aslam, M., Niaki, S. T. A., Mughal, A. R. (2018). A fuzzy EWMA attribute control chart to monitor process mean. Information, 9(12), 312. DOI 10.3390/info9120312. [Google Scholar] [CrossRef]

20. Aslam, M., Shafqat, A., Albassam, M., Malela-Majika, J. C., Shongwe, S. C. (2021). A new CUSUM control chart under uncertainty with applications in petroleum and meteorology. PLoS One, 16(2), e0246185. DOI 10.1371/journal.pone.0246185. [Google Scholar] [CrossRef]

21. Smarandache, F. (2014). Introduction to neutrosophic statistics. USA: Sitech and Education Publishing. [Google Scholar]

22. Chen, J., Ye, J., Du, S. (2017). Scale effect and anisotropy analyzed for neutrosophic numbers of rock joint roughness coefficient based on neutrosophic statistics. Symmetry, 9(10), 208. DOI 10.3390/sym9100208. [Google Scholar] [CrossRef]

23. Chen, J., Ye, J., Du, S., Yong, R. (2017). Expressions of rock joint roughness coefficient using neutrosophic interval statistical numbers. Symmetry, 9(7), 123. DOI 10.3390/sym9070123. [Google Scholar] [CrossRef]

24. Aslam, M. (2018). A new sampling plan using neutrosophic process loss consideration. Symmetry, 10(5), 132. DOI 10.3390/sym10050132. [Google Scholar] [CrossRef]

25. Aslam, M., Bantan, R. A., Khan, N. (2019). Design of a new attribute control chart under neutrosophic statistics. International Journal of Fuzzy Systems, 21(2), 433–440. DOI 10.1007/s40815-018-0577-1. [Google Scholar] [CrossRef]

26. Aslam, M., Bantan, R. A., Khan, N. (2019). Monitoring the process based on belief statistic for neutrosophic gamma distributed product. Processes, 7(4), 209. DOI 10.3390/pr7040209. [Google Scholar] [CrossRef]

27. Alevizakos, V., Chatterjee, K., Koukouvinos, C. (2021). The triple exponentially weighted moving average control chart. Quality Technology & Quantitative Management, 18(3), 326–354. DOI 10.1080/16843703.2020.1809063. [Google Scholar] [CrossRef]

28. Riaz, M., Abbas, Z., Nazir, H. Z., Abid, M. (2021). On the development of triple homogeneously weighted moving average control chart. Symmetry, 13(2), 360. DOI 10.3390/sym13020360. [Google Scholar] [CrossRef]

29. Letshedi, T. I., Malela-Majika, J. C., Castagliola, P., Shongwe, S. C. (2021). Distribution-free triple EWMA control chart for monitoring the process location using the Wilcoxon rank-sum statistic with fast initial response feature. Quality and Reliability Engineering International, 1–18. DOI 10.1002/qre.2842. [Google Scholar] [CrossRef]

30. Aslam, M., AL-Marshadi, A. H., Khan, N. (2019). A new X-bar control chart for using neutrosophic exponentially weighted moving average. Mathematics, 7(10), 957. DOI 10.3390/math7100957. [Google Scholar] [CrossRef]

31. Faisal, M., Zafar, R. F., Abbas, N., Riaz, M., Mahmood, T. (2018). A modified CUSUM control chart for monitoring industrial processes. Quality and Reliability Engineering International, 34(6), 1045–1058. DOI 10.1002/qre.2307. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.