
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2021.016870
ARTICLE
Reliability Modeling and Evaluation of Complex Multi-State System Based on Bayesian Networks Considering Fuzzy Dynamic of Faults
School of Intelligent Manufacturing, Chengdu Technological University, Chengdu, 611730, China
*Corresponding Author: Fangjun Zuo. Email: zuofangjun@126.com
Received: 04 April 2021; Accepted: 11 May 2021
Abstract: In the traditional reliability evaluation based on the Bayesian method, the failure probability of nodes is usually expressed by the average failure rate within a period of time. Aiming at the shortcomings of traditional Bayesian network reliability evaluation methods, this paper proposes a Bayesian network reliability evaluation method considering dynamics and fuzziness. The fuzzy theory and the dynamic of component failure probability are introduced to construct the dynamic fuzzy set function. Based on the solving characteristics of the dynamic fuzzy set and Bayesian network, the fuzzy dynamic probability and fuzzy dynamic importance degree of the fault state of leaf nodes are solved. Finally, through the dynamic fuzzy reliability analysis of CNC machine tool hydraulic system balance circuit, the application of this method in system reliability evaluation is verified, which provides support for fault diagnosis of CNC machine tools.
Keywords: Bayesian network (BN); dynamics; fuzzy; multi-state
Owing to the development of mechanical products becoming increasingly complex, reliability evaluation and prediction of such systems have always focused on reliability engineering research [1,2]. The relationship between the faulty logic and the fault probability of each component of the system with time is more and more complex. In the reliability evaluation, whether the quantification method with uncertain parameters is close to the actual engineering conditions has an important impact on the accuracy of the evaluation [3,4]. Nowadays, the development theory of system reliability analysis in static environments has been dramatically developed. A relatively perfect theoretical system has been formed: binary decision diagram analysis method, binary decision algorithm, recursive analysis method, fault tree analysis method, and Bayesian analysis method [4,5]. This static system reliability of the method is based on two fundamental assumptions (probability hypothesis and binary hypothesis) and four premises (event definition exists, a large number of samples with probability repeatability and good distribution, not influenced by human factors) [6,7]. However, due to the various performance indicators, working environments and small-batch customization of the complex system structure, the reliability state of a complex system is often associated with multiple performance indicators, and there is a specific correlation between multiple performance indicators [8]. Thus, the failure probability of a complex system has shown the characteristics of dynamic fuzziness [9–11]. The fuzziness of system and component behavior and the dynamic operating environment of the system brings additional difficulties to estimate the failure probability of important events accurately. In these cases, it is unrealistic and impossible to use determined values to represent component failure behavior.
In order to solve these problems, new theories are developed and applied to reliability analysis, including fuzzy theory [10–13], confidence interval estimation theory [14], imprecise probability theory [7], Dempster-Shafer evidence theory (DSET) [15], possibility theory [16], etc. The use of fuzzy mathematics to deal with the problem of reliability began in the mid-1970s. Kaufmann et al. [17] introduced the concept of possibility to represent the reliability of components in 1975. Yao et al. [18] proposed the concept of the structural fuzzy safety measure and proposed using fuzzy set theory to represent the reliability of structures, which made a significant development of fuzzy reliability theory. Ayyub et al. [19] reviewed the application of fuzzy mathematics to structural reliability. Spz et al. [10] used the function approximation method to estimate the random interval reliability of structures. In this work, fuzzy random variables are used for reliability analysis. Bayesian network is a standard method for system reliability analysis [16]. Compared with other reliability evaluation methods, Bayesian networks possess obvious advantages in modelling, analysis and calculation. In addition, the Bayesian network also has the advantage of reverse reasoning [5]. Considering the system's dynamic characteristics, many scholars have studied the relationship between dynamic fault trees and dynamic Bayesian networks [6]. By transforming a dynamic fault tree into a dynamic Bayesian network, the reliability modelling and evaluation of the dynamic system are realized [12]. Huang et al. [16] analyzed the reliability of fuzzy life data based on the Bayesian method. Wu [20] and Taheri et al. [21] modelled the system parameters with fuzzy random variables and established the fuzzy reliability evaluation method based on Bayesian inference with fuzzy prior distribution parameters. Zhang et al. [22] introduced variables into the construction of fuzzy support radius and proposed a Bayesian network based on fuzzy support radius for multi-state fault diagnosis. Simon et al. [23] used the Bayesian network to evaluate the reliability of complex systems with epistemic uncertainty. In a complex mechanical system, due to the influence of various factors such as its environment, its material performance, human operation and so on, its reliability index generally shows a decreasing trend with the increase of working time. The decreasing process is dynamic, so the influence of the time factor cannot be ignored in the reliability analysis of the system or components. Moreover, the failure data obtained is also discrete, so it is difficult to characterize the change rule of failure probability with a simple function [24–27]. Applying Bayesian networks to realize the reliability evaluation of such complex multi-state systems is a problem worthy of study.
In this paper, the dynamic fuzzy set theory has been proposed in the Bayesian network evaluation. The reliability of the complex multi-state system is studied by considering the fault dynamics and fuzzy. Section 1 retrospect the theoretical basis of this research. Section 2, introduces the node definition and network inference of multi-state network, section considering fault dynamics and fuzzy. Section 3, the presented method is applied to the hydraulic system balance circuit as an example, and a brief conclusion follows it in Section 4.
2 Modeling and Evaluation of Multi State Bayesian Networks
Bayesian networks (BN) have the characteristics of bidirectional reasoning, that is, forward reasoning and reverse reasoning [28]. The inference used to judge the tendency and possibility of system failure in the system design stage is called positive reasoning, and positive reasoning is also called causal reasoning. The reasoning used to determine the main reasons for system failure after a system failure is called reverse reasoning. Reverse reasoning is also known as diagnostic reasoning, according to which reverse reasoning can find the system's weak links to provide a basis for safety management and system design improvement [29,30].
BN is a subjective view based on probability. Suppose
where
BN is a representation and reasoning model of uncertain knowledge based on probability analysis and graph theory [27]. When the probability distribution of node variables is known, the Bayesian network can realize qualitative and quantitative uncertainty representation [28]. The Directed acyclic graphs (DAG) and conditional probability tables (CPT) are two parts of the BN model. The DAG can explain the logic structure of BN, which is a part of qualitative analysis [29]. Nodes without parents are called root nodes, nodes without sub-nodes are called leaf nodes, and other nodes are called intermediate nodes. The CPT is used for conditional probabilities under different fault states. The CPT represents the strength of the relationship between nodes which is a part of the quantitative analysis of BN [30].
The BN is depicted in Fig. 1. Here,
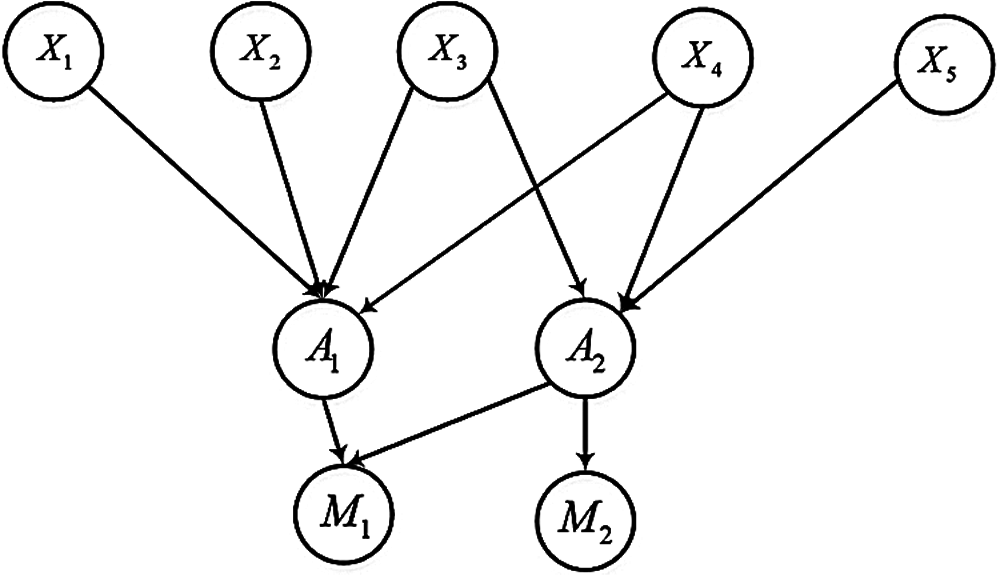
Figure 1: Bayesian network structure
When the node state in a Bayesian network goes out of the two-state assumption, i.e., the node has several states, the traditional Bayesian network will be extended to a multi-state Bayesian network. In practical engineering, systems and components often have various fault modes and present different fault states. Reliability modelling of multi-state systems is often based on fault tree analysis using the extended multi-state fault tree analysis method [16]. The CPT of the Bayesian network is reconstructed by using expert knowledge and practical experience so that the logic relationship, uncertainty and multi-state component fault, which traditional Bayesian networks cannot express, are reflected [21]. Therefore, when the Bayesian network is used to deal with the polymorphism of variables, different state values can be selected to represent different fault states of nodes, and only the CPT of corresponding nodes needs to be adjusted [22].
2.2 Definition Fuzzy Node of BN
In order to characterize the influence of subjective uncertainty on system reliability due to the lack of system cognition and limited information, some scholars proposed to further extend the continuous node variables of Bayesian networks to fuzzy node variables [31]. When the fault probability of a Bayesian network node is difficult to express with exact value, the fault probability of the node is expressed with a fuzzy subset. The definition of a fuzzy BN node is divided into two steps. The first step is to describe the failure state of the fuzzy node, and the second step is to describe the failure rate of the fuzzy node [32].
2.2.1 Description of the Fault States of Fuzzy Node
In engineering, due to the limitation of objective conditions and the influence of various uncertainties, we often encounter the situation of insufficient data or incomplete information. Therefore, the failure probability of parts is difficult to obtain in the reliability analysis. The fuzzy set theory provides a suitable modelling tool for some cases where the parameters are fuzzy numbers. Zadeh put forward the definition of a fuzzy subset in 1965 [13]. Latife introduced the fuzzy set theory into Bayesian networks to evaluate the fuzzy reliability of production management systems [33]. A fuzzy set is not a single value but a set of possibilities [17]. In fuzzy BN, we usually use fuzzy language variables to describe different fault states of the root node [8]. In this paper, the language information is adopted to describe the fault state, which can be divided into no fault, half fault and complete fault.
The membership functions of fuzzy subsets are of many forms, such as trapezoidal membership function, rectangular membership function, normal distribution membership function and lognormal membership function, etc. Because the triangle membership function is the most widely used and algebraic operation is simple, the triangular fuzzy number is considered in this paper.
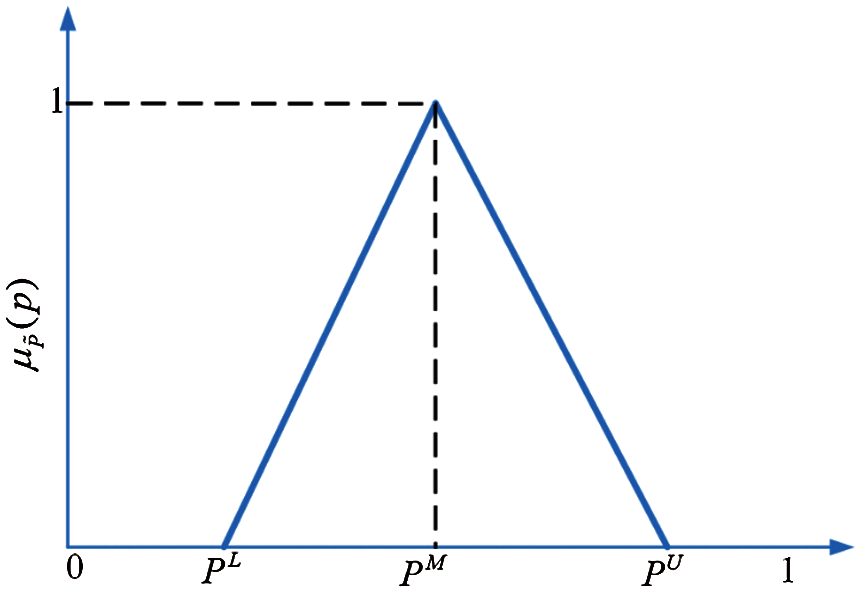
Figure 2: The membership function of triangular fuzzy number
The fuzziness and multi-state of nodes are considered in the above analysis. Due to the influence of various factors such as its environment, its material performance, human operation and so on, its reliability index generally shows a decreasing trend with the increase of working time. The decreasing process is dynamic, so the influence of the time factor cannot be ignored in the reliability analysis of the system or components. When the system reliability analysis is carried out, if any system's characteristic is ignored, the analysis result will produce an enormous error [8].
2.2.2 Quantification of Uncertainty of Root Node
In practice engineering, the failure probability of each component in the system varies with time, and the time variable is introduced, so the fuzzy dynamic function is used to describe the fuzzy state of each root node in this paper.
For a BN with finite nodes, the set of nodes is
where
where
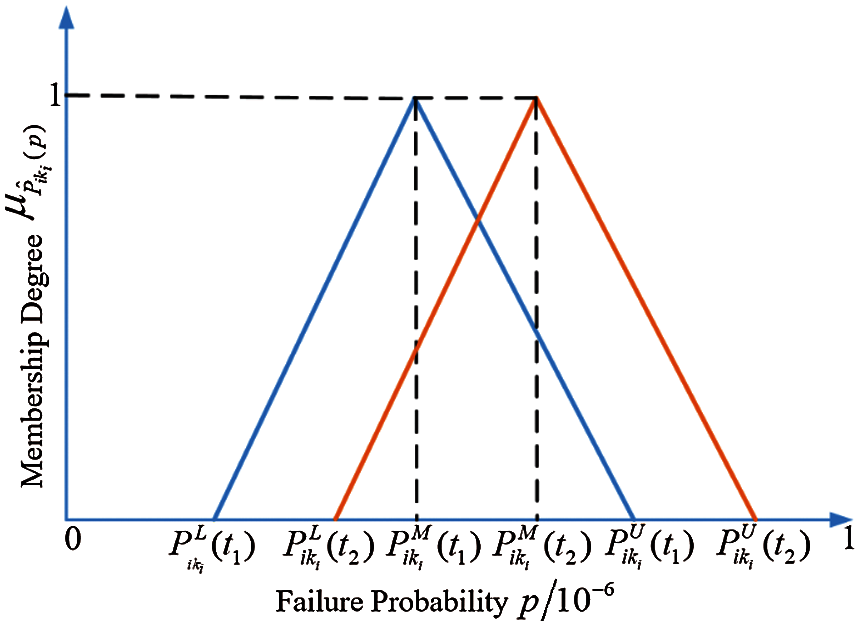
Figure 3: The membership function of
According to the characteristics of node failure probability changing with time and combining with the fuzzy subset of triangle membership function, a dynamic fuzzy set was established to describe the function relation of root node failure probability changing with time
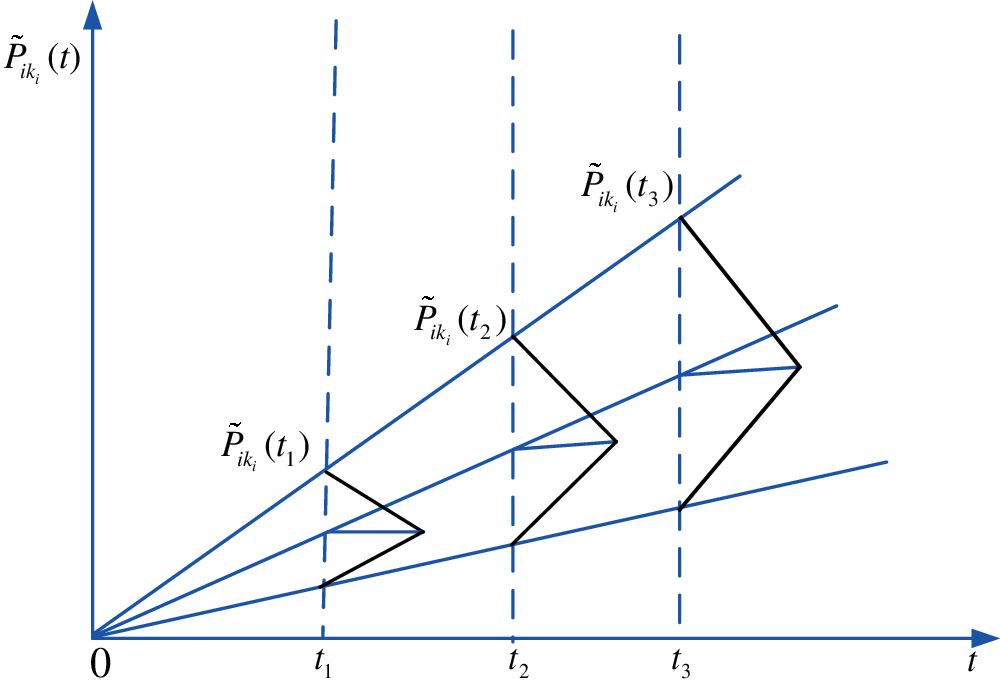
Figure 4: The failure probability of node with time
2.3 Analysis of Node Failure Possibility
In a multi-state BN system, which have
in which
where
2.4 Importance Analysis of Fuzzy Dynamic Root Node
The fuzzy importance degree of BN describes the evaluation of the importance degree when the leaf node is in a certain fault state, and the root node is in different fuzzy states in the multi-state system. The importance of the root node is an important part of quantitative analysis in system reliability analysis [24,27]. It represents the importance of components in the system and aims to quantify the contribution of the component failure to system failure [28]. The importance degree of the root node in the Bayesian network can be obtained by using the inference algorithms, such as graph reduction method, clique tree propagation and bucket elimination inference method [33–35]. In this paper, the clique tree reasoning method is used for calculation, and the clique tree is constructed according to the variable elimination method. According to the calculation process of variable elimination, the information is transferred to the root node for calculation [16].
If the failure state of
in which
According to the definition of a triangular fuzzy number, each triangular fuzzy number has a non-fuzzy number corresponding to it. The process of finding a value that can best characterize this fuzzy number is called deblurring, which is also commonly called deblurring. At present, there are many methods to remove ambiguity, including the mean area method, gravity center method, integration value method, etc. In this paper, we use the center of gravity method to de-fuzzily, so the fuzzy importance
when failure state of
where
3 Numerical Results and Comparative Analysis of Hydraulic System Balance Circuit
Hydraulic systems are widely used in aerospace, metallurgy, machinery, engineering, machinery and other fields. This paper takes the balance circuit of a heavy CNC machine tool as the research object, and analyzes and studies the reliability of the hydraulic system [24].
3.1 Hydraulic System Balance Circuit
Through the reliability distribution and FMECA analysis of a heavy CNC machine, it can be seen that there are serious reliability problems in the hydraulic system of the beam moving gantry machining center. In the hydraulic system, the valve core of the one-way valve is stuck. Usually, it is not completely stuck, and there is still fluid flow. The piston of the hydraulic cylinder does not fail, and it is not that the piston cannot act completely, but that the action is often incomplete; For the system as a whole, the failure of insufficient pressure is fuzzy. Therefore, it is necessary to introduce the method of fuzzy theory when doing fault tree analysis for the system. Moreover, the faults cannot be described by two states: normal and fault, and use fuzzy probability to describe the probability of component fault (occurrence of the bottom event) and system fault (occurrence of the top event) [32–36].
The balance circuit is composed of filter (j1), motor (r), hydraulic pump (p), filter (j2), pressure indicator (n1), cut-off valve (k1), pressure reducing valve (f1), one-way valve (a1), pressure indicator (n2), pressure relay (b2), cut-off valve (k2) and (k3), relief valve (i1), accumulator group (m1) and balance cylinder (h1). Any component failure can result in a system failure.
After the system starts, the hydraulic pump (p) provides oil and pressure to the whole system. During the operation of the hydraulic pump, the system presses the accumulator group. When the pressure reaches the range set by the pressure relay (b2), the hydraulic pump stops supplying pressure. During the operation of the balancing cylinder, when the pressure decreases, the accumulator group (m1) will make up the pressure and maintain the pressure of the whole system. Here, the accumulator group is regarded as series of components for fault tree modelling analysis.
According to the FMEA analysis results of the whole machine tool and hydraulic system, “no pressure or low pressure lift in the balance circuit” has been chosen as the top event. On the basis of the modelling rules of the fault tree, the fault mode of the system is analyzed from top to bottom. Causes leading to no pressure or low pressure lift in the top event balance loop include insufficient oil supply pressure, oil filter (j2) blocking, oil branch 1 fault, hydraulic cylinder (h1) fault and energy storage system failing to store energy. Secondly, the failure mode of each hydraulic component and the failure state of the components in the hydraulic component is analyzed. The fault mode and codes of the entire balance loop are shown in Tab. 1. The fault tree is presented in Fig. 5.

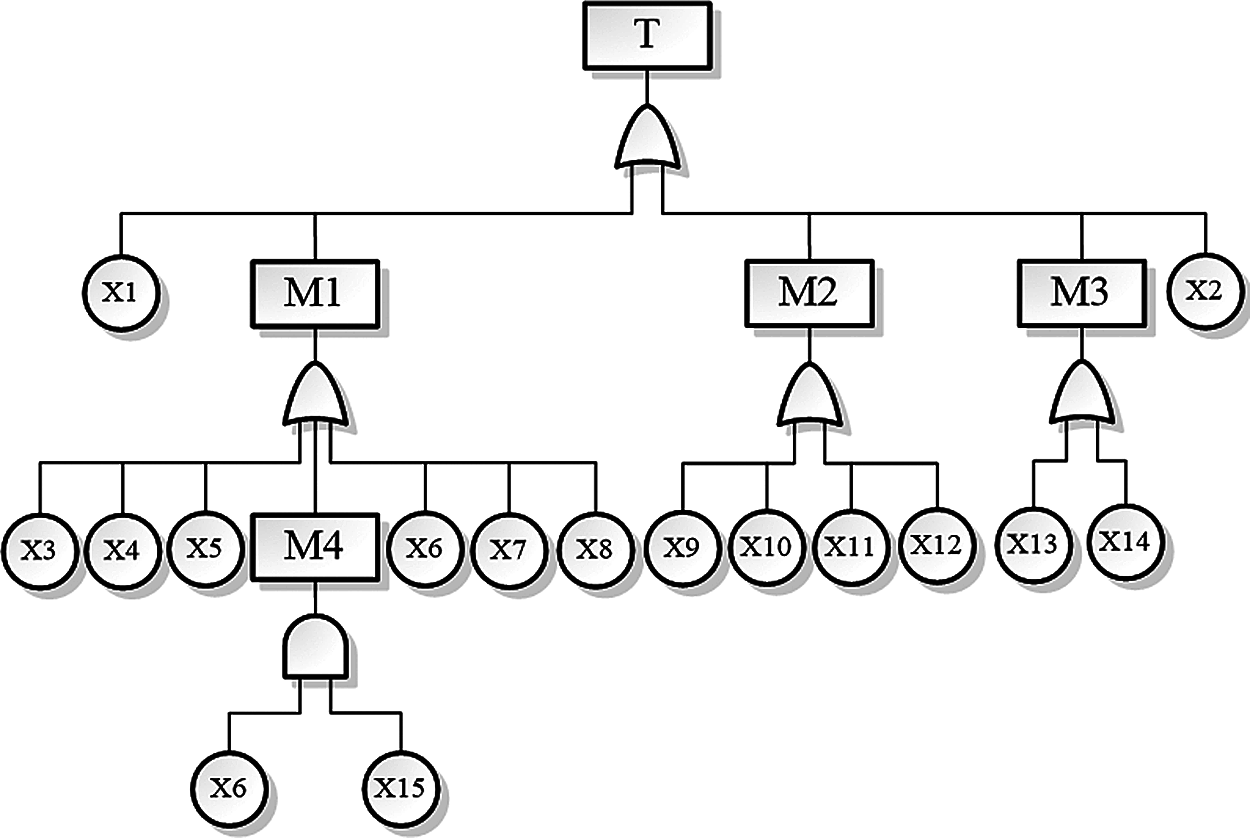
Figure 5: The FTA of the balance circuit
Based on the characteristics of the BN, the FTA is transformed into the BN model. Fig. 6 depicts the BN model of hydraulic system balance circuit fault accident. Here
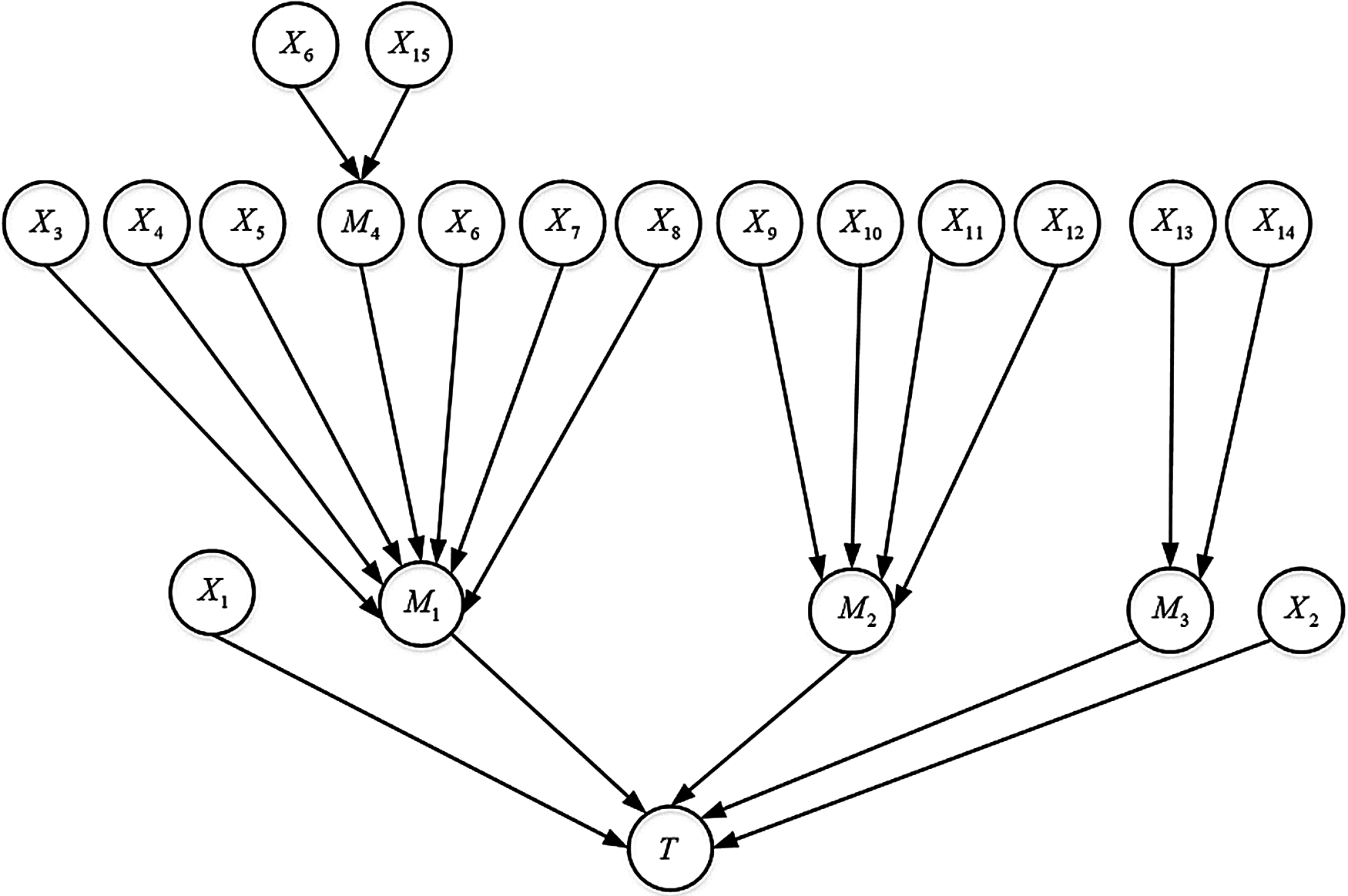
Figure 6: The BN model of the balance circuit
Due to the different structure and function of each root node itself, different root nodes have different influences on the system even under the same failure state. Therefore, this paper considers nodes





3.2 Dynamic Fuzzy Possibility Analysis of Leaf Nodes
Due to components in the hydraulic loop system having different performance and different working environments, the failure probability of each component varies with time. The dynamic fuzzy subset of failure probability of root node is obtained when the failure state of root node is 1 and 0.5 by analyzing the historical data and expertise, as shown in Tabs. 7 and 8.


According to Tabs. 2–6 and Eq. (7), when
when
The comparison between the results of the method presented in this paper and the results of the fault tree analysis method is obtained by using MATLAB software simulation, as depicted in Figs. 7 and 8.
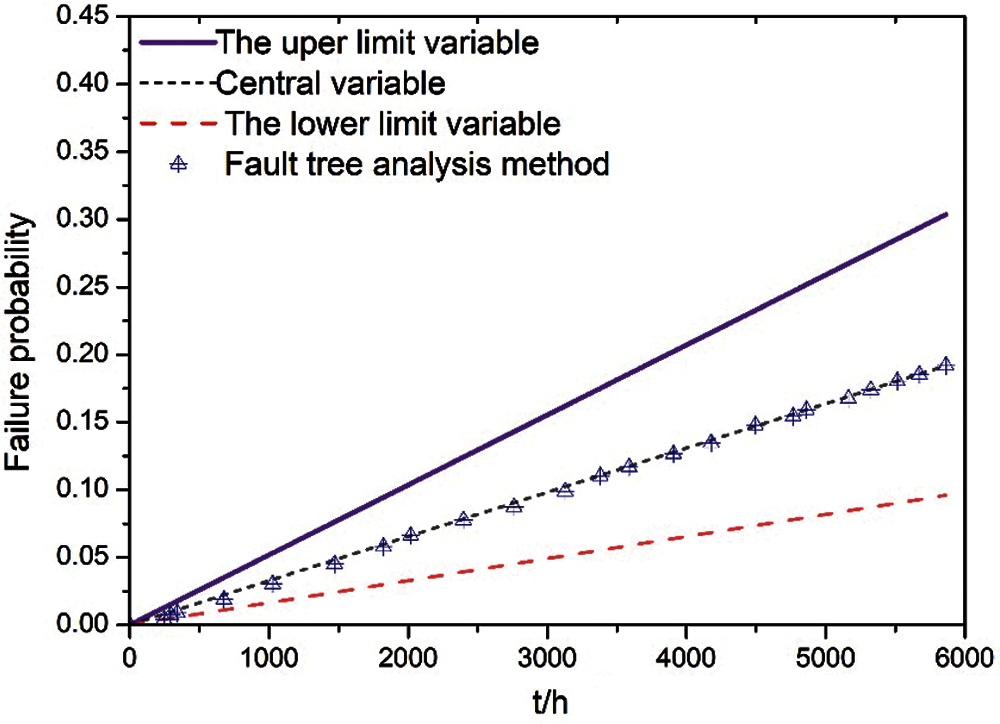
Figure 7: Comparison of the results (The state node T is 1)
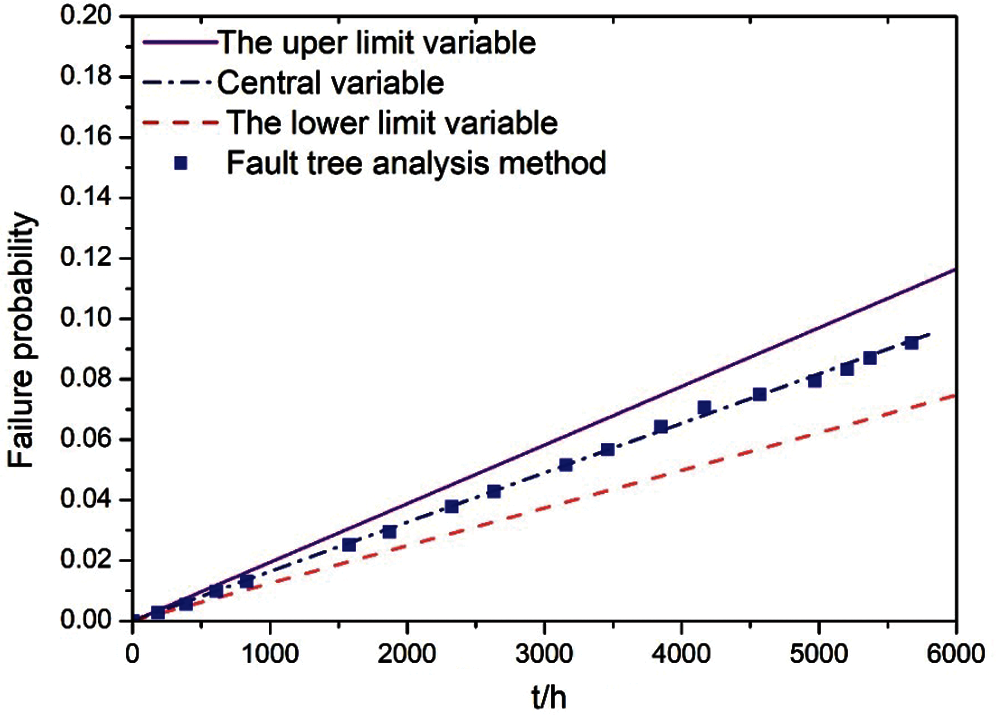
Figure 8: Comparison of the results (The state node T is 0.5)
Based on the above system possibility analysis, it can be concluded that: the dynamical fuzzy possibility analysis results of leaf nodes include the dynamical fuzzy subsets of upper variable, center variable and lower variable. The central variable is almost the same as the one obtained by the traditional fault tree method. For a simple system with sufficient information and a clear fault logic relationship, the fault tree analysis method can be used; for the complex system with a lack of fault information and uncertain fault logic relationship, this method can clearly quantify and express the impact of cognitive uncertainty on system reliability. It does not need fault tree analysis and minimum cut set calculation, and it does not need to determine the complex algebraic expression of system reliability. It can be found that the method proposed in this paper can effectively deal with the fuzziness caused by the lack of data or cognition in the engineering system.
3.3 Importance Analysis of Fuzzy Dynamic Root Node
According to Eq. (10), when
Similarly, when
According to Eqs. (10)–(12), when
Similarly, when leaf node
According to Eqs. (17) and (18), the fuzzy importance of root nodes at t = 3000 h are calculated and also listed in Tab. 9.
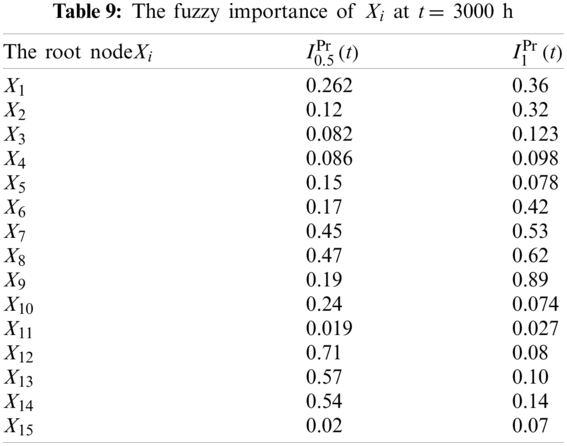
According to the fuzzy importance of nodes, the system fault diagnosis and maintenance detection can be effectively carried out. Firstly, the most important components are inspected and maintained. The qualitative and quantitative evaluation methods proposed in this paper can also provide a theoretical basis for system fault diagnosis and maintenance strategy formulation.
According to Eqs. (17) and (18), The importance of
It can be concluded that the system dynamic fuzzy importance analysis method is based on BN proposed in this paper. When the leaf node
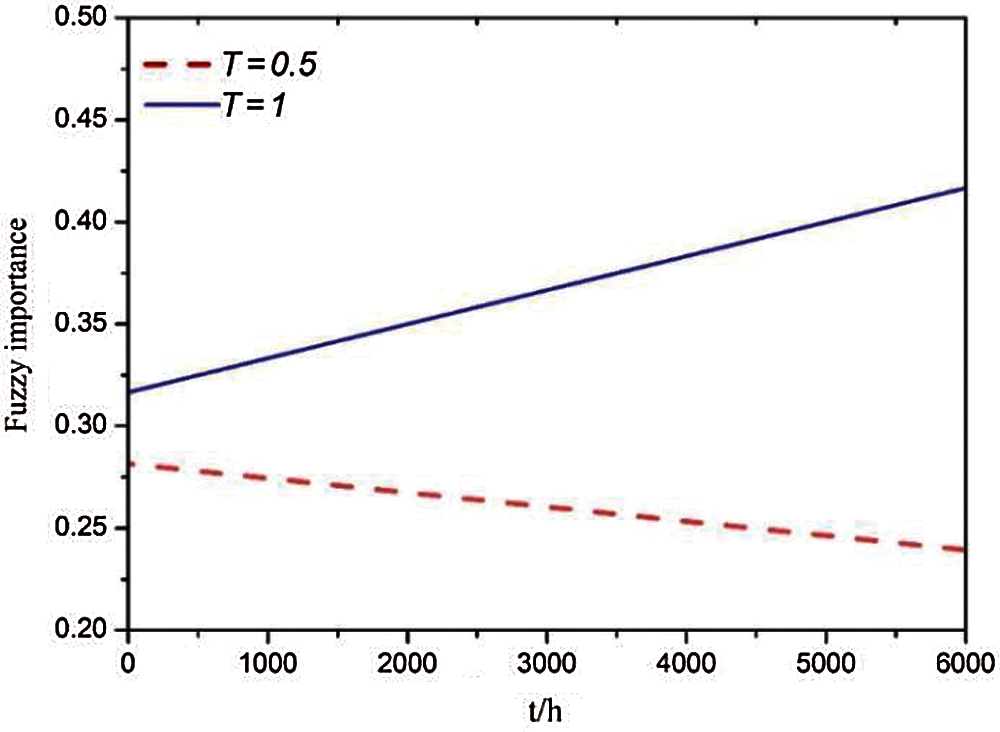
Figure 9: The importance of
In this paper, the dynamic fuzzy theory is used to represent the cognitive uncertainty in the system. Combined with the advantages of the Bayesian network in system structure expression and probabilistic reasoning, fuzzy theory and the Bayesian network are integrated to realize the logical relationship expression and probabilistic reasoning of complex multi-state systems with cognitive uncertainty. The linear fuzzy subset function is introduced into the Bayesian network, and the dynamic fuzzy subset is established to describe the variety of node failure probability with time instead of the exact value, which can effectively solve the fuzziness and dynamics of fault information. The fuzzy multi-state CTP is used to describe the fault relationship between components. Compared with the traditional system reliability analysis, the multi-state of system faults and the uncertainty of the logic relationship between faults are considered. We can apply this method to many practical problems that cannot be expressed in exact mathematics. In addition, the time-varying fault probability is considered. This method can make better use of the existing information of the system, and the analysis result is closer to the actual situation. This method makes full use of the advantages of the Bayesian network in probabilistic reasoning and can effectively represent and quantify the impact of cognitive uncertainty on system reliability without calculating the minimum cut set or determining the complex algebraic expression of system failure probability, which meets the actual needs of engineering. Therefore, the method proposed in this paper has certain significance in engineering.
Funding Statement: This research was supported by the Sichuan Science and Technology Department under Contract Nos. 2019YJ0396 and 2018JY0516, the National Natural Science Foundation of China under the Contract No. 51705041.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Sankararaman, S., Mahadevan, S. (2011). Likelihood-based representation of epistemic un-certainty due to sparse point data and/or interval data. Reliability Engineering & System Safety, 96(7), 814–824. DOI 10.1016/j.ress.2011.02.003. [Google Scholar] [CrossRef]
2. Kiureghian, A. D. (2008). Analysis of structural reliability under parameter uncertainties. Probabilistic Engineering Mechanics, 23(4), 351–358. DOI 10.1016/j.probengmech.2007.10.011. [Google Scholar] [CrossRef]
3. Hwang, C. L., Tillman, F. A., Lee, M. H. (1981). System-reliability evaluation techniques for complex/large systems—A review. IEEE Transaction Reliably, 30(5), 416–423. DOI 10.1109/TR.1981.5221152. [Google Scholar] [CrossRef]
4. Troffaes, M., Walter, G., Kelly, D. (2014). A robust Bayesian approach to modeling epistemic uncertainty in common-cause failure models. Reliability Engineering & System Safety, 125(1), 13–21. DOI 10.1016/j.ress.2013.05.022. [Google Scholar] [CrossRef]
5. Chen, D. (2012). Reliability analysis of multi-state system based on fuzzy Bayesian networks and application in hydraulic system. Journal of Mechanical Engineering, 48(16), 175–183. DOI 10.3901/JME.2012.16.175. [Google Scholar] [CrossRef]
6. Ding, Y., Zuo, M. J., Lisnianski, A., Tian, Z. (2008). Fuzzy multi-state system: General definition, and performance assessment. IEEE Transactions on Reliability, 57(4), 589–594. DOI 10.1109/TR.2008.2006078. [Google Scholar] [CrossRef]
7. Jafary, B., Fiondella, L. (2016). A universal generating function-based multi-state system performance model subject to correlated failures. Reliability Engineering & System Safety, 15(5), 16–27. DOI 10.1016/j.ress.2016.02.004. [Google Scholar] [CrossRef]
8. Liu, R., Wang, X. J., Chen, P. W. (2021). The role of tension-compression asymmetrical microcrack evolution in the ignition of polymer-bonded explosives under low-velocity impact. Journal of Applied Physics, 129(17), 175108. DOI 10.1063/5.0046011. [Google Scholar] [CrossRef]
9. Zhu, S. P., Keshtegar, B., Chakraborty, S., Trung, N. T. (2020). Novel probabilistic model for searching most probable point in structural reliability analysis. Computer Methods in Applied Mechanics and Engineering, 366, 113027. DOI 10.1016/j.cma.2020.113027. [Google Scholar] [CrossRef]
10. Spz, A., Bkb, C., Mb, D., Peng, H. E., Nttb, C. (2020). Novel hybrid robust method for uncertain reliability analysis using finite conjugate map. Computer Methods in Applied Mechanics and Engineering, 371, 113309. DOI 10.1016/j.cma.2020.113309. [Google Scholar] [CrossRef]
11. Zhu, S. P., Keshtegar, B., Tian, K., Trung, N. T. (2021). Optimization of load-carrying hierarchical stiffened shells: Comparative survey and applications of six hybrid heuristic models. Archives of Computational Methods in Engineering, 1–14. DOI 10.1007/s11831-021-09528-3 [Google Scholar] [CrossRef]
12. Bagheri, M., Keshtegar, B., Zhu, S. P., Meng, D., Jesus, A. (2020). Fuzzy reliability analysis using genetic optimization algorithm combined by adaptive descent chaos control. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 6(2), 4020022. DOI 10.1061/AJRUA6.0001064. [Google Scholar] [CrossRef]
13. Zadeh, L. A. (1978). Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets and Systems, 1(1), 3–28. DOI 10.1016/0165-0114(78)90029-5. [Google Scholar] [CrossRef]
14. Soundappan, P., Nikolaidis, E., Haftka, R. T., Grandhi, R., Canfield, R. (2004). Comparison of evidence theory and Bayesian theory for uncertainty modeling. Reliability Engineering & System Safety, 85(1), 295–311. DOI 10.1016/j.ress.2004.03.018. [Google Scholar] [CrossRef]
15. Li, H., Huang, H. Z., Li, Y. F., Zhou, J., Mi, J. (2018). Physics of failure-based reliability prediction of turbine blades using multi-source information fusion. Applied Soft Computing, 72, 624–635. DOI 10.1016/j.asoc.2018.05.015. [Google Scholar] [CrossRef]
16. Huang, H. Z., Zuo, M. J., Sun, Z. Q. (2006). Bayesian reliability analysis for fuzzy lifetime data. Fuzzy Sets and Systems, 157(12), 1674–1686. DOI 10.1016/j.fss.2005.11.009. [Google Scholar] [CrossRef]
17. Kaufmann, A., Press, A. (1975). Introduction to the fuzzy subsets. New York: Academic Press. [Google Scholar]
18. Yao, J. (1980). Discussion of the merging of fuzzy and crisp information. Journal of the Engineering Mechanics Division, 106(6), 1451–1452. DOI 10.1061/JMCEA3.0002683. [Google Scholar] [CrossRef]
19. Ayyub, B. M., Lai, K. L. (1992). Structural reliability assessment with ambiguity and vagueness in failure. Naval Engineers Journal, 104(3), 21–35. DOI 10.1111/j.1559-3584.1992.tb02221.x. [Google Scholar] [CrossRef]
20. Wu, H. C. (2004). Fuzzy reliability estimation using Bayesian approach. Computers and Industrial Engineering, 46(3), 467–493. DOI 10.1016/j.cie.2004.01.009. [Google Scholar] [CrossRef]
21. Taheri, S. M., Zarei, R. (2011). Bayesian system reliability assessment under the vague environment. Applied Soft Computing, 11(2), 1614–1622. DOI 10.1016/j.asoc.2010.04.021. [Google Scholar] [CrossRef]
22. Zhang, R. J., Zhang, L. L., Dong, M. X. (2015). Multi-state system importance analysis method of fuzzy Bayesian networks. International Journal of Industrial and Systems Engineering, 21(3), 395–414. DOI 10.1504/IJISE.2015.072272. [Google Scholar] [CrossRef]
23. Simon, C., Weber, P., Evsukoff, A. (2008). Bayesian networks inference algorithm to implement Dempster Shafer theory in reliability analysis. Reliability Engineering & System Safety, 93(7), 950–963. DOI 10.1016/j.ress.2007.03.012. [Google Scholar] [CrossRef]
24. Xiao, N. C., Huang, H. Z., Li, Y., Liu, Y., Wang, Z. (2012). Reliability analysis of series systems with multiple failure modes under epistemic and aleatory uncertainties. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 226(3), 295–304. DOI 10.1177/1748006X11421266. [Google Scholar] [CrossRef]
25. Jafary, B., Fiondella, L. (2016). A universal generating function-based multi-state system performance model subject to correlated failures. Reliability Engineering & System Safety, 152(5), 16–27. DOI 10.1016/j.ress.2016.02.004. [Google Scholar] [CrossRef]
26. Zhi, P., Xu, Y., Chen, B. (2020). Time-dependent reliability analysis of the motor hanger for EMU based on stochastic process. International Journal of Structural Integrity, 11(3), 453–469. DOI 10.1108/IJSI-07-2019-0075. [Google Scholar] [CrossRef]
27. Ding, Y., Lisnianski, A. (2008). Fuzzy universal generating function for multi-state system reliability assessment. Fuzzy Sets and Systems, 159(3), 307–324. DOI 10.1016/j.fss.2007.06.004. [Google Scholar] [CrossRef]
28. Li, Y. F., Yang, Y. J., Mi, J., Huang, H. Z. (2015). Dynamic fault tree analysis based on continuous time Bayesian networks under fuzzy numbers. Proceedings of the Institution of Mechanical Engineers, Part O, Journal of Risk and Reliability, 229(6), 530–541. DOI 10.1177/1748006X15588446. [Google Scholar] [CrossRef]
29. Mi, J., Li, Y. F., Peng, W., Huang, H. Z. (2018). Reliability analysis of complex multi-state system with common cause failure based on evidential networks. Reliability Engineering & System Safety, 174(2), 71–81. DOI 10.1016/j.ress.2018.02.021. [Google Scholar] [CrossRef]
30. Mi, J., Li, Y. F., Yang, Y. J., Peng, W. (2016). Reliability assessment of complex electromechanical systems under epistemic uncertainty. Reliability Engineering & System Safety, 152(5), 1–15. DOI 10.1016/j.ress.2016.02.003. [Google Scholar] [CrossRef]
31. Nahal, M., Khelif, R. (2021). A finite element model for estimating time-dependent reliability of a corroded pipeline elbow. International Journal of Structural Integrity, 12(2), 306–321. DOI 10.1108/IJSI-02-2020-0021. [Google Scholar] [CrossRef]
32. O'Connor, A. N. (2013). A general cause-based methodology for analysis of dependent failures in system risk and reliability assessments (Dissertations & Theses-Gradworks). University of Maryland. [Google Scholar]
33. Pliego Marugan, A., Garcia Marquez, F. P., Lev, B. (2017). Optimal decision-making via binary decision diagrams for investments under a risky environment. International Journal of Production Research, 55(17–18), 1–16. DOI 10.1080/00207543.2017.1308570. [Google Scholar] [CrossRef]
34. Abd Rahim, A. A., Abdullah, S., Singh, S. S. K., Nuawi, M. Z. (2019). Reliability assessment on automobile suspension system using wavelet analysis. International Journal of Structural Integrity, 10(5), 602–611. DOI 10.1108/IJSI-04-2019-0035. [Google Scholar] [CrossRef]
35. Ye, Z., Ying, L., Bo, H. (2014). Appearance design evaluation on CNC machine tools based on fuzzy synthetic evaluation model. International Journal of Multimedia and Ubiquitous Engineering, 9(2), 65–76. DOI 10.14257/ijmue.2014.9.2.07. [Google Scholar] [CrossRef]
36. He, Q., Zhang, R., Liu, T., Zha, Y., Liu, J. (2019). Multi-state system reliability analysis methods based on Bayesian networks merging dynamic and fuzzy fault information. International Journal of Reliability and Safety, 13(1/2), 44–60. DOI 10.1504/IJRS.2019.097016. [Google Scholar] [CrossRef]
37. Görkemli, L., Ulusoy, S. K. (2010). Fuzzy Bayesian reliability and availability analysis of production systems. Computer & Industrial Engineering, 59(4), 690–696. DOI 10.1016/j.cie.2010.07.020. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |