Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.017511

ARTICLE

Neutrosophic Mathematical Programming for Optimization of Multi-Objective Sustainable Biomass Supply Chain Network Design

Mohammad Fallah* and Hamed Nozari

Department of Industrial Engineering, Islamic Azad University, Central Tehran Branch, Tehran, Iran
*Corresponding Author: Mohammad Fallah. Email: mohammadfallah553@gmail.com
Received: 15 May 2021; Accepted: 21 June 2021

1  Introduction

In today’s competitive economics world, focusing on reducing costs or increasing revenue is essential to the long-term competitive advantage and financial profitability of organizations. In addition to economic challenges, the consequences of human activities in the environment and society (such as acid rain, climate change, deforestation, migration of workers to external borders, and reduced job opportunities) have been highlighted. Increasing social awareness of individuals about the social effects of the supply chain cannot be the only indicator of the sustainability of the supply chain economic considerations. In addition, the energy crisis and environmental issues have prompted researchers to move towards the development of renewable energy sources [1].

Plant fuels are a type of renewable energy that can be a good alternative to fossil fuels. Bioethanol is a type of plant fuel that is widely used today in the field of transportation as a substitute for diesel. First-generation bioethanols are crops such as corn and sugarcane, which have raised concerns such as food security and rising food prices due to the allocation of arable land to biomass crops and environmental sustainability [2]. To take advantage of second-generation bioethanol, some countries have enacted renewable energy laws that include rules and incentives for lignocellulosic-based bioethanol production. The Renewable Fuel Standard (RFS2) states the global need to produce 36,000 million gallons per year of plant fuels by 2022. It should be noted that to date, the production of second-generation bioethanol has not been commercialized globally [3]. On the other hand, rising global oil prices, declining fossil fuel reserves, rising global warming, improving the quality of life of the people, increasing world population, environmental and social issues have led many countries to use the “biomass supply chain and non-fossil energy” approach.

Thus, in recent years, different countries of the world have widely used new energy and non-fossil fuels, especially biomass energy and biofuels. Thus, the use of biomass energies is growing worldwide, and the debate between proponents and opponents of the use of such energies is expanding. Due to the increasing desire of people to use such energies, it is predicted that by the middle of the 21st century, the demand for biomass energy and biofuels will double; As a result, biofuels and biomass energy are expected to become an important part of the global energy mix and contribute greatly to energy demand. The structured and gradual replacement of fossil resources with biomass and the calculated construction of interconnected refineries (which in turn requires the expansion of agriculture and the production of strategic foodstuffs) and the production, consumption and export of refined biological products including biofuels are not only a choice but a definite strategic necessity. One of the important reasons for this necessity is that human beings are responsible for their health and environment, employment and food security for themselves and the people, as well as sustainable development [4].

In a general definition, residues and materials derived from living organisms are called biomass. In fact, all forms of organic matter are considered biomass; Such as plant and animal residues and wastes, municipal and factory wastes. Important sources of biomass include oilseeds (such as sunflower and soybeans), sugar and starch, lignocellulose (such as agricultural waste, forest residues, municipal solid waste, and perennial grasses), and algae with different conversion technologies, including biochemical processes (biodegradation, air fermentation). And alcohol, thermochemical (steam explosion, fireburn), biochemical (carboxylate pathway) and direct combustion, all kinds of energy are produced, including biodiesel, ethanol, biogas, methane, c-ethanol, hydrocarbon-bio-oil and bioelectricity [5].

In different sectors of the industry, the biomass supply chain includes growth (production), harvesting, transportation, collection, storage and conversion of biomass into the final product. Productivity and technology in each sector affect other sectors. The most important issues in the supply chain are the existence and communication with the biomass market and biomass supply. The choice of biomass, stability and profitability in the production of raw materials as well as the scale of production and conversion of biomass into valuable materials on a large scale are among the important issues in this field [6]. Among the issues that need to be addressed in the supply chain and concerns about it; These include seasonal supply, climatic conditions, collection and transportation, industry-supplier relationship, and supply sustainability. In addition, methods of biomass operation and crop production must be optimized [7]. The most important supply chain concerns are biomass storage.

If biomass production is seasonal, these concerns increase. On-site storage changes biomass characteristics and reduces the productivity of later stages. Storage in places between the place of production and the place of use also carries transportation costs. A more logical solution is to keep the biomass close to where it is used. Given the importance of biomass energy and biofuels in this paper, the aim is to provide a mathematical model of a sustainable biomass supply chain network. Global economic conditions and environmental importance lead to excessive attention of governments, private and governmental organizations and environmental companies to the development of mathematical models of supply chain network [8].

In this paper, by presenting a mathematical model, an attempt has been made to design a comprehensive network of supply, production, refining and supply of biomass products to customers in which social, economic and environmental issues have been observed.

The structure of the article is as follows, in the second part, the background of research related to the biomass supply chain is discussed and the research gap of the problem is shown. In the third part, an uncertain model of a stable biomass supply chain network is presented and the fuzzy planning and neutrosophic programming methods for controlling and solving the model are described. The fourth section presents the test results and its analysis. The fifth section concludes and presents future research proposals.

2  Literature Review

2.1 Biomass Supply Chain

The main obstacle to the commercialization of biofuel is its complex production processes. This complexity is due to various forms of various parameters. Uncertainty is one of the common forms of variability in biofuel supply chain parameters. Biomass supply, biofuel production and demand, price and logistics are common parameters that are associated with uncertainty [9]. Examining complex linear integer linear programming models, many studies can be observed that are related to biomass supply chain network optimization models under uncertainty. For example, Dal-Mas et al. [10] designed a dynamic randomized integer linear programming model to design a biofuel supply chain under market uncertaint. Giarola et al. [11] proposed a multi-period multi-level integer linear integer programming model to optimize the bioethanol supply chain network design taking into account biomass and carbon market uncertainties.

Ghaderi et al. [12] designed a mixed integer mathematical model for a biomass supply chain network in which demand was considered indefinitely. They conducted their study on a real issue in the state of North Dakota in the United States. Osmani et al. [13] applied stochastic optimization for a chain network to produce stable second-generation ethanol.

Their main goal in this paper was to maximize economic, environmental and social performance. They used the Banders analysis method to solve the model and conducted a logistics case study in the United States to prove the effectiveness of their proposed mathematical model. Ghaderi et al. [14] presented a robust multi-objective feasibility optimization model in designing a sustainable biomass supply chain network that simultaneously considered economic, social and environmental goals. Rabbani et al. [15] designed a network of sustainable biomass supply chains with conflicting economic, social and environmental goals. They used the Epsilon constraint method to solve their model and showed that in order to achieve a desirable level of social and environmental performance, the share of economic function should be increased by 15%. Petridis et al. [16] designed a sustainable biomass supply chain network in a paper. They provided an integrated mathematical framework for the transportation and storage of biomass at different nodes of the supply chain, using the ideal planning method to minimize the economic, social, and environmental goals of the problem.

Fattahi et al. [17] designed a biomass supply chain network under supply and demand uncertainty. In their model, they used the stochastic planning method and examined different supply and demand values in different scenarios. In their model, objective functions included environmental, economic and social goals. Foo et al. [18] presented a simple linear model for the optimal allocation of palm biomass in a multilevel supply chain network. Their main purpose in this paper was to maximize the benefits of grid design along with minimizing the cost of carbon dioxide emissions. Bragado et al. [19] developed a mathematical model for optimizing the flow system of biomass supply chain products. In this paper, they aimed to increase the profits from the design of the entire network and obtain the most optimal source of biomass energy storage and product distribution. khishtandar [20] designed a mathematical programming model in conditions of uncertainty for the biogas supply chain network.

In this paper, labor force, biomass demand and biomass price are considered unknown, and Monte Carlo simulations and evolutionary algorithms (genetic algorithm and differential evolution) are used to find the optimal solution. Akbarian et al. [21] proposed a mixed integer programming model for the sustainable biomass supply chain and used the BWM and TH methods to solve the problem. The results showed that adapting the appropriate ethanol distribution policy to a planning horizon could lead to a 33% reduction in total costs. Durmaz et al. [22] designed and planned the optimal biomass supply chain network, which includes the flow from poultry farms to biogas facilities.

In this research, two strategic decisions of facility location and a tactical decision of allocating flow between facilities have been considered. Cao et al. [23] proposed a routing location model in the biomass supply chain network and solved the model using a hierarchical method based on prohibited search. Thezozzo et al. [24] provided an optimization framework for the design of biorefinery. Ghahremani Nahr et al. designed a green closed loop supply chain under uncertainty. They developed a net robust possibilistic optimization method to control the uncertainty parameters. At the end, they used five meta-heuristic algorithms to solve the designed model [25].

2.2 Neutrosophic Programming

Kamal et al. designed a multi-objective selective maintenance allocation problem with fuzzy parameters under neutrosophic environment. They used a new defuzzification technique based on beta distribution to convert fuzzy parameters into crisp values [26]. Junaid et al. [27] studied a supply chain with aims at identifying and assessing supply chain risks and developing criteria for managing these risks. They presented a neutrosophic (N) theory is merged with the analytic hierarchy process (AHP) and technique for order of preference by similarity to ideal solution (TOPSIS) to deal with complexity, uncertainty, and vagueness. Abdel-Basset et al. desiged a framework to handle scheduling problems using neutrosophic activity duration times. They considered important aspects of time-cost tradeoffs while taking into account the real and uncertain situation surrounded by the projects [28].

Ahmad et al. designed a closed loop supply chain network under fuzzy number. They developed a fuzzy programming model to control the demand and transportation costs, anf used neutrosophic optimization model to optimization the model [29]. Edalatpanah designed a new model of DEA that the information on decision-making units is triangular neutrosophic numbers. In this paper, after comparative the conventional DEA model and the triangular neutrosophic numbers, an algorithm for solving the new model has been used [30]. Abdel-Baset et al. developed a green closed loop supply chain under uncertainty. In this paper the robust ranking technique with neutrosophic set to handle practices and performances in the developed model is used. The results display that “reverse logistics”, “supplier environmental collaboration”, “carbon management” are the significant in GSCM practices [31]. Edalatpanah proposed a new algorithm to solve the neutrosophic linear programming. In this paper, the variables andright-hand side represented with triangular neutrosophic numbers. The results show that the new algorithm is useful to design of a wide range of neutrosophic optimization [32].

Rizk-Allah et al. proposed a new algorithm for multi-objective transportation problem, which is inspired by Zimmermann's fuzzy programming and the neutrosophic set terminology. In this paper, a neutrosophic compromise programming model is constructed with the aim to find best compromise solution and optimization the all objectives is developed [33].

Pratihar et al. presented neutrosophic set to solve the Transportation problem under uncertainty. They considered supply, demand, and cell cost as uncertainty parameters, and used neutrosophic set to obtaint the optimum objective. neutrosophic set is a generalization of crisp sets, fuzzy set, and intuitionistic fuzzy set, which is handle the uncertain, unpredictable, and insufficient information in real-life problem [34]. Touqeer et al. solved a linear programming network problems with constraints concerning interval-valued neutrosophic numbers. For this, they used score function and upper and lower membership functions of interval-valued neutrosophic numbers [35].

In their research, four layers of interconnected decision are considered: biomass supply, conversion processes, storage and markets. This model is formulated as MILP to maximize net present operating value.

Tab. 1 compares some of the most important papers on the subject under study.

According to the literature review and the gaps in the studied papers, the innovations of the model are as follows:

•   Use of vehicle routing in the distribution of products from retail centers to demand centers.

•   Using fuzzy programming method in controlling model parameters and neutrosophic programming to solve the model.

•   Considering the limitation of increasing the quality of purchasing raw materials from cultivation centers with discounts.

3  Problem Definition and Modeling

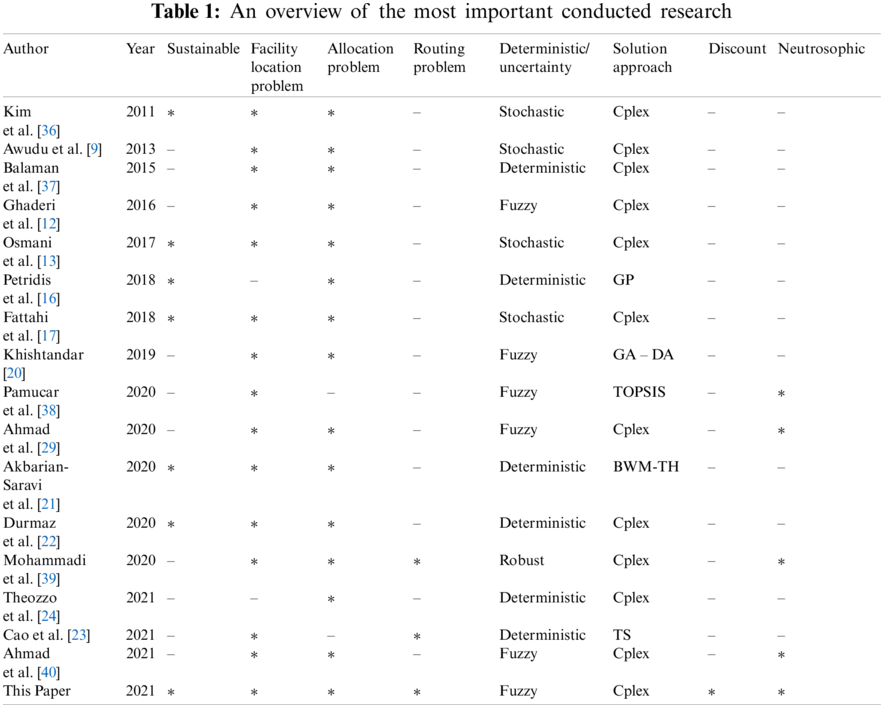
The importance of environmental problems and chain network design as well as the use of environmental fuel has led to the design of a sustainable biomass supply chain network in this paper. According to Fig. 1 in this network, 6 levels of cultivation center, pre-processing center, refinery, major distribution center, retail distribution center and customers are considered. In this network, cultivation centers in the first stage send the biomass raw materials needed for bioethanol production to pre-processing centers. Pre-processing centers, after performing the initial operations on the materials, send them to these centers for production in the refinery. Refineries also send processed products to major distributors and retailers for sale after producing processed products due to uncertain customer demand. Retail distribution centers also use optimal vehicle routing to distribute processed products. Therefore, the most important decision-making variables of this problem include strategic decision-making variables such as determining the optimal level of discount, determining the optimal number of cultivation centers, pre-processing centers, refining centers, major and retail distribution centers. Also, tactical decision-making variables in this issue include determining the optimal amount of bioethanol production, determining the optimal level of purchasing raw materials from cultivation centers, determining the optimal amount of inventory in distribution centers and determining the optimal amount of product transportation between centers.

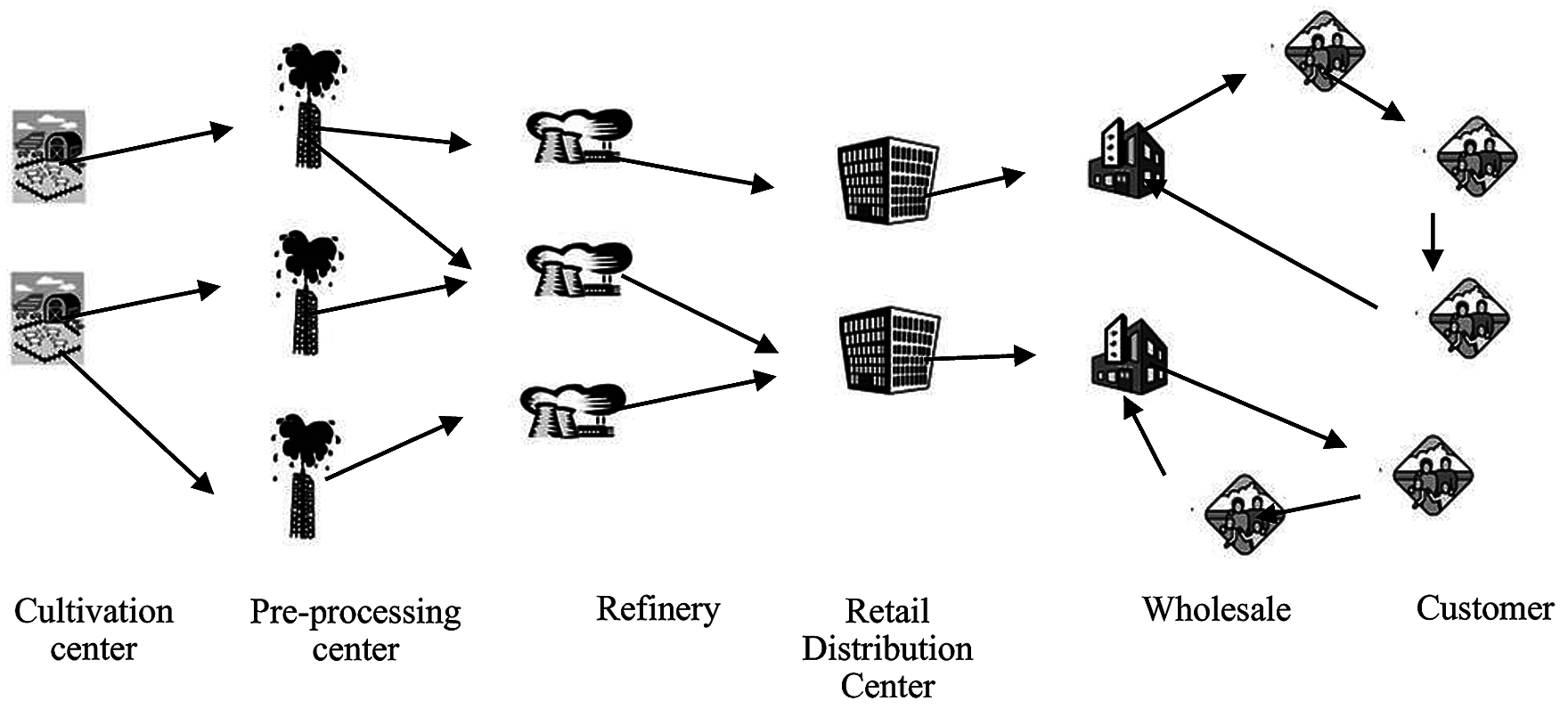
Figure 1: Biomass supply chain problem model

The assumptions of the sustainable biomass supply chain network model are as follows:

•   The optimal number and location of facilities such as cultivation centers, pre-processing centers, refineries, major distributors and retailers are unknown.

•   The capacity of retail and wholesale distributors as well as the elastic parameters of demand, transportation cost, transportation time are indefinite.

•   The capacity of vehicles in the optimal routing of processed products is known and

•   The purchase price of raw materials from cultivation centers is known.

3.1 Uncertain Model of Sustainable Biomass Supply Chain Network Problem Sets

In the following equations, the arc (ι,ϱ)=(i,j)∪(j,k)∪(k,l)∪(l,m)∪(mn,mn′) is considered for the transfer of products.

Parameters:

Decision variable:

3.2 Uncertain and Nonlinear Mathematical Model of the Problem

Eq. (1) shows the first objective function of the problem and includes minimizing the costs of the entire biomass supply chain network (transportation costs, fixed construction costs, maintenance costs, and the cost of purchasing discounted raw materials). In Eq. (2), the second objective function illustrates the problem and involves minimizing the amount of greenhouse gas emissions from vehicle traffic on the routes allocated to them. Eq. (3) shows the social objective function of the problem and includes maximizing the employment rate and employing people to create new centers. Eq. (4) is related to the fourth objective function of the problem and is to minimize the time of transfer of products and raw materials by freight vehicles on the routes allocated to them. Eq. (5) states that the optimal route of transport by a vehicle can be serviced if that vehicle has already been selected. Eq. (6) ensures that each optimal route of transport should only be traveled by a maximum of one selected vehicle. Eqs. (7) and (8) show that all customer products can only be delivered from the route for which a vehicle is intended. Eq. (9) ensures that vehicles must visit each node at most once. Eq. (10) guarantees that if a vehicle enters a node, it will inevitably leave that node. Eq. (11) ensures that the amount of product carried by each vehicle does not exceed the capacity intended for that product. Eq. (12) ensures that the maximum number of available vehicles can be used for each selected retail distribution center. Eq. (13) ensures that each retailer has the ability to distribute products and provide services to the maximum of its product capacity. Eqs. (14) and (15) are auxiliary constraints for sub-net removal. Eq. (16) shows the total amount of products distributed in each retail distribution center. Eqs. (17) and (18) show the balance of product flow in the retail and wholesale center, respectively, along with the amount of product inventory in these centers. Eq. (19) shows the amount of raw materials needed to convert products in each refinery. Eq. (20) shows the amount of raw materials transferred from each cultivation center to the pre-processing center. Relationships (21)–(24) calculate the optimal route of vehicles between each level of the supply chain network. Relationships (25)–(28) are related to the capacity constraints of each potential center, and if those centers are constructed, they can benefit from the services of the centers to the maximum of their capacity. Eqs. (29)–(31) show the constraints related to the general discount, so that in Eq. (29) shows the total amount of raw material purchased from each cultivation center, Eq. (30) expresses the optimal level of purchase discount from each cultivation center and Eq. (31) shows the guarantee of using a discount level for each crop in each cultivation center. Eqs. (32) and (33) show the type and nature of decision variables.

MinW1=∑v=1FixVv.ZVv,t+∑m=1FixMm.ZMm+∑j=1FixJj.ZJj+∑l=1FixLl.ZLl+∑i=1FixIi.ZIi+∑i=1∑j=1∑v=1∑t=1Tr~i,j.Gi,j,v,t′+∑j=1∑k=1∑v=1∑t=1Tr~j,k.Sj,k,v,t′+∑k=1∑l=1∑v=1∑t=1Tr~k,l.Rk,l,v,t′+∑mn=1∑mn′=1∑v=1∑t=1Tr~mn,mn′.Xm,n,v,t′+∑l=1∑m=1∑v=1∑t=1Tr~l,m.Ul,m,v,t′+∑m=1∑p=1∑t=1Hm,t.IPm,p,t+∑l=1∑p=1∑t=1Hl,t.IMl,p,t+∑i∑b∑c∑tpri,b,cMi,b,c,tΘi,c,t (1)

MinW2=∑mn=1∑mn′=1∑v=1∑t=1Co2mn,mn′,v.Xm,n,v,t′+∑l=1∑m=1∑v=1∑t=1Co2l,m,v.Ul,m,v,t′+∑k=1∑l=1∑v=1∑t=1Co2k,l,v.Rk,l,v,t′+∑j=1∑k=1∑v=1∑t=1Co2j,k,v.Sj,k,v,t′+∑i=1∑j=1∑v=1∑t=1Co2i,j,v.Gi,j,v,t′ (2)

MaxW3=∑i=1φFiZIi+∑j=1φEjZJj+∑k=1φDkZKk+∑l=1φClZLl+∑m=1φAmZMm+∑v=1∑t=1φBvZVv,t (3)

MinW4=∑mn=1∑mn′=1∑v=1∑t=1Ti~mn,mn′.Xm,n,v,t′+∑l=1∑m=1∑v=1∑t=1Ti~l,m.Ul,m,v,t′+∑k=1∑l=1∑v=1∑t=1Ti~k,l.Rk,l,v,t′+∑j=1∑k=1∑v=1∑t=1Ti~j,k.Sj,k,v,t′+∑i=1∑j=1∑v=1∑t=1Ti~i,j.Gi,j,v,t′ (4)

s.t:

∑m=1∑n=1Xm,n,v,t′≤ZVv,t,∀v,t (5)

∑v=1Yn,p,v,t′=1,∀n,p,t (6)

∑p=1Yn,p,v,t′≤M.∑mn=1Xmn,n,v,t′,∀n,v,t (7)

∑mn=1Xmn,n,v,t′≤∑p=1Yn,p,v,t′,∀n,v,t (8)

∑mn=1Xmn,n,v,t′≤1,∀n,v,t (9)

∑mn=1Xmn,mn′,v,t′=∑mn=1Xmn′,mn,v,t′,∀mn′,v,t (10)

∑n=1Dem~n,p,t.Yn,p,v,t′≤CapVvZVv,t,∀p,v,t (11)

∑n=1∑v=1Xm,n,v,t′≤DQm.ZMm,∀m,t (12)

∑n=1∑v=1Dem~n,p,t.Xm,n,v,t′≤CapM~m,p.ZMm,∀m,p,t (13)

∑m=1∑v=1STm,v=0 (14)

STmn,v+1≤STn,v+M(1−Xmn,n,v,t′),∀mn,n,v,t (15)

∑n=1∑v=1Dem~n,p,t.Xm,n,v,t′=Qm,p,t,∀m,p,t (16)

∑l=1∑v=1Ul,m,p,v,t+IPm,p,t−1−IPm,p,t=Qm,p,t,∀m,p,t (17)

∑k=1∑v=1Rk,l,p,v,t+IMl,p,t−1−IMl,p,t=∑k=1∑v=1Ul,m,p,v,t,∀l,p,t (18)

∑j=1∑v=1Sj,k,c,v,t=∑l=1∑v=1∑p=1Rk,l,p,v,tOc,p,∀c,k,t (19)

∑i=1∑v=1Gi,j,c,v,t=∑k=1∑v=1Sj,k,c,v,t,∀j,c,t (20)

∑p=1Ul,m,p,v,t≤M.Ul,m,v,t′,∀l,m,v,t (21)

∑p=1Rk,l,p,v,t≤M.Rk,l,v,t′,∀k,l,v,t (22)

∑c=1Sj,k,c,v,t≤M.Sj,k,v,t′,∀j,k,v,t (23)

∑c=1Gi,j,c,v,t≤M.Gi,j,v,t′,∀i,j,v,t (24)

∑m=1∑v=1Ul,m,p,v,t≤CapL~l,p.ZLl,∀l,p,t (25)

∑l=1∑v=1Rk,l,p,v,t≤CapKk,p.ZKk,∀k,p,t (26)

∑k=1∑v=1Sj,k,c,v,t≤CapJj,c.ZJj,∀j,c,t (27)

∑j=1∑v=1Gi,j,c,v,t≤CapIi,c.ZIi,∀i,c,t (28)

Θi,c,t=∑j=1∑v=1Gi,j,c,v,t,∀i,c,t (29)

Mi,b,c,tΨi,b,c,t≤Θi,c,t,∀i,b,c,t (30)

∑b=1Mi,b,c,t=ZIi,∀i,c,t (31)

ZVv,t,Xmm,mn′,v,t′,Yn,p,v,t′,Ul,m,v,t′,Rk,l,v,t′,Sj,k,v,t′,Gi,j,v,t′,ZMm,ZLl,ZKk,ZJj,ZIi,Mi,b,c,t∈{0,1},∀i,j,k,l,m,mn,mn′,v,t,b,c (32)

Qm,p,t,Θi,p,t,Ul,m,p,v,t,Rk,l,p,v,t,Sj,k,c,v,t,Gi,j,c,v,t,IPm,p,t,IMl,p,t,STmn,v≥0,∀m,p,t,i,l,v,k,j,n,c,mn (33)

3.3 Fuzzy Programming Method

Due to the uncertainty of the model parameters in the form of triangular fuzzy execution, in this section, the control of the uncertainty parameters of the model is discussed. Therefore, consider the following linear mathematical programming model with fuzzy parameters:

Min Z=c~txs.t.:x∈N(A~,B~)={x∈Rn|a~ix≥b~i,i=1,…,mx≥0}x∈N(A~,D~)={x∈Rn|a~ix≤d~i,i=1,…,mx≥0} (34)

where c~=(c~1,c~2,…,c~n),A=[a~ij]m×n,b~=(b~1,b~2,…,b~n)t,d~=(d~1,d~2,…,d~n)t, (fuzzy parameters used in the objective function of the problem) is the vector coefficient and the parameter to the right is the constraint. The probabilistic distribution function of fuzzy parameters is assumed based on the properties of fuzzy numbers. Finally, x=(x1,x2,…,xn) shows the decision vector. For the feasibility and optimization of the problem presented in the above model, it is necessary to control the uncertain parameters presented in the objective and constraint function. Therefore, assuming the α parameter as the minimum degree of constraint, the controlled model is as follows:

Min Z=EV(c~)xs.t.:[(1−α)E2ai+αE1ai]x≥(1−α)E1bi+αE2bi,i=1,…,mx≥0,α∈[0,1][(1−α)E1ai+αE2ai]x≤(1−α)E2di+αE1di,i=1,…,mx≥0,α∈[0,1] (35)

In the above relation EV(c~) is the expected value of the fuzzy number used in the objective function of the model, which is calculated as follows:

EV(c~)=E1c+E2c2 (36)

The possible distribution of the fuzzy parameter is denoted by C~=(Cp,Cm,Co). Cp and Cm, Co represent the optimistic, probable, pessimistic values of the fuzzy number C, which are determined by the decision maker. Therefore, the expected value of the fuzzy parameter of the objective function can be calculated as follows:

EI(c~)=[E1c,E2c]=[cp+cm2,cm+co2] (37)

As mentioned, the demand and cost parameters of delivery are considered as a triangular fuzzy number. Therefore, triangular fuzzy programming method has been used to control the uncertain parameters. As a result, the controlled model of the sustainable biomass supply chain network problem is as follows:

Min W1=∑v=1FixVv.ZVv,t+∑m=1FixMm.ZMm+∑j=1FixJj.ZJj+∑l=1FixLl.ZLl+∑i=1FixIi.ZIi+∑i=1∑j=1∑v=1∑t=1(Tri,jp+2Tri,jm+Tri,jo4).Gi,j,v,t′+∑j=1∑k=1∑v=1∑t=1(Trj,kp+2Trj,km+Trj,ko4).Sj,k,v,t′+∑i∑b∑c∑tpri,b,cMi,b,c,tΘi,c,t+∑k=1∑l=1∑v=1∑t=1(Trk,lp+2Trk,lm+Trk,lo4).Rk,l,v,t′+∑l=1∑p=1∑t=1Hl,t.IMl,p,t+∑mn=1∑mn′=1∑v=1∑t=1(Trmn,mn′p+2Trmn,mn′m+Trmn,mn′o4).Xm,n,v,t′+∑l=1∑m=1∑v=1∑t=1(Trl,mp+2Trl,mm+Trl,mo4).Ul,m,v,t′+∑m=1∑p=1∑t=1Hm,t.IPm,p,t (38)

Min W4=∑mn=1∑mn′=1∑v=1∑t=1(Timn,mn′p+2Timn,mn′m+Timn,mn′o4).Xm,n,v,t′+∑l=1∑m=1∑v=1∑t=1(Til,mp+2Til,mm+Til,mo4).Ul,m,v,t′+∑k=1∑l=1∑v=1∑t=1(Tik,lp+2Tik,lm+Tik,lo4).Rk,l,v,t′+∑j=1∑k=1∑v=1∑t=1(Tij,kp+2Tij,km+Tij,ko4).Sj,k,v,t′+∑i=1∑j=1∑v=1∑t=1(Tii,jp+2Tii,jm+Tii,jo4).Gi,j,v,t′ (39)

s.t.:

∑n=1(αDemn,p,t(m)+Demn,p,t(o)2+(1−α)Demn,p,t(p)+Demn,p,t(m)2).Yn,p,v,t′≤CapVvZVv,t,∀p,v,t (40)

∑n=1∑v=1(αDemn,p,t(m)+Demn,p,t(o)2+(1−α)Demn,p,t(p)+Demn,p,t(m)2).Xm,n,v,t′≤(αCapMm,p(p)+CapMm,p(m)2+(1−α)CapMm,p(m)+CapMm,p(o)2).ZMm,∀m,p,t (41)

∑n=1∑v=1(αDemn,p,t(m)+Demn,p,t(o)2+(1−α)Demn,p,t(p)+Demn,p,t(m)2).Xm,n,v,t′=Qm,p,t,∀m,p,t (42)

∑m=1∑v=1Ul,m,p,v,t≤(αCapLl,p(p)+CapLl,p(m)2+(1−α)CapLl,p(m)+CapLl,p(o)2).ZLl,∀l,p,t (43)

Eqs. (2), (3); Eq. (5)-Eqs. (10)-(12); Eqs. (14), (15); Eqs. (17)-(24); Eqs. (26)-(33) (44)

3.4 Neutrosophic Programming Method

Multi-objective decision models are the most common type of mathematical models that have conflicting goals. In such cases the goal is to achieve the optimal value of all conflicting objective functions simultaneously. In such problems, the decision maker expresses the importance of his preferences by providing an optimal weight β∈[0,1] to each objective function, So that with a high value of weight β in an objective function, decision maker preferences are higher in that objective function. Zimmermann [41] by introducing a multi-objective fuzzy programming method, maximized the decision maker's preferences in achieving the objective functions simultaneously. In the following years, Faizulkhakov [42] and Angelov [43] were able to solve a variety of mathematical problems with the development of Russian multi-objective fuzzy programming called intuitive fuzzy programming. In these planning methods, flexibility in element membership functions was also possible. This method has been extensively studied in various real life issues and problems. In recent years it has been observed that living conditions may have neutral thoughts about an element in the collection. Neutral or uncertain thoughts about the elements fall between a degree of falsehood and truth. Thus, with the development of the intuitive fuzzy programming method, Smarandache [44] examined the neutrosophic programming method, which has three membership sets: truth (degree of belonging), uncertainty (degree of belonging to some extent) and falsehood (degree of non-belonging). According to the developed method of neutrosophic programming, in this paper, the model of sustainable biomass supply chain network model with the objectives of four opposite objective functions is discussed. Hence, each objective function has three functions: truth membership, non-determination and falsehood. Therefore, the neutrosophic programming method plays an important role in optimizing multi-objective problems by considering neutral thoughts. Consider a multi-objective model with contrasting objective functions in which (D) represents a set of fuzzy decisions, (G) a set of fuzzy objective functions, and (C) fuzzy constraints. Therefore, the set of fuzzy decisions is represented as D=G∩C. Fuzzy neutrosophic Decision Set (Dn) with the set of neutrosophic fuzzy target functions (Go) and the set of neutrosophic constraints (Cm) [45]:

Dn=(⋂o=1OGo)(⋂m=1MCm)=(w,PD(w),QD(w),RD(w))s.t.:PD(w)={minPGo(w),∀o∈Os.t.PCm(w),∀m∈M}QD(w)={maxQGo(w),∀o∈Os.t.QCm(w),∀m∈M} (45)

RD(w)={maxRGo(w),∀o∈Os.t.RCm(w),∀m∈M}

In the above equation, PD(w) is a membership function of truth; QD(w) is the membership function of non-determination and RD(w) is the membership function of false under neutrosophic fuzzy decisions Dn. Each of the above membership functions has upper and lower bound, which is obtained as the following relation for all membership functions:

Uo=max(Zo(X)) (46)

Lo=min(Zo(X))

Therefore, the upper and lower bounds of the neutrosophic membership function can be calculated as follows for truth, non-determination, and falsehood, respectively:

UoP=Uo,LoP=Lo (47)

UoQ=LoP+ao,LoQ=Lo

UoR=UoP,LoR=LoP+bo

In the above relation ao and bo is a predefined value between 0 and 1. According to the above materials, the linear membership function for a neutrosophic fuzzy framework is as follows:

Dn=(⋂o=1OGo)(⋂m=1MCm)=(w,PD(w),QD(w),RD(w))s.t.:Po(Zo(X))={1ifZo(X)<LoPUoP−Zo(X)UoP−LoPifLoP≤Zo(X)≤UoP0if Zo(X)>UoP}Qo(Zo(X))={1ifZo(X)<LoQUoQ−Zo(X)UoQ−LoQifLoQ≤Zo(X)≤UoQ0ifZo(X)>UoQ}Ro(Zo(X))={1ifZo(X)>UoRZo(X)−LoRUoR−LoRifLoR≤Zo(X)≤UoR0ifZo(X)<LoR} (48)

Therefore, the controlled model of the sustainable biomass supply chain network problem with neutrosophic programming method based on the above relations is as follows:

max∑o=1(μo+ϑo−δo) (49)

s.t:

Po(Zo(X))≥μo,∀o

Qo(Zo(X))≥ϑo,∀o

Ro(Zo(X))≤δo,∀o

μo≥ϑo,∀o

μo≥δo,∀o

0≤δo+μo+ϑo≤3,∀o

δo,μo,ϑo∈(0,1)

Eqs. (38)–(44)

4  Analysis of Results

In this section, a small sample problem is analyzed using neutrosophic programming method. The problem of the small sample is designed according to the dimensions presented in Tab. 2 and based on the limits of the definite and non-definite parameters presented according to Tab. 3.

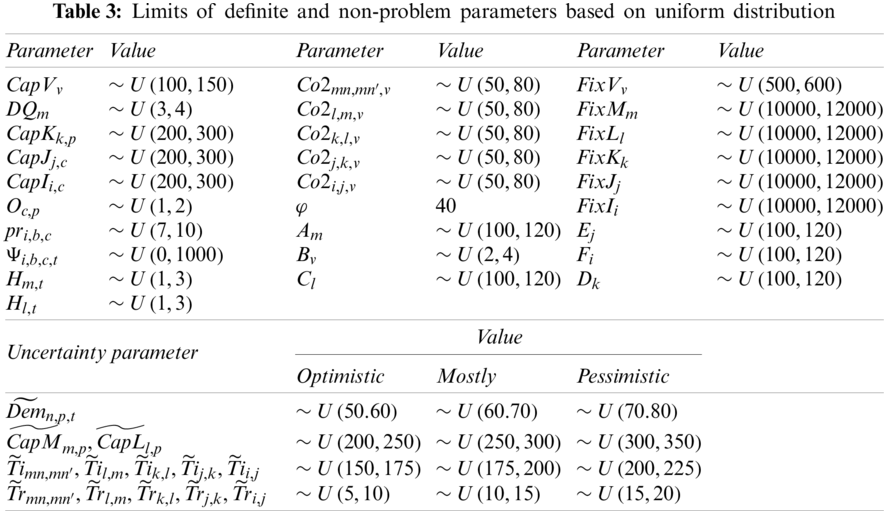
Due to the fact that the mathematical model has several objective functions, the neutrosophic programming method has been used to simultaneously achieve near-optimal solutions. Therefore, in Tab. 4, first, the optimal value of each objective function and the lower and upper bound of each objective function with respect to Eq. (46) are obtained assuming the uncertainty rate (α=0.5).

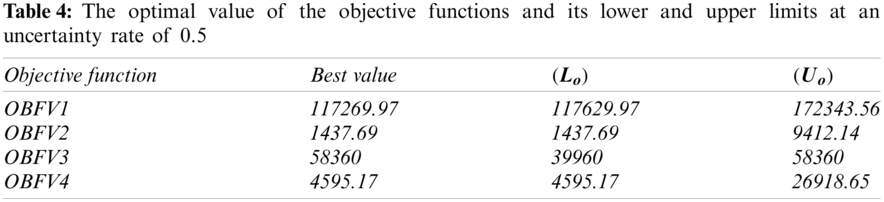
According to Tab. 4 the optimal value of each objective function is shown. Therefore, Tab. 5 shows the location of potential facilities obtained by solving objective functions by individual optimization method.

According to Tab. 5, the minimum number of facilities is used when the goal is to minimize the total network costs. If in other objective functions, facility location is not considered and the maximum number of potential facilities is used. Tab. 6 also shows the optimal transportation routing between retail centers and end customers in each time period and assuming the optimization of each objective function individually.

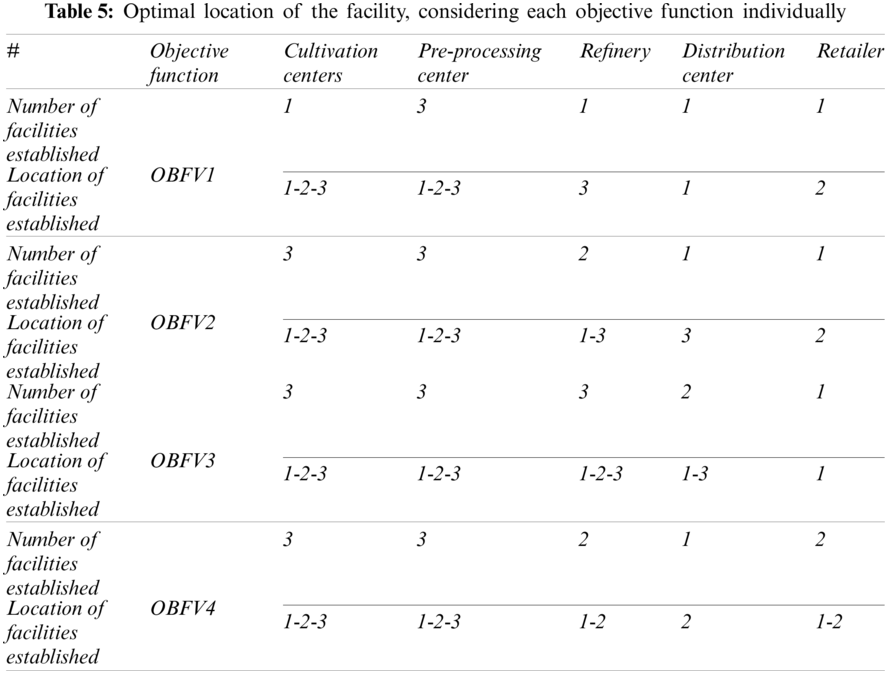
According to the results of Tab. 6, it can be seen that in the path of selecting a retailer, the vehicle routing to distribute biomass products to customers begins from that retailer. Since the model of sustainable biomass supply chain network has 4 contrasting objective functions, so to optimize all objective functions simultaneously, the neutrosophic programming method has been used. The lower and upper bounds of each objective function are obtained according to the states of truth, non-determination and falsehood according to Eq. (47) as described in Tab. 7.

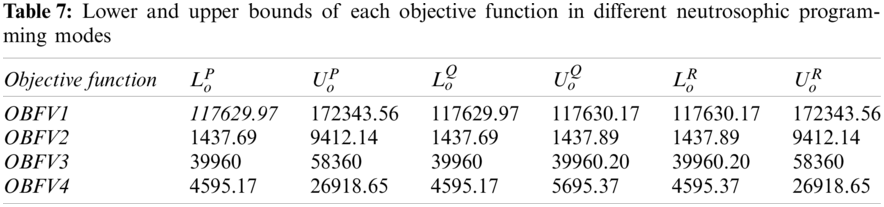
After forming the truth membership function, non-determination membership function and false membership function according to relation (48) and problem optimization (49), the value of the first objective function of the problem is 139384.30, the value of the second objective function of the problem is 1467.83, the value of the third objective function is 49440 and Finally, the value of the fifth objective function of the problem is 4631.72 units. According to the obtained results, the value of the objective functions obtained from the neutrosophic programming method is very close to the optimal value of the optimal objective functions of the problem. Accordingly, Fig. 2 shows the biomass supply chain network obtained from the neutrosophic programming method at an uncertainty rate of 0.5.

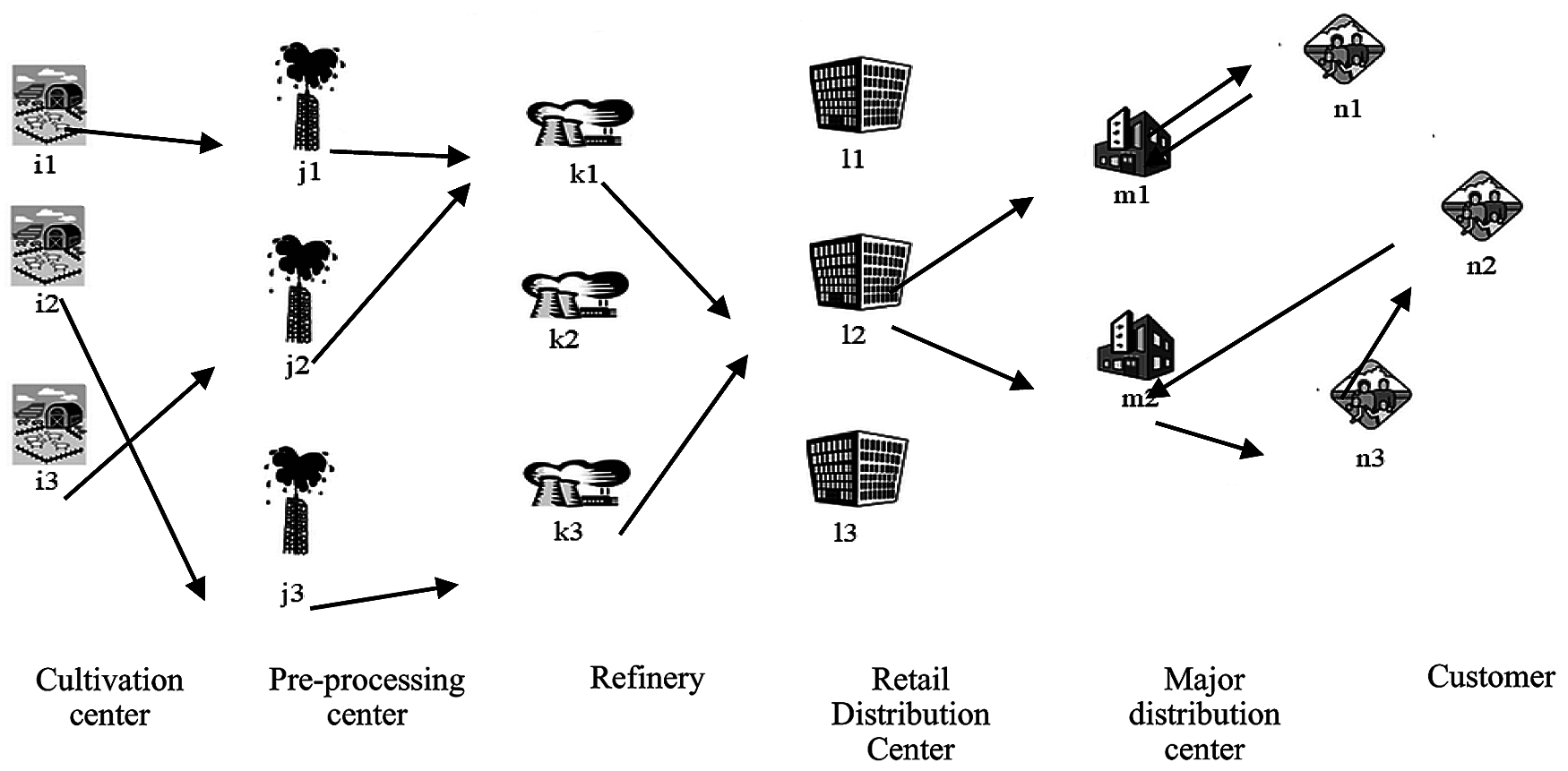
Figure 2: Biomass supply chain network with neutrosophic programming method

According to Fig. 2, all cultivation centers have been used to supply the raw material needed to produce biomass products. Also, pre-processing centers Nos. 1–3 are responsible for pre-processing of raw materials in the field of cultivation centers. Meanwhile, Refinery No. 2 and Major Distribution Centers Nos. 1 and 3 have not been used in the supply chain network. Tab. 8 shows the discount level obtained from the neutrosophic planning method for purchasing raw materials from cultivation centers.

The above analyzes in this section have been performed assuming an uncertainty rate of 0.5. Therefore, in order to analyze the sensitivity of the uncertainty rate on the values of the objective functions, the value of the uncertainty rate is changed from 0.1 to 0.9 and the values of the objective functions corresponding to each uncertainty rate with the neutrosophic programming method are shown in Tab. 9.

According to the results of Tab. 9, it is observed that with increasing uncertainty rate due to reduced capacity of facilities and increasing demand, the total cost of network design increases, also the amount of vehicle traffic and therefore greenhouse gas emissions and transportation time has increased. Also, in these circumstances, the employment rate has decreased with increasing uncertainty. Fig. 3 also shows the trend of changes in the objective functions of the problem at different rates of uncertainty according to Tab. 8.

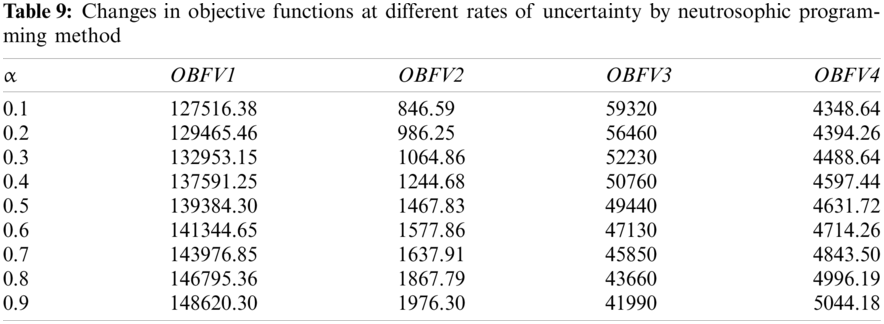
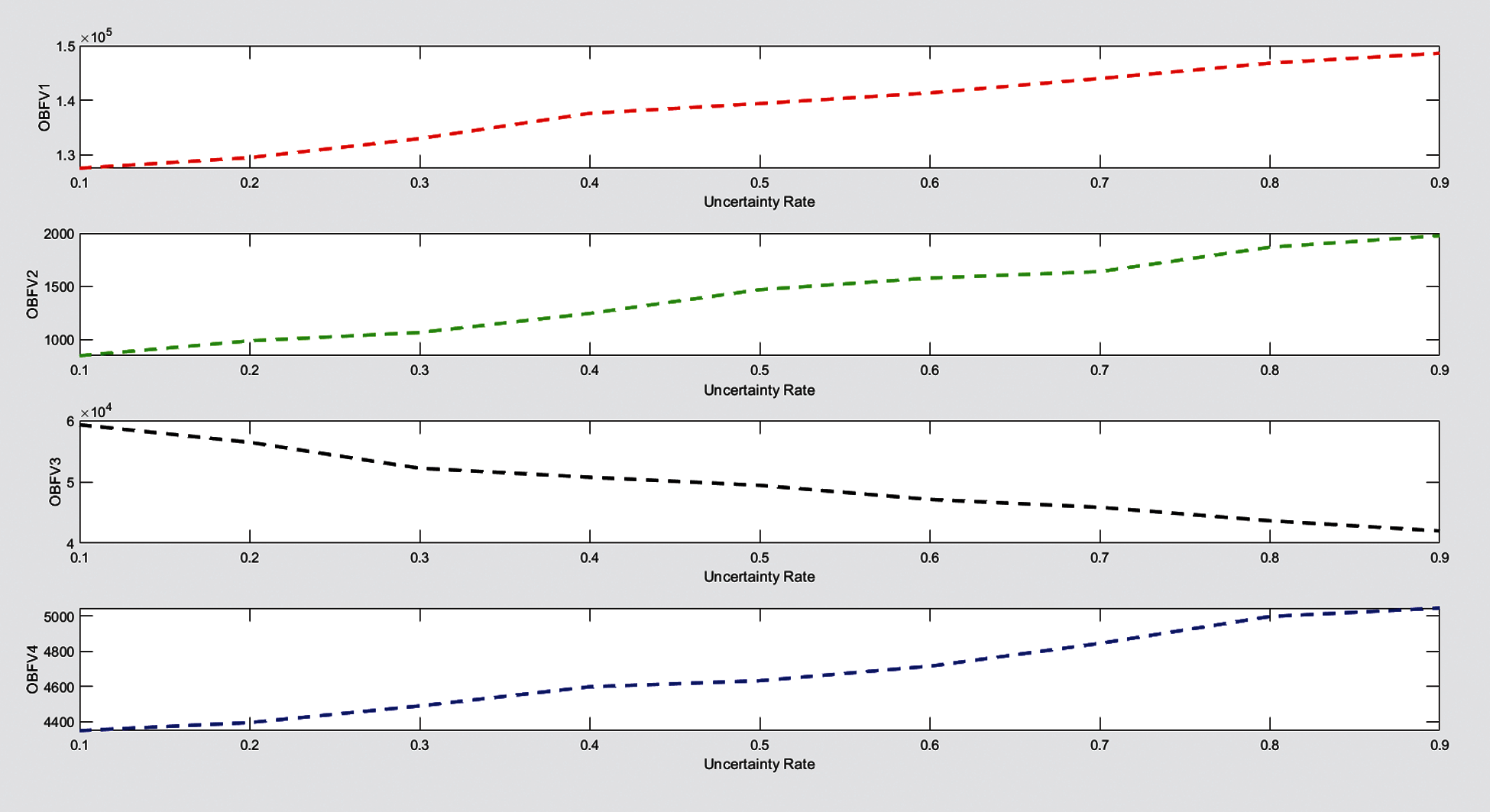
Figure 3: The trend of changes in objective functions at different rates of uncertainty

5  Conclusions and Future Suggestions

Given the importance of biomass energy and biofuels in this paper, a mathematical model of a sustainable biomass supply chain network under conditions of demand uncertainty, potential facility capacity, transportation costs and transmission time is presented. Sustainability in the proposed biomass supply chain network includes minimizing the total costs of the supply chain network, maximizing the employment rate and minimizing the amount of greenhouse gas emissions along with reducing the transmission time of biomass products. Different types of facility tracking decisions, optimal flow allocation and vehicle routing are considered in the proposed model. Also in this paper, cultivation centers provide the general raw materials needed to produce biomass products by offering a general discount. Triangular fuzzy programming method has been used to control the uncertain parameters of the problem and neutrosophic programming method has been used to solve the multi-objective model. In this method, each of the objective functions is considered in the three membership functions of truth, non-determination and falsehood. By implementing the neutrosophic programming method, the value of the objective functions obtained is very close to the optimal value of the objective function of the problem by the individual optimization method. Also, by examining the changes in uncertainty rates on the values of the objective functions of the problem, it was observed that with increasing uncertainty rates due to reduced capacity and increased demand, the total cost of network design has increased and vehicle traffic and therefore greenhouse gas emissions and transportation time has increased. Also, in these circumstances, the employment rate has decreased with increasing uncertainty. Since in the present paper, an attempt has been made to provide a comprehensive model of the biomass supply chain network, so more favorable results can be obtained by using the fuzzy stable method in controlling uncertain parameters. It is also proposed to consider the objective function of minimizing the maximum unmet demand as future research.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.