
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2021.017589
ARTICLE
Effective Elastic Properties of 3-Phase Particle Reinforced Composites with Randomly Dispersed Elastic Spherical Particles of Different Sizes
Dedicated to Professor Karl Stark Pister for his 95th birthday
1Civil Engineering and Construction Engineering Management, California State University, Long Beach, CA 90840-5101, USA
2Civil and Environmental Engineering, University of California, Los Angeles, CA 90095-1593, USA
*Corresponding Author: Yu-Fu Ko. Email: yu-fu.ko@csulb.edu
Received: 22 May 2021; Accepted: 05 August 2021
Abstract: Higher-order multiscale structures are proposed to predict the effective elastic properties of 3-phase particle reinforced composites by considering the probabilistic spherical particles spatial distribution, the particle interactions, and utilizing homogenization with ensemble volume average approach. The matrix material, spherical particles with radius
Keywords: Particle reinforced composites; micromechanics; spherical particle interactions; ensemble volume average; homogenization; probabilistic spatial distribution; higher-order bounds; multiscale
Composite materials can considerably enhance the following material properties including strength, stiffness, thermal insulation, thermal conductivity, fatigue life, acoustical insulation, wear resistance, corrosion resistance, etc. To achieve targeted engineering performance, composite materials consisting of two or more different materials to macroscopically form new materials are needed. The “inclusions” in composites can be in the forms of whiskers, fibers, and particulates. The “matrix” in composites is the binder material. The matrix material provides the support and protection to the inclusions. The matrix material also transfers stresses and strains through inclusion/matrix interfaces under complex 3-dimensional loading. Limited mechanical properties of conventional particle reinforced composites that contain a single material type of inclusions are observed such as tensile strength, compressive strength, impact resistance.
Alternatively, hybrid particle-reinforced composites, containing several different sizes and/or materials of particles into a matrix, demonstrate superior and excellent mechanical properties and have been largely employed in engineering applications, e.g., aerospace, civil engineering, automobile industries, and military equipment. The mechanical behaviors of hybrid composites, compared with conventional composites, are improved by the weighted summation of the individual particles with different material properties and distinct sizes. Therefore, enhanced engineering performance and cost could be obtained by appropriate engineering material design [1–5].
Numerous experimental research works have exhibited that mechanical behaviors of particle reinforced composites are controlled by particle sizes, micro-structural morphology, and interfacial properties between matrix material and particles [6–17]. Several theoretical methods have been developed in literatures to derive the effective elastic properties of multiphase composites such as variational methods, effective medium methods, direct micromechanical methods, and finite element methods.
Variational methods utilize linear comparison composites or variational principles to acquire mathematical upper and lower bounds for effective elastic properties of composites [18–27]. Hashin's bounds are referred to as the 2-point bounds. Furthermore, the “improved” higher-order mathematical bounds considering the statistical micro-structural information of composites were proposed [28–33]. For instance, Silnutzer [28] proposed improved bounds, referred to as 3-point bounds, on the effective in-plane shear modulus and bulk modulus. The 3-point bounds are narrower when compared with the 2-point bounds.
Effective medium methods employ effective medium to predict the effective elastic properties of composites [34–39]. Mori-Tanaka method, differential scheme, self-consistent method, and generalized self-consistent method are among the effective medium methods. These methods considered only the volume fractions and geometries of inclusions. Conversely, probabilistic distributions or spatial locations of inclusions are not considered. Therefore, the effective medium methods are best suited for low volume fractions of inclusions or some limited particular configurations.
Direct micromechanical methods consider specific geometric configurations of inclusions dispersed in the matrix and utilize approximations to determine effective elastic properties of composites with randomly located and interacting inclusions. Eshelby [40] proposed the renowned “Eshelby's equivalence principle” based on an ellipsoidal inclusion embedded in infinite matrix. Mura [41] primarily considered rigorous “local” micromechanics. Honein [42] proposed frameworks based on Kolosov-Muskhelishvili complex potentials to study circular inclusions in plane elastostatics. Moreover, the direct micromechanical methods are further utilized and studied [43]. Nonetheless, based on the above methods, “local” (not “overall”) field solutions could be achieved. To predict the effective properties of elastic multi-phase composites, Ju et al. [44,45], based on Eshelby [40], proposed a micromechanical ensemble volume average formulation, which is higher-order in volume fractions of inclusions
Finite element methods, i.e., numerical solutions, are obtained based on the “unit cell model” as well as assume particular periodic arrays of inclusions [50–53].
Finally, Ju and co-researchers, following the micromechanical frameworks [44,45], continue to study the effective elastoplastic with/without damage behaviors of advanced composite materials [54–81]. Additionally, Ko et al. [82,83] proposed new higher-order bounds on effective transverse elastic properties of 3-phase hybrid fiber-reinforced composites. The hybrid fiber-reinforced composites contain randomly located and unidirectionally aligned circular fibers featuring distinct fiber sizes and different elastic material properties.
Majority of research works on prediction of the effective elastic properties of particle reinforced composites focus on conventional composites containing one type of particle and did not consider the effects of different particle sizes. In addition, the “unit cell model,” commonly adopted within the 3-D RVE finite element models, assumes periodic arrays of particles, not randomly distributed.
The predictions of effective elastic properties of particle reinforced composites with different particle sizes are still limited in research works. The objective of this paper is to propose analytical frameworks based on the direct micromechanical methods to derive the effective elastic properties of 3-phase spherical particle reinforced composites featuring different particle sizes and same elastic material property of particle. All particles are considered randomly dispersed, non-intersection, and with perfect interfaces between matrix and particles. In addition, both “local” and “overall” ensemble volume averaged micromechanical field equations will be derived by rigorously considering the spherical particle interactions and the probabilistic spatial distribution of particles in formulations as well as utilizing homogenization technique with ensemble volume average approach.
Section 2 presents analytical local solutions of spherical particle interactions. The spherical particles are assumed to be elastic and randomly dispersed in the matrix material. 3-phase composites contain 2 inclusion phases featuring different particle sizes and same elastic properties. Consequently, Section 3 presents the derivations of the ensemble volume averaged eigenstrains based on the probabilistic particle interactions mechanism considering uniform radial distribution function (URDF). Additionally, 2 formulations with different orders, Formulation II and Formulation I, are proposed. In Section 4, the effective elastic properties of 3-phase composites consisting of spherical particles, which are randomly dispersed as well as featuring different particle sizes and same elastic material properties, are analytically obtained. In Section 5, our theoretical predictions are compared with available experimental data together with numerical examples to demonstrate the competence of the proposed frameworks. In Section 6, conclusions are presented.
2 Analytical Local Solutions of Spherical Particle Interactions
Consider a 3-phase particle reinforced composite consisting of randomly dispersed and spherical shaped elastic particles with different particle sizes embedded in an isotropic elastic matrix as shown in Fig. 1. The matrix material, spherical particles with radius
where
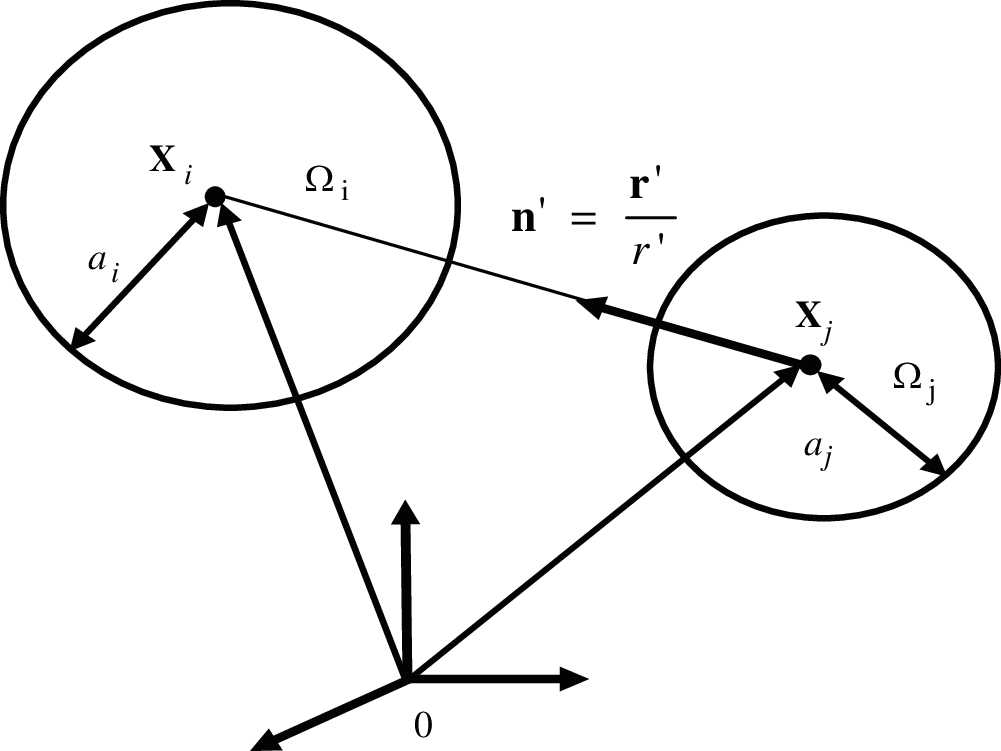
Figure 1: 2-particle interaction in a 3-phase composite
According to the eigenstrain concept of Eshelby [40], with the replacement of the spherical particles by the matrix material, the perturbed strain field
where
Due to the presence of the distributed eigenstrain
where V is volume of a representative volume element (RVE),
In addition, the 4th-order tensor G per Mura [41] is expressed as
where
We also define the components of the 4th-order tensor F in the Cartesian coordinates as (m = 1–6)
where
Making use of Eqs. (2) and (3),
By considering spherical particle interactions, Eq. (6) are rearranged as
where
To obtain the 1st-order solution for the eigenstrain
In addition, the 4th-order tensor S, known as interior-point Eshelby tensor of a spherical particle, is [41,58,59]
The components of S for a spherical particle are [41]
where v0 is the Poisson's ratio of the matrix material.
To obtain the effects of spherical particle interactions, Eq. (8) is subtracted by Eq. (9). Then, solving the integral equation
In addition, we define
In order to find the correction of
where the following equalities are employed.
Substitution of Eq. (14) to Eq. (12) yields
where volume of a spherical particle in the ith phase is
Moreover, the average fields shown in Eq. (16) are defined as
The 3rd-order tensor
It is noted that the leading order of
By conducting volume averaging of Eq. (16) over the
By setting i equal to 1 and j equal to 2, we obtained Eqs. (20)–(23).
in which
Similarly, by setting i equal to 2 and j equal to 1, we obtained Eqs. (24)–(27).
where
and the components of
Moreover, we define
Furthermore, Eqs. (20) and (24) are further rearranged:
Eq. (29) can be solved to obtain
It can be proved that the leading order is of
In addition,
Likewise, Eq. (31) can be expressed as
3 Averaged Eigenstrains of Spherical Particles by Ensemble Volume Average Approach
To find the solutions of averaged eigenstrains of spherical particles considering spherical particle interactions, ensemble volume average approach is adopted. The ensemble volume average process is stated as
where
In this paper, we adopt a statistically isotropic and uniform 2-point conditional probability density function known as uniform radial distribution function (URDF).
where r is the distance between the centers of the spherical particles in the ith phase and the spherical particles in the jth phase.
After substituting Eq. (32) into Eq. (35),
where
where
Additionally, we can prove that
in which,
Likewise, after substituting Eq. (33) into Eq. (36),
Similarly, we can also prove that
In the following sections, Formulation II (higher order) and Formulation I (lower order) will be presented to obtain the effective elastic properties of 3-phase particle reinforced composites. In this paper, Superscript II indicates Formulation II and Superscript I indicates Formulation I. It is noted that Formulation II represents higher-order formulation than Formulation I. In addition, with same elastic material property and same shape of spherical particles in the 1st phase and the 2nd phase,
With lengthy algebra together with employing identities Eqs. (18), (37) and (41),
where the isotropic tensor
where
Likewise,
where the isotropic tensor
where
Following similar procedures in Formulation II and dropping the higher-order components
where the isotropic tensor
Likewise,
where the isotropic tensor
4 Effective Elastic Properties of 3-Phase Particle Reinforced Composites with Randomly Dispersed Elastic Spherical Particles of Different Particle Sizes and Same Material Properties
We will employ the solutions of
The ensemble volume averaged field equations are [44]
where
With same elastic material properties of spherical particles (the 1st phase) and spherical particles (the 2nd phase), then we write
in which
Moreover, the effective shear modulus
In addition, the effective bulk modulus
where
Consequently, the effective Young's modulus
Effective properties of the composites based on Formulation I can be derived by replacing Superscript II based on Formulation II with I. It is also noted that our formulations are completely identical to Eqs. (48), (49), (55) and (56) in Lin et al. [46] when the particles featuring same particle sizes and same elastic material property.
5 Numerical Examples and Comparisons
We will present several analytical examples of 2-phase and 3-phase particle reinforced composites under consideration. In addition, the following notations will be adopted in the illustrations.
3-point upper bound of Silnutzer is SU; 2-point upper bound of Hashin is HU; 3-point lower bound of Silnutzer is SL; 2-point lower bound of Hashin is HL; Formulation II is FII; Formulation I is FI.
5.1 2-Phase Elastic Composites: Elastic Spherical Particles in Elastic Matrix
The analytical predictions of our proposed micromechanical framework are compared with the 2-point bounds [19], the 3-point bounds [30,32], and experimental data [84]. As a special case, i.e., particle size of the 1st phase and particle size of the 2nd phase are the same; the proposed formulations reduce to 2-phase formulas. The following material properties of experiments from Smith's data [84] are as follows:
The normalized effective shear modulus
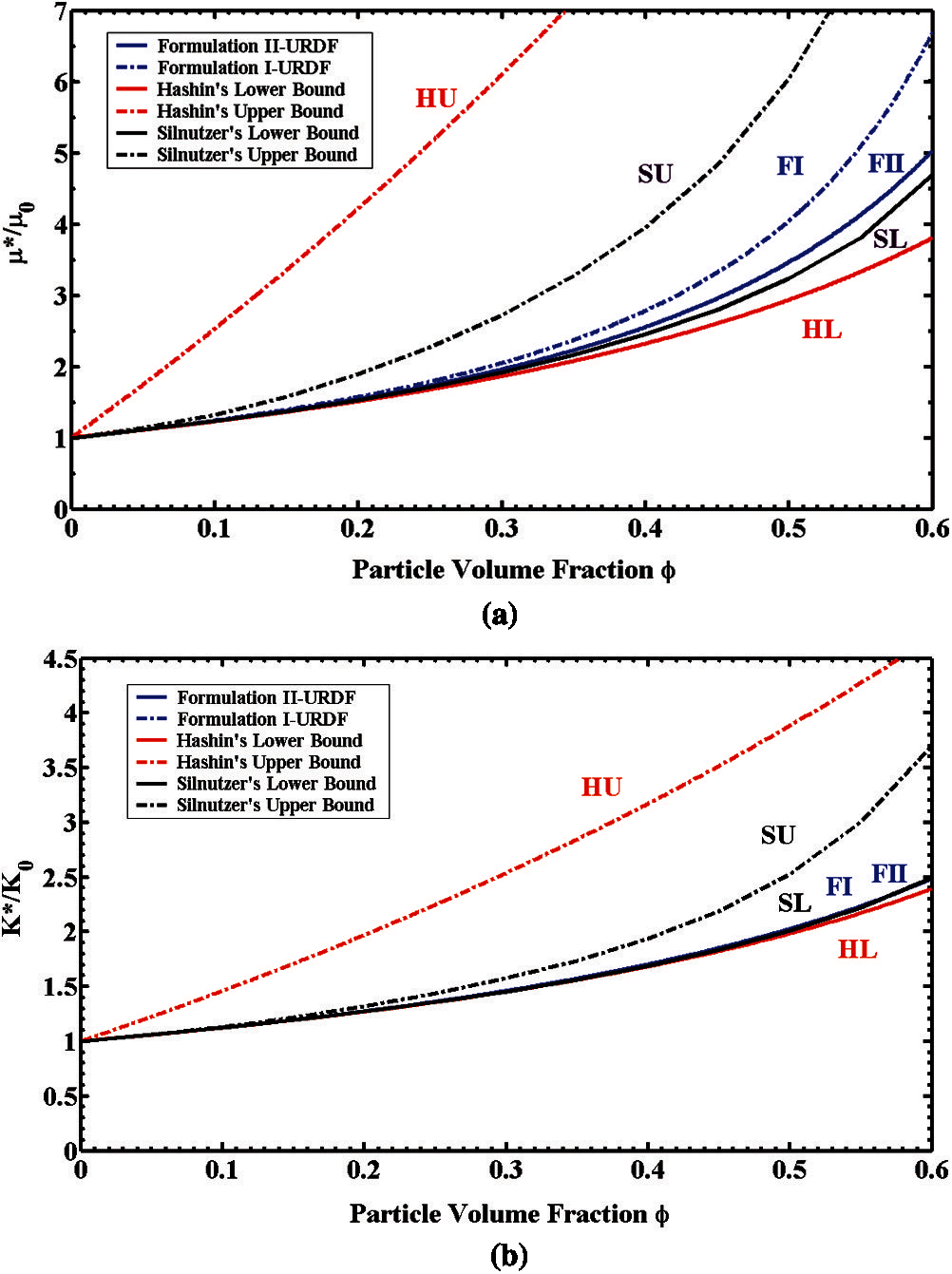
Figure 2: 2-phase elastic composites: (a) the normalized effective shear modulus
Comparisons among our analytical predictions, 2-point bounds [19], and the 3-point bounds [30,32]), and experimental data [84] on the normalized effective Young's modulus

Figure 3: 2-phase elastic composites: the normalized effective Young's modulus
5.2 3-Phase Particle Reinforced Composites-Varying Particle Volume Fractions at Different Particle Sizes
We assumed the 3-phase composites consist of only glassy spherical particles in both the 1st phase and the 2nd phase of particles with different ratios of particle size
Fig. 4a presented the normalized effective shear modulus
The normalized effective Young's modulus
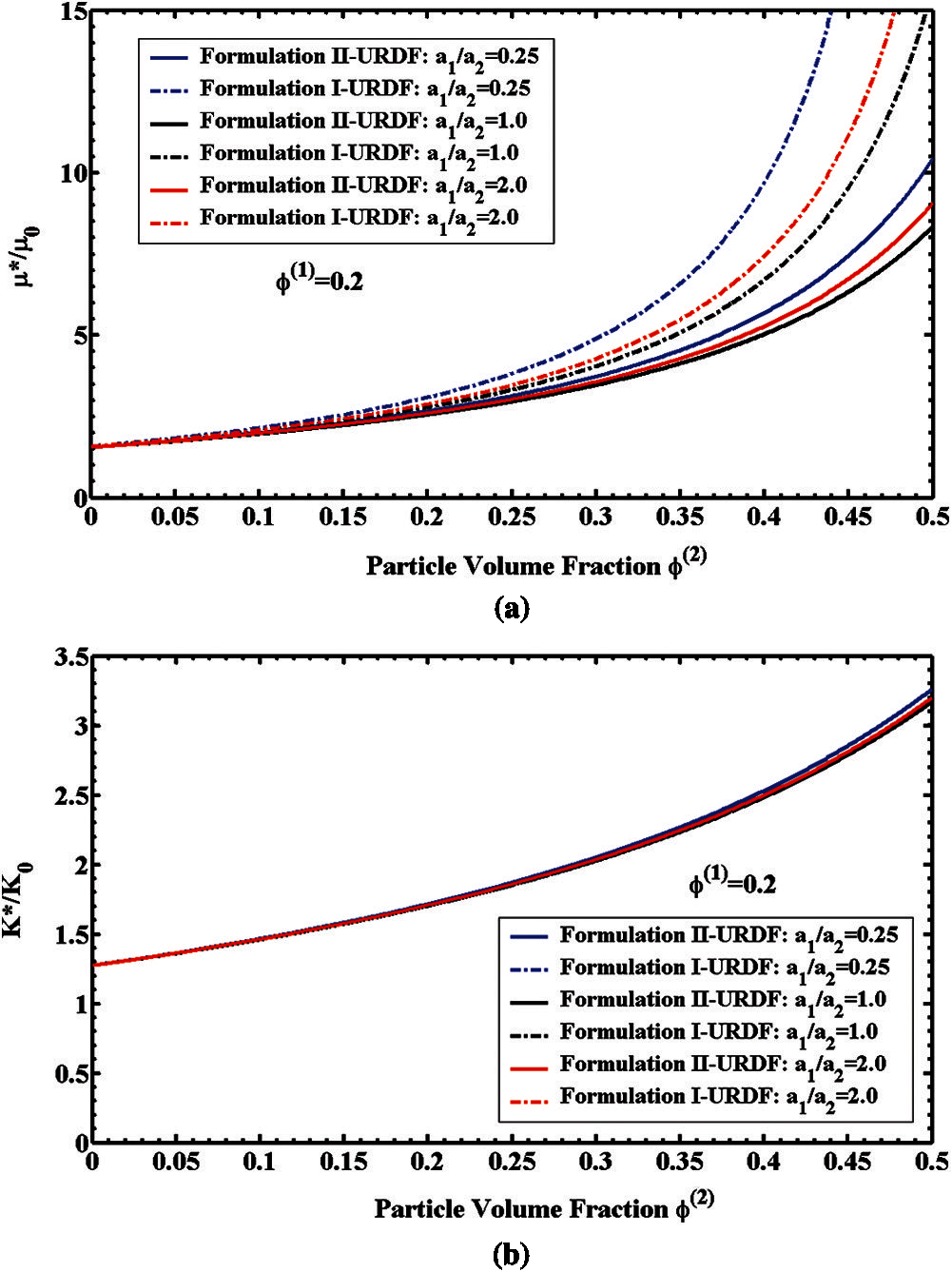
Figure 4: 3-phase elastic composites with different particle size ratios
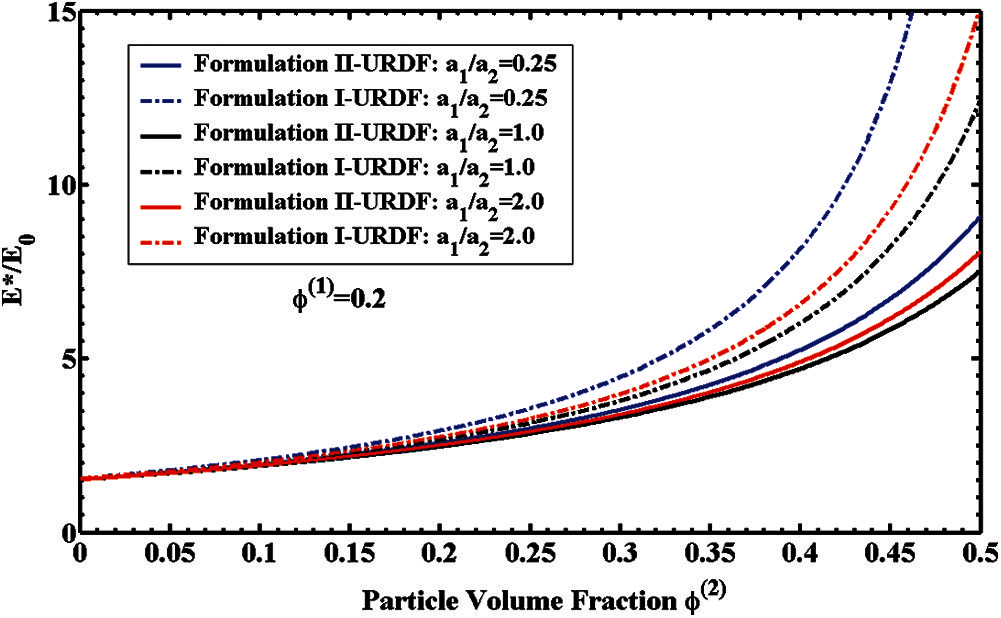
Figure 5: 3-phase elastic composites with different particle size ratios
5.3 3-Phase Particle Reinforced Composites-Varying Particle Size Ratios with a Mixture of Particle Volume Fractions
To examine the effects of varying particle size ratios, various micromechanics-based predictions were conducted. We assumed the 3-phase composites consist of only glassy spherical particles in both the 1st phase and the 2nd phase of particles with varying ratios of particle size
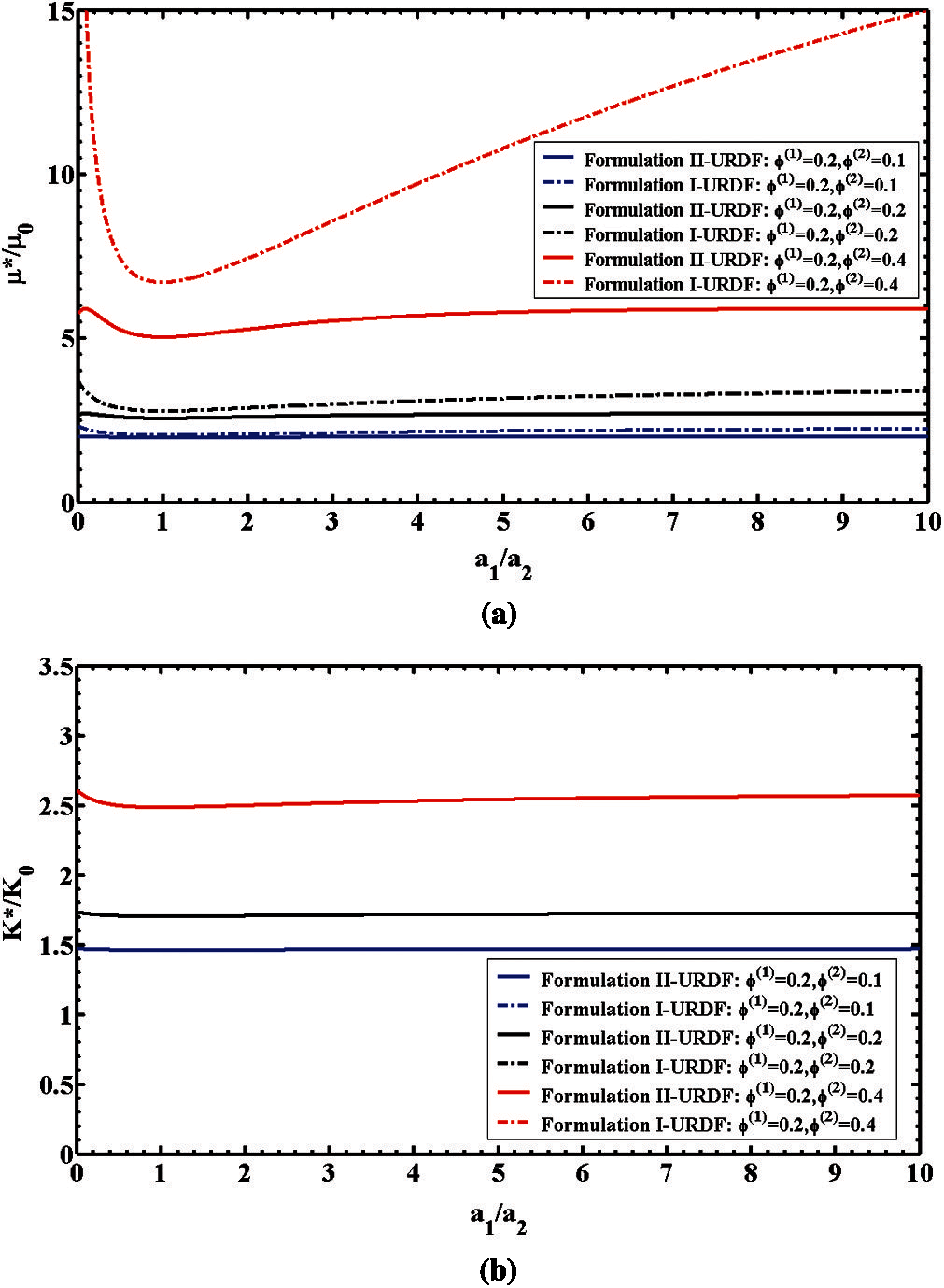
Figure 6: 3-phase elastic composites with varying particle size ratios
The normalized effective shear modulus
Fig. 7 exhibits the normalized effective Young's modulus
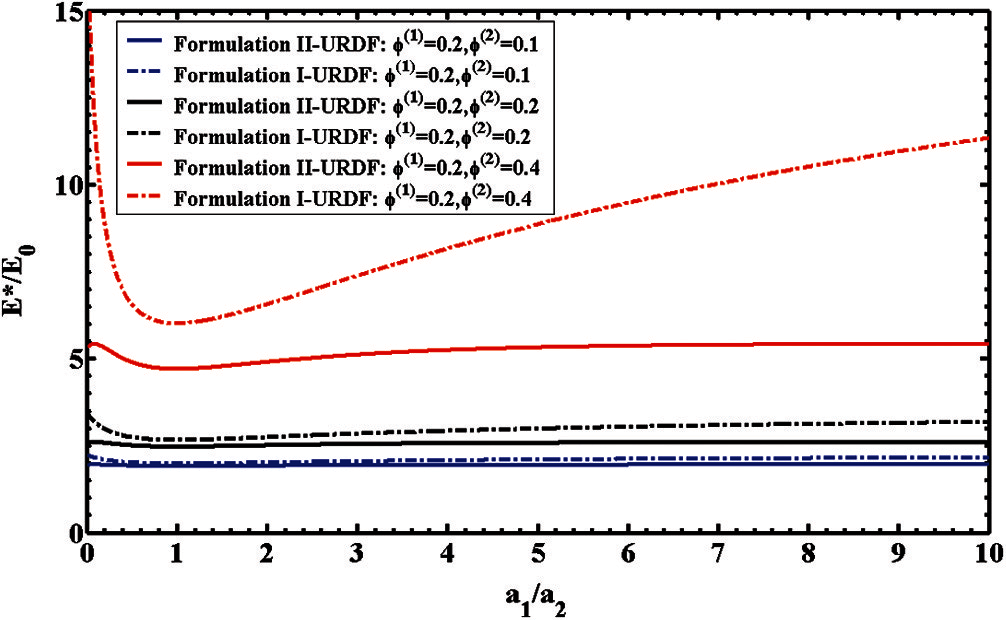
Figure 7: 3-phase elastic composites with varying particle size ratios
This paper obtains effective elastic properties of 3-phase particle reinforced composites containing randomly dispersed elastic spherical particles of different sizes and the same elastic material properties by our proposed innovative new higher-order micromechanical formulations. In particular, higher-order spherical particle interaction effects together with governing field equations are considered. The randomness of dispersed spherical particles is considered within the probabilistic ensemble volume average process. The averaged eigenstrains in spherical particles are approximately derived by ensemble volume average approach through the spherical particle interactions. Consequently, we obtained compact analytical formulations.
Moreover, improved higher-order bounds on effective elastic properties of 3-phase composites are derived by proposed Formulation II and Formulation I. This paper demonstrates major improvements over the prior works by other researchers based on the same spherical particle sizes in the matrix material. As a special case, i.e., particle size of the 1st phase is the same as particle size of the 2nd phase, the proposed formulations reduce to 2-phase formulas. Our proposed micromechanical frameworks demonstrate excellent agreement with selected experimental data. Our analytical predictions for 2-phase composites also fall within the 2-point bounds [19] and the 3-point bounds [30,32]. With our proposed analytical formulations, finite element calculations and Monte Carlo simulations can be circumvented. In addition, numerical simulations as well as comparisons presented in this paper cover a wide range of 3-phase particle reinforced elastic composites consisting of different spherical particle sizes and same elastic material properties, including varying particle size ratios as well as a mixture of particle volume fractions of the 1st phase particles and the 2nd phase particles.
To further calibrate the analytical frameworks proposed in this paper, experimental validations are the key procedures. When the associated experiment data of 3-phase elastic composites become available, additional comparisons as well as experimental validations will be conducted.
Acknowledgement: This work was in part sponsored by the 2015–2016 California State University Long Beach Research, Scholarship and Creative Activity (RSCA) Award.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Tan, X., Zhang, B., Liu, K., Yan, X. B., Han, J. et al. (2020). Microstructure and mechanical property of the 2024Al matrix hybrid composite reinforced with recycled SiCp/2024Al composite particles. Journal of Alloys and Compounds, 815, 152330. DOI 10.1016/j.jallcom.2019.152330. [Google Scholar] [CrossRef]
2. Satyanarayana, T., Rao, P. S., Krishna, M. (2019). Influence of wear parameters on friction performance of A356 aluminum–graphite/granite particles reinforced metal matrix hybrid composites. Heliyon, 5, e01770. DOI 10.1016/j.heliyon.2019.e01770. [Google Scholar] [CrossRef]
3. Arun prakash, V. R., Rajadurai, A. (2016). Thermo-mechanical characterization of siliconized E-glassfiber/hematite particles reinforced epoxy resin hybrid composite. Applied Surface Science, 384, 99–106. DOI 10.1016/j.apsusc.2016.04.185. [Google Scholar] [CrossRef]
4. Golla, S. K., Prasanthi, P. (2016). Micromechanical analysis of a hybrid composite—effect of boron carbide particles on the elastic properties of basalt fiber reinforced polymer composite. Materials Research Express, 3, 115303. DOI 10.1088/2053-1591/3/11/115303. [Google Scholar] [CrossRef]
5. Şenel, M. C., Gürbüz, M. (2020). Microstructure and wear behaviour of graphene–si3n4 binary particle-reinforced aluminium hybrid composites. Bulletin of Materials Science, 43, 148. DOI 10.1007/s12034-020-02124-4. [Google Scholar] [CrossRef]
6. Song, S. G., Shi, N., Gray, G. T., Roberts, J. A. (1996). Reinforcement shape effects on the fracture behavior and ductility of particulate-reinforced 6061-Al matrix composites. Metallurgical and Materials Transactions/a, 27, 3739–3746. DOI 10.1007/bf02595465. [Google Scholar] [CrossRef]
7. Qin, S., Chen, C., Zhang, G., Wang, W., Wang, Z. (1999). The effect of particle shape on ductility of SiCp reinforced 6061 Al matrix composites. Materials Science and Engineering A: Structure, 272, 363–370. DOI 10.1016/s0921-5093(99)00503-1. [Google Scholar] [CrossRef]
8. Ceschini, L., Minak, G., Morri, A. (2009). Forging of the AA2618/20% Al2O3p composite: Effects on microstructure and tensile properties. Composites Science and Technology, 69, 1783–1789. DOI 10.1016/j.compscitech.2008.08.027. [Google Scholar] [CrossRef]
9. Iqbal, A. A., Chen, S., Arai, Y., Araki, W. (2015). Study on stress evolution in SiC particles during crack propagation in cast hybrid metal matrix composites using ranman spectroscopy. Engineering Failure Analysis, 52, 109–115. DOI 10.1016/j.engfailanal.2015.03.007. [Google Scholar] [CrossRef]
10. Wu, C., Ma, K., Wu, J., Fang, P., Luo, G. et al. (2016). Influence of particle size and spatial distribution of B4C reinforcement on the microstructure and mechanical behavior of precipitation strengthened Al alloy matrix composites. Materials Science and Engineering A: Structure, 675, 421–430. DOI 10.1016/j.msea.2016.08.062. [Google Scholar] [CrossRef]
11. Behm, N., Yang, H., Shen, J., Ma, K., Kecskes, L. J. et al. (2016). Quasi-static and high-rate mechanical behavior of aluminum-based MMC reinforced with boron carbide of various length scales. Materials Science and Engineering A: Structure, 650, 305–316. DOI 10.1016/j.msea.2015.10.064. [Google Scholar] [CrossRef]
12. Williams, J. J., Piotrowski, G., Saha, R., Chawla, N. (2002). Effect of overaging and particle size on tensile deformation and fracture of particle-reinforced aluminum matrix composites. Metallurgical and Materials Transactions A, 33, 3861–3869. DOI 10.1007/s11661-002-0258-3. [Google Scholar] [CrossRef]
13. El-Kady, O., Fathy, A. (2014). Effect of SiC particle size on the physical and mechanical properties of extruded Al matrix nanocomposites. Materials & Design, 54, 348–353. DOI 10.1016/j.matdes.2013.08.049. [Google Scholar] [CrossRef]
14. Mordyuk, B. N., Prokopenko, G. I., Milman, Y. Iefimov, V., Grinkevych, M. O. et al. (2014). Wear assessment of composite surface layers in Al–6Mg alloy reinforced with AlCuFe quasicrystalline particles: Effects of particle size, microstructure and hardness. Wear, 319, 84–95. DOI 10.1016/j.wear.2014.07.011. [Google Scholar] [CrossRef]
15. Guo, X. L., Guo, Q., Nie, J. H., Liu, Z. Y., Li, Z. Q. et al. (2018). Particle size effect on the interfacial properties of SiC particle-reinforced Al-Cu-Mg composites. Materials Science & Engineering A, 711, 643–649. DOI 10.1016/j.msea.2017.11.068. [Google Scholar] [CrossRef]
16. Ekici, R., Kemal Apalak, M., Yıldırım, M., Nair, F. (2010). Effects of random particle dispersion and size on the indentation behavior of SiC particle reinforced metal matrix composites. Materials and Design, 31, 2818–2833. DOI 10.1016/j.matdes.2010.01.001. [Google Scholar] [CrossRef]
17. Qu, S. G., Lou, H. S., Li, X. Q. (2016). Influence of particle size distribution on properties of SiC particles reinforced aluminum matrix composites with high SiC particle content. Journal of Composite Materials, 50(8), 1049–1058. DOI 10.1177/0021998315586864. [Google Scholar] [CrossRef]
18. Hashin, Z. A., Shtrikman, S. (1962). On some variational principles in anisotropic and nonhomogeneous elasticity. Journal of the Mechanics and Physics of Solids, 10(4), 335–342. DOI 10.1016/0022-5096(62)90004-2. [Google Scholar] [CrossRef]
19. Hashin, Z., Shtrikman, S. (1962). A variational approach to the theory of the elastic behavior of multiphase materials. Journal of the Mechanics and Physics of Solids, 11(2), 127–140. DOI 10.1016/0022-5096(63)90060-7. [Google Scholar] [CrossRef]
20. Hill, R. (1964). Theory of mechanical properties of fiber-strengthened materials: I. Elastic behavior. Journal of the Mechanics and Physics of Solids, 12, 199–212. DOI 10.1016/0022-5096(64)90019-5. [Google Scholar] [CrossRef]
21. Hill, R. (1964). Theory of mechanical properties of fiber-strengthened materials: II. Inelastic behavior. Journal of the Mechanics and Physics of Solids, 12, 213–218. DOI 10.1016/0022-5096(64)90020-1. [Google Scholar] [CrossRef]
22. Hashin, Z., Rosen, B. W. (1964). The elastic moduli of fiber-reinforced materials. Journal of Applied Mechanics, 31, 223–232. DOI 10.1115/1.3629590. [Google Scholar] [CrossRef]
23. Hashin, Z. (1965). On elastic behavior of fiber reinforced materials of arbitrary transverse phase geometry. Journal of Applied Mechanics, 13, 119–134. DOI 10.1016/0022-5096(65)90015-3. [Google Scholar] [CrossRef]
24. Walpole, L. J. (1966). On bounds for overall elastic moduli of inhomogeneous systems: I. Journal of the Mechanics and Physics of Solids, 14, 151–162. DOI 10.1016/0022-5096(66)90035-4. [Google Scholar] [CrossRef]
25. Walpole, L. J. (1966). On bounds for overall elastic moduli of inhomogeneous systems: II. Journal of the Mechanics and Physics of Solids, 14, 289–301. DOI 10.1016/0022-5096(66)90025-1. [Google Scholar] [CrossRef]
26. Walpole, L. J. (1969). On the overall elastic moduli of composite materials. Journal of the Mechanics and Physics of Solids, 17(4), 235–251. DOI 10.1016/0022-5096(69)90014-3. [Google Scholar] [CrossRef]
27. Hashin, Z. (1972). Theory of fiber reinforced materials, NASA CR-1974. The National Aeronautics and Space Administration, USA. [Google Scholar]
28. Silnutzer, N. (1972). Effective constants of statistically homogeneous materials (Ph.D. Thesis). University of Pennsylvania. [Google Scholar]
29. Milton, G. W. (1982). Bounds on the elastic and transport properties of two-component composites. Journal of the Mechanics and Physics of Solids, 30(3), 177–191. DOI 10.1016/0022-5096(82)90022-9. [Google Scholar] [CrossRef]
30. Milton, G. W., Phan-Thien, N. (1982). New bounds on effective elastic moduli of two-component materials. Proceedings of the Royal Society of London. A, 380(1779), 305–331. DOI 10.1098/rspa.1982.0044. [Google Scholar] [CrossRef]
31. Sen, A. K., Lado, F. (1987). Bulk properties of composite media: II. Evaluation of bounds on the shear moduli of suspensions of impenetrable spheres. Journal of Applied Physics, 62(10), 4135–4141. DOI 10.1063/1.339130. [Google Scholar] [CrossRef]
32. Torquato, S., Lado, F. (1986). Effective properties of two-phase disordered composite media: II. Evaluation of bounds on the conductivity and bulk modulus of dispersions of impenetrable spheres. Physical Review B, 33(9), 6428–6434. DOI 10.1103/PhysRevB.33.6428. [Google Scholar] [CrossRef]
33. Torquato, S., Lado, F. (1992). Improved bounds of the effective elastic moduli of random arrays of cylinders. Journal of Applied Mechanics, 59, 1–6. DOI 10.1115/1.2899429. [Google Scholar] [CrossRef]
34. Hill, R. (1965). Theory of mechanical properties of fiber-strengthened materials: III. Self-consistent model. Journal of the Mechanics and Physics of Solids, 13, 189–198. DOI 10.1016/0022-5096(65)90008-6. [Google Scholar] [CrossRef]
35. Hill, R. (1965). A self-consistent mechanics of composite materials. Journal of the Mechanics and Physics of Solids, 13, 213–222. DOI 10.1016/0022-5096(65)90010-4. [Google Scholar] [CrossRef]
36. Christensen, R. M., Lo, K. H. (1979). Solutions for effective shear properties in three phase sphere and cylinder models. Journal of the Mechanics and Physics of Solids, 27(4), 315–330. DOI 10.1016/0022-5096(79)90032-2. [Google Scholar] [CrossRef]
37. Mori, T., Tanaka, K. (1973). Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metallurgica, 21(5), 571–574. DOI 10.1016/0001-6160(73)90064-3. [Google Scholar] [CrossRef]
38. Benveniste, Y. (1987). A new approach to the application of mori-tanaka's theory in composite materials. Mechanics of Materials, 6(2), 147–157. DOI 10.1016/0167-6636(87)90005-6. [Google Scholar] [CrossRef]
39. Weng, G. J. (1990). The theoretical connection between mori-tanaka's theory and the hashin-shtrikman-walpole bounds. International Journal of Engineering Science, 28(11), 1111–1120. DOI 10.1016/0020-7225(90)90111-U. [Google Scholar] [CrossRef]
40. Eshelby, J. D. (1957). The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proceedings of the Royal Society of London, A241, 376–396. DOI 10.1098/rspa.1957.0133. [Google Scholar] [CrossRef]
41. Mura, T. (1987). Isotropic inclusion. Micromechanics of defects in solids. 2nd edition. The Netherlands: Kluwer Academic. [Google Scholar]
42. Honein, E. (1991). Multiple inclusions in elastostatics (Ph.D. Dissertation). Stanford University. [Google Scholar]
43. Nemat-Nasser, S., Hori, M. (1993). Micromechanics: Overall properties of heterogeneous materials. The Netherlands: Elsevier Science Publisher B. V. [Google Scholar]
44. Ju, J. W., Chen, T. M. (1994a). Micromechanics and effective moduli of elastic composites containing randomly dispersed ellipsoidal inhomogeneities. Acta Mechanica, 103(1), 103–121. DOI 10.1007/BF01180221. [Google Scholar] [CrossRef]
45. Ju, J. W., Chen, T. M. (1994b). Effective elastic moduli of two-phase composites containing randomly dispersed spherical inhomogeneities. Acta Mechanica, 103(1), 123–144. DOI 10.1007/BF01180222. [Google Scholar] [CrossRef]
46. Ju, J. W., Zhang, X. D. (1998). Micromechanics and effective transverse elastic moduli of composites with randomly located aligned circular fibers. International Journal of Solids and Structures, 35(9–10), 941–960. DOI 10.1016/S0020-7683(97)00090-5. [Google Scholar] [CrossRef]
47. Ju, J. W., Yanase, K. (2010). Micromechanics and effective elastic moduli of particle-reinforced composites with near-field particle interactions. Acta Mechanica, 215(1), 135–153. DOI 10.1007/s00707-010-0337-2. [Google Scholar] [CrossRef]
48. Ju, J. W., Yanase, K. (2011). Micromechanical effective elastic moduli of continuous fiber- reinforced composites with near-field fiber interactions. Acta Mechanica, 216(1–4), 87–103. DOI 10.1007/s00707-010-0356-z. [Google Scholar] [CrossRef]
49. Lin, P. J., Ju, J. W. (2009). Effective elastic moduli of three-phase composites with randomly located and interacting spherical particles of distinct properties. Acta Mechanica, 208, 11–26. DOI 10.1007/s00707-008-0114-7. [Google Scholar] [CrossRef]
50. Adams, D. F., Crane, D. A. (1984). Finite element micromechanical analysis of a unidirectional composite including longitudinal shear loading. Computers & Structures, 18(6), 1153–1165. DOI 10.1016/0045-7949(84)90160-3. [Google Scholar] [CrossRef]
51. Nimmer, R. P., Bankert, R. J., Russell, E. S., Smith, G. A., Wright, P. K. (1991). Micromechanical modeling of fiber/matrix interface effects in transversely loaded SiC/Ti-6-4 metal matrix composites. Journal of Composites, Technology and Research, 13(1), 3–13. DOI 10.1520/CTR10068J. [Google Scholar] [CrossRef]
52. Doghri, I., Friebel, C. (2005). Effective elasto-plastic properties of inclusion-reinforced composites. study of shape, orientation and cyclic response. Mechanics of Materials, 37(1), 45–68. DOI 10.1016/j.mechmat.2003.12.007. [Google Scholar] [CrossRef]
53. Weng, L., Fan, T. X., Wen, M., Shen, Y. (2019). Three-dimensional multi-particle FE model and effects of interface damage, particle size and morphology on tensile behavior of particle reinforced composites. Composite Structure, 209, 590–605. DOI 10.1016/j.compstruct.2018.11.008. [Google Scholar] [CrossRef]
54. Ju, J. W., Chen, T. M. (1994c). Micromechanics and effective elastoplastic behavior of two-phase metal matrix composites. Journal of Engineering Materials and Technology, 116, 310–318. DOI 10.1115/1.2904293. [Google Scholar] [CrossRef]
55. Ju, J. W., Tseng, K. H. (1996). Effective elastoplastic behavior of two-phase ductile matrix composites: A micromechanical framework. International Journal of Solids and Structures, 33(29), 4267–4291. DOI 10.1016/0020-7683(95)00266-9. [Google Scholar] [CrossRef]
56. Ju, J. W., Tseng, K. H. (1997). Effective elastoplastic algorithms for ductile matrix composites. Journal of Engineering Mechanics, 123, 260–266. DOI 10.1061/(ASCE)0733-9399(1997)123:3(260). [Google Scholar] [CrossRef]
57. Ju, J. W., Zhang, X. D. (2001). Effective elastoplastic behavior of ductile matrix composites containing randomly located aligned circular fibers. International Journal of Solids and Structures, 38(22–23), 4045–4069. DOI 10.1016/S0020-7683(00)00270-5. [Google Scholar] [CrossRef]
58. Ju, J. W., Sun, L. Z. (2001). Effective elastoplastic behavior of metal matrix composites containing randomly located aligned spheroidal inhomogeneities. Part I: Micromechanics-based formulation. International Journal of Solids and Structures, 38(2), 183–201. DOI 10.1016/S0020-7683(00)00023-8. [Google Scholar] [CrossRef]
59. Sun, L. Z., Ju, J. W. (2001). Effective elastoplastic behavior of metal matrix composites containing randomly located aligned spheroidal inhomogeneities. Part II: Applications. International Journal of Solids and Structures, 38(2), 203–225. DOI 10.1016/S0020-7683(00)00026-3. [Google Scholar] [CrossRef]
60. Ju, J. W., Sun, L. Z. (1999). A novel formulation for the exterior-point eshelby's tensor of an ellipsoidal inclusion. Journal of Applied Mechanics, 66(2), 570–574. DOI 10.1115/1.2791090. [Google Scholar] [CrossRef]
61. Ju, J. W., Lee, H. K. (2000). A micromechanical damage model for effective elastoplastic behavior of ductile matrix composites considering evolutionary complete particle debonding. Computer Methods in Applied Mechanics and Engineering, 183(3–4), 201–222. DOI 10.1016/S0045-7825(99)00219-4. [Google Scholar] [CrossRef]
62. Ju, J. W., Lee, H. K. (2001). A micromechanical damage model for effective elastoplastic behavior of partially debonded ductile matrix composites. International Journal of Solids and Structures, 38(36–37), 6307–6332. DOI 10.1016/S0020-7683(01)00124-X. [Google Scholar] [CrossRef]
63. Sun, L. Z., Ju, J. W., Liu, H. T. (2003). Elastoplastic modeling of metal matrix composites with evolutionary particle debonding. Mechanics of Materials, 35, 559–569. DOI 10.1016/S0167-6636(02)00276-4. [Google Scholar] [CrossRef]
64. Sun, L. Z., Liu, H. T., Ju, J. W. (2003). Effect of particle cracking on elastoplastic behaviour of metal matrix composites. International Journal for Numerical Methods in Engineering, 56(14), 2183–2198. DOI 10.1002/(ISSN)1097-0207. [Google Scholar] [CrossRef]
65. Liu, H. T., Sun, L. Z., Ju, J. W. (2004). An interfacial debonding model for particle-reinforced composites. International Journal of Damage Mechanics, 13(2), 163–185. DOI 10.1177/1056789504041057. [Google Scholar] [CrossRef]
66. Liu, H. T., Sun, L. Z. (2004). Effects of thermal residual stresses on effective elastoplastic behavior of metal matrix composites. International Journal of Solids and Structures, 41(8), 2189–2203. DOI 10.1016/j.ijsolstr.2003.11.038. [Google Scholar] [CrossRef]
67. Ko, Y. F. (2005). Effective elastoplastic-damage model for fiber-reinforced metal matrix composites with evolutionary fibers debonding (Ph.D. Dissertation). University of California, Los Angeles. [Google Scholar]
68. Ju, J. W., Ko, Y. F., Ruan, H. N. (2006). Effective elastoplastic damage mechanics for fiber reinforced composites with evolutionary complete fiber debonding. International Journal of Damage Mechanics, 15(3), 237–265. DOI 10.1177/1056789506060747. [Google Scholar] [CrossRef]
69. Liu, H. T., Sun, L. Z., Ju, J. W. (2006). Elastoplastic modeling of progressive interfacial debonding for particle-reinforced metal matrix composites. Acta Mechanica, 181(1–2), 1–17. DOI 10.1007/s00707-005-02-79-2. [Google Scholar] [CrossRef]
70. Ju, J. W., Ko, Y. F., Ruan, H. N. (2008). Effective elastoplastic damage mechanics for fiber reinforced composites with evolutionary partial fiber debonding. International Journal of Damage Mechanics, 17(6), 493–537. DOI 10.1177/1056789507081688. [Google Scholar] [CrossRef]
71. Ju, J. W., Ko, Y. F. (2008). Micromechanical elastoplastic damage modeling of progressive interfacial Arc debonding for fiber reinforced composites. International Journal of Damage Mechanics, 17(4), 307–356. DOI 10.1177/1056789508089233. [Google Scholar] [CrossRef]
72. Ju, J. W., Yanase, K. (2008). Elastoplastic damage micromechanics for elliptical fiber composites with progressive partial fiber debonding and thermal residual stresses. Theoretical and Applied Mechanics, 35(1–3), 137–170. DOI 10.2298/TAM0803137J. [Google Scholar] [CrossRef]
73. Lee, H. K., Ju, J. W. (2008). 3-D micromechanics and effective moduli for brittle composites with randomly located interacting microcracks and inclusions. International Journal of Damage Mechanics, 17(5), 377–417. DOI 10.1177/1056789507077439. [Google Scholar] [CrossRef]
74. Ju, J. W., Ko, Y. F., Zhang, X. D. (2009). Multi-level elastoplastic damage mechanics for elliptical fiber reinforced composites with evolutionary complete fiber debonding. International Journal of Damage Mechanics, 18(5), 419–460. DOI 10.1177/1056789508097549. [Google Scholar] [CrossRef]
75. Ju, J. W., Yanase, K. (2009). Micromechanical elastoplastic damage mechanics for elliptical fiber-reinforced composites with progressive partial fiber debonding. International Journal of Damage Mechanics, 18(7), 639–668. DOI 10.1177/1056789508092418. [Google Scholar] [CrossRef]
76. Ju, J. W., Yanase, K. (2011). Size-dependent probabilistic micromechanical damage mechanics for particle reinforced metal matrix composites. International Journal of Damage Mechanics, 20(7), 1021–1048. DOI 10.1177/1056789510374165. [Google Scholar] [CrossRef]
77. Ko, Y. F., Ju, J. W. (2013). Effect of fiber-cracking on elastoplastic damage behavior of fiber-reinforced metal matrix composites. International Journal of Damage Mechanics, 22(1), 56–79. DOI 10.1177/1056789511433340. [Google Scholar] [CrossRef]
78. Zhang, Y., Ju, J. W., Zhu, H. H., Yan, Z. G. (2020). A novel multi-scale model for predicting the thermal damage of hybrid fiber reinforced concrete. International Journal of Damage Mechanics, 29(1), 19–44. DOI 10.1177/1056789519831554. [Google Scholar] [CrossRef]
79. Liu, X., Zhu, H., Ju, J. W., Chen, Q., Jiang, Z. et al. (2020). Investigation of the unbiased probabilistic behavior of the fiber-reinforced concrete's elastic moduli using stochastic micromechanical approach. International Journal of Damage Mechanics, 29(7), 1059–1075. DOI 10.1177/1056789520904007. [Google Scholar] [CrossRef]
80. Chen, Q., Zhu, H. H., Ju, J. W., Li, H. X., Yan, Z. G. (2020). Stochastic micromechanics-based investigations for the damage-healing of unsaturated concrete using electrochemical deposition method. International Journal of Damage Mechanics, 29(9), 1361–1378. DOI 10.1177/1056789520925868. [Google Scholar] [CrossRef]
81. Zhang, H., Ju, J. W., Zhu, W. L., Yuan, K. Y. (2021). A micromechanical model of elastic-damage properties of innovative pothole patching materials featuring high-toughness, low-viscosity nanomolecular resin. International Journal of Damage Mechanics, 1–24. DOI 10.1177/10567895211000089. [Google Scholar] [CrossRef]
82. Ko, Y. F., Ju, J. W. (2012). New higher-order bounds on effective transverse elastic moduli of three-phase fiber reinforced composites with randomly located and interacting aligned circular fibers. Acta Mechanica, 223(11), 2437–2458. DOI 10.1007/s00707-012-0696-y. [Google Scholar] [CrossRef]
83. Ko, Y. F., Ju, J. W. (2013). Effective transverse elastic moduli of three-phase hybrid fiber reinforced composites with randomly located and interacting aligned circular fibers of distinct elastic properties and sizes. Acta Mechanica, 224(1), 157–182. DOI 10.1007/s00707-012-0744-7. [Google Scholar] [CrossRef]
84. Smith, J. C. (1976). Experimental values for the elastic constants of a particulate-filled glassy polymer. Journal of Research of the National Bureau of Standards Section A Physics and Chemistry, 80A(1), 45–49. DOI 10.6028/jres.080A.008. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |