Near Future Perspective of ESBL-Producing <i>Klebsiella pneumoniae</i> Strains Using Mathematical Modeling

Cemile Bagkur; Emrah Guler; Bilgen Kaymakamzade; Evren Hincal; Kaya Suer

doi:10.32604/cmes.2022.016957

Near Future Perspective of ESBL-Producing Klebsiella pneumoniae Strains Using Mathematical Modeling

Cemile Bagkur1,*, Emrah Guler2,3, Bilgen Kaymakamzade4,5, Evren Hincal4,5 and Kaya Suer6

1Department of Medical Microbiology and Clinical Microbiology, Near East University, Nicosia, 99010, Cyprus
2Department of Nutrition and Dietetics, Near East University, Nicosia, 99010, Cyprus
3DESAM Institute, Near East University, Nicosia, 99010, Cyprus
4Department of Mathematics, Near East University, Nicosia, 99010, Cyprus
5Mathematics Research Center, Near East University, Nicosia, 99010, Cyprus
6Department of Infectious Diseases and Clinical Microbiology, Near East University, Nicosia, 99010, Cyprus
*Corresponding Author: Cemile Bagkur. Email: cemilebagkur@hotmail.com
Received: 14 April 2021; Accepted: 12 July 2021

Abstract: While antibiotic resistance is becoming increasingly serious today, there is almost no doubt that more challenging times await us in the future. Resistant microorganisms have increased in the past decades leading to limited treatment options, along with higher morbidity and mortality. Klebsiella pneumoniae is one of the significant microorganisms causing major public health problems by acquiring resistance to antibiotics and acting as an opportunistic pathogen of healthcare-associated infections. The production of extended spectrum beta-lactamases (ESBL) is one of the resistance mechanisms of K. pneumoniae against antibiotics. In this study, the future clinical situation of ESBL-producing K. pneumoniae was investigated in order to reflect the future scenarios to understand the severity of the issue and to determine critical points to prevent the spread of the ESBL-producing strain. For evaluation purposes, SIS-type mathematical modeling was used with retrospective medical data from the period from 2016 to 2019. Stability of the disease-free equilibrium and basic reproduction ratios were calculated. Numerical simulation of the SIS model was conducted to describe the dynamics of non-ESBL and ESBL-producing K. pneumoniae. In order to determine the most impactful parameter on the basic reproduction ratio, sensitivity analysis was performed. A study on mathematical modeling using data on ESBL-producing K. pneumoniae strains has not previously been performed in any health institution in Northern Cyprus, and the efficiency of the parameters determining the spread of the relevant strains has not been investigated. Through this study, the spread of ESBL-producing K. pneumoniae in a hospital environment was evaluated using a different approach. According to the study, in approximately seventy months, ESBL-producing K. pneumoniae strains will exceed non-ESBL K. pneumoniae strains. As a result, the analyses showed that hospital admissions and people infected with non-ESBL or ESBL-producing K. pneumoniae have the highest rate of spreading the infections. In addition, it was observed that the use of antibiotics plays a major role in the spread of ESBL-producing K. pneumoniae compared to other risk factors such as in-hospital transmissions. As a matter of course, recoveries from Klebsiella infections were seen to be the most effective way of limiting the spread. It can be concluded from the results that although the use of antibiotics is one of the most effective factors in the development of the increasing ESBL-producing K. pneumoniae, regulation of antibiotic use policy could be a remedial step together with effective infection control measures. Such steps may hopefully lead to decreased morbidity and mortality rates as well as improved medical costs.

Keywords: Mathematical modeling; Klebsiella pneumoniae; extended spectrum beta lactamases (ESBL)

Klebsiella pneumoniae (K. pneumoniae) is a member of the Enterobacteriaceae family, which is a saprophyte found in the gastrointestinal tract of humans. It is an opportunistic pathogen that causes complicated and difficult to treat community-acquired and nosocomial infections such as in the urinary system, soft tissue, pneumonia and bacteremia, and usually affects immunosuppressive and in-patients [1,2]. The increase in antibiotic-resistant K. pneumoniae species has caused outbreaks in hospitals in many countries, leading to high mortality rates in infected people [3].

The problem of antibiotic resistance is a major obstacle for clinicians, veterinarians and other infection control workers in the treatment and prevention of microorganisms that cause infections [4]. The most important mechanism of resistance seen in Klebsiella species is the production of extended spectrum beta-lactamase (ESBL). Carbapenem group antibiotics are the first choice agents in the treatment of infections caused by ESBL-producing gram-negative bacteria. As a result of the the widespread and improper use of carbapenems, resistance problems have arisen against this group of antibiotics. Outbreaks and sporadic cases caused by K. pneumoniae species producing ESBL and carbapenemase in all health institutions, especially in intensive care units, have been escalating with an increasing incidence rate around the world in recent years, which has led to global concern [1–5]. Many factors such as increased antimicrobial resistance, increased human interactions and dynamic human behavior have affected the prevention and control of infectious diseases, causing them to become international problems rather than just national issues. Against this complexity, mathematical models provide the necessary tools to synthesize information to understand epidemiological patterns and to develop the quantitative evidence base for making global health decisions. Mathematical models in epidemiology provide an insight into the underlying mechanisms that affect the spread of disease at the population level [6]. To help understand and control infectious diseases, mathematical models are increasingly being used, particularly to identify key parameters leading to disease spread, evaluate the impact of potential interventions, and predict the trajectory of outbreaks. Although the role of mathematical modeling in the control of emerging infections can be clearly observed, it is thought that it can be an effective tool in antimicrobial resistance control [7]. The studies conducted by Lipsitch et al. and Weinstein et al. [8,9] also support the idea that mathematical modeling can be useful for the investigation of antibiotic resistance of nosocomial pathogens.

In infectious diseases, the frequency of causative microorganisms and their antibiotic sensitivity can change over time. Therefore, in order to guide empirical treatment, changes in the active microorganism and antibiotic susceptibility should be determined by each institution. Correct determination of policies for use of antibiotics is critical in identifying the appropriate treatment and preventing the development of resistance [10].

Considering that 30 years have passed since the emergence of a new class of antibiotics, the treatment of resistant strains with new drugs seems unlikely to succeed. Taking precautions to prevent the increasing spread of resistance rather than waiting for new antibiotic classes is the most effective step that can be taken. For this reason, the rates of non-ESBL and ESBL-producing strains of K. pneumoniae over the years are calculated using mathematical modeling. The data used in the study are cumulative data of K. pneumoniae from 2016 to 2019. The aim is to determine the future distribution of non-ESBL and ESBL-producing K. pneumoniae strains in the hospital and to identify possible future problems in order to prevent them with the measures taken today.

Consequently, for the improvement of treatment options, reduction of medical costs and decrease of morbidity and mortality rates of resistant microorganisms, precautions must be taken and it is necessary to regulate the use of antibiotics and raise awareness on resistance.

Using mathematical models to predict outcomes in the medical field is helpful for clinicians as this practice enables our knowledge to be expanded further based on actual data. Limitations such as repeating studies, possible risks and researching on actual patients can be overcome. As nonlinear systems are inherently unpredictable, mathematical modeling can be used in the medical field, such as to describe the performance of an organ or to investigate the behavior of an organ system [11,12]. Therefore, mathematical modeling plays an important role in understanding many complex biological systems and investigating global events such as pandemics in detail [13].

As the spread of ESBL-producing K. pneumoniae is a global threat, investigations to determine the hospital departments in which it is more common and detailed examinations of clonal diversity through molecular genotyping have been performed by many researchers [14,15]. Control measures and public health interventions have also been evaluated through mathematical models [16,17]. This study shows what will await us in the future regarding ESBL-producing K.pneumoniae infections if the current situation continues and how much time remains for the worst-case scenario in which the ESBL-producing strains exceed the non-ESBL strains.

To the best of our knowledge, the present study is the first to examine data on ESBL-producing K. pneumoniae using mathematical modeling in a health institution in Northern Cyprus. By the means of numerical simulations and sensitivity analysis, we can predict what expects us in an estimated time and what are the significant parameters in terms of preventing increases in the rates of morbidity and mortality. The contribution of effective parameters in the infection process is also enlightened with the possibilities offered by mathematical modeling, and the study, which was carried out with the joint work of two different fields, sets an example in terms of the importance of a multidisciplinary approach in infection control.

The main contributions of this research can be summarized as follows: by using an SIS-type model, the dynamics of the non-ESBL and ESBL-producing K. pneumoniae strains for the near future were analyzed and the effects of these dynamics were discussed. Sensitivity analysis was performed to determine the effect of important parameters on the basic reproduction ratio for both non-ESBL and ESBL-producing K. pneumoniae strains.

The remainder of the article proceeds as follows. In Section 2, collected K. pneumoniae data are adapted to a SIS-type model. In Section 3, the values of the model in numerical simulation and sensitivity analysis are specified. In the last sections, a discussion of the results and concluding remarks are presented.

Klebsiella spp. strains detected in patients who presented to the university hospital between 2016 and 2019 were determined by selecting certain parameters from the hospital data system. In addition to parameters such as age, gender, culture samples (e.g., urine, sputum, aspirate), and relevant departments (e.g., intensive care, infection, internal medicine), the strains were also grouped according to whether they were ESBL positive (ESBL-producing) or ESBL negative (non-ESBL). The obtained data were evaluated by the mathematics department for mathematical modeling.

Culture samples were delivered to the microbiology laboratory of the university hospital. The samples were inoculated on blood and eosin methylene blue (EMB) media then incubated at 35°C for 24–48 h. Specimens with gram-negative growth were prepared in 0.5 McFarland bacterial suspension in accordance with the manufacturer's recommendations. Prepared suspensions were loaded into a BD Phoenix™ 100 device for identification and analysis of antimicrobial susceptibility tests.

In the SIS-type model, populations within the hospital are stated in three mutually exclusive ways: susceptible S(t), infected with ESBL+ K. pneumoniae E+(t) and infected with ESBL− K. pneumoniae E−(t). Here, it is assumed that individuals enter the hospital in one of these classes with the constant variable Λ.

The rate that individuals enter the hospital infected with ESBL- is m1, and for those infected with ESBL+ it is m2. The individuals exit from hospital either via death (μ) or hospital discharge (d). The susceptible class can be infected with ESBL- K. pneumoniae (δ1) or ESBL+ K. pneumoniae (δ2). The recovery rate from ESBL- is β1 and the recovery rate from ESBL+ is given by β2. The rate of transmission from ESBL- K. pneumoniae to ESBL+ K. pneumoniae is β2 With these assumptions, newly created differential equations in (1) are used for the model, where the meaning of the parameters/variables is presented in Table 1.

2.3.2 Stability of Disease Free Equilibrium Point (DFE) and Basic Reproduction Ratio

By equalizing each equation in the system (1) to zero and with the assumption m1=m2=0, we get the disease-free equilibrium (2):

then the basic reproduction number (R0) is the dominant eigenvalue of the fu−1, the basic reproduction ratio (R0) is found as R0={R0,E−,R0,E+}, where

Theorem 1: For the model (1), the disease-free equilibrium (2) is locally asymptotically stable whenever R0,E−<1 and R0,E+<1.

The eigenvalues of the Jacobian matrix are λ1=δ1S0−(cβ1+(1−c)β3+μ), λ2=δ2S0−(β2+μ), λ3=−(μ+d).

λ3 is always less than zero and λ1is less than zero whenever R0,E− (3) is less than zero and λ2 is less than zero whenever R0,E+ (4) is less than zero. Therefore, DFE is locally asymptotically stable when both R0,E− and R0,E+ are less than zero.

In this section, numerical results are calculated by simulating the model using the real data obtained the university hospital for the period 2016 and 2019. The model parameters used for this simulation are: S, E−,E+, Λ, m1, m2, C, δ1, δ2, β1, β2, β3.

The sensitivity analysis was used to understand the sensitivity of the basic reproduction number in relation to the important parameters used throughout the model. The computation of the expression of the basic reproduction number was carried out in Section 2.3.2 above and is denoted by

The computation of the normalized local sensitivity indices of R0 proportional to the parameters was performed. Here, the set of input parameters relative to R0 are

We denoted R0 by the normalized local sensitivity index with respect to a parameter found in γ, where γ is defined as

Using the above definition in (5), we computed the following indices (6)–(15) for the output R0 with respect to every parameter presented in.

ΩμR0,ESBL−=−Λδ1[cβ1+(1−c)β3+2μ]μ2(cβ1+(1−c)β3+μ)2μ2(cβ1+(1−c)β3+μ)δ1Λ=−[cβ1+(1−c)β3+2μ]cβ1+(1−c)β3+μ,(8)

ΩcR0,ESBL−=−Λδ1[β1−β3]μ(cβ1+(1−c)β3+μ)2μc(cβ1+(1−c)β3+μ)δ1Λ=−c[β1−β3]cβ1+(1−c)β3+μ,(9)

Ωβ1R0,ESBL−=−Λδ1cμ(cβ1+(1−c)β3+μ)2μβ1(cβ1+(1−c)β3+μ)δ1Λ=−β1ccβ1+(1−c)β3+μ,(10)

Ωβ3R0,ESBL−=−Λδ1(1−c)μ(cβ1+(1−c)β3+μ)2μβ3(cβ1+(1−c)β3+μ)δ1Λ=−β3(1−c)cβ1+(1−c)β3+μ,(11)

ΩμR0,ESBL+=−Λδ2[β2+2μ]μ2(β2+μ)2μμ(β2+μ)Λδ2=−[β2+2μ](β2+μ),(14)

In this paper, we studied an SIS-type model. The model shown in Fig. 1 demonstrates the transmission dynamics of Klebsiella bacteria with the acquisition of non-ESBL (ESBL−) or ESBL-producing (ESBL+) K. pneumoniae by susceptible patients and the acquisition of ESBL+ Klebsiella by ESBL− patients or the recoveries of either ESBL− orESBL+ K. pneumoniae patients into susceptible.

Figure 1: A compartment model of ESBL− and ESBL+ K. pneumoniae and susceptible individuals to K. pneumoniae infection in the hospital

By simulating the model, the values of the parameters calculated based on the data are presented in Table 2.

Basic reproduction numbers R0E+ and R0E− were found by using the next generation matrix method. The basic reproduction number R0 is the measurement of the potential of a disease to spread in a given population. In general, if R0<1, then the infection will die out, but if R0≥1, the infection will be able to spread.

Basic reproduction ratios of R0E+ and R0E− were calculated by plugging the values in Table 2 into the equations in (3) and (4).

Since both R0,E+ and R0,E−>1, there will be endemics for both resistant (ESBL+) and non- resistant (ESBL−) strains. However, the value of R0,E+ is greater than R0,E−, so the resistant group is more dangerous than the non-resistant group, which can be seen in Fig. 2.

We used local sensitivity analysis to illustrate the impact of each model parameter on R0. Plugging the values in Table 2 into the equations from (6)–(15), sensitivity values of each parameter are obtained. The calculated sensitivity values are shown in Table 3.

Table 3 demonstrates that increasing (respectively decreasing) any rate Λ, δ1 or δ2 by 10% will increase (respectively decrease) the value of R0 by 10%. Increasing (respectively decreasing) c by 10% will decrease (respectively increase) the value of R0 by about 6%. Increasing (respectively decreasing) the β1by 10%will decrease (respectively increase) the value of R0 by about 9%. Increasing (respectively decreasing) the β2 by 10% will decrease (respectively increase) the value of R0 by about 10%. Increasing (respectively decreasing) the β3 by 10% will decrease (respectively increase) the value of R0 by about 1%. Increasing (respectively decreasing) the μ by 10% will decrease (respectively increase) the value of R0 by about 10%. Graphical descriptions of the parameters are shown in Figs. 3–9.

Figure 3: Number of individuals infected with ESBL− (in (a)) and ESBL+ (in (b)) predicted by the model with original parameter values in Table 2 and with an increase of 10% in specific parameter Λ a. Impact of the variation of Λ on the number of ESBL− infections b. Impact of the variation of Λ on the number of ESBL+ infections

Figure 4: Number of individuals infected with ESBL− (in (a)) and ESBL+ (in (b)) predicted by the model with original parameter values in Table 2 and with an increase of 10% in specific parameter δ1 a. Impact of the variation of δ1 on the number of ESBL− infections b. Impact of the variation of δ1 on the number of ESBL+ infections

Figure 5: Number of individuals infected with ESBL− (in (a)) and ESBL+ (in (b)) predicted by the model with original parameter values in Table 2 and with an increase of 10% in specific parameter δ2 a. Impact of the variation of δ2 on the number of ESBL− infections b. Impact of the variation of δ2 on the number of ESBL+ infections

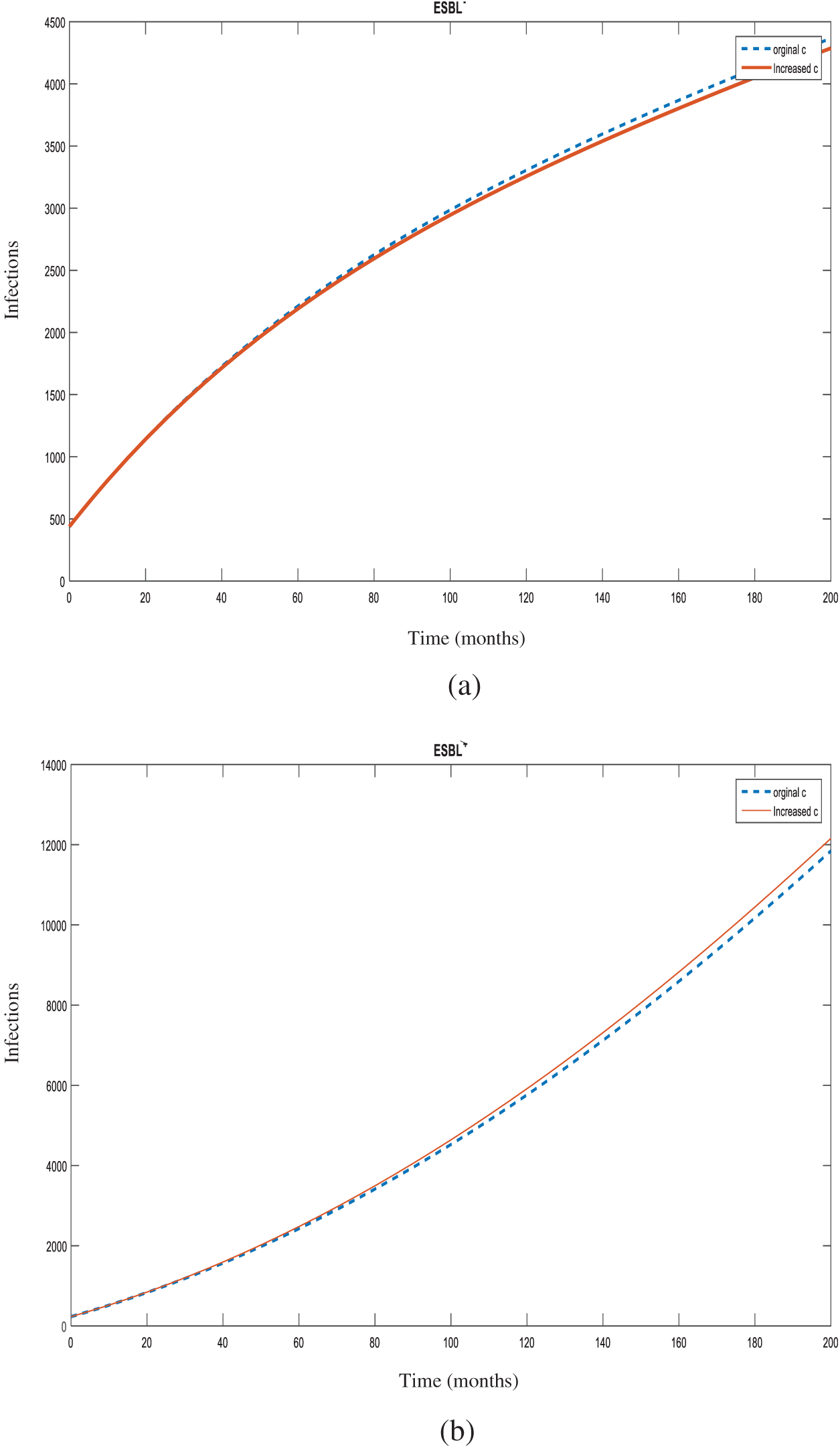
Figure 6: Number of individuals infected with ESBL− (in (a)) and ESBL+ (in (b)) predicted by model with original parameter values in Table 2 and with an increase of %10 of specific parameter c a. Impact of the variation of c on the number of ESBL− infections b. Impact of the variation of c in the number of ESBL+ infections

Figure 7: Number of individuals infected with ESBL− (in (a)) and ESBL+ (in (b)) predicted by the model with original parameter values in Table 2 and with an increase of 10% in specific parameter β1 a. Impact of the variation of β1 on the number of ESBL− infections b. Impact of the variation of β1 on the number of ESBL+ infections

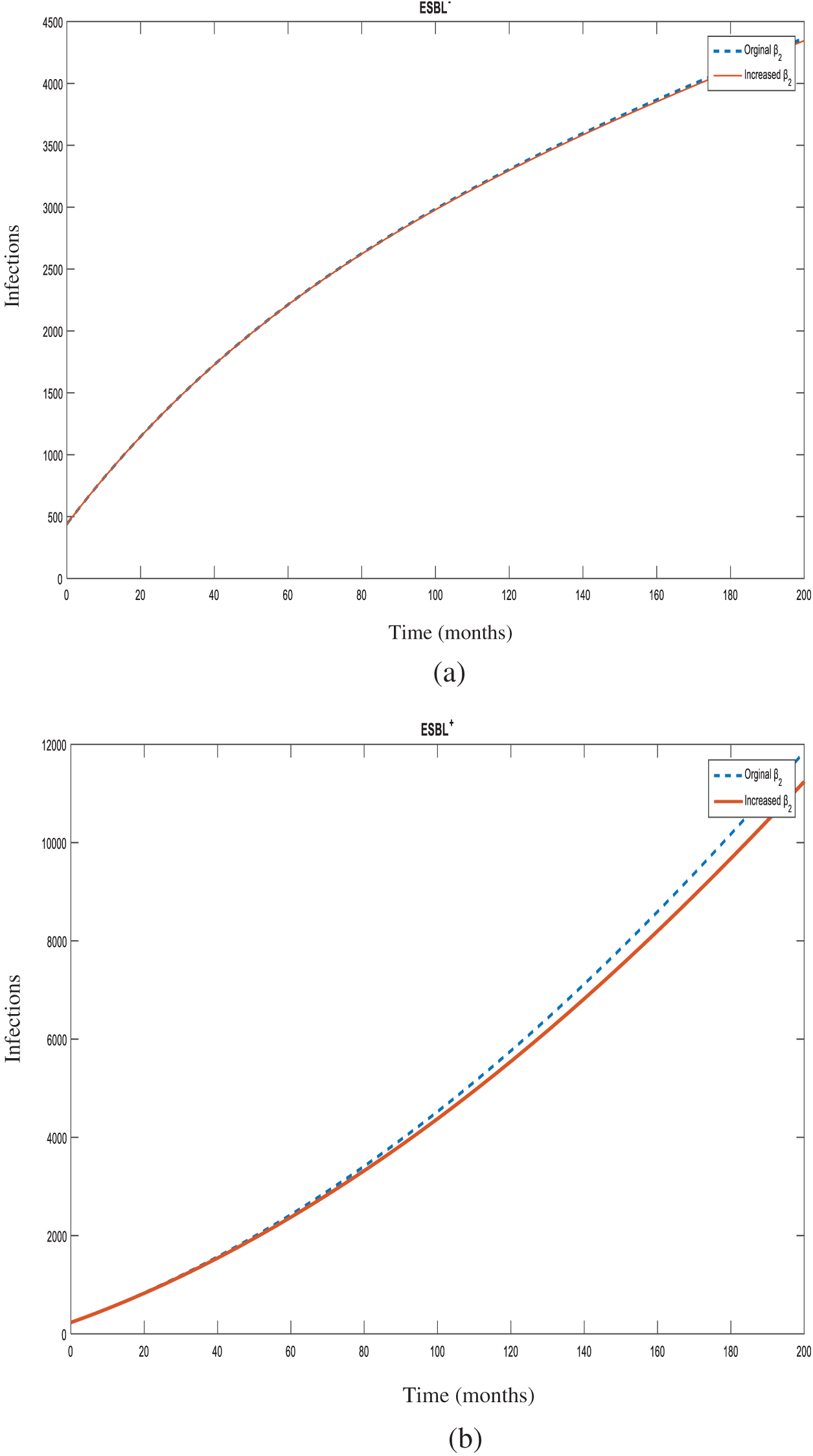
Figure 8: Number of individuals infected with ESBL− (in (a)) and ESBL+ (in (b)) predicted by the model with original parameter values in Table 2 and with an increase of 10% in specific parameter β2 a. Impact of the variation of β2 on the number of ESBL− infections b. Impact of the variation of β2 on the number of ESBL+ infections

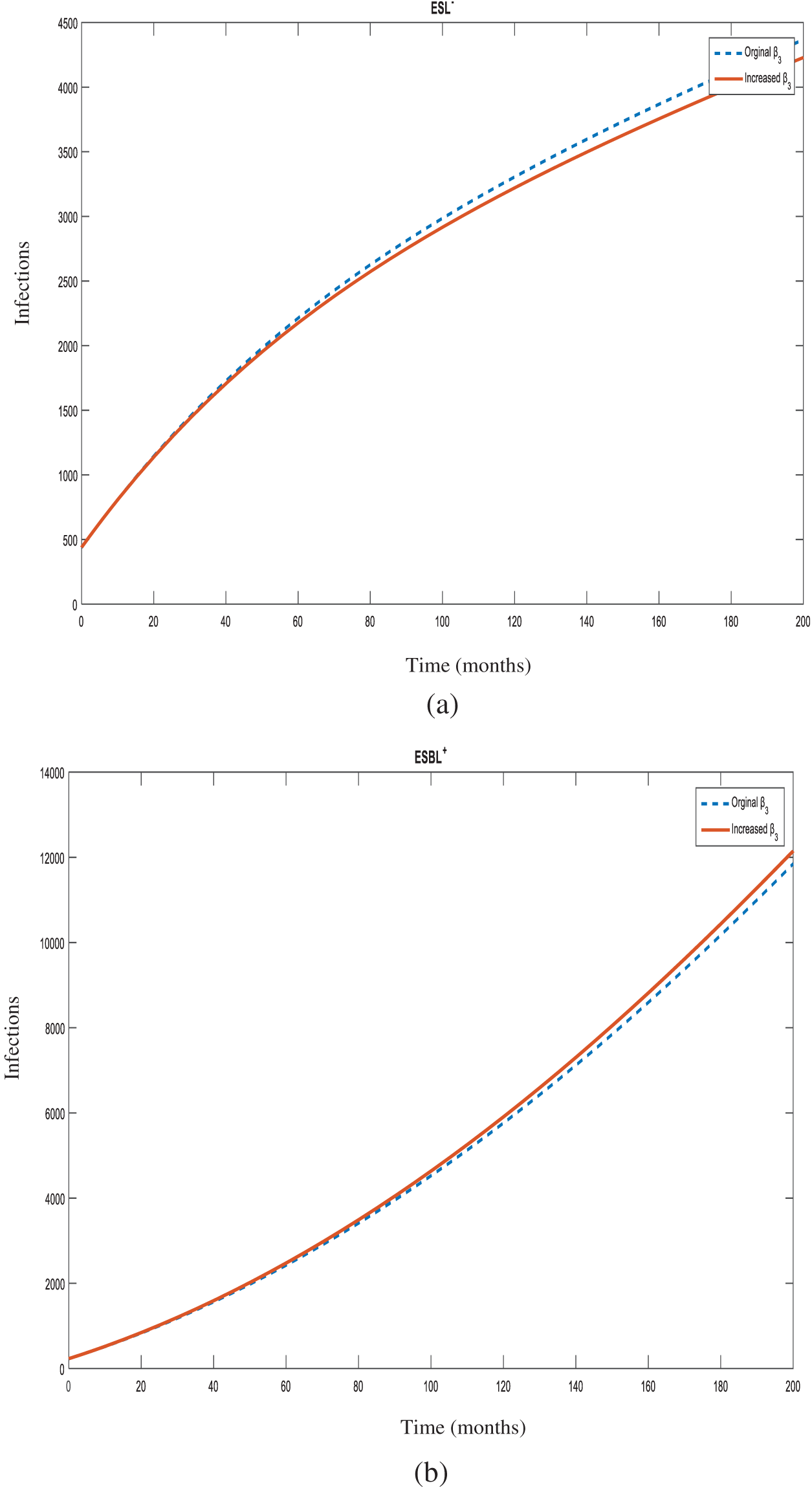
Figure 9: Number of individuals infected with ESBL− (in (a)) and ESBL+ (in (b)) predicted by the model with original parameter values in Table 2 and with an increase of 10% in specific parameter β3 a. Impact of the variation of β3 on the number of ESBL− infections b. Impact of the variation of β3 on the number of ESBL+ infections

The present study was carried out to evaluate the spread of non-ESBL and ESBL-producing K. pneumoniae strains in the hospital environment for the following years. In this context, based on the transmission dynamics of K. pneumoniae, an SIS-type model was created. Basic reproduction numbers R0E+ and R0E−were calculated by using the next-generation matrix method. In addition, local sensitivity analysis was used to illustrate the impact of each model parameter on R0.

The basic reproduction number (R0) is the measurement of the potential of a disease to spread in a given population. If a disease is introduced to a population by an infected individual in the absence of immunity to the particular disease, the subsequent generation of secondary cases is defined as R0 [18].

R0 < 1 is described as the situation where an infected individual can cause less than one new case on average during the individual's infection period. Then, the infection will die out and not spread. In this case, the disease free equilibrium is locally asymptotically stable. On the other hand, R0 > 1 is described as being when any infected individual can cause more than one new case on average so that the infection will be able to spread, indicating the possibility of an endemic. In this situation, the disease free equilibrium is locally asymptotically unstable [19].

According to the model parameters, which were calculated from the data collected from the hospital, R0E−was found to be approximately 1.998 and R0E+ was found to be approximately 2.342. Both R0 values are >1, which indicates that a major endemic caused by the spread of both strains is fairly possible. However, the greater value of R0E+ indicates that susceptible individuals and individuals infected with non-ESBL K. pneumoniae have a higher possibility of acquiring ESBL-producing strains compared to the likelihood of susceptible individuals acquiring non-ESBL strains of K. pneumoniae. This situation can be linked to the fact that ESBL-producing K. pneumoniae strains are more difficult to treat compared to non-ESBL ones as they are resistant to antibiotics and this limits the therapeutic options. Transferable resistance can occur between strains through conjugation or transformation [20]. Therefore, infections of ESBL-producing strains are more persistent making them higher risk than non-ESBL strains. In addition, it has been observed that ESBL-producing strains of K. pneumoniae can produce biofilms, which support the attachment to surfaces, prevent the activity of antibiotics and are challenging to eradicate [21,22].

Even though the R0E− value is less than R0E+, it is quite high according to the concept of the basic reproduction ratio as it is greater than one. As an opportunistic pathogen, K. pneumoniae can spread easily from the gastrointestinal tracts of patients and staff, as well as the hands of health-care workers in the hospital. Immunocompromised patients and patients with invasive devices have a higher risk of acquiring K. pneumoniae infections. The use of antibiotics and length of hospitalization also increase the colonization of nosocomial Klebsiella [23] and increase the possibility that non-ESBL strains will turn into ESBL positive strains by the acquisition of resistance under the antibiotic selective pressure [24].

Numerical results were calculated by simulating the model using real data obtained from the university hospital between the years of 2016 and 2019. The dynamics of non-ESBL and ESBL-producing strains are shown in Fig. 2. According to the table, at the present time, the number of ESBL-producing strains is less than non-ESBL strains. However, as time progresses, the ESBL-producing strain number approaches the number of non-ESBL strains in the fortieth month. From this point, the lines of ESBL-producing strains and non-ESBL strains seem to continue almost equally for thirty months. By the seventieth month, ESBL-producing strains start to increase gradually leaving the non-ESBL strains behind. This table shows that in forty months, ESBL-producing strains will arise, thus causing antibiotic resistance and difficulties in the treatment of resistant pathogens. In addition, as the treatment will be challenging, morbidity and mortality rates will also increase together with treatment costs. For two and a half years, while the rates of non-ESBL and ESBL-producing strains are expected to be equivalent, almost 6 years later, infections caused by ESBL-producing K. pneumoniae strains will exceed non-ESBL K. pneumoniae infections. To avoid such a situation, strict precautions must be taken by the hospital's infection control committee to prevent the spread of ESBL-producing strains. It is important that health-care workers are educated on how to take care of patients infected or colonized with ESBL-producing K. pneumoniae. Sanitation, disinfection and sterilization must be properly applied to these patients’ rooms and medical devices. Antimicrobial susceptibility tests must be performed to follow the resistance profiles of patients for efficient therapeutic applications.

A study carried out by Navon-Venezia et al. in 2017 produced a similar table showing that between 2005 and 2015, the resistance rates of K. pneumoniae steadily increased over the years. The study was carried four antibiotic classes including the third-generation cephalosporins, aminoglycosides, fluoroquinolones and carbapenems, and it was found that the resistance rates between countries varied [24].

In the case of the spread of an infection, in order to determine which parameter and at what magnitude would be the most effective in reducing the R0 value, sensitivity analysis is used. Determination of control measures informs the infection control committee which points require more attention. In this study, all increases were made at 10% for sensitivity analysis of the model. Increasing the rates of hospital admissions (Λ), transmission of susceptible individuals with non-ESBL K. pneumoniae (δ1) and transmission of susceptible individuals with ESBL-producing K. pneumoniae (δ2) seemed to increase the R0 value by 10%.

As an opportunistic pathogen, K. pneumoniae accounts for one third of all gram-negative infections causing urinary tract infections, pneumonia, wound infections, intra-abdominal infections and septicemia [24]. In addition, Klebsiella plays a role in community-acquired infections such as necrotizing pneumonia, pyogenic liver abscesses and endogenous endophthalmitis [23]. It is among the top three most causative agents of neonatal sepsis in most facilities [25]. ESBL-producing and carbapenem-resistant K. pneumoniae is accepted as a critical public health threat by the World Health Organization (WHO) that accounts for >90,000 infections with >7,000 deaths in Europe on an annual basis [26,27]. This high rate and the variety of infections certainly contribute to increased R0 values. Besides being a nosocomial pathogen, it can exhibit wide phenotypic and genetic diversity, as it can be found in many environmental and host-associated niches [28]. This increases the ease by which Klebsiella infections can be acquired.

The administration of any drug (c) to non-ESBL Klebsiella infections is seen to decrease the R0 value by about 6%, as it treats the infections caused by non-ESBL K. pneumoniae (Fig. 6a). However, if we take into account the possibility of resistance to the drug, the R0 value of ESBL-producing Klebsiella infections seems to increase (Fig. 6b) according to drug resistant strains and limited treatment options, leading to persistent infections.

As fluoroquinolones are broad-spectrum antibiotics, they were extensively used for empirical treatment of infections caused by gram-negative bacteria. Also, it was found that ESBLs frequently mediate the mechanisms of resistance to fluoroquinolones [29]. Accordingly, fluoroquinolone resistance emerged, thus making third-generation cephalosporins the choice of empirical treatment. Unfortunately, for the treatment of community-associated or healthcare-associated infections, ESBL-producing strains displayed resistance to third-generation cephalosporins [30]. Accordingly, for the treatment of non-ESBL infections, empirical treatment options must be chosen carefully. Regional patterns of resistance for community-associated infections and risk factors for patients in terms of acquiring resistance to third-generation cephalosporins must be considered. Another study carried out by Salzar-Vizcaya et al. in 2019 showed that public health interventions aimed at reducing antimicrobial consumption were observed to effectively reduce the prevalence of ESBL-producing K. pneumoniae [17]. The usage of antibiotics can lead to selective pressure by killing susceptible bacteria and allowing resistant bacteria to survive and then multiply. Hence, while treating non-ESBL infections, selective antimicrobial pressure should be avoided. For the treatment of ESBL-producing infections, choosing the proper drug is crucial, while the dosage and duration should be followed according to the severity of the illness.

Sensitivity analysis also showed that increasing the transmission rate from non-ESBL K. pneumoniae to susceptible individuals (β1) decreased the R0 value by about 9% (Fig. 7a). On the other hand, increasing the transmission rate from ESBL-producing K. pneumonia strains to susceptible individuals (β2) decreased the R0 value by about 10% (Fig. 8b). As the treatment of infections is expected to decrease the R0 values, it is seen that ESBL-producing strains are slightly more effective in decreasing the spread, which is consistent with the higher R0E+ value. Successful recovery from infections is accompanied by proper antibiotic administration indicating that the effectiveness of antibiotic use is a critical factor at this point.

Increasing the transmission rate from non-ESBL strains to ESBL-producing strains (β3), except for the use of antibiotics, decreases the R0 value of non-ESBL strains by about 1% (Fig. 9a). This actively demonstrates that in an inversely proportional way, the R0 value of ESBL-producing strains will increase (Fig. 9b). The hospital environment contains many risk factors with regard to the acquisition of ESBL-producing strains, such as the hands of healthcare workers, medical devices and colonized or infected patient rooms. As these infections emerge as nosocomial, the flora of the hospital and bacteriological surveillance of patients should be frequently monitored. Apart from contamination, ESBL-producing strains can also be acquired by spontaneous mutations of the genes [31]. Also, resistance elements can be gained horizontally by other strains, species or genera via mobile genetic elements such as plasmids and transposons [32]. According to a former study, controlling close proximity interactions (e.g., patients and staff) through proper hand hygiene in a hospital was found to be effective in reducing the spread of ESBL-producing K. pneumoniae [16].

The present study is the first to examine data on ESBL-producing K. pneumoniae using mathematical modeling in a health institution in Northern Cyprus. The contribution of effective parameters in the infection process was also enlightened with the possibilities offered by mathematical modeling, and the study, which was carried out with the joint work of two different fields, sets an example in terms of the importance of the multidisciplinary approach in infection control. To summarize, it seems clear that the use of antibiotics has a 6-times greater effect in the formation of the ESBL-producing K. pneumoniae strains compared to other factors such as in-hospital transmissions, horizontal gene transfers or mutations. Although antibiotics are seen as a remedy in the treatment of infections, negligent use of antibiotics can cause the phenomenon of resistance, which may cause medical treatment to return to the period before antibiotics were available. Hence, the study suggests that, as there is no new class of antimicrobial agents, existing ones should be used efficiently. The local population's resistance rates should be considered while using empiric therapy. Over-the-counter sales of antibiotics still exist in many parts of the world, which carries the possibility of causing resistance to antibiotics. The sale of antibiotics without medical prescription can lead to the occurrence of community-acquired ESBL infections. As it is already challenging to treat ESBL infections, the rational use of drugs, the choice of the right drug and adjustment of dosage, duration and administration are vital. Combination therapies should be considered using drugs that have a synergistic effect to prevent the formation of resistance. In cases where ESBL positive infections are present, the infection control committee must take appropriate measures in terms of both personnel and technical aspects in order to minimize in-hospital transmissions. Surveillance studies are very important in infection control. By obtaining more precise data with mathematical modeling, surveillance of the relevant strain can be conducted more effectively. In line with the data obtained, it seems necessary to take urgent measures. Through the regulation of antibiotic use policy and training of hospital staff about how to handle with resistance microorganisms, high morbidity and mortality rates can be prevented and the treatment of resistant infections can be improved. Therefore, it is believed that this will prevent the enormous increase in ESBL-producing K. pneumoniae infections over time, and will provide both therapeutic and financial improvements in the medical field. In order to extend the presented research, as a future recommendation, control strategies can be created to observe changes in the spread of ESBL-producing K. pneumoniae in the hospital using fractional models [33]. Fractional differential equations (FDEs) or delay differential equations (DDEs) can be used to examine and compare the subject with different approaches.

Limitations: The study has been conducted by ignoring death from Klebsiella pneumoniae infection.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

Buyuktuna, S. A., Hasbek, M., Celik, C., Unlusavuran, M., & Avci, O. N. U. R. (2020). Klebsiella pneumoniae infections in the intensive care unit: Risk factors related to carbapenem resistance and patient mortality. Mikrobiyoloji Bulteni, 54(3), 378-391. [Google Scholar] [CrossRef]
Kuş, H., Arslan, U., & Fındık, D. (2017). Investigation of various virulence factors of strains isolated from nosocomial infections. Mikrobiyoloji Bulteni, 51(4), 329-339. [Google Scholar] [CrossRef]
Li, G., Zhao, S., Wang, S., Sun, Y., & Zhou, Y. (2019). A 7-year surveillance of the drug resistance in from a primary health care center. Annals of Clinical Microbiology and Antimicrobials, 18(1), 1-7. [Google Scholar] [CrossRef]
Effah, C. Y., Sun, T., Liu, S., & Wu, Y. (2020). : An increasing threat to public health. Annals of Clinical Microbiology and Antimicrobials, 19(1), 1-9. [Google Scholar] [CrossRef]
Chung, P. Y. (2016). The emerging problems of infections: Carbapenem resistance and biofilm formation. FEMS Microbiology Letters, 363(20), 1-6. [Google Scholar] [CrossRef]
Heesterbeek, H., Anderson, R. M., Andreasen, V., Bansal, S., & de Angelis, D. (2015). Modeling infectious disease dynamics in the complex landscape of global health. Science, 347(6227), 1216-1226. [Google Scholar] [CrossRef]
Niewiadomska, A. M., Jayabalasingham, B., Seidman, J. C., Willem, L., & Grenfell, B. (2019). Population-level mathematical modeling of antimicrobial resistance: A systematic review. BMC Medicine, 17(1), 1-20. [Google Scholar] [CrossRef]
Lipsitch, M., Bergstrom, C. T., & Levin, B. R. (2000). The epidemiology of antibiotic resistance in hospitals: Paradoxes and prescriptions. Proceedings of the National Academy of Sciences, 97(4), 1938-1943. [Google Scholar] [CrossRef]
Weinstein, R. A., Bonten, M. J., Austin, D. J., & Lipsitch, M. (2001). Understanding the spread of antibiotic resistant pathogens in hospitals: Mathematical models as tools for control. Clinical Infectious Diseases, 33(10), 1739-1746. [Google Scholar] [CrossRef]
Temiz, H., Özbek, E., Vural, D. G., & Özekinci, T. (2015). Evaluation of antimicrobial resistance rates of isolates. Türk Mikrobiyoloji Cemiyeti Dergisi, 45, 68-74. [Google Scholar] [CrossRef]
Baleanu, D., Jajarmi, A., Mohammadi, H., & Rezapour, S. (2020). A new study on the mathematical modelling of human liver with caputo–Fabrizio fractional derivative. Chaos, Solitons & Fractals, 134, [Google Scholar] [CrossRef]
Baleanu, D., Sajjadi, S. S., Asad, J. H., Jajarmi, A., & Estiri, E. (2021). Hyperchaotic behaviors, optimal control, and synchronization of a nonautonomous cardiac conduction system. Advances in Difference Equations, 2021(1), 1-24. [Google Scholar] [CrossRef]
Gao, W., Veeresha, P., Baskonus, H. M., Prakasha, D. G., & Kumar, P. (2020). A new study of unreported cases of 2019-nCOV epidemic outbreaks. Chaos, Solitons & Fractals, 138, [Google Scholar] [CrossRef]
Müller-Schulte, E., Tuo, M. N., Akoua-Koffi, C., Schaumburg, F., & Becker, S. L. (2020). High prevalence of ESBL-producing klebsiella pneumoniae in clinical samples from central Côte d'Ivoire. International Journal of Infectious Diseases, 91, 207-209. [Google Scholar] [CrossRef]
Fils, P. E. L., Cholley, P., Gbaguidi-Haore, H., Hocquet, D., & Sauget, M. (2021). ESBL-Producing klebsiella pneumoniae in a university hospital: Molecular features, diffusion of epidemic clones and evaluation of cross-transmission. PLoS One, 16(3), e0247875. [Google Scholar] [CrossRef]
Duval, A., Obadia, T., Boëlle, P. Y., Fleury, E., & Herrmann, J. L. (2019). Close proximity interactions support transmission of ESBL- but not ESBL- in healthcare settings. PLoS Computational Biology, 15(5), e1006496. [Google Scholar] [CrossRef]
Salzar-Vizcaya, L., Atkinson, A., Kronenberg, A., Pluess, C., Kouyos, R. et al. (2019). The impact of public health interventions on the future prevalence of ESBL-producing Klebsiella pneumoniae: A population based mathematical modelling study. medRxiv, 19012765. DOI 10.1101/19012765. [CrossRef]
Bawa, M., Abdulrahman, S., Jimoh, O. R., & Adabara, N. U. (2013). Stability analysis of the disease-free equilibrium state for lassa fever disease. Journal of Science, Technology, Mathematics and Education, 9(2), 115-123. [Google Scholar]
Laukó, I. G. (2006). Stability of disease free sets in epidemic models. Mathematical and Computer Modelling, 43(11–12), 1357-1366. [Google Scholar] [CrossRef]
Vaidya, V. K. (2011). Horizontal transfer of antimicrobial resistance by extended-spectrum β lactamase-producing . Journal of Laboratory Physicians, 3(1), 37. [Google Scholar] [CrossRef]
Vuotto, C., Longo, F., Balice, M. P., Donelli, G., & Varaldo, P. E. (2014). Antibiotic resistance related to biofilm formation in . Pathogens, 3(3), 743-758. [Google Scholar] [CrossRef]
Surgers, L., Boyd, A., Girard, P. M., Arlet, G., & Decré, D. (2019). Biofilm formation by ESBL-producing strains of and . International Journal of Medical Microbiology, 309(1), 13-18. [Google Scholar] [CrossRef]
Podschun, R., & Ullmann, U. (1998). spp. as nosocomial pathogens: Epidemiology, taxonomy, typing methods, and pathogenicity factors. Clinical Microbiology Reviews, 11(4), 589-603. [Google Scholar] [CrossRef]
Navon-Venezia, S., Kondratyeva, K., & Carattoli, A. (2017). : A major worldwide source and shuttle for antibiotic resistance. FEMS Microbiology Reviews, 41(3), 252-275. [Google Scholar] [CrossRef]
Okomo, U., Akpalu, E. N., Le Doare, K., Roca, A., & Cousens, S. (2019). Aetiology of invasive bacterial infection and antimicrobial resistance in neonates in sub-saharan Africa: A systematic review and meta-analysis in line with the STROBE-NI reporting guidelines. The Lancet Infectious Diseases, 19(11), 1219-1234. [Google Scholar] [CrossRef]
World Health Organization (2017). Global priority list of antibiotic-resistant bacteria to guide research, discovery, and development of new antibiotics. World Health Organization.
Cassini, A., Högberg, L. D., Plachouras, D., Quattrocchi, A., & Hoxha, A. (2019). Attributable deaths and disability-adjusted life-years caused by infections with antibiotic-resistant bacteria in the EU and the european economic area in 2015: A population-level modelling analysis. The Lancet Infectious Diseases, 19(1), 56-66. [Google Scholar] [CrossRef]
Wyres, K. L., Lam, M. M., & Holt, K. E. (2020). Population genomics of . Nature Reviews Microbiology, 18(6), 344-359. [Google Scholar] [CrossRef]
Paterson, D. L., Mulazimoglu, L., Casellas, J. M., Ko, W. C., & Goossens, H. (2000). Epidemiology of ciprofloxacin resistance and its relationship to extended-spectrum β-lactamase production in isolates causing bacteremia. Clinical Infectious Diseases, 30(3), 473-478. [Google Scholar] [CrossRef]
Vardakas, K. Z., Tansarli, G. S., Rafailidis, P. I., & Falagas, M. E. (2012). Carbapenems versus alternative antibiotics for the treatment of bacteraemia due to producing extended-spectrum β-lactamases: A systematic review and meta-analysis. Journal of Antimicrobial Chemotherapy, 67(12), 2793-2803. [Google Scholar] [CrossRef]
Salverda, M. L., Koomen, J., Koopmanschap, B., Zwart, M. P., & de Visser, J. A. G. (2017). Adaptive benefits from small mutation supplies in an antibiotic resistance enzyme. Proceedings of the National Academy of Sciences, 114(48), 12773-12778. [Google Scholar] [CrossRef]
Woodford, N., Turton, J. F., & Livermore, D. M. (2011). Multiresistant gram-negative bacteria: The role of high-risk clones in the dissemination of antibiotic resistance. FEMS Microbiology Reviews, 35(5), 736-755. [Google Scholar] [CrossRef]
Jajarmi, A., Arshad, S., & Baleanu, D. (2019). A new fractional modelling and control strategy for the outbreak of dengue fever. Physica A: Statistical Mechanics and its Applications, 535, [Google Scholar] [CrossRef]