
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.017277
ARTICLE
Numerical Simulation for Bioconvection of Unsteady Stagnation Point Flow of Oldroyd-B Nanofluid with Activation Energy and Temperature-Based Thermal Conductivity Past a Stretching Disk
1School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an, 710049, China
2Department of Mathematics, Government College University Faisalabad, Layyah Campus, 31200, Pakistan
*Corresponding Author: Haihu Liu. Email: haihu.liu@xjtu.edu.cn
Received: 27 April 2021; Accepted: 22 June 2021
Abstract: A mathematical modeling is explored to scrutinize the unsteady stagnation point flow of Oldroyd-B nanofluid under the thermal conductivity and solutal diffusivity with bioconvection mechanism. Impacts of Joule heating and Arrhenius activation energy including convective boundary conditions are studied, and the specified surface temperature and constant temperature of wall (CTW) are discussed. The consequences of thermal conductivity and diffusivity are also taken into account. The flow is generated through stretchable disk geometry, and the behavior of non-linear thermal radiation is incorporated in energy equation. The partial differential equations governing the fluid flow in the structure is reduced into dimensionless nonlinear ODEs by applying suitable similarity variables. The obtained system of non-dimensional nonlinear ODEs is treated numerically with the help of bvp4c solver in Matlab under shooting algorithm. The impact of various prominent parameters on velocity profile, thermal profile, volumetric nanoparticle concentration and microorganism distribution is depicted in graphical form. The numerical outcomes for skin friction coefficient, heat transfer rate, Sherwood number as well as microorganism density number versus various parameters are listed in the tables. The results show that fluid velocity is reduced by increasing buoyancy ratio parameter, while the fluid flow increases with mixed convective parameter. The temperature profile is enhanced with the amount of nonlinear thermal radiation and temperature dependent thermal conductivity. Furthermore, concentration profiles of nanoparticles have opposite behavior for Brownian motion coefficient and thermophoresis diffusion parameter, and it is noticed that by varying Peclet number the microorganisms profile is declined. The proposed study is useful to control and optimize heat transfer in industrial applications.
Keywords: Oldroyd-B nanofluid; thermal conductivity; solutal diffusivity conductivity; bioconvective microorganisms; shooting algorithm
Nomenclature
| Surface temperature | |
| Constant wall temperature | |
| Relaxation time | |
| p | Pressure of fluid |
| C | Concentration |
| N | Microorganisms |
| Fluid heat diffusivity | |
| DB | Brownian diffusion coefficient |
| DT | Brownian thermophoresis coefficient |
| k1 | Chemical reaction constant |
| hT | Heat transfer coefficient |
| hC | Mass transfer coefficient |
| S | Unsteadiness parameter |
| M | Magnetic parameter |
| Nb | Brownian motion coefficient |
| Mixed convection parameter | |
| Ecr | Eckert number |
| Nt | Thermophoresis diffusion parameter |
| Nr | Buoyancy ratio parameter |
| Nc | Bioconvection Rayleigh number |
| K1 | Chemical reaction parameter |
| E | Activation energy parameter |
| Bi | Biot number |
| Pe | Peclet number |
| Microorganism difference variable | |
| Characteristics of velocity distribution | |
| Thermal profile | |
| Solutal field of nanomaterials | |
| Motile microorganism’s profiles | |
| E | Activation energy |
| Pe | Peclet number |
| Prandtl number | |
| Temperature ratio parameter | |
| Rd | Radiation parameter |
| Le | Lewis number |
| Lb | Bioconvection Lewis number |
| S | Unsteadiness parameter |
| Deborah number for relaxation to time parameter | |
| Deborah number for retardation to time parameter | |
| Thermal conductivity | |
| Solutal diffusivity parameter | |
| K | Velocity ratio parameter |
| T | Temperature |
| C | Concentration |
| Greek Symbols | |
| Density of fluid | |
| v | Kinematic viscosity |
Transmission of heat integrated liquid flow is necessary for a significant number of nuclear and thermal-hydraulic systems. The involvement of liquids in the these systems can help to reduce capital costs, enhance operating efficiency and improve the performance of the system. Amongst various conventional methods, air is one of the main techniques of cooling electrical devices. The cooling is necessary in order to maintain the required thermal efficiency in different scientific and technological products such as computers, engines, chemical processes, and so on. Nanofluids, due to their exceptional thermo-physical characteristics and relatively slower heat resistance, have recently obtained the most attractive interest. Nanoparticles are comparatively tiny-sized particles that are contained in the fluid. The main purpose of introducing such particles are to enhance the heat conductivity of commonly utilized base liquids. The definition of nanofluid was initiated by Choi [1] who demonstrated that a host liquid, including water or ethylene-glycol fluid, can increase its heat efficiency by incorporating nanoparticles. Later, Buongiorno [2] identified Brownian motion and thermophoresis elements for the development of nanoparticles associated with heat transport. Aminian et al. [3] studied the impacts of
Mass exchange method coupled with chemical processes through activation energy is usually important in geothermal and oil reservoirs manufacturing, chemical engineering, and water and oil emulsion system, food preparation, and so on. It is important to establish conceptual outcomes for estimating the effect of activation energy across flows. The terminology Arrhenius activation energy was initially pioneered by Svante Arrhenius scientist in 1889. It is the lowest energy needed to transform the reactants into materials. Using a numerical method, Bestman [16] studied the free convection boundary layer flow when the boundary wall moves in its own plane via Arrhenius activation energy. Ramesh [17] studied viscoelastic nanofluid influenced by activation energy and chemical processes. Abuzaid et al. [18] investigated numerically the mixed convective movement of Oldroyd-B nano liquid subjected to Arrhenius activation energy and binary chemical processes. Waqas et al. [19] researched the nonlinear radiation flow of Eyring-Powell nano liquid with magnet dipoles and Arrhenius activation energy. The consequence of activation energy for the Carreau-Yasuda nanofluid flow was examined by Khan et al. [20].
Non-Newtonian liquids have become very unique in the manufacturing and engineering sectors. Commonly non-Newtonian fluids are divided into three categories: (I) the differential type fluids, (II) the rate type fluids, and (III) the integral type non-Newtonian fluids. Oldroyd-B fluid is an important sub-class of the rate-type fluid. Such fluids play an important role in industrial processes such as pharmaceutical industries, paper production, food processing, drug delivery, and cancer treatment. The Oldroyd-B fluid model was first introduced by Oldroyd in 1950 [21], motivated by the research of Fröhlich et al. [22] who developed a structured method for the improvement of viscoelastic fluid modeling techniques. The 2-dimensional flow of Oldroyd-B nano liquid through the nonlinearly stretchable sheet with the Cattaneo Christov heat flux model was studied by Ibrahim et al. [23]. The improvement of dual stratification in the nonlinear radiative movement of Oldroyd-B nano liquid was explained by Irfan et al. [24]. Anwar et al. [25] evaluated the consequence of Newtonian thermal conductivity by the unsteady natural convectional movement of Oldroyd-B nanofluid contained in an infinite, vertical stationary plate. Interested readers may refer to [26,27] for more works on Oldroyd-B fluid.
Bioconvection is a naturally occurring phenomenon in swimming motile microorganisms. One type of motile microorganism, identified as the gyrotactic microorganism, is highly present in the aqueous system, which can swim in the flowing liquid along a specific direction with a fragile horizontal vortex and unstably fall in the flowing liquid with a significant horizontal vortex. Gyrotactic motile microorganism swimming components are important for understanding many ecological features of bioconvection. Microorganism molecules are used for the processing of agricultural materials including ethanol, fertilizers, biofuels, water plants as well as biodiesel. Bioconvection is an unrequested modification of macroscopic liquid patterns, including diminishing plumes. Two principal forms of up-swimming micro-organisms are normally utilized in convectional experimentation: low-heavy algae and solid oxytactic organisms. The terminology bioconvection was first proposed by Platt [28] in 1961, who described the formation of cells induced by microorganisms in the aqueous suspension. Mondal et al. [29] scrutinized the behavior of bioconvective phenomenon in nano liquid. Khan et al. [30] scrutinized the properties of a magnetic modified Newtonian fluid through bioconvection and chemically reactive organisms. Several investigators researched the bioconvection phenomenon, see [31–37]. Song et al. [38] conducted the analysis of the bioconvective phenomenon in micropolar nano liquid over the off-centered disk. The effects of exponential base heat source/sink and Cattaneo-Christov Laws on bioconvective Carreau nano liquid were analyzed by Farooq et al. [39]. Tlili et al. [40] scrutinized the use of Arrhenius energy with thermal radiative implications in the convectional flow of magnetic Oldroyd-B nanomaterials through a stretched cylinder. A mathematical method focusing on two-dimensional modified second-grade nano liquids against revolving Riga plate for the influence of the Arrhenius activation energy and bioconvection facets was examined by Waqas et al. [41].
In this work, a new class of fluid namely nanofluid is introduced, which has high thermal conductivity. Nanofluids are mostly utilized for their improved heat characteristics as a cooling medium in heat transformation equipment like radiators, cooling of microelectronics, and fuel cells. Inspired by the above studies, the main objective is to examine the impact of non-linearly thermal radiation on the stagnation point flow of bio-convective Oldroyd-B nano liquid past a stretchable disc with activation energy. The effects of temperature-based thermal efficiency and thermal diffusivity are investigated. The current model is explored for both constant wall temperature and prescribed surface temperature cases. The similarity transformations are used to obtain the ordinary differential equation from the developed system of PDEs. The numerical solution of ODEs is found by using the shooting scheme via the bvp4c MATLAB tool. The effect of flow governing parameters is illustrated for velocity profile, a thermal profile of species, concentration, and swimming microorganism field.
Consider unsteady, 2-D stagnation point fluid flow of electrical conducting Oldroyd-B nano liquid with bioconvective swimming microorganism above a linearly stretching disk. Select a polar coordinate arrangement
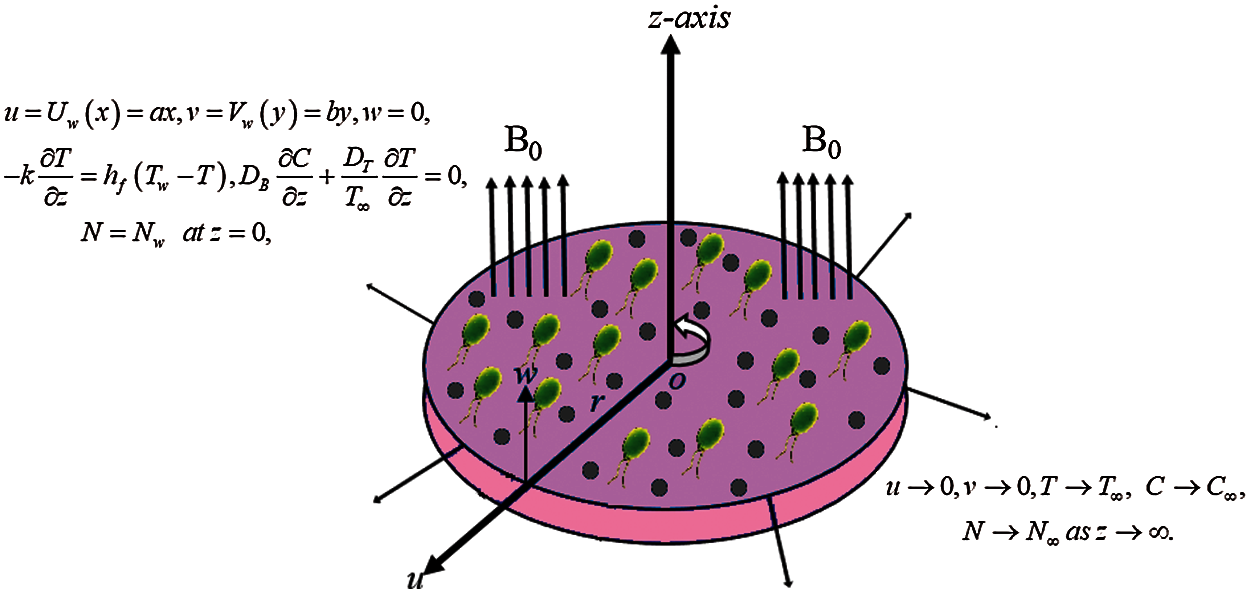
Figure 1: Physical layout of the flow
with the appropriate constraints:
Here, the relaxation time is denoted by
Variable conductivities for heat and mass are given below:
With the similarity transformations given by [44,45]
Eqs. (2)–(5) reduce to the following forms:
with
In the above equations,
The engineering quantities of interest include:
By adopting similarity transformations, the dimensionless form of engineering quantities are:
In this section, the obtained dimensionless nonlinear (ODEs) (9)–(13) subject to the boundary constraints (14), (15) are numerically integrated by applying bvp4c solver in MATLAB software. The shooting method is utilized to transform the higher-order non-dimensional flow system into the first ordered boundary value problem. For this purpose, we introduce some new variables such as:
Let us suppose that the transformed variables as
The unsteady natural convection of Oldroyd-B nano liquid via stretchable disk has been investigated. The numerical solution is obtained by utilizing MATLAB inbuilt function bvp4c, and the physical characteristics of the nanofluid is described by Buongiorno model. This section scrutinizes the influence of important physical parameters on quantities of substantial concentration. As sketched in Fig. 1, our aim is to visualize the characteristics of velocity distribution
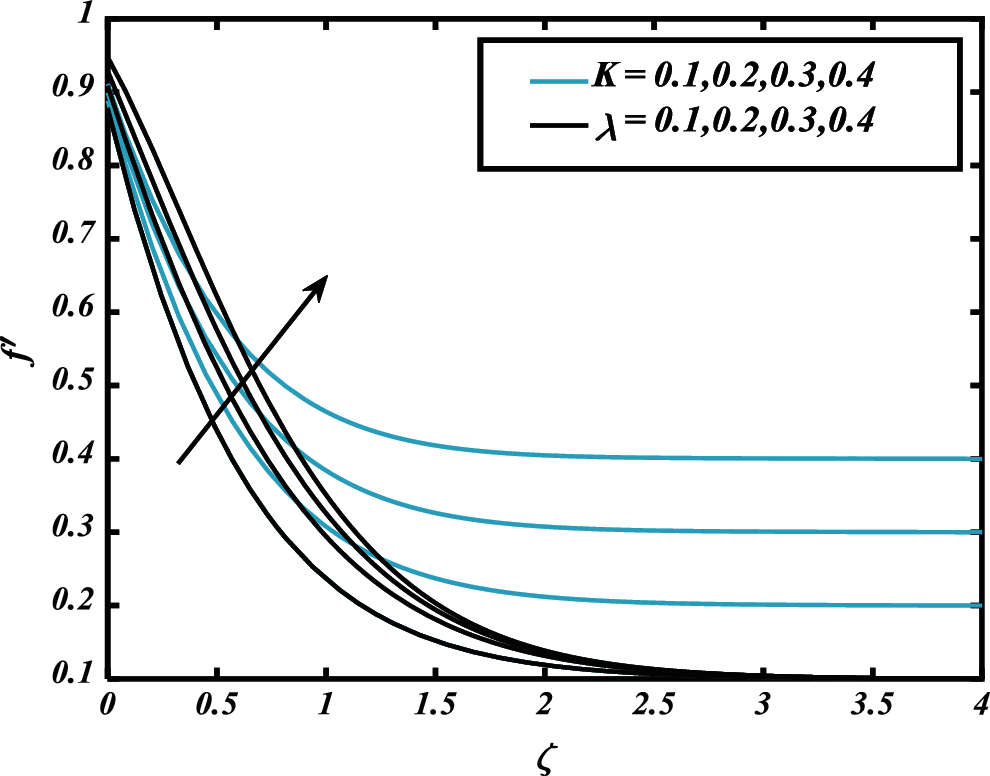
Figure 2:
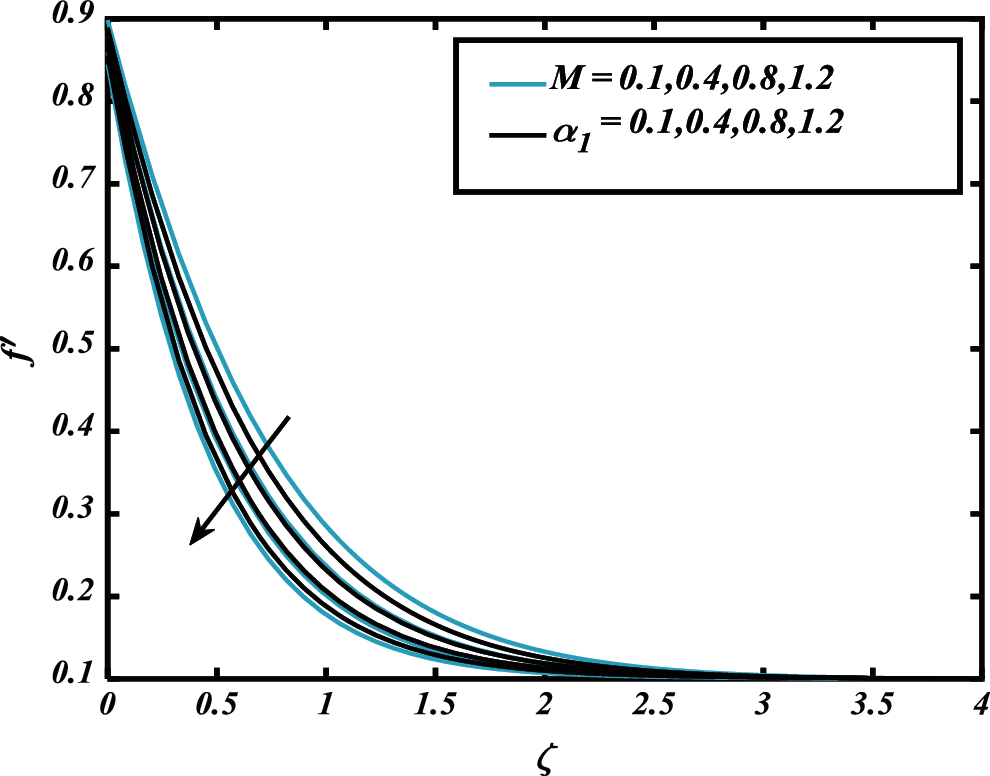
Figure 3:
Fig. 2 explores the effect of mixed convective parameter
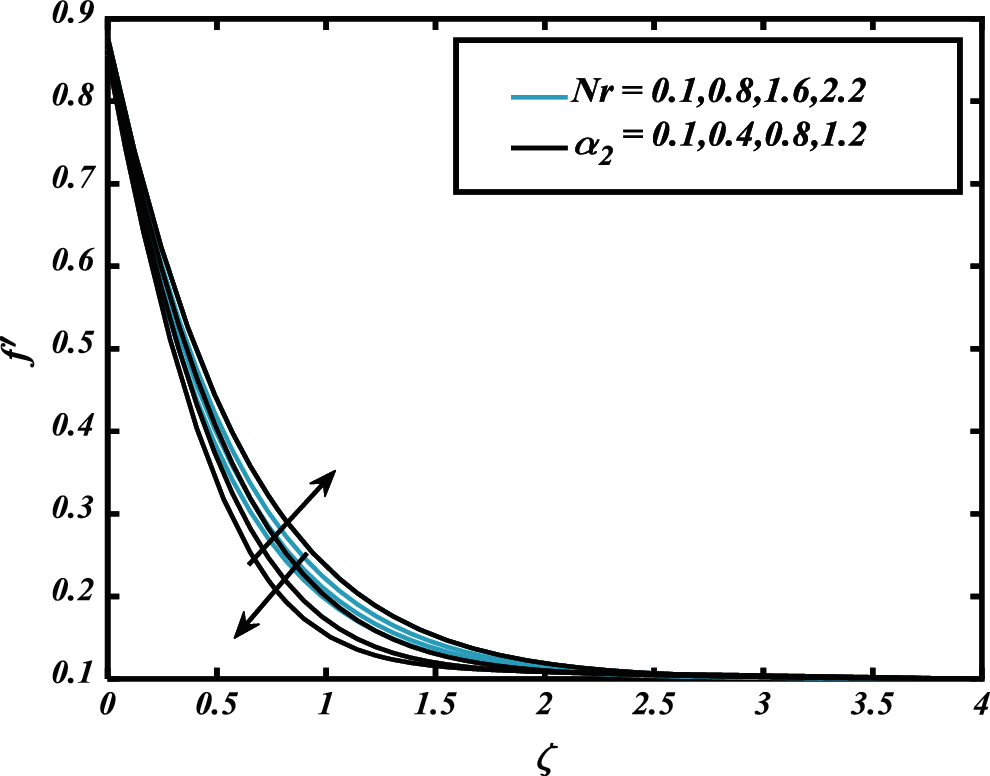
Figure 4:
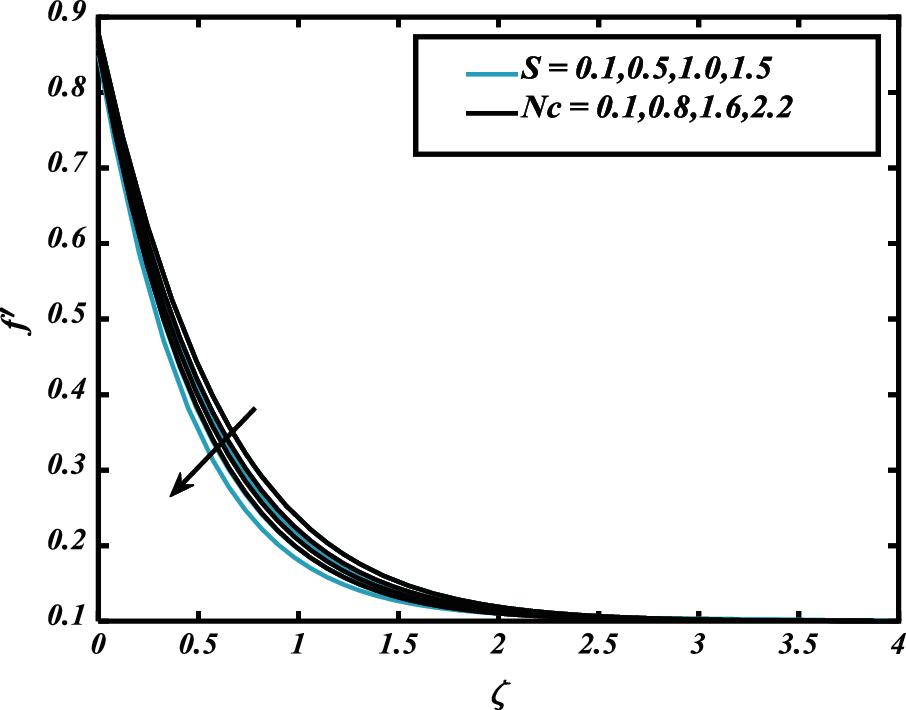
Figure 5:
The influence of radiation parameter Rd on a thermal profile
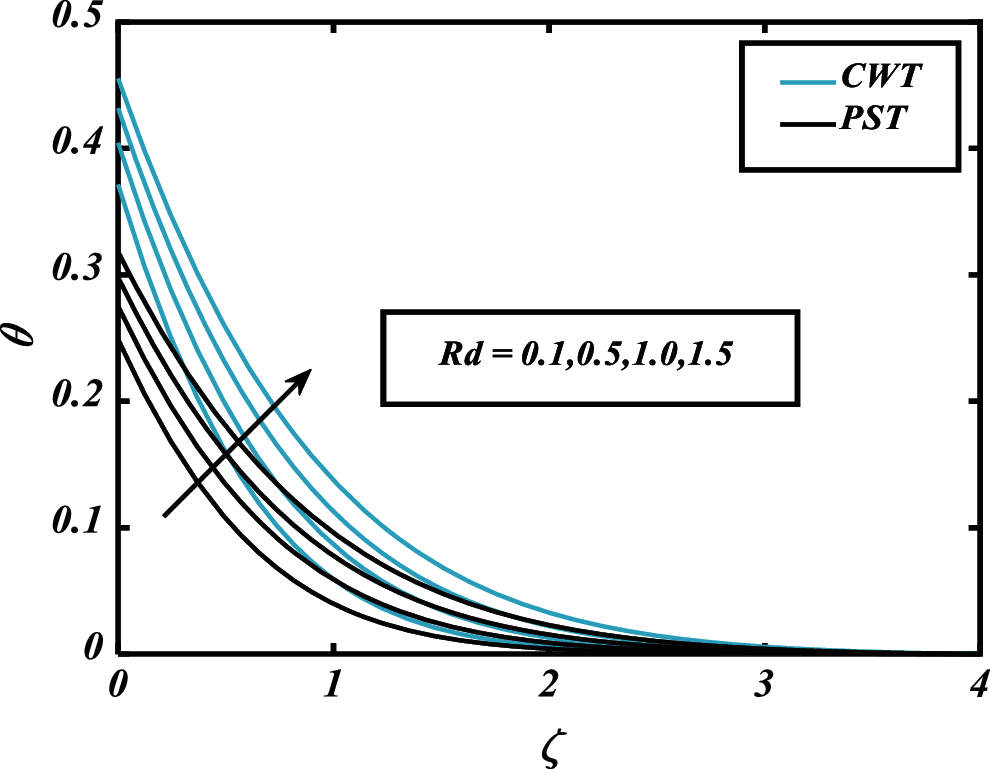
Figure 6:
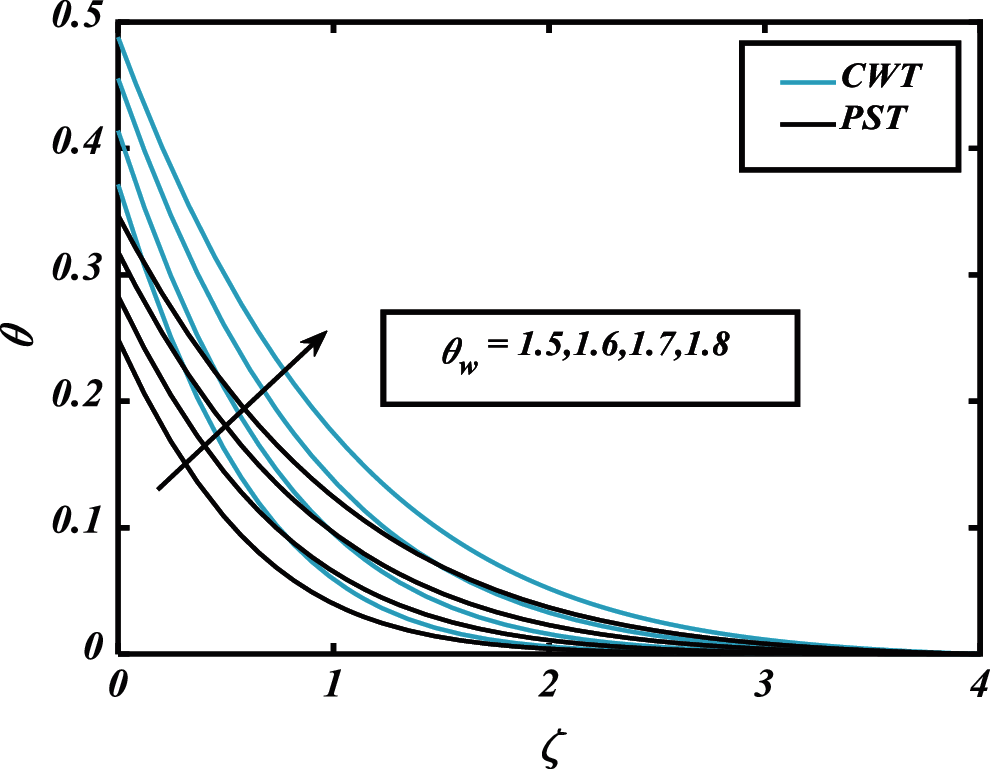
Figure 7:
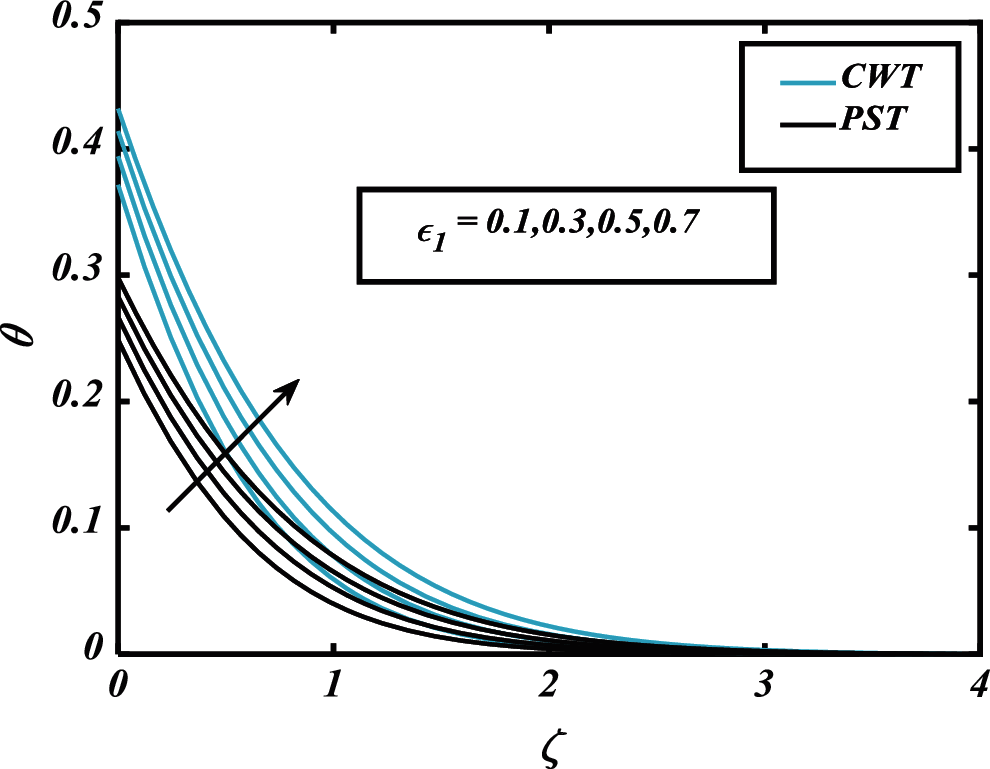
Figure 8:
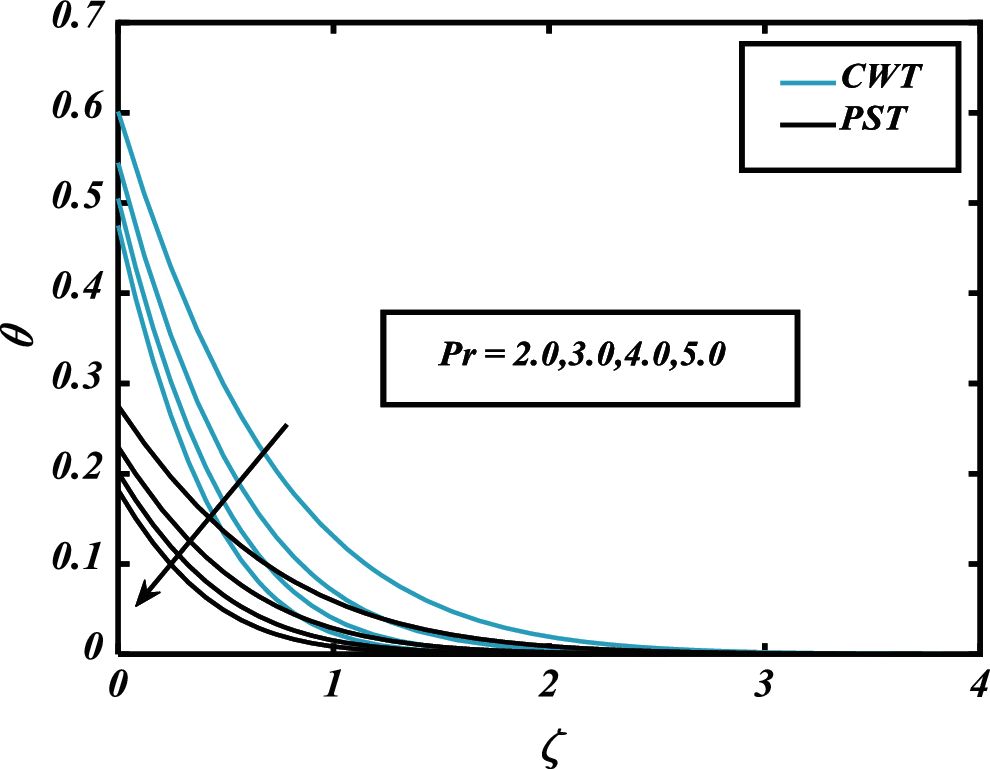
Figure 9:
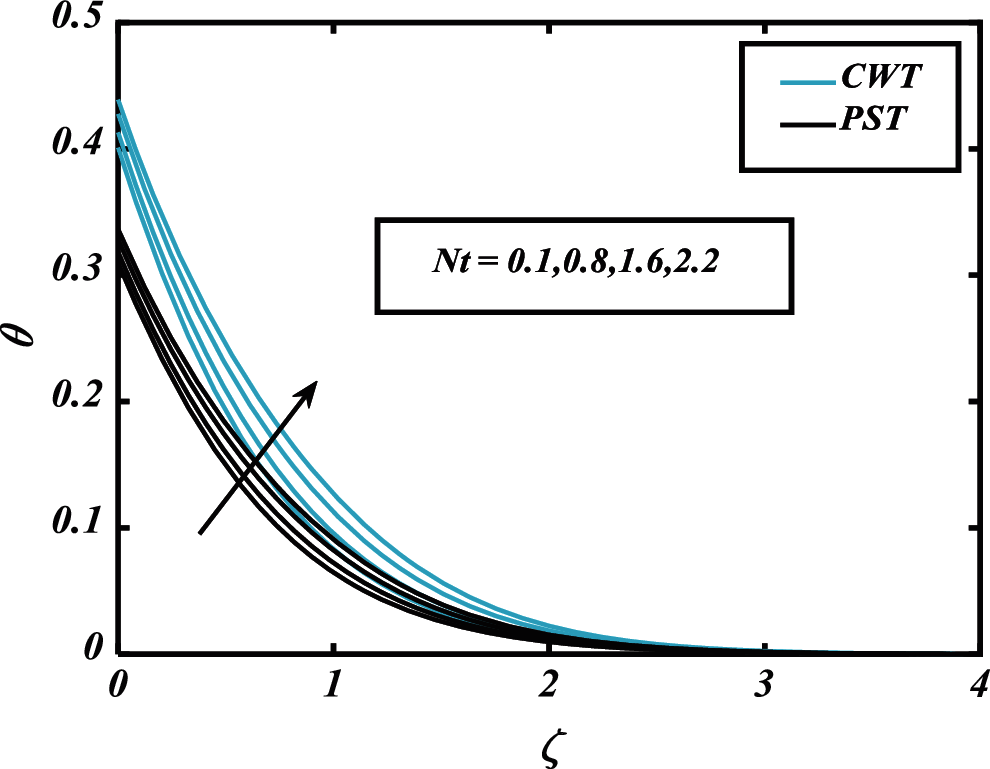
Figure 10:
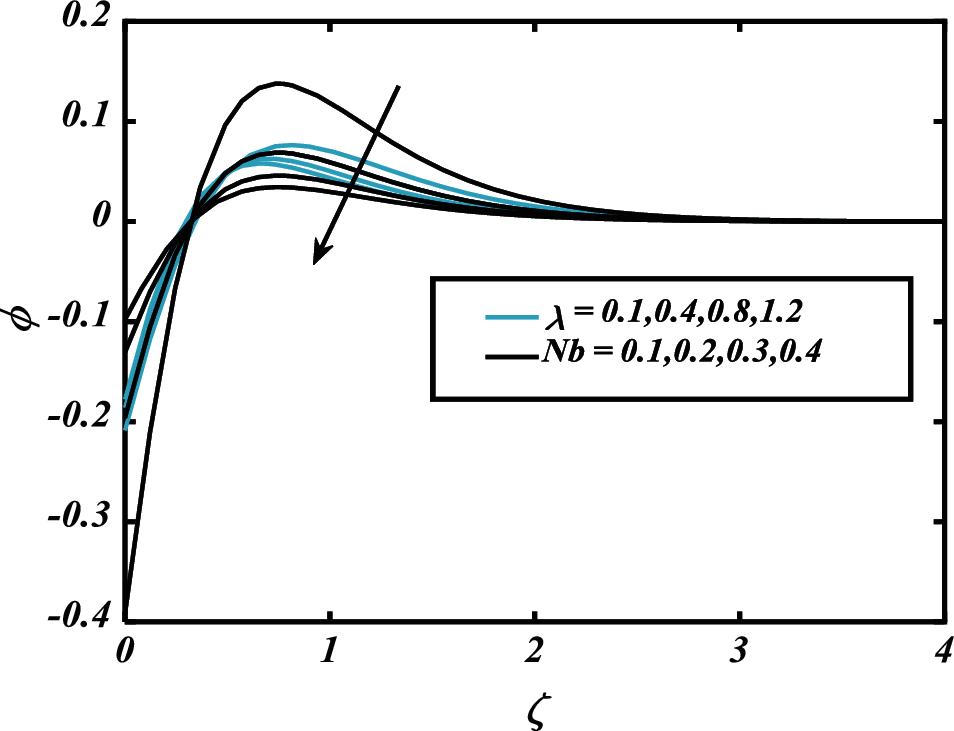
Figure 11:
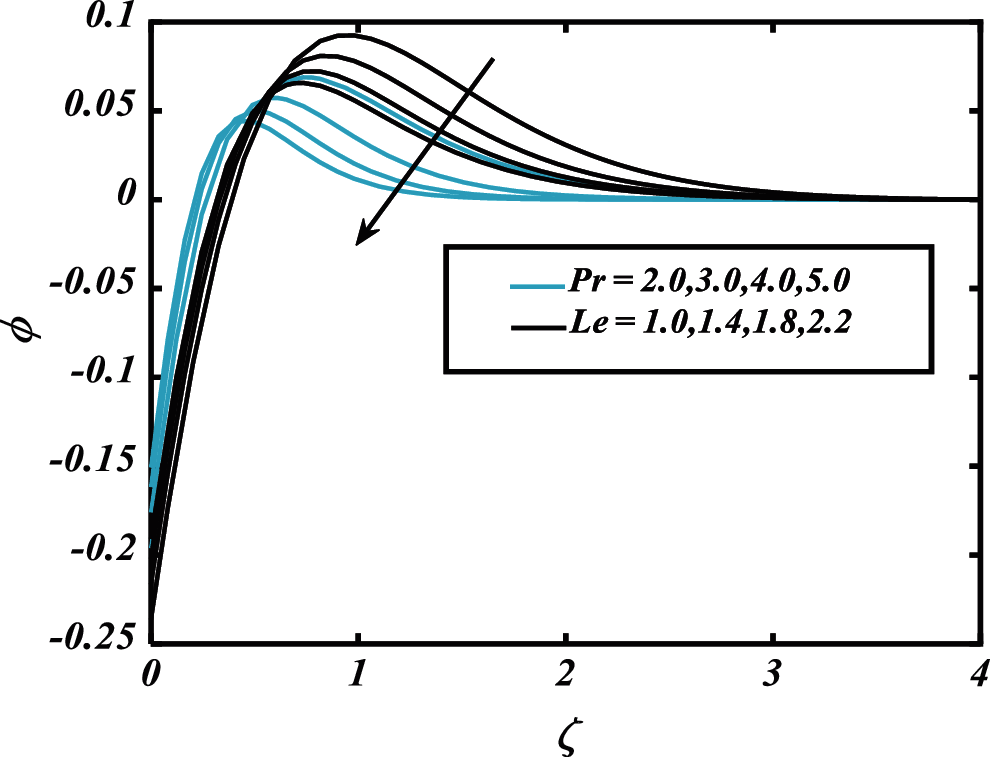
Figure 12:
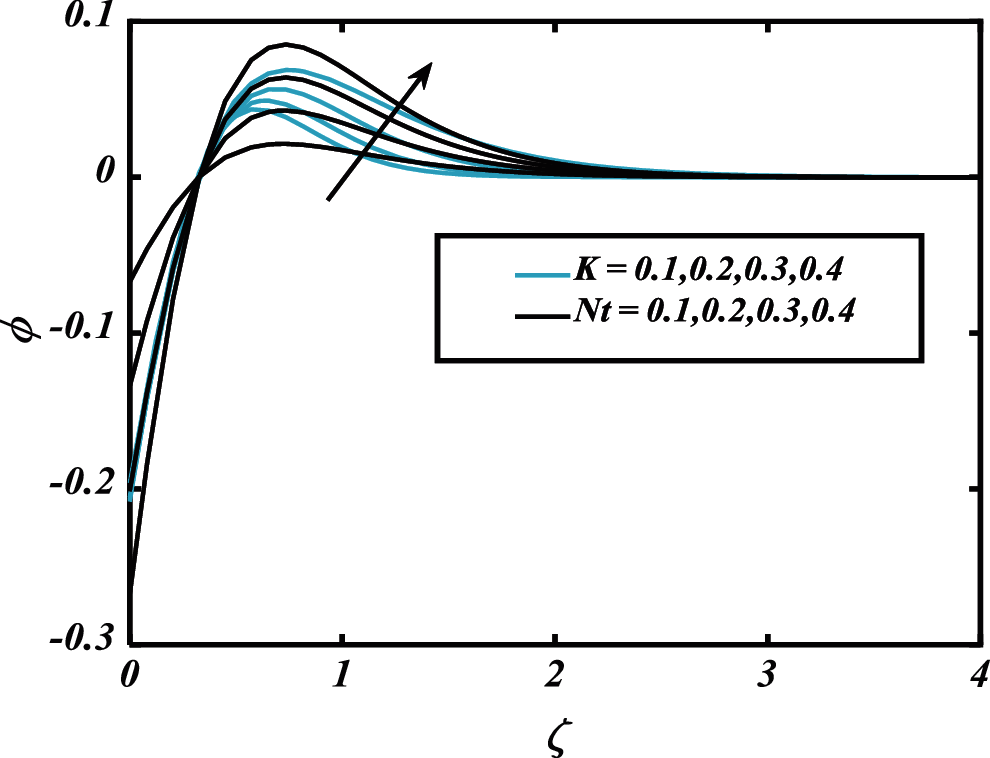
Figure 13:
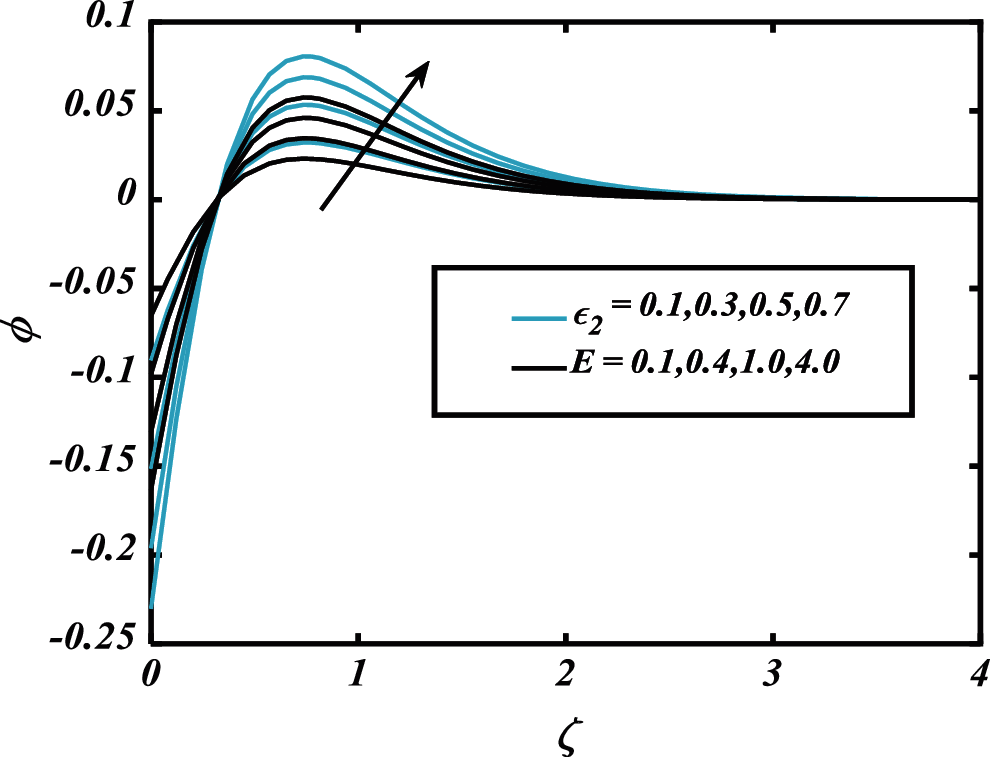
Figure 14:
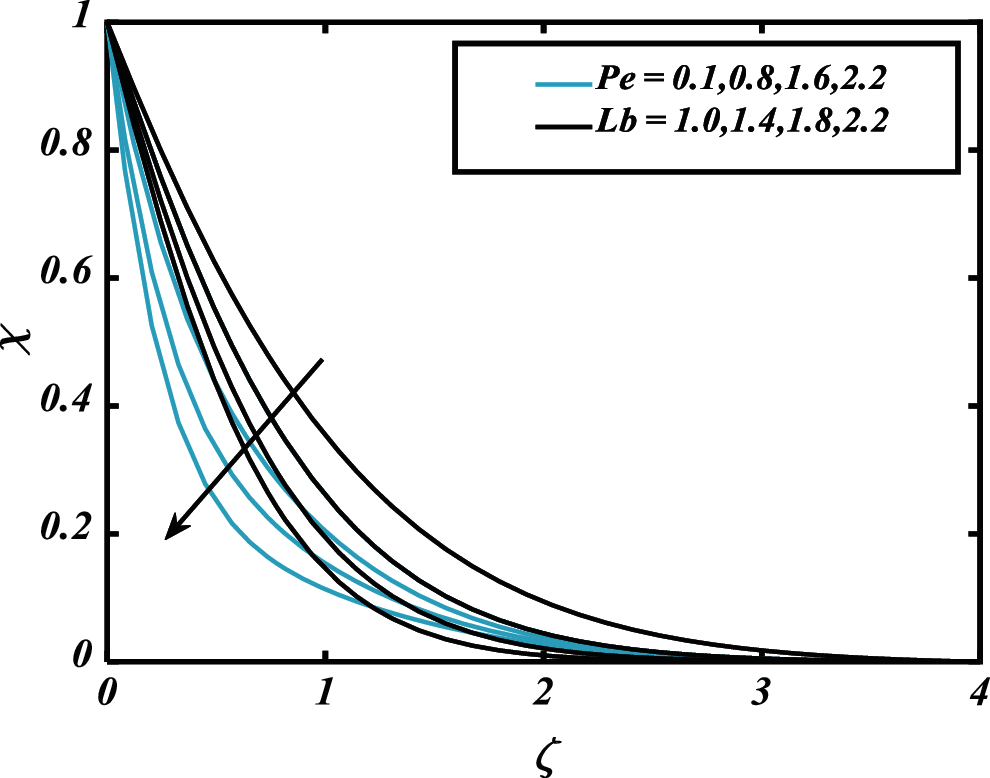
Figure 15:
Fig. 11 shows how the mixed convection parameter
Table 1 displays that drag forces coefficient
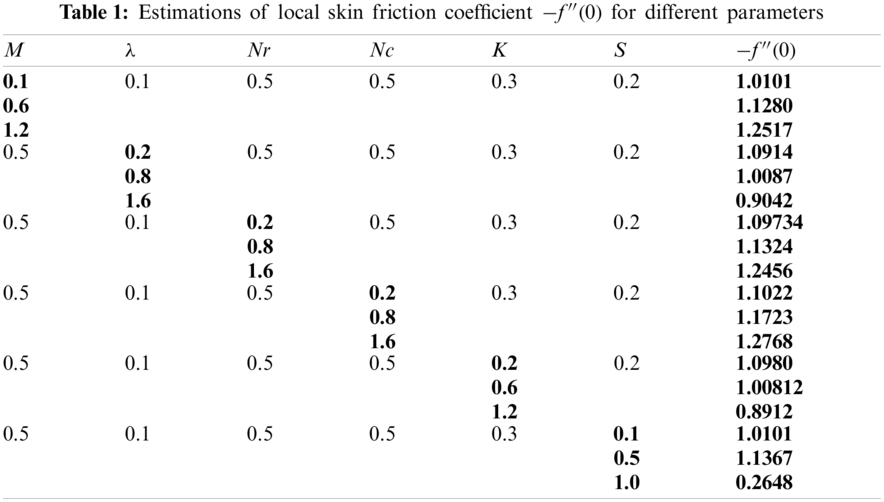
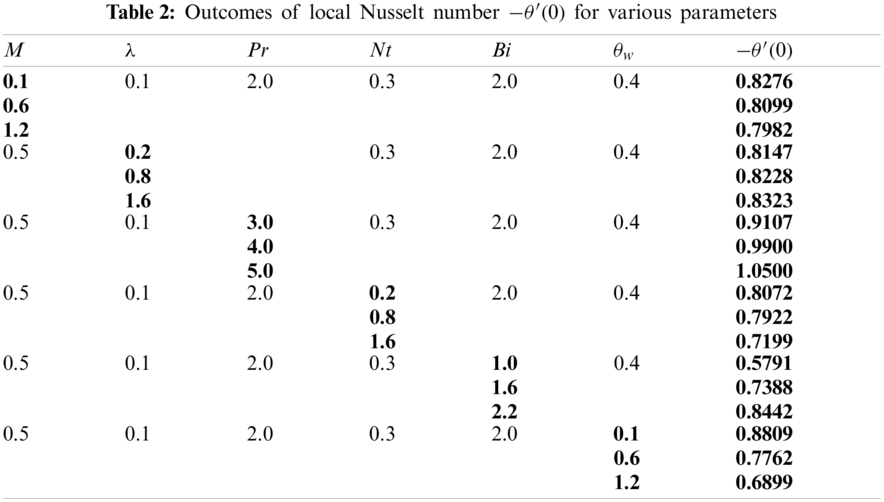
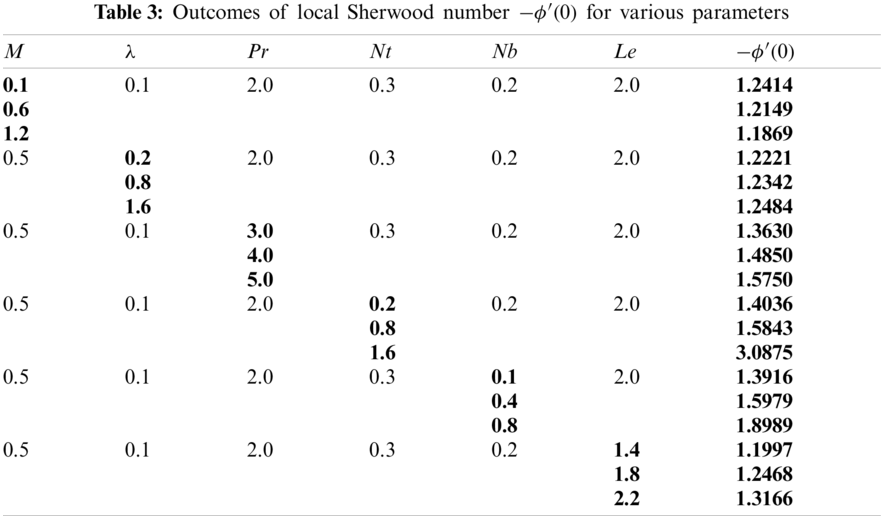
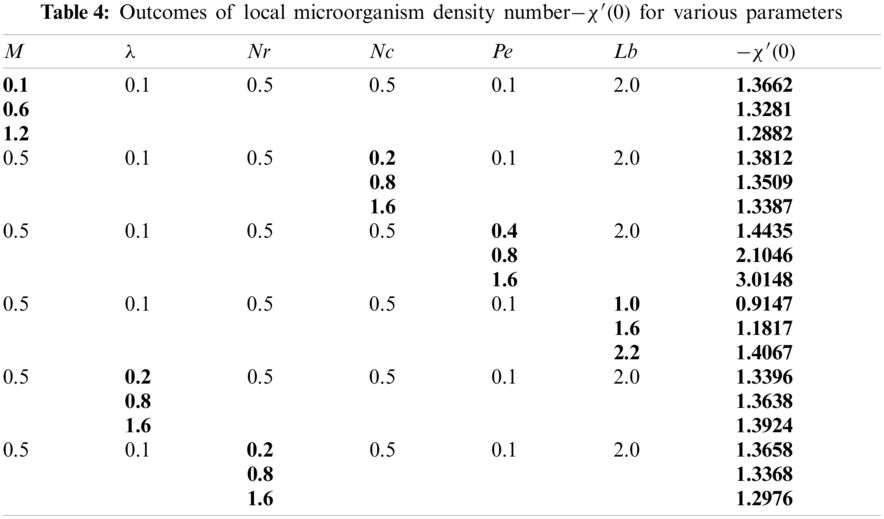
In this paper, we focus on the radiative Oldroyd-B nanofluid over stretchable disk with swimming microorganisms. The behavior of variable thermal and solutal diffusivity is investigated. Salient features of this work are:
• The larger buoyancy ratio parameter reduces the flow of fluid.
• The velocity field is improved by increasing the velocity ratio parameter and mixed convection parameter.
• Larger Deborah number of retardation time enhances the momentum distribution, while it decreases bioconvection Rayleigh number.
• The heat transformation is improved by dissolving nanomaterials in base fluid [48].
• The increment in the temperature ratio parameter boosts the temperature field.
• The concentration of nanoparticles is boosted with increasing thermophoretic parameters and Arrhenius activation energy.
• The concentration of nanoparticles is a decreasing function of the mixed convection parameter and the Lewis number.
• The larger Peclet number and bioconvection Lewis number decline the microorganism field.
Authors’ Contribution: All authors have an equivalent contribution.
Funding Statement: This work is supported by the National Natural Science Foundation of China (Nos. 51876170, 12072257), the Natural Science Basic Research Plan in Shaanxi Province of China (No. 2019JM-343) and the National Key Project (GJXM92579).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Choi, S. (1995). Enhancing thermal conductivity of fluids with nanoparticle, ASME Fluids Engineering Division, 231, 99–105. [Google Scholar]
2. Buongiorno, J. (2006). Convective transport in nanofluids. Journal of Heat Transfer, 128, 240–250. DOI 10.1115/1.2150834. [Google Scholar] [CrossRef]
3. Aminian, E., Moghadasi, H., Saffari, H. (2020). Magnetic field effects on forced convection flow of a hybrid nanofluid in a cylinder filled with porous media: A numerical study. Journal of Thermal Analysis and Calorimetry, vol. 141, 2019–2031. DOI 10.1007/s10973-020-09257-y. [Google Scholar] [CrossRef]
4. Saha, S. K. (2020). Magnetohydrodynamic buoyancy driven Al2O3-water nanofluid flow in a differentially heated trapezoidal enclosure with a cylindrical barrier. International Communications in Heat and Mass Transfer, 114, 104593. DOI 10.1016/j.icheatmasstransfer.2020.104593. [Google Scholar] [CrossRef]
5. Bhandari, A., Mishra, P. K. (2020). Heat and radiation absorption effects on casson nanofluid flow over a stretching cylinder in the presence of chemical reaction through mathematical modeling. Special Topics & Reviews in Porous Media: An International Journal, 11(2), 177–188. DOI 10.1615/SpecialTopicsRevPorousMedia.2020029260. [Google Scholar] [CrossRef]
6. Mondal, H., Das, S., Kundu, P. K. (2020). Influence of an inclined stretching cylinder over MHD mixed convective nanofluid flow due to chemical reaction and viscous dissipation. Heat Transfer, 49(4), 2183–2193. DOI 10.1002/htj.21714. [Google Scholar] [CrossRef]
7. Basha, H. T., Sivaraj, R., Prasad, V. R., Beg, O. A. (2020). Entropy generation of tangent hyperbolic nanofluid flow over a circular cylinder in the presence of nonlinear boussinesq approximation: A non-similar solution. Journal of Thermal Analysis and Calorimetry, 143(3), 2273–2289. DOI 10.1007/s10973-020-09981-5. [Google Scholar] [CrossRef]
8. Sheikholeslami, M., Arabkoohsar, A., Jafaryar, M. (2020). Impact of a helical-twisting device on the thermal–hydraulic performance of a nanofluid flow through a tube. Journal of Thermal Analysis and Calorimetry, 139(5), 3317–3329. DOI 10.1007/s10973-019-08683-x. [Google Scholar] [CrossRef]
9. Sudarsana Reddy, P., Sreedevi, P. (2020). Impact of chemical reaction and double stratification on heat and mass transfer characteristics of nanofluid flow over porous stretching sheet with thermal radiation. International Journal of Ambient Energy, 1–11. DOI 10.1080/01430750.2020.1712240. [Google Scholar] [CrossRef]
10. Mishra, A., Kumar, M. (2020). Velocity and thermal slip effects on MHD nanofluid flow past a stretching cylinder with viscous dissipation and joule heating. SN Applied Sciences, 2(8), 1–13. DOI 10.1007/s42452-020-3156-7. [Google Scholar] [CrossRef]
11. Khashi’ie, N. S., Waini, I., Zainal, N. A., Hamzah, K., Mohd Kasim, A. R. (2020). Hybrid nanofluid flow past a shrinking cylinder with prescribed surface heat flux. Symmetry, 12(9), 1493. DOI 10.3390/sym12091493. [Google Scholar] [CrossRef]
12. Saeed, A., Tassaddiq, A., Khan, A., Jawad, M., Deebani, W. et al. (2020). Darcy-forchheimer MHD hybrid nanofluid flow and heat transfer analysis over a porous stretching cylinder. Coatings, 10(4), 391. DOI 10.3390/coatings10040391. [Google Scholar] [CrossRef]
13. Jabbar, M. Y., Hamzah, H. K., Ali, F. H., Ahmed, S. Y., Ismael, M. A. (2020). Thermal analysis of nanofluid saturated in inclined porous cavity cooled by rotating active cylinder subjected to convective condition. Journal of Thermal Analysis and Calorimetry, 144, 1–25. DOI 10.1007/s10973-020-09668-x. [Google Scholar] [CrossRef]
14. Goudarzi, S., Shekaramiz, M., Omidvar, A., Golab, E., Karimipour, A. et al. (2020). Nanoparticles migration due to thermophoresis and brownian motion and its impact on Ag-MgO/Water hybrid nanofluid natural convection. Powder Technology, 375, 493–503. DOI 10.1016/j.powtec.2020.07.115. [Google Scholar] [CrossRef]
15. Ali, F. H., Hamzah, H. K., Hussein, A. K., Jabbar, M. Y., Talebizadehsardari, P. (2020). MHD mixed convection due to a rotating circular cylinder in a trapezoidal enclosure filled with a nanofluid saturated with a porous media. International Journal of Mechanical Sciences, 181, 105688. DOI 10.1016/j.ijmecsci.2020.105688. [Google Scholar] [CrossRef]
16. Bestman, A. R., (1990). Natural convection boundary layer with suction and mass transfer in a porous medium. Internationa Journal of Energy Research, 14, 389–396. DOI 10.1002/(ISSN)1099-114X. [Google Scholar] [CrossRef]
17. Ramesh, G. K. (2020). Analysis of active and passive control of nanoparticles in viscoelastic nanomaterial inspired by activation energy and chemical reaction. Physica A: Statistical Mechanics and its Applications, 550, 123964. DOI 10.1016/j.physa.2019.123964. [Google Scholar] [CrossRef]
18. Abuzaid, D., Ullah, M. Z. (2020). Numerical study for mixed convection flow of oldroyd-b nanofluid subject to activation energy and binary chemical reaction. Thermal Science, 174–174. DOI 10.2298/TSCI200214174A. [Google Scholar] [CrossRef]
19. Waqas, M., Jabeen, S., Hayat, T., Shehzad, S. A., Alsaedi, A. (2020). Numerical simulation for nonlinear radiated eyring-powell nanofluid considering magnetic dipole and activation energy. International Communications in Heat and Mass Transfer, 112, 104401. DOI 10.1016/j.icheatmasstransfer.2019.104401. [Google Scholar] [CrossRef]
20. Khan, M. I., Afzal, S., Hayat, T., Waqas, M., Alsaedi, A. (2020). Activation energy for the carreau-yasuda nanomaterial flow: Analysis of the entropy generation over a porous medium. Journal of Molecular Liquids, 297, 111905. DOI 10.1016/j.molliq.2019.111905. [Google Scholar] [CrossRef]
21. Oldroyd, J. G. (1950). On the formulation of rheological equations of state. Proceedings of the Royal Society A. Mathematical and Physical Sciences, 200(1063), 523–541. DOI 10.1098/rspa.1950.0035. [Google Scholar] [CrossRef]
22. Fröhlich, A., Sack, R. (1946). Theory of the rheological properties of dispersions. Proceedings of the Royal Society A. Mathematical and Physical Sciences, 185(1003), 415–430. DOI 10.1098/rspa.1946.0028. [Google Scholar] [CrossRef]
23. Ibrahim, W., Gadisa, G. (2020). Finite element solution of nonlinear convective flow of oldroyd-b fluid with cattaneo-christov heat flux model over nonlinear stretching sheet with heat generation or absorption. Propulsion and Power Research, 9(3), 304–315. DOI 10.1016/j.jppr.2020.07.001. [Google Scholar] [CrossRef]
24. Irfan, M., Khan, M., Khan, W. A., Alghamdi, M., Ullah, M. Z. (2020). Influence of thermal-solutal stratifications and thermal aspects of non-linear radiation in stagnation point oldroyd-b nanofluid flow. International Communications in Heat and Mass Transfer, 116, 104636. DOI 10.1016/j.icheatmasstransfer.2020.104636. [Google Scholar] [CrossRef]
25. Anwar, T., Kumam, P., Khan, I., Thounthong, P. (2020). Heat transfer analysis of unsteady natural convection flow of oldroyd-b model in the presence of newtonian heating and radiation heat flux. IEEE Access, 8, 92479–92489. DOI 10.1109/ACCESS.2020.2989348. [Google Scholar] [CrossRef]
26. Qi, H., Fatima, N., Waqas, H., Saeed, J. (2017). Analytical solution for the flow of a generalized Oldroyd-B fluid in a circular cylinder. Open Journal for Mathematics and Sciences, 1(1), 85–96. DOI 10.30538/oms2017.0009. [Google Scholar] [CrossRef]
27. Waqas, H., Imran, M., Muhammad, T., Sait, S. M., Ellahi, R. (2021). Numerical investigation on bioconvection flow of Oldroyd–B nanofluid with nonlinear thermal radiation and motile microorganisms over rotating disk. Journal of Thermal Analysis & Calorimetry, 145(2), 523–539. DOI 10.1007/s10973-020-09728-2. [Google Scholar] [CrossRef]
28. Platt, J. R. (1996). Bioconvection patterns in cultures of free–swimming organisms. Science, 133(3466), 1766–1767. DOI 10.1126/science.133.3466.1766. [Google Scholar] [CrossRef]
29. Mondal, S. K., Pal, D. (2020). Gyrotactic mixed bioconvection flow of a nanofluid over a stretching wedge embedded in a porous media in the presence of binary chemical reaction and activation energy. International Journal of Ambient Energy, 1–17. DOI 10.1080/01430750.2020.1814860. [Google Scholar] [CrossRef]
30. Khan, M., Salahuddin, T., Malik, M. Y., Alqarni, M. S., Alqahtani, A. M. (2020). Numerical modeling and analysis of bioconvection on MHD flow due to an upper paraboloid surface of revolution. Physica A: Statistical Mechanics and its Applications, 553, 124231. [Google Scholar]
31. Ahmad, R., Farooqi, A., Zhang, J. (2020). Analysis of transport and mixing phenomenon to invariant manifolds using LCS and KAM theory approach in unsteady dynamical systems. IEEE Access, 8, 141057–141065. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]
32. Farooqi, A., Ahmad, R., Khan, A. (2021). A comparative epidemiological stability analysis of predictor corrector type non-standard finite difference scheme for the transmissibility of measles. Results in Physics, 21, 103756. DOI 10.1016/j.rinp.2020.103756. [Google Scholar] [CrossRef]
33. Bary, G., Ahmed, W. (2021). Regio and stereoselective functionalization of alkenes with emphasis on mechanistic insight and sustainability concerns. Journal of Saudi Chemical Society, 25(7), 101260. DOI 10.1016/j.jscs.2021.101260. [Google Scholar] [CrossRef]
34. Ahmad, R., Farooqi, A., Farooqi, R., Khan, I., Sajid, M. et al. (2021). An analytical approach to study the blood flow over a nonlinear tapering stenosed artery in flow of carreau fluid model. Complexity, 21, 1–11. [Google Scholar]
35. Ahmad, R., Farooqi, A., Zhang, J. (2019). Steady flow of a power law fluid through a tapered non-symmetric stenotic tube. Applied Mathematics and Nonlinear Sciences, 4(1), 249–260. DOI 10.2478/AMNS.2019.1.00022. [Google Scholar] [CrossRef]
36. Sajid, M., Dehua, L., Zhao, X. (2021). Catalytic conversion of xylose to furfural by p-toluenesulfonic acid (pTSA) and chlorides: Process optimization and kinetic modeling. Molecules, 26(8), 2208. DOI 10.3390/molecules26082208. [Google Scholar] [CrossRef]
37. Sajid, M., Dehua, L., Zhao, X. (2020). Organic acid catalyzed production of platform chemical 5-hydroxymethylfurfural from fructose: Process comparison and evaluation based on kinetic modeling. Arabian Journal of Chemistry, 13(10), 7430–7444. DOI 10.1016/j.arabjc.2020.08.019. [Google Scholar] [CrossRef]
38. Song, Y. Q., Khan, S. A., Imran, M., Waqas, H., Khan, S. U. et al. (2021). Applications of modified darcy law and nonlinear thermal radiation in bioconvection flow of micropolar nanofluid over an off centered rotating disk. Alexandria Engineering Journal, 60(5), 4607–4618. DOI 10.1016/j.aej.2021.03.053. [Google Scholar] [CrossRef]
39. Farooq, U., Waqas, H., Khan, M. I., Khan, S. U., Chu, Y. M. et al. (2021). Thermally radioactive bioconvection flow of carreau nanofluid with modified cattaneo-christov expressions and exponential space-based heat source. Alexandria Engineering Journal, 60(3), 3073–3086. DOI 10.1016/j.aej.2021.01.050. [Google Scholar] [CrossRef]
40. Tlili, I., Waqas, H., Almaneea, A., Khan, S. U., Imran, M. (2019). Activation energy and second order slip in bioconvection of Oldroyd-B nanofluid over a stretching cylinder: A proposed mathematical model. Processes, 7(12), 914. DOI 10.3390/pr7120914. [Google Scholar] [CrossRef]
41. Waqas, H., Khan, S. U., Shehzad, S. A., Imran, M., Tlili, I. (2020). Activation energy and bioconvection aspects in generalized second-grade nanofluid over a Riga plate: A theoretical model. Applied Nanoscience, 10(12), 4445–4458. DOI 10.1007/s13204-020-01332-y. [Google Scholar] [CrossRef]
42. Hafeez, A., Khan, M., Ahmed, A. ( (2020). Stagnation point flow of radiative oldroyd-b nanofluid over a rotating disk. Computer Methods and Programs in Biomedicine, 191, 105342. DOI http://dx.doi.org/10.1016/j.cmpb.2020.105342. [Google Scholar]
43. Waqas, H., Imran, M., Muhammad, T., Sait, S. M., Ellahi, R. (2020). Numerical investigation on bioconvection flow of Oldroyd-B nanofluid with nonlinear thermal radiation and motile microorganisms over rotating disk. Journal of Thermal Analysis and Calorimetry, 145(2), 1–17. DOI 10.1007/s10973-020-09728-2. [Google Scholar] [CrossRef]
44. Ahmed, A., Khan, M., Ahmed, J., Hafeez, A., Iqbal, Z. (2020). Unsteady stagnation point flow of Maxwell nanofluid over stretching disk with joule heating. Arabian Journal for Science and Engineering, 45(7), 1–12. DOI 10.1007/s13369-020-04468-9. [Google Scholar] [CrossRef]
45. Zhou, S. S., Bilal, M., Khan, M. A., Muhammad, T. (2021). Numerical analysis of thermal radiative maxwell nanofluid flow over-stretching porous rotating disk. Micromachines, 12(5), 540. DOI 10.3390/mi12050540. [Google Scholar] [CrossRef]
46. Bary, G., Ru, P., Zhang, W. (2019). Normalized multi-pion hanbury–brown–twiss correlation functions of pion emitting sources with bose–einstein condensation. Journal of Physics G: Nuclear and Particle Physics, 46, 115107. DOI 10.1088/1361-6471/ab449a. [Google Scholar] [CrossRef]
47. Khan, S. A., Waqas, H., Naqvi, S., Alghamdi, M., Al-Mdallal, Q. (2021). Cattaneo-christov double diffusions theories with bio-convection in nanofluid flow to enhance the efficiency of nanoparticles diffusion. Case Studies in Thermal Engineering, 26, 101017. DOI 10.1016/j.csite.2021.101017. [Google Scholar] [CrossRef]
48. Maskeen, M. M., Zeeshan, A., Mehmood, O. U., Hassan, M. (2019). Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. Journal of Thermal Analysis and Calorimetry, 138(2), 1127–1136. DOI 10.1007/s10973-019-08304-7. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |