
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.017304
ARTICLE
Bioconvection Mangnetohydrodynamic Tangent Hyperbolic Nanofluid Flow with Quartic Chemical Reaction Past a Paraboloid Surface
1Department of Mathematics, Capital University of Science and Technology, Islamabad, Pakistan
2Department of Mechanical Engineering, College of Engineering, Prince Mohammad Bin Fahd University, Al Khobar, Saudi Arabia
3Department of Mathematics, University of Sargodha, Sargodha, Pakistan
4CAS Key Laboratory of Mechanical Behavior and Design of Materials, Department of Modern Mechanics, University of Science and Technology of China, Hefei, China
*Corresponding Authors: W. A. Khan. Email: wkhan1956@gmail.com; Muhammad Abbas. Email: muhammad.abbas@uos.edu.pk
Received: 30 April 2021; Accepted: 07 June 2021
Abstract: In this numerical study, the effect of quartic autocatalysis type of chemical reaction, buoyancy force and thermal radiation phenomenon and magnetic effect on tangent hyperbolic nanofluid past an upper horizontal surface of a paraboloid has been studied. By considering the Buongiorno model approach, a diffusion of unequal coefficients in the presence of gyrotactic microorganism is discussed. Implementation of microorganism's idea is used to stabilize the nanoparticles through bioconvection. The modeled PDEs of the problems are converted into nonlinear ODEs with the assistant of the similarity transformations. To tackle nonlinear ODEs, MATLAB package bvp4c is used. In addition, a hallmark of the Matlab code with the reported results in the literature is achieved by benchmarking. The variations in motion, concentration, temperature, and motile density due to sundry parameters have been analyzed in-depth via graphs. Our analysis shows that the density profile of motile of microorganism is hiked with an increment in the bioconvection Rayleigh number but decreases for higher thermal Grashof number.
Keywords: Quartic autocatalysis; tangent hyperbolic nanofluid; brownian motion; paraboloid of revolution; MHD flow; thermophoresis
The magnetohydrodynamic (MHD) studies have drawn substantial interest from researchers and scientists due to their vast applications in engineering and industry. The use of MHD in steaming, melting, stirring, and levitating liquid metals is very frequent. MHD has recently been shown to be helpful in many disease diagnosis processes. Flows under the influence of MHD, therefore attract significant interest from many researchers. As a consequence, MHD flows attain a great deal of focus from many researchers. A few of the recent developments are as follows: Hassan et al. [1] performed the comparison of non-magnetic and magnetic effect on nanoparticles past a wedge. Slip and thermal radiation effects on the MHD Casson effect were investigated by Raza [2] with concluding remarks that the concentration boundary layer thickness is hiked as the chemical reaction parameter gets higher. Yashkun et al. [3] highlighted the MHD hybrid radiative nanofluid past a shrinking/stretching surface. One of the conclusions was that suction parameter enhances the shrinking/stretching parameter range for which the solution exists. Anuar et al. [4] performed the stability analysis of magnetohydrodynamics flow past a deforming vertical surface and reported that only the first solution is linearly stable. Further detail in this regard can be seen in [5–9].
In the application of industry and engineering, non-Newtonian fluids are widespread; common examples are lubrications, drilling, high-speed objects, cooling processes, etc. The idea of including nanoparticles in some base fluids become very popular these days. The insertion of the nanoparticles in these fluids made the use of these fluid more significant for the improvement of thermal conductivity. The non-Newtonian fluids have been examined extensively due to their large applications in industries and engineering. These fluids have nonlinear relation between stress and strain in rheology. These shear effects play a significant role in the analysis of the heat transfer of the non-Newtonian fluids. A hyperbolic tangent fluid is one of the non-Newtonian fluids which are capable of describing the shear-thinning phenomenon. This rheological model has certain advantages over the other non-Newtonian fluids including its formulation simplicity, ease of computation and physical robustness. Furthermore, it is deduced from the kinetic theory of liquids rather than the empirical relation. From laboratory experiments, it is found that this model predicts the shear thinning phenomenon very precisely. Additionally, this model described the blood flow very accurately. Some of the recent developments may include, in the presence of the operative Prandtl model, Khan et al. [10] scrutinized the ferromagnetic nanofluid past a stretching surface. They concluded that the turbulence behavior could be controlled with magnetic dipole. Atif et al. [11] explored the micropolar behavior of Carreau nanofluid. Ahmed et al. [12] performed the thermal analysis on Maxwell nanofluid with thermal radiation effect and heat sink/source presence. They observed that Maxwell, curvature, and unsteadiness parameters upshots the concentration distribution. Tlili et al. [13] analyzed the entropy generation in Darcy Forchheimer nanofluid flow. One of the main observations was that the boosting Biot number hikes the energy of the fluid. Double stratification, chemical reaction and thermal radiation effects on tangent hyperbolic nanofluid were reported by Khan et al. [14]. A steady flow of a power-law fluid through a tapered non-symmetric stenotic tube was studied by Ahmad et al. [15]. The effect of solar radiation on MHD stagnation point nanofluid flow was discussed by Ghasemia et al. [16], with the key finding that the energy profile is hiked as each of the Biot number is upsurged. For a deeper understanding of nanofluids, the readers are referred to see [17–20].
Bioconvection is the development of random patterns due to the swimming of the microorganisms. This bioconvection phenomenon plays a vital role in the industry, food digestion, agriculture and antibiotics. Their inclusion in the base fluids improves the transfer of mass significantly. Kuznetsov et al. [21,22] presented the natural convection flow of nanofluid past a vertical sheet. Nima et al. [23] reported the behavior of non-Newtonian fluid with variable properties in the presence of the gyrotactic microorganisms. One of the key features was that the density profile is upsurged as the bioconvection Lewis number gets higher. Khan et al. [24] reported the Jaffery nanofluid with gyrotactic microorganisms in the presence of effective Prandtl number and Activation energy. The impact of heat generation on bioconvection MHD nanofluid flow was analyzed by Kotha et al. [25]. Atif et al. [26] examined the MHD micropolar fluid with stratification effects in the presence of nanoparticles and gyrotactic microorganisms with concluding remarks that density distribution is rambled as each of the mass stratification and buoyancy ratio parameter is boosted. When two or more reactants yield products, a chemical reaction occurs. This chemical reaction may be homogenous or heterogeneous depending upon whether the reaction takes place at the interface or due to a single-phase volume reaction [27]. Lotka [28] presented the idea of an autocatalytic chemical reaction. In this perspective, the simplest one is X + Y → Y + Y, which means that species X interacts with specie Y, and in the final product, whole species X is converted into species Y. Sapre [29] presented the idea of a quadratic and cubic autocatalytic chemical reaction. Animasaun et al. [30] analyzed the viscoelastic fluid flow by considering first-order reaction and cubic autocatalytic reaction schemes. The variable thickness of an object is one of the significant properties of the materials. In industry, there are many applications where the fluid flows over a non-uniform thickness surface. Patil et al. [31] looked in the double-diffusive flow past a stretching surface of variable thickness. One of the key findings of this study was that the enhancement in the Prandtl number depresses the 30% of the thermal boundary thickness. Qasim et al. [32] scrutinized the numerical and analytical solution of the mixed convection flow past a vertical sheet of variable thickness. One of the main observations of that study was that an increment in the surface drag is noticed as the wall thickness parameter is enhanced. Three-dimensional MHD Carreau fluid flow over a paraboloid surface with thermal radiation effects was inspected by Abdeljawad et al. [33]. An upper paraboloid surface (ups) phenomenon of bioconvection in Carreau fluid was discussed by Khan et al. [34] and conclude that velocity profile is declined as the bioconvection Rayleigh number is escalated. For non-Newtonian fluids past a paraboloid surface of revolution, flow properties were discussed by Santoshi et al. [35].
In the above-presented literature, it is noticeable that numerous researchers investigated the different non-Newtonian fluid flows past different geometries. However, no one studied the tangent hyperbolic nanofluid flow over a paraboloid surface with gyrotactic microorganisms. In this numerical computation, a tangent hyperbolic nanofluid past a horizontal paraboloid surface with a quartic autocatalytic type of chemical reaction is analyzed. The arising non-linear ODEs are tackled with Matlab package bvp4c which is a finite difference code that implements the 3-stage Lobatto IIIa formula. To use bvp4c from Matlab, first, Eqs. (15)–(19) are transformed into a set of a coupled first-order system of equations. This transformation is used to set up the system of equations as a boundary value problem (BVP) and use the BVP solver in Matlab to numerically solve this system, with the above boundary condition and assumed a suitable finite value for the far-field boundary condition, i.e.,
2 Formulation of the Governing Equations
Tangent hyperbolic nanofluid flow past ups in the presence of the gyrotactic microorganisms are analyzed. The flow analysis is carried out in the presence of magnetic and thermal radiation effects. For the stability of the nanoparticles, microorganisms are induced. The layer very next to ups is parallel to the sheet having velocity
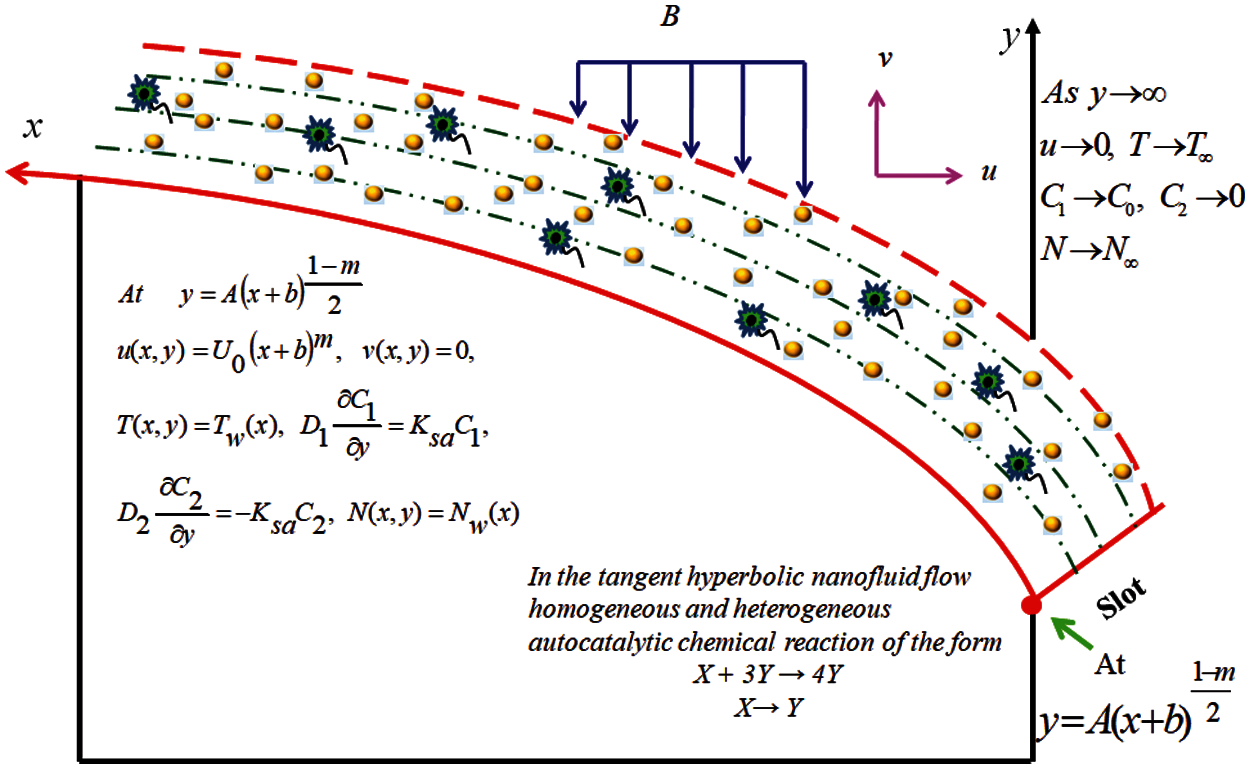
Figure 1: Flow configuration
The governing equations of the above-modeled problem
The boundary conditions are as follows
In order to obtain the nondimensional form of the modeled equations, a stream function
Here
It is noticeable that the continuity equation is satisfied automatically, and locally transformed ODEs are as follows:
It is noticeable that the least value of y is not the starting point of the slot. It is considering this fact, the BCs (7) cannot be imposed at
The BCs becomes:
In the above equations,
The dimensionless modelled equation Eqs. (9)–(13) are depending on
subject to BCs
In engineering and industry, the quantities which are the foremost interest are the surface drag
In the nondimensional form
The solution of the modeled BVP Eqs. (15)–(19) with BCs (20) has been achieved by MATLAB package bvp4c. It is not possible to find the solution of the equation for an infinite domain
For the validation of MATLAB code, the present results of skin friction are compared in the limiting case with Akbar et al. [38] and Malik et al. [39]. The tabulated results show a remarkable agreement with these results see Table 1.

5.1 The Skin Friction, Nusselt Number, and Density Number
Table 2 is presented to study the impact of important parameters on skin friction



The impact of the sundry parameters on different profiles is presented graphically and discussed in detail. For the whole study, the values of the parameters are considered as
Figs. 2a–2d are sketched to study the impact of the Brownian motion parameter
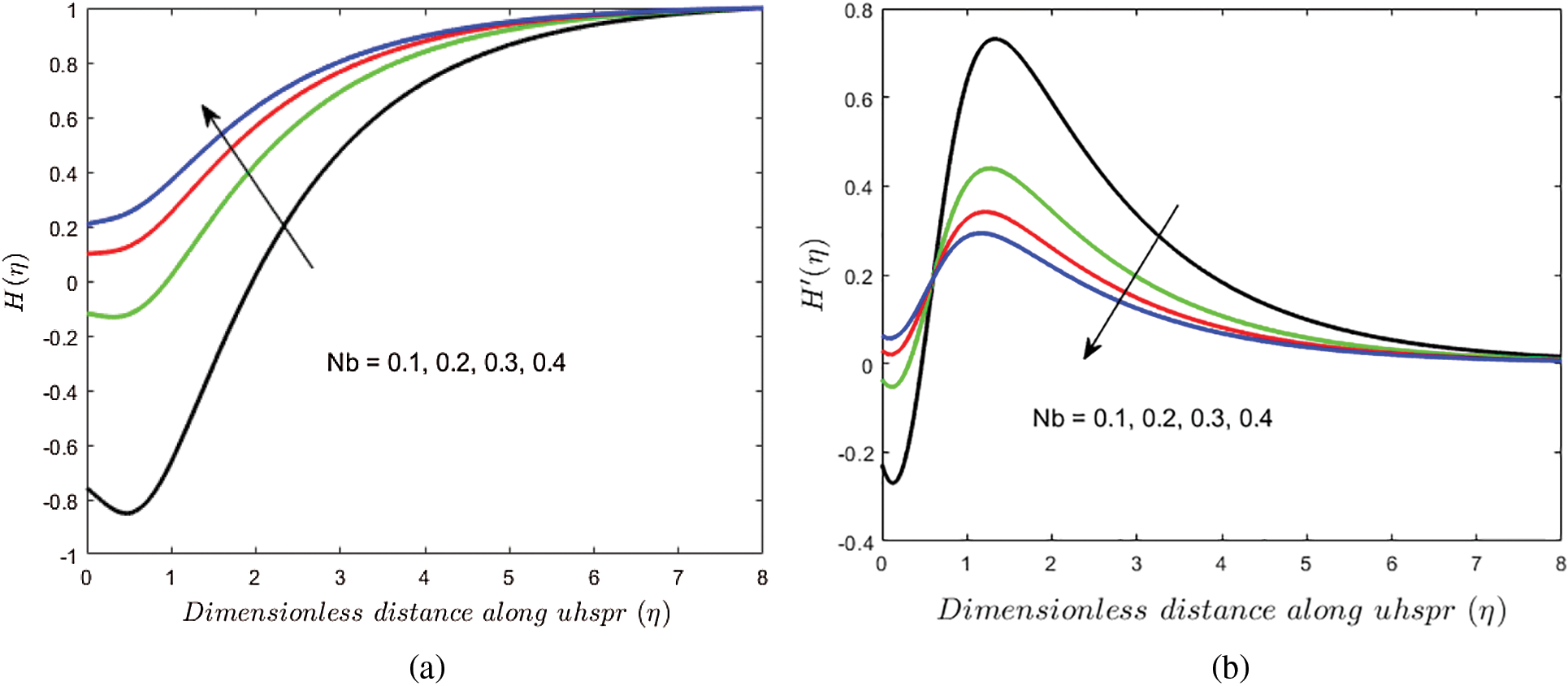
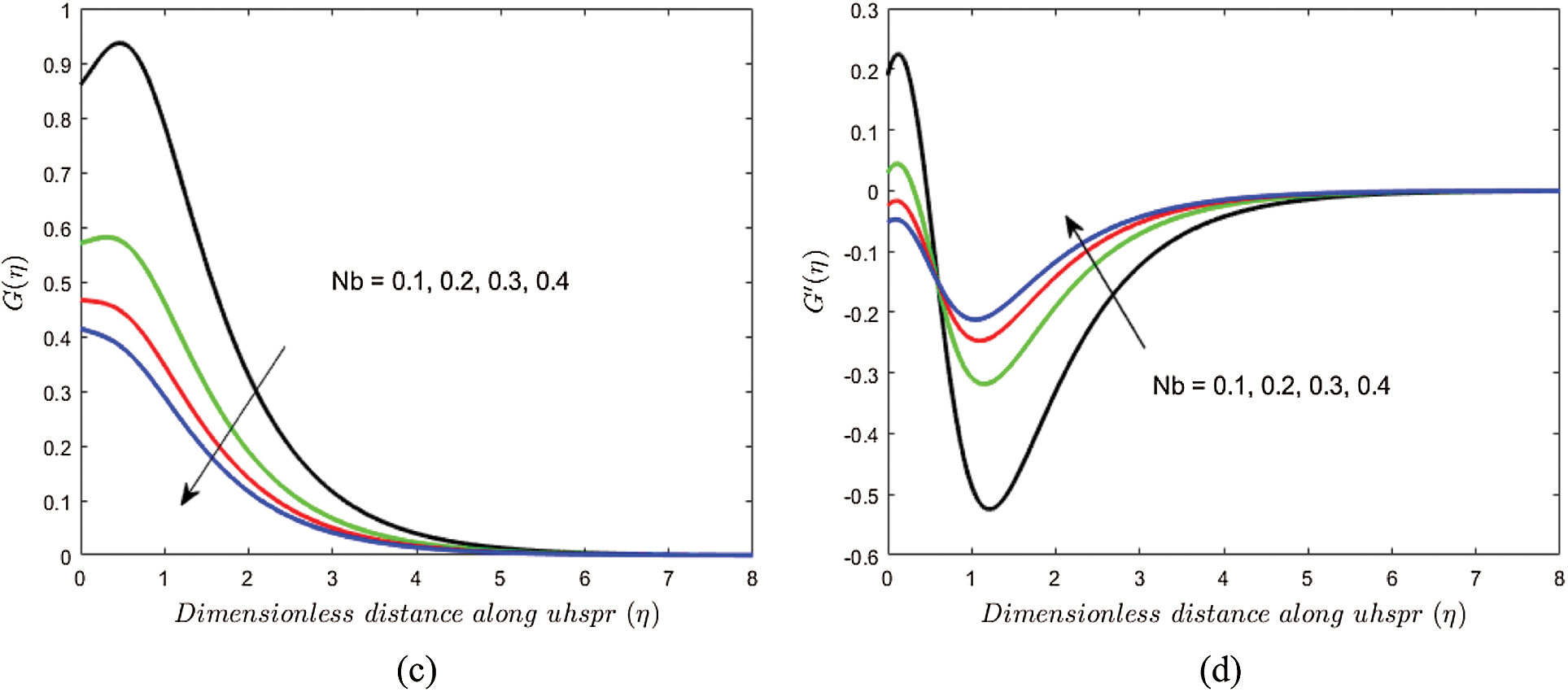
Figure 2: Variations in (a)
In order to view the influence of thermal Grashof number
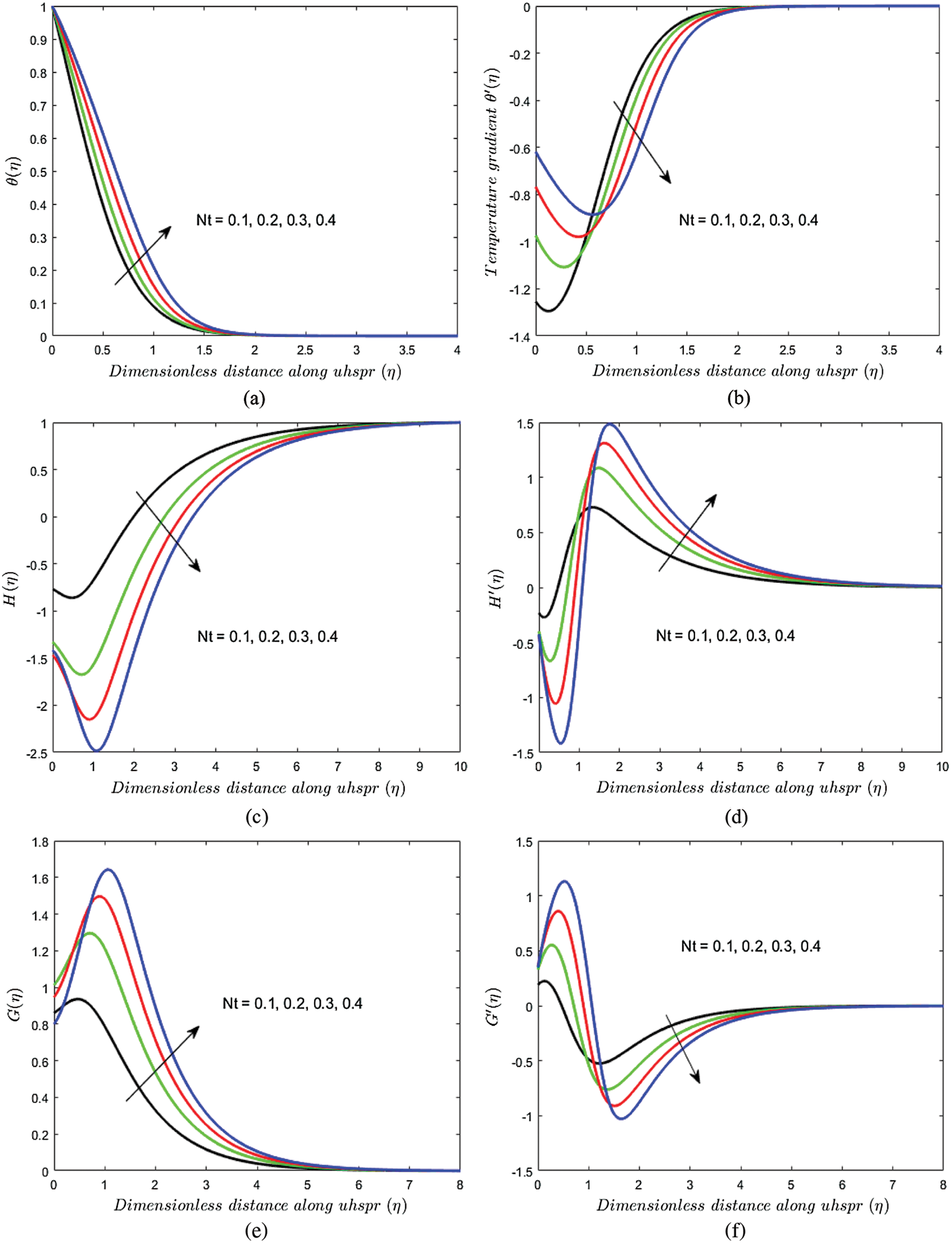
Figure 3: Variations in (a)

Figure 4: Variations in (a)
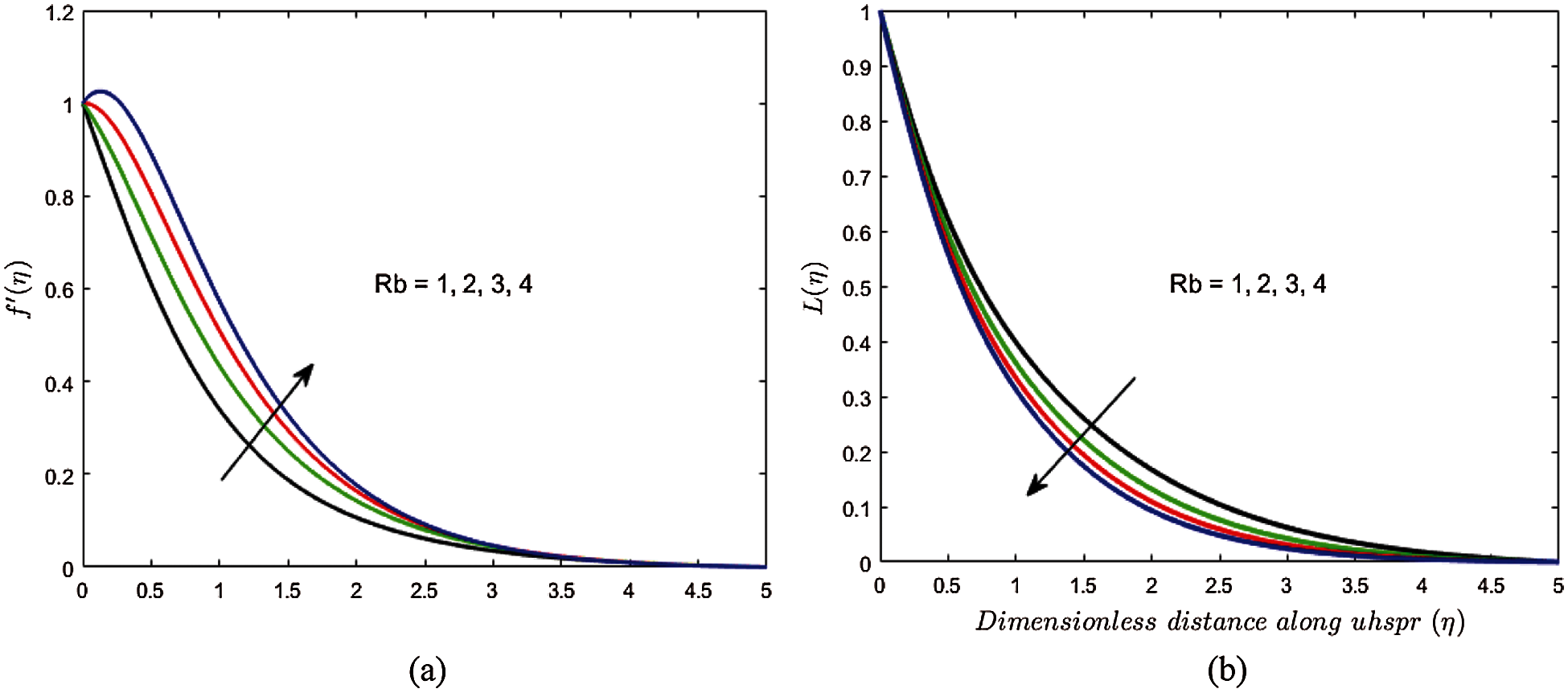
Figure 5: Variations in (a)
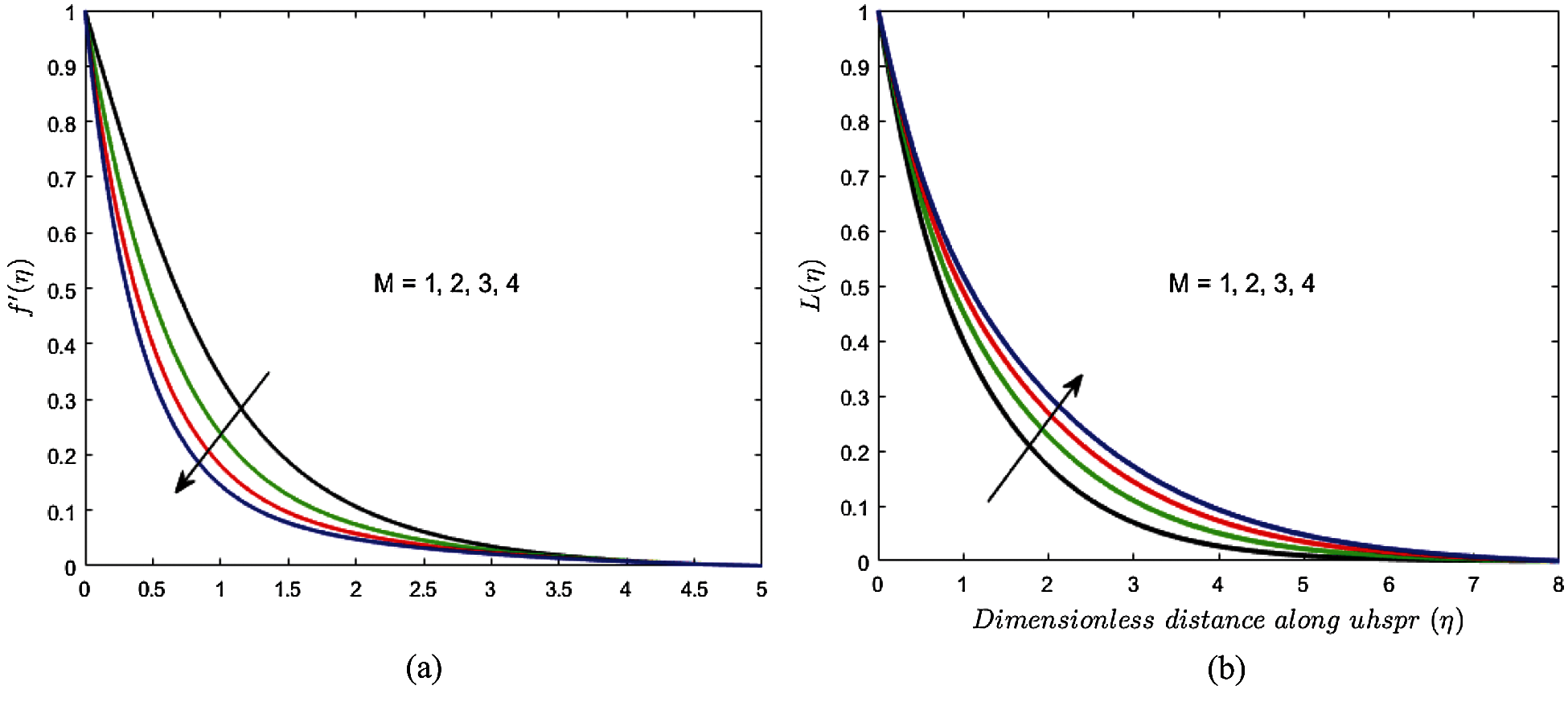
Figure 6: Variations in (a)
In this numerical study, the tangent hyperbolic nanofluid past the upper horizontal surface of paraboloid revolution with quartic autocatalysis chemical reaction has been studied. A few of the key results are:
• The velocity profile is declined, whereas the density profile is enhanced as the magnetic parameter is boosted.
• The impact of the Brownian motion parameter on the homogeneous fluid is increasing, whereas the thermophoresis parameter has the opposite impact.
• The density profile of motile microorganisms is hiked as the bioconvection Rayleigh number is upsurged, whereas it decreases for the increasing values of the thermal Grashof number.
• The Nusselt number and motile density number declined as the velocity power index was enhanced.
• The Skin friction coefficient is declined as each of the thermal Grashof numbers, power-law index, velocity power index, and bioconvection Rayleigh number are boosted.
• The influence of the Brownian motion parameter on the heterogeneous fluid is decreasing, whereas the opposite trend is noticed for the thermophoresis parameter.
Acknowledgement: We thank Dr. Muhammad Kashif Iqbal for his assistance in proofreading the manuscript.
Author's Contributions: All authors equally contributed to this work. All authors read and approved the final manuscript.
Funding Statement: The authors received no external funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Hassan, M., Ellahi, R., Bhatti, M. M., Zeeshan, A. (2019). A comparative study on magnetic and non-magnetic particles in nanofluid propagating over a wedge. Canadian Journal of Physics, 97(3), 277–285. DOI 10.1139/cjp-2018-0159. [Google Scholar] [CrossRef]
2. Raza, J. (2019). Thermal radiation and slip effects on magnetohydrodynamic (MHD) stagnation point flow of casson fluid over a convective stretching sheet. Propulsion and Power Research, 8(2), 138–146. DOI 10.1016/j.jppr.2019.01.004. [Google Scholar] [CrossRef]
3. Yashkun, U., Zaimi, K., Bakar, N. A. A., Ishak, A., Pop, I. (2020). MHD hybrid nanofluid flow over a permeable stretching/shrinking sheet with thermal radiation effect. International Journal of Numerical Methods for Heat & Fluid Flow, 31(3), 1014–1031. DOI 10.1108/HFF-02-2020-0083. [Google Scholar] [CrossRef]
4. Anuar, N. S., Bachok, N., Turkyilmazoglu, M., Arifin, N. M., Rosali, H. (2020). Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in carbon nanotubes. Alexandria Engineering Journal, 59(1), 497–507. DOI 10.1016/j.aej.2020.01.024. [Google Scholar] [CrossRef]
5. Kamran, A., Hussain, S., Sagheer, M., Akmal, N. (2017). A numerical study of magnetohydrodynamics flow in casson nanofluid combined with joule heating and slip boundary conditions. Results in Physics, 7, 3037–3048. DOI 10.1016/j.rinp.2017.08.004. [Google Scholar] [CrossRef]
6. Sajid, M., Shahzad, H., Mughees, M., Ali, N. (2019). Mathematical modeling of slip and magnetohydrodynamics effects in blade coating. Journal of Plastic Film & Sheeting, 35(1), 9–21. DOI 10.1177/8756087918777782. [Google Scholar] [CrossRef]
7. Lund, L. A., Omar, Z., Khan, I., Raza, J., Sherif, E. S. M. et al. (2020). Magnetohydrodynamic (MHD) flow of micropolar fluid with effects of viscous dissipation and joule heating over an exponential shrinking sheet: Triple solutions and stability analysis. Symmetry, 12(1), 142. DOI 10.3390/sym12010142. [Google Scholar] [CrossRef]
8. Atif, S. M., Hussain, S., Sagheer, M. (2018). Numerical study of MHD micropolar carreau nanofluid in the presence of an induced magnetic field. AIP Advances, 8(3), 035219. DOI 10.1063/1.5022681. [Google Scholar] [CrossRef]
9. Atif, S. M., Kamran, A., Shah, S. (2021). MHD micropolar nanofluid with non-Fourier and non-fick's law. International Communications in Heat and Mass Transfer, 122, 105114. DOI 10.1016/j.icheatmasstransfer.2021.105114. [Google Scholar] [CrossRef]
10. Khan, A., Gul, T., Zaheer, Z., Amiri, I. S. (2019). The flow of ferromagnetic nanofluid over an extending surface under the effect of operative prandtl model: A numerical study. Advances in Mechanical Engineering, 11(12), DOI 10.1177/1687814019896128. [Google Scholar] [CrossRef]
11. Atif, S. M., Hussain, S., Sagheer, M. (2019). Effect of thermal radiation on MHD micropolar Carreau nanofluid with viscous dissipation. Joule Heating, and Internal Heating. Scientia Iranica, 26(6), 3875–3888. DOI 10.24200/SCI.2019.51653.2294. [Google Scholar] [CrossRef]
12. Ahmed, A., Khan, M., Hafeez, A., Ahmed, J. (2020). Thermal analysis in unsteady radiative Maxwell nanofluid flow subject to heat source/sink. Applied Nanoscience, 10, 5489–5497. DOI 10.1007/s13204-020-01431-w. [Google Scholar] [CrossRef]
13. Tlili, I., Shahmir, N., Ramzan, M., Kadry, S., Kim, J. Y. et al. (2020). A novel model to analyze darcy forchheimer nanofluid flow in a permeable medium with entropy generation analysis. Journal of Taibah University for Science, 14(1), 916–930. DOI 10.1080/16583655.2020.1790171. [Google Scholar] [CrossRef]
14. Khan, M., Rasheed, A., Salahuddin, T. (2020). Radiation and chemical reactive impact on tangent hyperbolic fluid flow having double stratification. AIP Advances, 10(7), 075211. DOI 10.1063/5.0003717. [Google Scholar] [CrossRef]
15. Ahmad, R., Farooqi, A., Zhang, J., Ali, N. (2019). Steady flow of a power law fluid through a tapered non-symmetric stenotic tube. Applied Mathematics and Nonlinear Sciences, 4(1), 255–266. DOI 10.2478/AMNS.2019.1.00022. [Google Scholar] [CrossRef]
16. Ghasemi, S., Hatami, M. (2021). Solar radiation effects on MHD stagnation point flow and heat transfer of a nanofluid over a stretching sheet. Case Studies in Thermal Engineering, 25, 100898, DOI 10.1016/j.csite.2021.100898. [Google Scholar] [CrossRef]
17. Reddy, G. J., Kethireddy, B., Kumar, M., Hoque, M. M. (2018). A molecular dynamics study on transient non-newtonian MHD casson fluid flow dispersion over a radiative vertical cylinder with entropy heat generation. Journal of Molecular Liquids, 252, 245–262. DOI 10.1016/j.molliq.2017.12.077. [Google Scholar] [CrossRef]
18. Salawu, S. O., Ogunseye, H. A. (2020). Entropy generation of a radiative hydromagnetic powell-eyring chemical reaction nanofluid with variable conductivity and electric field loading. Results in Engineering, 5, 100072. DOI 10.1016/j.rineng.2019.100072. [Google Scholar] [CrossRef]
19. Hamid, A. (2020). Terrific effects of ohmic-viscous dissipation on casson nanofluid flow over a vertical thin needle: Buoyancy assisting & opposing flow. Journal of Materials Research and Technology, 9(5), 11220–11230. DOI 10.1016/j.jmrt.2020.07.070. [Google Scholar] [CrossRef]
20. Shah, S., Atif, S. M., Kamran, A. (2021). Radiation and slip effects on MHD Maxwell nanofluid flow over an inclined surface with chemical reaction. Heat Transfer, 50(4), 4062–4085. DOI 10.1002/htj.22064. [Google Scholar] [CrossRef]
21. Kuznetsov, A. V., Nield, D. A. (2010). Natural convective boundary-layer flow of a nanofluid past a vertical plate. International Journal of Thermal Sciences, 49(2), 243–247. DOI 10.1016/j.ijthermalsci.2009.07.015. [Google Scholar] [CrossRef]
22. Kuznetsov, A. V., Nield, D. A. (2011). Double-diffusive natural convective boundary-layer flow of a nanofluid past a vertical plate. International Journal of Thermal Sciences, 50(5), 712–717. DOI 10.1016/j.ijthermalsci.2011.01.003. [Google Scholar] [CrossRef]
23. Nima, N. I., Salawu, S. O., Ferdows, M., Shamshuddin, M. D., Alsenafi, A. et al. (2020). Melting effect on non-newtonian fluid flow in gyrotactic microorganism saturated non-darcy porous media with variable fluid properties. Applied Nanoscience, 10(10), 3911–3924. DOI 10.1007/s13204-020-01491-y. [Google Scholar] [CrossRef]
24. Khan, S. U., Tlili, I. (2020). Significance of activation energy and effective prandtl number in accelerated flow of jeffrey nanoparticles with gyrotactic microorganisms. Journal of Energy Resources Technology, 142(11). DOI 10.1115/1.4047248. [Google Scholar] [CrossRef]
25. Kotha, G., Kolipaula, V. R., Rao, M. V. S., Penki, S., Chamkha, A. J. (2020). Internal heat generation on bioconvection of an MHD nanofluid flow due to gyrotactic microorganisms. The European Physical Journal Plus, 135(7), 1–19. DOI 10.1140/epjp/s13360-020-00606-2. [Google Scholar] [CrossRef]
26. Atif, S. M., Hussain, S., Sagheer, M. (2019). Magnetohydrodynamic stratified bioconvective flow of micropolar nanofluid due to gyrotactic microorganisms. AIP Advances, 9(2), 025208. DOI 10.1063/1.5085742. [Google Scholar] [CrossRef]
27. Animasaun, I. L. (2015). Effects of thermophoresis, variable viscosity and thermal conductivity on free convective heat and mass transfer of non-darcian MHD dissipative casson fluid flow with suction and nth order of chemical reaction. Journal of the Nigerian Mathematical Society, 34(1), 11–31. DOI 10.1016/j.jnnms.2014.10.008. [Google Scholar] [CrossRef]
28. Lotka, A. J. (2002). Contribution to the theory of periodic reactions. The Journal of Physical Chemistry, 14(3), 271–274. DOI 10.1021/j150111a004. [Google Scholar] [CrossRef]
29. Sapre, A. V. (1989). Diffusional enhancement of autocatalytic reactions in catalyst particles. AIChE Journal, 35(4), 655–657. DOI 10.1002/aic.690350416. [Google Scholar] [CrossRef]
30. Animasaun, I. L., Raju, C. S. K., Sandeep, N. (2016). Unequal diffusivities case of homogeneous–heterogeneous reactions within viscoelastic fluid flow in the presence of induced magnetic-field and nonlinear thermal radiation. Alexandria Engineering Journal, 55(2), 1595–1606. DOI 10.1016/j.aej.2016.01.018. [Google Scholar] [CrossRef]
31. Patil, P. M., Roy, S., Moitsheki, R. J., Momoniat, E. (2017). Double diffusive flows over a stretching sheet of variable thickness with or without surface mass transfer. Heat Transfer—Asian Research, 46(8), 1087–1103. DOI 10.1002/htj.21261. [Google Scholar] [CrossRef]
32. Qasim, M., Riaz, N., Lu, D., Afridi, M. I. (2020). Mixed convection flow over a stretching sheet of variable thickness: Analytical and numerical solutions of self-similar equations. Heat Transfer, 49(6), 3882–3899. DOI 10.1002/htj.21813. [Google Scholar] [CrossRef]
33. Abdeljawad, T., Ullah, A., Alrabaiah, H., Ullah, I., Ayaz, M. et al. (2020). Thermal radiations and mass transfer analysis of the three-dimensional magnetite carreau fluid flow past a horizontal surface of paraboloid of revolution. Processes, 8(6), 656. DOI 10.3390/pr8060656. [Google Scholar] [CrossRef]
34. Khan, M., Hussain, A., Malik, M. Y., Salahuddin, T. (2017). Biconvection flow of carreau fluid over an upper paraboloid surface: A computational study. Results in Physics, 7, 4050–4057. DOI 10.1016/j.rinp.2017.10.023. [Google Scholar] [CrossRef]
35. Santoshi, P. N., Reddy, G. V. R., Padma, P. (2020). Flow features of non-newtonian fluid through a paraboloid of revolution. International Journal of Applied and Computational Mathematics, 6, 1–22. DOI 10.1007/s40819-020-00828-z. [Google Scholar] [CrossRef]
36. Chaudhary, M. A., Merkin, J. H. (1995). A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. I Equal diffusivities. Fluid Dynamics Research, 16(6), 311–333. DOI 10.1016/0169-5983(95)00015-6. [Google Scholar] [CrossRef]
37. Lynch, D. T. (1992). Chaotic behavior of reaction systems: Mixed cubic and quadratic autocatalysis. Chemical Engineering Science, 47(17–18), 4435–4444. DOI 10.1016/0009-2509(92)85121-Q. [Google Scholar] [CrossRef]
38. Akbar, N. S., Ebaid, A., Khan, Z. H. (2015). Numerical analysis of magnetic field effects on eyring-powell fluid flow towards a stretching sheet. Journal of Magnetism and Magnetic Materials, 382, 355–358. DOI 10.1016/j.jmmm.2015.01.088. [Google Scholar] [CrossRef]
39. Malik, M. Y., Salahuddin, T., Hussain, A., Bilal, S. (2015). MHD flow of tangent hyperbolic fluid over a stretching cylinder: Using keller box method. Journal of Magnetism and Magnetic Materials, 395, 271–276. DOI 10.1016/j.jmmm.2015.07.097. [Google Scholar] [CrossRef]
40. Zaimi, K., Ishak, A., Pop, I. (2014). Boundary layer flow and heat transfer over a nonlinearly permeable stretching/shrinking sheet in a nanofluid. Scientific Reports, 4(1), 1–8. DOI 10.1038/srep04404. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |