Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.017467

ARTICLE

Unsupervised Binary Protocol Clustering Based on Maximum Sequential Patterns

Jiaxin Shi1, Lin Ye1,2,*, Zhongwei Li3 and Dongyang Zhan1

1School of Cyberspace Science, Harbin Institute of Technology, Harbin, 150001, China
2Science and Technology on Communication Networks Laboratory, Shijiazhuang, 050081, China
3School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin, 150001, China
*Corresponding Author: Lin Ye. Email: hityelin@hit.edu.cn
Received: 12 May 2021; Accepted: 20 July 2021

1  Introduction

Network protocol stipulates the format and sequence of the messages exchanged between the entities at the two ends of the communication in the computer network, and the entities receive the protocol messages and make appropriate actions. It is composed of syntax, semantics, and timing, which determines the format of the protocol message [1]. With the rapid development of the Internet, many private protocols and network services have proliferated, resulting in a variety of protocol messages on the network. For example, the Internet-of-Things (IoT) technology has facilitated the development of a range of new devices, which increases the diversity of protocols [2–5]. But only a few of them use known protocol specifications. Considering economic interests, security, privacy, etc., most protocols do not disclose their specific details to the public. There are various protocols mixed together on the network, and malicious programs use private protocols to avoid being tracked and analyzed, which brings great challenges to network security. Especially in the industrial cyber-physical system, which faces various security threats, these programs can jeopardize the system’s stability [6,7]. In addition, well-known network protocols may have different formats due to different application requirements. For example, the P2P network adopted by the Bitcoin system in the blockchain has three types [8], so the P2P protocol of different networks may also have certain differences. Therefore, more and more attention has been paid to the detection and analysis of unknown protocols, and protocol reverse engineering (PRE) emerges to analyze unknown protocols.

Protocol reverse engineering is to speculate on the possible syntax, semantics and timing information of the protocol based on the content of the protocol messages and the behaviors of the communicating parties without relying on any protocol description [9]. The workload of manually analyzing the format specifications of the unknown protocol is large, time-consuming, and error-prone. For example, it takes 12 years for the SAMBA project to basically realize the extraction of the basic protocol specifications of the SMB protocol [10,11]. Therefore, it is very important to improve the analysis efficiency and reduce the error probability of PRE automation technology.

Protocol reverse analysis can be divided into two types: binary analysis of protocol implementation [12–15] and statistic analysis of unknown protocol traffic [16–19], which are realized by analyzing the program code of the communication entity program and the protocol message field, respectively.

The PRE process of the protocol includes input preprocessing, protocol format extraction and state machine inference [20–22]. First, the input preprocessing captures protocol messages on the network and transforms them into a format suitable for subsequent analysis. Second, protocol format extraction includes field identification and format inference. And it analyzes as much as possible to obtain a field format similar to the original protocol specification. Third, state machine inference completes the timing inference, which is used to describe the communication events.

There are many kinds of protocol messages on the network, which makes it difficult to perform reverse analysis on multiple protocols directly at the same time, and the accuracy of reverse analysis results is not satisfactory [23,24]. Therefore, in this paper, we mainly divide a variety of unknown protocol messages into different clusters, which will facilitate future protocol reverse work. Effective protocol message clustering necessitates the resolution of two critical issues: the measurement of protocol message distance and the design of clustering algorithm [25]. It is worth noting that the message distance is the basis of protocol clustering. Besides, the specifications vary greatly according to the protocol type [26]. Therefore, the distance between two different types of protocol messages is greater than the distance of the protocol messages in the same type, so it can be used as a basis for protocol clustering. For example, the protocol informatics project (PI) [27], Discover [19] and Netzob [18] use the progressive multiple sequence alignment algorithm in the field of bioinformatics [28] to achieve the sequence alignment and the calculation of message distance. The clustering algorithm can divide different protocol messages into different clusters, such as UPGMA [29] and the neural network [30–32] using different approaches to cluster protocol messages.

In this paper, we propose an unsupervised protocol message clustering method based on the fuzzy membership of maximum frequent sequences, which effectively solves the problem of clustering difficulties caused by different protocol message lengths. The main contributions are as follows:

1. We set the minimum support threshold and propose the maxBIDE algorithm based on the BIDE algorithm to mine the maximum frequent sequences.

2. Based on the fuzzy theory, we calculate the fuzzy membership of the maximum frequent sequences to each protocol message to construct the fuzzy membership vectors.

3. We introduce the number of protocol types as prior knowledge so that we can cluster the protocol messages, adjust different minimum support thresholds and calculate homogeneity, integrity and FMI to evaluate our method’s performance.

In summary, the rest of this paper is organized as follows: Section 2 introduces related research on protocol reverse engineering. Section 3 formulates the problem to be solved and gives relevant definitions. Section 4 designs the whole scheme of unknown binary protocol message clustering, including the problems mentioned above. Section 5 experiments with the method on the collected protocol messages and evaluates the clustering result, and this section also compares with the existing partial clustering methods. Moreover, we also evaluate our method when the distribution of the number of protocol messages is unbalanced. Finally, Section 6 gives the conclusion of the experiment and the direction for further research in the future.

2  Related Work

Network protocol can be divided into the binary protocol and text protocol. A text protocol message is composed of several human-understandable text strings, such as HTTP, SMTP, etc., while a binary protocol message is a combination of bit 0 and 1, such as ICMP, Modbus, etc. The binary protocol message is indistinguishable by the human-unreadable and it does not have any text encoding information, so prior knowledge is scarce, making manual analysis very difficult. The methods of distinguishing unknown protocol messages can be divided into three types: message format-oriented protocol clustering, state machine-oriented protocol clustering, and semantic template-oriented protocol clustering [33]. Message-oriented clustering focuses on key fields, and clusters messages based on the similarity of key fields among protocol messages. For example, PI [27] uses the Needleman–Wunsch algorithm [28] to complete the hierarchical clustering and extracts the statistical characteristics in the messages of the same type. Discoverer [19] further completes the token-level protocol message alignment on unknown protocol messages. Netzob [18] is a state machine-oriented protocol reverse tool, which uses a heuristic algorithm called the unweighted pair group method with arithmetic mean (UPGMA) [29] to cluster messages and a state machine to describe the interaction process between protocol entities. The semantic template-oriented method clusters protocol messages by analyzing the semantics. For example, ASAP [17] maps the message payloads to the vector space by constructing the marked letters derived from the separator and n-gram, and uses matrix factorization [34] to identify the basic direction and coordinate tuples to cluster different protocol messages. Sun et al. [25] defines Token Format Distance (TFD) and Message Format Distance (MFD) by introducing basic rules of Augmented Backus Naur Form (ABNF) [35] to calculate protocol message distances, then uses the DBSCAN algorithm [36] to cluster protocol messages, and uses Silhouette Coefficient and Dunn Validity Index [37] to determine the best clustering parameters to improve the quality of clustering performance.

Meanwhile, there are also many message clustering methods for binary protocol. ProDecoder [38] clusters messages by exploiting the semantics of protocol messages and using the information bottleneck(IB) algorithm [39], which is more applicable to asynchronous protocols compared to Netzob. Cai et al. [40] infers the binary protocol format by using the Hidden semi-Markov model (HSMM) [41], which maximizes the probability of message segmentation and keyword selection. And an affinity communication mechanism [42] is introduced to measure the similarity in protocol messages. Tao et al. [43] measures the tightness of clusters by calculating Silhouettes Coefficient [44]. In the preprocessing stage, K-means is used to implement hierarchical clustering of protocol messages, which avoids the problem of sparse message characteristics in the cluster.

3  Problem Statement

Let the protocol message set M contain several messages:

M=M1,M2,…,Mn (1)

where n represents the number of protocol messages, and each message contains several bytes:

mi=b1,b2,…,bli (2)

where bj is the possible value for each byte and bj ∈ [0, 255], and li denotes the length of mi.

Let α={a1,a2,…,al} be a sequence pattern, and mi = b1, b2, …, bli contain α when a1 = bi1, a2 = bi2, …, al = bil, which denotes α⊂mi. Therefore, the support of α in M is denoted as:

Sup(α)=∑i=1|M|I(α⊂mi)|M| (3)

where I is the indicator function, if α⊂mi, then I(α⊂mi)=1; otherwise I(α⊂mi)=0.

Given a threshold Γ, α is defined as a frequent sequence if Sup(α) ≥ Γ. Furthermore, given a frequent sequence set B, if there is no sequence β ∈ B and α⊂β, we define α as a maximum frequent sequence.

Let the set of maximum frequent sequences be C={c1,c2,…,ck}. The fuzzy membership vector of a protocol message denotes c(mi) = (wi1, wi2, …, wik), where wij reflects the membership of maximal frequent sequence cj to message mi, which is calculated by the following equation:

wij={1−(LCSS(cj,mi)length(cj))2LCSS(cj,mi)≤length(cj)2(LCSS(cj,mi)length(cj))2LCSS(cj,mi)>length(cj)2 (4)

where LCSS(cj,mi) is the length of the longest common subsequence between cj and mi, and length(cj) is the number of bytes that cj contains. The closer wij approaches to 0, the more similar the maximum frequent sequence is to the protocol message.

Suppose there are k types of protocol messages and the number of messages is n. These messages need to be divided into k clusters, which means the same type of protocol messages belong to the same cluster. In this paper, we use the above metrics related to the maximum frequent sequence to cluster protocol messages, and evaluate the clustering performance at last.

4  Unsupervised Clustering Based on Maximum Frequent Sequences

The unknown binary protocol message clustering based on statistics requires the diversity of the protocols, so as many protocol messages should be collected as possible on the network. Then the protocol messages are processed as shown in Fig. 1, including maximum frequent sequence mining, fuzzy membership calculation, and message clustering.

First, we collect the protocol messages to obtain the payloads. To extract their characteristics, we mine the maximum frequent sequences by using the maxBIDE algorithm, which is based on the BIDE algorithm [45]. Then, based on the fuzzy set theory, we transform each message into a fuzzy membership vector. Therefore, we obtain the vectors with the same dimension, which are used to subsequent message clustering. Finally, we use K-means++ to cluster the collected protocol messages with these vectors. Then we use homogeneity, completeness and Fowlkes and Mallows Index (FMI) [46] to evaluate the performance so that we can obtain the best clustering parameters.

Figure 1: Binary protocol clustering process

4.1 Maximum Frequent Sequence Mining

Since a protocol message is composed of several ordered binary bytes, there should also be an order relationship among bytes of maximum frequent sequences. There are many methods to mine frequent sequences such as CLOSET [47], CHARM [48], CloSpan [49], Prefixspan [50], etc. But most of them need to maintain the mined frequent sequences in memory to detect whether there is an already mined maximum sequence that includes the new mined sequence. Therefore, the memory requirement is high when the number of candidate sequences is too large.

To solve the problem of high memory requirements, Wang et al. [45] proposes the BIDE algorithm, designing a two-way extended closed frequent sequence detection technique, which defines a frequent sequence as a closed frequent sequence when there is no forward-extension event or backward-extension event. Since BIDE does not need to maintain any candidate sequences, it does not require high memory compared to these traditional algorithms. Therefore, in this paper, we propose the maxBIDE algorithm which takes the advantage of the BIDE algorithm to mine the maximum frequent sequences of the protocol messages by judging whether there are any two-way extension events in these sequences.

To determine whether a sequence is a maximum frequent sequence, we redefine the extension events as follows:

Definition 4.1. Given a sequence S = b1, b2, …, bn and a super-sequence whose Sup(S′) > Γ, where Γ is the minimum support threshold of the protocol messages. If there is a byte b′, where S′ = b1, b2, …, bn, b′, we define b′ as a max-forward-extension event. The byte is defined as a max-backward-extension event while the sequence S′ = b′, b1, b2, …, bn or S′ = b1, b2, …, b′, …, bn.

The BIDE algorithm uses Backscan to determine whether the sequence is prunable: Given a prefix sequence e = e1, e2, …, en, if there is a byte e′ shown in the i-th semi-maximum period of e, the prefix sequence will have a max-backward-extension event. Therefore, it cannot be a closed frequent sequence, which means it is prunable. In the maxBIDE algorithm, we define maxBackScan to determine whether we can prune the sequence: When the occurrence of byte e′ in the i-th semi-maximum period exceeds Γ, it means the support of e′, e1, e2, …, en or e1, e2, …, e′, …, en exceeds Γ, so e will not be a maximum frequent sequence. For example, suppose that the minimum support threshold is 3, the prefix B’s 1-th semi-maximum period is shown in Table 1. The support of byte A is 3, which is equal to the minimum support threshold, so AB is a frequent prefix. Therefore, these sequences whose prefix is B are not maximum sequences and we need to prune A.

The main idea of the maxBIDE algorithm is shown in Algorithms 1–3. Firstly, it obtains the frequent 1 sequence set F1 (Algorithm 1, Line 2), then each f1 ∈ F1 is used as a prefix to construct pseudo projected database [45] msgDBf1 (Algorithm 1, Lines 3 and 4), and we judge the frequent 1 sequences whether they have any max-backward-extension events by using maxBackScan (Algorithm 2). If not, it will calculate the number of max-forward-extension events by maxbide (Algorithm 3). If there is neither max-forward-extension event nor max-backward-extension event, we output it as a maximum frequent sequence. Otherwise, we extend it and process the maxbide recursively (Algorithm 3, Line 10).

4.2 Fuzzy Membership Vector Construction and Protocol Message Clustering

In order to divide messages into clusters, a metric is required to measure the distance among them. However, the lengths among these messages are quite different, their distances cannot be calculated by Euclidean distance [51], Manhattan distance [52], etc. Nevertheless, the characteristics of messages vary from protocol to protocol, so each protocol may have frequent subsequences that are significantly different from those of others. A protocol message sequence may not completely contain a mined frequent subsequence, but there may be a slight difference on 1–2 bytes, which is consistent with the ambiguity in nature. So this paper defines a fuzzy membership function based on the fuzzy set theory [53] to measure the membership of each maximum frequent sequence to each protocol message, so it can convert protocol messages with different lengths into the fuzzy membership vectors with the same dimension. Then we calculate the distance among these vectors and cluster messages by using the K-means++ [54] algorithm, which separates the cluster centers as much as possible.

Let X be a vector set. Firstly, we set the number of clustering centers to k, then K-means++ selects a fuzzy membership vector as an initial clustering center randomly. Second, it obtains the minimum distance from the remaining vectors to all current cluster centers Dx, x ∈ X. Each vector may be selected as the next clustering center with the possibility of Dx∑x∈XDx, until the number of clustering centers reaches k. Finally, the remaining vectors are clustered according to the distances.

5  Experiment and Analysis

In this section, we carry out the experiment on four protocols to evaluate the performance of our method, including Modbus/TCP, Ethernet/IP, ICMP and DHCP, where Modbus/TCP and Ethernet/IP protocol messages come from DARPA [55] and HAI [56], while ICMP and DHCP messages are obtained by monitoring the network. According to the analysis process shown in Fig. 1, we are able to divide mixed protocol messages into several clusters.

5.1 Evaluation Indexes

Overall, we expect the messages in a cluster to have the same protocol type. Since a cluster represents a type of unknown protocol, each cluster is supposed to contain all of the corresponding protocol messages. To evaluate these factors quantitatively, we introduce the three commonly used indexes: homogeneity is used to measure the closeness of each cluster contains only one type of unknown protocol messages, completeness indicates how much the protocol messages of the same class are assigned to the same cluster, and FMI is the overall evaluation of clustering performance.

The homogeneity and completeness are defined as follows:

homogeneity=1−H(G∣Q)H(G) (5)

completeness=1−H(Q∣G)H(Q) (6)

where H(G∣Q)=−∑g=1|G|∑q=1|Q|ng,qnlog⁡(ng,qn) and H(G)=−∑g=1|G|ngnlog⁡(ngn), ng is the number of messages whose protocol type is g, and ng, q is the number of messages whose protocol type is g but they are mistakenly clustered to the cluster whose protocol type is q. Completeness can be defined symmetrically. Homogeneity is used to measure the purity of each cluster’s protocol type, and the closer homogeneity is to 1, the more consistent the actual protocol type of the messages in the cluster are. Correspondingly, the closer completeness is to 1, the more completely a cluster contains a certain type of protocol message.

FMI is the geometric mean of precision rate and recall rate, which is used to comprehensively evaluate the clustering performance. Let message mi’s type be λi, and mj’s type be λj, they are clustered into λi′ and λj′. We can calculate the FMI of the clustering results:

FMI=a2(a+b)(a+c) (7)

where a, b, and c are calculated as follows:

a=|(mi,mj)|λi=λj, λi′=λj′, i<j| (8)

b=|(mi,mj)|λi=λj, λi′≠λj′, i<j| (9)

c=|(mi,mj)|λi≠λj, λi′=λj′, i<j| (10)

5.2 Experiment Results and Analysis

The numbers of the four types of protocol messages are shown in Table 2. We shuffle the messages and use the proposed method to cluster them, then use the above metrics to evaluate the performance.

We set the minimum support threshold to 0.10, and then perform the mining process and get the results shown in Table 3. Obviously, the support of each sequence in Table 3 exceeds the minimum support threshold.

The number of maximum frequent sequences is different according to the minimum support threshold, as shown in Fig. 2. When the minimum support threshold exceeds 0.45, there is only one maximum frequent sequence, which is inappropriate for protocol clustering. Therefore, we set the range of minimum support threshold to (0, 0.45], with 0.05 increment to cluster protocol messages and evaluate the performance. The higher the FMI, the better the clustering performance. Fig. 3 shows the results of homogeneity, completeness and FMI on different minimum support thresholds. According to the results, we find that the FMI reaches the maximum value of 0.9541 when the minimum support is 0.35. Although its completeness and homogeneity do not reach the maximum, the clustering performance outperforms all other minimum support thresholds.

Figure 2: The number of maximum frequent sequences with different minimum support threshold

Generally speaking, as the minimum support threshold increases, the number of maximum frequent sequences mined decreases, reducing the dimension of fuzzy membership vector, which results in poor clustering performance in homogeneity, completeness and FMI. However, experiments show that this is not the case. Fig. 3 shows that homogeneity, completeness and FMI change erratically. The reason is that some maximum frequent sequences accurately reflect the characteristics of messages, while others do not. When the threshold increases, some sequences are removed. As a result, the clustering performance improves or decades correspondingly. For example, the maximum frequent sequences of 0.30 minimum support threshold contain (0 × 01, 0 × 00) which is not in that of the 0.35 minimum support threshold. However, the performance of the 0.35 minimum support threshold drops dramatically, showing that (0 × 01, 0 × 00) has a positive influence on the clustering results in protocol messages clustering. Therefore, we only focus on when the overall clustering performance reaches the best and its corresponding minimum support threshold. Further research can be conducted to search for a solution to remove unreasonable maximum frequent sequences which have a negative influence on the performance of clustering.

Figure 3: Results of homogeneity, completeness and FMI of different minimum support threshold

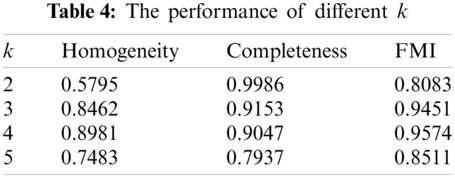
However, we cannot accurately determine the number of types of unknown protocols in advance. So many values of k are set to test our method’s performance. Suppose we have already known that there is more than one type of unknown protocol, which means k > 1, the best performance on the experiment of Table 2 for each k is shown in Table 4. Corresponding to other values, our method performs best when k = 4, which means that the performance of our method is influenced by k.

We also compare our method with the K-means algorithm based on the fixed-length prefix (FL-Kmeans) and Needlem-Wunsch (NW-Kmeans) in homogeneity, completeness and FMI. Due to the differences in the characteristics of different types of protocols, K-means based on fixed-length prefix extracts a certain length of message prefix as the protocol characteristic. Thus, the first 32 bytes of each message are intercepted as the basis of clustering. The K-means based on Needleman–Wunsch uses the idea of bioinformatics sequence alignment to compare protocol messages in pairs, and calculates the number of common bytes as the distance among messages as the basis for clustering. In Fig. 4, we find that FL-Kmeans algorithm’s performance is significantly lower than the other two algorithms. The possible reason is that it loses some key fields by dropping partial byte sequences of each message. The homogeneity of NW-Kmean is 1, reaching the highest level, while FL-Kmeans and our method are 0.7712 and 0.8891. However, the completeness and FMI of our method are higher than the other two methods, which are 0.9050 and 0.9541, indicating the advantage of our method in terms of overall performance.

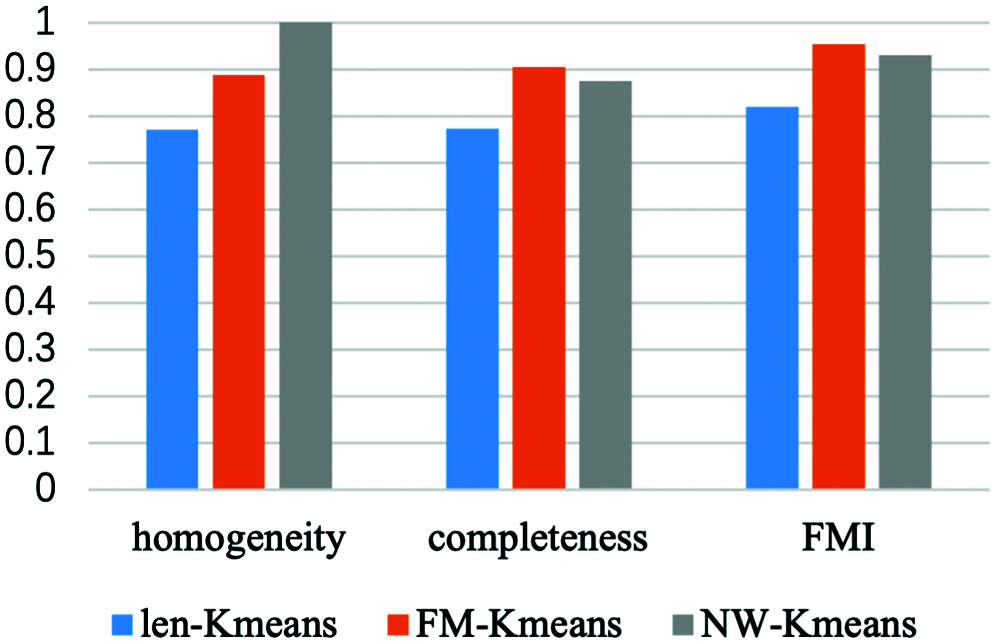
Figure 4: Comparison between FL-Kmeans, NW-Kmeans and this paper’s method on homogeneity, completeness and FMI

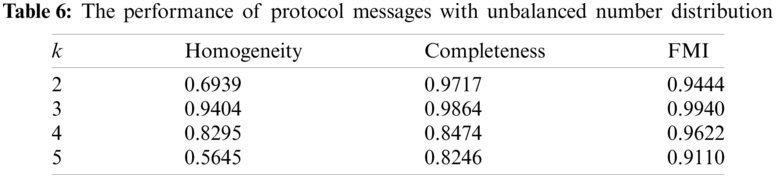
The performance of our method relies on the number of collected protocol messages, if the number of messages for a particular protocol is very small, it is too difficult to extract the characteristics of that protocol. For example, the numbers of collected messages are shown in Table 5, the Modbus/TCP messages far outnumber other types of protocol messages. In this condition, we use different minimum support thresholds to extract the characteristics of these messages, construct the fuzzy membership vectors and divide them into clusters. We also set several values of k to get the best performance. The results are shown in Table 6. Our method performs best when k = 3, with the maximum homogeneity, completeness and FMI, which are 0.9404, 0.9864 and 0.9940. In fact, Ethernet/IP, ICMP and DHCP messages account for only 3.73 percent of the total messages, so some characteristics of them may not be included in the fuzzy membership vectors, resulting in the above results. Although the performance of k = 4 is not the best, whose FMI is 0.0123 lower than that of k = 3, the overall performance is still satisfactory. So our method is also applicable to the condition where the number distribution of messages is unbalanced.

6  Conclusion and Future Work

In this paper, we propose a protocol clustering method based on the fuzzy membership of maximum frequent sequence to distinguish different types of unknown binary protocol messages. We first design the maxBIDE to mine maximum frequent sequences based on the BIDE algorithm, taking the advantage that it does not need to maintain the mined frequent sequences in memory. Then we calculate the fuzzy membership of a message to each maximum frequent sequence by (4) so that we can get the fuzzy membership vectors with the same length, and calculate the distances among these vectors to cluster messages by K-means++, whose inputs are the distances between each pair of messages. Besides, we constantly adjust the algorithm’s parameters to obtain the best evaluation performance. According to the results, we find the FMI reaches the maximum value of 0.9541 when the minSup is 0.35. Compared with FL-Kmeans and NW-Kmeans, although homogeneity and completeness are not the best, the FMI is better than other methods, which are 0.8199 and 0.9307, respectively. Therefore, our method is suitable for distinguishing different binary protocols. Although our method may be influenced by the number of each type of protocol messages, it is also applicable to protocol messages with an unbalanced number distribution. However, the maxBIDE algorithm produces some redundant sequences, which are similar to others, so some efforts can be made to remove these sequences in future work.

Funding Statement: This work was supported by National Natural Science Foundation of China under Grant No. 61872111 and Sichuan Science and Technology Program (No. 2019YFSY0049) and this work was also supported by the “Project for the Development and Application of Safety Testing and Verification Platform for Industrial Robots” of the Ministry of Industry and Information Technology.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Kurose, J. F. (2005). Computer networking: A top-down approach featuring the internet. London: Pearson Education India. [Google Scholar]

 2.  Qiu, J., Tian, Z., Du, C., Zuo, Q., Su, S. et al. (2020). A survey on access control in the age of Internet of Things. IEEE Internet of Things Journal, 7(6), 4682–4696. DOI 10.1109/JIOT.2020.2969326. [Google Scholar] [CrossRef]

 3.  Shafiq, M., Tian, Z., Bashir, A. K., Du, X., Guizani, M. (2020). Corrauc: A malicious bot-IoT traffic detection method in IoT network using machine-learning techniques. IEEE Internet of Things Journal, 8(5), 3242–3254. DOI 10.1109/JIOT.2020.3002255. [Google Scholar] [CrossRef]

 4.  Tian, Z., Luo, C., Qiu, J., Du, X., Guizani, M. (2019). A distributed deep learning system for web attack detection on edge devices. IEEE Transactions on Industrial Informatics, 16(3), 1963–1971. DOI 10.1109/TII.2019.2938778. [Google Scholar] [CrossRef]

 5.  Luo, C., Tan, Z., Min, G., Gan, J., Shi, W. et al. (2020). A novel web attack detection system for internet of things via ensemble classification. IEEE Transactions on Industrial Informatics, 17(8), 5810–5818. DOI 10.1109/TII.2020.3038761. [Google Scholar] [CrossRef]

 6.  Sun, Y., Tian, Z., Li, M., Su, S., Du, X. et al. (2020). Honeypot identification in softwarized industrial cyber-physical systems. IEEE Transactions on Industrial Informatics, 17(8), 5542–5551. DOI 10.1109/TII.2020.3044576. [Google Scholar] [CrossRef]

 7.  Shafiq, M., Tian, Z., Bashir, A. K., Du, X., Guizani, M. (2020). IoT malicious traffic identification using wrapper-based feature selection mechanisms. Computers & Security, 94(4), 101863. DOI 10.1016/j.cose.2020.101863. [Google Scholar] [CrossRef]

 8.  Crosby, M., Nachiappan, Pattanayak, P., Verma, S., Kalyanaraman, V. et al. (2016). Blockchain technology: Beyond bitcoin. Applied Innovation, 2(6–10), 71. [Google Scholar]

 9.  Team, C. C. (2021). Capec-capec-192: Protocol reverse engineering (version 2.6). https://web.archive.org/web/20140725160124/http://capec.mitre.org. [Google Scholar]

10. Sundaram, R. M., Vishnupriya, M. R., Biradar, S. K., Laha, G. S., Reddy, G. A. et al. (2008). Marker assisted introgression of bacterial blight resistance in samba mahsuri, an elite indica rice variety. Euphytica, 160(3), 411–422. DOI 10.1007/s10681-007-9564-6. [Google Scholar] [CrossRef]

11. Yun, X., Wang, Y., Zhang, Y., Zhou, Y. (2015). A semantics-aware approach to the automated network protocol identification. IEEE/ACM Transactions on Networking, 24(1), 583–595. DOI 10.1109/TNET.2014.2381230. [Google Scholar] [CrossRef]

12. Chen, Y., Lan, T., Venkataramani, G. (2019). Exploring effective fuzzing strategies to analyze communication protocols. Proceedings of the 3rd ACM Workshop on Forming an Ecosystem Around Software Transformation, pp. 17–23. London, UK. DOI 10.1145/33. [Google Scholar] [CrossRef]

13. Stute, M., Kreitschmann, D., Hollick, M. (2019). Reverse engineering and evaluating the apple wireless direct link protocol. GetMobile: Mobile Computing and Communications, 23(1), 30–33. DOI 10.1145/3351422.3351432. [Google Scholar] [CrossRef]

14. Ritsch, H., Sneed, H. (1993). Reverse engineering programs via dynamic analysis. Proceedings of Working Conference on Reverse Engineering, pp. 192–201. Baltimore, Maryland: IEEE Computer Society Press. [Google Scholar]

15. Newsome, J., Brumley, D., Franklin, J., Song, D. (2006). Replayer: Automatic protocol replay by binary analysis. Proceedings of the 13th ACM Conference on Computer and Communications Security, pp. 311–321. Alexandria, Virginia, USA. DOI 10.1145/1180405.1180444. [Google Scholar] [CrossRef]

16. Luo, J. Z., Yu, S. Z. (2013). Position-based automatic reverse engineering of network protocols. Journal of Network and Computer Applications, 36(3), 1070–1077. DOI 10.1016/j.jnca.2013.01.013. [Google Scholar] [CrossRef]

17. Krueger, T., Krämer, N., Rieck, K. (2010). ASAP: Automatic semantics-aware analysis of network payloads. International Workshop on Privacy and Security Issues in Data Mining and Machine Learning, pp. 50–63. Springer, Berlin, Heidelberg. DOI 10.1007/978-3-642-19896-0_5. [Google Scholar] [CrossRef]

18. Bossert, G., Guihéry, F., Hiet, G. (2014). Towards automated protocol reverse engineering using semantic information. Proceedings of the 9th ACM Symposium on Information, Computer and Communications Security, pp. 51–62. Kyoto, Japan. DOI 10.1145/2590296.2590346. [Google Scholar] [CrossRef]

19. Cui, W., Kannan, J., Wang, H. J. (2007). Discoverer: Automatic protocol reverse engineering from network traces. USENIX Security Symposium, pp. 1–14. Boston, MA, USA. [Google Scholar]

20. Narayan, J., Shukla, S. K., Clancy, T. C. (2015). A survey of automatic protocol reverse engineering tools. ACM Computing Surveys, 48(3), 1–26. DOI 10.1145/2840724. [Google Scholar] [CrossRef]

21. Duchene, J., Le Guernic, C., Alata, E., Nicomette, V., Kaâniche, M. (2018). State of the art of network protocol reverse engineering tools. Journal of Computer Virology and Hacking Techniques, 14(1), 53–68. DOI 10.1007/s11416-016-0289-8. [Google Scholar] [CrossRef]

22. Kleber, S., Maile, L., Kargl, F. (2018). Survey of protocol reverse engineering algorithms: Decomposition of tools for static traffic analysis. IEEE Communications Surveys & Tutorials, 21(1), 526–561. DOI 10.1109/COMST.2018.2867544. [Google Scholar] [CrossRef]

23. Shafiq, M., Tian, Z., Bashir, A. K., Jolfaei, A., Yu, X. (2020). Data mining and machine learning methods for sustainable smart cities traffic classification: A survey. Sustainable Cities and Society, 60(1), 102177. DOI 10.1016/j.scs.2020.102177. [Google Scholar] [CrossRef]

24. Shafiq, M., Tian, Z., Sun, Y., Du, X., Guizani, M. (2020). Selection of effective machine learning algorithm and bot-IoT attacks traffic identification for Internet of Things in smart city. Future Generation Computer Systems, 107(4), 433–442. DOI 10.1016/j.future.2020.02.017. [Google Scholar] [CrossRef]

25. Sun, F., Wang, S., Zhang, C., Zhang, H. (2019). Unsupervised field segmentation of unknown protocol messages. Computer Communications, 146(4), 121–130. DOI 10.1016/j.comcom.2019.06.013. [Google Scholar] [CrossRef]

26. Li, W., Dou, Z., Qi, L. (2020). Communication protocol classification based on LSTM and DBN. IEEE Access, 8, 91818–91828. DOI 10.1109/ACCESS.2020.2979768. [Google Scholar] [CrossRef]

27. Beddoe, M. A. (2004). Network protocol analysis using bioinformatics algorithms. Toorcon. http://phreakocious.net/PI/. [Google Scholar]

28. Needleman, S. B., Wunsch, C. D. (1970). A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology, 48(3), 443–453. DOI 10.1016/0022-2836(70)90057-4. [Google Scholar] [CrossRef]

29. Sokal, R. R. (1958). A statistical method for evaluating systematic relationships. The University of Kansas Science Bulletin, 38, 1409–1438. [Google Scholar]

30. Sun, R., Yang, B., Peng, L., Chen, Z., Zhang, L. et al. (2010). Traffic classification using probabilistic neural networks. Sixth International Conference on Natural Computation, vol. 4, pp. 1914–1919. Yantai, Shandong, China, IEEE. DOI 10.1109/ICNC.2010.5584648. [Google Scholar] [CrossRef]

31. Shen, F., Ren, X. (2007). Research of P2P traffic identification based on BP neural network. Third International Conference on Intelligent Information Hiding and Multimedia Signal Processing, vol. 2, pp. 75–78. Kaohsiung, Taiwan, IEEE. DOI 10.1109/IIH-MSP.2007.260. [Google Scholar] [CrossRef]

32. Raahemi, B., Kouznetsov, A., Hayajneh, A., Rabinovitch, P. (2008). Classification of peer-to-peer traffic using incremental neural networks (fuzzy ARTMAP). Canadian Conference on Electrical and Computer Engineering, pp. 719–724. Niagara Falls, ON, Canada, IEEE. DOI 10.1109/CCECE.2008.4564629. [Google Scholar] [CrossRef]

33. Sun, F., Wang, S., Zhang, C., Zhang, H. (2020). Clustering of unknown protocol messages based on format comparison. Computer Networks, 179(4), 107296. DOI 10.1016/j.comnet.2020.107296. [Google Scholar] [CrossRef]

34. Lee, D. D., Seung, H. S. (1999). Learning the parts of objects by non-negative matrix factorization. Nature, 401(6755), 788–791. DOI 10.1038/44565. [Google Scholar] [CrossRef]

35. Crocker, D., Overell, P. (1997). Augmented BNF for syntax specifications: ABNF. Technical report, RFC 4234. [Google Scholar]

36. Ester, M., Kriegel, H.-P., Sander, J., Xu, X. (1996). A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, vol. 96, pp. 226–231. Portland, Oregon. [Google Scholar]

37. Bezdek, J. C., Pal, N. R. (1995). Cluster validation with generalized dunn’s indices. Proceedings of Second New Zealand International Two-Stream Conference on Artificial Neural Networks and Expert Systems, pp. 190–193. Dunedin, New Zealand, IEEE. DOI 10.1109/ANNES.1995.499469. [Google Scholar] [CrossRef]

38. Wang, Y., Yun, X., Shafiq, M. Z., Wang, L., Liu, A. X. et al. (2012). A semantics aware approach to automated reverse engineering unknown protocols. 2012 20th IEEE International Conference on Network Protocols, pp. 1–10. Austin, TX, USA, IEEE. DOI 10.1109/ICNP.2012.6459963. [Google Scholar] [CrossRef]

39. Slonim, N., Tishby, N. (2000). Document clustering using word clusters via the information bottleneck method. Proceedings of the 23rd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, pp. 208–215. Athens, Greece. DOI 10.1145/345508.345578. [Google Scholar] [CrossRef]

40. Cai, J., Luo, J. Z., Lei, F. (2016). Analyzing network protocols of application layer using hidden semi-markov model. Mathematical Problems in Engineering, 2016, 1–14. DOI 10.1155/2016/9161723. [Google Scholar] [CrossRef]

41. Yu, S. Z. (2010). Hidden semi-markov models. Artificial Intelligence, 174(2), 215–243. DOI 10.1016/j.artint.2009.11.011. [Google Scholar] [CrossRef]

42. Frey, B. J., Dueck, D. (2007). Clustering by passing messages between data points. Science, 315(5814), 972–976. DOI 10.1126/science.1136800. [Google Scholar] [CrossRef]

43. Tao, S., Yu, H., Li, Q. (2016). Bit-oriented format extraction approach for automatic binary protocol reverse engineering. IET Communications, 10(6), 709–716. DOI 10.1049/iet-com.2015.0797. [Google Scholar] [CrossRef]

44. Rousseeuw, P. J. (1987). Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics, 20, 53–65. DOI 10.1016/0377-0427(87)90125-7. [Google Scholar] [CrossRef]

45. Wang, J., Han, J. (2004). Bide: Efficient mining of frequent closed sequences. Proceedings of 20th International Conference on Data Engineering, pp. 79–90. Boston, MA, USA, IEEE. DOI 10.1109/ICDE.2004.1319986. [Google Scholar] [CrossRef]

46. Fowlkes, E. B., Mallows, C. L. (1983). A method for comparing two hierarchical clusterings. Journal of the American Statistical Association, 78(383), 553–569. DOI 10.1080/01621459.1983.10478008. [Google Scholar] [CrossRef]

47. Fang, G., Wu, Y., Li, M., Chen, J. (2015). An efficient algorithm for mining frequent closed itemsets. Informatica, 39(1). http://informatica.si/index.php/informatica/article/view/754. [Google Scholar]

48. Zaki, M. J., Hsiao, C. J. (2002). Charm: An efficient algorithm for closed itemset mining. Proceedings of the SIAM International Conference on Data Mining, pp. 457–473. Arlington, VA, USA, SIAM. DOI 10.1137/1.9781611972726.27. [Google Scholar] [CrossRef]

49. Yan, X., Han, J., Afshar, R. (2003). Clospan: Mining: Closed sequential patterns in large datasets. Proceedings of the 2003 SIAM International Conference on Data Mining, pp. 166–177. San Francisco, CA, USA, SIAM. DOI 10.1137/1.9781611972733.15. [Google Scholar] [CrossRef]

50. Pei, J., Han, J., Mortazavi-Asl, B., Wang, J., Pinto, H. et al. (2004). Mining sequential patterns by pattern-growth: The prefixspan approach. IEEE Transactions on Knowledge and Data Engineering, 16(11), 1424–1440. DOI 10.1109/TKDE.2004.77. [Google Scholar] [CrossRef]

51. Danielsson, P. E. (1980). Euclidean distance mapping. Computer Graphics and Image Processing, 14(3), 227–248. DOI 10.1016/0146-664X(80)90054-4. [Google Scholar] [CrossRef]

52. de Maesschalck, R., Jouan-Rimbaud, D., Massart, D. L. (2000). The mahalanobis distance. Chemometrics and Intelligent Laboratory Systems, 50(1), 1–18. DOI 10.1016/S0169-7439(99)00047-7. [Google Scholar] [CrossRef]

53. Klir, G., Yuan, B. (1995). Fuzzy sets and fuzzy logic, vol. 4. New Jersey: Prentice Hall. [Google Scholar]

54. Arthur, D., Vassilvitskii, S. (2006). k-means++ The advantages of careful seeding. Technical Report. Stanford. [Google Scholar]

55. Clark, D. (1988). The design philosophy of the darpa internet protocols. Proceedings on Communications Architectures and Protocols, pp. 106–114. Cathedral Hill Hotel, San Francisco, CA, USA. DOI 10.1145/52324.52336. [Google Scholar] [CrossRef]

56. Shin, H. K., Lee, W., Yun, J. H., Kim, H. (2020). {HAI} 1.0: Hil-based augmented {ICS} security dataset. 13th {USENIX} Workshop on Cyber Security Experimentation and Test, pp. 1–5. Boston, MA, USA. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.