Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.018348

ARTICLE

Similarity Analytic Solutions of a 3D-Fractal Nanofluid Uncoupled System Optimized by a Fractal Symmetric Tangent Function

Rabha W. Ibrahim1,*, Ahmed M. Ajaj2, Nadia M.G. Al-Saidi3 and Dumitru Balean4,5,6

1Institute of Electrical and Electronics Engineers, Kuala Lumpur, Malaysia
2Department of Islamic Finance and Banking, College of Islamic Sciences, Iraqi University, Adhamiyah, Iraq
3Department of Applied Sciences, University of Technology, Baghdad, Iraq
4Department of Mathematics, Cankaya University, Ankara, Turkey
5Institute of Space Sciences, Magurele-Bucharest, Romania
6Department of Medical Research, China Medical University, Taichung, Taiwan
*Corresponding Author: Rabha W. Ibrahim. Email: rabhaibrahim@yahoo.com
Received: 18 July 2021; Accepted: 30 August 2021

1  Introduction

Similarity solution is an extension of the symmetric solution of dynamic processing systems, where its stability introduces the stability of the dynamic processing of any system. Maschler et al. [1] consider stability of the dynamic systems with applications in the game theory for the first time in 1967. Sakamoto et al. [2] introduced a dynamic system design of social struggle that chains approach variation system and game theory. Later, the stability of the game theory is studied using different approaches and different applications [3]. Bogdan et al. [4] investigate fractal dynamic game in 2011. Chaos game theory and its application is studied recently by Jampour et al. [5], while Li et al. [6] utilized the fractal in a case study for the game theory. Recent modification of this study including a symmetric analysis can be located in [7,8].

The theory of fractal (local fractional calculus), which was first offered by Kolwankar et al. [9] for the usual fractional calculus of Riemann-Liouville operators. It was utilized to deal with non-differentiable structures appearing in both science and engineering. Numerous other opinions and facts of fractal calculus were offered, such as the geometric fractal. Yang et al. [10] formulated what is called the cantor fractal in the logical extensions of the definitions to the subject of local derivative on fractals. Different studies and applications are indicated in the literature.

SAS is a type of solution which is similar to itself whenever the independent and dependent variables are accordingly sized. SAS approaches have been used in numerous engineering categories, particularly in the boundary layer flows. Because of its suitable computational performance and accuracy, there are restricted search in the field of fluid flow and heat transfer in absorbent media such as thermal sinks but the usage of this method is common in numerous other problems [11]. In this place, by utilizing SAS, flow and heat transfer of nanofluid have been examined in various geometries such as flow between two flat platters in revolving system, among clutching platters [12] and among parallel platters in the incidence of a magnetic field in view of thermal radiation properties [13,14]. Liu et al. [15] for special forms of shape presented the chaotic of nanofluid, for the first time. For this shape, Beebe et al. [16] improved particles of fluid pass in chaotic paths. Definitely, chaotic conduct of nanofluid can be shaped using some types of geometrical processes. Recently, Ibrahim et al. [17] discussed SAS for a special type of a set of differential equations using a multibrot fractal set.

The viewpoint of SAS including univalent solution (one-one) in the open unit disk deals with the preparation of functions, agreeing with the control and the uniqueness of the geometrical and analytic possessions. To dominate the dynamic process, we employ the subordination and majorization concepts, where the game theory provides the main conditions to get a stability. Recently, this concept is applied in different real life examples (see [18,19]). Based on the actions of the subordination and majorization concepts, we develop a new method to establish the SAS of the 3D-FNFS in the open unit disk. The boundary conditions are suggested on the boundary of the open unit disk. We have formulated conditions on the suggested FNFS subordinating by a chaotic function to obtain a SAS controlled by the same function.

2  Method

The geometry in this study is about the analysis of 2D-flow, which is called 2D-flow when the velocity sets on a fixed plane and controls not by the coordinate plane; and thermal transfer in a unit disk (or even in a cylinder). Fig. 1 indicates the preserving fluid arrives into the thermal descend in T in warm disk and uniform velocity V. Since the problem is 2D-symmetric, the calculation is suggested in the z−plane as follows: V(z)=υ1+iυ2,T(z)=τ1+iτ2 and Ξ(z)=χ1+iχ2, where z∈U:={z∈C:|z|<1}.

Figure 1: The geometry of the problem: 3-D system and boundary conditions

2.1 Fractal Definition

For ε>0 and |χ−χ0|<δ, the limit

f(α)(χ):=ð(α)f(χ)=limχ→χ0Γ(α+1)(f(χ)−f(χ0))(χ−χ0)α, f∈Cα(the fractal set) is finite and exists. Note that

The 2D-fractal derivative is considered for a complex function f(z=x+iy) defining on a fractal set of Cα(U), as follows ð(α)f(z)=limz→z0Γ(α+1)(f(z)−f(z0))(z−z0)α,z∈U.

For example f(zα)=zαn, has a fractal derivative ð(α)znα=(Γ(αn+1)Γ(α(n−1)+1))zα(n−1).

Therefore, in general for an analytic function f in a complex domain, we have the structure of fractal derivative as follows [20]-Theorem 9: ð(α)f(z)=∑n=1∞(Φn(a,b)Γ(α(n−1)+1))zα(n−1), where f is defined in some fractal set. In our study, we shall use a fractal function defining by the fractal sine function sinα⁡(zα)=∑n=0∞(−1)nz(2n+1)αΓ(1+(2n+1)α),α∈(0,1) and fractal cosine function cosα⁡(zα)=∑n=0∞(−1)nz2nαΓ(1+2nα),α∈(0,1) as follows:

sinα⁡(zα)1+cosα⁡(zα)=∑n=0∞−iδn((−2i)1+n(−η(n))2Γ(nα+1))zαn:=∑n=0∞Θnzαn≈tanα(zα2), (1)

where δn and η(n) indicate the delta and Dirichlet eta function respectively. It is clear that

|Θn|≈2nη(n)Γ(nα+1), where η(0)=12,η(1)=ln⁡(2),η(2)=π212,η(3)=3ζ(3)4=3.64,η(4)=7π4720,

2.2 Complex Fractal Uncoupled System

In order to study SAS of any nanofluid system, we introduce the similarity variables, which are formulated in the following chaotic system for the fractal function tan. The investigated issue can be recognized as a stagnation point flow. Thus, for solving the governing equations by SAS, similarity variables and functions are followed as in [21]. As a conclusion, we have the following structure:

z2V′′′(z)+℘zV′′(z)+V′(z)=tan⁡(ω1(z))z2T′′(z)+♭zT′(z)=tan⁡(ω2(z))z2Ξ′′(z)+lzΞ′(z)=tan⁡(ω3(z)), (2)

where ℘,♭,l are perturbation positive constants. Special cases for real variables of System (2) can be found in [14]. Our aim is to construct a set of conditions on the parameters of System (2). Now by using the reduced derivative ℏ(z)=V′(z)1+ϵ|V′(z)|,

System becomes

z2ℏ′′(z)+℘zℏ′(z)+ℏ(z)=tan⁡(ω1(z))∁[5pt]z2T′′(z)+♭zT′(z)=tan⁡(ω2(z))[5pt]z2Ξ′′(z)+lzΞ′(z)=tan⁡(ω3(z)), (3)

where C=1+ϵ|V′(z)|,z∈U,ϵ∈[0,1].

We selected the tangent fractal function because, in general, the tangent family provides a complete classification of their stable behavior (see Fig. 2) L={℧λ(z):=λtan⁡(z)=λ(z+z33+2z515+O(z6)),λ∈C∖{0}}.

In addition, it can be described by the hyperbolic mechanisms and gave an explanation their placement in the parameter plane. Precisely, the symmetry of the maps with respect to 0 implies that the stable and unstable sets are symmetric with respect to the origin, satisfying ℧λ(−z)=−℧λ(z),℧λ′(z)=℧λ′(−z).

We proceed to generalize System by using the fractal difference operator. For ϵ→0, the fractal system can be formulated as follows:

(z2α)ℏ(2α)(zα)+℘zαℏ(α)(zα)+ℏ(zα)=tanα⁡(zα2)(z2β)T(2β)(zβ)+♭zβT(β)(zβ)=tanβ⁡(zβ2)(z2γ)Ξ(2γ)(zγ)+lzγΞ(γ)(zγ)=tanγ⁡(zγ2), (4)

where α,β,γ∈(0,1] and ℘,♭,l are real constants. We suppose that ℏ(0)=T(0)=Ξ(0)=0, where 0 is the origin of U such that

ℏ(zα)=∑n=0∞hnznα,T(zβ)=∑n=0∞τnznβ,Ξ(zγ)=∑n=0∞ςnznγ. (5)

In view of Eq. (5), we have ℏ(α)(zα)=∑n=1∞hnΓ(αn+1)Γ(α(n−1)+1)zα(n−1), and

ℏ(2α)(zα)=∑n=2∞hnΓ(2αn+1)Γ(2α(n−1)+1)zα(n−2). Similarly for T and Ξ.

We aim to find SAS at ∂U bounded by the fractal tangent function. To reach our aim, we need more information.

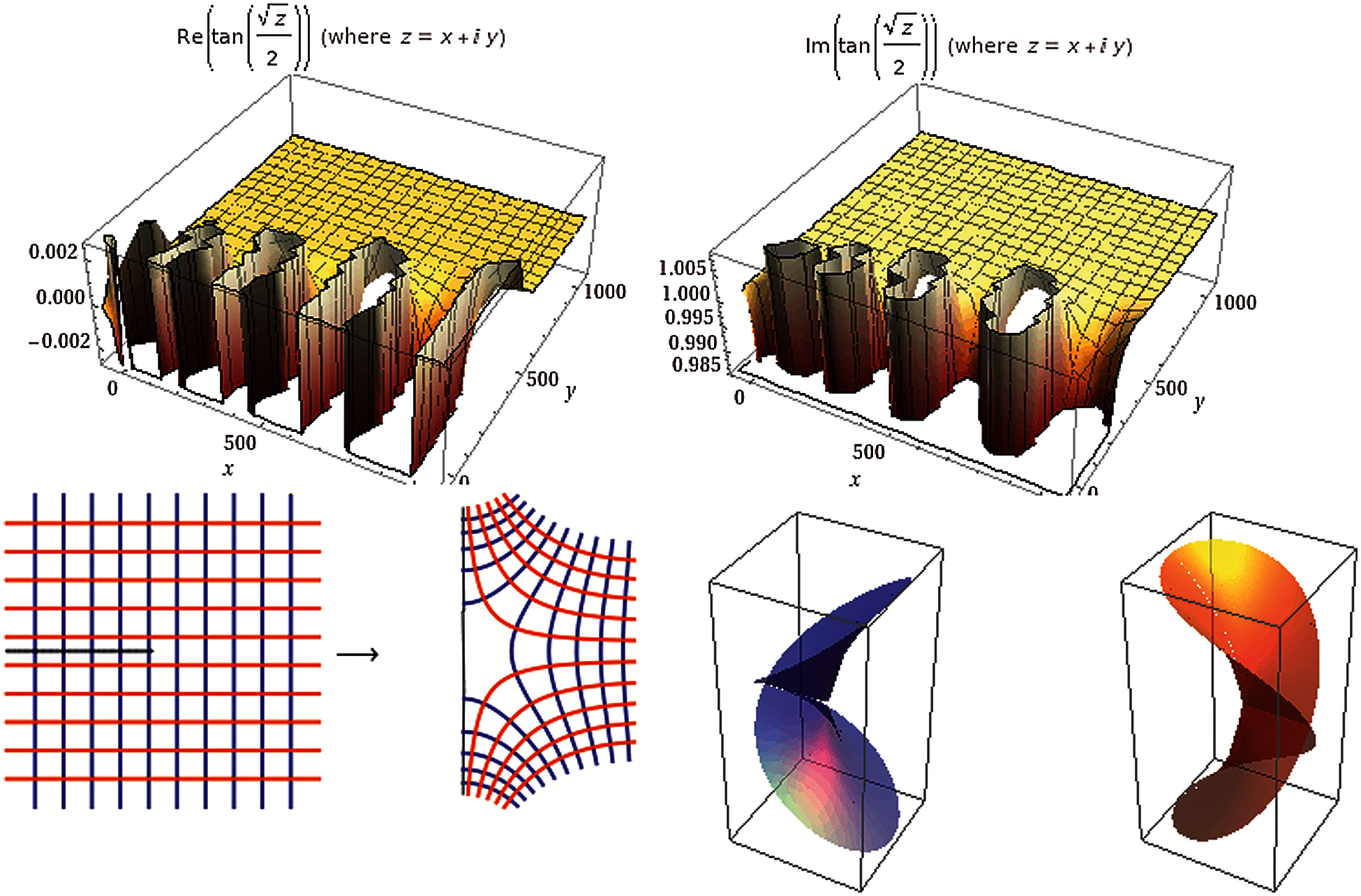
Figure 2: The plot of tan(z0.5/2)

2.3 Geometric Concepts

We request the following definition [22–24]:

Definition 1. Two analytic functions f and g in U, the function f(z)=∑n=0∞ϕnzn is majored by g=∑n=0∞ψnzn (f≪g) if there is an analytic function ϖ,|ϖ|<1 such that f(z)=ϖ(z)g(z). Note that f≪g if and only if |ϕn|≤|ψn|,∀n. If f(z)=g(ϖ(z)) then f is subordinated by g (f≺g).

Note that, there is a deep relation between these two concepts. It is well known, under some conditions on f and g, we have the information [22] f≺g⇔f≪g.

We aim to find the conditions on System (4), to get SAS for the inequalities

ℏ(z)≪tanα⁡(zα2),T(z)≪tanβ⁡(zβ2),Ξ(z)≪tanγ⁡(zγ2). (6)

In addition tan⁡(ς),ς∈U is univalent in the disk |z|<π/2 and convex in |z|<0.86033 (see [24]). Recently, this concept is used in different applications of fractional calculus and fractal [25]. Note that, in view of majorization and subordination theory, it is clear that tan⁡(z) can be majorized and then subordinated using the extreme convex function [22]-Corollary 1

tan⁡(z)≺z1−z,|z|<r,r∈(0.28,2−1). (7)

3  Results

In this section, we construct the analytic method to investigate the SAS of System (4), by using the majorization method.

3.1 Existence of Similarity Solutions

We have the following result:

Proposition 1. Consider System (4), (5). If the coefficients bound, satisfy the following inequalities:

then

ℏ(z)≪tanα⁡(zα2),T(z)≪tanβ⁡(zβ2),Ξ(z)≪tanγ⁡(zγ2). (8)

Proof. By using the series method of a fractal constructions of the functions ℏ,T and Ξ, in System (4) we have

A comparison implies

But in view of the first condition of the theorem, we have

which means that |hn|≤2nη(n)Γ(nα+1). Thus, by the definition of a majorization, we have ℏ(z)≪tanα⁡(zα2).

Now, we proceed to determine the upper bound of τn.

Consequently, we obtain |τn|≤2nη(n)(Γ(nβ+1)Γ(2βn+1)Γ(2β(n−1)+1)+♭Γ(nβ+1)Γ(βn+1)Γ(β(n−1)+1)).

By the second condition, we have

which leads to |τn|≤2nη(n)Γ(nβ+1)⇒T(z)≪tanβ⁡(zβ2).

Finally, a computation implies that |ςn|≤2nη(n)(Γ(nγ+1)Γ(2γn+1)Γ(2γ(n−1)+1)+lΓ(nγ+1)Γ(γn+1)Γ(γ(n−1)+1)).

The last condition of the theorem implies that

which confirms that |ςn|≤2nη(n)Γ(nγ+1)⇒Ξ(z)≪tanγ⁡(zγ2).

As a conclusion of the result, we obtain the desired inequalities ℏ(z)≪tanα⁡(zα2),T(z)≪tanβ⁡(zβ2),Ξ(z)≪tanγ⁡(zγ2).

Corollary 2. Let the conditions of Proposition 1 hold. Then the solution of Eqs. (4), (5) is convex satisfying ℏ′(z)≪1(1−z)2,T′(z)≪1(1−z)2,Ξ′(z)≪1(1−z)2,z∈U.

Proof. In view of Proposition 1, we have the majorization inequalities (8). But, for some α,β,γ∈(0,1) yields tanα⁡(zα)≺z1−z,tanα⁡(zβ)≺z1−z,tanα⁡(zγ)≺z1−z,(|z|<r,r∈(0.28,2−1),z1−z∈C), where C is the class of convex univalent functions in U. This implies that ℏ(z)≺z1−z,T(z)≺z1−z,Ξ(z)≺z1−z. Thus, in view of [22]-Theorem 3, we obtain ℏ′(z)≪(z1−z)′,T′(z)≪(z1−z)′,Ξ′(z)≪(z1−z)′, where (z1−z)′=1(1−z)2.

3.2 Evaluation of Solutions

The essential objective of the similar solutions is to exploit them from the game theory perspective. Moreover, due to the confidence, these solutions may correct their approaches in changing the variables and the parameters of the system. Therefore, the relationship with these variables is not infinitely considerable. On the other hand, throughout each obtaining cycle, these variables may regulate their schemes (or occupation performance) to maximize the solution in order to make dominated information periodically. Thus, in order to describe the phenomenon of similarity solutions among the variables of the system, an evolutionary game model is established in the green attaining relationship [26].

Proposition 3. The replicator dynamic system of (4) cab be formulated by

(z2α)ℏj(2α)(zα)+℘zαℏj(α)(zα)+ℏj(zα)=tanα⁡(zα2)(z2β)Tj(2β)(zβ)+♭zβTj(β)(zβ)=tanβ⁡(zβ2)(z2γ)Ξj(2γ)(zγ)+lzγΞj(γ)(zγ)=tanγ⁡(zγ2),j∈N. (9)

Then the origin is the stable fixed and equilibrium point in the open unit disk.

Proof. Since the only zero of the function tanα⁡(zα2)=∑n=0∞Θnzαn,z∈U is z=0, then in view of the majorization Proposition 1, we obtain the desired assertion. The stability comes from the convergence solutions (ℏ(z),T(z),Ξ(z)) to (tanα⁡(zα2),tanβ(zβ2),tanγ(zγ2)).

4  Discussion

In this section, we illustrate some special cases of System (4) to discuss its SAS. Similarity solution is very important in fractal studies, not only to provide a nice geometry of the solution, but also to study the behaviors in view of stability, oscillation and other important properties. Proposition 1 indicates a new method to investigate the SAS of a fractal system in a complex domain. We showed that whenever the system approximates to the fractal function (tanα(zα/2,tanβ(zβ/2,tanγ(zγ/2)), the SAS does also approximate.

•   Let ℘=♭=l=1 and α,β,γ=1, we have the following SAS:

•   Let ℘=♭=l=1 and α,β,γ=0.5, we have the following SAS:

•   Let ℘=1,♭=2,l=3 and α,β,γ=0.5, we have the following SAS:

•   Let ℘=1,♭=2,l=3 and α=0.5,β=0.75,γ=0.25, we have the following SAS:

where L(ℏ′,ℏ,z) is the Lagrangian. Note that the conditions of Proposition 1 are valid for some n≥1.

5  Conclusion

In this study, we introduced a new approach of similarity analytic solution (SAS) for a class of nanofluid systems dominated by the surface of the open unit disk. The outcomes presented that the solution of the system can be bounded by a fractal tangent function. These functions are solutions of the Lagrange equation and are computed through required performed flow conditions. We further demarcated the fluid flow formulated by a unique source and hypothesis a univalent function (one-one conformal function), so that the image of a source is also a source for a specific complex potential. The outcomes were selected via plot simulations, clarifying a flow’s absorption from a point (source) with straight streamlines, all essentially considered as circular appeared far from the center point.

Remark

• The optimal solution of System (4) satisfies the relation ℏ(z)≪tanα⁡(zα2),T(z)≪tanβ⁡(zβ2),Ξ(z)≪tanγ⁡(zγ2) .

which means, that (ℏ(z),T(z),Ξ(z)) is bounded by the tangent function. Therefore, we have 3D-complex system (ℏ(z),T(z),Ξ(z)) and 3D-parametric real system (α, β, γ). The efficiency of any dynamic system is measured as a ratio of the output and the input information. Since the tangent function optimizes the System (4), that is the output is converge to this function and hence it will be stable around the equilibrium point at the origin. Comparing with many works in this direction and by using the traditional analytical techniques, the suggested method, by using geometric function theory is more robust and stable with less mathematical computations. Fig. 3 shows the 3D-solution of System (4) for different fractal powers.

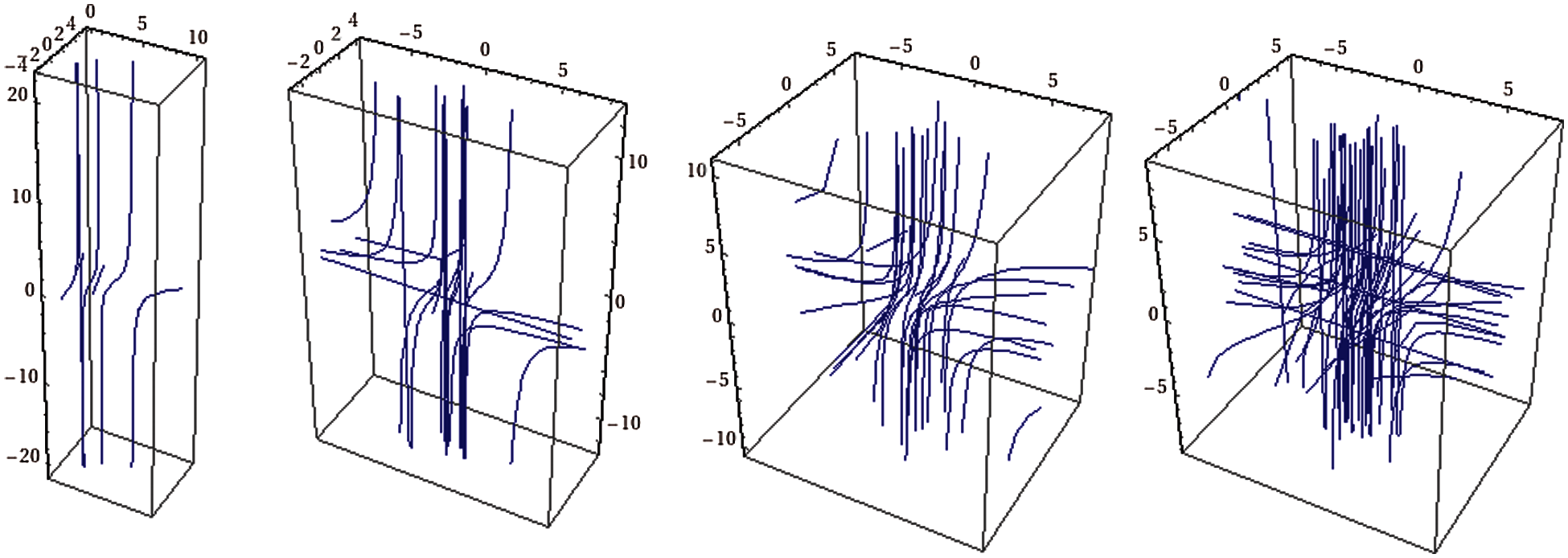
Figure 3: The conduct of solutions of System (4), for (α,β,γ), such that from the left respectively, (0.1,0.2,0.3),(0.3,0.2,0.4),(0.5,0.4,0.6),(0.4,0.3,0.5)

Acknowledgement: The authors would like to thanks the editor office for the deep advice to improve our work.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Maschler, M., Peleg, B. (1976). Stable sets and stable points of set-valued dynamic systems with applications to game theory. SIAM Journal on Control and Optimization, 14(6), 985–995. DOI 10.1137/0314062. [Google Scholar] [CrossRef]

 2.  Sakamoto, M., Hagihara, Y., Sugiman, T. (2004). A dynamic system model of social conflict that combines attitude change model and game theory. Asian Journal of Social Psychology, 7(3), 263–284. DOI 10.1111/j.1467-839X.2004.00151.x. [Google Scholar] [CrossRef]

 3.  Basar, T., Georges, Z. (2018). Handbook of dynamic game theory. New York, USA: Springer International Publishing. [Google Scholar]

 4.  Bogdan, P., Marculescu, R. (2011). A fractional calculus approach to modeling fractal dynamic games. 50th IEEE Conference on Decision and Control and European Control Conference, pp. 255–260. Orlando, FL, USA. [Google Scholar]

 5.  Jampour, M., Naserasadi, A. (2019). Chaos game theory and its application for offline signature identification. IET Biometrics, 8(5), 316–324. DOI 10.1049/iet-bmt.2018.5188. [Google Scholar] [CrossRef]

 6.  Li, S., Liao, L., Chang, S. H. (2020). A game model of supply chain management based on fractal analysis of time series. Fractals–An Interdisciplinary Journal on the Complex Geometry of Nature, 28(8), 2040023. DOI 10.1142/S0218348X2040023X. [Google Scholar] [CrossRef]

 7.  Peng, Y., Xiao, Y., Lu, Q., Wu, X., Zhao, Y. (2020). Chaotic dynamics in cournot duopoly model with bounded rationality based on relative profit delegation maximization. Physica A: Statistical Mechanics and its Applications, 560, 125174. DOI 10.1016/j.physa.2020.125174. [Google Scholar] [CrossRef]

 8.  Cao, L., Wu, B. (2021). Eco-evolutionary dynamics with payoff-dependent environmental feedback. Chaos, Solitons & Fractals, 150(suppl_3), 111088. DOI 10.1016/j.chaos.2021.111088. [Google Scholar] [CrossRef]

 9.  Kolwankar, K. M., Gangal, A. D. (1996). Fractional differentiability of nowhere differentiable functions and dimensions. Chaos: An Interdisciplinary Journal of Nonlinear Science, 6(4), 505–513. DOI 10.1063/1.166197. [Google Scholar] [CrossRef]

10. Yang, X. J., Baleanu, D., Srivastava, H. M. (2015). Local fractional integral transforms and their applications. USA: Academic Press. [Google Scholar]

11. Al-Saidi, N. M., Ali, A. H. (2017). Towards enhancing of fractal image compression performance via block complexity. Annual Conference on New Trends in Information & Communications Technology Applications, pp. 246–251. Baghdad, Iraq. [Google Scholar]

12. Al-Saidi, N. M., Al-Bundi, S. S., Al-Jawari, N. J. (2018). A hybrid of fractal image coding and fractal dimension for an efficient retrieval method. Computational and Applied Mathematics, 37(2), 996–1011. DOI 10.1007/s40314-016-0378-9. [Google Scholar] [CrossRef]

13. Siavashi, M., Rasam, H., Izadi, A. (2019). Similarity solution of air and nanofluid impingement cooling of a cylindrical porous heat sink. Journal of Thermal Analysis and Calorimetry, 135(2), 1399–1415. DOI 10.1007/s10973-018-7540-0. [Google Scholar] [CrossRef]

14. Naqvi, S. M. R. S., Muhammad, T., Saleem, S., Kim, H. M. (2020). Significance of non-uniform heat generation/absorption in hydromagnetic flow of nanofluid due to stretching/shrinking disk. Physica A: Statistical Mechanics and its Applications, 553, 123970. DOI 10.1016/j.physa.2019.123970. [Google Scholar] [CrossRef]

15. Liu, R. H., Stremler, M. A., Sharp, K. V., Olsen, M. G., Santiago, J. G. et al. (2000). Passive mixing in a three-dimensional serpentine microchannel. Journal of Microelectromechanical Systems, 9(2), 190–197. DOI 10.1109/84.846699. [Google Scholar] [CrossRef]

16. Beebe, D. J., Adrian, R. J., Olsen, M. G., Stremler, M. A., Aref, H. et al. (2001). Passive mixing in microchannels: Fabrication and flow experiments. Mécanique & Industries, 2(4), 343–348. DOI 10.1016/S1296-2139(01)01114-9. [Google Scholar] [CrossRef]

17. Ibrahim, R. W., Baleanu, D. (2021). Analytic solution of the langevin differential equations dominated by a multibrot fractal set. Fractal and Fractional, 5(2), 50. DOI 10.3390/fractalfract5020050. [Google Scholar] [CrossRef]

18. Miller, S. S., Mocanu, P. T. (2000). Differential subordinations: Theory and applications. USA: CRC Press. [Google Scholar]

19. Ibrahim, R. W., Baleanu, D. (2021). On quantum hybrid fractional conformable differential and integral operators in a complex domain. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas, 115, 1–13. DOI 10.1007/s13398-020-00982-5. [Google Scholar] [CrossRef]

20. Carlo, C., Srivastava, H. M., Yang, X. J. (2015). Fractional dynamics. Berlin/Boston: Walter de Gruyter GmbH. [Google Scholar]

21. Sepasgozar, S., Faraji, M., Valipour, P. (2017). Application of differential transformation method (DTM) for heat and mass transfer in a porous channel. Propulsion and Power Research, 6(1), 41–48. DOI 10.1016/j.jppr.2017.01.001. [Google Scholar] [CrossRef]

22. Campbell, D. M. (1973). Majorization-subordination theorems for locally univalent functions. II. Canadian Journal of Mathematics, 25(2), 420–425. DOI 10.4153/CJM-1973-042-6. [Google Scholar] [CrossRef]

23. MacGregor, T. H. (1967). Majorization by univalent functions. Duke Mathematical Journal, 34(1), 95–102. DOI 10.1215/S0012-7094-67-03411-4. [Google Scholar] [CrossRef]

24. Goodman, A. W. (1979). An invitation on the study of univalent and multivalent functions. International Journal of Mathematics and Mathematical Sciences, 2(2), 163–186. DOI 10.1155/S016117127900017X. [Google Scholar] [CrossRef]

25. Ibrahim, R. W., Baleanu, D. (2021). Geometric behavior of a class of algebraic differential equations in a complex domain using a majorization concept. AIMS Mathematics, 6(1), 806–820. DOI 10.3934/math.2021049. [Google Scholar] [CrossRef]

26. Ji, P., Ma, X., Li, G. (2015). Developing green purchasing relationships for the manufacturing industry: An evolutionary game theory perspective. International Journal of Production Economics, 166(12), 155–162. DOI 10.1016/j.ijpe.2014.10.009. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.