Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2021.017310

ARTICLE

A Chaos Sparrow Search Algorithm with Logarithmic Spiral and Adaptive Step for Engineering Problems

Andi Tang, Huan Zhou*, Tong Han and Lei Xie

Aeronautics Engineering College, Air Force Engineering University, Xi'an, 710038, China
*Corresponding Author: Huan Zhou. Email: kgy_zhouh@163.com
Received: 30 April 2021; Accepted: 15 July 2021

1  Introduction

The optimization problem is a common real-world problem that requires seeking the maximum or minimum value of a given objective function and they can be classified as single-objective optimization problems and multi-objective optimization problems [1,2]. There are two types of methods commonly used for optimization problems. One type is the traditional gradient-based approach. One is the metaheuristic algorithm [3,4]. Generally speaking, the traditional gradient-based methods often encounter difficulties in solving complex engineering problems [5]. The existing research shows that the traditional mathematical or numerical programming methods are difficult to deal with many non-differentiable and discontinuous problems efficiently [6]. In order to overcome these shortcomings, a kind of metaheuristic optimization algorithm is proposed and used to solve global optimization problems. Metaheuristic algorithms are usually divided into three categories: evolutionary algorithms, physics-based algorithms, and swarm-based algorithms. Evolutionary algorithm is a kind of algorithm inspired by the mechanism of natural evolution. Genetic Algorithm (GA) [7] based on Darwin's theory of survival of the fittest is one of the most famous evolutionary algorithms. There are also some other evolutionary algorithms such as Evolution Strategy (ES) [8], Evolutionary Programming (EP) [9], Differential Evolution (DE) [10] and Biogeography Based Optimization (BBO) [11]. Physical-based algorithms are based on physical concepts to establish optimization models, such as Simulated Annealing (SA) [12], Gravity Search Algorithm (GSA) [13], Nuclear Reaction Optimization (NRO) [14], and Black Hole Algorithm (BHA) [15]. Swarm-based algorithms based on the characteristics of group behavior are the focus of research in recent years. These algorithms establish optimization models by imitating the behavior of gregarious animals [16]. Particle Swarm Optimization (PSO) [17] is the most well-known swarm intelligence optimization algorithm among these algorithms and has been applied to many fields. Other swarm intelligence optimization algorithms include Ant Colony Optimization (ACO) [18], Monarch Butterfly Optimization (MBO) [19], Moth Search Algorithm (MSA) [20], and Harris Hawk Optimization (HHO) [21]. In addition to the algorithms mentioned above, there are more algorithms proposed, such as Earthworm Optimisation Algorithm (EOA) [22], Elephant Herding Optimization (EHO) [23] and Slime Mould Algorithm (SMA) [24]. Besides proposing new algorithms to solve the optimization problems, more researchers also solve them by modifying existing algorithms. Gao et al. [25] propose a new selection mechanism to improve the DE performance and apply it to solve the job-shop scheduling problem. To enhance the population diversity of the equilibrium optimizer, Tang et al. [26] suggested the utilization of distribution estimation strategies and selection pools and perform well in solving the UAV path planning problem. Chen et al. [27] enhanced the performance of neighborhood search algorithm by introducing ad hoc destroy/repair heuristics and a periodic perturbation procedure, with successful solution of the dynamic vehicle routing problem Wang et al. [28] proposed a new newsvendor model and apply a histogram-based distribution estimation algorithm to solve it. However, the no free lunch theory states that no single algorithm can solve all problems well [29]. This motivates us to continuously propose and improve algorithms to be applicable to more problems. SSA is a new swarm-based optimization algorithm based on sparrow foraging principle proposed by XUE in 2020 [30], which has the advantages of simple structure and few control parameters. In SSA, each sparrow finds the best position by looking for food and anti-predation behavior.

However, similar to other metaheuristic algorithms, there are also problems such as reduction of population diversity and early convergence in the late iterations when solving complex optimization problems.

Based on the discussion above, a chaos sparrow search algorithm based on logarithmic spiral search strategy and adaptive step size strategy (CLSSA) is proposed in this paper, which employs three strategies to enhance the global search ability of SSA. In CLSSA, different chaotic maps are used to change the random values of the parameters in the SSA. Logarithmic spiral search strategy is used to expand the search space and enhance population diversity. Two adaptive step size strategies are applied to adjust the development and exploration ability of the algorithm. To verify the performance of CLSSA, 23 benchmark functions and three engineering problems were used for the tests. Simulation results show that the CLSSA proposed in this paper is superior to the existing methods in terms of accuracy, convergence speed and stability.

The rest of this article is organized as follows: Section 2 introduces the principle and structure of SSA. Section 3 introduces the improvement strategy of CLSSA. Section 4 introduces the experimental results and analysis based on benchmark functions and engineering problems. In Section 5, the full text is summarized, and the direction of further research is pointed out.

2  The Basic Sparrow Search Algorithm

SSA is a novel swarm-based optimization algorithm that mainly simulates the process of sparrow foraging. The sparrow foraging process is a kind of discoverer-follower model, and the detection and early warning mechanism is also superimposed. Individuals with good fitness in sparrows are the producers, and other individuals are the followers. At the same time, a certain proportion of individuals in the population are selected for detection and early warning. If a danger is found, these individuals fly away to find new position.

There are producers, followers, and guards in SSA. The location update is per-formed according to their respective rules. The update rules are as follows:

Xi,jt+1={Xi,jt×exp(−iα×itermax)if R2<STXi,jt+Q×Lif R2≥ST(1)

where t indicates the current iteration, Xi,jt represents the value of the jth dimension of the ith sparrow at iteration t. itermax is a constant with the largest number of iterations. α∈(0,1] is a random number. R2(R2∈(0,1)) and ST(ST∈[0.5,1)) represent the alarm value and the safety threshold respectively, where R2 is randomly generated and ST is usually set to 0.8. Q is a random number which obeys normal distribution. L shows a matrix of 1 × D for which each element inside is 1.

Xi,jt+1={Q×exp(Xworstt−Xi,jti2)if i>n/2Xpt+1+|Xi,jt+−Xpt+1|×A+×Lif others(2)

where Xp indicates the best position occupied by the discoverer, Xworst indicates the current worst position, and A is a matrix with a row of multi-dimensional elements of 1 or −1.

Xi,jt+1={Xbestt+β×|Xi,jt−Xbestt|if fi>fgXi,jt+K×(|Xi,jt−Xworstt|(fi−fw)+ε)if fi=fg(3)

where Xbest is the current global best position, β is a step size control parameter that obeys Gaussian distribution, K∈(−1,1) is a random number, fi is the fitness of the current sparrow, fg and fw is the best fitness and the worst fitness at present, and εis a constant to avoid zero denominator. The pseudo code of SSA is shown in Algorithm 1:

3  The Improved Sparrow Search Algorithm

In Section 3, we introduce a new SSA variant called CLSSA, which can improve the performance of the basic SSA. We introduce three strategies to improve the SSA algorithm. Firstly, we use chaotic map sequence to replace the random parameter R2 of the algorithm. Secondly, we use the combination of logarithmic helix strategy and original search strategy to balance the discoverer's development and exploration ability. finally, we use two adaptive step size strategies to update the alert position and adjust the algorithm exploitation and exploration ability.

3.1 Chaotic Maps

Chaos is a random phenomenon in nonlinear dynamic systems, which is regular and random, and is sensitive to initial conditions and ergodicity. According to these characteristics, chaotic graphs represented by different equations are constructed to update the random variables in the optimization algorithm. Table 1 and Fig. 1 show ten chaotic maps which are used in the experiments. These ten chaotic maps have different effects in generating numerical values. More details about the 10 chaotic maps can be found in the literature [31,32]. Many researchers have demonstrated the effectiveness of chaotic maps in their studies, investigating the contribution of chaotic operators in the HHO [33], Krill Herd Algorithm (KHA) [34] and WOA [35].

3.2 Logarithmic Spiral Strategy

Through experiments, it is found that the original SSA is easy to fall into the local optimum, which leads to premature convergence. As shown in Fig. 2b, each iteration update of its discoverer approaches the individual optimal solution straight line, which has a strong exploitation ability, but loses the exploration of the nearby search space in the process of approaching the optimal individual, the population diversity is reduced, and it is easy to fall into the local optimum. Therefore, we introduce a logarithmic spiral search model [21] to solve this problem. The mathematical model is described as follows:

Xpbestt=|Xi,jt−Xpbestt|⋅eal⋅cos⁡(2πθ)+Xpbestt(4)

l=2(1−t/itermax)−1(5)

where a is constant that determines the shape of the spiral, whose value is 1, l is a parameter that linearly decreases from 1 to −1, and Xpbest is the optimal position of the current iteration individual.

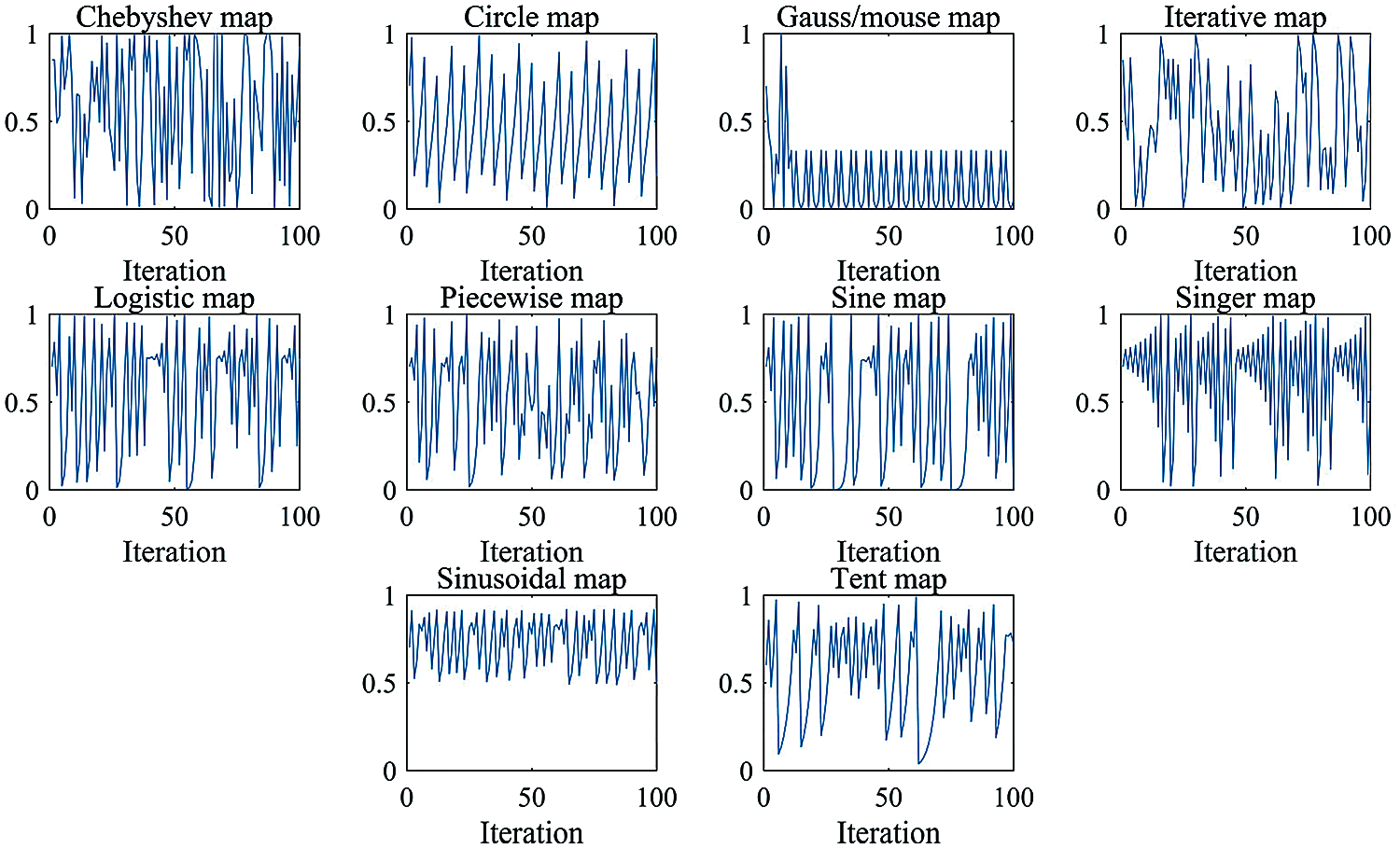
Figure 1: Chaotic maps visualization

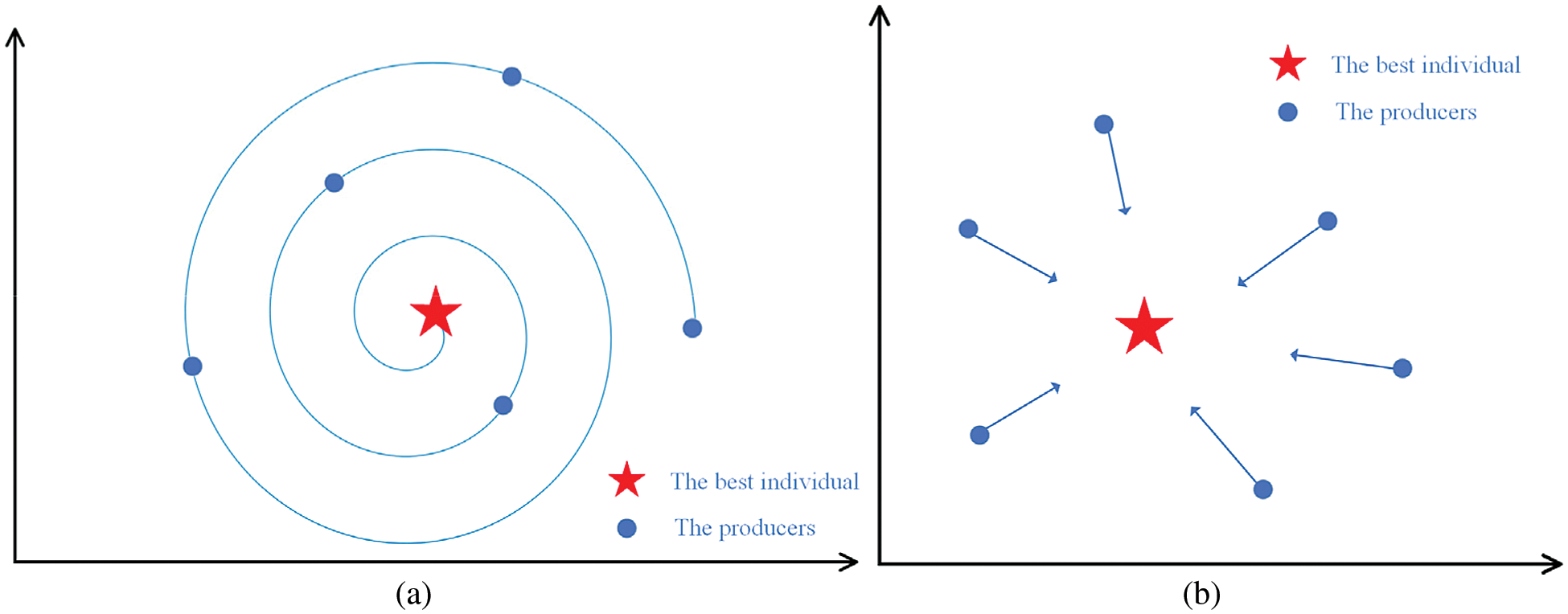
Figure 2: The illustration of two search model (a) the logarithmic spiral search model (b) the original search model

It can be seen from the Fig. 2a that when individuals of each generation update their positions, they gradually approach in a spiral shape, increasing the search for the surrounding space, maintaining the diversity of the population, and enhancing the exploration ability of the algorithm. Based on this analysis, the position update formula is adjusted as follows:

Xpbestt={Xpbestt×exp(−iα×itermax)if R2<ST & if R3<p|Xi,jt−Xpbestt|×eal×cos⁡(2πθ)+Xpbesttif R2<ST & if R3≥pXi,jt+Q×Lif R2≥ST(6)

where R3 is a uniformly distributed random number from 0 to 1, p is a constant and the value is 0.5.

3.3 Adaptive Step Strategy

In the SSA, two strategies are used for the location update of the guards. The Gaussian distribution is used to generate the step size for individuals with poor fitness. It can be seen from the Fig. 3 that the probability of the Gaussian distribution producing a smaller step size is higher. Conducive to the global search of the algorithm. The random step strategy is used for individuals with better fitness, and there is still a greater probability of large step in the later iterations, which is not conducive to algorithm convergence. Based on the above analysis, in order to balance the exploitation and exploration capabilities of the algorithm and enhance the convergence speed of the algorithm, an adaptive step size update formula is proposed for two strategies:

β={Cauchyrnd()if fitmeanSEL(t)≥fitmeanSEL(t+1)Gaussianrnd()if fitmeanSEL(t)<fitmeanSEL(t+1)(7)

K=(2rand−1)×(1−t/itermax)1/2(8)

Xi,jt+1={Xbestt+β×|Xi,jt−Xbestt|if fi>fgXi,jt+K×(|Xi,jt−Bworstt|(fi−fw)+ε)if fi=fg(9)

where fitmeanSEL is the average fitness of the dominant population and SEL is the ratio of the dominant population which is 0.35.

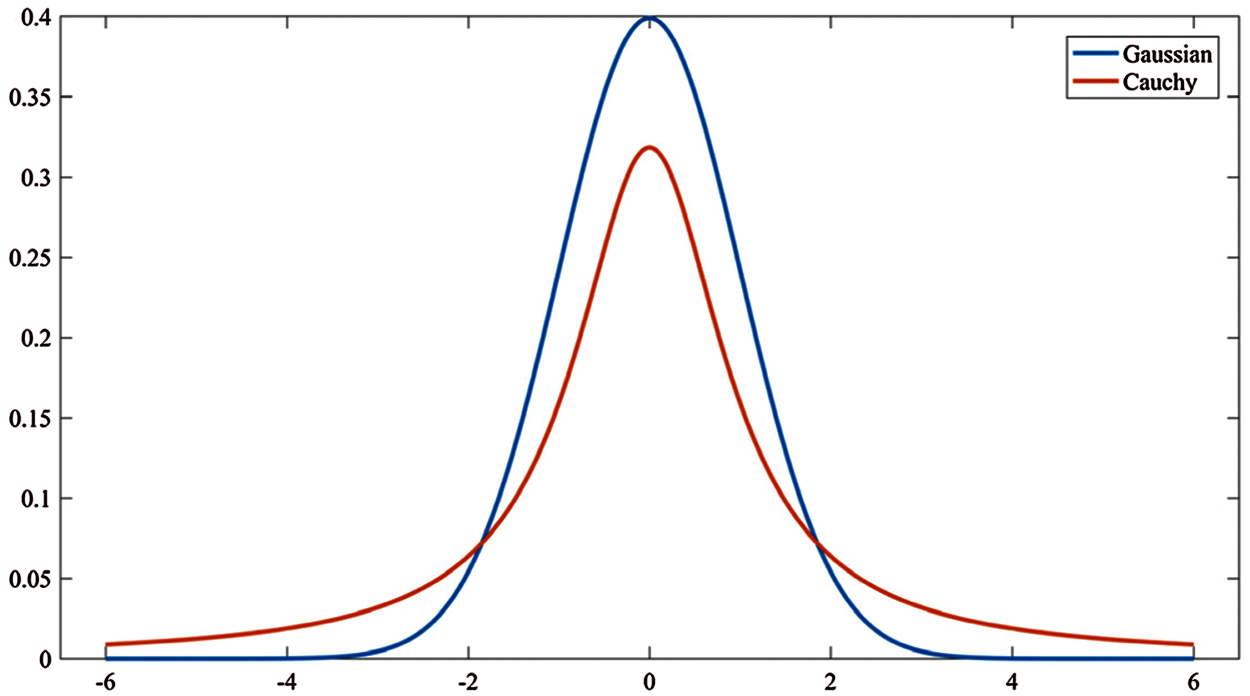
Figure 3: Gauss-cauchy distribution density function

Figure 4: Comparison of new and old step strategies

For the individuals with poor fitness, when the dominant population of the updated sparrow is better than the dominant population of the previous generation, the larger step size of the Cauchy distribution is used to make the poor individual approach to the dominant population quickly; while when the dominant population of the updated sparrow is weaker than the dominant population of the previous generation, indicating that the renewal effect of this generation is not good, the smaller step size of Gaussian distribution is used to strengthen the search of the space near the individual. For individuals with better fitness, the adaptive step strategy is used. As can be seen from the Fig. 4, the large step size produced by the large probability in the early stage is beneficial for the individual to jump out of the local optimization, maintain the population diversity, increase the probability of small step size in the later stage, and impose only a small disturbance on the dominant individual, which is conducive to the convergence of the algorithm.

The pseudo code and flow chart of CLSSA is shown in Algorithm 2 and Fig. 5.

Figure 5: Flow chart of CLSSA

4  Experimental Results and Discussion

In Section 4, the benchmark function will be used to evaluate various chaotic map combination algorithms, and then determine which chaotic map sequence to replace the original SSA parameters. Secondly, we need to explore the impact of different improvement strategies in CLSSA on the optimization performance of the algorithm. Finally, we evaluate the performance of the CLSSA and compare the results with other latest algorithms.

4.1 Introduction of Benchmark Function

In this paper, 23 classical test functions are employed, including 7 unimodal functions, 6 multimodal functions and 10 fixed dimensional functions. The above test functions are all single-objective functions. The unimodal function F1–F7 has only one global optimal value, which is mainly used to test the development ability of the algorithm; the multimodal function has multiple local minima, which can be used to test the exploration ability of the algorithm. The benchmark function is shown in Table 2. The 3D view of each test function is shown in Figs. 6a–6d.

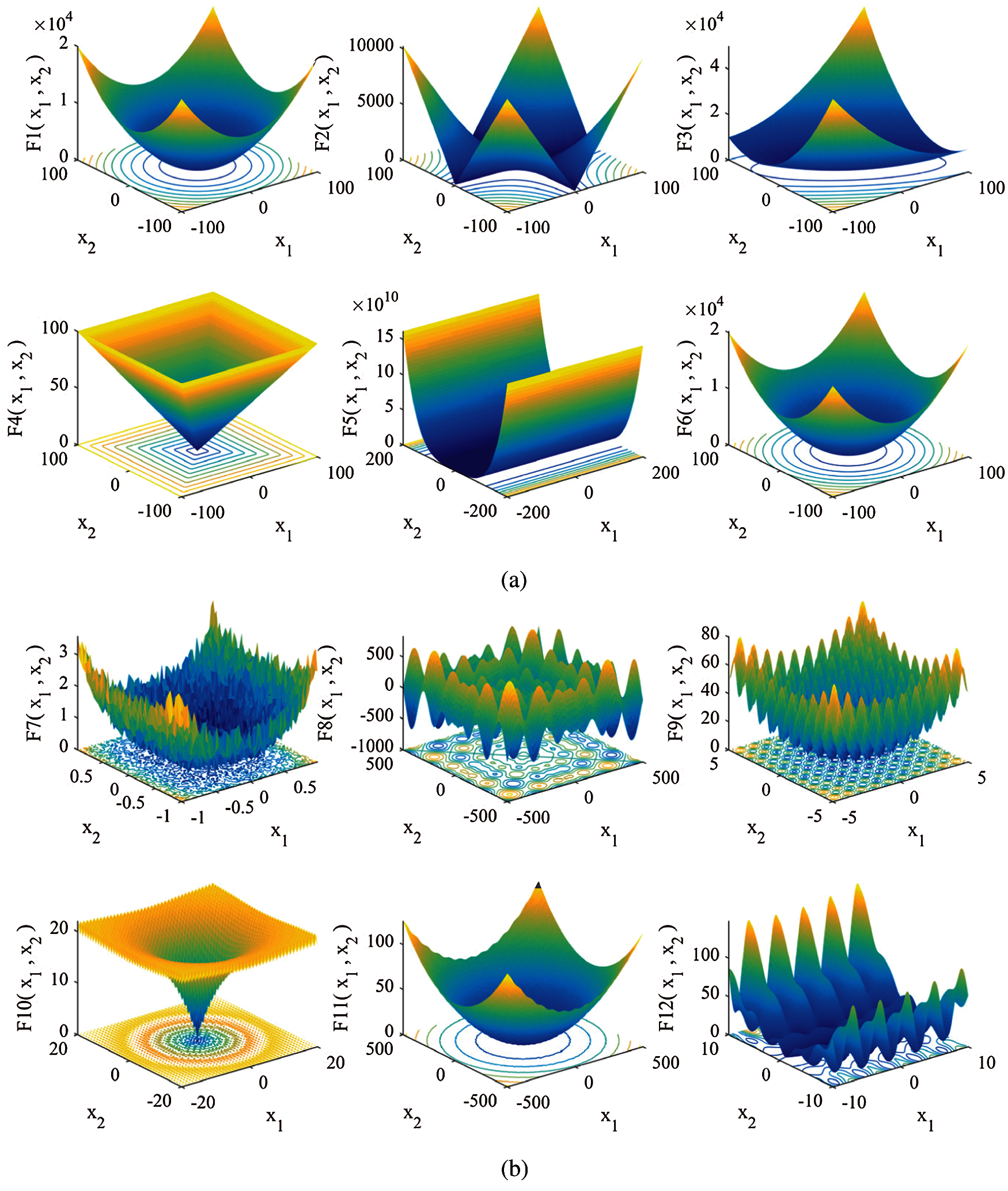
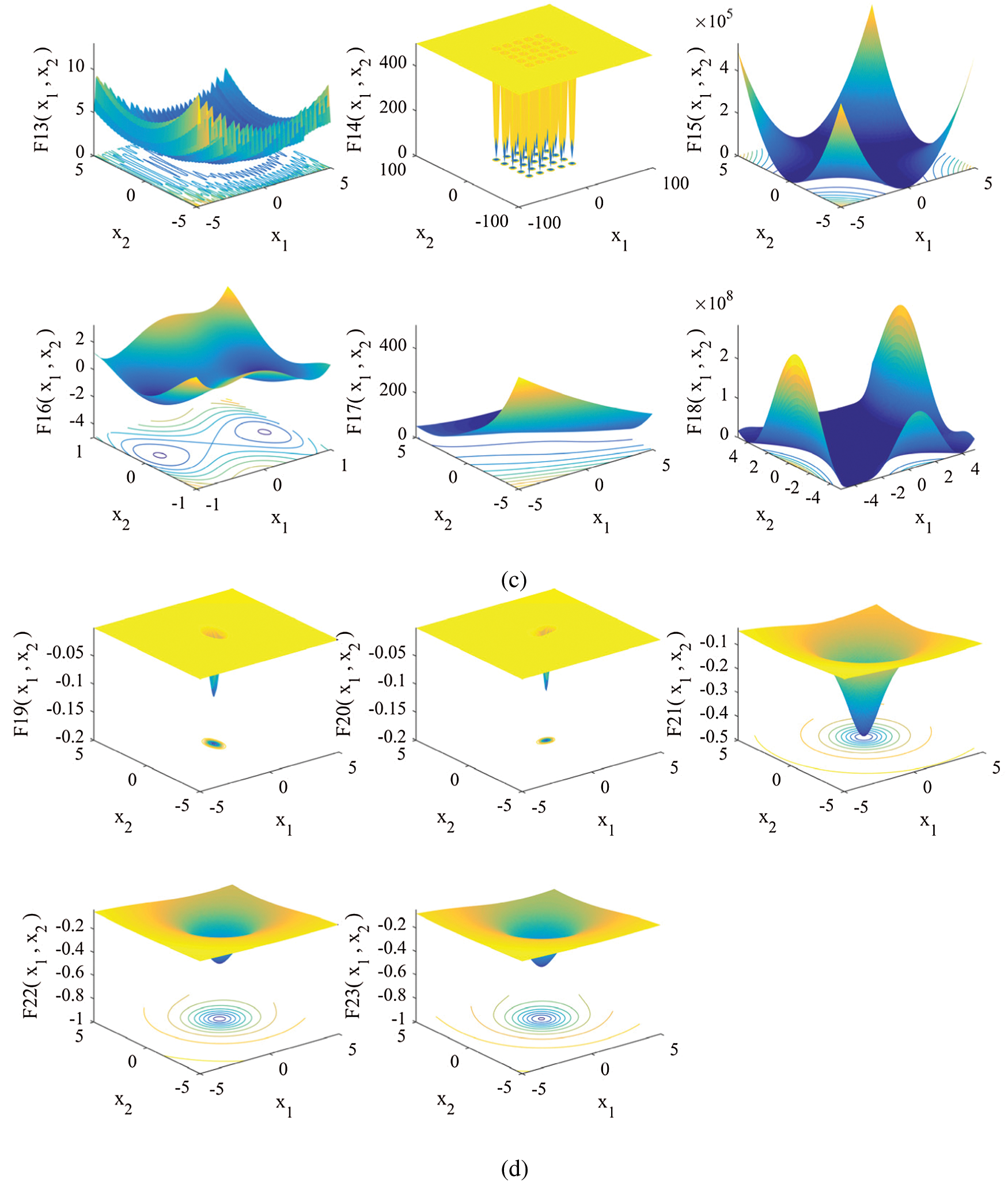
Figure 6: 3D view of benchmark functions (a) 3D view of benchmark F1–F6 (b) 3D view of benchmark F7–F12 (c) 3D view of benchmark F13–F18 (d) 3D view of benchmark F19–F23

4.2 Chaos Map Test

Ten kinds of chaotic maps are combined with SSA algorithm to form new algorithms, the first chaotic map combined algorithm is named SSA-1, the second chaotic map combined algorithm is named SSA-2, and so on. The ten combined algorithms are compared with SSA in the benchmark function. In order to make a fair comparison, on the same experimental platform, the number of populations is set to 50, and the maximum number of iterations is 300. Except for using chaotic sequences to replace parameter R2, the other parameters are consistent with the original literature, and the initial values of chaotic mapping sequences are set to 0.7. All the algorithms are implemented in MATLAB R2016a and the test environment is set up on a computer with AMD R7 4700U CPU@1.80 GHz 16GB RAM, running on Windows 10. The average value is used to measure the accuracy of the algorithm, and the standard deviation is used to measure the robustness of the algorithm, so the average value and standard deviation are used to measure the performance of the algorithm. The results are recorded in Table 3. The last row in this table presents the count of the better than, equal to or worse than SSA obtained by each chaotic map over all functions.

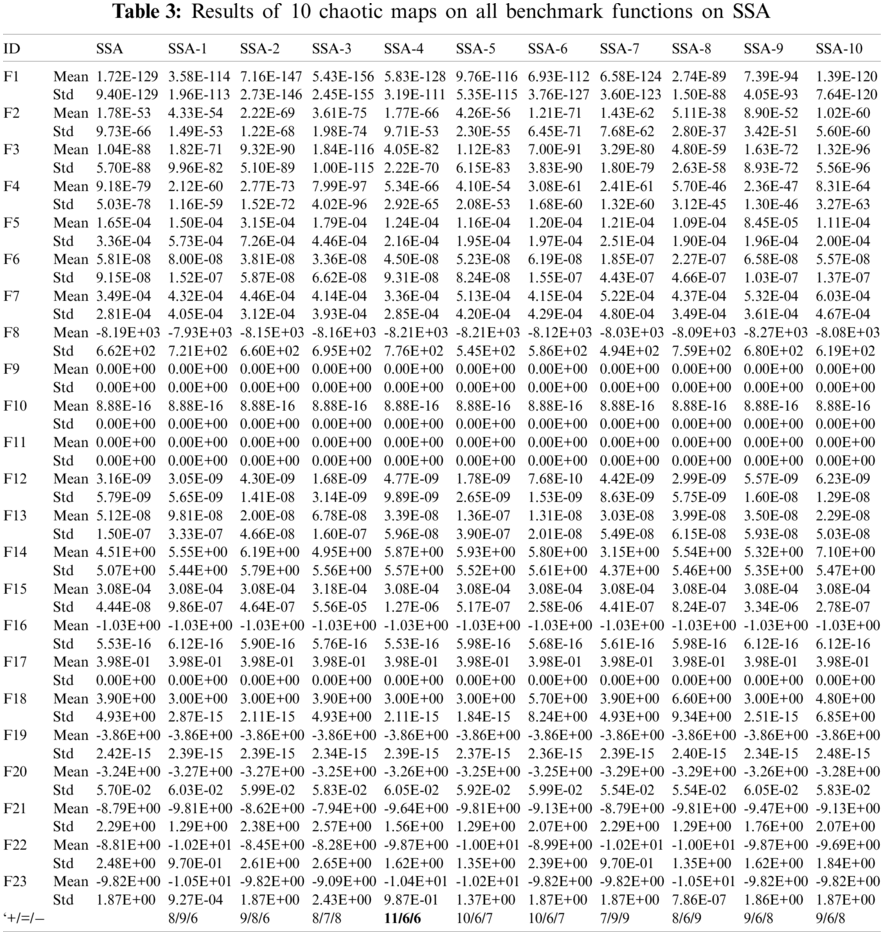
It can be observed from Table 3 that SSA-8 (Singer map) outperforms or equals SSA in 14 test functions. SSA-3 (Gauss map), SSA-9 (Sinusoidal map) and SSA-10 (Tent map) perform better than or equal to SSA in 15 test functions. SSA-5 (Logistic map), SSA-6 (Precewise map) and SSA-7 (Sine map) perform better than or equal to SSA in 16 test functions. SSA-1 (Chebyshev map), SSA-2 (Circle map) and SSA-4 (Iterative map) are superior or equal to SSA in 17 test functions.

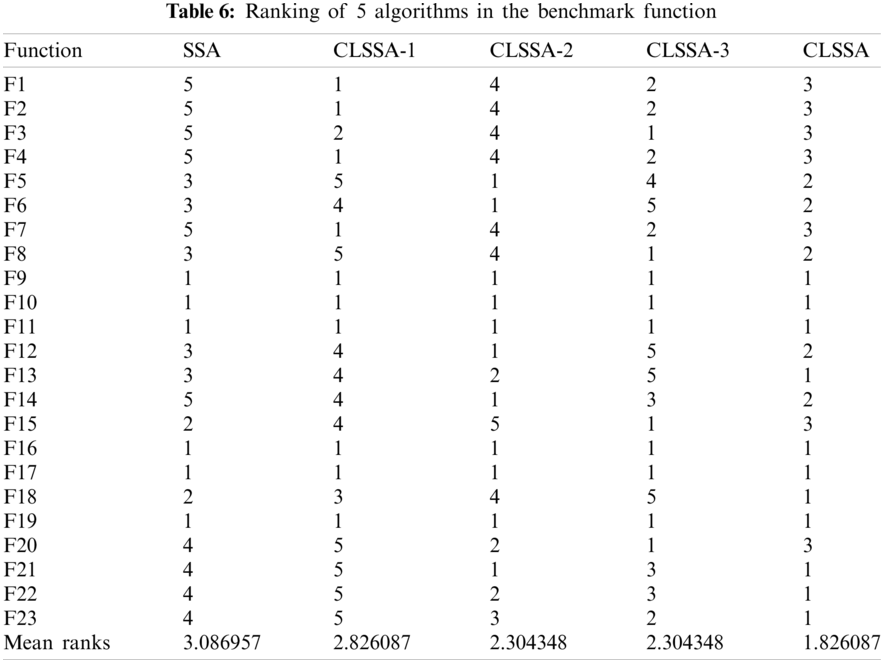
In order to further analyze the optimization ability of the eleven algorithms, the results of these algorithms in each test function are compared and sorted according to the mean value of Table 3. The results are shown in Table 4, and the average sorting results of each algorithm in the last behavior of the table. SSA-4 ranks first, indicating that iterative mapping is the best alternative to the original parameter R2. In addition to SSA-4, SSA-2, SSA-3, SSA-5, and SSA-7 also rank higher than SSA. The above analysis shows that using chaotic map sequence to replace the random parameter R2 in the algorithm can better improve the algorithm's optimization performance, and each chaotic map sequence has different improvement effects on the algorithm. In order to visually show the performance of each algorithm in different test functions, a block diagram is used to plot the ranking results in Table 4, as shown in Fig. 7. The larger the area of the circle in the Fig. 7, the darker the color, indicating that the algorithm has a stronger performance in this test function, and the numbers in the figure indicate the ranking of each algorithm in each test function. It can be seen from Fig. 7 that SSA-4 performs better in the test function, and only performs poorly on F12 and F14.

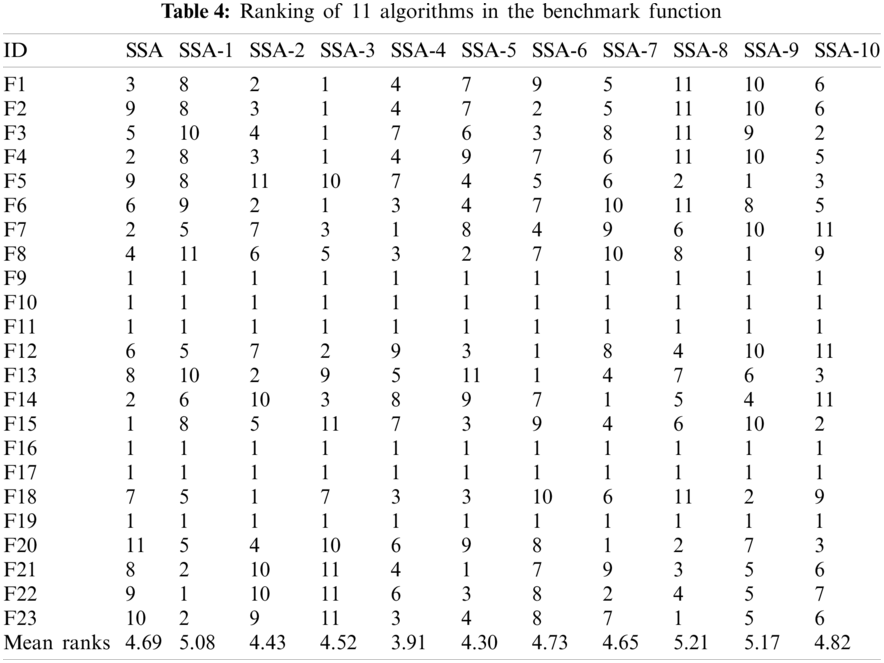
Figure 7: Block diagram of algorithm ranking

In order to further prove the effectiveness of using chaotic sequences to replace SSA algorithm parameter, Figs. 8 and 9 list the convergence curves and box plots of eleven algorithms. It can be seen from Fig. 8 that SSA performs generally in each test function, and all chaotic mapping combination algorithms are better than SSA in convergence speed and convergence accuracy. The box diagram is used to show the distribution of the solutions of each algorithm. It can be seen from Fig. 9 that the optimal, median and worst values of the improved algorithm are better than those of SSA in most functions.

Figure 8: Convergence graphs of 11 algorithms on 23 representative functions

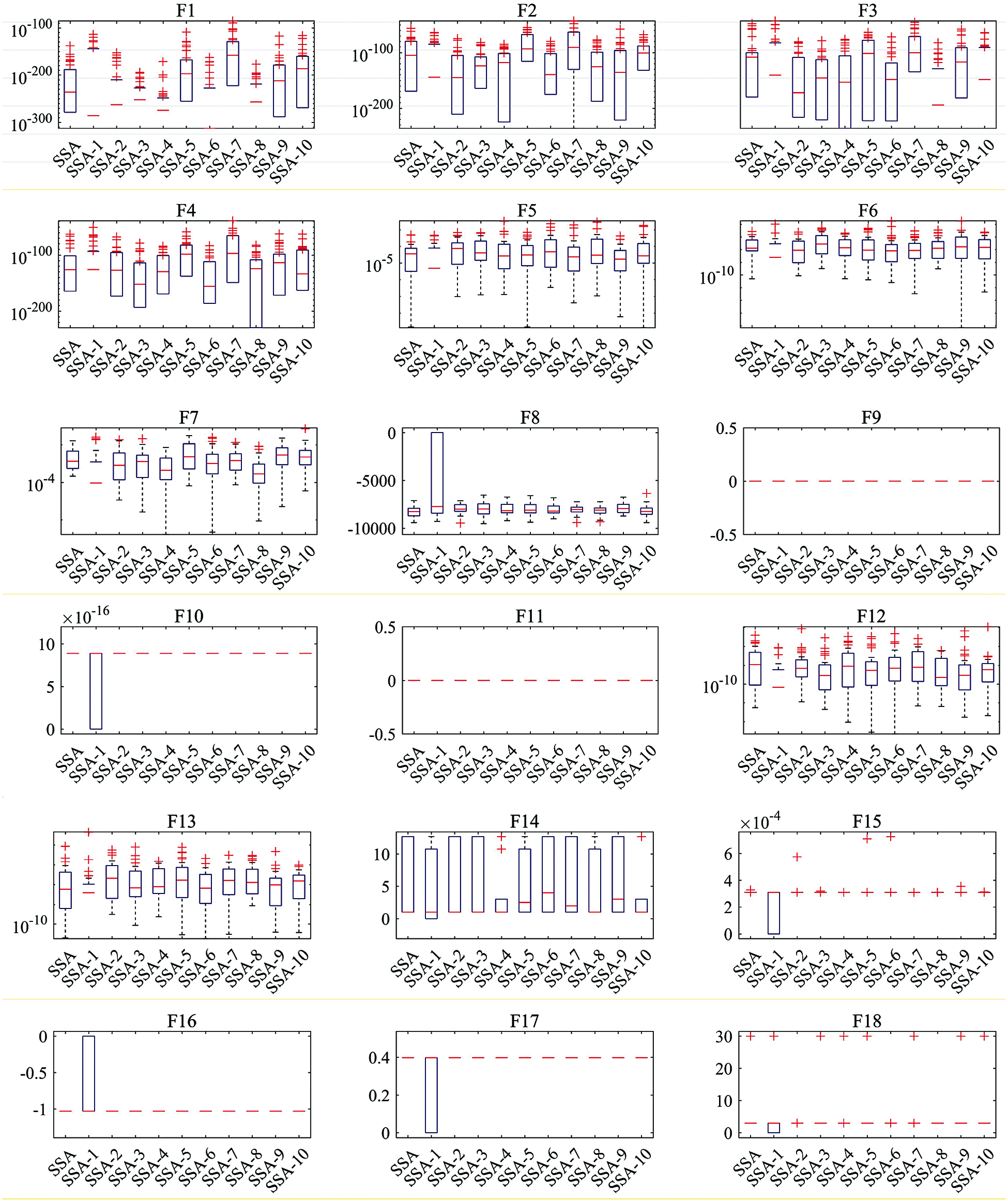
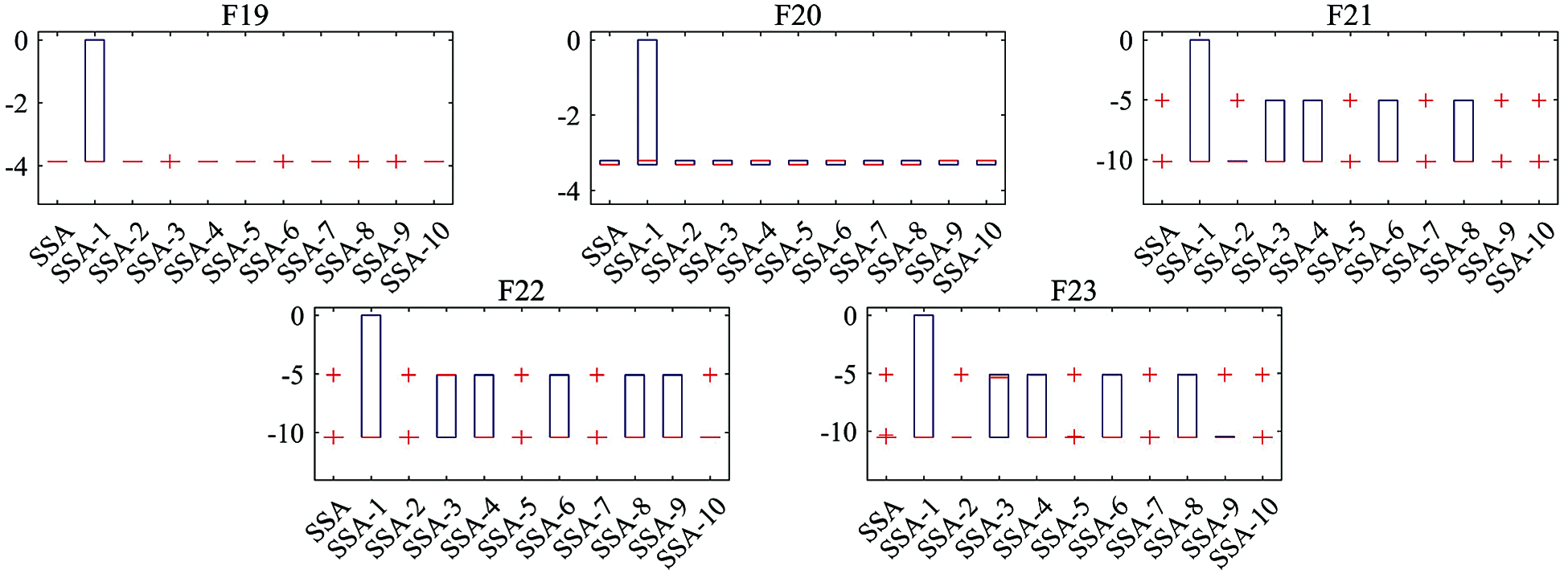
Figure 9: Box diagrams of solutions obtained by 11 algorithms on 23 benchmark functions with 30 independent runs

Combined with the above analysis, the chaotic mapping sequence can promote the improvement of SSA performance, and iterative mapping has the best effect on improving the performance of the SSA. Therefore, in the next part of the CLSSA performance test, the iterative mapping sequence is used to replace the random value parameter R2 in the SSA.

4.3 Comparison of Different Improvement Strategies

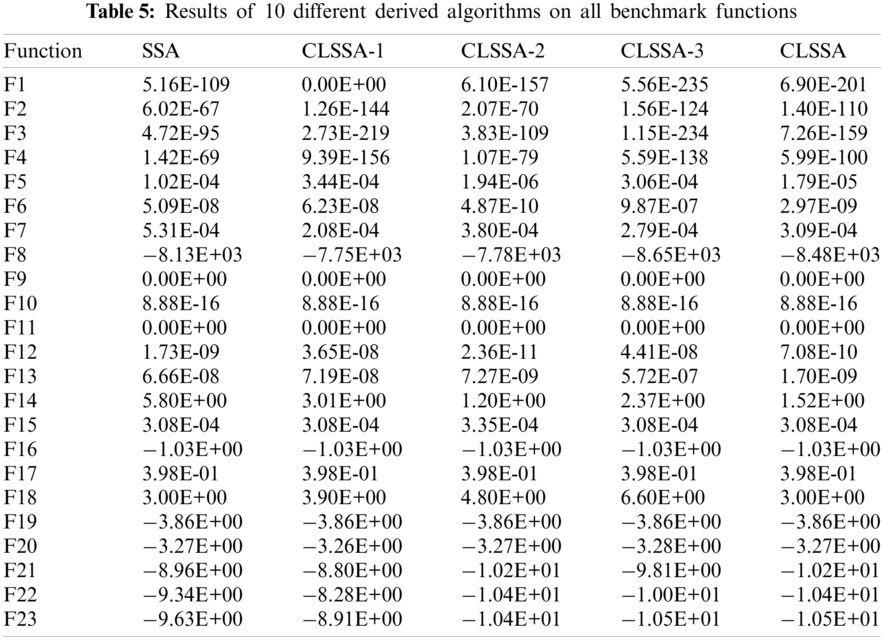
As mentioned above, this paper mainly uses three strategies to improve SSA, so three different derivative algorithms are designed to evaluate the impact of these three strategies on the algorithm. These three derivation algorithms are obtained by removing the corresponding improvement strategy from CLSSA. CLSSA-1 removes both logarithmic spiral strategy and adaptive step strategy; CLSSA-2 removes chaotic map and adaptive step strategy at the same time; CLSSA-3 removes chaotic map strategy and logarithmic spiral strategy at the same time. 23 benchmark functions are used to compare the performance of the three derived algorithms with SSA and CLSSA. Each algorithm runs 30 times independently on each test function, and the statistical average results are shown in Tables 5 and 6 show the ranking of each algorithm in the test function. Obviously, CLSSA which includes all the improvement strategies, performed best, ranking first on average. The performance of the derived algorithm with one improved strategy is better than that of SSA. From the specific optimization results and sorting table provided by the Table 6, the chaotic mapping strategy mainly improves the development ability, while the logarithmic spiral strategy enhances the exploration ability of the algorithm, while the adaptive step strategy enhances the exploitation ability and exploration ability of the algorithm to some extent. The above analysis proves the effectiveness of each improvement strategy.

4.4 Performance Test of CLSSA

In order to verify the performance of CLSSA, the proposed CLSSA is compared with the SSA, WOA, BSO [36], PSO, GSA, HHO, GWO [37], SCA [38], MVO [39], MFO [40], BBO, FPA [41] Flower pollination algorithm for global optimization. The experimental environment is the same as the previous article, the number of populations is set to 50, the maximum number of iterations is 300, and the parameters of each algorithm are consistent with the original literature. Meanwhile, to reduce the influence of randomness on the experimental results, all algorithms need to run 30 times independently. Table 7 lists the best fitness, mean fitness and standard deviation, in which the best mean fitness is marked in bold.

As shown in Table 7, when solving the unimodal test functions F1–F7, CLSSA can stably converge to the optimal value in F1–F4 and F6, and the performance is better than the comparison algorithm. CLSSA could not obtain the optimal value of F5, but it was 19 orders of magnitude higher than SSA. HHO perform best on F7, with CLSSA in second position. In the unimodal test functions F1–F7, CLSSA is better than SSA, indicating that the proposed chaotic map sequence substitution strategy can effectively improve the local search ability of the algorithm.

When solving the multimodal test functions F8–F13, GSA, PSO, BBO and MFO outperform CLSSA in solving F8. For F9–F11, CLSAA, SSA, HHO can all stably converge to the optimal value. WOA can obtain the optimal value, but it is not stable. The CLSSA has the highest accuracy for F12–F13, with optimal values improved by 17 and 11 orders of magnitude compared to SSA. When solving the fixed-dimensional multimodal functions F14–F23, the CLSSA performs poorly for F14, outperforming only SSA, WOA, GSA, GWO and BBO. For the F15, optimal values can be obtained for CLSSA and SSA, but CLSSA is more stable than SSA. All algorithms have similar performance at F16, and all can obtain optimal values. GSA is the most stable and CLSAA is the second most stable. The CLSSA outperforms WOA, HHO, GSA, CSA, MVO, BBO and FPA for F17, with performance comparable to other algorithms. As for F18, the stability of CLSSA is only weaker than BSO, PSO, and GSA. The CLSSA outperforms all comparison algorithms for F19, F21 and F23. The GSA performs best for F22, with the CLSSA second best. In all multimodal test functions, CLSSA performs better than SSA, which shows that the logarithmic spiral strategy proposed in this paper can significantly improve the performance of algorithm exploration.

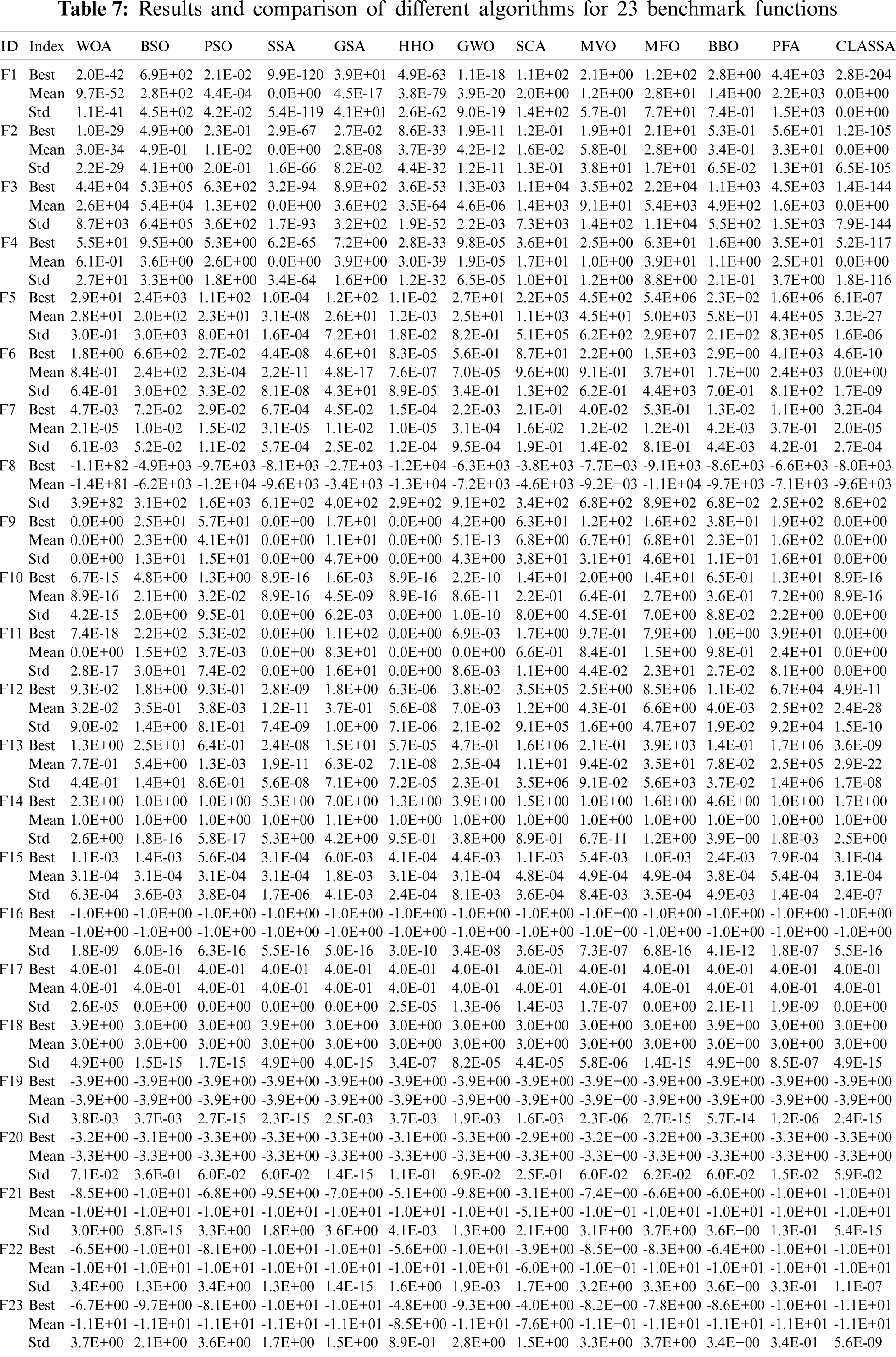
Combined with the above analysis, the CLSSA proposed in this paper is better than all the comparison algorithms in 12 of the 23 benchmark functions, 11 comparison algorithms in 6 test functions, 9 comparison algorithms in 3 test functions, and CLSSA is better than SSA, in all test functions, which proves that our proposed CLSSA has obvious advantages in optimization accuracy.

In order to directly show the performance differences of each algorithm in solving the test function, the algorithms are sorted according to the mean fitness of Table 7, the results are shown in Table 8, and the last column is the average ranking of each algorithm.

Fig. 10 is drawn according to the ranks in Table 8. The smaller the area of the algorithm performance curve, the better the performance of the algorithm.

Figure 10: Ranks of average of 13 algorithms

The black bold line is the sorting result curve of CLSSA, and it can be seen intuitively that the performance of CLSSA is in the middle level on F8 and F14, and performs better in other test functions, and its surrounding area is the smallest, indicating that CLSSA has the best optimization performance as a whole.

To further illustrate the convergence performance of CLSSA, Fig. 11 lists the mean convergence curves of 13 algorithms to solve these functions. For the unimodal test function F1–F7, CLSSA has the best performance, the convergence speed is faster than all comparison algorithms, and the convergence accuracy is also higher than all comparison algorithms. For the multimodal functions F8–F23, CLSSA performs best in most of them. However, for functions F14, F17, and F18, CLSSA converges slowly in the early iterations. The CLSSA converges slower in the early iterations on F21 and F22 but can converge to better results afterwards. CLSSA converges faster than SSA on all test functions, which shows that the variable step strategy proposed in this paper can effectively improve the convergence speed.

Figure 11: Convergence graphs of 13 algorithms on 23 representative functions

To analyze the distribution characteristics of each algorithm in the test function, Fig. 12 lists box plots of 13 algorithms. Compared with other comparison algorithms, the CLSSA proposed in this paper performs well on most functions, and the obtained maximum, minimum, and median values are almost the same as the optimal solution, especially for F9, F10, F11, F16, F17, F19 and F20. In other test functions, although there are individual outliers, the overall distribution is still more concentrated than the comparison algorithm. Therefore, the CLSSA proposed in this paper has stronger stability.

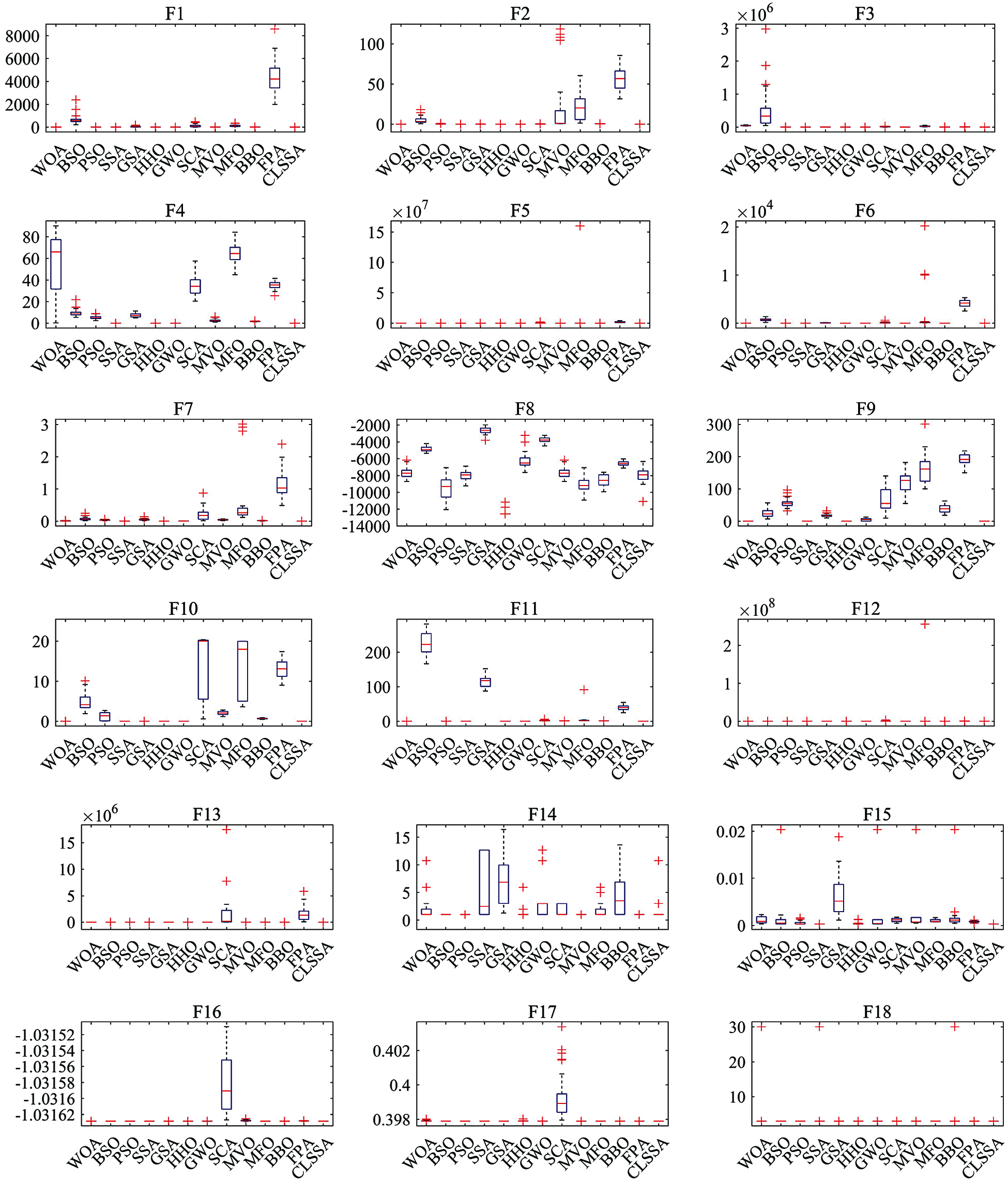
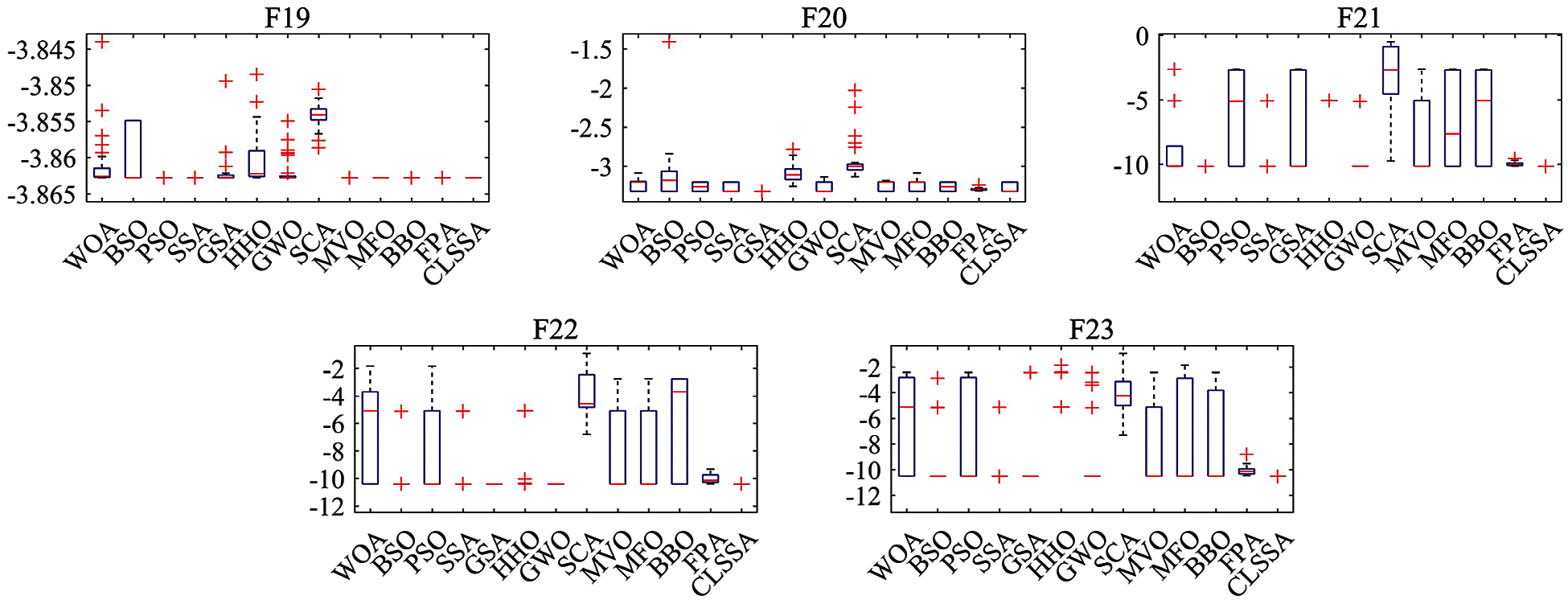
Figure 12: Box diagrams of solutions obtained by 13 algorithms on 23 benchmark functions with 30 independent runs

The above analysis shows that CLSSA shows strong optimization ability on low-dimensional functions. However, the optimization algorithm is prone to fail in solving high-dimensional complex function problems. Real-world optimization problems are mostly large-scale complex optimization problems. Therefore, to verify the performance of CLSSA in high-dimensional problems, 13 algorithms were compared on the 100D test functions, and the experimental results are shown in Table 9. CLSSA is better than all comparison algorithms in F1–F6 and F12–F13. HHO performs best in F7 and F8, CLSSA ranks second and third respectively. When solving F9–F11, CLSSA and SSA can get the best value. It can also be seen from Figs. 13 and 14 that CLSSA performs well in other test functions except for the pool performance on F8 and can steadily and quickly converge to a better value.

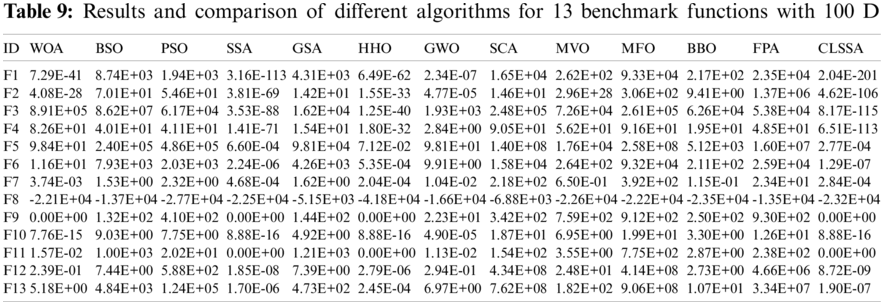
Figure 13: Box diagrams of solutions obtained by 13 algorithms on 13 benchmark functions with 30 independent runs

In summary, compared with other algorithms, the CLSSA proposed in this paper is competitive, and the proposed improvement strategy can handle the relationship between exploitation and exploration well.

4.5 CLSSA for Engineering Problems

Engineering design problem is a nonlinear optimization problem with complex geometric shapes, various design variables and many practical engineering constraints. The performance of the proposed algorithm is evaluated by solving practical engineering problems. In the simulation, the population size is set to 50, and the maximum iterations is 500. The results of 30 independent runs of CLSSA are compared with those in other literatures.

4.5.1 Pressure Vessel Design Problem

The pressure vessel design optimization problem shown in Fig. 15 is a typical hybrid optimization problem, whose goal is to reduce the total cost, including forming cost, material cost and welding cost. There are four different variables: container thickness Ts(x1), head thickness Th(x2), inner diameter R(x3) and container cylindrical section length L(x4). The comparison results are shown in Table 10. The problem can be described as Eq. (10).

minf(x1,x2,x3,x4)=0.6224x1x3x4+1.7781x2x32+3.1661x12x4+19.84x12x3(10)

Figure 14: Convergence graphs of 13 algorithms on 13 representative functions

Figure 15: Schematic of the pressure vessel design problem

4.5.2 Tension/Compression Spring Design Problem

The tension/compression spring design problem is a mechanical engineering design optimization problem, which can be used to evaluate the superiority of the algorithm. As shown in Fig. 16, the goal of this problem is to reduce the weight of the spring. It includes four nonlinear inequalities and three continuous variables: wire diameter w(x1), coil average diameter d(x2), coil length or number L(x3). The comparison results are shown in Table 11. The mathematical model of this problem can be described as Eq. (11).

minf(x1,x2,x3)=(x3+2)x12x2(11)

Figure 16: Schematic of tension/compression spring design problem

Figure 17: Schematic of welded beam design problem

4.5.3 Welded Beam Design Problem

As shown in Fig. 17, the main purpose of the welded beam design problem is to reduce the manufacturing cost of the welded beam, which mainly involves four variables: the width h (x1) and length l (x2) of the weld zone, the depth t (x3) and the thickness b (x4), and subject to the constraints of bending stress, shear stress, maximum end deflection and load conditions. The comparison results are shown in Table 12. The mathematical model of the problem is described as Eq. (12).

minf(x1,x2,x3,x4)=1.10471x12x2+0.04811x3x4(14.0+x2)(12)

where

In this paper, 15 algorithms are selected and compared with CLSSA. The simulation results show that CLSSA achieves the optimal values in all three engineering problems, which proves that CLSSA is highly competitive.

5  Conclusions

In this paper, we use three strategies combining chaos theory, logarithmic spiral search and adaptive steps to modify the basic sparrow search algorithm. First, the chaotic mapping is used to generate the values of the parameter R2. Second, the logarithmic spiral search strategy is used to expand the search of SSA to the surrounding area, thus enhancing the population diversity and avoiding falling into local optimum. In addition, the adaptive step control strategy is proposed to effectively balance the exploitation and exploration of SSA. To evaluate the performance of the proposed CLSSA, 23 classical test functions are used for verification. The simulation results show that it is effective to improve the SSA performance by using chaotic mapping to generate the value of parameter R2, in which the iterative mapping has the best impact. Three improvement strategies can improve the performance of SSA. Compared with eleven advanced algorithms, CLSSA has higher convergence accuracy, faster convergence speed and more stable performance. In addition, CLSSA was applied to three engineering optimization problems. The results show that CLSSA has excellent performance in terms of convergence rate and accuracy for structural engineering design problems. In future work, we plan to further improve the performance of CLSSA. We can hybridize CLSSA with other algorithms, such as combining with MBO, EHO, etc., with the same excellent performance, to achieve the effect of 1 + 1 > 2. We can also further study the impact of SSA parameter settings on performance. In addition, we plan to apply it to solve some real world problems, such as unmanned combat aerial vehicles task allocation and unmanned combat aerial vehicles path planning.

Funding Statement: The author acknowledges funding received from the following science foundations: The Science Foundation of Shanxi Province, China (2020JQ-481, 2021JM-224), Aero Science Foundation of China (201951096002).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wang, F., Li, Y., Liao, F., Yan, H. (2020). An ensemble learning based prediction strategy for dynamic multi-objective optimization. Applied Soft Computing, 96, 106592. DOI 10.1016/j.asoc.2020.106592. [Google Scholar] [CrossRef]

 2.  Sun, J., Miao, Z., Gong, D., Zeng, X. J., Li, J. et al. (2020). Interval multiobjective optimization with memetic algorithms. IEEE Transactions on Systems, Man, and Cybernetics, 50(8), 3444–3457. DOI 10.1109/TCYB.2019.2908485. [Google Scholar] [CrossRef]

 3.  Wang, G. G., Tan, Y. (2019). Improving metaheuristic algorithms with information feedback models. IEEE Transactions on Cybernetics, 49(2), 542–555. DOI 10.1109/TCYB.2017.2780274Y. [Google Scholar] [CrossRef]

 4.  Feng, Y., Deb, S., Wang, G. G., Alavi, A. H. (2021). Monarch butterfly optimization: A comprehensive review. Expert Systems with Applications, 168, 114418. DOI 10.1016/j.eswa.2020.114418. [Google Scholar] [CrossRef]

 5.  Wu, G. (2016). Across neighborhood search for numerical optimization. Information Sciences, 329, 597–618. DOI 10.1016/j.ins.2015.09.051. [Google Scholar] [CrossRef]

 6.  Wu, G., Pedrycz, W., Suganthan, P. N., Mallipeddi, R. (2015). A variable reduction strategy for evolutionary algorithms handling equality constraints. Applied Soft Computing, 37, 774–786. DOI 10.1016/j.asoc.2015.09.007. [Google Scholar] [CrossRef]

 7.  Goldberg, D. E. (1989). Genetic algorithms in search, optimization, and machine learning. USA: Addison-Wesley. [Google Scholar]

 8.  Beyer, H. G., Schwefel, H. P. (2002). Evolution strategies-a comprehensive introduction. Natural Computing, 1(1), 3–52. DOI 10.1023/A:1015059928466. [Google Scholar] [CrossRef]

 9.  Yao, X., Liu, Y., Lin, G. (1999). Evolutionary programming made faster. IEEE Transactions on Evolutionary Computation, 3(2), 82–102. DOI 10.1109/4235.771163. [Google Scholar] [CrossRef]

10. Sarker, R. A., Elsayed, S. M., Ray, T. (2014). Differential evolution with dynamic parameters selection for optimization problems. IEEE Transactions on Evolutionary Computation, 18(5), 689–707. DOI 10.1109/TEVC.2013.2281528. [Google Scholar] [CrossRef]

11. Simon, D. (2008). Biogeography-based optimization. IEEE Transactions on Evolutionary Computation, 12(6), 702–713. DOI 10.1109/TEVC.2008.919004. [Google Scholar] [CrossRef]

12. Dupanloup, I., Schneider, S., Excoffier, L. G. L. (2002). A simulated annealing approach to define the genetic structure of populations. Molecular Ecology, 11(12), 2571–2581. DOI 10.1046/j.1365-294X.2002.01650.x. [Google Scholar] [CrossRef]

13. Rashedi, E., Nezamabadi-pour, H., Saryazdi, S. (2009). GSA: A gravitational search algorithm. Information Sciences, 179(13), 2232–2248. DOI 10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]

14. Wei, Z., Huang, C., Wang, X., Han, T., Li, Y. (2019). Nuclear reaction optimization: A novel and powerful physics-based algorithm for global optimization. IEEE Access, 7, 66084–66109. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]

15. Hatamlou, A. (2013). Black hole: A new heuristic optimization approach for data clustering. Information Sciences, 222, 175–184. DOI 10.1016/j.ins.2012.08.023. [Google Scholar] [CrossRef]

16. Yang, X. S. (2010). Nature-inspired metaheuristic algorithms. Second Edition, UK: Luniver Press. [Google Scholar]

17. Eberhart, R., Kennedy, J. (1995). A new optimizer using particle swarm theory. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan. [Google Scholar]

18. Colorni, A., Dorigo, M., Maniezzo, V., Varela, F., Bourgine, P. (1992). Distributed optimization by ant colonies. Toward a practice of autonomous systems: Proceedings of the first european conference on artificial life, pp. 134–142. Massachusetts. [Google Scholar]

19. Wang, G. G., Deb, S., Cui, Z. (2019). Monarch butterfly optimization. Neural Computing and Applications, 31(7), 1995–2014. DOI 10.1007/s00521-015-1923-y. [Google Scholar] [CrossRef]

20. Wang, G. G. (2018). Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Computing, 10(2), 151–164. DOI 10.1007/s12293-016-0212-3. [Google Scholar] [CrossRef]

21. Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M. M. et al. (2019). Harris hawks optimization: Algorithm and applications. Future Generation Computer Systems, 97, 849–872. DOI 10.1016/j.future.2019.02.028. [Google Scholar] [CrossRef]

22. Wang, G. G., Deb, S., Coelho, L. D. S. (2015). Earthworm optimisation algorithm: A bio-inspired metaheuristic algorithm for global optimisation problems. International Journal of Bio-Inspired Computation, 12(1), 1–22. DOI 10.1504/IJBIC.2018.093328. [Google Scholar] [CrossRef]

23. Li, J., Lei, H., Alavi, A. H., Wang, G. G. (2020). Elephant herding optimization: Variants, hybrids, and applications. Mathematics, 8(9), 1415. DOI 10.3390/math8091415. [Google Scholar] [CrossRef]

24. Li, S., Chen, H., Wang, M., Heidari, A. A., Mirjalili, S. (2020). Slime mould algorithm: A new method for stochastic optimization. Future Generation Computer Systems, 111, 300–323. DOI 10.1016/j.future.2020.03.055. [Google Scholar] [CrossRef]

25. Gao, D., Wang, G. G., Pedrycz, W. (2020). Solving fuzzy job-shop scheduling problem using de algorithm improved by a selection mechanism. IEEE Transactions on Fuzzy Systems, 28(12), 3265–3275. DOI 10.1109/TFUZZ.91. [Google Scholar] [CrossRef]

26. Tang, A. D., Han, T., Zhou, H., Xie, L. (2021). An improved equilibrium optimizer with application in unmanned aerial vehicle path planning. Sensors, 21(5), 1814. DOI 10.3390/s21051814. [Google Scholar] [CrossRef]

27. Chen, S., Chen, R., Wang, G. G., Gao, J., Sangaiah, A. K. (2018). An adaptive large neighborhood search heuristic for dynamic vehicle routing problems. Computers & Electrical Engineering, 67, 596–607. DOI 10.1016/j.compeleceng.2018.02.049. [Google Scholar] [CrossRef]

28. Wang, F., Li, Y., Zhou, A., Tang, K. (2020). An estimation of distribution algorithm for mixed-variable newsvendor problems. IEEE Transactions on Evolutionary Computation, 24(3), 479–493. DOI 10.1109/TEVC.2019.2932624. [Google Scholar] [CrossRef]

29. Wolpert, D. H., Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1), 67–82. DOI 10.1109/4235.585893. [Google Scholar] [CrossRef]

30. Xue, J., Shen, B. (2020). A novel swarm intelligence optimization approach: Sparrow search algorithm. Systems Science & Control Engineering, 8(1), 22–34. DOI 10.1080/21642583.2019.1708830. [Google Scholar] [CrossRef]

31. Wang, G. G., Deb, S., Gandomi, A. H., Zhang, Z., Alavi, A. H. (2016). Chaotic cuckoo search. Soft Computing, 20, 3349–3362. DOI 10.1007/s00500-015-1726-1. [Google Scholar] [CrossRef]

32. Wang, G. G., Gandomi, A. H., Alavi, A. H. (2013). A chaotic particle-swarm krill herd algorithm for global numerical optimization. Kybernetes, 42(6), 962–978. DOI 10.1108/K-11-2012-0108. [Google Scholar] [CrossRef]

33. Ewees, A. A., Elaziz, M. E. A. (2020). Performance analysis of chaotic multi-verse harris hawks optimization: A case study on solving engineering problems. Engineering Applications of Artificial Intelligence, 88, 103370. DOI 10.1016/j.engappai.2019.103370. [Google Scholar] [CrossRef]

34. Wang, G. G., Guo, L., Gandomi, A. H., Hao, G., Wang, H. (2014). Chaotic krill herd algorithm. Information Sciences, 274, 17–34. DOI 10.1016/j.ins.2014.02.123. [Google Scholar] [CrossRef]

35. Kaur, G., Arora, S. (2018). Chaotic whale optimization algorithm. Journal of Computational Design and Engineering, 5(3), 275–284. DOI 10.1016/j.jcde.2017.12.006. [Google Scholar] [CrossRef]

36. Wang, T., Yang, L., Liu, Q. (2020). Beetle swarm optimization algorithm: Theory and application. Filomat, 34(15), 5121–5137. DOI 10.2298/FIL2015121W. [Google Scholar] [CrossRef]

37. Mirjalili, S., Mirjalili, S. M., Lewis, A. (2014). Grey wolf optimizer. Advances in Engineering Software, 69, 46–61. DOI 10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

38. Mirjalili, S. (2016). SCA: A sine cosine algorithm for solving optimization problems. Knowledge Based Systems, 96, 120–133. DOI 10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

39. Mirjalili, S., Mirjalili, S. M., Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications, 27(2), 495–513. DOI 10.1007/s00521-015-1870-7. [Google Scholar] [CrossRef]

40. Mirjalili, S. (2015). Moth-flame optimization algorithm. Knowledge Based Systems, 89, 228–249. DOI 10.1016/j.knosys.2015.07.006. [Google Scholar] [CrossRef]

41. Yang, X. S. (2012). Flower pollination algorithm for global optimization. Proceedings of the 11th International Conference on Unconventional Computation and Natural Computation, pp. 240–249. Orleans. [Google Scholar]

42. Zhang, Z., Ding, S., Jia, W. (2019). A hybrid optimization algorithm based on cuckoo search and differential evolution for solving constrained engineering problems. Engineering Applications of Artificial Intelligence, 85, 254–268. DOI 10.1016/j.engappai.2019.06.017. [Google Scholar] [CrossRef]

43. He, Q., Wang, L. (2007). A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization. Applied Mathematics and Computation, 186(2), 1407–1422. DOI 10.1016/j.amc.2006.07.134. [Google Scholar] [CrossRef]

44. Deb, K., Goyal, M. (1996). A combined genetic adaptive search (GeneAS) for engineering design. Journal of Computer Science and Informatics, 26, 34–45. [Google Scholar]

45. Sadollah, A., Bahreininejad, A., Eskandar, H., Hamdi, M. (2013). Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Applied Soft Computing, 13, 2592–2612. DOI 10.1016/j.asoc.2012.11.026. [Google Scholar] [CrossRef]

46. Guo, W., Chen, M., Wang, L., Wu, Q. (2016). Backtracking biogeography-based optimization for numerical optimization and mechanical design problems. Applied Intelligence, 44(4), 894–903. DOI 10.1007/s10489-015-0732-4. [Google Scholar] [CrossRef]

47. Mirjalili, S. (2015). The ant lion optimizer. Advances in Engineering Software, 83, 80–98. DOI 10.1016/j.advengsoft.2015.01.010. [Google Scholar] [CrossRef]

48. Huang, F. Z., Wang, L., He, Q. (2007). An effective co-evolutionary differential evolution for constrained optimization. Applied Mathematics and Computation, 186(1), 340–356. DOI 10.1016/j.amc.2006.07.105. [Google Scholar] [CrossRef]

49. Yan, X., Liu, H., Zhu, Z., Wu, Q. (2017). Hybrid genetic algorithm for engineering design problems. Cluster Computing, 20(1), 263–275. DOI 10.1007/s10586-016-0680-8. [Google Scholar] [CrossRef]

50. Kaveh, A., Dadras, A. (2017). A novel meta-heuristic optimization algorithm. Advances in Engineering Software, 110, 69–84. DOI 10.1016/j.advengsoft.2017.03.014. [Google Scholar] [CrossRef]

51. Kamboj, V. K., Nandi, A., Bhadoria, A., Sehgal, S. (2020). An intensify harris hawks optimizer for numerical and engineering optimization problems. Applied Soft Computing, 89, 106018. DOI 10.1016/j.asoc.2019.106018. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.