Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.018739

ARTICLE

Group Decision-Making Model of Renal Cancer Surgery Options Using Entropy Fuzzy Element Aczel-Alsina Weighted Aggregation Operators under the Environment of Fuzzy Multi-Sets

Jing Fu1,2, Jun Ye3 and Liping Xie1,*

1Department of Urology, The First Affiliated Hospital, College of Medicine, Zhejiang University, Hangzhou, 310003, China
2Department of Urology, Shaoxing Second Hospital, Shaoxing, 312000, China
3School of Civil and Environmental Engineering, Ningbo University, Ningbo, 315211, China
*Corresponding Author: Liping Xie. Email: xielp@zju.edu.cn
Received: 14 August 2021; Accepted: 28 September 2021

1  Introduction

The incidence of renal cell carcinoma (RCC) accounts for 2%–3% of adult malignant tumors. RCC is second only to prostate cancer and bladder cancer in urologic tumors, but it is the malignant tumor with the highest mortality rate in the urinary system [1]. The incidence rate is increasing every year in most countries and regions [1,2]. In recent years, with the widespread application of imaging techniques such as B-mode ultrasound, computed tomography (CT), and magnetic resonance imaging (MRI), as well as the increase in physical examination and screening, more and more patients with T1 stage RCC (tumor less than 7cm in diameter) have been diagnosed early. Currently, surgery is the preferred treatment for T1 stage RCC [3,4]. Localized renal tumor surgery methods include open surgery, laparoscopic surgery, etc., which can be performed by transperitoneal or retroperitoneal (translumbar) approach, including radical nephrectomy or partial nephrectomy. At present, the selection of surgical methods mainly depends on the physician’s past training skills and personal experience/judgment. Generally, surgical treatment options (STOs) for T1 stage RCC depend not only on its anatomical characteristics, but also on the hospital’s medical conditions, the patient’s financial ability, physical fitness and so on. It is obvious that existing renal cancer STOs lack a scientifical and reasonable evaluation/decision-making model in clinical applications.

In fact, the physician’s experience and judgment on the anatomical characteristics of RCC and some medical assessments of a renal cancer patient are also incomplete, uncertain, and vague because they cannot give accurate arguments in the medical diagnosis/assessment. In this case, fuzzy sets [5] are very suitable for the representment and processing of incomplete and uncertain information. Hence, fuzzy sets have been widely applied in medical diagnosis/evaluation problems. Then, many medical diagnosis/evaluation methods are mainly based on fuzzy relations of diseases and symptoms to obtain diagnosis/evaluation results of patients [6–10]. In hesitant situations, hesitant fuzzy sets (HFSs) and cubic HFSs have been utilized in medical diagnosis [11] and assessments of prostate hyperplasia symptoms and prostatic cancer [12,13]. However, due to the hesitation feature, HFS lacks the same fuzzy value information in the hesitation fuzzy elements, which shows its insufficiency in the expression of hesitation information. Since fuzzy multi-sets (FMSs) [14] can occur more than once with the different and/or identical membership values, El-Azab etal. [15] proposed correlation measures of FMSs and used them for medical diagnosis problems. Then, Turkarslan etal. [16] introduced a conversion method for transforming FMS into a consistency fuzzy set (CFS) based on the mean and consistency level (complement of standard deviation) of a fuzzy sequence in FMS, then they proposed the correlation coefficient and cosine similarity measure of CFSs and applied it to medical diagnosis problems in the setting of FMSs.

FMS has a number of properties that make it suitable for the expression of multivalued information (the group evaluation information) with the different and/or same fuzzy values, which are usually occurred in group evaluation process of a patient’s medical diagnosis and treatment. Since the existing STO for a renal cancer patient is mainly dependent on the clinical experience and judgment of physicians, the determination of the best STO for a renal cancer patient lacks a scientific and reasonable decision-making model in the existing literature. However, in existing clinical applications, there is no fuzzy decision-making/evaluation model for the most suitable STO regarding a patient with T1 stage RCC. Therefore, it is necessary to develop an effective group decision-making (GDM) model to determine the most suitable STO corresponding to a fuzzy multivalued/group evaluation information for the renal cancer patient. Then, the STO problem is a multicriteria GDM problem, where the medical team (a group of physicians) is required to assess the situations of the renal cancer patient and decide the most suitable STO for the patient. Although some authors recently applied three-way decision methods [17–19] to decision-making problems with fuzzy or fuzzy rough information, they cannot handle GDM problems with FMS information.

However, the GDM problem usually contains uncertain, incomplete, and vague evaluation information in the assessment process of a patient with T1 stage RCC because no physician can give an accurate evaluation value of the patient’s condition. Then, the FMS information is very suitable for the information expression of the GDM problem of STOs. In a GDM problem, the consistency level can be reflected by the complement of standard deviation of group evaluation values [16]. Since there is a certain degree of approximately linear relationship between the standard deviation and Shannon/probability entropy [20], the larger the standard deviation, the smaller the Shannon/probability entropy value. Therefore, the Shannon/probability entropy measure can also reflect the consistency level of group evaluation values. Thus, we can effectively express the group evaluation information based on the average value and entropy value of a fuzzy sequence in FMS to reasonably simplify information expression and operations between different fuzzy sequence lengths. Motivated by these ideas, this study proposes a multicriteria GDM model based on the Aczel-Alsina aggregation operators and score function of entropy fuzzy elements (EFEs) to solve the GDM problem of STOs regarding the patient with T1 stage RCC under the environment of FMSs. To do so, the aims of this work are (1) to propose a conversion method for transforming FMSs into entropy fuzzy sets (EFSs), a score function of EFE for ranking EFEs, and operation relations of EFEs based on the Aczel-Alsina t-norm and t-conorm operations [21,22], (2) to present the EFE Aczel-Alsina weighted arithmetic averaging (EFEAAWAA) and EFE Aczel-Alsina weighted geometric averaging (EFEAAWGA) operators and their properties, (3) to develop a multicriteria GDM model of the renal cancer STOs, and (4) to apply the proposed GDM model to two clinical cases of renal cancer patients for deciding the most suitable STO for each renal cancer patient in the setting of FMSs and verifying the efficiency and rationality of the proposed GDM model.

In this study, the proposed GDM model can overcome the flaw of the traditional STOs and provide a new effective way for determining the best STO for a renal cancer patient. Then, the GDM applications of two clinical cases show the effectiveness and rationality of the proposed GDM model in the setting of FMSs. Comparative analysis indicates that the merits of the proposed model are more reasonable and flexible than existing methods in information expression and decision-making algorithms.

The rest of this paper consists of the following sections: Section 2 presents a conversion method for transforming FMSs into EFSs based on the mean and Shannon entropy of a fuzzy sequence in FMS, a score function of EFE for ranking EFEs, and the Aczel-Alsina t-norm and t-conorm operations of EFEs. Section 3 proposes the EFEAAWAA and EFEAAWGA operators. In Section 4, a multicriteria GDM model of renal cancer STOs is established based on the EFEAAWAA and EFEAAWGA operators and the score function in the setting of FMSs. Finally, the GDM applications of two clinical cases show the effectiveness and rationality of the proposed GDM model in the setting of FMSs in Section 5. Section 6 indicates some conclusions and future research.

2  EFSs and Operations of EFEs in the FMS Environment

This section proposes a conversion method that converses FMSs into EFSs based on the mean and Shannon entropy of fuzzy sequences in FMS, and then defines the score function and ranking rules of EFEs. Then, operational relations of EFEs are presented based on the Aczel-Alsina t-norm and t-conorm operations [21,22].

2.1 EFSs Based on the Mean and Shannon Entropy of Fuzzy Sequences in FMS

This part proposes a conversion method that converses FMSs into EFSs based on the mean and Shannon entropy of fuzzy sequences in FMS, and then defines the score function and ranking rules of EFEs.

First, we introduce the concept of the Shannon/probability entropy [20].

Let B={b1,b2,…,bn} be a probability distribution on a random variable set. Then, the Shannon entropy of the probability distribution B is defined as

P(B)=−∑j=1nbjln⁡(bj), (1)

where bj∈ [0,1] and ∑j=1nbj=1.

Especially when all values of bj (j=1,2,…,n) are the same, the Shannon entropy reflects the maximum value of P(B), which means the perfect consistency of bj. To some extent, there is an approximately linear relationship between Shannon entropy and standard deviation: the smaller the standard deviation (the better the consistency level), the larger the entropy value.

Then, we introduce the concept of FMS [14].

Let U={u1,u2,…,un} be a finite set. Then, the FMS F on U is defined as

where MF(uj) is an increasing fuzzy sequence MF(uj)=(ζF1(uj),ζF2(uj),…,ζFsj(uj))(j=1,2,…,n), simply denoted as the j-th fuzzy sequence MFj=(ζFj1,ζFj2,…,ζFjsj).

In the following, we present a conversion method for transforming FMS into EFS.

Definition 2.1. Let U={u1,u2,…,un} be a finite set. Then, the EFS E on U is defined below:

Example 1. Let U={u1,u2,u3} be the universal set. Assume that there is , in U. Then, using Eqs. (2) and (3) we have the following results:

Thus, the FMS F can be transformed into the EFS , E= { <u1, (0.6, 1)>, <u2, (0.625, 0.9893)>, <u3, (0.6667, 0.9835)> }.

To compare EFEs, we define the score function and ranking rules of EFEs.

Definition 2.2. Set two EFEs as pEj = < mEj, eEj > (j = 1, 2). Then, the score function of pEj is defined below:

2.2 Aczel-Alsina T-Norm and T-Conorm Operations of EFEs

Aczel-Alsina [21] and Alsina etal. [22] presented the t-norms Sδ(g,h): [0,1]2→ [0,1] and t-conorms Tδ(g,h): [0,1]2→ [0,1] for g,h∈ [0,1] with any parameter δ≥0 and defined the following t-norms and t-conorms:

(i) The Aczel-Alsina t-norms are defined by

(ii) The Aczel-Alsina t-conorms are defined by

where S0(g, h) and T0(g, h) are the drastic t-norm and the drastic t-conorm, respectively, which are represented below:

Regarding the Aczel-Alsina t-norm and t-conorm with δ≥1, we can define some operations of EFEs.

Definition 2.3. Let pE1 = < mE1, eE1 > and pE2 = < mE2, eE2 > be two EFEs, δ≥1, and ω>0. Then, their operational rules are defined as follows:

3  Aczel-Alsina Aggregation Operators of EFEs

This section proposes the EFEAAWAA and EFEAAWGA operators according to the operational relations in Definition 2.3 and indicates their properties.

3.1 EFEAAWAA Operator

This part proposes the EFEAAWAA operator according to the operational relations in Definition 2.3.

Definition 3.1 Let j=1,2,…,n be a group of EFEs, along with their corresponding weight vector ω=(ω1,ω2,…,ωn) for ωj∈ [0,1] and ∑j=1nωj=1. Then, the EFEAAWAA operator is defined by

According to the operational relations in Definition 2.3, the EFEAAWAA operator contains the following theorem.

Theorem 3.1 Set pEj = < mEj, eEj > as a group of EFEs (j=1,2,…,n) with their corresponding weight vector ω=(ω1,ω2,…,ωn) for ωj∈ [0,1] and ∑j=1nωj=1. Then, the aggregated value of the EFEAAWAA operator is also EFE, which is obtained by the following formula:

Proof: Theorem 3.1 can be proved by mathematical induction.

(a) If n = 2, according to Definition 3.1 and Esq. (5) there is the following result:

EFEAAWAA(pE1,pE2)=ω1pE1⊕ω2pE2=〈1−e−(ω1(−ln(1−mE1))δ)1/δ,1−e−(ω1(−ln(1−eE1))δ)1/δ〉                 ⊕〈1−e−(ω2(−ln(1−mE2))δ)1/δ,1−e−(ω2(−ln(1−eE2))δ)1/δ〉                  =〈1−e−(∑j=12ωj(−ln(1−mEj))δ)1/δ,1−e−(∑j=12ωj(−ln(1−eEj))δ)1/δ〉. (7)

(b) If Eq. (6) for n = k is true, there exists the equation:

EFEAAWAA(pE1,pE2,…,pEk)=j=1⊕kωjpEj= 〈1−e−(∑j=1kωj(−ln(1−mEj))δ)1/δ,1−e−(∑j=1kωj(−ln(1−eEj))δ)1/δ〉 (8)

(c) If n = k + 1, according to Eqs. (7) and (8) we yield the result:

Based on the results of (a), (b), and (c), Eq. (6) can exist for any n.

Clearly, the EFEAAWAA operator of Eq. (6) contains the following properties.

Theorem 3.2 The EFEAAWAA operator implies the following properties:

Proof: (p1) Since j=1,2,…,n, using Eq. (6) we obtain the result:

(p2) The property is straightforward.

(p3) Since the inequalities minj(pEj)≤pEj≤maxj(pEj) and minj(eEj)≤eEj≤maxj(eEj) exist, we can yield the following inequalities:

Based on the property (p1) and the ranking rules, we have pEmin≤j=1⊕nωjpEj≤pEmax, i.e., pEmin≤EFEAAWAA(pE1,pE2,…,pEn)≤pEmax.

(p4) Since pEj≤pEj∗(j=1,2,…,n), there is j=1⊕nωjpEj≤j=1⊕nωjpEj∗. Then, EFEAAWAA(pE1, pE2,…,pEn)≤EFEAAWAA(pE1∗,pE2∗,…,pEn∗) exists.

Especially when δ=1, the EFEAAWAA operator is reduced to the EFE weighted arithmetic averaging (EFEWAA) operator:

EFEWAA(pE1,pE2,…,pEn)=j=1⊕nωjpEj=⟨1−∏j=1n(1−mEj)ωj,1−∏j=1n(1−eEj)ωj⟩ (9)

3.2 EFEAAWGA Operator

In this part, the EFEAAWGA operator is proposed based on the operational relations in Definition 2.3.

Definition 3.2 Set j=1,2,…,n as a group of EFEs with their corresponding weight vector ω=(ω1,ω2,…,ωn) for ωj∈ [0,1] and ∑j=1nωj=1. Then, the EFEAAWGA operator is defined by

According to the operational relations in Definition 2.3, the EFEAAWG operator contains the following theorem.

Theorem 3.3 Set j=1,2,…,n as a group of EFEs with their corresponding weight vector ω=(ω1,ω2,…,ωn) for ωj∈ [0,1] and ∑j=1nωj=1. Then, the aggregated value of the EFEAAWGA operator is also EFE, which is yielded by the formula:

Based on the similar verification of Theorem 3.1, Theorem 3.3 can be easily proved, which is omitted here.

However, the EFEAAWGA operator also contain the following properties.

Theorem 3.4 The EFEAAWGA operator contains the following properties:

Based on the similar proof method of Theorem 3.2, Theorem 3.4 can be easily proved, which is not repeated here.

Especially when δ=1, the EFEAAWGA operator of Eq. (11) is reduced to the EFE weighted geometric averaging (EFEWGA) operator:

EFEWGA(pE1,pE2,…,pEn)=j=1⊗npEjωj=⟨∏j=1nmEjωj,∏j=1neEjωj⟩ (12)

4  GDM Model of Renal Cancer STOs

Renal cancer is a disease that starts in the kidneys, where kidney cells become malignant (cancerous) and grow out of control to form a tumor. Then, renal cell carcinoma is the most common type of renal cancer in adults and usually appears in one or both kidneys. Other less common types of kidney cancer can occur. Once kidney cancer occurs, the physician will perform tests to determine whether the cancer has spread in the kidneys or other parts of the body. This process is named staging. The higher the stage, the more serious the cancer. First, the physician must know the stage before determining a treatment option. Then, surgery is the most common treatment for most people with early stage renal cancer (T1 stage) to remove all or part of the kidney. However, the treatment options will depend on the stage, general health, age, and other factors of the cancer patient.

To effectively determine a suitable STO for a kidney cancer patient in clinical medicine, physicians usually choose a better STO for the patient among the common STOs based on their experience and judgment of the patient’s situations. However, due to various influencing factors, such as RENAL nephrometry score (a comprehensive standardized system for quantitating renal tumor size) [23], tumor kidney location, tumor adjacent to renal pedicle vessel, mayo adhesive probability score [24], and treatment effect, it is difficult for physicians to directly give a cancer patient the most suitable STO. Hence, this is a GDM problem of STOs, which usually contains uncertain, incomplete, and vague evaluation information in the treatment issue of a kidney cancer patient. In this case, due to the uncertainty and ambiguity of the cognition/judgment of physicians regarding a kidney cancer patient, each physician in the medical treatment group gives his/her own fuzzy evaluation values of STOs over various influencing factors/criteria of a kidney cancer patient during the medical evaluation process. Thus, the FMS information is very suitable for the information expression of the group evaluation problem of STOs. Therefore, this section proposes a multicriteria GDM model of STOs regarding the patient with T1 stage renal cancer under the environment of FMSs.

Regarding current medical techniques for patients with T1 stage kidney cancer, physicians usually consider the six potential STOs (alternatives): open radical nephrectomy (ORN), transperitoneal laparoscopic radical nephrectomy (TLRN), retroperitoneal laparoscopic radical nephrectomy (RLRN), open partial nephrectomy (OPN), transperitoneal laparoscopic partial nephrectomy (TLPN), and retroperitoneal laparoscopic partial nephrectomy (RLPN), which can be constructed as a set of STOs T = {ORN, TLRN, RLRN, OPN, TLPN, RLPN} = {T1, T2, T3, T4, T5, T6}. To decide the best STO in the available set of STOs (alternatives) for a renal cancer patient, the six potential STOs (alternatives) must be satisfactorily assessed by the main influencing factors/criteria: RENAL nephrometry score (q1), tumor kidney location (q2), tumor adjacent to renal pedicle vessel (q3), mayo adhesive probability score (q4), hospital stay (q5), postoperative complications (q6), patient’s financial capacity (q7), technical skills (q8), medical condition (q9), and patient’s physical condition before surgery (q10), which are constructed as a set of criteria Q={q1,q2,q3,q4,q5,q6,q7,q8,q9,q10}. Then, the importance weight vector of the ten criteria is specified as ω=(ω1,ω2,…,ω10) for ωj∈ [0,1] and ∑j=110ωj=1.

In this decision-making problem, we can establish a multicriteria GDM model of renal cancer STOs and give the following decision process.

Step 1: In the assessment process, the medical treatment group of physicians, such as the chief physician, deputy chief physician, and physician, gives their suitable evaluation values of the six alternatives over the ten criteria. Based on their evaluated fuzzy values, we can establish the FMS evaluation/decision matrix M=(MFij)6×10, where MFij=(ζFij1,ζFij2,…,ζFijsj) (j=1,2,…,10; i=1,2,…,6) are fuzzy sequences.

Step 2: Using Eqs. (2) and (3), we transform FMSs in M into EFSs. Then, all EFSs are constructed as the EFS matrix P=(pEij)6×10, where pEij = < mEij, eEij > (j=1,2,…,10;i=1,2,…,6) are EFEs.

Step 3: The aggregated EFEs pEi for Ti(i=1,2,…,6) are yielded by the EFEAAWAA operator or the EFEAAWGA operator:

lpEi=EFEAAWAA(pEi1,pEi2,…,pEi10)=j=1⊕10ωjpEij=〈1−e−(∑j=110ωj(−ln(1−mEij))δ)1/δ,1−e−(∑j=110ωj(−ln(1−eEij))δ)1/δ〉 (13)

or

pEi=EFEAAWGA(pEi1,pEi2,…,pEi10)=j=1⊗10pEijωj=⟨e−(∑j=110ωj(−ln⁡mEij)δ)1/δ,e−(∑j=110ωj(−ln⁡eEij)δ)1/δ⟩ (14)

Step 4: The score values of R(pEi)(i=1,2,…,6) are calculated by Eq. (4).

Step 5: The alternatives are ranked in a descending order corresponding to the score values, then the best STO is given for a renal cancer patient.

Step 6: End.

5  GDM Cases of STOs for Renal Cancer Patients

To show the applicability and efficiency of the proposed GDM model, two clinical cases of renal cancer patients are provided to decide the most suitable STO for each renal cancer patient by the proposed GDM model in the setting of FMSs. Then, comparison with existing related methods shows the feasibility and rationality of the proposed model in the case of FMSs.

5.1 Applications of Two Actual Cases

Case 1 There is a patient at the First Affiliated Hospital, College of Medicine, Zhejiang University, China. She is a 62-year-old woman with a history of hypertension for more than 10 years. During her physical examination in December 2020, she had the posterior segment of the right kidney (right kidney tumor) through the related examinations of CT renal tumor assessment and angiography (CTA) (kidney tumors and blood vessels). Then, her detailed diagnosis results indicated: (1)the RENAL nephrometry score was low risk, (2)the tumor kidney location was uncertain, (3)the tumor was not adjacent to renal pedicle vessel, (4)the mayo adhesive probability score was low.

Regarding this clinical case of the renal cancer patient, we can apply the established GDM model of renal cancer STOs to the decision-making problem of STOs for the renal cancer patient and give the following decision process.

First, the medical treatment team consisting of three physicians (the chief physician, deputy chief physician, and physician) gave their appropriate assessments of the six alternatives over the ten criteria during the patient assessment process, then their fuzzy evaluation results can be established as the FMS matrix M=(MFij)6×10, where MFij=(ζFij1,ζFij2,…,ζFijsj) (j=1,2,…,10; i=1,2,…,6; sj = 3) are fuzzy sequences, which are shown in Table 1.

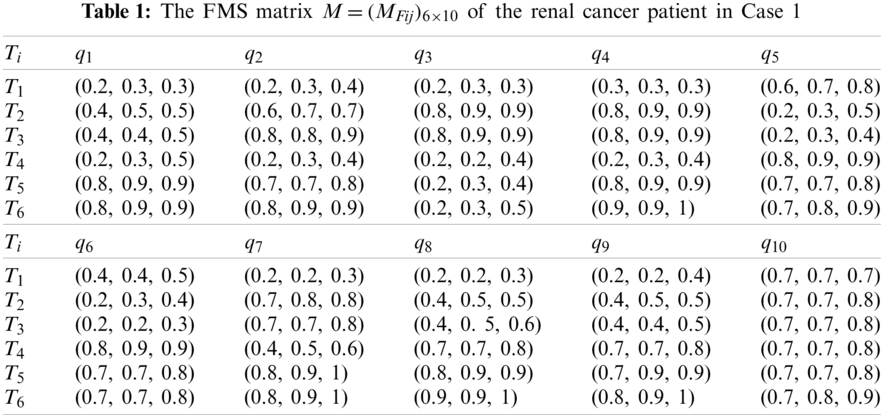
Second, using Eqs. (2) and (3), we transform the FMS matrix M=(MFij)6×10 in Table 1 into the EFS matrix P=(pEij)6×10 in Table 2, where pEij = < mEij, eEij > (j=1,2,…,10; i=1,2,…,6) are EFEs.

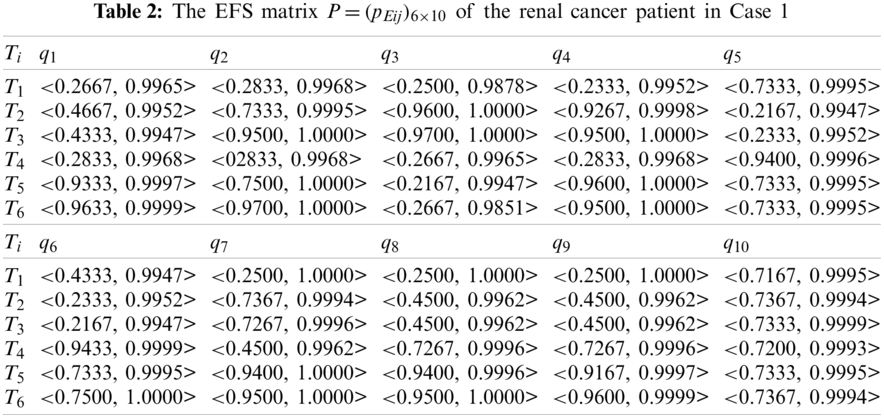
In this case, we do not consider the important differences among the ten criteria. Thus, the weight values of the ten criteria are specified as ωj=1/10(j=1,2,…,10). Using the EFEAAWAA operator of Eq. (13) or the EFEAAWGA operator of Eq. (14), the aggregated EFEs pEi for Ti(i=1,2,…,6) and the score values of R(pEi) are obtained by taking δ=1,2,3. Then the decision results are shown in Table 3.

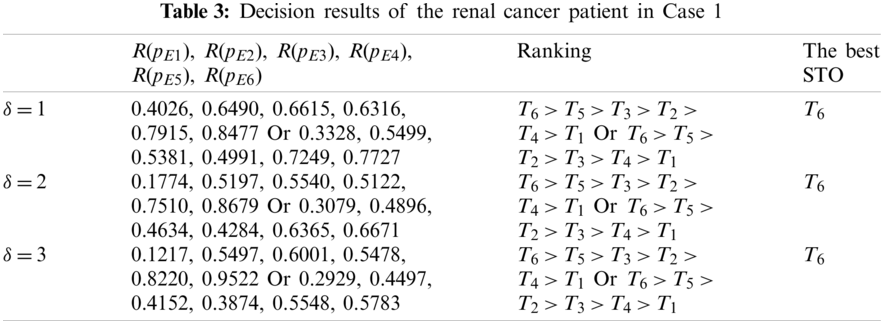
In Table 3, the ranking orders reflect their difference corresponding to different aggregation operators. Based on the ranking results in Table 3, the best STO T6 can be decided for the patient with renal cancer, and then the STS T5 can also be given as the second option. Meanwhile, we see that the different values of δ cannot impact on the ranking orders of STOs, which show some robustness of ranking orders in this case. In clinical applications, physicians may select a preference aggregation operator and value of δ in actual decision process so as to determinate the best STO for a patient.

In Case 1, the medical treatment group specified the best STS T6 for the renal cancer patient. After she underwent surgery through the retroperitoneal laparoscopic partial nephrectomy (RLPN), she had no postoperative complications, and then followed up well after half a year.

Case 2 There is another patient at the First Affiliated Hospital, College of Medicine, Zhejiang University, China. He is a 67-year-old man and has no past medical history. In April 2021, he had the right kidney tumor through the related examinations of CT renal tumor assessment and angiography (CTA) and CT urography in the hospital. Then, his detailed diagnosis results indicated: (1) the RENAL nephrometry score was high risk, (2) the location of the tumor’s kidney was uncertain, (3) the tumor was adjacent to renal pedicle vessel, and (4) the mayo adhesive probability score was low.

Regarding this clinical case of the renal cancer patient, we can also apply the established GDM model of renal cancer STOs to the decision-making problem of STOs for the renal cancer patient and give the following decision process.

First, the medical treatment team consisting of three physicians (the chief physician, deputy chief physician, and physician) gave their suitable fuzzy assessments of the six alternatives over the ten criteria in the patient assessment process, then their evaluation results can be established as the FMS matrix M=(MFij)6×10, where MFij=(ζFij1,ζFij2,…,ζFijsj) (j=1,2,…,10; i=1,2,…,6; sj=3) are fuzzy sequences, which are shown in Table 4.

Second, using Eqs. (2) and (3), we transform the FMS matrix M=(MFij)6×10 in Table 4 into the EFS matrix P=(pEij)6×10 in Table 5, where pEij = < mEij, eEij > (j=1,2,…,10; i=1,2,…,6) are EFEs.

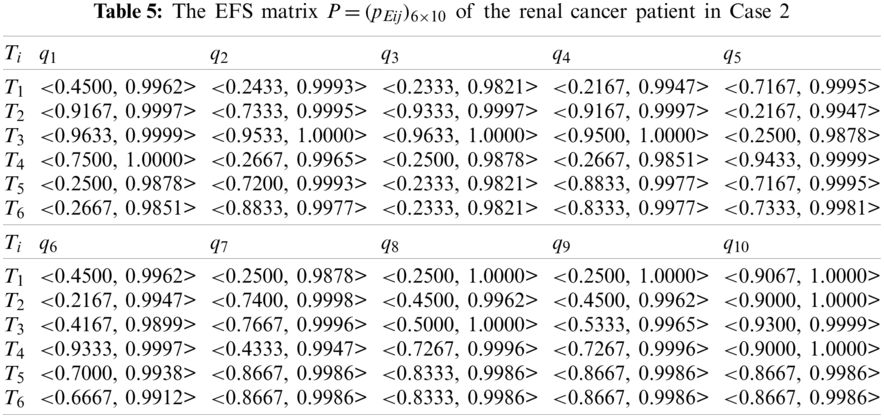
Similarly, we do not consider the important differences among the ten criteria. Thus, the weight values of the ten criteria are specified as ωj=1/10(j=1,2,…,10). by the EFEAAWAA operator of Eq. (13) or the EFEAAWGA operator of Eq. (14), the aggregated EFEs pEi for Ti(i=1,2,…,6) and the score values of R(pEi) are yielded corresponding to δ=1,2,3. Thus, the decision results are shown in Table 6.

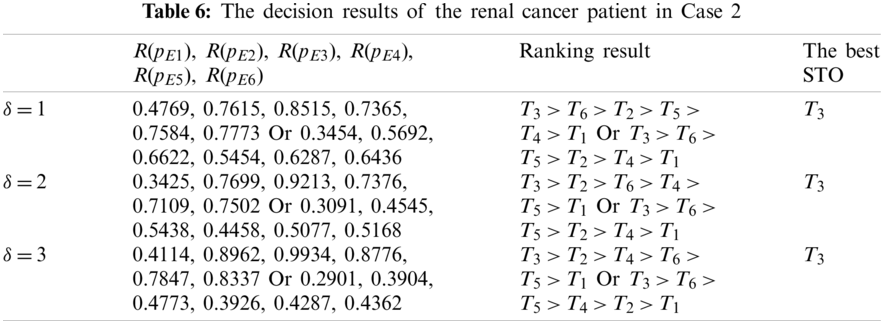
In Table 6, the ranking results reflect their difference corresponding to different aggregation operators and values of δ. Based on the ranking results in Table 6, the best STO T3 can be given to the patient with renal cancer. Since the different aggregation operators and values of δ can impact on the ranking orders of STOs in this case, the ranking orders show some flexibility and sensitivity to the two aggregation operators and values of δ. In clinical applications, physicians may select a preferred aggregation operator and value of δ in actual decision process so as to determinate the best STO for a patient.

In Case 2, the medical treatment team used the best STO T3 for the renal cancer patient. After he underwent surgery through the retroperitoneal laparoscopic radical nephrectomy (RLRN), he had no postoperative complications, and then followed up well after half a year.

Since the traditional method of STOs mainly depends on physicians’ clinical experience and judgment for a renal cancer patient, the determination of the best STO for the renal cancer patient lacks a scientifical and reasonable decision-making/evaluation model. Then, the GDM model proposed in this study can overcome this flaw of the existing selection method and provide a new effective way for the determination of the best STO for a renal cancer patient. However, the GDM applications of two clinical cases indicate that the proposed GDM model of the renal cancer STOs shows the advantages of the usability and rationality in the setting of FMSs.

5.2 Comparison with the Related Methods

In this original study, we propose the GDM model of renal cancer STOs for the first time. Then, there are no existing methods/models for solving renal cancer STO problems in the current literature or clinical applications. Therefore, it is difficult to make a qualitative comparison with the existing methods. However, we have to address the comparison of the following characteristics in the expression of information and the GDM method of STOs in the case of FMSs.

Since the traditional method of STOs mainly depends on physicians’ clinical experience and judgment for a renal cancer patient, the determination of the best STO for the renal cancer patient lacks a scientific and reasonable decision-making/evaluation model in current clinical applications. Then, the GDM model proposed in this study can overcome this flaw of the existing selection method and provide a new effective way for the determination of the best STO for a renal cancer patient. Through the clinical application of the best STOs in the two actual cases, there were no postoperative complications, and the follow-up for half a year showed good results, reflecting the effectiveness and rationality of the best STOs in the clinical application. However, the applications of GDM in two clinical cases indicate that the proposed GDM model of renal cancer STOs shows the advantages of its feasibility and rationality in the setting of FMS.

In the case of FMSs, El-Azab er al. [15] presented correlation coefficients of FMSs for medical diagnosis. Then, Turkarslan etal. [16] introduced the concept of CFS in terms of the average value and consistency degree (complement of standard deviation) of a fuzzy sequence in FMS and proposed GDM methods using the weighted correlation coefficient and weighted cosine similarity measure of CFSs. However, existing methods [15,16] cannot be applied to the two actual cases because we cannot find a desired/ideal STO/CFS Ti∗ in current clinical applications and existing literature and use the correlation coefficient or cosine similarity measure between the STO Ti and the desired CFS Ti∗. Obviously, our GDM model without considering the ideal STO/CFS can solve the STO problem and reflect its superiority over the existing methods in clinical applications. In addition, the conversion method using the complement of the standard deviation (degree of consistency) [16] is generally only suitable for the normal distribution, which shows its limitations, then we can make up for this gap by using the normalized entropy conversion method. Therefore, our model reflects its highlighting merits in the information expression of EFS, flexible aggregation operations, and the GDM method of STOs in the case of FMSs.

6  Conclusion

In view of the lack of scientific and reasonable decision-making models in the commonly used STO methods for renal cancer patients, this article established a multicriteria GDM model of renal cancer STOs to overcome the flaws of the existing methods. In this study, regarding FMSs evaluated by the medical group in the assessment process of a renal cancer patient, we proposed a conversion method for conversing FMSs into EFSs based on the mean and Shannon entropy of each fuzzy sequence in FMS to reasonably simplify the information expression and operations of FMSs and defined the score function and ranking rules of EFEs. Then, we proposed the EFEAAWAA and EFEAAWGA operators based on the Aczel-Alsina t-norm and t-conorm operations of EFEs. Furthermore, a multicriteria GDM model was established based on the EFEAAWAA and EFEAAWGA operators and the score function to solve the decision-making problems of STOs for renal cancer patients in the setting of FMSs. Finally, the GDM applications of two clinical cases indicated that the proposed GDM model can show the advantages of the efficiency and rationality under the environment of FMSs. The decision-making results of the two cases demonstrated that the GDM model proposed in this study can overcome the flaw of the existing traditional STO method and provide a new effective way to determine the best STO for a renal cancer patient in the FMS environment.

In future research, we can extend the proposed GDM model to STOs of other cancer patients, such as prostate and bladder cancer patients under the FMS environment. Furthermore, we further also propose new fuzzy multivalued measure algorithms and GDM models to solve diagnosis/assessment problems of cancer patients with group fuzzy evaluation values.

Funding Statement: This study has received funding by the Science and Technology Plan Project of Keqiao District (No. 2020KZ58).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wein, A. J., Kavoussi, L. R., Partin, A. W., Peters, C. A. (2015). Campbell-walsh urology. 11 edition, pp. 1320–1321. Amsterdam: Elsevier. [Google Scholar]

 2.  Sung, H., Ferlay, J., Siegel, R. L. (2021). Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer Journal for Clinicians, 71(3), 209–249. DOI 10.3322/caac.21660. [Google Scholar] [CrossRef]

 3.  Escudier, B., Porta, C., Schmidinger, M. (2019). Renal cell carcinoma: ESMO clinical practice guidelines for diagnosis, treatment and follow-up. Annals of Oncology, 30(5), 706–720. DOI 10.1093/annonc/mdz056. [Google Scholar] [CrossRef]

 4.  Campbell, S. C., Clark, P. E., Chang, S. S. (2021). Renal mass and localized renal cancer: Evaluation, management, and follow-up: AUA guideline: Part I. Journal of Urology, 206(2), 199–208. DOI 10.1097/JU.0000000000001911. [Google Scholar] [CrossRef]

 5.  Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI http://dx.doi.org/10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]

 6.  Adlassnig, K. P. (1986). Fuzzy set theory in medical diagnosis. IEEE Transactions on Systems, Man, and Cybernetics, 16(2), 260–265. DOI 10.1109/TSMC.1986.4308946. [Google Scholar] [CrossRef]

 7.  Khanale, P. B., Ambilwade, R. P. (2011). A fuzzy inference system for diagnosis of hypothyroidism. Journal of Artificial Intelligence, 4(1), 45–54. DOI 10.3923/jai.2011.45.54. [Google Scholar] [CrossRef]

 8.  Choi, H., Han, K., Choi, K., Ahn, J. (2016). A fuzzy medical diagnosis based on quintiles of diagnostic measures. Journal of Intelligent & Fuzzy Systems, 31(6), 3197–3202. DOI 10.3233/JIFS-169205. [Google Scholar] [CrossRef]

 9.  Choi, G., Mun, J., Ahn, C. (2012). A medical diagnosis based on interval valued fuzzy set. Biomedical Engineering: Applications, Basis and Communications, 24(4), 349–354. DOI 10.4015/S1016237212500305. [Google Scholar] [CrossRef]

10. Oye, N. D., Thomas, L. L. (2019). Fuzzy model for diagnosis of bacterial meningitis. International Journal of Computer Applications Technology and Research, 8(02), 33–51. DOI 10.7753/IJCATR0802.1001. [Google Scholar] [CrossRef]

11. Farhadinia, B. (2016). Utility of correlation measures for weighted hesitant fuzzy sets in medical diagnosis problems. Mathematical Modelling and Applications, 1(2), 36–45. DOI 10.11648/j.mma.20160102.12. [Google Scholar] [CrossRef]

12. Fu, J., Ye, J., Cui, W. H. (2018). An evaluation method of risk grades for prostate cancer using similarity measure of cubic hesitant fuzzy sets. Journal of Biomedical Informatics, 87(8), 131–137. DOI 10.1016/j.jbi.2018.10.003. [Google Scholar] [CrossRef]

13. Fu, J., Ye, J., Cui, W. (2019). The Dice measure of cubic hesitant fuzzy sets and its initial evaluation method of benign prostatic hyperplasia symptoms. Scientific Reports, 9(1), 60. DOI 10.1038/s41598-018-37228-9. [Google Scholar] [CrossRef]

14. Yager, R. R. (1986). On the theory of bags. International Journal of General Systems, 13(1), 23–37. DOI 10.1080/03081078608934952. [Google Scholar] [CrossRef]

15. El-Azab, M. S., Shokry, M., Abo Khadra, R. A. (2017). Correlation measure for fuzzy multisets. Journal of the Egyptian Mathematical Society, 25(3), 263–267. DOI 10.1016/j.joems.2017.02.007. [Google Scholar] [CrossRef]

16. Turkarslan, E., Ye, J., Unver, M., Olgun, M. (2021). Consistency fuzzy sets and a cosine similarity measure in fuzzy multiset setting and application to medical diagnosis. Mathematical Problems in Engineering, 2021(9), 1–9. DOI 10.1155/2021/9975983. [Google Scholar] [CrossRef]

17. Zhan, J., Jiang, H., Yao, Y. (2020). Three-way multi-attribute decision-making based on outranking relations. IEEE Transactions on Fuzzy Systems, 29(10), 2844–2858. DOI 10.1109/TFUZZ.2020.3007423. [Google Scholar] [CrossRef]

18. Zhang, K., Zhan, J., Wu, W. Z. (2021). On multi-criteria decision-making method based on a fuzzy rough set model with fuzzy α-neighborhoods. IEEE Transactions on Fuzzy Systems, 29(9), 2491–2505. DOI 10.1109/TFUZZ.2020.3001670. [Google Scholar] [CrossRef]

19. Zhan, J., Ye, J., Ding, W., Liu, P. (2021). A novel three-way decision model based on utility theory in incomplete fuzzy decision systems. IEEE Transactions on Fuzzy Systems (in Press). DOI 10.1109/TFUZZ.2021.3078012. [Google Scholar] [CrossRef]

20. Shannon, C. E. (1948). A mathematical theory of communication. The Bell System Technical Journal, 27(3), 379–423. DOI 10.1002/j.1538-7305.1948.tb01338.x. [Google Scholar] [CrossRef]

21. Aczel, J., Alsina, C. (1982). Characterization of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements. Aequationes Mathematicae, 25(1), 313–315. DOI 10.1007/BF02189626. [Google Scholar] [CrossRef]

22. Alsina, C., Frank, M. J., Schweizer, B. (2006). Associative functions: Triangular norms and copulas. Danvers, MA: World Scientific Publishing. [Google Scholar]

23. Kutikov, A., Uzzo, R. G. (2009). The R.E.N.A.L. nephrometry score: A comprehensive standardized system for quantitating renal tumor size, location and depth. Journal of Urology, 182(3), 844–853. DOI 10.1016/j.juro.2009.05.035. [Google Scholar] [CrossRef]

24. Davidiuk, A. J., Parker, A. S., Thomas, C. S., Leibovich, B. C., Castle, E. P. et al. (2014). Mayo adhesive probability score: An accurate image-based scoring system to predict adherent perinephric fat in partial nephrectomy. European Urology, 66(6), 1165–1171. DOI 10.1016/j.eururo.2014.08.054. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.