
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.019159
ARTICLE
Research on Normal Pythagorean Neutrosophic Set Choquet Integral Operator and Its Application
1Department of Computer Science, Shaoxing University, Shaoxing, China
2College of Management Shenzhen University, Shenzhen, China
3Information Technology R&D Innovation Center of Peking University, Shaoxing, China
*Corresponding Author: Jihong Chen. Email: jihongchen@szu.edu.cn
Received: 06 September 2021; Accepted: 26 October 2021
Abstract: We first propose the normal Pythagorean neutrosophic set (NPNS) in this paper, which synthesizes the distribution of the incompleteness, indeterminacy, and inconsistency of the Pythagorean neutrosophic set (PNS) and normal fuzzy number. We also define some properties of NPNS. For solving the decision-making problem of the non-strictly independent and interacting attributes, two kinds of NPNS Choquet integral operators are proposed. First, the NPNS Choquet integral average (NPNSCIA) operator and the NPNS Choquet integral geometric (NPNSCIG) operator are proposed. Then, their calculating formulas are derived, their properties are discussed, and an approach for solving the interacting multi-attribute decision making based on the NPNS is studied. Finally, the two kinds of operators are applied to validate the stability of the new method.
Keywords: Normal pythagorean neutrosophic set (NPNS); NPNS choquet integral average (NPNSCIA) operator; NPNS choquet integral geometric (NPNSCIG) operator; multi-attribute decision making (MADM)
As an important branch of modern decision theory, MADM is widely used in many fields such as economy, management, military, and engineering. One of the core problems of MADM is how to give the attribute values under each attribute. Since Zadeh [1] proposed the concept of fuzzy set (FS), FS has become a hot research topic. Different scholars apply various methods and new theories to fuzzy decision making, improve and optimize the existing problems in fuzzy decision making, and make its development more perfect and reasonable. To popularize the FS, in 1986, Atanassov [2] introduced the concept of intuitionistic fuzzy set (IFS) and studied it. IFS can express membership degree and non-membership degree at the same time, and their sum is less than or equal to 1. Compared with traditional fuzzy sets, IFS is more suitable for describing fuzziness and uncertainty in practical problems. However, in the process of dealing with decision making, the sum of membership degree and non-membership degree may be greater than 1. So Yager [3] proposed the Pythagorean fuzzy set (PFS), which allows the sum of membership degree and non-membership degree to be greater than 1, but its sum of squares is not more than 1. PFS is an extension of IFS. Therefore, the processing of fuzzy and uncertain information has a stronger performance. On the basis of Yager's research, different scholars applied various methods and new theories to Pythagorean fuzzy decision making. For example, Peng et al. [4] put forward the Pythagoras soft set by integrating Pythagoras with the soft set. Liang and Peng et al. [5,6] studied interval-valued Pythagorean fuzzy sets. Liu et al. [7] proposed the Pythagorean hesitation fuzzy set by combining the Pythagorean and hesitation fuzzy set. Fan et al. [8] generalized the membership degree and non-membership degree of the Pythagorean fuzzy number and proposed the triangular Pythagorean fuzzy set. But IFS can only deal with incomplete information but not with uncertain and inconsistent information. Therefore, Smarandache [9,10] proposed the neutrosophic set (NS) theory based on IFS. It is a generalization of FS and IFS by adding independent uncertainty on the basis of IFS. In the NS theory, decision-makers can use the degree of truth, indeterminacy, and falsity to describe the evaluation of objective things. Since it was proposed, it has attracted extensive attention and research. Wang et al. [11] proposed a concept of single-valued neutrosophic sets (SVNS). Liu et al. [12] proposed a weighted aggregation operator and decision making method based on interval value neutrosophic sets (IVNS). Fan et al. [13–15] proposed decision making methods based on SVNS, linguistic neutrosophic multisets(LNM), and refined-SVNS. Liu et al. [16,17] proposed the normal neutrosophic set (NNS). Ye [18] proposed Correlation Coefficients of NNS. Jansi et al. [19] in 2019 proposed Pythagorean neutrosophic set (PNS) as an extension of Ajay et al. applied PNS in fuzzy graphs [20].
Ideally, the constructed decision indicator system should have the conditions of completeness, representativeness, and independence. However, in many practical cases, these attributes are usually not independent but correlated. In order to solve the MADM problem of attribute correlation, Marichal [21] in 2000 generalized the fuzzy measure defined by Sugeno [22] and proposed the Choquet integral [23]. Since Choquet integral was put forward, it has been hotly discussed by many scholars. Xu [24] applied Choquet integral to multi-attribute decision making of intuitional fuzzy sets and proposed intuitional fuzzy correlated average operator, intuitional fuzzy correlated geometric operator, etc. Tan et al. [25] proposed intuitionistic fuzzy Choquet integral average operator and intuitionistic fuzzy Choquet integral geometric operator. Qu et al. [26] applied the Choquet integral to the interval-hesitation fuzzy multi-attribute decision making and proposed the interval-hesitation fuzzy Choquet integral operator. Peng et al. [27] applied Choquet integral to The Pythagorean fuzzy decision making environment and proposed the Pythagorean fuzzy Choquet integral average operator and geometric operator. Dong et al. [28] proposed Generalized Choquet Integral Operator of Triangular Atanassov's Intuitionistic Fuzzy Numbers. Wan et al. [29] proposed Generalized Shapley Choquet integral operator based method for interactive interval-valued hesitant fuzzy uncertain linguistic. When solving MADM problems, Choquet integral operator can effectively deal with the redundant part of attribute compatibility, and solve the problem of attribute correlation by balancing the influence degree between attributes. In view of the Choquet integral operator can be used to consider the relationship between information, this paper proposes the normal Pythagorean neutrosophic set (NPNS) and generalize Choquet integral operator to the NPNS environment. NPNS synthesizes the distribution of the incompleteness, indeterminacy, and inconsistency of PNS and the normal neutrosophic number, which is more reasonable than PNS and NNS on expressing the decision making information. NPNS Choquet integral operator not only considers the importance between attributes but also reflects the relation between attributes. Then the properties of this operator are discussed, and an algorithm for solving the MADM problem is proposed based on this operator.
We organize the paper as follows. Section 2 describes basic concepts. Section 3 defines two Choquet integral operators of NPNS. Section 4 establishes the DM model based on NPNSCIA or NPNSCIG Operator. Section 5 provides an example. Section 6 gives conclusions.
2.1 Pythagorean Fuzzy set (PFS)
Definition 1 [3]. Set Y as an object set, a PFS is expressed as
Definition 2 [30]. Set
Definition 3 [10,11]. Set Y as an object set,
2.4 Pythagorean Neutrosophic Set (PNS)
Definition 4 [19]. Set Y as an object set,
2.5 Normal Pythagorean Neutrosophic Set (NPNS)
Definition 5. Set Y is an object set,
For convenience, a normal Pythagorean neutrosophic element (NPNE) is denoted as
Definition 6. Set
Definition 7. Set
and its accuracy functions are
Definition 8. Set
if
if
if
if
if
if
if
if
Definition 9 [22]. Set D(Y) as the power set to
i.
ii.
iii.
If
If
For
Definition 10 [21]. Set
In which
3 Two Choquet Integral Operators of NPNS
In this section, we define two normal Pythagorean neutrosophic set based Choquet integral operators, one is the normal Pythagorean neutrosophic set Choquet integral averaging (NPNSCIA) operator, and the other is the normal Pythagorean neutrosophic set Choquet integral geometric (NPNSCIG) operator. Meantime, we discuss some properties of them.
Definition 11. Set
NPNSCIA is called the NPNS Choquet integral averaging operator, in which (
According to some relevant operation rules of NPNE, we can get the form of the NPNSCIA operator shown in Theorem 1.
Theorem 1. Set
In which
Now, we proof Eq. (13).
Proof:
When n = 1, we can easily get Eq. (13).
When n = 2, we get:
Making a hypothesis, when n=
Then n=
This proves Theorem 1.
Theorem 2. Set
Proof:
Since
for
Theorem 3. Set
It is easy to prove it according to Definition 11, here we omit.
Theorem 4. Set
Proof:
Since
Since
Then, with Eq. (5),
Theorem 4 has been proved.
Theorem 5. (Boundedness). Set
Proof:
To Theorem 2,
To Theorems 3–4,
Then
Definition 12. Set
NPNSCIG is called the NPNS Choquet integral geometric operator, in which (
According to some relevant operation rules of NPNSs, we can get the form of the NPNSCIG operator shown in Theorem 6.
Theorem 6. Set
Theorem 7. Set
Theorem 8. Set
Theorem 9. Set
Theorem 10. (Boundedness). Set
It is easy to prove Theorems 6–10.
4 Decision Making Methods Based on NPNSCIA or NPNSCIG Operator
The multi-attribute decision problem with decision information of NPNS is described as follows: There are m schemes
Step 1: Build up C=
Step 2: Calculate the fuzzy measure of attribute sets;
Step 3: Calculate by using the NPNSCIA or NPNSCIG operator;
Step 4: Calculate each scheme's score value;
Step 5: Choose the best scheme.
The company plans to choose one of the four suppliers
Step 1: In Table 1, the decision makers give the evaluation values described by NPNE.
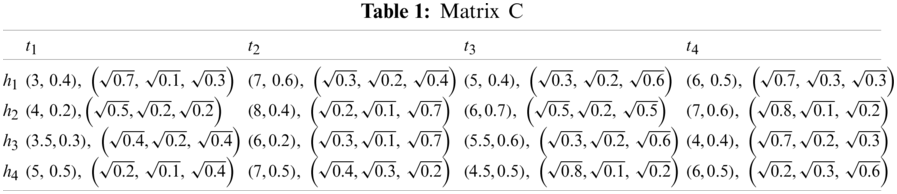
Step 2: Using Eq. (10), we calculate
Step 3: Using Eq. (9) and
Step 4: Using the NPNSCIA operator, we calculate each supplier's comprehensive value.
Step 5: Each supplier's score value can be gotten by using Eqs. (5), (6);
Step 6: According to the value
While using NPNSCIG operator:
Step 1’–3’: Just as Steps 1–3;
Step 4’: Using the NPNSCIG operator, we calculate each supplier's comprehensive value.
Step 5’: Each supplier's score value can be gotten by using Eqs. (5), (6).
Step 6’: According to the value
Compared with the literatures [16–19], NPNS Choquet integral operator can not only model the weight of attributes and attribute-set in MADM problem, measure the correlation, complementary correlation, and preference correlation between attributes, but also can fully consider the importance between attributes, so as to make the decision results more objective.
In this paper, NPNS and Choquet integral operators are combined to define the NPNSCIA operator and NPNSCIG operator, which can consider the incidence relation between indicators. It is proved that they have power equality, displacement invariance, ordered monotonicity, and boundedness. A nonlinear programming model is established and the FM of indicators and indicator sets is solved objectively. In the NPNS environment, by using the defined operators and the established model, the problem of related MADM with attribute weight information unknown or partially attribute weight information unknown is solved effectively. Finally, the case proves that this method is easy and reasonable. This study extended the Choquet integral to NPNS, making the Choquet integral better applied and developed in the related MADM problems.
Funding Statement: This research was funded by the National Natural Science Foundation of China, Grant No. 61703280; Zhejiang Provincial Natural Science Foundation of China, Grant No. LY20F020011; Social Sciences and Humanities Youth Foundation of Ministry of Education, Grant No. 21YJCZH039; Natural Science Foundation of Zhejiang Province, Grant No. TY22F025548; the Public Welfare Technology Research Project of Zhejiang Province, Grant No. GG22F015473 and Key scientific research project of Shaoxing University, Grant No. 2020LG1004.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Zedeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
2. Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
3. Yager, R. R. (2013). Pythagorean fuzzy subsets. IFSA World Congress and NAFIPS Annual Meeting, 2013, 57–61. DOI 10.1109/IFSA-NAFIPS.2013.6608375. [Google Scholar] [CrossRef]
4. Peng, X. D., Yang, Y., Song, J. P., Jiang, Y. (2015). Pythagorean fuzzy soft set and its application. Computer Engineering, 41(7), 224–229. DOI 10.3969/j.issn.1000-3428.2015.07.043. [Google Scholar] [CrossRef]
5. Liang, W., Zhang, X., Liu, M. (2015). The maximizing deviation method based on interval-valued pythagorean fuzzy weighted aggregation operator for multiple criteria group decision analysis. Discrete Dynamics in Nature and Society, 2015, 1–15. DOI 10.1155/2015/746572. [Google Scholar] [CrossRef]
6. Peng, X., Yang, Y. (2016). Fundamental properties of interval-valued pythagorean fuzzy aggregation operators. International Journal of Intelligent Systems, 31(5), 444–487. DOI 10.1002/int.21790. [Google Scholar] [CrossRef]
7. Liu, W. F., He, X.(2016). Pythagoras hesitation fuzzy set. Fuzzy Systems and Mathematics, 30(4), 107–115. [Google Scholar]
8. Fan, J. P., Yan, Y., Wu, M. Q. (2019). Multi-criteria decision making method based on triangle pythagorean fuzzy set. Control and Decision Making, 34(8), 1601–1608. [Google Scholar]
9. Smarandache, F. (1998). Neutrosophy: Neutrosophic probability, set, and logic. Rehoboth, DE, USA: American Research Press. [Google Scholar]
10. Smarandache, F. (1999). A unifying field in logics. In: Neutrosophy: Neutrosophic probability, set and logic. Rehoboth: American Research Press. [Google Scholar]
11. Wang, H., Smarandache, F., Zhang, Y. Q., Sunderraman, R. (2010). Single valued neutrosophic sets. Multispace and Multistructure, 4, 410–413. [Google Scholar]
12. Liu, P. D., Tang, G. L. (2016). Some power generalized aggregation operators based on the interval neutrosophic numbers and their application to decision making. Journal of Intelligent & Fuzzy Systems, 30, 2517–2528. DOI 10.3233/IFS-151782. [Google Scholar] [CrossRef]
13. Fan, C. X. (2019). Correlation coefficients of refined-single valued neutrosophic sets and their applications in multiple attribute decision-making. Journal of Advanced Computational Intelligence and Intelligent Informatics, 23(3), 421–426. DOI 10.20965/jaciii.2019.p0421. [Google Scholar] [CrossRef]
14. Fan, C. X., Hu, K. L., Feng, S., Ye, J., Fan, E. (2019). Heronian mean operators of linguistic neutrosophic multisets and their multiple attribute decision-making methods. International Journal of Distributed Sensor Networks, 15(4),155014771984305. DOI 10.1177/1550147719843059. [Google Scholar] [CrossRef]
15. Fan, C. X., Fan, E., Chen, J. H., Ye, J., Zhou, K. (2020). Single-value neutrosophic cosine measure for evaluation of port logistics competitiveness. Journal of Intelligent & Fuzzy Systems, 39(3), 4667–4675. DOI 10.3233/JIFS-200598. [Google Scholar] [CrossRef]
16. Liu, P. D., Teng, F. (2018). Multiple attribute decision-making method based on normal neutrosophic generalized weighted power averaging operator. International Journal of Machine Learning and Cybernetics, 9(2), 281–293. DOI 10.1007/s13042-015-0385-y. [Google Scholar] [CrossRef]
17. Liu, P. D., Li, H. G. (2017). Multiple attribute decision-making method based on some normal neutrosophic Bonferroni mean operators. Neural Computing and Applications, 28, 179–194. DOI 10.1007/s00521-015-2048-z. [Google Scholar] [CrossRef]
18. Ye, J. (2017). Multiple attribute decision-making method using correlation coefficients of normal neutrosophic sets. Symmetry, 9, 80. DOI 10.3390/sym9060080. [Google Scholar] [CrossRef]
19. Jansi, R., Mohana, K., Smarandache, F. (2019). Correlation measure for pythagorean neutrosophic sets with t and f as dependent neutrosophic components. Neutrosophic Sets and Systems, 30, 202–212. [Google Scholar]
20. Ajay, D., Chellamani, P. (2020). Pythagorean neutrosophic fuzzy graphs. International Journal of Neutrosophic Science, 11(2), 108–114. DOI 10.5281/zenodo.4172124. [Google Scholar] [CrossRef]
21. Marichal, J. L. (2001). An axiomatic approach of the discrete choquet integral as a tool to aggregate interacting criteria. IEEE Transactions on Fuzzy Systems, 8(6), 800–807. DOI 10.1109/91.890347. [Google Scholar] [CrossRef]
22. Sugeno, M. (1974). Theory of fuzzy integral and its application (Doctorial Dissertation). Tokyo Institute of Technology. [Google Scholar]
23. Choquet, G. (1954). Theory of capacities. Ann Institut Fourier, 5, 131–295. DOI 10.5802/aif.53. [Google Scholar] [CrossRef]
24. Xu, Z. S. (2010). Choquet integrals of weighted intuitionistic fuzzy information. Information Sciences, 180, 726–736. DOI 10.1016/j.ins.2009.11.011. [Google Scholar] [CrossRef]
25. Tan, C. Q., Chen, X. H. (2010). Intuitionistic fuzzy choquet integral operator for multi-criteria decision making. Expert Systems with Applications, 37(1), 149–157. DOI 10.1016/j.eswa.2009.05.005. [Google Scholar] [CrossRef]
26. Qu, G., Qu, W., Li, C. (2018). Some new interval-valued dual hesitant ant fuzzy choquet integral aggregation opeators and their applications. Journal of Intelligent & Fuzzy Systems, 34, 245–266. DOI 10.3233/JIFS-171162. [Google Scholar] [CrossRef]
27. Peng, X., Yang, Y. (2016). Pythagorean fuzzy choquet integral based MMBAC method for multiple attribute group decision making. International Journal of Intelligent Systems, 31(10), 989–1020. DOI 10.1002/int.21814. [Google Scholar] [CrossRef]
28. Dong, J. Y., Lin, L. L., Wan, S. P., Feng, W. (2016). Generalized choquet integral operator of triangular atanassov's intuitionistic fuzzy numbers and application to multi-attribute group decision making, international journal of uncertainty. Fuzziness and Knowledge-Based Systems, 24(5), 647–683. DOI 10.1142/S0218488516500306. [Google Scholar] [CrossRef]
29. Wan, S. P., Xiao, J. (2020). Generalized shapley choquet integral operator based method for interactive interval-valued hesitant fuzzy uncertain linguistic multi-criteria group decision making. IEEE Access, 8, 202194–202215. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]
30. Wang, J. Q., Li, K. J., Zhang, H. Y., Chen, X. H. (2013). A score function based on relative entropy and its application in intuitionistic normal fuzzy multiple criteria decision making. Journal of Intelligent & Fuzzy Systems, 25, 567–576. DOI 10.3233/IFS-120662. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |