Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.017391

ARTICLE

Bioconvection Cross Diffusion Effects on MHD Flow of Nanofluids over Three Different Geometries with Melting

Tahir Kamran, Muhammad Imran*, Muhammad N. Naeem and Mohsan Raza

Department of Mathematics, Government College University Faisalabad, Faisalabad, 38000, Pakistan
*Corresponding Author: Muhammad Imran. Email: drmimranranchaudhry@gmail.com
Received: 07 May 2021; Accepted: 09 June 2021

1  Introduction

Magnetohydrodynamics (MHD) has a vital role in several flow phenomena, including industry. The MHD is applied in various fields, including multidisciplinary technological areas like biochemical manufacturing heat transfer, automotive sector, ceramic technology, aerodynamic performance, metallurgical technology, mental operating techniques, and fluid dynamics. Magnetohydrodynamic initiation changes the flow field’s preferred direction by fluctuating boundary layer configuration flow. Electromagnetic fields play an important role in convection mechanisms like metallic casting, material processing fields, and nuclear reactor control plants. Zheng et al. [1] investigated the heat transformation in the two-dimensional flow of magnetohydrodynamic (MHD) by considering temperature and velocity slip effects through a shrinking porous surface. It was stated that the thermal boundary layer flow declined to owe to an increase in the shrinking parameters. The heat transmission and magnetohydrodynamic flow through the porous plate and shrinking surface were studied by Chauhan et al. [2]. The central concept was that the cooling rate was controlled by the electromagnetic number and suction parameter over channels bounded. Attia [3] examined the different physiological properties of the unsteady MHD Couette flowing heat exchange in a dusty fluid flow with variable viscosity. Kumar et al. [4] explored mass and heat transport across a vertical plate under the cross-diffusion impact in radiative mixed convective cases of magnetohydrodynamic fluid flow. The fluid movement increased with an increase in both the buoyancy force variables and the mixed convection parameter. Ibrahim et al. [5,6,7] observed heat exchange and MHD boundary layer nanofluid flow via vertical surfaces and a non–isothermal expanding surface using the similarity transformation technique. Ibrahim et al. [8,9] described nanoparticles’ MHD boundary layer flow through a stretched surface, influenced by double stratification and diffusion. Muhammad et al. [10] discussed the Eyring- Powell nanofluid with thermal radiation effects. Waqas et al. [11] checked the melting effects in a modified second-grade nanofluid. Danish et al. [12] explore the EMHD effects in Williamson nanofluid with activation energy and nonlinear thermal radiation. Waqas et al. [13] analyzed the flow and heat transfer improvement in radiative hybrid nanofluid flow across the disk. Mabood et al. [14] analyzed radiative nanofluid across the thin needle.

Several investigators studied heat transfer due to its various applications in applied technologies, manufacturing, and refrigeration. Thermally conductive fluid has subsequently become a common research topic for scientists. Nanotechnology is becoming a subject of significant interest in manufacturing and engineering for investigators as its requirement grows in industrial sectors. Non-Newtonian fluids are now a big subject for scientists and physiologists [15–17]. Moreover, the world is experiencing an energy problem because of global heating and pollution. As a result, researchers are working to develop new heat transfer techniques to make improvements that can be justified. Nanotechnology is one of the researchers' most recent techniques to help alleviate energy shortages. Choi et al. [18] introduced the nanofluids, and they have since achieved boundless attention. Nanofluids are the most using coolants in the industry. The thermal properties of a combination of nanometer-sized particles immersed in a fluid identified as nanofluids or base fluids improved due to the involvement of these nanomaterials. Buongiorno [19] explored how to augment the convection rate of heat transformation in two significantly slip situations: thermophoresis diffusion and Brownian motion behavior.

Bioconvection occurs because the microorganisms are denser than water; therefore, a motile gyrotactic microorganism moves upwardly in water. The production of the base fluid increased as the dynamically self-propelled motile gyrotactic microorganisms moved in a particular direction. Bioconvection is used in various areas, including fertilizer, biofuel, and manufacturing systems. Nanofluid bioconvection is considered for density stratified as well as patron formation due to nanomaterials apprentice, buoyancy forces, including microorganisms. Kuznetsov [20] reported that bioconvection in nanofluids is expected to occur if the concentration of nanoparticles is small so that nanoparticles do not cause any significant increase in the viscosity of the base fluid. Ali et al. [21] studied the bio-convectional of micropolar nanofluids in water-based concentrations containing microorganisms and nanoparticles. Nayak et al. [22] scrutinized the effects of velocity, temperature, solutal and motile gyrotactic microorganism slip lying on the biologically neutral Casson nano liquid flow across an exponential expanding electro- magnetic surface with chemical effects. Khan et al. [23] analyzed the bioconvection impact in the rheological nano liquid stress coupled with Arrhenius activation energy and Wu’s slip with magnetic properties. The bioconvection motion of nanofluids caused by gyrotactic motile microorganisms was mentioned by Kotha et al. [24]. The motile gyrotactic microorganisms and thermal radiation for the chemical bonded bio-convectional flow of tangent hyperbolic nanofluids were reported by Al-Khaled et al. [25]. For dispersing gyrotactic motile microorganisms and the density of gyrotactic microorganisms, including velocity profiles, are declining, the Schmidt number is performed by Makinde et al. [26]. The bioconvection Rayleigh number and the local thermal Grashof number are diminishing functions for motile gyrotactic microorganism diffusion is evaluated by Makinde et al. [27]. Saleem et al. [28] examined the density computed for motile gyrotactic microorganisms shrinks above the Peclet number under the bio convection effect. Waqas et al. [29] examined bioconvection effects on modified second-grade nanofluid microorganisms. Chu et al. [30] discussed the modified diffusion in tangent hyperbolic nanofluid under the bioconvection phenomenon. Many researchers [31–38] explore the bioconvection phenomenon in nanofluid flow.

Furthermore, affiliation with a related domain that is closely suitable in real life has a significant impact. Because of their significance in multiple fields of technology agriculture, including manufacturing applications, the flows generated through a wedge, cone, and vertical plate have gotten a lot of attention. Vajravelu et al. [39] developed a mathematical mechanism for transmitting heat reacting to flow via a cone and wedge. Chamkha [40] explained that the heat source parameter improved the local Nusselt number by considering the flow, including porosity. Many investigators in various fields, specifically fluid dynamics, used wedge as the geometry in their experiments because they implemented the above–mentioned work. Khan et al. [41] observed the flow of a nano liquid throughout a rotating wedge under the chemical process, including thermal radiation. Interestingly, fluid dynamics scientists are currently considering the action of heat transformation over wedge flows.

Whereas mass and heat transport occurs continuously in a moveable fluid. Compared to the Dufour effect, the Soret effect is negligible in fluids. Numerous researchers have reported cross-diffusion influences in boundary layer flow in recent decades. Abd El-Aziz [42] discussed the consequences of Dufour, radiation, Soret parameters, and Magnetohydrodynamic over a porous sheet that is often stretched. He discovered that the Dufour and Soret parameters have an important impact on temperature, momentum, and assemble distributions. Eckert et al. [43] and Mortimer et al. [44] have addressed a variety of flow events, including those in geophysics, where thermal diffusion and diffusion thermo consequences are highly suspected. Thermal–diffusion and Diffusion–thermo are imperative when density differences occur in the fluid flow, according to Devi et al. [45]. Thermal–diffusion and Diffusion–thermo influences have been most significant for interfering molecular weight gases in binary processes frequently confronted in chemical technology mechanisms.

MATLAB is an essential software tool for numerically solving and comparing the outcomes of various models, including physics, technology, and a variety of others. The variable flowing and thermal characteristics when a decelerating rotating disc is modified scrutinized by Rafiq et al. [46]. The consequence of thermal conductivity and the variable viscosity overheat transmission rates and drag was discovered in a two-way analysis for a numerical solution using Matlab-bvp4c and R-K shooting methods.

The study of bioconvection in nanofluid is beneficial in different fields like biofuels cells, biotechnology, bioengineering, oil refineries, biofuels, and agriculture engineering. To the author’s best knowledge, no studies have yet reported analyzing bioconvections for the heat and mass transfer of the MHD flow with cross-diffusion impacts by considering three different geometries by considering the thermal and solutal Robin’s conditions. So, we filled this gap with the assistance of the above-cited studies. The prime motive of this study is to investigate the consequences of the occurrence of motile microorganisms on nanofluid flow with thermal radiation, activation energy, and melting phenomena past the geometries cone, wedge, and the plate. Appropriate similarity transformations are used to convert the PDEs into ODEs, and these equations are solved by numerical technique through shooting methods using bvp4c solver. Outcomes are exposed graphically and conferred numerical values for various physical parameters.

2  Mathematical Development of the Problem

Assume an incompressible, convective, time independent, laminar MHD flow over geometries of three different shapes like cone, wedge and plate. The melting mechanism is measured. In the plane xy, we considered surface of the body is measured by x and normally outward to the surface measured by y. Fig. 1 shows that strength B0 of transverse electro–magnetic field is applying perpendicularly along the flow on surface of the geometry. The half angle of cone represented by α and full angle of wedge represented by Ω, the cone radius shown by r. Let ξ be the stream velocity function. The temperature of fluid, concentration and bioconvection near the plate is presented as Tw=T0+axs,Cw=C0+bxq and Nw=N0+cxn, here (a, b and c) are real constants, (s,q and n) are the energy, concentration, and bioconvection parameters for wall (the energy, concentration, and bioconvection over wall is constant when (s=q=n=0), (T0,C0 and N0) are the ambient temperature, concentration and bioconvection. Mixed convection heat flux, cross diffusion impacts are included in the given problem.

For the above considered problem the basic coupled nonlinear dimensional equations are given below [47]:

∂∂x(rm∂ξ∂y)−∂∂y(rm∂ξ∂x)=0,(1)

∂ξ∂y∂2ξ∂x∂y−∂ξ∂x∂2ξ∂y2=ν∂3ξ∂y3+(βt(T−T∞)+βc(C−C∞)+βn(N−N∞))gcos⁡α−σβ02ρ∂ξ∂y,(2)

∂ξ∂y∂T∂x−∂ξ∂x∂T∂y=kρcp∂2T∂y2+1(ρcp)f∂∂y(K(T)∂T∂y)+τ[DB∂C∂y∂T∂y+DTT∞(∂T∂y)2],(3)

∂ξ ∂y ∂C ∂x − ∂ξ ∂x ∂C ∂y = 1 (ρ c p ) f ∂ ∂y ( D(C) ∂C ∂y )+ D B ∂ 2 C ∂ y 2 + D T T ∞ ( ∂ 2 T ∂ y 2 ) − K 1 r 2 (C− C ∞ ) ( T T ∞ ) 2 exp( − E a κT ), (4)

∂ξ∂y∂N∂x+∂ξ∂x∂N∂y+[∂∂y(N∂C∂y)]bWc(Cw−C∞)=Dm∂∂y(∂N∂y).(5)

Figure 1: Schematic flow with coordinate system

The applied boundaries conditions are [48]

u(x,0)= u w =νx/ l 2 ,v(x,0)=0, k ∂T ∂y = h f ( T w −T), D B ∂C ∂y = h g ( C w −C), D m ∂N ∂y = h n ( N w −N), u→0,T→ T ∞ ,C→ C ∞ ,N→ N ∞ asy→∞. (6a)

−k ∂T ∂y | y=0 =ρ[ λ 0 +( T m − T 0 ) c s ] (6b)

1.    If m=0 and α≠0 then flow problem for wedge.

2.    If m=1 and α≠0 then flow problem for cone.

3.    If m=0 and α=0 then flow problem for plate.

Introduced the suitable similarities variables

ζ=yl−1,u=νxl−2∂f∂ζ,v=−ν(m+1)l−1f(ζ),θ(ζ)(Tw−T∞)+T∞=T,ϕ(ζ)(Cw−C∞)+C∞=C,χ(ζ)(Nw−N∞)+N∞=N.(7)

Transformation equations are as follows:

d3fdζ3+(m+1)fd2fdζ2−(dfdζ)2−Mdfdζ+λ(θ+Grϕ+Ncχ)cos⁡α=0,(8)

(1+ε1θ)d2θdζ2+ε1(dθdζ)2+Pr(Nbdθdζdϕdζ+Nt(dθdζ)2)+Pr((m+1)fdθdζ−sdfdζθ)=0,(9)

(1+ε2ϕ)d2ϕdζ2+ε2(dϕdζ)2+LePr((m+1)fdϕdζ−sdfdζϕ)+NtNbd2θdζ2−LePrσ∗∗(1+δθ)nϕexp⁡(−E1+δθ)=0,(10)

d2χdζ2+Lb((m+1)fdχdζ−sdfdζχ)−Pe[d2ϕdζ2(χ+δ1)+dχdζdϕdζ]=0,(11)

where s representing the temperature parameter.

The dimension-less conditions are as follows:

Meθ′(0)+Prf(0)=0,dfdζ=1,dθdζ=−Ω1(1−θ(0)),dϕdζ=−Ω2(1−ϕ(0))=0,dχdζ=−Ω3(1−χ(0))atζ=0(12)

dfdζ=0,θ=0,ϕ=0,χ=0asζ→0.(13)

In above equations M is the magnetic field, l is the characteristic length, λ is mixed convection parameter, Gr designed for Grashof number for concentration, Nc describe the Grashof number for microorganisms, Pr explain the Prandtl number, Nb demonstrate the Brownian motion, Nt illustrate the thermophoresis diffusion parameter, Lb confirm the bioconvection Lewis number, Pe represent the Peclet number, δ is the temperature difference parameter, microorganisms difference parameter denoted by δ1 and thermal Biot number characterized by Ω1, solutal Biot number indicated by Ω2 and the microorganisms Biot number symbolized by Ω3, ε1 is the temperature dependent thermal conductivity, ε2 denotes the Concentration diffusivity, σ∗∗ denotes the chemical reaction parameter and melting parameter can be defined as Me.

M=σ0β02l2ρν,λ=l2gβt(Tw−T∞)νuw,Gr=l2gβc(Cw−C∞)νuw,Nc=l2gBn(Nw−N∞)νuw,Pr=μcpk,Nb=τDB(Cw−C∞)ν,Nt=τDT(Tw−T∞)νT∞,Lb=νDm,Pe=bWcν,δ1=N∞Nw−N∞,Ω1=hfkl,Ω2=hgDBl,Ω3=hnDMl,Me=cp(T∞−Tm)λ0+cs(Tm−T0).(14)

The friction factor Cf, local Nusselt number Nu, local Sherwood number Sh and Sn defined as

Cf=Cf∗μuw=−d2fdζ2|ζ=0,Nu=hlk(Tw−T∞)=−dθdζ|ζ=o,Sh=hmlk(Cw−C∞)=−dϕdζ|ζ=0,Sn=hnlk(Nw−N∞)=−dχdζ|ζ=0.(15)

3  Numerical Scheme

In this portion the nonlinear dimensionless ordinary differential equations with appropriate boundary conditions are solved numerically through the solver bvp4c package in computational MATLAB. The higher order ODEs are converted into linear one by introducing the following variables such as

f=p,dfdζ=p1,d2fdζ2=p2,d3fdζ3=p′2,θ=p3,dθdζ=p4,d2θdζ2=p′4,ϕ=p5,dϕdζ=p6,d2ϕdζ2=p′6,χ=p7,dχdζ=p8,d2χdζ2=p′8.(16)

p2′=−(m+1)pp2+(p1)2+Mp1−λ(p3+Grp5+Ncp7)cos⁡γ,(17)

p4′=−ε1(p4)2−Pr(Nbp4p6+Nt(p4)2)−Pr((m+1)pp4−sp1p3)(1+ε1p3),(18)

p6′=−ε2(p6)2−LePr((m+1)pp6−sp1p5)−NtNbp′4+LePrσ∗∗(1+δp3)np5exp⁡(−E1+δp3)(1+ε2p5),(19)

p8′=−Lb((m+1)pp8−sp1p7)+Pe[p′6(p7+δ1)+p8p6],(20)

With

Mep4(0)+Prp(0)=0,p1=1,p4=−Ω1(1−p3(0)),p6=−Ω2(1−p5(0))=0,p8=−Ω3(1−p7(0))atζ=0(21)

p1=0,p3=0,p5=0,p7=0asζ→0.(22)

4  Description of the Results

In this section all the results of graphs are embellished and created by using the computational software MATLAB–16a (bvp4c) solver. For the understanding of figures, we must have to know about the color of curves demonstrated. The black curve demonstrates for wedge, red for cone and blue for sheet. The iterations of effective goods parameters increased or decreased with their individual behaviors. In this segment the graphic outcome interoperate for the different values of different parameters, like Pr=2.0, Pe=0.1, E=0.1, ε2=0.1, Lb=1.2, Le=1.2, Nb=0.1, Nt=0.1, Ω1=0.1, Ω2=0.2, Ω3=0.1, M=0.5, Nr=0.1, Nc=0.1, Me=0.5.

The influence of buoyancy ratio parameter Nr and velocity distribution f′ is illustrated in Fig. 2. It is noticed from this figure that for the highest values of Nr, f′ decreases (Fig. 3). Illustrates the fluctuation of the bioconvection Rayleigh number Nc with respect to the microorganism field with in the velocity profile f′. Such that the value of bioconvection Rayleigh number Nc increase due to the increased value of microorganism graph. The relationship between the buoyancy and viscosity is known as Rayleigh number within the fluids. The significant magnetic field parameter M against velocity distribution f′ has been examined in Fig. 4. The velocity of the fluid decreased with the increased value of M. Once more this behavior is defined as the Hartmann number is interlinked with the occurrence of Lorentz force. Figs. 5–8 are examines the variation of Me on motile density profile χ, concentration profile φ, temperature profile θ and velocity profile f′ respectively for three different geometries (wedge, cone and sheet). The fluctuation in Me reduces the motile density profile χ, concentration profile φ, temperature profile θ and velocity profile f′.

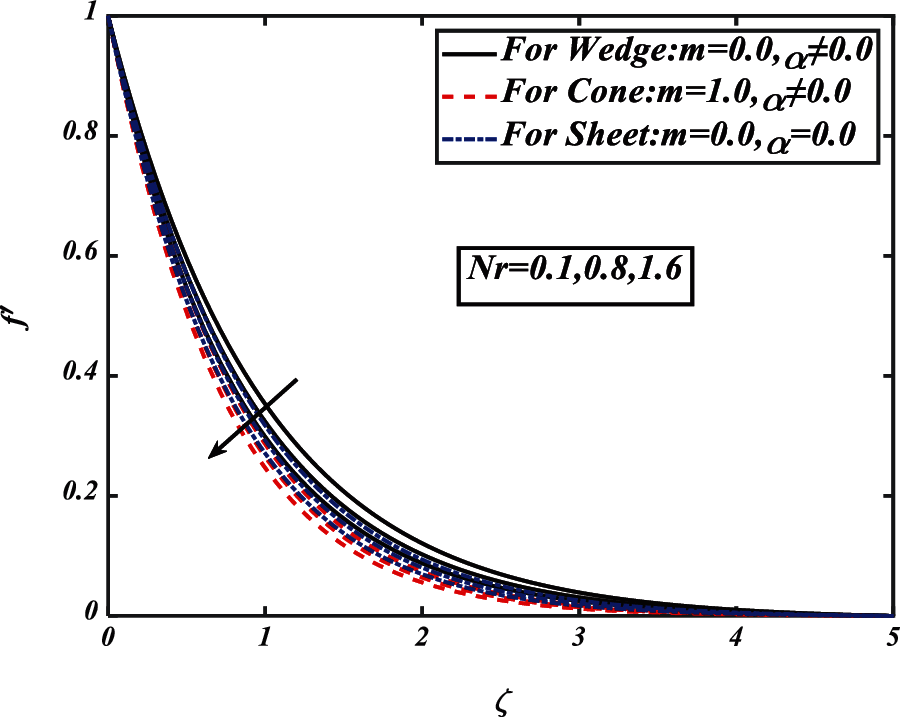
Figure 2: Pictogram of Nr over f′

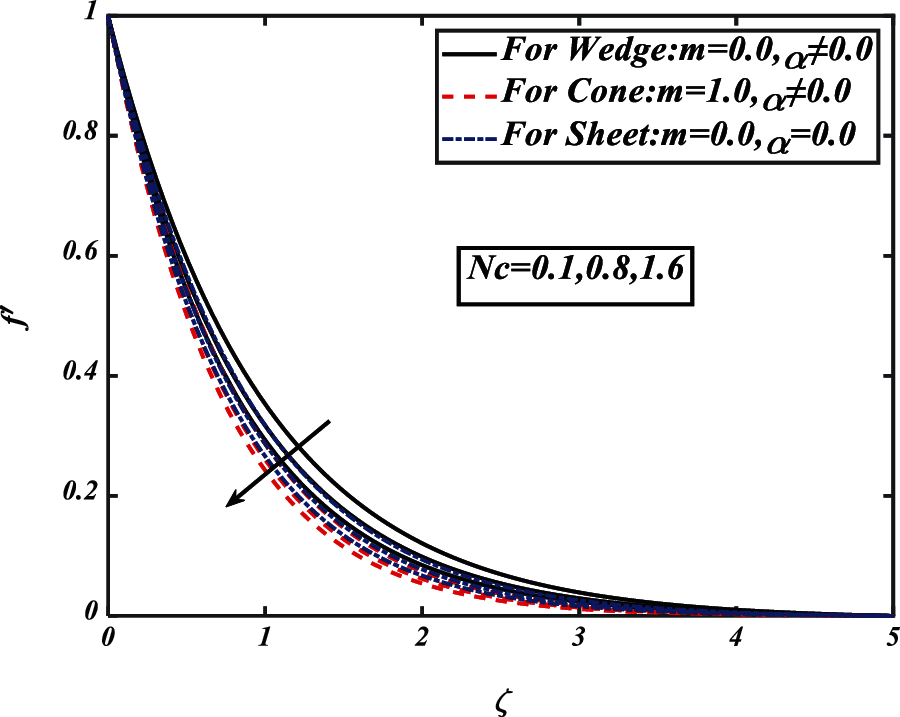
Figure 3: Pictogram of Nc over f′

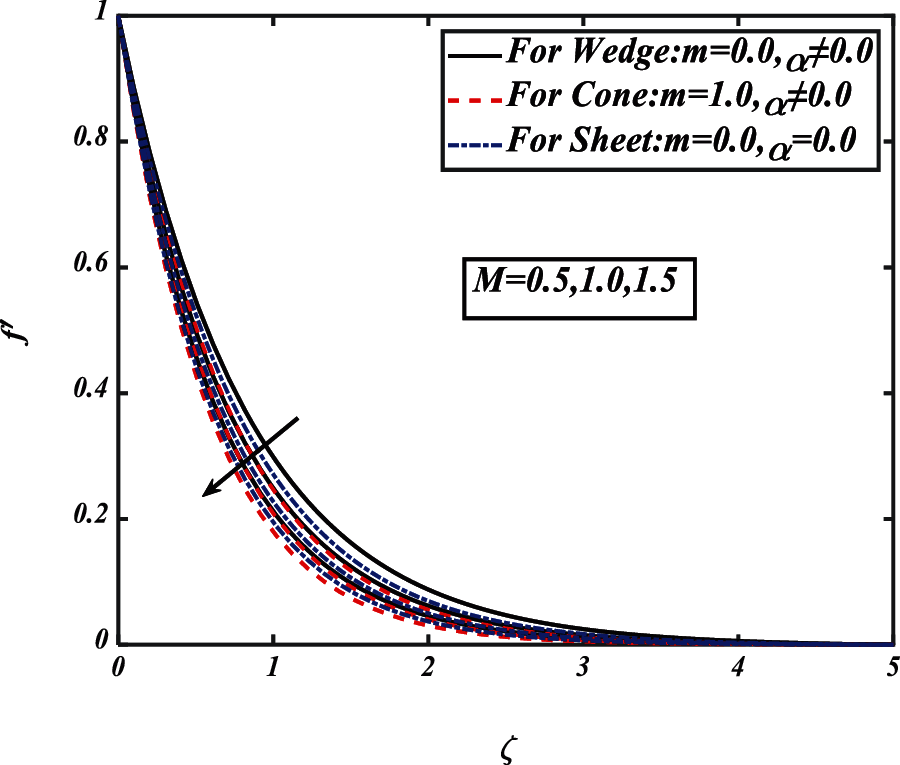
Figure 4: Pictogram of M over f′

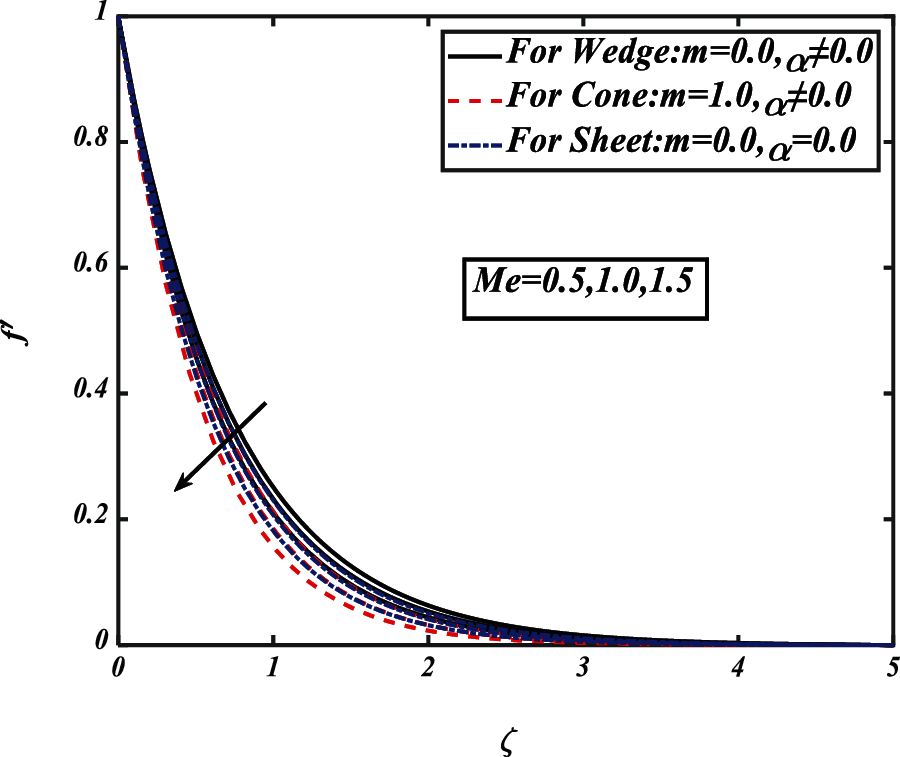
Figure 5: Pictogram of Me over f′

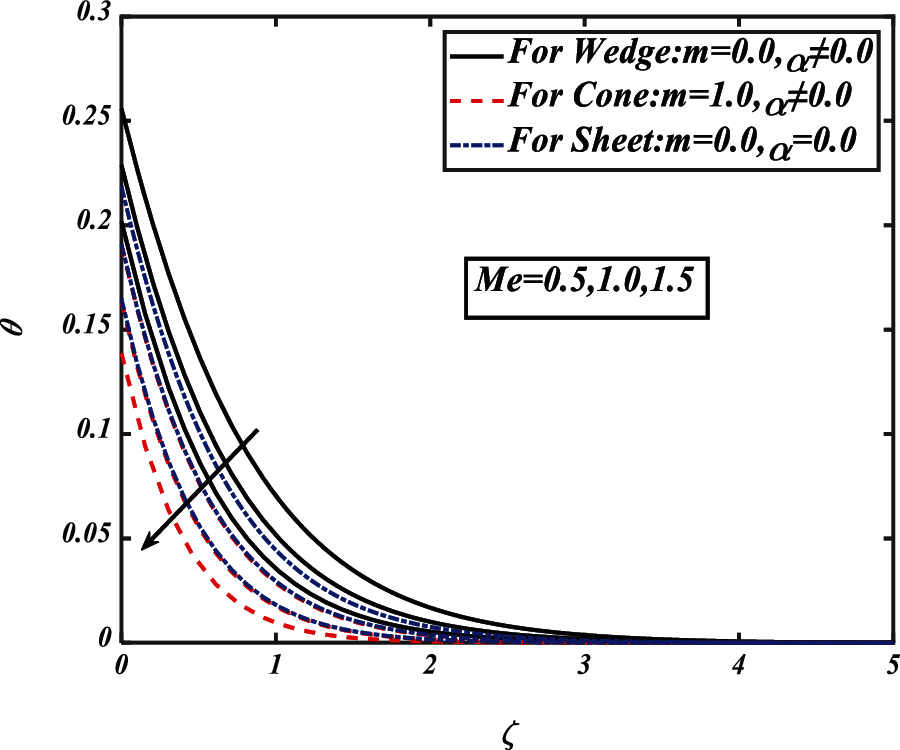
Figure 6: Pictogram of Me over θ

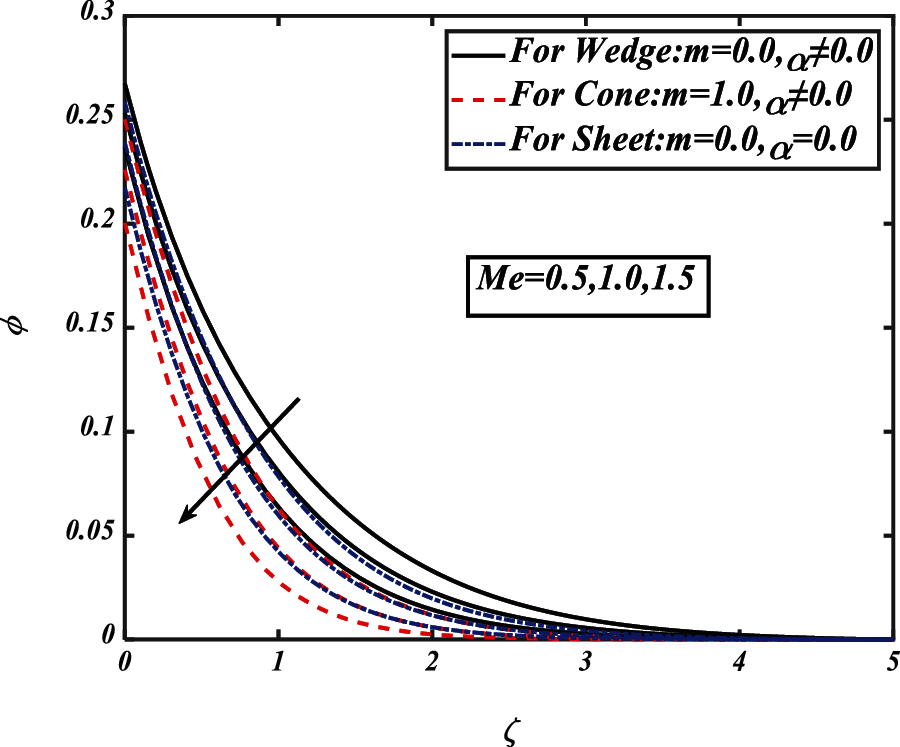
Figure 7: Pictogram of Me over ϕ

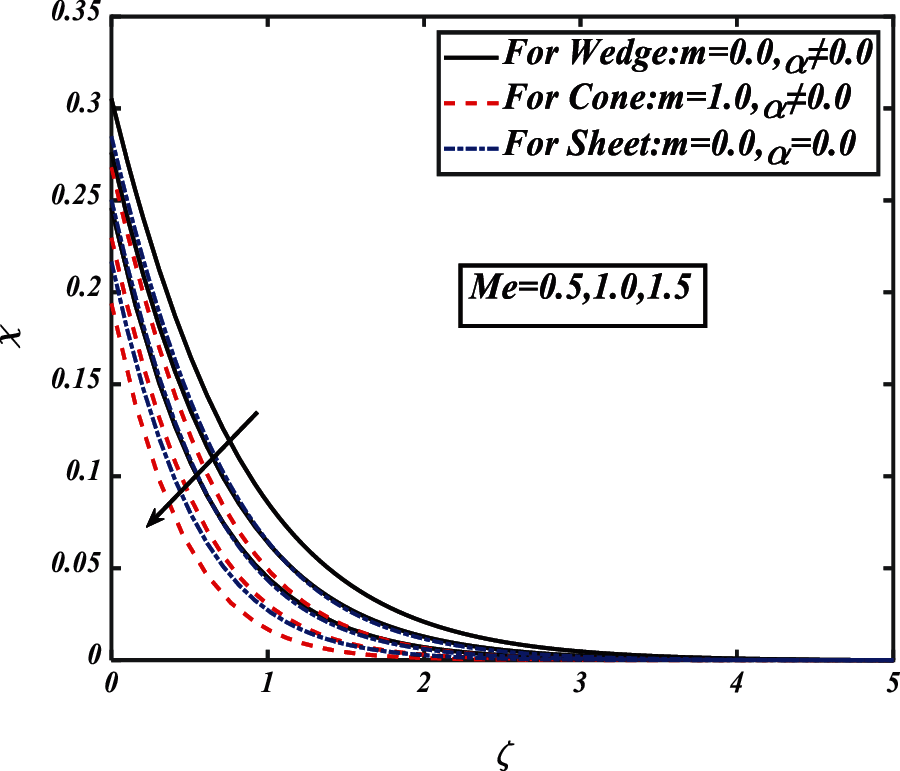
Figure 8: Pictogram of Me over χ

Fig. 9 illustrates the impact of the Prandtl number over temperature distribution respectively for different value of m for cone, wedge and sheet. Fig. 10 demonstrates the impact of thermal Biot number via temperature distribution for different geometries for several values of m and α. For cone m=1.0 and for other two geometries its zero. Fig. 11 depicts that concentration is reduced via larger Prandtl number Pr. In Fig. 12 the activation energy E parameter is communicated for the nanoparticles volume distribution. In this graph when the value of E is increasing then the rate of reaction is decline due to higher temperature and greatest activation energy which develop the nanoparticles volume fraction. The concentration profile for ε2 is deeply observed in the Fig. 13. Concentration dependent thermal diffusivity enhances the concentration field of nanoparticles. Fig. 14 analyzed the effect of Lewis number Le over concentration ϕ. The decreasing in ϕ is noticed for demonstrative value of Le for three different geometries. The Le is defined to be the ratio of mass and thermal diffusivity. The ϕ is decreased for the higher value of Le in these geometries. Fig. 15 represented the variation of φ for the Brownian motion parameter Nb. The relationship between Nb and nanoparticles concentration is inverse. φ. From Fig. 16 the temperature distribution is upswing owing to the growing value of thermophoresis parameter Nt. For Nt the temperature profile improved, so the migration of particles from region to region exists as hot to cold region. Multi industrial processes use this concept now a days. The profile of concentration is increased for given value of Nt. The components of representational non–dimensional nanoparticles concentration ϕ is purposed through allotting unique values to Nt for three different geometries.

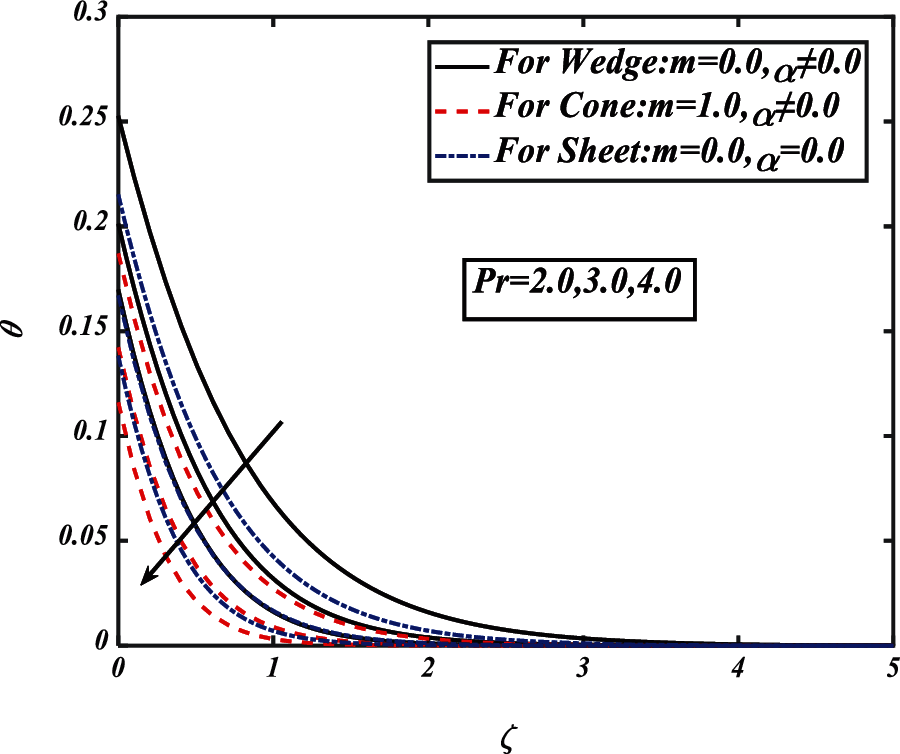
Figure 9: Pictogram of Pr over θ

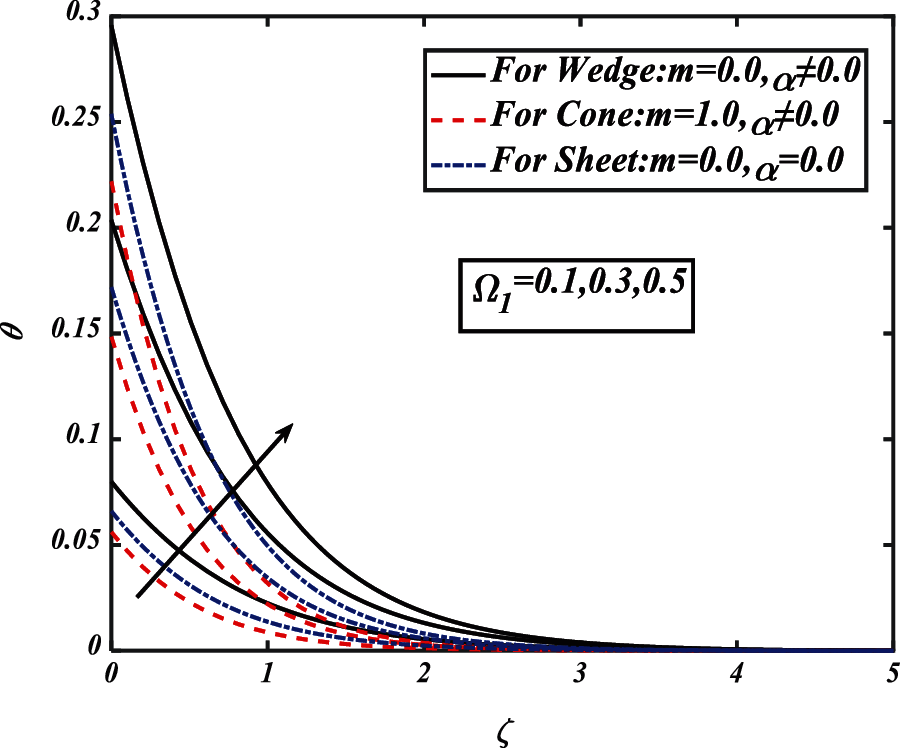
Figure 10: Pictogram of Ω1 over θ

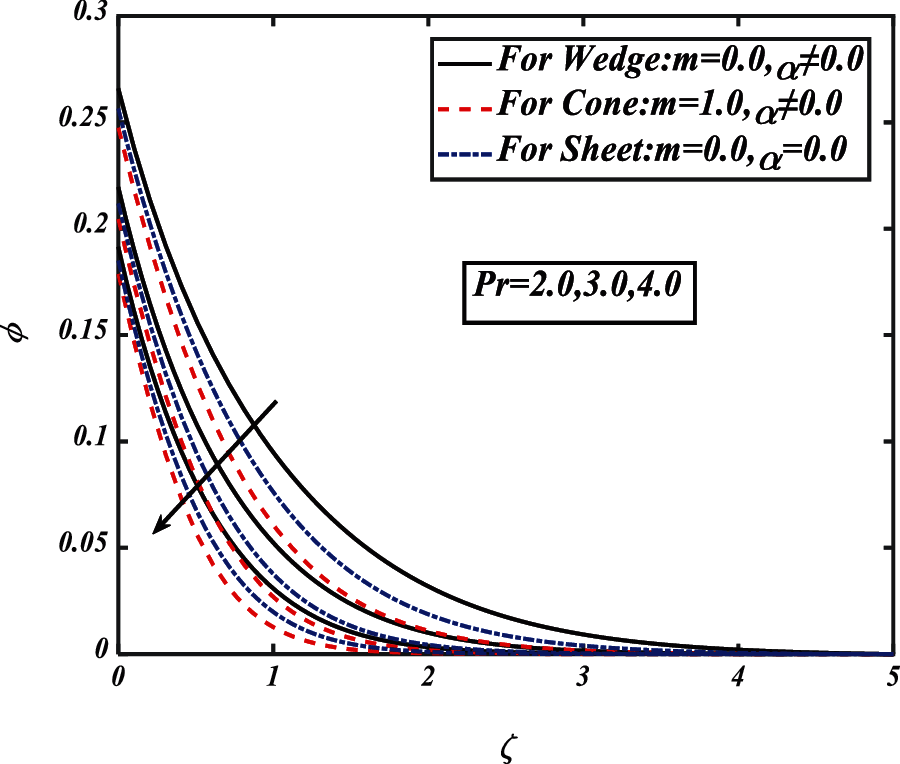
Figure 11: Pictogram of Pr over φ

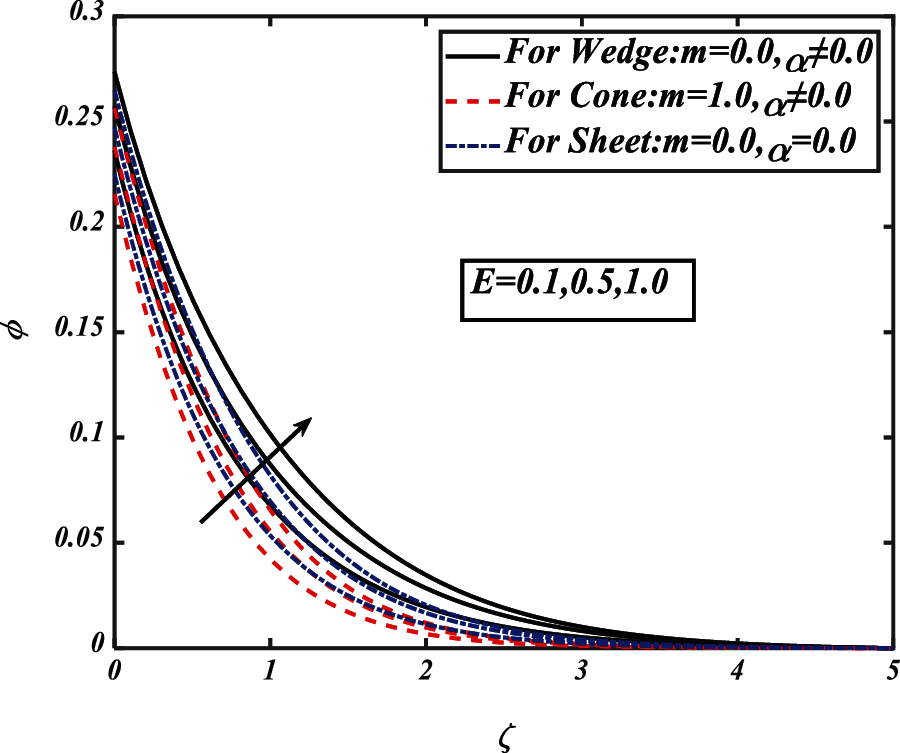
Figure 12: Pictogram of E over φ

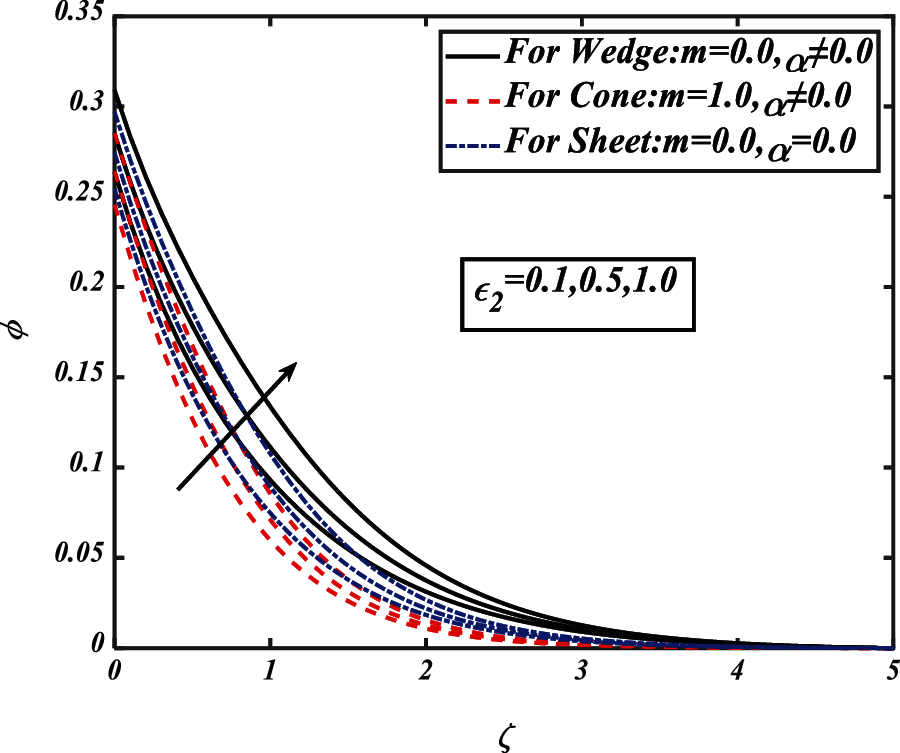
Figure 13: Pictogram of ε2 over φ

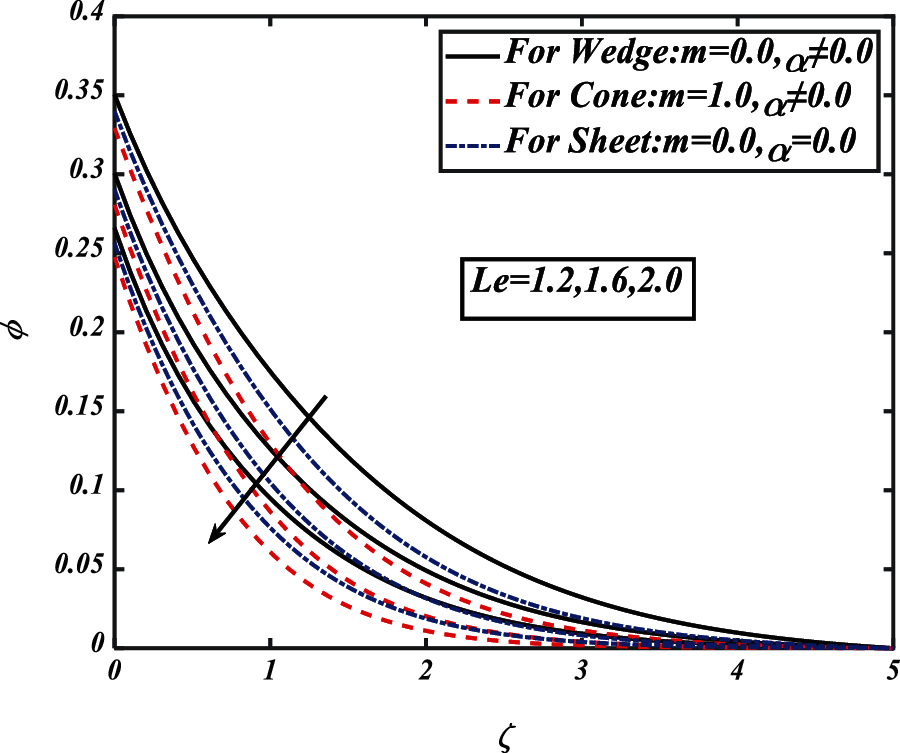
Figure 14: Pictogram of Le over φ

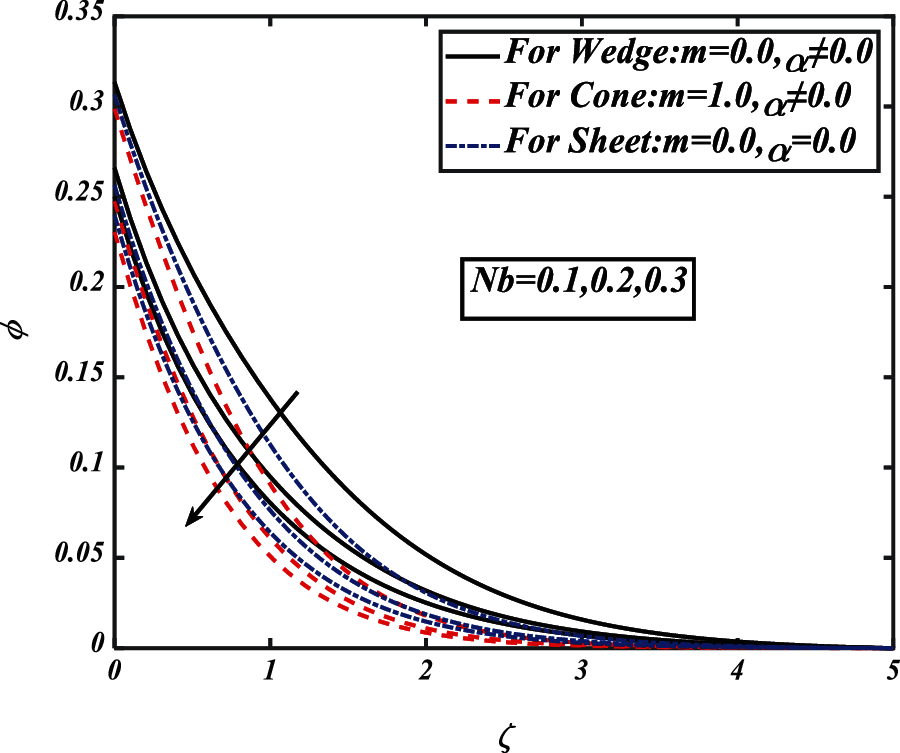
Figure 15: Pictogram of Nb over φ

Figs. 17 and 18 explain the variation of solutal Biot number Ω2, and microorganism Biot numbers Ω3 respectively for concentration and motile density profiles. The concentration and motile density profile depends upon the Biot number for all three conditions with respect to all three different geometries (wedge, cone and sheet). Here concentration and microorganism's field boosted for larger Biot numbers. Fig. 19 illustrates the impact of Peclet number on χ for three different geometries like wedge, cone and sheet. Largest values of Peclet number diminish the microorganism distribution. Fig. 20 illustrates that the bioconvection Lewis number Lb is a decreasing function for motile density profile χ of three geometries (wedge, cone and sheet). The χ diminished and the value of Lb are higher for the cause of increase in the diffusivity of the motile microorganism.

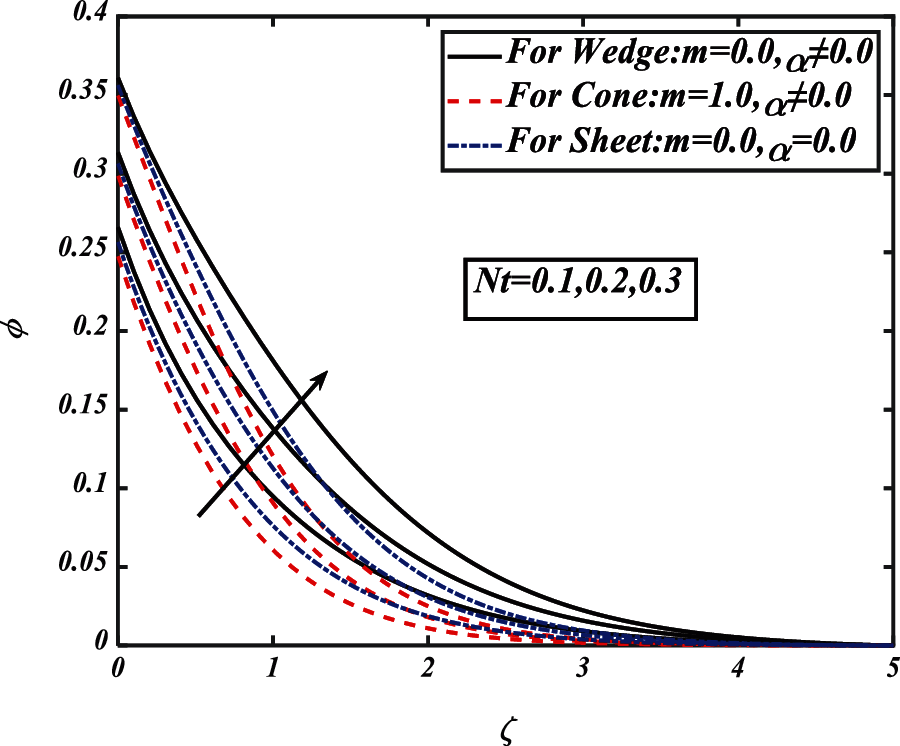
Figure 16: Pictogram of Nt over φ

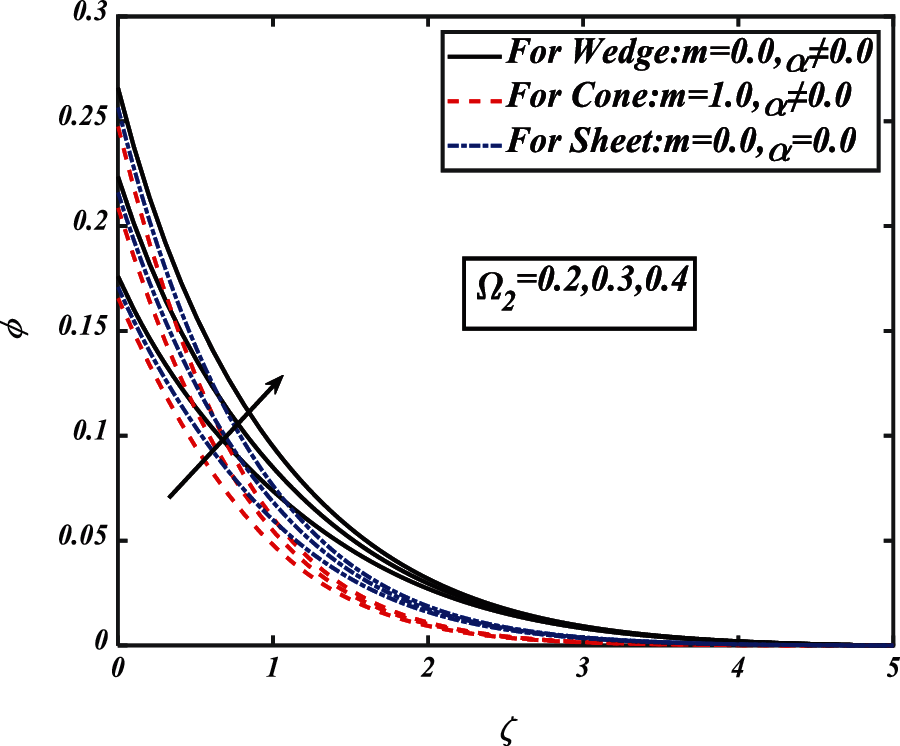
Figure 17: Pictogram of Ω2 over φ

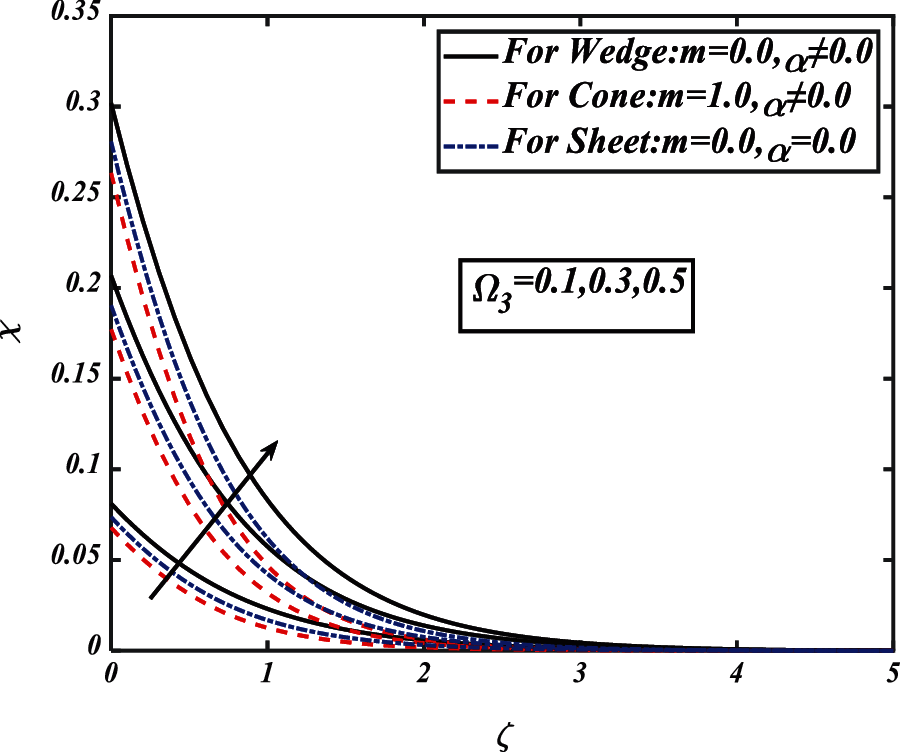
Figure 18: Pictogram of Ω3 over χ

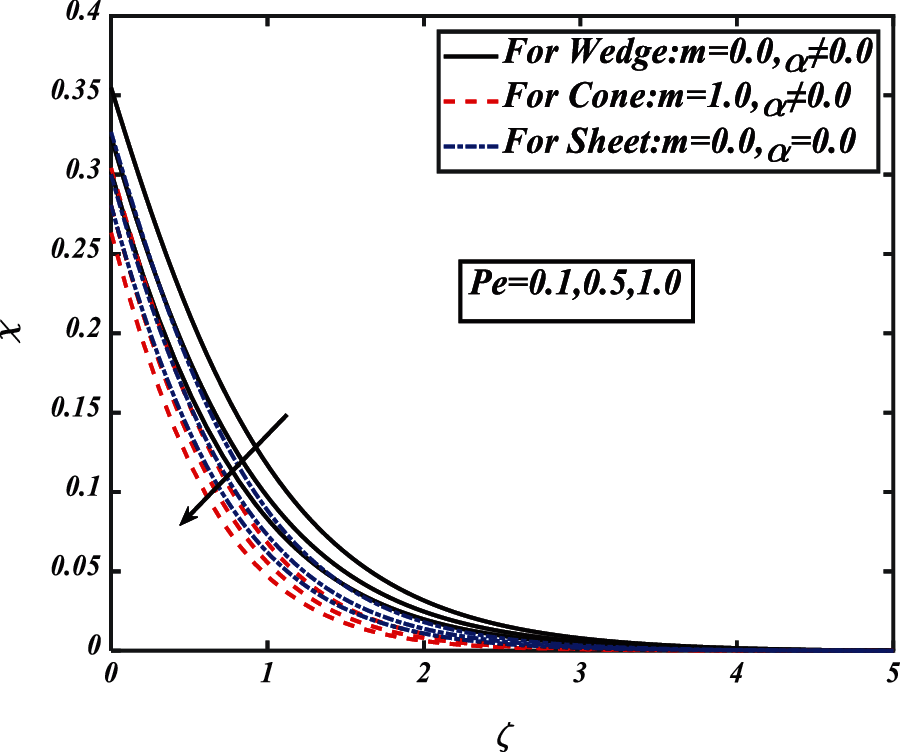
Figure 19: Pictogram of Pe over χ

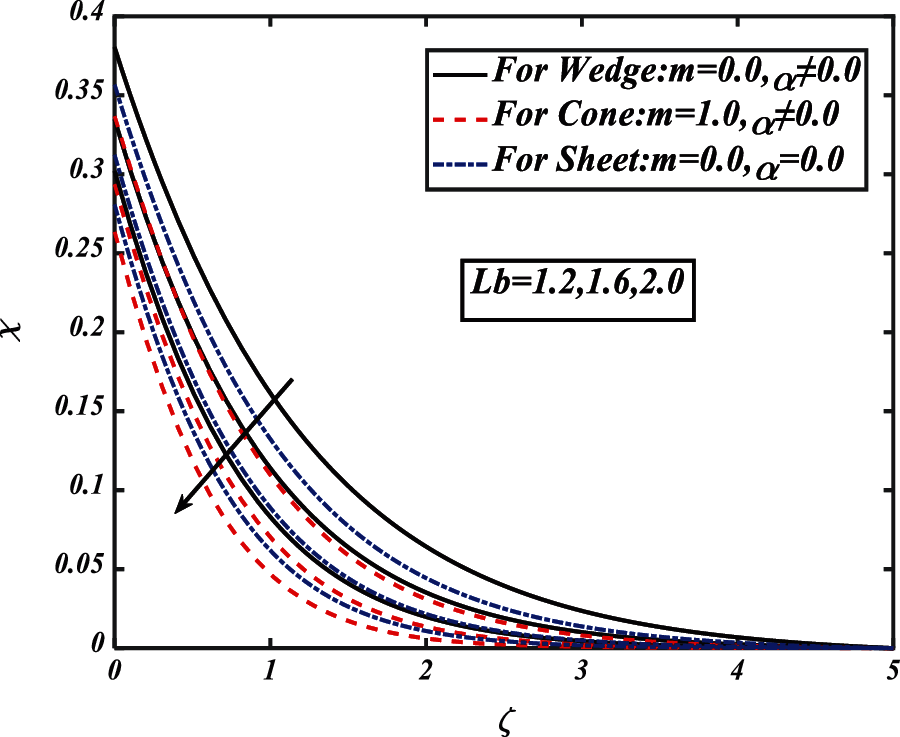
Figure 20: Pictogram of Lb over χ

5  Final Remarks

Heat and mass transformation of the nanofluid bioconvection flow under the melting mechanisms is scrutinized in the existence of cross-diffusion impacts. Mathematical modeling is fixed to scrutinize the flowing performance on vertically three different geometries (cone, wedge, and plate). Some significant remarks are synopsized below:

•   Fluid exposure, the fluid velocity is highest for the flow over the plate as compared with the other two geometries (cone and wedge).

•   The transformation rate of mass and heat is much better for the flow via cone than flow over the wedge.

•   It is investigated that both the Brownian motion diffusion parameter and thermophoretic diffusion parameter are directly proportional to the temperature of the fluid. At the same time, concentration is directly proportional to the thermophoretic parameter but inversely proportional to the Brownian diffusion parameter.

•   The temperature and concentration profile performance increased for the highest value in the thermophoretic parameter.

•   The microorganisms’ density is inversely proportional to the Peclet number and Lewis number.

•   This study analyzed the flow characteristics of non-Newtonian fluids extended for the present mathematical model.

•   Reducing the amount of melting enhanced the heat transfer rate and velocity of the fluid.

Funding Statement: This work is financially supported by the Government College University, Faisalabad and Higher Education Commission, Pakistan.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Zheng, L., Niu, J., Zhang, X., Gao, Y. (2012). MHD flow and heat transfer over a porous shrinking surface with velocity slip and temperature jump. Mathematical and Computer Modelling, 56(5–6), 133–144. DOI 10.1016/j.mcm.2011.11.080. [Google Scholar] [CrossRef]

 2.  Chauhan, D. S., Agrawal, R. (2013). MHD flow and heat transfer in a channel bounded by a shrinking sheet and a porous medium bed: Homotopy analysis method. International Scholarly Research Notices, 2013, 291270. DOI 10.1155/2013/291270. [Google Scholar] [CrossRef]

 3.  Attia, H. A. (2006). Unsteady MHD couette flow and heat transfer of dusty fluid with variable physical properties. Applied Mathematics and Computation, 177(1), 308–318. DOI 10.1016/j.amc.2005.11.010. [Google Scholar] [CrossRef]

 4.  Kumar, K. G., Archana, M., Gireesha, B. J., Krishanamurthy, M. R., Rudraswamy, N. G. (2018). Cross diffusion effect on MHD mixed convection flow of nonlinear radiative heat and mass transfer of casson fluid over a vertical plate. Results in Physics, 8, 694–701. DOI 10.1016/j.rinp.2017.12.061. [Google Scholar] [CrossRef]

 5.  Ibrahim, W., Shanker, B. (2012). Boundary-layer flow and heat transfer of nanofluid over a vertical plate with convective surface boundary condition. Journal of Fluids Engineering, 134(8), 081203. DOI 10.1115/1.4007075. [Google Scholar] [CrossRef]

 6.  Ibrahim, W., Shanker, B. (2014). Magnetohydrodynamic boundary layer flow and heat transfer of a nanofluid over non–isothermal stretching sheet. Journal of Heat Transfer, 136(5), 051701. DOI 10.1115/1.4026118. [Google Scholar] [CrossRef]

 7.  Ibrahim, W., Shanker, B. (2015). MHD boundary layer flow and heat transfer due to a nanofluid over an exponentially stretching non–isothermal sheet. Journal of Nanofluids, 4(1), 16–27. DOI 10.1166/jon.2015.1125. [Google Scholar] [CrossRef]

 8.  Ibrahim, W., Makinde, O. D. (2013). The effect of double stratification on boundary–layer flow and heat transfer of nanofluid over a vertical plate. Computers Fluids, 86, 433–441. DOI 10.1016/j.compfluid.2013.07.029. [Google Scholar] [CrossRef]

 9.  Ibrahim, W., Makinde, O. D. (2015). Double-diffusive in mixed convection and MHD stagnation point flow of nanofluid over a stretching sheet. Journal of Nanofluids, 4(1), 28–37. DOI 10.1166/jon.2015.1129. [Google Scholar] [CrossRef]

10. Muhammad, T., Waqas, H., Khan, S. A., Ellahi, R., Sait, S. M. (2021). Significance of nonlinear thermal radiation in 3D eyring-powell nanofluid flow with arrhenius activation energy. Journal of Thermal Analysis and Calorimetry, 143(2), 929–944. DOI 10.1007/s10973-020-09459-4. [Google Scholar] [CrossRef]

11. Waqas, H., Khan, S. A., Farooq, U., Khan, I., Alotaibi, H. et al. (2021). Melting phenomenon of non-linear radiative generalized second grade nanoliquid. Case Studies in Thermal Engineering, 26, 101011. DOI 10.1016/j.csite.2021.101011. [Google Scholar] [CrossRef]

12. Danish, G. A., Imran, M., Tahir, M., Waqas, H., Asjad, M. I. et al. (2021). Effects of non-linear thermal radiation and chemical reaction on time dependent flow of williamson nanofluid with combine electrical MHD and activation energy. Journal of Applied and Computational Mechanics, 7(2), 546–558. DOI 10.22055/JACM.2020.35122.2568. [Google Scholar] [CrossRef]

13. Waqas, H., Farooq, U., Naseem, R., Hussain, S., Alghamdi, M. (2021). Impact of MHD radiative flow of hybrid nanofluid over a rotating disk. Case Studies in Thermal Engineering, 26, 101015. DOI 10.1016/j.csite.2021.101015. [Google Scholar] [CrossRef]

14. Mabood, F., Muhammad, T., Nayak, M. K., Waqas, H., Makinde, O. D. (2020). EMHD flow of non-newtonian nanofluids over thin needle with Robinson's condition and arrhenius pre-exponential factor law. Physica Scripta, 95(11), 115219. DOI 10.1088/1402-4896/abc0c3. [Google Scholar] [CrossRef]

15. Shah, N. A., Hajizadeh, A., Zeb, M., Ahmad, S., Mahsud, Y. et al. (2018). Effect of magnetic field on double convection flow of viscous fluid over a moving vertical plate with constant temperature and general concentration by using new trend of fractional derivative. Open Journal of Mathematical Sciences, 2(1), 253–265. DOI 10.30538/oms2017. [Google Scholar] [CrossRef]

16. Qi, H., Fatima, N., Waqas, H., Saeed, J. (2017). Analytical solution for the flow of a generalized oldroyd-b fluid in a circular cylinder. Open Journal of Mathematical Sciences, 1(1), 85–96. DOI 10.30538/oms2017. [Google Scholar] [CrossRef]

17. Farooq, M. U., Khan, M. S., Hajizadeh, A. (2019). Flow of viscous fluid over an infinite plate with caputo-Fabrizio derivatives. Open Journal of Mathematical Sciences, 3(1), 115–120. DOI 10.30538/oms2017. [Google Scholar] [CrossRef]

18. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. Proceeding of the International Mechanical Engineering Congress and Exhibition, San Francisco. [Google Scholar]

19. Buongiorno, J. (2005). Convective transport in nanofluids. Journal of Heat Transfer, 128(3), 240–250. DOI 10.1115/1.2150834. [Google Scholar] [CrossRef]

20. Kuznetsov, A. V. (2011). Nanofluid bioconvection in water–based suspensions containing nanoparticles and oxytactic microorganisms: Oscillatory instability. Nanoscale Research Letters, 6(1), 1–13. DOI 10.1186/1556-276X-6-100. [Google Scholar] [CrossRef]

21. Ali, L., Liu, X., Ali, B., Mujeed, S., Abdal, S. (2019). Finite element simulation of multi-slip effects on unsteady mhd bioconvective micropolar nanofluid flow over a sheet with solutal and thermal convective boundary conditions. Coatings, 9(12), 842. DOI 10.3390/coatings9120842. [Google Scholar] [CrossRef]

22. Nayak, M. K., Prakash, J., Tripathi, D., Pandey, V. S., Shaw, S. et al. (2020). 3D bioconvective multiple slip flow of chemically reactive casson nanofluid with gyrotactic micro-organisms. Heat Transfer–Asian Research, 49(1), 135–153. DOI 10.1002/htj.21603. [Google Scholar] [CrossRef]

23. Khan, S. U., Waqas, H., Bhatti, M. M., Imran, M. (2020). Bioconvection in the rheology of magnetized couple stress nanofluid featuring activation energy and Wu's slip. Journal of Non-Equilibrium Thermodynamics, 45(1), 81–95. DOI 10.1515/jnet-2019-0049. [Google Scholar] [CrossRef]

24. Kotha, G., Kolipaula, V. R., Rao, M. V. S., Penki, S., Chamkha, A. J. (2020). Internal heat generation on bioconvection of an MHD nanofluid flow due to gyrotactic microorganisms. The European Physical Journal Plus, 135(7), 1–19. DOI 10.1140/epjp/s13360-020-00606-2. [Google Scholar] [CrossRef]

25. Al-Khaled, K., Khan, S. U., Khan, I. (2020). Chemically reactive bioconvection flow of tangent hyperbolic nanoliquid with gyrotactic microorganisms and nonlinear thermal radiation. Heliyon, 6(1), e03117. DOI 10.1016/j.heliyon.2019.e03117. [Google Scholar] [CrossRef]

26. Makinde, O. D., Animasaun, I. L. (2016). Bioconvection in MHD nanofluid flow with nonlinear thermal radiation and quartic autocatalysis chemical reaction past an upper surface of a paraboloid of revolution. International Journal of Thermal Sciences, 109, 159–171. DOI 10.1016/j.ijthermalsci.2016.06.003. [Google Scholar] [CrossRef]

27. Makinde, O. D., Animasaun, I. L. (2016). Thermophoresis and brownian motion effects on MHD bioconvection of nanofluid with nonlinear thermal radiation and quartic chemical reaction past an upper horizontal surface of a paraboloid of revolution. Journal of Molecular Liquids, 221, 733–743. DOI 10.1016/j.molliq.2016.06.047. [Google Scholar] [CrossRef]

28. Saleem, S., Rafiq, H., Al-Qahtani, A., El-Aziz, M. A., Malik, M. Y. et al. (2019). Magneto jeffrey nanofluid bioconvection over a rotating vertical cone due to gyrotactic microorganism. Mathematical Problems in Engineering, 2019, 1–12. DOI 10.1155/2019/3478037. [Google Scholar] [CrossRef]

29. Waqas, H., Khan, S. U., Hassan, M., Bhatti, M. M., Imran, M. (2019). Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic microorganisms and nanoparticles. Journal of Molecular Liquids, 291, 111231. DOI 10.1016/j.molliq.2019.111231. [Google Scholar] [CrossRef]

30. Chu, Y. M., Waqas, H., Hussain, S., Yasmein, S., Khan, S. U. et al. (2021). Joule heating, activation energy and modified diffusion analysis for 3D slip flow of tangent hyperbolic nanofluid with gyrotactic microorganisms. Modern Physics Letters B, 35(16), 2150278. DOI 10.1142/S021798492150278X. [Google Scholar] [CrossRef]

31. Waqas, H., Khan, S. A., Alghamdi, M., Alqarni, M. S., Muhammad, T. (2021). Numerical simulation for bio-convection flow of magnetized non-newtonian nanofluid due to stretching cylinder/plate with swimming motile microorganisms. The European Physical Journal Special Topics, 230, 1–18. DOI 10.1140/epjs/s11734-021-00041-z. [Google Scholar] [CrossRef]

32. Waqas, H., Imran, M., Bhatti, M. M. (2021). Bioconvection aspects in non-newtonian three-dimensional carreau nanofluid flow with cattaneo-christov model and activation energy. The European Physical Journal Special Topics, 230, 1–14. DOI 10.1140/epjs/s11734-021-00046-8. [Google Scholar] [CrossRef]

33. Waqas, H., Imran, M., Bhatti, M. M. (2020). Influence of bioconvection on Maxwell nanofluid flow with the swimming of motile microorganisms over a vertical rotating cylinder. Chinese Journal of Physics, 68, 558–577. DOI 10.1016/j.cjph.2020.10.014. [Google Scholar] [CrossRef]

34. Song, Y. Q., Khan, S. A., Imran, M., Waqas, H., Khan, S. U. et al. (2021). Applications of modified darcy law and nonlinear thermal radiation in bioconvection flow of micropolar nanofluid over an off centered rotating disk. Alexandria Engineering Journal, 60(5), 4607–4618. DOI 10.1016/j.aej.2021.03.053. [Google Scholar] [CrossRef]

35. Song, Y. Q., Waqas, H., Al-Khaled, K., Farooq, U., Khan, S. U. et al. (2021). Bioconvection analysis for sutter by nanofluid over an axially stretched cylinder with melting heat transfer and variable thermal features: A marangoni and solutal model. Alexandria Engineering Journal, 60(5), 4663–4675. DOI 10.1016/j.aej.2021.03.056. [Google Scholar] [CrossRef]

36. Waqas, H., Manzoor, U., Muhammad, T., Hussain, S. (2021). Thermo-bioconvection transport of nanofluid over an inclined stretching cylinder with cattaneo-christov double-diffusion. Communications in Theoretical Physics, 73, 075006. DOI 10.1088/1572-9494/abfcb9. [Google Scholar] [CrossRef]

37. Akram, S., Razia, A. (2021). Hybrid effects of thermal and concentration convection on peristaltic flow of fourth grade nanofluids in an inclined tapered channel: Applications of double-Diffusivity. Computer Modeling in Engineering & Sciences, 127(3), 901–922. DOI 10.32604/cmes.2021.014469. [Google Scholar] [CrossRef]

38. Ejaz, A., Abbas, I., Nawaz, Y., Arif, M. S., Shatanawi, W. et al. (2020). Thermal analysis of MHD non–newtonian nanofluids over a porous media. Computer Modeling in Engineering & Sciences, 125(3), 1119–1134. DOI 10.32604/cmes.2020.012091. [Google Scholar] [CrossRef]

39. Vajravelu, K., Nayfeh, J. (1992). Hydromagnetic convection at a cone and a wedge. International Communications in Heat and Mass Transfer, 19(5), 701–710. DOI 10.1016/0735-1933(92)90052-J. [Google Scholar] [CrossRef]

40. Chamkha, A. J. (1996). Non-darcy hydromagnetic free convection from a cone and a wedge in porous media. International Communications in Heat and Mass Transfer, 23(6), 875–887. DOI 10.1016/0735-1933(96)00070-X. [Google Scholar] [CrossRef]

41. Khan, M. S., Karim, I., Islam, M. S., Wahiduzzaman, M. (2014). MHD boundary layer radiative, heat generating and chemical reacting flow past a wedge moving in a nanofluid. Nano Convergence, 1(1), 1–13. DOI 10.1186/s40580-014-0020-8. [Google Scholar] [CrossRef]

42. Abd El-Aziz, M. (2008). Thermal-diffusion and diffusion-thermo effects on combined heat and mass transfer by hydromagnetic three-dimensional free convection over a permeable stretching surface with radiation. Physics Letters A, 372(3), 263–272. DOI 10.1016/j.physleta.2007.07.015. [Google Scholar] [CrossRef]

43. Eckert, E. R. G., Drake, R. M. (1971). Analysis of heat and mass transfer. USA: McGraw-Hill. [Google Scholar]

44. Mortimer, R. G., Eyring, H. (1980). Elementary transition state theory of the soret and dufour effects. Proceedings of the National Academy of Sciences, 77(4), 1728–1731. DOI 10.1073/pnas.77.4.1728. [Google Scholar] [CrossRef]

45. Devi, S. A., Devi, R. U. (2011). Soret and dufour effects on MHD slip flow with thermal radiation over a porous rotating infinite disk. Communications in Nonlinear Science and Numerical Simulation, 16(4), 1917–1930. DOI 10.1016/j.cnsns.2010.08.020. [Google Scholar] [CrossRef]

46. Rafiq, T., Mustafa, M., Farooq, M. A. (2020). Modeling heat transfer in fluid flow near a decelerating rotating disk with variable fluid properties. International Communications in Heat and Mass Transfer, 116, 104673. DOI 10.1016/j.icheatmasstransfer.2020.104673. [Google Scholar] [CrossRef]

47. Raju, C. S. K., Sandeep, N. (2016). Falkner-skan flow of a magnetic-Carreau fluid past a wedge in the presence of cross diffusion effects. The European Physical Journal Plus, 131(8), 1–13. DOI 10.1140/epjp/i2016-16267-3. [Google Scholar] [CrossRef]

48. Waqas, M., Hayat, T., Alsaedi, A., Khan, W. A. (2020). Analytical evaluation of oldroyd-B nanoliquid under thermo-solutal robin conditions and stratifications. Computer Methods and Programs in Biomedicine, 196, 105474. DOI 10.1016/j.cmpb.2020.105474. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.