
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.019770
REVIEW
Analysis of Multi-AGVs Management System and Key Issues: A Review
1Shanghai Key Laboratory of Intelligent Manufacturing and Robotics, School of Mechatronic Engineering and Automation, Shanghai University, Shanghai, 200444, China
2National Demonstration Center for Experimental Engineering Training Education, Shanghai University, Shanghai, 200444, China
*Corresponding Author: Tao Song. Email: songtao43467226@shu.edu.cn
Received: 14 October 2021; Accepted: 22 December 2021
Multiple Automatic Guided Vehicle (multi-AGVs) management systems provide an effective solution to ensuring stable operations of multi-AGVs in the same scenario, such as flexible manufacturing systems, warehouses, container terminals, etc. This type of systems need to balance the relationship among the resources of the system and solve the problems existing in the operation to make the system in line with the requirement of the administrator. The multi-AGVs management problem is a multi-objective, multi-constraint combinatorial optimization problem, which depends on the types of application scenarios. This article classifies and compares the research papers on multi-AGVs management in detail. Firstly, according to the different dimensions of the problem, the multi-AGVs management system is analyzed from three perspectives, namely, 1) task dimension- dispatch, 2) spatial dimension-path, and 3) time dimension-scheduling. The detailed comparison between the three dimensions and their respective solutions are discussed in detail as well. Secondly, according to their utility, the multi-AGVs management problems are divided into three categories: 1) cost reduction, resource-oriented, 2) efficiency improvement, problem-oriented, 3) personalized demand, goal-oriented. The algorithm and methods of the different utility-oriented are analyzed and discussed. The related literature is summarized and corresponds to the composition of the multi-AGVs management system and the multi-AGVs management problems. Finally, according to the literature review, suggestions are made for further research.
Keywords: Multiple automatic guided vehicle; dispatch; route; schedule
Nomenclature
| AGV: | Automated Guided Vehicles |
| WMS: | Warehouse Management System |
| STT: | Shortest Travel Time |
| STD: | Shortest Travel Distance |
| MQS: | Maximum Queue Size |
| LWT: | Longest Waiting Time |
| SAWM: | Simple Additive Weighting Method |
| MAWM: | Modified Additive Weighting Method |
| RW: | Random Work center rule |
| STT/D: | Shortest Travel Time/Distance rule |
| LTT/D: | Longest Travel Time/Distance rule |
| MOQS: | Maximum Outgoing Queue Size rule |
| MROQS: | Minimum Remaining Outgoing Queue Space |
| MFGPS: | Modified First Come-First Serve rule |
| RV: | Random Vehicle rule |
| NV: | Nearest Vehicle rule |
| PV: | Farthest Vehicle rule |
| LIV: | Longest Idle Vehicle rule |
| LUV: | Least Utilized Vehicle rule |
| NWF: | Nearest-Workstation-First rule |
| NVF: | Nearest-Vehicle-First |
| LIV: | Longest-Idle-Vehicle |
| FCFS: | First-Come-First-Served |
| STTF: | Shortest-Travel-Time-First |
| NVFTP: | Nearest-Vehicle-First with Time Priority |
| DQN: | Deep Q-Network |
| VRP: | Vehicle Routing Problem |
| GA-PSO: | Genetic Algorithm–Particle Swarm Optimization |
| FMS: | Flexible Manufacture System |
| PGA-B: | Proposed Genetic Algorithm with Bidirectional layout |
| GACO: | Guided Ant Colony Optimization algorithm |
Automated Guided Vehicles (AGV) are one of the fastest growing areas in robotic industry. Multi-AGVs systems in warehousing and manufacturing facilities have been widely recognized as a practical means to increasing production efficiency while substantially reducing operational costs. To ensure that each vehicle in the multi-AGVs system executes the designated mobile tasks in accordance with certain rules, multi-AGVs management systems have become an important strategy tool. Many scholars have studied multi-AGVs management systems.
A multi-AGVs management system can decide when, where and how each vehicle should act to perform tasks along given routes [1]. The management of multi-AGVs can be divided into three parts: scheduling, dispatching and routing [1–3]. Scheduling includes the issue of dispatching and routing over time to ensure that each task is carried out without conflict and congestion. Dispatching is the process of selecting and assigning tasks to vehicles, i.e., determining which vehicle should be assigned to perform a specific task. Routing refers to the selection of the specific paths taken by AGVs to reach their destinations.
The dispatching issue has already been studied by some groups by dividing this problem into single-attribute and multi-attribute dispatching with two categories: work center initiated task assignment and vehicle initiated task assignment [1,4]. The routing issue has been researched by researchers in considering different categories [5–7]. The scheduling issue has been researched by researchers in Xu et al. [8]. Some groups studied the combination problems of these issues, e.g., dispatching and routing, routing and scheduling [7,9]. Multi-AGVs systems have been widely discussed by researchers. Vivaldini et al. [10] contributed to the clarification of AGVs dispatching, scheduling and routing, and provided a comprehensive review of the main existent methods to solve, which focused on the solution of macro problems. Franciscatto [11] presented developments on the facility layout design and the scheduling in FMS. Angra et al. [12] compared and evaluated the performance of five different conventional job selection dispatching rules for multi-AGVs system. Fragapane et al. [13] identified and classifies works related to the planning and control of AGV in intralogistics, which highlights how AGV technological advances affect planning and control decisions. Chawla et al. [14] described multi-AGVs system for material handling and analyzed some specific problems in the FMS. Vis [15] specified research perspectives in the design and control of AGV systems in distribution, transshipment and transportation systems. Torres et al. [16] had focused their optimization studies on AGVs design and control optimization. Jiang et al. [17] divided the scheduling problem into three types: static scheduling, dynamic scheduling and simultaneous scheduling with other resources. Qiu et al. [7,18–20] summarized one or more problems in multi-AGVs systems from different aspects. Fazlollahtabar et al. [21] analyzed and studied the AGV problem in FMS in detail from the algorithm used, which included mathematical methods, simulation studies, metaheuristic techniques and artificial intelligence.
Multi-AGVs management systems involve coordinating system’s resources, track layout of the system, the number of AGVs required by the system and the buffer queue size. The track layout of the system was divided into two categories: unidirectional-guide-path and bidirectional-guide-path [18]. An effective evolutionary approach was proposed to minimize the number of AGVs [22]. The maximum exit buffer queue size of work center is included as a reference in the dispatch issue [23]. There are conflict issues, deadlock issue and idle-vehicle positioning problem which often need to be solved during operation. In most cases, the less time required and the shorter AGV travel distance are the optimization goals pursued. the idle-vehicle positioning problem was researched using an exact polynomial-time algorithm [24]. Optimization of the time required for multi-AGVs system has been studied which aims to find the shortest time routes, with avoidance of deadlock and blocking in the system [25]. The idle-vehicle positioning issue was researched using an exact polynomial-time algorithm [24]. The number of AGVs to execute a given transportation order was determined by the task allocation method proposed by Vivaldini et al. [26]. Reduction in time required by the system and the path congestion were proposed by decreasing the start-stop frequency [16].
This article aims to conduct a survey including two aspects: the multi-AGVs management system and the multi-AGVs management problem. The multi-AGVs management system is further split into scheduling, dispatching and routing. The detailed comparison between the three dimensions and their respective solutions is discussed in detail in Section 2. In Section 3, three kinds of multi-AGVs management problems with different applications are studied according to the references, and the solutions and algorithms are discussed and compared in detail. Section 4 corresponds the literature to the two dimensions and comments on different issues. Finally, in Section 5, future development directions for the multi-AGVs management systems are provided.
2 Modular Analysis of the Multi-AGVs System
The multi-AGVs can be described as the system that coordinates dispatching, routing and scheduling functions to control a number of AGVs for shared tasks. As shown in Fig. 1, the Warehouse Management System (WMS) distributes orders to the multi-AGVs management system which outputs executable order information to each AGV. The multi-AGVs management system includes three parts: dispatching, routing, and scheduling. Specifically, the dispatching module assigns orders to each AGV according to specific strategies and decides which AGV should perform a certain task. The routing module finds available paths for each AGV to perform the assigned tasks. At the time level, the scheduling module decides when the tasks are to be executed and how to deal with the accidents during the operation, such as conflicts and deadlocks along the path. When each AGV is running, it feeds back its own status and the task implementation status to the management system or the WMS in real time. If the order execution fails, it would be redistributed and transported again. The entire system forms a closed loop to ensure the execution of the task smoothly. In the following text, the main solution algorithms of the three parts are described and compared in detail.
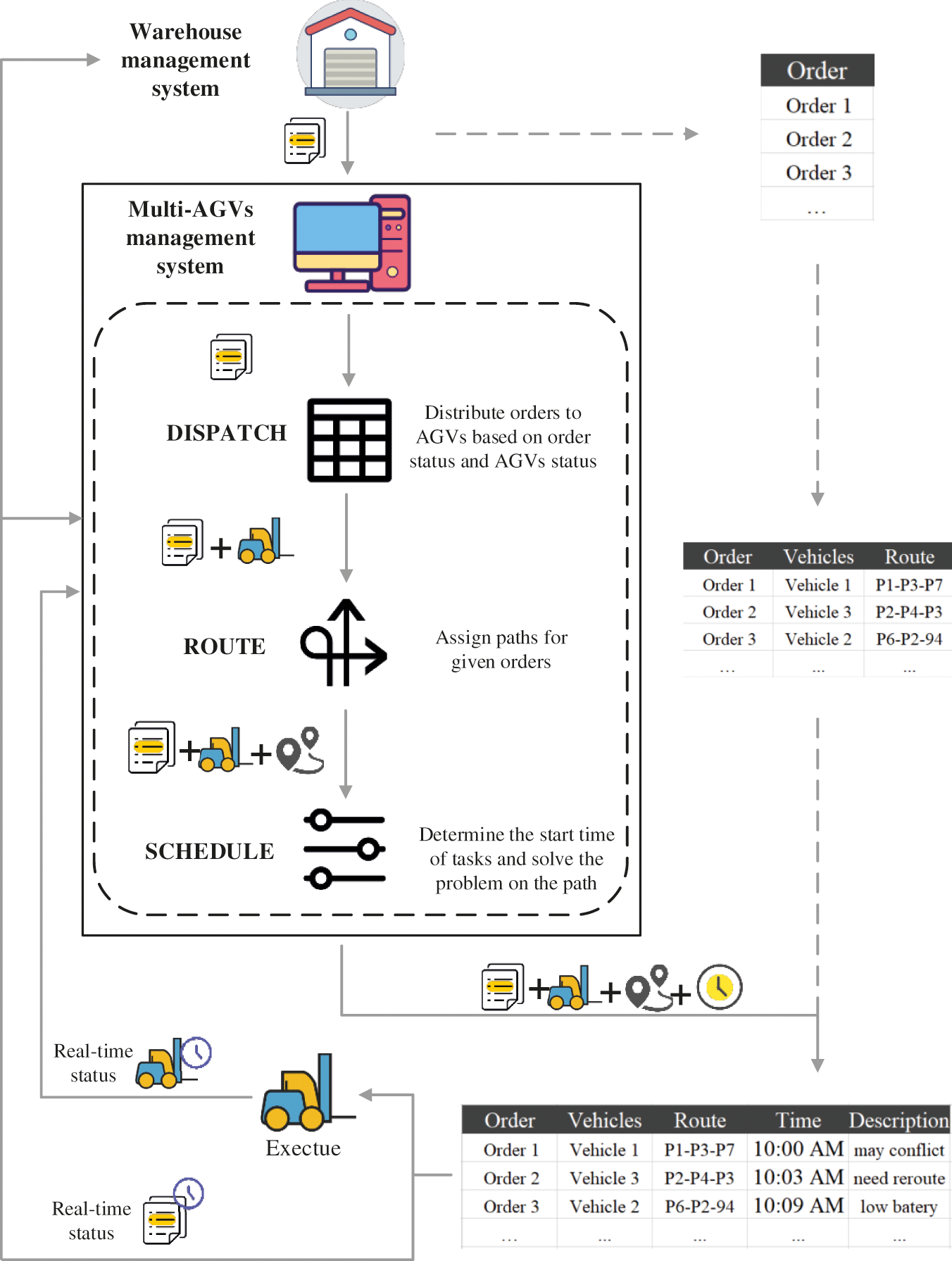
Figure 1: The role of the multi-AGVs management system in the warehousing process
Dispatch module solves the problem of task dimension and adopts a strategy based on the goals set by the administrator and decides which AGV should perform a certain task [2]. As shown in Fig. 2, there are orders (the S2 represents the station-02) to be executed and idle AGVs that need to be allocated by the dispatch function. There are three orders: S1–S7, S2–S6 and S5–S4 which can represent the tasks to move goods from one station to another. There are some AGVs in idle state waiting for the orders to be allocated. The dispatch strategy is divided into single-attribute strategies and multi-attribute strategies [1]. For single-attribute strategies, there are Shortest Travel Time/Distance (STT/D) rule [4], Maximum Queue Size (MQS) rule [27] and Longest Waiting Time (LWT) rule [28]. For multi-attribute rules, there are Simple Additive Weighting Method (SAWM) [29], Yager’s Multi-attribute Decision Making Method (YAGER) [30] and Modified Additive Weighting Method (MAWM) [31]. The AGV dispatch problem is divided into two categories: vehicle initiated task assignment and work center initiated task assignment [4]. The former deals with the problem that the AGV chooses a task to execute, which usually involves a single AGV and multiple work centers. About this method, there are heuristic rules such as Random Work center (RW) rule, Shortest Travel Time/Distance (STT/D) rule, Longest Travel Time/Distance (LTT/D) rule, Maximum Outgoing Queue Size (MOQS) rule, Minimum Remaining Outgoing Queue Space (MROQS) rule and Modified First Come-First Serve (MFGPS) rule discussed [4]. The latter deals with the issues for the work center to select an idle AGV to perform the task, which usually involves a single work center and one or more AGVs. There are Random Vehicle (RV) rule, Nearest Vehicle (NV) rule, Farthest Vehicle (PV) rule, Longest Idle Vehicle (LIV) rule, Least Utilized Vehicle (LUV) rule [4].
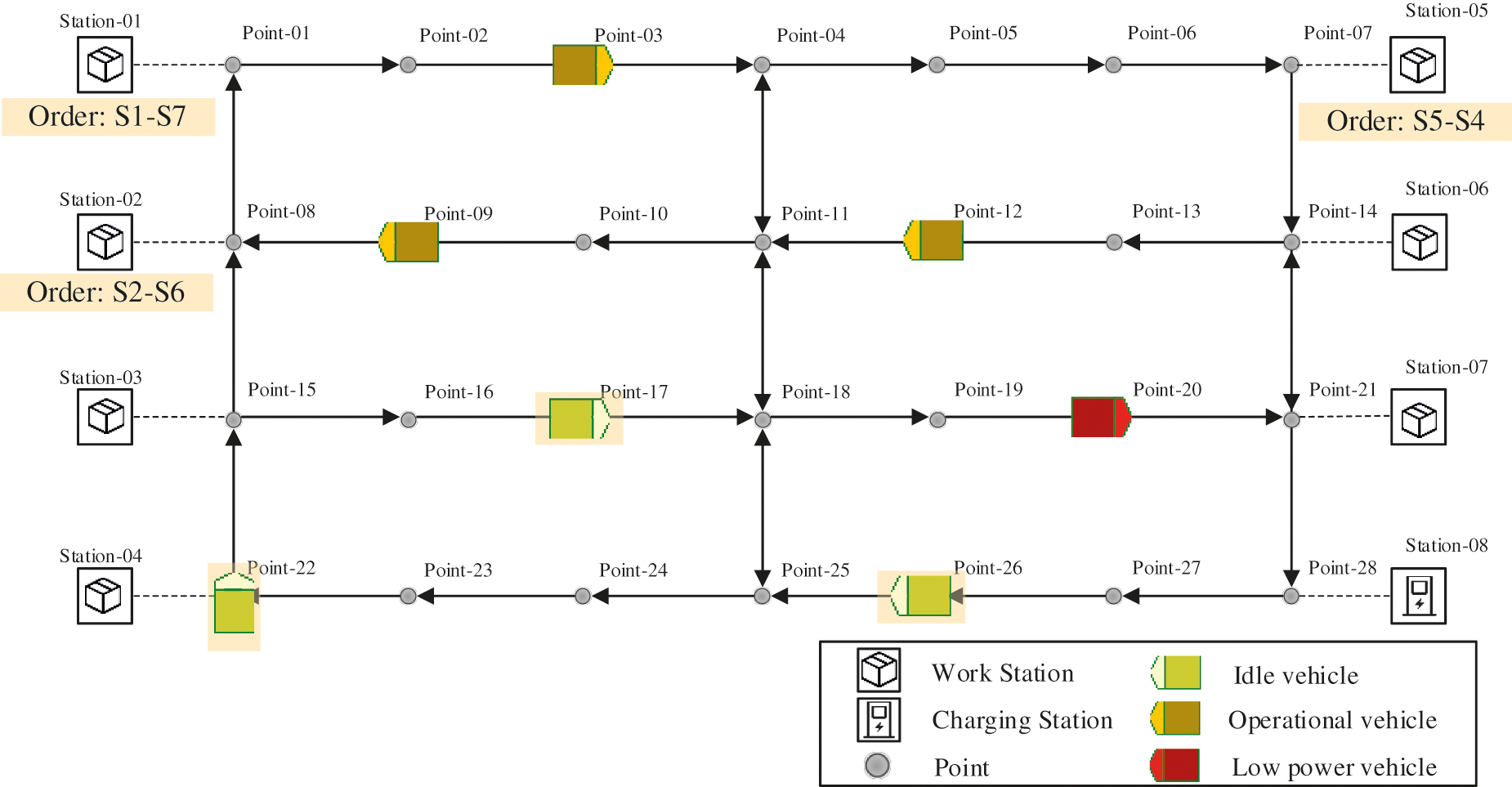
Figure 2: The dispatch function of multi-AGVs management system
Generally speaking, multi-attribute strategies can meet more targets than the single-attribute strategies, that is to simultaneously consider two or more of the following objectives: minimizing waiting time, minimizing queue length, minimizing travel distance, maximizing throughput, and maximizing vehicle and machine utilization. Compared with single-attribute rules, multi-attribute strategies can be more robust. This section also discusses the vehicle initiated task assignment multi-attribute dispatch and work center initiated task assignment multi-attribute dispatch in detail.
2.1.1 Single-Attribute Strategies
Single-attribute dispatch strategies are generally simple and applicable. The common single-attribute dispatch strategies include: Nearest-workstation-First (NWF) [32], Nearest-Vehicle-First (NVF) [33], Longest-Idle-Vehicle (LIV) [34], First-Come-First-Served (FCFS) [35,36] and Shortest-Travel-Time-First (STTF) [4]. NWF is the dispatch strategy initiated by AGVs, and the idle AGVs search for the nearest workstation to perform tasks. The disadvantage is sensitive to the layout of the map. Namely, the tasks would probably never be carried out if they were located outside the often-visited locations. As to NVF, the work center has the initiative to allocate tasks. Namely, the available AGV that is closest to the work center has the priority to receive the tasks for execution. It means that AGVs far away from the work center cannot take full advantage [37]. The FCFS may result in poor transportation efficiency of the system that assigns the vehicles to the earliest request (longest waiting load) at the station. Compared with the above dispatch rules, the threshold of time is set and AGVs with long wait time obtain the priority-promotion in Nearest-Vehicle-First with Time Priority (NVFTP) [37]. The system prioritizes it when the load reaches the thresh-old value. The threshold value should be decided for the specific situation.
2.1.2 Multi-Attribute Strategies
a. Vehicle Initiated Task Assignment Multi-Attribute Strategies
A workload-balancing algorithm is developed to deal with the pickup-dispatching problem that determines which job should be assigned to an AGV [38]. A multi-attribute dispatch approach was proposed based on vehicle-initiated task assignment by Jeong et al. [39]. This method considered the remaining space in the output buffer of a workstation, the distance between the idle AGVs and the workstation, and the remaining space in the input buffer of the work destination. In the multi-attribute strategy, the weight of each attribute is difficult to determine, which is why the author developed a dynamic method based on the neuronal network to adjust the weight over time. Moreover, the author used different performance indicators to compare the methods proposed with the single-attribute method and subsequently demonstrated the superiority of multi-attribute dispatch method. A multiple-attribute method was proposed to take slack time, waiting time and distance into consideration [40]. Tasks were evaluated by three attributes and the tasks with the greatest evaluation value would be served by the AGV. A model was presented based on deep Q network training (DQN) to assign the task with the departure point closest to the idle AGV, and the least vehicles in the path to improve the completion time and avoid conflicts during operation [41]. The neural network method needs to be retrained when the environment changes.
b. Work Center Initiated Task Assignment Multi-Attribute Strategies
The task assignment initiated by the work center is to decide the system selection of an AGV from the idle group for a given task. A vehicle priority dispatch method was presented based on NVF that used the global information and current status to allocate resources [42]. A dynamic dispatching strategy was proposed by Li et al. [43] to find a suitable AGV to conduct the task with reduced total travel distance and wait time. Both vehicle-initiated task assignment and work center-initiate task assignment were discussed by Bilge et al. [44]. The authors proposed multiple attribute rules and dynamic weight rules based on the traditional single-attribute dispatch rules: STTF and Minimum-Remaining-Outgoing-Queue-Space (MROQS). In addition, the authors verified the robustness of the rules by simulation. A deadlock-free multi-attribute dispatching method with dynamically adjustable weights (AWMA) was proposed in [45,46]. Travel distance, input, and output buffer statuses were selected as dispatching attributes according to the efficiency and deadlock avoidance requirement [45]. The load balance and deadlock avoidance were taken into consideration according to the system resources by Guan et al. [46]. A dual task allocation mechanism was designed based on task priority and FCFS [47]. Specifically, each AGV was configured with a sequence of tasks, and each sequence consisted of two tasks: i) the task under execution, ii) the task to be performed. This mechanism required that the termination point of the previous task be the start point of the next task, to reduce the idle AGV and improve the work efficiency of the multi-AGVs system. The disadvantage was that this distribution method was difficult to achieve in some cases. A single AGV dual task allocation mechanism was proposed to divide the tasks of AGVs into transportation tasks and self-generating tasks by Wu et al. [48]. These two kinds could be assigned to an AGV, and the simulation result showed that the method could increase the operation efficiency by 20%.
Route is the function to set a specific path for an AGV to reach its destination. The route function handles the issue of which path the two AGVs should take from the start point to the end point. As shown in Fig. 3, there are two AGVs at S7 and S8, and the route module has assigned two optional routes to each car (represented by two colors). The route issue was mentioned as a more complicated variant of the traditional Vehicle Routing Problem (VRP) [7]. The complexity of the route issue lies in the fact that the unpredictable collision problem in the actual work scenario must be considered. Generally speaking, the path obtained by the shortest path strategy and the shortest time strategy are not the same in multi-AGVs management systems, and sometimes it is necessary to reroute to solve the conflict and deadlock problem. As shown in Fig. 3, it can be seen that each idle AGV (the AGVs at point-07 and point-08) has two alternative routes (each color represents one route). For each AGV, the optimal route may not be the shortest one. This is because during the movement, an AGV is easily affected by the other AGVs on the same path. In the multi-AGVs management system, not only does route module select a path that meets certain condition for a single vehicle, but also need to take into account the path selection of other vehicles in order to avoid congestion or collision problem. Many scholars have proposed more complex and intelligent solutions about route module, which can be mainly divided into two categories: static routing algorithms and dynamic routing algorithms. The static routing method refers to the system operation mode in which the vehicle route does not change during operation. In the dynamic routing situation, the management system can re-plan or reselect a route based on the real-time information during the execution process.
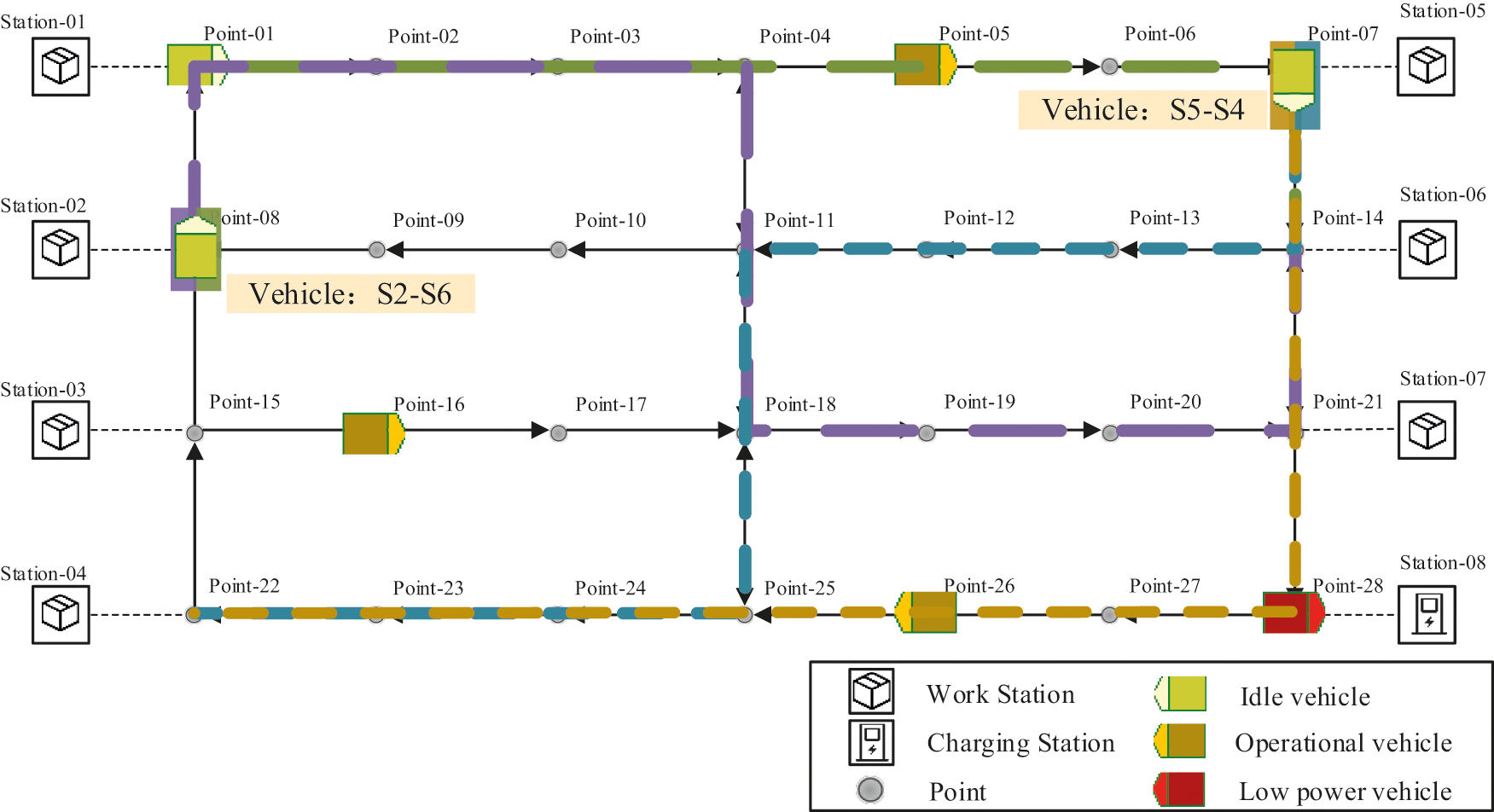
Figure 3: The route function of multi-AGVs management system
2.2.1 Static Routing Algorithms
The shortest travel distance is the main solution to static routing planning. The algorithms include Dijkstra algorithm [49], A*star algorithm [50], genetic algorithm [51], etc. An optimal route selection method was put forward for the shortest travel distance by improving the genetic algorithm [52]. For small-scale problems, the better results than traditional genetic algorithm can be obtained. A static method was proposed to solve the conflict-free path problem of AGVs [53]. This method included a two-stage routing method. The first stage modeled the road network and the second stage detected avoided deadlock. A conflict-free route by preplanning for the AGV was be proposed by Maza et al. [54], which included three steps: checking space feasibility, checking time feasibility and checking potential conflicts. With this method, the execution may not be accurately predicted and then the system may pause or even crash.
2.2.2 Dynamic Routing Algorithms
Compared with the static routing algorithms, dynamic routing algorithms is more adaptable to unexpected situations. An adaptive routing planning algorithm was proposed as follows: firstly, Dijkstra algorithm was used to perform preliminary routing of AGVs to obtain candidate paths, and then the nodes which may lead to conflict in the candidate path were sorted out and an adaptive method was then used to solve the conflict problem caused by these nodes [55]. The downside is that it may increase the complexity of the problem because of the reroute strategy. The estimated cost of the A* algorithm was improved by increasing the penalty value of the path that AGVs shared with each other to alleviate traffic congestion and collision [56]. Use of this reroute method would obtain a less complex reroute and better reroute effects. The shortest distance was employed to propose a routing planning algorithm using time windows in a vector form [57]. Although there are some problems, such as the complexity of rerouting and the real-time performance, the dynamic routing method is more appropriate in most cases of multi-AGVs management systems.
Scheduling is the issue that brings the time dimension into dispatch and route to decide when the dispatch occurs and how to resolve conflicts on the route. As shown in Fig. 4, the highlighted part represents the application scenario of the scheduling function, which is responsible for deciding to whom and when the resource should be given first. There are two AGVs (the AGVs at point-04 and point-12) competing for point-11 and other two AGVs (the AGVs at point-16 and point-17) competing for point-17. Schedule function solves the problem as to when the cross point (resource) can be allocated to which AGV. Vivaldini et al., [10,18] divided the scheduling problem into two categories: offline schedule and online schedule. In offline schedule method, all issues need to be considered before beginning of the task, and the system will generate a set of skeds and run according to them. Obviously, if all tasks are to be performed and any potential accidents that may occur are known during the planning period, the offline schedule strategy can be used. However, in practice, it is generally impossible to know all the precise information on tasks and accidents. Small changes in the arrival time of the AGV at the site or short-term congestion on the route will affect or even destroy the entire sked. The online schedule method makes it possible to obtain information and implement decisions in real time, monitor the evolution of the schedule and manage unforeseen events. There is also an alternative combining offline schedule strategies with the online schedule strategies. For example, Yan et al. [58], who used the Floyd algorithm, initially generated routes. Besides, the Particle Swarm optimization algorithm and the rerouting strategy were integrated for the dynamic schedule.
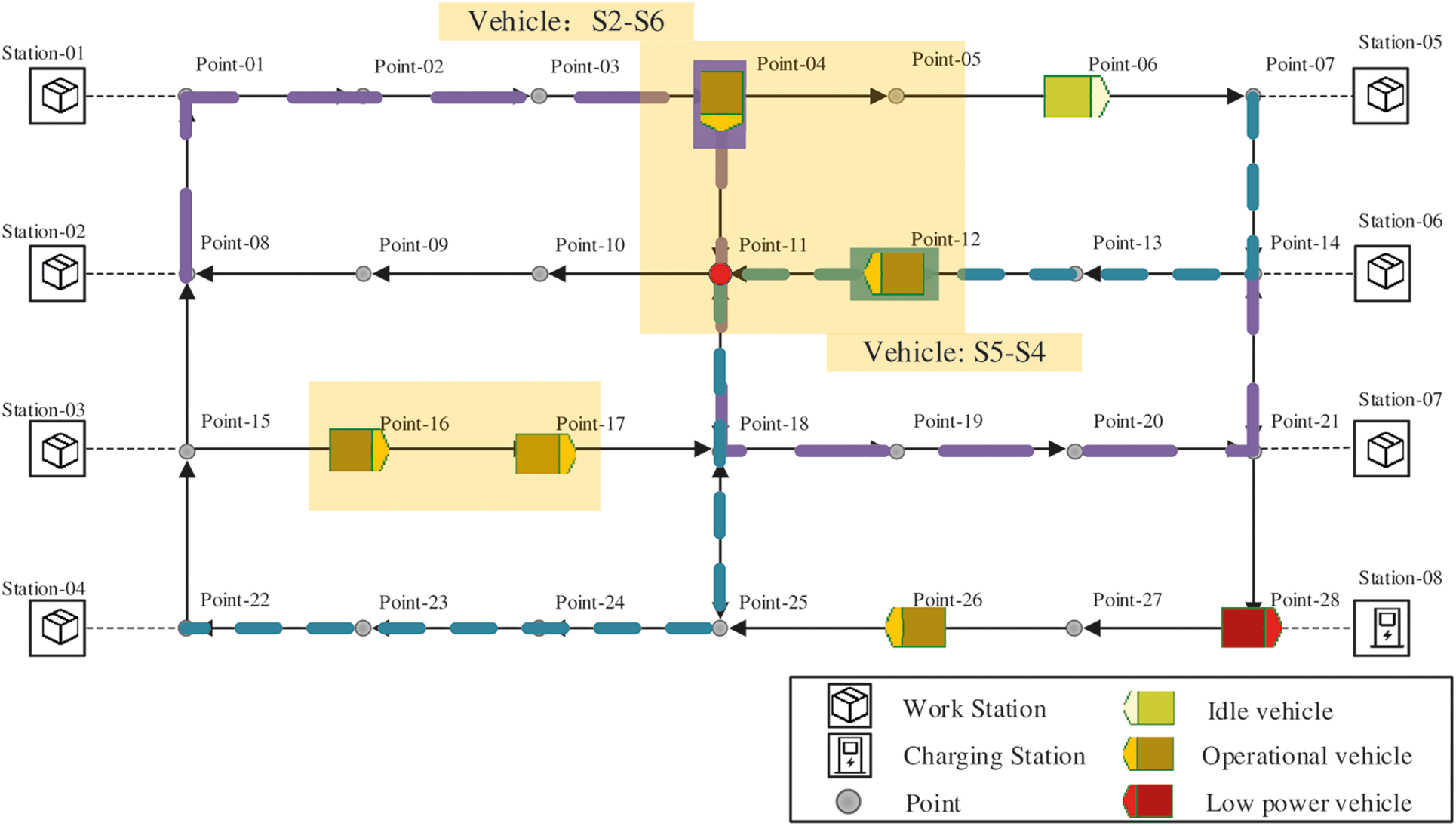
Figure 4: The schedule function of multi-AGVs management system
2.3.1 Online Real-Time Schedule Approach
In multi-AGVs management systems, the environments are usually stochastic (the travel time, loading and unloading times fluctuate, and vehicles may break down), so the schedule has to be adapted dynamically in time [56]. Correa et al. [59] proposed a hybrid method to solve AGVs schedule problems and conflict-free path problems in FMS, by taking the former as the main problem and the latter as the sub-problems. The authors modeled the main problem with constraint programming and the subproblem with mixed integer programming. It was proved that this method could be used on 6 AGVs. A similar bilevel decomposition algorithm was used by Nishi et al. [60] by decomposing a mixed integer formulation into two levels: the upper level master problem of task assignment and scheduling; and the lower level routing subproblem. The effectiveness of the proposed method was investigated by computational experiments. A schedule model was established to minimize the number of AGVs by considering the AGV battery charge [61]. A fuzzy hybrid GA-PSO (Genetic Algorithm–Particle Swarm Optimization) was used to optimize the model that verifies the feasibility and performance of the model. A load-exchangeable AGV (EX-AGV) system was exhibited, where vehicles could exchange loads, scheduled transportation tasks, and even the vehicle numbers when they move in opposite directions to ensure that the load is always on the shortest path [62].
2.3.2 Two-Stage Schedule Method
The hierarchical scheduling method combines the benefits of the offline scheduling strategy and the online scheduling strategy. Xu [8] proposed a schedule strategy based on a two-stage method. At the offline stage, the genetic algorithm is used to plan the optimal obstacle avoidance path for the AGV in a static environment. At the online stage, the system sorts and resolves conflicts in the operation. The benefits of offline scheduling and online scheduling were combined to consider the improvement of the multi-AGVs system performance [54]. The method planned to establish conflict-free path in the first stage, and in the second stage, an interruption method was adopted to avoid deadlock. As shown in Fig. 5, Yan et al. [58] proposed a three-level scheduling scheme to generate route schemes (the off-line route generation in Fig. 5) for any two workstations at the first level. In the second stage, the authors developed a mathematical delivery time model, and combined the real-time schedule (the scheduling task sequence in Fig. 5) with the Particle Swarm Operation algorithm to perform tasks allocation and dynamic schedule. The authors used heuristic rules to avoid collisions and deadlocks between AGVs based on the real-time operating status of AGVs in the third layer. An optimization process was proposed by Giglio [63] based on three sequential phases. In the first phase, the number of AGVs to be allocated to each arrived truck was determined; in the second phase, an AGV-to-truck assignment problem was solved; in the third phase, the single tasks were assigned to and sequenced on the AGVs. Bilge et al. [44] presented two methods were to solve the schedule problem: parameter method and dynamic method. The parameter method calculated the weight over the planning period, and the dynamic method used statistical information to update the weights over the cause of the evolution.
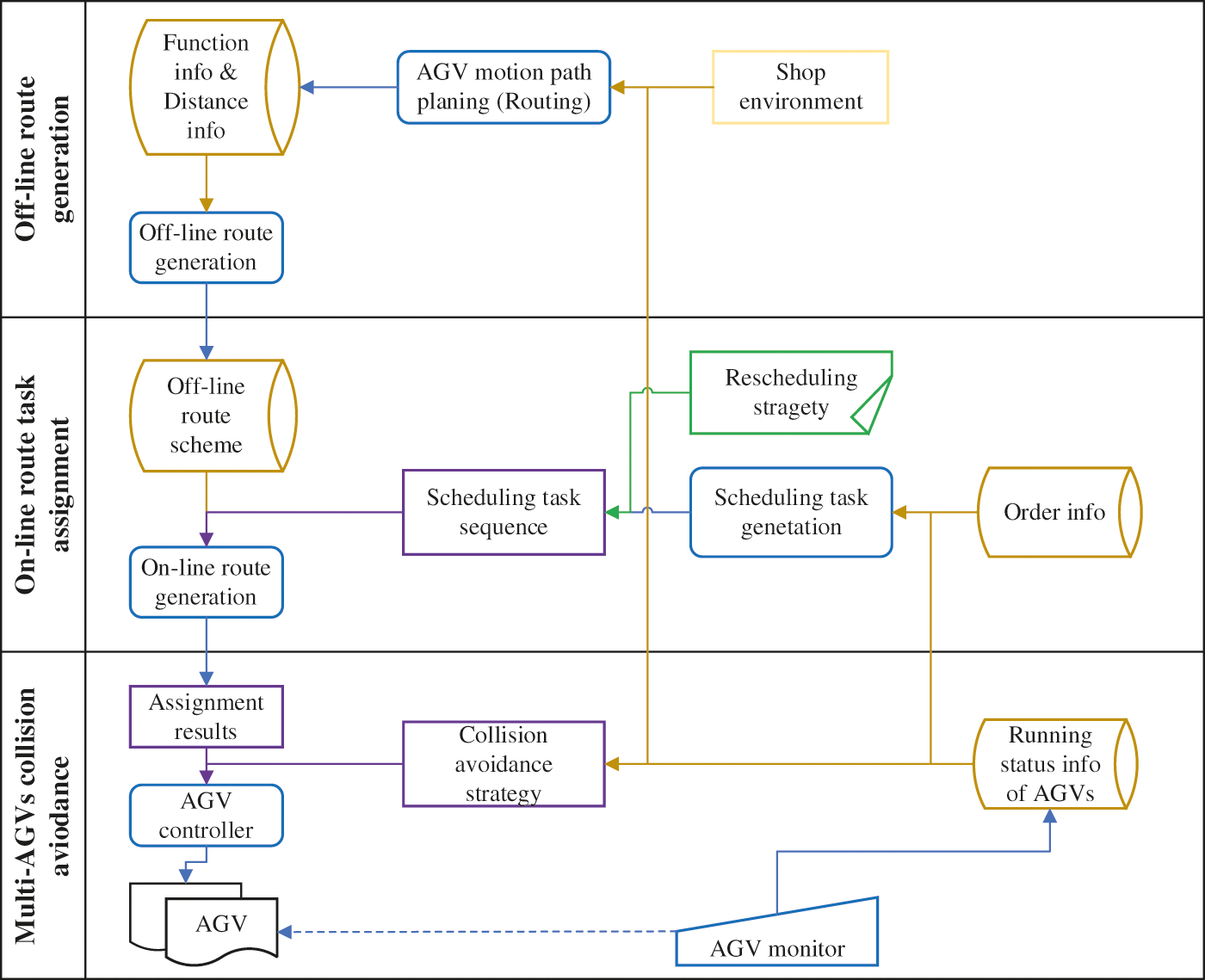
Figure 5: Structure of three-level scheduling scheme of [58]
This chapter divided the multi-AGVs management system into three parts and gave a detailed explanation respectively. It can be concluded from the literature that the multi-AGVs management system needs to synthesize the information (AGV position and status, order status, path status, station status) in the entire system and make judgments, which requires the real time information with high quality. Therefore, the multi-attribute dispatch strategies and the dynamic routing algorithms are more suitable complex application scenarios. Schedule defines the allocation process of AGVs for tasks while considering the time and cost operations and ensuring conflict-free routes, which is an essential part of a multi-AGVs system [64]. The integration of dispatch, route and schedule together is a very difficult NP-hard optimization issue. Solving them at the same time may reduce the real-time performance and quality of the solution due to insufficient computing power in some large scenarios. The offline methods can sacrifice time to ensure the optimum solution in certain computational power conditions. The hierarchical method combines the advantages of the online method and the offline method. Although there may be problems that need to be re-solved when the environment changes, it is favored by many scholars. The multi-AGVs management problem is a multi-objective, multi-constrained optimization problem. Different utilization scenarios have different resource constraints and optimization objectives. The detailed description of the multi-AGVs management problem will be elaborated on in the next chapter.
3 Analysis of Key Issues in Multi-AGVs Management System
The main purpose of the multi-AGVs management system is to properly allocate tasks to each AGV and ensure the conflict-free execution of the tasks. To solve the problem of allocating resources of the multi-AGVs management system, the number and form of resources in the system should first be determined. The resource-oriented problem can be seen as the issue about the cost reduction, which is related to the decision-making process at different levels. Problem of conflict and deadlock, as well as the problem of idle-vehicle position, may be considered to improve the performance of the system. In terms of system optimization, the administrator may pursue a shorter time or a shorter path consumption, which is called goal-oriented. There are interactions between different levels, as the type of the maps may directly influence complexity of the system, and the number of AGVs may also affect the time of tasks required.
The first step to research the multi-AGVs management system is to determine the resources in the system. Saravanan et al., [65,66] introduced the different layouts in the manufacturing system. A review was presented on facility layout design of an AGV in FMS [67]. The map layout design was proposed as a major issue in multi-AGVs system, and this article also compared three common methods of classifying the map, including flow topology, number of parallel lanes and flow direction, as shown in Table 1 [18]. This article used the flow direction as the classification method. AGVs are the main role of the system, which is responsible for the cargo transportation and coordination with other operations. The number of AVGs has an indirect impact on the time it takes and the complexity of the system. An appropriate number of AGVs can improve the efficiency of the management system and reduce the risk of accidents.

3.1.1 The Layout Design of the Map in the System
Depending on the direction of the traffic, there are two main ways to classify the vehicle paths: unidirectional-guide-path and bidirectional-guide-path. As shown in Fig. 6, in the unidirectional-guide-path, the vehicle can only travel along one direction of the path, and while in the bidirectional-guide-path, the vehicle can travel in both directions in the path according to actual needs. The unidirectional path system is more stable in operation than the bidirectional path system, especially for preventing system conflicts and deadlocks. Designing the path of the multi-AGVs system as a unidirectional path is a relatively simple deadlock avoidance method. In most seaport container terminals, a single-loop guide-path is usually used, and it is almost impossible for AGVs to block each other during operation [68]. A single direction traffic rule was proposed for the system by creating loops over the network, which significantly reduced the vehicle conflicts [69]. Zheng et al. [70] considered the problem of minimizing the makespan in unidirectional flow path design. The issues that determine the loop for the motion of an AGV and the location of pickup and delivery (P/D) stations in the cells in unidirectional single loop systems were considered by Farahani et al. [71]. The deadlock and blocking avoidance algorithm was proposed for unidirectional-path, mentioning that the conflict avoidance for opposite direction should be considered if there is a bidirectional layout [72]. Because the unidirectional path problem is usually easier than the bidirectional path solution, some scholars have converted the latter to the former [24].
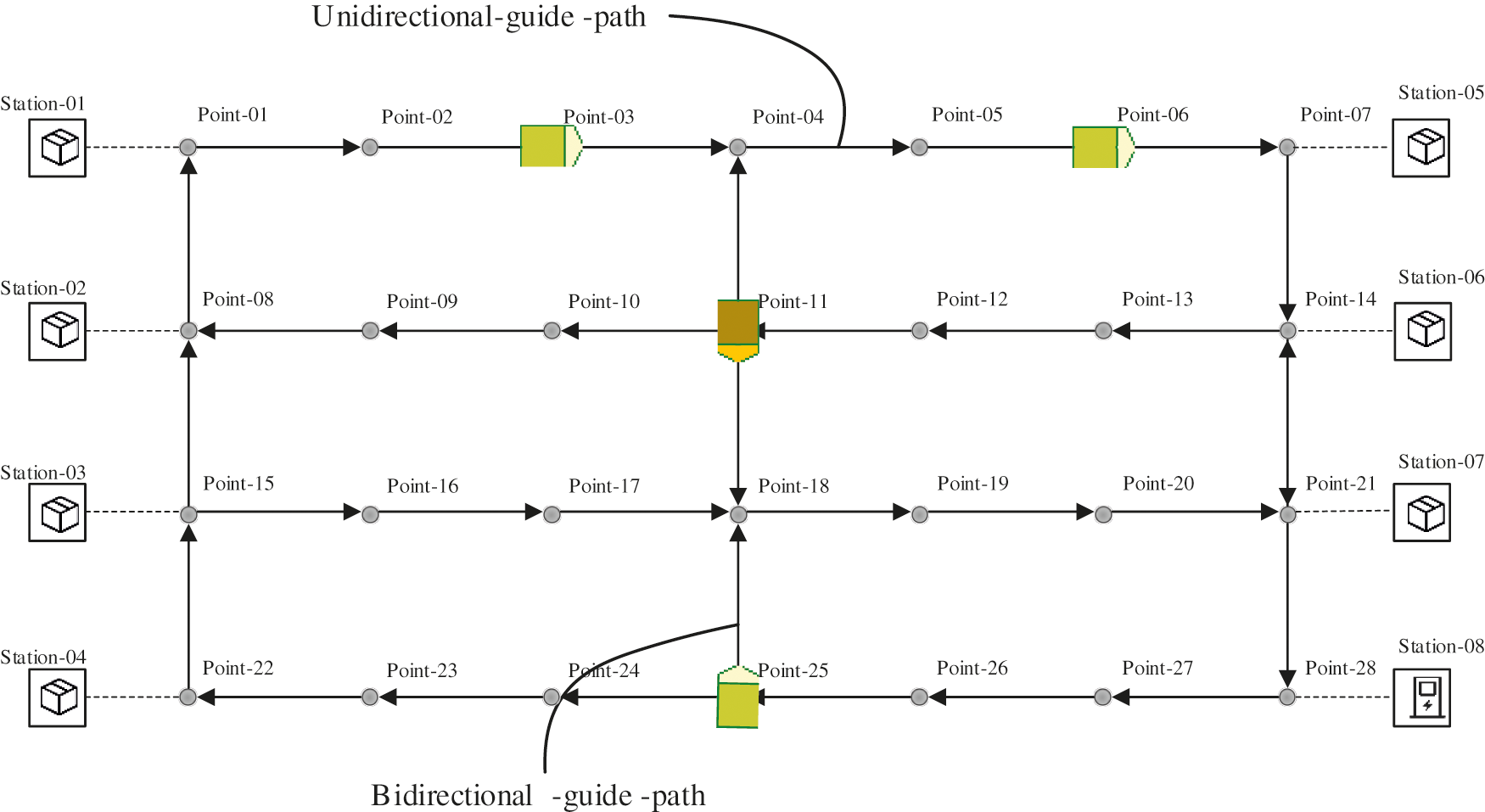
Figure 6: The difference of bidirectional-guide-path and Unidirectional-guide-path
The bidirectional-path solution has a higher degree of freedom than the unidirectional-path solution, so it works better than the unidirectional-path solution under certain conditions. Bidirectional paths were used to model and optimize FMS systems, and a genetic algorithm was also proposed to combine with the Dijkstra algorithm to minimize the makespan while considering the influence of the number of AGVs [73]. In this paper, the author tested four layouts and ten jobs respectively. The PGA-B (proposed genetic algorithm with bidirectional layout) was shown effective in 25 experiments. Sarker et al. [74] proposed a path selection algorithm to ensure that the AGVs path was conflict-free to achieve the minimum travel distance. An ant colony system (ACS) algorithm was developed to solve the shortest path design problem (SPDP) on bidirectional path topology [75]. Simultaneous scheduling and routing problem for AGVs was investigated with bidirectional-path environment [76]. A Petri net decomposition approach was addressed for simultaneous dispatching and conflict-free routing for bidirectional automated guided vehicle AGV systems in dynamic environments [77]. In this algorithm, the entire Petri net was decomposed into task and AGV subnets. The penalty function method was used to derive a solution for all subnets. A deadlock avoidance method was embedded in the proposed methodology to ensure the feasibility and the quality of the solution. Bahari [78] presented a bidirectional path flow layout and a routing algorithm that could guarantee conflict-free and shortest time routes for AGVs. A bidirectional routing planning and AGV path selection algorithm was proposed [79]. In order to minimize the space required for the map layout, the critical conditions of some key parameters between the paths and the AGV were derived to provide more complex path layout and routing algorithms. When considering the complexity of the system alone, the unidirectional-path solution was often preferred to minimize AGVs’ collisions in the performance of tasks [80], and the bidirectional-path solution was more suitable for the multi-AGVs management systems with higher performance requirements. The designer should also select an appropriate layout of the map balancing the requirements the physical capability of the system.
3.1.2 The Number of AGVs in the System
In many instances, the number of AGVs and the time required by the system and the time required to complete tasks are two competing issues. The aim of Fathi et al. [81] is to optimally schedule the delivery of raw material at assembly lines while using the minimum number of vehicles. Aiming at determining the number of AGVs required in a container terminal, a network model was established and a corresponding solution method was constructed to determine the minimum number of AGVs needed at the terminal [82]. Fu et al. [83] defined the AGV vehicle requirement determination as a general optimization problem, and developed a new AGV vehicle requirement determination method capable of effective solving the problem. An investigation for fleet size optimization of AGVs in FMS by application of the analytical method and grey wolf optimization algorithm (GWO) was carried out by Chawla et al. [84]. Choobineh et al. [85] modeled the steady-state behavior of the closed queuing network by a linear program with the optimal value being the estimate of the required fleet-size. A mathematical model in the form of multi-objective integer programming model was developed to obtain the optimal number of vehicles by Wang et al. [86], with an illustrative example presented to verify the proposed model. Hamdy [87] developed a simulation model to determine the optimized number of AGVs capable of increasing throughput while meeting the material handling requirements of the system. A mathematical model was proposed to identify the MHRs requirement to perform the material handling activities in the FMS by Chawla et al. [88]. Moorthy et al. [89] designed three experiments: 20, 40, and 80 AGVs to simulate the proposed model. The results showed that the deadlock rate with 80 AGVs was only slightly higher than the rate with 40 AGVs. However, the reduction of the number of AGVs will cause the system to proceed slowly, so the authors proposed that any attempt to reduce the number of AGVs in order to reduce the occurrence of deadlock was not worthwhile based on the proposed models and experiments. In order to minimize the number of AGV, Lyu et al. [73] investigated the problem of optimum number of AGV. The problem of the shortest transportation time and the problem of conflict-free routing were solved by using genetic algorithm based on time window combined with Dijkstra algorithm. The article highlighted the importance of selecting an appropriate number of AGVs through experiments. Chawla et al. [90] found that AGV speed and AGVs fleet size had a significant role in the increase or decrease of throughput of the FMS. Wu et al. [91] discussed the interaction between the number of AGVs and the load capacity of AGVs in the manufacturing system. In practical applications, the number of AGVs in the system should be determined by careful trade-offs between vehicle cost, queuing capacity, and other design factors.
The essence of the multi-AGVs management problem is the proper allocation of resources. The improper allocation of resources will cause a series of problems such as conflicts and deadlocks in the system. The conflict will occur when the same resource is allocated to two targets at the same time or the system cannot decide which target to allocate the resource. If the conflicts are not discovered or resolved in time, they may cause collisions or congestion among the AGVs, which will reduce system throughput. The appearance of deadlock will lead to a partial stagnation of the system, which may lead to the crashing of the system. Proper handling of idle vehicle positions in the system can reduce the time and distance consumed by the system.
Conflicts arise when resources cannot be allocated reasonably. In a multi-AGVs system, conflicts can be divided into three categories: node conflicts (as shown in Fig. 7a, there are two paths across the point-05), pursuit conflicts (as shown in Fig. 7b, there are two AGVs compete for the point-05) and opposite conflicts (as shown in Fig. 7c, there are two AGVs running opposite each other) [8]. They are all caused by improper node allocation and route allocation. Generally, there are three ways to solve conflicts: (1) resolving by resetting the path layout more suitable for the system; (2) using sensors that can perceive the environment to identify impending conflicts or collisions, and avoid them through vehicle backtracking or rerouting; (3) developing certain routing strategies to prevent conflicts and deadlocks, such as adjusting the speed when the conflict is about to happen.
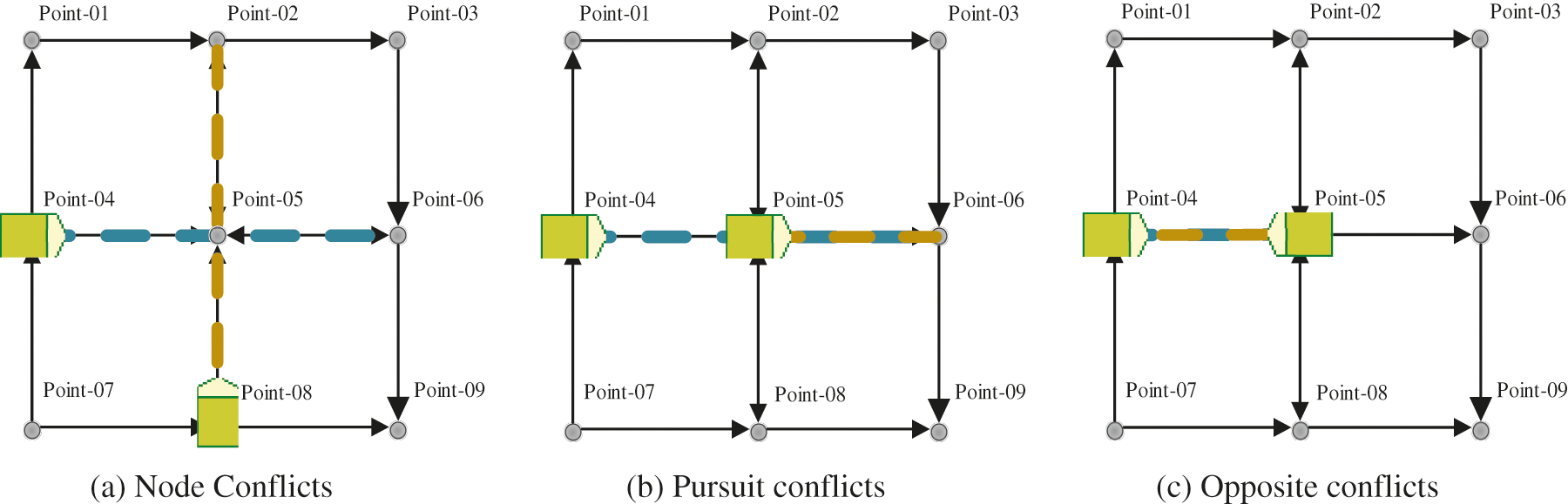
Figure 7: Three kinds of conflict issues: (a) node conflicts (there are two paths across the point-05 and compete for this point), (b) pursuit conflicts (the AGV behind wants to compete for the point where the AGV in front is located) and (c) opposite conflicts (two AGVs are going opposite each other on the same road)
Kłosowski et al. [92] proposed a scheme to design the layout of the map to solve the conflict issue by dividing the workspace into zones and switching stations. The authors assigned an AGV to each zone and used the switching stations to exchange goods for conflict avoidance (as shown in Fig. 8a, there are four zones and one switching station). Zhang et al. [93] took a similar approach to that of Kłosowski et al. [92], by dividing the warehouse environment into five zones, and then performed route planning. The FMS was split into six flexible manufacturing cells and served by six MHRs deployed in each partitioned area for efficient material handling operations [94]. This solution is not recommended when there are many charges that must be exchanged frequently between different zones as it will greatly increase the probability of conflict. Xu [8] devised a two-step method, and in the offline step, a high degree of genetic algorithm was used to make the plans in the static environment. The authors used the rate adjustment method and the reroute method to solve the conflicts in the online stage. For the two AGVs where the node conflict occurred, the one with high priority can go first, and the others will be parked or decelerated. Pursuit conflicts can be resolved by improving the speed of the former AGV or reducing the speed of the latter AGV. For the opposite conflicting, rerouting planning and windows backwards can be used to solve (as shown in Fig. 8b). A dynamic adjustment method based on conflict probability for AGVs was designed by Li et al. [95] focusing on the Pursuit conflicts. To solve the conflict and deadlock problem, a solution based on two AGVs exchanging loads and numbers was proposed (as shown in Fig. 8c) [62]. With the special structure of the AGV, the conflict problem can be solved when two AGVs meet. Li et al. [96] developed a conflict-free AGV model considering wait times and proposed a guided ant colony optimization (GACO) algorithm to resolve it. Moreover, the efficacy of the model and the solution method was verified through simulation. Draganjac et al. [97] used a decentralized control algorithm to propose a priority-based vehicle conflict resolution solution (as shown in Fig. 8d). There is a negotiation process aiming to agree upon the execution of a set of coordinated removal and passing actions which intended to free the path for the blocked vehicle and ensured its safe motion toward the allocated private zone. The process was initiated by the removal requested message sent by the blocked vehicle to all AGV blocks along their paths. To achieve conflict-free AGV path planning, a priority-based speed control strategy was used in conjunction with the Dijkstra depth-first search algorithm to solve the model [98]. The multi-AGVs system was formulated as an integer program, and then, local/random search methods were proposed to solve the conflict-free routing problem [99]. Wang et al. [100] used the concept of abstract time windows (ATWs) to represent the movement of robots. The conditions for detecting conflicts in the ATW representation were introduced along with the necessary operations for resolving conflicts. Guo et al. [101] designed an architecture of AGV’s system based on Multi-Agent System (MAS) to improve the speed control method and the method of determining AGV priority based on time cost are used as the AGV negotiation strategy. The study showed that the control method based on MAS was more suitable for the conflict-free path planning of more than 30 AGVs. For the system with a clear classification of tasks or AGV, the priority may be used first and the decentralized control method can be used in the system with a relatively simple layout. Whether it is a priority-based conflict resolution solution or a decentralized control method, the problem will not be well resolved when the number of AGVs reaches a certain number.
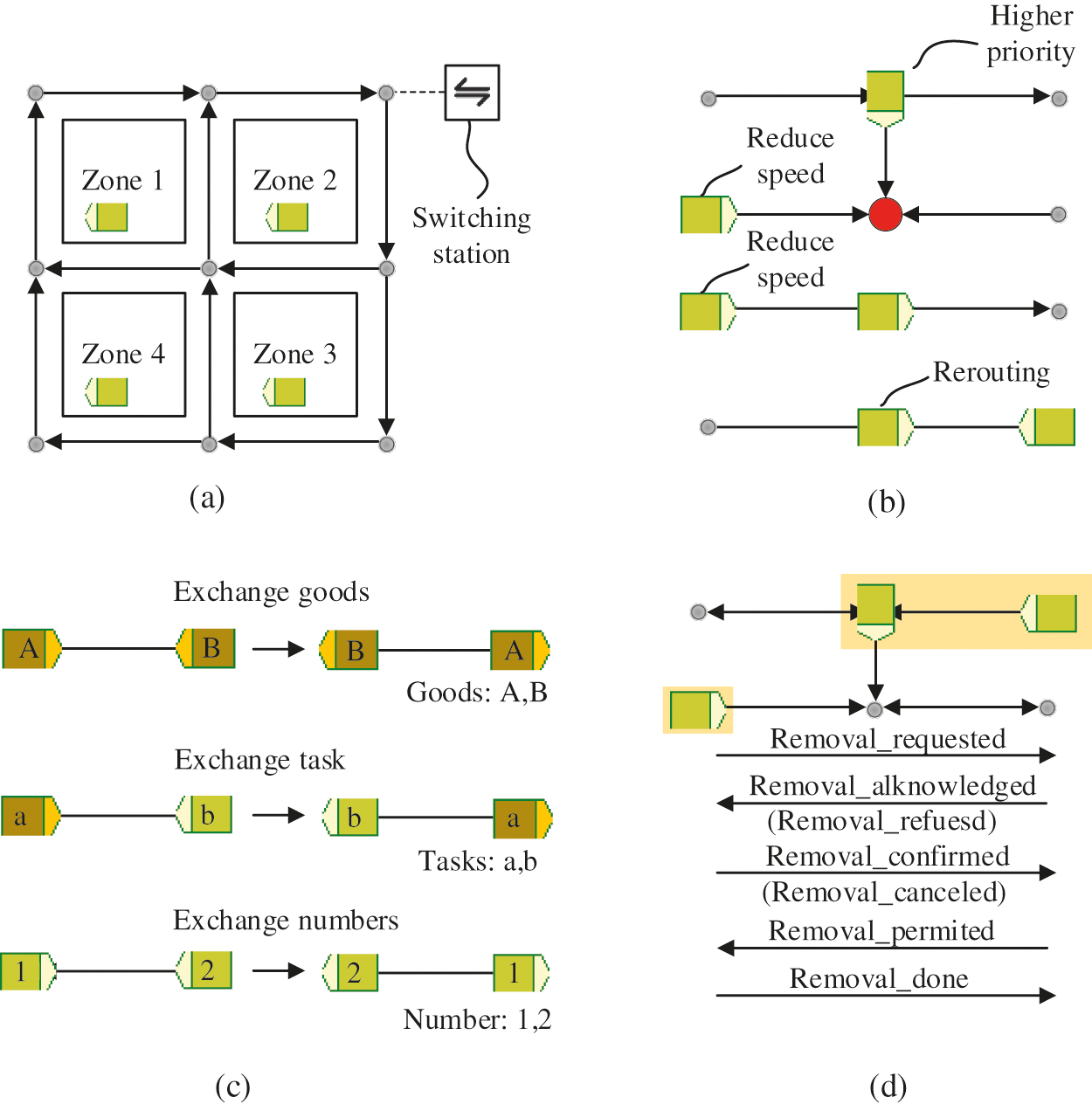
Figure 8: Four solutions of conflict problems
The deadlock problem is defined as follows: “A situation where one or more concurrent processes in a system are blocked forever because the requests for resources by the processes can never be satisfied” [102], as shown in Fig. 9, Each point represents a resource and each color represents a route. The status of the resource is occupied if there is an AGV at this point (point-02) and the resource will be released (point-01) when the AGV leaves. There are four AGVs and their routes form a circular. The scene that each AGV requires resources occupied separately and none of the resources can be released is called blocked, which can lead to deadlock. The deadlock may result in the failure to execute part of the system and will gradually extend to the entire system, eventually leading to a constant state of blockage of the integrated system [103]. There are three causes of deadlock in the multi-AGVs system: (1) insufficient system resources, (2) improper dispatch sequence and (3) improper resource allocation. Generally speaking, there are three main methods for deadlock problems: deadlock avoidance/prevention, deadlock detection, and deadlock resolution [104,105].
The banker’s algorithm is a classic algorithm for deadlock prevention. The common path of different vehicles in the route is called the shared path where the deadlock problem may occur. Felko [106] used Smith Waterman algorithm to analyze the shared path of different AGVs to determine the path segments where deadlock may occur, and combined the banker algorithm to avoid deadlock. The authors defined a structural precondition for deadlock occurrence: if AGVs allocate resources within the same critical section simultaneously or if one AGV enters a critical section while the other is already within, a deadlock will occur (as showed in Fig. 10a). Wu et al. [107] modeled automated manufacturing systems with a resource-oriented Petri net (ROPN) and presented some condition under deadlock avoidance. Zhang et al. [108] proposed a revised ISC deadlock prevention policy in the Petri net framework. Fanti et al. [109] emphasized the specifications of the deadlock avoidance strategy based on graph theory approaches. Yoo et al. [110] proposed a deadlock avoidance method based on the graph-theoretic approach, which was more convenient to modify the model than the petri net method when the environment changed. The paper included two types of routing strategies: the shortest path algorithm and the load-based path algorithm. The author proposed that the shortest path algorithm could provide a shorter path but it may result in a deadlock situation and the load-based path algorithm provided a relatively long distance which could prevent a deadlock situation (as shown in Fig. 10b). Moorthy et al. [89] developed a deadlock prediction and avoidance method for multiple AGV systems, which included 80 AGVs (as shown in Fig. 10c). The AGVs will execute the deadlock prediction algorithm if they want to enter the empty node; they will wait until the deadlock to clear once they find an impending deadlock, which is called ‘wait and proceed’ method. Kim et al. [111] proposed a method for reserving grid-blocks in advance to prevent deadlocks which assumed that the traveling area for AGVs was divided into a large number of grid-blocks, and, as a traffic control method, grid-blocks were reserved in advance. AGVs breakdowns may also cause deadlocks in the multi-AGVs system. To avoid vehicle collisions and deadlocks with the occurrence of vehicle breakdowns, Li et al. [112] included one extra vehicle event that allowed each vehicle to probe further ahead while moving on the guide-path and designed an emergency traffic control scheme as supplementary to the normal traffic control rules.
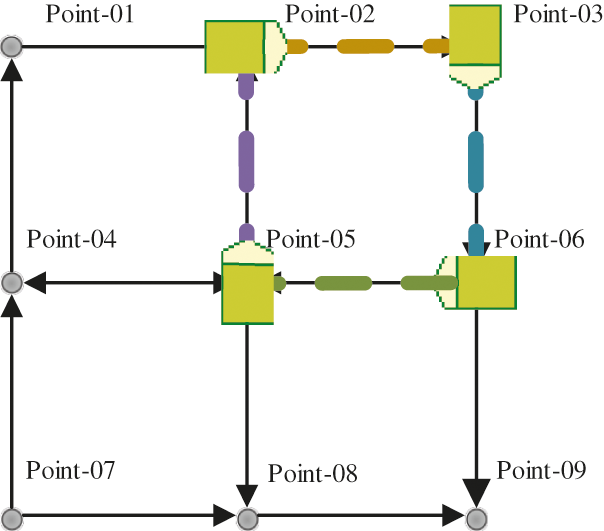
Figure 9: An example of the deadlock problem
Lehmann et al. [68] proposed two detection methods of the deadlock problem, namely matrix representation based on the resource allocation system and graph-oriented deadlock detection. The resource allocation system mainly examined the state of the terminal during the simulation phase to trigger the deadlock resolution procedures. The graph-oriented deadlock detection sacrificed some nonessential information and worked better. This paper proposed three different deadlock resolution procedures, namely: Modify Sc Sequence, Advance Order and Reassign Order. The Modify SC Sequence was the easiest to implement since it required the least changes in the schedules of the resources. It was effective when the stacking order of multiple goods and the handling order of multiple AGVs were inappropriate, by adjusting the sequence to reduce wait time of AGVs. The Advance Order was suitable for more complicated situations than the previous one by adjusting the order of the order to solve the deadlock. The Reassign Order could be used when the condition was not solved by the previous strategies, through the use of standby AGVs, reassignment of the order to resolve the deadlock and re-allocation of orders by adding spare vehicles to solve the problem.
A traffic control model based on semaphores was proposed to resolve conflict and deadlock problems in application of multi-AGVs system [113]. Prototype experiments have been conducted to validate the function and performance of the proposed model. Guo et al. [114] proposed a dynamic unlock algorithm for multi-AGV scheduling problem and proved its effectiveness. Han et al. [115] adopted the coordinated control method of the distributed mix area control model and the traffic rule method, to reduce the possibility of system deadlock and solve the conflict and deadlock problem of AGV online. In case of occurrence of conflict or deadlock, the adjacent zone controller sends a message to identify the state of the other’s path status. After finding a collision-free path, the AGV in the area was scheduled to a new path through the controller of the conflict area, and the AGV could reach the task node through the new path. Although many academics have done extensive research, there is still no universal and effective solution to the deadlock problem in different AGV systems, which explains why the deadlock problem remains.
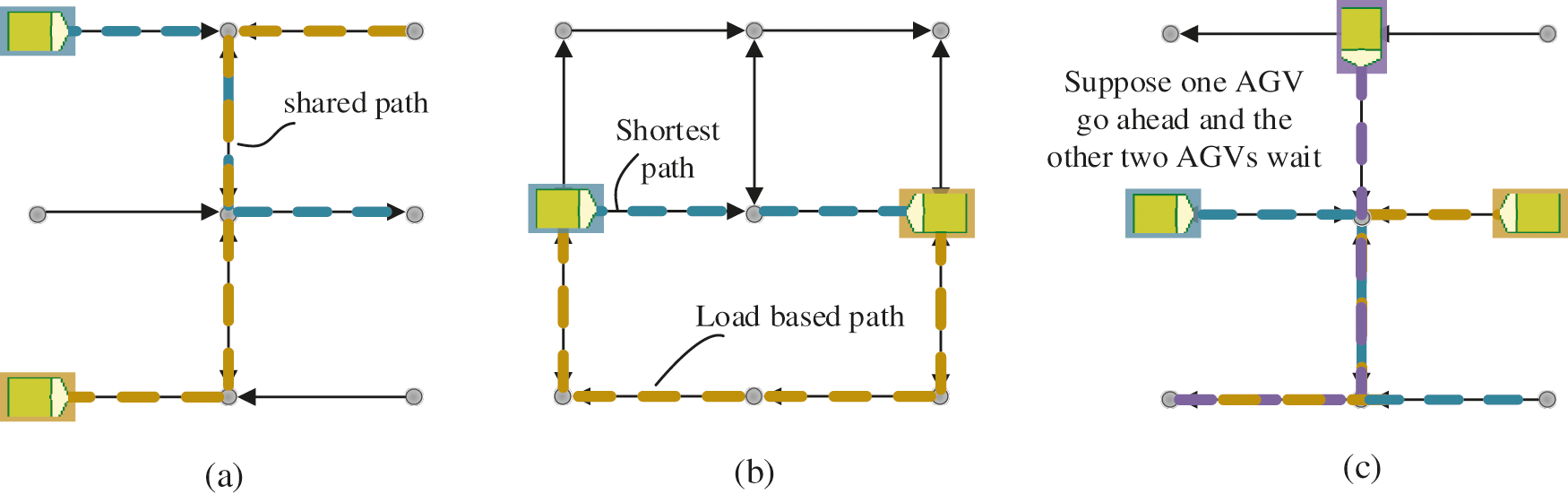
Figure 10: Three kinds of solution of the deadlock
3.2.3 Idle-Vehicle Positioning Problem
AGVs idling is a discrete process, and each instance of vehicle idling involves a period. Resolving the problem of vehicle idling is helpful for the efficient operation of the entire management system. Currently, there are two main methods to resolve idle-vehicle positioning: one is static and another is dynamic. In static method, a series of fixed parking spots is set, and the vehicles will automatically go to the parking places and wait there when no task to perform. The latter is to plan the route according to the point of the following order that can move the AGV with some specific strategies. The static method can reduce system complexity but will increase the consumption of the system. The dynamic method can improve resource utilization but may increase the complexity of the route strategies and the schedule strategies.
Ventura et al. [116] addressed the issue of optimally localization of dwell points for a given number of AGVs in a general guide-path layout. Based on an optimality property, the author proposed new mixed integer linear programming (MILP) formulations and developed a generic genetic algorithm that can be applied to this problem. A dynamic programming algorithm to solve this issue in unidirectional single loop systems was developed to minimize the maximum response time [117]. This polynomial time algorithm finds optimal dwell points when all requests from a given pick-up station are handled by a single AGV. Hale et al. [118] presented a general procedure to determine the optimal dwell point location for an arbitrary service device within a defined region. Two fast and effective heuristics were proposed and tested to dynamically determine the home positions Bruno et al. [119]. Lee et al. [120] considered the optimal number of AGV as well as the optimal number of workstations for automatic warehouses. Li et al. [121] proposed an approach to address the issue of idle AGVs positioning with an artificial neural network. This method was used to forecast the future tasks of the multi-AGVs system and decide whether an AGV should arrive at the start of the next task in advance in combination with the best time to initialize the task. And the result of the simulation showed that it was around 20%~30% higher than the traditional method. According to the above paper, the problem of idle-vehicle positioning has a significant impact on system efficiency. Deep learning has proven to be very effective in task prediction, and the method combining traditional AGVs algorithms with deep recurrent neural networks is worth pursuing.
The essence of the problem to find the best place to charge the AGVs is like the idle-vehicle positioning problem. Simulation models were developed to investigate how the routing of an AGV towards a battery station could affect the productivity of a manufacturing facility [122]. An integrated mathematical model of job shop and AGV scheduling with respect to the location of a battery charging storage was proposed [123]. This method took into consideration the number of AGVs, machines, parts and other problem parameters, and obtained the optimal cost and location of battery charging storage. Baras et al. [124] proposed an algorithm that utilized more than one robot simultaneously to allocate tasks and tailor the navigation path of each robot based on its characteristics, such as its speed, type and current location within the warehouse so as to minimize the task delivery timing and find the optimal location for the placement of power stations.
The resource-oriented and problem-oriented research is for the better performance of the system. The performance of the system generally includes two indicators: time and distance. In the multi-AGVs system, the shortest path in the spatial dimension is generally not the optimal path in time domain, and the minimum time and the shortest distance are a pair of contradictory questions. Many researchers have optimized the distance and time required by the system in accordance with the working environment.
3.3.1 The Shortest Travel Distance in System
The goal of the VRP is the shortest route, the shortest travel distance is also one of the goals of the multi-AGVs management system. Han et al. [64] proposed a multi-AGVs path planning method based on an improved genetic algorithm to minimize the total path distance of all AGVs by selecting individuals with big fitness values, and minimize each AGV path distances by the three-exchange heuristic crossover operator method. The simulation results showed that all AGV travel distances and the longest single AGV travel distances were shortened by using the improved genetic algorithm. Hsueh et al. [62] proposed a shortest route method using a load-exchangeable AGV (EX-AGV) system that allowed two AGVs to exchange their loads, tasks and even vehicle numbers. The method proposed in this article can also be used to solve conflicts and deadlocks. The disadvantage of this method is that it is based on AGVs with a specific structure. Chawla et al. [125] applied clonal selection algorithm (CSA) for the simultaneous scheduling to reduce backtracking and the distance travelled by AGVs in the FMS. Bennewitz et al. [126] proposed an approach to perform a randomized search with hill-climbing to find solutions and to minimize the overall path lengths, which have been implemented and tested on the real robots and in extensive simulations. Li et al. [127] presented a two-layer path planning method based on speed pre-allocation to produce the shortest travel paths in the offline phase to generate the path library, and select the vehicle’s conflict-free path depending on the library in the online phase. The data to be regenerated is a common problem with offline database methods when the system changes.
3.3.2 The Shortest Time to Complete
Zhang et al. [128] proposed a greedy upper bounding and Lagrangian relaxation algorithm to select a route for minimization of the total expected travel time. The authors established a model to consider various workflow interruptions, improve the efficiency of transportation by rerouting traffic when encountering congestion, and prove the effectiveness in reducing the completion time. Investigations were carried out for the multi-objective scheduling of AGVs to minimize the travel time of AGVs in the FMS, which was carried out by the application of nature-inspired grey wolf optimization algorithm (GWO) [129]. The application of a novel modified memetic particle swarm optimization algorithm (MMPSO) was presented for simultaneous workload balancing and travel time minimization of automatic guided vehicles (AGVs) in the flexible manufacturing system (FMS) [130]. Xia et al. [131] used the same method used to minimize the time for the multi-AGV to complete the transportation. A mathematical optimization program was proposed in order to minimize the total earliness and total tardiness of AGVs in the manufacturing system and the Artificial Immune System (AIS) algorithm was used to obtain the optimal solution [132]. A method was proposed to estimate the waiting time of each vehicle which resulted from the interferences among AGVs during travelling [133]. The author used the Q-learning technology and constructed the shortest-time routing matrix for each given position of the quay cranes to estimate the wait time for each vehicle. The method solved the issue of extended completion time caused by interference between vehicles. Zhou et al. [134] used an improved anisotropic Q-learning routing algorithm to find the shortest-time routes, and achieve 9.5% improvement in optimization effectiveness compared to the method of Jeon et al. [133]. Reduction of AGV travel distance and reduction of operating time were modelled together [135]. The authors also proposed a three-stage decomposition algorithm by combining the benefits of the pre-planning algorithm with the real-time planning algorithm. The algorithm combined the A* algorithm with the time window principle to plan the path of each AGV in chronological order. Finally, the efficiency of this method in trajectory research and time optimization has been demonstrated. The method of bi-objective optimization was also used to express the dispatching and conflict-free path problem for AGVs as a bi-objective optimal firing sequence problem for Petri Net [136]. In this research, two objective functions were set, one for the deviation of delivery time from an initial position to a destination, and another for the sum of the total traveling time. A different algorithm was proposed to reduce the delivery time to utilize multiple AGV, based on its specifications, i.e., speed, type and current position to tailor the path for each AGV [137]. In addition to the above, many scholars have researched the relationship of the time spent in the system to other factors. Ventura et al. [24] optimized the completion time by improving the parking position of idle AGVs and minimizing the maximum response time. The deep Q-NET method was used to shorten the average time of the task and minimize the completion time [41]. An effective evolutionary approach was used to minimize completion time and the number of AGVs at the same time [22].
With the usage of AGVs in more and more fields, research on multi-AGVs system is also growing. Different scholars have used different methods for classification and research to make meaningful contributions to the development of multi-AGVs systems. From our literature review, the conclusions can be drawn that the problems of the multi-AGVs management system are intertwined with each other and that the results of each solution have mutual influence, for example, the number of AGVs required and the time required to complete the system are contradictory. The relationship between different parts is shown in Fig. 9. This literature review covers the multi-AGVs management system, including dispatch and routing together, or schedule and route together. In view of the problems in the management system, the conflict problem and the deadlock problem have been considered by most research, and the optimization of the multi-AGVs management system such as less path consumption and shorter time has also been widely studied. A summary of approaches is presented in Table 2, which combines different modules in different multi-AGVs management systems with different types of problems. The abscissa and ordinate in the table represent different modules of the system and different types of problems in the system. Respectively, the numbers in the table represent the references that contain this module or contain the solutions to the problem. The relationship between the various parts of the multi-AGVs management system is shown in Fig. 11. The multi-AGVs systems are the hub of Enterprise Resource Planning (ERP), Warehouse Management System (WMS), Order Management System (OMS) etc. The classification and solutions of the different system modules may be mapped and different system modules should exchange information. The two-stage thinking was adopted by some scholars in solving problems to weaken the differences between the various aspects of the system and strengthen the connections between the different parts. For the optimization issue in the multi-AGVs management system, certain heuristic rules have been proven to be effective, such as genetic algorithm [22,64], randomized search algorithm [126], colony algorithm [96]. For complex multi-attribute optimization problems, the size of the weight is sometimes difficult to determine, and the emergent neural network algorithm can be used.
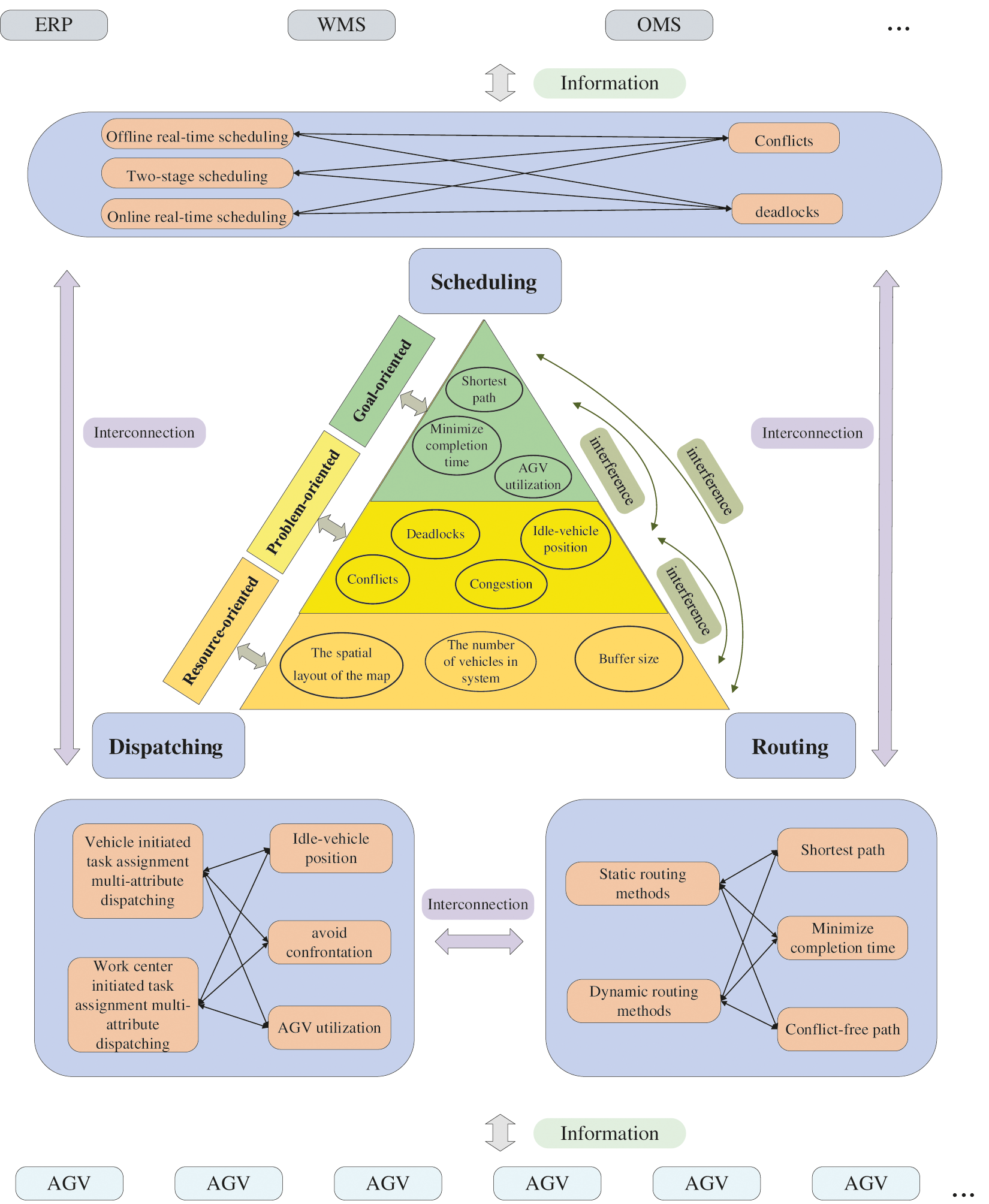
Figure 11: Multi-AGVs management system framework
5 Conclusions and Research Perspectives
In summary, the classification methods and related issues of multi-AGVs management systems have been detailed. The research on multi-AGVs systems has evolved from the simple unidirectional path and offline management to increasingly complex models. For different problems, traditional methods, intelligent methods, and more mature methods in other areas are used to investigate and resolve the problem in the multi-AGVs management system. On the base of the literature survey, the following conclusions and future research prospective are determined:
1. Most scholars have put forward effective solutions to certain problems of the multi-AGVs system, and their experiments were based on multiple assumptions, some of which cannot be fully satisfied in practice. In the future research, the problem assumptions of research should be more standardized.
2. Some researchers have checked the proposed programming models or solving algorithms by calculation or simulation but have not performed sufficient experiments in a real environment. For future studies, it is recommended to increase the proportion of actual experiments to validate the algorithm results.
3. With the development of the multi-AGVs system, the traditional single-attribute strategies cannot meet the system target well. The strategies which combine two or more strategies can achieve better results, such as the combination of NVF strategy, the Time Priority and the NWF.
4. Most of algorithms and strategies can handle a limited number of AGVs in the system. The decentralized control (system) allows the robots to exchange information on their current states and their intended actions by use of inter-robot communication [144]. Not only can this distribute the load of the computer but also simplify the algorithm. The decentralized approach can be studied further.
5. The development of many intelligent algorithms provides new ideas for solving the problems in multi-AGVs systems, and among them, the genetic algorithms are widely used, not only in the routing module but also in the scheduling module. The improvement of genetic algorithms or the combination with other algorithms may bring a better result, such as Lin et al., [22,64].
6. The multi-AGVs management system is not an independent system. In practical applications, the multi-AGVs system needs to be used in conjunction with other parts, such as WMS. Research into cooperation between multi-AGVs systems and other systems should be carefully examined.
7. The development of the fifth generation communication technology (5G), Artificial Intelligence (AI), Digital Twins and other technologies have provided more possibilities for multi-AGVs system. These new technologies can provide the multi-AGVs system with better real-time performance and new functions, which is a promising direction.
Funding Statement: This research was funded by the National Key Research and Development Program of China (No. 2019YFB1310003), by the National Natural Science Foundation of China (Nos. U1913603, 61803251 and 51775322). This research was also funded by the Shanghai Collaborative Innovation Center of Intelligent Manufacturing Robot Technology for Large Components (No. ZXZ20211101).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Klei, C. M., Kim, J. (1996). AGV dispatching. International Journal of Production Research, 34(1), 95–110. DOI 10.1080/00207549608904893. [Google Scholar] [CrossRef]
2. Co, C. G., Tanchoco, J. M. A. (1991). A review of research on AGVS vehicle management. Engineering Costs and Production Economics, 21(1), 35–42. DOI 10.1016/0167-188X(91)90016-U. [Google Scholar] [CrossRef]
3. Umar, U. A., Ariffin, M. K. A., Ismail, N., Tang, S. H. (2015). Hybrid multiobjective genetic algorithms for integrated dynamic scheduling and routing of jobs and automated-guided vehicle (AGV) in flexible manufacturing systems (FMS) environment. International Journal of Advanced Manufacturing Technology, 81(9–12), 2123–2141. DOI 10.1007/s00170-015-7329-2. [Google Scholar] [CrossRef]
4. Egbelu, P. J., Tanchoco, J. M. A. (2007). Characterization of automatic guided vehicle dispatching rules. International Journal of Production Research, 22(3), 359–374. DOI 10.1080/00207548408942459. [Google Scholar] [CrossRef]
5. Hasan, H. S., Abidin, M. S. Z., Mahmud, M. S. A., Muhamad Said, M. F. (2019). Automated guided vehicle routing: Static, dynamic and free range. International Journal of Engineering and Advanced Technology, 8(5C), 1–7. DOI 10.35940/ijeat.E1001.0585C19. [Google Scholar] [CrossRef]
6. Pillac, V., Gendreau, M., Gueret, C., Medaglia, A. L. (2013). A review of dynamic vehicle routing problems. European Journal of Operational Research, 225(1), 1–11. DOI 10.1016/j.ejor.2012.08.015. [Google Scholar] [CrossRef]
7. Qiu, L., Hsu, W. J., Huang, S. Y., Wang, H. (2002). Scheduling and routing algorithms for AGVs: A survey. International Journal of Production Research, 40(3), 745–760. DOI 10.1080/00207540110091712. [Google Scholar] [CrossRef]
8. Xu, W. (2017). Path planning for multi-AGV systems based on two-stage scheduling. International Journal of Performability Engineering, 13, 1347. DOI 10.23940/ijpe.17.08.p16.13471357. [Google Scholar] [CrossRef]
9. Zhong, M. S., Yang, Y. S., Dessouky, Y., Postolache, O. (2020). Multi-AGV scheduling for conflict-free path planning in automated container terminals. Computers & Industrial Engineering, 142(12), 106371. DOI 10.1016/j.cie.2020.106371. [Google Scholar] [CrossRef]
10. Vivaldini, K. C. T., Rocha, L. F., Becker, M., Moreira, A. P. (2015). Comprehensive review of the dispatching, scheduling and routing of AGVs. Proceedings of the 11th Portuguese Conference on Automatic Control, vol. 10, pp. 505–514. Portugal. DOI 10.1007/978-3-319-10380-8_48. [Google Scholar] [CrossRef]
11. Jahagirdar, E., Harish (2021). Flexible manufacturing technology: A review of facility design and the scheduling. International Journal of Advance Research, Ideas and Innovations in Technology, 7(4), 1610–1615. [Google Scholar]
12. Angra, S., Chanda, A. K., Chawla, V. K. (2018). Comparison and evaluation of job selection dispatching rules for integrated scheduling of multi-load automatic guided vehicles serving in variable sized flexible manufacturing system layouts: A simulation study. Management Science Letters, 8, 187–200. DOI 10.5267/j.msl.2018.3.002. [Google Scholar] [CrossRef]
13. Fragapane, G., de Koster, R., Sgarbossa, F., Strandhagen, J. O. (2021). Planning and control of autonomous mobile robots for intralogistics: Literature review and research agenda. European Journal of Operational Research, 294, 405–426. DOI 10.1016/j.ejor.2021.01.019. [Google Scholar] [CrossRef]
14. Chawla, V. K., Chanda, A. K., Angra, S. (2019). Automatic guided vehicle systems in flexible manufacturing system–A review. International Journal of Industrial Engineering-Theory Applications and Practice, 26, 737–765. DOI 10.23055/ijietap.2019.26.5.3746. [Google Scholar] [CrossRef]
15. Vis, I. F. A. (2006). Survey of research in the design and control of automated guided vehicle systems. European Journal of Operational Research, 170, 677–709. DOI 10.1016/j.ejor.2004.09.020. [Google Scholar] [CrossRef]
16. Torres, I. R., Dessens, L. F. R., Flores, J. L. M., Benítez, E. O. (2015). Review of comprehensive approaches in optimizing AGV systems. In: Operational excellence in logistics and supply chains: Optimization methods, data-driven approaches and security insights, pp. 203–232. Germany. [Google Scholar]
17. Fu, J. L., Zhang, H. Z., Zhang, J., Jiang, L. K. (2020). Review on AGV scheduling optimization. Journal of System Simulation, 32, 1664–1675. DOI 10.16182/j.issn1004731x.joss.19-0042. [Google Scholar] [CrossRef]
18. Le-Anh, T., de Koster, M. B. M. (2006). A review of design and control of automated guided vehicle systems. European Journal of Operational Research, 171(1), 1–23. DOI 10.1016/j.ejor.2005.01.036. [Google Scholar] [CrossRef]
19. Mor, A., Speranza, M. G. (2020). Vehicle routing problems over time: A survey. 4OR–A Quarterly Journal of Operations Research, 18(2), 129–149. DOI 10.1007/s10288-020-00433-2. [Google Scholar] [CrossRef]
20. Mehrabian, A., Tavakkoli-Moghaddam, R., Khalili-Damaghani, K. (2017). Multi-objective routing and scheduling in flexible manufacturing systems under uncertainty. Iranian Journal of Fuzzy Systems, 13, 45–77. DOI 10.22111/IJFS.2017.3133. [Google Scholar] [CrossRef]
21. Fazlollahtabar, H., Saidi-Mehrabad, M. (2015). Methodologies to optimize automated guided vehicle scheduling and routing problems: A review study. Journal of Intelligent & Robotic Systems, 77(3–4), 525–545. DOI 10.1007/s10846-013-0003-8. [Google Scholar] [CrossRef]
22. Lin, L., Shinn, S. W., Gen, M., Hwang, H. (2006). Network model and effective evolutionary approach for AGV dispatching in manufacturing system. Journal of Intelligent Manufacturing, 17(4), 465–477. DOI 10.1007/s10845-005-0019-4. [Google Scholar] [CrossRef]
23. Nanvala, H. B. (2011). Dispatching AGVs to work centers for transport of a part in online FMS scheduling. International Journal of Engineering Science Technology, 3. [Google Scholar]
24. Ventura, J. A., Lee, C. (2003). Optimally locating multiple dwell points in a single loop guide path system. IIE Transactions, 35(8), 727–737. DOI 10.1080/07408170304346. [Google Scholar] [CrossRef]
25. Wu, N. Q., Zhou, M. (2007). Shortest routing of bidirectional automated guided vehicles avoiding deadlock and blocking. IEEE/ASME Transactions on Mechatronics, 12(1), 63–72. DOI 10.1109/TMECH.2006.886255. [Google Scholar] [CrossRef]
26. Vivaldini, K., Rocha, L. F., Martarelli, N. J., Becker, M., Moreira, A. P. (2015). Integrated tasks assignment and routing for the estimation of the optimal number of AGVS. International Journal of Advanced Manufacturing Technology, 82(1–4), 719–736. DOI 10.1007/s00170-015-7343-4. [Google Scholar] [CrossRef]
27. Nguyen, D. H., Nguyen, H., Renault, E. (2017). Performance evaluation of E-MQS scheduler with Mobility in LTE heterogeneous network. 2017 IEEE International Conference on Communications (ICC), pp. 1–6. France. [Google Scholar]
28. Wu, T. L. (2020). Conditional waiting time distributions of runs and patterns and their applications. Annals of the Institute of Statistical Mathematics, 72(2), 531–543. DOI 10.1007/s10463-018-0696-3. [Google Scholar] [CrossRef]
29. Zavadskas, E. K., Nunic, Z., Stjepanovic, Z., Prentkovskis, O. (2018). A novel rough range of value method (R-ROV) for selecting automatically guided vehicles (AGVs). Studies in Informatics and Control, 27(4), 385–394. DOI 10.24846/v27i4y201802. [Google Scholar] [CrossRef]
30. Taghaboni, F., Tanchoco, J. M. A. (2007). A LISP-based controller for free-ranging automated guided vehicle systems. International Journal of Production Research, 26(2), 173–188. DOI 10.1080/00207548808947852. [Google Scholar] [CrossRef]
31. Prasad, R. K., Jaya, T. (2019). Optimal network selection in cognitive radio network using simple additive weighting method with multiple parameters. 2019 International Conference on Smart Systems and Inventive Technology (ICSSIT), India. [Google Scholar]
32. Nguyen, M. S., Lee, K. J., Hong, J. (2018). Dispatching of multiple autonomous intelligent vehicles considering stochastic travel times by genetic algorithm. 2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV), pp. 454–459. Singapore. [Google Scholar]
33. Hu, H., Jia, X. L., He, Q. X., Fu, S. F., Liu, K. (2020). Deep reinforcement learning based AGVs real-time scheduling with mixed rule for flexible shop floor in Industry 4.0. Computers & Industrial Engineering, 149(2), 106749. DOI 10.1016/j.cie.2020.106749. [Google Scholar] [CrossRef]
34. Heger, J., Voss, T. (2019). Dynamic priority based dispatching of AGVs in flexible job shops. 12th Cirp Conference on Intelligent Computation in Manufacturing Engineering, 79(1), 445–449. DOI 10.1016/j.procir.2019.02.119. [Google Scholar] [CrossRef]
35. Johnson, M. E. (2001). Modelling empty vehicle traffic in AGVS design. International Journal of Production Research, 39(12), 2615–2633. DOI 10.1080/00207540110048990. [Google Scholar] [CrossRef]
36. Yin, J., Ma, Y., Hu, Y., Han, K., Yin, S. et al. (2021). Delay, Throughput and emission tradeoffs in airport runway scheduling with uncertainty considerations. International Journal of Production Research, 21(1), 85–122. DOI 10.1007/s11067-020-09508-3. [Google Scholar] [CrossRef]
37. de Koster, R. M. B. M., Le-Anh, T., van der Meer, J. R. (2004). Testing and classifying vehicle dispatching rules in three real-world settings. Journal of Operations Management, 22(4), 369–386. DOI 10.1016/j.jom.2004.05.006. [Google Scholar] [CrossRef]
38. Li, M. (2017). Design and analysis of multiple-load automated guided vehicle dispatching algorithms. Winter Simulation Conference, pp. 3311–3322. USA. [Google Scholar]
39. Jeong, B. H., Randhawa, S. U. (2001). A multi-attribute dispatching rule for automated guided vehicle systems. International Journal of Production Research, 39(13), 2817–2832. DOI 10.1080/00207540110051860. [Google Scholar] [CrossRef]
40. Ho, Y. C., Liu, H. C., Yih, Y. (2012). A multiple-attribute method for concurrently solving the pickup-dispatching problem and the load-selection problem of multiple-load AGVs. Journal of Manufacturing Systems, 31(3), 288–300. DOI 10.1016/j.jmsy.2012.03.002. [Google Scholar] [CrossRef]
41. Li, M. P., Sankaran, P., Kuhl, M. E., Ptucha, R., Ganguly, A. et al. (2019). Task selection by autonomous mobile robots in a warehouse using deep reinforcement learning. 2019 Winter Simulation Conference (WSC), pp. 680–689. USA. DOI 10.1109/WSC40007.2019.9004792. [Google Scholar] [CrossRef]
42. Liu, F. H., Hung, P. C. (2002). Control strategy for dispatching multi-load automated guided vehicles in a deadlock-free environment. Journal of Mathematical Modelling and Algorithms, 1(2), 117–134. DOI 10.1023/A:1016564209985. [Google Scholar] [CrossRef]
43. Li, X., Zhang, C., Yang, W., Qi, M. (2018). Multi-AGVs conflict-free routing and dynamic dispatching strategies for automated warehouses. International Conference on Mobile and Wireless Technology, pp. 277–286. Singapore. [Google Scholar]
44. Bilge, U., Esenduran, G., Varol, N., Ozturk, Z., Aydin, B. et al. (2006). Multi-attribute responsive dispatching strategies for automated guided vehicles. International Journal of Production Economics, 100(1), 65–75. DOI 10.1016/j.ijpe.2004.10.004. [Google Scholar] [CrossRef]
45. Guan, X. P., Dai, X. Z. (2009). Deadlock-free multi-attribute dispatching method for AGV systems. International Journal of Advanced Manufacturing Technology, 45(5–6), 603–615. DOI 10.1007/s00170-009-1996-9. [Google Scholar] [CrossRef]
46. Guan, X. P., Dai, X. Z. (2008). Multi-attribute dispatching method with dynamically adjustable weights for multirobot transportation systems. 2008 International Conference on Information and Automation, 1–4, 1368–1373. DOI 10.1109/Icinfa.2008.4608215. [Google Scholar] [CrossRef]
47. Li, S. N., Xing, K. X., Lin, Y. G., Zhang, G. J. (2019). Research on multi-AGV scheduling method of logistics warehouse based on petri net. High Technology, 29, 494–502. DOI 10.3772/j.issn.1002-0470.2019.05.011. [Google Scholar] [CrossRef]
48. Wu, G., Sun, X. (2020). AGV task distribution study. Journal of Physics: Conference Series, 1486(7), 072016. DOI 10.1088/1742-6596/1486/7/072016. [Google Scholar] [CrossRef]
49. Dijkstra, E. W. (1959). A note on two problems in connexion with graphs. Numerische Mathematik, 1(1), 269–271. DOI 10.1007/BF01386390. [Google Scholar] [CrossRef]
50. Hart, P. E., Nilsson, N. J., Raphael, B. (1968). A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Science and Cybernetics, 4(2), 100–107. DOI 10.1109/TSSC.1968.300136. [Google Scholar] [CrossRef]
51. Goldberg, D. E. G. A. J. H. (1988). Genetic algorithms and machine learning. Machine Learning, 3, 95–99. DOI 10.1007/BF00113892. [Google Scholar] [CrossRef]
52. Li, C., Cao, C., Gao, Y. (2018). Path planning for multiple AGV systems using genetic algorithm in warehouse. 2018 3rd International Conference on Communications, Information Management and Network Security (CIMNS 2018). China. [Google Scholar]
53. Klimm, M., Gawrilow, E., Möhring, R. H., Stenzel, B. (2008). Conflict-free vehicle routing: Load balancing and deadlock prevention. Euro Journal on Transportation & Logistics, 1(1–2), 87–111. DOI 10.1007/s13676-012-0008-7. [Google Scholar] [CrossRef]
54. Maza, S., Castagna, P. (2005). A performance-based structural policy for conflict-free routing of bi-directional automated guided vehicles. Computers in Industry, 56(7), 719–733. DOI 10.1016/j.compind.2005.03.003. [Google Scholar] [CrossRef]
55. Zheng, Z., Guo, Q., Yuan, P. (2017). Conflict-free route planning of automated guided vehicles based on conflict classification. 2017 IEEE International Conference on Systems, Man and Cybernetics (SMC), pp. 1459–1464. Canada. [Google Scholar]
56. Yuan, R., Dong, T., Li, J. (2016). Research on the collision-free path planning of multi-AGVs system based on improved A* algorithm. American Journal of Operations Research, 6(6), 442–449. DOI 10.4236/ajor.2016.66041. [Google Scholar] [CrossRef]
57. Smolic-Rocak, N., Bogdan, S., Kovacic, Z., Petrovic, T. (2010). Time windows based dynamic routing in multi-AGV systems. IEEE Transactions on Automation Science and Engineering, 7(1), 151–155. DOI 10.1109/TASE.2009.2016350. [Google Scholar] [CrossRef]
58. Yan, J. H., Zhang, M. Y., Fu, Z. M. (2019). Scheduling optimization for multi-AGVs in intelligent assembly workshop. Proceeding of the 24th International Conference on Industrial Engineering and Engineering Management, pp. 110–119. Thailand. DOI 10.1007/978-981-13-3402-3_13. [Google Scholar] [CrossRef]
59. Correa, A. I., Langevin, A., Rousseau, L. M. (2007). Scheduling and routing of automated guided vehicles: A hybrid approach. Computers & Operations Research, 34(6), 1688–1707. DOI 10.1016/j.cor.2005.07.004. [Google Scholar] [CrossRef]
60. Nishi, T., Hiranaka, Y., Grossmann, I. E. (2011). A bilevel decomposition algorithm for simultaneous production scheduling and conflict-free routing for automated guided vehicles. Computers & Operations Research, 38(5), 876–888. DOI 10.1016/j.cor.2010.08.012. [Google Scholar] [CrossRef]
61. Mousavi, M., Yap, H. J., Musa, S. N., Dawal, S. Z. M. (2017). A fuzzy hybrid Ga-Pso algorithm for multi-objective Agv scheduling in FMS. International Journal of Simulation Modelling, 16(1), 58–71. DOI 10.2507/IJSIMM16(1)5.368. [Google Scholar] [CrossRef]
62. Hsueh, C. F. (2010). A simulation study of a bi-directional load-exchangeable automated guided vehicle system. Computers & Industrial Engineering, 58(4), 594–601. DOI 10.1016/j.cie.2009.12.008. [Google Scholar] [CrossRef]
63. Giglio, D. (2014). Task scheduling for multiple forklift AGVs in distribution warehouses. 2014 IEEE Emerging Technology and Factory Automation (Etfa), pp. 1–6. Spain. DOI 10.1109/ETFA.2014.7005360. [Google Scholar] [CrossRef]
64. Han, Z., Wang, D., Liu, F., Zhao, Z. (2017). Multi-AGV path planning with double-path constraints by using an improved genetic algorithm. PLoS One, 12(7), e0181747. DOI 10.1371/journal.pone.0181747. [Google Scholar] [CrossRef]
65. Saravanan, M., Kumar, S. G. (2013). Different approaches for the loop layout problems: A review. International Journal of Advanced Manufacturing Technology, 69(9–12), 2513–2529. DOI 10.1007/s00170-013-5133-4. [Google Scholar] [CrossRef]
66. Asef-Vaziri, A., Goetschalckx, M. (2008). Dual track and segmented single track bidirectional loop guidepath layout for AGV systems. European Journal of Operational Research, 186(3), 972–989. DOI 10.1016/j.ejor.2007.02.049. [Google Scholar] [CrossRef]
67. Gutta, P. R., Chinthala, V. S., Manchoju, R. V., Charan, M. V. N. V., Purohit, R. (2018). A review on facility layout design of an automated guided vehicle in flexible manufacturing system. Materials Today-Proceedings, 5(2), 3981–3986. DOI 10.1016/j.matpr.2017.11.656. [Google Scholar] [CrossRef]
68. Lehmann, M., Grunow, M., Gunther, H. O. (2006). Deadlock handling for real-time control of AGVs at automated container terminals. OR Spectrum, 28(4), 631–657. DOI 10.1007/s00291-006-0053-4. [Google Scholar] [CrossRef]
69. Zhou, C. H., Li, H. B., Lee, L. H., Chew, E. P. (2018). Single direction traffic rule for GRID system–An innovative automated material handling system. 2018 IEEE 14th International Conference on Automation Science and Engineering (Case), pp. 843–848. Germany. DOI 10.1109/COASE.2018.8560590. [Google Scholar] [CrossRef]
70. Zheng, Y., Xiao, Y., Seo, Y. (2016). A hybrid heuristic algorithm for integrated problem of machine scheduling and unidirectional flow path design. International Journal of Industrial Engineering-Theory Applications and Practice, 22, 717–728. DOI 10.23055/ijietap.2015.22.6.1566. [Google Scholar] [CrossRef]
71. Farahani, R. Z., Pourakbar, M., Miandoabchi, E. (2007). Developing exact and Tabu search algorithms for simultaneously determining AGV loop and P/D stations in single loop systems. International Journal of Production Research, 45(22), 5199–5222. DOI 10.1080/00207540600824912. [Google Scholar] [CrossRef]
72. Tanaka, Y., Nishi, T., Inuiguchi, M. (2010). Dynamic optimization of simultaneous dispatching and conflict-free routing for automated guided vehicles-petri net decomposition approach. Journal of Advanced Mechanical Design Systems and Manufacturing, 4(3), 701–715. DOI 10.1299/jamdsm.4.701. [Google Scholar] [CrossRef]
73. Lyu, X. F., Song, Y. C., He, C. Z., Lei, Q., Guo, W. F. (2019). Approach to integrated scheduling problems considering optimal number of automated guided vehicles and conflict-free routing in flexible manufacturing systems. IEEE Access, 7, 74909–74924. DOI 10.1109/ACCESS.2019.2919109. [Google Scholar] [CrossRef]
74. Sarker, B. R., Gurav, S. S. (2005). Route planning for automated guided vehicles in a manufacturing facility. International Journal of Production Research, 43(21), 4659–4683. DOI 10.1080/00207540500140807. [Google Scholar] [CrossRef]
75. Hamzheei, M., Farahani, R. Z., Rashidi-Bajgan, H. (2013). An ant colony-based algorithm for finding the shortest bidirectional path for automated guided vehicles in a block layout. International Journal of Advanced Manufacturing Technology, 64(1–4), 399–409. DOI 10.1007/s00170-012-3999-1. [Google Scholar] [CrossRef]
76. Fazlollahtabar, H., Hassanli, S. (2017). Hybrid cost and time path planning for multiple autonomous guided vehicles. Applied Intelligence, 48(2), 482–498. DOI 10.1007/s10489-017-0997-x. [Google Scholar] [CrossRef]
77. Nishi, T., Tanaka, Y. (2012). Petri net decomposition approach for dispatching and conflict-free routing of bidirectional automated guided vehicle systems. IEEE Transactions on Systems Man and Cybernetics Part A–Systems and Humans, 42(5), 1230–1243. DOI 10.1109/TSMCA.2012.2183353. [Google Scholar] [CrossRef]
78. Fazlollahtabar, H., Saidi-Mehrabad, M. (2014). Studies in systems, decision and control. Automated guided vehicles routing, vol. 20. Springer. [Google Scholar]
79. Qiu, L., Hsu, W. J. (2001). A bi-directional path layout for conflict-free routing of AGVs. International Journal of Production Research, 39(10), 2177–2195. DOI 10.1080/00207540110038531. [Google Scholar] [CrossRef]
80. Bechtsis, D., Tsolakis, N., Vouzas, M., Vlachos, D. (2017). Industry 4.0: Sustainable material handling processes in industrial environments, 40(4), 2281–2286. DOI 10.1016/B978-0-444-63965-3.50382-2. [Google Scholar] [CrossRef]
81. Fathi, M., Syberfeldt, A., Ghobakhloo, M., Eskandari, H. (2018). An optimization model for material supply scheduling at mixed-model assembly lines. 51st Cirp Conference on Manufacturing Systems, 72(1–4), 1258–1263. DOI 10.1016/j.procir.2018.03.274. [Google Scholar] [CrossRef]
82. Vis, I. F. A., de Koster, R., Roodbergen, K. J., Peeters, L. W. P. (2001). Determination of the number of automated guided vehicles required at a semi-automated container terminal. Journal of the Operational Research Society, 52(4), 409–417. DOI 10.1057/palgrave.jors.2601094. [Google Scholar] [CrossRef]
83. Fu, J. L., Zhang, J., Ding, G. F., Qin, S. F., Jiang, H. F. (2021). Determination of vehicle requirements of AGV system based on discrete event simulation and response surface methodology. Proceedings of the Institution of Mechanical Engineers Part B: Journal of Engineering Manufacture, 235(9), 1425–1436. DOI 10.1177/0954405421995602. [Google Scholar] [CrossRef]
84. Chawla, V. K., Chanda, A. K., Angra, S. (2018). Automatic guided vehicles fleet size optimization for flexible manufacturing system by grey wolf optimization algorithm. Management Science Letters, 8, 79–90. DOI 10.5267/j.msl.2017.12.004. [Google Scholar] [CrossRef]
85. Choobineh, F. F., Asef-Vaziri, A., Huang, X. L. (2012). Fleet sizing of automated guided vehicles: A linear programming approach based on closed queuing networks. International Journal of Production Research, 50(12), 3222–3235. DOI 10.1080/00207543.2011.562560. [Google Scholar] [CrossRef]
86. Wang, H. F., Chan, C. H. (2014). Multi-objective optimisation of automated guided dispatching and vehicle routing system. International Journal of Modelling in Operations Management, 4(1/2), 35–52. DOI 10.1504/IJMOM.2014.063585. [Google Scholar] [CrossRef]
87. Hamdy, A. (2019). Optimization of automated guided vehicles (AGV) fleet size with incorporation of battery management (Doctoral Dissertation). Old Dominion University. [Google Scholar]
88. Chawla, V. K., Chanda, A. K., Angra, S. (2019). Material handling robots fleet size optimization by a heuristic. Journal of Project Management, 4(3), 177–188. DOI 10.5267/j.jpm.2019.4.002. [Google Scholar] [CrossRef]
89. Moorthy, R. L., Hock-Guan, W., Wing-Cheong, N., Chung-Piaw, T. (2003). Cyclic deadlock prediction and avoidance for zone-controlled AGV system. International Journal of Production Economics, 83(3), 309–324. DOI 10.1016/S0925-5273(02)00370-5. [Google Scholar] [CrossRef]
90. Chawla, V. K., Chanda, A. K., Angra, S. (2018). Simultaneous dispatching and scheduling of multi-load AGVs in FMS-A simulation study. Materials Today-Proceedings, 5(11), 25358–25367. DOI 10.1016/j.matpr.2018.10.339. [Google Scholar] [CrossRef]
91. Wu, N., Zhou, M. (2005). Modeling and deadlock avoidance of automated manufacturing systems with multiple automated guided vehicles. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 35(6), 1193–1202. DOI 10.1109/TSMCB.2005.850141. [Google Scholar] [CrossRef]
92. Kłosowski, G., Gola, A., Amila, T. (2018). Computational intelligence in control of AGV multimodal systems. IFAC-PapersOnLine, 51(11), 1421–1427. DOI 10.1016/j.ifacol.2018.08.315. [Google Scholar] [CrossRef]
93. Zhang, Z., Guo, Q., Chen, J., Yuan, P. J. (2018). Collision-free route planning for multiple AGVs in an automated warehouse based on collision classification. IEEE Access, 6, 26022–26035. DOI 10.1109/ACCESS.2018.2819199. [Google Scholar] [CrossRef]
94. Chawla, V., Chanda, A. K., Angra, S., Bonyadi Naeini, A. (2020). Coexistent scheduling in the tandem flow path configuration of a flexible manufacturing system by using an advanced grey wolf optimizer. Scientia Iranica, 27, 1–24. DOI 10.24200/sci.2020.54152.3618. [Google Scholar] [CrossRef]
95. Li, J. J., Xu, B. W., Postolache, O., Yang, Y. S., Wu, H. F. (2018). Impact analysis of travel time uncertainty on AGV catch-up conflict and the associated dynamic adjustment. Mathematical Problems in Engineering, 2018(5), 1–11. DOI 10.1155/2018/4037695. [Google Scholar] [CrossRef]
96. Li, J. J., Xu, B. W., Yang, Y. S., Wu, H. F. (2017). A guided ant colony optimization algorithm for conflict-free routing scheduling of AGVs considering waiting time. IAES International Journal of Robotics and Automation (IJRA), 6(2), 69. DOI 10.11591/ijra.v6i2.pp69-79. [Google Scholar] [CrossRef]
97. Draganjac, I., Miklic, D., Kovaci, Z., Vasiljevic, G., Bogdan, S. (2016). Decentralized control of multi-AGV systems in autonomous warehousing applications. IEEE Transactions on Automation Science and Engineering, 13(4), 1433–1447. DOI 10.1109/TASE.2016.2603781. [Google Scholar] [CrossRef]
98. Zhong, M. S., Yang, Y. S., Sun, S., Zhou, Y. M., Postolache, O. et al. (2020). Priority-based speed control strategy for automated guided vehicle path planning in automated container terminals. Transactions of the Institute of Measurement and Control, 42(16), 3079–3090. DOI 10.1177/0142331220940110. [Google Scholar] [CrossRef]
99. Miyamoto, T., Inoue, K. (2016). Local and random searches for dispatch and conflict-free routing problem of capacitated AGV systems. Computers & Industrial Engineering, 91, 1–9. DOI 10.1016/j.cie.2015.10.017. [Google Scholar] [CrossRef]
100. Wang, C. B., Wang, L., Qin, J., Wu, Z. Z., Duan, L. H. et al. (2015). Path planning of automated guided vehicles based on improved A-Star algorithm. 2015 IEEE International Conference on Information and Automation, pp. 2071–2076. China. DOI 10.1109/ICInfA.2015.7279630. [Google Scholar] [CrossRef]
101. Guo, K., Zhu, J. (2020). Multi-agent AGV conflict free path planning based on improved speed control method in automated terminals. International Core Journal of Engineering, 6, 386–398. DOI 10.6919/ICJE.202009_6(9). 0049. [Google Scholar] [CrossRef]
102. Kim, C. W., Tanchoco, J. M. A., Koo, P. H. (1997). Deadlock prevention in manufacturing systems with AGV systems: Banker’s algorithm approach. Journal of Manufacturing Science and Engineering-Transactions of the ASME, 119(4B), 849–854. DOI 10.1115/1.2836834. [Google Scholar] [CrossRef]
103. Kim, C. O., Kim, S. S. (1997). An efficient real-time deadlock-free control algorithm for automated manufacturing systems. International Journal of Production Research, 35(6), 1545–1560. DOI 10.1080/002075497195119. [Google Scholar] [CrossRef]
104. Qiu, G., Ou, C. X., Han, T. R. (2016). Research on map construction and scheduling algorithms based on intelligent warehouse multi-AGV. Industrial Control Computer, 29, 117–119. DOI 10.3969/j.issn.1001-182X.2016.12.053. [Google Scholar] [CrossRef]
105. Fanti, M. P., Zhou, M. C. (2004). Deadlock control methods in automated manufacturing systems. IEEE Transactions on Systems Man and Cybernetics Part A: Systems and Humans, 34(1), 5–22. DOI 10.1109/TSMCA.2003.820590. [Google Scholar] [CrossRef]
106. Felko, I. (2011). Simulation-based deadlock avoidance and optimization in bidirectional AGVS. 4th International ICST Conference on Simulation Tools and Techniques, 7, 152–161. DOI 10.4108/icst.simutools.2011.245542. [Google Scholar] [CrossRef]
107. Wu, N. Q., Zhou, M. C., Hu, G. (2013). One-step look-ahead maximally permissive deadlock control of AMS by using petri nets. ACM Transactions on Embedded Computing Systems, 12(1), 1–23. DOI 10.1145/2406336.2406346. [Google Scholar] [CrossRef]
108. Zhang, Z. M., Wu, W. M. (2013). Sequence control of essential siphons for deadlock prevention in petri nets. ACM Transactions on Embedded Computing Systems, 12(1), 1–22. DOI 10.1145/2406336.2406344. [Google Scholar] [CrossRef]
109. Fanti, M. P., Maione, B., Turchiano, B. (2018). Deadlock avoidance policies in production systems by a digraph approach. Formal Methods in Manufacturing, 8, 229–258. DOI 10.1201/9781315216140-8. [Google Scholar] [CrossRef]
110. Yoo, J. W., Sim, E. S., Cao, C., Park, J. W. (2004). An algorithm for deadlock avoidance in an AGV System. International Journal of Advanced Manufacturing Technology, 26(5–6), 659–668. DOI 10.1007/s00170-003-2020-4. [Google Scholar] [CrossRef]
111. Kim, K. H., Jeon, S. M., Ryu, K. R. (2006). Deadlock prevention for automated guided vehicles in automated container terminals. OR Spectrum, 28(4), 659–679. DOI 10.1007/s00291-006-0055-2. [Google Scholar] [CrossRef]
112. Li, Q., Pogromsky, A., Adriaansen, T., Udding, J. T. (2016). A control of collision and deadlock avoidance for automated guided vehicles with a fault-tolerance capability. International Journal of Advanced Robotic Systems, 13(2), 64. DOI 10.5772/62685. [Google Scholar] [CrossRef]
113. Shao, S. J., Xia, Z. Y., Chen, G. D., Zhang, J., Hu, Y. et al. (2014). A new scheme of multiple automated guided vehicle system for collision and deadlock free. 2014 4th Ieee International Conference on Information Science and Technology (Icist), pp. 606–610. China. DOI 10.1109/ICIST.2014.6920551. [Google Scholar] [CrossRef]
114. Guo, Y. J., Huang, H. S., Gao, F. Q., Qiao, X. H. (2017). Improving the performance of multi-AGV systems with a dynamic unlock algorithm. 2017 10th International Conference on Intelligent Computation Technology and Automation (Icicta 2017), 1, pp. 39–43. DOI 10.1109/Icicta.2017.16. [Google Scholar] [CrossRef]
115. Han, Z., Wang, D. (2017). Research of multi-AGV scheduling system based on a new mixed regional control model. 2017 Chinese Automation Congress (CAC), pp. 2641–2645. China. DOI 10.1109/CAC.2017.8243222. [Google Scholar] [CrossRef]
116. Ventura, J. A., Pazhani, S., Mendoza, A. (2015). Finding optimal dwell points for automated guided vehicles in general guide-path layouts. International Journal of Production Economics, 170(1), 850–861. DOI 10.1016/j.ijpe.2015.03.007. [Google Scholar] [CrossRef]
117. Ventura, J. A., Rieksts, B. Q. (2009). Optimal location of dwell points in a single loop AGV system with time restrictions on vehicle availability. European Journal of Operational Research, 192(1), 93–104. DOI 10.1016/j.ejor.2007.09.014. [Google Scholar] [CrossRef]
118. Hale, T. S., Hanna, M. E., Huq, F. (2009). The generalised dwell point location problem. International Journal of Industrial Systems Engineering, 4(4), 446–454. DOI 10.1504/IJISE.2009.024072. [Google Scholar] [CrossRef]
119. Bruno, G., Ghiani, G., Improta, G. (2000). Dynamic positioning of idle automated guided vehicles. Journal of Intelligent Manufacturing, 11(2), 209–215. DOI 10.1023/A:1008947018074. [Google Scholar] [CrossRef]
120. Lee, C. K. M., Keung, K. L., Ng, K. K. H., Lai, D. C. P. (2018). Simulation-based multiple automated guided vehicles considering charging and collision-free requirements in automatic warehouse. 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEE IEEM), pp. 1376–1380. Thailand. DOI 10.1109/IEEM.2018.8607396. [Google Scholar] [CrossRef]
121. Li, D., Ouyang, B., Wu, D., Wang, Y. (2019). Artificial intelligence empowered multi-AGVs in manufacturing systems. arXiv preprint arXiv:.03373. [Google Scholar]
122. Kabir, Q. S., Suzuki, Y. (2019). Comparative analysis of different routing heuristics for the battery management of automated guided vehicles. International Journal of Production Research, 57(2), 624–641. DOI 10.1080/00207543.2018.1475761. [Google Scholar] [CrossRef]
123. Dehnavi-Arani, S., Sabaghian, A., Fazli, M. (2018). A job shop scheduling and location of battery charging storage for the automated guided vehicles (AGVs). Journal of Optimization in Industrial Engineering, 12, 121–129. DOI 10.22094/joie.2018.543203.1511. [Google Scholar] [CrossRef]
124. Baras, N., Chatzisavvas, A., Ziouzios, D., Dasygenis, M. (2021). Improving automatic warehouse throughput by optimizing task allocation and validating the algorithm in a developed simulation tool. Automation, 2(3), 116–126. DOI 10.3390/automation2030007. [Google Scholar] [CrossRef]
125. Chawla, V. K., Chanda, A. K., Angra, S. (2018). A clonal selection algorithm for minimizing distance travel and back tracking of automatic guided vehicles in flexible manufacturing system. Journal of The Institution of Engineers (IndiaSeries C, 100(3), 401–410. DOI 10.1007/s40032-018-0447-5. [Google Scholar] [CrossRef]
126. Bennewitz, M., Burgard, W., Thrun, S. (2001). Optimizing schedules for prioritized path planning of multi-robot systems. IEEE International Conference on Robotics and Automation, pp. 271–276. Korea. [Google Scholar]
127. Li, X., Liao, K., Chen, W. (2019). Two-stage multi-AGV path planning based on speed pre-allocation. 2019 IEEE 3rd Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), China. [Google Scholar]
128. Zhang, M., Batta, R., Nagi, R. (2009). Modeling of workflow congestion and optimization of flow routing in a manufacturing/warehouse facility. Management Science, 55(2), 267–280. DOI 10.1287/mnsc.1080.0916. [Google Scholar] [CrossRef]
129. Chawla, V. K., Chanda, A. K., Angra, S. (2019). The scheduling of automatic guided vehicles for the workload balancing and travel time minimi-zation in the flexible manufacturing system by the nature-inspired algorithm. Journal of Project Management, 4(1), 19–30. DOI 10.5267/j.jpm.2018.8.001. [Google Scholar] [CrossRef]
130. Chawla, V. K., Chanda, A. K., Angra, S. (2019). Simultaneous workload balancing and travel time minimization of automatic guided vehicles. Journal of Physics: Conference Series, 1240(1), 012001. DOI 10.1088/1742-6596/1240/1/012001. [Google Scholar] [CrossRef]
131. Xia, P. P., Xu, A., Zhang, Y. (2020). A multi-AGV optimal scheduling algorithm based on particle swarm optimization. International Conference on Artificial Intelligence and Security, pp. 527–538. Singapore. [Google Scholar]
132. Murugesan, R. (2017). Optimization algorithm for minimizing the earliness/tardiness of automated guided vehicles using artificial immune system. International Journal of Applied Engineering Research, 12, 11913–11919. DOI 10.15406/iratj.2017.02.00006. [Google Scholar] [CrossRef]
133. Jeon, S. M., Kim, K. H., Kopfer, H. (2010). Routing automated guided vehicles in container terminals through the Q-learning technique. Logistics Research, 3(1), 19–27. DOI 10.1007/s12159-010-0042-5. [Google Scholar] [CrossRef]
134. Zhou, P. F., Lin, L., Kim, K. H. (2021). Anisotropic Q-learning and waiting estimation based real-time routing for automated guided vehicles at container terminals. Journal of Heuristics, DOI 10.1007/s10732-020-09463-9. [Google Scholar] [CrossRef]
135. Hu, Y. J., Dong, L. C., Xu, L. (2020). Multi-AGV dispatching and routing problem based on a three-stage decomposition method. Mathematical Biosciences and Engineering, 17(5), 5150–5172. DOI 10.3934/mbe.2020279. [Google Scholar] [CrossRef]
136. Eda, S., Nishi, T., Mariyama, T., Kataoka, S., Shoda, K. et al. (2012). Petri net decomposition approach for bi-objective routing for AGV systems minimizing total traveling time and equalizing delivery time. Journal of Advanced Mechanical Design Systems and Manufacturing, 6(5), 672–686. DOI 10.1299/jamdsm.6.672. [Google Scholar] [CrossRef]
137. Baras, N., Dasygenis, M. (2019). An algorithm for routing heterogeneous vehicles in robotized warehouses. 2019, 153–156. DOI 10.1109/PACET48583.2019. [Google Scholar] [CrossRef]
138. Fazlollahtabar, H., Saidi-Mehrabad, M., Masehian, E. (2015). Mathematical model for deadlock resolution in multiple AGV scheduling and routing network: A case study. Industrial Robot–The International Journal of Robotics Research and Application, 42(3), 252–263. DOI 10.1108/IR-12-2014-0437. [Google Scholar] [CrossRef]
139. Nishi, T., Morinaka, S., Konishi, M. (2007). A distributed routing method for AGVs under motion delay disturbance. Robotics and Computer-Integrated Manufacturing, 23(5), 517–532. DOI 10.1016/j.rcim.2006.10.007. [Google Scholar] [CrossRef]
140. Yangl, Z., Li, C., Zhao, Q. (2018). Dynamic time estimation based AGV dispatching algorithm in automated container terminal. 37th Chinese Control Conference (CCC), pp. 7868–7873. China. [Google Scholar]
141. Chawla, V. K., Chanda, A. K., Angra, S., Rani, S. (2019). Effect of nature-inspired algorithms and hybrid dispatching rules on the performance of automatic guided vehicles in the flexible manufacturing system. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 41(10), 1–17. DOI 10.1007/s40430-019-1894-5. [Google Scholar] [CrossRef]
142. Rezapour, S., Zanjirani-Farahani, R., Miandoabchi, E. (2011). A machine-to-loop assignment and layout design methodology for tandem AGV systems with single-load vehicles. International Journal of Production Research, 49(12), 3605–3633. DOI 10.1080/00207543.2010.489056. [Google Scholar] [CrossRef]
143. Chang, K. H., Chang, A. L., Kuo, C. Y. (2014). A simulation-based framework for multi-objective vehicle fleet sizing of automated material handling systems: An empirical study. Journal of Simulation, 8(4), 271–280. DOI 10.1057/jos.2014.6. [Google Scholar] [CrossRef]
144. Azarm, K., Schmidt, G. (1997). Conflict-free motion of multiple mobile robots based on decentralized motion planning and negotiation. Proceedings of International Conference on Robotics and Automation, pp. 3526–3533. USA. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |