Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.017914

ARTICLE

Numerical Simulation of Reiner–Rivlin Nanofluid Flow under the Influence of Thermal Radiation and Activation Energy over a Rotating Disk

Arfan Shahzad1,2, Muhammad Imran1,*, Muhammad Nawaz Naeem1 and Mohsan Raza1

1Department of Mathematics, Government College University Faisalabad, Faisalabad, 38000, Pakistan
2Department of Sciences & Humanities, National University of Computer and Emerging Sciences, Chiniot-Faisalabad Campus, Faisalabad, 38000, Pakistan
*Corresponding Author: Muhammad Imran. Email: drmimranchaudhry@gmail.com
Received: 16 June 2021; Accepted: 23 November 2021

Nomenclature

1  Introduction

The flow of spinning disks is critical in both theoretical and practical considerations. In principle, such flows are among the fluid mechanics’ problems that the Navier–Stokes equations may effectively solve. These flows are realistically based on the cases such as geophysics, microbiology, and other industrial implementations such as turbomachinery. Whether the vortex formed, or small eddy motion created automatically leads to the talk of rotating fluids. The flow of spinning disks is typically employed in many tracts viz., nutriment processing, chemical reactors, designing turbines, engine gearing and brake components, disk cleaners, viscometry, medical gadgetry, typical rotating geometry of internal cooling, compressors, rotors, and cyclone separator. The study of the heat transfer phenomenon in the presence of thermal radiation has also achieved great attention by scientists in recent decades. The impact of thermal radiation at high temperatures cannot be denied as it encountered a variety of interesting applications in power generation, solar energy systems, nuclear industries, missiles technology, semiconductor wafers, etc.

Non-Newtonian fluid flows are found more in research and technology than Newtonian fluids. Scientists, biologists, and mathematicians worked tirelessly to explain and grasp the rheological characteristics of non-Newtonian fluids. These fluids have difficult nature of the operation and are complicated to apply in industries owing to their changeable composition. Therefore, this work discusses the bioconvective, steady, and incompressible flow of the Reiner–Rivlin nanofluid over a rotating disk. An empirical approach using a bvp4c method is proposed for the current study. Nanofluid is classified as nanometer-sized particles suspended in normal fluids with a diameter of less than 100 nm. Nanofluids have properties that make them potentially useful in many applications of heat transfer. They exhibit enhanced thermal conductivity and the convective heat transfer coefficient compared to the base fluid. Nanofluids are useful in a variety of science and industrial applications, including biomedicine, automotive cooling, transformer cooling, electrical device cooling, heat exchanger, the development of liquid displays, and nuclear power plants [1 –5]. Hafeez et al. [6] analyzed the stagnation point flow of Oldroyd-B fluid over a rotatory disk. Hayat et al. [7] studied the influence of magnetohydrodynamics (MHD) 3-dimensional flow of nanoliquids and thermal transport of convective boundary conditions. Ellahi et al. [8] investigated slip’s role in two-phase nanofluid flow. Alsaedi et al. [9] examined entropy production in MHD Eyring–Powell nanofluid flow because of viscous dissipation, nonlinear mixed convection, and Joule heating. Khan et al. [10] studied the effect of thermal and solutal transport behavior in the Maxwell flow of nanofluid on the solar radiative expansion surface. Gireesha et al. [11] created a numerical model of nonlinearly thermal radiation as well as chemical reactions on a Maxwell nanofluid layer. Heat and mass diffusion of Maxwell nanoparticles were combinedly studied by Khan et al. [12] as they traveled through a linearly stretching surface. Nadeem et al. [13] analyze numerically the heat transformation process for Maxwell nanofluids. Khan et al. [14] investigate the impact of nonlinear heat radiation with nanomaterials and Arrhenius activation energy on the flowing of a generalized 2nd-grade nanofluid. Alghamdi [15] investigated the erratic flow of carbon nanotubes-type fluids between two moveable discs. Ullah et al. [16] proposed a computational model of the Darcy–Forchheimer nanoliquids motion by a rotating disc with partial slip. Tabassum et al. [17] investigated the numerical behavior of non-Newtonian Reiner–Rivlin nanofluid partial slip and heat transportation basis on a spinning disc. Attempts [18–20] offer more detail on the Reiner–Rivlin fluid.

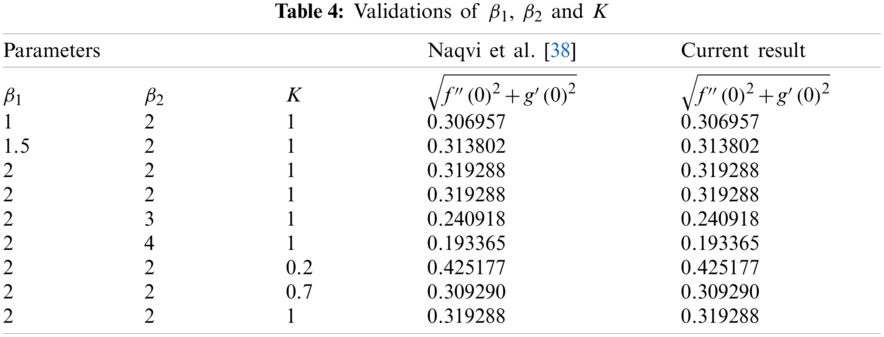
Bioconvection models (swimming of motile microorganisms) have a crucial role in various real life-fields including model construction, pharmaceutical manufacturing, hydrodynamics system, sedimentary waterways, micro-fluidics machines, biofuels, food processing, gas-bearing, hydrodynamics fabrication, microbial increased oil recovery, lubrication materials, polymer construction, etc. Microorganisms are used in medicines as antibiotics and help to create vaccines. Furthermore, there has been reported to be a great combination of nanoliquids and bioconvective processes. The bioconvection of motile microorganisms is utilized alongside nanofluids to provide stability to enhanced thermal transportation. Microorganism particles are used in a wide range of commercial and industrial product categories, such as ethanol, biodiesel, biofuels, microsystems, and bio-fertilizers. Ansari et al. [21] scrutinized the effects of motile swimming microorganisms and nanomaterials over the bioconvection magnetohydrodynamics (MHD) movement of Casson-type liquid at the nonlinearly stretched boundary. Rashad et al. [22] addressed the bio-convection process in nanoliquid flow by the circular cylinder. The mass movement of steady incompressible MHD liquid immediately the stagnation level with the deferral of microscopic particles under the stretchable surface is evaluated by Mamatha et al. [23]. Iqbal et al. [24] discussed the effect of motile gyrotactic microorganisms absorbed in the nanoliquid is often by control of mass flux, bio-convection, as well as energy convection. Kasaragadda et al. [25] inspected the consequence of highly hydrophobic surfaces on the acceptance of nanoparticle-reinforced biomaterial structures. Waqas et al. [26] used both cylinder and plate to observe the bioconvective flow by considering Wu’s slip conditions. Amirsom et al. [27] focused on a bi-axial stretched layer for the 3-dimensional motion of gyrotactic motile microorganisms in bioconvection nanoliquids. Uddin et al. [28] studied the mathematical model of bio-nano-convection transition with blowing and multiple slips through the horizontal layer. Ferdows et al. [29] discovered the conceptual boundary layer flow of cylinder heat and mass transportation in the motile microorganism living in a viscous liquid. Khan et al. [30] examine bioconvection in two stretchable rotating disks utilizing entropy imitation. Li et al. [31] examined the behavior of a transformed second grade nanofluid with bioconvection properties in the presence of Wu’s slip. Muhammad et al. [32] used slip results from a wedge to discover the cause of bioconvection in Carreau nanofluid. More research on bioconvection is being conducted [33–35]. Zhang et al. [36] examined the influence of thermal radiation on the stretching/shrinking of a disc in a bioconvective rate type nanofluid with Arrhenius activation energy. Waqas et al. [37] examined the passage of an Oldroyd-B fluid around a spinning disk containing swimming motile microorganisms. Naqvi et al. [38] scrutinized the bioconvection flow of a few stress fluids involving nanomaterials, magnetic fields, and gyrotactic microorganisms in rotating disks.

1.1 Scope of the Study

The heat transfer in electronic devices is the main challenge in the world due to shorter sizing. To fulfill this gap nanofluids with bioconvection are more useful due to the higher thermal conductivity of nanoparticles. Therefore, in this article, we explore the bioconvection analysis of Reiner–Rivlin nanofluid flow over a rotating disk. For innovative physical situations, the consequences of motile microorganisms along with multiple slip effects are also part of this study. The bioconvection of motile microorganisms is utilized alongside nanofluids to provide stability to enhanced thermal transportation. In literature, the structure of the proposed problem under the impacts of multiple slip constraints is not discussed yet so pertinent results are given importance to fill this gap. The effects of some asymmetrical controlling parameters including wall slip parameters, thermophoresis parameter, Brownian motion parameter, Reiner–Revlin fluid parameter, Prandtl number, Peclet number, Lewis number, bioconvection Lewis number, and the mixed convection parameter on the flow, concentration, density of motile microorganism, and thermal field are examined thoroughly. The numerical outcomes are obtained by using the bvp4c method in MATLAB software. The graphical trend of different controlling parameters besides subjective flow fields is discussed and elaborated.

2  Mathematical Modeling

Consider the three-dimensional, steady, and incompressible flow of Reiner–Rivlin nanofluid containing gyrotactic motile microorganisms over a rotating disk. The rotation of nanofluid is taken about the z–-axis normal to the surface with angular velocity ω, (u,v,w) the velocity components along r,ϕ,z (see Fig. 1). The flow formulation is developed by addressing the effects of thermal radiation to the energy Eq. (5) and Arrhenius activation energy to the nanoparticle’s concentration Eq. (6). It is presumed that Tw, Cw, Nw and T∞, C∞, N∞ are the temperature, concentration of nanoparticles, the density of motile microorganisms at the surface and far away from the surface respectively. The highly nonlinear equations of the flow problem are transformed into ordinary ones with suitable similarities. For this purpose, we employed the bvp4c scheme. The tensor of Reiner–Rivlin fluid is given by [17]:

τij=−pδij+μeij+μceikekj;ejj=0. (1)

Figure 1: The geometrical shape of the problem

Here τij,p,μc,δijandeij=(∂ui/∂xj)+(∂uj/∂xi) designate the deformation rate tensor, pressure, and stress tensor and cross-viscosity coefficient, respectively. The governing flow equations are proposed by [17,37]:

ur+ur+wz=0, (2)

ρ(uur+wuz+v2r)=∂r(τrr)+∂r(τrz)+τrr−τϕϕr,(3)

ρ(uur+wuz+uvr)=1r2ur(r2τrϕ)+∂z(τzϕ)+τrϕ−τϕrrρ(uur+wuz)=1r2∂r(rτrz)+∂z(τzz)+1ρf[(1−Cf)ρfβ∗∗g∗(T−T∞)−(ρp−ρf)g∗(C−C∞)−(N−N∞)g∗γ(ρm−ρf)], (4)

uTr+wTz=αm(Trr+1rTr+Tzz)+(ρc)ρ(ρc)f(DB(TrCr+TzCz))+DTT∞((Tr)2+(Tz)2)+1(ρc)f16σ∗T∞33k∗Tzz, (5)

uCr+wCz=DB(Crr+1rCr+Czz)+DTT∞(Trr+1rTr+Tzz)−Kr2(C−C∞)(TT∞)nexp⁡(−EaK1T), (6)

uNr+wNz+bWc(Cw−C∞)[∂z(NCz)]=DmNzz, (7)

Furthermore, distortion rate tensor’s components are [17]:

err=2ur;eϕϕ=2ur;ezz=2wz;erϕ=eϕr=r∂r(vr),ezϕ=eϕz=vz,erz=ezr=uz+wr (8)

Stress tensor components are assumed to be defined as [17]:

τrr=−p+μ(2ur)+μc{4(ur)2+(uz+wr)2+(vr−vr)2}, (9)

τzr=μ(uz+wr)+μc{(uz+wr)(2ur)+(vz)(vr−vr)+(2wz)(uz+wr)}, (10)

τϕϕ=−p+μ(2ur)+μc{4u2r2+(vz)2+(vr−vr)2}, (11)

τrϕ=μ(vr−vr)+μc{(vr−vr)(2ur)+(2ur)(vr−vr)+(vz)(uz+wr)}, (12)

τzϕ=μvz+μc{(uz+wr)(vr−vr)+2((vz)(ur)+(wz)(vz))}, (13)

τzz=−p+2μ(wz)+μc{4(wz)2+(vz)2+(uz+wr)2}, (14)

The physical boundary conditions are [17,37]:

u(r,0)=β1τrz(r,0),v(r,0)=β2τzϕ(r,0)+rω,w=0,T(r,0)=Tw+β3Tz(r,0),C(r,0)=Cw+β4Cz(r,0),N(r,0)=Nw+β5Nz(r,0),u(r,0)→0,v(r,0)→0,T(r,0)→T∞,C(r,0)→C∞,N(r,0)→N∞asz→∞} (15)

where T stands for the temperature of nanofluid, C stands for the concentration of nanomaterials, N stands for the concentration of motile microorganisms, αm=k/(ρc)f for thermal diffusivity, (ρc)p for the heat capacity of nanomaterials, (ρc)f for base fluid heat capacity, ρ signifies the fluid density, k for thermal conductivity, DT for the coefficient of thermophoresis diffusion, DB for Brownian diffusion coefficient, the term 16σ∗T∞3/3k∗ in Eq. (5) depicts the thermal radiative heat transfer. The term Kr2(C−C∞)(TT∞)nexp⁡(−EaK1T) in Eq. (6) represents the modified Arrhenius function where Ea denotes the activation energy and Kr is the chemical reaction rate, n power-law index, Dm the mass diffusion coefficient, Wc the maximum swimming speed of microorganism cell and β1,β2 are wall slip parameters.

The similarity transformations are [17,37]:

ζ=(ω/v)12z,(u,v,w)=(rωf′(ζ),rωg(ζ),−2vωf′(ζ)),(p,T,C,N)=(p∞−ωμP(ζ),T∞+(Tw−T∞)θ(ζ),C∞+(Cw−C∞)ϕ(ζ),N∞+(Nw−N∞)χ(ζ)) (16)

where f(ζ) and g(ζ) are the non-dimensional stream functions, θ(ζ) is the non-dimensional temperature of nanofluid, ϕ(ζ) is the non-dimensional nanoparticles concentration function, χ(ζ) is the non-dimensional microorganisms density field, and ζ is the similarity transformation variable.

The following dimensionless ordinary differential equations are obtained by applying suitable similarity transformations [17,37]:

f‴−f′2+2ff″+g2+λ(f″2−2f′f‴−g′2)+B∗(θ−Rbϕ−Rcχ)=0, (17)

g″−2f′g+2fg′−2λ(f′g″−f″g′)=0, (18)

(1+43Rd)θ″+Pr(fθ′+Nbθ′ϕ′+Ntθ′2)=0, (19)

ϕ″+NtNbθ″+LePrfϕ′−PrLeσ∗(1+δθ)nexp⁡(−E/(1+δθ))ϕ=0, (20)

χ″+Lbfχ′−Pe[ϕ″(χ+δ1)+χ′ϕ′]=0. (21)

where the Reiner–Rivlin fluid parameter is λ=(μcωμ), Rb=(γ(ρm−ρf)(Nw−N∞)ρf(1−C∞)(Tw−T∞)β∗∗) and Rc=((ρp−ρf)(Cw−C∞)(Tw−T∞)β∗∗ρf(1−Cf)) for bioconvection Rayleigh number as well as buoyancy ratio parameter, respectively, Rd=4σT∞3/kk∗ thermal radiation parameter, B∗=(β∗∗g∗(1−Cf)(Tw−T∞)(1−γt))/ωr for mixed convection parameter, activation energy parameter read as E=Ea/kT∞, Le=(α1/DB) Lewis number, Prandtl number denoted by Pr=(μCpk), Nb=(τDB(CW−C∞)ν) denotes Brownian diffusion parameter, Nt=(τDT(TW−T∞)νT∞) be the thermophoresis parameter, Lb=(νDm),Pe=(bWcDm) and δ1=(N∞Nw−N∞) for bioconvection Lewis number, Peclet number and microorganisms differences parameter, respectively.

Here γ1=(β3ν/ω),γ2=(β4ν/ω) and γ3=(β5ν/ω) for thermal, concentration and microorganisms slip coefficients where β3,β4&β5 are slip coefficients. Thus, the boundary conditions are transformed also [17,37]:

f(0)=0,f′(0)=β1f″(0)(1−2λf′(0)),g(0)=β2g′(0)(1−2λf′(0))+1,θ(0)=1+γ1θ′(0),ϕ(0)=1+γ2ϕ′(0),χ(0)=1+γ3χ′(0)f′→0,g→0,θ→0,ϕ→0,χ→0asζ→∞.} (22)

Torque T0 is specified by definite integral such as:

T0=−∫0Rτzϕ|z=0(2πr2)dr=−πρω2ωvR4G′(0) (23)

The engineering quantities of interest are local skin friction coefficient Cf (explain the shear stress on the surface), local Nusselt number Nu (explain the rate of heat transfer), Sherwood number Sh (explain the rate of mass transfer), as well as the local density number of motile microorganisms Sn (explain the motile microorganisms flux) are presented as:

Cf=τr2−τϕ2ρ(rω)2,Nu=rqwk(Tw−T∞),Sh=rjwDB(Cw−C∞),Sn=rjmDm(Nw−N∞) (24)

where qw, jw and jm denotes shear stress, local heat flux, local mass flux, and motile microorganisms’ flux on the surface, respectively.

Thus from (24), we have dimensionless quantities as:

Cf=(ωr2v)−12(F″(0))2−(G′(0))2,Nu=(ωr2v)12θ′(0),Sh=(ωr2v)12ϕ′(0),Sn=(ωr2/v)12χ′(0) (25)

3  Numerical Scheme

The ordinary differential Eqs. (17)–(21) under the boundary conditions (22) are tackled by bvp4c method with the comfort of computing software MATLAB. The arrangement of non-linear governing ordinary differential equations (ODEs) is restructured to the initial-order ordinary differential equation (ODEs). Let

f=q1,f′=q2,f′′=q3,f′′′=q′3,g=q4,g′=q5,g′′=q′5,θ=q6,θ′=q7,θ′′=q′7,ϕ=q8,ϕ′=q9,ϕ′′=q′9,χ=q10,χ′=q11,χ′′=q′11 (26)

q3′=q22−2q1q3−q42−λ(q32−q52)−B∗(q6−Rbq8−Rcq10)1−2λq2, (27)

q5′=2q2q4−2q1q5−2λq3q51−2λq2, (28)

q7′=−Pr(q1q7+Nbq7q9+Ntq72),(1+43Rd) (29)

q9′=−NtNbq7′−LePrq1q9+PrLeσ∗(1+δq6)nexp⁡(−E(1+δq6))q8, (30)

q11′=−Lbq1q11+Pe[q9′(q10+δ1)+q10q9] (31)

with

q1(0)=0,q2(0)=β1q3(0)(1−2λq2(0)),q4(0)=β2q5(0)(1−2λq2(0))+1,q6(0)=1+γ1q7(0),q8(0)=1+γ2q9(0),q10(0)=1+γ3q11(0)q2→0,q4→0,q6→0,q8→0,q10→0asζ→∞}. (32)

4  Results and Discussion

The numerical solution of non-linear dimensionless ordinary differentiated structures (17)–(21) with boundary constraints given in expression (22) has been attained by the bvp4c function on MATLAB using a mathematical shooting scheme. The major focus of the current work is to observe the effect of several developing specific parameters against axial velocity f(ζ), radial velocity f′(ζ), azimuthal velocity g(ζ), the thermal field θ(ζ) of nanomaterials, the concentration field ϕ(ζ) of nanomaterials, and the motile microorganisms field χ(ζ). The outcomes of dimensionless profiles are analyzed briefly with the aid of graphs and tabular data. Figs. 2–27 are delineated the effects of prominently involved parameters vs. flow fields.

Fig. 2 is depicted to see the impact of distinct estimations of wall slip parameters β1,β2 on the axial velocity profile f of Reiner–Rivlin nanofluid. It is manifest from the figure that increasing values of wall slip parameters diminishes the axial velocity profiles. Fig. 3 is designed to analyze the inspiration of wall slip parameters β1,β2 vs. radial fluid velocity f′. From the figure, it is also witnessed that radial fluid velocity decreases by enhancing the estimation of wall slip parameters. The significance of wall slips parameters β1,β2 on azimuthal velocity g is elaborated through Fig. 4. It is depicted that azimuthal velocity is depressed by enlarging wall slips parameters. Physically, wall slip occurs due to liquid-to-solid transitions under shear stress so crucially dependent on liquid-to-wall molecular interactions.

Figure 2: Axial velocity profile f for distinct values of wall slip parameters β1,β2

Figure 3: Radial velocity profile f′ for distinct values of wall slip parameters β1,β2

Figure 4: Azimuthal velocity profile g for distinct values of wall slip parameters β1,β2

Figs. 5 and 6 demonstrate the inspiration of bioconvection Rayleigh number Rb against the axial and radial velocities f, f′ of the fluid. It is observed that declination in velocities occurs with augmenting magnitudes of bioconvection Rayleigh number. Physically, the bioconvection Rayleigh number Rb measures the instability between layers of fluid due to the variation of temperature and density from top to bottom. The significance of the Reiner–Rivlin fluid parameter λ vs. axial and radial velocities f, f′ are provided in Figs. 7 and 8. The rise in magnitudes of the Reiner–Rivlin fluid parameter λ diminishes both velocity fields of the fluid. Furthermore, radial velocity boosts up away from the disk. The variations of axial and radial velocities f, f′ for distinct values of buoyancy ratio parameter Rc and mixed convection parameter B∗ are presented in Figs. 9–12. The velocities escalate with higher magnitudes of mixed convection parameter while an opposing trend has been detected forbuoyancy ratio parameter. As mixed convection parameter exemplifies ratio among buoyancy to viscous force and large value of this parameter conveys higher buoyancy force, while buoyancy ratio develops further progressive for larger Rc which reduce velocities.

Figure 5: Axial velocity profile f for distinct values of bioconvection Rayleigh number Rb

Figure 6: Radial velocity profile f′ for distinct values of bioconvection Rayleigh number Rb

Figure 7: Axial velocity profile f for distinct values of Reiner–Revlin parameter λ

Figure 8: Radial velocity profile f′ for distinct values of Reiner–Revlin parameter λ

Figure 9: Axial velocity profile f for distinct values of buoyancy ratio parameter Rc

Figure 10: Axial velocity profile f for distinct values of mixed convection parameter B∗

Figure 11: Radial velocity profile f′ for distinct values of mixed convection parameter B∗

Figure 12: Radial velocity f′ for distinct values of buoyancy ratio parameter Rc

The dependence of temperature profile θ on relevant parameters is explained in Figs. 13–17. Fig. 13 demonstrates the outcomes of dimensionless temperature field θ against a varying range of Prandtl numbers Pr. Here, the temperature of nanofluid and its thermal boundary layer thickness declines for enlarging magnitudes of Prandtl number. Physically, when the Prandtl number boosted, the thermal diffusivity de-escalated and consequently led to the decrement in the ability of energy, so the thermal boundary layer declined. Fig. 14 discloses the stimulus of thermal slip coefficient γ1 against a thermal field of species. The temperature field diminishes with rising numbers of thermal slip parameters. Fig. 15 is interpreted as the influence of distinct estimations of wall slip parameters β1,β2 on the temperature profile of Reiner–Rivlin nanofluid. It is apparent from the figure that emerging values of wall slip parameters β1,β2 boosted the concentration of the temperature field. The upshots of thermophoresis parameter Nt vs. temperature distribution θ are demonstrated in Fig. 16. Temperature distribution is increased by enlarging variation of thermophoresis parameter. Physically, this phenomenon occurs because the thermophoresis parameter raises the density of the thermal boundary layer, and suspended particles are transported from warmer to a cooler region which raises fluid temperature significantly. Therefore, temperature increases with an increase in Nt. Fig. 17 explaines the effects of thermal radiationRdon the thermal profile θ of nanofluids. The thermal field goes up due to augmentation in the values of the thermal radiation parameter. Physically, larger radiation parameter Rd leads to enhancement in the kinetic energy of fluid particles and hence increases the temperature profile of fluid.

Figure 13: Temperature profile θ for distinct values of Prandtl number Pr

Figure 14: Temperature profile θ for distinct values of thermal slip coefficient γ1

Figure 15: Temperature profile θ for distinct values of wall slip parameters β1,β2

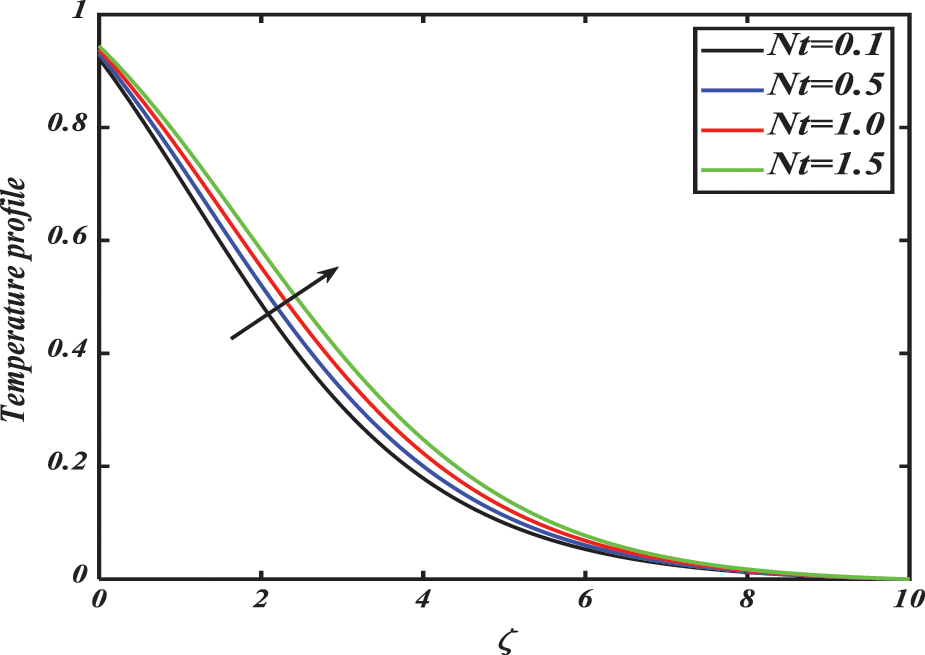
Figure 16: Temperature profile θ for distinct values of thermophoresis parameter Nt

Figure 17: Temperature profile θ for distinct values of thermal radiation parameter Rd

Figs. 18–23 reveal a dependence of concentration distribution ϕ on the relevant parameters. Fig. 18 decelerates the consequence of the Brownian motion parameter Nb via the concentration profile ϕ of nanoparticles. It is inferred that the concentration of nanomaterials retarded down for larger estimations of the Brownian motion parameter. Physically, the greater Brownian motion results in an arbitrary movement of nanoparticles so the extra heat is produced. Due to this extra heat, the temperature of nanoparticles is also increased causes reduced nanoparticles concentration profile. Fig. 19 delineates the characteristics of Lewis number Le over concentration profile of species. Diminution in the concentration of Reiner–Rivlin nanofluid can be noticed for enlarging magnitudes of Lewis number. Physically, the Lewis number decreases the mass diffusivity and hence reduces the permeation depth of the boundary layer. Fig. 20 discloses the consequences of activation energy E against the volumetric concentration of nanoparticles. The volumetric concentration of nanoparticles is boosted by the intensification in the values of activation energy. Activation energy, the minimum energy required to start a chemical reaction. So, the volumetric concentration profile increases as E. The properties of the wall slip parameter on the solutal field of species are demonstrated in Fig. 21. Solutal profile decreases for larger magnitudes of concentration slip coefficient γ2. Fig. 22 is deliberated to investigate the inspiration of wall slip parameters β1,β2 against the volumetric distribution of nanofluid. It is viewed that volumetric nanoparticle concentration enhancing parallel to the enlarging estimations of wall slip parameters β1,β2.

Figure 18: Nanoparticle concentration profile ϕ for distinct values of Brownian diffusion parameter Nb

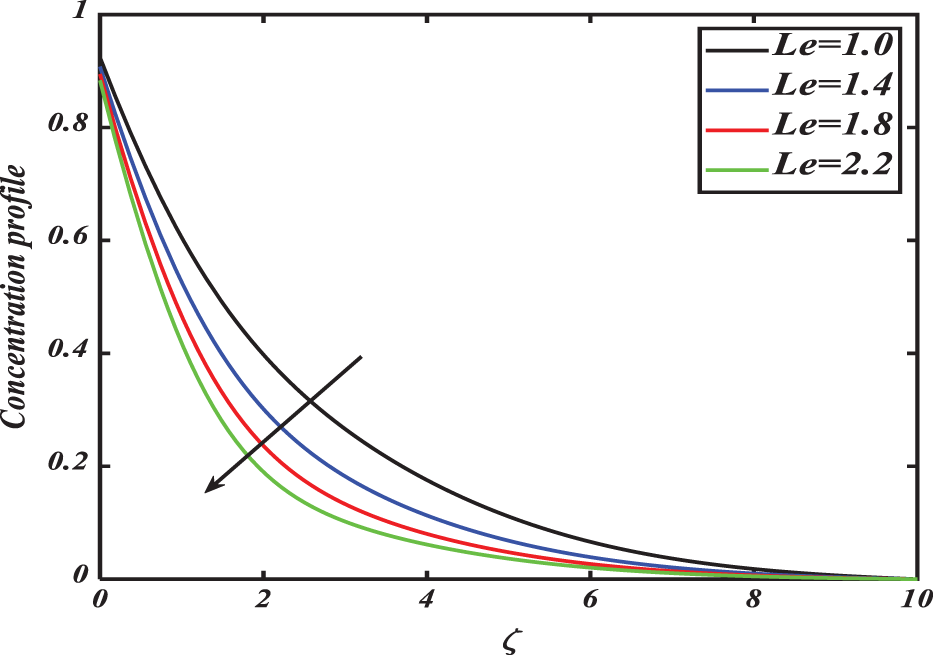
Figure 19: Nanoparticle concentration profile ϕ for distinct values of Lewis number Le

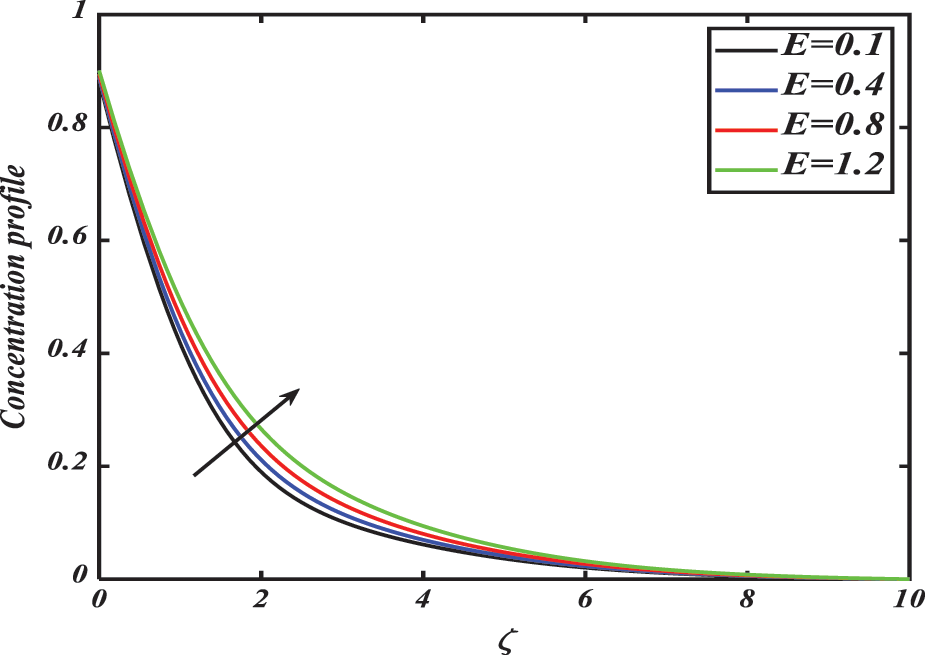
Figure 20: Nanoparticle concentration profile ϕ for distinct values of activation energy E

Figure 21: Nanoparticle concentration profile ϕ or distinct values of concentration slip coefficient γ2

Figure 22: Nanoparticle concentration profile ϕ for distinct values of wall slip parameters β1,β2

Fig. 23 is considered to study the upshot of thermophoresis parameter Nt on the solutal field ϕ of nanomaterials. It is observed that the thermophoresis parameter strongly enhanced the concentration field of species. Physically, in the thermophoresis phenomenon, the tiny particles of fluid are pulled back from the warm to a cold area. Then the particles of the nanofluid move back from the heated surface and consequently nanoparticles’ volume profile is enhanced.

Figure 23: Nanoparticle concentration profile ϕ for distinct values of thermophoresis number Nt

Figs. 24–27 revealed the effectiveness of bioconvection Lewis number Lb, Peclet number Pe, microorganism slip coefficient γ3, and wall slip parameters β1,β2 over the swimming motile microorganism’s concentration field χ. Fig. 24 is plotted to allocate the influence of bioconvection Lewis number Lb over the swimming motile microorganism’s concentration field χ. It is conceivable to note that the motile microorganisms’ profile χ diminishes by positive variations of bioconvection Lewis number Lb. This happens, as the increasing values Lb increase the rate of viscous diffusion, and the density profile of motile microorganisms decreases in the boundary layer. Fig. 25 is drawn to outline the significance of bioconvection Peclet number Pe of motile gyrotactic microorganism’s distribution χ. From the curves, it is promising to observe that the motile microorganisms’ field χ reduces when the Peclet number boosts. As bioconvection Peclet number Pe=bWcDm increases, the cell swimming speed Wc also increases, and hence density profile of motile microorganisms decreases. Fig. 26 exhibits the variation of microorganism slip coefficient γ3 against motile microorganism’s distribution profile χ. From the graphs, it is perceived that the concentration of motile microorganism’s profile curve declined for distinct estimations of microorganism slip coefficient. Fig. 27 reports the assortment of motile microorganisms’ fields χ for evident estimations of wall slip parameters β1,β2. Enhancement in the wall slip parameters boosted the density of the motile microorganism’s field.

Figure 24: Motile microorganism density profile χ for distinct values of bioconvection Lewis number Lb

Figure 25: Motile microorganism density profile χ for distinct values of Peclet number Pe

Figure 26: Motile microorganism density profile χ for distinct values of microorganisms slip coefficient γ3

Figure 27: Motile microorganism density profile χ for distinct values of wall slip parameters β1,β2

Figs. 28a–28c show the streamlines at different values of the β1,β2. The contour of Nusselt number and Sherwood number against subjective parameters is shown in Figs. 29a and 29b. From the figures we observed that the Shewood number and Nusselt number are enhanced via larger subjective parameters. The 3-D plot of Nusslet number via Rb and Rc drawn in Fig. 30. Furthermore, the 3D plot of microorganism’s density number for different estimations of the Pe and Lb given in Fig. 31.

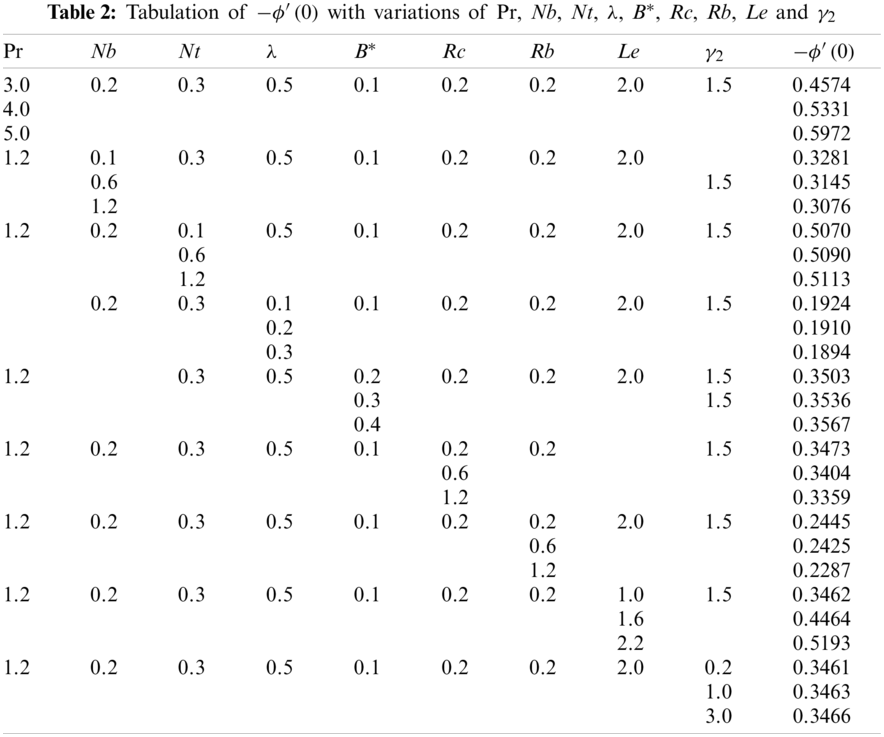
Tables 1–3 are pinched to estimate the variations of the local Nusselt number, the local Sherwood number, as well as the local density number of swimming microorganisms against various mentioned parameters. From Table 1, it can be noted that the local Nusselt number (heat transfer rate) decreases through λ and Pr. Furthermore, the local Sherwood number (mass transfer rate) declined for larger magnitudes of the parameters Rb&Rc, and increases as γ2 shown in Table 2. From Table 3, it is concluded that the local density number of microorganisms (motile microorganisms’ flux) rises with Pe and Lb. Table 4 gives the comariosion of resuts between current study and results by Naqvi et al. [38].

Figure 28: (a–c) Aspects of streamline Nr and β1=β2

Figure 29: (a and b) Aspects of Contour line Sherwood and Nusselt number

Figure 30: 3D plot of Rb&Rc on Nusselt number

Figure 31: 3D plot of Lb&Pe on Microorganism’s profile

5  Conclusions

In this manuscript, we have discussed the steady and incompressible bioconvection flow of Reiner–Rivlin nanofluid over a rough rotational disk containing motile microorganisms with thermal radiation and Arrhenius activation energy. The effects of some asymmetrical controlling parameters including wall slip parameters, thermophoresis parameter, Brownian motion parameter, Reiner–Revlin nanofluid parameter, Prandtl number, Peclet number, Lewis number, bioconvection Lewis number, and the mixed convection parameter on the flow, the concentration of nanoparticles, thermal field, and density of motile microorganisms are examined thoroughly.

•   The velocity profiles of nanofluid escalate for higher magnitudes of mixed convection parameter B∗ while an opposing trend has been detected for buoyancy ratio parameter Rc, Reiner–Rivlin fluid parameter λ, wall slip parameters β1&β2, and bioconvection Rayleigh number Rb.

•   The temperature profile of nanofluid goes up due to augmentation in the values of thermal radiation parameter Rd, thermophoresis number Nt, and wall slip parameters β1&β2 while an opposing trend has been noticed for enlarging magnitudes of Prandtl number Pr.

•   The concentration profile is boosted up by the thermophoresis number Nt and wall slip parameters β1&β2.

•   The concentration profile of nanoparticles grows by intensification in activation energy E.

•   Brownian motion Nb and Lewis number Le consequences show a decrement in the concentration profile of nanoparticles.

•   The motile microorganisms’ profile diminishes by positive variations of bioconvection Lewis number Lb and Peclet number Pe while escalating for wall slip parameters β1&β2.

•   The temperature, concentration, and microorganisms’ density profiles decrease for enlarging values of thermal, concentration, and microorganisms slip coefficients γ1,γ2&γ3, respectively.

Funding Statement: This work is financially supported by the Government College University, Faisalabad, and Higher Education Commission, Pakistan.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Choi, S. U., Eastman, J. A. (1995). Enhancing the thermal conductivity of fluids with nanoparticles(No. AL/MSD/CP-84938; CONF-951135-29). IL, USA: Argonne National Lab. [Google Scholar]

 2.  Buongiorno, J. (2005). Convective transport in nanofluids. ASME Journal of Heat Transfer, 128(3), 240–250. DOI 10.1115/1.2150834. [Google Scholar] [CrossRef]

 3.  Sheikholeslami, M., Bhatti, M. M. (2017). Forced convection of nanofluid in presence of constant magnetic field considering shape effects of nanoparticles. International Journal of Heat and Mass Transfer, 111(7), 1039–1049. DOI 10.1016/j.ijheatmasstransfer.2017.04.070. [Google Scholar] [CrossRef]

 4.  Waqas, H., Farooq, U., Naseem, R., Hussain, S., Alghamdi, M. (2021). Impact of MHD radiative flow of hybrid nanofluid over a rotating disk. Case Studies in Thermal Engineering, 26(1), 101015. DOI 10.1016/j.csite.2021.101015. [Google Scholar] [CrossRef]

 5.  Bhatti, M. M., Rashidi, M. M. (2016). Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. Journal of Molecular Liquids, 221(4), 567–573. DOI 10.1016/j.molliq.2016.05.049. [Google Scholar] [CrossRef]

 6.  Hafeez, A., Khan, M., Ahmed, J. (2020). Stagnation point flow of radiative Oldroyd-B nanofluid over a rotating disk. Computer Methods and Programs in Biomedicine, 191(17), 105342. DOI 10.1016/j.cmpb.2020.105342. [Google Scholar] [CrossRef]

 7.  Hayat, T., Imtiaz, M., Alsaedi, A. (2015). MHD 3D flow of a nanofluid in the presence of convective conditions. Journal of Molecular Liquids, 212(5), 203–208. DOI 10.1016/j.molliq.2015.09.012. [Google Scholar] [CrossRef]

 8.  Ellahi, R., Hussain, F., Abbas, S. A., Sarafraz, M. M., Goodarzi, M. et al. (2020). Study of two-phase Newtonian nanofluid flow hybrid with Hafnium particles under the effects of slip. Inventions, 5(1), 6. DOI 10.3390/inventions5010006. [Google Scholar] [CrossRef]

 9.  Alsaedi, A., Hayat, T., Qayyum, S., Yaqoob, R. (2020). Eyring-Powell nanofluid flow with nonlinear mixed convection: Entropy generation minimization. Computer Methods and Programs in Biomedicine, 186(3), 105183. DOI 10.1016/j.cmpb.2019.105183. [Google Scholar] [CrossRef]

10. Khan, M., Salahuddin, T., Tanveer, A., Malik, M. Y., Hussain, A. (2019). Change in internal energy of thermal diffusion stagnation point Maxwell nanofluid flow along with solar radiation and thermal conductivity. Chinese Journal of Chemical Engineering, 27(10), 2352–2358. DOI 10.1016/j.cjche.2018.12.023. [Google Scholar] [CrossRef]

11. Gireesha, B. J., Krishnamurthy, M. R., Ganeshkumar, K. (2019). Nonlinear radiative heat transfer and boundary layer flow of Maxwell nanofluid past stretching sheet. Journal of Nanofluids, 8(5), 1093–1102. DOI 10.1166/jon.2019.1661. [Google Scholar] [CrossRef]

12. Khan, M., Malik, M. Y., Salahuddin, T., Khan, F. (2019). Generalized diffusion effects on Maxwell nanofluid stagnation point flow over a stretchable sheet with slip conditions and chemical reaction. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 41(3), 138. DOI 10.1007/s40430-019-1620-3. [Google Scholar] [CrossRef]

13. Nadeem, S., Haq, R. U., Khan, Z. H. (2014). Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. Journal of the Taiwan Institute of Chemical Engineers, 45(1), 121–126. DOI 10.1016/j.jtice.2013.04.006. [Google Scholar] [CrossRef]

14. Khan, S. U., Tlili, I., Waqas, H., Imran, M. (2020). Effects of nonlinear thermal radiation and activation energy on modified second-grade nanofluid with Cattaneo–Christov expressions. Journal of Thermal Analysis and Calorimetry, 143(2), 1175–1186. DOI 10.1007/s10973-020-09392-6. [Google Scholar] [CrossRef]

15. Alghamdi, M. (2020). On magnetohydrodynamic flow of viscoelastic nanofluids with homogeneous-heterogeneous reactions. Coatings, 10(1), 55. DOI 10.3390/coatings10010055. [Google Scholar] [CrossRef]

16. Ullah, M. Z., Serra-Capizzano, S., Baleanu, D. (2020). A numerical simulation for Darcy–Forchheimer flow of nanofluid by a rotating disk with partial slip effects. Frontiers in Physics, 7, 219. DOI 10.3389/fphy.2019.00219. [Google Scholar] [CrossRef]

17. Tabassum, M., Mustafa, M. (2018). Numerical treatment for partial slip flow and heat transfer of non-Newtonian Reiner–Rivlin fluid due to rotating disk. International Journal of Heat and Mass Transfer, 123, 979–987. DOI 10.1016/j.ijheatmasstransfer.2018.03.040. [Google Scholar] [CrossRef]

18. Motsa, S., Makukula, Z. (2013). On spectral relaxation method approach for steady von Kármán flow of a Reiner–Rivlin fluid with Joule heating, viscous dissipation, and suction/injection. Open Physics, 11(3), 363–374. DOI 10.2478/s11534-013-0182-8. [Google Scholar] [CrossRef]

19. Akbar, N. S., Nadeem, S. (2010). Simulation of heat and chemical reactions on Reiner–Rivlin fluid model for blood flow through a tapered artery with stenosis. Heat and Mass Transfer, 46(5), 531–539. DOI 10.1007/s00231-010-0595-5. [Google Scholar] [CrossRef]

20. Baker, M., Ericksen, J. L. (1954). Inequalities restricting the form of the stress-deformation relations for isotropic elastic solids and Reiner–Rivlin fluids. Journal of the Washington Academy of Sciences, 44(2), 33–35. [Google Scholar]

21. Ansari, M. S., Otegbeye, O., Trivedi, M., Gogo, S. P. (2021). Magnetohydrodynamic bio-convective Casson nanofluid flow: A numerical simulation by paired quasi linearisation. Journal of Applied and Computational Mechanics, 7(4), 2024–2039. DOI 10.22055/JACM.2020.31205.1839. [Google Scholar] [CrossRef]

22. Rashad, A. M., Nabwey, H. A. (2019). Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. Journal of the Taiwan Institute of Chemical Engineers, 99(21), 9–17. DOI 10.1016/j.jtice.2019.02.035. [Google Scholar] [CrossRef]

23. Mamatha, S. U., Babu, K. R., Prasad, P. D., Raju, C. S. K., Varma, S. V. K. (2020). Mass transfer analysis of two-phase flow in a suspension of microorganisms. Archives of Thermodynamics, 41, 175–192. DOI 10.24425/ather.2020.132954. [Google Scholar] [CrossRef]

24. Iqbal, Z., Mehmood, Z., Azhar, E., Maraj, E. N. (2017). Numerical investigation of nanofluid transport of gyrotactic microorganisms submerged in the water towards the Riga plate. Journal of Molecular Liquids, 234, 296–308. DOI 10.1016/j.molliq.2017.03.074. [Google Scholar] [CrossRef]

25. Kasaragadda, S., Alarifi, I. M., Rahimi-Gorji, M., Asmatulu, R. (2020). Investigating the effects of surface superhydrophobicity on moisture ingression of nanofiber-reinforced bio-composite structures. Microsystem Technologies, 26(2), 447–459. DOI 10.1007/s00542-019-04507-y. [Google Scholar] [CrossRef]

26. Waqas, H., Imran, M., Muhammad, T., Sait, S. M., Ellahi, R. (2021). On bio-convection thermal radiation in Darcy–Forchheimer flow of nanofluid with gyrotactic motile microorganism under Wu’s slip over stretching cylinder/plate. International Journal of Numerical Methods for Heat & Fluid Flow, 31(5), 1520–1546. DOI 10.1108/HFF-05-2020-0313. [Google Scholar] [CrossRef]

27. Amirsom, N. A., Uddin, M. J., Basir, M. F. M., Ismail, A., Beg, O. A. et al. (2019). Three-dimensional bioconvection nanofluid flow from a biaxial stretching sheet with anisotropic slip. Sains Malaysiana, 48(5), 1137–1149. DOI 10.17576/jsm-2019-4805-23. [Google Scholar] [CrossRef]

28. Uddin, M. J., Kabir, M. N., Alginahi, Y., Bég, O. A. (2019). Numerical solution of bio-nano-convection transport from a horizontal plate with blowing and multiple slip effects. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 233(19–20), 6910–6927. DOI 10.1177/0954406219867985. [Google Scholar] [CrossRef]

29. Ferdows, M., Reddy, M. G., Alzahrani, F., Sun, S. (2019). Heat and mass transfer in a viscous nanofluid containing a gyrotactic micro-organism over a stretching cylinder. Symmetry, 11(9), 1131. DOI 10.3390/sym11091131. [Google Scholar] [CrossRef]

30. Khan, N. S., Shah, Q., Bhaumik, A., Kumam, P., Thounthong, P. et al. (2020). Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Scientific Reports, 10(1), 4448. DOI 10.1038/s41598-020-61172-2. [Google Scholar] [CrossRef]

31. Li, Y., Waqas, H., Imran, M., Farooq, U., Mallawi, F. et al. (2020). A numerical exploration of modified second-grade nanofluid with motile microorganisms, thermal radiation, and Wu’s slip. Symmetry, 12(3), 393. DOI 10.3390/sym12030393. [Google Scholar] [CrossRef]

32. Muhammad, T., Alamri, S. Z., Waqas, H., Habib, D., Ellahi, R. (2020). Bioconvection flow of magnetized Carreau nanofluid under the influence of slip over a wedge with motile microorganisms. Journal of Thermal Analysis and Calorimetry, 143(2), 945–957. DOI 10.1007/s10973-020-09580-4. [Google Scholar] [CrossRef]

33. Song, Y. Q., Waqas, H., Al-Khaled, K., Farooq, U., Khan, S. U. et al. (2021). Bioconvection analysis for Sutter by nanofluid over an axially stretched cylinder with melting heat transfer and variable thermal features: A Marangoni and solutal model. Alexandria Engineering Journal, 60(5), 4663–4675. DOI 10.1016/j.aej.2021.03.056. [Google Scholar] [CrossRef]

34. Al-Mubaddel, F. S., Farooq, U., Al-Khaled, K., Hussain, S., Khan, S. U. et al. (2021). Double stratified analysis for bioconvection radiative flow of Sisko nanofluid with generalized heat/mass fluxes. Physica Scripta, 96(5), 055004. DOI 10.1088/1402-4896/abeba2. [Google Scholar] [CrossRef]

35. Farooq, U., Waqas, H., Khan, M. I., Khan, S. U., Chu, Y. M. et al. (2021). Thermally radioactive bioconvection flow of Carreau nanofluid with modified Cattaneo–Christov expressions and exponential space-based heat source. Alexandria Engineering Journal, 60(3), 3073–3086. DOI 10.1016/j.aej.2021.01.050. [Google Scholar] [CrossRef]

36. Zhang, T., Khan, S. U., Imran, M., Tlili, I., Waqas, H. et al. (2020). Activation energy and thermal radiation aspects in bioconvection flow of rate type nanoparticles configured by a stretching/shrinking disk. Journal of Energy Resources Technology, 142(11), 112102. DOI 10.1115/1.4047249. [Google Scholar] [CrossRef]

37. Waqas, H., Imran, M., Muhammad, T., Sait, S. M., Ellahi, R. (2021). Numerical investigation on bioconvection flow of Oldroyd-B nanofluid with nonlinear thermal radiation and motile microorganisms over a rotating disk. Journal of Thermal Analysis and Calorimetry, 145(2), 523–539. DOI 10.1007/s10973-020-09728-2. [Google Scholar] [CrossRef]

38. Naqvi, S. M. R. S., Kim, H. M., Muhammad, T., Mallawi, F., Ullah, M. Z. (2020). Numerical study for slip flow of Reiner–Rivlin nanofluid due to a rotating disk. International Communications in Heat and Mass Transfer, 116(6), 104643. DOI 10.1016/j.icheatmasstransfer.2020.104643. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.