Computer Modeling in Engineering & Sciences

DOI: 10.32604/cmes.2022.018343

ARTICLE

Image Encryption Algorithm Based on New Fractional Beta Chaotic Maps

Rabha W. Ibrahim1,*, Hayder Natiq2, Ahmed Alkhayyat3, Alaa Kadhim Farhan4, Nadia M. G. Al-Saidi5 and Dumitru Baleanu6,7,8

1Institute of Electrical and Electronics Engineers, Kuala Lumpur, 59200, Malaysia
2Information Technology College, Imam Ja'afar Al-Sadiq University, Baghdad, 10001, Iraq
3Department of Computer Technical Engineering, College of Technical Engineering, Islamic University, Najaf, 192122, Iraq
4Department of Computer Sciences, University of Technology, Baghdad, 10066, Iraq
5Department of Applied Sciences, University of Technology, Baghdad, 10066, Iraq
6Department of Mathematics, Cankaya University, Balgat, Ankara, 06530, Turkey
7Institute of Space Sciences, Magurele-Bucharest, R76900, Romania
8Department of Medical Research, China Medical University, Taichung, 40402, Taiwan
*Corresponding Author: Rabha W. Ibrahim. Email: rabhaibrahim@yahoo.com
Received: 17 July 2021; Accepted: 07 December 2021

1  Introduction

The recent advancements in communications and computer technologies facilitate data transmission over the internet networks [1]. However, the major problems with data transmission over the internet are the safety of the information from unauthorized users. In recent years, image encryption has been an attractive area for research. It is extensively recognized as a useful technique for secure transmission. Every image encryption algorithm is aimed to keep information secret [2,3]. Image cryptographic models are based on mathematical functions to generate a combination of different keys to encrypt the input image. The encrypted images are dependent on two important features; the compensation of generating the key and the strength of the encryption algorithm [4]. Many encryption models have been proposed. The most known image encryption algorithms are based on chaotic encryption [5]. Image encryptions and chaos provide a good combination for image encryptions. The chaotic image encryption demonstrates the use of chaos theories to do various encryption tasks. Many new chaotic maps have been developed to produce more security with better encryption performances [4,6].

Fractional calculus plays a major role in many sciences and its applications [7–9]. It developed, improved, and even created new rules, algorithms and proceedings in computer science and engineer studies. Nowadays, the list of fractional calculus is very long to include many fractional operators (differential and integral) [10–12]. Over the years, chaos theory has been applied in science and engineering. It especially got much attention in the field of image encryption. Zhang et al. [13] proposed a new chaotic logistic map called tent delay-sine cascade (TDSCL). The proposed TDSCL has better initial value sensitivity with a larger chaotic parameter interval compared with the original chaotic logistic map. The image encryption algorithm that is based on TDSCL achieved both the confusion and diffusion at the same time. Zhang et al. [14] proposed a new fractional-order logistic map based on S-boxes. The proposed fractional-order chaotic system provided a larger key space to make the image encryption more efficient against cryptanalyst attacks. The proposed S-boxes are used for the encryption confusion process.

Fractional calculus is utilized to generalize chaotic systems, chaotic maps, optimization, operation, and other theories of chaos and has been employed in an extensive choice of this field including entropy concept [9,15–18]. Fractional calculus models are now widely used in image security due to their infinite boundary property. Wang et al. [19] proposed a novel image encryption algorithm that employs fractal geometry of colored images. This proposed image encryption algorithm has a large key space with a complex behavior to produce the confusion behavior. The confusion behavior of the proposed model helped to shuffle the pixel positions to avoid the correlation between image pixels. Chaos theory focuses on describing the behavior of a nonlinear dynamic system, which sensitivity to initial conditions is high. The common features between chaotic and encryption models have led to developing different chaos-based image encryption modes. Recently, chaotic maps employed in different ways in image encryption algorithms and related to security applications. Xu et al. [20] presented a chaotic tablet code for image encryption using the concept of the matrix semi-tensor. Yu et al. [21] proposed a method based on the compressive identifying and a hyperactive chaotic map. Jithin et al. [22] formulated a chaotic map based on the phase-truncated short-time fractional Fourier transform. The DNA sequence is utilized to define an encryption, image algorithm based on an Arnold map by Ul Haq et al. [23]. Zhang et al. [24] formulated a chaotic map in RGB image encryption. Zig Zag diffusion and RNA generated a Hyper-Chaotic Color Image Encryption transformed Operation which is given by Jiao et al. [25]. Finally, Arnold map and RSA algorithm are used by Zahmoul et al. [26]. Beta function is utilized in various types of applications in image processing and engineering, especially in bio-medical signal and image compression, image detection [27–36]. Other works can be located in [37–49].

Therefore, looking for a new chaotic mapping technique, which produces better security performances compared with other methods of image encryption, is very important and superior performance with respect to the trade-offs between the security and efficiency. To further increase, the security performances of the image encryption based on chaos, a new chaotic map based on fractional beta function has been proposed to achieve strong chaotic key generations. The structure of the paper is as follows: Section 2 deals with the fractional beta map; Section 3 includes the experimental results; Section 4 involves the conclusion and future works.

2  Fractional Beta Chaotic (FBC) Maps

Chaos theory focuses on describing the behavior of a nonlinear dynamic system, which sensitivity to initial conditions is high. The common features between chaotic and encryption models have led to developing different chaos-based image encryption modes. Recently, chaotic map approaches have been used in different ways in image encryption algorithms and related to security applications. Zahmoul et al. [26] proposed the beta map for the first time using the formula

β(χ;ρ,ϱ,χ1,χ2)=(χ−χ1χγ−χ1)ρ(χ2−χχ2−χγ)ϱ,(1)

where χ;ρ,ϱ,χ1,χ2 ∈R(the set of real numbers) and

χγ=ρχ2+ϱχ1ρ+ϱ,ρ≠−ϱ,χ∈(χ1,χ2), where γ is a fixed constant.

Hence, the β− map is defined by: χn+1=κβ(χn;ρ,ϱ,χ1,χ2),

where κ is a parameter of chaotic map, which is used to adjust the value of β-map and indicate the bifurcation parameter. Beta function is utilized in various types of applications in image processing and engineering, especially in bio-medical signal and image compression, image detection [27–31].

The motivation for this study is to employ the concept of the fractional calculus to generalize and improve the β-map. We call the consequence of this generalization the fractional β-map. Then we employ the new look of this function to design a hybrid model for image encryption based on fractional-chaotic maps. Our contribution is to develop a new chaotic map based on fractional-chaotic map is proposed. The proposed fractional-chaos have a large range of bifurcation parameter with the strong chaotic behavior which increases the protection of the image encryption schemes.

2.1 Proposed Fractional Chaos-Based (FBC)Model

In this section, a new mathematical fractional-chaotic maps model has proposed to as a new image encryption algorithm. Consider the polynomial function ϕ (χ) taking the form

ϕ(χ)=χn.(2)

The first derivative is known by the formula

[ϕ(χ)]′=ddχϕ(χ)=nχn−1.(3)

Accumulating this yields the general formula

dℵdχℵχn=n!(n−ℵ)!χn−ℵ.(4)

Now, generalize the factorial by the gamma function, we have the generalized calculus

dℵdχℵχn=Γ(n+1)Γ(n−ℵ+1)χn−ℵ,n>0.(5)

For negative integer power n, we obtain the following relation:

dℵdχℵχ−n=(−1)ℵΓ(n+ℵ)Γ(n)χ−(n+ℵ) for n≥0.(6)

By using the above conclusion, dℵdχℵχn:=χn(ℵ),κ ∈R, we present the FBM, as follows:

βℵ(χn+1;ρ,ϱ,χ1,χ2)=(χn(ℵ)−χ1χγ−χ1)ρ(χ2−χn(ℵ)χ2−χγ)ϱ         ≈(Γ(n+1)Γ(n−ℵ+1)χnn−ℵ−χ1χγ−χ1)ρ(χ2−Γ(n+1)Γ(n−ℵ+1)χnn−ℵχ2−χγ)ϱ,     n=⌈ℵ⌉.(7)

2.2 β–Algorithm

The encryption dynamic of the suggested system recognized by the following steps:

•   Suppose that a picture of size M∗N. Replace the selected image by a square dimension picture;

•   Produce two dissimilar quasi-random arrangements subsequently constructing numerous recipes of FBM. Via the understanding of the chaotic purpose of the considerable difference in the initial condition, numerous random arrangements might be made;

•   At this stage, the produced arrangements of the FBM are utilized to waddle the plaintext copy's rows and columns. Organizing elements of Q_pro and Q1_pro whose elements are M * N in matrix system and find Q and Q1 matrices with M * N dimension. The variation procedure affects the original feature pixels by variation them inside columns, utilizing Q1 matrices coefficient's locations. The coefficients of the consequential matrix are formulated, using Q2 within rows;

•   Share the consequential matrix into four blocks of equivalent dimension. Transform every block to a quasi-random matrix W, where every matrix additional transformed by the utilities;

UN(δ)=⊤(δ)modIUR(δ)=⊤⌊(δ)⌋modIUS(δ)=⊤(δ2)modIUD(δ)=⊤(2δ)modIW=(UN(βℵ(1,1))UR(βℵ(1,2))US(βℵ(1,3))UD(βℵ(1,4))UR(βℵ(2,1))US(βℵ(2,2))UD(βℵ(2,3))UN(βℵ(2,4))US(βℵ(3,1))UD(βℵ(3,2))UN(βℵ(3,3))UR(βℵ(3,4))UD(βℵ(4,1))UN(βℵ(4,2))UR(βℵ(4,3))US(βℵ(4,4)))

•   The operator ⊤ means a truncation of a decimal to form an integer for every digit of the consequential matrix W, while I designates the feature category, for (I = 256) it is an 8-bit gray image, and for (I = 2) it is a binary feature. Thus, we obtain an original accidental integer matrix J. Formerly, we get a code text picture I with the next equality (for encryption):

Gencr=(P+J)modI,P=(Gencr−J)modI;

•   Diffusion imitates the assets that the termination in the data and figures of the plain text is dissolute in the cipher text;

•   Finally, the encryption procedure upgrades the security of pictures critically. The decryption structure of the process can be investigated as the converse of the encryption scheme utilizing the matching key.

2.3 Image Processing by β–Algorithm

The proposed image encryption algorithm consisted of the following steps:

1-Resize the input image in square equal dimension.

2-Produce different random sequences by using different combinations of beta chaotic maps.

3-The generated sequences are used for shuffling the rows and columns of input image.

4-The substitution process of input image pixels by: f(r) = T(r) mod I. Where I is the input image

and T is the truncation function.

5-The decryption process is the reverse of the encrypted using the same key.

The fractional β map βℵ(X) diagram is used to illustrate in Fig. 1, to show the behavior of the proposed fractional β map through different value of ϱ. Essentially, the FBC maps can be governed by two parameters (ρ and ϱ).

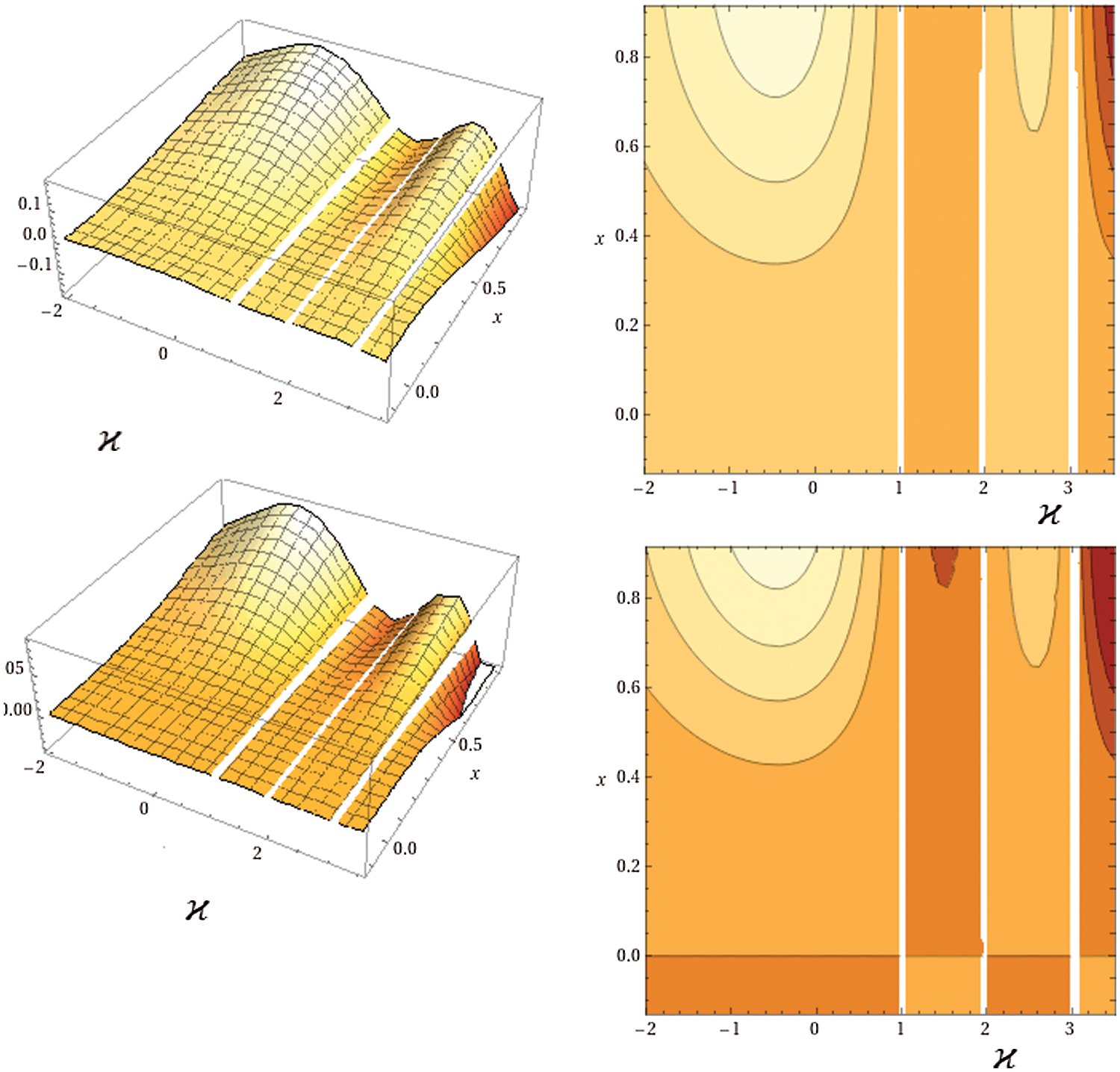
Figure 1: The plot of the fractional β map βℵ(χ) when ρ= ϱ = 2, ρ = 2, and ϱ = 3 respectively

3  Experimental Results

In this section, the performance of the proposed image encryption model is demonstrated using standard test images, commonly known as Lena, Pepper, and Baboon. We employed statistical analyses to assess the model's performance.

3.1 The Histogram Analysis

The image histogram represents the relationship between the pixel gray level and the frequency of occurrence. In this study, the histograms of different original and encrypted images are illustrated in Fig. 2. The histogram of the plain picture has large spikes as shown in Fig. 2b. In comparison, the histogram of the encrypted image is more uniformed as shown in Fig. 2d. We can conclude that there is a important alteration in the shape of histograms of the plain and of the encrypted images.

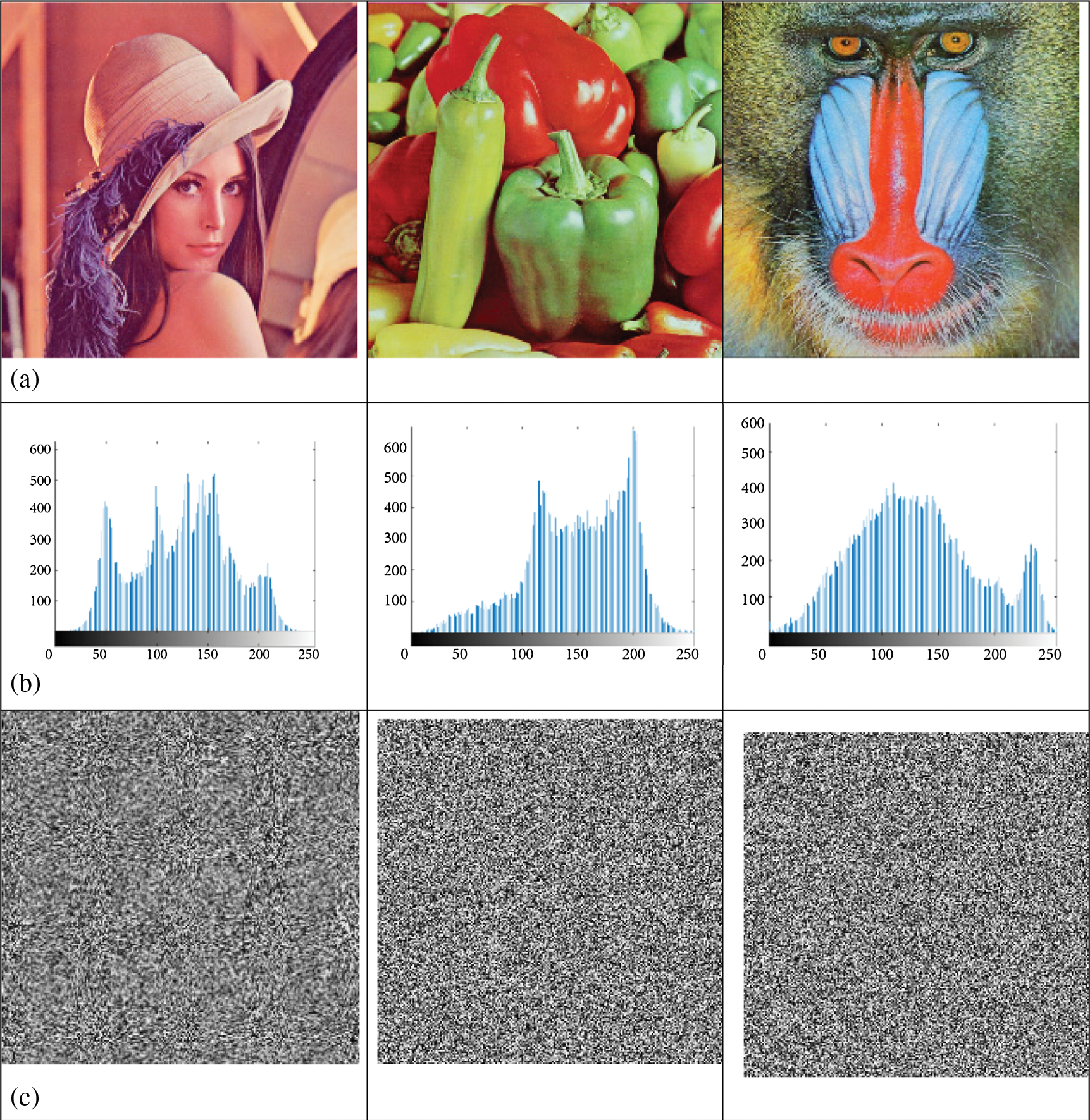
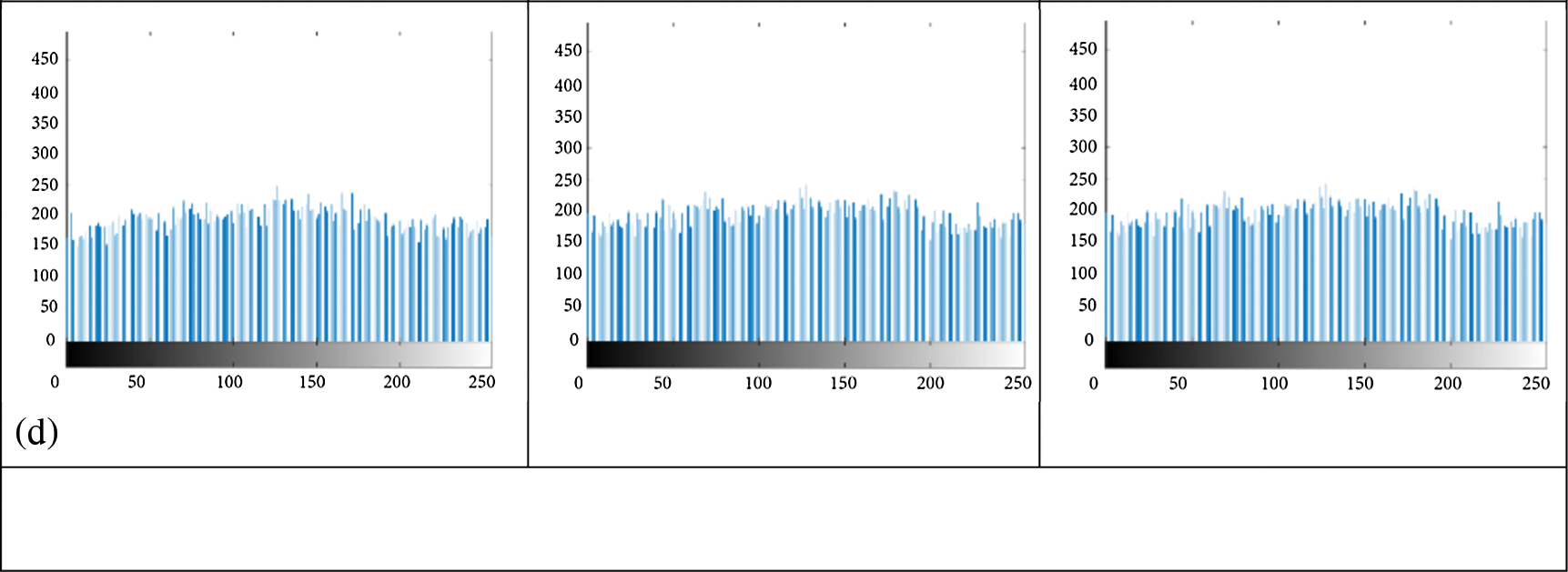
Figure 2: Histograms analysis (a) Input images, (b) Input images histograms, (c) Encrypted images, (d) Encrypted images histograms

3.2 Information Entropy Analysis

The entropy measures the degree of unpredictability of information. The information entropy is calculated for encrypted images to measure the degree of uncertainties; however, any certain degree of predictability will threaten the encryption security [31]. Table 1 is a test of the information entropy of the plaintext and the encrypted image of the proposed FBC maps model.

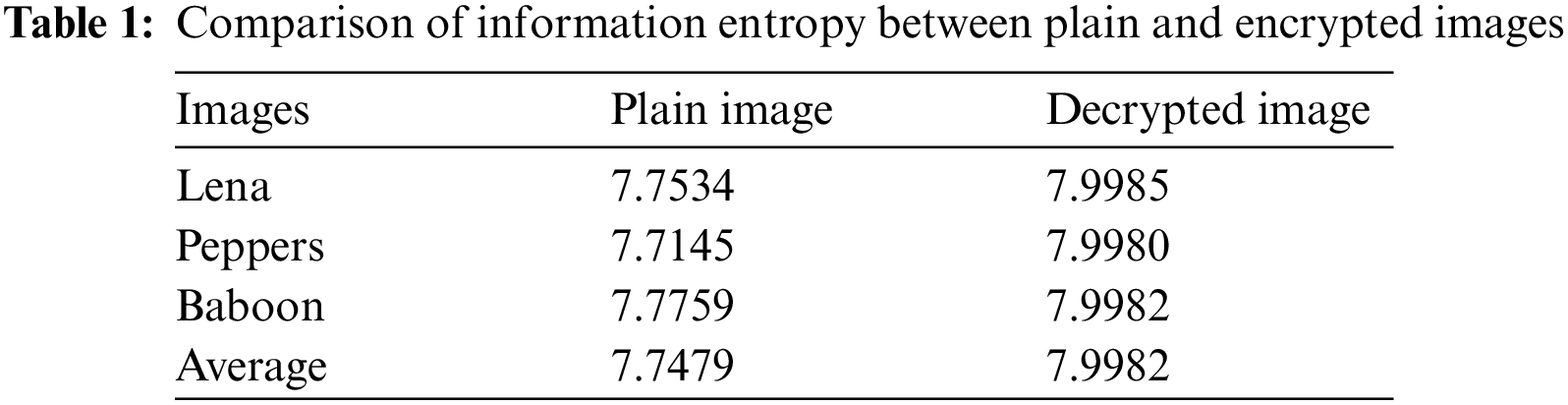
The results of Table 1 illustrated that the calculated entropies of the mentioned encrypted images are almost close to number 8. Therefore, we can conclude that our suggested FBC map process has an entropy average of 7.9982. Therefore, the proposed FBC maps are robust against any types of entropy attacks. Moreover, Table 2 illustrates the comparison of information entropy of several algorithms using Lena as a test image. From Table 2, it is clear that the values of entropy of the decrypted image achieved by the proposed FBC map algorithm are almost close to the number 8, which shows that the encrypted Lena image is near to a random source.

3.3 Correlation Analysis

The aim of the image encryption algorithm is to decrease the correlation among the image pixels in order to make the prediction of any given pixel from its neighbors more difficult. The next formula indicates the correlation coefficient between each pair:

Cor(x,y)=∑i=1N⁡(xi−1N∑j=1N⁡xj)(yi−1N∑j=1N⁡yj)∑i=1N⁡(xi−1N∑j=1N⁡xj)2∑i=1N⁡(yi−1N∑j=1N⁡yj)2,

where xi and yi from i-th couple of horizontal (H), vertical (V) and diagonal (D) adjacent pixels, N signifies the entire number of couples of the contiguous pixels. The correlation constants in the three directions of neighboring pixels for two couples of the basic pictures cited above and their associated encrypted pictures are indicated in Tables 3 and 4.

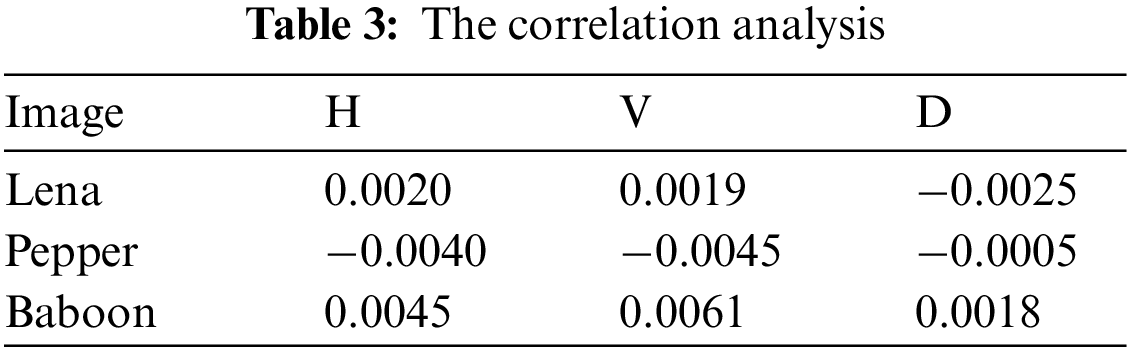
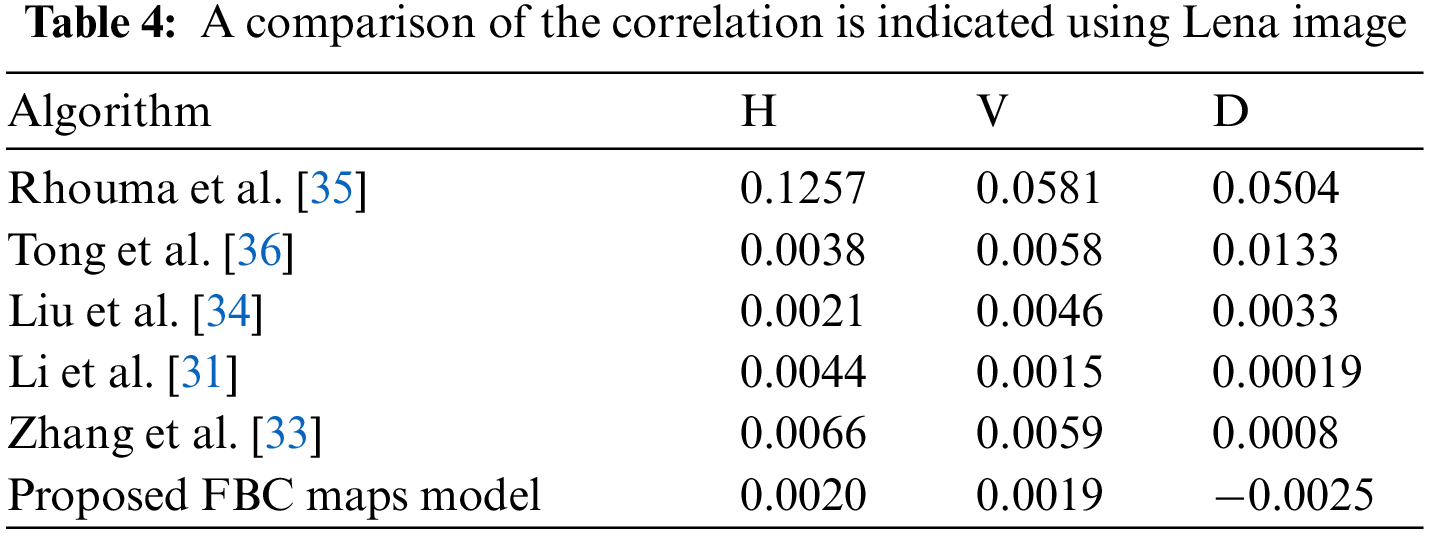
Table 3 illustrates the correlation coefficients of input images and encrypted images. The calculated correlation coefficients illustrate that the correlation coefficients of encrypted images are close to zero, which proves that the proposed FBC maps of the proposed model can efficiently reduce the correlations among the adjacent image pixels of the input images in three directions: The horizontal (H); the vertical (V) and diagonal (D). The low record values in all the three directions (H, V and D) indicated that the pixel pattern of decrypted images is unbreakable by the attackers.

Taking the Lena (256 × 256) image as an experimental object, the comparison of correlation between different encryption algorithms in the horizontal (H), vertical (V) and diagonal (D) directions is illustrated in Table 4. The correlation values in the three directions obtained from the proposed FBC map algorithm for Lena images are smaller than the values of study in the shown in Table 4, which indicated that the proposed FBC map method is secure against statistical attacks.

3.4 The Structural Similarity (SSIM)

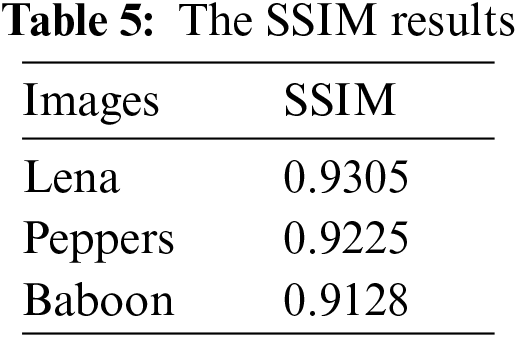
The SSIM measure is used to measure the similarity between the input image and the decrypted image. The close pixels have strong SSIM when they are close. The range of SSIM is between −1 and 1. Table 5 shows the SSIM value of three testing images. The best value of SSIM is close to 1.

3.5 Key Sensitivity Analysis

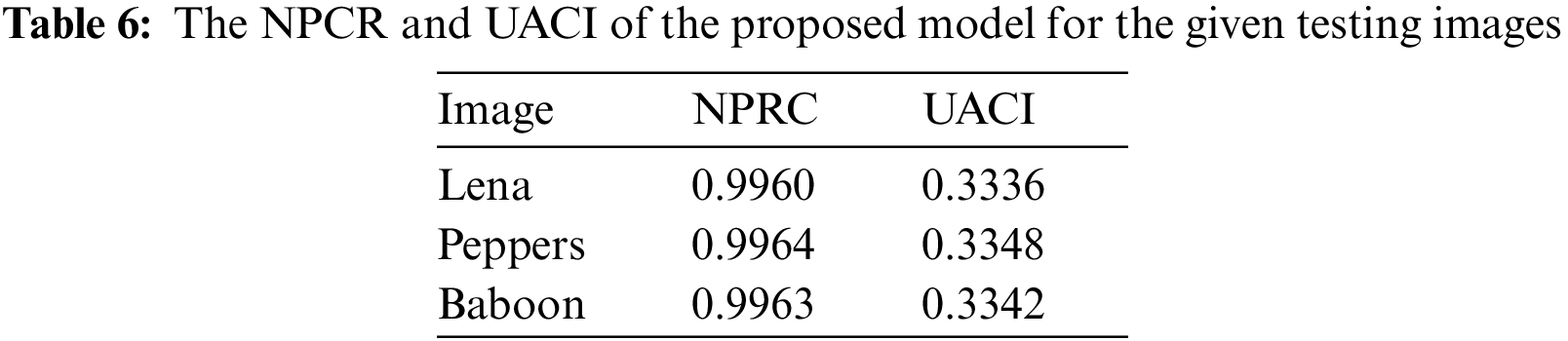
The image encryption algorithm primarily depends on the key sensitivity. Even one bit change to the key combinations can produce a different encrypted image. The two measures used for the key sensitivity analysis are the “Number of Changing Pixel Rate (NPCR) and the Unified Averaged Changed Intensity (UACI)”. The NPCR measures the total distinct pixels between two given images, while UACI represents the average of the intensity. These parameters are defined as follows:

NPRC=[∑i,jN⁡A(i,j)H]×100,(8)

UACI=1H[∑i,jN⁡|G1(i,j)−G2(i,j)|255]×100,(9)

where

A(j,j)={1,(G1(i,j)≠G2(i,j))0,otherwise,(10)

where, G1 and G2 are two pixels with the same coordinates, and H represents the image size.

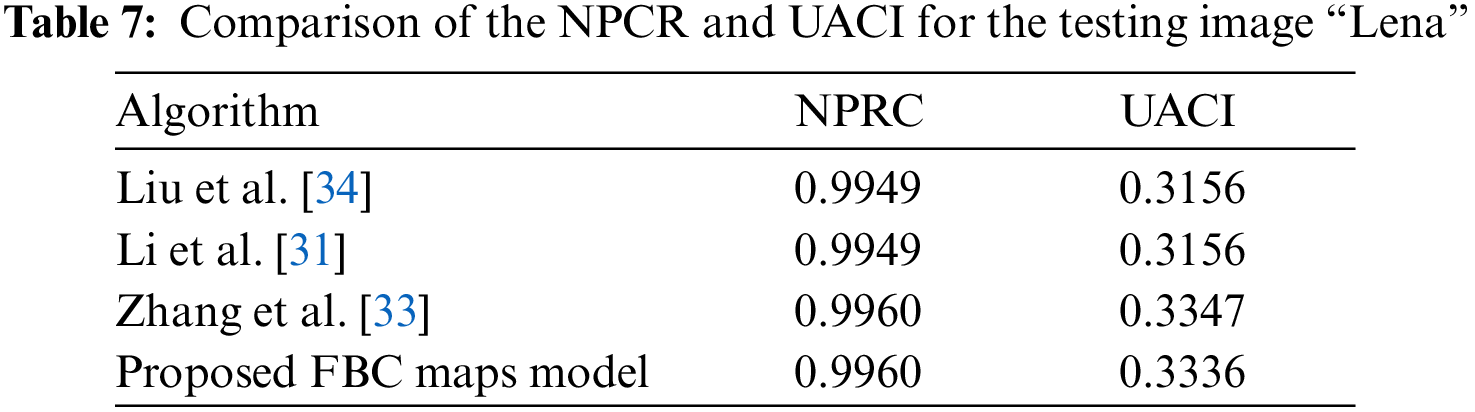
Generally, the NPCR value of a ‘good’ chaotic image encryption model needs to be more than 90% and UACI value more than 33%. Table 6 shows the NPRC and UACI for the proposed FBC maps encryption algorithm. Furthermore, the comparison of NPCR and UACI for the “Lena” image with other algorithms is presented in Table 7. The values of NPCR and UACI for the proposed FBC map method are achieved 0.9960 and 0.3336, respectively, and these values show how closeness to the theoretical values.

4  Conclusion

In this study, a new algorithm of image encryption based on new fractional beta chaotic maps is proposed. All of the experimental results demonstrated that the FBC map algorithm offers a large key space with high sensitivity to all the secret keys. The comparison with other image encryption works indicates that the proposed FBC map model provided the best performance. The proposed FBL map model is preferment and thus valuable for image encryption applications. For future work, further improvements on the encryption system can be assumed including a new fractional chaotic model for image encryption application.

Acknowledgement: The authors would like to thank the editor office for the deep advice to improve our work.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Al-Saidi, N. M., Younus, D., Natiq, H. K. Ariffin, M. R., Asbullah, M. A. et al. (2020). A new hyperchaotic map for a secure communication scheme with an experimental realization. Symmetry, 12(11), 1–17. DOI 10.3390/sym12111881. [Google Scholar] [CrossRef]

 2.  Veeman, D., Natiq, H., Al-Saidi, N. M., Rajagopal, K., Jafari, S. et al. (2021). A new megastable chaotic oscillator with blinking oscillation terms. Complexity, 2021, 1–12. DOI 10.1155/2021/5518633. [Google Scholar] [CrossRef]

 3.  Alhudhaif, A., Ahmad, M., Alkhayyat, A., Tsafack, N., Farhan, A. K. et al. (2021). Block cipher nonlinear confusion components based on New 5-D hyperchaotic system. IEEE Access, 2018, 1–11. DOI 10.1109/ACCESS.2021.3090163. [Google Scholar] [CrossRef]

 4.  Al-Saidi, N. M., Al-Bundi, S. S., Al-Jawari, N. J. (2018). A hybrid of fractal image coding and fractal dimension for an efficient retrieval method. Computational and Applied Mathematics, 37(2), 996–1011. DOI 10.1007/s40314-016-0378-9. [Google Scholar] [CrossRef]

 5.  Zahmoul, R., Ejbali, R., Zaied, M. (2017). Image encryption based on new beta chaotic maps. Optics and Lasers in Engineering, 96, 39–49. DOI 10.1016/j.optlaseng.2017.04.009. [Google Scholar] [CrossRef]

 6.  Al-Shamasneh, A. A. R., Jalab, H. A., Palaiahnakote, S., Obaidellah, U. H., Ibrahim, R. W. et al. (2018). A new local fractional entropy-based model for kidney MRI image enhancement. Entropy, 20(5), 344. DOI 10.3390/e20050344. [Google Scholar] [CrossRef]

 7.  Roy, S., Shivakumara, P., Jalab, H. A., Ibrahim, R. W., Pal, U. et al. (2016). Fractional poisson enhancement model for text detection and recognition in video frames. Pattern Recognition, 52, 433–447. DOI 10.1016/j.patcog.2015.10.011. [Google Scholar] [CrossRef]

 8.  Jalab, H. A., Ibrahim, R. W., Hasan, A. M., Karim, F. K., Al-Shamasneh, A. A. R. et al. (2021). A new medical image enhancement algorithm based on fractional calculus. Computers Materials & Continua, 68(2), 1467–1483. DOI 10.32604/cmc.2021.016047. [Google Scholar] [CrossRef]

 9.  Kilbas, A. A., Srivastava, H. M., Trujillo, J. J. (2006). Theory and applications of fractional differential equations, vol. 204. Singapore: elsevier. [Google Scholar]

10. Zhou, Y., Wang, J., Zhang, L. (2016). Basic theory of fractional differential equations. Germany: World Scientific. [Google Scholar]

11. Gonzalez-Feliu, J., Semet, F., Routhier, J. L. (2014). Sustainable urban logistics: Concepts, methods and information systems, pp. i--iii. Berlin, Heidelberg: Springer Berlin Heidelberg. [Google Scholar]

12. Zhang, G., Ding, W., Li, L. (2020). Image encryption algorithm based on tent delay-sine cascade with logistic map. Symmetry, 12(3), 355. DOI 10.3390/sym12030355. [Google Scholar] [CrossRef]

13. Zhang, Y. Q., Hao, J. L., Wang, X. Y. (2020). An efficient image encryption scheme based on S-boxes and fractional-order differential logistic map. IEEE Access, 8, 54175–54188. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]

14. Ibrahim, R. W., Altulea, D. (2020). Controlled homeodynamic concept using a conformable calculus in artificial biological systems. Chaos, Solitons & Fractals, 140, 110132. DOI 10.1016/j.chaos.2020.110132. [Google Scholar] [CrossRef]

15. Meshram, C., Ibrahim, R. W., Meshram, S. G., Kalare, K. W., Bagde, S. D. (2020). An efficient ID-based cryptographic technique using IFP and GDLP. Security and Privacy, 3(5), e119. DOI 10.1002/spy2.119. [Google Scholar] [CrossRef]

16. Ibrahim, R. W. (2020). A new image denoising model utilizing the conformable fractional calculus for multiplicative noise. SN Applied Sciences, 2(1), 1–11. DOI 10.1007/s42452-019-1718-3. [Google Scholar] [CrossRef]

17. Ibrahim, R. W. (2021). Water engineering modeling controlled by generalized Tsallis entropy. Montes Taurus Journal of Pure and Applied Mathematics, 3(3), 227–237. MTJPAM-D-20-00040. [Google Scholar]

18. Sangavi, V., Thangavel, P. (2019). An image encryption algorithm based on fractal geometry. Procedia Computer Science, 165, 462–469. DOI 10.1016/j.procs.2020.01.007. [Google Scholar] [CrossRef]

19. Wang, X., Gao, S. (2020). Image encryption algorithm based on the matrix semi-tensor product with a compound secret key produced by a Boolean network. Information Sciences, 539, 195–214. DOI 10.1016/j.ins.2020.06.030. [Google Scholar] [CrossRef]

20. Xu, C., Sun, J., Wang, C. (2020). An image encryption algorithm based on random walk and hyperchaotic systems. International Journal of Bifurcation and Chaos, 30(4), 2050060. DOI 10.1142/S0218127420500601. [Google Scholar] [CrossRef]

21. Yu, S. S., Zhou, N. R., Gong, L. H., Nie, Z. (2020). Optical image encryption algorithm based on phase-truncated short-time fractional Fourier transform and hyper-chaotic system. Optics and Lasers in Engineering, 124, 105816. DOI 10.1016/j.optlaseng.2019.105816. [Google Scholar] [CrossRef]

22. Jithin, K. C., Sankar, S. (2020). Colour image encryption algorithm combining Arnold map, DNA sequence operation, and a Mandelbrot set. Journal of Information Security and Applications, 50, 102428. DOI 10.1016/j.jisa.2019.102428. [Google Scholar] [CrossRef]

23. Ul Haq, T., Shah, T. (2020). 12 × 12 S-box design and its application to RGB image encryption. Optik, 217, 164922. DOI 10.1016/j.ijleo.2020.164922. [Google Scholar] [CrossRef]

24. Zhang, D., Chen, L., Li, T. (2021). Hyper-chaotic color image encryption based on transformed zigzag diffusion and RNA operation. Entropy, 23(3), 361. DOI 10.3390/e23030361. [Google Scholar] [CrossRef]

25. Jiao, K., Ye, G., Dong, Y., Huang, X., He, J. (2020). Image encryption scheme based on a generalized arnold map and RSA algorithm. Security and Communication Networks, 2020, 1–14. DOI 10.1155/2020/9721675. [Google Scholar] [CrossRef]

26. Zahmoul, R., Zaied, M. (2016). Toward new family beta maps for chaotic image encryption. 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary. [Google Scholar]

27. Yasser, I., Khalifa, F., Mohamed, M. A., Samrah, A. S. (2020). A new image encryption scheme based on hybrid chaotic maps. Complexity, 2020, 1–23. DOI 10.1155/2020/9597619. [Google Scholar] [CrossRef]

28. Ding, Y., Tan, F., Qin, Z., Cao, M., Choo, K. K. R. et al. (2021). Deepkeygen: A deep learning-based stream cipher generator for medical image encryption and decryption. IEEE Transactions on Neural Networks and Learning Systems, 2021, 1–15. DOI 10.1109/TNNLS.5962385. [Google Scholar] [CrossRef]

29. Musanna, F., Dangwal, D., Kumar, S. (2021). Novel image encryption algorithm using fractional chaos and cellular neural network. Journal of Ambient Intelligence and Humanized Computing, 1, 1–22. DOI 10.1007/s12652-021-02982-8. [Google Scholar] [CrossRef]

30. Kumar, M., Saxena, A., Vuppala, S. S. (2020). A survey on chaos based image encryption techniques. In: Multimedia security using chaotic maps: Principles and methodologies, pp. 1–26. Germany: Springer. [Google Scholar]

31. Li, T., Du, B., Liang, X. (2020). Image encryption algorithm based on logistic and two-dimensional lorenz. IEEE Access, 8, 13792–13805. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]

32. Wang, X., Guo, K. (2014). A new image alternate encryption algorithm based on chaotic map. Nonlinear Dynamics, 76(4), 1943–1950. DOI 10.1007/s11071-014-1259-7. [Google Scholar] [CrossRef]

33. Zhang, F., Zhang, X., Cao, M., Ma, F., Li, Z. (2021). Characteristic analysis of 2D Lag-complex logistic Map and its application in image encryption. IEEE MultiMedia, 2021, 96–106. DOI 10.1109/MMUL.2021.3080579. [Google Scholar] [CrossRef]

34. Liu, L., Miao, S. (2016). A new image encryption algorithm based on logistic chaotic map with varying parameter. SpringerPlus, 5(1), 1–12. DOI 10.1186/s40064-016-1959-1. [Google Scholar] [CrossRef]

35. Rhouma, R., Meherzi, S., Belghith, S. (2009). OCML-Based colour image encryption. Chaos, Solitons & Fractals, 40(1), 309–318. DOI 10.1016/j.chaos.2007.07.083. [Google Scholar] [CrossRef]

36. Tong, X. J., Wang, Z., Zhang, M., Liu, Y., Xu, H. et al. (2015). An image encryption algorithm based on the perturbed high-dimensional chaotic map. Nonlinear Dynamics, 80(3), 1493–1508. DOI 10.1007/s11071-015-1957-9. [Google Scholar] [CrossRef]

37. Kumar, S. (2014). A new analytical modelling for fractional telegraph equation via Laplace transform. Applied Mathematical Modelling, 38(13), 3154–3163. DOI 10.1016/j.apm.2013.11.035. [Google Scholar] [CrossRef]

38. Ghanbari, B., Kumar, S., Kumar, R. (2020). A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative. Chaos, Solitons & Fractals, 133, 1–11. DOI 10.1016/j.chaos.2020.109619. [Google Scholar] [CrossRef]

39. Goufo, E. F. D., Kumar, S., Mugisha, S. B. (2020). Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos, Solitons & Fractals, 130, 1–7. DOI 10.1016/j.chaos.2019.109467. [Google Scholar] [CrossRef]

40. Kumar, S., Kumar, R., Agarwal, R. P., Bessem, S. (2020). A study of fractional Lotka-Volterra population model using Haar wavelet and Adams-Bashforth-Moulton methods. Mathematical Methods in the Applied Sciences, 43(8), 5564–5578. DOI 10.1002/mma.6297. [Google Scholar] [CrossRef]

41. Kumar, S., Surath, G., Bessem, S., Emile, F. (2020). An analysis for heat equations arises in diffusion process using new yang-Abdel-Aty-Cattani fractional operator. Mathematical Methods in the Applied Sciences, 43(9), 6062–6080. DOI 10.1002/mma.6347. [Google Scholar] [CrossRef]

42. Kumar, S., Kumar, R., Cattani, C., Bessem, S. (2020). Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons & Fractals, 135, 1–12. DOI 10.1016/j.chaos.2020.109811. [Google Scholar] [CrossRef]

43. Kumar, S., Ahmadian, A., Kumar, R., Kumar, D., Singh, J. et al. (2020). An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets. Mathematics, 4, 1–22. DOI 10.3390/math8040558. [Google Scholar] [CrossRef]

44. Sheikh, N., Dennis, L., Khan, I., Kumar, D., Kottakkaran, S. (2020). A new model of fractional Casson fluid based on generalized Fick's and Fourier's laws together with heat and mass transfer. Alexandria Engineering Journal, 59(5), 2865–2876. DOI 10.1016/j.aej.2019.12.023. [Google Scholar] [CrossRef]

45. Jumani, T. A., Mustafa, M. W., Hussain, Z., Rasid, M. M., Saeed, M. S. et al. (2020). Jaya optimization algorithm for transient response and stability enhancement of a fractional-order PID based automatic voltage regulator system. Alexandria Engineering Journal, 59(4), 2429–2440. DOI 10.1016/j.aej.2020.03.005. [Google Scholar] [CrossRef]

46. Abro, K. A., Gomez-Aguilar, J. F., Khan, I., Nisar, K. (2019). Role of modern fractional derivatives in an armature-controlled DC servomotor. The European Physical Journal Plus, 134(11), 1–9. DOI 10.1140/epjp/i2019-12957-6. [Google Scholar] [CrossRef]

47. Shaikh, A. S., Nisar, S. (2019). Transmission dynamics of fractional order Typhoid fever model using Caputo–Fabrizio operator. Chaos, Solitons & Fractals, 128, 355–365. DOI 10.1016/j.chaos.2019.08.012. [Google Scholar] [CrossRef]

48. Al-Dhaifallah, M., Nassef, A., Hegazy, R., Nisar, S. (2020). Optimal parameter design of fractional order control based INC-MPPT for PV system. Solar Energy, 159, 650–664. DOI 10.1016/j.solener.2017.11.040. [Google Scholar] [CrossRef]

49. Shaikh, A. S., Iqbal, N. S., Nisar, S. (2020). A mathematical model of COVID-19 using fractional derivative: Outbreak in India with dynamics of transmission and control. Advances in Difference Equations, 2020(1), 1–19. DOI 10.1186/s13662-020-02834-3. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.