
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.019941
ARTICLE
Partial Bell Polynomials, Falling and Rising Factorials, Stirling Numbers, and Combinatorial Identities
1College of Mathematics and Physics, Inner Mongolia Minzu University, Tongliao, 028043, China
2School of Mathematics and Informatics, Henan Polytechnic University, Jiaozuo, 454010, China
3School of Mathematical Sciences, Tiangong University, Tianjin, 300387, China
*Corresponding Authors: Bai-Ni Guo. Email: bai.ni.guo@gmail.com; Feng Qi. Email: qifeng618@gmail.com
Received: 25 October 2021; Accepted: 24 January 2022
Abstract: In the paper, the authors collect, discuss, and find out several connections, equivalences, closed-form formulas, and combinatorial identities concerning partial Bell polynomials, falling factorials, rising factorials, extended binomial coefficients, and the Stirling numbers of the first and second kinds. These results are new, interesting, important, useful, and applicable in combinatorial number theory.
Keywords: Connection; equivalence; closed-form formula; combinatorial identity; partial Bell polynomial; falling factorial; rising factorial; binomial coefficient; Stirling number of the first kind; Stirling number of the second kind; problem
In this paper, we use the notation
The partial Bell polynomials, also known as the Bell polynomials of the second kind, in combinatorics can be denoted and defined by
for
for
The double factorial of negative odd integers −(2k+1) is defined by
The falling factorial
and
respectively. It is easy to verify that
and
See page 167 in [2] and related texts in the paper [3].
The Stirling numbers of the first kind s(n, k) for
and can be explicitly computed (see Corollary 2.3 in [4]) by
for
and can be explicitly computed (see TheoremA on page 204 in [1]) by
For more information on the Stirling numbers of the first and second kinds s(n, k) and S(n, k), please refer to the papers [5,6] and the monographs [7,8].
The extended binomial coefficient
in terms of the falling factorial
On page 206 in [1] and on page 165 in [7], there are two relations
and
The falling factorial
for
In this paper, we will collect, discuss, and find out several connections, equivalences, closed-form formulas, and combinatorial identities concerning partial Bell polynomials
Among the Stirling numbers of the first and second kinds s(n, k) and S(n, k), the falling factorial
Theorem 2.1. For
and
Proof. In Remark 3.1 of [11], the formula
for
for
The formulas (11) and (12) can be rewritten respectively as
and
for
Considering the formulas (6), (7), and (8) in the formulas (12) or (13), we can derive
for
Combining (12), (13), and (14) results in
for
3 Simpler Closed-Form Formulas
When taking
Theorem 3.1. For
and
Proof. By the definition (1), we can easily deduce that, for
where we used the relation (15). See also pages 167–168 in [2]. The identity (16), which recovers the first one in (28) below, is thus proved.
In Theorem 5.1 of [13] and in Section 3 of [14], the formula
was established for
for
In the proof of Theorem 3.2 in [2], it was obtained that
for
Replacing
for
in Section 1.5 of [15] and in Theorem 1.2 of [16], we derive
for
Employing the relation (25) and using the identities
and
in Sections 1.3 and 1.9 of [15] and in Lemma 6 of [17], we acquire
and
The identities (19) and (20) are thus derived. The proof of Theorem 3.1 is complete.
Remark 3.1. We can regard those identities from (17) to (20) in Theorem 3.1 as generalizations of the orthogonality relations
listed on page 171 in [7].
Theorem 3.2. For
and
Proof. Combining (12) and (14) yields
Accordingly, similar to arguments in Lemma 2.2 of [18], we acquire
for
which is a special case x = 0 and
in the formula (1.48) on pages 27–28 of [8], we used the relation (7) twice, and we used the equality
which is a special case r = 1 and p = m of the identity
in the formula (X.5) on page 132 of [8]. Further applying relations in (15), we conclude those relations in (29).
Replacing
Remark 3.2. The last equality in (29) can be rewritten as
Theorem 12.1 on page 171 of [7] reads that, if
Applying Theorem 12.1 on page 171 in [7] to the second equality in (33), we find
Considering the explicit formula (6) and utilizing (31) and (32), we arrive at
for
which is a recovery of the well-known relation
in the equation (1.27) on page 19 of [10].
4 Several Combinatorial Identities
In items (3.163) and (3.164) on pages 91–92 of [8], we find two identities
and
Lemma 2.2 in [18] reads that
We can also find some discussions and alternative proofs for these three identities at the sites https://math.stackexchange.com/q/1098257 and https://math.stackexchange.com/q/4235171.
Theorem 4.1. For
and the identity (34) are valid.
Proof. For the case
For the case
for all
The proof of Theorem 4.1 is complete.
Remark 4.1. The identity (35) can be simplified as
for
The identities (36), (37), and (39) in Theorem 4.1 are probably new.
Theorem 4.2. For
and
Proof. From (29), we conclude that
for
Substituting (21) into (46) gives
The identity (39) is thus proved.
Substituting (23) into (46) results in
The identity (40) is verified.
Utilizing the relations (2) and (5), we can reformulate the identity (26) as
Substituting this equality into (46) arrives at
The formula (41) follows.
Utilizing the relations (2) and (5), we can reformulate the identity (27) as
Substituting this equality into (46) and employing (31) reveal
and
The fourth equality (42) in Theorem 4.2 is thus proved.
Employing (31), we can rearrange the identity (43) as
The equality (43) is deduced.
In Theorem 3.2 of [2], on page 5 in [15], and in Theorem 4.2 of [19], there is the equality
for
for
Combining the last one with the relation
which is obtained by applying
Substituting (24) into (46) leads to
which is a recovery of the formula (44).
For
Letting Sn = ( −1)n22n and sn = ( −1)n2n(n+1), considering (40), applying the inversion theorem expressed by (47), and simplifying figure out the identity (45).
Remark 4.2. The formula (44) is also alternatively established in the proof of Theorem 3.2 in [18] and in Remark 5.3 of [21].
Remark 4.3. The identity (34) established in Lemma 2.2 of [18] and recovered in Theorem 4.1, the identity (36) in Theorem 4.1, and the formula (43) in Theorem 4.2 were announced at https://math.stackexchange.com/a/4268339 and https://math.stackexchange.com/a/4268341 online.
Remark 4.4. In Remark 3.4 of [18], applying the inversion theorem expressed by (47), we obtained
and
5 Several Problems and Numerical Demonstrations
Can one find out simpler closed-form formulas like those in Theorem 3.1 for the quantities
for
By the methods used in this paper, can one find out more combinatorial identities like those in Theorems (4.1) and 4.2?
In general, can one find explicit and closed-form formulas of the quantities
for some special values
For better understanding the above problems, by the Wolfram Mathematica 12, we numerically compute the quantity
for
If fixing k = 4, 5 and n = 7, 8 and regarding
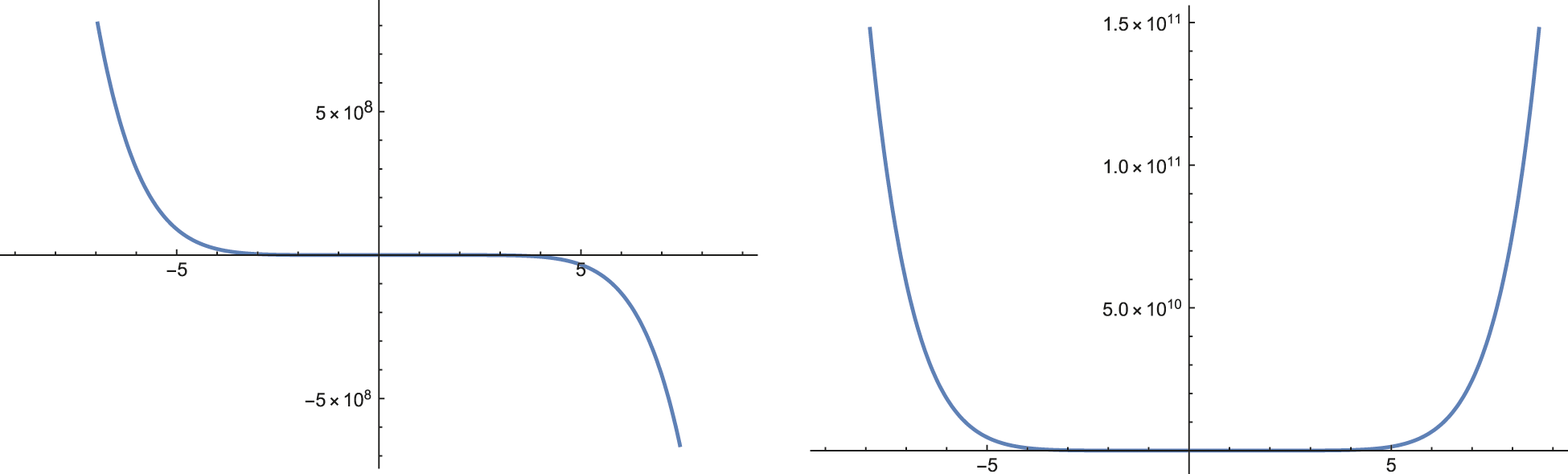
Figure 1: The graphs of
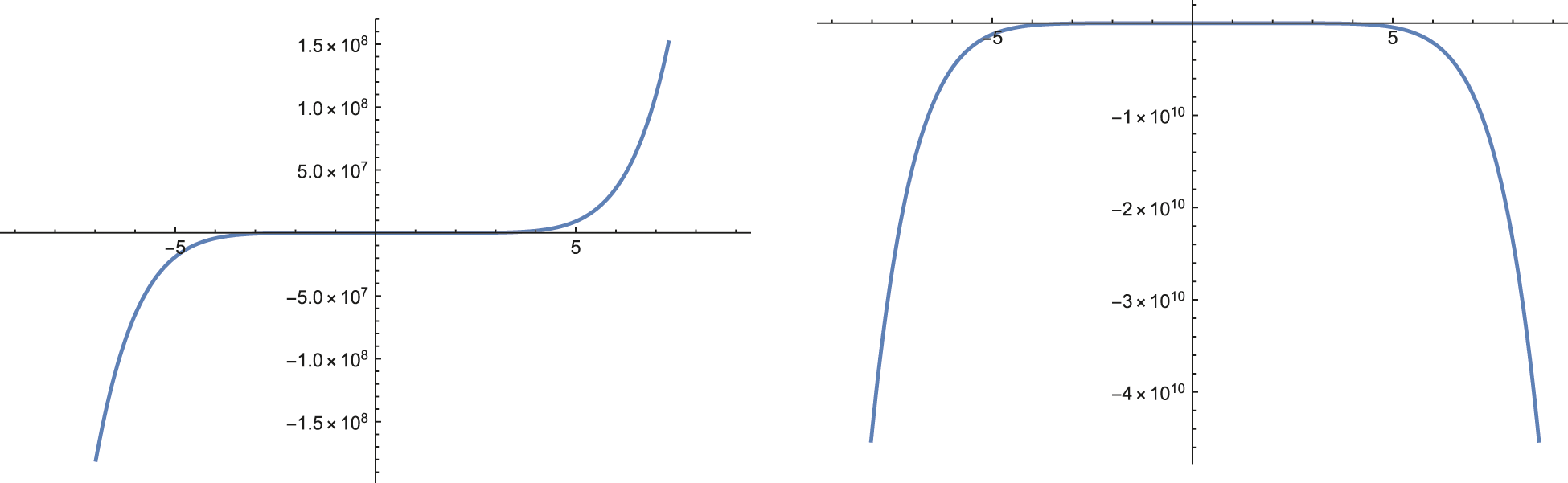
Figure 2: The graphs of
In this paper, we collected, discussed, and found out significant connections, equivalences, closed-form formulas, and combinatorial identities concerning partial Bell polynomials
Acknowledgement: The authors thank anonymous referees for their careful corrections, helpful suggestions, and valuable comments on the original version of this paper.
Funding Statement: This work was supported in part by the National Natural Science Foundation of China (Grant No.12061033), by the Research Program of Science and Technology at Universities of Inner Mongolia Autonomous Region (Grants No. NJZY20119), and by the Natural Science Foundation of Inner Mongolia (Grant No. 2019MS01007), China.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Comtet, L. (1974). Advanced combinatorics: The art of finite and infinite Expansions. Revised and Enlarged Edition. D. Reidel Publishing Co., Dordrecht–Boston. [Google Scholar]
2. Qi, F., Niu, D. W., Lim, D., Guo, B. N. (2020). Closed formulas and identities for the bell polynomials and falling factorials. Contributions to Discrete Mathematics, 15(1), 163–174. DOI 10.11575/cdm.v15i1.68111. [Google Scholar] [CrossRef]
3. Qi, F., Shi, X. T., Liu, F. F. (2016). Several identities involving the falling and rising factorials and the Cauchy. Lah, and stirling numbers. Acta Universitatis Sapientiae Mathematica, 8(2), 282–297. DOI 10.1515/ausm-2016-0019. [Google Scholar] [CrossRef]
4. Qi, F. (2014). Explicit formulas for computing Bernoulli numbers of the second kind and stirling numbers of the first kind. Filomat, 28(2), 319–327. DOI 10.2298/FIL1402319O. [Google Scholar] [CrossRef]
5. Qi, F., Guo, B. N. (2018). A diagonal recurrence relation for the stirling numbers of the first kind. Applicable Analysis and Discrete Mathematics, 12(1), 153–165. DOI 10.2298/AADM170405004Q. [Google Scholar] [CrossRef]
6. Qi, F., Lim, D., Guo, B. N. (2018). Some identities related to eulerian polynomials and involving the stirling numbers. Applicable Analysis and Discrete Mathematics, 12(2), 467–480. DOI 10.2298/AADM171008014Q. [Google Scholar] [CrossRef]
7. Quaintance, J., Gould, H. W. (2016). Combinatorial identities for stirling numbers (The unpublished notes of H. W. Gould. With a foreword by George E. Andrews). Singapore: World Scientific Publishing Co. Pte., Ltd. [Google Scholar]
8. Sprugnoli, R. (2006). Riordan array proofs of identities in gould’s book. Italy: University of Florence. [Google Scholar]
9. Wei, C. F. (2022). Integral representations and inequalities of extended central binomial coefficient. In: Mathematical methods in the applied sciences (in Press). DOI 10.1002/mma.8115. [Google Scholar] [CrossRef]
10. Temme, N. M. (1996). Special functions: An introduction to classical functions of mathematical physics. New York: A Wiley-Interscience Publication, John Wiley & Sons, Inc. [Google Scholar]
11. Guo, B. N., Qi, F. (2021). Viewing some ordinary differential equations from the angle of derivative polynomials. Iranian Journal of Mathematical Sciences and Informatics, 16(1), 77–95. DOI 10.29252/ijmsi.16.1.77. [Google Scholar] [CrossRef]
12. Guo, B. N., Lim, D., Qi, F. (2022). Maclaurin’s series expansions for positive integer powers of inverse (hyperbolic) sine and tangent functions, closed-form formula of specific partial Bell polynomials, and series representation of generalized logsine function. Applicable Analysis and Discrete Mathematics, 16(1). [Google Scholar]
13. Qi, F., Guo, B. N. (2017). Explicit formulas for special values of the bell polynomials of the second kind and for the euler numbers and polynomials. Mediterranean Journal of Mathematics, 14(3), 140, DOI 10.1007/s00009-017-0939-1. [Google Scholar] [CrossRef]
14. Qi, F., Zheng, M. M. (2015). Explicit expressions for a family of the bell polynomials and applications. Applied Mathematics and Computation, 258, 597–607. DOI 10.1016/j.amc.2015.02.027. [Google Scholar] [CrossRef]
15. Qi, F., Niu, D. W., Lim, D., Yao, Y. H. (2020). Special values of the bell polynomials of the second kind for some sequences and functions. Journal of Mathematical Analysis and Applications, 491(2), 124382. DOI 10.1016/j.jmaa.2020.124382. [Google Scholar] [CrossRef]
16. Qi, F., Shi, X. T., Liu, F. F., Kruchinin, D. V. (2017). Several formulas for special values of the bell polynomials of the second kind and applications. Journal of Applied Analysis and Computation, 7(3), 857–871. DOI 10.11948/2017054. [Google Scholar] [CrossRef]
17. Qi, F., Shi, X. T., Guo, B. N. (2016). Two explicit formulas of the schröder numbers. Integers, 16. DOI 10.13140/RG.2.1.2676.3283. [Google Scholar] [CrossRef]
18. Qi, F., Ward, M. D. (2021). Closed-form formulas and properties of coefficients in maclaurin’s series expansion of Wilf’s function. https://arxiv.org/abs/2110.08576v1. [Google Scholar]
19. Qi, F., Wu, G. S., Guo, B. N. (2019). An alternative proof of a closed formula for central factorial numbers of the second kind. Turkish Journal of Analysis and Number Theory, 7(2), 56–58. DOI 10.12691/tjant-7-2-5. [Google Scholar] [CrossRef]
20. Qi, F., Zou, Q., Guo, B. N. (2019). The inverse of a triangular matrix and several identities of the Catalan numbers. Applicable Analysis and Discrete Mathematics, 13(2), 518–541. DOI 10.2298/AADM190118018Q. [Google Scholar] [CrossRef]
21. Li, W. H., Qi, F., Kouba, O., Kaddoura, I. (2021). A further generalization of the Catalan numbers and its explicit formula and integral representation. Authorea. DOI 10.22541/au.159844115.58373405/v3. [Google Scholar] [CrossRef]
22. Duran, U., Araci, S., Acikgoz, M. (2021). Bell-based Bernoulli polynomials with applications. Axioms, 10(1), 29. DOI 10.3390/axioms10010029. [Google Scholar] [CrossRef]
23. K¡x0131/¿z¡x0131/¿lateş, C. (2021). New families of horadam numbers associated with finite operators and their applications. Mathematical Methods in the Applied Sciences, 44(18), 14371–14381. DOI 10.1002/mma.7702. [Google Scholar] [CrossRef]
24. K¡x0131/¿z¡x0131/¿lateş, C., Du, W. S., Qi, F. (2022). Several determinantal expressions of generalized tribonacci polynomials and sequences. Tamkang Journal of Mathematics, 53 (in Press). DOI 10.5556/j.tkjm.53.2022.3743. [Google Scholar] [CrossRef]
25. Qi, F., K¡x0131/¿z¡x0131/¿lateş, C., Du, W. S. (2019). A closed formula for the horadam polynomials in terms of a tridiagonal determinant. Symmetry, 11(6), 782. DOI 10.3390/sym11060782. [Google Scholar] [CrossRef]
26. Wang, Y., Dağl¡x0131/¿, M. C., Liu, X. M., Qi, F. (2021). Explicit, determinantal, and recurrent formulas of generalized eulerian polynomials. Axioms, 10(137. DOI 10.3390/axioms10010037. [Google Scholar] [CrossRef]
27. Xie, C., He, Y. (2021). New expressions for sums of products of the Catalan numbers. Axioms, 10(4), 330. DOI 10.3390/axioms10040330. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |