
 | Computer Modeling in Engineering & Sciences |  |
DOI: 10.32604/cmes.2022.020598
ARTICLE
Group Decision-Making Method with Incomplete Intuitionistic Fuzzy Preference Relations Based on a Generalized Multiplicative Consistent Concept
1School of Computer Science, Qinghai Normal University, Xining, 810008, China
2School of Science, Shanghai Institute of Technology, Shanghai, 201418, China
3School of Statistics, Jiangxi University of Finance and Economics, Nanchang, 330013, China
4School of Information Technology, Jiangxi University of Finance and Economics, Nanchang, 330013, China
∗Corresponding Author: Jiuying Dong. Email: jiuyingdong@126.com
Received: 02 December 2021; Accepted: 26 January 2022
Abstract: Based on the analyses of existing preference group decision-making (PGDM) methods with intuitionistic fuzzy preference relations (IFPRs), we present a new PGDM framework with incomplete IFPRs. A generalized multiplicative consistent for IFPRs is defined, and a mathematical programming model is constructed to supplement the missing values in incomplete IFPRs. Moreover, in this study, another mathematical programming model is constructed to improve the consistency level of unacceptably multiplicative consistent IFPRs. For group decision-making (GDM) with incomplete IFPRs, three reliable sources influencing the weights of experts are identified. Subsequently, a method for determining the weights of experts is developed by simultaneously considering three reliable sources. Furthermore, a targeted consensus process (CPR) is developed in this study with reference to the actual situation of the consensus level of each IFPR. Meanwhile, in response to the proposed multiplicative consistency definition, a novel method for determining the optimal priority weights of alternatives is redefined. Lastly, based on the above theory, a novel GDM method with incomplete IFPRs is developed, and the comparative and sensitivity analysis results demonstrate the utility and superiority of this work.
Keywords: Intuitionistic fuzzy preference relations; multiplicative consistency; consensus; optimization model; group decision-making
Multi-attribute decision-making (MADM) aims to identify the best alternative from a set of finite feasible alternatives by considering multiple attributes that are used extensively in numerous fields of modern life [1–3]. However, because of the many evaluation factors of complex decision-making problems, it is difficult for experts to provide a corresponding evaluation value for each factor, leading to the emergence of preference DMs (PDMs) [4,5]. The PDM is used to identify the best alternative from a set of finite feasible alternatives using preference relations (PRs) between alternatives offered by experts, which is simpler and more convenient than MADM. PR is a form of pairwise comparison between alternatives, and was initially reported by Saaty [6] in the analytic hierarchy process. Since PRs are highly consistent with people’s evaluation habits and experts can provide them easily, consequently, PDM has received widespread attention in recent years. Currently, there are two primary types of PRs, i.e., additive preference relations [7] and multiplicative preference relations [8]. With extensive research on PDM, many derivatives of the two PRs have emerged through the intervention of various fuzzy sets, such as interval fuzzy preference relations (IVFPRs) [9,10], intuitionistic fuzzy preference relations (IFPRs) [11], intuitionistic multiplicative preference relations (IMPRs) [12], complex intuitionistic fuzzy preference relations (CIFPRs) [13], hesitant fuzzy preference relations (HFPRs) [14], probabilistic hesitant fuzzy preference relations (PHFPRs) [15], etc. [16]. Among them, since IFPRs can express the pairwise comparison between alternatives from the following three dimensions: affirmative, negative, and hesitant, IFPRs are more popular in group decision-making (GDM) when expressing the pairwise comparison between alternatives with uncertain information. Therefore, GDM with IFPRs is an interesting topic. Generally, it is necessary to perform three processes for GDM with IFPRs. First, the consistency of IFPRs is an essential issue in GDM, the quality of which directly affects the reasonability and acceptability of the final DM result. Researches related to the consistency of IFPRs in GDM includes how to define, check, and repair the consistency. Second, the consensus among individual IFPRs is another crucial issue in GDM with IFPRs, the quality of which directly impacts the recognition and acceptance of the final DM result by all members in the group. Researches related to consensus in GDM with IFPRs includes checking and improving the consensus. In addition to the above two issues, the ranking process of alternatives is the third issue that must be solved in GDM with IFPRs. Research on the ranking process of alternatives primarily refers to the selection of a reasonable method for determining the priority weight vector of the alternatives. Although many achievements have been made in the research on GDM with IFPRs, these methods are imperfect for numerous reasons. Therefore, this study continued to study GDM with IFPRs.
The remainder of the paper is organized as follows. Section 2 briefly recalls the literature review of GDM with IFPRs. This section also resumes the research motivations, novelties and research methodology of this study. In Section 3, the concepts regarding IFPRs are reviewed. In Section 4 a generalized multiplicative consistency definition of IFPRs is presented. Section 5 constructs respectively two mathematically programming models to supplement the default values in incomplete IFPRs and improve the consistency level of the unacceptably consistent IFPRs. After that develops a new consistency improving method with incomplete IFPRs. Section 6 introduces a new method of generating the experts’ weights, and then designs a targeted CPR and develops a method determining priority weight vector of alternatives. Further, based on the above theoretical basics, a new GDM method with incomplete IFPRs is developed. In Section 7, an application example is supplied to verify the practicability of the method presented in this study, comparative and sensitivity analysis result shows the advantages of this method. Concluding remarks are given in Section 8.
As an extension of the conventional fuzzy set portrayed by Atanassov [17], the intuitionistic fuzzy set (IFS) theory uses three-dimensional (3D) degrees to characterize the experts’ positive, negative, and indeterminate cognitions. Owing to its robust advantages in describing the uncertainty and vagueness of human thinking, the IFS has received special attention in the field of DM. Therefore, many DM methods based on the IFS have also been developed. For instance, Liao et al. manifested the intuitionistic fuzzy Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE) [18], Liao et al. [19] extended Analytic Network Process (ANP) into intuitionistic fuzzy environments and developed the intuitionistic ANP (IFANP) method, and Wan et al. [20] introduced the Best-worst method with IFPRs, and Efe [21] proposed IF modelling-based risk assessment approaches using IF numbers-based quality function deployment (QFD) and VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) technique. Stanujkić et al. [22] proposed a new extension of the WASPAS method for DM problems with intuitionistic fuzzy numbers. Moreover, Kushwaha et al. [23] presented an integrated framework based on Intuitionistic Fuzzy-Failure Mode Effect Analysis (IF-FMEA) and IF-Technique for Order Preference by Similarity to Ideal Solution (IF-TOPSIS) techniques to rank the listed failure causes, etc. Among the methods based on IFS for handling DM problems, the DM method based on IFPRs is one of the fundamental and efficient methods for modeling DM issues. In recent years, many achievements have been made regarding DM with IFPRs. Xu et al. [24] developed a consensus analysis method for GDM with IFPRs based on a defined similarity measure between IFSs. Xu et al. [25] first presented the multiplicative consistency definition and used it to estimate probable missing elements in an incomplete IFPR, after which they developed a GDM method with incomplete IFPRs. Based on the consistency definition [25], Xu et al. [26] developed an approach to enhance the consistency level of unacceptably consistent IFPRs and extended the classic analytic hierarchy process (AHP) into intuitionistic fuzzy AHP (IFAHP). Furthermore, Liao et al. [27] found that the multiplicative consistency condition proposed in [25] conflicts with Saaty’s multiplicative transitivity property because of stringent constraints and proposed a general multiplicative consistency definition of IFPRs and developed a novel approach to derive the priority weights from an IFPR. Based on the multiplicative consistency definition presented in [27], Liao et al. [28] devised an iterative algorithm to enhance the consistency level of IFPRs, and then presented an interesting consensus reaching process, and Xu et al. [29] constructed an optimization model to repair the consistency of the unacceptably consistent IFPRs and developed a GDM method with IFPRs by simultaneously considering the acceptable consensus and consistency. Jin et al. [30] developed a novel approach to derive the priority weights from an IFPR and proposed a GDM method with IFPRs. In addition, according to the isomorphism between IVFPRs and IFPRs, Gong et al. [31] introduced the definition of multiplicative consistent IFPR, based on which the intuitionistic fuzzy priority weight vector (IFPWV) was produced through some goal programming models. Moreover, Wu et al. [32] initiated multiplicative consistency of IFPRs by a proposed multiplicative consistency definition for IVFPRs, and designed a consistency and consensus improving method based on feedback mechanism. Based on the multiplicative consistency of IFPRs presented in [32], Wu et al. [33] constructed a multiplicative consistency-based multi-objective programming (MOP) model to derive the priority vector from an IFPR. More recently, Meng et al. [34] provided an innovative multiplicative consistency definition of IFPRs based on the quasi-interval-based transitivity equation of IVFPRs and constructed a consensus model to enhance consensus among experts. Based on Krejčí [35] multiplicative consistency definition of IVFPRs, Meng et al. [36] redefined the multiplicative consistency of IFPRs, and Wang [37] presented a novel multiplicative consistency definition of IFPRs and developed a representable uninorm based IFAHP.
The literature reviews reveal that the above mentioned achievements are effective in dealing with real DM problems; however, there are some gaps in the following aspects, which can be summarized as follows:
(1) The first gap obtained from existing studies is in terms of consistency management in GDM with IFPRs. In [24], the multiplicative consistency of individual IFPRs was not considered, which could lead to an unreasonable DM result. In [37], Wang pointed out that these multiplicative consistency definitions for IFPRs presented in [25,27,32] are not intuitionistic fuzzy extensions of Tanino’s multiplicative consistency. Therefore, the DM outcomes obtained by GDM methods [28,29,32], which were respectively developed based on the consistency definitions in [25,27,32] may lack rationality and persuasiveness. Moreover, because the GDM method with IFPRs [34] is developed based on complete multiplicative consistency, and the DM result is produced at the cost of a large amount of original information loss (it can be seen from the comparative analysis in Section 6). For GDM methods [30,31], the consistency of the IFPRs has not been considered. Given the shortcomings of consistency management in GDM with IFPRs [25,27–29,32,34], it is essential to present a more reasonable consistency management framework for GDM with IFPRs, which is the first motivation of this study.
(2) The second gap obtained from existing studies is in terms of the method of determining the weights of experts. In these methods [24,25,28,30,31], the experts’ weights are assigned in advance, which makes it difficult to avoid subjective randomness. In [29], the experts’ weights were derived by simultaneously considering the consistency index and confidence degree. In [32], experts’ weights were derived by considering the consistency index. In [34], experts’ weights were derived by considering the degree of confidence. Although these methods determine experts’ weights in [29,32,34] effectively avoid the subjective randomness of the experts’ weights, they only consider one or two aspects affecting experts’ weights. In fact, some factors, such as the hesitancy degree of the IFPRs and the ability to retain the original information, have a greater impact on the experts’ weights. In view of this fact, it is essential to propose a method determining the experts’ weights that comprehensively considers these aspects, which is the second motivation of this research.
(3) The third gap obtained from existing studies is in terms of the consensus-reaching process (CRP) in GDM with IFPRs. In the methods [25,30,31], group consensus among experts was not considered. In [24,28,32,34], the information loss of the original individual IFPRs was ignored in CRP. In [29], although the information loss of the original individual IFPRs has gained attention, the adjustments for individual IFPRs were accomplished by modifying all individual IFPRs via an optimization model, which illustrates the adjustment without the target. Thus, the final adjusted individual IFPRs may not be optimal in terms of preserving the original information (it is evident from the comparative analysis in Section 6). In view of the shortcomings of the CRP proposed in [24,28–32,34], it is essential to develop a more reasonable consensus-improving method, which is the third motivation of this study.
(4) The fourth gap obtained from existing studies exist in terms of the method employed for obtaining the priority weights of alternatives. In the methods [25,28,29,32,34], the priority weights of alternatives have been primarily determined by some aggregation operator; however, for some situations, it may cause a number of information losses if this method is adopted. However, although the priority weights of alternatives are derived by the optimization model in [27,30,31], which effectively prevents the loss of information, the DM result may lack persuasiveness because the priority weights of alternatives are generated based on the group IFPR without checking the consistency. In view of the shortcomings of methods for obtaining the priority weights of alternatives in [25,27–32,34], it is necessary to develop a more reasonable method to obtain the priority weights of alternatives, which is the fourth motivation of this study.
To bridge the above four research motivations, this study aims to develop a novel GDM method using IFPRs, the key novelties of which are listed below:
(1) A more generalized multiplicative consistency definition for IFPRs is presented, which compensates for the defects of the existing multiplicative consistency definitions for IFPRs. Furthermore, a more reasonable consistency management framework for GDM with IFPRs is presented, in which the acceptable multiplicative consistency of individual IFPRs is considered.
(2) Three reliable sources influencing experts’ weights were first identified by analyzing the factors affecting experts’ weights, and a method of determining experts’ weights was developed by simultaneously considering three reliable sources.
(3) A targeted consensus-improving method is developed by which the individual IFPRs obtained retain the original information to the greatest extent while achieving an acceptable consensus and consistency level.
(4) The priority weights of the alternatives were derived from the acceptably multiplicative consistent IVFPR via the optimization model, which prevents information loss and enhances the persuasiveness of the obtained DM result.
To achieve the goal mentioned above, the research methodology for the present study is shown in Fig. 1.
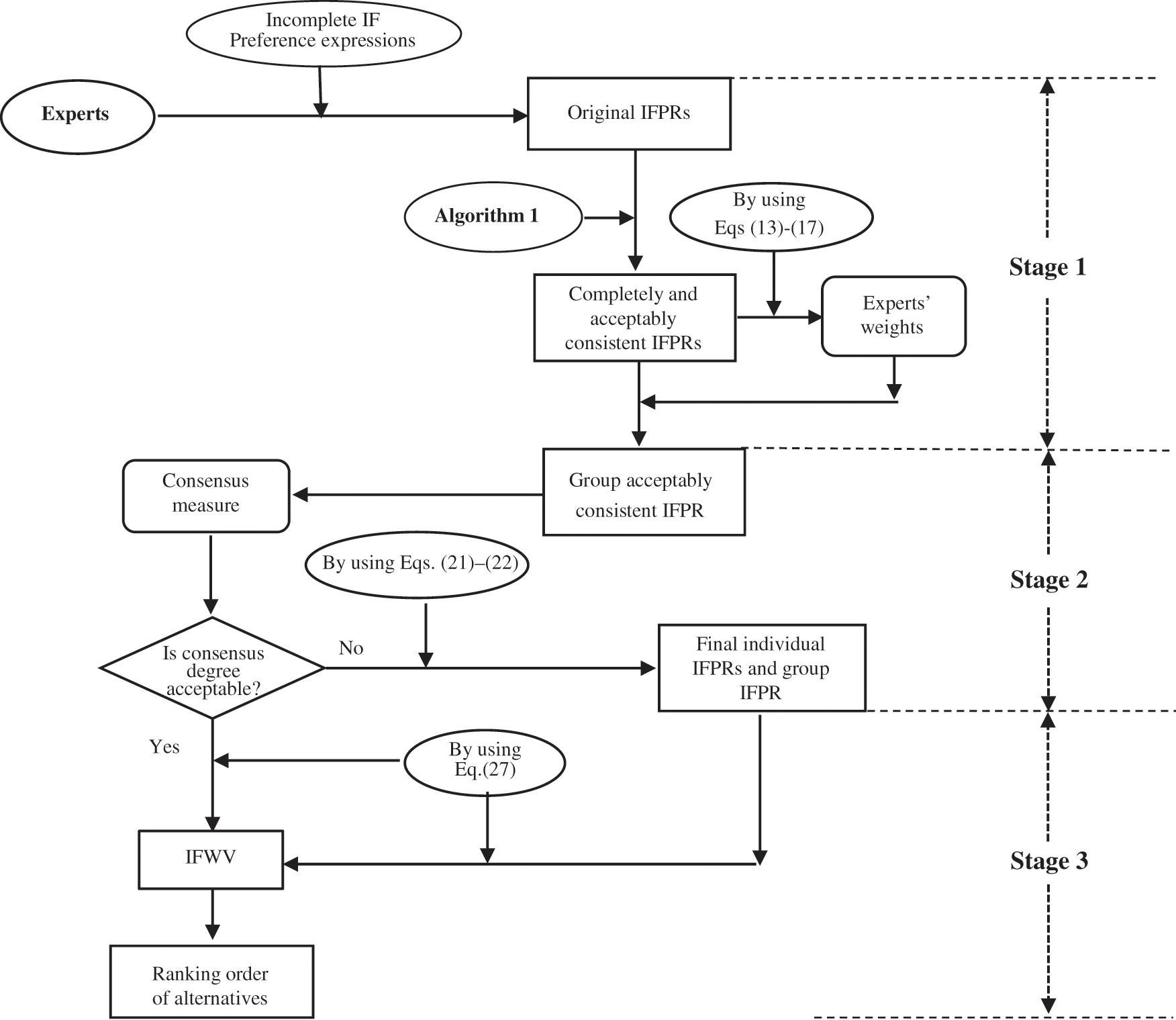
Figure 1: Research methodology
Stage 1: Consistency improving phase: Based on the proposed multiplicative consistency definition for IFPRs, two mathematical programming models are respectively constructed to supplement the default values in incomplete IFPRs and improve the consistency level of unacceptably consistent IFPRs.
Stage 2: Consensus improving phase: This stage introduces a new method of generating experts’ weights, and then designs a targeted consensus improving method to enhance the consensus level of individual IFPRs.
Stage 3: Exploitation phase: Based on the proposed multiplicative consistency definition for IFPRs, a method determining the priority weights of alternatives is developed.
This section mainly reviews some relevant concepts of IFSs and IFPRs. Let
Definition 3.1. [17] Assume that
In addition, Xu et al. [38] introduced the intuitionistic fuzzy number (IFN), which is generally denoted as
Definition 3.2. [39] Assume that
Definition 3.3. [11] Let
4 A New Multiplicative Consistency Framework for IFPRs
In this section, based on the multiplicative consistency definition for IFPRs proposed by Meng et al. [36], a new consistency index for IFPRs is first defined, after which the corresponding acceptably multiplicative consistency definition for IFPRs is presented.
Definition 4.1. [36] Let
Then
Property 4.1. [36] Let
Then
Since
By taking the logarithm on both sides of Eq. (4), we can obtain
It should be noted that Eq. (5) holds only when the IFPR
where the symbol “
then Eq. (6) can be rewritten as
where
In what follows, based on the above linear membership functions for fuzzy constraint given in Eq. (7), a new multiplicative consistency index to quantify the multiplicative consistency level of IFPRs is presented.
Definition 4.2. Let
where
Remark 4.1. It is apparent that
Definition 4.3. Let
However, due to the complexity and uncertainty of DM problems involved in real life, it is not an easy thing for experts to provide acceptably consistent IFPRs. For these unacceptably consistent IFPRs, generally, the judgments of IFPRs needs to be adjusted by establishing related optimization model to make the IFPRs reach an acceptable consistency level.
5 A New Method for Improving the Consistency of the Incomplete IFPRs
It is common to encounter information default in DM because of experts’ limited expertise and time pressure or the complex DM environment. Therefore, it is very necessary to present an effective method to deal with the DM problems with incomplete information under intuitionistic fuzzy context. To do this, we first need to supplement these missing values. In this section, based on the above multiplicative consistency measure concept, the missing values in an incomplete IFPR are estimated by constructing related optimization model.
5.1 Optimization Model for Estimating Missing Values in Incomplete IFPRs
Before constructing the optimization model to estimate missing values in incomplete IFPRs, the relevant concepts for incomplete IFPRs are first introduced in the following.
Definition 5.1. Let
In this paper,
Definition 5.2. Let
In fact, for an incomplete IFPR
where
5.2 Optimization Model for Improving Consistency Level of Complete IFPRs
The consistency level of PR has a crucial impact on the final DM result. It happens too often that an unreasonable DM result may be generated from a PR with poor consistency. In fact, a complete IFPR
where
To solve Eq. (11) conveniently, let
By solving Eq. (12), we can obtain the optimal solutions
5.3 Algorithm Description for Obtaining the Acceptably Multiplicative Consistent IFPRs
Based on the above theory, a new method for obtaining the acceptably multiplicative consistent IFPRs is brought forward as follows:

It is well known that in real life, when facing a complex DM problem, experts or scholars from related fields are usually invited to make decisions collectively, namely, GDM. This section focuses on introducing a new GDM method with incomplete IFPRs. To this end, two parts need to be completed: derivation of experts’ weights and consensus improvement. Without loss of generality, assume that
6.1 Derivation of Experts’ Weights
After obtaining the individual acceptably multiplicative consistent IFPR
Generally, the degree of confidence reflects the degree of support from other experts. An expert with a higher confidence degree should be given a larger weight, whereas an expert with a lower confidence degree should be allocated less weight. Moreover, the confidence index
The similarity between the original complete IFPR obtained by solving Eq. (10) (or given by experts) and the acceptably multiplicative consistent IFPR obtained by solving Eq. (11) reflects the degree to which the adjusted IFPR retains original information. More specifically, the larger the deviation, the lesser weight given to the expert, whereas the smaller the deviation degree, the more weight given to the expert. In general, the similarity index between
Furthermore, the hesitancy degree of the IFPR provided by an expert was considered an expert feature. The smaller the hesitancy of the IFPR, the more the weight given to the expert, whereas the bigger the hesitancy of the IFPR, the lesser the weight given to the expert. In general, the hesitancy index of IFPR
Based on the above three reliable sources influencing experts’ weights, a comprehensive index of expert
Let
Consensus measures applied to quantify the recognition degree of individual opinions among a group of experts are divided into two types [41]: (1) based on the distance to the group PR [42] and (2) based on the distance between experts’ PRs [43]. Without loss of generality, the first type is employed in this study to measure the consensus level among individual IFPRs. Prior to presenting the consensus measure concept, we first introduce the calculation of the group IFPRs.
Theorem 6.1. [44] Let
where
Theorem 6.2. Let
Proof: As per Eqs. (9) and (18), we have
Since
Therefore,
Remark 6.1. Theorem 6.2 shows that the prerequisite for a group IFPR to be acceptably multiplicative consistent is that all of individual IFPRs used to aggregate into it by Eq. (18) must be acceptably multiplicative consistent. Furthermore, according to Theorem 6. 2, we can also obtain that if all of individual IFPRs are completely multiplicative consistent, then the group IFPR aggregated by these individual IFPRs is completely multiplicative consistent.
6.2 Consensus Improving Process for GDM with IFPRs
In what follows, based on the group IFPR, we first give the concept of consensus measure of the individual IFPRs. Then, a mathematical programming model is constructed to improve the consensus level of individual IFPRs which do not meet the requirement of consensus.
Definition 6.3. Let
Clearly, it is
Property 6.1. Let
Proof: First, we proof
In addition, since
Furthermore, as per
Therefore, according to Definition 3.3,
As per Eqs. (9) and (20), we have
Since
Based on above analysis, to improve the consensus level of all acceptably multiplicative consistent individual IFPRs, we construct the following mathematical programming model:
where
To solve Eq. (21) conveniently, let
By solving model (22), the optimal solutions
6.3 Deriving the Priority Weights of Alternatives from an IFPR
The determination of the weight vector of alternatives from an IFPR is a necessary step in GDM with IFPRs. In what follows, a new way for obtaining IFPWV of IFPR based on Definition 4.2 is developed.
Definition 6.4. [45] Let
Then
Based on the normalized IFPWV, a new matrix
Theorem 6.3. Let
Proof: First, we prove the matrix
As
According to Property 4.1,
Corollary 6.1. Let
then
Furthermore, since
Obviously, as per Corollary 6.1, an IFPR
The smaller the deviations, the better the multiplicative consistent level of judgement. Therefore, we construct the following linear program model to derive an IFPWV from an acceptably multiplicative consistent IFPR
solving Eq. (27), the IFPWs
6.4 Algorithm Description for GDM with Incomplete IFPRs
Based on the above theoretical basis, in what follows, a new GDM method with incomplete IFPRs is brought forward to derive ranking order of alternatives.
Remark 6.2. If Steps 5 to 6 in Algorithm 2 are omitted, then Algorithm 2 become an algorithm for individual DM method with incomplete IFPR. In addition, we find the individual IFPRs obtained by Algorithm 2 satisfy the requirements of acceptable consensus and consistency, and the group IFPR obtained by Algorithm 2 is acceptably consistent. Therefore, the DM result obtained by Algorithm 2 is reasonable and persuasive.

7 Numerical Examples and Comparison Analyses
In this section, several numerical examples are given to illustrate the effectiveness of this method in solving practical GDM problems, after which the advantages of this method are illustrated by comparative and sensitivity analysis results.
7.1 Example and Comparison Analyses for GDM with IFPR
Example 7.1. With the progress and development of the society, great changes have taken place in our lives. Urban traffic congestion is one of the phenomena caused by this change. The traffic congestion and even chaos caused by the increase of traffic facilities in cities have brought great inconvenience to people’ s life, this inconvenience forces people to find high-tech and effective means to solve this inconvenience. The intelligent parking lot is a high-tech product that meets the needs of this era. To effectively solve the traffic chaos caused by random parking, The head of Guanghua Community plans to install a parking lot computer charging management system in the near future. After earlier period inspection and analysis, four alternative systems are preliminarily determined, namely,
Step 1: Let

Step 2: Use Eqs. (13)–(17) to determine the experts’ weights as:
Step 3: Let
Step 4: Use Eqs. (21) and (22) to obtain the adjusted individual IFPRs
Step 5: Use Eq. (27) to derive the group IFPWVs from
Step 6: Calculate the similarity measures
Different values of tolerance parameters may bring diverse DM results. Therefore, it is necessary to conduct sensitivity analyses. Tables 2 and 3 represent the obtained missing values and the consistency degrees of the corresponding complete IFPRs under different values of tolerance parameters
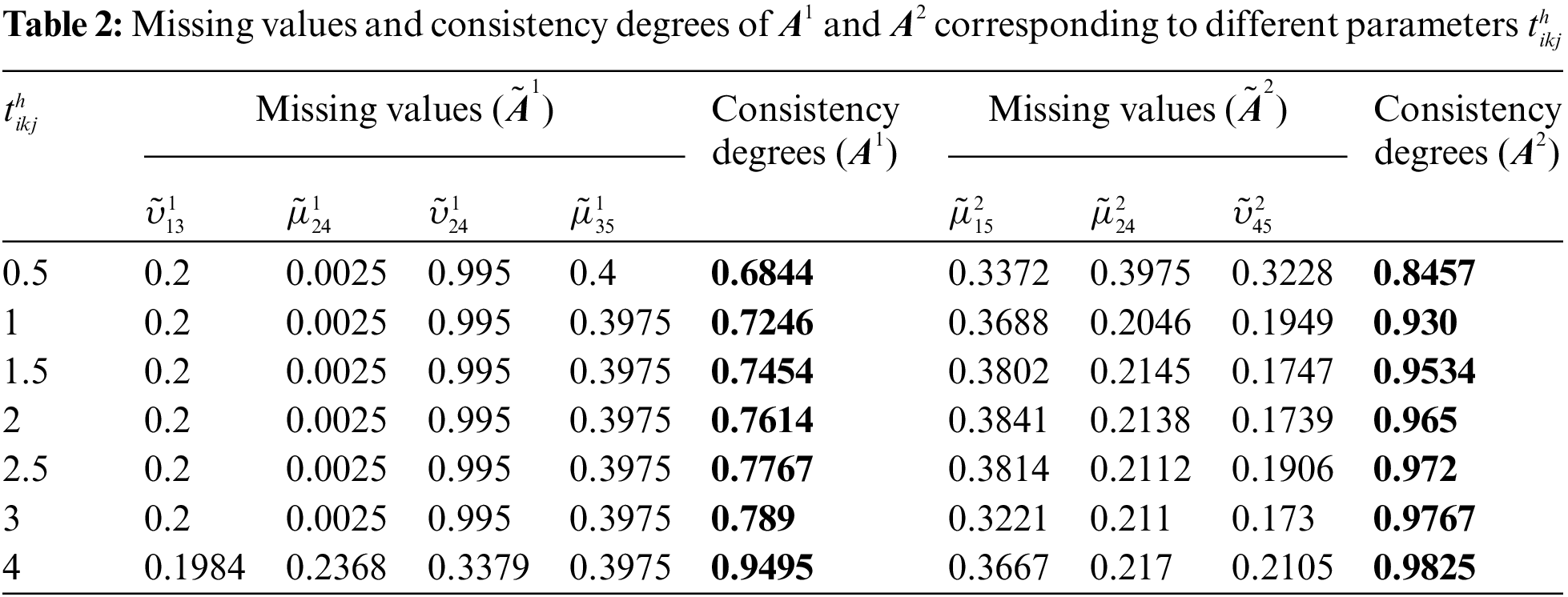
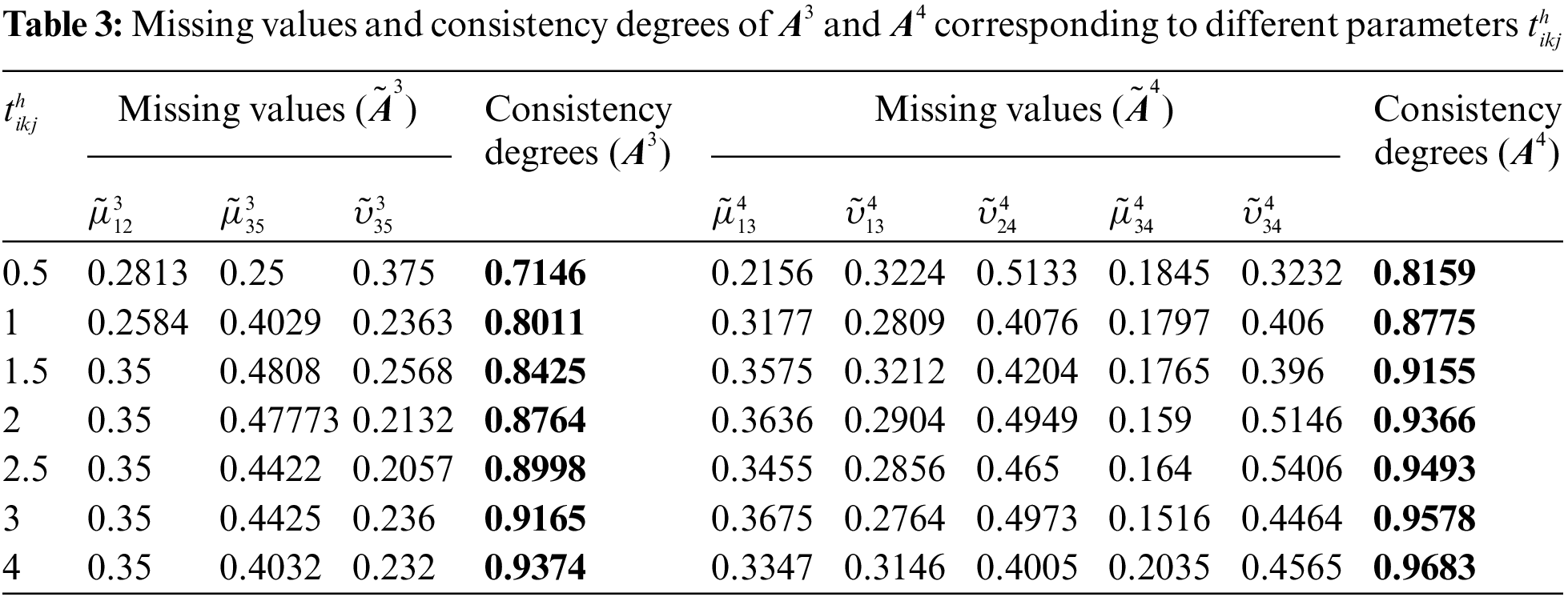
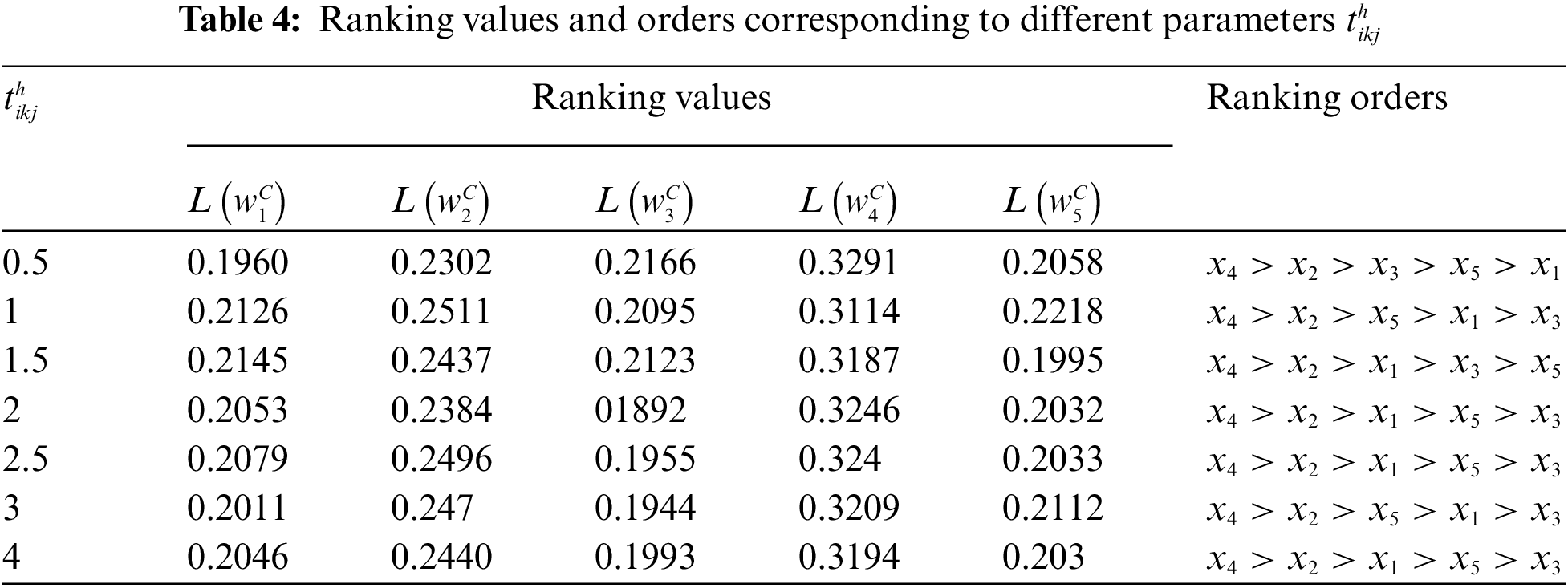
Table 4 shows the related ranking values and orders of the alternatives respectively under different values of tolerance parameters
From Tables 2 and 3, we can conclude that experts can set different values of tolerance parameters
7.3 Comparison Analyses with Existing GDM Methods with IFPRs
As for the existing GDM methods with IFPRs [24,28–32,34], because Meng et al. conducted theoretical and numerical analyses in [34], we primarily compared the GDM method proposed in this study with the two methods mentioned in [29,34].
7.3.1 Comparative Analyses for GDM Methods with Complete IFPRs [29,34]
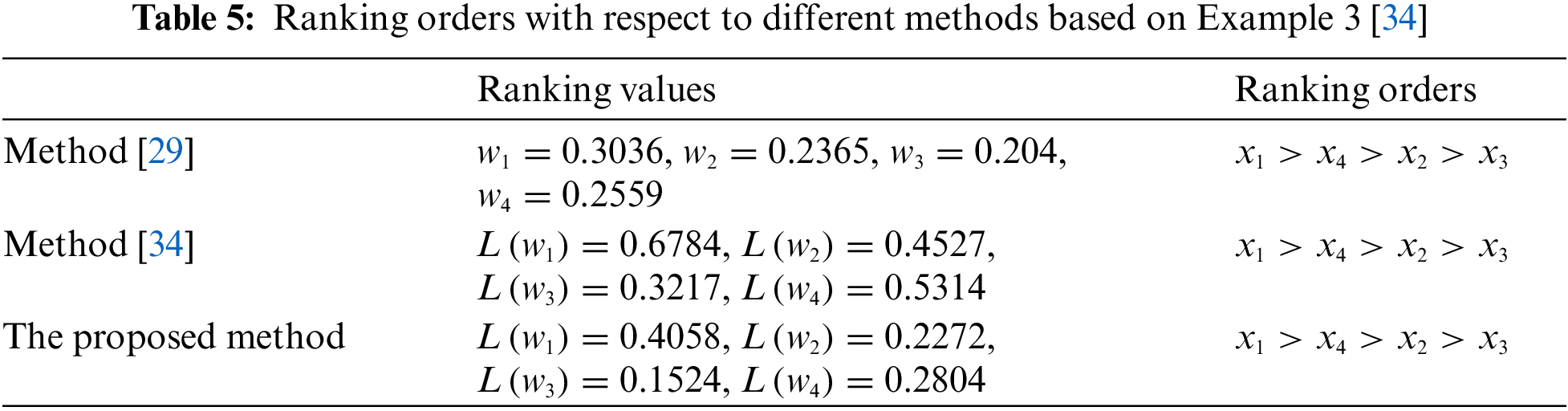
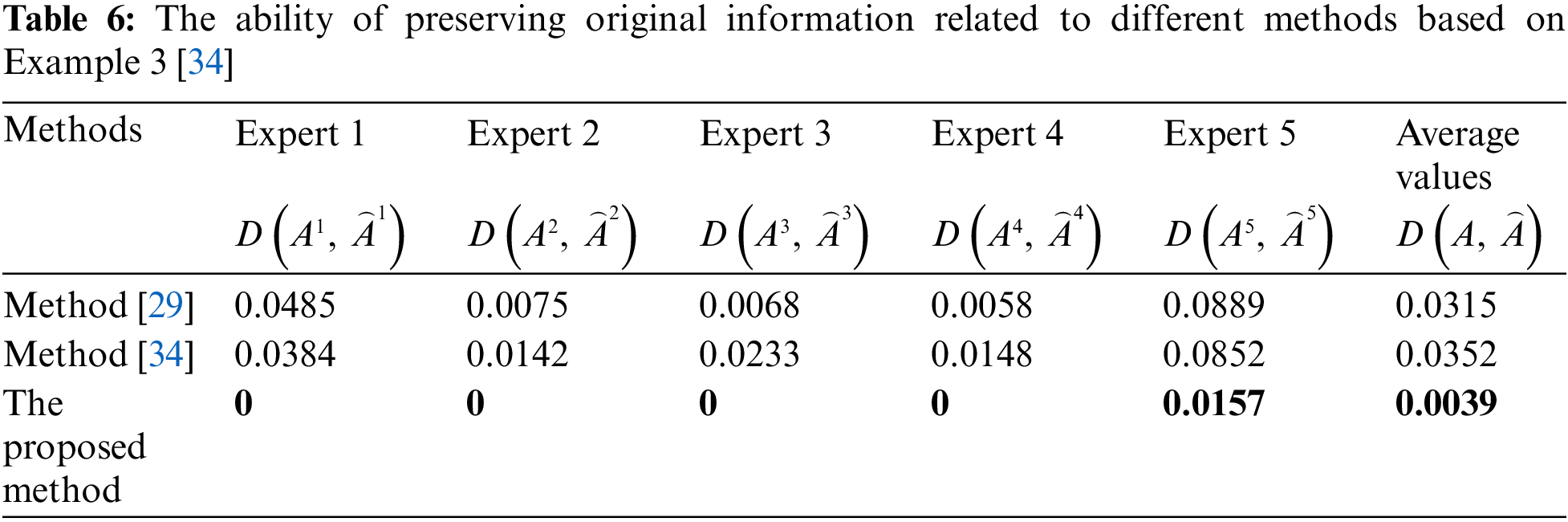
The GDM with a complete IFPR problem (Example 3) proposed in [34] aims to choose PhD students to study in overseas universities. Algorithm 2 is applied to handle the GDM problem presented in [34] (let
7.3.2 Comparative Analyses for GDM Method with Incomplete IFPRs [34]
Algorithm 2 is used to handle the GDM problem (Example 4) with incomplete IFPRs, to illustrate the rationality and superiority of Algorithm 2 in solving the GDM problem with incomplete IFPRs, as shown in [34] (let



From the above comparative analysis, the proposed method has the following advantages over the method in [29,34]:
(1) Compared with the consistency improvement framework proposed in [29,34], the framework proposed in this study is more reasonable. Considering the consistency improvement framework proposed in [29], as described in Section 4, since the multiplicative consistent definition for IFPRs presented in [29] is not a natural extension of Tanino’s multiplicative consistency definition of PRs, the obtained DM result based on the definition lacks a certain degree of persuasiveness. The consistency improvement framework introduced in [34] is based on the definition of complete consistency. However, owing to the difference in professional knowledge, it takes considerable time and energy to achieve the complete consistency of all experts. Meanwhile, the accomplishment of complete consistency is often at the cost of a considerable information loss, which can be found in the above examples.
(2) The CRP proposed in [29] adopts an optimization-based consensus to reach consensus among experts, because its adjustment is not targeted; that is, all individual IFPRs have been adjusted in this process, the final adjusted individual IFPRs may not be optimal in preserving the original information. For the CRP proposed in [34], although the individual IFPRs with the lowest level of consensus were selected and adjusted, its adjustment was targeted. However, the degree of retention of the original information is not considered in the adjustment process. In this study, we first select all individual IFPRs whose consensus is lower than the prescribed value and then adjust them through the optimization model to generate corresponding individual IFPRs satisfying the consensus requirements. Indeed, the method in this study combines the merits of the two methods, so it has more advantages in terms of consensus improvement over the method in [29,34].
(3) Compared with the method for determining the priority weights of alternatives proposed in [29,34], the method proposed in this study uses an optimization model to determine the priority weights of alternatives, whereas the methods in [29,34] used an aggregation operator to obtain the priority weights of alternatives. However, in certain situations, the use of these aggregation operators may lead to missing information. Thus, the method of determining the priority weights of alternatives proposed in this study is more convincing.
Therefore, considering the defects of existing GDM methods with incomplete IFPRs based on multiplicative consistency, this study develops a new method.
The contributions of this study are as follows: First, a new generalized multiplicative consistency for IFPRs is introduced, based on which two mathematical programming models are constructed to supplement the default values in incomplete IFPRs and improve the consistency level of unacceptably consistent IFPRs. Then, for GDM with incomplete IFPRs, a novel method for determining the weights of experts is introduced, and a targeted CRP to improve the consensus level of individual IFPRs is developed. Lastly, a new GDM with incomplete IFPRs is presented, the practicability of which is confirmed through an application example, and its superiority and rationality are explained through comparative and sensitivity analyses.
The benefits of this study are as follows. (1) The multiplicative consistency definition for IFPRs presented in this study, which compensates for the defects of the existing multiplicative consistency definitions for IFPRs, provides a somewhat theoretical guarantee for obtaining reasonable DM results. (2) The CRP presented in this study combines the merits of the existing CPR in GDM with IFPRs to enhance the efficiency of consensus and provides a certain theoretical guarantee for obtaining the DM result recognized by all experts. (3) The method using an optimization model to determine the priority weights of alternatives, avoids information loss, and provides a more convincing DM result.
The limitations of this study are as follows: since the decision data depend on the subjective information provided by the experts, the obtained DM result may have an element of inaccuracy and personal bias, and the consistency and consensus thresholds are provided in advance, which also lacks objectivity.
The implication of this study is that its findings can help community managers effectively reduce the confusion caused by chaotic parking in the community, thereby improving people’s quality of life. Moreover, the method proposed in this study can be applied to other real-world problems, such as supplier selection, risk evaluation, hotel location selection, etc.
Furthermore, the additive consistency of IFPRs is another tool used to evaluate the quality of pairwise comparisons of alternatives provided by the expert. Therefore, the application of our method to GDM problems based on additive consistent IFPRs is worth studying in the future. In addition, extending the method proposed in this study to other fuzzy environments, such as trapezoidal neutral data [47], m-polar set [48], nonlinear Pentagon intuitionistic fuzzy number [49], and intuitionistic multiplicative set [50,51], are also some interesting topics in the future.
Funding Statement: This research was supported by the National Natural Science Foundation of China (Nos. 71740021, 11861034, and 61966030), the Humanities Social Science Programming Project of Ministry of Education of China (No. 20YJA630059), the Natural Science Foundation of Jiangxi Province of China (No. 20192BAB207012), the Natural Science Foundation of Qinghai Province of China (No. 2019-ZJ-7086).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Du, C., Ye, J. (2021). Weighted parameterized correlation coefficients of indeterminacy fuzzy multisets and their multicriteria group decision making method with different decision risks. Computer Modeling in Engineering & Sciences, 129(1), 341–354. DOI 10.32604/cmes.2021.016758. [Google Scholar] [CrossRef]
2. Ye, J. (2017). Bidirectional projection method for multiple attribute group decision making with neutrosophic numbers. Neural Computing and Applications, 28(5), 1021–1029. DOI 10.1007/s00521-015-2123-5. [Google Scholar] [CrossRef]
3. Luo, H. S., Li, L. J., Zhang, Y. K., Fang, S. Y., Chen, X. Y. (2021). Link prediction in multiplex networks using a novel multiple-attribute decision-making approach. Knowledge-Based Systems, 219(11), 106904. DOI 10.1016/j.knosys.2021.106904. [Google Scholar] [CrossRef]
4. Wan, S. P., Wang, F., Dong, J. Y. (2016). A novel group decision making method with intuitionistic fuzzy preference relations for RFID technology selection. Applied Soft Computing, 38(2), 405–422. DOI 10.1016/j.asoc.2015.09.039. [Google Scholar] [CrossRef]
5. Zhang, Z. M., Chen, X. M. (2021). Group decision making based on multiplicative consistency and consensus preference analysis for incomplete q-rung orthopair fuzzy preference relations. Information Sciences, 574(7), 653–673. DOI 10.1016/j.ins.2021.07.044. [Google Scholar] [CrossRef]
6. Saaty, T. L. (1986). Axiomatic foundation of the analytic hierarchy process. Management Science, 32(7), 841–855. DOI 10.1287/mnsc.32.7.841. [Google Scholar] [CrossRef]
7. Orlovsky, S. A. (1978). Decision-making with a fuzzy preference relation. Fuzzy Sets and Systems, 1(3), 155–167. DOI 10.1016/0165-0114(78)90001-5. [Google Scholar] [CrossRef]
8. Chiclana, F., Herrera, F., Herrera-Viedma, E. (2001). Integrating multiplicative preference relations in a multipurpose decision-making model based on fuzzy preference relations. Fuzzy Sets and Systems, 122(2), 277–291. DOI 10.1016/S0165-0114(00)00004-X. [Google Scholar] [CrossRef]
9. Xu, Z. S., Chen, J. (2008). Some models for deriving the priority weights from interval fuzzy preference relations. European Journal of Operational Research, 184(1), 266–280. DOI 10.1016/j.ejor.2006.11.011. [Google Scholar] [CrossRef]
10. Wan, S. P., Wang, F., Dong, J. Y. (2018). A group decision making method with interval valued fuzzy preference relations based on the geometric consistency. Information Fusion, 40(1), 87–100. DOI 10.1016/j.inffus.2017.06.003. [Google Scholar] [CrossRef]
11. Xu, Z. S. (2007). Intuitionistic preference relations and their application in group decision making. Information Sciences, 177(11), 2363–2379. DOI 10.1016/j.ins.2006.12.019. [Google Scholar] [CrossRef]
12. Garg, H. (2018). Generalized interaction aggregation operators in intuitionistic fuzzy multiplicative preference environment and their application to multicriteria decision-making. Applied Intelligence, 48(8), 2120–2136. DOI 10.1007/s10489-017-1066-1. [Google Scholar] [CrossRef]
13. Rani, D., Garg, H. (2021). Complex intuitionistic fuzzy preference relations and their applications in individual and group decision-making problems. International Journal of Intelligent Systems, 36(4), 1800–1830. DOI 10.1002/int.22361. [Google Scholar] [CrossRef]
14. Wan, S. P., Zhong, L. G., Dong, J. Y. (2020). A new method for group decision making with hesitant fuzzy preference relations based on multiplicative consistency. IEEE Transactions on Fuzzy Systems, 28(7), 1449–1463. DOI 10.1109/TFUZZ.2019.2914008. [Google Scholar] [CrossRef]
15. Jin, F. F., Garg, H., Pei, L. D., Liu, J. P., Chen, H. Y. (2020). Multiplicative consistency adjustment model and data envelopment analysis-driven decision-making process with probabilistic hesitant fuzzy preference relations. International Journal of Fuzzy Systems, 22(7), 2319–2332. DOI 10.1007/s40815-020-00944-4. [Google Scholar] [CrossRef]
16. Garg, H. (2022). SVNMPR: A new single-valued neutrosophic multiplicative preference relation and their application to decision-making process. International Journal of Intelligent Systems, 37(3), 2089–2130. DOI 10.1002/int.22767. [Google Scholar] [CrossRef]
17. Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
18. Liao, H. C., Xu, Z. S. (2014). Multi-criteria decision making with intuitionistic fuzzy PROMETHEE. Journal of Intelligent & Fuzzy Systems, 27(4), 1703–1717. DOI 10.3233/IFS-141137. [Google Scholar] [CrossRef]
19. Liao, H. C., Mi, X. M., Xu, Z. S., Xu, J. P., Herrera, F. (2018). Intuitionistic fuzzy analytic network process. IEEE Transactions on Fuzzy Systems, 26(5), 2578–2590. DOI 10.1109/TFUZZ.2017.2788881. [Google Scholar] [CrossRef]
20. Wan, S. P., Dong, J. Y. (2021). A novel extension of best-worst method with intuitionistic fuzzy reference comparisons. IEEE Transactions on Fuzzy Systems, 30(6), 1698–1711. DOI 10.1109/TFUZZ.2021.3064695. [Google Scholar] [CrossRef]
21. Efe, B. (2019). Analysis of operational safety risks in shipbuilding using failure mode and effect analysis approach. Ocean Engineering, 187(4), 106214. DOI 10.1016/j.oceaneng.2019.106214. [Google Scholar] [CrossRef]
22. Stanujkić, D., Karabašević, D. (2018). An extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: A case of website evaluation. Operational Research in Engineering Sciences: Theory and Applications, 1(1), 29–39. DOI 10.31181/oresta19012010129s. [Google Scholar] [CrossRef]
23. Kushwaha, D. K., Panchal, D., Sachdeva, A. (2020). Risk analysis of cutting system under intuitionistic fuzzy environment. Reports in Mechanical Engineering, 1(1), 162–173. DOI 10.31181/rme200101162k. [Google Scholar] [CrossRef]
24. Xu, Z. S., Yager, R. R. (2009). Intuitionistic and interval-valued intutionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group. Fuzzy Optimization and Decision Making, 8(2), 123–139. DOI 10.1007/s10700-009-9056-3. [Google Scholar] [CrossRef]
25. Xu, Z. S., Cai, X. Q., Szmidt, E. (2011). Algorithms for estimating missing elements of incomplete intuitionistic preference relations. International Journal of Intelligent Systems, 9(26), 787–813. DOI 10.1002/int.20494. [Google Scholar] [CrossRef]
26. Xu, Z. S., Liao, H. C. (2014). Intuitionistic fuzzy analytic hierarchy process. IEEE Transactions on Fuzzy Systems, 22(4), 749–761. DOI 10.1109/TFUZZ.2013.2272585. [Google Scholar] [CrossRef]
27. Liao, H. C., Xu, Z. S. (2014). Priorities of intuitionistic fuzzy preference relation based on multiplicative consistency. IEEE Transactions on Fuzzy Systems, 22(6), 1669–1681. DOI 10.1109/TFUZZ.2014.2302495. [Google Scholar] [CrossRef]
28. Liao, H. C., Xu, Z. S., Zeng, X. J., Merigó, J. M. (2015). Framework of group decision making with intuitionistic fuzzy preference information. IEEE Transactions on Fuzzy Systems, 23(4), 1211–1227. DOI 10.1109/TFUZZ.2014.2348013. [Google Scholar] [CrossRef]
29. Xu, G. L., Wan, S. P., Wang, F., Dong, J. Y., Ze, Y. F. (2016). Mathematical programming methods for consistency and consensus in group decision making with intuitionistic fuzzy preference relations. Knowledge-Based Systems, 98, 30–43. DOI 10.1016/j.knosys.2015.12.007. [Google Scholar] [CrossRef]
30. Jin, F. F., Ni, Z. W., Chen, H. Y., Li, Y. P. (2016). Approaches to group decision making with in intuitionistic fuzzy preference relations based on multiplicative consistency. Knowledge-Based Systems, 97(1), 48–59. DOI 10.1016/j.knosys.2016.01.017. [Google Scholar] [CrossRef]
31. Gong, Z. W., Li, L. S., Zhou, F. X., Yao, T. X. (2009). Goal programming approaches to obtain the priority vectors from the intuitionistic fuzzy preference relations. Computers & Industrial Engineering, 57(4), 1187–1193. DOI 10.1016/j.cie.2009.05.007. [Google Scholar] [CrossRef]
32. Wu, J., Chiclana, F. (2014). Multiplicative consistency of intuitionistic reciprocal preference relations and its application to missing values estimation and consensus building. Knowledge-Based Systems, 71(1), 187–200. DOI 10.1016/j.knosys.2014.07.024. [Google Scholar] [CrossRef]
33. Wu, J., Chiclana, F., Liao, H. C. (2018). Isomorphic multiplicative transitivity for intuitionistic and interval-valued fuzzy preference relations and its application in deriving their priority vectors. IEEE Transactions on Fuzzy Systems, 26(1), 193–202. DOI 10.1109/TFUZZ.2016.2646749. [Google Scholar] [CrossRef]
34. Meng, F. Y., Tang, J., Xu, Z. S. (2017). A 0-1 mixed programming model based method for group decision making with intuitionistic fuzzy preference relations. Computers & Industrial Engineering, 112, 289–304. DOI 10.1016/j.cie.2017.08.027. [Google Scholar] [CrossRef]
35. Krejčí, J. (2017). On multiplicative consistency of interval and fuzzy reciprocal preference relations. Computers & Industrial Engineering, 111(3), 67–78. DOI 10.1016/j.cie.2017.07.002. [Google Scholar] [CrossRef]
36. Meng, F. Y., Chen, S. M., Yuan, R. P. (2020). Group decision making with heterogeneous intuitionistic fuzzy preference relations. Information Sciences, 523(1), 197–219. DOI 10.1016/j.ins.2020.03.010. [Google Scholar] [CrossRef]
37. Wang, Z. J. (2020). A representable uninorm based intuitionistic fuzzy analytic hierarchy process. IEEE Transactions on Fuzzy Systems, 28(10), 2555–2569. DOI 10.1109/TFUZZ.2019.2941174. [Google Scholar] [CrossRef]
38. Xu, Z. S., Yager, R. R. (2006). Some geometric aggregation operators based on intuitionistic fuzzy sets. International Journal of General Systems, 35(4), 417–433. DOI 10.1080/03081070600574353. [Google Scholar] [CrossRef]
39. Szmidt, E., Kacprzyk, J. (2000). Distances between intuitionistic fuzzy sets. Fuzzy Sets and Systems, 114(3), 505–518. DOI 10.1016/S0165-0114(98)00244-9. [Google Scholar] [CrossRef]
40. Tanino, T. (1984). Fuzzy preference orderings in group decision making. Fuzzy Sets and Systems, 12(2), 117–131. DOI 10.1016/0165-0114(84)90032-0. [Google Scholar] [CrossRef]
41. Palomares, I., Estrella, F. J., Martínez, L., Herrera, F. (2014). Consensus under a fuzzy context: Taxonomy, analysis framework AFRYCA and experimental case of study. Information Fusion, 20(2), 252–271. DOI 10.1016/j.inffus.2014.03.002. [Google Scholar] [CrossRef]
42. Herrera, F., Herrera-Viedma, E., Verdegay, J. (1996). A model of consensus in group decision making under linguistic assessments. Fuzzy Sets and Systems, 78(1), 73–87. DOI 10.1016/0165-0114(95)00107-7. [Google Scholar] [CrossRef]
43. Herrera, F., Herrera-Viedma, E., Verdegay, J. (1997). Linguistic measures based on fuzzy coincidence for reaching consensus in group decision making. International Journal of Approximate Reasoning, 16(3–4), 309–334. DOI 10.1016/S0888-613X(96)00121-1. [Google Scholar] [CrossRef]
44. Xu, Z. S., Xia, M. M. (2014). Iterative algorithms for improving consistency of intuitionistic preference relations. Journal of the Operational Research Society, 65(5), 708–722. DOI 10.1057/jors.2012.178. [Google Scholar] [CrossRef]
45. Wang, Z. J. (2013). Derivation of intuitionistic fuzzy weights based on intuitionistic fuzzy preference relations. Applied Mathematical Modelling, 37(9), 6377–6388. DOI 10.1016/j.apm.2013.01.021. [Google Scholar] [CrossRef]
46. Zhang, X. M., Xu, Z. S. (2012). A new method for ranking intuitionistic fuzzy values and its application in multi-attribute decision making. Fuzzy Optimization and Decision Making, 11(2), 135–146. DOI 10.1007/s10700-012-9118-9. [Google Scholar] [CrossRef]
47. Haque, T. S., Chakraborty, A., Mondal, S. P., Alam, S. (2021). New exponential operational law for measuring pollution attributes in mega-cities based on MCGDM problem with trapezoidal neutrosophic data. Journal of Ambient Intelligence and Humanized Computing, 77(4), 438. DOI 10.1007/s12652-021-03223-8. [Google Scholar] [CrossRef]
48. Hashmi, M. R., Riaz, M., Smarandache, F. (2020). m-polar neutrosophic topology with applications to multi-criteria decision-making in medical diagnosis and clustering analysis. International Journal of Fuzzy Systems, 22(1), 273–292. DOI 10.1007/s40815-019-00763-2. [Google Scholar] [CrossRef]
49. Chakraborty, A., Pal, S., Mondal, S. P., Alam, S. (2021). Nonlinear pentagonal intuitionistic fuzzy number and its application in EPQ model under learning and forgetting. Complex & Intelligent Systems, 8(2), 1307–1322. DOI 10.1007/s40747-021-00574-9. [Google Scholar] [CrossRef]
50. Garg, H. (2020). Exponential operational laws and new aggregation operators for intuitionistic multiplicative set in multiple-attribute group decision making process. Information Sciences, 538(1), 245–272. DOI 10.1016/j.ins.2020.05.095. [Google Scholar] [CrossRef]
51. Garg, H. (2021). Multi-attribute group decision-making process based on possibility degree and operators for intuitionistic multiplicative set. Complex and Intelligent Systems, 7(2), 1099–1121. DOI 10.1007/s40747-020-00256-y. [Google Scholar] [CrossRef]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |