Computer Modeling in Engineering & Sciences

---

DOI: 10.32604/cmes.2022.020495

ARTICLE

Implementation of OpenMP Parallelization of Rate-Dependent Ceramic Peridynamic Model

Haoran Zhang1, Yaxun Liu2, Lisheng Liu2,*, Xin Lai2,*, Qiwen Liu2 and Hai Mei2

1Department of Engineering Structure amd Mechanics, Wuhan University of Technology, Wuhan, 430070, China
2Hubei Key Laboratory of Theory and Application of Advanced Materials Mechanics, Wuhan University of Technology, Wuhan, 430070, China
*Corresponding Authors: Lisheng Liu. Email: liulish@whut.edu.cn; Xin Lai. Email: laixin@whut.edu.cn
Received: 27 November 2021; Accepted: 30 January 2022

1  Introduction

The ceramic composite armor has garnered significant research attention as the main protective material for modern military systems. The protective performance of ceramic composite armor is closely related to the damage, destruction process and structure of the ceramic material, as well as the ductility of the metallic back-plate. During projectile penetration, the ceramic front plate is the main energy-absorbing structure, and the metal or composite back-plate plays a supporting role [1]. Therefore, it is necessary to establish a numerical model that can accurately describe the dynamic mechanical properties of ceramic materials under impact load to understand the dynamic response. So far, in the field of computational mechanics, researchers have proposed a series of numerical methods based on traditional continuum theory to simulate the dynamic response of ceramic materials. However, these methods are all based on the framework of continuum mechanics, and their motion control equations are based on the partial derivative of the space coordinate. One should note that the partial derivative on the crack surface, where the displacement field is discontinuous, cannot be defined. The continuity assumption is essentially insufficient to model cracks [2] and it is necessary to redefine the discrete body to eliminate the discontinuous displacement field. Therefore, a non-local continuum theory, called peridynamic (PD), has been proposed by Silling et al. [3] to handle discontinuous problems, such as crack propagation and damage. The proposed theory utilizes the spatial integral equation for discontinuous body instead of the differential equation in continuum theory, which is more suitable for simulating crack initiation and propagation [4]. The peridynamic theory can be divided into two distinct branches, i.e., bond-based peridynamics (BB-PD) and state-based peridynamics (SB-PD) [5,6]. The BB-PD theory, as originally proposed by Silling et al., has been successfully applied to the damage and fracture simulation of brittle materials, such as concrete [7–9], ice [10] and geomaterials [11]. The state-based peridynamics theory [5,6] proposed by Silling overcomes the constraint of Poisson's ratio in the bond-based peridynamics, describes the interaction between two material points through the force state, and can accurately describe the constitutive relationship of elastic-plastic materials. It has also been successfully applied to the fracture simulation of brittle materials such as ceramics [12], glass [13] and ice [14]. However, due to the computational complexity and resource consumption of state-based peridynamics method, it is more expensive than the bond-based peridynamics. The bond-based peridynamic theory is relatively simple, easier to understand and implement, and suitable for coupling with molecular dynamics during multi-scale analysis [15]. Therefore, it has been developed and applied to also study some solid fracture and impact problems. For instance, Lee et al. [16] have proposed a new contact algorithm to simulate the contact and impact problems in peridynamic and non-peridynamic domains, e.g., conventional finite elements and rigid bodies, under high velocities. Ma et al. [17] have utilized the PD method to simulate and calculate the damage process of round glass with different thicknesses, curvatures and inclinations under impact load.

Moreover, based on the von Mises yield criterion, Kazemi et al. [18] have used the state-based PD constitutive relation to capture the ductile fracture induced by a high-speed impact steel strips, and studied the effects of impact velocity and strain hardening on steel strips. Deng et al. [19] have investigated the mechanism of impact and crushing of two spherical particles using a PD model. According to the simulation data, the initiation and growth of different types of cracks are dynamically captured, and the relationship between various crushing methods and impact speed is discussed in detail. Moreover, the crack growth speed under different conditions is simulated. Liu et al. [20] have proposed a coupling method between the bond-based peridynamic model for solids and the updated Lagrangian particle hydrodynamics (ULPH) model of fluids to simulate the interaction between ice and seawater, and applied this method to simulate a rigid ball impacting on an ice plate floating in water pool, the results obtained captured the main characteristics of the dynamic ice-breaking process successfully. Chen et al. [21] have developed a peridynamic fiber-reinforced concrete model based on the bond-based peridynamic model with rotation effect (BBPDR). the frictional effect between the fibers and the concrete matrix is considered, and the numerical examples validate the proposed model's effectiveness in modelling the fracture behavior of fiber-reinforced concrete. Chu et al. [22] have considered the tensile-brittle response, compressive plastic softening and strain rate effects of ceramics, improved the micro-elastic brittleness (PMB) model, and established the rate-dependent PD model to describe the anti-penetration behavior of ceramic materials. The constitutive model successfully captures the overall dynamic process of ceramics, and studies the fracture mechanism of ceramic materials during ballistic impact. However, since the model is based on the classical PD theory, the material Poisson's ratio is always limited to 0.25 in the case of three-dimensional problems. Therefore, the application range of ceramic materials is greatly restricted and it is necessary to modify the proposed model. Later, Liu et al. [23] have introduced the concept of rotation angle based on Chu et al.'s work, and established a rate-dependent bond-based PD constitutive model to describe the ceramic penetration behavior, eliminating the influence of Poisson's ratio from the BB-PD theory.

Although the PD method has obvious advantages in simulating impact-induced structural damage, the model needs to be separated into a series of material points when analyzing discontinuities, such as crack propagation, and each material point stores corresponding material information. Furthermore, it is necessary to build the neighbor list according to material points and store other material points that interact with them. Hence, it will require more computational resources when carrying out large-scale loop computation of the bond force and damage of material points according to different constitutive equations under the time step loop. For the rate-dependent BB-PD constitutive model [22], it is considered that the material is brittle under tensile load, and the fracture occurs when the relative stretch of the bond exceeds the critical stretch. Under the compression load, the plastic softening behavior of the material is considered. When the relative compression deformation of the bond is less than the elastic compression limit, the relationship between bond force and relative compression deformation is linear. Once the elastic compression limit is exceeded, the damage accumulation in the bond leads to the reduction of the critical force of the bond. When the relative compression deformation of the bond reaches the compression limit, the damage of the bond reaches 1, indicating that the bond is broken. However, the bond can continue to bear the compression load after reaching the compression limit, and the critical force remains at a fixed value. The rate-dependent BB-PD constitutive model, considering the rotation effect [23], eliminated the limitation of Poisson's ratio of the traditional BB-PD model due to the introduction of rotation angle. It is considered that there is a rotation effect between material points along with the tension and compression of the bond. Also, the rotation angle exhibits a linear relationship with the tangential bond force of the bond. When the rotation angle of the bond exceeds the critical angle, a brittle fracture occurs in the tangential direction. When solving the bond force between the particle and neighboring particles in the model, it is necessary to store and calculate the bond force and bond damage of particles at both ends of the bond at the same time. Therefore, there are several problems in large-scale models, such as high computational complexity and vast computing [24]. Therefore, the improvement in calculation efficiency has become a practical problem.

It is worth noting that parallel computing is currently the main method for large-scale computations, where some of the codes can be parallelly executed to improve the computational efficiency of complex and large-scale computations of PD programs. In parallel computing, the usually adopted methods include MPI parallel [25], CPU-based OpenMP parallel architecture [26], GPU-based CUDA parallel architecture [24] and GPU-based OpenCL parallel architecture [27]. Extensive studies have been conducted on the performance of PD programs based on the above parallelization methods, such as: Parks et al. [28] implemented the PMB material model within the framework of the classical molecular dynamics package LAMMPS which ultilized MPI. And the PD package in LAMMPS is called PD-LAMMPS, it's also one of the open-source PD codes. Diehl et al. [29] proposed a GPU based CUDA parallel architecture to accelerate the nearest neighbor search algorithm. The algorithm can be used in any particle method and is suitable for neighborhood update at each time step in dynamic particle cloud. Boys et al. [30] developed a lightweight, open source and high-performance Python package for GPU acceleration using OpenCL to solve the peridynamics problem in solid mechanics. The package takes advantage of the heterogeneity of OpenCL, so it can be executed on any platform with different hardware, i.e., CPU and GPU cores. The HPX library is a C++ standard compliant Asynchronous Many Task (AMT) run time system tailored for high performance computing (HPC) applications, which is considered by Diehl et al. [31] . And the methdology is shown on how to take advantage of the fine-grain parallelism arising on modern supercomputers. In all methods mentioned above, the OpenMP framework is used mainly for loop parallelism, which can effectively overcome the shortcomings of poor portability and expansion performance of parallel programming, makes small changes to the program, and can quickly realize the parallelization of PD simulations.

In rate-dependent PD simulations of ceramics, where the rotation effect is considered and the model contains n material points, the complexity of establishing the nearest neighbor list is about O(n2) and the loop statements are executed about n × (n + 1)/2. In the time step cycle, the force, displacement and damage state of the material points need to be updated. The complexity of calculating displacement, velocity and acceleration of the material point in a unit time step is about O(n), and the execution time of the cycle statement is about 3n. However, the complexity of bond force update in a unit time step is about O(n × m × k), where m refers to the number of neighbors in the horizon size of the particle and k denotes the number of iterations to obtain the true normal bond force. This is different from the traditional PD model. At the same time, the calculation process is more time-consuming than the traditional PD model owing to the uncertainty of the number of iterations. The complexity of the updated part of the total damage of particles is about O(n × m), and the number of executions of the loop statement is about n × m.

The rate-dependent BB-PD constitutive model considering rotation effect can accurately simulate the dynamic mechanical response and crack propagation of brittle materials, such as ceramics, under impact loading. However, considering the strain-rate dependence and rotation effect, a large amount of computation time is required for calculations. Herein, according to the characteristics of the rate-dependent PD model considering the rotation effect, we investigate the parallel implementation of the PD numerical simulations based on the OpenMP and the program structure is summarized and modified. Parallelization is set for time-consuming modules in the program to realize multi-threaded and efficient parallel computing. Based on the theoretical framework of Liu et al. [23], the dynamic response of a ceramic plate under the impact of a steel column is simulated and the results are reproduced. Also, three models with different particle sizes are simulated, and the number of parallel threads in OpenMP mode and the influence of particle size on computing efficiency are compared. Moreover, the main reasons for the gradual decrease of parallel efficiency with the increase of thread number are analyzed and discussed. Overall, the results reveal the promise of parallelization process in terms of accuracy and stability.

2  Rate-dependent BB-PD Theory and Simulation Algorithm of the Ceramic Model

Peridynamic theory is a non-local continuity theory proposed by Silling et al., which is mainly divided into bond-based peridynamics theory [3] (BB-PD) and state-based peridynamics theory (SB-PD) [5]. In the BB-PD model, the equation of motion for a material point xi at time t can be given by Eq. (1):

ρxiu¨xi(x,t)=∫Hxif(ξ,η)dVxj+b(xi,t)(1)

where ρxi refers to the mass density of the particle xi, u(xi, t) and ü(xi, t) denote the displacement vector field and accelerating vector field of the material point xi at time t, respectively, f(ξ, η) represents a pairwise force function to describe interactions between material points of the bond, and b(xi, t) refers to the body force density of the material point xi at time t.

In BB-PD theory, the essence of the solution is an iteration calculation of the interaction force f(ξ, η) between particles at the point of matter and the particles within its horizon based on the time step. f(ξ, η) is calculated according to the constitutive properties of the selected material.

Liu et al. [23] have introduced the concept of rotation angle based on rate-dependent BB-PD theory [22], and constructed the rate-dependent BB-PD constitutive model considering the rotation effect. This also eliminates the influence of Poisson's ratio of the traditional BB-PD theory. Herein, when the bond is subjected to tensile-shear loads, the relationship between bond force and deformation of the bond can be expressed by Eq. (2):

f(η,ξ)={μ(t,ξ)(csn+κγ)λ<10λ≥1(2)

where the dimensionless value λ in the peridynamics theory can be given by Eq. (3):

λ=(ss0)2+(γγ0)2(3)

where s0 and γ0 denote the critical relative stretch and critical tangential angle, which can be obtained from the fracture energy (G0) and the shear fracture energy (Gs), respectively [23], as shown in Eqs. (4) and (5):

G0=∫0δ∫02π∫0δ∫0cos−1z/ξ(cs02ξ2)ξ2sin⁡ϕdϕδξdθdz=πcs02δ510(4)

Gs=∫0δ∫02π∫0δ∫0cos−1z/ξ(cγ02ξ2)ξ2sin⁡ϕdϕδξdθdz=πcγ02δ510(5)

The constitutive relationship is shown in Fig. 1. Also, μ(t,ξ) is a scalar function, whose value is 1 and 0 for λ < 1 and λ ≥ 1, respectively. s and γ represent the relative stretch of the bond and tangential rotation angle of the bond, respectively. c and κ denote the normal micro-elastic modulus and tangential micro-elastic modulus parameters, respectively [32], as shown in Eqs. (6) and (7):

c=6Eπδ4(1−2ν)(6)

κ=6E(1−4ν)πδ4(1+ν)(1−2ν)(7)

where E denotes the elastic modulus, δ refers to the size of neighborhood horizon, and ν represents the Poisson's ratio.

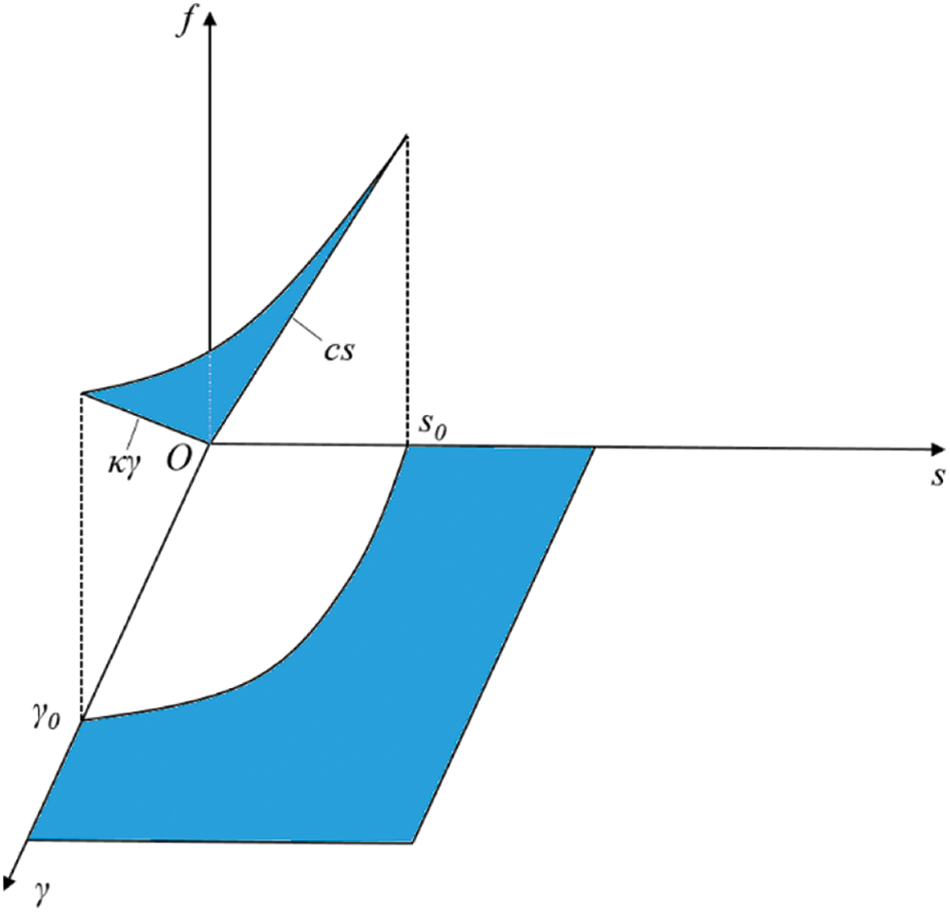
Figure 1: The constitutive relationship under tension-shear load

The judgment of bond damage is controlled by the damage function φ(x, t), as shown in Eq. (8). φ(x,t)=0 indicates that the material points are intact and φ(x, t) = 1 indicates that all the bonds in the horizon of a material point are disconnected.

φ(x,t)=1−∫Hxμ(x,t,ξ)dVξ∫HxdVξ(8)

When the bond is under compressive-shear load, there are two failure modes, i.e., compression failure and shear failure. The constitutive relationship between the normal compression bond force (fn) and the relative elongation (s) of the bond is shown in Fig. 2, where se represents the elastic deformation limit under compression and s1 denotes the critical fracture deformation. For the tangential bond force, it is considered that the tangential bond force is linearly related to the relative rotation angle of the pair-wise bond. When the angle exceeds the critical value γ0, a brittle fracture occurs in the tangential direction and the tangential bond force (ft) becomes 0. When the compression damage variable (D) reaches 1, the bond is completely broken. The normal bond force is the critical force (pf) for complete damage and the tangential bond force ft becomes 0.

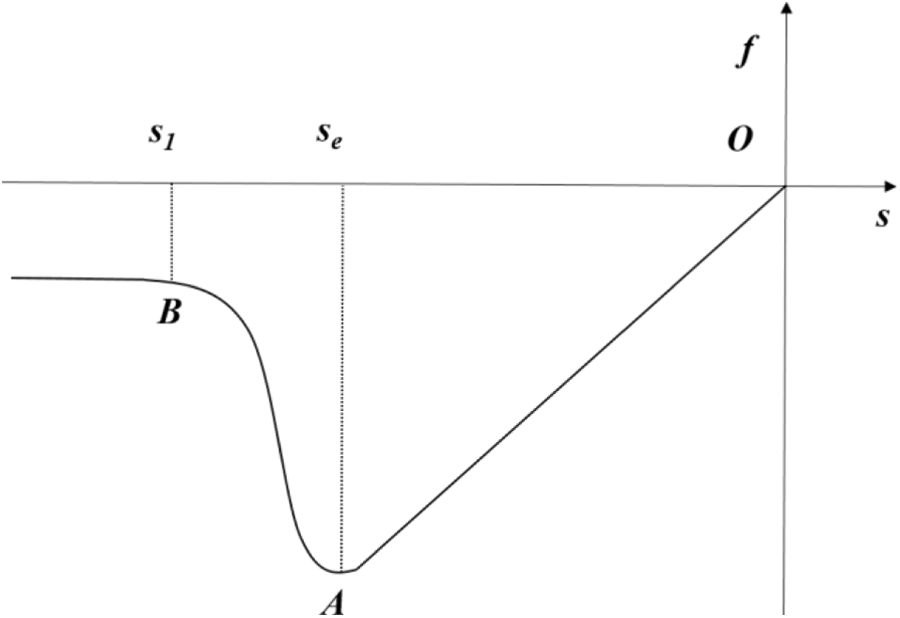
Figure 2: The constitutive model under compressive load

The relationship between bond force and bond deformation can be expressed by Eq. (9):

f(η,ξ)={|fn+κγ|D<1andγ<γ0fnD<1 and γ≥γ0pfD≥1(9)

The calculation method of the normal compression bond force \; (fn) of the bond is consistent with the calculation method of the compression failure part in Chu et al.'s work [22], in whicn the plastic softening behavior is considered when the relative compression deformation of the bond exceeds the elastic compression limit. The current critical bond force (p) on normal can be given by Eq. (10):

p=pi−D(pi−pf)(10)

where D represents the cumulative damage of the bond after plastic deformation, and can be expressed by Eq. (11):

D=∑sps1−se(11)

in which sp represents the relative plastic compressive deformation in a time step increment, ∑sp denotes the cumulative plastic compressive deformation, se corresponds to the elastic limit of the bond during compressive deformation, and s1 represents the critical relative compressive deformation of the bond. pi and pf refer to the intact strength and fracture strength of the bond, respectively [22]. And they are expressed by Eqs. (12) and (13):

pi=p0(1+αln⁡s˙)(12)

pf=βp0(1+αln⁡s˙)(13)

in which p0 is the rate-independent static strength, β and α are material constants, and S˙ refers to the rate-independent relative compression deformation rate of the bond, and can be expressed by Eq. (14):

s˙=η˙⋅(ξ+η)||ξ||⋅||ξ+η||(14)

Considering the plastic deformation of the bond with the elastic relative compression deformation limit, the bond force function can be given by Eq. (15):

fn=c(s−sp)(15)

where sp is the relative plastic compressive deformation, which can be obtained by the product of S˙p and time step (Δt). And S˙p can be expressed by Eq. (16):

s˙p=cc−Hs˙(16)

where H=(1−β)pis1−se.

The flow chart of the serial program is illusttrated in Fig. 3. This program is programmed in Fortran. The computational process of the program mainly includes data input and storage, model spatial discretization, horizon construction, initialization, boundary condition application, calculation of acceleration, velocity and displacement of the material point, calculation of the current bond force and bond damage, and data acquisition. Fig. 4 presents the bond force update algorithm that is based on the constitutive model of the rate-dependent BB-PD considering the rotation effect. The bond is discussed separately under tensile-shear load and compressive-shear load. When the bond is under tensile-shear load, the bond force is calculated according to Eq. (2). When the bond is subjected to compressive-shear load, the bond force is calculated according to Eq. (9). This part is located in the time step cycle. When calculating the bond force, the particles are first cycled and, then, the nearest neighbors of particles are cycled. Therefore, the time complexity of this part is O(n × m × k), where n represents the total number of particles, m refers to the number of neighbors in the horizon size of the particle, and k denotes the number of iterations.

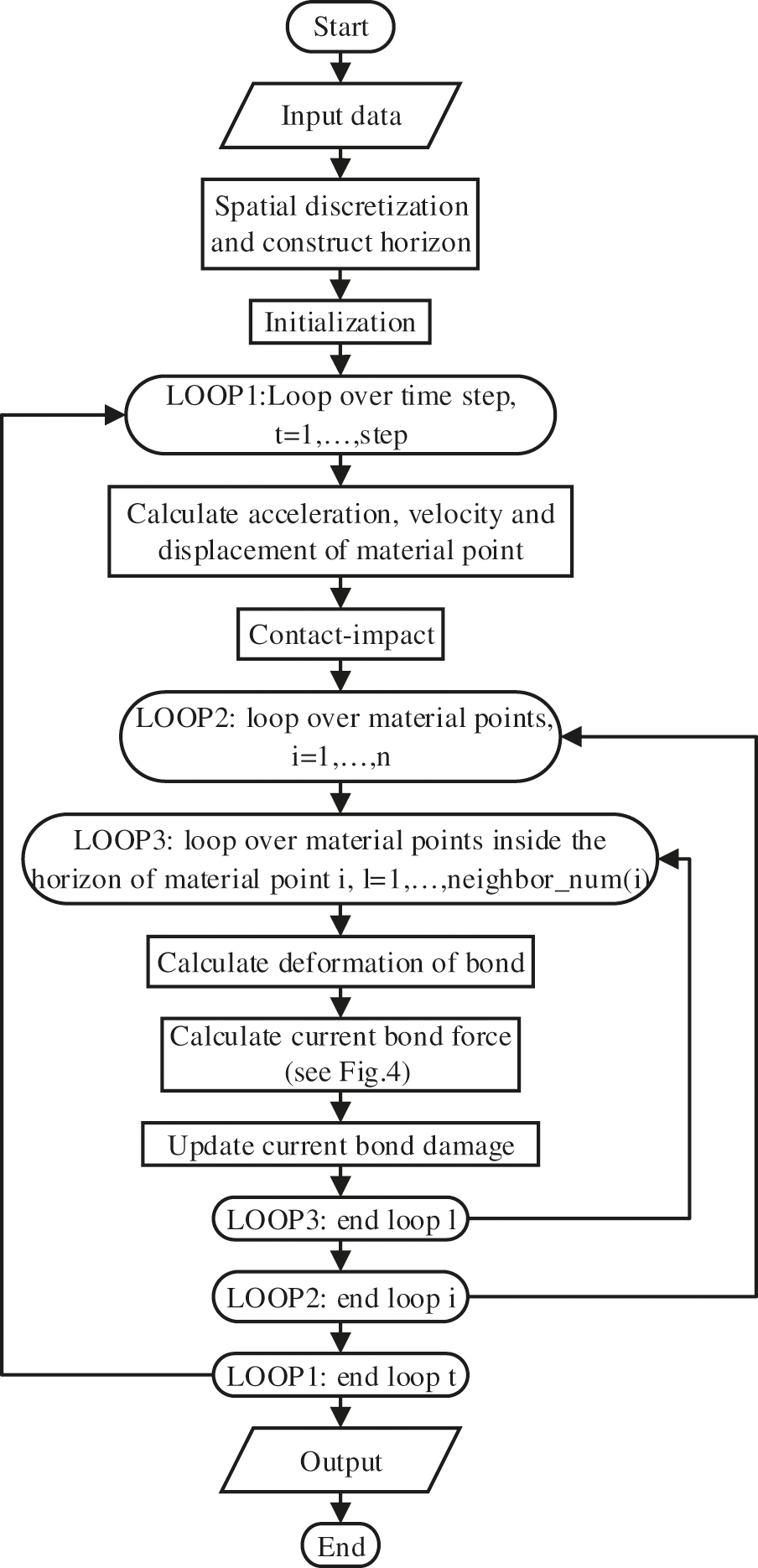
Figure 3: Flow chart of the serial program

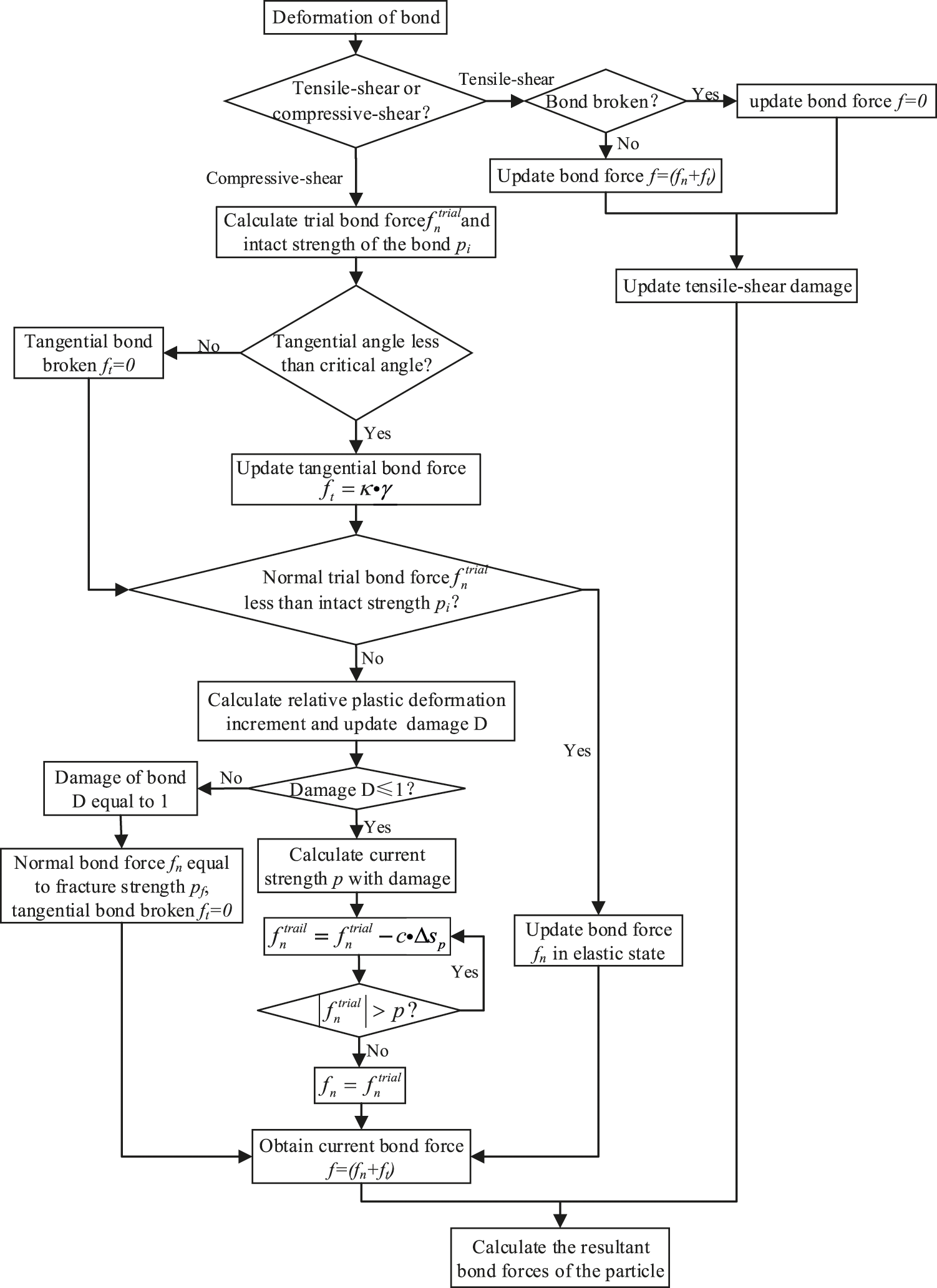
Figure 4: Flow chat for update bond force

3  Implementation of OpenMP Parallelization of Rate-Dependent PD Model

3.1 OpenMP

OpenMP is an application interface that directly controls shared memory parallel programming and is a parallel language for multi-threaded processors with shared memory. The parallelism of the model is realized based on the combination of compiler instructions, library routines and environment variables [33]. The OpenMP code can only run-on shared memory machines, and each thread can access a shared memory unit and read/write data on the shared memory unit. Since the memory is shared, the data written to the shared memory by a certain thread will be immediately accessed by other threads.

OpenMP makes use of a parallel design pattern called the Fork-Join model [33], as shown in Fig. 5. Initially, there is only one running thread called the master thread. When the master thread runs the project, it encounters the OpenMP boot statement and several sub-threads are derived according to the environment variables and actual needs. At this time, the sub-thread and the master thread run at the same time. During the process, if the child thread encounters a parallel guidance statement, it will spawn a child thread again. All threads form a thread group to complete a task together. After the completion of parallel codes, the derived sub-threads converge to form the master program, continue to execute the final program code and exit.

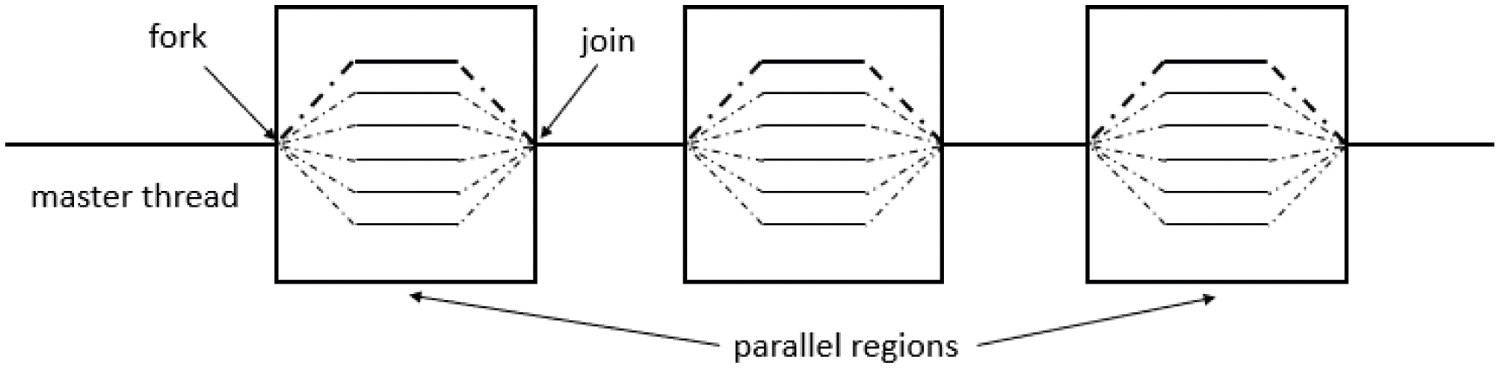
Figure 5: The schematic illustration of the Fork-Join model

OpenMP is mainly for loops in parallel. After the loop is parallelized, the program does not need to wait for the end of the previous loop to start the next loop like a serial program. On the other hand, before entering the loop, the entire loop is divided and is equally distributed in different threads. This can maximize the performance of multi-core multi-thread computers. When modifying programs in parallel, make sure that there is no data competition between threads. Not all loops can be parallelized. Only the variables between loops do not have circular dependencies and data competition. Although some data dependencies can be eliminated through various instructions in the program, the actual time consumed is not much different from that before parallelization. Therefore, not all programs are suitable for changing into parallel programs in OpenMP mode.

3.2 Parallelization of the Programs of Rate-Dependent BB-PD Model

In this part, we shall discuss the detailed implementation of the rate-dependent BB-PD model by using OpenMP parallel computation. Hence, we first implement the program in serial with the model descritized into 90 × 90 × 12 particles with impact speed 175 m/s to determine the most time-consuming part of the code. The results reveal that the total time spent in the serial program is 28,784 s, and the time spent on the calculation module of the bond force between the particles in the material point and its horizon takes 72.59% of the total calculation time. On the other hand, the time spent on the calculation module of the bond damage between the particles in the material point and its horizon accounts for about 27.12% of the total calculation time in the serial program. Other modules including initialization module, neighborhood module and contact update module and motion status update module in the time cycle only take 0.29% of the total calculation time. Therefore, this paper mainly focuses on the parallelization of two modules: bond force update and damage update. In the part without cycle dependence, OpenMP compiling guidance statement is added to parallelize the module.

In the BB-PD theory, each material point interacts with the points within its horizon. The interactions between material points can be called bond interactions. Each bond is independent and the bond forces appear in pairs, collinear, equal in size and opposite in direction. Therefore, when calculating the bond force and damage of particles at both ends of the bond, it is only necessary to solve the bond force and damage of particles at one end of the bond and assign the obtained bond force and damage directly to particles at the other end. In order to reduce the calculation time, this paper labels the particles at both ends of the bond by defining the logical array mark. Only the particles at one end of the label are calculated and directly assigned to the particles at the other end of the bond, as shown in Fig. 6.

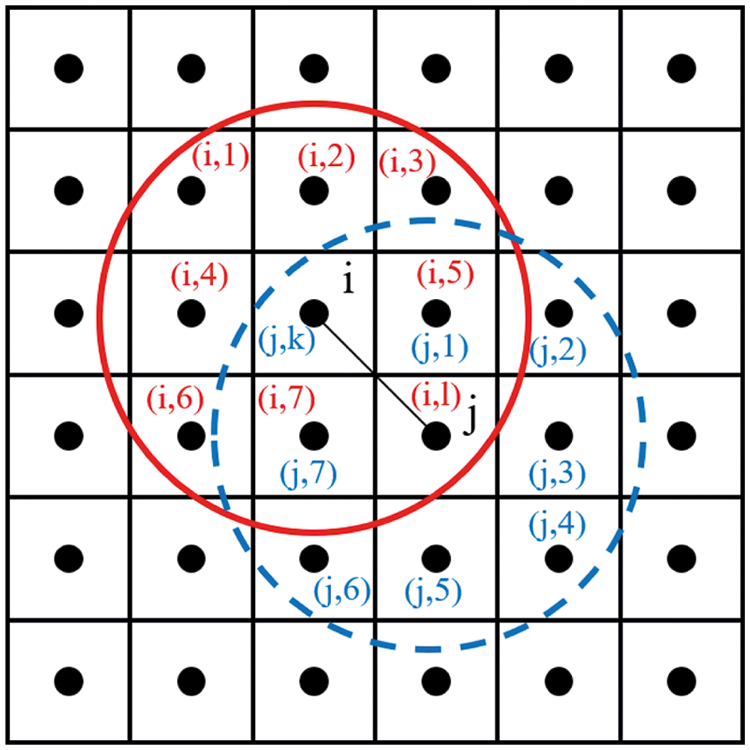
Figure 6: The logical array tag on the particles at both ends of the bond

As shown in Fig. 6, the j particle is located in the lth nearest neighbor of the ith particle horizon range list, and the corresponding i particle is located in the kth nearest neighbor of the j particle horizon range list. Marking mark(i, l) as true, the corresponding mark(j, k) is marked as false, as shown in Eq. (17). When the bond force at both ends of the particle is updated in the time step loop, the bond force and damage of the particle at one end of the bond are calculated by identifying the logical array mark, and the obtained bond force and damage result are directly assigned to the particle at the other end of the bond.

{mark(i,l)=.true.mark(j,k)=.false.(17)

When the program of the bond force update module is parallelly rewritten, it is found that there is a layer of time step cycle outside the module. However, two loops before and after the time step loop are interdependent. So, OpenMP cannot be used for parallel optimization of the time step loop. Therefore, the particle cycle under the time step cycle is optimized in parallel and the program flow chart is shown in Fig. 7. The pseudocode for bond force update is shown in Table 1. As shown in the parallel region in Fig. 7, the loops about the particles are assigned to three threads in sequence. So, the task assigned to each thread is about (n × m)/3. In addition, each thread recognizes the logical array of the particles at both ends of the bond at runtime and directly assigns the obtained values to the particles at the other end of the bond after updating the bond force. Therefore, the number of tasks allocated to each thread is approximately (n × m)/6, and the number of tasks allocated to each thread gradually decreases with the increase in number of threads.

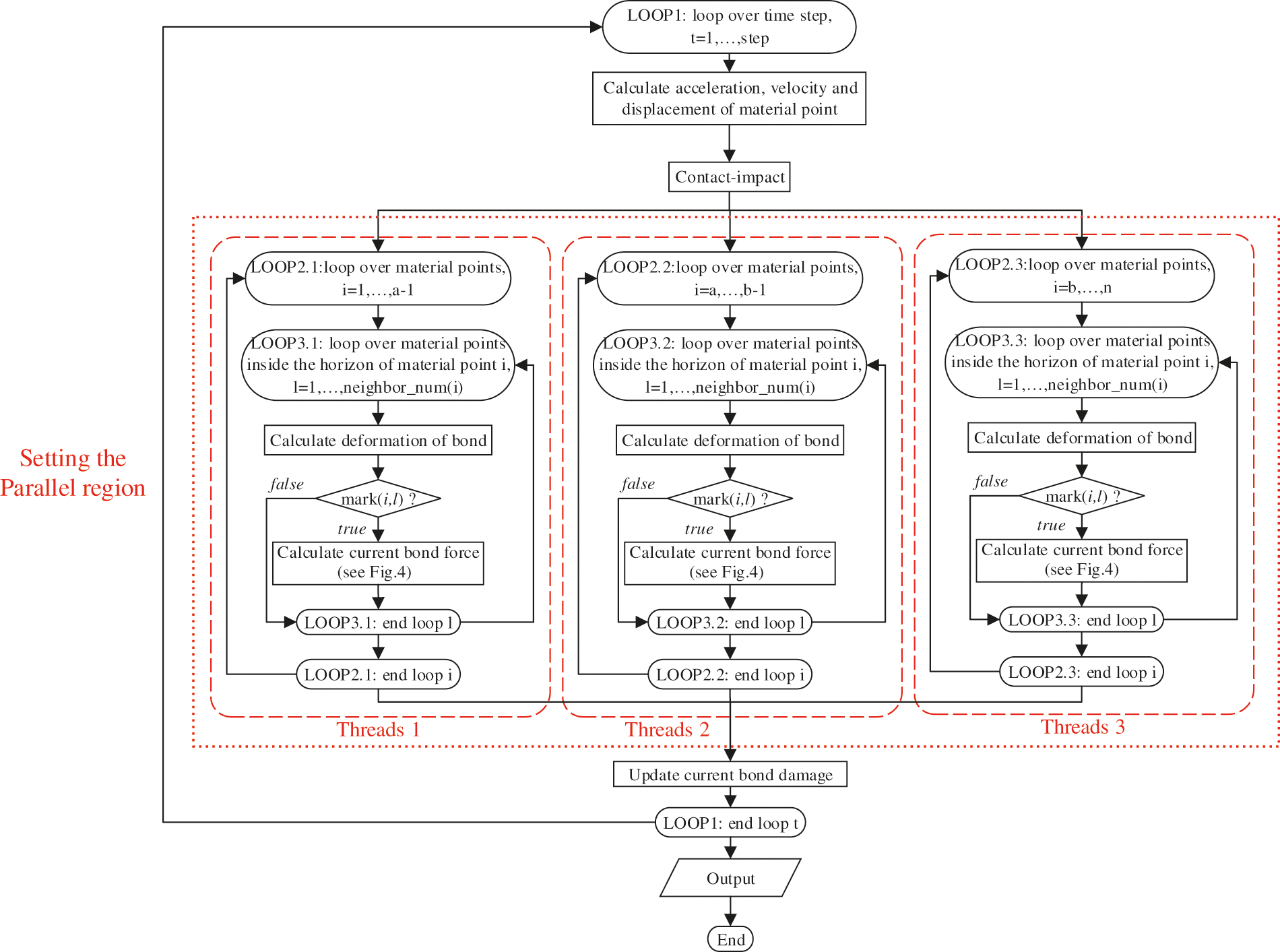
Figure 7: The parallelization flow chart of the bond force update module

After setting the parallel area of the program, in order to avoid possible data competition, we need to define the variables of the program, as shown in Fig. 8. One should note that certain arrays are only used for reading, such as initial coordinates of the particles, current coordinates, total displacement, displacement in a unit time step. Moreover, in the particle loop, the array with clear directivity is only read and written once, such as the array bond_force_n(:,:,:), whereas the bond_force_t(:,:) is used to store the tangential bond force and normal bond force of the bond pair. As there is no competition during operation, it is set as a public variable. The array ten_broken(i) is used to store the number of bonds broken by tensile-shear. Owing to the role of logical array mark(:,:), it may be read and written in multiple threads at the same time. When it is defined as a public variable, the atomic clause in the OpenMP function library can be added before writing to the array to prevent multiple threads from rewriting the same address in memory concurrently. For cyclic variables and the one-dimensional array used to store the information of bonds between material points, such as ξij, ηij, s, s˙, γ, λ in line number 12 to 17 in Table 1, if it is set as a public variable, each thread will read and write it, leading to severe data competition. Therefore, it can only be set as a private variable and stored in the private variable copy of each sub-thread. Each child thread can only read and write copies of its private variable copy, avoiding the phenomenon of data competition.

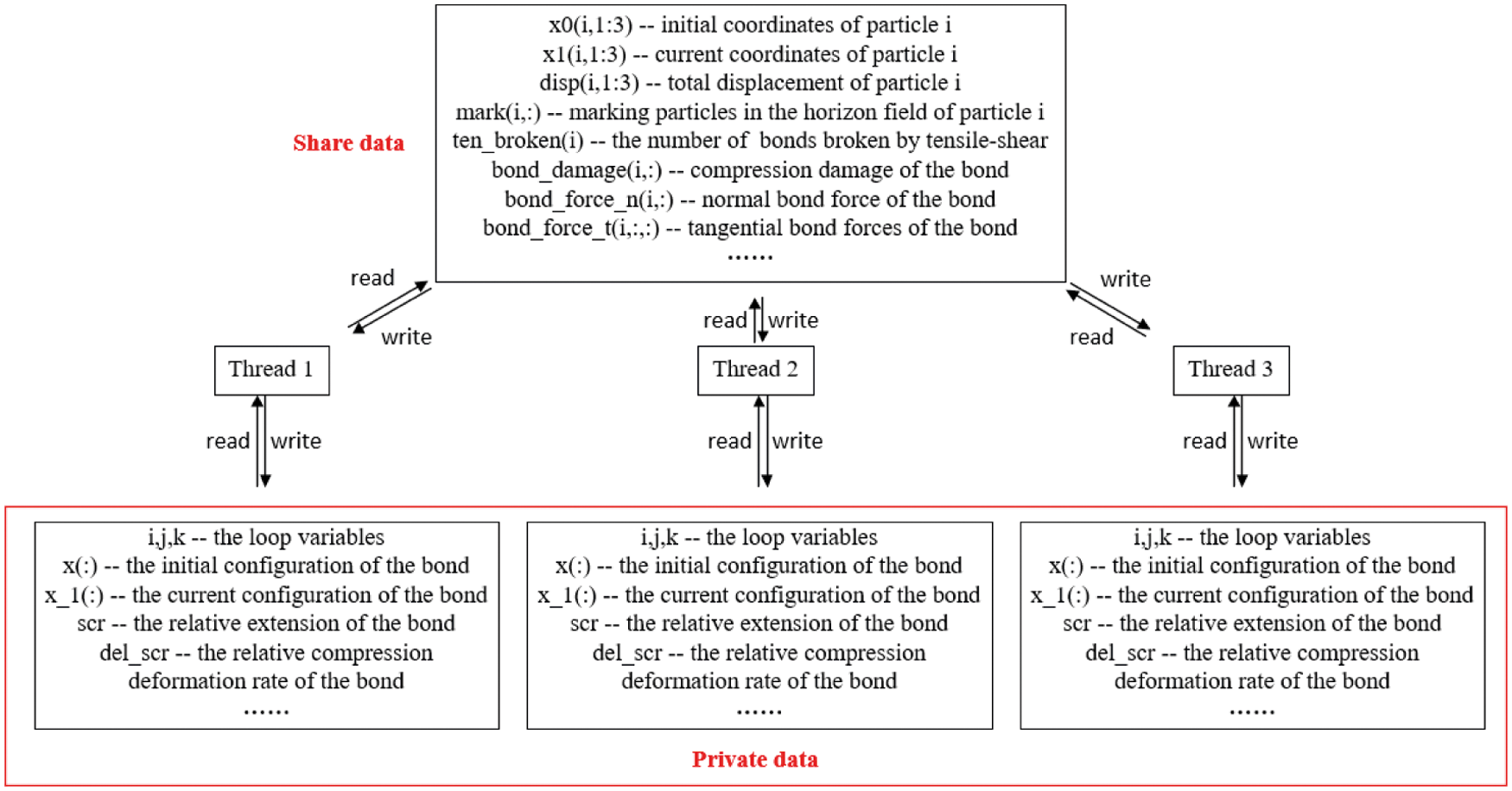
Figure 8: The definition of data when setting the parallel area

During bond force calculation, the calculation time of bond force for each particle and all particles in its horizon range is different due to the different number of adjacent particles of each particle. OpenMP is mainly parallelized for the loop body. The loop will be allocated to each thread for calculations, and the calculation time of each thread will not necessarily be the same. Also, the completed thread will not be integrated into the main program until the completion of other threads, leading to the imbalance of computing load. Therefore, this paper selects the guiding scheduling method to schedule the threads during the bond force calculation module and adds the schedule (guided) clause after the parallel statement (line 5 in Table 1). The scheduling process is shown in Fig. 9. The guided scheduling will first divide the loop into task blocks of different sizes according to the differences of nodes in each particle neighborhood. The iteration block allocated to each thread will be relatively large at the beginning and gradually reduce later, ensuring the load balance of threads during execution.

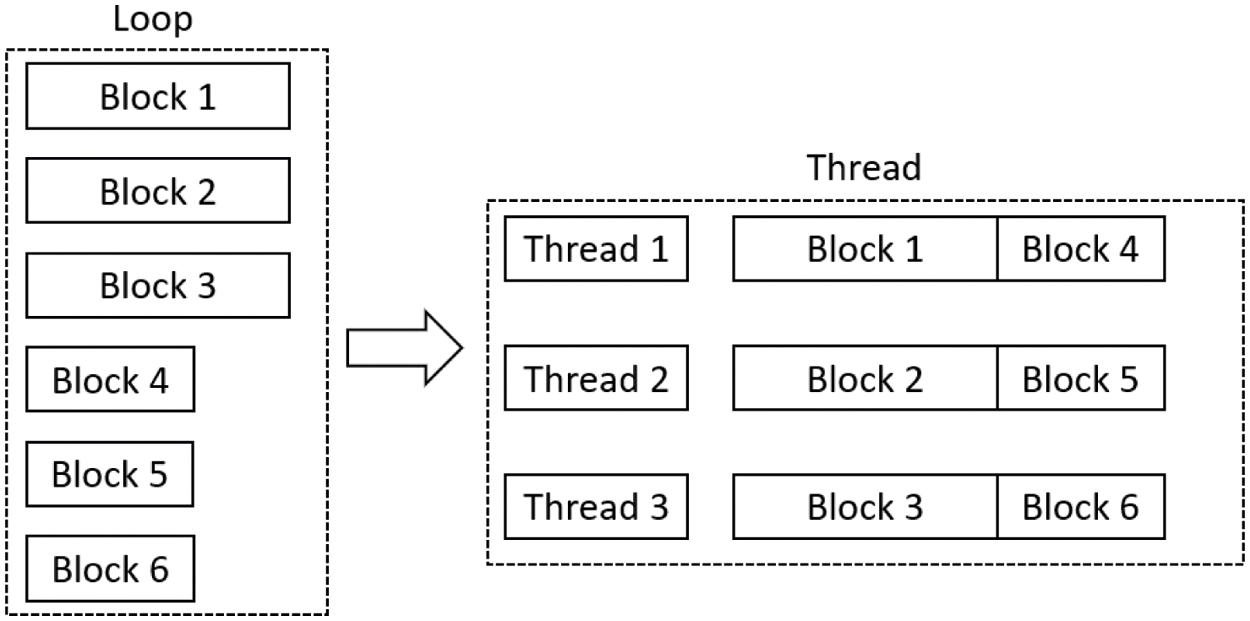
Figure 9: The process of guided schedule

For damage calculations, the calculations are performed based on the combined damage conditions between the material point and neighboring points. After the bond is damaged by the tensile-shear load, the bond no longer continues to bear the load. In the bond force calculation module, when it is determined that the bond is broken by the tensile-shear load, the number of bond breaks of the particle is calculated through the shared variable array ten_broken. When the bond is subjected to compressive-shear load, the damage will be stored in the two-dimensional public variable array bond_damage. It can be seen from the damage function of Eq. (8) that the total damage of a particle is calculated based on the bond loss between the particle and neighbors. The default static scheduling method is adopted, i.e., the total number of loop iterations is n, the total number of threads in the parallel domain is p, and each thread is allocated approximately n/p consecutive iterations.

In the process of parallelization and debugging of the entire program, different operating functions under the OpenMP runtime environment are used, such as omp_set_num_threads for setting thread functions and omp_get_wtime for measuring time. These functions can only be called from outside the parallel region.

4  Results and Efficiency

The simulation of dynamic response of SiC ceramic plates, with three different particle sizes under the impact of steel columns, was conducted with number of threads (N), ranging from 1 to 32 in a CPU model of dual-socket Intel(R) Xeon(R) Gold 6248R CPU@3.00 GHz. The OpenMP fortran90 code was compiled by using the Intel Parallel Studio XE 2013. The model size is shown in Fig. 10, where a steel column impacts a silicon carbide (SiC) ceramic target plate (60 × 60 × 8 mm3), and normal fixed constraints were applied on the backside of the plate. The material properties of SiC and steel used in this paper are shown in Table 2. The elastic compressive limit and the compression limit are specified as se = 0.0061 and s1 = 0.0213. The diameter of the rigid steel column is 10 mm, the height is 15 mm and the mass is 9.3 g. Herein, the steel column is modeled to impact on the SiC ceramic plates at different initial speeds, and four different impact speeds of 175 m/s, 300 m/s, 400 m/s and 500 m/s are chosen, respectively. The spacing Δx of three sizes of particles is 1 mm, 0.67 mm and 0.5 mm, respectively, and the size of particles corresponding to the model is 60 × 60 × 8, 90 × 90 × 12 and 120 × 120 × 16. The neighborhood horizon was set as 3 times of particle spacing, i.e., δ = 3Δx. The unit time step was Δt = 2.0 × 10−9s and the total calculation time step was 12,000 steps.

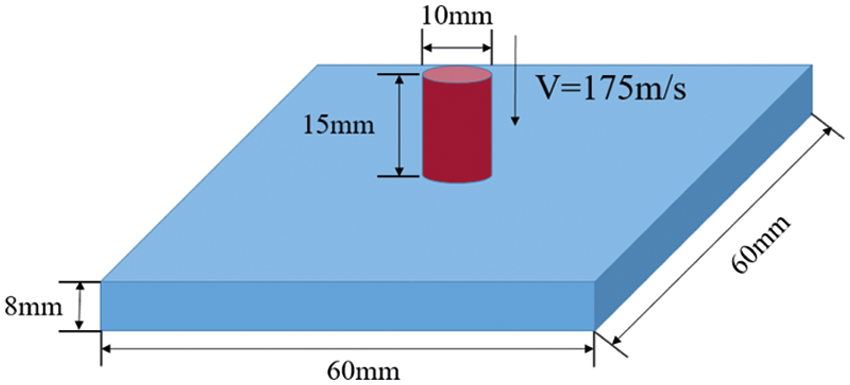
Figure 10: The schematic illustration of the SiC ceramic impact-loading

In order to verify the correctness of the calculation results, the serial results of three examples are compared with the parallel results. The results reveal that the parallel results are consistent with the serial results, and the parallel calculations do not affect the accuracy. The simulation results are compared with the experimental results [34], as shown in Fig. 11. Example 1, example 2 and example 3 correspond to three different particle size models of 60 × 60 × 8, 90 × 90 × 12 and 120 × 120 × 16 at an impact velocity of 175 m/s. The simulation results of the same particle model (90 × 90 × 12) at different initial speeds are compared, as shown in Table 3.

Figure 11: The comparison between simulation and experimental results

Fig. 11 shows that, when SiC ceramic plate with the same model size and different particle sizes is impacted by the steel column, the simulation results of three examples are consistent with the experimental results. On the other hand, it can be seen that the smaller particle spacing corresponds to denser damage crack and more accurate description of the crack path. It can be seen from the damage of ceramic plate under impact at different speeds in Table 3 that with the increase of impact speed of steel column, Table 3 shows that the conical and radial crack of ceramics at low to high impact velocity can be well captured, with the propagation and superposition degree of stress wave in the ceramic plate increases, the damage range on the back of ceramic plate increases in turn, the damage degree is more serious, and the radial cracks on the top and back are more dense.

In order to compare the calculation efficiency, the concepts of speed-up ratio and parallel efficiency [35] in parallel computing are used to compare the improvement of calculation efficiency. For the overall program, the number of threads performing parallel part of the work is N, and the potential speed-up can be given by Eq. (18):

Si=11−P+P/N(18)

Among them, P is the parallel code part of the program. For the serial program obtained from the three examples, the running time of each module shows that the strictly non-parallel part of the code is less than 0.29%. In parallel programming, the speed-up ratio Sp of a code can be defined as Eq. (19):

SP=TcTb(19)

where Tc is the time spent in CPU calculations of the serial algorithm. In this paper, we regard the parallel code has the same computational efficient with the serial code when it is running with single thread. And Tb represents the time consumed in CPU calculations of the parallel algorithm with different numbers of threads, and the parallel efficiency Ep can be defined as Eq. (20):

EP=SPN(20)

In the abovementioned three examples, the overall running time of the program under different thread numbers is shown in Fig. 12, showing simulation time vs. the number of threads participated in the computations. The speed-up ratio (Sp) and efficiency (Ep) of the code are also plotted with their respective ideal cases of a strictly non-parallel portion 0.29% in Fig. 13.

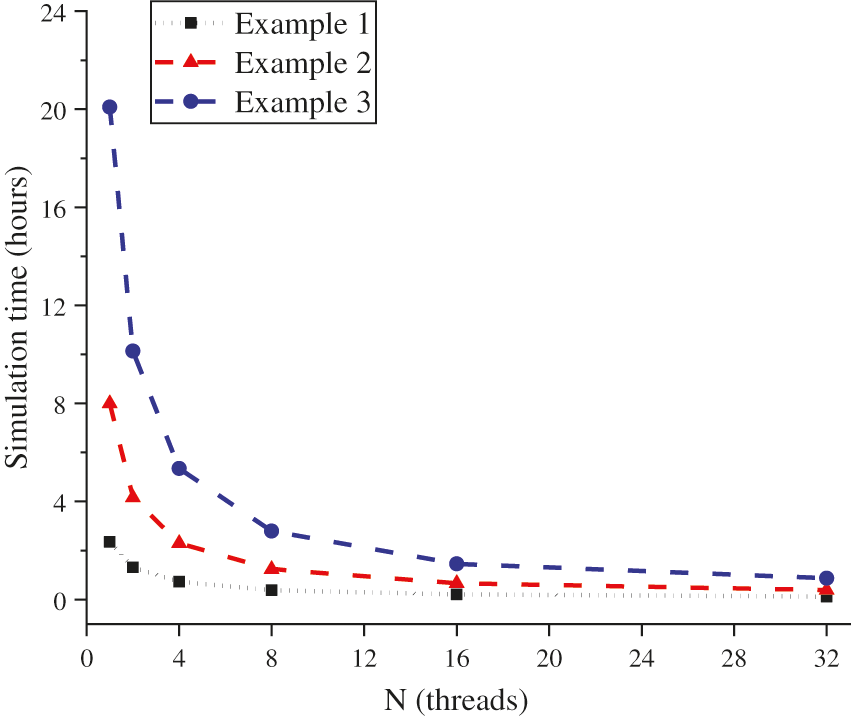
Figure 12: The simulation time cost vs. the number of threads participated (unit: h)

As shown in Fig. 12, in all three cases, it can be clearly seen that the simulation time decreases rapidly during first few number of threads and gradually slows down until almost reaching a plateau.

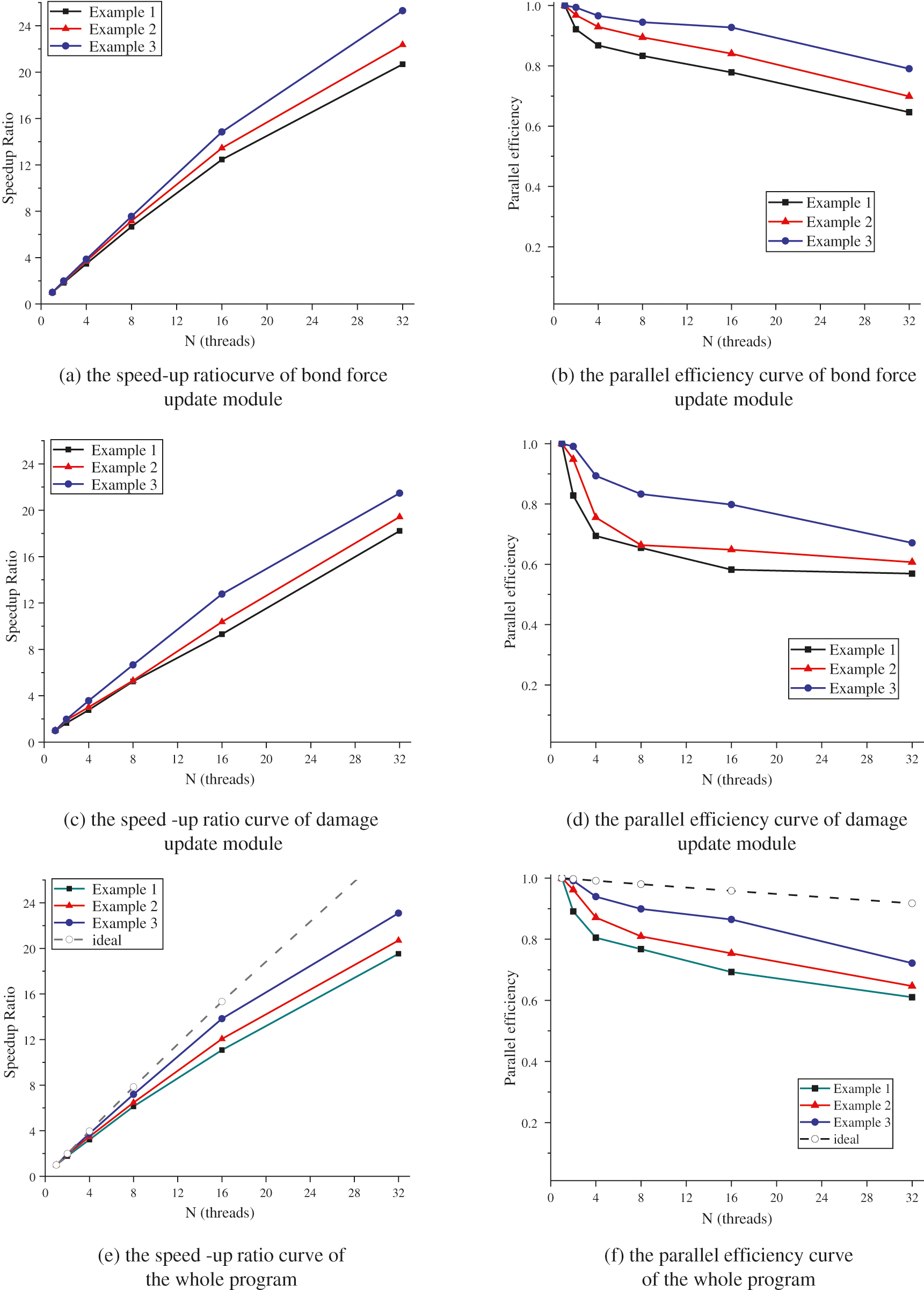
Figure 13: The performance of OpenMP parallel code

Fig. 13 shows that the acceleration ratio curves exhibited an upward trend with increasing number of threads. Moreover, an increase in particle size enhanced the speed-up ratio when the same number of threads is allocated because the overhead of managing threads increased to a certain extent with the increase of allocated threads. This is the overhead of OpenMP's own parallelism and it gradually increases with the increase of number of threads. In the case of a smaller particle size, less time is required for calculations. Therefore, for three examples with different particle sizes, the higher number of parallel threads resulted in obvious differences in parallel speed-up ratio.

Furthermore, the efficiency curves exhibited an obvious downward trend with increasing particle size, which can be explained by several reasons. First, the threads set in the parallel area may have sufficient computing power but, since the processor shares the memory bandwidth, the computing performance declines when the threads compete for the shared memory bandwidth. Therefore, there is a critical number of threads for the fixed scale particle model. When the number of threads exceeds the critical value, the increase in number of parallel threads does not reduce the simulation time. Second, data synchronization requires that sequential processes are completed. In a particular computation block, some threads may complete the assigned task in advance, but they cannot continue until all threads are completed. In addition, the comparison of acceleration ratio and parallel efficiency curves of the parallel module with the overall acceleration ratio and parallel efficiency curves indicates that the overall acceleration ratio and parallel efficiency curve are lower than the acceleration ratio and parallel efficiency curve obtained by each module. One should note that all programs are not parallelized in this paper. Considering the overhead between parallelization and thread allocation of modules with a small time-consuming proportion, this paper only parallelizes the bond force update part and damage update part with a large time-consuming proportion. At the same time, many other common problems in parallel computing may also affect the overall speed of the program, such as memory hierarchy of the processor, data writing and acquisition.

5  Conclusions

The integral form of the peridynamic equation renders certain advantages in analyzing and dealing with discontinuities. Moreover, the rate-dependent BB-PD model considering the rotation effect can more accurately describe the dynamic response of ceramic materials under the impact load. However, considering the strain rate effect during the compression stage and accumulation of damage caused by compressive plastic softening, the calculation amount of bond force and damage part is larger, which is also one of the problems in practical applications. Herein, we have discussed the computational and algorithmic structure of the OpenMP parallelization of the rate-dependent BB-PD model considering the rotation effect in detail. A numerical example of the projectile, penetrating a ceramic target, has been performed using OpenMP parallel computing. By running the simulations with number of threads (1–32), the computational time, speed-up ratio, and parallel efficiency of the proposed model have been analyzed. The results revealed that, compared with the serial program, the parallel program obtained a speed-up ratio of 1.7–23 times under the condition of ensuring the calculation accuracy, and the running time of the program has been greatly reduced. However, the parallel efficiency decreased with an increase in number of threads. Herein, we have demonstrated that OpenMP could effectively deal with the time-consuming part of the large-scale rate-dependent BB-PD model and save computing time. However, with the increase in number of threads, the parallel efficiency declined owing to the imbalance between computing load and data storage structure. In the future, we shall further test and optimize the data storage structure and program scheduling of parallel programs.

Funding Statement: This research is supported by the National Natural Science Foundation of China (Nos. 11972267, 11802214 and 51932006) and the Fundamental Research Funds for the Central Universities (WUT: 2020lll031GX).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study

References

 1.  Dong, B., Wei, R. B., Zong, H., Wang, X. W., Zhang, W. T. et al. (2020). The energy absorption mechanism and influential factors of ceramic/fiber reinforced polymer composite hybrid armour. Ordnance Material Science and Engineering, 43(5), 128–136. DOI 10.14024/j.cnki.1004-244x.20200616.001. [Google Scholar] [CrossRef]

 2.  Zhou, X. P., Wang, Y. T., Shou, Y. D., Kou, M. M. (2018). A novel conjugated bond linear elastic model in bond-based peridynamics for fracture problems under dynamic loads. Engineering Fracture Mechanics, 188(1), 151–183. DOI 10.1016/j.engfracmech.2017.07.031. [Google Scholar] [CrossRef]

 3.  Silling, S. A. (2000). Reformulation of elasticity theory for discontinuities and long-range forces. Journal of the Mechanics and Physics of Solids, 48(1), 175–209. DOI 10.1016/S0022-5096(99)00029-0. [Google Scholar] [CrossRef]

 4.  Silling, S. A. (2003). Dynamic fracture modeling with a meshfree peridynamic code. Computational Fluid and Solid Mechanics, 2003, 641–644. DOI 10.1016/B978-008044046-0.50157-3. [Google Scholar] [CrossRef]

 5.  Silling, S. A., Epton, M., Weckner, O., Xu, J., Askari, E. (2007). Peridynamic states and constitutive modeling. Journal of Elasticity, 88(2), 151–184. DOI 10.1007/s10659-007-9125-1. [Google Scholar] [CrossRef]

 6.  Silling, S. A. (2010). Linearized theory of peridynamic states. Journal of Elasticity, 99(1), 85–111. DOI 10.1007/s10659-009-9234-0. [Google Scholar] [CrossRef]

 7.  Gerstle, W. H., Sau, N., Sakhavand, N. (2009). On peridynamic computational simulation of concrete structures. Special Publication, 265(1), 245–264. [Google Scholar]

 8.  Tuniki, B. K. (2012). Peridynamic constitutive model for concrete. Mexico: Osmania University. [Google Scholar]

 9.  Yang, D., Dong, W., Liu, X. F., Yi, S. H., He, X. Q. (2018). Investigation on mode-I crack propagation in concrete using bond-based peridynamics with a new damage model. Engineering Fracture Mechanics, 199(1), 567–581. DOI 10.1016/j.engfracmech.2018.06.019. [Google Scholar] [CrossRef]

10. Liu, M. H., Wang, Q., Wei, L. (2017). Peridynamic simulation of brittle-ice crushed by a vertical structure. International Journal of Naval Architecture and Ocean Engineering, 9(2), 209–218. DOI 10.1016/j.ijnaoe.2016.10.003. [Google Scholar] [CrossRef]

11. Lai, X., Ren, B., Fan, H. F., Li, S. F., Wu, C. T. et al. (2015). Peridynamics simulations of geomaterial fragmentation by impulse loads. International Journal for Numerical Analytical Methods in Geomechanics, 39(12), 1304–1330. DOI 10.1002/nag.2356. [Google Scholar] [CrossRef]

12. Lai, X., Liu, L. S., Li, S. F., Zeleke, M., Liu, Q. W. et al. (2018). A Non-ordinary state-based peridynamics modeling of fractures in quasi-brittle materials. International Journal of Impact Engineering, 111(1), 130–146. DOI 10.1016/j.ijimpeng.2017.08.008. [Google Scholar] [CrossRef]

13. Zhao, J. J., Lu, G. D., Zhang, Q., Du, W. C. (2021). Modelling of contact damage in brittle materials based on peridynamics. Computer Modeling in Engineering & Sciences, 129(2), 519–539. DOI 10.32604/cmes.2021.017268. [Google Scholar] [CrossRef]

14. Song, Y., Yan, J. L., Li, S. F., Kang, Z. (2019). Peridynamic modeling and simulation of ice craters by impact. Computer Modeling in Engineering & Sciences, 121(2), 465–492. DOI 10.32604/cmes.2019.07190. [Google Scholar] [CrossRef]

15. Tupek, M. R., Radovitzky, R. (2014). An extended constitutive correspondence formulation of peridynamics based on nonlinear bond-strain measures. Journal of the Mechanics and Physics of Solids, 65(1), 82–92. DOI 10.1016/j.jmps.2013.12.012. [Google Scholar] [CrossRef]

16. Lee, J., Liu, W. Y., Hong, J. (2016). Impact fracture analysis enhanced by contact of peridynamic and finite element formulations. International Journal of Impact Engineering, 87(1), 108–119. DOI 10.1016/j.ijimpeng.2015.06.012. [Google Scholar] [CrossRef]

17. Ma, P. F., Li, S. C., Zhou, H. Y., Zhao, S. S., Wang, P. C. et al. (2021). Peridynamic method to determine energy absorption characteristics of ordinary glass under impact load. International Journal of Crashworthiness, 26(2), 227–235. DOI 10.1080/13588265.2019.1701890. [Google Scholar] [CrossRef]

18. Kazemi, S. R. (2020). Plastic deformation due to high-velocity impact using ordinary state-based peridynamic theory. International Journal of Impact Engineering, 137(3), 103470.1–103470.9. DOI 10.1016/j.ijimpeng.2019.103470. [Google Scholar] [CrossRef]

19. Deng, X., Sun, S. (2019). Numerical investigation of impact breakage mechanisms of two spherical particles. Powder Technology, 364(10), 954–962. DOI 10.1016/j.powtec.2019.10.059. [Google Scholar] [CrossRef]

20. Liu, R. W., Yan, J. L., Li, S. F. (2019). Modeling and simulation of ice–water interactions by coupling peridynamics with updated lagrangian particle hydrodynamics. Computational Particle Mechanics, 7(11–12), 241–255. DOI 10.1007/s40571-019-00268-7. [Google Scholar] [CrossRef]

21. Chen, Z., Chu, X. H. (2021). Peridynamic modeling and simulation of fracture process in fiber-reinforced concrete. Computer Modeling in Engineering & Sciences, 127(1), 241–272. DOI 10.32604/cmes.2021.015120. [Google Scholar] [CrossRef]

22. Chu, B. F., Liu, Q. W., Liu, L. S., Lai, X., Mei, H. (2020). A Rate-dependent peridynamic model for the dynamic behavior of ceramic materials. Computer Modeling in Engineering & Sciences, 124(1), 151–178. DOI 10.32604/cmes.2020.010115. [Google Scholar] [CrossRef]

23. Liu, Y. X., Liu, L. S., Mei, H., Liu, Q. W., Lai, X. (2022). A modified rate-dependent peridynamic model with rotation effect for dynamic mechanical behavior of ceramic materials. Computer Methods in Applied Mechanics & Engineering, 388(24), 114246. DOI 10.1016/j.cma.2021.114246. [Google Scholar] [CrossRef]

24. Liu, S. S., Hu, Y. L., Yu, Y. (2016). Parallel computing method of peridynamic models based on GPU. Journal of Shanghai Jiaotong University, 50(9), 1362–1367. DOI 10.16183/j.cnki.jsjtu.2016.09.005. [Google Scholar] [CrossRef]

25. Navid, S. (2011). Parallel simulation of reinforced concrete structures using peridynamics. Albuquerque: University of New Mexico. [Google Scholar]

26. Xu, F. Z., Zhang, J. F. (2020). Parallel implementation of peridynamic simulation based on OpenMP. Journal of Henan Polytechnic University, 39(5), 130–138. DOI 10.16186/j.cnki.1673-9787.2020.5.19. [Google Scholar] [CrossRef]

27. Mossaiby, F., Shojaei, A., Zaccariotto, M., Galvanetto, U. (2017). OpenCL implementation of a high performance 3D peridynamic model on graphics accelerators. Computers and Mathematics with Applications, 74(8), 1856–1870. DOI 10.1016/j.camwa.2017.06.045. [Google Scholar] [CrossRef]

28. Parks, M. L., Lehoucq, R. B., Plimpton, S. J., Silling, S. A. (2007). Implementing peridynamics within a molecular dynamics code. Computer Physics Communications, 179(11), 777–783. DOI 10.1016/j.cpc.2008.06.011. [Google Scholar] [CrossRef]

29. Diehl, P., Schweitzer, M. A. (2015). Efficient neighbor search for particle methods on GPUs. In: Meshfree methods for partial differential equations VII, vol. 100, pp. 81–95. Springer. [Google Scholar]

30. Boys, B., Dodwell, T. J., Hobbs, M., Girolami, M. (2021). PeriPy--A high performance OpenCL peridynamics package. Computer Methods in Applied Mechanics and Engineering, 386(1), 114085. DOI 10.1016/j.cma.2021.114085. [Google Scholar] [CrossRef]

31. Diehl, P., Jha, P. K., Kaiser, H., Lipton, R., Lévesque, M. (2020). An asynchronous and task-based implementation of peridynamics utilizing HPX-the C++ standard library for parallelism and concurrency. SN Applied Sciences, 2(12), 1–21. DOI 10.1007/s42452-020-03784-x. [Google Scholar] [CrossRef]

32. Zhu, Q. Z., Ni, T. (2017). Peridynamic formulations enriched with bond rotation effects. International Journal of Engineering Science, 121(1), 118–129. DOI 10.1016/j.ijengsci.2017.09.004. [Google Scholar] [CrossRef]

33. Liu, Q. K., Teng, R. D., Liu, F., Gong, L. D., Zhang, J. Q. (2011). Application of multi-core parallel technology in molecular dynamic simulation. Computer Engineering and Design, 32(10), 3395–3398. DOI 10.1080/01932691003662381. [Google Scholar] [CrossRef]

34. Zinszner, J. L., Forquin, P., Rossiquet, G. (2015). Experimental and numerical analysis of the dynamic fragmentation in a SiC ceramic under impact. International Journal of Impact Engineering, 76, 9–19. DOI 10.1016/j.ijimpeng.2014.07.007. [Google Scholar] [CrossRef]

35. Fan, H. F., Li, S. F. (2017). Parallel peridynamics–SPH simulation of explosion induced soil fragmentation by using OpenMP. Computational Particle Mechanics, 4(2), 199–211. DOI 10.1007/s40571-016-0116-5. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.