Computer Modeling in Engineering & Sciences

---

DOI: 10.32604/cmes.2022.020793

ARTICLE

Performance Analysis of an Artificial Intelligence Nanosystem with Biological Internet of Nano Things

Saied M. Abd El-atty1,* Nancy A. Arafa1, Atef Abouelazm1, Osama Alfarraj2, Konstantinos A. Lizos3 and Farid Shawki1

1Department of Electronics and Electrical Communications Engineering, Faculty of Electronic Engineering, Menoufia University, Menouf, Egypt
2Computer Science Department, Community College, King Saud University, Riyadh, Saudi Arabia
3Department of Informatics, Faculty of Mathematics and Natural Sciences, University of Oslo (UiO), Oslo, Norway
*Corresponding Author: Saied M. Abd El-atty. Email: sabdelatty@el-eng.menofia.edu.eg
Received: 13 December 2021; Accepted: 11 February 2022

1  Introduction

Nanotechnology has recently allowed scientists to view intra-body systems, allowing us to create a synthetic nano-scale system that matches the natural cell system. This technique offers a wide range of applications, particularly in the field of nanomedicine. The nanotransmitter nanomachine (TN) and the nanoreceiver nanomachine (RN) are the two nanoscale machines that make up a nanosystem. Such a system could be implanted into the human body and could be used for medical applications, such as healthcare monitoring, disease detection and treatment, or advanced targeted drug delivery (ATDD) systems. The biological system, as is well known, is made up of groupings of entities or organs (cellular networks) that work together to fulfill a certain activity in the human body. The cellular network of body organs (brain, liver, heart, lung, kidney, etc.) must be recognized appropriately. Naturally, each disease in the body is caused or exacerbated by a breakdown in the communication between the organ's cells. We investigate the occurrence of diseases as a result of failure/irregular communication among biological entities in the human body to contextualize this engineering problem. Furthermore, nanotechnology has suggested that the prospective molecular communications technology is the best way to define the TN-RN connectivity framework [1]. Recently, significant efforts have been made to integrate 6G and nanonetwork-based molecular communication for modeling targeted drug delivery [2–4]. In reality, due to its biocompatibility, molecular communication (MC) is the preferred approach for AI technology utilized in nanomedical applications, highlighting advanced targeted nanomedicine (ATN) [5]. MC is founded on the idea of using biochemical signaling to understand the information exchange between naturally occurring and/or artificially created nanosystems over short distances. As a result, the MC is regarded as a communication engineering problem that delivers relevant information for nanomedical applications, particularly in the healthcare industry (HCI) [6,7].

In the prospective ATN, AI technology can be used to manage medicine delivery to the desired site. Furthermore, due to the Coronavirus disease (COVID 19), medical doctors can use the Internet of biological Nano Things (IoBNT)-based AI technology to contact their patients remotely and therefore avoid getting sick. Fig. 1 depicts an illustrative example of the ATN based on the IoBNT paradigm and the intelligent nanosystem [5]. The IoBNT is based on the Internet of Things (IoT) in order to achieve communication coordination between the AI nanosystems and external network such as Internet and similar to the social networks based on Internet of Thing (IoT) which is based on the AT technology [8,9]. The function of the biocyber interface, on the other hand, is to convert an electromagnetic (EM) wave into a biological signal, as described in [10,11]. The intra-body area network (IBAN)-based MC system is implemented using the following artificial intelligence nano-scale machines, as shown in Fig. 1: nanotransmitter (TN) for drug information molecule emission, molecular channel for propagation (i.e., vessel blood medium), and nanoreceiver (RN) for reception. Furthermore, various nanosensors were used to capture the essential data and transfer it to a nanotransmitter or nanoreceiver. Additionally, the nanosensor is actually a nanomachine, similar to a transceiver that can send and receive molecular information from the bio-cyber interface. For example, it detects/collects variations in the implanted nanonetwork environment (which represents the status of the diseased cell), and then sends the information to the bio-cyber, delivered to medical personnel to make a decision. We explore a scenario in which ATN-based IoBNT is used to diagnose and treat diseased cells in any biological system, including the heart, respiratory, nervous, and circulatory systems. We use AI nanosystem made up of TN and RN that is implanted near the diseased cell. In molecular communication (MC), the drug information is conveyed from TN to RN via the propagation property, while molecules transport the required information at the same time, according to cell-cell communication. There are several propagation schemes for transporting information molecules, including free diffusion [7], also known as Brownian motion; in this propagation scheme, the molecules carry drug information from the TN to the RN while simultaneously receiving energy from naturally occurring adenosine triphosphate (ATP). One of the most well-known propagation strategies in life science is the flow diffusion approach, which simulates propagation in the bloodstream [12]. Another nanomachine mobility-based propagation techniques, such as mobile MC systems [6,13,14], have been proposed.

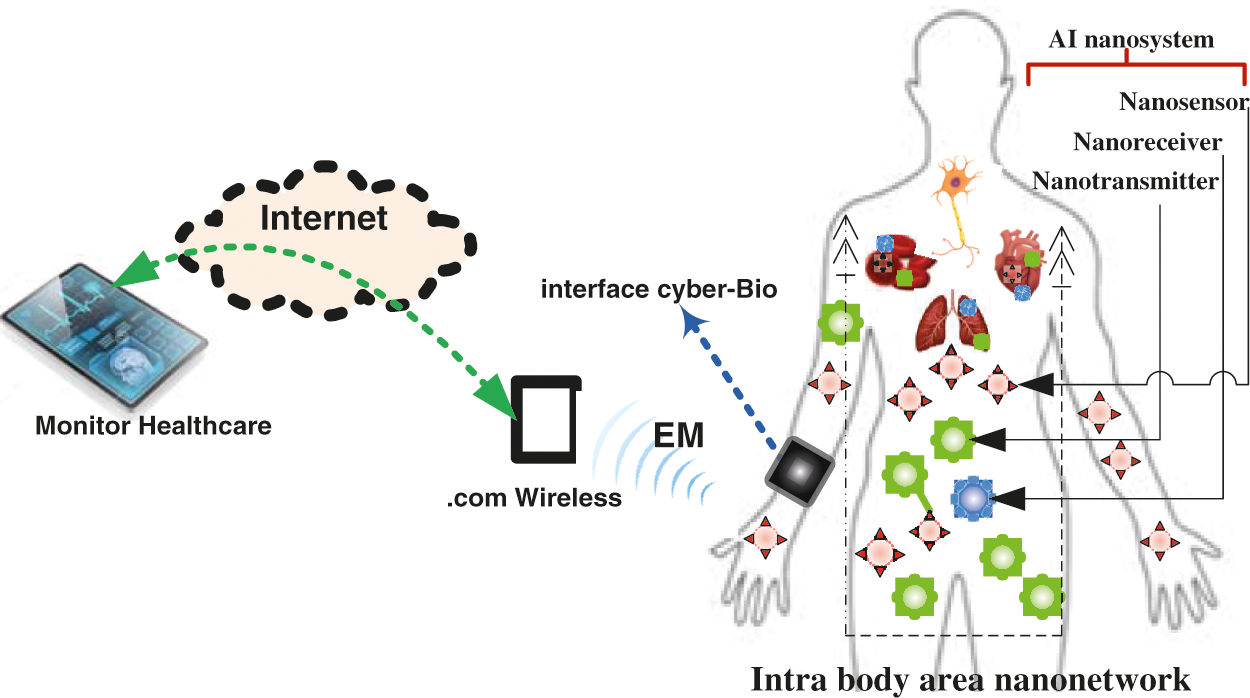
Figure 1: An illustrative design of IoBNT-based AI nanosystem

In molecular communication systems, binary information can be transferred on a time slot-by-slot basis, i.e., each time slot carries the appropriate information, as inspired by wireless communication networks. Furthermore, many forms of binary modulation techniques for transferring molecular information have been developed. To produce the appropriate signal, the transmitted binary bits can be modulated in the form of molecular concentration [15,16], molecule type [17], or molecule releasing time [18]. The detecting process at the RN, which is based on chemical reactions or the ligand-receptor mechanism, ensures successful molecular transport. The RN can be either a passive or an active receiver. The passive receiver employs passive reception methods and does not obstruct signaling molecule movement. In the MC literature, this style of receiver is frequently used to good effect [19]. Absorption by the active receiver may impact the mobility of signaling molecules. More precisely, when the released molecules meet the receiver's receptors, they are either absorbed instantly [20] or chemically react with them (i.e., the output signal is generated by the reversible reaction of the released molecules with the receptors at the receiver surface) [21].

2  Main Contributions and Motivation

The increased focus on nanotechnology and artificial intelligence has resulted in a wide range of applications, particularly in the nanomedicine field. The challenging issue of the nanomedicine framework is determining the patient's status and controlling nanomedical processes such as diagnostic, monitoring, and therapeutic using real-time information. Actually, ATN is based on information exchange and communication between the human intra-body network and an external network such as the Internet. Furthermore, molecular communications based on nanosystems can provide interconnection between the nanosystem and the external network to acquire treatment course and dose decisions. Exploring the benefits of nanomedicine necessitates the use of a diverse set of techniques, such as artificial intelligence nanosystems and AI tools, to improve the efficacy of future healthcare systems. However, in addition to these enablers, several challenges in the development of nanosystems have been identified. In order to overcome such challenges, researchers are encouraged to develop and implement solutions for the communication engineering complexity that occurs in such artificial intelligence nanosystems. As a result, in this study, the ATN is viewed as a molecular communication (MC) engineering problem based on the Internet of biological nanothings and AI technology. For example, in order to determine the desired therapeutic drug concentration at the targeted diseased cell, we must consider the changing of channel conditions caused by noise and ISI, as well as other physical parameters in the human body.

In this paper, we inspect the channel capacity of the proposed AI nanosystem in the presence of noise and inter-symbol interference (ISI). Noise is caused by a chemical reaction within the blood channel media, whereas ISI is caused by a concentration overlap between the current and previously received molecules from a TN. As a result, we investigate the impact and influence of physical characteristics in the human body, such as blood pressure, blood viscosity, and vascular size, on channel capacity. Blood pressure readings are important predictors of therapeutic decisions, and they are one of the most commonly measured clinical indicators. The thickness and stickiness of a person’s blood is measured by blood viscosity. It is a measurement of the ability of blood to flow through blood vessels.

The remainder of this paper is organized as follows. Section 3 introduces the related work. The system model and design of the molecular communication system are provided in Section 4. Section 5 provides the performance of the proposed AI nanosystems in the presence of noise and ISI, while Section 4 discusses the performance analysis of the channel capacity. Section 6 presents the numerical results, while Section 7 contains the conclusions.

3  Related Works

The application of molecular communication in nanomedicine has gotten a lot of interest in recent days. The channel capacity of molecular communication systems is an important problem that should be thoroughly researched because the blood vessel serves as the channel medium. In [22], a closed-form mathematical expression for diffusion-based molecular communication’s information capacity is derived. Based on this, the authors investigated the effects of physical parameters such as temperature, molecule number, transmitting power, and system bandwidth. The authors of [23] presented a complete model of the MC system, from drug injection to drug delivery onto the targeted cell via the vascular blood vessel in the human body. As a result, they developed a mathematical expression for the capacity of particulate drug delivery systems under noise constraints. In [24], a closed-form diffusion formula based on channel capacity was obtained by accounting for the effects of channel memory and molecular noise, and the upper bound of the capacity was analytically derived. The authors of [25] presented a deterministic capacity expression by assuming a single instantaneous emission of molecules by introducing a more realistic channel model for molecular communication. In [26], a discrete memory less approximation for the molecular channel-based diffusion is introduced, in the context of which the MC capacity is computed based on a binary coding scheme. The authors of [27] created a model for a molecular single-access channel and derived channel capacity expressions by employing the multiple-access method, which allows multiple transmitters to communicate with a single receiver. The capacity of the MC system in the case of a discrete noiseless system is examined in [28] by taking the channel memory effect into account.

Furthermore, the diffusion with drift is taken into account in specific literature. The authors of [29], for example, used a simulation program to determine the mutual information between the transmitter and receiver. They also considered how nanomachines and emitted molecules move through a fluid medium with Brownian motion and drift velocity. The authors have considered a molecular communication, with molecules propagating to the receiver through a fluid medium, in reference to [30]. They created a theoretical model for the additive inverse Gaussian noise channel and investigated whether the proposed model is more appropriate for molecular communications in fluid media with drift. The authors of [31] proposed a receiver scheme after modeling molecular communications inside blood vessels by considering mobile transmitters diffuse in the blood towards fixed receivers attached to the vessel walls.

Although the preceding works used MC-based diffusion, they ignored the main property of diffusion (slow velocity profile) as well as the physical parameters influencing the performance of the MC system. In this study, we consider a more realistic intelligent nanosystem MC system based on flow-based propagation found in the bloodstream, highlighting parameters such as temperature and viscosity in the cardio vascular channel, blood flow/velocity profile, and the influence of chemical reactions processed on propagating information molecules. Furthermore, we investigate the effect of the inter-symbol interference phenomenon on the efficiency of the investigated system in conjunction with the probability of error. In addition, we derive a closed-form expression for error probability.

4  System Model and Analysis

We consider an intelligent nanosystem paradigm that is implanted into the intra-body nanonetwork close to the diseased cell. The phenomena which include releasing the intelligence nanosystem onto the body, propagation through blood vessel network, physical design and the contact with targeted vessel wall (diseased cell), are elaborately presented in [32]. As a result, the movement of an intelligent nanosystem from its insertion into the intra-body nanonetwork to its final destination can be classified as an engineering communication phenomenon. Fig. 2 depicts the components of the proposed intelligent nanosystem. The intelligent nanosystem paradigm is made up of two fixed nanomachines: the nanotransmitter nanomachine (TN) and the nanoreceiver nanomachine (RN). The distance d between TN and RN, is illustrated in Fig. 2. The TN and RN communicate via a flow diffusion–based advection mechanism [33], which mimics a cardiovascular channel. Following that, information molecules (therapeutic drugs) are freely diffused in the cardiovascular channel due to Brownian motion and advection phenomena [32]. Unlike the electromagnetic (EM) channel, the cardiovascular channel has unique properties such as viscosity, distance factor, adhesion, reaction, and absorption that are heavily influenced by physical parameters such as temperature and pH within the intra-body nanonetwork. In summary, the following assumptions have been made for the proposed nanosystem:

•   As shown in Fig. 2, we consider a cross-sectional view of the cardiovascular system with length L and radius R.

•   TN is a point source that transports the same molecules as the cardiovascular channel (which is considered as the propagation medium).

•   We consider a binary transmission scheme based on a priori probability, a with ON/OFF keying, a bit 1 for IM (Information molecule) transport and a bit 0 otherwise.

•   Inspired by wireless networks, the cardiovascular channel is divided into T-second time slots that carry the binary IM.

•   TN and RN are considered perfectly synchronized by the proposed work in [34].

•   According to the characteristics of the cardiovascular channel, the IM follows the advection diffusion equation with positive drift due to the pressure of the bloodstream [35].

•   The reception of a molecular signal in the proposed nanosystem is occurred by binding mechanism, with binding reaction rate. The association and disassociation constant rates are denoted as kf and kr, respectively.

•   The additive noise and inter-symbol interference (ISI) are taken into account because of the chemical reaction with other nanoparticles (noise effect) in the blood vessel media and the residual influence of all previous transmitted bits at RN (ISI effect).

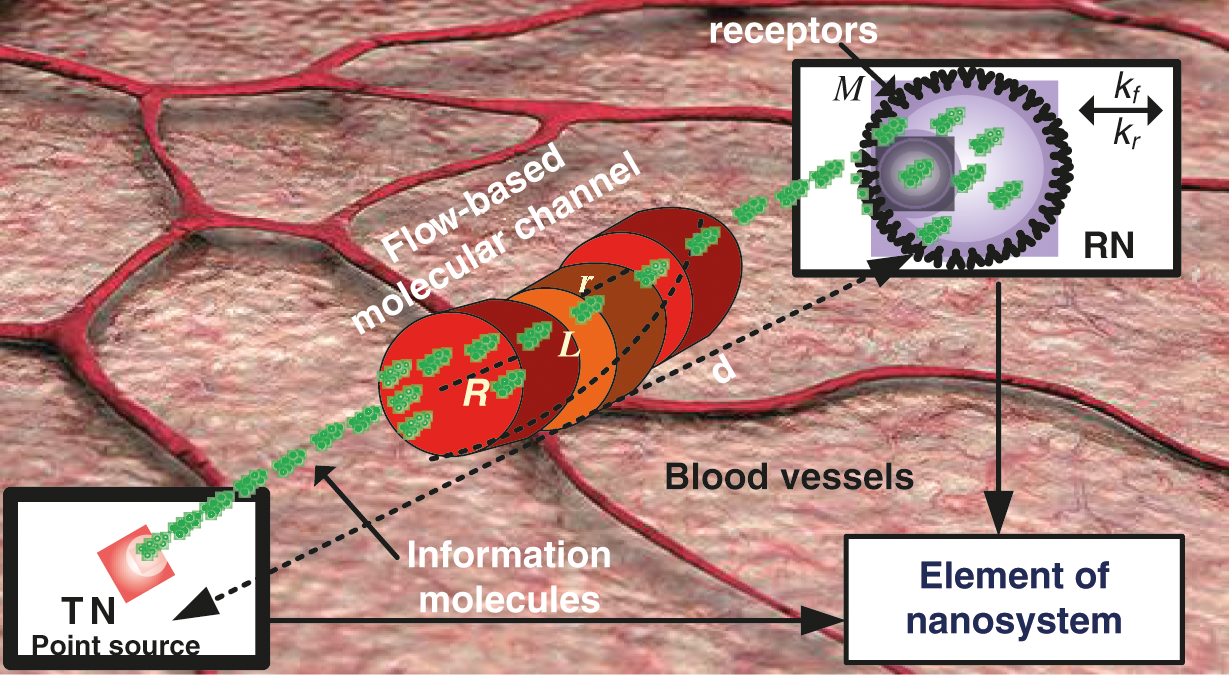
Figure 2: Illustration of the proposed nanosystem

As illustrated in the following subsections, the proposed molecular communications paradigm is inspired by conventional communication systems and is described by three successive processes: a) transmission, b) propagation, and c) reception.

4.1 Transmission Process

According to the proposed system model, we consider that the proposed nanosystem is settled down close to the targeted cell, inside the intra-body area network highlighting the circulatory system. As illustrated in Fig. 2, the TN and RN can communicate with each other via information molecules (IM) which swim in the cardiovascular channel as signaling molecules. The TN is considered as the point source, which releases molecules onto the fluid medium by using OOK scheme. Additionally, when the TN is excited to emit the desired number of molecules or concentration, the molecules transmitted in each time slot (T) are in a sequence number of n slots.

Based on biological science, certain cells can secrete a hormonal substance that spreads to the targeted cell via a flow mechanism within the bloodstream. As a result, we assume that the proposed method is a flow-based propagation with velocity v, to which the advection-diffusion model can be applied. Obviously, the velocity of flow is affected not only by the distinct space between the TN and the RN, but also by physical parameters found within the bloodstream, such as blood pressure, blood viscosity, and vessel diameter. As a result, the flow velocity in the cardiovascular channel can be expressed as [36]:

v=14ηΔpL(R2−r2)(1)

Eq. (1) includes the physical parameters of the cardiovascular channel such as the blood viscosity, η, the pressure, Δp drop along a vessel dimension, L, R and r is the longitudinal axis of the vessel, as illustrated in Fig. 2.

4.2 Propagation Process

Unlike propagation in a stationary medium or free diffusion medium, the proposed method takes into account flow-based propagation with velocity v. Following that, depending on the propagation speed, the concentration of IM, c can reach the RN in a slow or fast fashion. As a result, the advection-diffusion equation is used in the following way [33]:

∂c∂t+∇.(vc)=D∇2c(2)

where D denotes the drug molecules’ (IM) coefficient of diffusion in the cardiovascular channel and ∇ denotes the gradient operator.

Eq. (2), in fact, depicts the transmission of particle drug information via two processes: advection and diffusion. As a result, using flow-based molecular communication makes the propagation of IM inside the cardiovascular channel more realistic. We consider a one-dimensional (1D) environment inspired by transmission within a directed vessel network. As a result, Varshney et al. [33] provided the solution to Eq. (2) is given in Eq. (3), in terms of the probability density function (PDF) for the first passage time of the IM arriving at RN.

f(t)=d4πDt3exp⁡(−(d−vt)24Dt),t>0(3)

Similar to a wireless communication system, a molecular signal degrades as a result of time and distance. As a result, the concentration of IM that diffuses from TN to RN is always less than the original concentration. The former statement was validated by plotting the concentration distribution of f(t) against t for the proposed intelligent nanosystem with and without a flow-based mechanism. We consider the following parameters: D = 30 µm2/s, d = 10 µm, and v = 10 µm/s. At first glance, we can see from Figs. 3a and 3b that the concentration behaviour expresses about the channel impulse response (CIR) of the proposed system, which changes over time. Furthermore, all concentration plots begin to reside/reduce dramatically immediately after reaching their maximum (for example, at t = 1 s). According to the results of the investigation, the intelligent nanosystem with flow-based mechanism outperforms the non-flow-based method. As a result, it is critical to investigate the parameters and outline the framework that influences the drug delivery mechanism to the targeted cell.

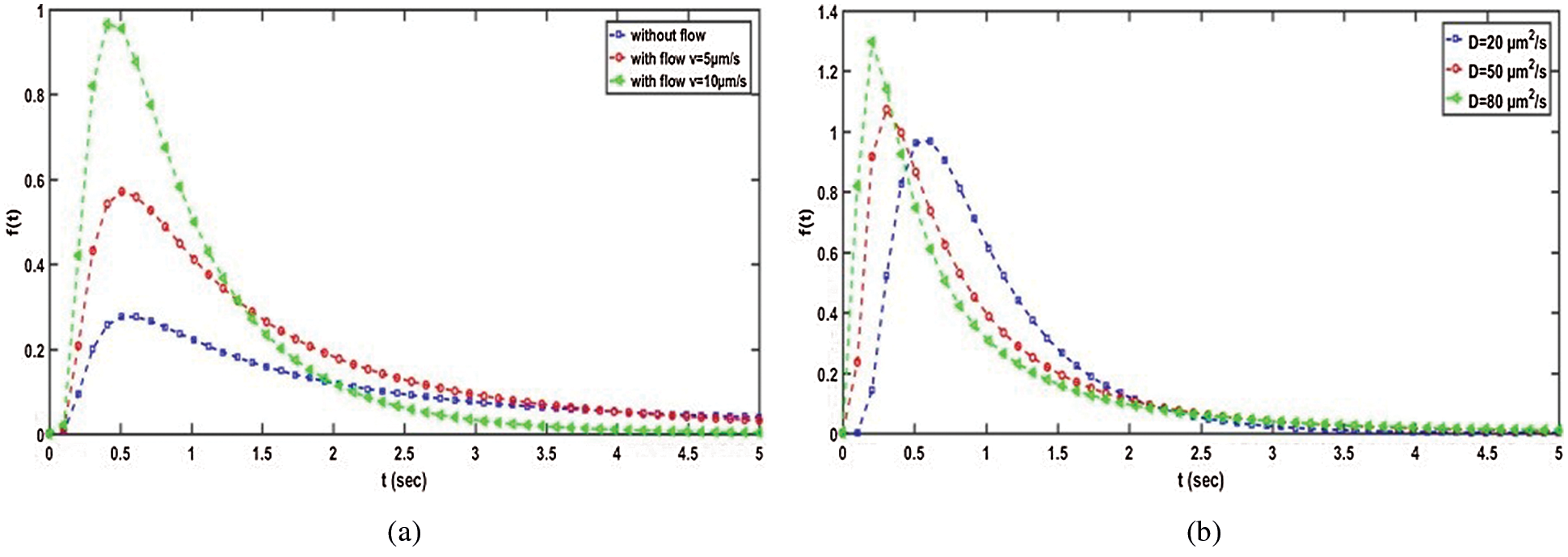
Figure 3: Concentration distribution in the proposed intelligence nanosystem-based flow

4.3 Reception Process

We consider the ligand-receptor binding kinetic reaction in the proposed scenario, where the emitted molecules are denoted by L and the receiving receptor is denoted by R, and thus the forward and reverse reaction rates are kf and kr, respectively. The process of binding mechanism is depicted in Fig. 4 based on the kinetic reaction.

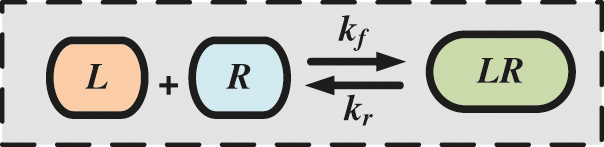
Figure 4: Kinetic reaction based-ligand-receptor binding mechanism

Given that the number of receptors on the RN’s surface is M, as shown in Fig. 2, the probability of successful reception at the RN is equal to Mkf/kr [31]. As a result, we assume that the number of slots is n and the slot duration is T. At the start of, T, the TN emits Q molecules in the cardiovascular channel with a priori probability of bit 1, otherwise, the transmission of information symbol is 0 bit. As a result, as shown in Fig. 5, the probability of a molecule transmitted in time slot j∈1, 2,…, n arriving in time slot n, qn-j can be expressed as Eq. (4) [37]

qn−j=Mkfkr∫(n−j)T(n−j+1)T∫t∞f(t)m(z)dtdz(4)

where m(z) denotes the molecule life expectancy over time, is expressed by an exponential distribution function: m(z) = λe-zλ with average value 1/λ [37].

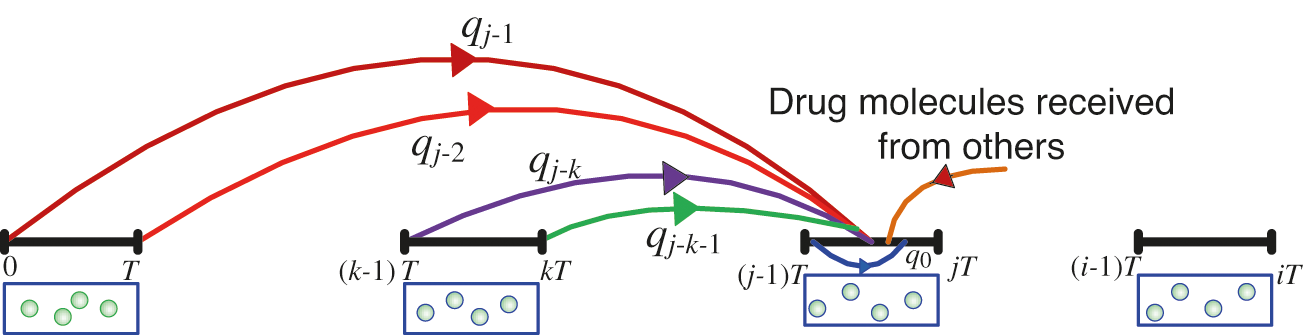
Figure 5: Illustration of the probability occurrence, qn-j. Analysis of proposed intelligent nanosystem approach in the presence of ISI

In this section, we present the bit error probability performance of the proposed intelligent nanosystem approach based on flow mechanism in the presence of noise and inter symbol interference (ISI). In fact, the purpose of this analysis is to investigate the performance of a cardiovascular channel in the presence of noise and ISI distortion. According to the previously discussed transmission mechanism, the required concentration is emitted in a sequence of time slots, and due to diffusion dynamics, some molecules may arrive after their intended time slot, as shown in Fig. 6.

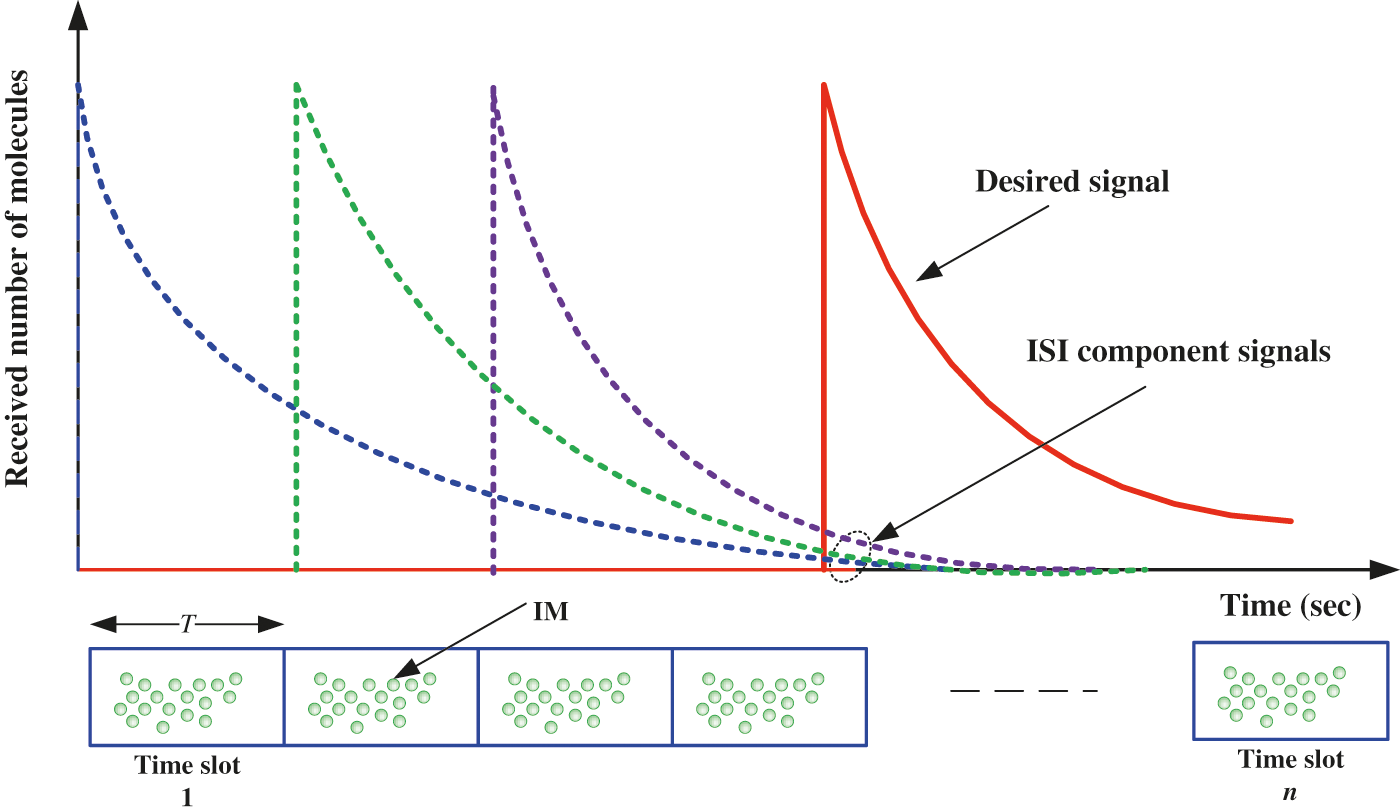
Figure 6: Illustration of ISI component in the proposed nanosystem system

As a result, this type of noise is known as residual noise, and it is responsible for the ISI component [38]. Fig. 7 depicts the proposed nanosystem’s block diagram in the presence of ISI and noise. The receiver received the required concentration of drug molecules sent by the TN in the current time slot as well as the concentration of drug molecules sent in the previous time slot.

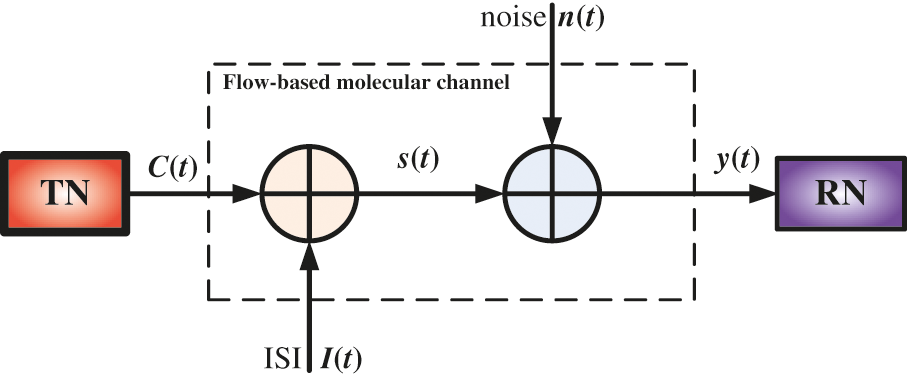
Figure 7: The block diagram of the proposed intelligent nanosystem

The received concentration, Rs [j] at the RN during time slot [(j-1)T, jT] can be expressed by Eq. (5):

Rs[j]=S[j]+I[j]+CN[j](5)

S[j] denotes the number of molecules received in the current slot, I[j] denotes the ISI resulting from transmission in the previous j-1 slots, and CN[j] denotes the counting error caused by received noise at the RN.

Eq. (6) expresses the expected noise which assumed to be a Gaussian distribution with a zero mean and signal variance, as used in [39]:

CN[j]≈N[0,y(t)/VR](6)

where VR denotes the volume of the spherical reception space with radius R.

We can model the interference signal, I[j] in Eq. (7), similarly to a conventional communication system:

I[j]=I[1]+I[2]+⋯+I[j−1](7)

The received drug molecules are detected by the RN by comparing the received number of molecules Rs [j] with the threshold, ξ and the detected symbol is given by Eq. (8):

a={1ifRs[j]≥ζ0ifRs[j]<ζ(8)

As a result, when TN sends drug molecules, the total number of molecules, Rs[j], is given by Eq. (9):

Rs[j]=S[j]+I[1]+I[2]+⋅⋅⋅+I[j−1]+CN[j](9)

In the absence of drug transmission, however, the output number of drug molecules Rs[j] is given by Eq. (10):

Rs[j]=I[1]+I[2]+I[2]+⋅⋅⋅+I[j−1]+CN[j](10)

Then the binary hypotheses are expressed by Eq. (11):

H0:R0[j]=I[1]+I[2]+⋅⋅⋅+I[j−1]+CN[j]H1:R1[j]=S[j]+I[1]+I[2]+⋅⋅⋅+I[j−1]+CN[j](11)

The binary hypotheses H0 and H1 correspond to the absence (sending 0) and presence (sending 1) of drug, respectively. As a result, the RN's expected error probabilities are given by Eq. (12):

P(1|0)=P(μ0≥ζ|H0)P(0|1)=P(μ1<ζ|H1)(12)

Accordingly, Eq. (12) can be expressed by Eqs. (13) and (14):

P(0|1)=∫ζ∞12πσ02exp⁡[−(u−μ0)22σ02]du=Q(ζ−μ0σ0)(13)

P(1|0)=∫−∞ζ12πσ12exp⁡[−(u−μ1)22σ12]du=1−Q(ζ−μ1σ1)(14)

where µ0, µ1, σ0, σ1 are the mean and variances under the hypothesis H0 and H1, respectively.

Finally, the average probability of error, Pe for slots 1 to n at the RN is given by Eq. (15):

Pe=∑j=1n1n(α[Q(ζ−μ1[j]σ1[j])]+(1−α)[Q(ζ−μ0[j]σ0[j])])(15)

where Q (.) is the Q function defined as in [32].

5  Performance Analysis of Channel Capacity

The purpose of measuring the information channel capacity for the proposed nanosystem-based flow diffusion mechanism is very important to know the concentration of the drug molecules inside the targeted cell site (i.e., RN). According to Shannon information theory that formulates the engineering context for information exchange among biological entities [30]. Without loss of generality, we assume that the transmitted molecular information message (IM) from TN in slot time n is Xn while the received IM at RN in the same time slot is Yn. According to the flow based diffusion mechanism, we mimics the block diagram of proposed nanosystem for mutual information communication between TN and RN as illustrated in Fig. 8, the mutual information of the transmitted IM and the received IM in time slot n can be expressed by I(Xn; Yn).

For instance, the closed-form expression for channel capacity in the proposed nanosystem can be expressed as the maximum value of mutual information I(Xn; Yn) as illustrated in Eq. (16):

C=max{I(Xn;Yn)}(16)

where, I(Xn; Yn) denotes the mutual information, in time slot n, it can be expressed by Eq. (17):

I(Xn;Yn)=H(Yn)−H(Yn|Xn)(17)

where H(Xn | Yn) is the entropy per time slot n of the transmitted IM, X given the received IM, Y. H(Yn) is the entropy per time slot n of the received IM, Y. H( . ) is the binary entropy function expressed by the two possibilities with probabilities β and 1-β as illustrated in Eq. (18):

H(.)=−βlog⁡β−(1−β)log⁡(1−β)(18)

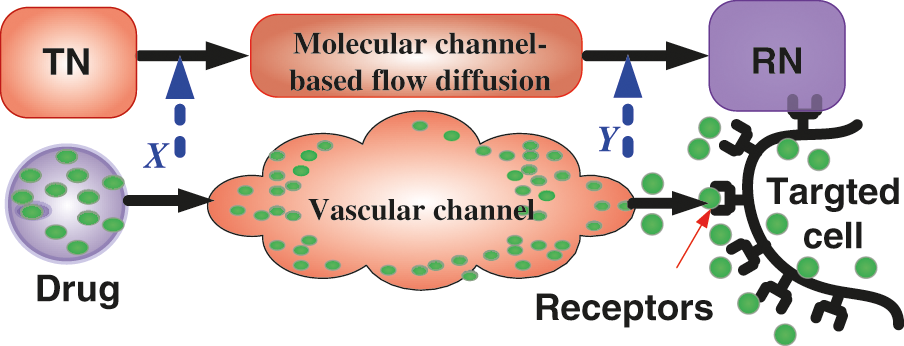
Figure 8: The mutual information in the proposed AI nanosystem

Using Eq. (4) and the derivation in [37], we develop a new expression of mutual information based on ISI considerations. The sum of the mutual information between the TN and RN in time slot n containing the received drug molecules is given by Eq. (19):

I(Xn;Yn)=H((1−α)∏j=1n−1(1−αqj)+α(1−(1−q0)∏j=1n−1(1−αqj)))−{αH(1−(1−q0)∏j=1n−1(1−αqi)+(1−α)H(∏j=1n−1(1−αqi)))}(19)

where q0 is the chance that a molecule will transmit in the first slot (i.e., n = 1). As a result of the binary transmission scheme ON/OFF keying, the maximum mutual information from slot 1 to n can be expressed by Eq. (20):

C=(∑j=1nmaxI(Xj;Yj)n)/Tbits/sec(20)

6  Numerical Results

The numerical results of the proposed intelligent nanosystems are presented in this section. The goal is to investigate the effect of flow on channel capacity and to observe changes in molecular channel capacity as physical parameters such as the distance, r, between the intelligent TN and the RN change. We also want to look into the effect of biological parameters in the human intra-body network on channel capacity. The obtained results were computed numerically for a common set of parameters listed in Table 1 and obtained from [33,40].

6.1 Effect of the Flow Velocity

Fig. 9 depicts the capacity of the proposed intelligent nanosystem’s cardiovascular channel, C in (bps), with varying a priori probability, for various flow velocities. We notice that the curve of C is always a convex function (that is, it increases with and thus reaches its peak value before decreasing until it reaches zero); this indicates that a priori probability is an effective parameter for determining channel capacity. We also notice that is a critical parameter with a maximum value for capacity at a value that is not close to 1 or 0. The figure depicts the effect of cardiovascular flow velocity on channel capacity in the opposite direction. As expected, the capacity of the cardiovascular channel increases as the flow velocity increases. Furthermore, we find that the capacity of the cardio vascular channel without considering fluid flow is very low when compared to the proposed intelligent nanosystem.

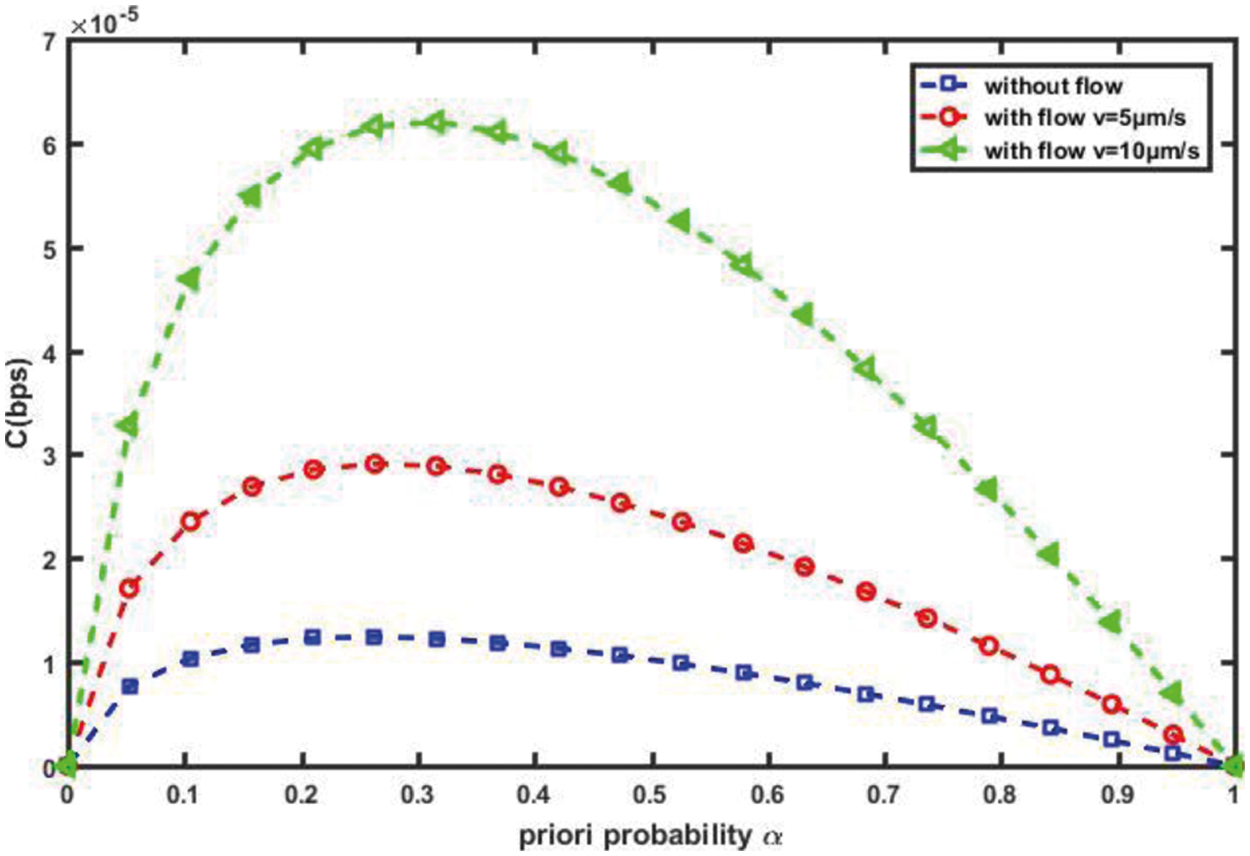
Figure 9: Channel capacity against α for different v (T = 1 s, D = 30 µm2/s, d = 10 µm)

Fig. 10 shows C in (bps) vs. for various values of the separation distance, d, between TN and RN in the proposed nanosystem when v = 1 μm/s. The capacity of the cardio vascular channel is very sensitive to distance, as shown in the figure, and as the distance between the TN and the RN increases, the capacity of the cardio vascular channel decreases significantly. This is due to the fact that molecules cannot move long distances using the diffusion property; if this occurs, the molecules are lost in the cardio vascular channel and thus cannot reach the target cell.

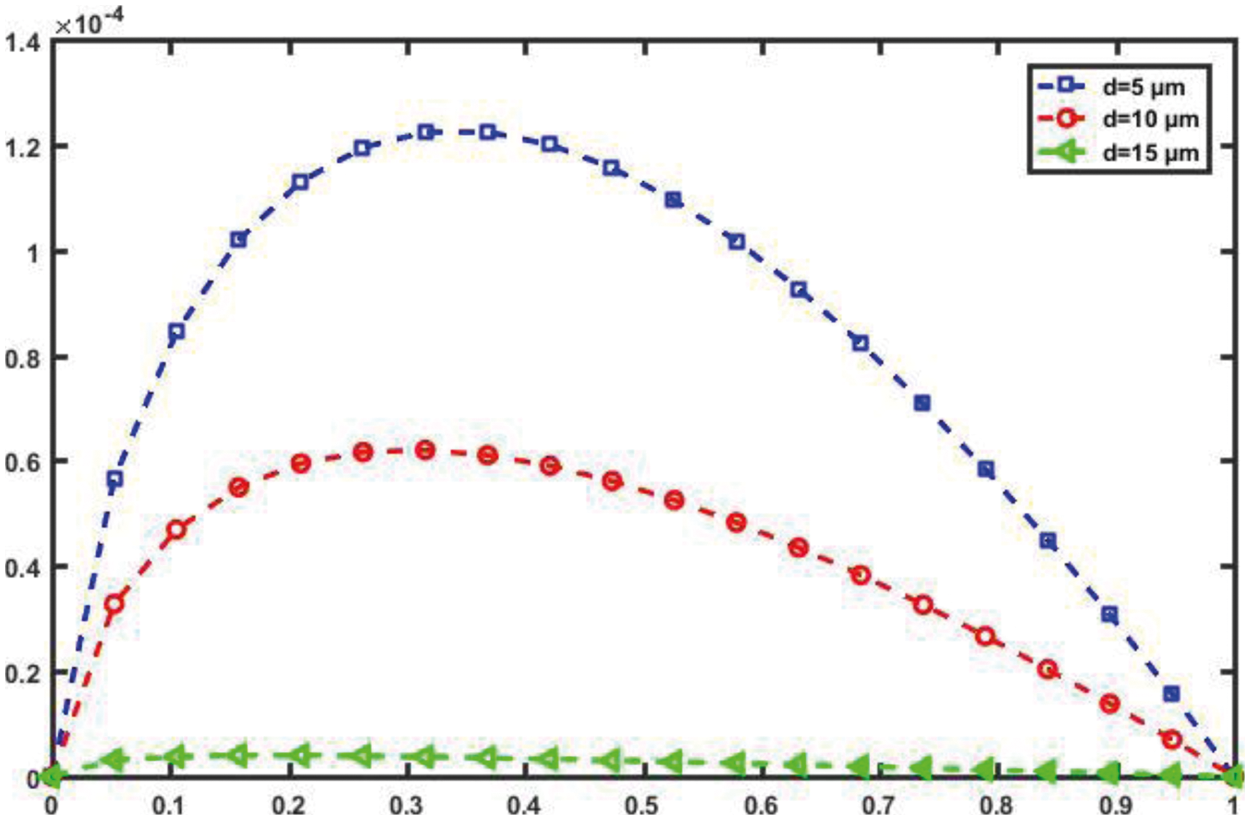
Figure 10: Channel capacity against α for different d (T = 1 s, D = 30 µm2/s, v = 10 µm/s)

On the other hand, we show the effect of the time slot length (in sec) on the capacity of the vascular channel, C in (bps), in Fig. 11. This information can assist medical personnel through IoBNT paradigm in adjusting the required drug concentration to the target cell. As we can see, when the transmitted time slot is long, the capacity increases. In other words, the higher the channel capacity, the longer the time slots. Because of the longer time slot, RN receives more drug concentration. Furthermore, this observation can be translated into the difficult issue of pharmacokinetics and bio-distribution during the introduction of the proposed intelligent nanosystem into the IBAN (intra-body area network).

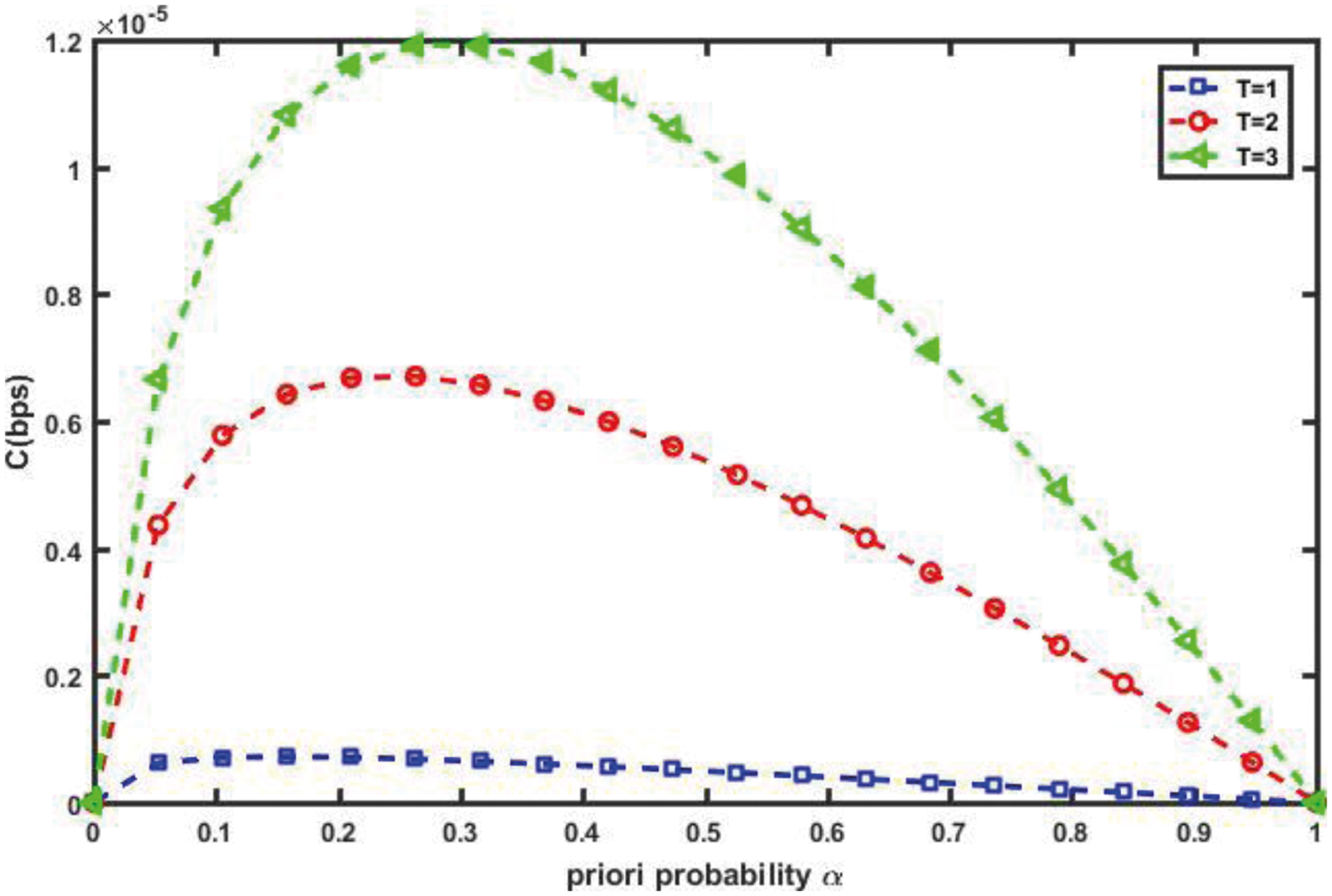
Figure 11: Channel capacity against α for different time slot, T (D = 30 µm2/s, d = 10 µm, v = 10 µm/s)

6.2 Effect of the Physical Parameters

In this section, we look at how physical parameters of the human body affect channel capacity. Actually, we are investigating the effect of blood viscosity on system capacity, which will aid medical personnel in managing/controlling/tracking targeted drug delivery.

As shown in Fig. 12, as the plasma viscosity in a blood vessel increases from normal to hyper viscosity, the channel capacity decreases, because high blood viscosity values indicate high resistance to flow along the blood vessel. As a result, the proposed nanosystem's efficiency suffers in such environmental conditions. Blood pressure, on the other hand, is the pressure exerted by circulating blood on the walls of the body’s blood vessels, and it is one of the critical parameters measured on virtually every patient in every healthcare setting. Poiseuille's Equation states that Δp is the pressure drop along a vessel section of length L; as Δp increases, blood flow increases, and thus vascular channel capacity improves, as shown in Fig. 13.

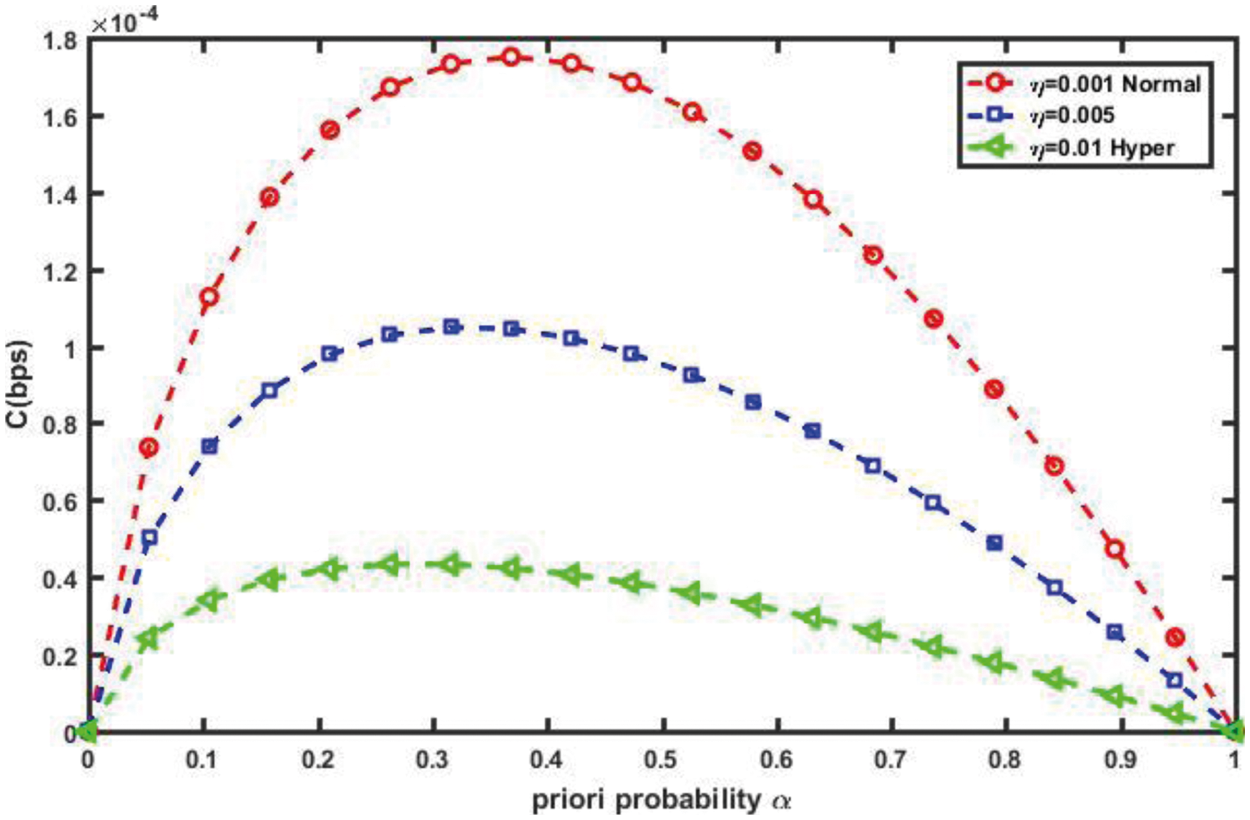
Figure 12: Impact of blood viscosity,η on channel capacity (at L = 30 mm, R = 30 µm, r = 1 µm, Δp = 10 Pa)

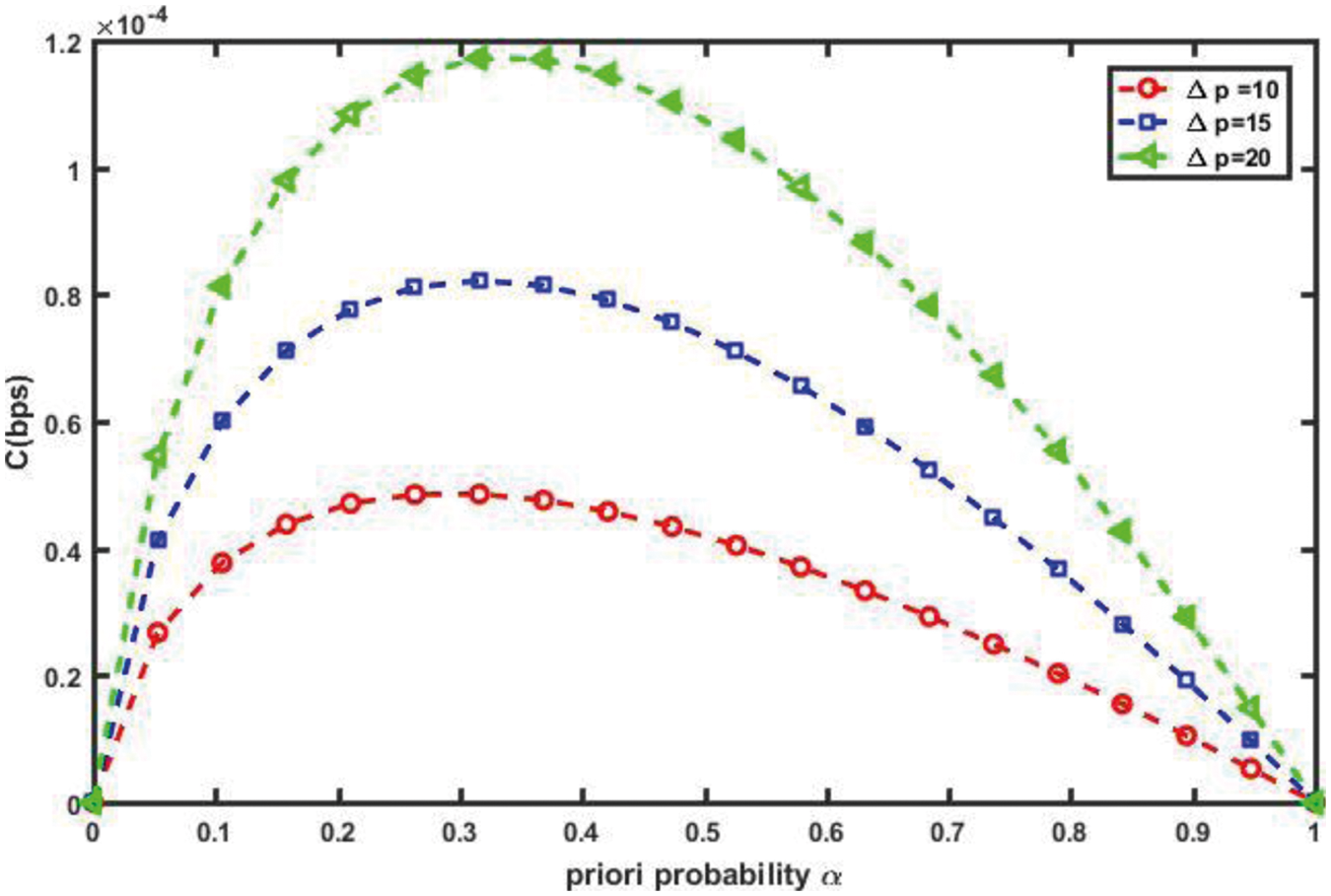
Figure 13: Impact of pressure drops, Δp on channel capacity (L = 30 mm, R = 30 µm, r = 1 µm, η = 0.001 cP)

According to the type of vessel, the diameter of blood vessels may be changed throughout the intra-body area network (IBAN). The increasing of the diameter means that there is less blood contacting to the vessel wall, result in reducing the friction and thus low resistance, result in increasing the flow velocity. Obviously, small increase in the diameter of vessel causes increasing in flow, and then the capacity in the proposed nanosystem will be increased as depicted in Fig. 14. On the other hand, the length of a vessel is inversely proportional to the blood flow, the longer the vessel is, and the lower the flow velocity is. Therefore, when the length of a vessel increases, the proposed nanosystem capacity will be decreased as shown in Fig. 15. This is because of increasing the length of vessel cause of dispersion of the molecules diffusion. Thereby the expected number of therapeutic drug molecules that may be counted at the RN over time after the transmission process is decreased and thus the channel capacity is decreased too.

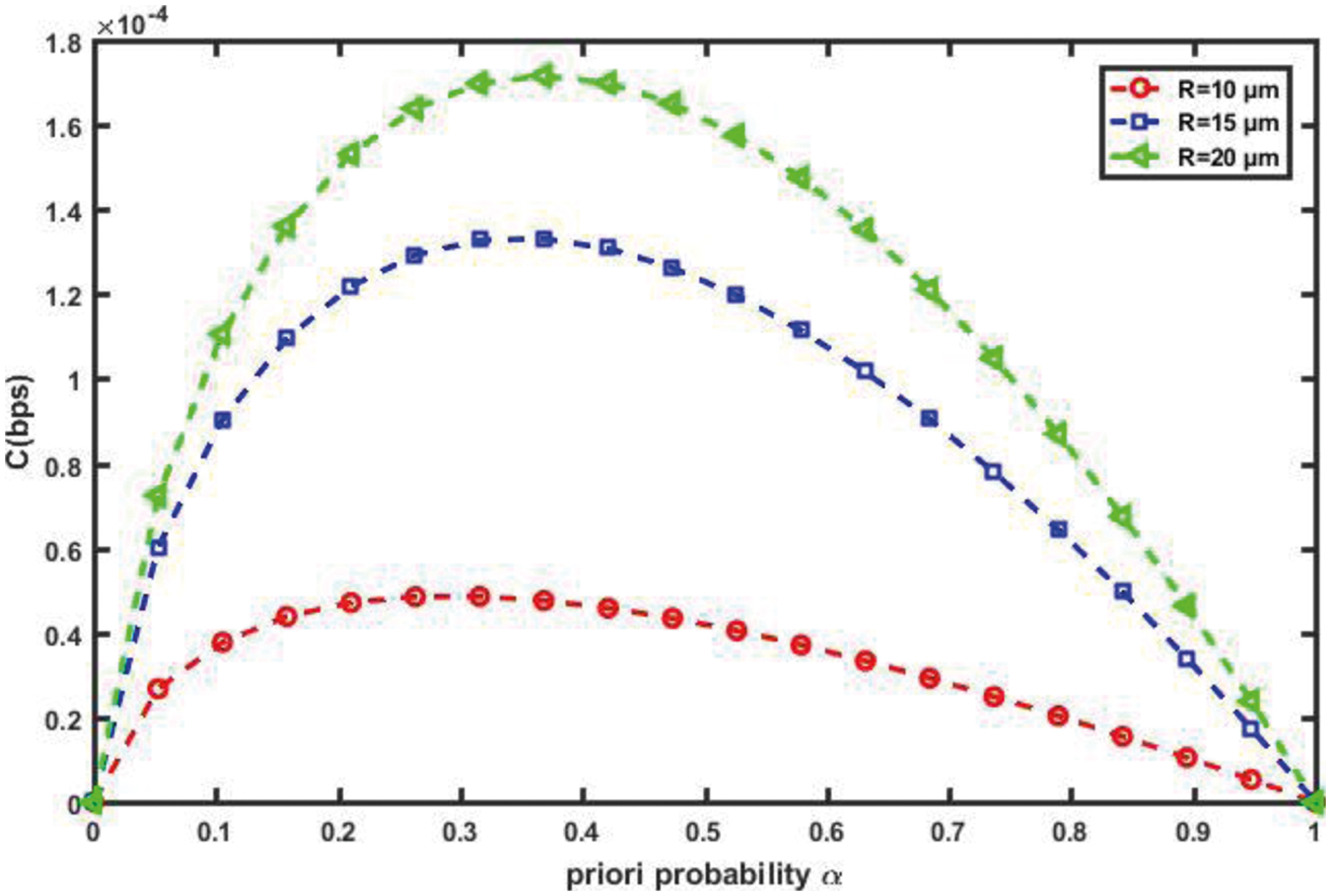
Figure 14: Impact of diameter of blood vessel, R on channel capacity (L = 30 mm, r = 1 µm, η = 0.001 cP)

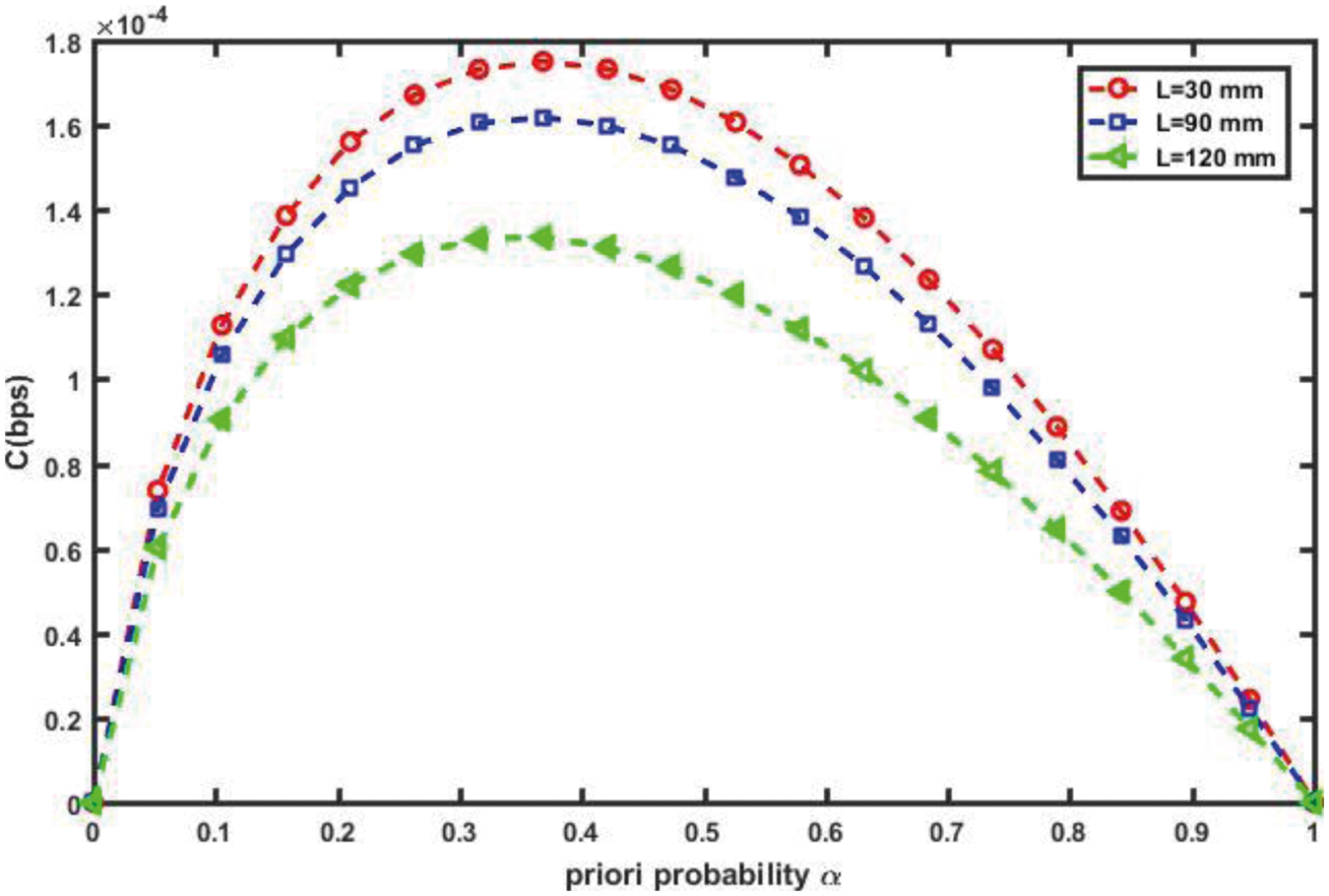
Figure 15: Impact of length of vessel, L on channel capacity (R = 30 µm, r = 1 µm, Δp = 10 Pa, η = 0.001 cP)

We can conclude from the results discussion that the proposed intelligent nanosystem-based IoBNT paradigm is suitable for nanomedicine applications involving short distances, such as transporting drug molecules from the extracellular to intracellular of diseased cells via the plasma membrane. The proposed nanosystem, on the other hand, can be used for long-distance nanomedical scenarios in which we could use nanomachines as relay nano-nodes (future scope). Furthermore, the capacity of the vascular channel used for therapeutic drug transmission varies significantly with the physical parameters of the intra-body area network (IBAN).

6.3 Performance of Error Probability in AI Nanosystem

We present the performance of error probability for transmission therapeutic drug using the proposed nanosystem in this section. In fact, we investigate the performance of the proposed nanosystem in the presence of noise and an ISI component. We adjusted the main parameters of the proposed nanosystem before running the simulation campaign with the system parameters D = 30 μm2/s, d = 20 μm and v = 5 μm/s.

The average error probability in the proposed nanosystem is plotted against the detection threshold that can be used at RN in Fig. 16. As we can see, the minimum error probability occurs when the detection threshold at the RN is set to the appropriate value. Furthermore, as expected, the error probability of the proposed nanosystem-based flow diffusion outperforms that of the nanosystem without flow-based because the velocity of blood flow is considered, and thus the probability of error decreases. Clearly, we can see that the proposed nanosystem is capable of achieving the lowest error probability, especially when the flow velocity is high.

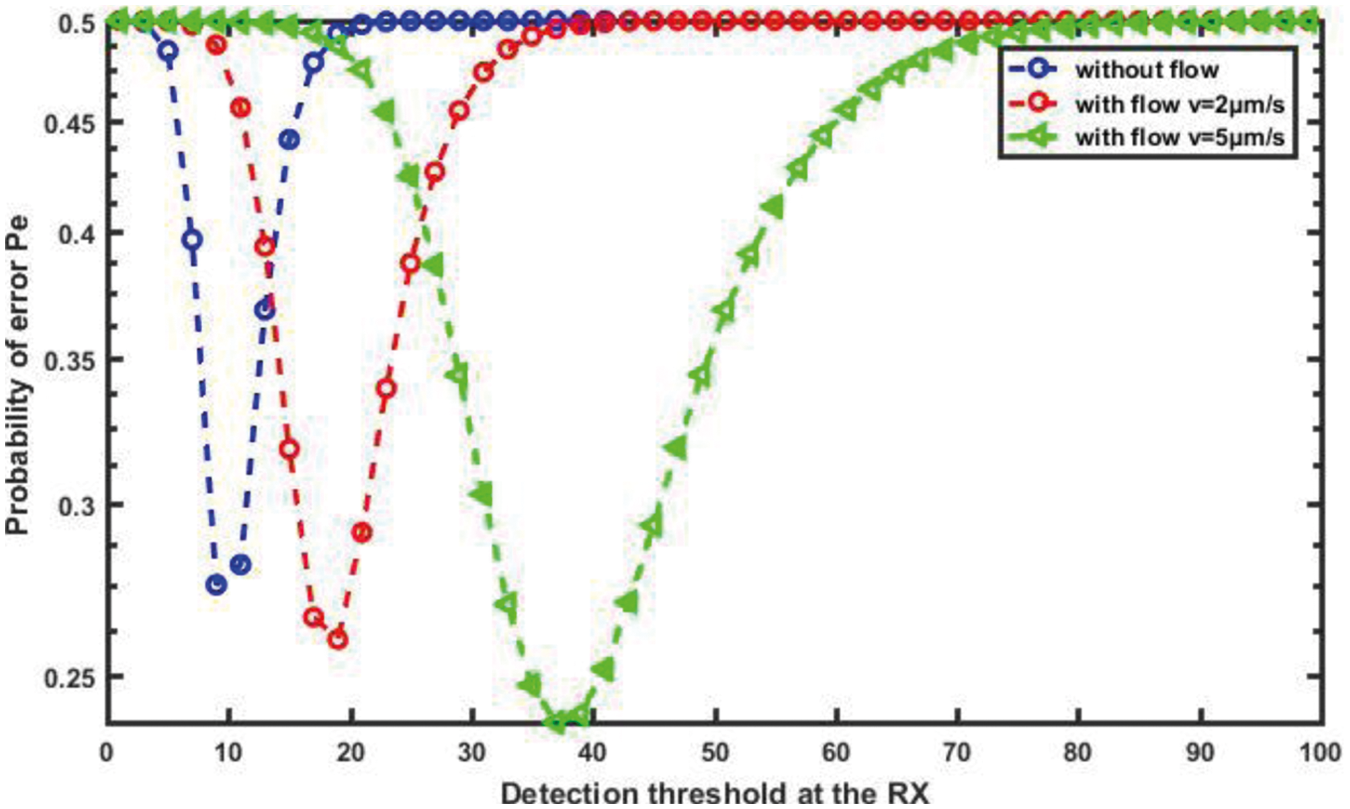
Figure 16: Probability of error against the detection threshold for different flow velocity

For a more detailed explanation of the results, we plot the error probability against the detection threshold at the RN for different numbers of molecules, Q, which are transmitted on a slot-by-slot basis, as shown in Fig. 17. Clearly, as the number of molecules released Q increases, the optimal value of the threshold that achieves minimum, Pe, increases. Furthermore, in order to evaluate the performance of the probability of error and the channel capacity for the proposed nanosystem with variations in the diffusion coefficient, D, we can see in Figs. 18 and 19, respectively, which as D increases, the probability of error decreases while the channel capacity increases.

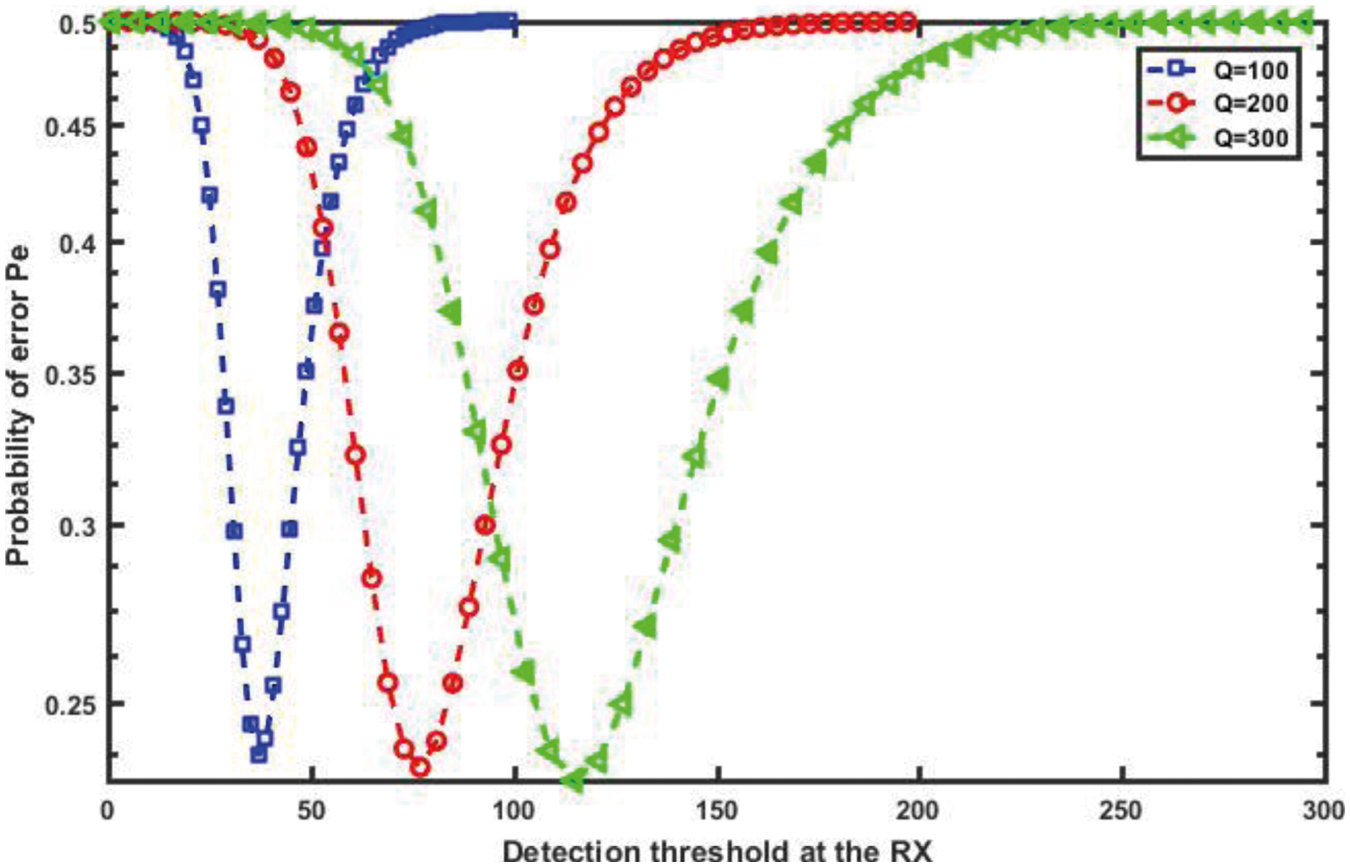
Figure 17: Probability of error against detection threshold for different number of molecules

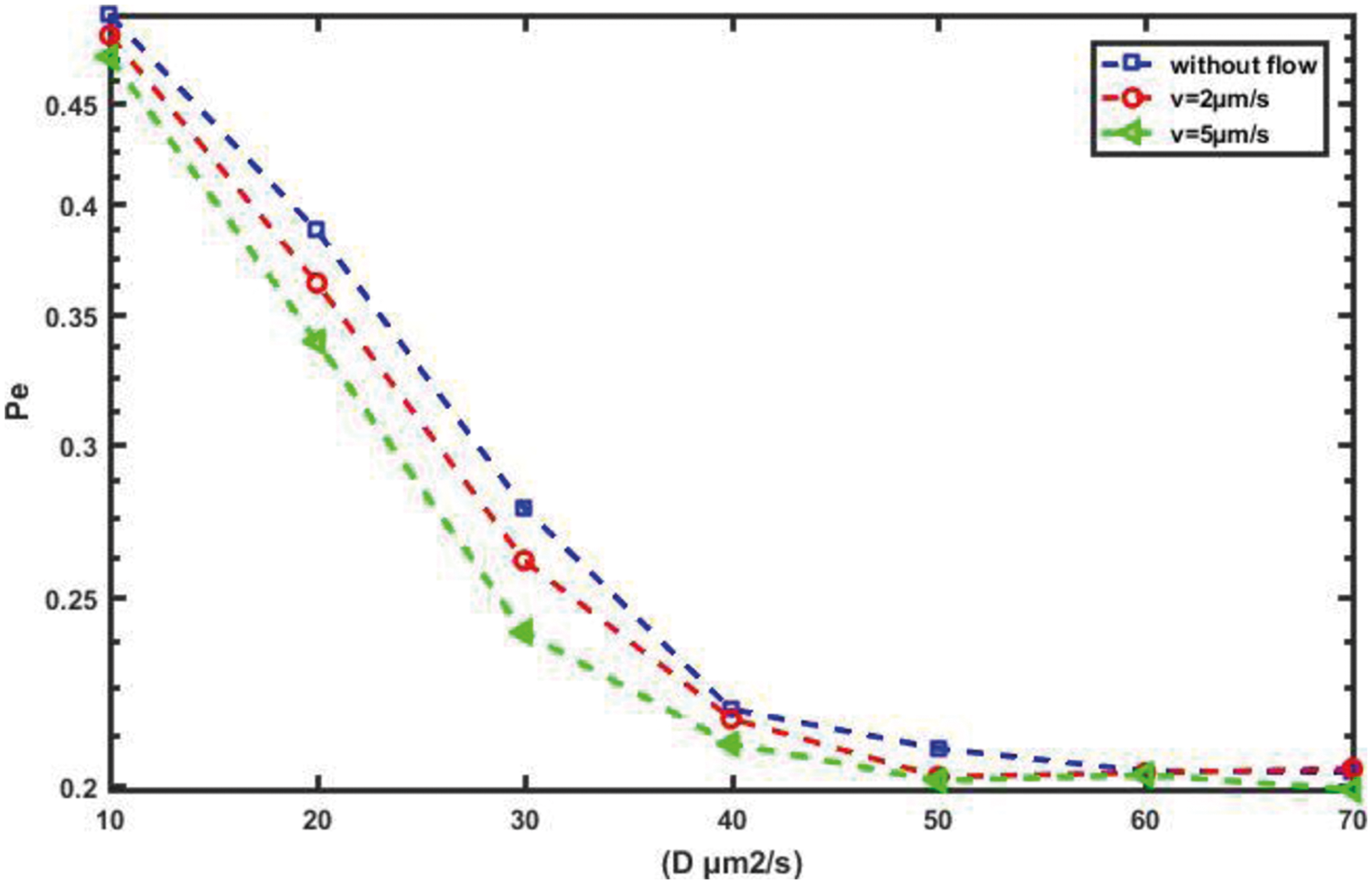
Figure 18: Probability of error against D for different flow velocity

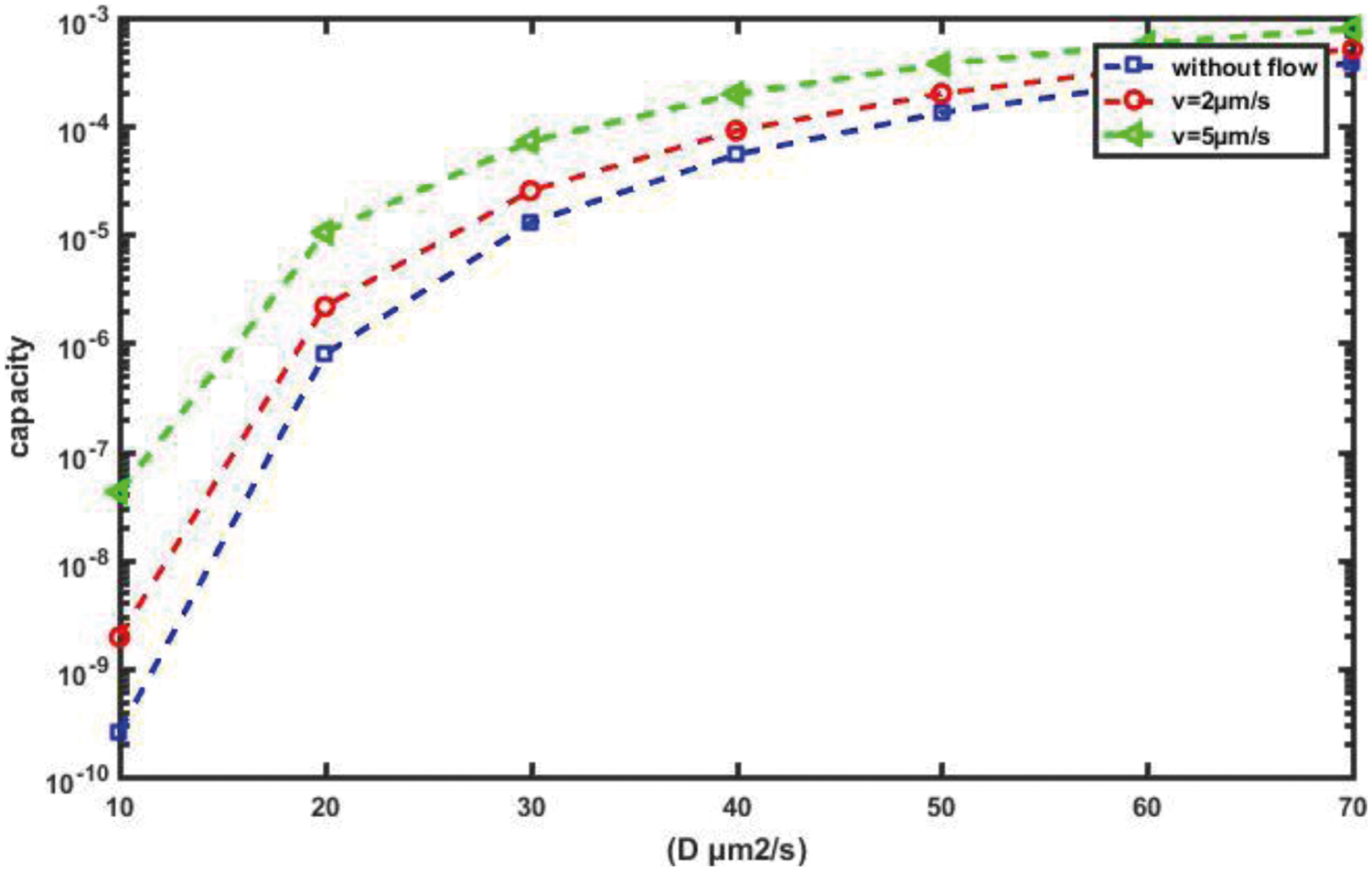
Figure 19: Channel capacity against D for different flow velocity

Based on the results, we can conclude that the proposed nanosystem-based flow diffusion is superior. Furthermore, the diffusion of molecules with drift in the cardiovascular channel mimics the turbulence (i.e., blood or pheromones) environment and thus delivers to the RN. Furthermore, we will be able to develop diagnostic, therapeutic, and monitoring capabilities in the intra-body area network by implementing the proposed AI nanosystem. This section examines how physical parameters of the human body influence channel capacity. Actually, we are looking into how blood viscosity affects system capacity, which will help medical personnel manage/control/track targeted drug delivery.

7  Conclusions

The performance of channel capacity for nanosystem based on the artificial intelligent (AI) and the Internet of biological nanothings is presented in this paper. A more realistic channel suitable for nanomedical applications, as well as a receiver design structure resembling that of a living cell, were considered. In addition, the analysis took into account the effect of channel parameters as well as biological parameters. The numerical results show that increasing the channel capacity is possible when the flow velocity in the cardiovascular channel is high and the blood viscosity is low. According to the proposed channel capacity analysis, the proposed AI nanosystem can assist medical personnel in transmitting the desired dose to the patient. Furthermore, the proposed AI nanosystems are thought to be a promising tool for real-time diagnostics in healthcare technology.

Funding Statement: This work was funded by the Researchers Supporting Project No. (RSP-2021/102) King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Pierobon, M., Akyildiz, I. F. (2011). Information capacity of diffusion based molecular communication in nanonetworks. IEEE International Conference on Computer Communications, pp. 506–510. Shanghai, China. [Google Scholar]

 2.  Ning, Z. L., Yang, Y. X., Wang, X. J., Guo, L., Gao, X. B. et al. (2021). Dynamic computation offloading and server deployment for UAV-enabled multi-access edge computing. IEEE Transactions on Mobile Computing, 1. DOI 10.1109/TMC.2021.3129785. [Google Scholar] [CrossRef]

 3.  Ning, Z. L., Dong, P. R., Wen, M. W., Wang, X. J., Guo, L. et al. (2021). 5G-Enabled UAV-to-community offloading: Joint trajectory design and task scheduling. IEEE Journal on Selected Areas in Communications, 39(11), 3306–3320. DOI 10.1109/JSAC.2021.3088663. [Google Scholar] [CrossRef]

 4.  Shen, Q. L., Wu, J., Li, J. H., Zhang, X. F., Wang, K. (2021). Communication modeling for targeted delivery under Bio-DoS attack in 6G molecular network. IEEE International Conference on Communications, pp. 1–5. Montreal, Canada. [Google Scholar]

 5.  Abd El-atty, S. M., Tolba, A. (2019). A cross layer approach for optimization of MolCom systems towards the Internet of Bio Nano Things. IEEE Systems Journal, 30(3), 2751–2762. DOI 10.1109/JSYST.2018.2877207. [Google Scholar] [CrossRef]

 6.  Nakano, T., Moore, M., Enomoto, A., Suda, T. (2011). Molecular communication technology as a biological ICT. Berlin, Heidelberg: Springer. [Google Scholar]

 7.  Nakano, T., Moore, M. J., Wei, F., Vasilakos, A. V., Shuai, J. (2012). Molecular communication and networking: Opportunities and challenges. IEEE Transactions on Nano Bioscience, 11(2), 135–148. DOI 10.1109/TNB.2012.2191570. [Google Scholar] [CrossRef]

 8.  El-Fatyany, A., Wang, H., Abd El-atty, S. M. (2020). On mixing reservoir targeted drug delivery Modeling-based Internet of Bio-NanoThings. Wireless Networks, 26(5), 3701–3713. DOI 10.1007/s11276-020-02294-3. [Google Scholar] [CrossRef]

 9.  Ullah, N., Kong, X., Ning, Z., Tolba, A., Alrashoud, M. et al. (2020). Emergency warning messages dissemination in vehicular social networks: A trust based scheme. Vehicular Communications, 22(2), 1–16. DOI 10.1016/j.vehcom.2019.100199. [Google Scholar] [CrossRef]

10. Abd El-atty, S. M., Bidar, R., El-Rabaie, E. S. M. (2020). MolCom system with downlink/uplink biocyber interface for Internet of Bio-NanoThings. International Journal of Communication Systems, 23(1), 1–21. DOI 10.1002/dac.4171. [Google Scholar] [CrossRef]

11. El-Fatyany, A., Wang, H., Abd El-atty, S. M., Khan, M. (2020). Biocyber interface-based privacy for Internet of Bio-NanoThings. Wireless Personal Communications, 114(2), 1465–1483. DOI 10.1007/s11277-020-07433-9. [Google Scholar] [CrossRef]

12. Kim, N. R., Eckford, A. W., Chae, C. B. (2014). Symbol interval optimization for molecular communication with drift. IEEE Transactions on NanoBioscience, 13(3), 223–229. DOI 10.1109/TNB.2014.2342259. [Google Scholar] [CrossRef]

13. Gregori, M., Akyildiz, I. F. (2010). A new nanonetwork architecture using flagellated bacteria and catalytic nanomotors. IEEE Journal on Selected Areas in Communications, 28(4), 612–619. DOI 10.1109/JSAC.2010.100510. [Google Scholar] [CrossRef]

14. Cobo, L. C., Akyildiz, I. F. (2010). Bacteria-based communication in nanonetworks. Nano Communication Networks, 1(4), 244– 256. DOI 10.1016/j.nancom.2010.12.002. [Google Scholar] [CrossRef]

15. Mahfuz, M. U., Makrakis, D., Mouftah, H. T. (2010). On the characterization of binary concentration-encoded molecular communication in nanonetworks. Nano Communication Networks, 1(4), 289–300. DOI 10.1016/j.nancom.2011.01.001. [Google Scholar] [CrossRef]

16. Kuran, M. Ş., Yilmaz, H. B., Demirkol, I., Farsad, N., Goldsmith, A. et al. (2021). A survey on modulation techniques in molecular communication via diffusion. IEEE Communications Surveys & Tutorials, 23(1), 7–28. DOI 10.1109/COMST.2020.3048099. [Google Scholar] [CrossRef]

17. Rudsari, H. K., Javan, M. R., Orooji, M., Mokari, N., Jorswieck, E. A. (2021). TDMA-MTMR-Based molecular communication with ligand-binding reception. IEEE Transactions on Molecular, Biological and Multi-Scale Communications, 7(2), 111–116. DOI 10.1109/TMBMC.2021.3054902. [Google Scholar] [CrossRef]

18. Pierobon, M., Akyildiz, I. F. (2010). A physical end-to-end model for molecular communication in nanonetworks. IEEE Journal on Selected Areas in Communications, 28(4), 602–611. DOI 10.1109/JSAC.2010.100509. [Google Scholar] [CrossRef]

19. Meng, L. S., Yeh, P. C., Chen, K. C., Akyildiz, I. F. (2014). On receiver design for diffusion-based molecular communication. IEEE Transaction on Signal Processing, 62(22), 6032–6044. DOI 10.1109/TSP.2014.2359644. [Google Scholar] [CrossRef]

20. Yilmaz, H. B., Heren, A. C., Tugcu, T., Chae, C. B. (2014). Three-dimensional channel characteristics for molecular communications with an absorbing receiver. IEEE Communications Letters, 18(6), 929–932. DOI 10.1109/LCOMM.2014.2320917. [Google Scholar] [CrossRef]

21. Pierobon, M., Akyildiz, I. F. (2011). Noise analysis in ligand-binding reception for molecular communication in nanonetworks. IEEE Transactions on Signal Processing, 59(9), 4168–4182. DOI 10.1109/TSP.2011.2159497. [Google Scholar] [CrossRef]

22. Llatser, I., Cabellos-Aparicio, A., Pierobon, M., Alarcón, E. (2013). Detection techniques for diffusion-based molecular communication. IEEE Journal on Selected Areas in Communications, 31(12), 726–734. DOI 10.1109/JSAC.2013.SUP2.1213005. [Google Scholar] [CrossRef]

23. Chahibi, Y., Akyildiz, I. F. (2014). Molecular communication noise and capacity analysis for particulate drug delivery systems. IEEE Transactions on Communications, 62(11), 3891–3903. DOI 10.1109/TCOMM.2014.2360678. [Google Scholar] [CrossRef]

24. Pierobon, M., Akyildiz, I. F. (2013). Capacity of a diffusion-based molecular communication system with channel memory and molecular noise. IEEE Transactions on Information Theory, 59(2), 942–954. DOI 10.1109/TIT.2012.2219496. [Google Scholar] [CrossRef]

25. Atakan, B., Akan, O. B. (2010). Deterministic capacity of information flow in molecular nanonetworks. Nano Communication Networks, 1(1), 31–42. DOI 10.1016/j.nancom.2010.03.003. [Google Scholar] [CrossRef]

26. Arifler, D. (2011). Capacity analysis of a diffusion-based short-range molecular nano-communication channel. Computer Networks, 55(6), 1426–1434. DOI 10.1016/j.comnet.2010.12.024. [Google Scholar] [CrossRef]

27. Liu, Q., Yang, K. (2013). Multiple-access channel capacity of diffusion and ligand-based molecular communication. ACM International Conference on Modeling, Analysis & Simulation of Wireless and Mobile Systems, pp. 151–158. New York, USA. [Google Scholar]

28. Einolghozati, A., Sardari, M., Beirami, A., Fekri, F. (2011). Capacity of discrete molecular diffusion channels. IEEE International Symposium on Information Theory, pp. 603–607. Petersburg, Russia. [Google Scholar]

29. Kadloor, S., Adve, R. S., Eckford, A. W. (2012). Molecular communication using brownian motion with drift. IEEE Transactions on NanoBioscience, 11(2), 89–99. DOI 10.1109/TNB.2012.2190546. [Google Scholar] [CrossRef]

30. Srinivas, K. V., Eckford, A. W., Adve, R. S. (2012). Molecular communication in fluid media: The additive inverse gaussian noise channel. IEEE Transactions on Information Theory, 58(7), 678– 4692. DOI 10.1109/TIT.2012.2193554. [Google Scholar] [CrossRef]

31. Felicetti, L., Femminella, M., Reali, G. (2013). Establishing digital molecular communications in blood vessels. First International Black Sea Conference on Communications and Networking (BlackSeaCom), pp. 1–5. Batumi, Georgia. [Google Scholar]

32. Chude-Okonkwo, U., Malekian, R., Maharaj, B. T. (2019). Advanced targeted nanomedicine: A Communication engineering solution. Berlin, Heidelberg: Springer. [Google Scholar]

33. Varshney, N., Haselmayr, W., Guo, W. (2018). On flow-induced diffusive mobile molecular communication: First hitting time and performance analysis. IEEE Transactions on Molecular, Biological and Multi-Scale Communications, 4(4), 195–207. DOI 10.1109/TMBMC.2019.2928543. [Google Scholar] [CrossRef]

34. Lin, L., Yang, C., Ma, M., Ma, S., Yan, H. (2016). A clock synchronization method for molecular nanomachines in bionanosensor networks. IEEE Sensors, 16(19), 7194–7203. DOI 10.1109/JSEN.2016.2591823. [Google Scholar] [CrossRef]

35. Farsad, N., Yilmaz, H. B., Eckford, A., Chae, C. B., Guo, W. (2016). A comprehensive survey of recent advancements in molecular communication. IEEE Communications Surveys & Tutorials, 18(3), 1887–1919. DOI 10.1109/COMST.2016.2527741. [Google Scholar] [CrossRef]

36. Chen, Y. L., Bai, G. Q., Ren, L. X., Bai, Y., Sun, M. Y. et al. (2020). Blood physiological and flow characteristics within coronary artery circulatory network for human heart based on vascular fractal theory. Advances in Mechanical Engineering, 12(7), 1–13. DOI 10.1177/1687814020933385. [Google Scholar] [CrossRef]

37. Liu, Q., Yang, K. (2015). Channel capacity analysis of diffusion based molecular communication system with ligand receptors. International Journal of Communication Systems, 8(8), 1508–1520. DOI 10.1002/dac.2730. [Google Scholar] [CrossRef]

38. Dissanayake, M. B., Ekanayake, N. (2021). On the exact performance analysis of molecular communication via diffusion for Internet of Bio-Nano Things. IEEE Transactions on NanoBioscience, 20(3), 291–295. DOI 10.1109/TNB.2021.3072230. [Google Scholar] [CrossRef]

39. Wang, X., Higgins, M. D., Leeson, M. S. (2015). Distance estimation schemes for diffusion based molecular communication systems. IEEE Communications Letters, 19(3), 399–402. DOI 10.1109/LCOMM.2014.2387826. [Google Scholar] [CrossRef]

40. ShahMohammadian, H., Messier, G. G., Magierowski, S. (2013). Modelling the reception process in diffusion based molecular communication channels. 2013 IEEE International Conference on Communications Workshops (ICC), pp. 782–786. DOI 10.1109/ICCW.2013.6649339. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.