Computer Modeling in Engineering & Sciences

---

DOI: 10.32604/cmes.2022.021127

ARTICLE

A Hybrid Local/Nonlocal Continuum Mechanics Modeling of Damage and Fracture in Concrete Structure at High Temperatures

Runze Song1, Fei Han1,*, Yong Mei2,*, Yunhou Sun2 and Ao Zhang2

1Department of Engineering Mechanics, State Key Laboratory of Structural Analysis for Industrial Equipment, International Research Center for Computational Mechanics, Dalian University of Technology, Dalian, 116023, China
2Institute of Defense Engineering, AMS, Beijing, 100036, China
*Corresponding Authors: Fei Han. Email: hanfei@dlut.edu.cn; Yong Mei. Email: meiyong1990@126.com
Received: 29 December 2021; Accepted: 29 March 2022

1  Introduction

As a major engineering material with many advantages, concrete plays a main role in supporting most architectural structures. Under some circumstances, concrete structures are expected to be working under high-temperature or even ultra-temperature conditions. For instance, the temperature of the inner wall of an industrial chimney can reach 500°C∼600°C. In nuclear reactor pressure vessels and containment structures, concrete is generally exposed to ultra-temperature conditions. Within a very short time, the fierce heat in a fire accident can reach over 1000°C [1]. High-temperature conditions accelerate the microstructure damage of concrete, leading to the degradation of the macroscopic mechanical property of concrete. Studies about concrete structure accidents show that many cracks in the failure of concrete structures were caused due to insufficient tensile strength and tensile deformation limit, especially under high-temperature conditions [2]. Concrete used to be regarded as a tensile brittle material. However, experimental data have shown that concrete is a typical quasi-brittle material, for its stress-strain curve reveals an inherent tensile softening behavior that alters along with the rising of temperature [3]. Thus, the key to establishing a reasonable mechanical model for concrete materials is to effectively reflect these intrinsic thermomechanical features in the constitutive relation.

As a branch of solid mechanics, damage mechanics is expected to be a theoretical solution to the irreversible thermodynamic dissipation problem dominated by microcracking. It is noted that damage mechanics has been introduced into investigations of concrete since 1976 [4] and proven qualified to describe the constitutive behavior of concrete materials in a physical sense. Based on experimental data, there have been many discussions on the form of concrete damage model under tensile loading. A damage model with a linear softening curve was firstly developed for concrete material by Loland [5], and then Mazars proposed another one with a nonlinear softening curve [6,7]. Moreover, a great number of works [8,9] have been conducted regarding the thermal damage modeling of concrete for better understanding of the thermal impact on concrete material.

In previous works on the failure simulations of concrete structures, various damage mechanical models were adopted within the framework of classical continuum mechanics (CCM). However, CCM based on the continuity assumption loses its applicability when it comes to simulating the process from continuous deformation to discontinuous deformation (i.e., the initiation and propagation of cracks). To this end, we intend to propose a peridynamic damage model for failure simulation of concrete structures considering the temperature in this study.

Peridynamics is a nonlocal theory of solid mechanics firstly proposed by Silling in 2000 [10] and has become a popular method for fracture analysis. In peridynamics, the equilibrium relation was redefined with integral equations in replacement of partial differential equations to avoid invalidation in the presence of a discontinuity in the deformation field. Moreover, it has been demonstrated that the peridynamic stress tensor has the exact mathematical expression as that of the first Piola-Kirchhoff static Virial stress [11], providing solid theoretical basis for the numerical calculations of peridynamic models. Also, crack nucleation and propagation can be spontaneously predicted without extra crack propagation criteria. Thus, peridynamics has an inherent and unique capacity for investigating failure or fracture of engineering materials. Studies have validated the applicability of peridynamics on concrete [12], soil [13,14], rock [15], glass [16] and composite materials [17–19]. Additionally, for the concrete material we focus on, a peridynamic fiber-reinforced concrete model is developed based on the bond-based peridynamic model with rotation effect [20], where the interactions and frictional effect between fibers and concrete matrix are all considered properly. Nevertheless, one of the main challenges peridynamics may encounter is its computational cost. On that account, considerable efforts have been made over the past few years. Various coupling methods between peridynamics and CCM, such as the variable horizon method [21], the force-based coupling method [22,23], the Arlequin coupling method [24], and the Morphing method [25], have been developed and widely implemented. A superposition-based coupling method was then proposed and applied to damage analysis of the cut-off wall in a landslide dam, in which the accuracy of the coupling model was verified by experimental tests [26,27]. Moreover, an energy-based multivariate coupling scheme [28] and a quasi-nonlocal coupling method [29] have been presented and proven very effective to eliminate the ghost force in the coupling methods. Regarding the thermomechanical formulation we are interested in, a fully-coupled peridynamic model has been developed with constant micromodulus [30]. Also, a coupling approach of the peridynamic and finite element method was proposed for modeling the thermal fractures in brittle solids and showed great performance of capturing the complex crack patterns involving heat transfer [31].

On this basis, another indispensable part in the thermomechanical damage model of concrete materials would be an applicable damage constitutive relation. At first, Silling et al. proposed a linear microelastic damage model within the framework of bond-based peridynamic theory to simulate the failure of prototype microelastic brittle materials [32]. Up until today, this microelastic brittle model has been widely employed and proven steady for capturing the fracture process of various complex structures. But as aforementioned, the brittle constitutive model appears to be incapable of reproducing the softening behavior of concrete in the tensile stress-strain curve. Therefore, the work on the failure behavior of concrete should be extended to the quasi-brittle constitutive model of peridynamics.

In recent years, a few quasi-brittle constitutive models have been developed within the bond-based peridynamic framework. For example, a linear softening curve was embedded in the microelastic model and was utilized to simulate the fracture behavior of reinforced concrete structures, and then the parameters were determined [33]. For better fitting of the experimental load-displacement curve of concrete, bilinear [34] and exponential [35] tensile softening constitutive models were further adopted in the peridynamics for concrete. However, the thermal influence on the damage model has yet to be involved in these investigations on the peridynamic damage model for concrete so far.

In this paper, we attempt to associate the classic damage model of concrete with the peridynamic bond damage constitutive to numerically simulate the damage and fracture behavior of concrete at high temperatures. For this work, the remainder of this paper is organized as follows: In Section 2, a bond-based thermomechanical peridynamic formula is briefly reviewed, where the equilibrium equation and constitutive equation are reformulated. The equivalent relations of the stiffness and thermal parameters between the local and nonlocal models are established. Section 3 is devoted to stating the peridynamic quasi-brittle thermomechanical damage model we propose. A hybrid local/nonlocal continuum mechanics model was adopted in Section 4 to optimize the computational efficiency of the proposed model. In Section 5, several relevant numerical examples regarding concrete structures at different temperatures are conducted for comparison and verification. Finally, concluding remarks are provided in Section 6.

2  The Bond-Based Thermomechanical Peridynamics

In this section, we introduce a thermal parameter into the bond-based peridynamics and reformulate the bond-based peridynamic model for thermomechanical problems.

2.1 The Equilibrium Equation

In the classical bond-based peridynamic model, a material point x interacts with all the points in its neighborhood, Hδ(x). Based on the nonlocal integral relation and Newton’s second law, the motion equation in the bond-based peridynamic model was stated [32]. In this study, we consider a quasi-static problem under a constant-temperature environment. A temperature-dependent parameter T¯, denoting the temperature difference between the current environment T1 and the base temperature T0 (i.e., T¯=T1−T0), is introduced here. So the thermomechanical equilibrium equation can be written as Eq. (1):

∫Hδ(x)f(x′,x,T¯)dVξ+b(x)=0,(1)

In Eq. (2),  f(x′,x,T¯) is the bond force function between point x and point x′. We regard f(x′,x,T¯) as the superposition of two interactions:

f(x′,x,T¯)=f^(x′,x,T¯)−f^(x,x′,T¯),(2)

where f^(x′,x,T¯) (respectively f^(x,x′,T¯)) is the partial interaction due to the action of point x′ over point x (with respect to point x over point x′).

2.2 The Constitutive Model

Under the assumptions of linear elasticity and small deformations, the undamaged constitutive model for the thermomechanical problem can be written as Eq. (3):

f^(x′,x,T¯)=12c(x,ξ)(ηξ(x′,x)−a(x,ξ)T¯)eξ,(3)

where the relative position vector ξ=x′−x denotes the bond; the direction vector eξ=ξ/|ξ|; ηξ is the relative displacement along ξ:

ηξ(x′,x)=uξ(x′)−uξ(x).(4)

In Eq. (4), uξ(x) and uξ(x′) respectively denote the displacement of x and x′ along ξ; c(x,ξ) is the peridynamic micromodulus tensor; here we define a(x,ξ) as the coefficient of thermal expansion for peridynamics and we let

λ(x,ξ)=c(x,ξ)a(x,ξ).(5)

We consider a homogeneous material, such that

c(x,ξ)=c(x′,ξ)=c0(|ξ|),(6)

Also, we consider the thermal parameter to be homogeneous in the structure, such that

a(x,ξ)=a(x′,ξ)=a0(|ξ|).(7)

Substituting Eqs. (6) and (7) into Eq. (5), we have

λ(x,ξ)=λ(x′,ξ)=λ0(|ξ|).(8)

Based on Eqs. (3)–(8), the strain energy density of the thermomechanical peridynamic model at point x can be derived as Eq. (9):

W(x,T¯)=14∫Hδ(x)c0(|ξ|)(ηξ(x′,x)−a0(|ξ|)T¯)2dVξ=14∫Hδ(x)c0(|ξ|)ηξ(x′,x)2dVξ−12∫Hδ(x)λ0(|ξ|)T¯ηξ(x′,x)dVξ+14∫Hδ(x)a0(|ξ|)λ0(|ξ|)T¯2dVξ.(9)

2.3 The Energy Equivalent Relations between Local and Non-Local Models

Note that all the peridynamic parameters in Eq. (9) can be obtained from the CCM model by the energy equivalent relations. Assuming both material and strain are homogeneous over the neighborhood, we consider an infinitesimal homogeneous transformation over the neighborhood of point x, such that

ε(x′)≃ε(x)=ε¯andηξ(x′,x)=ξ⋅ε¯⋅ξ|ξ|,∀x′∈Hδ(x),(10)

where ε is the strain tensor. The strain energy density of an equivalent CCM model regardless of the thermal parameter is given as

12ε(x):E0:ε(x)=14∫Hδxc0(|ξ|)ηξ(x′,x)2dVx′,(11)

where E0 is the stiffness tensor of the homogeneous material in the CCM model. Substituting Eq. (10) into the Eq. (11), the stiffness tensor yields

E0=12∫Hδ(x)c0(|ξ|)ξ⊗ξ⊗ξ⊗ξ|ξ|2dVx′.(12)

Similarly, we can get the other energy density equivalent relation between the local and nonlocal model thermal parameters:

ε(x):β0T¯=12∫Hδ(x)λ0(|ξ|)T¯ηξ(x′,x)dVx′,(13)

where β0 is the coefficient of thermal expansion in the CCM model. Accordingly, we substitute Eq. (10) into Eq. (13), such that

β0=12∫Hδ(x)λ0(|ξ|)ξ⊗ξ|ξ|dVx′.(14)

To this point, both the stiffness and thermal peridynamic parameters can be obtained from those of the CCM model, which is essential for simulation analysis of engineering problems. Moreover, the energy equivalent relations have also laid a solid foundation for a practical and proper coupling method between peridynamics and CCM.

3  Damage Model for Concrete under High Temperatures

Concrete shows the characteristic of a typical quasi-brittle material under tensile loading conditions, which includes not only a linear elastic deformation stage but a nonlinear damage deformation stage as well. Therefore, the peridynamic bond constitutive function for concrete ought to be formulated by appending a nonlinear deformation stage for the damage accumulation. In this paper, we intend to link the classical damage mechanics theory to the proposed thermomechanical bond-based peridynamic model.

3.1 A Thermomechanical Damage Framework for Bond-Based Peridynamics

As a fundamental characteristic parameter in the damage theory within the framework of CCM, a damage variable D is often introduced into the constitutive model to characterize the degradation of the material. Based on the Lemaitre strain equivalent assumption [36], the basic damage constitutive equation in the one-dimensional case can be expressed as Eq. (15):

σ=Ewε,(15)

in which the Ew is defined as the damaged elastic modulus, defined as Eq. (16):

Ew=(1−D)E0,(16)

where D, E0 respectively denote the damage variable and the undamaged elastic modulus. According to the degree of damage, the damage variable D goes from 0 to 1 and does not decrease, indicating the irreversibility of damage evolution.

Similarly, we introduce a damage variable Dm into the constitutive force function of the bond-based peridynamics, indicating the historical damage of the bond at a certain moment. For a specific bond, Dm also ranges from 0 to 1 and does not decrease. By this definition, we here present a damage model capable of describing the tensile quasi-brittle damage characteristic of concrete within the framework of bond-based peridynamics.

For the thermomechanical peridynamic model described above, the scalar force function of damage constitutive model for concrete at high temperatures can be simplified as Eq. (17):

fw=cw(ηξ−aT¯),(17)

where cw denotes the peridynamic micromodulus in the damage model:

cw=(1−Dm)c0,(18)

in Eq. (18), c0 is the undamaged peridynamic micromodulus.

As a multi-phase composite material, concrete is generally composed of coarse aggregate, sand, and cement paste, with quite a large number of randomly distributed micro-pores and micro-cracks inside. The disparity of thermal properties among those components gives rise to a series of complex physical and chemical reactions inside the concrete in high-temperature environments, causing the tremendous upheaval in the microstructure of concrete. Under high-temperature conditions, the combined action of loading and heating reflects on the damage exacerbation process of concrete in a nonlinear way [37]. Here we decompose the bond damage variable Dm into two parts, Df and Dh, respectively denoting the bond damage caused by loading and heating:

Dm=1−(1−Df)(1−Dh)=Df+Dh−DfDh.(19)

This coupling relation stated in Eq. (19) can be explained as: the thermal damage arises due to the initiation and propagation of micro-pores and micro-cracks caused by thermal expansion between coarse aggregates, sand, and cement paste, resulting in the deterioration of the mechanical performance of concrete; the applied loading leads to slip and dislocation between crystal grains, which interplay with the thermal damage effect, inevitably altering the mechanical properties of concrete; the coupling effect of temperature and loading damage weakens the total damage [37].

3.2 The Bond Damage Law for Concrete

Experimental data show that the full stress-strain curve from deformation to failure of concrete under tensile load presents an obvious damage softening stage [38]. Based on some former studies and experimental data, Mazars established an elaborate continuous concrete damage model [6,7], in which the evolution equation of the concrete damage variable under tensile load is summarized as Eq. (20):

D={00⩽ε<εc1−εc(1−A)ε−Aexp⁡[B(ε−εc)]ε⩾εc(20)

where A and B are two tensile material constants corresponding to the property of concrete, and εc denotes the peak strain at the peak stress in the stress-strain curve (hereinafter referred to as the peak strain). Depending on the concrete material property, the values of A and B vary, and usually the value of A ranges between 0.7 and 1.2 while B usually takes the value between 104 and 0.5×105 [39]. The Mazars damage model is a classical damage model widely employed in the damage and failure analysis of concrete structures owing to its fine consistency with the softening characteristic of concrete.

In this study, we present a bond constitutive function for concrete within the framework of bond-based peridynamics based on the above damage model of concrete. The stretch of the bond in the bond-based peridynamics is defined as Eq. (21):

s=|η+ξ|−|ξ||ξ|.(21)

There is a physical resemblance between the bond force constitutive relation in peridynamics and the stress-strain relation in CCM, for both of them describe the constitutive feature of the material. Here we assume that the linear and nonlinear relations between them are consistent with each other under one-dimensional conditions [40,41]. Following the Mazars damage evolution law, in which we switch the strain with bond stretch, the peridynamic bond damage variable Df can be acquired:

Df={00⩽s<sc1−sc(1−Af)s−Afexp⁡[Bf(s−sc)]sc⩽s⩽sb1s>sb(22)

In Eq. (22), sc denotes the critical stretch of the bond, in accordance with εc in the classic Marzars damage model, representing the stretch threshold where the bond goes into damage stage. Furthermore, to reduce the calculation cost of the peridynamic model, we introduce another critical break stretch sb into the model, indicating the breakage of the bond. We assume that when the bond damage variable of a certain bond approaches 1 extremely close, the bond breaks without restorability.

From the above bond damage evolution equation, we see that when the bond stretch s is no more than sc, we believe that the bond stays undamaged, in which case the bond constitutive function presents linear elasticity; when the bond stretch exceeds sc, the bond damage begins, with the bond decreasing quickly. After that, the bond reaches breakage, that is, the two material points connected with the bond no longer interact with each other. Also, by the two parameters Af and Bf corresponding to the two material constants from the Mazars formula, a specific bond damage curve can be obtained for a certain concrete material, given the property parameters.

3.3 Temperature Effects on the Damage Evolution

In the previous section, we discussed the damage constitutive model of concrete and established the bond damage function without thermal effects. However, as observed from experimental data, high-temperature environments have a great influence on the tensile damage process of concrete [38]. The tensile strength of concrete decreases rapidly as temperature increases and even more sharply at higher temperatures. Therefore, the tensile constitutive relation we present above ought to be further modified for concrete failure analysis under high-temperature conditions. Therefore, we tend to conduct a thorough investigation about the thermal effects on the damage constitutive model of concrete for the damage and fracture simulation of concrete structures in high-temperature environments.

On the one hand, as the test temperature rises, the peak stress of the concrete material gradually shifts down, making the stress-strain curve flattened at higher temperatures [38]. Besides, the peak strain of concrete  (i.e., εc in the Mazars damage evolution equation) at high temperatures is much larger than that of low-temperature environments. The experimental results of relation between temperature and the peak strain ratio(the ratio of the peak strain at T°C to the original peak strain, that is, ηT=εTc/εc) has been integrated and displayed in [38]. In order to reflect this temperature effect on the bond constitutive, the value of the damage critical stretch at a certain temperature T, sTc, is acquired by multiplying the original critical stretch sc by the peak strain ratio ηT:

sTc=sc⋅ηT.(23)

The ηT in Eq. (23) is determined by the experimental data in [38].

On the other hand, a high-temperature environment also affects the inherent material properties of concrete. For instance, the heat takes on a rather severe influence on the elastic modulus of concrete materials [38,42]. As a consequence, the slope of the concrete damage curve decreases significantly at higher temperatures. Under the action of high temperature, due to the intensified thermal movement of the concrete microstructure and the incoordination of the thermal expansion of the various grain boundaries, considerable thermal stress is generated inside, resulting in the initiation and propagation of micro-cracks [37]. As those micro-cracks expand and penetrate constantly, the macroscopic material mechanical properties deteriorate as a result. Here we use the thermal damage variable Dh to quantify this process of progressive failure of concrete caused by the accumulation of those micro-defects. According to the theory of macroscopic damage mechanics, this thermal damage of concrete can be phenomenologically characterized by the degradation of the material mechanical property [37]. The thermal damage variable Dh is expressed as Eq. (24):

Dh=1−ETE0,(24)

where ET denotes the elastic modulus of the material at the temperature of T. There have been many experimental studies on the thermal effect on the material properties of concrete [3,38]. The results vary with different specimens and test conditions, but the observed patterns are in substantial agreement, that is, the elastic modulus of concrete materials decreases approximatively in a linear way as the temperature rises. In addition, experimental studies also show that the tensile strength, aggregate types, water-cement ratio, and other properties of concrete are all related to the degree of temperature effects [1].

By these experimental data, we can detect and summarize the thermal effect law of the damage evolution equation of concrete, and present a practical thermal damage model for concrete.

3.4 The Peridynamic Thermomechanical Damage Model for Concrete

To sum up, the bond damage function of concrete at the temperature of T is obtained

Dm={1−ETE00⩽s<sTc1−ETE0[sTc(1−Af)s+Afexp⁡[Bf(s−sTc)]]sTc⩽s⩽sb1s>sb(25)

Substituting Eq. (25) into Eq. (17), the damage bond force constitutive function yields

fw={ETE0c0(ηξ−aT¯)0⩽s<sTcETE0[sTc(1−Af)s+Afexp⁡[Bf(s−sTc)]]c0(ηξ−aT¯)sTc⩽s⩽sb0s>sb(26)

Eq. (25) denotes the peridynamic concrete constitutive function under high-temperature conditions (see Fig. 1).

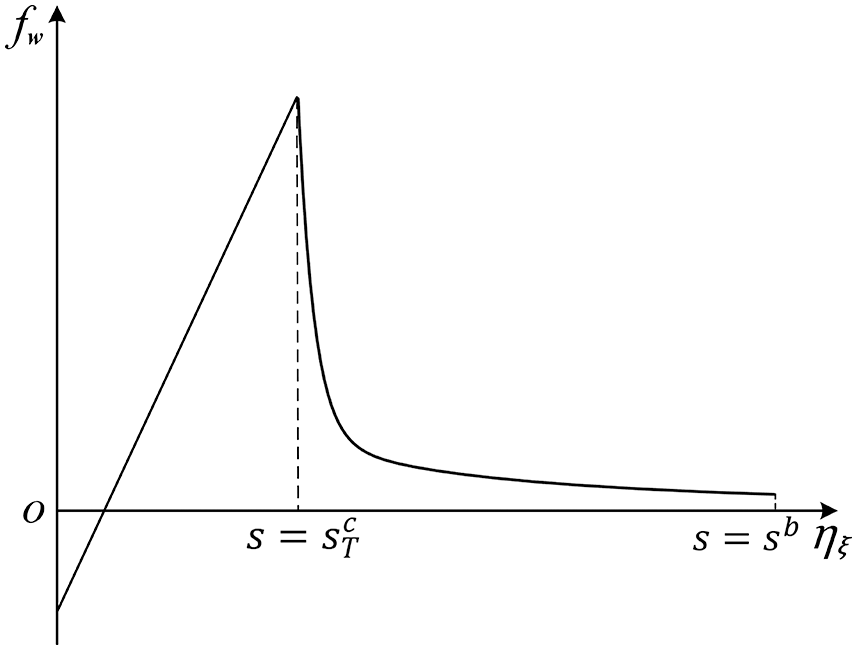
Figure 1: The damage bond force constitutive function at T∘C

A clear conclusion can be drawn based on the above discussion that the influence of temperature on the overall damage evolution process of concrete is complex and profound. To this end, we have introduced the thermal damage variable into our thermomechanical peridynamic model, to fully capture this intricate process and ultimately develop an accurate numerical model for the high-temperature fracture simulation of concrete structures.

4  The Hybrid Local/Nonlocal Continuum Thermomechanical Model

As a nonlocal theory of solid mechanics, peridynamics shows great performances for the full simulation of material mechanical response from deformation to failure. Yet the high computational cost has greatly diminished the practicability of peridynamics in engineering problems. On this account, a Morphing coupling method of peridynamics and CCM is proposed [25]. This Morphing coupling method is employed here to establish a local/nonlocal hybrid thermomechanical model with decent computational efficiency.

4.1 The Governing Equations

In the hybrid local/nonlocal continuum model, Ω denotes the overall domain and can be divided into three subdomains Ω1, Ω2 and Ωm (see Fig. 2). In this model, the CCM model is adopted in Ω1, and the peridynamic model is adopted in Ω2 while the hybrid model is applied in subdomain Ωm. The displacement u¯ is imposed on the boundary Γu. The external traction F¯ is exerted on the boundary ΓF, and n denotes the outward direction vector normal to ΓF.

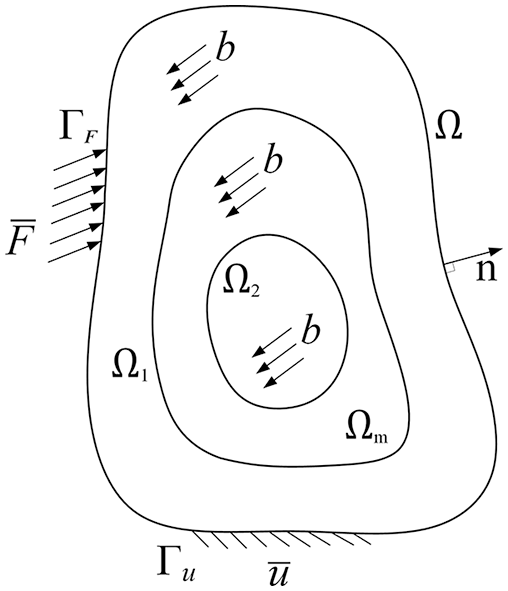
Figure 2: The subdomains of the hybrid local/nonlocal continuum model

The governing equations of the hybrid local/nonlocal continuum model for the linearly elastic, isotropic, homogeneous solid can be summarized as Eqs. (27)–(33) [25]:

•   Kinematic admissibility and compatibility

ε(x)=12(∇u(x)+(∇u)T(x))∀x∈Ω∖Ω2(27)

ηξ(x′,x)=uξ(x′)−uξ(x)∀x,x′∈Ω∖Ω1(28)

u(x)=u¯(x)   ∀x∈Γu(29)

•    Static admissibility

divσ(x,T¯)+∫Hδ(x)f^(x′,x,T¯)−f^(x,x′,T¯)dVx′=−b(x)∀x∈Ω(30)

(σ(x,T¯)+β(x)T¯)⋅n(x)=F¯(x)∀x∈ΓF(31)

•    Constitutive equations

σ(x,T¯)=E(x):ε(x)−β(x)T¯∀x∈Ω∖Ω2(32)

f^(x′,x,T¯)=12c(x,ξ)ηξ(x′,x)eξ−12λ(x,ξ)T¯eξ∀x,x′∈Ω∖Ω1(33)

where ε and σ denote the infinitesimal strain tensor and Cauchy stress tensor in the CCM model, respectively.

4.2 The Morphing Functions in the Coupling Method

In the above formula, E(x) denotes the stiffness tensor of the CCM model at the point x, while c(x,ξ) denotes the peridynamic micromodulus at the point x; β and λ are the thermal parameters in the CCM model and the peridynamic model, respectively. If we introduce a Morphing function w(x), such that

c(x,ξ)=w(x)c0(|ξ|).(34)

By Eq. (34), the stiffness coefficients in different subdomains of the hybrid local/nonlocal model can be completely formulated by two functions, E(x) and w(x), both of which are determined by the location of x. In particular, for the stiffness of a point x completely located in the peridynamics subdomain, we let E(x)=0 and w(x)=1, x′∈Hδ(x); similarly, the stiffness of a point x completely located in the CCM subdomain can be expressed as: E(x)=E0 and w(x)=0, x′∈Hδ(x). Generally speaking, a unified stiffness formulation for the local/nonlocal model can be derived by E(x) and w(x). Based on the energy equivalence at a certain material point and the assumption of approximate homogeneous deformation over the neighborhood [25], this constraint relation can be expressed as Eq. (35):

E(x)=E0−12∫Hδ(x)c0(|ξ|)w(x)+w(x′)2ξ⊗ξ⊗ξ⊗ξ|ξ|2dVx′.(35)

For the thermal parameters in the hybrid local/nonlocal thermomechnical model, we also introduce a corresponding Morphing function v(x), such that

a(x,ξ)=v(x)a0(|ξ|).(36)

Substituting Eq. (36) to Eqs. (5) and (8), we have

λ(x,ξ)=w(x)v(x)λ0(|ξ|).(37)

By Eq. (37), the constraint relation between the thermal parameters of these two models can be obtained as Eq. (38):

β(x)=β0−12∫Hδ(x)λ0(|ξ|)w(x′)v(x′)+w(x)v(x)2ξ⊗ξ|ξ|dVx′(38)

So far, we have established the overall local/nonlocal coupling model considering thermal effects, and have explained the constraint relations between the CCM model and peridynamic model with respect to both stiffness and thermal parameters. Moreover, the parameter formulations throughout the overall domain have been unified by a couple of Morphing functions.

4.3 Numerical Algorithm for the Thermomechanical Damage Model

By the hybrid local/nonlocal thermomechanical model presented previously, we are enabled to develop the numerical algorithm for failure simulation of concrete structures under high-temperature conditions.

Firstly, we perform the finite element discretization of the hybrid model. Following the principle of minimum potential energy, the discretized formula of the hybrid model can be derived [43]. It is noted that the subdomains Ω1 and Ωm are to be discretized using the continuous finite elements (CFEs) while the subdomain Ω2 is to be discretized into the discrete finite elements (DFEs), i.e., each element does not share nodes with the adjacent elements. In the peridynamic subdomain Ω2, DFEs are connected to their relevant elements via peridynamic bonds. These DFEs ensure that the initiation and propagation of cracks during the failure process can be simulated spontaneously by the breakage of the bonds passing via the element edge.

After implementation of the discretization, we incorporate the proposed progressive damage model of concrete into the numerical simulation. Fig. 3 illustrates the iterative algorithm for the damage and failure simulation process of concrete structures under thermal effects. Here, the bond no longer breaks in the form of brittle fracture but degrades according to a temperature-related historical damage variable. In each iteration step, the damage variable of each bond will be calculated, updated according to the bond stretch, and assembled in the element stiffness matrix. When there is no new broken bond and the damage of any bond no longer evolves in the current loading step, the iteration calculation of the loading step is considered complete, and then the next loading step is imposed. After all the loading steps have been applied, the whole calculation ends, indicating that the failure response of the concrete structure is obtained. It is noted that the algorithm is designed for quasi-static problems, given the absence of time parameters. In addition, the thermodynamic failure model in this study is developed for the structural fracture under constant-temperature conditions. During each calculation, the temperature condition is set to a constant value to implement the failure simulation of the concrete structure at a given temperature.

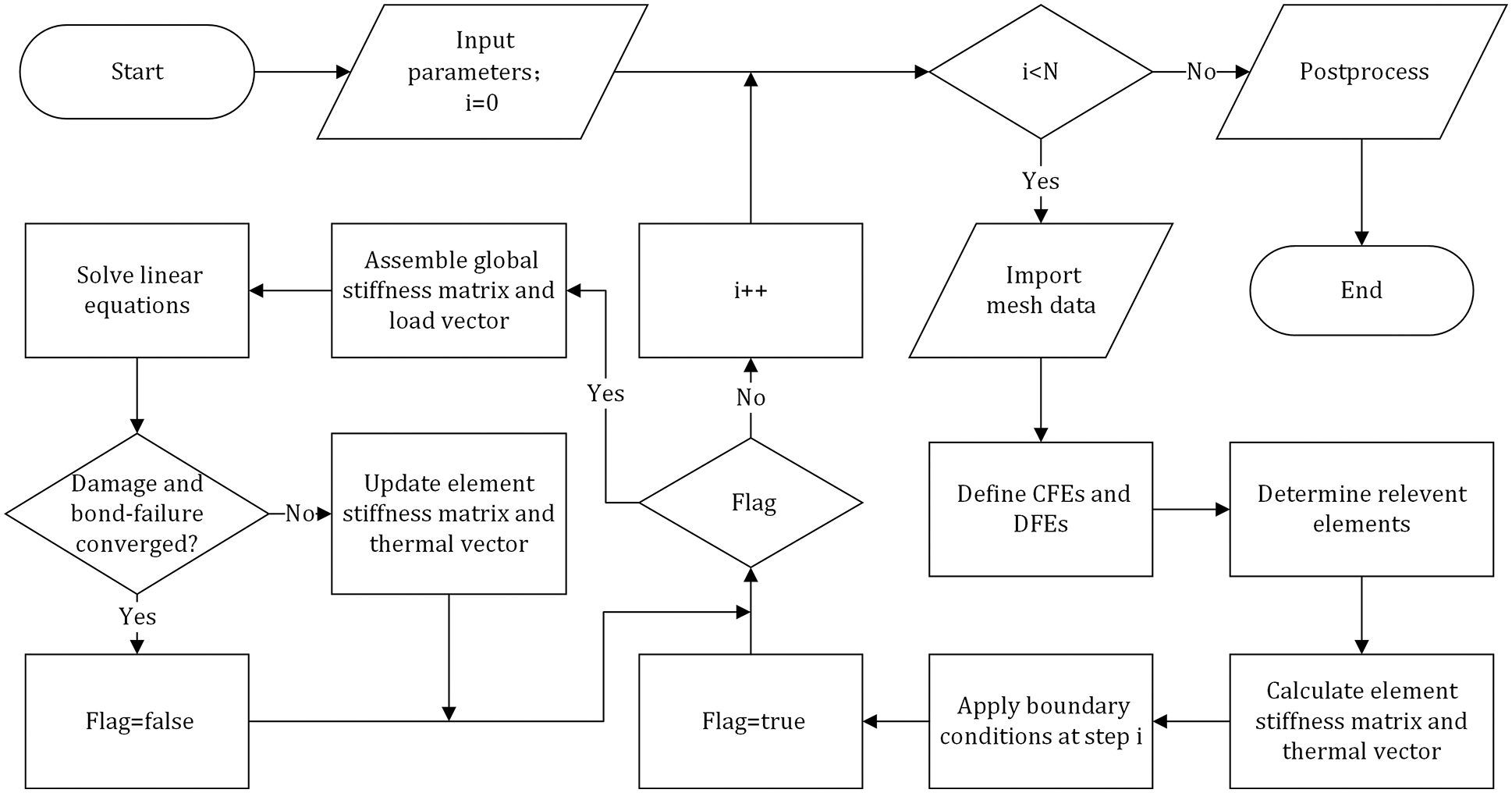
Figure 3: Flowchart of the iterative algorithm for the hybrid thermomechanical damage model, where N is the number of iterations

5  Numerical Examples

Three two-dimensional numerical examples are adopted in this section to verify the effectiveness of the proposed model, where the numerical results are compared with the experimental results. In these examples, univariate analyses of the temperature effect on the failure characteristics of concrete structures, such as crack tip location and propagation path, are conducted.

5.1 Wedge-Splitting Test

A two-dimensional wedge-splitting problem is firstly simulated to objectify the influence of temperature on the fracture performance of concrete, in which a pre-cracked plate gets split under quasi-static loads implemented on both sides of the crack. Fig. 4 shows the dimensions, boundary conditions, and distribution of the subdomains for this numerical example. The plate is considered an isotropic homogeneous concrete material. The displacement load on both sides is 0.4 m. The whole loading process is accomplished in 200 steps to imitate the quasi-static loading.

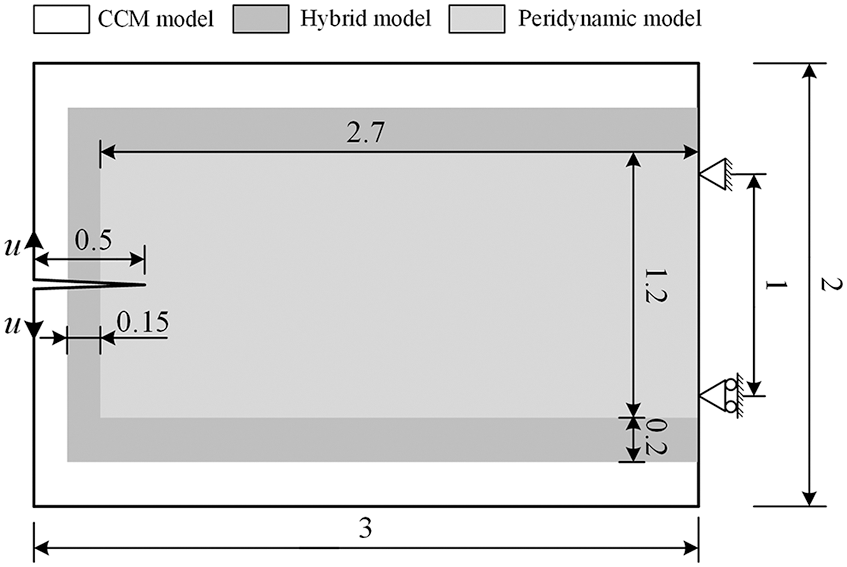
Figure 4: Dimensions, boundary conditions and subdomain divisions of a wedge-splitting test (unit of length: m)

Firstly, we conduct a convergence verification regarding the mesh size influence on the numerical results. The peridynamic mesh size, Δ, is set to four different values in the simulation, and the peridynamic horizon δ=3Δ. The obtained force-displacement curves are demonstrated in Fig. 5. It can be concluded that as the mesh size gets smaller, the curves gradually become stabler and smoother, and the numerical results ultimately converge, providing the numerical stability verification that we needed. For the balance of numerical stability and the computational efficiency, we set the mesh size to 0.05 m for the following simulation.

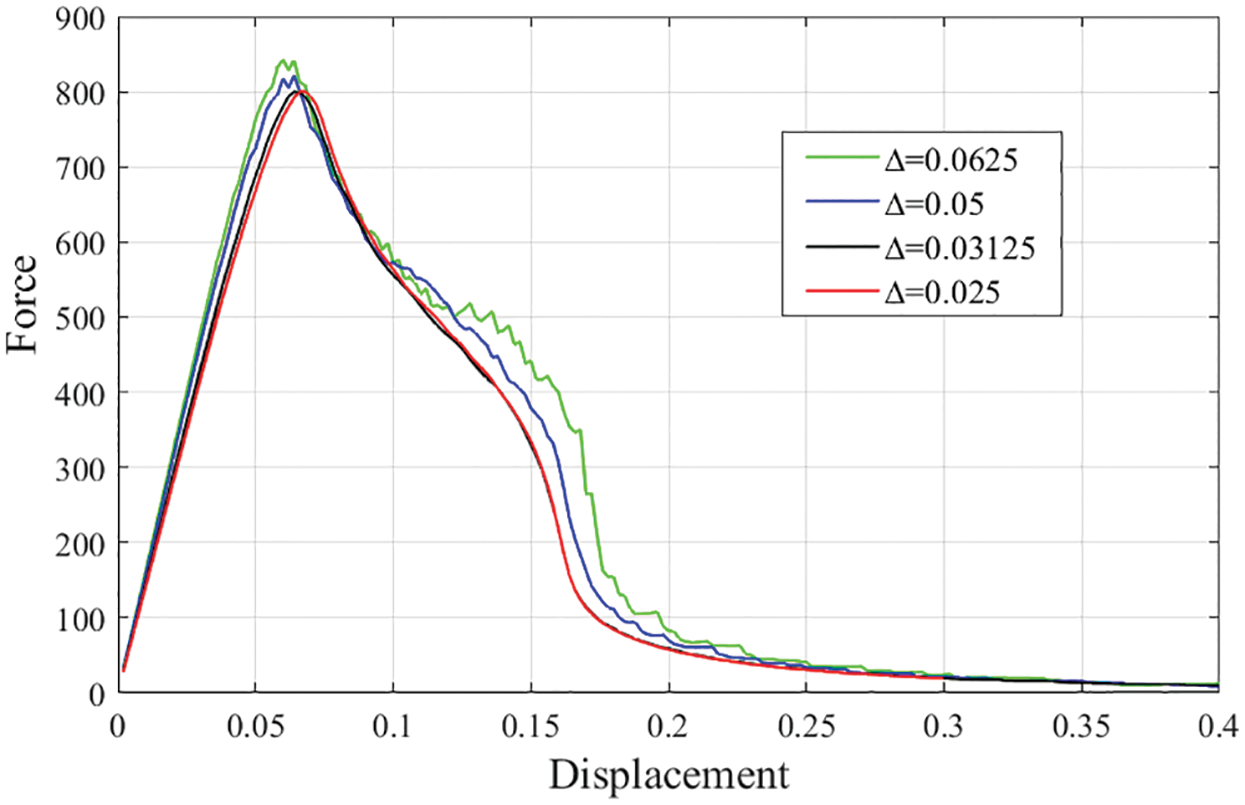
Figure 5: Force-displacement curves of the wedge-splitting tests with different mesh sizes (units: force/kN; displacement/m)

Then, we select 6 temperature conditions, T=0∘C, 100∘C, 200∘C, 300∘C, 600∘C, 800∘C, as the ambient temperatures for comparison. Note that we set the base temperature T0 to be 0∘C for all the cases in our examples, such that T¯=T1−T0=T1=T. We take the thermal expansion coefficient for concrete to be 5×10−6/∘C. Note that the two parameters in the damage model Af and Bf are respectively set as 0.7 and 10000 during all calculations in this study. Under different temperature conditions, we set the elastic modulus of concrete and the critical stretch of the peridynamic bond to different values according to the experimental law in [38,42]. The specific values are tabulated as Table 1.

Fig. 6 shows six force-displacement curves obtained from the wedge-splitting tests at various temperatures. We can find that as the temperature increases, the peak value of the force-displacement curve gradually decreases with increasing amplitude. This also reflects that the bearing capacity of concrete structures decreases sharply as the temperature rises. Meanwhile, we can see that below 200∘C, the temperature change does not significantly affect the fracture characteristics of concrete. However, when the temperature reaches above 200∘C, the curve quickly shows a flattening tendency, which is also consistent with the variation trend of concrete constitutive relations with rising temperature [3].

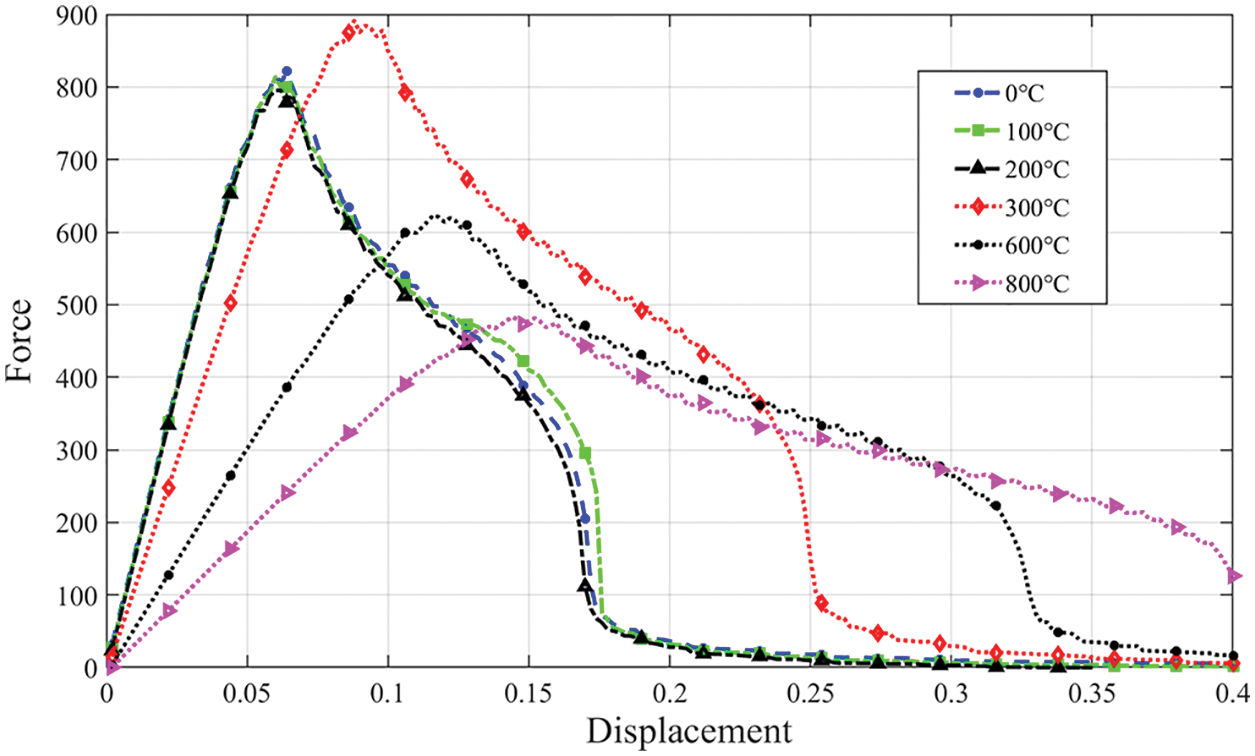
Figure 6: Force-displacement curves of the wedge-splitting tests at different temperatures (units: force/kN; displacement/m)

The temperature effect on the crack propagation in the wedge-splitting test can be concluded from Fig. 7. We take the results of step 70 at various temperatures to observe the crack propagation in the concrete structures. When the temperature rises, the damage characteristic of the structure becomes more and more obvious, and the material shows a softening trend, leading to the tardiness of the crack propagation. According to the results above, the proposed model is very much competent to capture the damage and failure characteristics of concrete under high-temperature conditions.

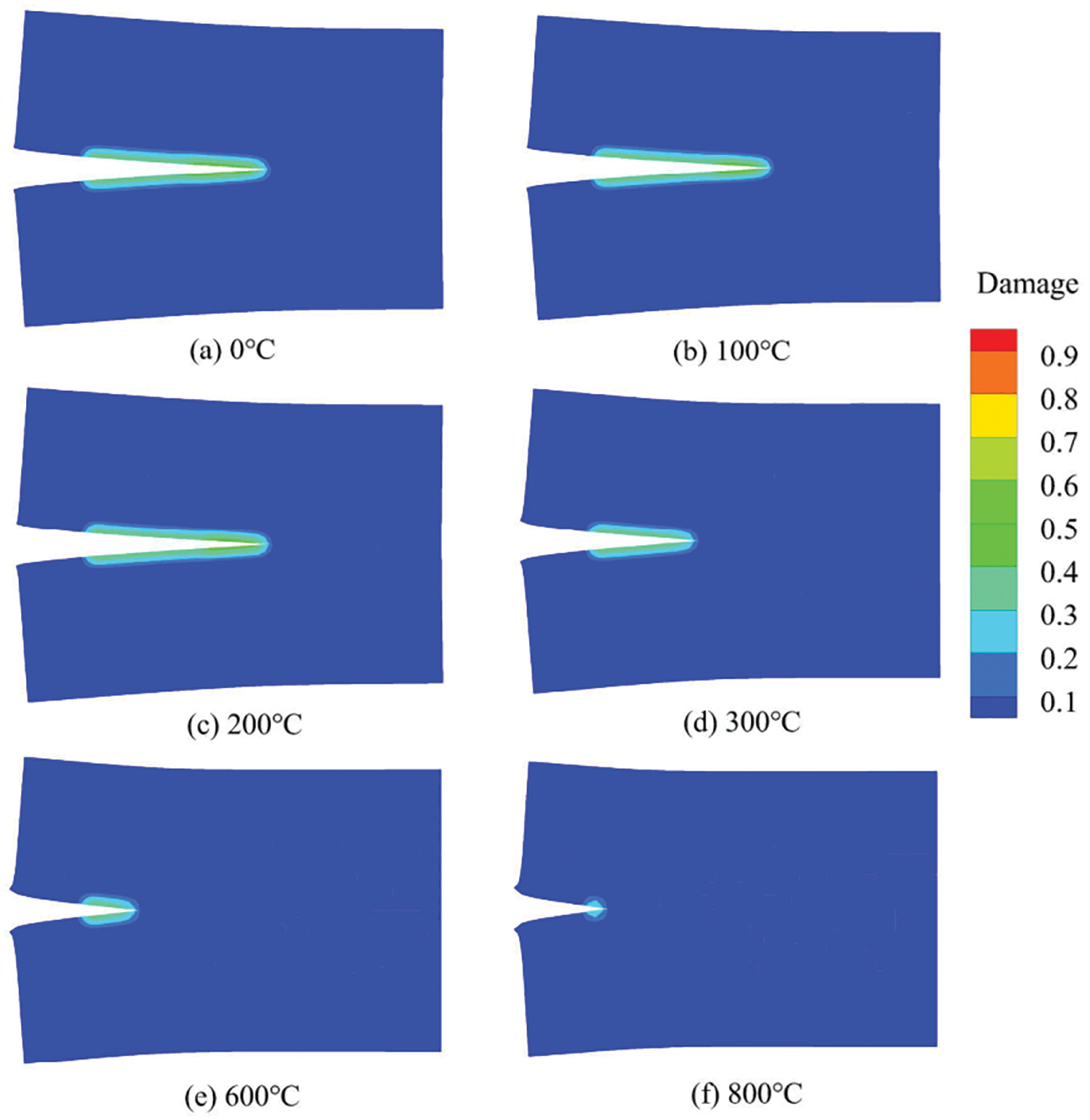
Figure 7: Damage contour images at the 70th step under different temperature conditions

5.2 Three-Point Bending Test

A decenter-notched three-point bending example is numerically conducted to verify the accuracy of the proposed model. The dimensions, boundary conditions and distribution of the subdomains are shown in Fig. 8.

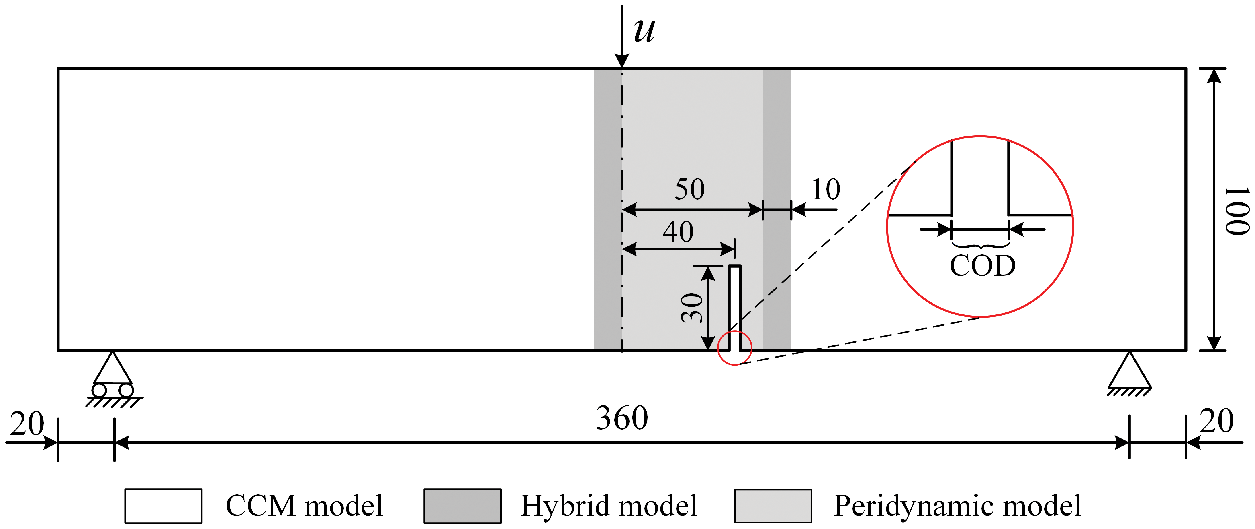
Figure 8: Test setup and configuration for three-point bending test (unit of length: mm)

The displacement load u=30 mm. Here, we take the peridynamic mesh size as Δ=2 mm, and δ=3Δ. In this section, we take four temperatures, T=0∘C, 200∘C, 400∘C, 600∘C, as ambient temperatures. The material parameters at each temperature are selected and listed in Table 2. And the coefficient of thermal expansion for concrete material is still 5×10−6/∘C.

The simulated crack path shows great agreement with the experimental observation (see Fig. 9). The force-displacement curves at four temperatures are compared in Fig. 10. We can easily find that below 200∘C, the bearing capacity of concrete is merely affected by temperature, and the deviation of the peak force value alters within the range of 5%. But as the temperature rises, the peak force of the concrete structure drops sharply. Under low-temperature conditions, for instance, at 0∘C, the entire structure is more likely to fracture in a brittle way, where the curve quickly climbs to the highest value and then drops sharply. However, under high-temperature conditions, the entire curve shows a flattening trend, and the trailing part of the curve under high-temperature conditions is relatively longer than that of low-temperature conditions. These appearances manifest the damage aggravation in the entire concrete structure under high-temperature conditions, which is rather distinguishable by contrast with the brittle feature exhibited under the low-temperature condition.

Figure 9: Comparison of numerical simulation results (a) and experimental results in [44] (b)

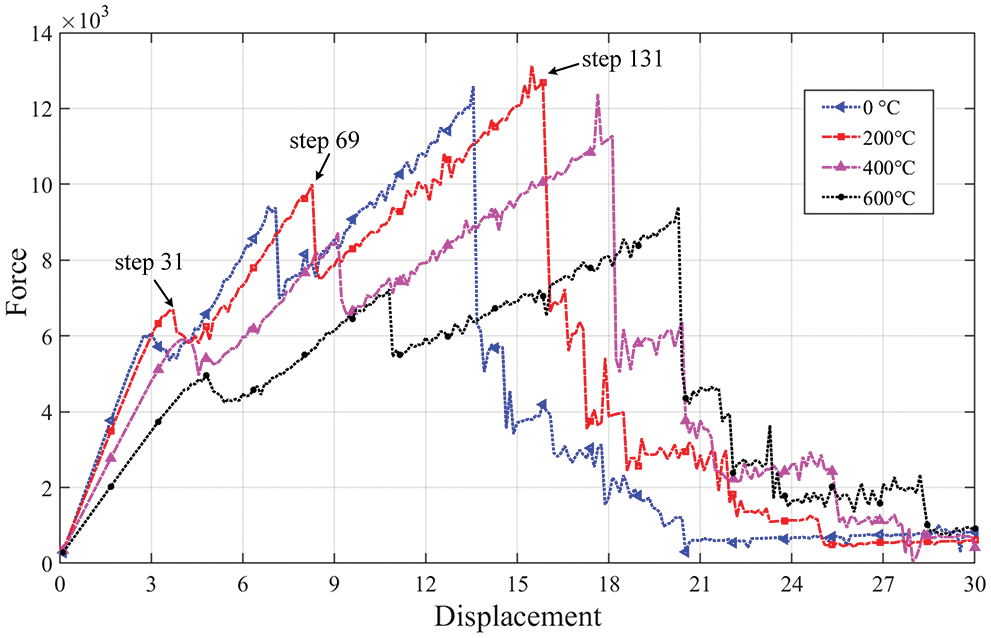
Figure 10: Force-displacement curves of failure process of three-point bending structure at different temperatures (units: force/N; displacement/mm)

In addition, it is very clear that the force-displacement curves at the four temperatures are all in similar tri-peak forms, which is closely relevant to the crack propagation in the structural fracture process. Let’s take the ambient temperature of 200∘C as an example. We take out the fracture images corresponding to the three peaks and the final fracture respectively(see Fig. 11): at step 31, the crack initiates, hence the first peak; at step 69, that is, the second peak in Fig. 10, the crack starts to deflect for the first time and extends to the left; at step 131, the crack deflects again and starts going to the upper left, and the bearing capacity of the entire three-point bending decreases rapidly, which leads to the third and also the largest peak; at last, the structure has approached complete failure and lost its bearing capacity at step 250.

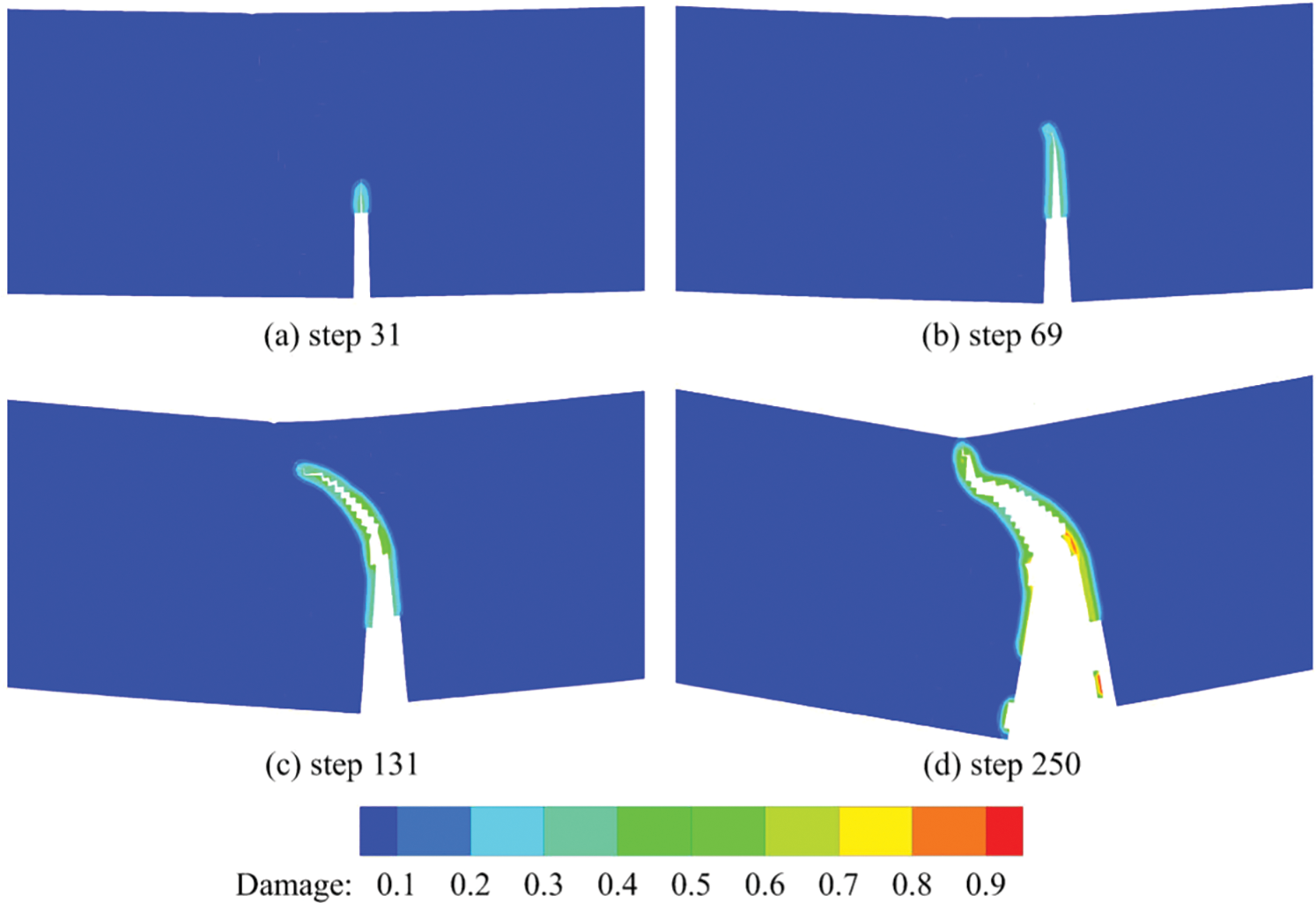
Figure 11: Crack propagation of different loading steps at 200∘C

We can also see that at the same loading step, the crack opening displacements (CODs) under different temperature conditions are quite different. We take the damage image at step 135 as an example. As shown in Fig. 12, under low-temperature conditions like 0∘C, the crack propagation of the concrete structure is rather rapid and more inclined to brittle fracture. However, under high-temperature conditions such as 400°C and 600°C, the damage degree increases, and the crack propagation process is more gentle than that of lower temperature conditions, showing more obvious damage characteristics. This also proves that the proposed model is capable of capturing the damage feature of concrete materials in high-temperature environments.

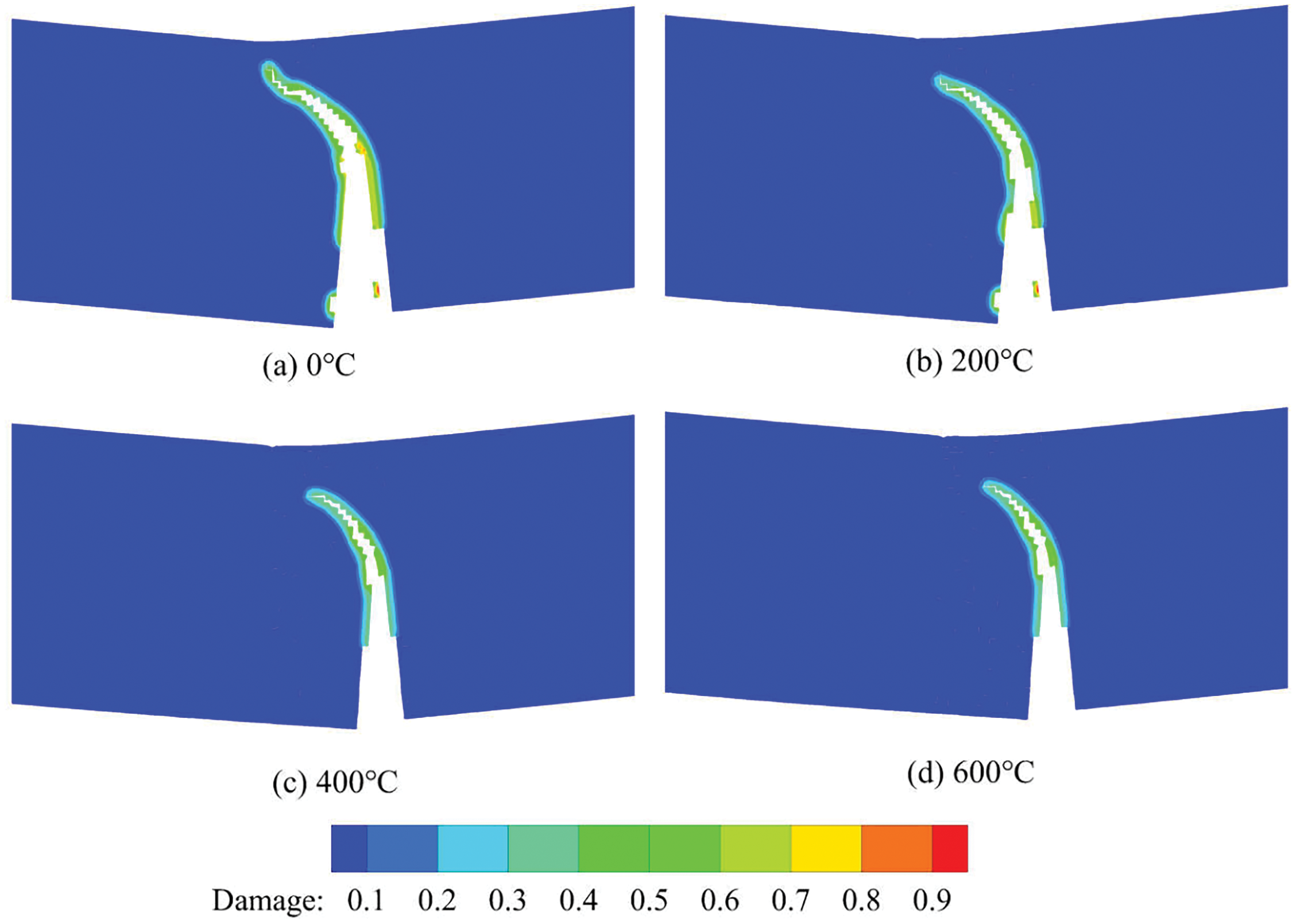
Figure 12: Fracture images of three-point bending structure under different temperatures conditions at step 135

The growth curves of COD at the four temperatures are shown in Fig. 13. The curves of the COD corresponding to the loading displacement show a similar positive correlaton. Also, in each curve, there are two minor leaps and a major leap, corresponding to the three peaks in the force-displacement curve (see Fig. 10). The major leap indicates the structure going through a sudden breakage, which soon leads to the failure of the structure. Fig. 14 shows the failure form at each temperature when the three-point bending structure reaches complete failure and the slope of the COD curve in Fig. 13 is stabilized. The fracture responses of the three-point bending under the high-temperature conditions are more severe, and the CODs are larger than that of the low-temperature condition, which also reflects the high-temperature conditions undermining the bearing capacity and strength of the concrete structures.

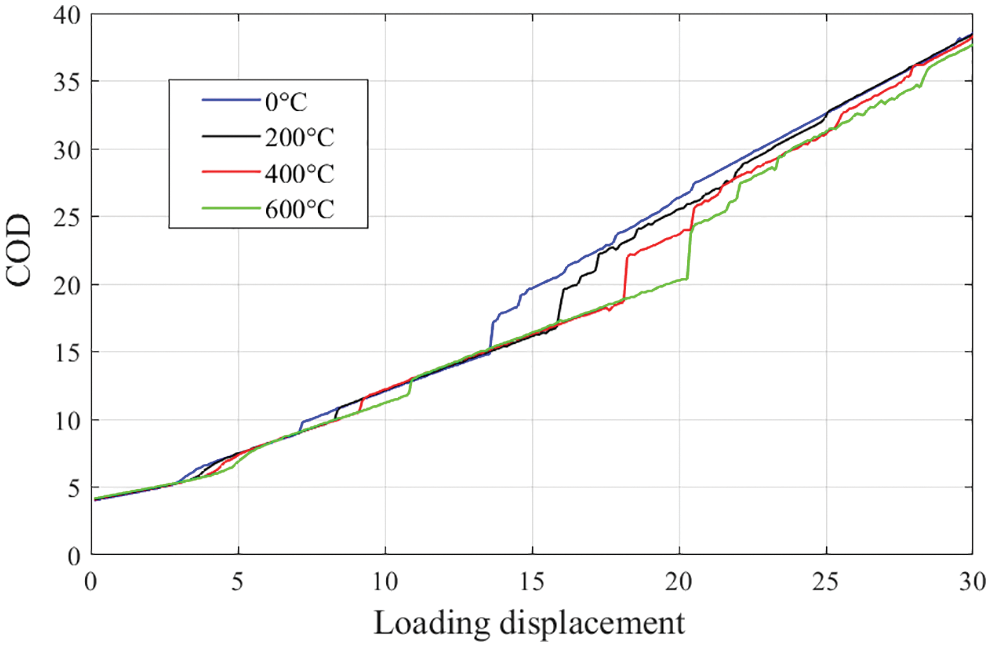
Figure 13: Growth curves of the COD corresponding to loading displacement at the four temperatures (unit of length: mm)

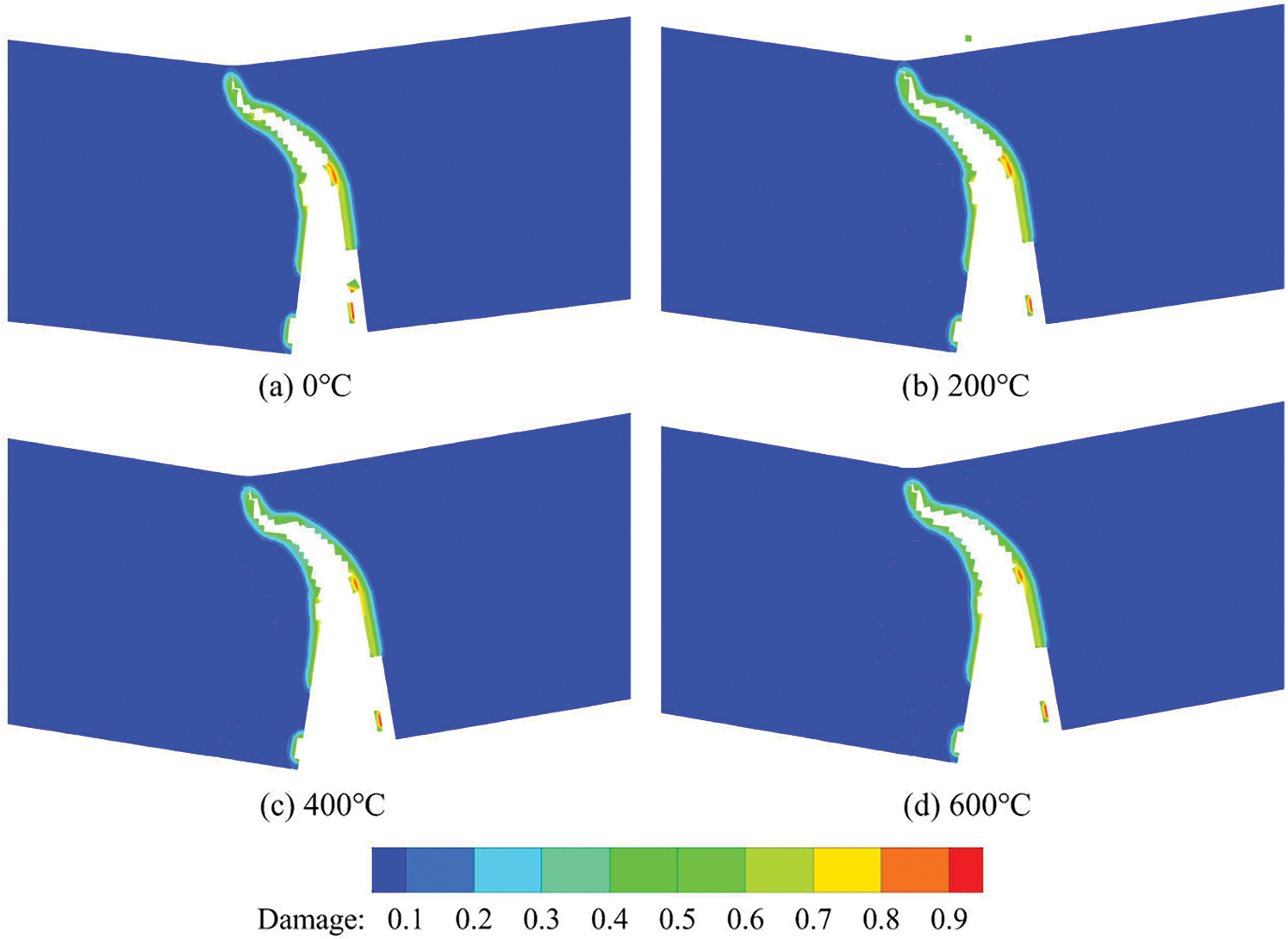
Figure 14: Failure forms of the three-point bending structure at different temperatures

5.3 Double-Edge-Notched Specimen under Tension-Shear Combined Loads

Next, a double-edge-notched specimen under tension-shear combined loads is taken as a numerical example [45]. The geometry, load condition, and subdomain distribution of the numerical example are shown in Fig. 15. In this part, the elastic modulus of the material we use at 0∘C is E=50 GPa, and the critical bond stretch is s0=1.02. Firstly, the problem is simulated in the absence of temperature impact, where the tension-shear load ratio is set to be ut/us=1. The whole structure is discretized into quadrilateral elements of size Δ=2 mm, and δ=3Δ. We compare the numerical results with the experimental observation in [45] (see Fig. 16). It can be observed that the crack path reproduced by the proposed model matches the experimental results very well. Next, to further study the fracture behavior of concrete structures under high-temperature conditions, the fracture simulations of concrete structures with different thermal expansion coefficients are conducted at the ambient temperature of 800∘C. We take the elastic modulus of the concrete material at 800∘C as E=20 GPa, and the critical bond stretch is s0=1.04. The thermal expansion coefficients are selected as 5×10−6/∘C, 1.0×10−5/∘C, 1.5×10−5/∘C, respectively.

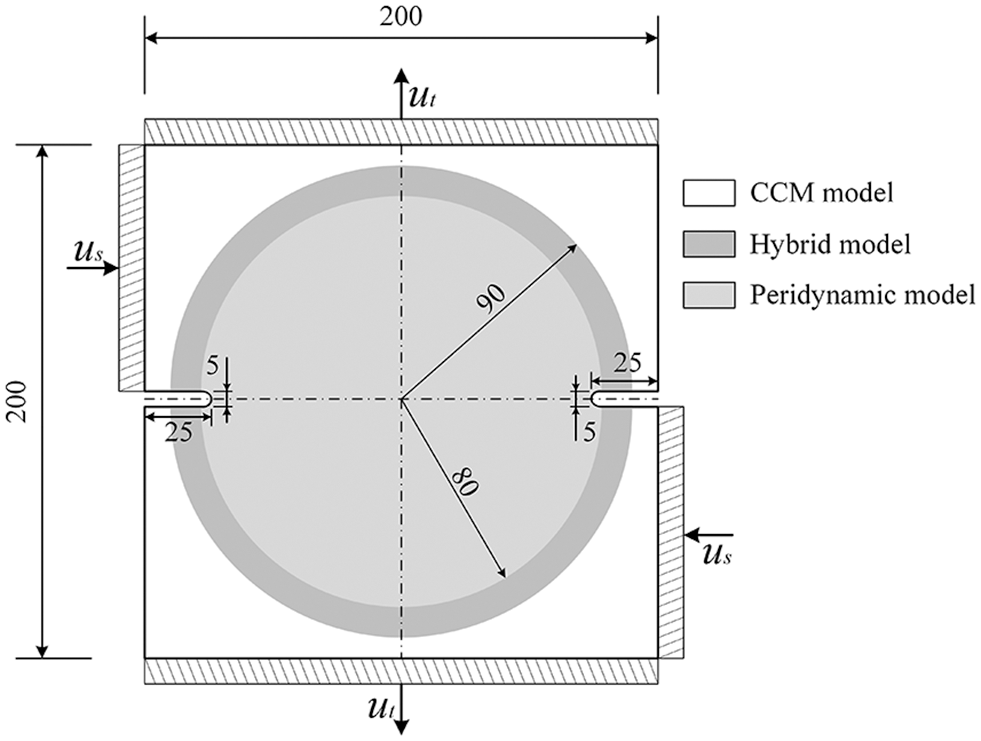
Figure 15: Double-edge-notched specimen under tension-shear combined loads (unit of length: mm)

Figure 16: The simulated result (a) and the experimental observation in [45] (b)

Fig. 17 indicates that as the thermal expansion coefficient gradually increases, the deflection angle of the crack caused by the shear-tension combined loads gets magnified. The reason is that under the same temperature condition, as the thermal expansion coefficient increases, the extension of the bonds in the structure gradually increases, which enhances the effect of the tensile load yet offsets the shear effect to a certain extent. And with the increase of the expansion coefficient, this influence shows more obviously, meaning that the effective tensile/shear load ratio of the structure rises consequently, ultimately leading to the crack deflection. This phenomenon appears to be in accordance with experimental law in [45]. In addition, for the structure with higher expansion rates (see Fig. 17c), the structural damage is more severe than that of lower expansion rates. We can see both the damage associated with the loading around the cracks and the destruction caused by thermal expansion between the cracks. This issue has been addressed in [42] regarding the spalling damage caused by the expansion of concrete materials in high-temperature environments. In high-temperature environments, the internal micro-cracks emerge in large numbers due to heat-induced changes in the components of the concrete structure and the microstructure, causing local damage to intensify and eventually evolve into the macroscopic damage of the concrete structure. This also proves that the model proposed in this study essentially reflects the effect of various parameters on the fracture and failure behavior of concrete structures under high-temperature conditions from a multiscale perspective.

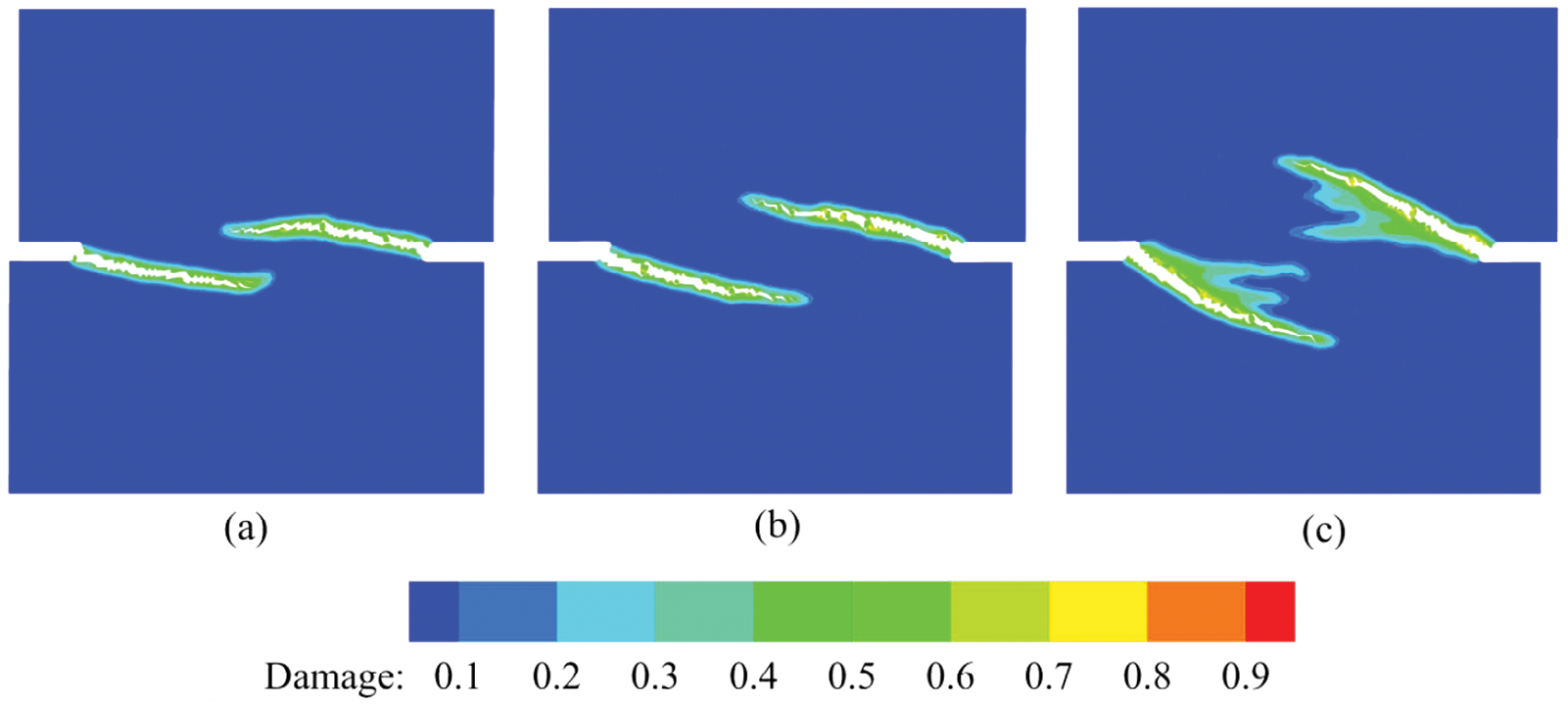
Figure 17: The damage contour of the facture results at 800∘C for concrete structures with various thermal expansion coefficients: (a) 5×10−6/∘C, (b) 1.0×10−5/∘C, (c) 1.5×10−5/∘C

6  Conclusion

A hybrid local/nonlocal thermomechanical model is developed in this paper for the damage and fracture simulation of concrete structures under high-temperature conditions. The proposed model can capture the damage characteristic of concrete and predict the fracture process of concrete structures under high-temperature conditions naturally and efficiently.

The validity and effectiveness of the proposed model are verified by comparison with experimental results. We further explore the influence of temperature on the damage process of various concrete structures. It was found that the high-temperature environment has a devastating effect on the load-bearing capacity of the concrete structure, and the crack path in the concrete structure also alters depending on the different material properties and high-temperature conditions.

Furthermore, we expect to carry on for more extension work based on this study. First of all, the presented model is more focused on the fracture of concrete under steady-state temperature conditions. It is undeniable that a fully coupled thermo-mechanical model is necessary for a more comprehensive and precise study of the failure behavior of concrete or other materials, in which the formulas need to be reconstructed for thermal diffusion. There have been many profound studies on this issue [30,31], providing a promising prospect for the extension to establish a hybrid peridynamic and CCM model for the thermo-mechanical damage and fracture problems with transient temperature distributions.

Besides, this proposed model generalizes the degradation induced by the microstructure of concrete using the framework of damage mechanics from a macroscopical perspective. For future elaborate study on the fracture behavior of concrete at high temperatures (including spalling) on the basis of this study, we need to model the microstructure of concrete more clearly. The main causes of heat-induced fracture include increased elastic energy due to suppressed thermal expansion and pore pressure caused by the continuous vaporization of water within the concrete pores [46]. To this end, more precise modeling of the material properties and interactions of coarse aggregate, sand, and cement paste in concrete material ought to be investigated for further advances.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper. The authors also are deeply thankful for the support and contribution from journal editors.

Funding Statement: The authors gratefully acknowledge the financial support received from the National Natural Science Foundation of China (11872016), National Key Laboratory of Shock Wave and Detonation Physics (JCKYS2021212003), Fundamental Research Funds for the Central Universities (DUT20LAB203), Key Research and Development Project of Liaoning Province (2020JH2/10500003).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Qin, L. (2014). Study on the strength and deformation of concrete under multiaxial stress after high-temperature of freeze-thaw cycling (Ph.D. Thesis). Dalian University of Technology, China (in Chinese). [Google Scholar]

 2.  Xie, D., Qian, Z. (1998). Research on bond and tension of concrete after high temperature. Journal of Zhejiang University(Natural Science Edition), 32(5), 597–602 (in Chinese). [Google Scholar]

 3.  Ma, Q., Guo, R., Zhao, Z., Lin, Z., He, K. (2015). Mechanical properties of concrete at high temperature—A review. Construction and Building Materials, 93, 371–383. DOI 10.1016/j.conbuildmat.2015.05.131. [Google Scholar] [CrossRef]

 4.  Dougill, J. W. (1976). On stable progressively fracturing solids. Zeitschrift für Angewandte Mathematik und Physik(ZAMP), 27(4), 423–437. DOI 10.1007/BF01594899. [Google Scholar] [CrossRef]

 5.  Loland, K. E. (1980). Continuous damage model for load-response estimation of concrete. Cement and Concrete Research, 10(3), 395–402. DOI 10.1016/0008-8846(80)90115-5. [Google Scholar] [CrossRef]

 6.  Mazars, J. (1981). Mechanical damage and fracture of concrete structures. Advances in Fracture Research, 4, 1499–1506. [Google Scholar]

 7.  Mazars, J. (1986). A description of micro-and macroscale damage of concrete structures. Engineering Fracture Mechanics, 25(5–6), 729–737. DOI 10.1016/0013-7944(86)90036-6. [Google Scholar] [CrossRef]

 8.  Barragan, B. E., Giaccio, G. M., Zerbino, R. L. (2001). Fracture and failure of thermally damaged concrete under tensile loading. Materials and Structures, 34(5), 312–319. DOI 10.1007/BF02482211. [Google Scholar] [CrossRef]

 9.  Chen, B., Li, C., Chen, L. (2009). Experimental study of mechanical properties of normal-strength concrete exposed to high temperatures at an early age. Fire Safety Journal, 44(7), 997–1002. DOI 10.1016/j.firesaf.2009.06.007. [Google Scholar] [CrossRef]

10. Silling, S. A. (2000). Reformulation of elasticity theory for discontinuities and long-range forces. Journal of the Mechanics and Physics of Solids, 48(1), 175–209. DOI 10.1016/S0022-5096(99)00029-0. [Google Scholar] [CrossRef]

11. Li, J., Li, S., Lai, X., Liu, L. (2022). Peridynamic stress is the static first piolakirchhoff virial stress. International Journal of Solids and Structures, 241, 111478. DOI 10.1016/j.ijsolstr.2022.111478. [Google Scholar] [CrossRef]

12. Gerstle, W., Sau, N., Silling, S. A. (2007). Peridynamic modeling of concrete structures. Nuclear Engineering and Design, 237(12–13), 1250–1258. DOI 10.1016/j.nucengdes.2006.10.002. [Google Scholar] [CrossRef]

13. Fan, H., Bergel, G., Li, S. (2016). A hybrid peridynamics–SPH simulation of soil fragmentation by blast loads of buried explosive. International Journal of Impact Engineering, 87, 14–27. DOI 10.1016/j.ijimpeng.2015.08.006. [Google Scholar] [CrossRef]

14. Fan, H., Li, S. (2017). A Peridynamics-SPH modeling and simulation of blast fragmentation of soil under buried explosive loads. Computer Methods in Applied Mechanics and Engineering, 318, 349–381. DOI 10.1016/j.cma.2017.01.026. [Google Scholar] [CrossRef]

15. Lai, X., Ren, B., Fan, H., Li, S., Wu, C. et al. (2015). Peridynamics simulations of geomaterial fragmentation by impulse loads. International Journal for Numerical and Analytical Methods in Geomechanics, 39(12), 1304–1330. DOI 10.1002/nag.2356. [Google Scholar] [CrossRef]

16. Kilic, B., Madenci, E. (2009). Prediction of crack paths in a quenched glass plate by using peridynamic theory. International Journal of Fracture, 156(2), 165–177. DOI 10.1007/s10704-009-9355-2. [Google Scholar] [CrossRef]

17. Xu, J., Askari, A., Weckner, O., Silling, S. (2008). Peridynamic analysis of impact damage in composite laminates. Journal of Aerospace Engineering, 21(3), 187–194. DOI 10.1061/(ASCE)0893-1321(2008)21:3(187). [Google Scholar] [CrossRef]

18. Kilic, B., Agwai, A., Madenci, E. (2009). Peridynamic theory for progressive damage prediction in center-cracked composite laminates. Composite Structures, 90(2), 141–151. DOI 10.1016/j.compstruct.2009.02.015. [Google Scholar] [CrossRef]

19. Han, F., Azdoud, Y., Lubineau, G. (2014). Computational modeling of elastic properties of carbon nanotube/polymer composites with interphase regions. Part ii: Mechanical modeling. Computational Materials Science, 81, 652–661. DOI 10.1016/j.commatsci.2013.07.008. [Google Scholar] [CrossRef]

20. Chen, Z., Chu, X. (2021). Peridynamic modeling and simulation of fracture process in fiber-reinforced concrete. Computer Modeling in Engineering & Sciences, 127(1), 241–272. DOI 10.32604/cmes.2021.015120. [Google Scholar] [CrossRef]

21. Silling, S. A., Littlewood, D., Seleson, P. (2015). Variable horizon in a peridynamic medium. Journal of Mechanics of Materials and Structures, 10(5), 591–612. DOI 10.2140/jomms. [Google Scholar] [CrossRef]

22. Seleson, P., Beneddine, S., Prudhomme, S. (2013). A force-based coupling scheme for peridynamics and classical elasticity. Computational Materials Science, 66, 34–49. DOI 10.1016/j.commatsci.2012.05.016. [Google Scholar] [CrossRef]

23. Seleson, P., Ha, Y. D., Beneddine, S. (2015). Concurrent coupling of bond-based peridynamics and the navier equation of classical elasticity by blending. International Journal for Multiscale Computational Engineering, 13(2), 91–113. DOI 10.1615/IntJMultCompEng.2014011338. [Google Scholar] [CrossRef]

24. Han, F., Lubineau, G. (2012). Coupling of nonlocal and local continuum models by the arlequin approach. International Journal for Numerical Methods in Engineering, 89(6), 671–685. DOI 10.1002/nme.3255. [Google Scholar] [CrossRef]

25. Lubineau, G., Azdoud, Y., Han, F., Rey, C., Askari, A. (2012). A morphing strategy to couple non-local to local continuum mechanics. Journal of the Mechanics and Physics of Solids, 60(6), 1088–1102. DOI 10.1016/j.jmps.2012.02.009. [Google Scholar] [CrossRef]

26. Sun, W., Fish, J. (2019). Superposition-based coupling of peridynamics and finite element method. Computational Mechanics, 64(1), 231–248. DOI 10.1007/s00466-019-01668-5. [Google Scholar] [CrossRef]

27. Sun, W., Zhang, G., Zhang, Z. (2021). Damage analysis of the cut-off wall in a landslide dam based on centrifuge and numerical modeling. Computers and Geotechnics, 130, 103936. DOI 10.1016/j.compgeo.2020.103936. [Google Scholar] [CrossRef]

28. Jiang, F., Shen, Y., Cheng, J. (2020). An energy-based ghost-force-free multivariate coupling scheme for bond-based peridynamics and classical continuum mechanics. Engineering Fracture Mechanics, 240, 107316. DOI 10.1016/j.engfracmech.2020.107316. [Google Scholar] [CrossRef]

29. Jiang, F., Shen, Y. (2022). A Quasi-nonlocal coupling method for bond-based peridynamics with classical continuum mechanics. Engineering Computations, 39(2), 554–573. DOI 10.1108/EC-05-2020-0246. [Google Scholar] [CrossRef]

30. Oterkus, S., Madenci, E., Agwai, A. (2014). Fully coupled peridynamic thermomechanics. Journal of the Mechanics and Physics of Solids, 64, 1–23. DOI 10.1016/j.jmps.2013.10.011. [Google Scholar] [CrossRef]

31. Sun, W., Lu, W., Bao, F., Ni, P. (2021). A PD-FEM coupling approach for modeling thermal fractures in brittle solids. Theoretical and Applied Fracture Mechanics, 116, 103129. DOI 10.1016/j.tafmec.2021.103129. [Google Scholar] [CrossRef]

32. Silling, S. A., Askari, E. (2005). A meshfree method based on the peridynamic model of solid mechanics. Computers & Structures, 83(17–18), 1526–1535. DOI 10.1016/j.compstruc.2004.11.026. [Google Scholar] [CrossRef]

33. Zaccariotto, M., Luongo, F., Sarego, G., Galvanetto, U. (2015). Examples of applications of the peridynamic theory to the solution of static equilibrium problems. The Aeronautical Journal, 119(1216), 677–700. DOI 10.1017/S0001924000010770. [Google Scholar] [CrossRef]

34. Yang, D., Dong, W., Liu, X., Yi, S., He, X. (2018). Investigation on mode-I crack propagation in concrete using bond-based peridynamics with a new damage model. Engineering Fracture Mechanics, 199, 567–581. DOI 10.1016/j.engfracmech.2018.06.019. [Google Scholar] [CrossRef]

35. Gerstle, W., Sau, N., Sakhavand, N. (2009). On peridynamic computational simulation of concrete structures. ACI Special Publication, 265, 245–264. [Google Scholar]

36. Lemaitre, J. (2012). A course on damage mechanics. Springer Science & Business Media. [Google Scholar]

37. Nechnech, W., Meftah, F., Reynouard, J. M. (2002). An elasto-plastic damage model for plain concrete subjected to high temperatures. Engineering Structures, 24(5), 597–611. DOI 10.1016/S0141-0296(01)00125-0. [Google Scholar] [CrossRef]

38. Chen, X., Bu, J., Zhou, W., Wang, Q. (2019). Effect of pre-cyclic damage and high temperature on residual tensile behavior of concrete. Fire Safety Journal, 108, 102853. DOI 10.1016/j.firesaf.2019.102853. [Google Scholar] [CrossRef]

39. Xu, L., Wang, S., Jin, Y. (2021). Nonlocal concrete mazars model and its numerical implementation and validation. Journal of China Three Gorges University (Natural Sciences), 43(1), 7–12 (in Chinese). DOI 10.13393/j.cnki.issn.1672-948x.2021.01.002. [Google Scholar] [CrossRef]

40. Shi, H., Qian, S., Yuan, Q., Xu, T., Zhang, G. (2017). Construction of the constitutive force function of quasi-brittle materials based on the peridynamic theory. Chinese Journal of Computational Mechanics, 34(4), 422–427 (in Chinese). [Google Scholar]

41. Yu, H., Chen, X., Sun, Y. (2020). A generalized bond-based peridynamic model for quasi-brittle materials enriched with bond tension–rotation–shear coupling effects. Computer Methods in Applied Mechanics and Engineering, 372, 113405. DOI 10.1016/j.cma.2020.113405. [Google Scholar] [CrossRef]

42. Liu, J., Tan, K., Yao, Y. (2018). A new perspective on nature of fire-induced spalling in concrete. Construction and Building Materials, 184, 581–590. DOI 10.1016/j.conbuildmat.2018.06.204. [Google Scholar] [CrossRef]

43. Wang, Y., Han, F., Lubineau, G. (2019). A hybrid local/nonlocal continuum mechanics modeling and simulation of fracture in brittle materials. Computer Modeling in Engineering & Sciences, 121(2), 399–423. DOI 10.32604/cmes.2019.07192. [Google Scholar] [CrossRef]

44. Carpinteri, A., Brighenti, R. (2010). Fracture behaviour of plain and fiber-reinforced concrete with different water content under mixed mode loading. Materials & Design, 31(4), 2032–2042. DOI 10.1016/j.matdes.2009.10.021. [Google Scholar] [CrossRef]

45. Nooru-Mohamed, M., Schlangen, E., van Mier, J. (1993). Experimental and numerical study on the behavior of concrete subjected to biaxial tension and shear. Advanced Cement Based Materials, 1(1), 22–37. DOI 10.1016/1065-7355(93)90005-9. [Google Scholar] [CrossRef]

46. Cheng, P., Zhu, H., Zhang, Y., Jiao, Y., Fish, J. (2022). Coupled thermo-hydro-mechanical-phase field modeling for fire-induced spalling in concrete. Computer Methods in Applied Mechanics and Engineering, 389, 114327. DOI 10.1016/j.cma.2021.114327. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.