DOI:10.32604/biocell.2022.020806

| BIOCELL DOI:10.32604/biocell.2022.020806 |  |
| Viewpoint |
Cell bioenergetics: Simple logics, complex solution
Instituto de Histología y Embriología de Mendoza (IHEM, Universidad Nacional de Cuyo, CONICET), Facultad de Ciencias Exactas y Naturales, Mendoza, 5500, Argentina
*Address correspondence to: Luis S. Mayorga, lmayorga@mendoza-conicet.gob.ar
Received: 15 December 2021; Accepted: 23 February 2022
Abstract: Cells are open systems that exchange energy and molecules with their environment. As any material system, they perform all the complex activities required for homeostasis and reproduction, obeying the thermodynamic laws. This viewpoint will argue that the basic logic governing the energy flux required to preserve cell organization and function is simple: to decrease the activation energy (Ea) of specific processes. Almost none of the possible chemical reactions and energy transformations inside a cell occur at a measurable speed at room or body temperature. Enzymes or other macromolecular structures speed up particular transformations by decreasing the corresponding energetic barriers. However, to maintain the systems in a homeostatic state, capable of sophisticated functions based on this simple strategy requires an inconceivably complex solution. The conclusion will point to the challenging and intricate problems that cells have solved to carve the highly regulated channel through which the energy flows, fueling the work of these nanoscale machines.
Keywords: Thermodynamics; Cellular logics; Self-organization; Complexity
Cells are sophisticated nanoscale systems that preserve their structures and perform intricate functions far from the thermodynamic equilibrium. How is such an unusual condition for a physicochemical system attained by obeying the thermodynamic laws?
Boxes: A brief and informal visit to the thermodynamics laws
The thermodynamic laws establish that all systems constantly evolve to more probable conditions preserving the total energy during the process. These two requirements are summarized by stating that systems progress, at constant temperature and pressure, decreasing the Gibbs free energy (Box 1). An intuitive way to visualize these laws at a molecular level is to represent the energy in the height of a box (Fig. 1A) (Mayorga et al., 2012). As temperature increases, molecules populate higher energy levels (following a Boltzmann distribution). Moreover, suppose the box is divided into two compartments. Then, a chemical reaction can be quantitatively represented by adjusting the difference of floor levels to the ΔH of the reaction and the difference in the width of the compartments calculated from the ΔS. Accordingly, more stable compounds will have lower floor levels, and less rigid compounds with more freedom degrees will have wider compartments. A folded protein will be represented by a compartment with a lower floor (less energy) and a narrower width (less conformational freedom), than an unfolded protein. It is easy to see how balls tend to populate wide compartments (large entropy) with lower floors (less energy). Therefore, suppose that a wall separating the two sectors is introduced in the box (Fig. 1B). The height of this barrier accurately represents the reaction activation energy (Ea); this is the energy necessary to jump from one compartment to the other.

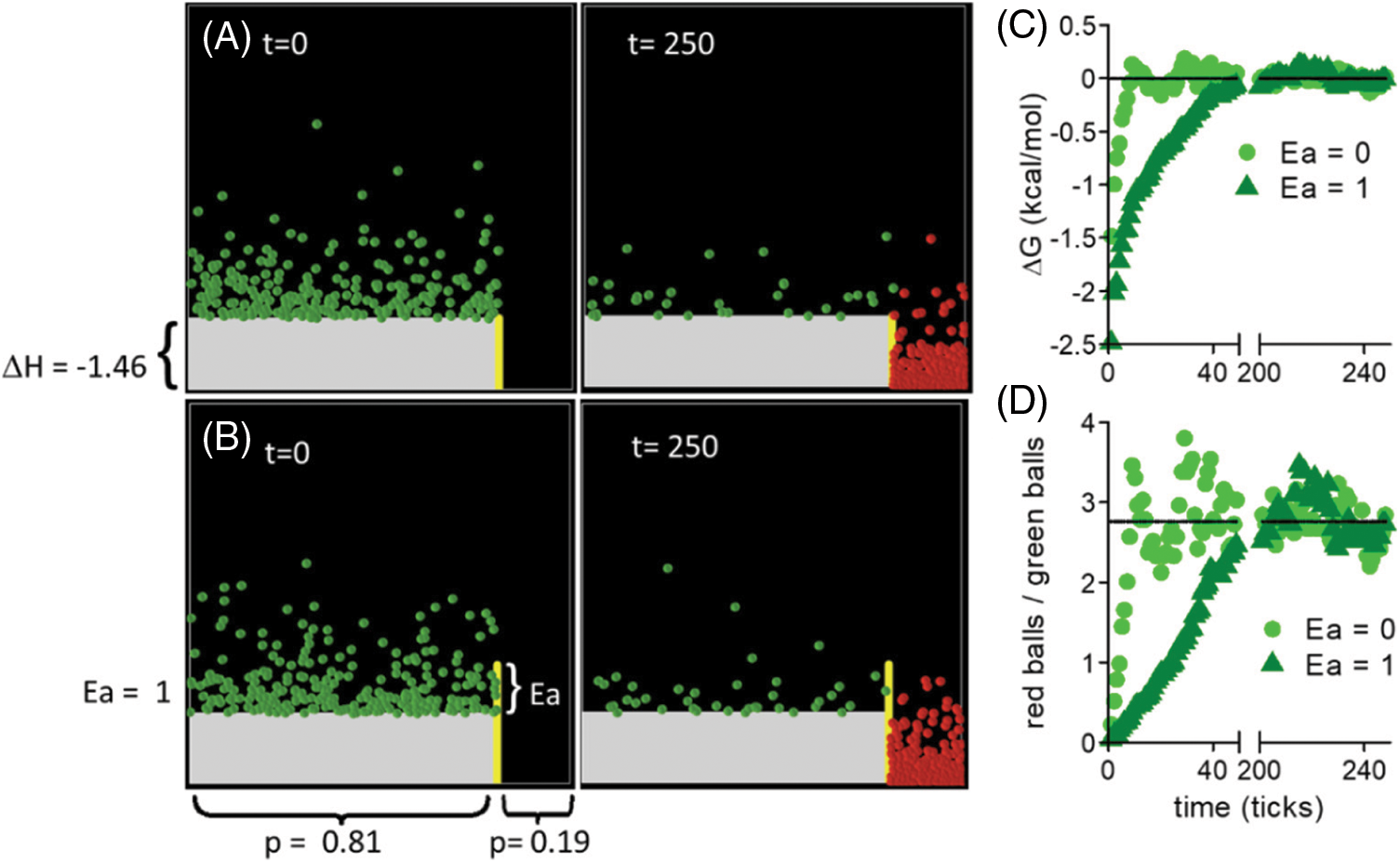
Figure 1: Thermodynamics in a box. A chemical reaction can be accurately represented in a box with two compartments (Mayorga et al., 2012). The ΔH° of the reaction is equivalent to the floor difference, and the width of the compartments (the relative probability p of each state) can be calculated from ΔS°. A) The ATP + AMP ←→ 2 ADP reaction has been represented (ΔH° = –1.46 kcal/mol, ΔS° = –2.88 cal/mol/°K) (Alberty, 1969) in a box. Balls jump to populate energy levels according to the system’s temperature (following a Boltzmann distribution). In this simulation, the temperature was set to 298°K. At time = 0, only reactants are present. When the simulation is run, balls jump all over the box until they reach an equilibrium where balls going from right to left are compensated by balls jumping from left to right (left panel, t = 250). At the equilibrium, the ΔG of the reaction is zero, and the number of red/green balls fluctuated around a fixed value (the equilibrium constant of the reaction). B) The same reaction is represented, but with a barrier (Ea = 1 kcal/mol) between reactants and products. The same equilibrium is reached but at a later time. C) The ΔG of the reaction was calculated at different time of simulation for Boxes in A (circles) and B (triangles) using ΔG = ΔG° + R × T × ln (red balls/green balls), where ΔG° = ΔH° – T × ΔS°, T = 298°K, and R = 0.001987 kcal/mol/°K (gas constant). D) The red balls/green balls ratio was calculated at different simulation times. Notice that in C and D, the equilibrium values were not altered by the imposed barrier (Ea). However, the time to reach the equilibrium was longer. See also that a 1 kcal/mol Ea is very low. Organic reactions involve the break of strong chemical bonds (in the order of 100 kcal/mol). The simulation was implemented in Netlogo (a platform for Agent-based modeling, http://ccl.northwestern.edu/netlogo/) (Wilensky, 1999; Wilensky, 2002). Time is measured in ticks, which indicate the number of times the simulation was iterated.
Cellular metabolism as a dynamic maze
Now, suppose that all possible chemical reactions among all metabolites in the cell are represented by boxes (Fig. 2). The cell cannot change the shape of the boxes, which are determined by the physicochemical properties of reactants and products; the only parameter amenable to manipulation is Ea. It can only decrease the Ea by providing an enzyme that catalyzes the reaction. It is worth noticing that this statement is an oversimplification; cells can manipulate parameters that affect the free energy of reactions, such as pH and ion concentrations. Notice however that the strategy is similar; to activate ion channels or specific membrane pumps.
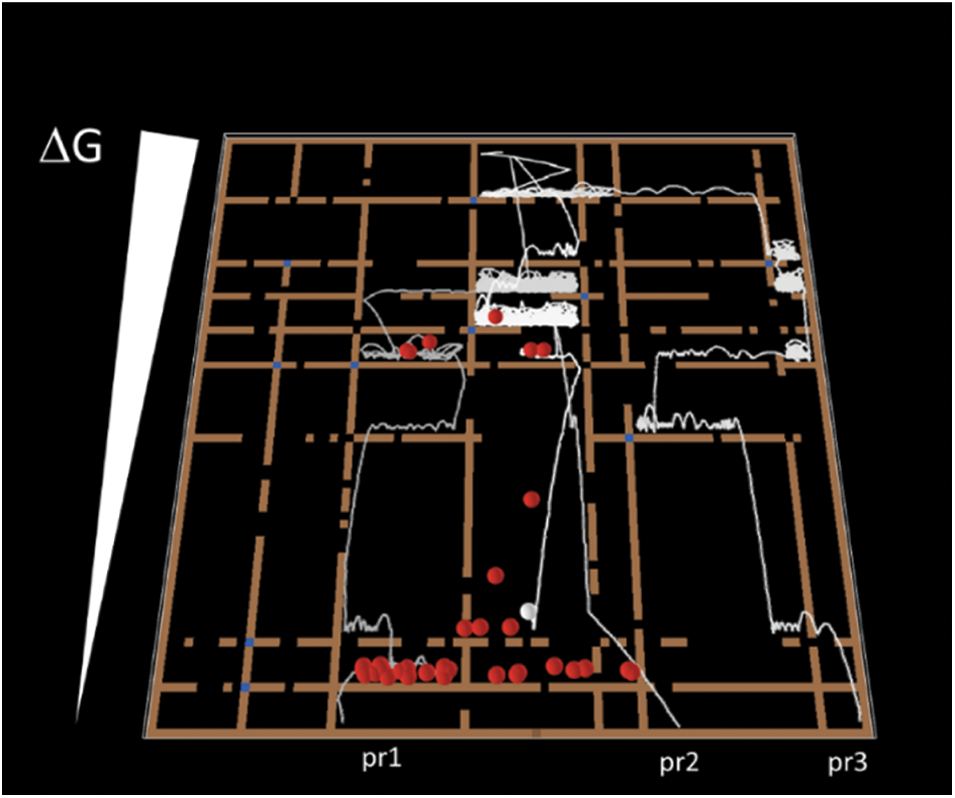
Figure 2: The metabolic maze. Balls jump in a complex box having multiple compartments. The walls of this maze can be opened (decrease of Ea), allowing balls to travel downhill the free energy landscape following different paths. Four balls were individually traced along with the simulation (gray-white lines). Three balls from the same initial state suffered different “chemical reactions” and arrived at different products. The fourth ball (white) is still bouncing in the maze. The simulation was implemented in Netlogo (Wilensky, 2002).
For the cell function, it is crucial to notice that the Ea for the great majority of the chemical reaction in the cell is high enough to prevent them from proceeding at room temperature at a speed compatible with the cellular metabolism. For example, glucose does not react with atmospheric oxygen at room temperature. In contrast, glucose is rapidly oxidized to CO2 and H2O inside the cell. Therefore, the cellular strategy to guide the energy gradient available in the environment to fuel its activity is quite simple: dig the appropriate channels lowering the necessary Ea to direct the energy flux.
The general principle is then straightforward to understand (Box 2). The box shapes cannot be modified; only the walls separating the compartments can be lowered. However, the task for these nano-machines is formidable: to direct the energy flux in a self-regulated way that assures their homeostasis. According to the signals sensed from the environment, which enzymatic path will be active at the necessary level, needs to be determined automatically to guarantee the cell survival and proper function. In the box analogy, the cell metabolism can be represented by an intricate maze lying downhill the energy landscape. Walls (Eas) prevent the flux of energy, which can only follow a few opened pathways. But, like a deceiving maze, the walls change over time in a coordinated way that allows the building of more wall-regulation devices, ultimately preserving the maze function.

Life, the more probable outcome?
Considering the second law of Thermodynamics, it is hard to imagine how a highly organized cell can be the more probable outcome of a nano-scale system made out of ordinary atoms and molecules. There is not a central computer making decisions to preserve the cell and fulfill its functions; instead, the cell acts according to the present situation, without any teleological aims. Local control switches turn on/off the pathways by allosteric mechanisms regulated by the substrates or products of the metabolic routes. Enzymes are also sensitive to more global indicators, such as the ATP/(ADP + AMP) proportions, to assess the energetic state of the cell, or the NADH/NAD+ ratio, to test the redox conditions. A few signals can trigger subtle protein modifications -such as a covalent phosphate addition- that completely change their function and switch the cell metabolism from an anabolic to a catabolic state. Proteins are synthesized and degraded in a coordinated way, according to complex switches involving promotor activation, changes in chromatin structure, ribosomal function, proteasome targeting, and many other still poorly understood processes. Again, none of these switches is manipulated by a central decision-maker with teleological objectives.
Self-organization dictated by physicochemical forces
Several functions do not require a central decision-maker system. Certainly, self-organization appears as a common property of cellular structures (Karsenti, 2008). For example, most proteins acquire their precise folding upon synthesis. Moreover, their conformations dictate their many functions. Complementary DNA strains assemble in double helixes in a test tube, and sets of macromolecules spontaneously form complex organelles, such as microtubules and proteoliposomes. Highly complex cellular processes occur in cell-free systems. DNA replication, protein synthesis, or membrane fusion can be reproduced in cell extracts that are no longer part of a cell. For example, given a DNA polymerase, a template chain, and a set of deoxynucleotide triphosphates (dNTPs), the more probable nucleotide that will be incorporated to the 3’ end of the primer is the one complementary to the template chain. Hundreds of collisions will happen in a fraction of a second, enough to have a high probability that the right dNTP will be positioned at the enzyme reaction center, and the phosphodiester bond will be formed. Amazingly, the more probable outcome is the miracle that a highly ordered sequence is formed. Nevertheless, self-organization is not enough. Therefore, the exquisite regulation required to preserve cellular homeostasis needs high-order switches to turn on/off specific processes that are still far from being fully understood.
Considering the sophisticated organization of any cell, why life is so frequent on earth?
It is exceptionally challenging to envision the tremendous complexity of the cellular machinery at work. However, on earth, life is inevitable in a system where an energy source is available and a machine with the required information to use this energy is present (i.e., a viable cell). We, cell biologists, know how difficult it is to preserve sterility in the lab. This paradox will be addressed in the following viewpoint by analyzing the interconnection between thermodynamics, probability, and information. Maxwell demon, Szilard machine, Landauer principle, and Shannon entropy will be introduced intuitively to address this conundrum.
Acknowledgement: I would like to thank the comments and suggestions by L. Mariano Polo and María Roqué.
Author Contribution: The author confirms sole responsibility for study conception and design and manuscript preparation.
Availability of Data and Materials: The simulations were uploaded in ModelingCommons of Netlogo and can be accessed from the following links: MolecularThermodynamicsInBoxes: http://modelingcommons.org/browse/one_model/6895. CellularMetabolismLabyrinth: http://modelingcommons.org/browse/one_model/6897. The simulations can be run in NetLogo Web or downloaded and executed with the free software available from: https://ccl.northwestern.edu/netlogo.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.
Alberty RA (1969). Standard Gibbs free energy, enthalpy, and entropy changes as a function of pH and pMg for several reactions involving adenosine phosphates. Journal of Biological Chemistry 244: 3290–3302. DOI 10.1016/S0021-9258(18)93127-3. [Google Scholar] [CrossRef]
Karsenti E (2008). Self-organization in cell biology: A brief history. Nature Reviews Molecular Cell Biology 9: 255–262. DOI 10.1038/nrm2357. [Google Scholar] [CrossRef]
Mayorga LS, Lopez MJ, Becker WM (2012). Molecular thermodynamics for cell biology as taught with boxes. CBE—Life Sciences Education 11: 31–38. DOI 10.1187/cbe.11-07-0053. [Google Scholar] [CrossRef]
Wilensky U (1999). NetLogo. Evanston, IL: Center for Connected Learning and Computer-Based Modeling, Northwestern University. [Google Scholar]
Wilensky U (2002). NetLogo GasLab Gravity Box Model. Evanston, IL: Center for Connected Learning and Computer-Based Modeling, Northwestern University. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |