DOI:10.32604/cmc.2020.012505
| Computers, Materials & Continua DOI:10.32604/cmc.2020.012505 | |
| Article |
Effects of Combined Heat and Mass Transfer on Entropy Generation due to MHD Nanofluid Flow over a Rotating Frame
1Department of Information Technology, Fanshawe College London, ON, N5Y 5R6, Canada
2Department of Mathematics, University of Ilorin, Ilorin, Kwara, 240003, Nigeria
3Department of Mathematics, Faculty of Science, Aswan University, Aswan, 81528, Egypt
4Department of Mechanical Engineering, College of Engineering, Prince Mohammad Bin Fahd University, Al Khobar, 31952, Saudi Arabia
5Department of Mathematics, College of Science and Humanities in Al-Kharj, Prince Sattam bin Abdulaziz University, Al-Kharj, 11942, Saudi Arabia
6Department of Basic Engineering Science, Faculty of Engineering, Menoufia University, Shebin El-Kom, 32511, Egypt
*Corresponding Author: W. A. Khan. Email: wkhan1956@gmail.com
Received: 02 July 2020; Accepted: 22 August 2020
Abstract: The current investigation aims to explore the combined effects of heat and mass transfer on free convection of Sodium alginate-Fe3O4 based Brinkmann type nanofluid flow over a vertical rotating frame. The Tiwari and Das nanofluid model is employed to examine the effects of dimensionless numbers, including Grashof, Eckert, and Schmidt numbers and governing parameters like solid volume fraction of nanoparticles, Hall current, magnetic field, viscous dissipation, and the chemical reaction on the physical quantities. The dimensionless nonlinear partial differential equations are solved using a finite difference method known as Runge-Kutta Fehlberg (RKF-45) method. The variation of dimensionless velocity, temperature, concentration, skin friction, heat, and mass transfer rate, as well as for entropy generation and Bejan number with governing parameters, are presented graphically and are provided in tabular form. The results reveal that the Nusselt number increases with an increase in the solid volume fraction of nanoparticles. Furthermore, the rate of entropy generation and Bejan number depends upon the magnetic field and the Eckert number.
Keywords: Nanofluid flow; entropy generation; heat and mass transfer; viscous dissipation; chemical reaction
Most of the conventional liquids such as saltwater, liquid metal, plasma, etc. are conducting fluids that have over the years captured immense attention of renowned researchers to the study of the dynamics of these fluids because of their significant engineering applications like MHD generators, flow meters, metal purification, metallurgy, geothermal energy extractions, and polymer technology. Some studies [1–3] involve fluid flow analysis of the electrically conducting fluids. However, Hall current effect is significant for a strong magnetic field and a low density [4]. In the pioneering work of [5], the Hall current effect was taken into consideration to examine the magnetohydrodynamic flow of a viscous ionized gas passing through parallel plates. Further studies of Hall effects have been communicated by [6] who reviewed the peristaltic flow of a Jeffrey non-Newtonian fluid over vertical walls in the presence of porous medium and Hall influence. Muthucumaraswamy et al. [7] studied the unsteady flow of a viscous fluid over an exponential plate accelerating due to density difference with Hall effects and thermal radiation.
Hydromagnetic fluid flow problems are essential in the field of earth science, Meteorology. Interestingly, the Hall current induces both the primary and secondary flows in fluid governed of Coriolis force. Very recently, Krishna et al. [8] have been analyzed the mixed convection laminar flow of hydromagnetic viscous rotating fluid flow over a porous vertical sheet with Hall effects. Hall current influence on the unsteady flow of an oscillating fluid over an exponential slip plate with chemical reaction is investigated by [9]. They concluded that the Coriolis force and Hall current tend to augment the fluid velocity in the secondary flow direction whereas, in the primary flow direction, Ion-slip current enhanced. Given these applications, Hall current effects on rotating magnetohydrodynamic have been studied in various flow geometries, for example [10,11].
Above mentioned literature was performed in the fluid flow models of a conventional fluid flow of an electrically conducting fluid. Still, fluids with the inclusion of nanometer-sized particles (nanofluid) behave quite differently from that of the traditional fluid in several vital aspects. A report from the current trend in research has shown that heat transfer is enhanced in the thermal system through the embedded nanoparticle into conventional liquids. The applications exist in a solar receiver, nuclear reactor, microbial fuel cell, thermal storage, biomedical applications, heat exchangers, industrial cooling medium. Authors have established several results about nanofluid flow in various geometries, for example, see Ali et al. [12,13].
In energy management, minimizing entropy production in a thermal system cannot be overemphasized because of its limited percentage of energy available as heat. It is, however, imperative to improve the amount of energy available for work through entropy generation. Some relevant articles that analyzed the flow and heat transfer using the 2nd law of thermodynamics are [14–17]. Opanuga et al. [18] have examined the Hall current and ion-slip on a steady flow of micropolar fluid through an infinite vertical channel with entropy generation.
The objective of the current analysis is to examine the rate of entropy optimization on MHD Brinkman-type nanofluid flow over a vertical rotating plate with the influence of radiation and chemical reaction. It is, therefore, pertinent to examine the effect of this feature because entropy production occurs in moving fluid with high temperature. To the best of our knowledge, the present study has not remained investigated. By applying suitable transformations, the governing equations of the model are converted to non-dimensional form and then solved by employing the Runge–Kutta–Fehlberg scheme. Effects of all the pertinent parameters on velocity, temperature, nanoparticle concentration, skin friction coefficient, Nusselt number, Sherwood number, entropy generation, and the Bejan number profiles are shown through graphs and extensively discussed.
A magnetohydrodynamic convective flow of Sodium alginate-Fe3O4 based Brinkmann type nanofluid is examined in a vertical rotating frame. The flow is assumed to be incompressible and time-dependent.
Fig. 1 explains the coordinate system of the vertical rotating frame in a nanofluid. The system spins about the normal axis with an angular velocity 
. Consider the physical quantities depend only on y. Also, a magnetic field of constant strength 
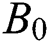is introduced in a direction parallel to the y-axis in direction to the fluid flow. Considering the effects of thermal radiation and chemical reaction, the governing equations are:
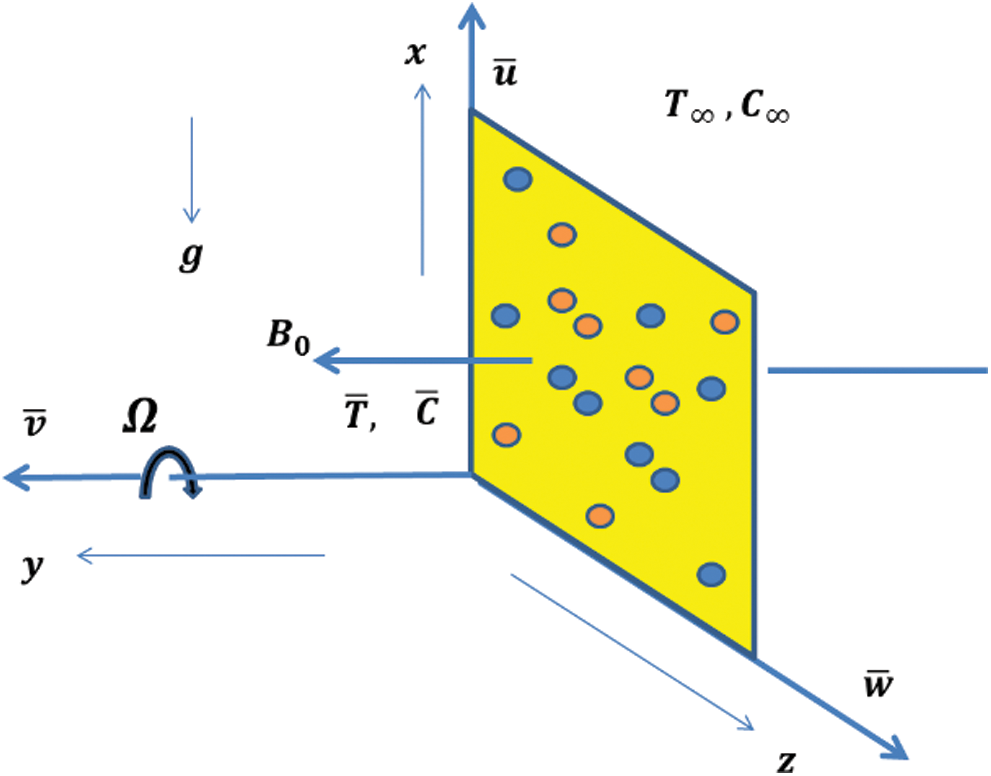
Figure 1: Schematic diagram
Subject to the initial and boundary conditions
Defining
The dimensionless variables are given by
Thus, the governing equations are:
The boundary conditions are given by
where the parameters are defined by
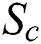(Schmidt number);
(Diffusive constant parameter);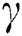 
(Brinkmann parameter); 
(Ideal gas constant); 
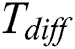(Temperature difference); 
(Concentration difference);
(Thermal Grashof number);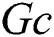 
(Solutal Grashof number); 
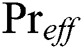(Effective Prandtl number); 
(Prandtl number); 
(Radiation parameter); 
(Eckert number); 
(Magnetic parameter); 
(Chemical reaction parameter); 
(Hall current parameter); 
(Acceleration due to gravity); 
(Induced magnetic field); 
(Non dimensional rotation parameter).
The local skin friction 
, Nusselt number 
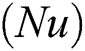, and the Sherwood number 
are:
The wall shear stress is 
the heat transfer rate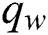 
and the rate of mass transfer 
The dimensionless form
The expression for the entropy generation of this model may be written as
Here, the characteristic entropy 
, the dimensionless form of entropy generation yields
In dimensionless form, Bejan number may be written as
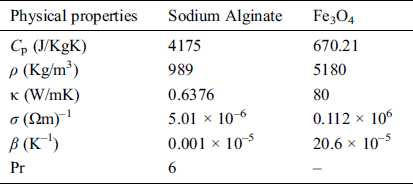
The physical properties of the base fluid and nanoparticles have been reported in the Tab. 1.
Table 1: Thermophysical properties of base fluid (Sodium Alginate) and nanoparticle
The system of partial differential Eqs. (8)–(11) with associated initial and boundary conditions Eq. (12) are solved numerically using a finite difference method. In all cases, we have adopted the following default values of parameters 
,
Unless individually shown in the appropriate separately. Variations of the dimensionless velocities 
(P/velocity) and 
(S/velocity) with 
(magnetic field) depicted in Fig. 2. Figs. 2a and 2b display the influence of the primary and secondary velocities with increasing values
. Higher values of 
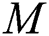cause both velocities plots to decelerate. The physics of this trend is that as the magnetic field is applied, a resistance force opposing the fluid motion is produced, thereby causing a decrease in the velocity of the liquid. Comparatively, a gradual drop in the secondary velocity is noticed, as shown in Fig. 2b.
Figure 2: Effects of magnetic parameter on (a) primary and (b) secondary velocities
The impacts of 
(magnetic parameter), 
(thermal radiation parameter), 
(volume fraction parameter), and 
(Eckert number) on the temperature profile 
are shown in the Figs. 3 and 4. Fig. 3a elucidates the impact of 
on 
. Inside the thermal boundary layer, the dimensionless temperature increases with the magnetic field. In this plot, higher estimations of 
connects presence of Lorentz heating in the flow, the force boost the fluid temperature, and a distinct trend is perceived within 
. The impact of the radiation parameter on the dimensionless temperature 
is presented in Fig. 3b. However, an enhancement in the temperature profile is observed at all points in the presence of thermal radiation. The reason for this trend is that bigger estimations of Nr produce more heat into the fluid, causing a rise in the temperature.
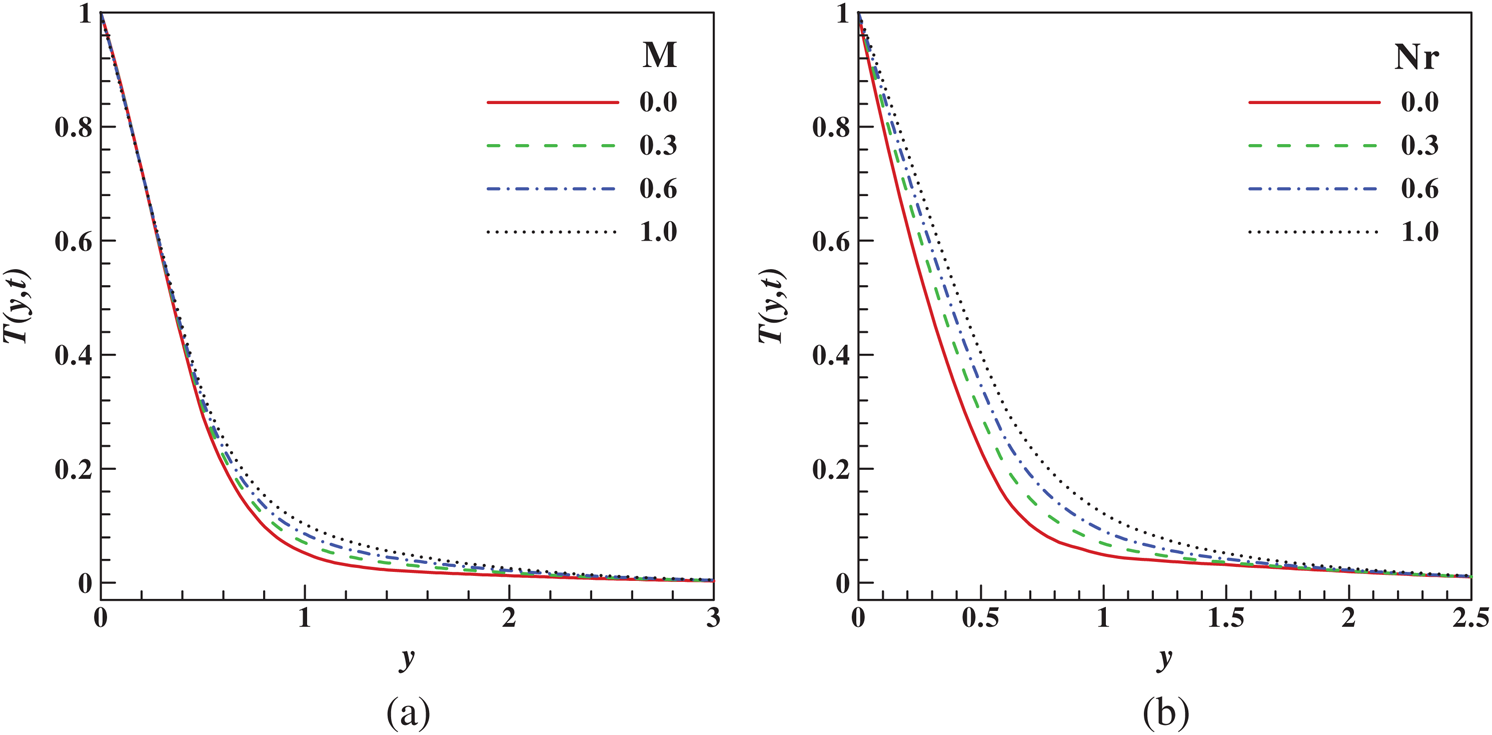
Figure 3: Variation of temperature with (a) magnetic (b) radiation parameters
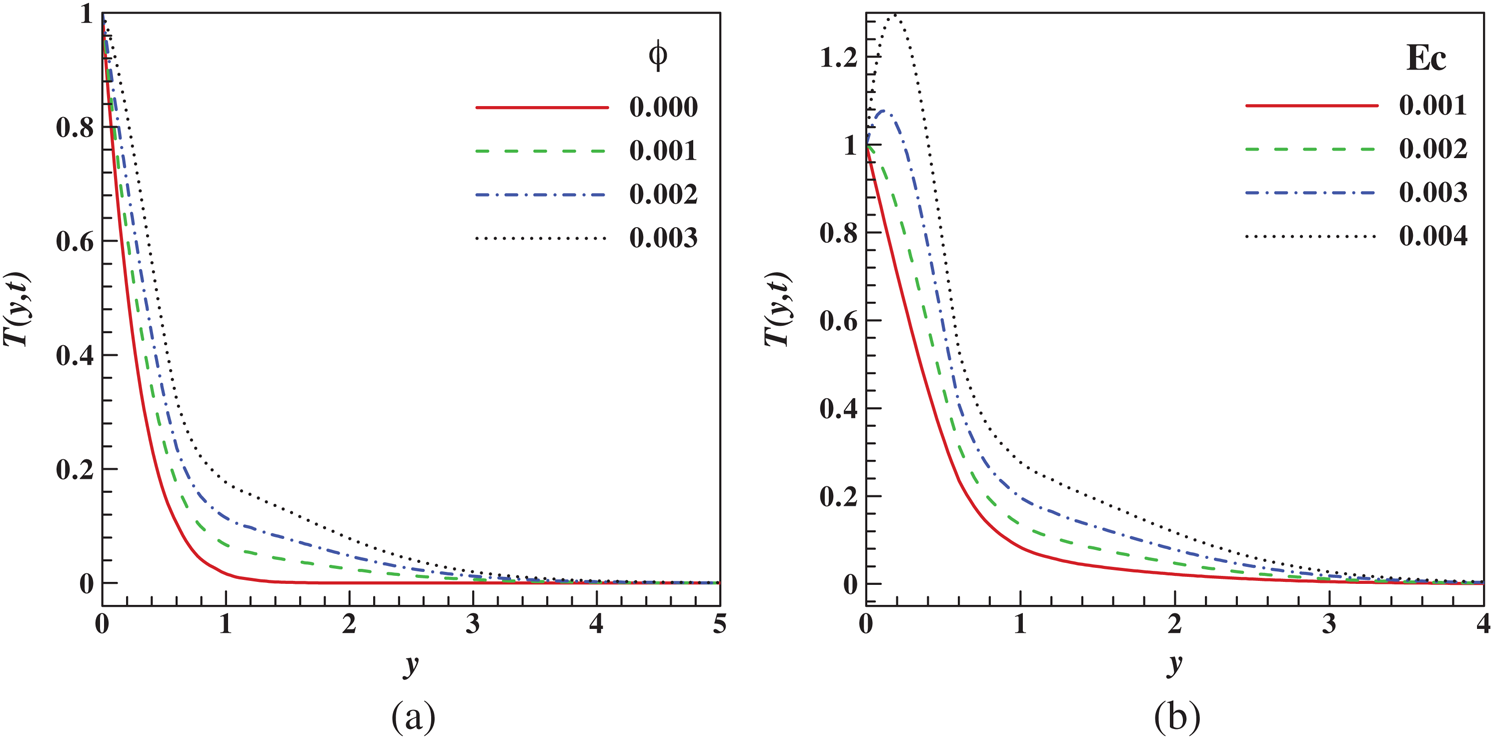
Figure 4: Variation of temperature with (a) solid volume fraction (b) Eckert number
The effects of the solid volume fraction of nanoparticles and Eckert number on the dimensionless temperature are shown in the Figs. 4a and 4b respectively. As shown in Fig. 4a that enhancement in the solid volume fraction of nanoparticles 
leads to an increase in the temperature profile. Moreover, an increase in Ec corresponds to a significant rise in the temperature profile. Fig. 4b demonstrates this behavior. Physically, frictional heating produces more heat with an increase in Ec.
Figs. 5a and 5b illustrate the impacts of the chemical reaction 
and Schmidt number 
on the dimensionless concentration, respectively. The behavior of the dimensionless concentration for different values of destructive chemical reaction parameters 
is portrayed in Fig. 5a. It is noticed that the dimensionless concentration is a decreasing function of 
. In true sense, the amount of nanomaterials presence in the fluid becomes smaller as the destructive chemical reaction occurs. Meanwhile, Fig. 5b displays the concentration profile decreases rapidly with an increase in the Schmidt number. Physically, 
is the ratio of the momentum to the mass diffusivity, so the relative effect of momentum diffusion to species diffusion is signified by Schmidt number. A drop in concentration profile gives the impression that the diffusion of species dominates the momentum diffusivity.
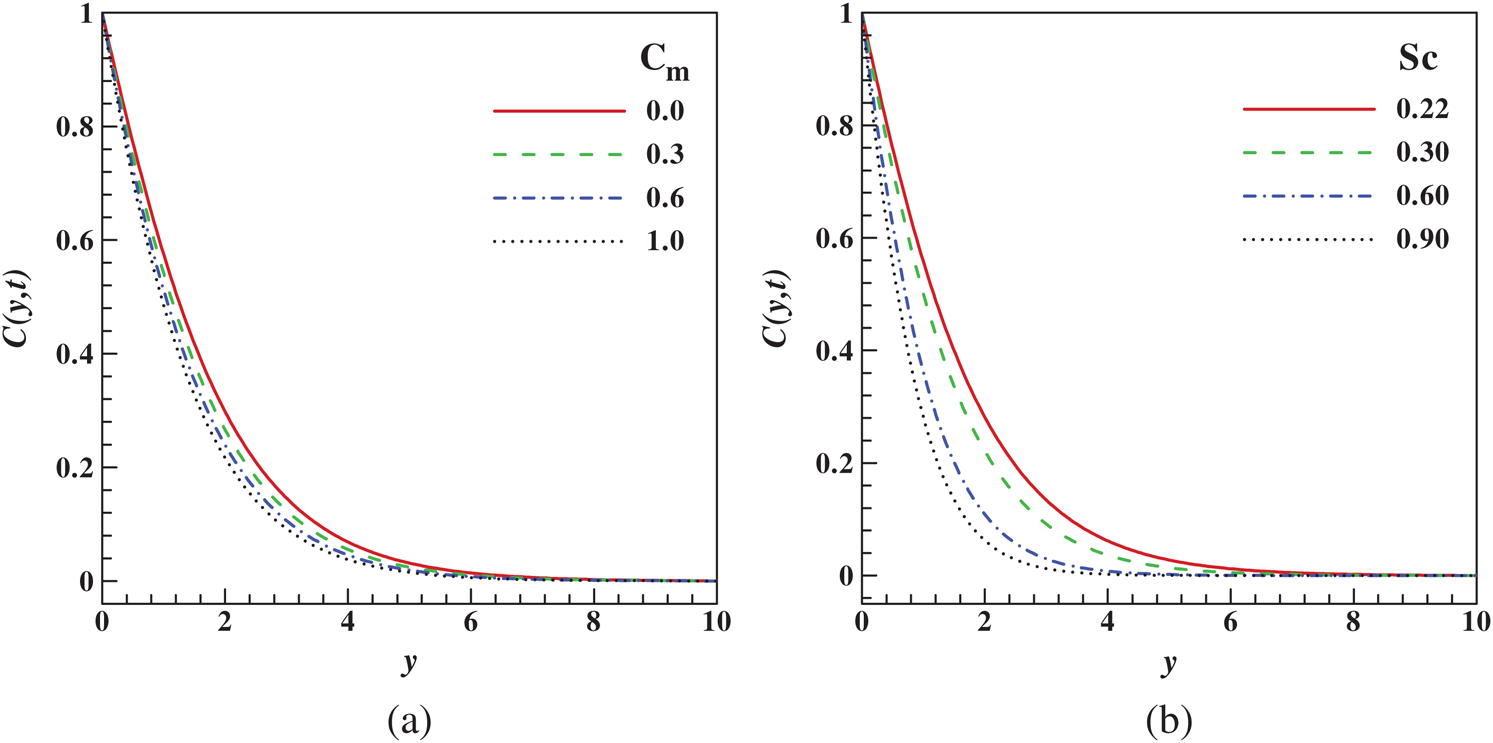
Figure 5: Variation of concentration (a) chemical reaction parameter (b) Schmidt number
Plots of physical quantities such as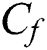 
(Skin friction coefficient) 
(rate of heat transfer) and the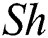 
(rate of mass transfer) as a function of 
are shown in Figs. 6a and 6b for various pertinent parameters. The behavior of the magnetic parameter 
, Brinkman parameter 
, Hall current parameter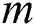 
, and the thermal Grashof number 
on the skin friction coefficient is displayed in Figs. 6a and 6b. The rise in the magnitude of 
has been noticed for higher values of 
. The physics behind this is an increase in M generates a drag like force which reduces the friction on the wall surface. As the Brinkmann parameter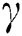 
rises and for all values of 
, a high impact of skin factor at the wall is observed (see Tab. 2). Similarly, from Fig. 6b, the skin factor enhanced with increasing values of parameters 
and 
.
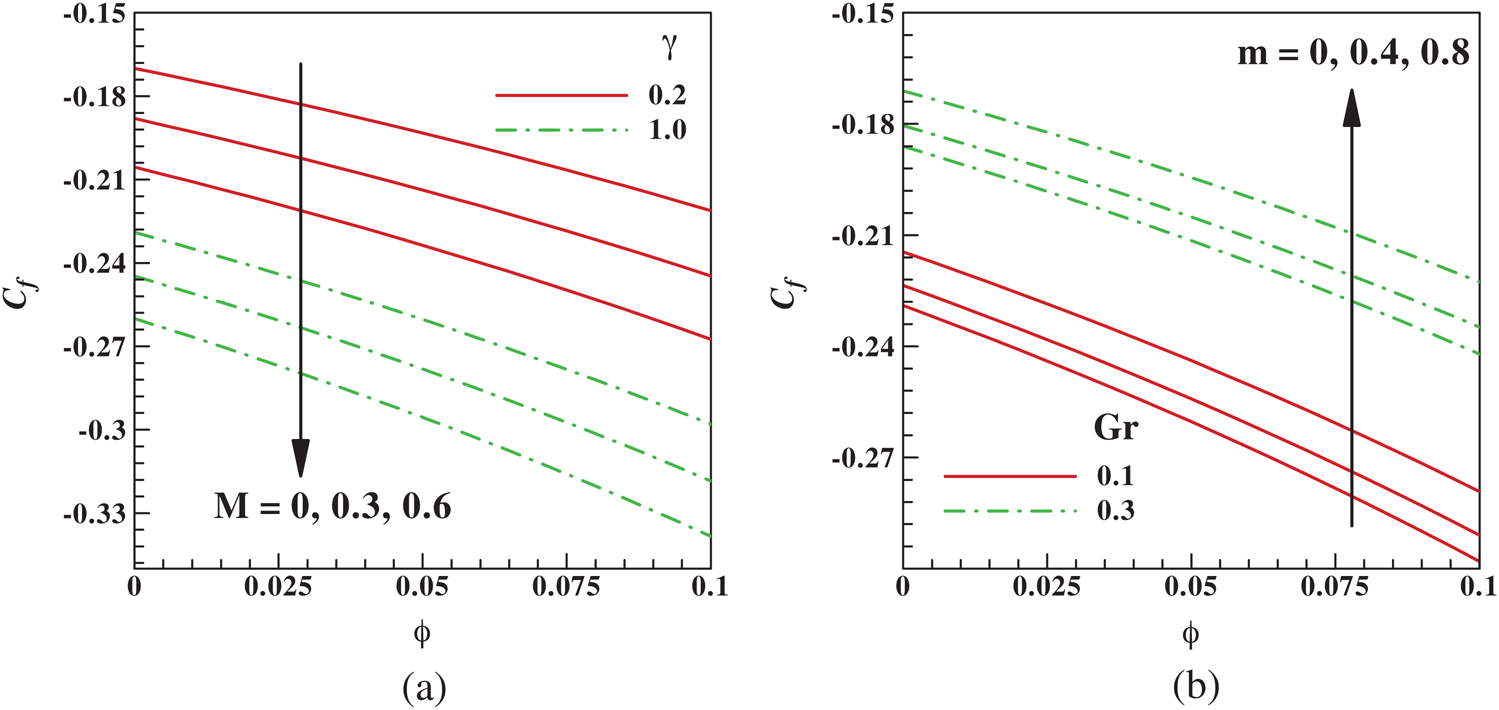
Figure 6: Variation of skin friction with 
(a) M and γ (b) Gr and m
Table 2: Skin friction values when 
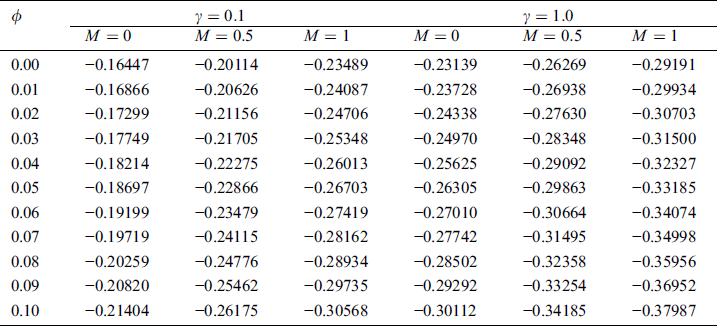
The rate of heat transfer as a function of 
is exhibited in Fig. 7. for different values of 
. These plots show that due to the temperature gradient, the heat flux is an increasing function of 
. Tab. 3 reports that the Nusselt number increases with an increase in the volume fraction of nanoparticles and the radiation parameter. The higher rate of heat transfer from the moving fluid to the wall with larger values of the Brinkman parameter 
. However, as shown in Fig. 7, an augmented 
and slow down the heat transfer rate 
. Physically, enhancement in 
corresponds to upsurge in the thermal field via dissipation, hence, boosting the heat transfer rate.
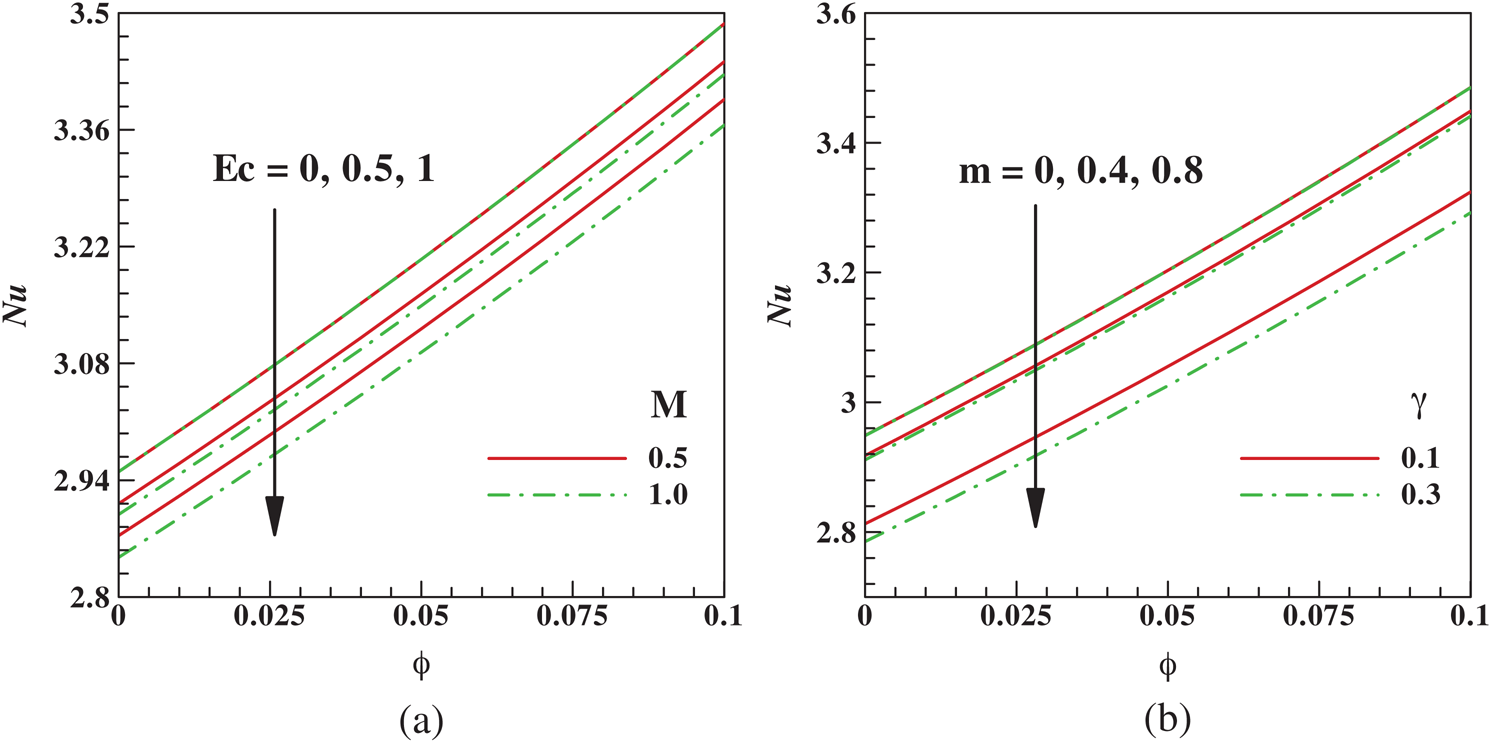
Figure 7: Variation of Nusselt number with 
(a) M and Ec (b) 
and m
Table 3: Nusselt number values when 
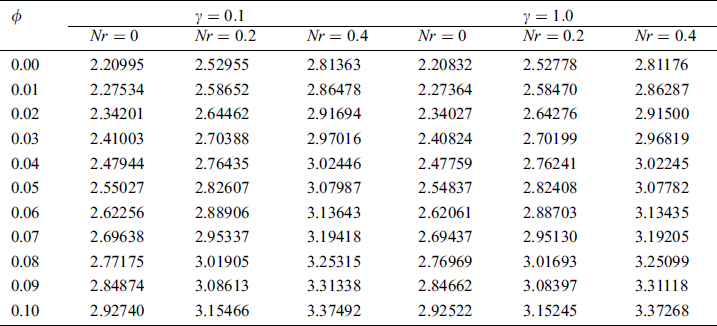
The influence of the Schmidt number 
and chemical reaction parameter 
on the Sherwood number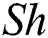 
is displayed in Fig. 8 and Tab. 4. It may be noted that with a rise in the concentration gradient, mass transport increases for increasing values of both 
and 
.
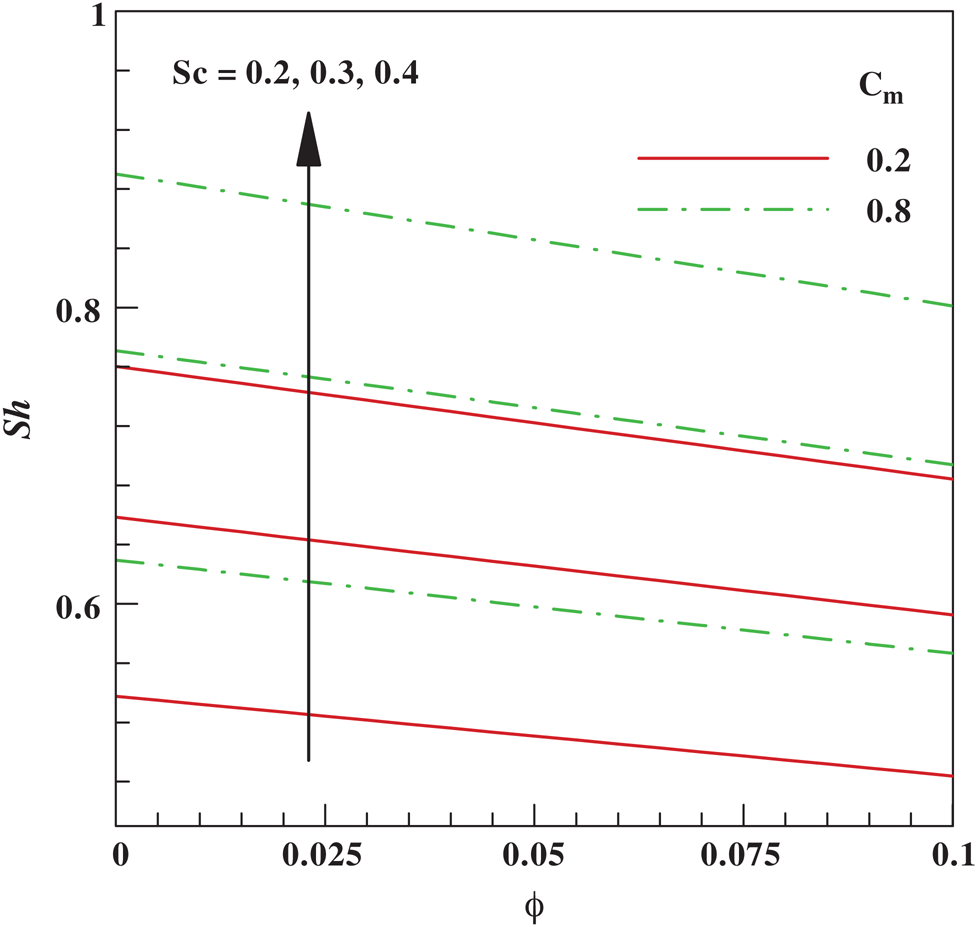
Figure 8: Variation of Sherwood number with 
for different values of 
and 
Table 4: Sherwood number values when 
The impacts of governing parameters, including 
, and 
on the entropy generation rate,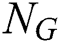 
are shown in Fig. 9. It is noticed that the rate of disorderliness becomes low in the absence of 
. However, the magnetic field produces a Lorentz force, which boosts the rate of entropy generation. Also, higher values of 
escalate the entropy production. It is observed from the same plot that improving the magnitude of 
marginally suppressed the rate of entropy generation. Moreover, throughout the fluid system, enhanced 
suppressed the rate of entropy generation. This is an indication that there is more fluid-particle disorder via augmentation in 
, and 
.
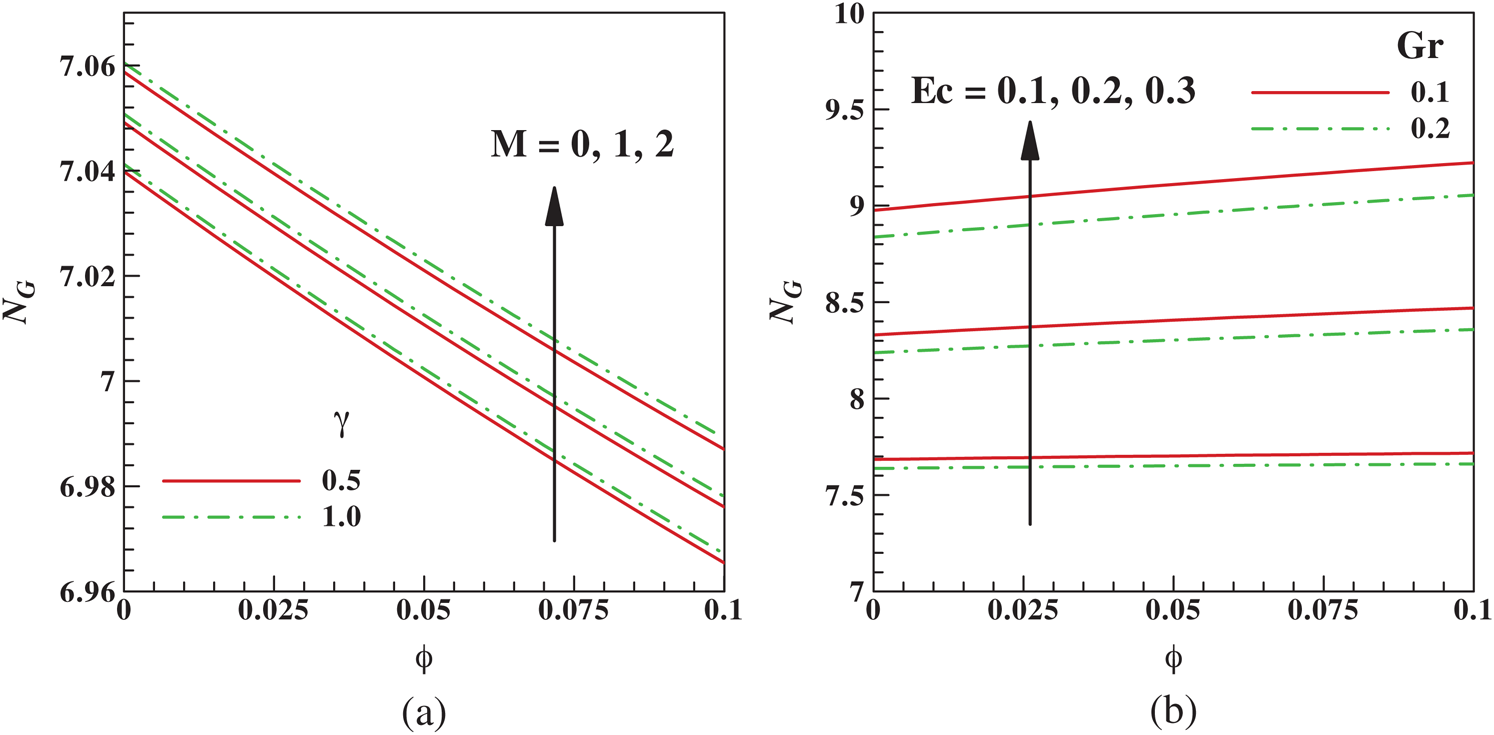
Figure 9: Variation of entropy generation rate with 
(a) M and γ (b) Gr and Ec
Fig. 10 elucidates the Bejan number 
against 
for different values of 
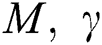
, and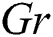 
. The contribution of fluid friction is more dominant via enhancement of 
, and 
. Also, since an increase in 
and 
correspondingly reduce the Bejan number, the fluid friction irreversibility dominates throughout the mainstream. Generally, we observed that the governing parameters enhance the rate of entropy production and correspondingly decrease the Bejan number.
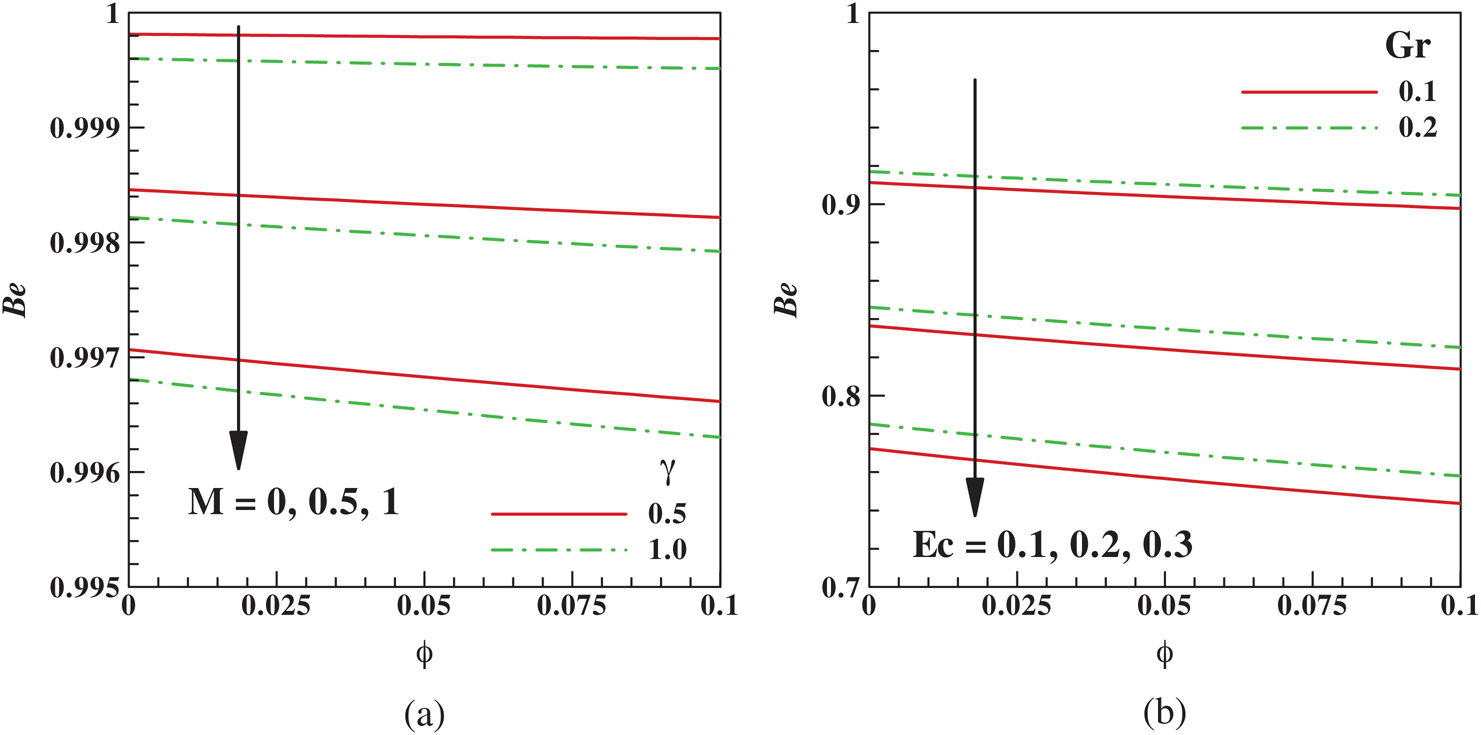
Figure 10: Variation of Bejan number with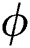 
(a) M and γ (b) Gr and Ec
In this paper, the effects of viscous dissipation and chemical reaction on MHD flow with combined heat and mass transfer of incompressible sodium-alginate based Fe3O4 in a rotating frame have been analyzed. The following are the main results of the present study:
•The dimensionless velocity 
increases with the augmentation of 
and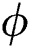 
while it peters out via incremented 
.
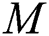•The dimensionless temperature 
increases with the augmentation of 
and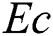 
.
•An increase in the chemical reaction parameter and Schmidt number has shown a declining trend for the dimensionless concentration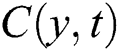 
.
•Viscous drag decreases due to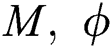 
, and 
while shows the opposite fashion via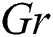 
and 
.
•The rate of heat transfer is decreasing due to the rise in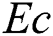 
and 
.
•The mass transfer rate increases with an increase in
while it decreases with 
.
•Rate of Entropy generation and Bejan number shows the opposite trend for 
and 
.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. F. Mabood, R. G. Abdel-Rahman and G. Lorenzini. (2016). “Effect of melting heat transfer and thermal radiation on Casson fluid flow in porous medium over moving surface with magnetohydrodynamics,” Journal of Engineering Thermophysics, vol. 25, no. 4, pp. 536–547.
2. F. Mabood, R. G. Abdel-Rahman and G. Lorenzini. (2016). “Numerical study of unsteady Jeffery fluid flow with magnetic field effect and variable fluid properties,” Journal of Thermal Science and Engineering Applications, vol. 8, no. 4, pp. 19.
3. F. Mabood, G. Lorenzini, N. Pochai and S. Shateyi. (2018). “Homotopy analysis method for radiation and hydrodynamic-thermal slips effects on MHD flow and heat transfer impinging on stretching sheet,” Defect and Diffusion Forum, vol. 388, pp. 317–327.
4. T. Nagy and Z. Demendy. (1995). “Effects of Hall currents and Coriolis force on Hartmann flow under general wall conditions,” Acta Mechanica, vol. 113, no. 1-4, pp. 77–91.
5. H. Sato. (1961). “The Hall effect in the viscous flow of ionized gas between parallel plates under transverse magnetic field,” Journal of the Physical Society of Japan, vol. 16, no. 7, pp. 1427–1433.
6. M. V. Krishna, K. Bharathi and A. J. Chamkha. (2018). “Hall effects on MHD peristaltic flow of Jeffrey fluid through porous medium in a vertical stratum,” Interfacial Phenomena and Heat Transfer, vol. 6, no. 3, pp. 253–268.
7. R. Muthucumaraswamy and K. M. A. Prema. (2016). “Hall effects on flow past an exponentially accelerated infinite isothermal vertical plate with mass diffusion,” Journal of Applied Fluid Mechanics, vol. 9, no. 2, pp. 889–897.
8. M. V. Krishna, B. V. Swarnalathamma and A. J. Chamkha. (2019). “Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate,” Journal of Ocean Engineering and Science, vol. 4, no. 3, pp. 263–275.
9. J. K. Singh and C. T. Srinivasa. (2018). “Unsteady natural convection flow of a rotating fluid past an exponential accelerated vertical plate with Hall current, ion-slip and magnetic effect,” Multidiscipline Modeling in Materials and Structures, vol. 14, no. 2, pp. 216–235.
10. M. V. Krishna and A. J. Chamkha. (2020). “Hall and ion slip effects on MHD rotating flow of elastico-viscous fluid through porous medium,” International Communications in Heat and Mass Transfer, vol. 113, 104494.
11. M. V. Krishna, G. S. Reddy and A. J. Chamkha. (2018). “Hall effects on unsteady MHD oscillatory free convective flow of second grade fluid through porous medium between two vertical plates,” Physics of Fluids, vol. 30, no. 2, pp. 1–9.
12. F. Ali, B. Aamina, I. Khan, N. A. Sheikh and M. Saqib. (2017). “Magnetohydrodynamic flow of brinkman-type engine oil based MoS2-nanofluid in a rotating disk with hall effect,” International Journal of Heat and Technology, vol. 4, no. 35, pp. 893–902.
13. N. Acharya, R. Bag and P. K. Kundu. (2019). “Influence of Hall current on radiative nanofluid flow over a spinning disk: A hybrid approach,” Physica E: Low-Dimensional Systems and Nanostructures, vol. 111, no. 7, pp. 103–112.
14. F. Mabood, T. A. Yusuf and W. A. Khan. (2020). “Cu-Al 2 O 3-H 2 O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation,” Journal of Thermal Analysis and Calorimetry, vol. 141, no. 4, pp. 1–12.
15. M. I. Afridi, M. Qasim and I. Khan. (2018). “Entropy generation minimization in MHD boundary layer flow over a slendering stretching sheet in the presence of frictional and Joule heating,” Journal of the Korean Physical Society, vol. 73, no. 9, pp. 1303–1309.
16. T. A. Yusuf, S. O. Adesanya and J. A. Gbadeyan. (2020). “Entropy generation in MHD Williamson nanofluid over a convectively heated stretching plate with chemical reaction,” Heat Transfer, vol. 49, no. 4, pp. 1982–1999.
17. T. A. Yusuf and F. Mabood. (2020). “Slip effects and entropy generation on inclined MHD flow of Williamson fluid through a permeable wall with chemical reaction via DTM,” Mathematical Modelling of Engineering Problems, vol. 7, no. 1, pp. 1–9.
18. A. A. Opanuga, J. A. Gbadeyan, H. I. Okagbue and O. O. Agbolla. (2018). “Hall current and suction/injection effects on the entropy generation of third-grade fluid,” International Journal of Advanced and Applied Sciences, vol. 5, no. 7, pp. 108–115.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |