DOI:10.32604/cmc.2020.012334

| Computers, Materials & Continua DOI:10.32604/cmc.2020.012334 |  |
| Article |
Analysis of Convective Transport of Temperature-Dependent Viscosity for Non-Newtonian Erying Powell Fluid: A Numerical Approach
1Centre for Mathematical Sciences, UMP, Gambang, 26300, Malaysia
2Faculty of Computer and Math Sciences, UiTM Johor, Pasir Gudang Campus, Masai, 81750, Malaysia
3Manufacturing Engineering Technology Section, UniKL, Italy Design Institute, Kuala Lumpur, 56100, Malaysia
*Corresponding Author: Abdul Rahman Mohd Kasim. Email: rahmanmohd@ump.edu.my
Received: 26 June 2020; Accepted: 26 July 2020
Abstract: Non-Newtonian is a type of fluid that does not comply with the viscosity under the Law of Newton and is being widely used in industrial applications. These include those related to chemical industries, cosmetics manufacturing, pharmaceutical field, food processing, as well as oil and gas activities. The inability of the conventional equations of Navier–Stokes to accurately depict rheological behavior for certain fluids led to an emergence study for non-Newtonian fluids’ models. In line with this, a mathematical model of forced convective flow on non-Newtonian Eyring Powell fluid under temperature-dependent viscosity (TDV) circumstance is formulated. The fluid model is embedded with the Newtonian heating (NH) boundary condition as a heating circumstance and is assumed to move over a stretching sheet acting vertically. Using appropriate similarity variables, the respective model was converted into ordinary differential equations (ODE), which was later solved utilizing the Keller box approach. The present model is validated by comparing the existing output in literature at certain special limiting cases, where the validation results display a firm agreement. The current outputs for the proposed model are shown in tabular and graphical form for variation of skin friction plus Nusselt number, velocity and temperature distribution, respectively.
Keywords: Temperature-dependent viscosity; erying powell fluid; vertical stretching sheet; numerical solution; boundary layer
Over recent decades, several wide-ranging investigations have been conducted on heat transference in a non-Newtonian fluid. Fluids with a non-Newtonian nature are partly or wholly made up of macromolecules or dual-phase materials. These fluids are typically described as those equipped with the capacity chronology of flow. As a rule, the categorization of the numerous forms of non-Newtonian type of fluid is realized on the shear stress equation. Unlike Newtonian fluid behaviors, industrial materials, such as polymeric liquids, paste, melts, emulsions, muds, foodstuffs, condensed milk, soaps, shampoos, molten plastics, etc., are able to follow the characteristics of non-Newtonian fluid. Therefore, the fluid flow modeling and estimation have fundamental and practical importance in the applications of engineering and its businesses. The behaviors rheological of such fluid flow are substantial inside the flows of nuclear gasoline slurries, paper coating, greases and lubrication with heavy oils, plasma and mercury, polymers, etc. Besides, one of the essential characteristics of fluids under investigation herein is the pressure tensor, which is associated with the fee of deformation tensor utilizing non-linear courting. Valuable contributions to the investigation of the properties of such fluids are highlighted by following experts [1–5].
The new development underwritten in fluid mechanics has paved the way for innovative methods in investigating the two-dimensional flow, where the non-Newtonian fluids’ flow mathematical system is far complex. Most known modules are the second grade of the non-Newtonian, which contains Maxwell, Oldroyd-B, as well as the power law of mathematical model. Eyring and Powell proposed a whole new mathematical model for non-Newtonian fluids in 1944 called the Eyring Powell model. Thus, very scant research has been involved in the fluid model of Eyring Powell on a two-dimensional type even though the model is better in several ways than other forms of non-Newtonian fluid models. Eyring Powell’s model has possessed numerous benefits for two main reasons. First, it is based on the theory of kinetic towards objects instead of that experimental formulas. Apart from that, the modeling of Eyring Powell reacts accordingly to low and high behavior of Newtonian’ shear rates.
Despite facing the challenges of solving the Eyring Powell model due to its complexity, Jalil et al. [6] took the challenge of solving the non-Newtonian Eyring Powell problem passing a permeable surface that is continuously moving parallel with the free stream. Besides, an analytical solution for the effects of convective boundary conditions over a surface moving with convective boundary conditions under a constant free stream movement has been analyzed by Hayat et al. [7]. Moreover, the ordinary equation arising from the partial governing differential upon applying proper transformation has been solved in a numerical manner using the Keller box method (KBM). Furthermore, Khader et al. [8] employed a numerical approach to investigate an unsteady flow and thermal conduction of Eyring Powell fluids in a laminar fluid-filled on a horizontal stretch surface under the condition of internal thermal generation. Likewise, Jalil et al. [9] and Javed et al. [10] devoted their study on fluids’ flow of the non-Newtonian Eyring Powell on the thin layer moving over a horizontal stretching sheet solved utilizing a finite difference approach. Moreover, Malik et al. [11] discussed a boundary layer of Eyring Powell for variable viscosity of a stretched cylinder.
Apart from that, Akbar et al. [12] deliberated the impact on free convection flow, mass and heat of viscous dissipation employing the numerical technique for computation. Also, Roşca et al. [13] discussed the flow and heat transfer of Powell Eyring fluids on a shrinking surface aligned with the free stream movement. Also, the effects of magnetohydrodynamics of Powell Eyring fluids with heat transfer were examined by Hayat et al. [14], Akbar et al. [15], Ellahi et al. [16], Hayat et al. [17], Gireesha et al. [18]. Moreover, Abbasi et al. [19] and Hina [20] concentrated on investigating the peristaltic fluid of Eyring Powell. In contrast, Hayat et al. [21] and Rauf et al. [22] solved such fluid using optimal control embedded with double-diffusive Cattaneo–Christov heat and mass flux theories, respectively. The series comparing numerical solutions of Eyring-Powell fluid flow with NH and heat generation is presented by Hayat et al. [23] and Rehman et al. [24], separately. Furthermore, the study on Prandtl-Eyring fluids forced convection flow Eyring Powell and its theoretical similarity was carried out by Shukla et al. [25]. Moreover, Sajid et al. [26] and Khan et al. [27] solved the fluid flow problem of Maxwell and Erying Powel models, respectively in the existence of nanoparticles with the effect of non-linear thermal radiation on a stretched surface.
Motivated by researchers examined above, the incompressible boundary layer of forced convection in two dimensions over a stretching sheet can be considered with the NH boundary condition as a heating circumstance. This recent study is dedicated to examining the forced convective of Eyring Powell fluid’s flow incorporated with TDV along a vertical stretching sheet through embedded NH boundary conditions. Numerical solutions are worked out by employing the KBM, and the solution is expressed through the graphical and tabular arrangement.
This study aims to investigate the characteristic of Eyring fluid under the influence of TDV embedded with the Newtonian heating (NH) boundary condition. The flow is assumed to flow over a vertical stretching sheet. It is presumed that the sheet stretches in the direction and moves with uniform velocity, where the x-axis is defined as an upward direction alongside the sheet. At the same time, the y-axis assumes its upward direction concerning the surface. The geometric configuration of the study case is shown in Fig. 1.
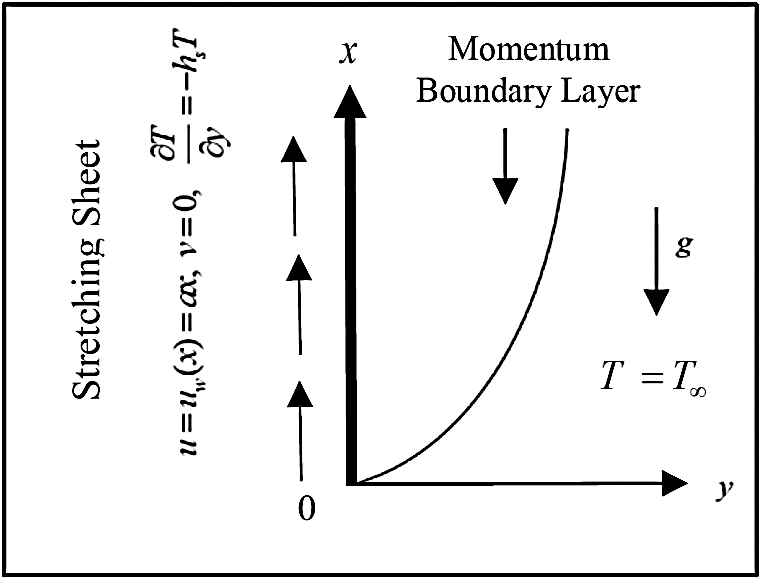
Figure 1: Physical configuration of problem
The derivation of the Eyring Powell model is based on rate processes theory to demonstrate the sheer of non-Newtonian flow. Summing up from the assumptions mentioned above and adopting the boundary layer approximation in the Cartesian coordinate system, the equations representing the model of fluid with TDV can be conveyed as

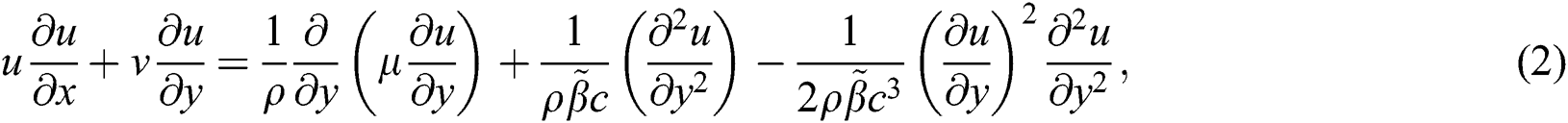

where  ,
,  ,
, 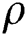 ,
, 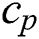 ; and
; and 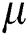 respectively refer to velocity components in
respectively refer to velocity components in  directions, temperature, density, constant pressure of specific heat, and fluid’s viscosity coefficient while
directions, temperature, density, constant pressure of specific heat, and fluid’s viscosity coefficient while 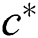 and
and 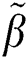 are the Powell Eyring parameters’ fluid model which has (time-1) dimension.
are the Powell Eyring parameters’ fluid model which has (time-1) dimension.
The model is referred to conditions at the boundary as
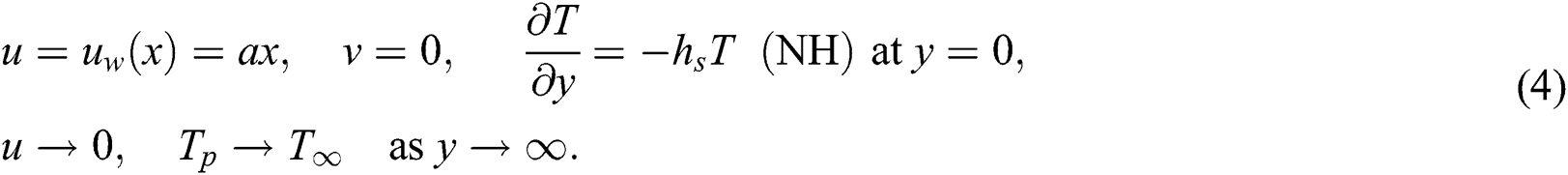
In Eq. (4), the parameters 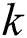 ,
, 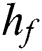 ,
, 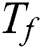 and
and 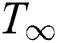 correspond to thermal conductivity, heat transference coefficient, hot fluid and ambient temperature, respectively. To obtain the set of similarity equations in the form of ODE, the similarity transformation variables as in Eq. (5) are adopted and applied to the governing Eqs. (1) to (4).
correspond to thermal conductivity, heat transference coefficient, hot fluid and ambient temperature, respectively. To obtain the set of similarity equations in the form of ODE, the similarity transformation variables as in Eq. (5) are adopted and applied to the governing Eqs. (1) to (4).
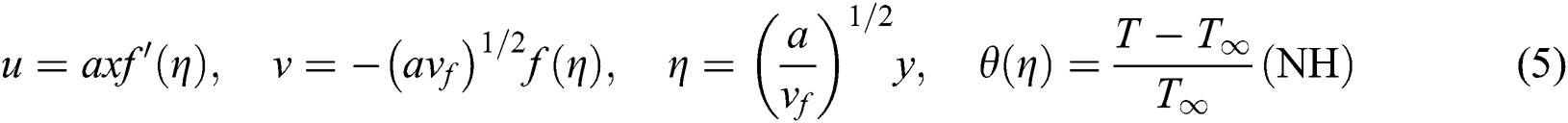
To simulate temperature-dependent viscosity variation, we adopt the Reynolds exponential viscosity model which provides an accurate approach, given by:

where the inverse linear function of temperature is assumed for variation of fluid viscosity. The resulting equations are obtained as follows:
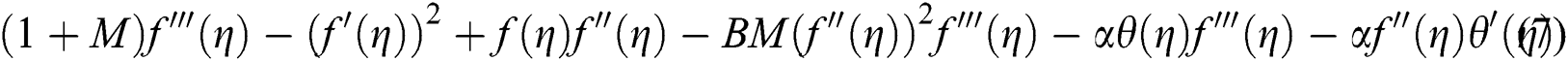

together with the reformed boundary conditions given by:
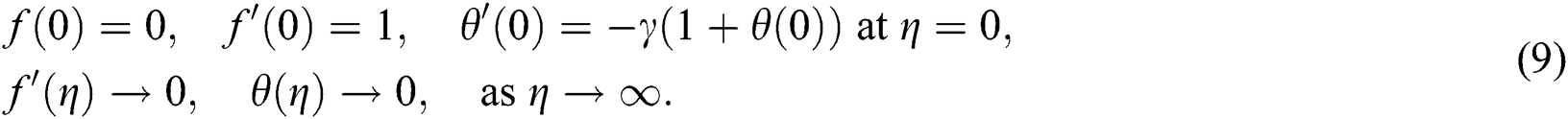
The obtained equations under the arrangement of a set of ODE is solved by employing the Keller box technique. Eqs. (8) and (9) subjected to the boundary conditions (10) are reduced to the system of first order. For that matter, the independent variables are demonstrated as follows

Then, the respective equations can be written as
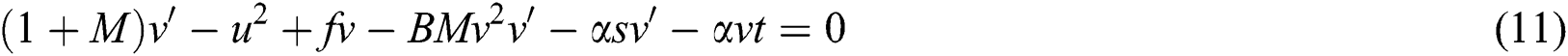

In Eqs. (7) to (12), the prime notation 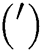 corresponds to the differentiation with respect to
corresponds to the differentiation with respect to 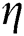 . Additionally, fluid parameters,
. Additionally, fluid parameters, 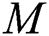 and
and 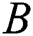 , Prandtl number,
, Prandtl number,  , specific heat ratio of mixture,
, specific heat ratio of mixture, 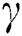 , thermal diffusivity,
, thermal diffusivity, 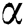 and fluid kinematic viscosity,
and fluid kinematic viscosity, 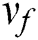 can be defined as follows
can be defined as follows
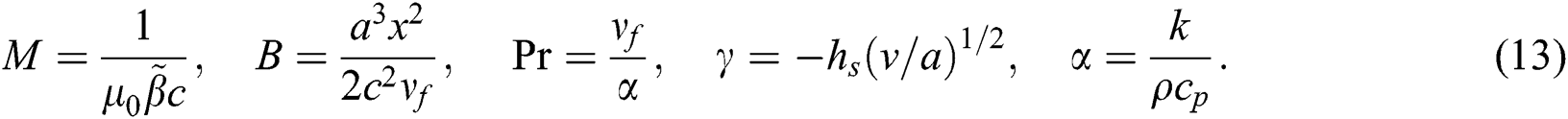
The net rectangle in the 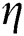 level is considered as in Fig. 2. The points of net are denoted as
level is considered as in Fig. 2. The points of net are denoted as
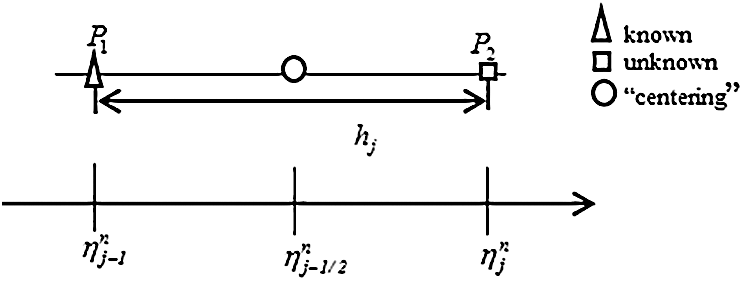
Figure 2: Net rectangle for difference approximations
where  is the
is the  -spacing and
-spacing and 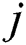 is the order of numbers specifying the coordinate location.
is the order of numbers specifying the coordinate location.
Eqs. (10)–(12) are predicted by expending the central difference at mid-point 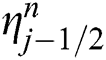 of the segment
of the segment  . Thus, the following set of equations are obtained
. Thus, the following set of equations are obtained



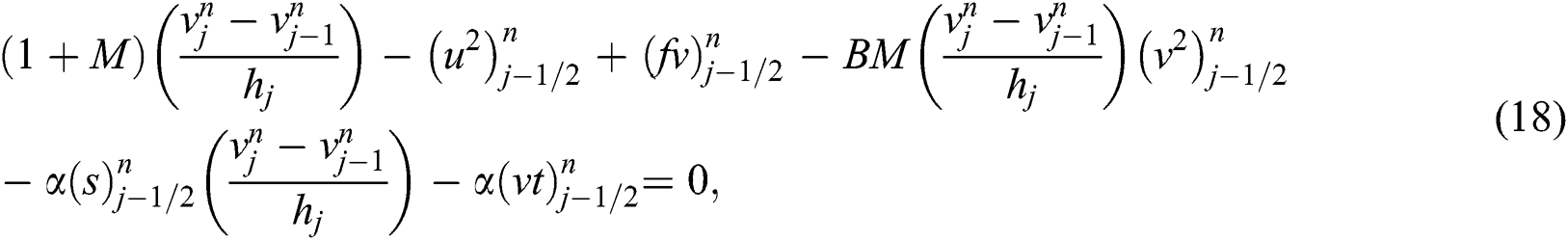

Eqs. (15)–(19) are computed for 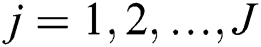 at the given
at the given 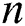 where the boundary conditions (9) become
where the boundary conditions (9) become
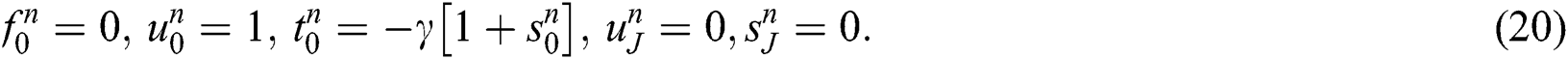
Suppose 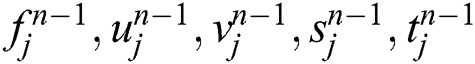 are known for
are known for 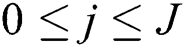 , then Eqs. (16)–(20) form a system of the unknown variables
, then Eqs. (16)–(20) form a system of the unknown variables 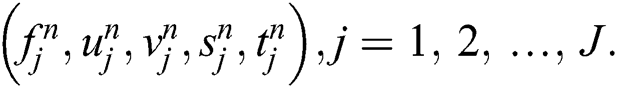 For simplification, the unknown variables
For simplification, the unknown variables 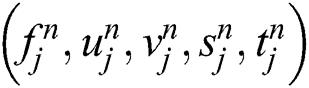 are written as
are written as 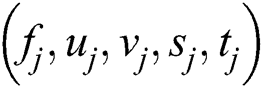 . Generally, Newton’s method is employed to linearize Eqs. (16) to (20) by introducing the subsequent iterates
. Generally, Newton’s method is employed to linearize Eqs. (16) to (20) by introducing the subsequent iterates

Upon performing algebraic manipulation and releasing the quadratic plus higher-order terms in 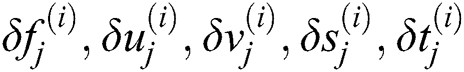 as well as the superscript
as well as the superscript 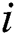 for simplicity, the following linear tridiagonal system is obtained as follows
for simplicity, the following linear tridiagonal system is obtained as follows
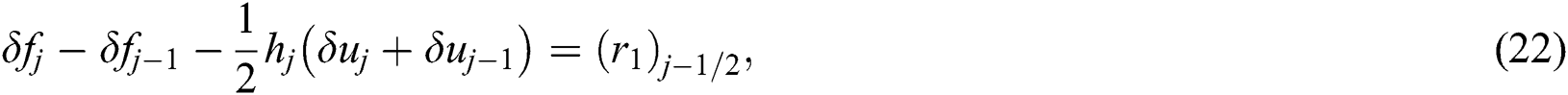
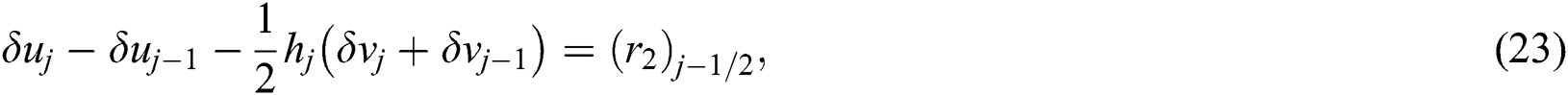
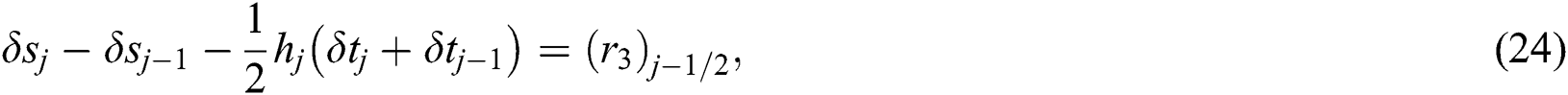
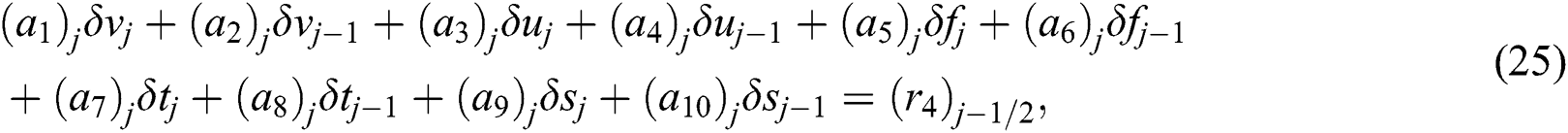
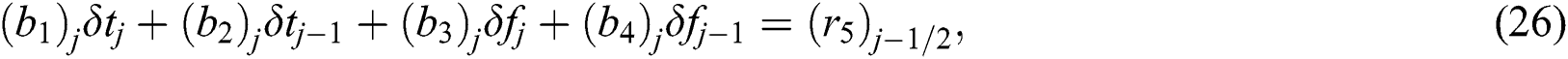
where
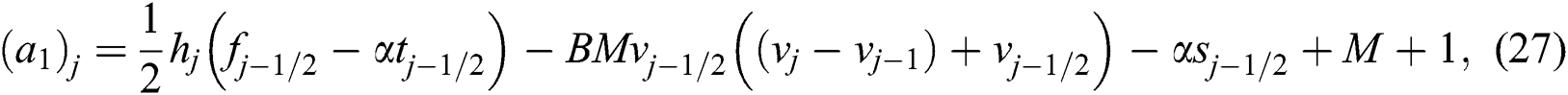
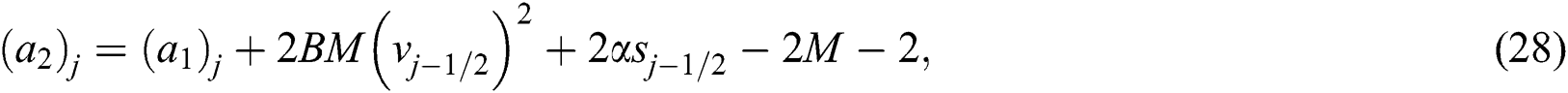



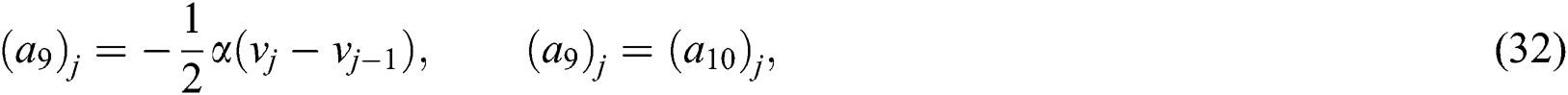



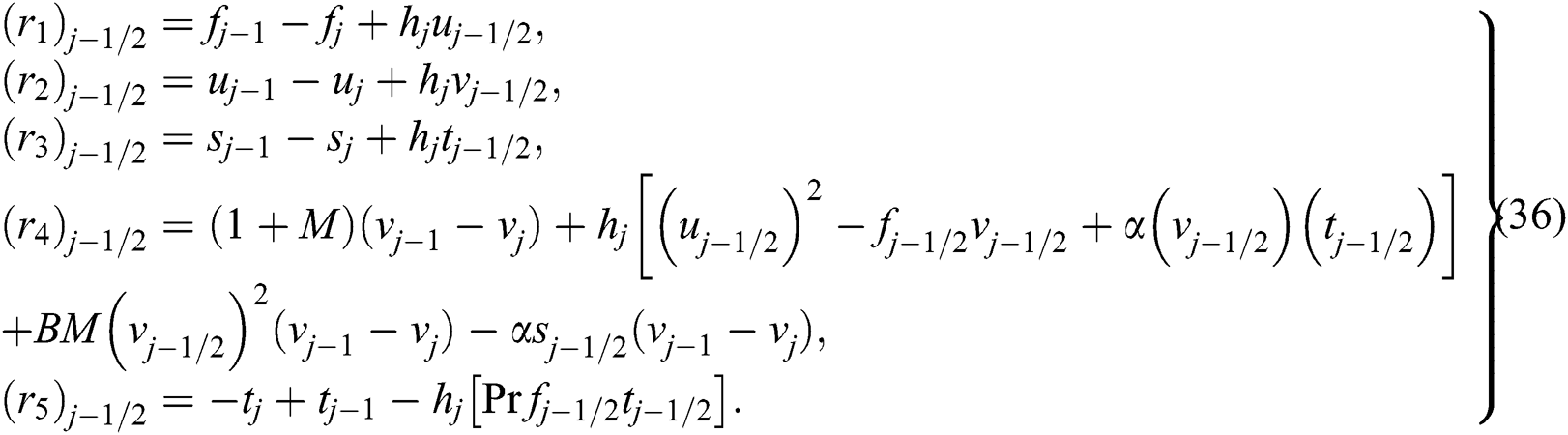
To uphold the correct values for the entire iterates, the assumption of 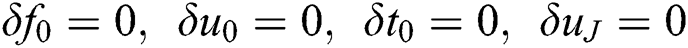 and
and 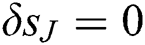 is required. To perform the linearized difference equations using the block elimination procedure, the elements of block matrices must be defined using three different cases where the corresponding matrix can be inscribed as
is required. To perform the linearized difference equations using the block elimination procedure, the elements of block matrices must be defined using three different cases where the corresponding matrix can be inscribed as

where
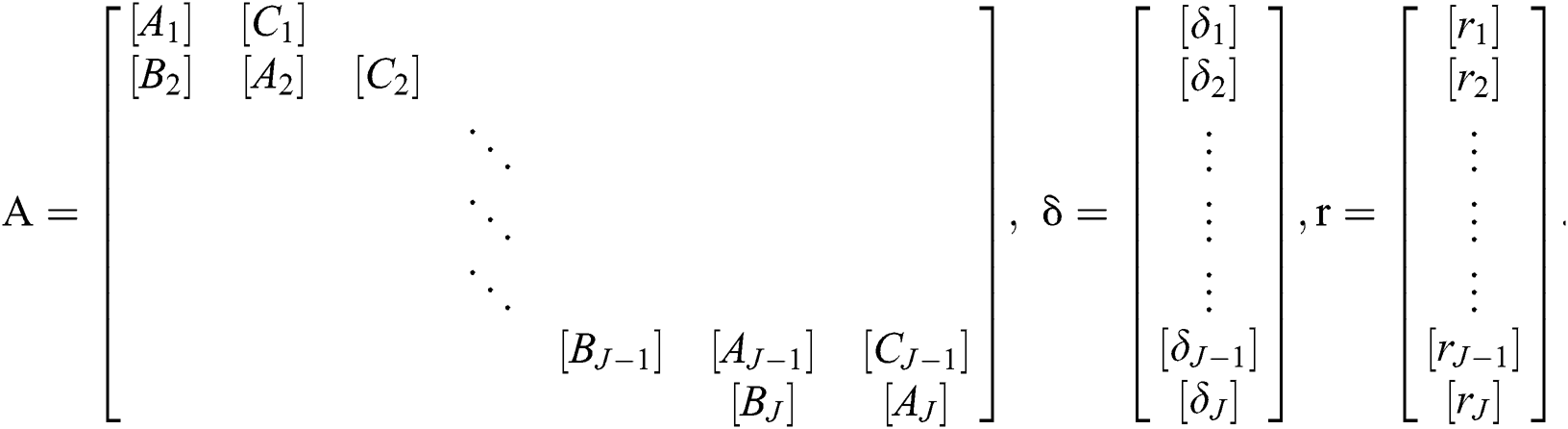
The elements of the matrices are given by

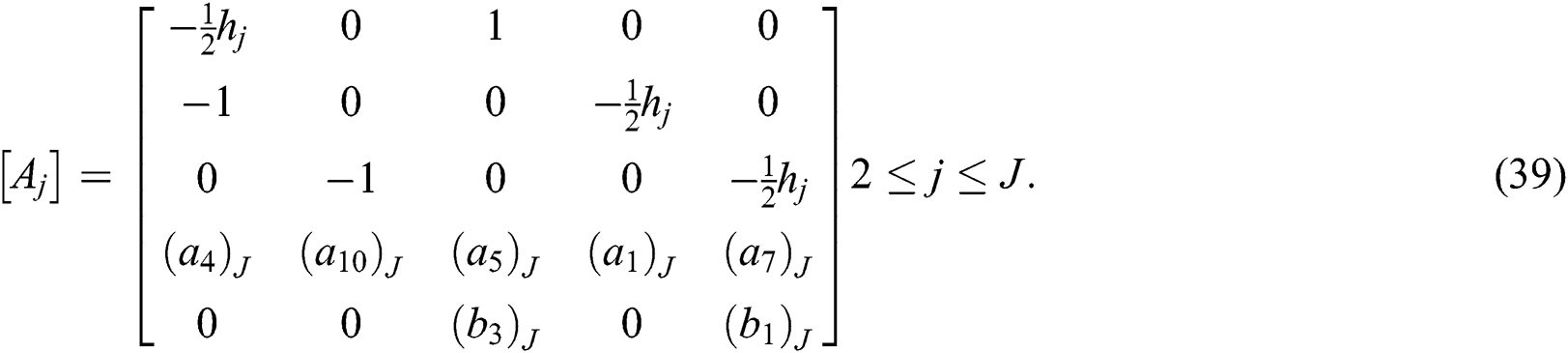
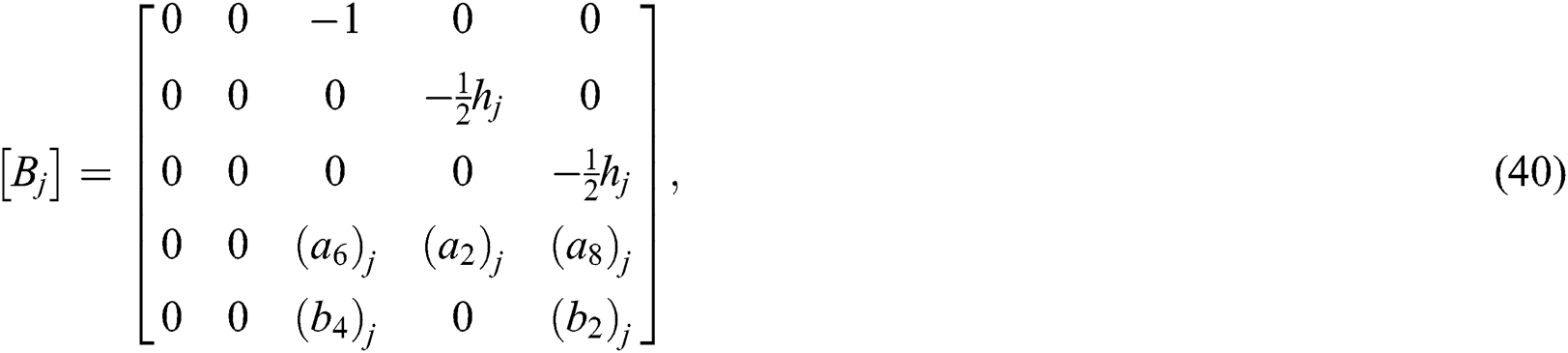

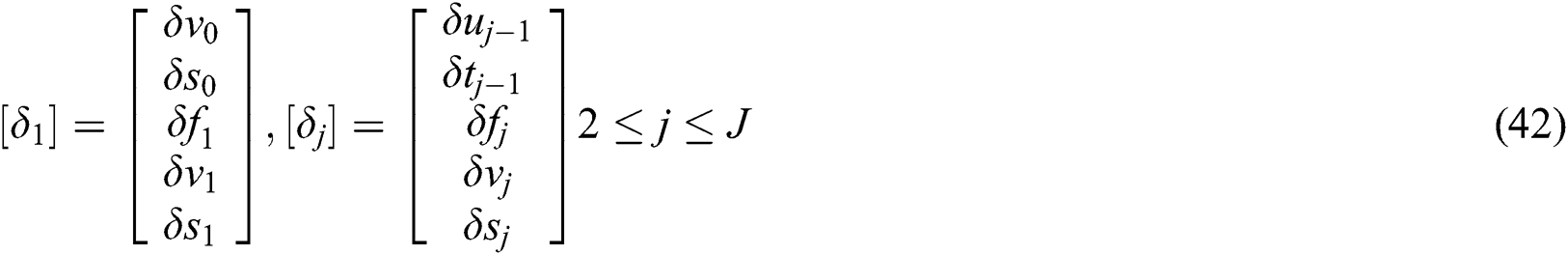
and

The matrix A is acknowledged as a tridiagonal matrix having zero elements except for its main diagonal. The respective system can be elucidated by using a block elimination technique with the assumption that the matrix A is non-singular and able to be factorized in the form of

The numerical results for this current investigation was computed using KBM. The outcome of fluid parameters (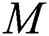 and
and 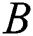 ), Prandtl number (
), Prandtl number ( ), and thermal diffusivity (
), and thermal diffusivity (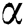 ) on fluids’ velocity and temperature against
) on fluids’ velocity and temperature against 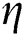 are computed using MATLAB software. It is well known that this method is undeniably one of the suitable approaches for solving the flow problem based on its wide application in many previous and recent studies within this research area. By having the finite boundary layer thickness,
are computed using MATLAB software. It is well known that this method is undeniably one of the suitable approaches for solving the flow problem based on its wide application in many previous and recent studies within this research area. By having the finite boundary layer thickness, 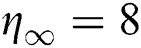 , the boundary conditions of this study are fully satisfied based on both velocity and temperature profiles attaining the asymptotic behavior. It is important to mention that the exact solution for skin friction coefficient for Eq. (12) without the parameter representing Eyring Powell fluid and viscosity is given by
, the boundary conditions of this study are fully satisfied based on both velocity and temperature profiles attaining the asymptotic behavior. It is important to mention that the exact solution for skin friction coefficient for Eq. (12) without the parameter representing Eyring Powell fluid and viscosity is given by

The exact expression of Eq. (41) has also been documented by Salleh et al. [28]. It is worth mentioning here that the comparative outcomes with the exact solution are necessary to claim the current model and its output are acceptable. The physical measures of skin friction as well as Nusselt number for this present mathematical model are given as
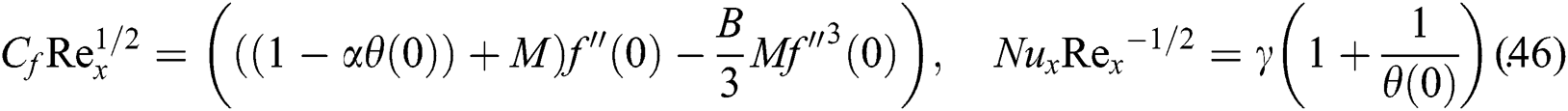
Besides that, the present model can be reduced to the existing equation, as in the literature. The following summaries are presented to show its connection to the model.
This present paper concentrates on the discussion of the solutions obtained (tabular and graphical form). The results were computed under the NH boundary condition for various parameter 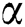 ,
, 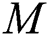 ,
, 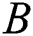 , and
, and  . The computation is performed by assigning a set of fixed values of the parameter, where the value of
. The computation is performed by assigning a set of fixed values of the parameter, where the value of 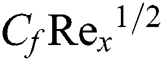 and
and 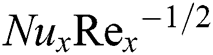 are later computed one by one. The direct comparison study with the exact expression (46) as well as the existing study reported by Salleh et al. [28], Gorla et al. [29], and Vajravelu et al. [30] carried out to corroborate the numerical solutions acquired in this study. From Tabs. 1 and 2, an excellent agreement is achieved, which indicates that the current model and its findings are acceptable.
are later computed one by one. The direct comparison study with the exact expression (46) as well as the existing study reported by Salleh et al. [28], Gorla et al. [29], and Vajravelu et al. [30] carried out to corroborate the numerical solutions acquired in this study. From Tabs. 1 and 2, an excellent agreement is achieved, which indicates that the current model and its findings are acceptable.
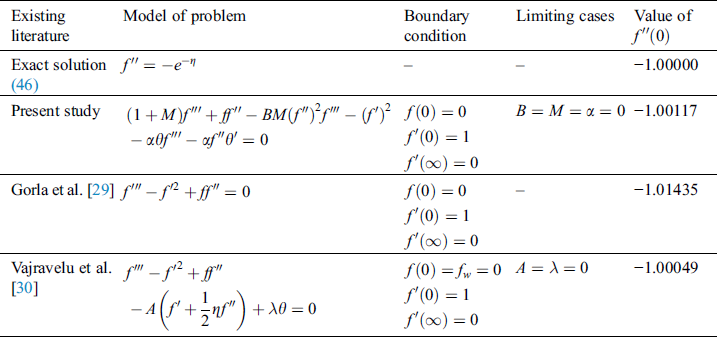
Table 2: Comparative study on value 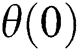 and
and 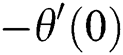

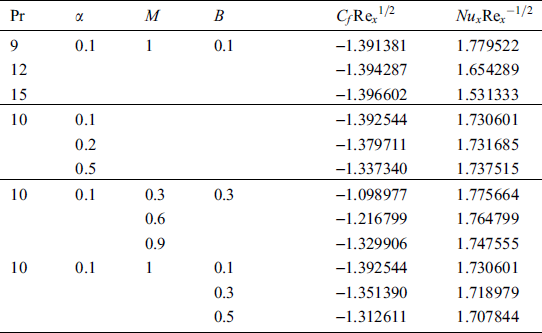
Tab. 3 depicts the variations of 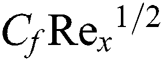 and
and 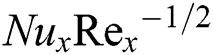 with the variation of the values of the parameter involved. For the entire computation, the value
with the variation of the values of the parameter involved. For the entire computation, the value 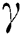 was taken as 1. It is noticed that for larger values of
was taken as 1. It is noticed that for larger values of  and
and 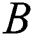 , the skin friction coefficient increases while decreasing trend is observed for larger values of
, the skin friction coefficient increases while decreasing trend is observed for larger values of 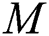 and
and  . On the other hand, the variant of Nusselt number increases only for larger values of
. On the other hand, the variant of Nusselt number increases only for larger values of 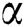 , while a decreasing trend for
, while a decreasing trend for  ,
, 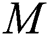 and
and 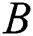 is observed. The increment in skin friction is due to the enhancement of drag forces occurring on the surface, and the increase in Nusselt number attributes to the store of heat from the process of fluid movement. It can be noticed that all the parameters existing in the present model affects the fluid flow characteristics.
is observed. The increment in skin friction is due to the enhancement of drag forces occurring on the surface, and the increase in Nusselt number attributes to the store of heat from the process of fluid movement. It can be noticed that all the parameters existing in the present model affects the fluid flow characteristics.
Table 3: Numerical results of 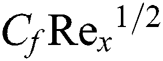 and
and 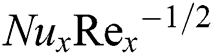 for numerous values of
for numerous values of  ,
, 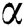 , M and B
, M and B
Furthermore, the analysis on parameters of 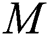 ,
, 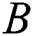 ,
,  and
and 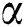 on velocity and temperature of fluid, respectively, are described in Figs. 3 to 10. An increased behavior of velocity can be seen in larger values of
on velocity and temperature of fluid, respectively, are described in Figs. 3 to 10. An increased behavior of velocity can be seen in larger values of  and
and 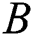 , as captured in Figs. 5 and 7, respectively. This is because the properties of those parameters characterize the ability to exchange thermal energy with its surroundings, which reduces the viscosity of fluid particles. Meanwhile, a contradict behavior on velocities of fluid can be seen for larger values of
, as captured in Figs. 5 and 7, respectively. This is because the properties of those parameters characterize the ability to exchange thermal energy with its surroundings, which reduces the viscosity of fluid particles. Meanwhile, a contradict behavior on velocities of fluid can be seen for larger values of 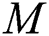 and
and 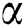 , as illustrated in Figs. 3 and 9, correspondingly. The temperature distribution shows a decreasing trend for larger values of
, as illustrated in Figs. 3 and 9, correspondingly. The temperature distribution shows a decreasing trend for larger values of 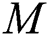 ,
, 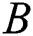 and
and  whereas an increasing trend for larger
whereas an increasing trend for larger 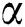 is obtained, as captured in Figs. 4, 6, 8 and 10, respectively. This is due to lessen heat loss and viscosity. Besides that, all the figures indicate that the velocity and temperature of the fluid asymptotically approaches zero, which fittingly fulfils the boundary condition.
is obtained, as captured in Figs. 4, 6, 8 and 10, respectively. This is due to lessen heat loss and viscosity. Besides that, all the figures indicate that the velocity and temperature of the fluid asymptotically approaches zero, which fittingly fulfils the boundary condition.
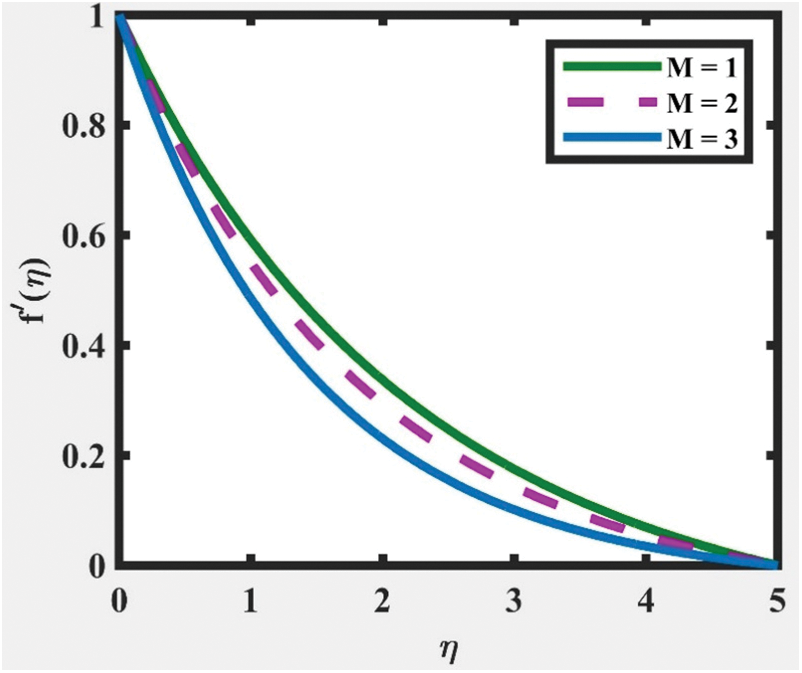
Figure 3:  at
at  ,
,  and
and 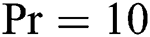 for various values of
for various values of 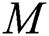
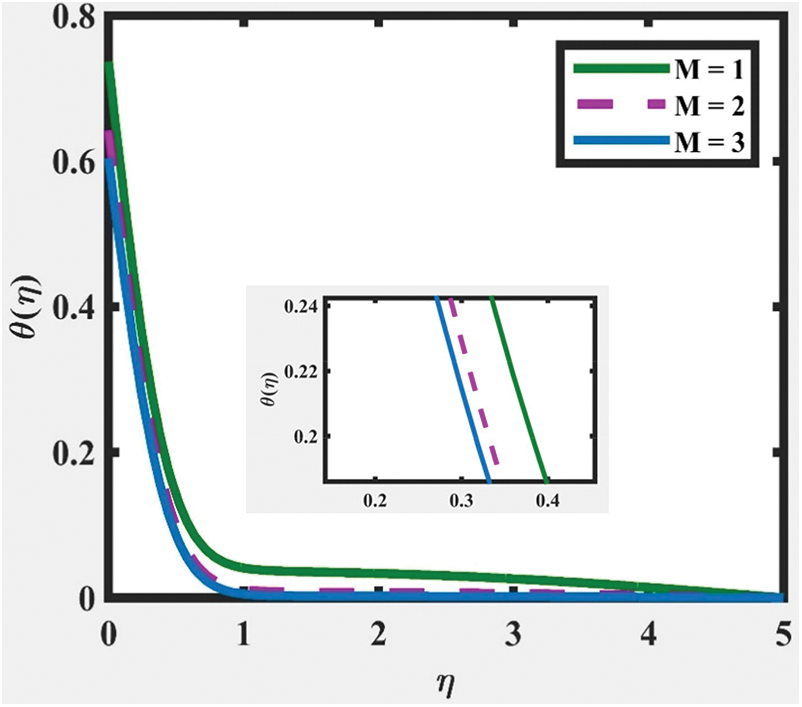
Figure 4:  at
at 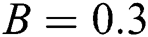 ,
, 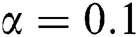 and
and 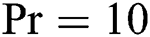 for various values of
for various values of 
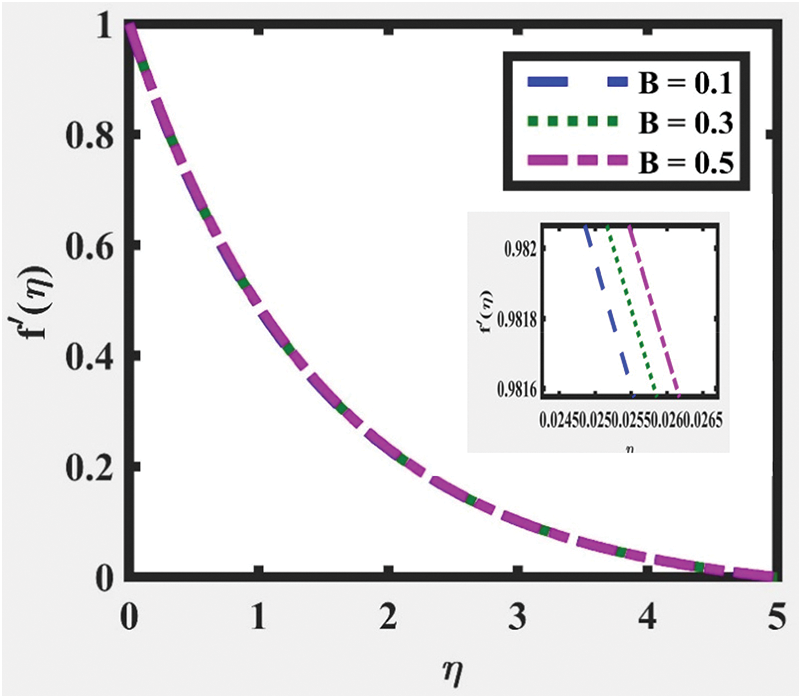
Figure 5: 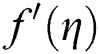 at
at 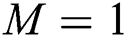 ,
, 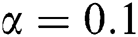 and
and 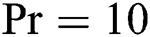 for various values of
for various values of 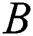
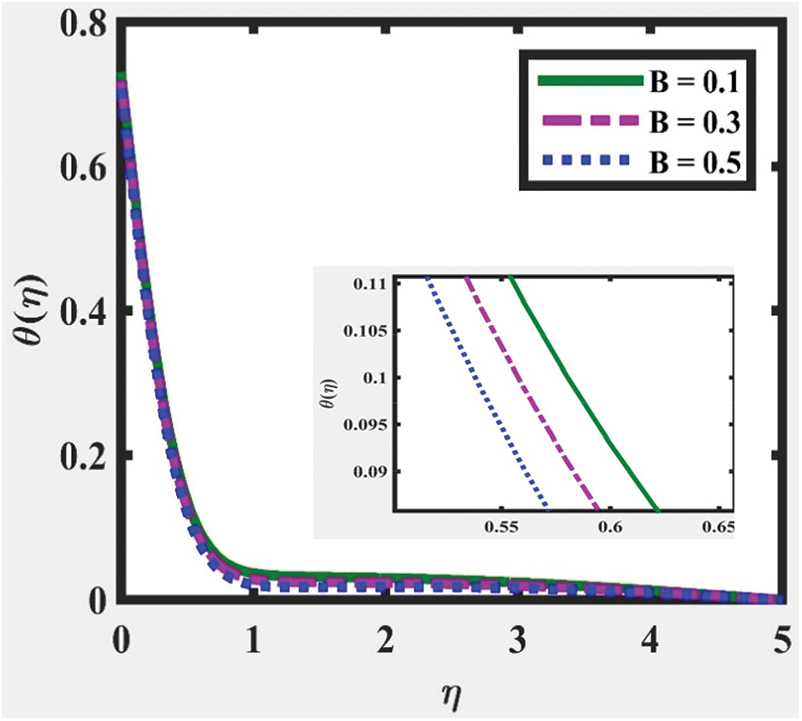
Figure 6:  at
at 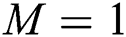 ,
, 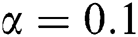 and
and 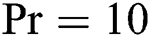 for various values of
for various values of 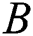
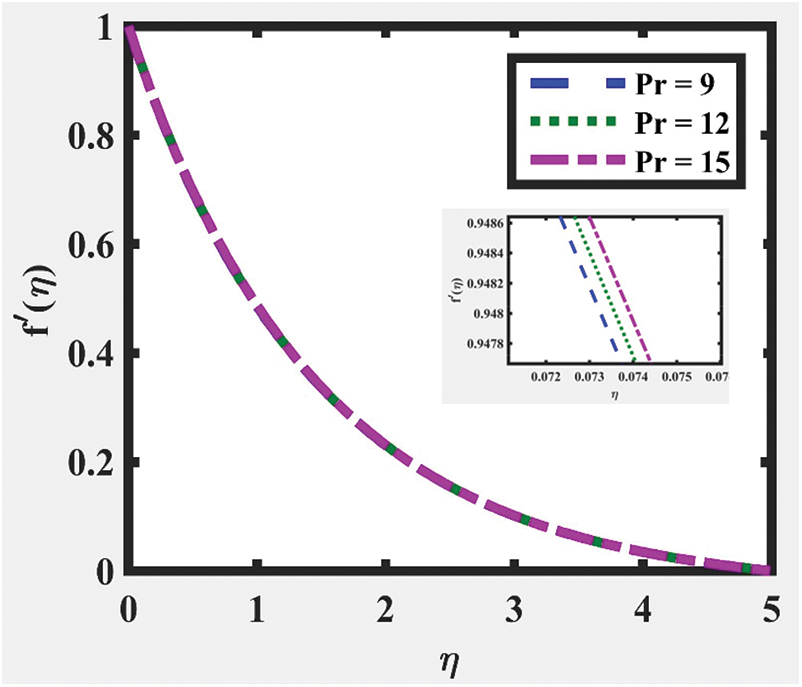
Figure 7: 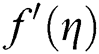 at
at 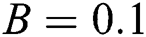 ,
, 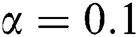 and
and 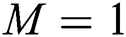 for various values of
for various values of 
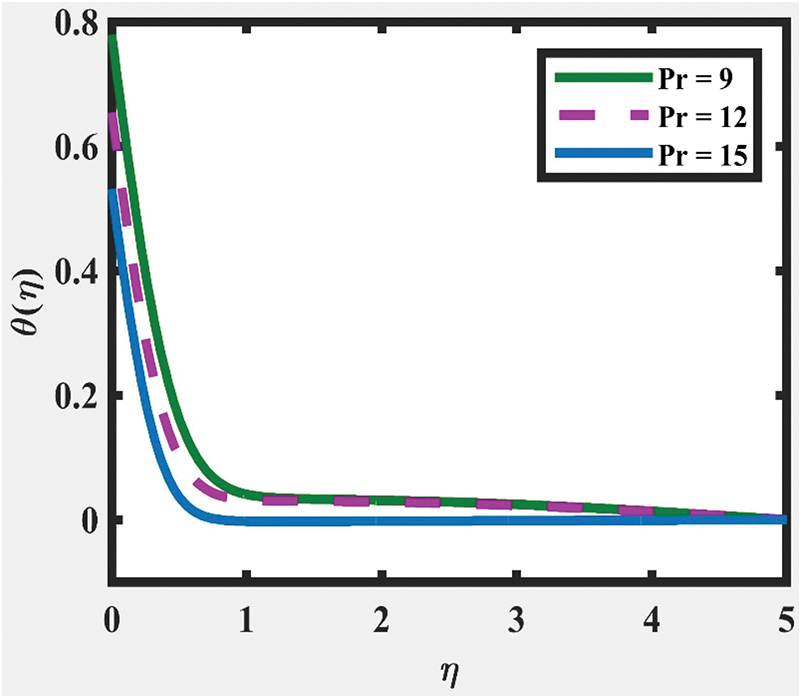
Figure 8:  at
at 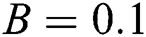 ,
, 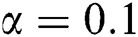 and
and 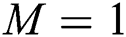 for various values of
for various values of 
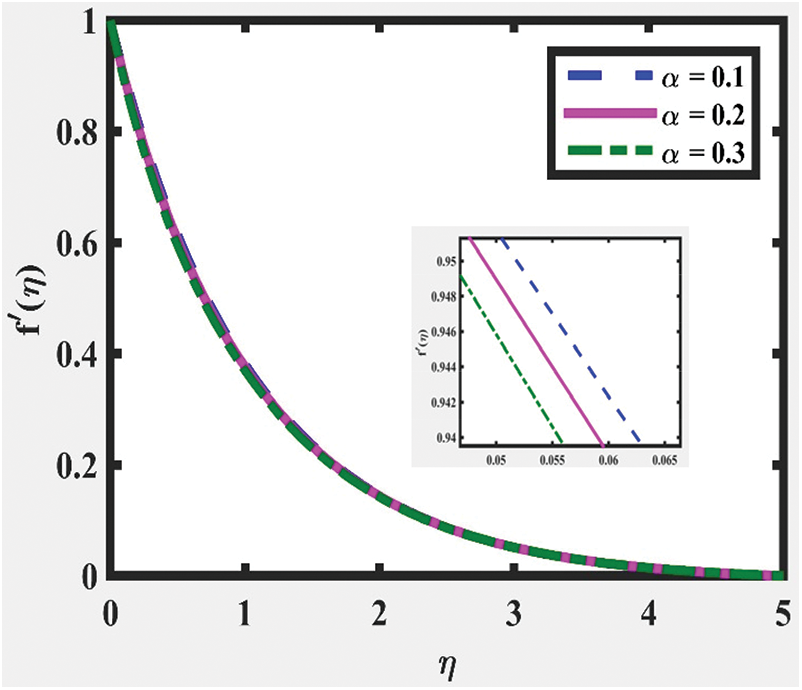
Figure 9: 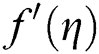 at
at 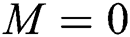 ,
, 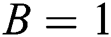 and
and 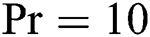 for various values of
for various values of 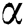
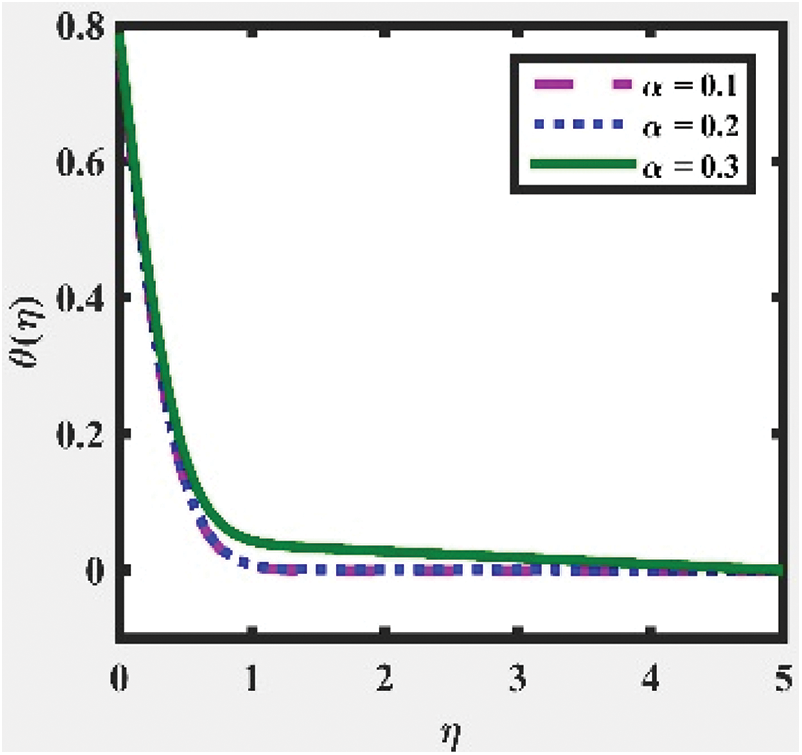
Figure 10:  at
at  ,
, 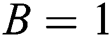 and
and 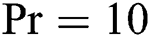 for various values of
for various values of 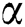
In this research, the convective force of an Eyring Powell fluid along vertical stretch plate has been discussed by highlighting the effect of TDV involved the parameters of 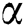 ,
, 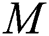 ,
, 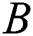 , and
, and  . A similar trend can be noticed from the mathematical analysis in the motion and temperature distributions of fluid, respectively, when parameters are increased. The utilization of KBM has developed a numerical solution, where the given graphs and tables demonstrate the effects of parameters. Nevertheless, the deviations on the distribution of velocity and the temperature of fluid exhibit the significance of the parameters studied. The findings in this study are expected to contribute to a better understanding of single-phase fluid flow characteristics as much as the solutions of its flow problems.
. A similar trend can be noticed from the mathematical analysis in the motion and temperature distributions of fluid, respectively, when parameters are increased. The utilization of KBM has developed a numerical solution, where the given graphs and tables demonstrate the effects of parameters. Nevertheless, the deviations on the distribution of velocity and the temperature of fluid exhibit the significance of the parameters studied. The findings in this study are expected to contribute to a better understanding of single-phase fluid flow characteristics as much as the solutions of its flow problems.
Funding Statement: This project has been supported by Universiti Malaysia Pahang & Ministry of Higher Education under The Fundamental Research Grant Scheme for Research Acculturation of Early Career Researchers (FRGS-RACER) (Ref: RACER/1/2019/STG06/UMP//1) through RDU192602.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1B. Sahoo. (2010), “Flow and heat transfer of a non-Newtonian fluid past a stretching sheet with partial slip. ,” Communications in Nonlinear Science and Numerical Simulation, vol. 15, no. (3), pp, 602–615, .
2T. Hayat and M. Qasim. (2010), “Influence of thermal radiation and Joule heating on MHD flow of a Maxwell fluid in the presence of thermophoresis. ,” International Journal of Heat and Mass Transfer, vol. 53, no. (21–22), pp, 4780–4788, .
3W. Khan and I. Pop. (2010), “Boundary-layer flow of a nanofluid past a stretching sheet. ,” International Journal of Heat and Mass Transfer, vol. 53, no. (11–12), pp, 2477–2483, .
4S. Nadeem, R. U. Haq and Z. Khan. (2014), “Numerical solution of non-Newtonian nanofluid flow over a stretching sheet. ,” Applied Nanoscience, vol. 4, no. (5), pp, 625–631, .
5T. Hayat, S. Asad, M. Mustafa and A. Alsaedi. (2015), “MHD stagnation-point flow of Jeffrey fluid over a convectively heated stretching sheet. ,” Computers & Fluids, vol. 108, pp, 179–185, . [Google Scholar]
6M. Jalil, S. Asghar and S. Imran. (2013), “Self similar solutions for the flow and heat transfer of Powell-Eyring fluid over a moving surface in a parallel free stream. ,” International Journal of Heat and Mass Transfer, vol. 65, pp, 73–79, . [Google Scholar]
7T. Hayat, Z. Iqbal, M. Qasim and S. Obaidat. (2012), “Steady flow of an Eyring Powell fluid over a moving surface with convective boundary conditions. ,” International Journal of Heat and Mass Transfer, vol. 55, no. (7–8), pp, 1817–1822, . [Google Scholar]
8M. Khader and A. Megahed. (2013), “Numerical studies for flow and heat transfer of the Powell-Eyring fluid thin film over an unsteady stretching sheet with internal heat generation using the Chebyshev finite difference method. ,” Journal of Applied Mechanics and Technical Physics, vol. 54, no. (3), pp, 440–450, . [Google Scholar]
9M. Jalil and S. Asghar. (2013), “Flow and heat transfer of Powell-Eyring fluid over a stretching surface: A Lie group analysis. ,” Journal of Fluids Engineering, vol. 135, no. (12), pp, 26, . [Google Scholar]
10T. Javed, N. Ali, Z. Abbas and M. Sajid. (2013), “Flow of an Eyring-Powell non-Newtonian fluid over a stretching sheet. ,” Chemical Engineering Communications, vol. 200, no. (3), pp, 327–336, . [Google Scholar]
11M. Malik, A. Hussain and S. Nadeem. (2013), “Boundary layer flow of an Eyring-Powell model fluid due to a stretching cylinder with variable viscosity. ,” Scientia Iranica, vol. 20, no. (2), pp, 313–321, . [Google Scholar]
12N. S. Akbar and S. Nadeem. (2013), “Effects of induced magnetic field on the peristaltic flow of an Eyring-Powell fluid. ,” Journal of Aerospace Engineering, vol. 26, no. (4), pp, 835–841, . [Google Scholar]
13A. V. Roşca and I. Pop. (2014), “Flow and heat transfer of Powell-Eyring fluid over a shrinking surface in a parallel free stream. ,” International Journal of Heat and Mass Transfer, vol. 71, pp, 321–327, . [Google Scholar]
14T. Hayat, M. Awais and S. Asghar. (2013), “Radiative effects in a three-dimensional flow of MHD Eyring-Powell fluid. ,” Journal of the Egyptian Mathematical Society, vol. 21, no. (3), pp, 379–384, . [Google Scholar]
15N. S. Akbar, A. Ebaid and Z. H. Khan. (2015), “Numerical analysis of magnetic field effects on Eyring-Powell fluid flow towards a stretching sheet. ,” Journal of Magnetism and Magnetic Materials, vol. 382, pp, 355–358, . [Google Scholar]
16R. Ellahi, E. Shivanian, S. Abbasbandy and T. Hayat. (2016), “Numerical study of magnetohydrodynamics generalized Couetteflow of Eyring-Powell fluid with heat transfer and slip condition. ,” International Journal of Numerical Methods for Heat & Fluid Flow, vol. 26, no. 5, pp. 1433–1445, . [Google Scholar]
17T. Hayat, Z. Hussain, M. Farooq and A. Alsaedi. (2018), “Magnetohydrodynamic flow of Powell-Eyring fluid by a stretching cylinder with Newtonian heating. ,” Thermal Science, vol. 22, no. (1), pp, 371–382, . [Google Scholar]
18B. J. Gireesha, R. S. R. Gorla and B. Mahanthesh. (2015), “Effect of suspended nanoparticles on three-dimensional MHD flow, heat and mass transfer of radiating Eyring-Powell fluid over a stretching sheet. ,” Journal of Nanofluids, vol. 4, no. (4), pp, 474–484, . [Google Scholar]
19F. M. Abbasi, A. Alsaedi and T. Hayat. (2014), “Peristaltic transport of Eyring-Powell fluid in a curved channel. ,” Journal of Aerospace Engineering, vol. 27, no. (6), pp, 04014037, . [Google Scholar]
20S. Hina. (2016), “MHD peristaltic transport of Eyring-Powell fluid with heat/mass transfer, wall properties and slip conditions. ,” Journal of Magnetism and Magnetic Materials, vol. 404, pp, 148–158, . [Google Scholar]
21T. Hayat, S. Makhdoom, M. Awais, S. Saleem and M. M. Rashidi. (2016), “Axisymmetric Powell-Eyring fluid flow with convective boundary condition: Optimal analysis. ,” Applied Mathematics and Mechanics, vol. 37, no. (7), pp, 919–928, . [Google Scholar]
22A. Rauf, Z. Abbas, S. Shehzad, A. Alsaedi and T. Hayat. (2018), “Numerical simulation of chemically reactive Powell-Eyring liquid flow with double diffusive Cattaneo-Christov heat and mass flux theories. ,” Applied Mathematics and Mechanics, vol. 39, no. (4), pp, 467–476, . [Google Scholar]
23T. Hayat, S. Ali, M. A. Farooq, A. Alsaedi and Z. K. Gao. (2015), “On comparison of series and numerical solutions for flow of Eyring-Powell fluid with Newtonian heating and internal heat generation/absorption. ,” PLoS One, vol. 10, no. (9), e0129613, . [Google Scholar]
24K. U. Rehman, M. Y. Malik, T. Salahuddin and M. Naseer. (2016), “Dual stratified mixed convection flow of Eyring-Powell fluid over an inclined stretching cylinder with heat generation/absorption effect. ,” AIP Advances, vol. 6, no. (7), 075112, . [Google Scholar]
25H. Shukla, J. Patel, H. C. Surati, M. Patel and M. Timol. (2017), “Similarity solution of forced convection flow of Powell-Eyring & Prandtl-Eyring fluids by group-Theoretic method. ,” Mathematical Journal of Interdiciplinary Sciences, vol. 5, no. (2), pp, 151–165, . [Google Scholar]
26T. Sajid, M. Sagheer, S. Hussain and M. Bilal. (2018), “Darcy-Forchheimer flow of Maxwell nanofluid flow with nonlinear thermal radiation and activation energy. ,” AIP Advances, vol. 8, no. (3), 035102, . [Google Scholar]
27M. Khan, M. Irfan, W. A. Khan and A. S. Alshomrani. (2017), “A new modeling for 3D Carreau fluid flow considering nonlinear thermal radiation. ,” Results in Physics, vol. 7, pp, 2692–2704, . [Google Scholar]
28M. Z. Salleh, R. Nazar and I. Pop. (2010), “Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. ,” Journal of the Taiwan Institute of Chemical Engineers, vol. 41, no. (6), pp, 651–655, . [Google Scholar]
29R. S. R. Gorla and I. Sidawi. (1994), “Free convection on a vertical stretching surface with suction and blowing. ,” Applied Scientific Research, vol. 52, no. (3), pp, 247–257, . [Google Scholar]
30K. Vajravelu, K. V. Prasad and C. O. Ng. (2013), “Unsteady convective boundary layer flow of a viscous fluid at a vertical surface with variable fluid properties. ,” Nonlinear Analysis: Real World Applications, vol. 14, no. (1), pp, 455–464, . [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |