DOI:10.32604/cmc.2020.011110
| Computers, Materials & Continua DOI:10.32604/cmc.2020.011110 | |
| Article |
Hospital Bed Allocation Strategy Based on Queuing Theory during the COVID-19 Epidemic
1Department of Rehabilitation Medicine, Children’s Hospital of Nanjing Medical University, Nanjing, 210008, China
2College of Science and Engineering Management, Anhui University of Technology, Ma’anshan, 243002, China
3Huai’an TCM Hospital Affiliated to Nanjing University of Chinese Medicine, Huai’an, 223002, China
4Department of Physics and Astronomy, University College London, London, 0044, UK
*Corresponding Author: Gang Hu. Email: hug_2004@126.com
Received: 20 April 2020; Accepted: 26 July 2020
Abstract: During the current epidemic, it is necessary to ensure the rehabilitation treatment of children with serious illness. At the same time, however, it is essential to effectively prevent cross-infection and prevent infections from occurring within the hospital setting. To resolve this contradiction, the rehabilitation department of Nanjing Children’s Hospital adjusted its bed allocation based on the queuing model, with reference to the regional source and classification of the children’s conditions in the rehabilitation department ward. The original triple rooms were transformed into a double room to enable the treatment of severely sick children coming from other places. A M/G/2 queuing model with priority was also applied to analyze the state of patient admissions. Moreover, patients in Nanjing were also classified into mild and severe cases. The M/M/1 queuing model with priority was used for analysis of this situation, so that severely ill children could be treated in time while patients with mild symptoms could be treated at home. This approach not only eases the bed tension in the ward, but also provides suitable conditions for controlling cross-infection.
Keywords: COVID-19; bed allocation; queuing theory
It was on December 26 2019 when Zhang Jixian, Director of the Department of Respiratory Medicine at the Hospital of Integrated Traditional Chinese and Western Medicine in Hubei Province, reported the first case of viral pneumonia (later confirmed as new coronavirus pneumonia) known as the Coronavirus Disease 2019 (COVID-19). On January 23, 2020, the epidemic prevention and control headquarters in Wuhan issued the announcement that the city would be closed; this included buses, subways, ferries, long-distance buses and all flights being forced into emergency shutdown. The government issued specific rules ordering that citizens of Wuhan could not leave the city without a special reason. A total of 11 million Wuhan citizens were at risk due to the new coronavirus pneumonia vortex [1]. Moreover, at 8:30 on January 23, 574 people had been diagnosed across the country, 17 of whom had died; most of those had either lived in Wuhan for a long period, were in Wuhan briefly to visit relatives or friends, or were just on a leisurely travel. After the first-level emergency public health response was implemented on January 23 in the Hunan and Guangdong provinces of Zhejiang, 22 other provinces and municipalities of the country were subsequently placed under level one major public health emergency response conditions, with the exception of five autonomous regions, two special administrative regions and the Taiwan Province. Three days later, other provinces, cities, districts, counties and townships closed their roads; as a result, locals could not leave, and visitors coud not get in [2–4].
At the same time as these restrictions were in effect, there were also children with serious illnesses requiring rehabilitation treatment (such as post-brain trauma surgery, heart disease surgeries, small mandibular surgeries, and encephalitis recovery treatment). If a child is infected with COVID-19, any accompanying persons or medical workers in hospitals are also susceptible to being infected in the closed hospital environment. Accordingly, controlling the source of infection and cutting off transmission routes are important and difficult tasks that all hospital management teams and doctors must pay attention to. This article will analyze and conduct research into this issue.
In Geneva on February 11, WHO director-general Tan Desai announced that the disease caused by the novel coronavirus had been officially named Coronavirus Disease 2019 (COVID-19). Since December 2019, Wuhan City has identified multiple cases of viral pneumonia, all diagnosed as viral pneumonia/pulmonary infection. Due to the new type of pneumonia which exists interpersonal transmission, National Health Commission of the PRC decided to include the COVID-19 as the legal class B infectious disease, and implemented managements as a legal class A infectious disease [5,6].
On January 20, Xi Jinping provided important instructions regarding the COVID-19 pneumonia epidemic. He emphasized that the safety and health of the people should be the priority, along with resolutely curbing the spread of the epidemic. On January 30, 2020, WHO released guidance stating that the new coronavirus infection pneumonia epidemic was a public health emergency of international concern, while emphasizing that travel and trade restrictions were not recommended. Meanwhile, the WHO agreed with China’s strategic and tactical approach to the epidemic. On March 11, the director-general of the WHO announced that the new coronavirus constituted a global pandemic [7].
At 11:00, 2020-04-12, there were a total of more than 1.7 million confirmed cases worldwide, with 532,879 confirmed cases in the United States. In China, there were 83,482 diagnosed persons, of whom 3,349 were dead and 78,028 were cured and discharged; 67,803 of these cases were diagnosed in Hubei [8,9].
2.2 Nanjing Children’s Hospital
Nanjing Children’s Hospital, affiliated with Nanjing Medical University (Jiangsu Children’s Medical Center, Nanjing Children’s Hospital), is a large-scale third-class comprehensive children’s hospital integrating medical treatment, rehabilitation, and healthcare. The annual number of outpatients and emergency admissions is 2,929,700, while the daily number of outpatient visits sits at about 800. The Rehabilitation Department, which is a key focus of development in Nanjing, is a standardized training base for rehabilitation therapists of the Jiangsu Provincial Health Commission. This department not only undertakes the rehabilitative medical care of children from all ethnic groups across the country, but also administers a large number of clinical internships and teaching positions. Children admitted include those with various types of cerebral palsy, comprehensive developmental delay and other delayed developmental indicators, various post-traumatic and brain trauma-related conditions, those requiring neurological rehabilitation, those in need of various types of encephalitis recovery treatment, those being treated for and recovering from heart disease, and those with orthopedic needs. The child patients come from all regions of the country, including Jiangsu, Anhui, Zhejiang, and Xinjiang. The average number of hospitalizations is 2,000 people/year, and the bed utilization rate is 100%.
The rehabilitation department of Nanjing Children’s Hospital implemented an online appointment queuing system for patients during the epidemic. Each patient is discharged from the hospital after a treatment course of 21 days, and the hospital discharge service department registers the discharge time. However, the closure of cities and roads in each province made it impossible for children there to come after appointment, which caused these children to lose some of their valuable treatment time. Moreover, the requirements for rehabilitating children after post-traumatic brain injury surgery, post-cardiac surgery, small mandibular surgery, and encephalitis recovery have not diminished during the outbreak.
To deal with this issue, the hospital implemented the “Administrative System and Regulations for Children with New Coronavirus Pneumonia,” stating that it would strictly conduct screening, diagnosis, and treatment of the children. Moreover, depending on the regional origin and condition classification of the children in rehabilitation wards, the hospital increased prevention and adjusted bed positions. These new policy decisions ensure that rehabilitation treatment for seriously ill children can be carried out actively and normally, while also effectively preventing cross-infection and ensuring that zero new infections occur in the hospital during the outbreak.
The hospital bed is one of the most important resources in a hospital. Some empirical articles have been published that investigate how hospital bed usage impacts on the length of hospital stay and mortality. Kuntz et al. [10,11] analyzed the relationship between in-hospital mortality and bed occupancy rate using a discrete-time survival model and found that when the bed occupancy rate exceeded 92.5%, the patient mortality rate increased dramatically. Similarly, Berry et al. [12,13] explored the relationship between bed occupancy and the length of hospitalization in the inpatient department. By modeling the length of hospitalization using a piecewise linear spline model, these authors found that the bed occupancy rate and the patient’s hospitalization time exhibited an N-shaped curve when plotted. Once the bed occupancy rate passed the second critical point of −93%, an increase in bed occupancy rate would lead to an increase in hospitalization duration.
The relevant literature on hospital bed capacity planning mainly uses simulation, queuing theory and optimization theory. Zhu et al. [14,15] used simulation models to estimate ICU (Intensive Care Unit) bed capacity via discrete event simulation. Thomas et al. [16–18] used discrete-time simulation models to analyze the impact of different emergency bed allocation schemes on system performance, which reduced the number of patients overflowing in the system. Finally, simulation experiments were used to verify the model robustness and the applicability of the conclusions.
Domestic scholars primarily study the arrangement and allocation of hospital beds by constructing mathematical programming models. Li et al. [19,20] established a linear programming model to address the bed arrangement problem by considering the costs incurred by patients waiting for admission and surgery. Jiang et al. [21] used queuing theory to establish an optimal model for the rational allocation of ophthalmic beds. Xu et al. [22,23] used the mixed-integer programming model to solve admission scheduling for gynecological patients. Cao et al. [24] analyzed the current situation and problems associated with the allocation of bed resources in medical institutions in Shanghai. An et al. [25,26] established a non-linear programming model for ophthalmology bed arrangement, which was scored using the established evaluation indicators. Finally, the Monte Carlo method was used to test the robustness of the model.
Normal bed allocations in the rehabilitation department.
Before the outbreak occurred, all children in need of rehabilitation were admitted to the hospital for treatment regardless of their race, gender or region of origin. The waiting time for severely ill children was slightly less than that for mildly ill children. Moreover, there are three beds in each ward of the rehabilitation department, and 27 wards overall, for a total of 81 beds. Accordingly, the priority M/G/3 queuing theory model is used to analyze this case, as shown in Fig. 1.
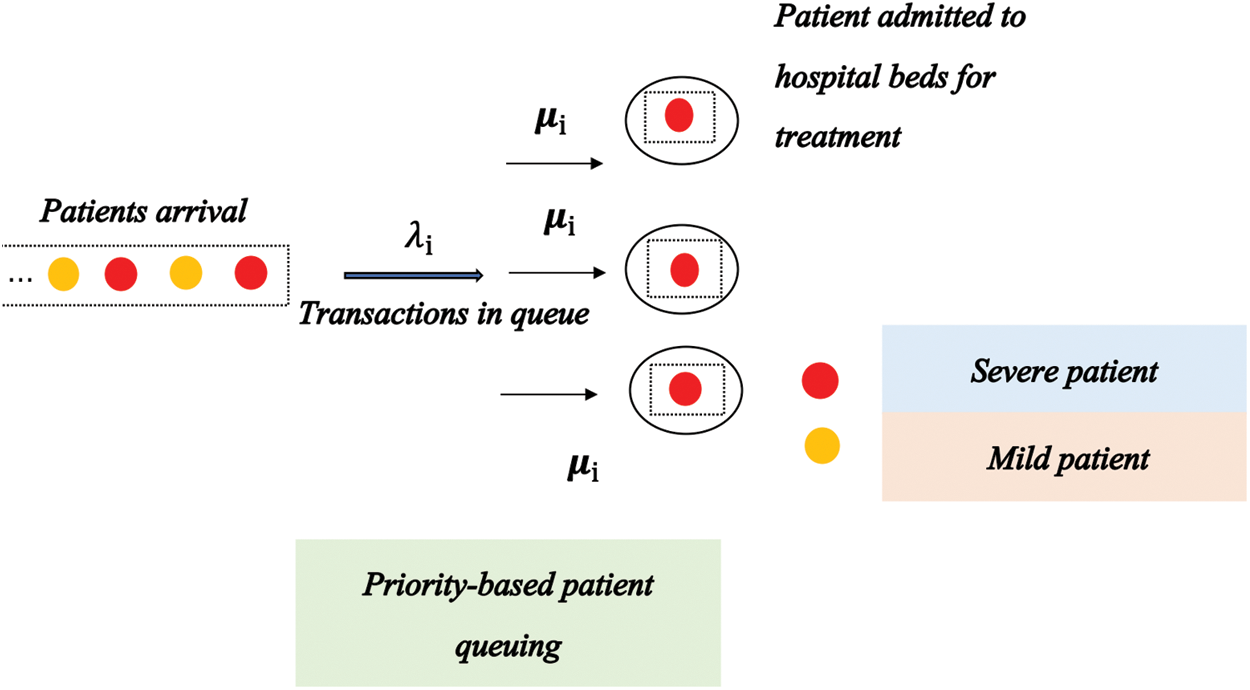
Figure 1: Rehabilitation bed allocation model based on the priority M/G/3 queuing theory
There are two types of severe and mild patients in children patients, and the arrival process of the 
th patient 
conforms to the Poisson process. Thus, the service time is 
,
, 
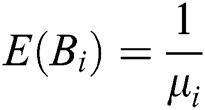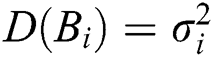. The priority of patients in category 
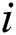is higher than that of patients in category 
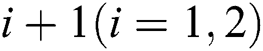; moreover, patients of the same type need to follow the first-come-first-served (FCFS) treatment as well.
Moreover, a non-preemptive model is utilized; this means that under circumstances when severe patients with high priority arrive at the ward, the treatment of mild patients with low priority is not terminated. Based on the assumption that the arrival process of the two types of patients is independent of each other, the treatment time of patients of the same type is believed to have the same distribution.
where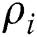 
is the service strength of the system, while 
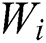is the waiting time of the 
th patient; moreover,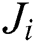 
is the arrival interval of the 
th patient, and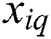 
is the queue length of the 
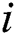th patient when the new patient arrives 
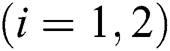.The hospital treatment system is stable, meaning that 
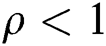. The waiting time for critically ill patients can be broken down into two parts. The first part is the time remaining before patients are treated by the medical system, 
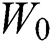. If patients are being treated, then 
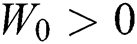; if there are no patients, then 
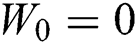. Considering that in patients are treated in parallel within the system, moreover, another part is one-third of the total treatment time required for all critical patients; that is, 
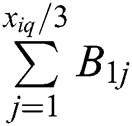, where 
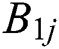is the service time of the 
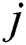th critical patient in the critical patient cohort. Furthermore, all 
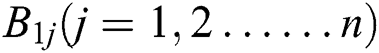are independent of each other and have the same distribution as 
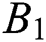. Finally, 
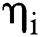is the remaining treatment time of the 
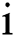th patient. Thus, we can obtain the following formula:
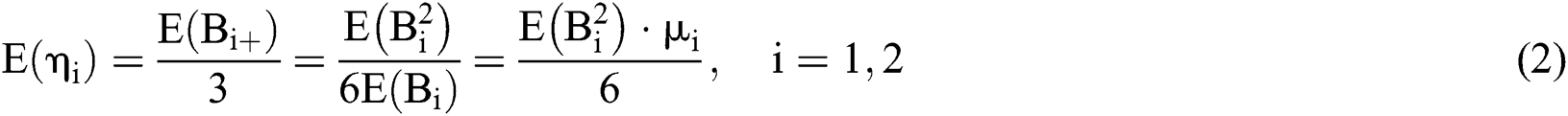
Accordingly, the probability that a patient arriving at any moment will belong to the category of the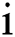 
th patient is 
. The probability that the bed is occupied by the 
th patient is therefore as follows:
Thus, we obtain the following result:
The following results can thus be obtained:
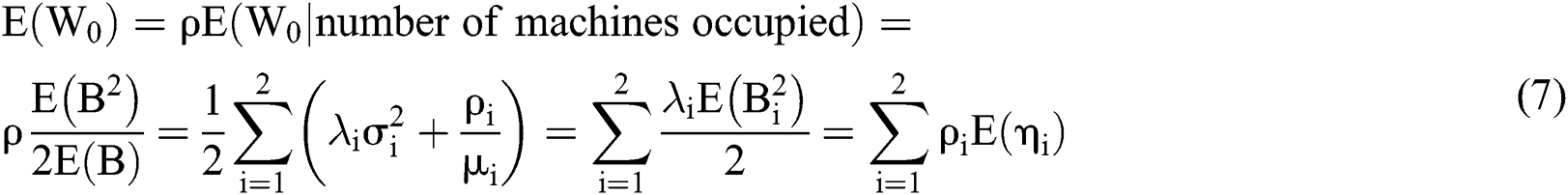
1) For critically ill patients, the waiting time is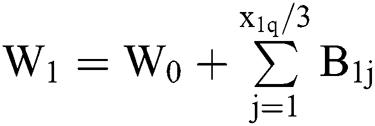 
. Therefore, the average waiting time for critically ill patients is as follows:
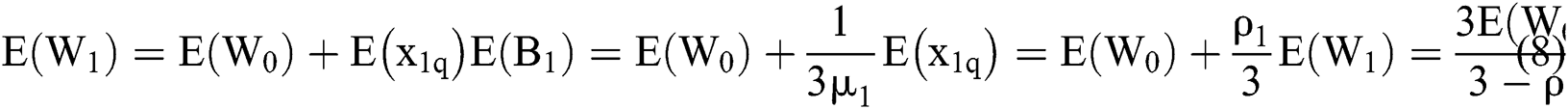
2) For mild patients, their priorities are lower than those of severe patients. Thus, we have the following formula:
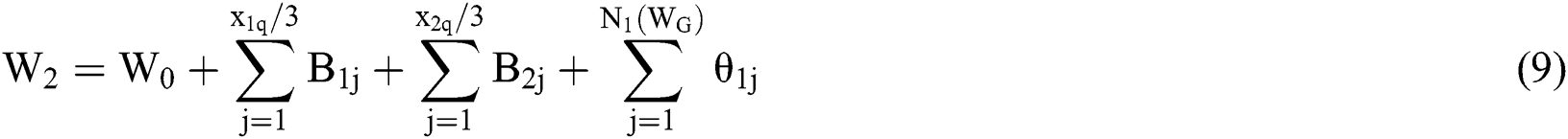
Set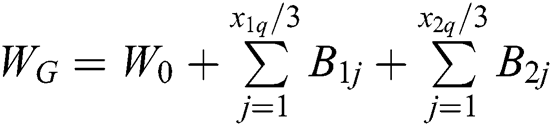 
, 
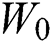is the remaining treatment time in the system when the mild patient arrives in the system, while 
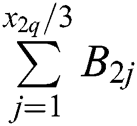defines treatment volume for mild patients in the system. 
means that the arrival time is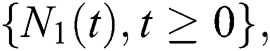 
while the service time is the busy period in the M/G/3 system. Each of the elements in 
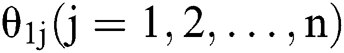are independent of each other and all have the same distribution as 
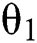, which is 
.
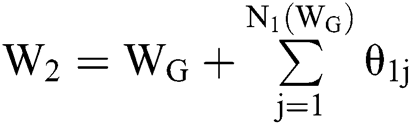Thus, the following can be concluded from the above derivation:
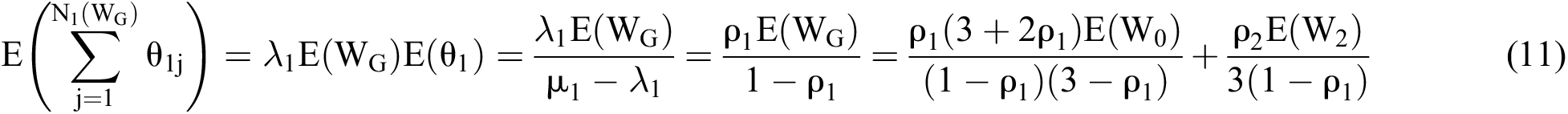
The average waiting time for the mild patients, as obtained by the simultaneous formula, is as follows:
Through calculation, it can be concluded that the waiting time until hospitalization for relatively severe children is about 21 days, while the waiting time until hospitalization for relatively mild children is about 45 days. These data are consistent with the actual situation.
3 Bed Allocation in Rehabilitation Department during the COVID-19 Epidemic
3.1 Each Ward Allocates Two Beds
During the epidemic, the children who can enter the hospital for treatment are all critically ill children in urgent need of treatment due to the COVID-19 restrictions implemented in various regions. In order to prevent cross-infection, the three beds A, B, and C previously available in each original ward were adjusted to beds A and C, with the bed B in the middle of ward being temporarily left vacant. Therefore, the queuing theory model based on priority M/G/2 is used. This process is illustrated in Fig. 2.
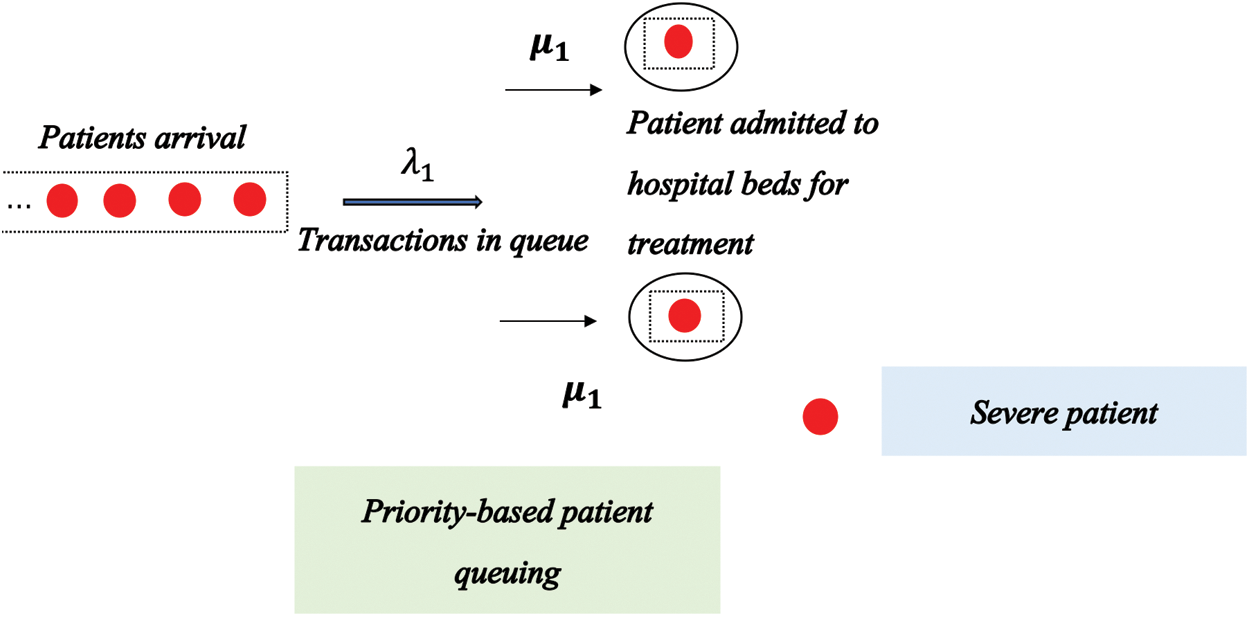
Figure 2: Rehabilitation bed allocation model based on the priority M/G/2 queuing theory
We define the patient input process 
to be a Poisson process with the parameter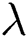 
, meaning that the inter-arrival time series 
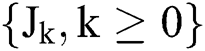is an independently identically distribution (
) random variable sequence, while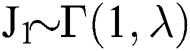 
. Because there are two beds, the treatment process for each bed is independent and has the same distribution of treatment time 
,
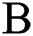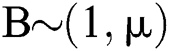; that is, the patient’s treatment time series 
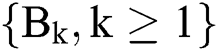is a sequence of 
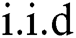random variables. 
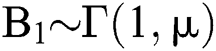, while 
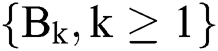and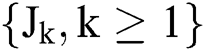 
are independent.
where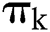 
represents the probability of 
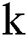patients entering the system after the system is in balance. When the distribution of the system is stable, 
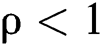; here, ρ is referred to as the treatment intensity of the system. From this stable distribution, several quantitative indicators based on the M/M/2 system can be obtained: namely, the average captain and the average waiting captain.
We use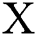 
to represent the captain of the system when 
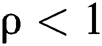, while 
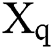is the waiting captain of the system. Thus, the following formulas can be obtained:
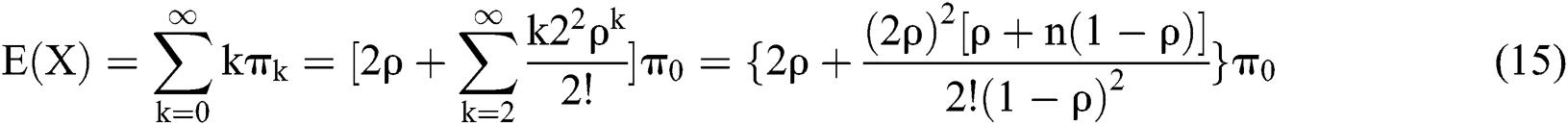
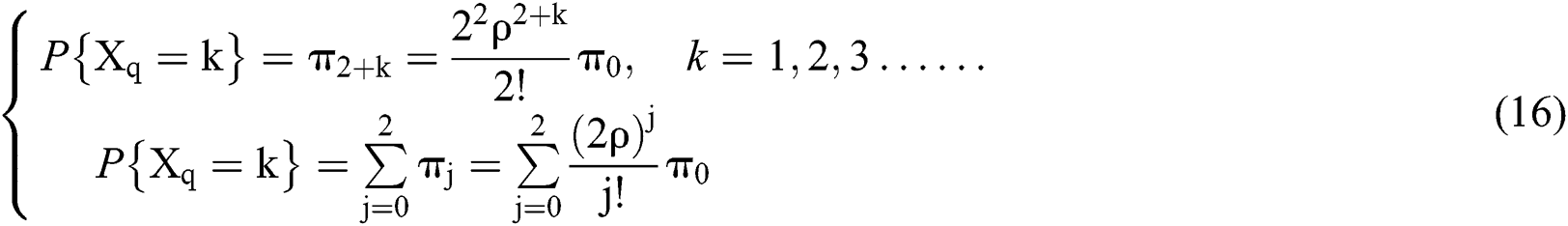
If we introduce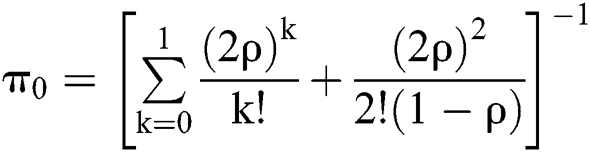 
into the above formulas, the following formula can be obtained:
Moreover,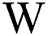 
denotes the waiting time of the next patient under the steady distribution condition 
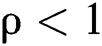. Thus,
As for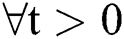 
, the distribution function of 
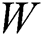is as follows:
According to the probability theory, the following can be obtained:
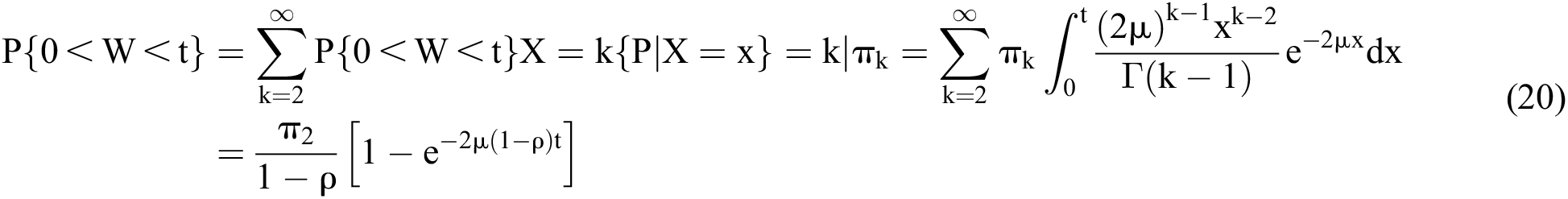
The distribution function of time is therefore as follows:
Since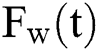 
is discontinuous at t = 0, W is not a continuous random variable; moreover, the graph of 
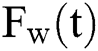is not stepped, which is further evidence that W is not a discrete random variable. Thus, the density function of W is as follows:
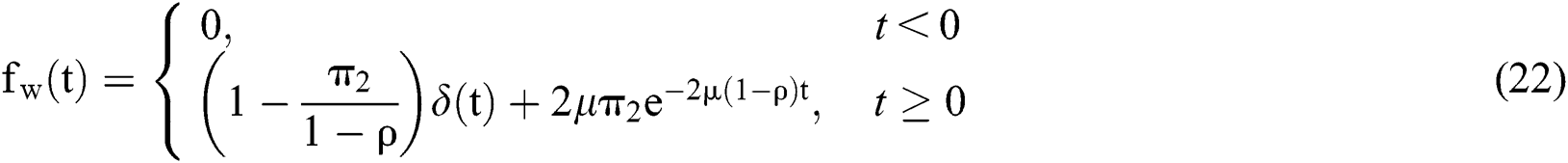
where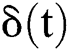 
is the Dirac function. And the properties of this function are as follows:
(1) When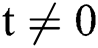 
, 
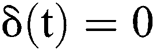; when 
, 
.
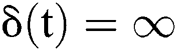(2) 
.
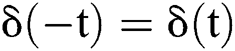(3) For any function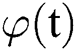 
, there is 
.
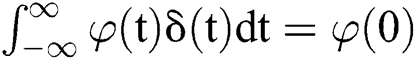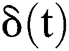can be seen as a unit jump function: 
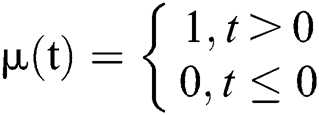. Thus, 
.
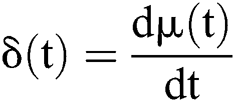From the density function of time, the expected time is as follows:
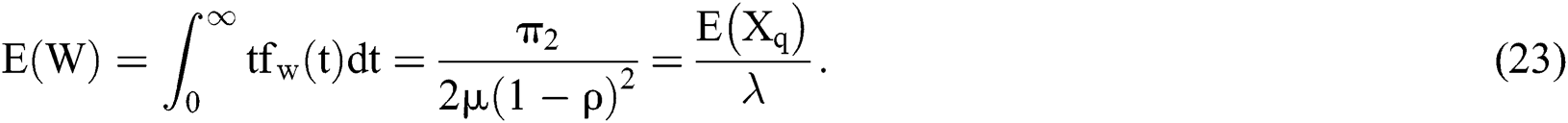
From the above calculations, it can be concluded that the waiting time for the hospitalization of relatively serious child patients in the field is about 18 days, which is three days shorter than the waiting time before the outbreak. This is because all of the child patients who come to Nanjing for treatment from other places are seriously ill enough that they cannot be treated effectively in their cities. The rehabilitation department of Nanjing Children’s Hospital (affiliated with Nanjing Medical University) is a medical institution with good medical conditions and advanced technology located in East China. To prevent cross-infection, the department reserved two beds (specifically the A and C beds) out of the three beds available in each ward for these critically ill children, which both reduced the number of beds and negatively impacted the ability to treat the local children of Nanjing.
According to the disease classification system, local children are categorized into two patient types: Severe and mild patients. Severe children have the right to priority treatment. To prevent cross-infection, the local children with moderate and severe illness can use only bed A or C on the ward. This situation can therefore be analyzed using the above M/G/2 queuing model.
For children with relatively mild illness in Nanjing who require rehabilitative services, the rehabilitation department of the Children’s Hospital is still the preferable choice. A small number of the B beds can be opened after both the A and C beds have been filled during the epidemic. The priority level of relatively mild patients is lower than that of the severe patient. Based on the above, the queuing theory model with priority M/M/1 was utilized to analyze the children with mild illness requiring rehabilitation. This process is illustrated in Fig. 3 below.
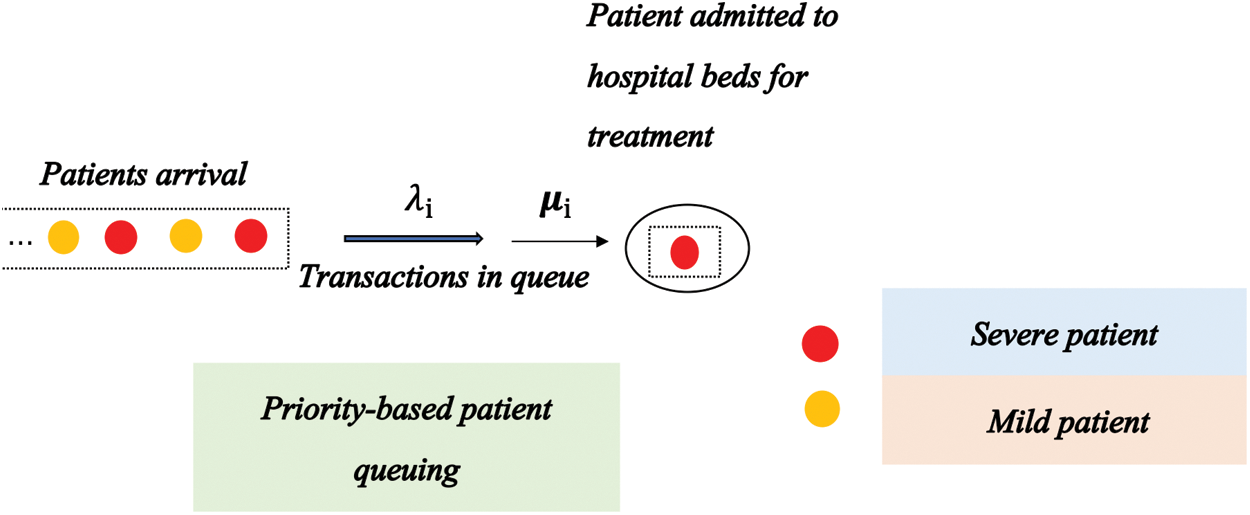
Figure 3: Rehabilitation bed allocation model based on the priority M/M/1 queuing theory
The following formula can thus be obtained:
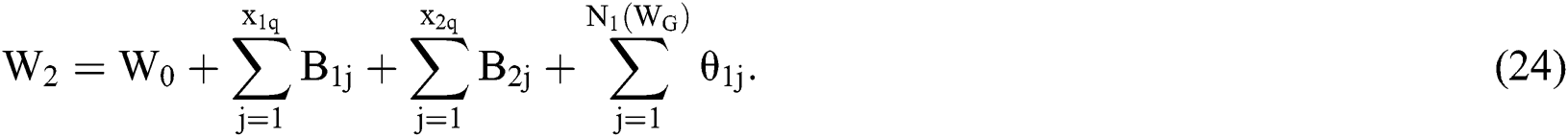
Assuming 
, 
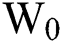denotes the remaining treatment time within the system when the mild patient enters the system. 
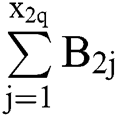is the treatment volume for mild patients in the system. 
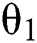indicates that the arrival time is 
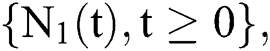while the service time is the busy period of the M/M/1 system. Similar to 
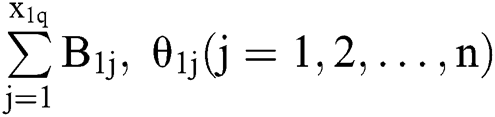are independent of each other, and are all distributed in the same as 
.
Thus, the following formulas can be obtained from the above derivation:
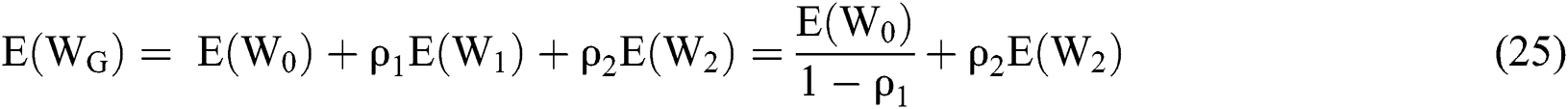
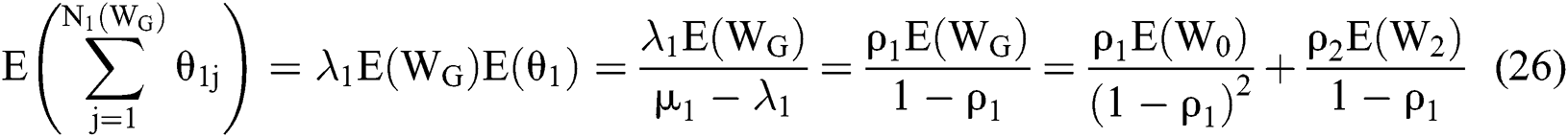
The average waiting time for mild patients is as follows:
It is concluded that the waiting time for local children with relatively mild conditions is about 78 days.
During the epidemic period, the waiting time in Nanjing for children with severe cases has not been extended; meanwhile, the waiting time for hospitalization of children with relatively mild illness who require rehabilitative services is 78 days.
In addition to rehabilitation treatment in outpatient clinics, children with a relatively mild illness can also undergo home rehabilitation treatment. Internet technology can be used to provide rehabilitation guidance to these children. Under this approach, the child’s parent reports recent details of the child’s condition to the medical team through a remote consultation system, after which doctors, nurses and therapists in the hospital determine the child’s short-term rehabilitation goals. Moreover, documents pertaining to various rehabilitation training guidance programs and department dynamics have been published on the undergraduate department’s consultation platform. Furthermore, the treatment group in hospital actively interacted with the parents of the children to alleviate the parents’ anxiety, achieving good social benefits.
During this epidemic, it is vital to improve the level of rehabilitation specialist knowledge possessed by child rehabilitation professionals in first- and second-level medical institutions. Among the group of children who are usually hospitalized, some children with growth retardation and generalized developmental delays can early enter the first- and second-level medical institutions for rehabilitation training after being diagnosed by the third-level medical institutions. For various reasons, these patients still enter into the queuing system of the third-level diagnosis and treatment institution’s rehabilitation ward, as this results in the best use of medical resources. If this problem is to be solved, it will also be necessary to design an advanced diagnosis and treatment model that will classify the child’s condition in detail, as this will also enable the limited medical resources to be utilized more reasonably.
The new coronavirus spreading rapidly all over the world is transmitted through respiratory droplets and via contact transmission. Moreover, as a hospital is a relatively centralized environment, it is important to control the sources of infection and cut off the transmission routes in these locations. During the epidemic, to prevent cross-infection between children, the rehabilitation department reduced the number of beds and controlled the number of caregivers in hospital, which enabled expansion of the bed space between each hospitalized child. It is a difficult business to appropriately treat children and configure the beds under these circumstances. In this paper, a queuing model with priority was applied to analyze the state of patient admission. This approach not only ensures that children with serious illnesses will get timely, effective and safe treatment, but also enables the occurrence of infections on the ward to be effectively controlled.
Funding Statement: This work is supported by the NSFC (61772280). Gang Hu is the corresponding author.
Conflicts of Interest: The authors declare that we have no conflicts of interest to report regarding the present study.
References
1Y. Bai, L. Yao, T. Wei, T. Tian, D.Jin. (2020). et al., “Presumed asymptomatic carrier transmission of COVID-19. ,” Journal of the American Medical Association, vol. 323, no. (14), pp, 1406–1407, .
2Y. Dong, X. Mo, Y. Hu, X. Qi and F. Y. Jiang. (2020), “Epidemiology of COVID-19 among children in China. ,” Pediatrics, vol. 145, no. (6), e20200702, . [Google Scholar]
3H. Fan and H. Zhu. (2019), “Motion vector detection based on local autocorrelation coefficient. ,” Cluster Computing, vol. 22, no. (5), pp, 11633–11639, .
4L. Fang, C. Yin, X. Yun, Z. Wen, S. Ji. (2019). et al., “THP: A novel authentication scheme to prevent multiple attacks in SDN-based IoT network. ,” IEEE Internet of Things Journal, vol. 7, no. (7), pp, 5745–5759, . [Google Scholar]
5X. Jiang, M. Coffee, A. Bari, J. Wang and X. Jiang. (2020), “Towards an artificial intelligence framework for data-driven prediction of coronavirus clinical severity. ,” Computers, Materials & Continua, vol. 63, no. (1), pp, 537–551, . [Google Scholar]
6J. Wang, W. B. Wu, Z. F. Liao, R. S. Sherratt, G. J. Kim et al., “A probability preferred priori offloading mechanism in mobile edge computing,” IEEE Access, vol. 8, no. 1, pp. 39758–39767, 2020. [Google Scholar]
7J. Wu, K. Leung and G. Leung. (2020), “Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. ,” Lancet, vol. 395, no. (10225), pp, 689–697, . [Google Scholar]
8Y. C. Mao, J. H. Zhang, H. Qi and L. B. Wang. (2019), “DNN-MVL: DNN-multi–view-learning–based recover block missing data in a dam safety monitoring system. ,” Sensors, vol. 2019, no. (19), pp. 2895, . [Google Scholar]
9X. Xu, P. Chen, J. Wang, J. Feng, W. Zhong. (2020). et al., “Evolution of the novel coronavirus from the ongoing Wuhan outbreak and modeling of its spike protein for risk of human transmission. ,” Science China Life Sciences, vol. 63, no. (3), pp, 457–460, . [Google Scholar]
10L. Gong, B. Yang, T. Xue, J. Chen and W. L. Wang. (2018), “Secure rational numbers equivalence test based on threshold cryptosystem with rational numbers. ,” Information Sciences, vol. 466, pp, 44–54, . [Google Scholar]
11L. Kuntz, R. Mennicken and S. Scholtes. (2014), “Stress on the ward-evidence of safety tipping points in hospitals. ,” Management Science, vol. 61, no. (4), pp, 754–771, . [Google Scholar]
12J. Berry and A. Tucker. (2016), “Past the point of speeding up: The negative effects of workload saturation on efficiency and patient severity. ,” Management Science, vol. 63, no. (4), pp, 1042–1062, . [Google Scholar]
13W. Zhao, J. Liu, H. Guo and T. Hara. (2018), “Etc-IoT: Edge-node-assisted transmitting for the cloud-centric Internet of Things. ,” IEEE Network, vol. 32, no. (3), pp, 101–107, . [Google Scholar]
14Z. Zhu, H. Hoon and T. Liang. (2012), “Estimating ICU bed capacity using discrete event simulation. ,” International Journal of Health Care Quality Assurance, vol. 25, no. (2), pp, 134–144, . [Google Scholar]
15J. Xu, Y. Zhang, L. Fu and S. Peng. (2019), “SGX-based secure indexing system. ,” IEEE Access, vol. 7, pp, 77923–77931, . [Google Scholar]
16L. Thomas, A. Schneider, P. Besselink, M. Zondefland, R. Boucherie. (2018). et al., “ Allocating emergency beds improves the emergency admission flow. ,” Interfaces, vol. 48, no. (4), pp, 384–394, . [Google Scholar]
17J. Wang, X. J. Gu, W. Liu, A. K. Sangaiah and H. J. Kim, “An empower hamilton loop based data collection algorithm with mobile agent for WSNs,” Human-centric Computing and Information Sciences, vol. 9, no. 1, pp. 1–14, 2019.
18C. Wang, X. Shao, Z. Gao, C. Zhao and J. Gao. (2019), “Common network coding condition and traffic matching supported network coding aware routing for wireless multihop network. ,” International Journal of Distributed Sensor Networks, vol. 15, no. (6), pp, 1–20, . [Google Scholar]
19Z. Li, W. Zhou and B. Liu. (2020), “Linear programming method for hospital sickbed arrangement problem. ,” Operations Research and Management Science, vol. 19, no. (6), pp, 1–5, . [Google Scholar]
20Y. Ren, Y. Liu, S. Ji, A. K. Sangaiah and J. Wang. (2018), “Incentive mechanism of data storage based on blockchain for wireless sensor networks. ,” Mobile Information Systems, vol. 2018, pp, 1–10, . [Google Scholar]
21Q. Jiang, S. Hua, Q. Han and C. Chang. (2013), “The optimal collocate model about the sickbeds of eye administration and its computer simulation. ,” Mathematics in Practice and Theory, vol. 2013, no. (2), pp, 7–13, . [Google Scholar]
22Y. Ren, Y. Len, Y. Cheng and J. Wang. (2019), “Secure data storage based on blockchain and coding in edge computing. ,” Mathematical Biosciences and Engineering, vol. 16, no. (4), pp, 1874–1892, . [Google Scholar]
23L. Xu, N. Li and Z. Zhang. (2013), “Mixed integer programming for gynecological ward bed planning. ,” Industrial Engineering and Management, vol. 13, no. (6), pp, 147–151, . [Google Scholar]
24X. H. Cao, X. S. He, W. Zhang, L. D. Li and Y. Z. Zhou. (2014). et al., “Study of adjustment strategy of licensed beds in medical institutions in Shanghai. ,” Chinese Hospital Management, vol. 14, no. (3), pp, 8–11, . [Google Scholar]
25B. An, B. Xu and G. Wang. (2016), “Optimization model of hospital bed arrangement based on nonlinear programming. ,” Statistics & Decision, vol. 36, no. (13), pp, 82–85, . [Google Scholar]
26Y. Ren, F. Zhu, P. K. Sharmr, T. Wang, J. Wang. (2020). et al., “Data query mechanism based on hash computing power of blockchain in Internet of Things. ,” Sensors, vol. 20, no. (1), pp, 207, . [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |