DOI:10.32604/cmc.2020.012255
| Computers, Materials & Continua DOI:10.32604/cmc.2020.012255 | |
| Article |
Robust Hybrid Artificial Fish Swarm Simulated Annealing Optimization Algorithm for Secured Free Scale Networks against Malicious Attacks
1Anna University, Chennai, 600025, India
2Department of ECE, C. Abdul Hakeem College of Engineering and Technology, Vellore, India
3Department of ECE, Excel Engineering College, Salem, India
*Corresponding Author: Ganeshan Keerthana. Email: gkeerthu21@gmail.com
Received: 22 June 2020; Accepted: 10 September 2020
Abstract: Due to the recent proliferation of cyber-attacks, highly robust wireless sensor networks (WSN) become a critical issue as they survive node failures. Scale-free WSN is essential because they endure random attacks effectively. But they are susceptible to malicious attacks, which mainly targets particular significant nodes. Therefore, the robustness of the network becomes important for ensuring the network security. This paper presents a Robust Hybrid Artificial Fish Swarm Simulated Annealing Optimization (RHAFS-SA) Algorithm. It is introduced for improving the robust nature of free scale networks over malicious attacks (MA) with no change in degree distribution. The proposed RHAFS-SA is an enhanced version of the Improved Artificial Fish Swarm algorithm (IAFSA) by the simulated annealing (SA) algorithm. The proposed RHAFS-SA algorithm eliminates the IAFSA from unforeseen vibration and speeds up the convergence rate. For experimentation, free scale networks are produced by the Barabási–Albert (BA) model, and real-world networks are employed for testing the outcome on both synthetic-free scale and real-world networks. The experimental results exhibited that the RHAFS-SA model is superior to other models interms of diverse aspects.
Keywords: Free scale networks; robustness; malicious attacks; fish swarm algorithm
Wireless Sensor Networks (WSN) has been applied for collecting data regarding the physical parameters in diverse application areas. As a promising technology it brings about a faster development in the area of advanced wireless telecommunication. The Internet of Things (IoT) has gained significant interest and offers advantageous to numerous real-time applications. Sensor interfacing devices are needed to detect different types of sensing data in the IoT environment. WSN plays a vital role in sensing the atmosphere and collecting the data. For sensing the ecological metrics, a massive number of sensors, like a sink and sensor nodes, have been deployed in wider regions. Such nodes tend to develop a multi-hop ad hoc network and implement desired operations based on the essential applications [1]. WSN can be installed in homes, constructions, forests, hills, and so on. The sensor network topology defines the wireless communications that take place among diverse sensors in WSN and it is based on the development of diverse network communication protocols and routing protocols [2] that is considered to be more significant in-network features, like network lifespan, power utilization, stability, and latency. With the rapid growth in cyber-attacks, improvising the efficiency of WSN has become a vital task. In this model, it mainly focuses on enhancing the robustness of the network topologies for WSN. It refers that, the main objective is to deploy a model where the connection of massive nodes is conserved after the occurrence of node failures which results from cyber attacks. The term target selection for attacks, which is of 2 types namely, the random and the MA. In the case of random attacks, an attacker randomly selects the nodes from a network topology as the required targets, while MAs involve in selecting the nodes with maximum node degrees as the targets. At this point, specific network topology and scale-free topology has been examined for WSN.
The scale-free topology comes under the tedious network hypothesis that is comprised of extensive domains of real-time applications, like the global transportation system [3], cooperation networks, social networks, as well as mobile networks [4]. For complex network theory, the small-world topology and the scale-free topology are assumed to be the 2 conventional techniques. In the case of a small-world approach, it is further classified into two types, smaller average path length, and maximum clustering coefficient. It applied to thedeveloping heterogeneous network topologies [5]. Unlike, the scale-free model can be employed in designing homogeneous network topologies; thereby it is more applicable for the WSN where the maximum number of nodes is constrained with the same communication range and bandwidth. A node degree in a scale-free topology uses a power-law definition. It is referred that, a greater number of nodes in a scale-free network has minimized degrees. Therefore, in case of random attacks, lower degree nodes are often selected. But, Li et al. [6] stated that a scale-free topology could be delicate for the MA. Therefore, improving the robustness of a scale-free topology enables the WSN to deal with MAs which has been assumed to be a more significant research.
To produce the power-law distribution of node degrees in scale-free networks, it is projected with a model named BA, under the application of 2 procedures to attain a scale-free topology. Initially, Growth: new nodes consecutively combine with the network. A newly merged node links with a previous node with a possible degree. These procedures tend to provide a maximum node connection where it receives novel connections. Hence, it is named as the “Mathew Effect”. This criterion is effectively applied to produce the power-law distribution of node degrees that is evident from Fornasier et al. [7]. Due to the reduced transmission radius of WSN, every node suffers from insufficient neighboring nodes which are unable to deploy a greater number of edge nodes. Therefore, the preferred attachment feature of the BA approach could not be directly induced in WSN. Liu et al. [8] projected a complex network method based on the heterogeneous networks applied in WSN. It is comprised with a small world as well as scale-free systems. The shortest path feature in scale-free networks has developed a comparatively effective transporation system. Zheng et al. [9] modeled 2 robust scale-free network topologies namely, the Linear Growth Evolution Model (LGEM) and the Accelerated GEM (AGEM). These topologies mainly focus on the absence or presence of nodes and the reformation of edges. Jian et al. [10] and Dandekar et al. [11] projected a novel energy-aware scale-free model based on a BA scheme, termed an energy-aware BA (EABA). Li et al. [12] applied with tunable coefficients to manage the node connection as well as the power application of a scale-free network topology. Few developers have consumed the energy management as well as the transmission operation that improves the data overhead at the time of developing an approach.
In scale-free networks, a lower count of nodes is comprised of higher degrees, where the networks are more vulnerable for MA. The whole network topology has been segmented rapidly. Hence, the major aim of this method is to boost the robustness of scale-free networks in WSN for MAs. Additionally, edge nodes are capable of solving the issues involved in this model. Several models have been presented and available in the literature. Peng et al. [13] and Xiao et al. [14] established a novel robustness feature. It is assumed with a larger connected cluster and defined as robustness by the proportion of remaining nodes from every network node, Herrmann et al. [15] implied with a hill-climbing framework that depends upon the robustness metric R, which results in making network topologies that reflects a reliable onion-like architecture by swapping the edges. But the multimodal criteria might eliminate the technique of shifting the local optimum.
Louzada et al. [16] applied a smart rewiring technique that computes the edges which have to be compared under the application of 2-fold selections. Zhou et al. [17] developed a memetic approach that belongs to a significant enhancing model to combine the global as well as the local searching to increment the robust value of scale-free networks over MA with no alteration of degree distribution. Therefore, a smart rewiring as well as a memetic technique, Mancilla et al. [18] does not assume the constraints of the transmission radius for the network nodes which is not applicable for WSN. The fragileness of scale-free networks with MA belongs to a heavy-tailed property that results in the loss of a node connectivity if a node hub has failed. Hence, the main goal of this approach is to study the way of improving the robustness of scale-free networks over MA. A solution for this issue is to include the links, however, extra links tend to improve the costs. Hence, the network robustness has to be improved over HDAs with no alteration of degree distribution in primary networks.
Wang et al. [19] deployed a simple rewiring approach that does not change the nodal degree, and network robustness could be improved slightly with reduced assortativity coefficient. Schneider et al. [20] established a novel value for robustness, that assumes the linked cluster while processing the whole attacks, and applied this value to develop a heuristic approach to reduce the MA. Using the same value, Buesser et al. [21] signified a SA model and Louzada et al. [22] presented a simple rewiring approach to resolve these problems. These techniques manifest an optimized function to enhance the network robustness against the primary networks. Therefore, these models could be incremented by applying the probability of global searches in the optimizing task. Hence, effective models are capable to perform global and local searches that are required for optimizing the network architecture. Evolutionary algorithms (EAs), is a type of stochastic global optimization evolved by biological evolution and heredity that is effectively applied in solving diverse types of complex optimization issues.
Tnag et al. [23] identified the malicious users and the unstable energy providers, the mechanism of identification and processing (MIP) for the malicious users and unstable energy providers is proposed. Xiong et al. [24] developed a robust dynamic network traffic partitioning scheme to defend against malicious attacks and the experimental results indicate that our proposed scheme outperforms the conventional ones in terms of packet distribution performance, especially the robustness against malicious attacks. Su et al. [25] deployed a simple work that describes a novel HTTP traffic flow mining approach to detect and categorize Android malware and unsafe ad library. In this paper, we exploit spatial and semantic conventional features extracted from the convolutional neural networks in continuous object tracking [26].
Kuang et al. [27] established a novel value for robustness, a novel support vector machine (SVM) model by combining the kernel principal component analysis (KPCA) with improved chaotic particle swarm optimization (ICPSO) is proposed to deal with intrusion detection. Lipschitz aggregation property and copula characteristics of t-norms and implications are discussed [28]. The robustness of rule-based fuzzy reasoning is investigated and the relationships among input perturbation, rule perturbation, and output perturbation are presented. Yu et al. [29] modelled to address the issues encountered by zeroing neural network (ZNN), by suggesting a new nonlinear activation function, a robust and fixed-time zeroing neural dynamics (RaFT-ZND) model is proposed and analyzed for the time-variant nonlinear equation (TVNE).
To achieve robustness in the network and to improve the network security, this paper introduces a new Robust Hybrid Artificial Fish Swarm Simulated Annealing Optimization (RHAFS-SA) Algorithm over malicious attacks (MA) with no change in degree distribution. The proposed RHAFS-SA is an enhanced version of the Improved Artificial Fish Swarm algorithm (IAFSA) and the SA model. The proposed RHAFS-SA algorithm discards the IAFSA from unforeseen vibration and improves the convergence value. For experimentation, free scale networks are produced by the BA and the real-world networks are employed for testing the outcomes on synthetic-free scale and real-world networks. The experimental results exhibited that the RHAFS-SA model is superior to the other models interms of diverse aspects. The remaining sections of the paper has been organized in the following order. Section 2 introduces the proposed RHAFS-SA algorithm and the experimental details are provided in Section 3. At last, the paper is concluded in Section 4.
2 The Proposed RHAFS-SA Algorithm
AFSA is said to be the current heuristic searching approach that has been evolved from the food hunting nature of fish. IAFSA is an extended version of improved exploration potential to identify the position with maximum food concentration. But, IAFSA is not assumed to be the ideal process as it provides the outcomes which have a minimum accuracy because of the unknown vibrations, in case of minimum visibility. Besides, SA is named as a global optimization model based on the annealing of solids. It is capable of finding global optimum under the application of stochastic searching methodologies. The main aim is to explore the global optimum, but it is vulnerable due to the sensitivity of the annealing schedule as well as the perturbation method. Therefore, SA is comprised of a better local stability and concatenated with alternate models such as AFSA to supply optimal simulation outcomes. In this approach, it is proposed with an alternative hybrid optimization technique that integrates the IAFSA and the SA to boost the searching efficiency and convergence of global optimum.
A network can be expressed as a graph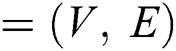 
, where 
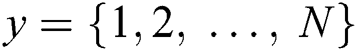denotes the collection of 
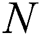nodes, and 
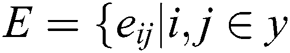and 
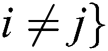implies the group of 
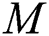links. Here, it is mainly concentrated on the desired attacks of an undirected as well as an unweighted system with a long-tailed degree distribution, such as the undirected and the unweighted scale-free networks. The targeted attacks are attentive as it is assumed to be more fragile with desired damage. Therefore, scale-free networks have been identified between significant networks in public as well as biological systems that refers to these features as more significant.
In developing the scale-free networks, the popular BA model has been employed. The BA initiates with a minimum clique of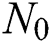 
nodes. For every iteration, a novel node has been included and the 
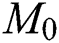is added in a link to the 
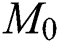of the previous nodes, where 
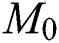represents a smaller value when compared with the number of previous nodes. If a new node has been linked to the traditional node and the possibility of the existing node selection to be proportional to a degree in which the nodes are predefined then the massive links would be selected. It is considered that the MA is HDA, and the network nodes have been sorted in a reduced degree order and a maximum degree node has been eliminated together with each link. Once the links have been removed, vertices degree undergoes revaluation and sorts the list, a few locations are modified with the attacking phase, and follows the first node until the network is isolated. Recently, the percolation theory concentrated on the largest component if there are frequent eliminations of the highest-degree vertices of a network, and projected a novel value, 
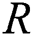, to measure the network robustness, that is represented by He et al. [30,31] as,
where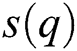 
signifies the fraction of nodes in a widely connected cluster once the removal of 
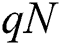nodes are completed. The normalization factor 
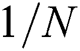assures the robustness of the networks with a diverse size. The measure of 
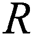comes under the range of
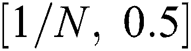. In fact, the higher value of 
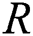is highly robust. Followed by, 
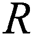has been employed as an objective function, such as the FF in EA which is applied for network optimization and it becomes more robust by resisting the MA.
2.2 Artificial Fish Swarm Algorithm (AFSA)
AFSA is a current heuristic that has been developed by searching the global optimum. It is considered to be a randomized search as well as an optimizing model assisted by the strategies of the fish swarm. It offers closer optimized solutions of the objective function. AFSA, the metrics of search space undergoes the encoding as 
. An arithmetical function has been related to every AF which calculates the degree of FF of an encoded solution. In general, inspired operators, such as prey, the swarm of iterations is to produce a capable
. AFSA is used to resolve the optimizing issues in signal processing, NN classification model as well as the tedious function optimization problems. The working function of the AFSA has outperformed with a prospective model in resolving the optimization issues. In recent times, SI and artificial life has led to the higher interests of the researchers. Tab. 1 defines the parameters applied by the AFSA technique. The nature of the AF has been defined as follows:
Table 1: Parameters definition of the AFSA algorithm
(1) Fprcy:
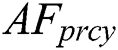is defined as a fundamental nature of food hunting. AF has to transfer to a location in water that has maximum food concentration. It is assisted by the corresponding vision. Fig. 1 depicts the vision of 
.
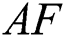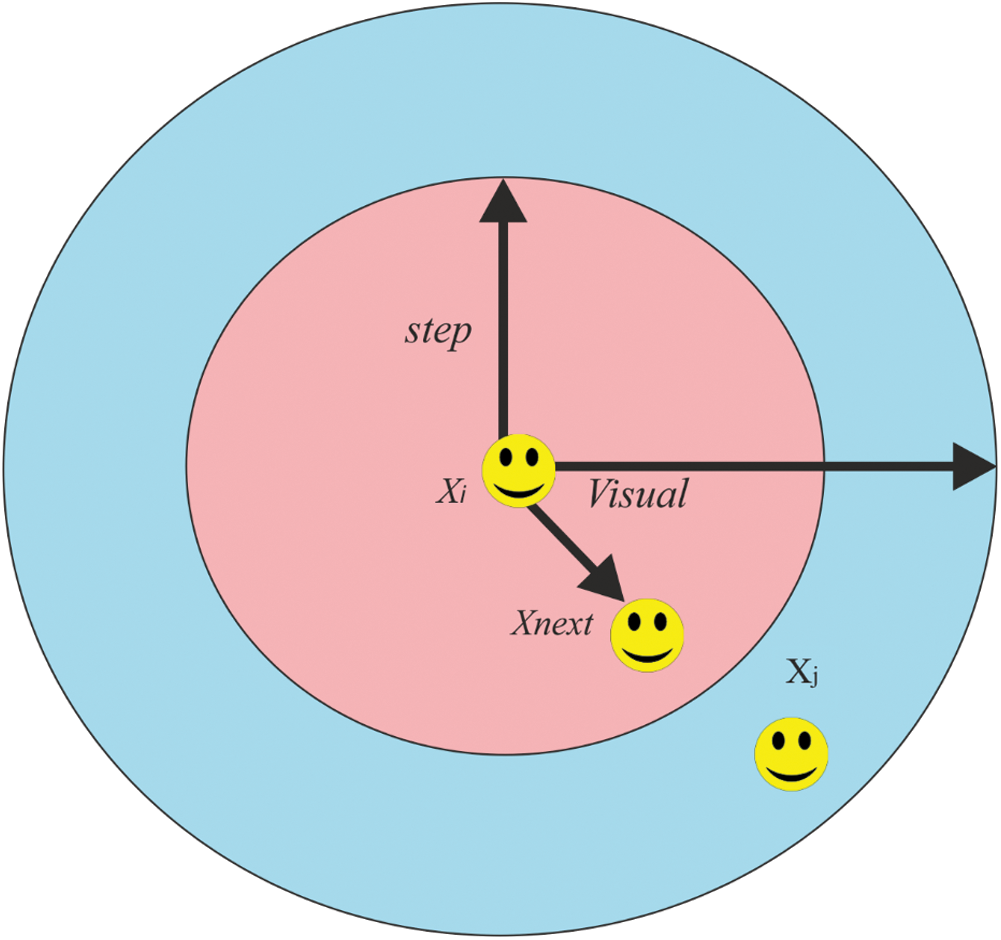
Figure 1: Vision concept of AFSA
It is considered that the recent position of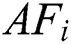 
is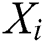 
, and the visual area of 
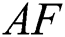, it selects the position 
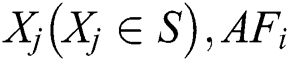swims to 
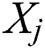in an arbitrary direction when 
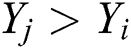. The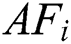 
repeats the searching from the visual area and selects an alternate position 
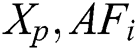would move to 
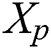in a random direction while 
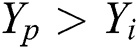. When 
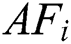cannot be effectively placed for maximum food concentration inside a visual area after try-number iterations, 
again swims in the minimum distance in a random direction. These features are randomly enabled with AF reducing from the local optimal. These functions are expressed as,
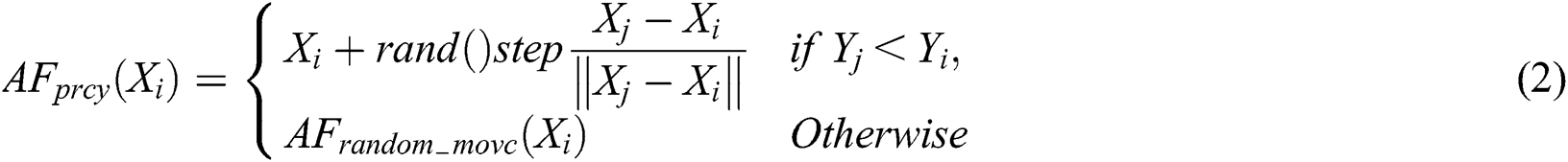
where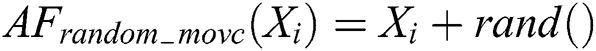 
step,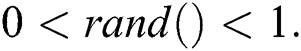 
It is pointed out that, the higher number of inspecting iterations by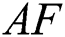 
, the maximum data regarding the entire condition of vision AF learns.
(2) AFswarm:
Fish often collects the process to hold a colony and eliminates the potential issues. When the current position of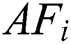 
is 
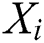, and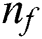 
neighbors are present within the visual area S, 
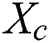denotes the neighbors, if 
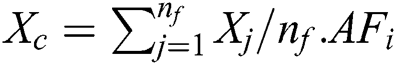swim in the 
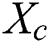direction while 
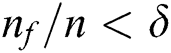and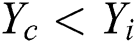 
. It refers to the process of sufficient sharing by every fish in an intermediate area. Else, 
repeats the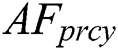 
behavior, that is shown by:
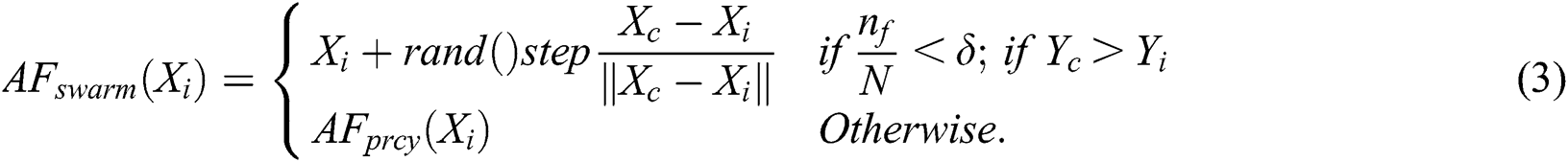
(3) AFfollow:
If a single fish identifies the food by using the moving process of the fish swarm, AFs have the movement of the following fish to obtain the optimal food-concentration position. Assume that the recent location of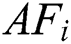 
is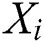 
and that it comprises of 
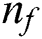neighbors inside a visual region S. 
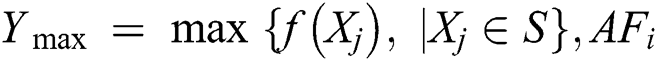would swim in a random direction to 
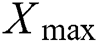in case of 
and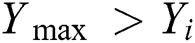 
. Else, 
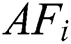resumes the 
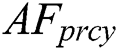behavior which is written as,
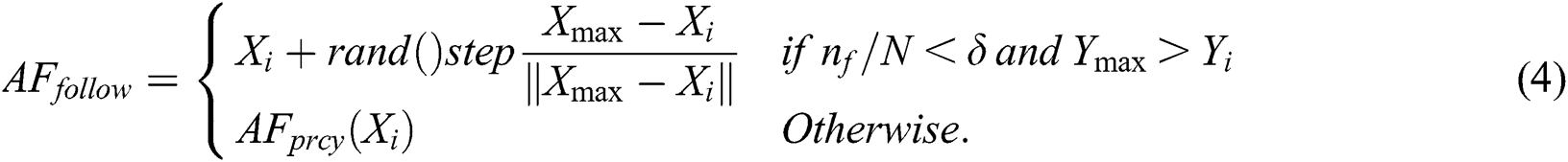
Generally, the behaviors of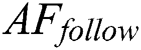 
and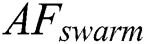 
would be accelerated after every iteration. The nature of providing AF an optimal position using food concentration can be decided. AFSA is capable of producing every selected nature of AF at the same time. It adopts a random trend of 
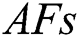, when it does not identify a maximum food concentration location that lowers the feasibility of AFs movement of local optimums.
(4) AFlcap:
The AFSA and the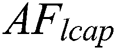 
behavior is termed as the IAFSA. The leaping behavior of AF is proposed in [31]. The preying nature, swarming and following nature are assumed to be the local behaviors. When the optimal fitness measure has not been enhanced after maximum rounds, it manifests the AF population that comes under the local optimum. The FF values are encoded in all the AF to make reliable and possibile reductions in the local optimum. To improve the likelihood in searching the global optimum, the leaping nature has been included to 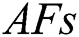the 
. The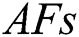 
’leaping behavior can be defined in the follows: When the measures of an objective function among the iterations are similar the variations are minimal when compared with 
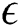which is a small positive constant while the provided iterations are selected randomly from the AFs to process the leaping behavior. 
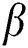implies the parameter which simulates the AF.
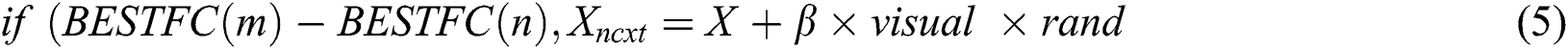
It is evident that, when the best AF present in a population has been chosen to implement the leaping behavior, immediate vibration occurs in the successive iteration task. Finally, it gradually decreases the converging speed. For increasing the convergence speed, optimized AFs could not be selected for implementing the leaping behavior.
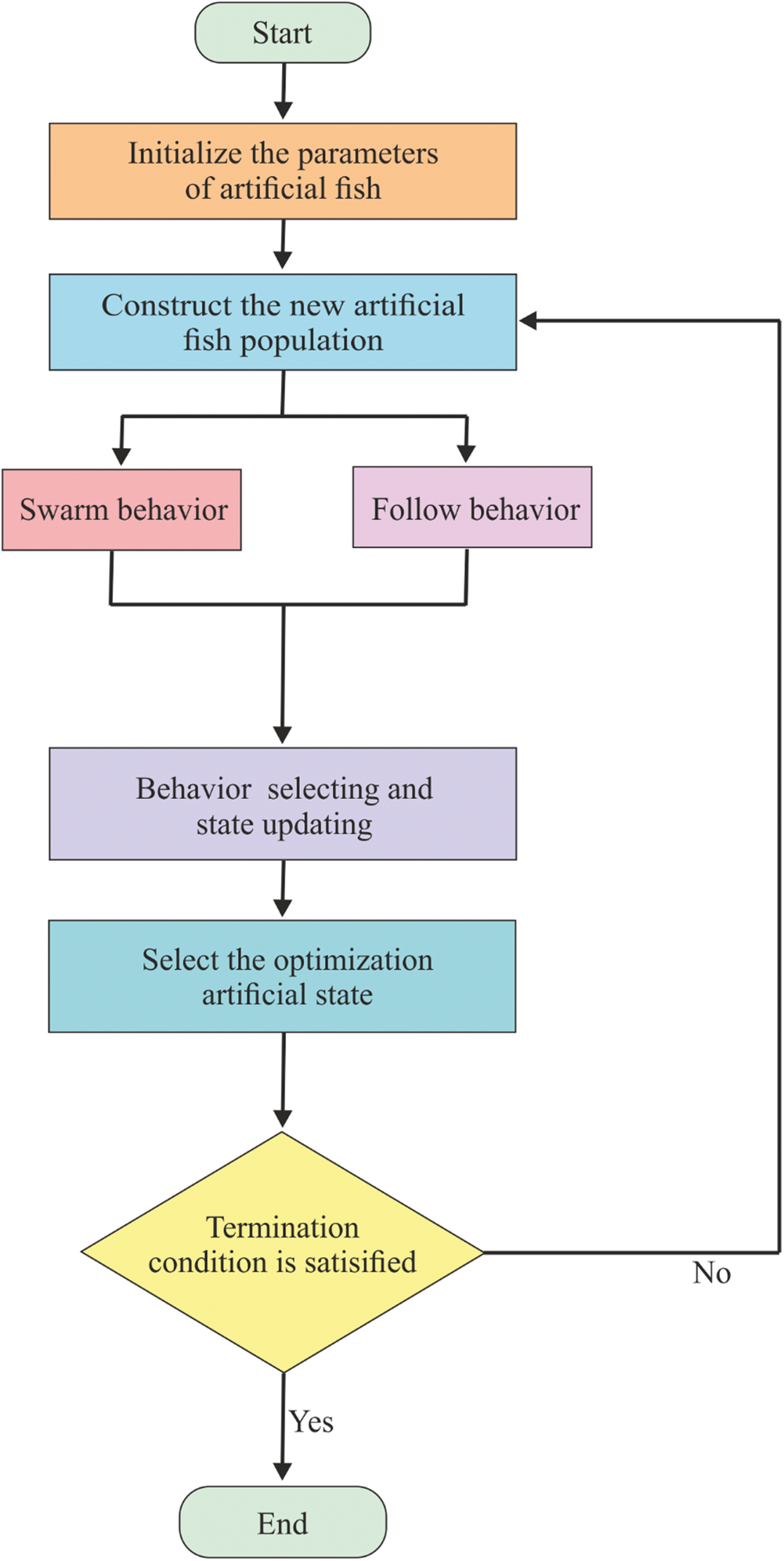
Figure 2: Flowchart of AFSA
Step 1: Compute Parameter Encoding
Describes the number of clusters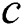 
and the vector 
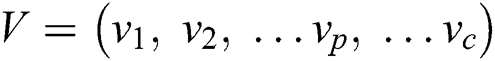showcases the centroids of the clusters; which is one among the 
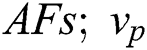is a centroid of the 
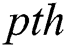cluster 
. 
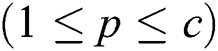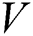is named as a vector with 
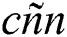dimensions. The final position of 
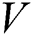is referred to as the optimal cluster centroids.
Step 2: Initialization
Load the population of AF,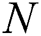 
, fuzziness exponent 
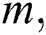termination condition, the visual distance of 
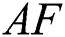, step of 
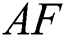, crowd factor 
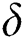and the try-number. Compute the higher iteration 
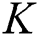for AFSA, fix the iteration value 
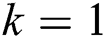and initiate the AF population:
where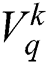 
is a location of qth AF at 
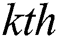iteration; 
is the population of 
Step 3: Global Search
(a) Based on the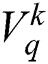 
, evaluate the MF matrix 
Implement IAFSA with the application of Eq. (1) as an objective function.
(b) Go to Step 4 if the result meets the termination condition, else,
Improve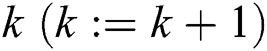 
and go back to Step 3(a).
Step 4: Local Search
(a) Identify the optimal individual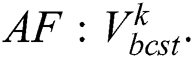 
(b) Determine the MF matrix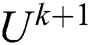 
using F-CM.
(c) Upgrade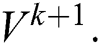 
(d) Terminate the iteration when the result meets the termination condition, else, improve 
and go back to Step 4(b).
2.3 Simulated Annealing (SA) Algorithm
The initial SA model has been presented by Metropolis et al. It has been evolved from the annealing of solids. Annealing is defined as the task of melting the solids to high temperatures by a lower cooling pattern by reducing the environmental temperature of the ecology. Here, the temperature has to be provisioned in a reliable state for a given time interval which is enough to attain the thermal equilibrium. For thermal equilibrium, it is comprised of several configurations linked with the diverse energy levels. The likelihood of a solid is to approve the modification from a recent configuration to the novel function of variations in the energy levels between 2 states. At the initial stage, a trial configuration has been attained by a randomly produced perturbation of a recent configuration. It has been considered that the Ec and the Et imply the corresponding energy levels of the present trial configurations. When Ec > Et, the trial configuration is approved to be a novel configuration. Besides, the Ec|Et, the trial configuration is named only when the positive probability is as expressed in Eq. (7).
Also, it is referred to the ad Metropolis Law. From the recent temperature T cur, it has been followed ‘Markov Length’ number of times as well as minimizes the temperature based on the annealing schedule. On the other hand, Markov Length computes the count of the trial configurations at every particular temperature. Since the temperature T is 0, the possibility of accepting a trial configuration is 0. The thermal equilibrium can be attained only with an enhanced energy level.
2.4 Hybrid Optimization Approach Based on IAFSA and SA
SA has been incorporated with the AF prey behavior. The AFs arbitrary selection of position inside the visual region and moving forward towards the direction of maximum food concentration takes place. When there is a forwarding condition that could not be satisfied once the iterations are completed, the AFs move to a distance in a random direction. The random migration behavior enables the model to eliminate the complexity in the local minimum. But, the AF seeks global optimum, without the vibration. Hence, it has to be presented with a novel hybrid model that integrates the IAFSA with the SA. The AF accepts an arbitrary position with a probability exp(-(deltaJ)/T cur), else, the AF remains in its recent position, asAs the acceptance rule has been computed by the current temperature, in the primary iterations. AF accepts the random position and exists from the local optimum. On the other hand, the value of FF is enabled to become poor inside an assertive extent in the primary events. As the temperature reduces in all iterations, the search area seeks for a neighborhood of the global optimum, and accepting the hypothesized optimal AF minimizes the irregular vibration. Finally, the reliability and convergence speed of a model can be enhanced.
This section discusses the experimental analysis of the RHAFS-SA algorithm. The proposed RHAFS-SA algorithm has been simulated using MatLab 8.1 simulation. The performance of the RHAFS-SA model has been validated under several aspects. The parameters used for simulation is shown in Tab. 2. The performance here is evaluated for a varying number of features at different circumstances. The results are compared with the existing methodologies such as the EROSE and the SPRT (L&H) interms of delay, packet delivery ratio (PDR), packet drop ratio (PDPR), residual energy, and communication overhead.
Tab. 3 and Fig. 3 show the analysis of the results of the RHAFS-SA algorithm with the existing methods interms of delay under a varying number of nodes. The table values point out that the EROSE algorithm possesses maximum delay over the RHAFS-SA algorithm and the SPRT (L&H) model. At the same time, it is noted that the SPRT (L&H) model acquires slightly better performance over the EROSE algorithm by offering lower delay. But, it does not compete with the proposed RHAFS-SA algorithm which requires a minimum amount of delay over the earlier models on all the varying numbers of nodes.
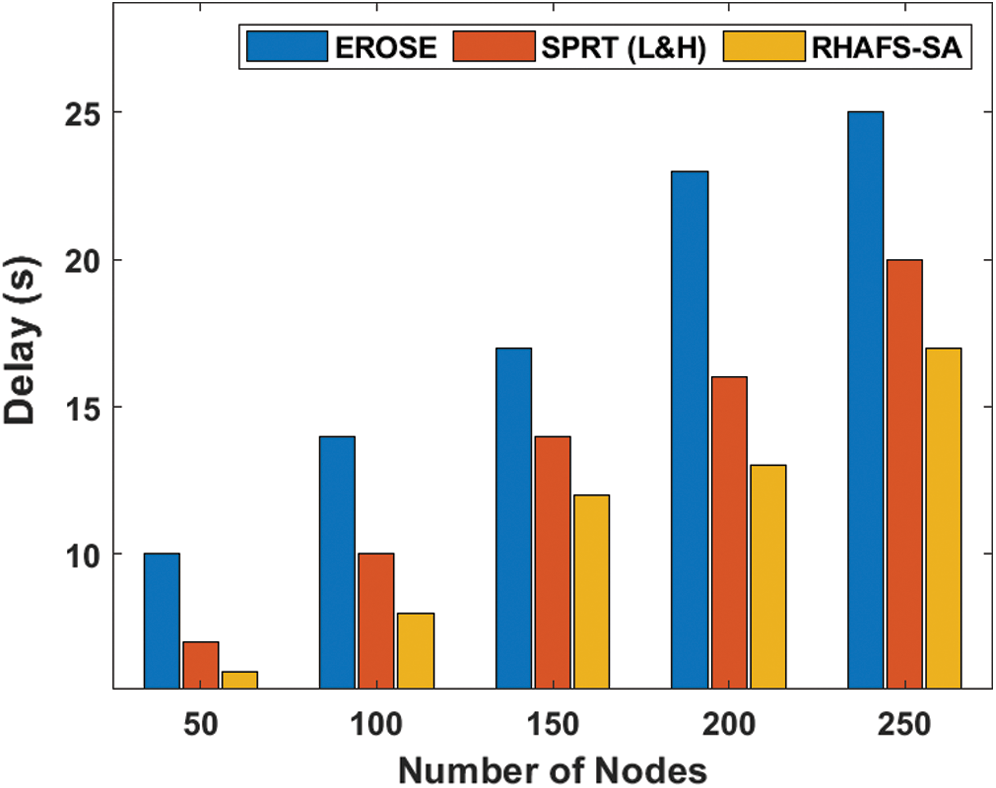
Figure 3: Delay analysis under varying node count
Table 3: Result analysis of delay (Sec) with existing and proposed method
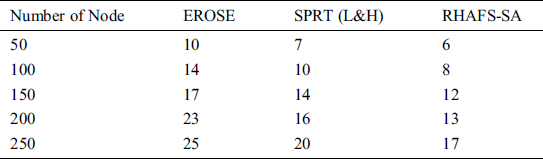
Tab. 4 and Fig. 4 portray the results of the RHAFS-SA algorithm with the existing models interms of the PDR under a varying node count. From Fig. 4, it is exhibited that the RHAFS-SA algorithm has demonstrated superior performance over the EROSE and the SPRT (L&H) models by attaining maximum PDR. At the same time, it is observed that the SPRT (L&H) model has provided slightly lower performance by achieving lower PDR over the RHAFS-SA algorithm. In the same way, the ineffective performance of the EROSR model has been ensured from the minimal PDR under a varying node count. The maximum value of the PDR offered by the RHAFS-SA algorithm shows its superiority over the existing methods.
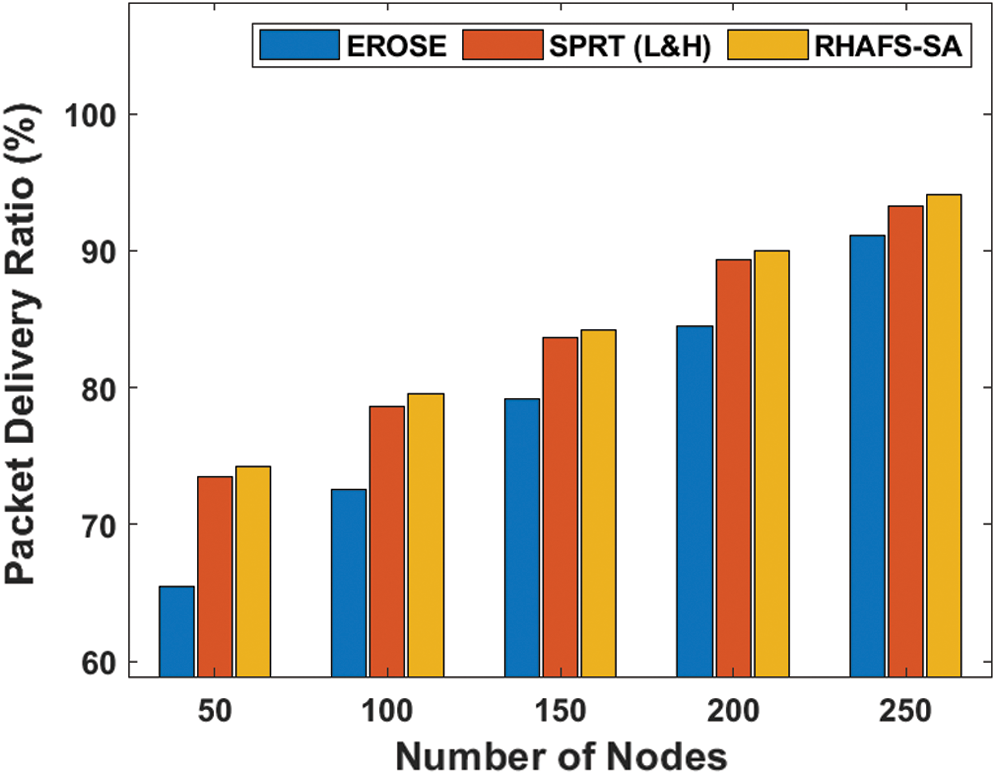
Figure 4: PDR analysis under varying node count
Table 4: Result analysis of packet delivery ratio (%) with existing and proposed method
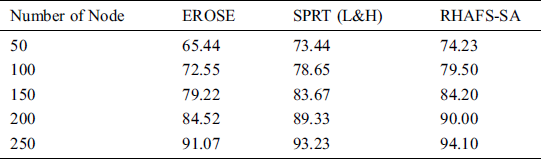
A detailed PDPR analysis is made between the RHAFS-SA algorithm and the existing methods as shown in Fig. 5 and Tab. 5. The table values denoted that the RHAFS-SA algorithm performs well and offers a minimum PDPR. Concurrently, it is denoted that the SPRT (L&H) model has shown slightly lower performance over the proposed method and offered a moderate PDPR. Simultaneously, it is demonstrated that the EROSE model has achieved a maximum PDPR indicating the ineffectiveness of transmitting data packets successfully.
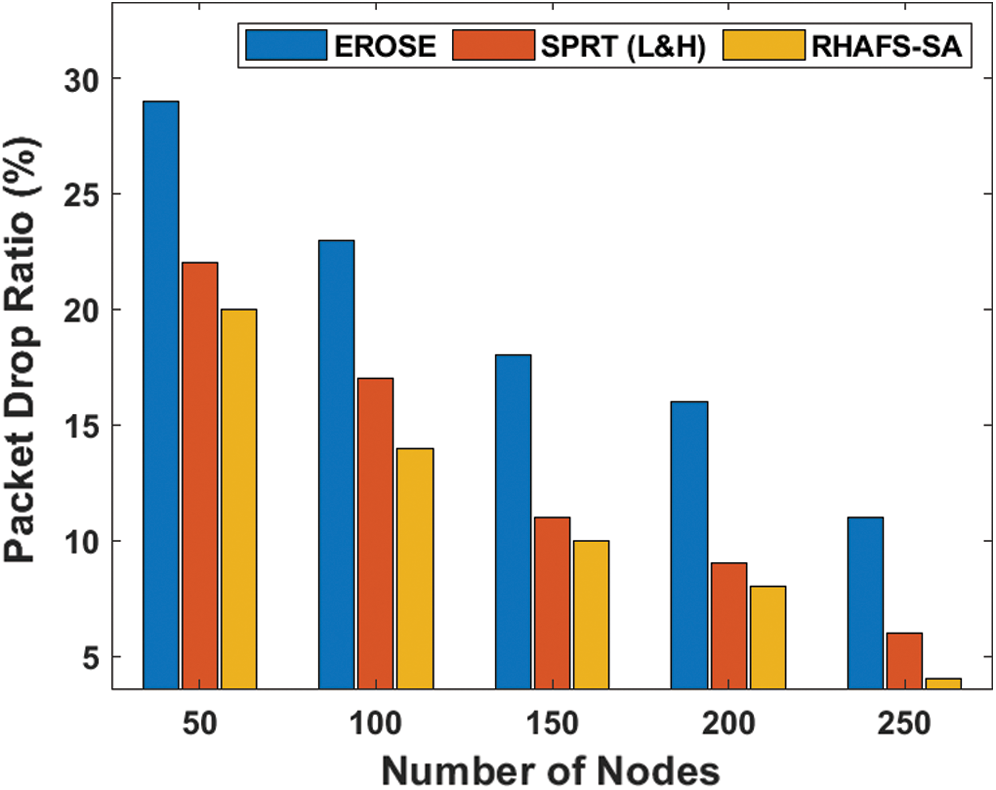
Figure 5: PDRP analysis of diverse models
Table 5: Result analysis of PDRP (%) with existing and proposed method
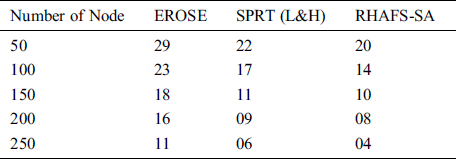
Tab. 6 and Fig. 6 investigate the residual energy analysis of the RHAFS-SA algorithm with the existing methods under a varying number of nodes. The experimental results indicate that the EROSE model has consumed more amount of energy over the compared methods and leads to a lower residual energy indicating energy dissipation at a faster rate. At the same time, it is noticed that the SPRT (L&H) model has achieved better energy efficiency over the EROSE by offering a moderate residual energy. Furthermore, it is observed that the RHAFS-SA algorithm has resulted in maximum energy efficiency by providing higher residual energy over the compared methods.
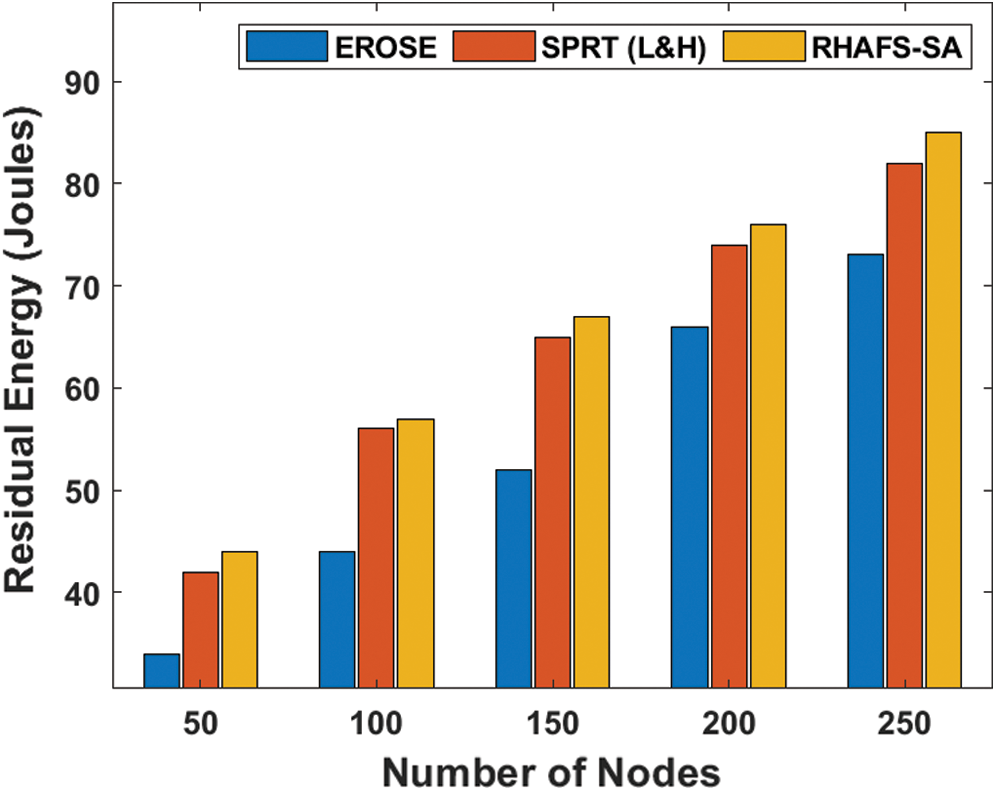
Figure 6: Residual energy analysis under a varying number of nodes
Table 6: Result analysis of residual energy (Joules) with existing and proposed method
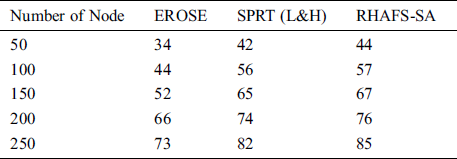
An extensive communication overhead analysis takes place between the RHAFS-SA algorithm and the compared methods under a varying numbers of nodes as given in Tab. 7 and Fig. 7. The EROSE model has acquired a maximum communication overhead indicating its ineffective performance under the all nodes count. In line with, it is noted that the SPRT (L&H) model has burdened with a moderate amount of communication overhead, which is lower than the EROSE, but not the proposed RHAFS-SA algorithm.
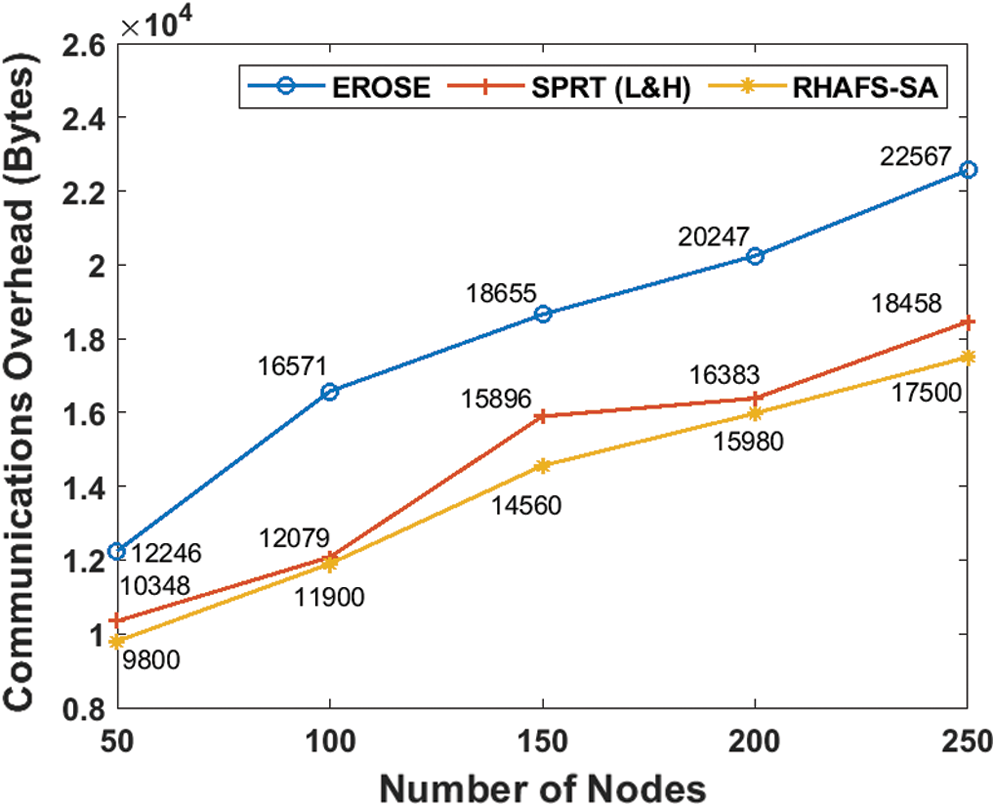
Figure 7: Communication overhead analysis
Table 7: Result analysis of communications overhead (bytes) with existing and proposed method
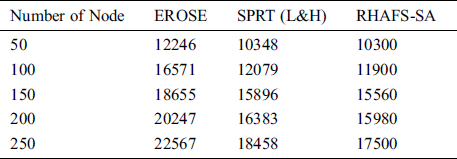
At last, it is depicted that an effective performance is exhibited by the RHAFS-SA algorithm by attaining a minimal communication overhead under all the applied scenarios. By looking into the above-mentioned tables and figures, it is ensured that the RHAFS-SA algorithm has offered superior performance over the existing methods interms of delay, PDR, PDPR, residual energy and communication overhead.
This paper has presented an effective RHAFS-SA Algorithm over the MA for the free scale networks with no change in degree distribution. The proposed RHAFS-SA is a hybridization of the IAFSA and the SA algorithms. The presented RHAFS-SA system discards the IAFSA from the unforeseen vibration and speeds up the convergence rate. For experimentation, free scale networks are produced by the BA model as well as the real-time networks are employed for testing the outcome on synthetic-free scale and real-world networks. The experimental results exhibited that, the RHAFS-SA model is superior to other models interms of diverse aspects such as delay, PDR, PDPR, residual energy, and communication overhead. In the future, the performance of the proposed model can be enhanced by the use of deep learning models.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1P. Eugster, V. Sundaram and X. Zhang. (2015), “Debugging the Internet of Things: The case of wireless sensor networks. ,” IEEE Software, vol. 32, no. (1), pp, 38–49, .
2Z. Li and H. Shen. (2014), “A QoS-oriented distributed routing protocol for hybrid wireless networks. ,” IEEE Transactions on Mobile Computing, vol. 13, no. (3), pp, 693–708, . [Google Scholar]
3A. Háznagy, I. Fi, A. London and T. Nemeth. (2015), “Complex network analysis of public transportation networks: A comprehensive study. ,” in Proc. of Int. Conf. on Models Technology in Intelligent Transport System (MT-ITS), Budapest, Hungary: , pp, 371–378, . [Google Scholar]
4X. Xia, X. Wang, W. Wei and X. Zhou. (2013), “Measuring the mobile app market: A complex network approach. ,” Information Technology Journal, vol. 12, no. (11), pp, 2090–2100, . [Google Scholar]
5S. Singh and J. G. Andrews. (2014), “Joint resource partitioning and offloading in heterogeneous cellular networks. ,” IEEE Transaction on Wireless Communication, vol. 13, no. (2), pp, 888–901, . [Google Scholar]
6R. H. Li, J. X. Yu, X. Huang, H. Cheng and Z. Shang. (2012), “Measuring robustness of complex networks under MVC attack. ,” in Proc. of the 21st ACM Int. Conf. on Information Knowledge Management, New York, NY, USA: , pp, 1512–1516, . [Google Scholar]
7M. Fornasier and F. Solombrino. (2014), “Mean-Field optimal control, ESAIM: Control. ,” Optimisation and Calculus of Variations, vol. 20, no. (4), pp, 1123–1152, . [Google Scholar]
8L. Liu, X. Qi, J. Xue and M. Xie. (2014), “A topology construct and control model with small-world and scale-free concepts for heterogeneous sensor networks. ,” International Journal of Distributed Sensor Networks, vol. 10, no. (3), pp, 1–8, . [Google Scholar]
9G. Zheng, S. Liu and X. Qi. (2012), “Scale-free topology evolution for wireless sensor networks with reconstruction mechanism. ,” Computers & Electrical Engineering, vol. 38, no. (3), pp, 643–651, . [Google Scholar]
10Y. Jian, E. Liu, Y. Wang, Z. Zhang and C. Lin. (2013), “Scale-free model for wireless sensor networks. ,” in Proc. of the IEEE Wireless Communication Networks Conf., Shanghai, China: , pp, 2329–2332, . [Google Scholar]
11D. R. Dandekar and P. R. Deshmukh. (2013), “Energy balancing multiple sink optimal deployment in multi-hop wireless sensor networks. ,” Proc. of the 3rd Int. Advance Computing Conf., Ghaziabad, India, pp, 408–412, . [Google Scholar]
12H. J. Li, Z. Bu, Z. Wang, J. Cao and Y. Shi. (2018), “Enhance the performance of network computation by a tunable weighting strategy. ,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 2, no. (3), pp, 214–223, . [Google Scholar]
13H. Peng, S. Si, M. K. Awad, N. Zhang, H. Zhao et al. (2016). , “Toward energy-efficient and robust large-scale WSNs: A scale-free network approach. ,” IEEE Journal on Selected Areas in Communications, vol. 34, no. (12), pp, 4035–4047, . [Google Scholar]
14Y. D. Xiao, S. Y. Lao, L. Hou and L. Bai. (2015), “Mitigation of malicious attacks on network observation. ,” International Journal of Modern Physics, vol. 26, no. (10), 1550108, . [Google Scholar]
15H. J. Herrmann, C. M. Schneider, A. A. Moreira, J. S. Andrade Jr. and S. Havlin. (2011), “Onion-like network topology enhances robustness against malicious attacks. ,” Journal of Statistical Mechanics: Theory and Experiment, vol. 20, no. (1), pp, 1–9, . [Google Scholar]
16V. H. P. Louzada, F. Daolio, H. J. Herrmann and M. Tomassini. (2013), “Smart rewiring for network robustness. ,” Journal Complex Networks, vol. 1, no. (2), pp, 150–159, . [Google Scholar]
17M. Zhou and J. Liu. (2014), “A memeticalgorithm for enhancing the robustness of scale-free networks against malicious attacks. ,” Physica A: Statistical Mechanics and Its Applications, vol. 410, pp, 131–143, . [Google Scholar]
18M. C. Mancilla, J. G. O. Cabrera, E. L. Mellado and A. M. Vazquez. (2013), “Design and implementation of a robust wireless sensor network. ,” in Proc. of the 23rd Int. Conf. on Electronics, Communications and Computing, Cholula, Mexico: , pp, 230–235, . [Google Scholar]
19S. Wang and J. Liu. (2019), “Designing comprehensively robust networks against intentional attacks and cascading failures. ,” Information Science, vol. 478, pp, 125–140, . [Google Scholar]
20C. M. Schneider, A. A. Moreira, J. S. Andrade Jr., S. Havlin and H. J. Herrmann. (2011), “Mitigation of malicious attacks on networks. ,” Proceedings of National Academy Science, vol. 108, no. (10), pp, 3838–3841, . [Google Scholar]
21P. Buesser, F. Daolio and M. Tomassini. (2011), “Optimizing the robustness of scale-free networks with simulated annealing. ,” in Proc. of the 10th Int. Conf. on Adaptive Natural Computing Algorithms, Ljubljana, Slovenia: , pp, 167–176, . [Google Scholar]
22V. H. P. Louzada, F. Daolio, H. J. Herrmann and M. Tomassini. (2013), “Smart rewiring for network robustness. ,” Journal of Complex Networks, vol. 1, pp, 150–159, . [Google Scholar]
23Q. Tang, K. Yang, D. Zhou, Y. Luo and F. Yu. (2015), “A real-time dynamic pricing algorithm for smart grid with unstable energy providers and malicious users. ,” IEEE Internet of Things Journal, vol. 3, no. (4), pp, 554–562, . [Google Scholar]
24B. Xiong, K. Yang, J. Y. Zhao and K. Q. Li. (2017), “Robust dynamic network traffic partitioning against malicious attacks. ,” Journal of Network and Computer Applications, vol. 87, pp, 20–31, . [Google Scholar]
25X. Su, X. C. Liu, J. C. Lin, S. M. He, Z. J. Fu et al. (2017). , “De-cloaking malicious activities in smartphones using HTTP flow mining. ,” KSII Transactions on Internet and Information Systems, vol. 11, no. (6), pp, 3230–3253, . [Google Scholar]
26J. M. Zhang, X. K. Jin, J. Sun, J. Wang and A. K. Sangaiah. (2018), “Spatial and semantic convolutional features for robust visual object tracking. ,” Multimedia Tools and Applications, vol. 79, no. (21–22), pp, 15095–15115, . [Google Scholar]
27F. J. Kuang, S. Y. Zhang, Z. Jin and W. H. Xu. (2015), “A novel SVM by combining kernel principal component analysis and improved chaotic particle swarm optimization for intrusion detection. ,” Soft Computing, vol. 19, no. (5), pp, 1187–1199, . [Google Scholar]
28F. Chen, W. H. Xu, C. Z. Bai and X. M. Gao. (2016), “A novel approach to guarantee good robustness of fuzzy reasoning. ,” Applied Soft Computing, vol. 41, pp, 224–234, . [Google Scholar]
29F. Yu, L. Liu, L. Xiao, K. L. Li and S. Cai. (2019), “A robust and fixed-time zeroing neural dynamics for computing time-variant nonlinear equation using a novel nonlinear activation function. ,” Neurocomputing, vol. 350, pp, 108–116, . [Google Scholar]
30S. He, N. Belacel, A. Chan, H. Hamamand and Y. Bouslimani. (2016), “A hybrid artificial fish swarm simulated annealing optimization algorithm for automatic identification of clusters. ,” International Journal of Information Technology & Decision Making, vol. 15, no. (5), pp, 949–974, . [Google Scholar]
31S. Wang and J. Liu. (2019), “Community robustness and its enhancement in interdependent networks. ,” Applied Soft Computing, vol. 77, pp, 665–677, . [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |