DOI:10.32604/cmc.2020.012610

| Computers, Materials & Continua DOI:10.32604/cmc.2020.012610 |  |
| Article |
An Iterative Scheme of Arbitrary Odd Order and Its Basins of Attraction for Nonlinear Systems
Department of Mathematical Sciences,Universiti Kebangsaan Malaysia, Bangi Selangor, 43600, Malaysia
*Corresponding Author: Ishak Hashim. Email: ishak_h@ukm.edu.my
Received: 06 July 2020; Accepted: 02 August 2020
Abstract: In this paper, we propose a fifth-order scheme for solving systems of nonlinear equations. The convergence analysis of the proposed technique is discussed. The proposed method is generalized and extended to be of any odd order of the form 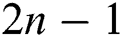 . The scheme is composed of three steps, of which the first two steps are based on the two-step Homeier’s method with cubic convergence, and the last is a Newton step with an appropriate approximation for the derivative. Every iteration of the presented method requires the evaluation of two functions, two Fréchet derivatives, and three matrix inversions. A comparison between the efficiency index and the computational efficiency index of the presented scheme with existing methods is performed. The basins of attraction of the proposed scheme illustrated and compared to other schemes of the same order. Different test problems including large systems of equations are considered to compare the performance of the proposed method according to other methods of the same order. As an application, we apply the new scheme to some real-life problems, including the mixed Hammerstein integral equation and Burgers’ equation. Comparisons and examples show that the presented method is efficient and comparable to the existing techniques of the same order.
. The scheme is composed of three steps, of which the first two steps are based on the two-step Homeier’s method with cubic convergence, and the last is a Newton step with an appropriate approximation for the derivative. Every iteration of the presented method requires the evaluation of two functions, two Fréchet derivatives, and three matrix inversions. A comparison between the efficiency index and the computational efficiency index of the presented scheme with existing methods is performed. The basins of attraction of the proposed scheme illustrated and compared to other schemes of the same order. Different test problems including large systems of equations are considered to compare the performance of the proposed method according to other methods of the same order. As an application, we apply the new scheme to some real-life problems, including the mixed Hammerstein integral equation and Burgers’ equation. Comparisons and examples show that the presented method is efficient and comparable to the existing techniques of the same order.
Keywords: System of nonlinear equations; root finding method; iterative method; order of convergence; Burgers’ equation
One popular research area in mathematics is to find the solution 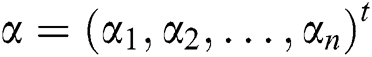 of the system of nonlinear equation
of the system of nonlinear equation 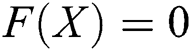 , where
, where 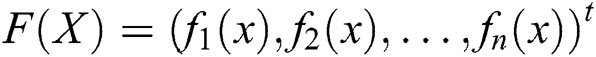 , and
, and 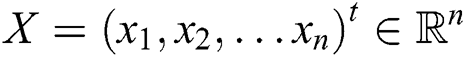 . This type of problems occurs in many applied sciences like engineering, physics, biology and chemistry. Many researchers developed iterative methods for solving this kind of systems using different techniques. The most popular iterative method for solving system of nonlinear equations is the well-known Newton’s method which has second order of convergence [1]. To improve the order of convergence and increase the accuracy of the solution obtained, many researchers tried to improve Newton’s method. Some authors used different forms and modifications based on Adomian decomposition technique for solving systems of nonlinear equations, see for instance [2–6]. Another way to improve some schemes for systems of nonlinear equation is by using homotopy analysis method and homotopy perturbation method, see for example [7,8]. Grau-Sánchez et al. [9] used the harmonic mean of the derivative to improve an iterative scheme for solving systems of nonlinear equations. By applying some quadrature formulas, some researchers implement their techniques to solve systems of nonlinear equations, for instance [10–12]. Also, some derivative-free schemes for systems of nonlinear equations were proposed, see for example [13–15] and the references therein. One of the well-known modifications of Newton method is Jarratt method of order four. Cordero et al. [16] extended Jarratt method to solve systems of nonlinear equations preserving the same order of convergence. Many variants of Jarratt type methods have been developed, see for example [17–19] and the references therein. Many other different orders of convergence schemes for nonlinear modules can be found in the literature, see for example [20,21] and the references therein.
. This type of problems occurs in many applied sciences like engineering, physics, biology and chemistry. Many researchers developed iterative methods for solving this kind of systems using different techniques. The most popular iterative method for solving system of nonlinear equations is the well-known Newton’s method which has second order of convergence [1]. To improve the order of convergence and increase the accuracy of the solution obtained, many researchers tried to improve Newton’s method. Some authors used different forms and modifications based on Adomian decomposition technique for solving systems of nonlinear equations, see for instance [2–6]. Another way to improve some schemes for systems of nonlinear equation is by using homotopy analysis method and homotopy perturbation method, see for example [7,8]. Grau-Sánchez et al. [9] used the harmonic mean of the derivative to improve an iterative scheme for solving systems of nonlinear equations. By applying some quadrature formulas, some researchers implement their techniques to solve systems of nonlinear equations, for instance [10–12]. Also, some derivative-free schemes for systems of nonlinear equations were proposed, see for example [13–15] and the references therein. One of the well-known modifications of Newton method is Jarratt method of order four. Cordero et al. [16] extended Jarratt method to solve systems of nonlinear equations preserving the same order of convergence. Many variants of Jarratt type methods have been developed, see for example [17–19] and the references therein. Many other different orders of convergence schemes for nonlinear modules can be found in the literature, see for example [20,21] and the references therein.
Some techniques to improve the order of convergence of the iterative schemes for systems of nonlinear equations have been proposed, for instance, see [22,23]. In general, obtaining a higher-order iterative method is not the only important thing; as the computational and the time cost are crucial issue also. So, establishing a high order iterative method based on low computational and time cost is very important.
In this paper, we develop a new multi-step scheme of arbitrary odd order for nonlinear equations. The proposed method can be used in the multidimensional case preserving the same order. The convergence analysis of the new scheme is discussed. Several examples are given to show the efficiency of the generalized method and its comparison with other iterative schemes of the same order. To confirm the applicability of the new technique, we apply the new technique to some real-life problems.
In this section we will derive the proposed technique for nonlinear modules. We begin by writing the function 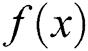 as:
as:
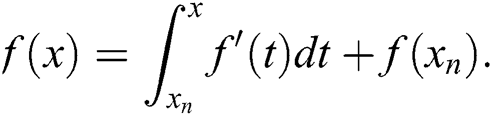
As we want 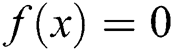 , and by using midpoint quadrature formula and writing the equation as an iterative scheme, one gets
, and by using midpoint quadrature formula and writing the equation as an iterative scheme, one gets
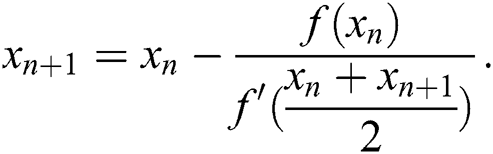
Now, to write the iterative scheme (2) in explicit form, replace 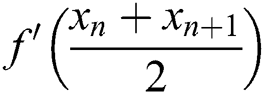 by
by 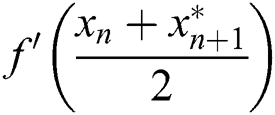 where
where 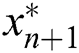 is the Newton step. So, scheme (2) becomes:
is the Newton step. So, scheme (2) becomes:
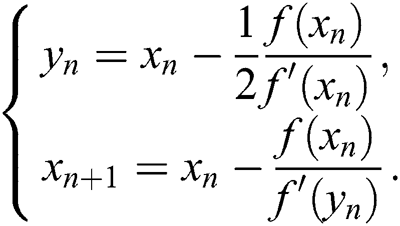
The iterative method (3) was proposed by Frontini and Sormani [10]. The multidimensional case of scheme (3) was discussed by Homeier [24] and can be written as:
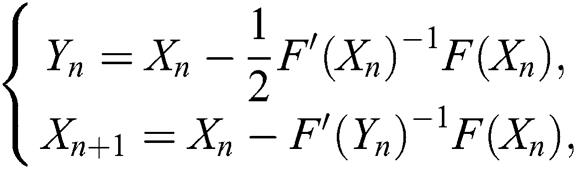
where 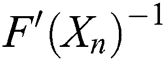 and
and 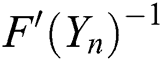 are the inverse of the first Fréchet derivative of
are the inverse of the first Fréchet derivative of 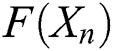 and
and 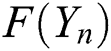 respectively. Scheme (4) is of third-order of convergence, and requires at each iteration the evaluation of one function, two Fréchet derivatives and two matrix inversions. In order to increase the convergence order and the computational efficiency of scheme (4) Sharma et al. [20] proposed a new scheme of the fifth-order of convergence by adding one step to scheme (4):
respectively. Scheme (4) is of third-order of convergence, and requires at each iteration the evaluation of one function, two Fréchet derivatives and two matrix inversions. In order to increase the convergence order and the computational efficiency of scheme (4) Sharma et al. [20] proposed a new scheme of the fifth-order of convergence by adding one step to scheme (4):
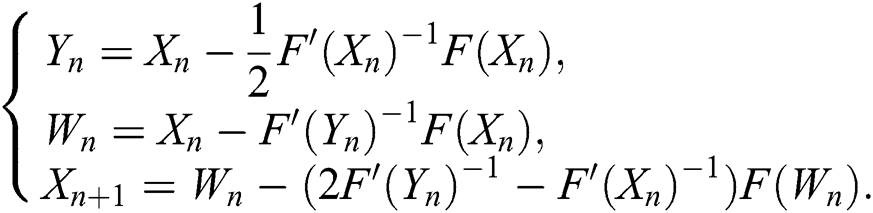
Per iteration, scheme (5) requires the evaluations of two functions, two Fréchet derivatives and two matrix inversions.
Now, to derive the new scheme for solving systems of nonlinear equations, we start by composing scheme (3) to additional Newton step, that is:
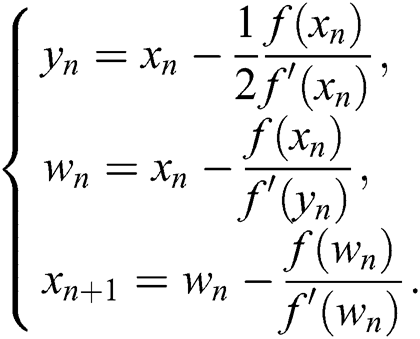
Now, to reduce number of functional evaluations at each iteration, we will use divided difference approximation to write the derivative 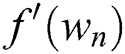 using some already computed functions from the previous steps. To do that, one can write
using some already computed functions from the previous steps. To do that, one can write
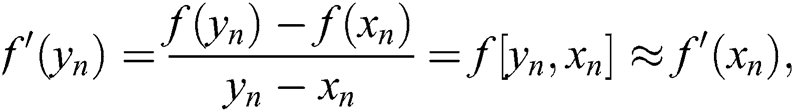
in the same manner, we have
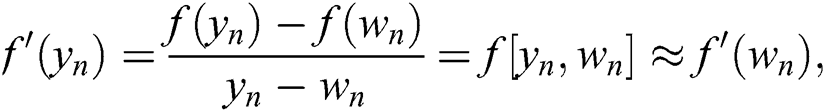
by adding (7) and (8), one easily can conclude that
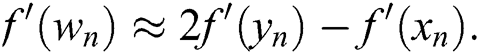
Now, if we substitute (9) in (6), then we will have a new scheme for solving nonlinear equations:
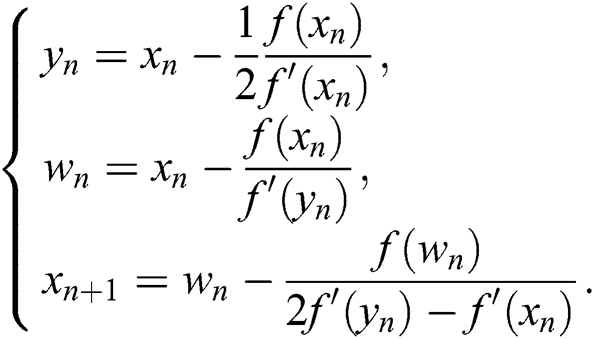
To generalize scheme (10) to the multidimensional case to solve systems of nonlinear modules, the scheme becomes:
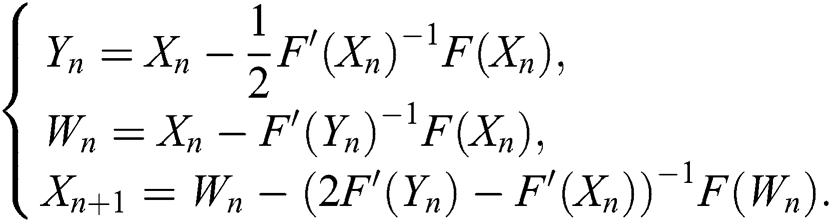
Scheme (11) requires at each iteration the evaluation of two functions, two Fréchet derivatives and three matrix inversions. The proposed scheme is of fifth-order of convergence as we will see in the next section.
If we repeat using the same idea of the derivation of scheme (11), we can write a general scheme for solving system of nonlinear equations, and this is the main motivation of our work. The general scheme can be written as:
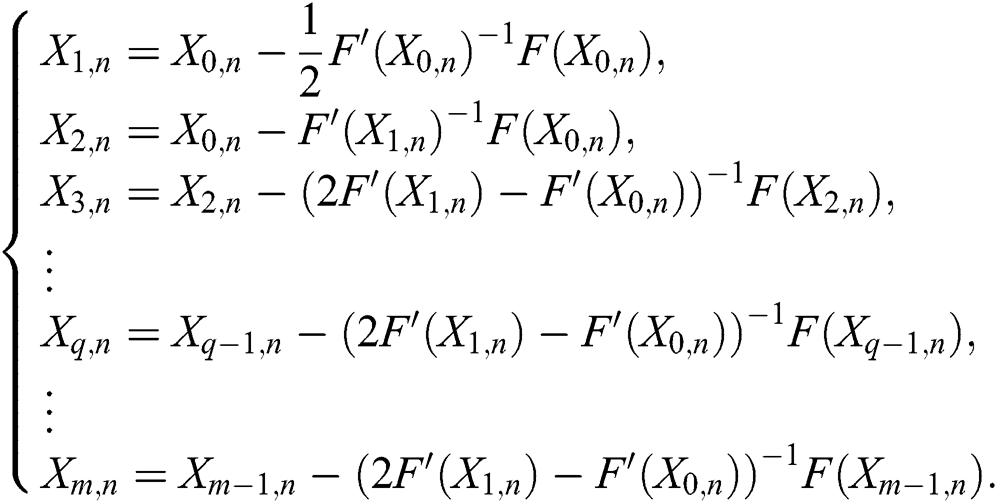
Per iteration, scheme (12) requires the evaluation of 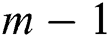 functions, two Fréchet derivatives and three matrix inversions. We will prove in the next section that scheme (12) is of order
functions, two Fréchet derivatives and three matrix inversions. We will prove in the next section that scheme (12) is of order 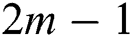 for any integer
for any integer 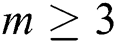 .
.
We will discuss in this section the order of convergence of the proposed schemes (11) and (12). Assume for the next theorems that 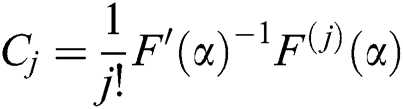 ,
, 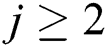 , and
, and 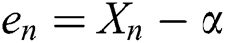 .
.
Theorem 1 Let 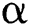 be the solution of the system
be the solution of the system 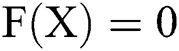 where
where 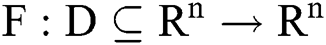 be a sufficiently differentiable function on a neighborhood
be a sufficiently differentiable function on a neighborhood 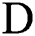 of
of 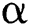 . Suppose that
. Suppose that 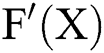 is continuous and nonsingular in
is continuous and nonsingular in 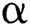 . If
. If 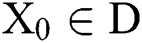 is an initial approximation which is close enough to
is an initial approximation which is close enough to 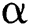 , then the sequence
, then the sequence 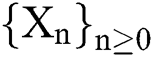 obtained by scheme (11) converges to the root
obtained by scheme (11) converges to the root 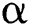 , and the order of convergence equals
, and the order of convergence equals 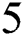 , with asymptotic equation
, with asymptotic equation 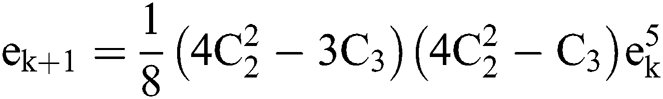 .
.
Proof. By using the Taylor expansion of  we can write
we can write 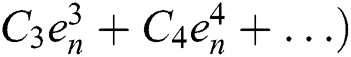 . Now, we use the following Mathematica code to show the convergence order of scheme (11) for
. Now, we use the following Mathematica code to show the convergence order of scheme (11) for 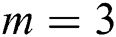 :
:
In[1]:= F[e_]:= 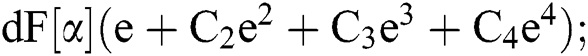
In[2]:= 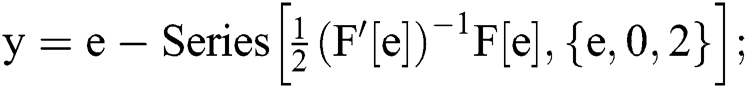
In[3]:= 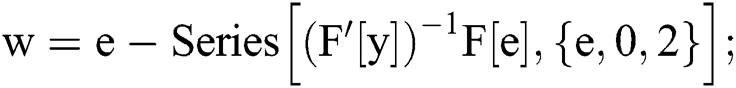
In[4]:= 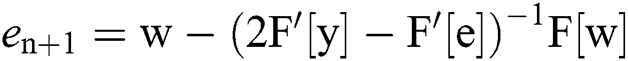 //FullSimplify
//FullSimplify
Out[4]:= 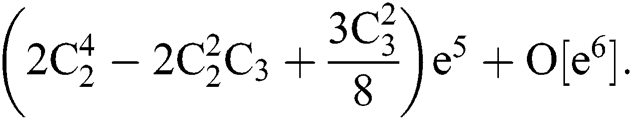
the code shows that we have 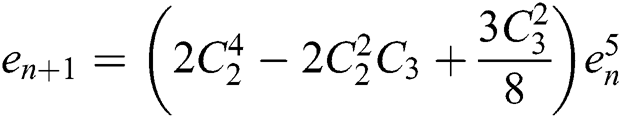 , which can be written as:
, which can be written as:
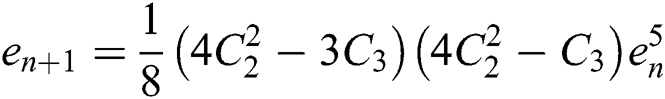 .
.
By this, we show that scheme (11) is at least of fifth-order of convergence.
Now, we want to discuss the order of convergence of the generalized scheme given by (12).
Theorem 2 Let 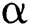 be the solution of the system
be the solution of the system 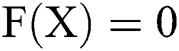 where
where 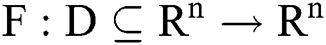 be a sufficiently differentiable function on a neighborhood
be a sufficiently differentiable function on a neighborhood 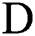 of
of 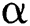 . Suppose that
. Suppose that 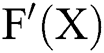 is continuous and nonsingular in
is continuous and nonsingular in 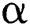 . If
. If 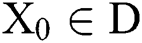 is an initial approximation which is close enough to
is an initial approximation which is close enough to 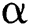 , then the sequence
, then the sequence 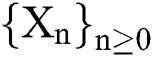 obtained by scheme (12) converges to the root
obtained by scheme (12) converges to the root 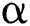 , and the order of convergence equals
, and the order of convergence equals 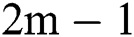 , for any integer
, for any integer 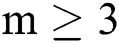 , with asymptotic equation of the form
, with asymptotic equation of the form 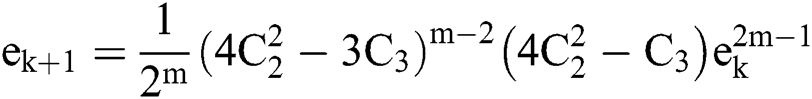 .
.
Proof. We will use the mathematical induction to prove the convergence order of scheme (12).
Firstly, we will prove that scheme (12) is convergent for 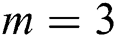 , and the convergence order satisfies
, and the convergence order satisfies 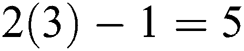 . Note that for
. Note that for 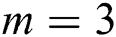 , scheme (12) reduces to scheme (11) which we have been proved that it has the fifth-order of convergence in the previous theorem. Now, to complete the proof using the mathematical induction, suppose that scheme (12) is true and converges for all
, scheme (12) reduces to scheme (11) which we have been proved that it has the fifth-order of convergence in the previous theorem. Now, to complete the proof using the mathematical induction, suppose that scheme (12) is true and converges for all 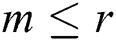 for some positive
for some positive 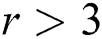 and satisfy the given asymptotic equation. We need to show that the scheme converges for
and satisfy the given asymptotic equation. We need to show that the scheme converges for 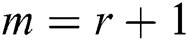 , and satisfy the given asymptotic equation. To do so, consider the following code of Mathematica:
, and satisfy the given asymptotic equation. To do so, consider the following code of Mathematica:
In[1]:= F[e_]:= 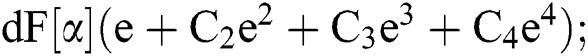
In[2]:= 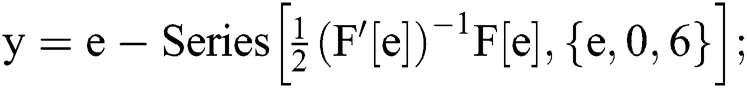

In[3]:= 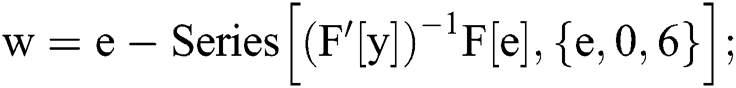
In[4]:= x[m_]:=x[m] 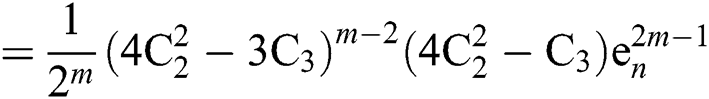 //FullSimplify
//FullSimplify
In[5]:= 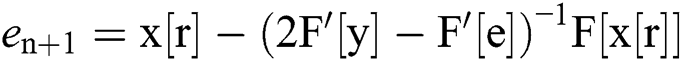 //FullSimplify
//FullSimplify
Out[5]:= 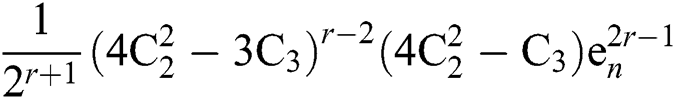

Hence, this shows that for 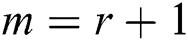 , we have
, we have 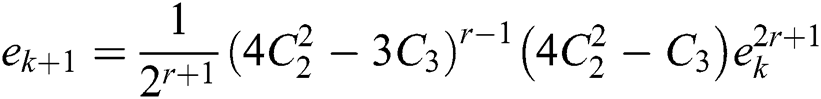 .
.
In this section, we compare the efficiency index of our proposed method with other methods in the literature. Commonly in the literature, the efficiency index 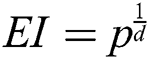 is used, where
is used, where 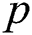 is the order of convergence of the iterative scheme, and
is the order of convergence of the iterative scheme, and 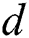 is the number of functions needed to be found per iteration in the iterative scheme. Another common index that can be used in the comparison between iterative scheme is the computational efficiency index
is the number of functions needed to be found per iteration in the iterative scheme. Another common index that can be used in the comparison between iterative scheme is the computational efficiency index 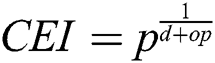 , where
, where 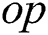 is the number of operations per iteration in the iterative scheme. The evaluation of any scalar function is considered as an operation.
is the number of operations per iteration in the iterative scheme. The evaluation of any scalar function is considered as an operation.
To find the number of functions required to be found per iteration in an iterative scheme, the following rules applied: Any computation of 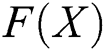 needs
needs 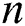 evaluations of scalar functions. Any computation of the Jacobian
evaluations of scalar functions. Any computation of the Jacobian 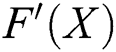 needs
needs 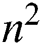 evaluations of scalar functions. Also, the floating points for obtaining the LU factorization are
evaluations of scalar functions. Also, the floating points for obtaining the LU factorization are 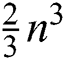 , and to solve the triangular system we need
, and to solve the triangular system we need 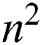 floating points operations. Finally,
floating points operations. Finally, 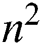 operations required to find a matrix-vector multiplication, and
operations required to find a matrix-vector multiplication, and 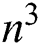 operations needed to find a matrix-matrix multiplication.
operations needed to find a matrix-matrix multiplication.
We compare the efficiency index and the computational efficiency index for the proposed method (PM) (11) to the following iterative schemes:
• The third-order Frontini-Sormani method (FS) [10] given by (4).
• The fifth order scheme (CHMT) proposed by Cordero et al. [23], given by
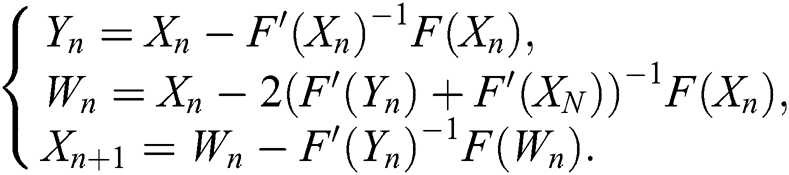
• The fifth order scheme (MMK) proposed by Waseem et al. [4], which is given by:
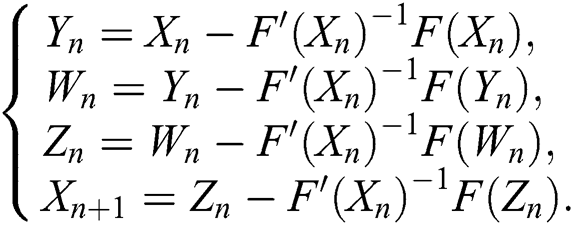
• The fifth-order iterative scheme (SG) presented by Sharma et al. [20], which is defined by scheme (5).
A comparison of the number of functional evaluations of the selected iterative schemes is illustrated in Tab. 1. Also, the computational efficiency indices of the selected schemes are compared (for 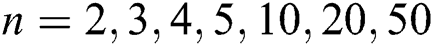 ), see Fig. 1. Note that the proposed scheme does not attain the best efficiency in this comparison, especially for small
), see Fig. 1. Note that the proposed scheme does not attain the best efficiency in this comparison, especially for small 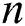 . We will see in the next two sections that this issue does not affect the scheme negatively when applied to some numerical tests.
. We will see in the next two sections that this issue does not affect the scheme negatively when applied to some numerical tests.
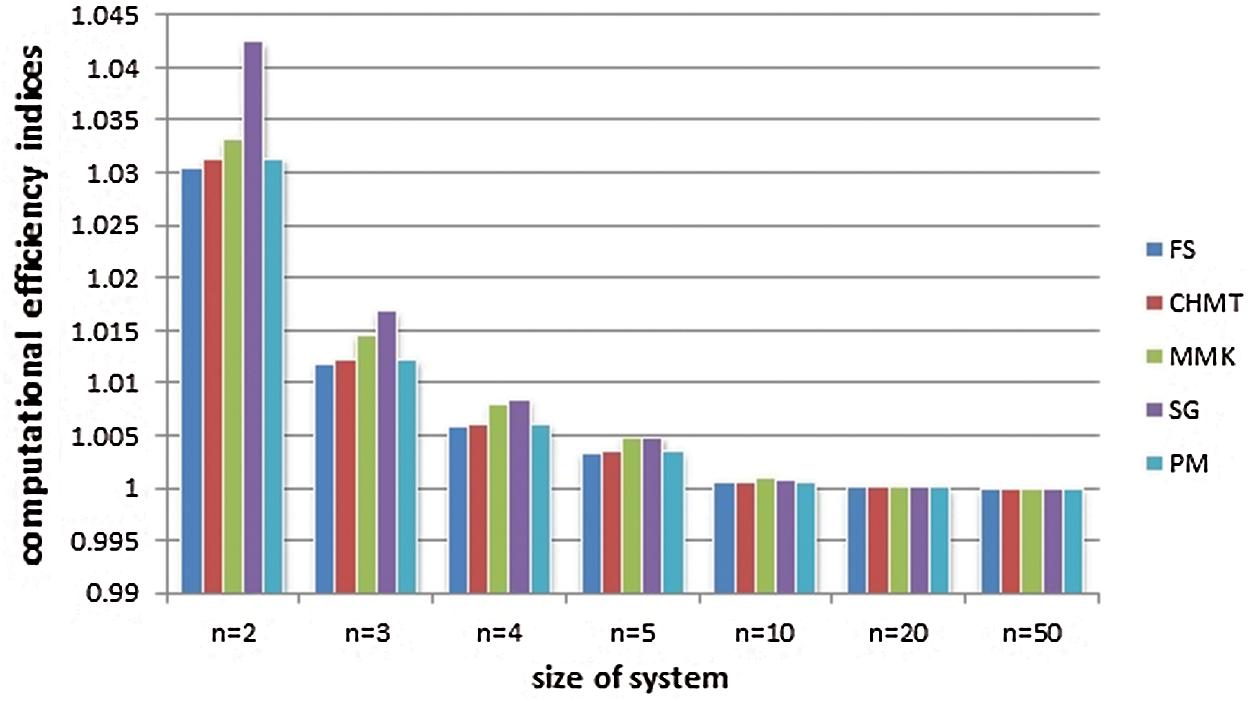
Figure 1: Computational efficiency indices for different sizes of system
Table 1: Comparisons of required functional evaluations per iteration

Fig. 2 illustrates the efficiency indices for the selected methods. Note that CHMT, SG and our proposed method have the same efficiency indices. However, this does not guarantee that they have the same behavior, accuracy and computational time cost.
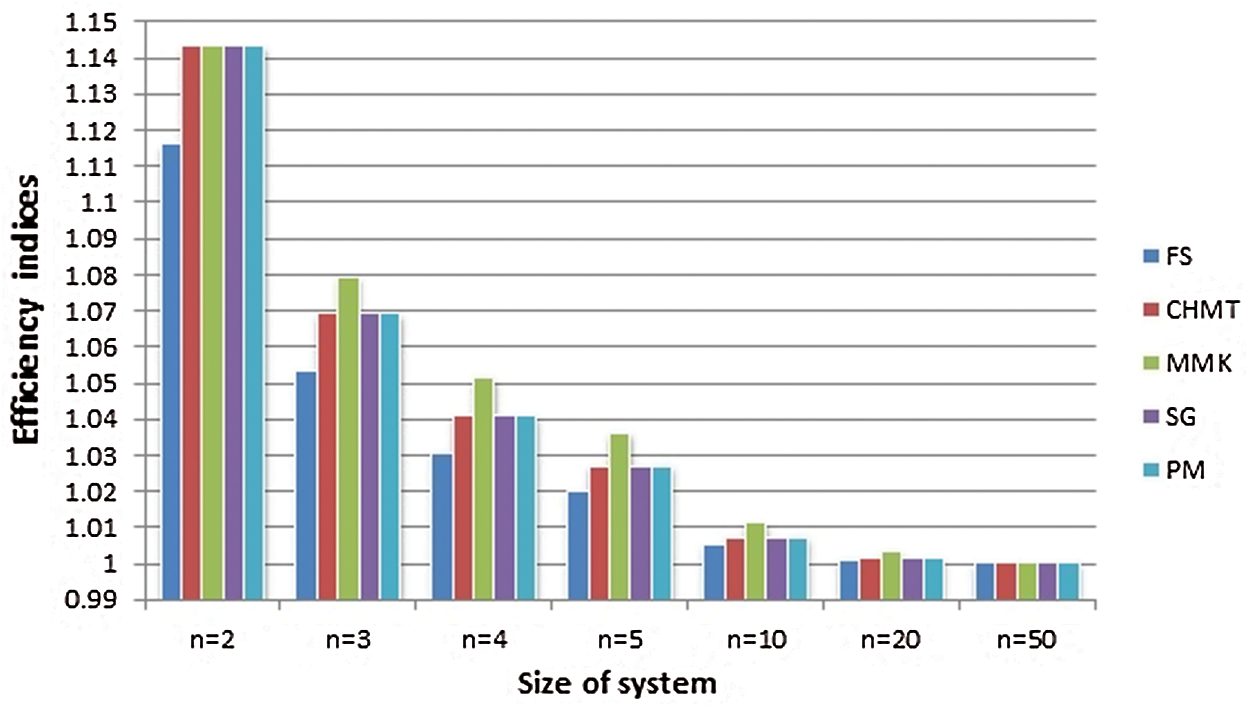
Figure 2: Efficiency indices for different values of 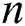
The concept of basins of attraction is a method to show how different starting points affect the behavior of the function. In this way, we can compare different root-finding schemes depending on the convergence area of the basins of attraction. In this sense, the iterative scheme is better if it has a larger area of convergence. Here, we mean by the area of convergence, the number of convergent points to a root 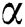 of
of 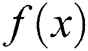 in a selected range.
in a selected range.
To check the stability and the area of convergence of our proposed method, we select the case 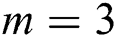 of scheme (12). We denote the proposed method by PM
of scheme (12). We denote the proposed method by PM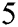 . For comparison, we compare PM
. For comparison, we compare PM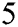 with the following schemes of the same order of convergence: The scheme CHMT given by Cordero et al. (13), the scheme SG proposed by Sharma and Gupta (5), and the scheme MMK presented by Waseem et al. (14). We choose three test examples to visualize the basins of attraction. All examples are polynomials with roots of multiplicity one. The test polynomials are
with the following schemes of the same order of convergence: The scheme CHMT given by Cordero et al. (13), the scheme SG proposed by Sharma and Gupta (5), and the scheme MMK presented by Waseem et al. (14). We choose three test examples to visualize the basins of attraction. All examples are polynomials with roots of multiplicity one. The test polynomials are
• 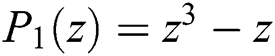 , with roots
, with roots 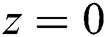 ,
, 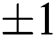 .
.
• 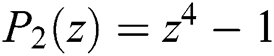 , with roots
, with roots 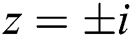 ,
, 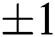 .
.
• 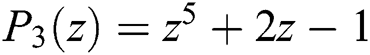 , with roots
, with roots 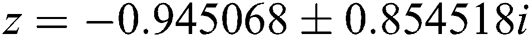 ,
, 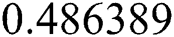 ,
, 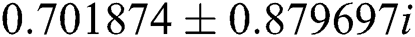
A  region is centered at the origin to cover all the zeros of the selected polynomials. The step size selected is
region is centered at the origin to cover all the zeros of the selected polynomials. The step size selected is 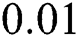 ; thus,
; thus, 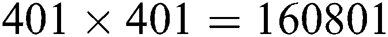 points in a uniform grid are selected as initial point for the iterative schemes to generate the basins of attraction. The exact roots were assigned as black dots on the graph. If the scheme needs less number of iterations to converge to a specific root, then the region of that roots appears darker. The convergence criterion selected is a tolerance of
points in a uniform grid are selected as initial point for the iterative schemes to generate the basins of attraction. The exact roots were assigned as black dots on the graph. If the scheme needs less number of iterations to converge to a specific root, then the region of that roots appears darker. The convergence criterion selected is a tolerance of 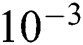 with a maximum of
with a maximum of 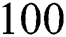 iterations. All calculations have been performed on Intel Xeon CPU-E5-2690 0@2.90 GHz with 32 GB RAM, using Microsoft Windows 10, 64 bit based on X64-based processor. Mathematica 9 has been used to generate all graphs and computations. The dynamics of the four test problems are shown in Figs. 3–5 respectively.
iterations. All calculations have been performed on Intel Xeon CPU-E5-2690 0@2.90 GHz with 32 GB RAM, using Microsoft Windows 10, 64 bit based on X64-based processor. Mathematica 9 has been used to generate all graphs and computations. The dynamics of the four test problems are shown in Figs. 3–5 respectively.

Figure 3: Basins of attraction of 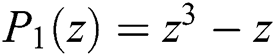 . The top row from left to right: CHMT and MMK. The bottom row from left to right: SG and PM
. The top row from left to right: CHMT and MMK. The bottom row from left to right: SG and PM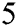
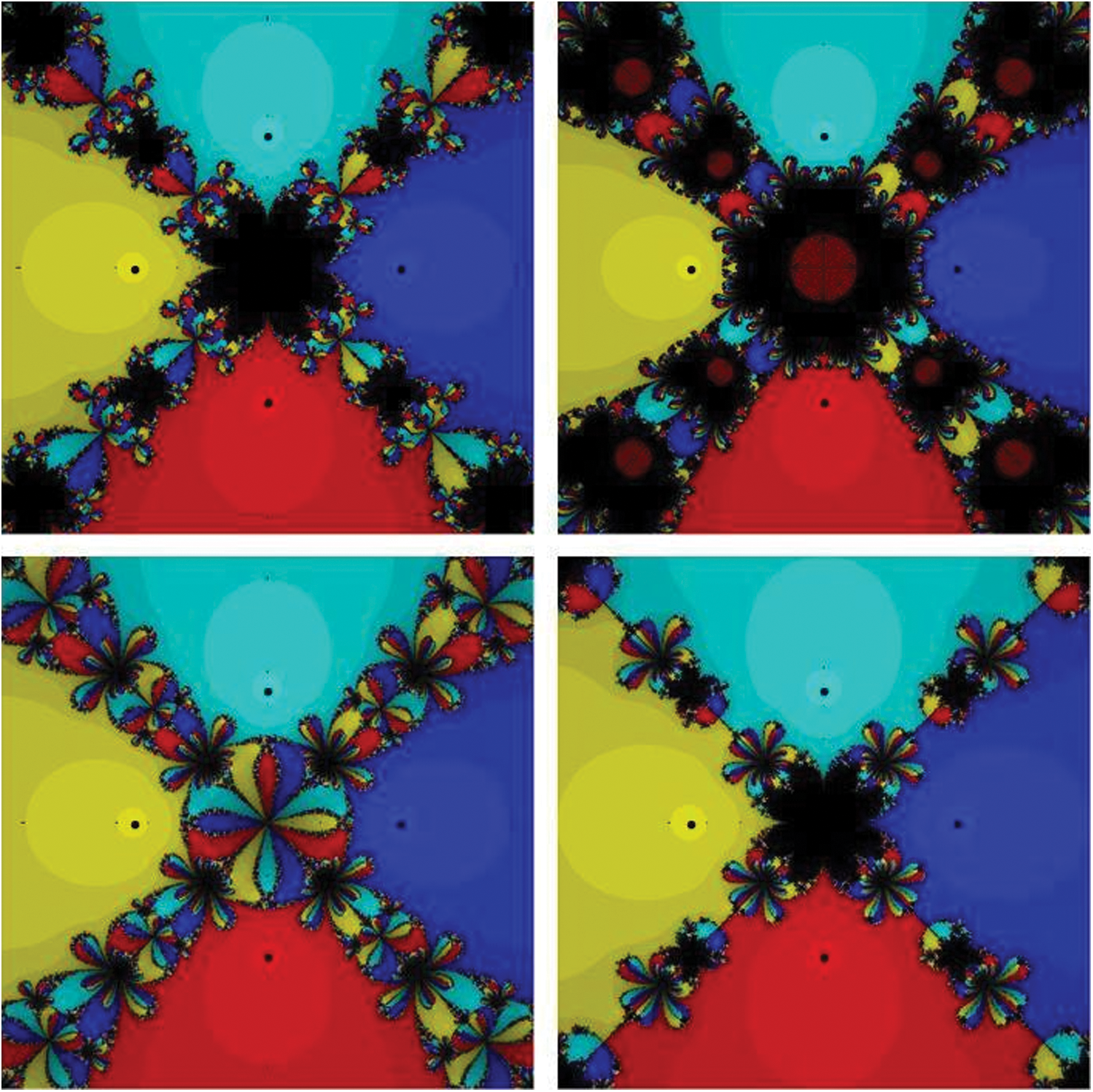
Figure 4: Basins of attraction of 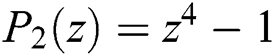 . The top row from left to right: CHMT and MMK. The bottom row from left to right: SG and PM5
. The top row from left to right: CHMT and MMK. The bottom row from left to right: SG and PM5

Figure 5: Basins of attraction of 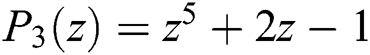 . The top row from left to right: CHMT and MMK. The bottom row from left to right: SG and PM5
. The top row from left to right: CHMT and MMK. The bottom row from left to right: SG and PM5

Basins of attraction of PM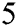 shows that the proposed method is comparable to other methods of the same order, with an area of convergence which is larger or the same as the areas of convergence of the other methods used in the comparison.
shows that the proposed method is comparable to other methods of the same order, with an area of convergence which is larger or the same as the areas of convergence of the other methods used in the comparison.
6 Numerical Tests and Applications
In this part, we consider some numerical problems to clarify the computational efficiency and convergence behavior of the proposed scheme. All calculations have been performed using 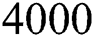 significant digits on Mathematics 9. For comparisons, we find the number of iterations
significant digits on Mathematics 9. For comparisons, we find the number of iterations 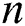 needed to satisfy the stopping criterion
needed to satisfy the stopping criterion 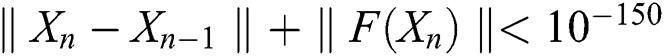 for each selected method. Also, we use the approximated computational order of convergence for each iterative scheme, which can be found by
for each selected method. Also, we use the approximated computational order of convergence for each iterative scheme, which can be found by
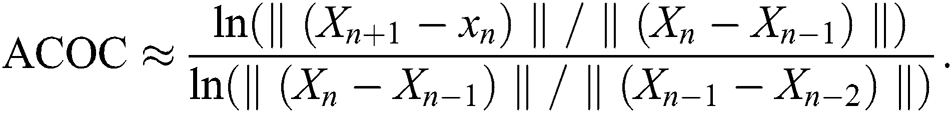
Finally, we compare for the selected schemes the distance between two consecutive iterations 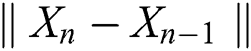 and the value of
and the value of 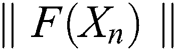 for
for 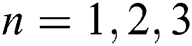 .
.
To be consistent in the comparison, we compare the proposed scheme PM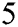 defined by scheme (12) for
defined by scheme (12) for 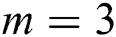 , to the original method which we derived from, that is, FS scheme given by (4). Also, we use the following fifth-order iterative schemes in the comparison: CHMT
, to the original method which we derived from, that is, FS scheme given by (4). Also, we use the following fifth-order iterative schemes in the comparison: CHMT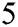 method defined by scheme (13), MMK method defined by (14), and SG method defined by (5). To test the efficiency of the extension of our proposed scheme to higher orders schemes, we compare the proposed scheme PM
method defined by scheme (13), MMK method defined by (14), and SG method defined by (5). To test the efficiency of the extension of our proposed scheme to higher orders schemes, we compare the proposed scheme PM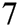 of seventh-order given by scheme (12) for
of seventh-order given by scheme (12) for 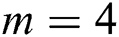 , to the extension of CHMT
, to the extension of CHMT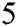 to the seventh-order scheme CHMT
to the seventh-order scheme CHMT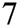 given by:
given by:
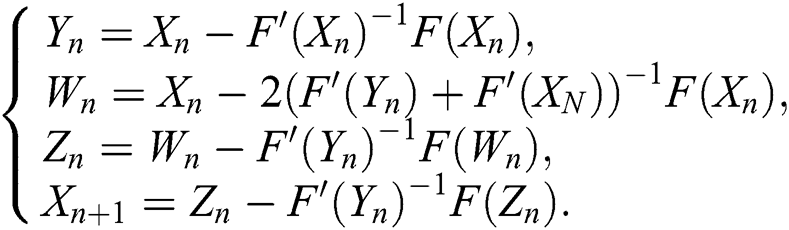
To be not selective in our examples, we choose most test problems from the same papers which contain the schemes used in the comparisons, see [4,20,23]. Also, we choose two distinct initial guesses for all problems to test the validity and the applicability of iterative schemes. We consider the following test problems and applications:
Example 1 Consider the following system of two nonlinear equations:
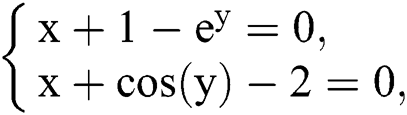
with initial guesses 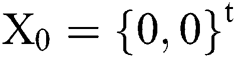 and
and 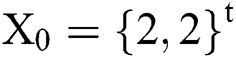 . The exact solution of this problem is
. The exact solution of this problem is 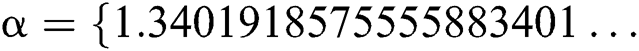 ,
, 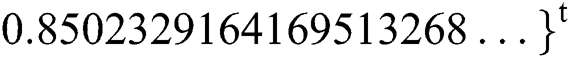 .
.
Example 2 Consider the following system of three nonlinear equations:
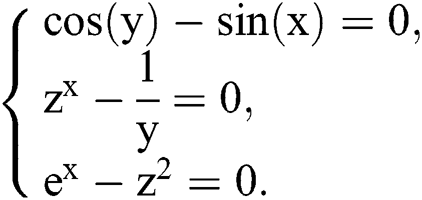
We consider as an initial solution 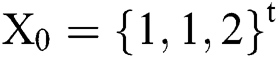 and
and 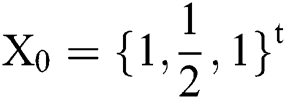 . The exact solution of this problem is
. The exact solution of this problem is 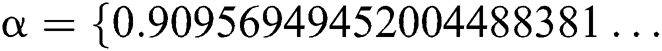 ,
, 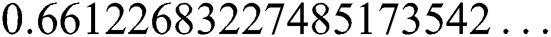 ,
, 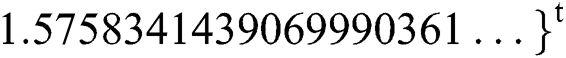 .
.
Example 3 Consider the following system
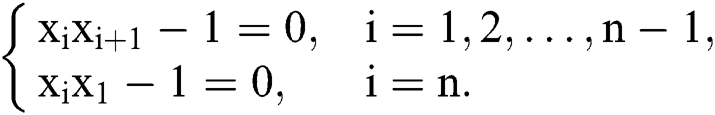
For odd 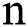 , the exact zeros of F(X) are
, the exact zeros of F(X) are 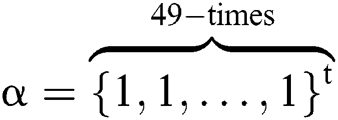 and
and 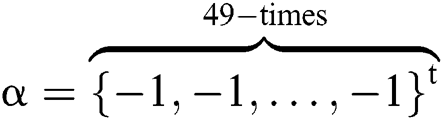 . For
. For 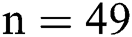 , we select as an initial guess
, we select as an initial guess 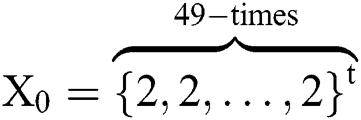 and
and 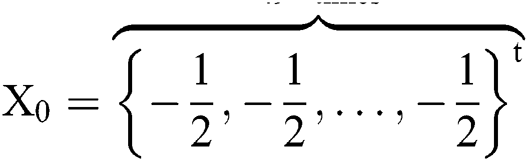 .
.
Example 4 Consider the nonlinear boundary value problem:
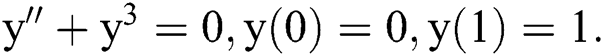
Assume the following partitioning for the interval 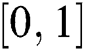 :
:
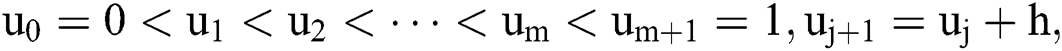
where 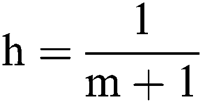 is the step size,
is the step size, 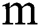 is the system size. Let
is the system size. Let 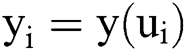 for
for 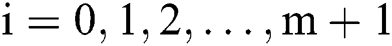 . We use the finite difference method to solve the problem, in which the second derivative
. We use the finite difference method to solve the problem, in which the second derivative 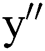 will be replaced by the central difference
will be replaced by the central difference 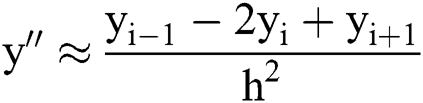 ,
, 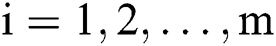 . By this, we obtain
. By this, we obtain  system given by:
system given by:
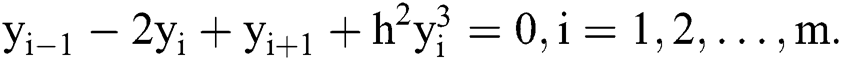
We solve this system for 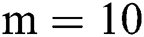 by selecting
by selecting 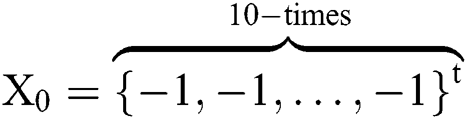 , and
, and 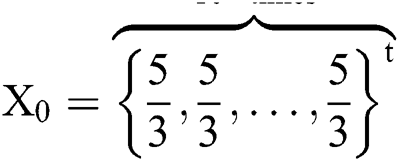 as initial guesses. The exact solution for this problem is
as initial guesses. The exact solution for this problem is 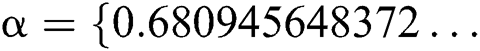 ,
, 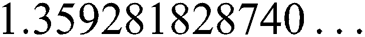 ,
, 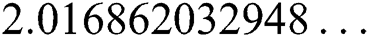 ,
, 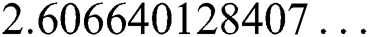 ,
, 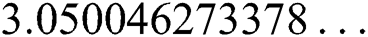 ,
, 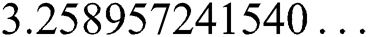 ,
, 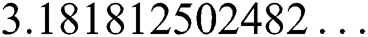 ,
, 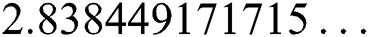 ,
, 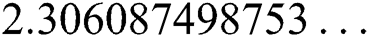 ,
, 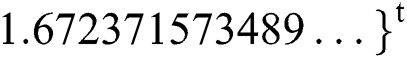 .
.
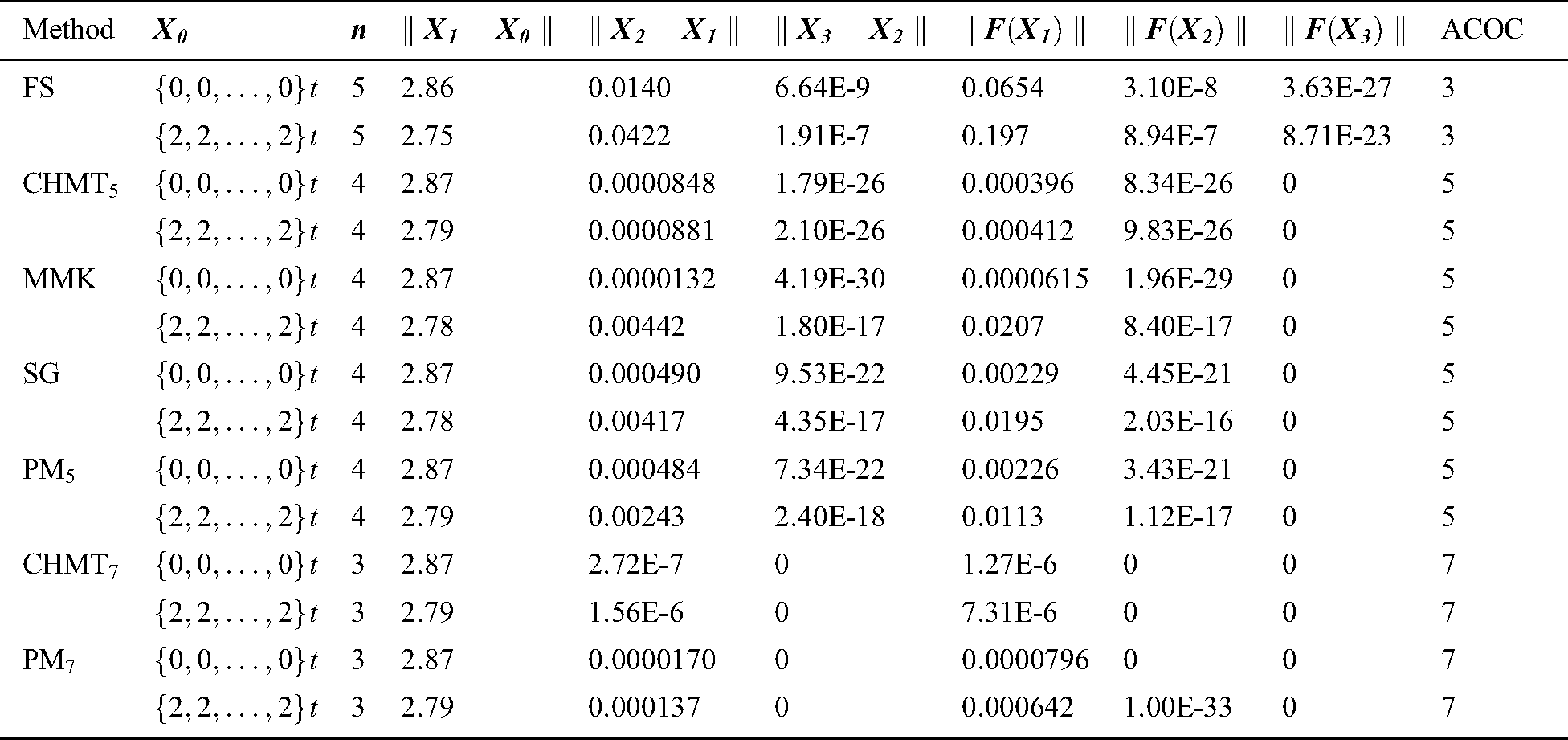
Tabs. 2–5 show that our proposed methods PM and PM
and PM are efficient with a good performance and comparable to the other methods of the same order. The proposed methods converge to the desired solution either by less number of iterations based on the convergence criterion (Examples 1 and 2), or by the same number of iterations needed to satisfy the convergence criterion with more accurate answers (Examples 3 and 4).
are efficient with a good performance and comparable to the other methods of the same order. The proposed methods converge to the desired solution either by less number of iterations based on the convergence criterion (Examples 1 and 2), or by the same number of iterations needed to satisfy the convergence criterion with more accurate answers (Examples 3 and 4).
Table 2: Comparisons between different methods for Example 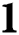
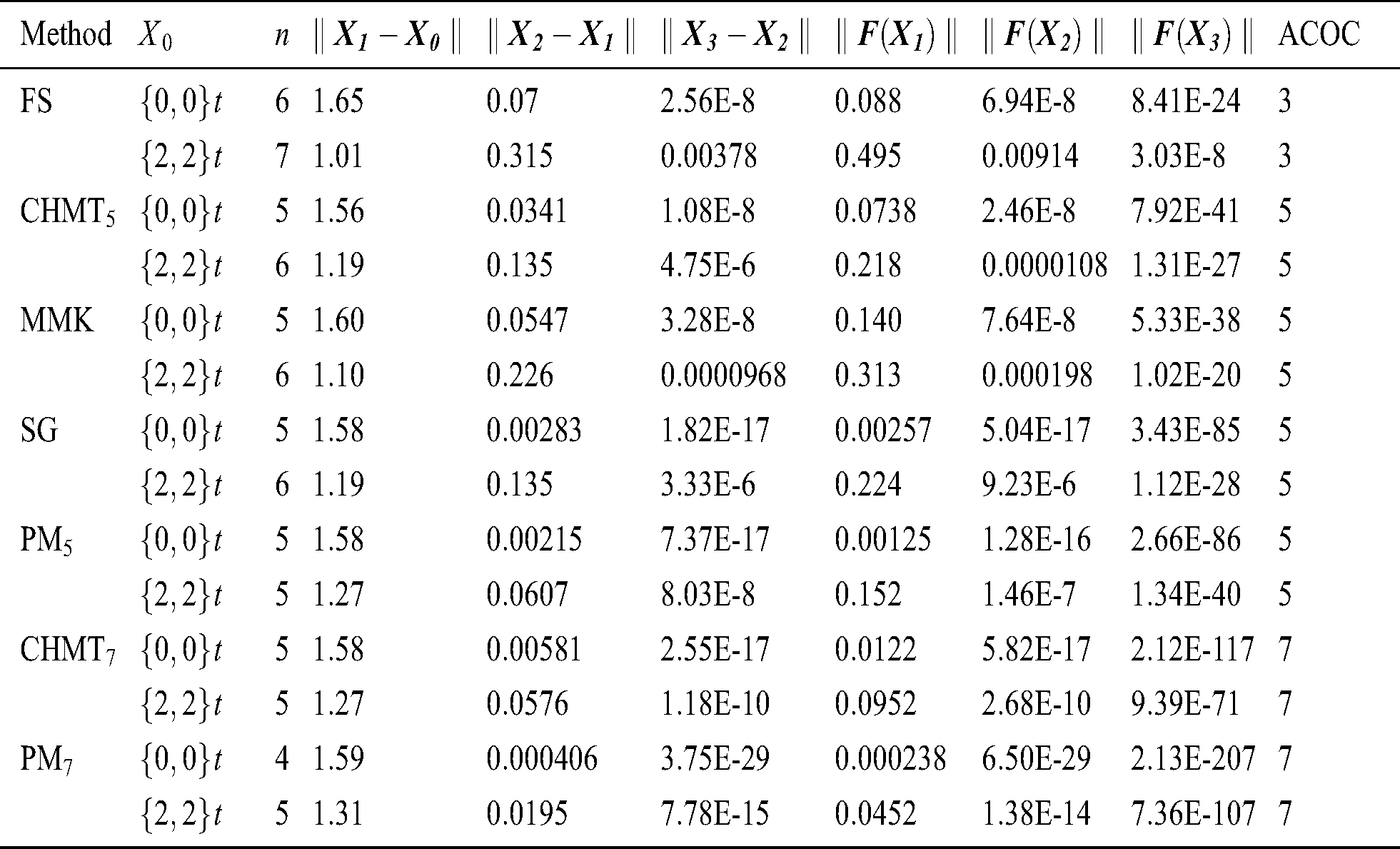
Table 3: Comparisons between different methods for Example 
Table 4: Comparisons between different methods for Example 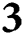
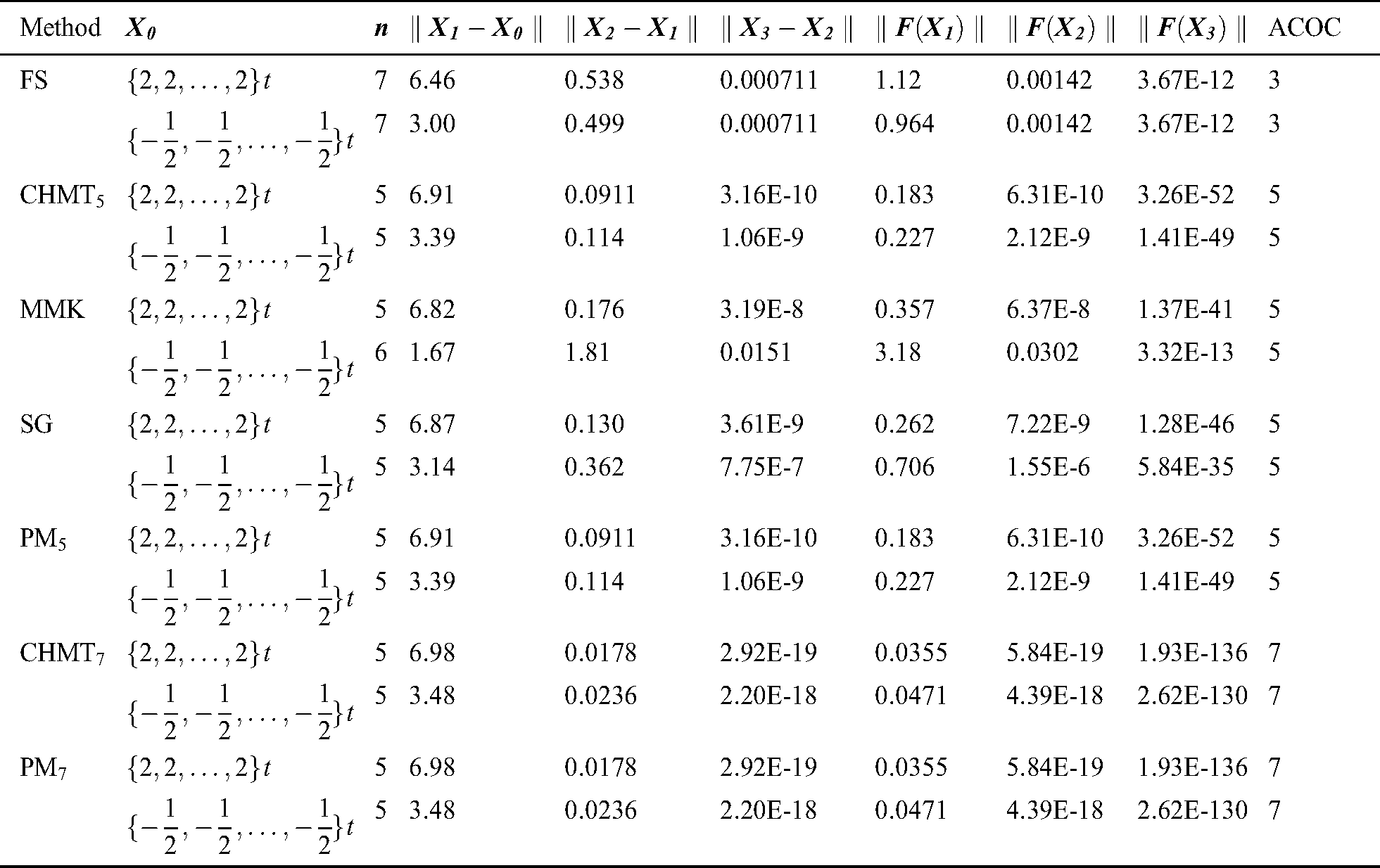
Table 5: Comparisons between different methods for Example 
To check the applicability of the proposed scheme on real-life problems, we apply it on the mixed Hammerstein integral equation and Burgers’ equation.
Problem 1 Consider the mixed Hammerstein integral equation:
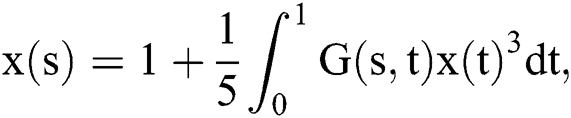
such that 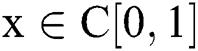 , and
, and 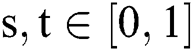 , and the kernel
, and the kernel 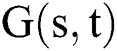 is given by
is given by
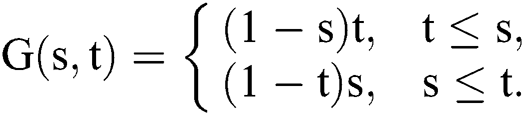
The integral equation is transformed into a finite-dimensional problem using the Gauss-Legender quadrature formula given by
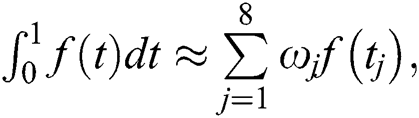
where the abscissas 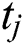 and the weights
and the weights 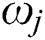 are determined for
are determined for 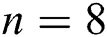 by the Gauss–Legendre quadrature formula. If we set
by the Gauss–Legendre quadrature formula. If we set 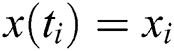 , for
, for 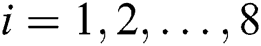 , then we obtain the following system of nonlinear equations
, then we obtain the following system of nonlinear equations
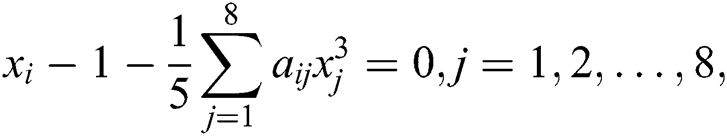
where
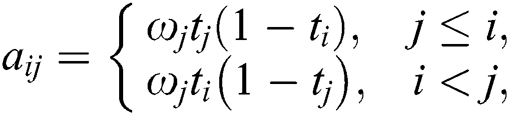
where the abscissas 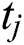 and the weights
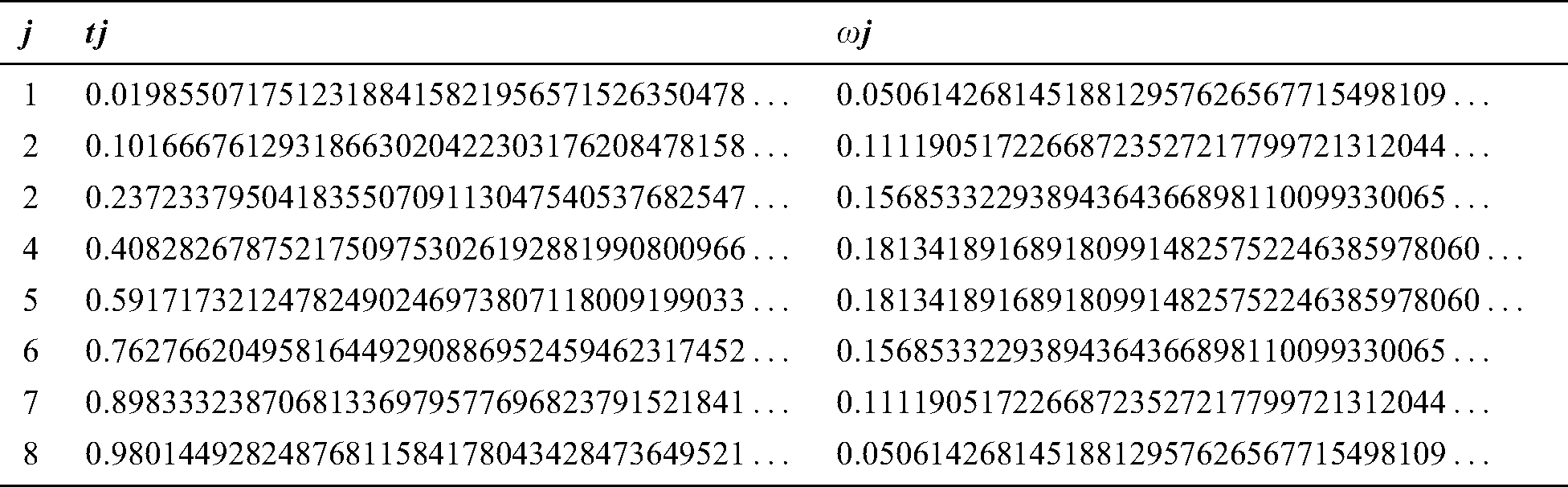
and the weights 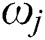 are known and presented in Tab. 6 for
are known and presented in Tab. 6 for 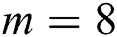 . The initial solutions considered are
. The initial solutions considered are 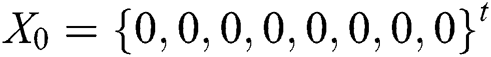 and
and 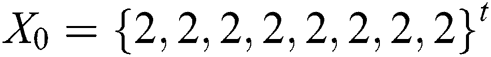 . The exact solution of this problem is
. The exact solution of this problem is 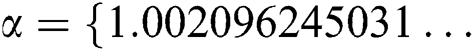 ,
, 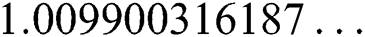 ,
, 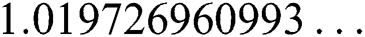 ,
, 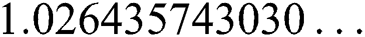 ,
, 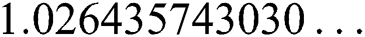 ,
, 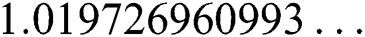 ,
, 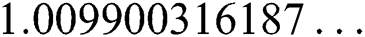 ,
, 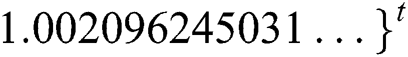 .
.
Table 6: Abscissas and weights and of Gauss-Legendre quadrature formula for 
Comparisons in Tab. 7 show that the proposed schemes have a good functioning and comparable to the other iterative methods of the same order.
Table 7: Comparisons between different methods for Problem 
Problem 2 Consider the following Burgers’ equation selected from [25]:
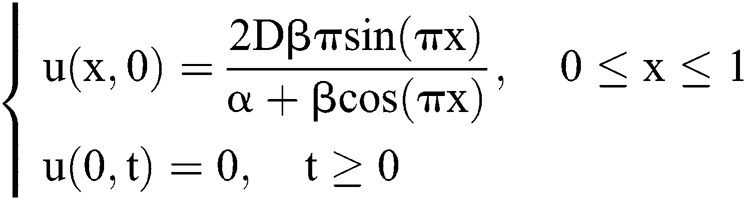
We use discretization to solve this problem. Let 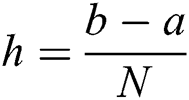 , and
, and 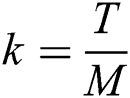 be the spatial and temporal step sizes respectively, where
be the spatial and temporal step sizes respectively, where 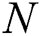 and
and 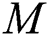 are numbers of subintervals in
are numbers of subintervals in 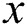 and
and 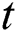 directions respectively. Therefore, for this problem we select points
directions respectively. Therefore, for this problem we select points 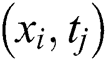 from a grid of domain
from a grid of domain  , where,
, where, 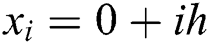 ,
, 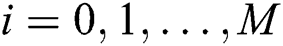 and
and 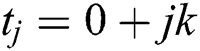 ,
, 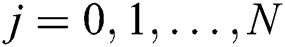 . Let
. Let 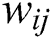 be the approximate solution at
be the approximate solution at 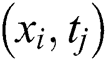 . By applying the central differences to
. By applying the central differences to 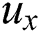 and
and 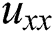 , and the backward difference to
, and the backward difference to 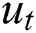 , we get the following nonlinear system:
, we get the following nonlinear system:
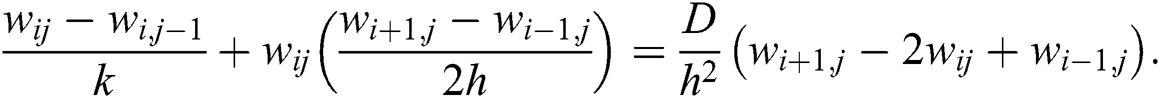
If we let 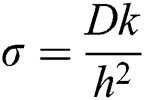 , and
, and 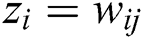 , then we are trying to solve the following system of equations:
, then we are trying to solve the following system of equations:
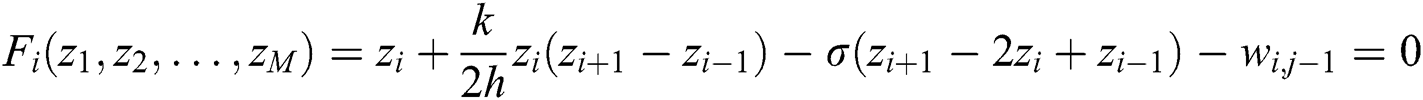 .
.
For the unknowns  . The last term
. The last term 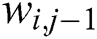 is known from the previous time step. The first and the last equations in the system can be replaced by using the given boundary conditions. In our problem, the first and the last equations in the system are
is known from the previous time step. The first and the last equations in the system can be replaced by using the given boundary conditions. In our problem, the first and the last equations in the system are
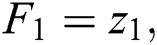
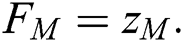
So, we have 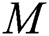 equations with
equations with 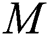 unknowns.
unknowns.
We find the approximate solution of the problem using the proposed method PM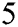 at
at 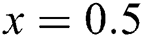 and
and 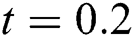 . To check the effect of the temporal step sizes on the solution, we select different values for
. To check the effect of the temporal step sizes on the solution, we select different values for 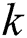 , which means a different number of steps to reach the wanted time. Consider for our problem that the diffusion coefficient
, which means a different number of steps to reach the wanted time. Consider for our problem that the diffusion coefficient 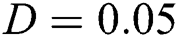 ,
, 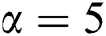 , and
, and 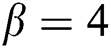 . The exact solution of the given Burgers’ equation is given by:
. The exact solution of the given Burgers’ equation is given by:
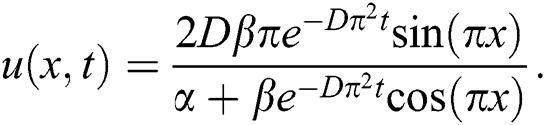
The exact solution for this problem is 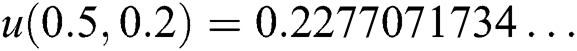 . Based on spatial step size equals
. Based on spatial step size equals 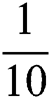 , we choose
, we choose 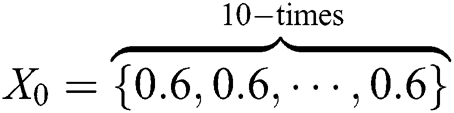 . Tab. 8 illustrates the numerical results of this problem. The effect of the selected
. Tab. 8 illustrates the numerical results of this problem. The effect of the selected 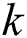 is clear. The results become better whenever we have a smaller temporal step size. Based on that, we will compare our proposed schemes to the other schemes for
is clear. The results become better whenever we have a smaller temporal step size. Based on that, we will compare our proposed schemes to the other schemes for 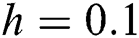 and
and 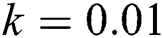 . We compare the approximate solutions at
. We compare the approximate solutions at 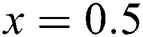 and
and 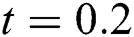 for
for 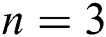 and
and 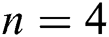 , that is
, that is 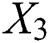 and
and 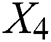 . Also, we find the norms of the functions
. Also, we find the norms of the functions 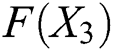 and
and 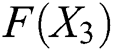 . Finally, we find the norm of the difference between the two consecutive iterations
. Finally, we find the norm of the difference between the two consecutive iterations 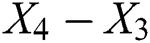 for each selected method. Comparisons results are shown in Tab. 9. It is clear that the proposed schemes perform in a good way, and in general, give results which are better than the other selected schemes.
for each selected method. Comparisons results are shown in Tab. 9. It is clear that the proposed schemes perform in a good way, and in general, give results which are better than the other selected schemes.
Table 8: Numerical results for Problem 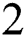
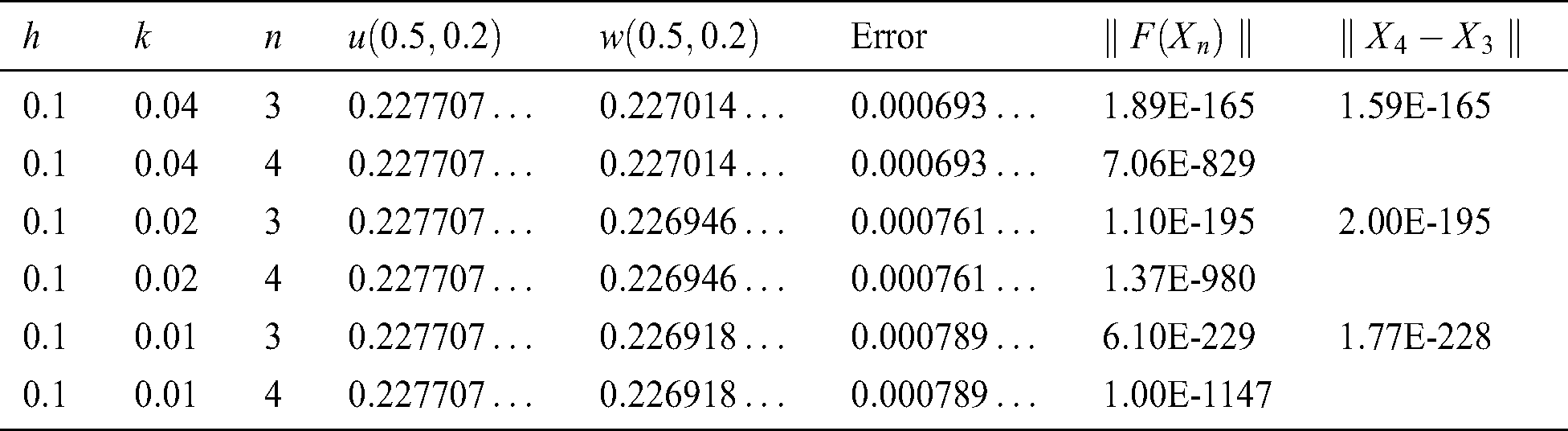
Table 9: Comparisons between different methods for Problem 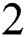
In this study, we have proposed an iterative scheme for systems of nonlinear equations of fifth-order of convergence. We have improved the proposed scheme to a generalized scheme of arbitrary odd order. The proposed method is based on Frontini–Sormani iterative method and developed using additional step with the usage of first derivative approximation. The software Mathematica has been used to show the order of convergence of the proposed method. Different comparisons were used to compare our proposed scheme to the other schemes of the same order, including the efficiency index, computational efficiency index, basins of attractions and several numerical problems. Comparisons show that the efficiency index and the computational efficiency index need not be proper tools for the efficiency of the iterative scheme. As an application, we test the proposed method on the mixed Hammerstein integral equation and Burgers’ equation. Comparisons show that the proposed scheme is of excellent performance and overall, it is comparable to the other iterative techniques used in the comparisons regarding the convergence speed, accuracy and the area of convergence in the basins of attraction.
Funding Statement: We are grateful for the financial support from UKM’s research Grant GUP-2019-033.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. M. Ortega and W. C. Rheinboldt. (1970). Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, New York, NY, USA. [Google Scholar]
2. H. Jafari and V. Daftardar-Gejji. (2006). “Revised Adomian decomposition method for solving a system of nonlinear equations,” Applied Mathematics and Computation, vol. 175, no. 1, pp. 1–7. [Google Scholar]
3. D. Kaya and S. M. El-Sayed. (2004). “Adomian’s decomposition method applied to systems of nonlinear algebraic equations,” Applied Mathematics and Computation, vol. 154, no. 2, pp. 487–493. [Google Scholar]
4. M. Waseem, M. A. Noor and K. I. Noor. (2016). “Efficient method for solving a system of nonlinear equations,” Applied Mathematics and Computation, vol. 275, pp. 134–146. [Google Scholar]
5. A. Cordero, E. Martnez and J. R. Torregrosa. (2009). “Iterative methods of order four and five for systems of nonlinear equations,” Journal of Computational and Applied Mathematics, vol. 231, no. 2, pp. 541–551. [Google Scholar]
6. M. T. Darvishi and A. Barati. (2007). “A third-order Newton-type method to solve systems of nonlinear equations,” Applied Mathematics and Computation, vol. 187, no. 2, pp. 630–635. [Google Scholar]
7. F. Awawdeh. (2010). “On new iterative method for solving systems of nonlinear equations,” Numerical Algorithms, vol. 54, no. 3, pp. 395–409. [Google Scholar]
8. A. Golbabai and M. Javidi. (2007). “Newton-like iterative methods for solving system of nonlinear equations,” Applied Mathematics and Computation, vol. 192, no. 2, pp. 546–551. [Google Scholar]
9. M. Grau-Sánchez, A. Grau and M. Noguera. (2011). “On the computational efficiency index and some iterative methods for solving systems of nonlinear equations,” Journal of Computational and Applied Mathematics, vol. 236, no. 6, pp. 1259–1266. [Google Scholar]
10. M. Frontini and E. Sormani. (2003). “Some variants of Newton’s method with third-order convergence,” Applied Mathematics and Computation, vol. 140, no. 2–3, pp. 419–426. [Google Scholar]
11. S. Weerakoon and T. G. I. Fernando. (2000). “A variant of Newton’s method with accelerated third-order convergence,” Applied Mathematics Letters, vol. 13, no. 8, pp. 87–93. [Google Scholar]
12. J. Kou, Y. Li and X. Wang. (2006). “A modification of Newton method with third-order convergence,” Applied Mathematics and Computation, vol. 181, no. 2, pp. 1106–1111. [Google Scholar]
13. F. Ahmad, F. Soleymani, F. K. Haghani and S. Serra-Capizzano. (2017). “Higher order derivative-free iterative methods with and without memory for systems of nonlinear equations,” Applied Mathematics and Computation, vol. 314, pp. 199–211. [Google Scholar]
14. A. Cordero, C. Jordán, E. Sanabria and J. R. Torregrosa. (2019). “A new class of iterative processes for solving nonlinear systems by using one divided differences operator,” Mathematics, vol. 7, no. 9, pp. 776. [Google Scholar]
15. J. R. Sharma, D. Kumar and L. Jäntschi. (2019). “On a reduced cost higher order Traub–Steffensen-like method for nonlinear systems,” Symmetry, vol. 11, no. 7, pp. 891. [Google Scholar]
16. A. Cordero, J. L. Hueso, E. Martínez and J. R. Torregrosa. (2010). “A modified Newton–Jarratt’s composition,” Numerical Algorithms, vol. 55, no. 1, pp. 87–99. [Google Scholar]
17. M. U. D. Junjua, S. Akram, N. Yasmin and F. Zafar. (2015). “A new Jarratt-type fourth-order method for solving system of nonlinear equations and applications,” Journal of Applied Mathematics, vol. 2015, no. 2, pp. 1–14. [Google Scholar]
18. A. K. H. Alzahrani, R. Behl and A. S. Alshomrani. (2018). “Some higher-order iteration functions for solving nonlinear models,” Applied Mathematics and Computation, vol. 334, pp. 80–93. [Google Scholar]
19. R. Behl, D. Sarría, R. González and Á. A. Magreñán. (2019). “Highly efficient family of iterative methods for solving nonlinear models,” Journal of Computational and Applied Mathematics, vol. 346, pp. 110–132. [Google Scholar]
20. J. R. Sharma and P. Gupta. (2014). “An efficient fifth order method for solving systems of nonlinear equations,” Computers and Mathematics with Applications, vol. 67, no. 3, pp. 591–601. [Google Scholar]
21. H. Esmaeili and M. Ahmadi. (2015). “An efficient three-step method to solve system of nonlinear equations,” Applied Mathematics and Computation, vol. 266, pp. 1093–1101. [Google Scholar]
22. X. Xiao and H. Yin. (2017). “Achieving higher order of convergence for solving systems of nonlinear equations,” Applied Mathematics and Computation, vol. 311, pp. 251–261. [Google Scholar]
23. A. Cordero, J. L. Hueso, E. Martínez and J. R. Torregrosa. (2012). “Increasing the convergence order of an iterative method for nonlinear systems,” Applied Mathematics Letters, vol. 25, no. 12, pp. 2369–2374. [Google Scholar]
24. H. H. H. Homeier. (2004). “A modified Newton method with cubic convergence: The multivariate case,” Journal of Computational and Applied Mathematics, vol. 169, no. 1, pp. 161–169. [Google Scholar]
25. T. Sauer. (2012). Numerical Analysis. 2nd ed. Boston, MA, USA: Pearson Education. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |