DOI:10.32604/cmc.2021.012696
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012696 | |
| Article |
A Novel Semi-Quantum Private Comparison Scheme Using Bell Entangle States
1School of Cybersecurity, Chengdu University of Information Technology, Chengdu, 610225, China
2Natural Resource Ecology Laboratory, Colorado State University, Fort Collins, CO 80523, USA
*Corresponding Author: Lili Yan. Email: yanlili@cuit.edu.cn
Received: 09 July 2020; Accepted: 21 September 2020
Abstract: Private comparison is the basis of many encryption technologies, and several related Quantum Private Comparison (QPC) protocols have been published in recent years. In these existing protocols, secret information is encoded by using conjugate coding or orthogonal states, and all users are quantum participants. In this paper, a novel semi-quantum private comparison scheme is proposed, which employs Bell entangled states as quantum resources. Two semi-quantum participants compare the equivalence of their private information with the help of a semi-honest third party (TP). Compared with the previous classical protocols, these two semi-quantum users can only make some particular action, such as to measure, prepare and reflect quantum qubits only in the classical basis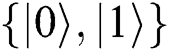 
, and TP needs to perform Bell basis measurement on reflecting qubits to obtain the results of the comparison. Further, analysis results show that this scheme can avoid outside and participant attacks and its’ qubit efficiency is better than the other two protocols mentioned in the paper.
Keywords: Cryptography; Bell entangled states; a semi-honest TP; security analysis; semi-quantum private comparison
Since Bennett and Brassard published the initial Quantum Key Distribution (QKD) protocol [1] in 1984, many quantum cryptography protocols have been published to solve security problems, such as Quantum Key Distribution (QKD) [1–4], Quantum Secure Direct Communication(QSDC) [5–12], Quantum Secret Sharing (QSS) [13–15], Quantum Secure Multiparty Computation (QSMC) [16–23], and so on.
Secure Multiparty Computing (SMC), also known as secure function evaluation, is a primitive basic form of distributed computation. It can correctly distribute computing to outputs when inputs are given by a group of distrustful users. As a subfield of QSMC, Quantum Private Comparison (QPC) was first established as a computing task by Yao [24] in 1982, “a socialist millionaire problem”, in which two millionaires want to know who is richer without publishing their properties to each other. Like QSMC, QPC is used to compare the quantum bits sent by two participants to determine whether the secret inputs of two participants are equal. Since then, many QPC protocols [25–41] have been proposed by using different kinds of quantum states and technologies. For example, Bell states were used in References [28,35,38], Reference [33] uses χ-Type State, single-photon was used in References [32–40], GHZ states were used in Reference [37]. Meanwhile, three kinds of TP are mentioned in related protocols: semi-honest [32,33], dishonest [34], almost-dishonest [42]. In most protocols, TP does not need to be completely honest, but only needs to execute the protocol honestly to make the TP know the comparison result 0 or 1 and the length of secret input.
Boyer et al. [43,44] proposed the first semi-quantum cryptography protocol based on the classical BB84 protocol in 2007. In this protocol, some participants have not quantum ability to participate in key distribution, but they can communicate by following the semi-quantum operation rules in quantum channel: (1) Reflect qubits back to the sender without any interference (referred to as REFLECT), and (2) Measure qubits in the basis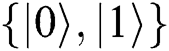 
and prepare the same quantum states, then resend them back to the sender (referred to as MEASURE). Compared with traditional quantum cryptography, semi-quantum cryptography can make some participants need neither complete quantum capabilities nor participating in the preparation and measurement of quantum superposition states. Based on this concept, semi-quantum Private Comparison (SQPC) protocols [45–47] had been put forward recently. In 2016, Chou et al. [45] published the first SQPC protocol under an almost dishonest third party. After that, Thapliyal et al. [46] proposed one QPC protocol and one SQPC protocol in 2018 by using Bell state as quantum resources. In their studies, they not only allow classical users to participate in the protocol, but also create a unique method of security detection and avoid TP from obtaining additional information in the process. In the same year, Lang et al. [47] published two SQPC protocols using single photons as quantum resources, which are modified schemes of Sun et al. [48].
In order to improve the qubits’ efficiency and make classical users be involved in quantum private comparison, we propose an SQPC protocol based on Bell state. Two semi-quantum users can compare their private information with the help of a semi-honest TP. Nevertheless, both of them can only make specific actions, such as measuring, preparing and reflecting the quantum qubits on the classical basis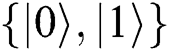
. With the help of a pre-shared key, this protocol can eliminate participant attacks by making Alice and Bob choose the same semi-quantum operation simultaneously. The encoding of private information is hidden in the returned particles after Alice and Bob choose the MEASURE operation. In addition, quantum TP only needs to prepare 2N Bell states as quantum resources, and releases one qubit to announce the comparison.
The rest of this paper is arranged as follows. The detailed description of the SQPC protocol is described in Section 2, and the security analysis of the protocol is explained in Section 3. In Section 4, the discussion and conclusion of this protocol are provided, and the following semi-quantum research work is analyzed and arranged.
2 The Novel SQPC Scheme Based on Bell Entangled States
In the following, the detailed description of an SQPC scheme is provided step by step. Two semi-quantum participants, Alice and Bob, are involved. Both of them have the same length of secret information.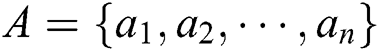 
and 
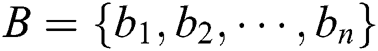
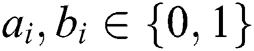(n is the length of private information). The third participant is a semi-honest quantum host TP, who always follows the process of the protocol but does not insure the safety of the protocol. Before performing the protocol, Alice and Bob share a master key KAB ( 
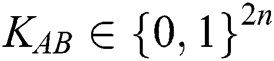) by using Semi-quantum Key Distribution (SQKD) protocol [49]. KAB is used for indicating Alice and Bob to choose the operation of MEASURE or REFLECT. When 
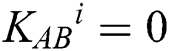, Alice and Bob will choose the MEASURE operation. Otherwise, they will choose the REFLECT operation.
The description of the scheme is the following steps.
Step 1: Semi-honest TP arranges 2n-bit Bell state sequence randomly chosen from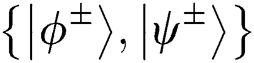 
, and splits every single Bell state into q1 and q2, consisting of sequences S1 and S2. Then TP sends the qubits S1 and S2 to Alice and Bob one by one, respectively.
Step 2: According to KAB, Alice (Bob) performs the operational rules of semi-quantum, MEASURE or REFLECT, on each qubit of S1 (S2) sequence. When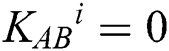 
, Alice (Bob) chooses the MEASURE operation on the qubit to obtain result ci for calculating 
(
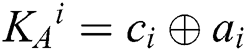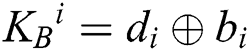). Then she (he) prepares a single photon according to the result of KAi (if 
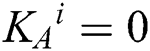, prepare
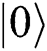; Otherwise, prepare
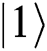) and send it back to TP. When 
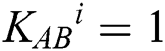, Alice (Bob) will reflect the qubit back to TP without any disturbance.
Step 3: TP makes Bell basis measurement with related qubits (the same position of S1' and S2') and records the result. Then TP confirms through a public channel.
Step 4: After receiving the announcement, Alice and Bob publishes the value of KAB to TP through the public channel. If these two KAB are not the same, TP terminates the protocol. Otherwise, TP proceeds to the next step.
Step 5: According to KAB, TP divides the result of measurement into MEASURE (M) and REFLECT (R) sequences (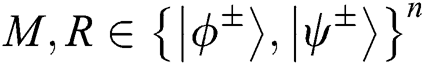
). When 
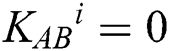, TP splits it into M sequence; When 
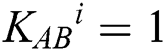, TP splits it into R sequence. For example:
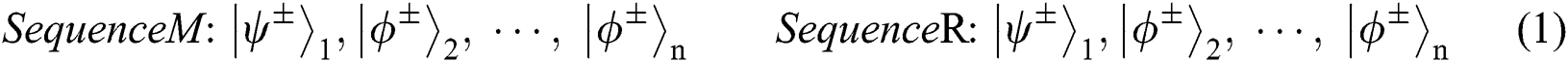
Then TP takes the next two steps:
1. Verifying the equivalence. Assume that TP prepares the initial Bell state to be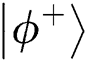 
. If the result of measurement in the same position is 
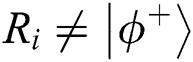, TP believes that eavesdropping exists in the channel. After finishing the comparison, TP calculates its error rate. If the error rate is above the predefined threshold, TP terminates the process of the protocol. Otherwise, TP announces the result of the comparison by operating.
2. Publishing the result of comparison. Assume that TP prepares the initial Bell state to be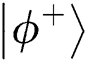 
and the measurement result at the same position is 
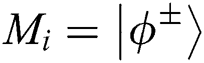, then TP thinks the secret information of Alice and Bob at the same position are same. When the measurement result at the same position is 
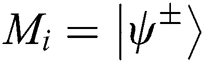, TP recognizes the secret information of Alice and Bob at the same position are different. After checking all n bits, TP announces one qubit 0 or 1. If all of them are the same, TP publishes 0. Otherwise, TP publishes 1 through the public channel.
For clarity, we describe the flowchart of the proposed protocol in Fig. 1 and provide an example to illustrate the further procedure of comparison. Suppose that TP prepares 8 bits Bell state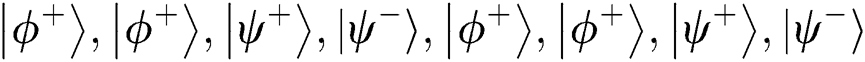 
, the master key is 
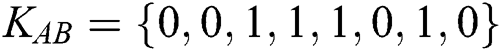. Moreover, Alice and Bob have private information of 
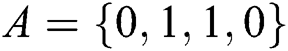and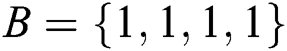 
. In Step 4, TP knows the 3rd, 4th, 5th and 7th qubits are used for security detection. If the results of Bell basis measurement are not 
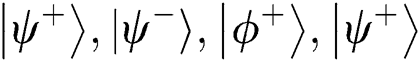, TP terminates the protocol. As for the comparison, assume that the two MEASURE sequences Alice and Bob made are 
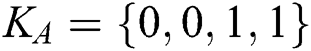and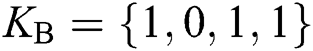 
. After making Bell basis measurement and comparison, TP will know that Alice and Bob just have the same qubit in the 2nd and 3rd positions. Thus TP announces 1. It can be concluded that TP has finished the comparison and cannot obtain any secret information from both sides.
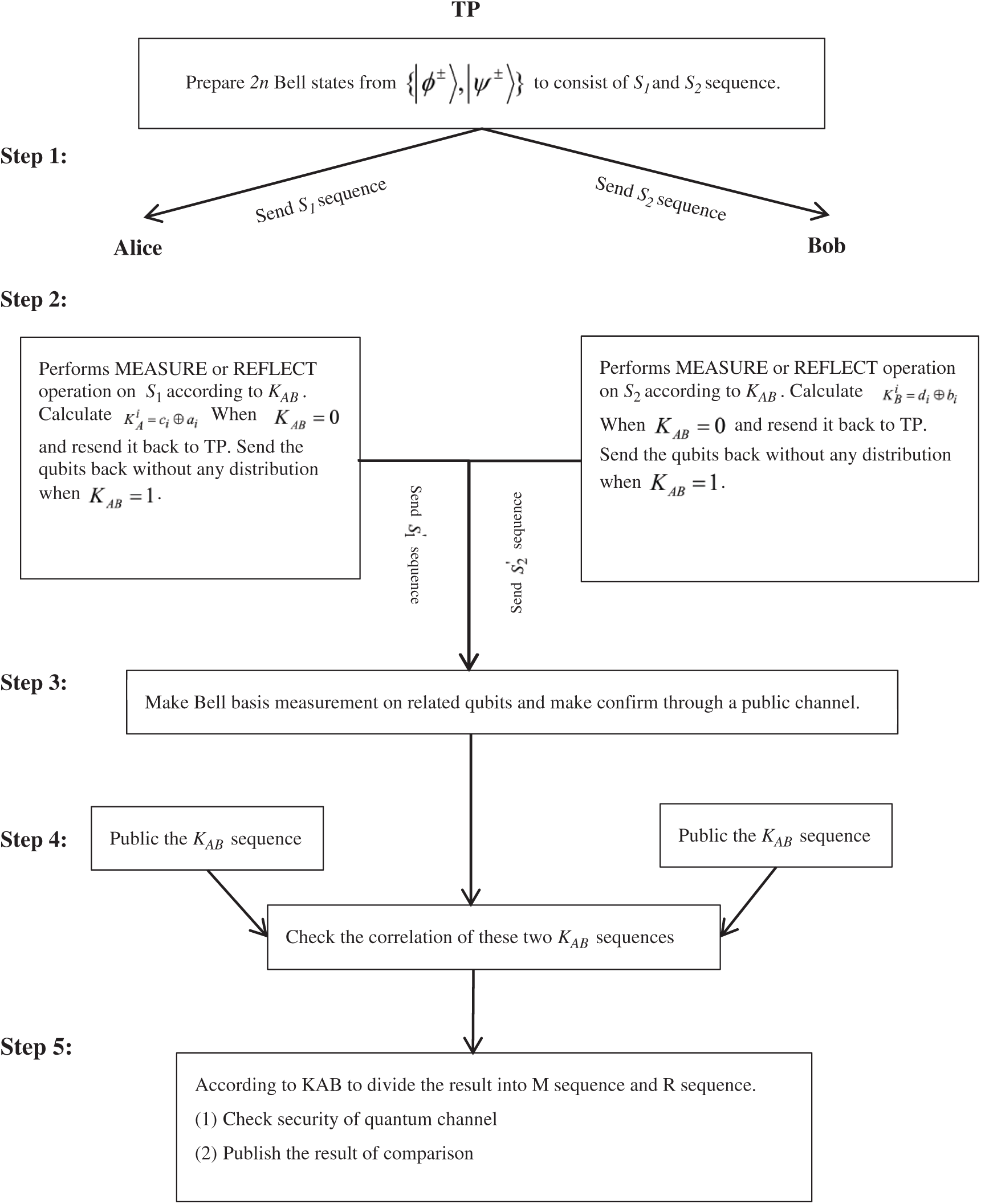
Figure 1: The flow chart of the proposed protocol
In this section, the security of the proposed protocol is analyzed from two aspects: (1) The secret information of participants is plagued by external eavesdroppers, and (2) Dishonest users or the semi-honest TP may steal the secret information in the procedure of the scheme. Then, the efficiency analysis of the scheme with some previous SQPC protocols are provided.
We will give out the eavesdropping detection that Eve may take at every step of the proposed protocol.
3.1.1 Security Analysis of Trojan Horse Attack
In Step 1, When TP sends S1 and S2 to Alice and Bob, respectively, Eve may launch an attack on the quantum channel. The attack is titled the Trojan horse attack [50,51], and can be prevented by adding a legitimate wavelength filter and a photon number splitter to both sides of Alice and Bob.
3.1.2 Security Analysis of Intercept-resend Attack
The external eavesdropper Eve intercepts the Bell states sent from TP to Alice (Bob) and prepares two-particle states according to measurement results, then she sends these qubits to Alice and Bob. Eve will be inevitably detected for two reasons: (1) Two-particle states can only be prepared randomly because this is the closest method to simulating the original sequence, and (2) Alice and Bob’s operation are still random to Eve, even though Alice and Bob publish the sequence KAB in Step 4. For example, the initial Bell state TP prepared is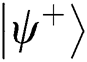 
. If Eve prepares the two-particles state to be 
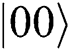and then send 
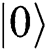to Alice and 
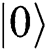to Bob.
When Alice and Bob choose REFLECT operation, TP makes Bell basis measurement on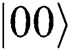 
and then TP has equal probability to obtain 
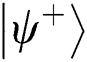and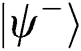 
. After analyzing all kinds of situation, TP finds out that Eve has a probability of 50% (All kinds of situation have been analyzed in Tab. 1).
Table 1: All kinds of situation of analysis when initial Bell state is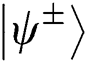 
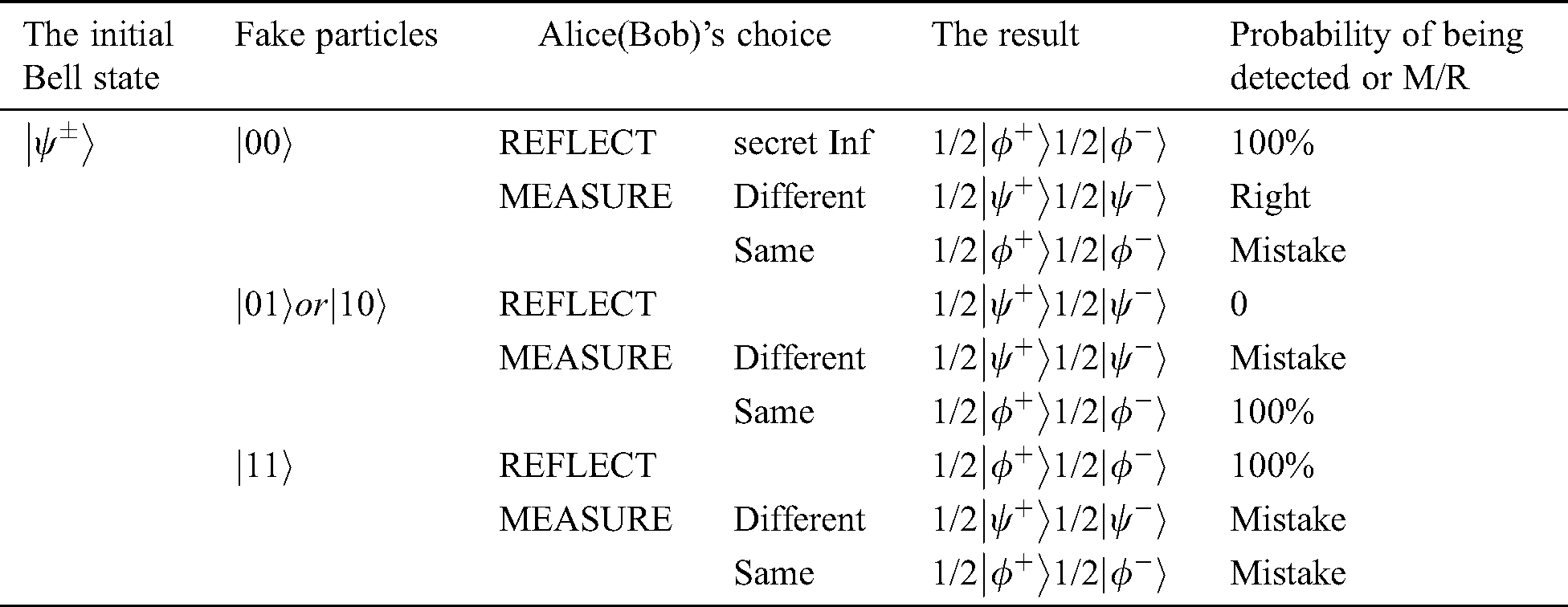
It should also be pointed out that Even Eve cannot obtain any secret information by performing intercept-resend attacks. She can still affect the comparison of secret information in some cases. The protocol can avoid Eve’s mistake by performing the detection firstly (Step 5).
3.1.3 Security Analysis of Measure-Resend Attack
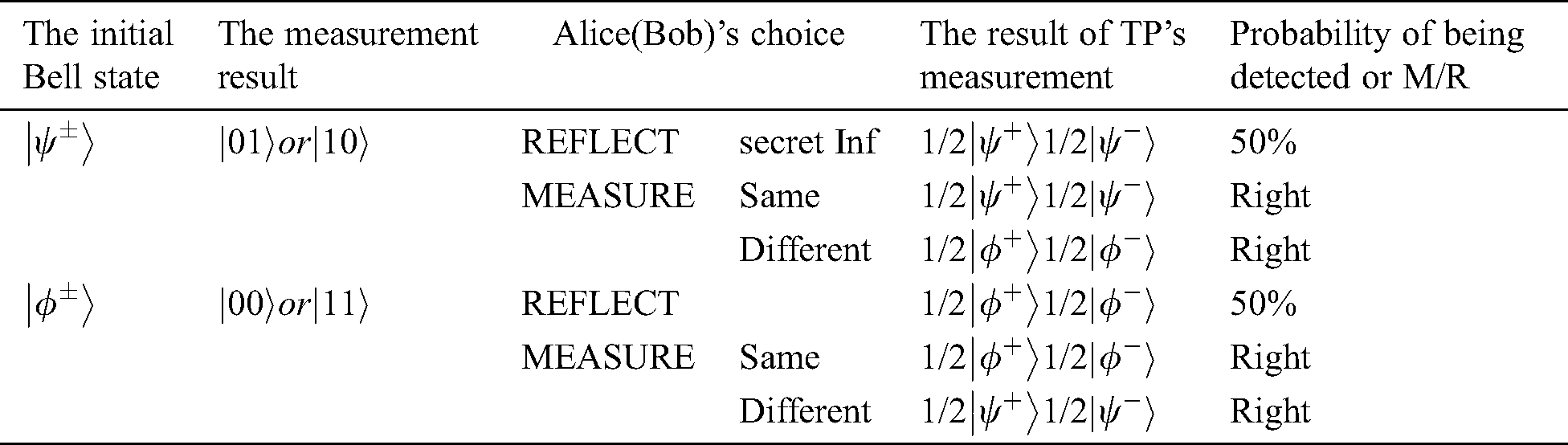
The measure-resend attack refers to that Eve intercepts the particles sent from TP to Alice (Bob), measures them, then sends the measured states to Alice (Bob). She inevitably causes the original Bell state to collapse into two-particle states. When Alice and Bob choose REFLECT operation, TP only has 50% possibility to obtain the initial Bell state. For the MEASURE operation, Eve cannot be detected and does not cause any interfere with the comparison result. In Tab. 2 are shown all situations.
Table 2: All situation after suffering this attack
3.1.4 Security Analysis of Flip Attack
During the flip attack, Eve interferes with the correctness of the comparison by modifying the intercepted particles’ information. This scheme can use the entanglement correlation of the Bell states to avoid this attack. Assuming that TP prepares the initial Bell state to be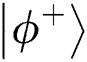 
, then sends the first qubit to Alice and the second one to Bob. Eve intercepts and measures it with the classical basis. If she obtains result 0 (1), she prepares single-photon 
(
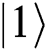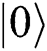) and sends it to Alice (Bob). If Alice (Bob) chooses MEASURE, Eve will not be found without causing any mistakes. If they choose REFLECT, TP performs Bell basis measurement on these qubits 
(
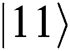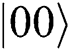), then obtains 
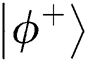and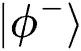 
with the same probability. When TP finishes the Bell basis measurement on all reflected qubits. The probability of Eve being found is 
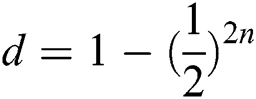. When n is large enough, the probability of being detected will reach 100%. In Tab. 2 are shown all situations.
3.1.5 Security Analysis of Entangle-Measure Attack
The entangle-measure attack means that Eve performs attack (UE,UF) on the Bell states among TP, Alice and Bob. UE and UF share a common probe space with initial state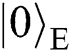 
. As the explanation in Refs. [43,56], the shared probe enables Eve to launch an attack on the returning qubits depending on the information acquired by UE. Assume that the initial Bell state is 
.
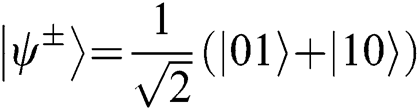Case 1: When Alice and Bob choose the REFLECT operation, Eve may obtain any secret information from (UE,UF).
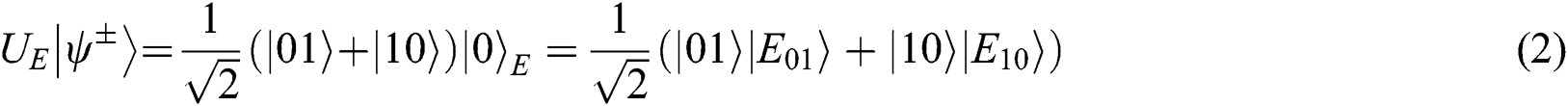
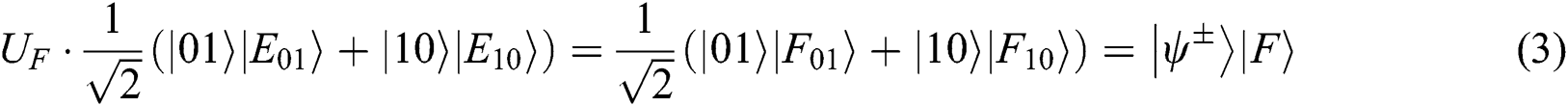
Thus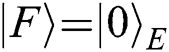 
. It means that Eve cannot obtain any information from this attack.
Case 2: When Alice and Bob choose the MEASURE operation, Eve loses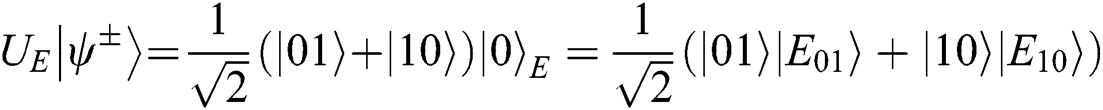 
even if 
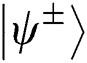collapse into 
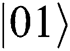or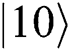
. She only can rely on 
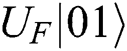or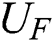 
. Eve has the same probability to obtain 01 or 10, but it is useless.
In the proposed protocol, dishonest users and semi-honest TP may try to obtain secret information. We analyze them in two ways.
Case 1: Alice or Bob eavesdrops the other’s secret information or disturbs the protocol’s process.
In Step 1, TP sends S1 to Alice and S2 to Bob. Firstly, both Alice and Bob can never perform certain operations on the other sequence. TP performs all joint measurements. This is the reason why Alice or Bob cannot obtain other’s secret information. Besides, if Alice or Bob deliberately choose different KAB sequence, it will be checked out in Step 4. In the last step, TP only uses 1 qubit to stand for the equivalence of their private information. They have no way to know the different of secret information.
Case 2: Semi-honest TP eavesdrops Alice and Bob’s private information.
The Semi-honesty determines that TP must implement the protocol base on the rules. Therefore, TP has only one way to obtain the private information of participants through M sequence (the sequence are all qubits that participants encode with their private information). For example, if the M sequence is 00 11 01 10, Eve only has the probability of 1/2 to obtain the initial state. When n is large enough, the probability of obtaining the private information of Alice is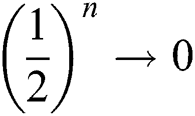 
.
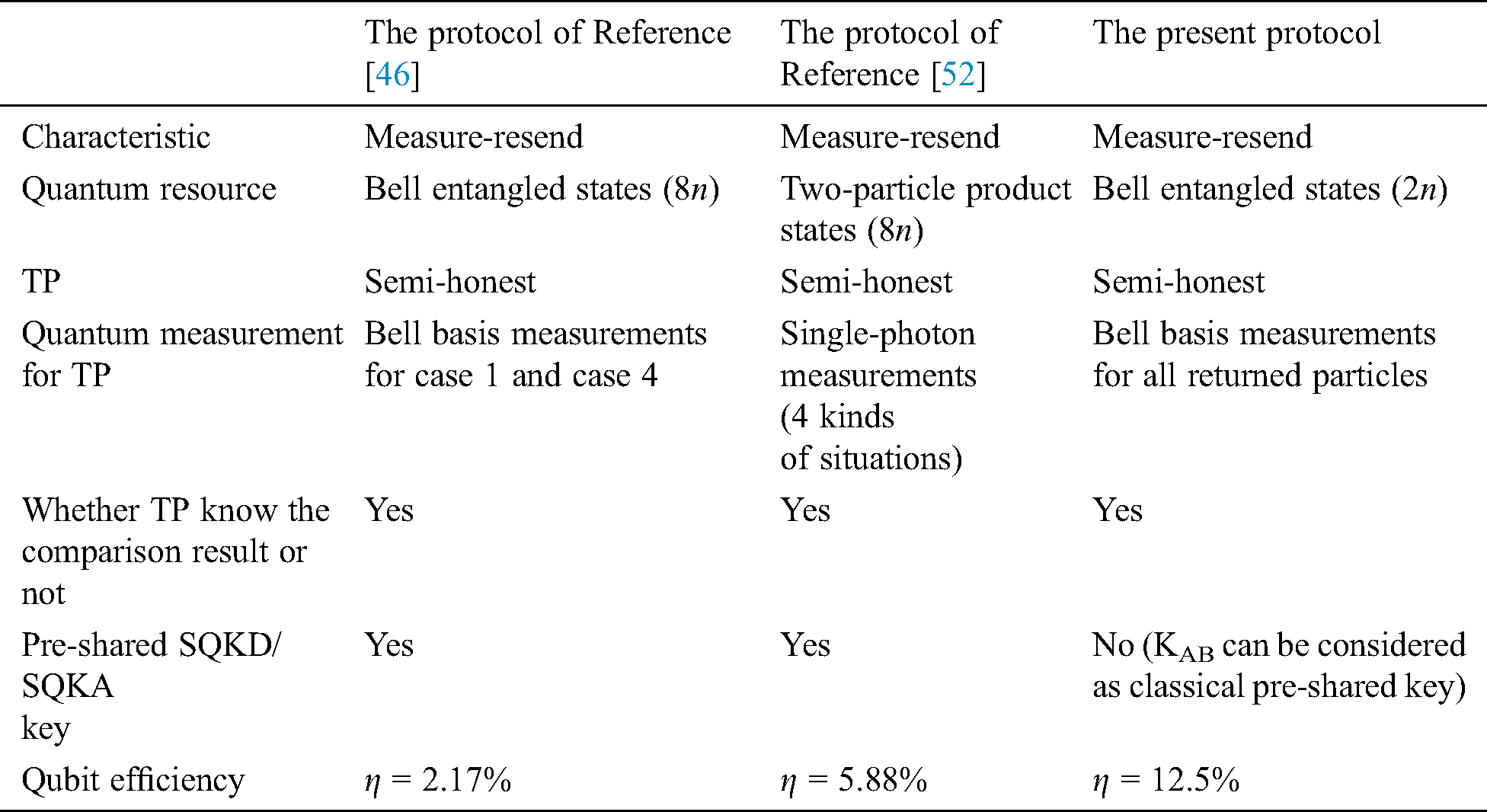
In this subsection, we aim to compare the efficiency of the proposed protocol with an SQPC protocols from References [46,52] .
In terms of the quantity of the preparation of initial states and workload of the participants, this protocol is better than Reference [46]. Assuming that the lengths of secret information of all three protocols are the same, the initial two qubits states we need to prepare (2n bits) are 1/4 of the previous protocols of References [46,52]. According to the value of KAB, classical Alice and Bob perform the MEASURE or REFLECT operation, which is different from the previous protocols. Meanwhile, TP does not need to classify the returned particles and make Bell basis measurement.
In addition, the qubits’ efficiency of the proposed protocol is highest among these three protocols. The qubits efficiency [53] of the proposed SQPC protocol is defined as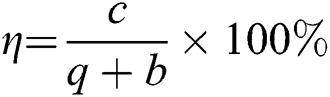 
, where c, q and b are the numbers of secret bits, the qubits used and the classical bits involved, respectively.
As for the proposed protocol, in order to compare n-bit secret information of Alice and Bob (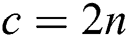
), TP needs to prepare 2n-bit Bell states (4n), and Alice and Bob prepare 2n-bit new qubits to send back to TP. Thus 
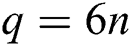. As for the classical bits of the protocol, the length of secret information is n bits. Alice and Bob share KAB (2n) before preforming the protocol, and they need to publish the sequence of KAB in Step 4. Meanwhile, TP needs to publish the announcement by using three qubits. Thus 
. Its qubit efficiency is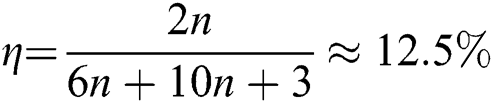 
. In addition, the qubit efficiencies of SQPC protocol from References [46,52] are 
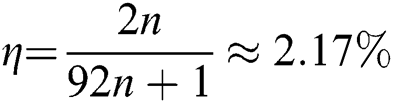and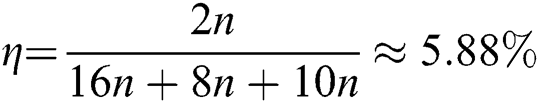 
, respectively. References [46,52] the comparison results are summarized in Tab. 3.
Table 3: The comparison of our SQPC protocol and the two similar SQOC protocols
In this paper, we have proposed a novel SQPC protocol with detailed procedures based on Bell entangled states. As the only quantum participant, TP can calculate the equivalence of private information of Alice and Bob, but he cannot obtain any private information of them. In addition, TP only needs to release 1 qubit through public channel to announce whether their private information is same. In addition, the paper has shown the detail of security against some eavesdropping attacks, and the qubit efficiency of the proposed scheme is higher than two other protocols.
Meanwhile, the quantum participants need several techniques in the scheme, such as the generation of Bell states in Reference [54] and the quantum storage techniques in Reference [55]. After focusing on semi-quantum use, we are looking forward to analyzing the effect of noisy environment or noise channel. As mentioned in References [46,52] , there are various noise models, such as amplitude damping (AD) channels, bit flip (BF) channels, phase flip (PF) channels and depolarizing channels (DC). Different noise environments have different influence on quantum states and need to be analyzed separetedly.
As for the decoherence noise channel, the coupling of the quantum system to the environment will cause the decay of quantum information. It can be described as:
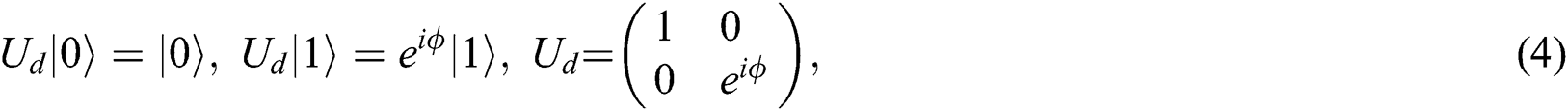
where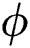 
is the parameters of the noise. It means that 
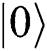does not change and 
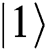has a phase shift of 
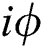after transferring in the noise channel. Furthermore, we also find out that 
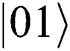and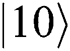 
cannot change in the channel because they have the same phase shift of 
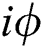. In this protocol, TP needs to prepare 2N Bell states as quantum resources. TP can prepare the Bell state 
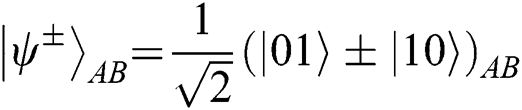in the state of 
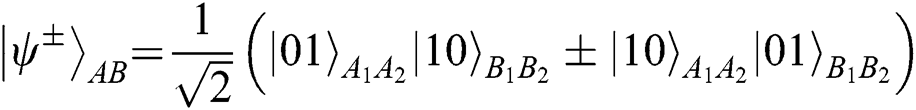to ensure that the Bell states will not change, but it only works in the situation of Alice and Bob’s choosing the operation of REFLECT. Once they make MEASURE, 
(
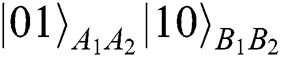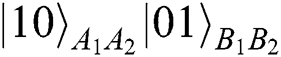), it will induce error. They only have the ability of single-photon measurement in the classical basis, and TP cannot obtain the actual results of comparison.
Further, future studies will focus on analyzing the impact of the noise channel to quantum cryptography protocols and preventing the classical users’ operations from the influence of noise channels. Our studies also continue to track the possibilities between block-chain and quantum secure communication in Reference [56].
Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant Nos. 61402058, 61572086), Major Project of Education Department in Sichuan (Grant No. 18ZA0109), and Web Culture Project Sponsored by the Humanities and Social Science Research Base of the Sichuan Provincial Education Department (Grant No. WLWH18-22).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. C. H. Bennett, H. Charles and G. Brassard. (2014). “Quantum cryptography: Public key distribution and coin tossing,” Theoretical Computer Science, vol. 560, no. 1, pp. 7–11. [Google Scholar]
2. A. K. Ekert. (1991). “Quantum cryptography based on Bell’s theorem,” Physical Review Letters, vol. 67, no. 6, pp. 661.
3. C. H. Bennett, G. Brassard and N. D. Mermin. (1992). “Quantum cryptography without Bell’s theorem,” Physical Review Letters, vol. 68, no. 5, pp. 557.
4. P. W. Shor and J. Preskill. (2000). “Simple proof of security of the BB84 quantum key distribution protocol,” Physical Review Letters, vol. 85, no. 2, pp. 441–444. [Google Scholar]
5. G. L. Long and X. S. Liu. (2002). “Theoretically efficient high-capacity quantum-key-distribution scheme,” Physical Review A, vol. 65, no. 3, pp. 644. [Google Scholar]
6. W. Zhang, D. S. Ding, Y. B. Sheng, L. Zhou, B. S. Shi et al. (2017). , “Quantum secure direct communication with quantum memory,” Physical Review Letters, vol. 118, no. 22, pp. 220501.
7. F. Zhu, W. Zhang, Y. Sheng and Y. Huang. (2017). “Experimental long-distance quantum secure direct communication,” Science Bulletin, vol. 62, no. 22, pp. 1519–1524.
8. P. H. Niu, Z. R. Zhou, Z. S. Lin, Y. B. Sheng, L. G. Yin et al. (2018). , “Measurement-device-independent quantum communication without encryption,” Science Bulletin, vol. 63, no. 20, pp. 1345–1350.
9. J. Y. Hu, B. Yu, M. Y. Jing, L. T. Xiao, S. T. Jia et al. (2016). , “Experimental quantum secure direct communication with single photons,” Light: Science & Applications, vol. 5, no. 9, e16144.
10. R. Qi, Z. Sun, Z. Lin, P. Niu, W. Hao et al. (2019). , “Implementation and security analysis of practical quantum secure direct communication,” Light: Science & Applications, vol. 8, no. 1, pp. 22.
11. Y. Sun, Y. L. Chen, A. Haseeb and H. W. Zhan. (2019). “An asymmetric controlled bidirectional quantum state transmission protocol,” Computers, Materials & Continua, vol. 59, no. 1, pp. 215–227.
12. J. F. Zhong, Z. H. Liu and J. Xu. (2018). “Analysis and improvement of an efficient controlled quantum secure direct communication and authentication protocol,” Computers, Materials & Continua, vol. 57, no. 3, pp. 621–633. [Google Scholar]
13. C. Kurtsiefer, P. Zarda, M. Halder, P. M. Gorman, P. R. Tapster et al.,. (2002). “Quantum optics in computing and communications,” S. Liu, G. Guo, H. K. Lo and N. Imoto (eds.Bellingham, WA: SPIE, vol. 4917, 25. [Google Scholar]
14. A. Karlsson, M. Koashi and N. Imoto. (1999). “Quantum entanglement for secret sharing and secret splitting,” Physical Review A, vol. 59, no. 1, pp. 162–168.
15. L. Xiao, G. L. Long, F. G. Deng and J. W. Pan. (2004). “Efficient multiparty quantum-secret-sharing schemes,” Physics, vol. 69, no. 5, pp. 521–524. [Google Scholar]
16. R. Cleve, D. Gottesman and H. K. Lo. (1999). “How to share a quantum secret,” Physical Review Letters, vol. 83, no. 3, pp. 648–651. [Google Scholar]
17. H. Mark, V. Buzĕk and A. Berthiaume. (1999). “Quantum secret sharing,” Physical Review Letters A, vol. 59, no. 3, pp. 1829–1834.
18. A. Karlsson, M. Koashi and N. Imoto. (1999). “Quantum entanglement for secret sharing and secret splitting,” Physical Review A, vol. 59, no. 1, pp. 162–168.
19. S. J. Qin, F. Gao, Q. Y. Wen and F. C. Zhu. (2006). “Improving the security of multiparty quantum secret sharing against an attack with a fake signal,” Physics Letters A, vol. 357, no. 2, pp. 101–103.
20. Y. G. Yang, Y. Wang, H. P. Chai, Y. W. Teng and H. Zhang. (2011). “Member expansion in quantum (t, n) threshold secret sharing schemes,” Optics Communications, vol. 284, no. 13, pp. 3479–3482.
21. Q. Li, D. Y. Long, W. H. Chan and D. W. Qiu. (2011). “Sharing a quantum secret without a trusted party,” Quantum Information Processing, vol. 10, no. 1, pp. 97–106.
22. R. H. Shi, L. S. Huang, W. Yang and H. Zhong. (2011). “Asymmetric multi-party quantum state sharing of an arbitrary m-qubit state,” Quantum Information Processing, vol. 10, no. 1, pp. 53–61.
23. H. Y. Jia, Q. Y. Wen, T. T. Song and F. Gao. (2011). “Quantum protocol for millionaire problem,” Optics Communications, vol. 284, no. 1, pp. 545–549. [Google Scholar]
24. A. C. Yao. (1982). “Protocols for secure computations,” in Proc. of the 23rd Annual IEEE Symposium on Foundations of Computer Science, pp. 160–164. [Google Scholar]
25. Y. G. Yan and Q. Y. Wen. (2009). “An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement,” Journal of Physics A, vol. 42, no. 26, pp. 30. [Google Scholar]
26. X. B. Chen, G. Xu, X. X., Q. Y. Wen and Y. X. Yang. (2010). “An efficient protocol for the private comparison of equal information based on the triplet entangled state and single-particle measurement,” Optics Communications, vol. 283, no. 7, pp. 1561–1565.
27. L. Olejnik. (2011). “Secure quantum private information retrieval using phase-encoded queries,” Physical Review A, vol. 84, no. 2, pp. 3242–3244.
28. H. Y. Tseng, J. Lin and T. Hwang. (2012). “ New quantum private comparison protocol using EPR pairs,” Quantum Information Processing, vol. 11, no. 2, pp. 373–384. [Google Scholar]
29. H. Y. Jia, Y. B. Li and F. Gao. (2012). “Quantum private comparison using genuine four-particle entangled states,” International Journal of Theoretical Physics, vol. 51, no. 4, pp. 1187–1194.
30. W. Liu, Z. T. Jiang and Y. Z. Cao. (2012). “A protocol for the quantum private comparison of equality with -type State,” International Journal of Theoretical Physics, vol. 51, no. 1, pp. 69–77.
31. Y. G. Yang, W. F. Cao and Q. Y. Wen. (2009). “Secure quantum private comparison,” Physica Scripta, vol. 80, no. 6, pp. 65002.
32. B. Liu, F. Gao, H. Y. Jia, W. Huang, W. W. Zhang et al. (2013). , “Efficient quantum private comparison employing single photons and collective detection,” Quantum Information Processing, vol. 12, no. 2, pp. 887–897. [Google Scholar]
33. W. Liu, Y. B. Wang, Z. T. Jiang, Y. Z. Cao and W. Cui. (2012). “New quantum private comparison protocol using χ-type state,” International Journal of Theoretical Physics, vol. 51, no. 6, pp. 1953–1960. [Google Scholar]
34. Y. G. Yang, J. Xia and X. Jia. (2013). “Comment on quantum private comparison protocols with a semi-honest third party,” Quantum Information Processing, vol. 12, no. 2, pp. 877–885. [Google Scholar]
35. L. Wen, Y. B. Wang and W. Cui. (2012). “Quantum private comparison protocol based on bell entangled states,” Communications in Theoretical Physics, vol. 57, no. 4, pp. 583–588. [Google Scholar]
36. J. Lin, H. Y. Tseng and T. Hwang. (2011). “Intercept-resend attacks on Chen et al.’s quantum private comparison protocol and the improvements,” Optics Communications, vol. 284, no. 9, pp. 2412–2414.
37. Y. J. Chang, C. W. Tsai and T. Hwang. (2013). “Multi-user private comparison protocol using GHZ class states,” Quantum Information Processing, vol. 2, no. 2, pp. 1077–1088. [Google Scholar]
38. S. Lin, Y. Sun, X. F. Liu and Z. Q. Yao. (2013). “Quantum private comparison protocol with d-dimensional Bell states,” Quantum Information Processing, vol. 12, no. 1, pp. 559–568. [Google Scholar]
39. T. Y. Ye and Z. X. Ji. (2017). “Two-party quantum private comparison with five-qubit entangled states,” International Journal of Theoretical Physics, vol. 56, no. 5, pp. 1517–1529.
40. C. Q. Ye and T. Y. Ye. (2018). “Multi-party quantum private comparison of size relation with d-level single-particle states,” Quantum Information Processing, vol. 17, no. 10, pp. 252. [Google Scholar]
41. H. G. Ping. (2018). “Device-independent quantum private comparison protocol without a third party,” Physica Scripta, vol. 93, no. 9, pp. 95001. [Google Scholar]
42. L. Huang, T. Sheng, P. Hwang and P. Gope. (2016). “Multi-Party quantum private comparison protocol with an almost-dishonest third party using GHZ states,” International Journal of Theoretical Physics, vol. 55, no. 6, pp. 1–8. [Google Scholar]
43. M. Boyer, D. Kenigsberg and T. Mor. (2007). “Quantum key distribution with classical Bob,” Physical Review Letters, vol. 99, no. 14, pp. 140501. [Google Scholar]
44. M. Boyer, G. Gelles, R. Kenigsberg and T. Mor. (2009). “Semi-quantum key distribution,” Physical Review A, vol. 79, no. 3, pp. 32341. [Google Scholar]
45. W. H. Chou, T. Hwang and J. Gu. (2016). “Semi-quantum private comparison protocol under an almost-dishonest third party. arXiv preprint, vol. 1607, no. 7961. [Google Scholar]
46. K. Thapliyal, R. D. Sharma and A. Pathak. (2018). “Orthogonal-state-based and semi-quantum protocols for quantum private comparison in noisy environment,” International Journal of Quantum Information, vol. 16, no. 5, pp. 1850047. [Google Scholar]
47. Y. F. Lang. (2018). “Semi-quantum private comparison using single photons,” International Journal of Theoretical Physics, vol. 57, no. 10, pp. 3048–3055. [Google Scholar]
48. Z. Sun, J. Yu, P. Wang, L. Xu and C. Wu. (2015). “Quantum private comparison with a malicious third party,” Quantum Information Processing, vol. 14, no. 6, pp. 2125–2133. [Google Scholar]
49. W. O. Krawec. (2015). “Mediated semi-quantum key distribution,” Physical Review A, vol. 91, no. 3. [Google Scholar]
50. Q. Y. Cai. (2006). “Eavesdropping on the two-way quantum communication protocols with invisible photons,” Physics Letters A, vol. 351, no. 1–2, pp. 23–25. [Google Scholar]
51. F. G. Deng, X. H. Li, H. Y. Zhou and Z. J. Zhang. (2005). “Improving the security of multiparty quantum secret sharing against Trojan horse attack,” Physical Review A, vol. 72, no. 4, pp. 44302–44450. [Google Scholar]
52. T. Y. Ye and C. Q. Ye. (2018). “Measure-resend semi-quantum private comparison without entanglement,” International Journal of Theoretical Physics, vol. 57, no. 12, pp. 3819–3834. [Google Scholar]
53. A. Cabello. (2000). “Quantum key distribution in the Holevo limit,” Physical Review Letters, vol. 85, no. 1, pp. 5635–5638. [Google Scholar]
54. B. B. Vladimir. (1994). “Quantum measurement,” Physics Today, vol. 47, no. 1, pp. 46–47. [Google Scholar]
55. D. F. Phillips, A. Fleischhauer, A. Mair, R. L. Walsworth and M. D. Lukin. (2001). “Storage of light in atomic vapor,” Physical Review Letters, vol. 86, no. 5, pp. 783. [Google Scholar]
56. Y. Ren, F. Zhu, P. K. Sharma, T. Wang, O. Alfarraj et al. (2020). , “Data query mechanism based on hash computing power of block-chain in Internet of Things,” Sensors, vol. 20, no. 1, pp. 207. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |