DOI:10.32604/cmc.2021.012698
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012698 | |
| Article |
The Controllability of Quantum Correlation under Geometry and Entropy Discords
1School of Information and Software Engineering, University of Electronic Science and Technology of China, Chengdu, 610054, China
2School of Physics, University of Electronic Science and Technology of China, Chengdu, 610054, China
3Department of Chemistry and Biochemistry, Utah State University, Logan, Utah, 84322, USA
4School of Computer Science, Southwest Petroleum University, Chengdu, 610000, China
*Corresponding Author: Qinsheng Zhu. Email: zhuqinsheng@gmail.com
Received: 09 July 2020; Accepted: 25 October 2020
Abstract: Quantum correlation plays a critical role in the maintenance of quantum information processing and nanometer device design. In the past two decades, several quantitative methods had been proposed to study the quantum correlation of certain open quantum systems, including the geometry and entropy style discord methods. However, there are differences among these quantification methods, which promote a deep understanding of the quantum correlation. In this paper, a novel time-dependent three environmental open system model is established to study the quantum correlation. This system model interacts with two independent spin-environments (two spin-environments are connected to the other spin-environment) respectively. We have calculated and compared the changing properties of the quantum correlation under three kinds of geometry and two entropy discords, especially for the freezing phenomenon. At the same time, some original and novel changing behaviors of the quantum correlation under different time-dependent parameters are studied, which is helpful to achieve the optimal revival of the quantum discord and the similar serrated form of the freezing phenomenon. Finally, it shows the controllability of the freezing correlation and the robustness of these methods by adjusting time-dependent parameters. This work provides a new way to control the quantum correlation and design nanospintronic devices.
Keywords: Spin environment; quantum correlation; nanospintronic devices; quantum information; freezing phenomenon
As an important part of quantum theory, quantum correlation shows some unimaginable properties of composite quantum systems that cannot be reproduced by classical systems. It has been widely studied in many physical fields, such as quantum information [1] and condensed matter physics [2]. Ollivier et al. [3], Henderson et al. [4] extend the mutual information concept of classical information theory to the quantum field and give the concept of quantum discord (QD) to quantify the quantum correlation by the von Neumann entropy, it has been demonstrated that entanglement represents a portion of the quantum correlation and can cover the latter for a global pure state entirely [5]. The minimum is required for all in quantum discord calculation and the tool of tomography [6] is usually needed to quantify the von Neumann entropy. Many efforts have been devoted to find the new quantification methods (QMS) in recent years, including Hilber–Schmidt [7], Bures distance, trace-norm and Hellinger [8] and the Rènyi entropy discord(RED) [9,10]. Generally, it is still an open problem about how to search the most optimal quantification method for a deterministic model, because there are subtle discrepancies between different methods. There are some subtle differences [9] not only between these geometry discord (GD) under the same condition, but also between the QD and GD. In prior studies, the Rènyi entropy had been found easy to implement experiment and probe as an equivalent definition of quantified information in information theory (Shannon and the Rènyi definition), which has aroused much attention to the Rènyi entropy discord (RED) [10].
In the realistic world, the quantum correlation of a quantum system unavoidably decreases with the system information continuously losing due to the experimental observation and applied field or the interaction between the surrounding environment and the system. Therefore, it is necessary to study the quantum correlation of the quantum open systems (QQS) [11]. From the dynamics process perspectives of these QQS, the dynamics of QQS can be represented as a quantum channel mapping from an initial state to a final state. Meanwhile, these channels generally show Markovian and non-Markovian dynamical behaviors and arouse many unique properties of the quantum system for different QQS models, such as the revival and the freezing [5,12] phenomenon of the quantum correlation. Under Markovian condition, the quantum system exhibits the irreversible dynamics features governed by a nonunitary time evolution, and quantum correlation also exhibits monotone decrease or disappearance at a finite time and freezing phenomenon. However, the non-Markovian process shows the reversible dynamic features for local time. It displays the system information feedback from environments to the system. The freezing phenomenon may also appear for some QQS [3,12] models because the revival phenomenon (feedback process). It is natural to ask, when the freezing phenomenon occurs, what are the conditions corresponding to various quantization methods and whether these conditions are the same.
In the application of quantum correlation, the quantum engineering has developed an alternative approach to improve the efficiency of computation, communication and metrology [1,13] in the last 30 years. For an open quantum system, the main obstacle is that the relatively fragile quantum correlation is easily destroyed, which has led to the research of how to control and maintain quantum correlation. In the previous manuscript [13], the quantum effect (such as memory effect) of the model is awakened by applying some time-dependent control fields (the quantum time-dependent open systems.), such as sequentially switching on/off plus fields. Therefore, it presents an interesting problem with the control of the quantum memory effect, including revival and freezing quantum correlation.
According to the above problems and our previous works [9,12,14,15], a time-dependent open system model is proposed, and several geometric and entropy-type incompatible quantum correlations are further studied. At the same time, several different time-dependent parameter conditions are studied to achieve the controllability of quantum correlation (resurrection correlation and freezing correlation), including the coupling parameters q12(t) and q23(t) between the environment and the time-dependent control field.
2 The Different Quantification Method of QC
Based on the Hilbert–Schmidt distance, Dakic introduced the geometric measure of discord [7] as Eq. (1):
The minimum is under the set of zero-discord states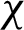 
.
Piani [16] later indicated that a factor could be introduced for the quantum correlation by a factorized local ancillary state on the unmeasured party. Another geometric measure of discord was put forward based on the classical Hellinger distance [17], which was defined as Eq. (2):
Here the minimum is taken over all local von Neumann measurement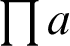 
on party a and ||.|| is the Hilbert-Schmidt distance.
Recently, the Bures distance describing the geometric distance between any two quantum states in projective Hilbert space has been used to quantify the quantum correlation. The discord-type correlations Q of a state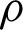 
is defined as Eq. (3) [5]:
where the set of classical-quantum states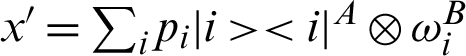 
, pi is a probability distribution, 
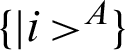denotes an orthonormal basis for subsystem A, 
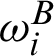is an arbitrary ensemble of states for subsystem B. 
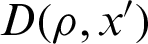is the square of the Bures distance. Then, a common Bures distance between two states 
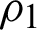and 
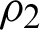is defined as Eq. (4):
where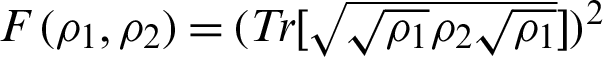 
is the Uhlmann fidelity [1].
For a given quantum state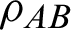 
of a composite system AB, the quantum discord of the state 
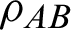under measurement 
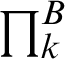can be defined as Eq. (5) [3,4]:
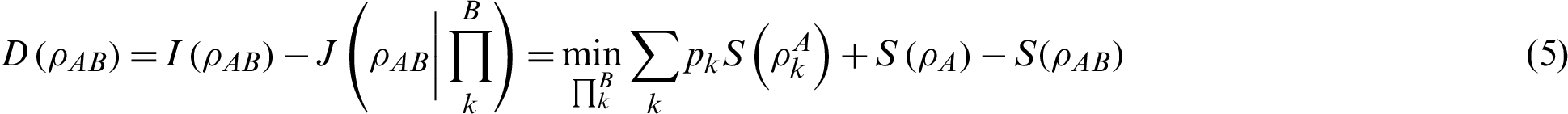
Here the von Neumann entropy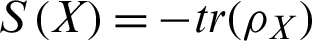 
is for the density operator 
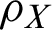of system X and 
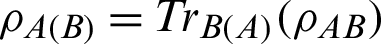is the reduced density matrix by tracing out the degree of system B(A). 
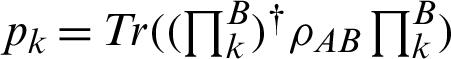and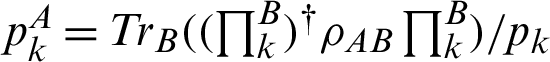 
.
Usually, Rènyi entropy is defined as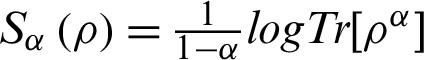 
, with the parameter 
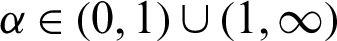and the natural logarithm of the base 2. Notably, the Rènyi entropy can reduce to the von Neumann entropy when 
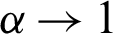. This has exhibited some superiority from quantum physics to gravity field, especially in the experimental probe problem of entropy [18]. Therefore, the 
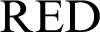is defined as Eq. (6) [19]:
with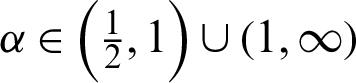 
and
Here the minimum is taken over all the density matrices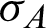 
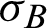and 
, and
with Pi performing rank-1 projective measurements.
Despite the different Rènyi generalizations of the quantum discord, we only focus on the properties of quantum correlation, where the relationship of different Rènyi discord definition is not considered here. Thus we choose the Rènyi discord of Eq. (6) with the similar form to Eq. (5).
3 The Hamiltonian of Quantum System
Two independent spin particles 1 and 3 (each with spin 1/2) are constructed, forming a two qubits system, and each spin particle interacts with one Fermi-environment (E1 or E3, with spin 1/2 for each particle), respectively [9]. These two Fermi-environments are related by interacting with the third Fermi-environment E2 (each particle rotates 1/2). Simultaneously, a time-dependent controlling field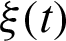 
is applied to the environments with the time-dependent interaction parameters q12(t) and q23(t) between the environments. This model can be realized by a spin cluster adsorbed on graphene substrate [20]. The Hamiltonian of this open system is given as Eq. (11) (ℏ = 1):
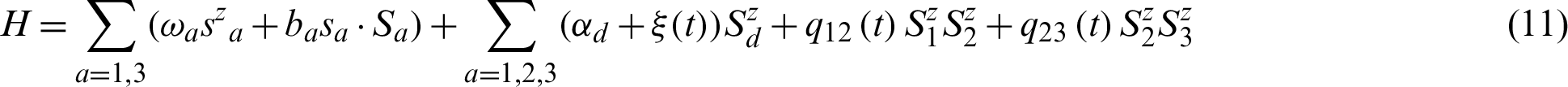
where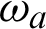 
(a = 1, 3) and 
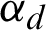(d = 1, 2, 3) are the frequencies of the qubit (characterized by spin operators si) and the environments, respectively. q12(t) (q23(t)) is the time-dependent coupling parameters between the environment 1 (3) and the environment 2. Each environment consists of Nd particles and 
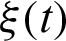is the controlling field. The interaction intensity between the spin particle 1 (3) and the environment 1 (3) is b1 (b3); 
, 
, 
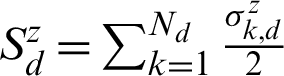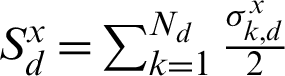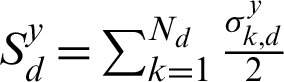are the collective spin operators of environments. 
,
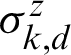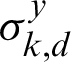and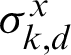 
are the Pauli matrices.
The reduced density operator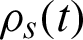 
of the system can be obtained by integrating out the degrees of freedom of the environments for the density operator 
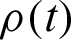of the total system shown as Eq. (12).
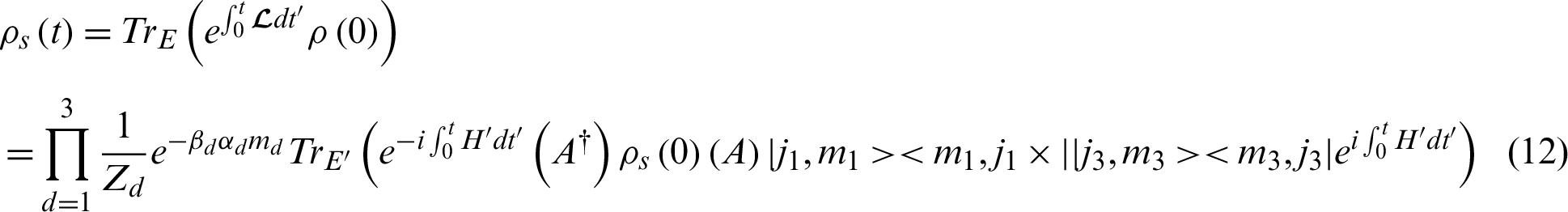
where the super operator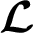 
satisfies 
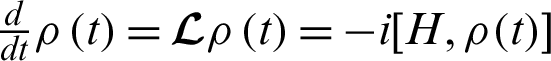and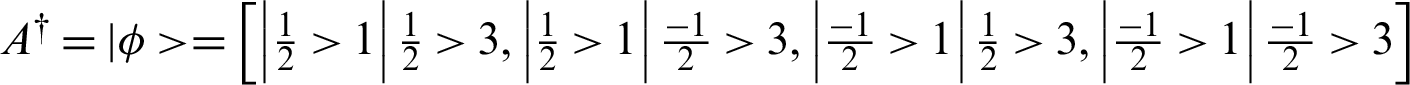 
; 
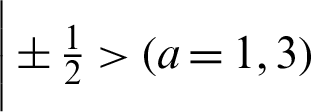denotes the spin of particle a.
Ding et al. [9] had the similar detailed calculation process with Eq. (12), because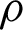 
s (t) has a complicated analytical expression.
4 The Quantum Correlation of X and SCI States
Figs. 1–5 show the revival and freezing phenomenon of the quantum correlation for X [5] and SCI [21] initial states by DHS, DHL, DBR, QD and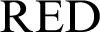 
. The revival phenomenon displays the periodical oscillation (the oscillation period depends on the parameter b [9]), with the maximum of the revival strengthen monotonously decreasing with time t. The freezing phenomenon also exists for different parameter conditions. Here, Tab. 1 compares some characteristics of different QMS in terms of recovery and freezing of quantum correlation. The following properties can be obtained:
1. The numerical searches indicate that the maximal revival strengthen has the same or approximately equal value for X and SCI initial states.
2. The different changing behaviors of quantum correlation only exist for non-maximal revival strengthens of X and SCI initial states.
3. Although all DHS, DHL, DBR and QD show the freezing phenomenon for the same and different initial states, The freezing phenomenon of different quantifiers definitely answers a question: “Is the freezing phenomenon purely a mathematical accident, due to the specific choice of quantum-related quantifiers, or must it be manifested independently of the measures used? [5]” (It only answer No to the geometric quantify measurement). At the same time, it also implies that the quantum-related freezing phenomenon is a universal quantum feature and has profound physical significance.
4. For the same SCI initial states, the DHL, DBR and QD show the conformity behavior of the freezing phenomenon. This property also means that the DHL, DBR and QD are better than DHS for the quantification of quantum correlation (References [5,16,17] have discussed some bad properties of DHS).
5. In the geometric quantification DHS, DHL and DBR, the value of the frozen platform satisfies DBR > DHS = DHL. It also hints that the Bures distance quantification method [5] is better than the other two measurement methods.
6. From the last two columns of Tab. 1, the SCI and X initial states of freezing conditions have the same diagonal and anti-diagonal elements. However, only DBR can present the contribution of the non-diagonal elements to the quantum correlation. This property can not only be useful for the experimental measurement of the quantum correlation but also shows the advantages of the Bures distance over the other geometric quantification measurements.
7. Since searching for the minimum relative entropy distance of the states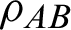 
and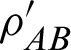 
from the set of all completely uncorrelated states 
is complicated, the analytic and numerical solutions of Eq. (6) are quite difficult for general states. Considering our model, the symmetries of the X initial states are researched under the symmetrical environment (Avijit et al. [19] also discussed some special states). Fig. 5 shows the changing behaviors of RED for a X initial state with a = 0:4; b = c = 0:1; 
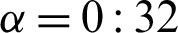and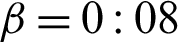 
under different parameters 
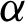. Similar to the above discord, some properties in Fig. 4 are obtained as follows. (i) The revival phenomenon also exists and displays the periodical oscillation for different parameters 
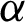. (ii) For different 
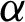, the minimum value of RED is not equal to zero and remains constant in several periods. So the freezing phenomenon also exists. (iii) The value of RED is not monotonous with the parameter 
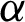[10]. (iv) The maximum of RED increases with the increase of 
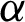. The comparison between RED and the other methods is presented in Tab. 12. Notably, Eq. (12) does not give the changing behaviors for 
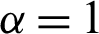because of the divergence [10].
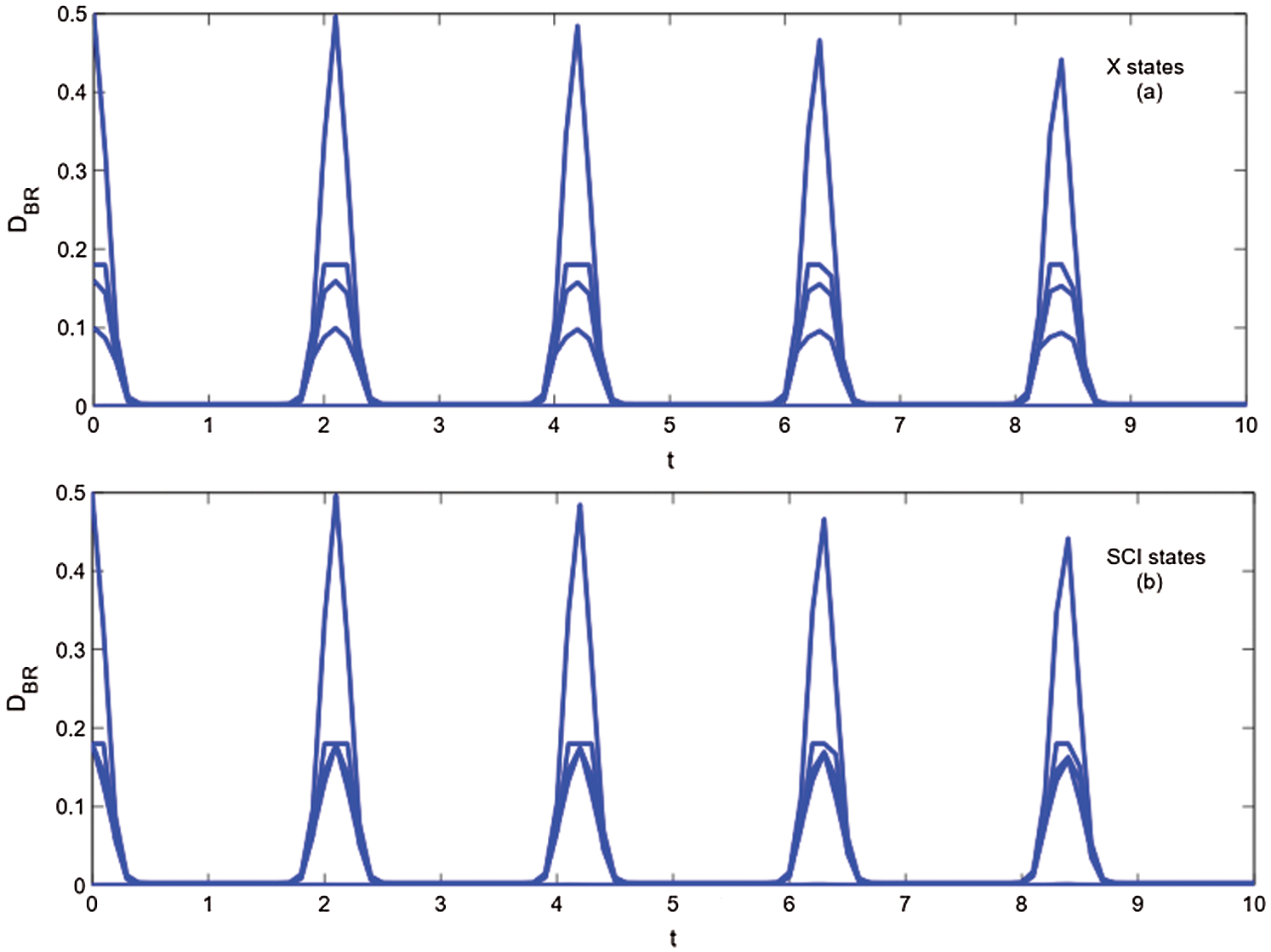
Figure 1: The properties of Bures distance discord as a function of time t for X initial states. The parameters are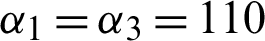 
ps−1, 
ps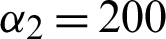−1, 
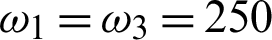ps−1;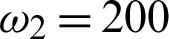 
ps−1, q12(t) = q23(t) = 50 ps−1, 
, 
, 
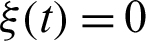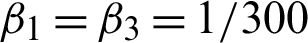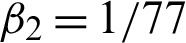, N1 = N3 = 10, N2 = 30 and b1 = b3 = 3 ps−1 for this and also the following Figs. 2–5
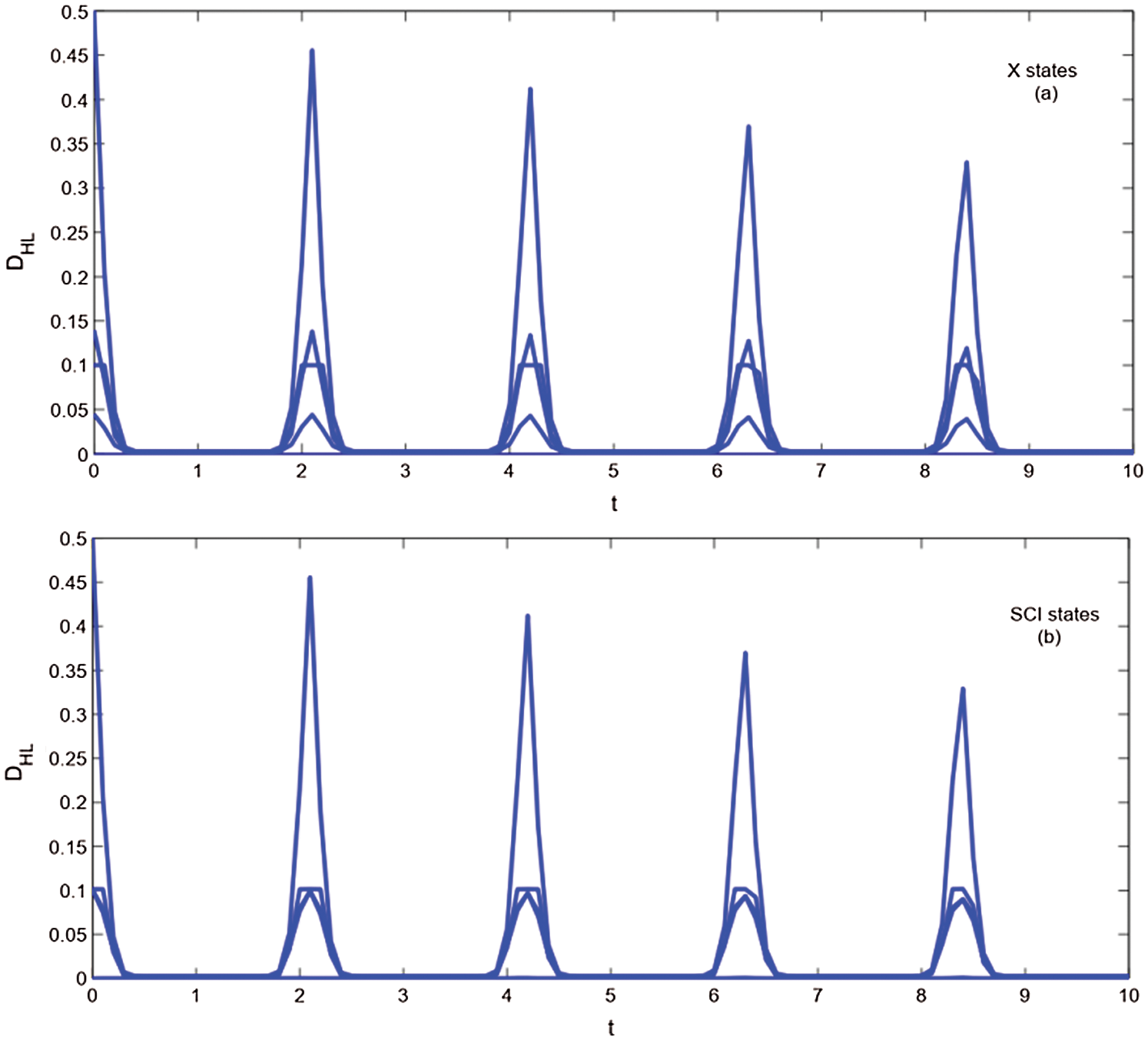
Figure 2: The properties of Hellinger distance discord as a function of time t for X initial states
Figure 3: The properties of Hilber–Schmidt distance discord as a function of time t for X initial states
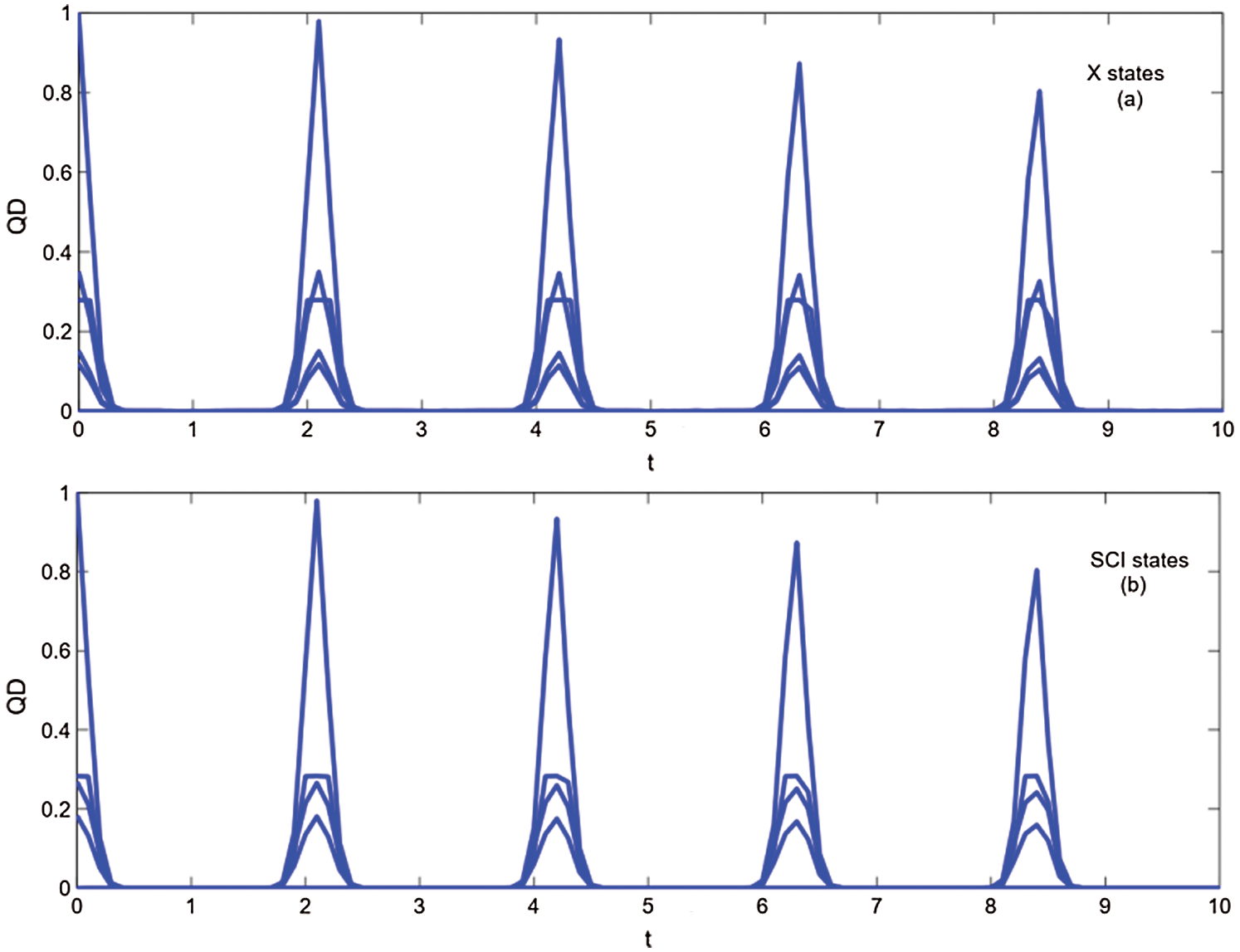
Figure 4: The properties of quantum discord as a function of time t for X initial states
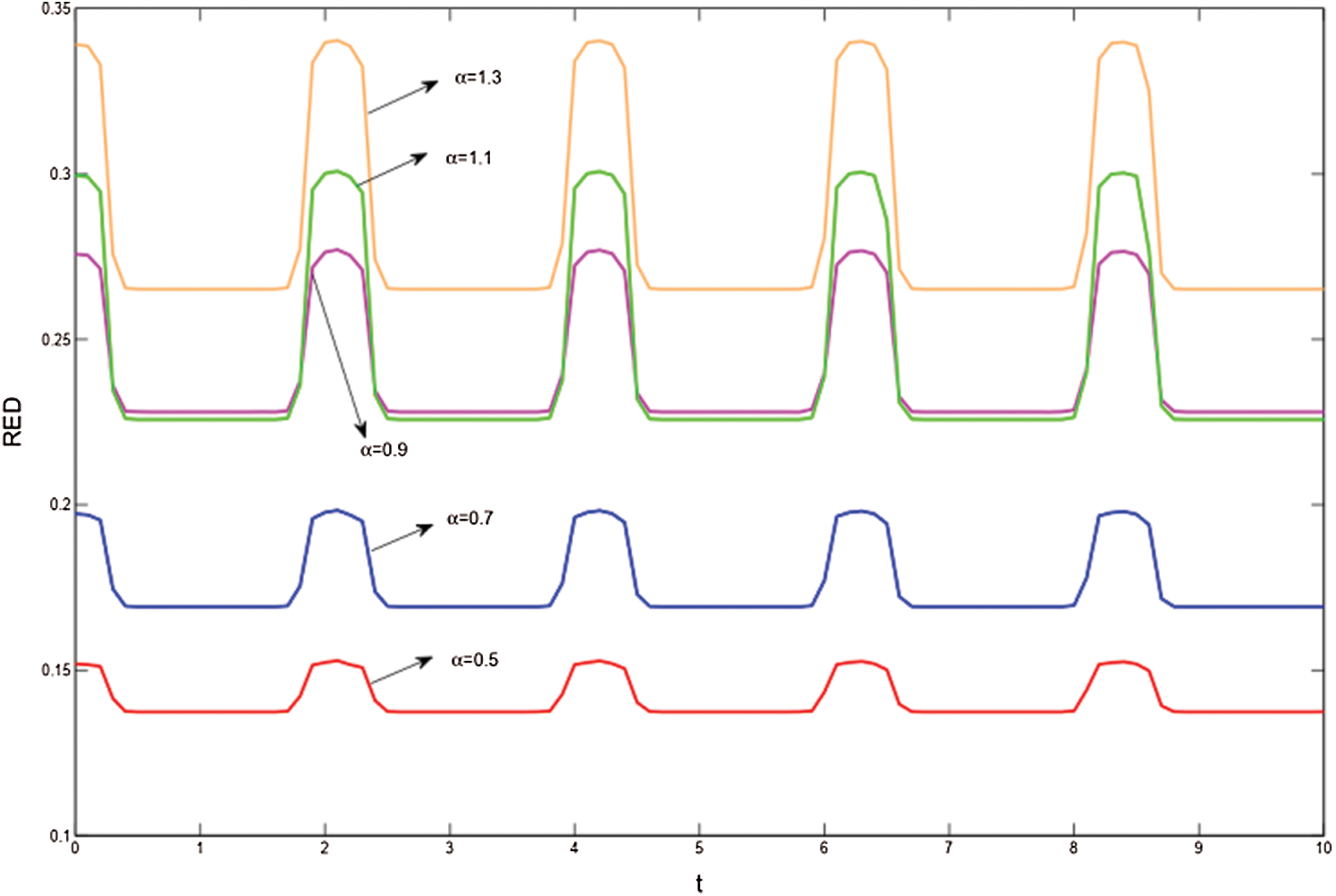
Figure 5: The properties of Rènyi entropy discord as a function of time t for X initial state which satisfies a = 0.4; b = c = 0.1;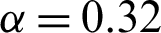 
and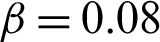 
Table 1: Comparison of the various QMS
5 The Controllability of Quantum Correlation
In this section, we study the influence of time-dependent parameters q12(t), q23(t) and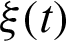 
on quantum correlation to show the controllability of quantum correlation. According to the nature of the resurrection and freezing phenomenon in Figs. 1–5, the controllability of the maximum resurrection and freezing phenomenon of the X state is proved by the method of Bures distance inconsistency.
5.1 The Controllability of the Freezing Phenomenon
By using the Bures distance inconsistency, the freezing phenomenon is shown as a function of the time t of X initial states, as shown in Fig. 6. Some special properties are obtained: (1) The red solid line shows the similar serrated form of the freezing phenomenon with q12(t) = q23(t) flip back and forth between 0 and 50 ps−1. (2) Comparing the behaviors of red solid line with blue dash line, the platform can soon collapse for smaller q12(t) and q23(t) which may affect the appearance of the freezing platform. Noticing the different styles of red solid line and blue dash line at the time t = 2 s, it stems from q12(t) and q23(t) jumping from 50 to 0 ps−1 at this time and arouses the collapse of the freezing platform. Then the freezing platform recovers with q12(t) = q23(t) jumping to 50 ps−1 in the next time interval.
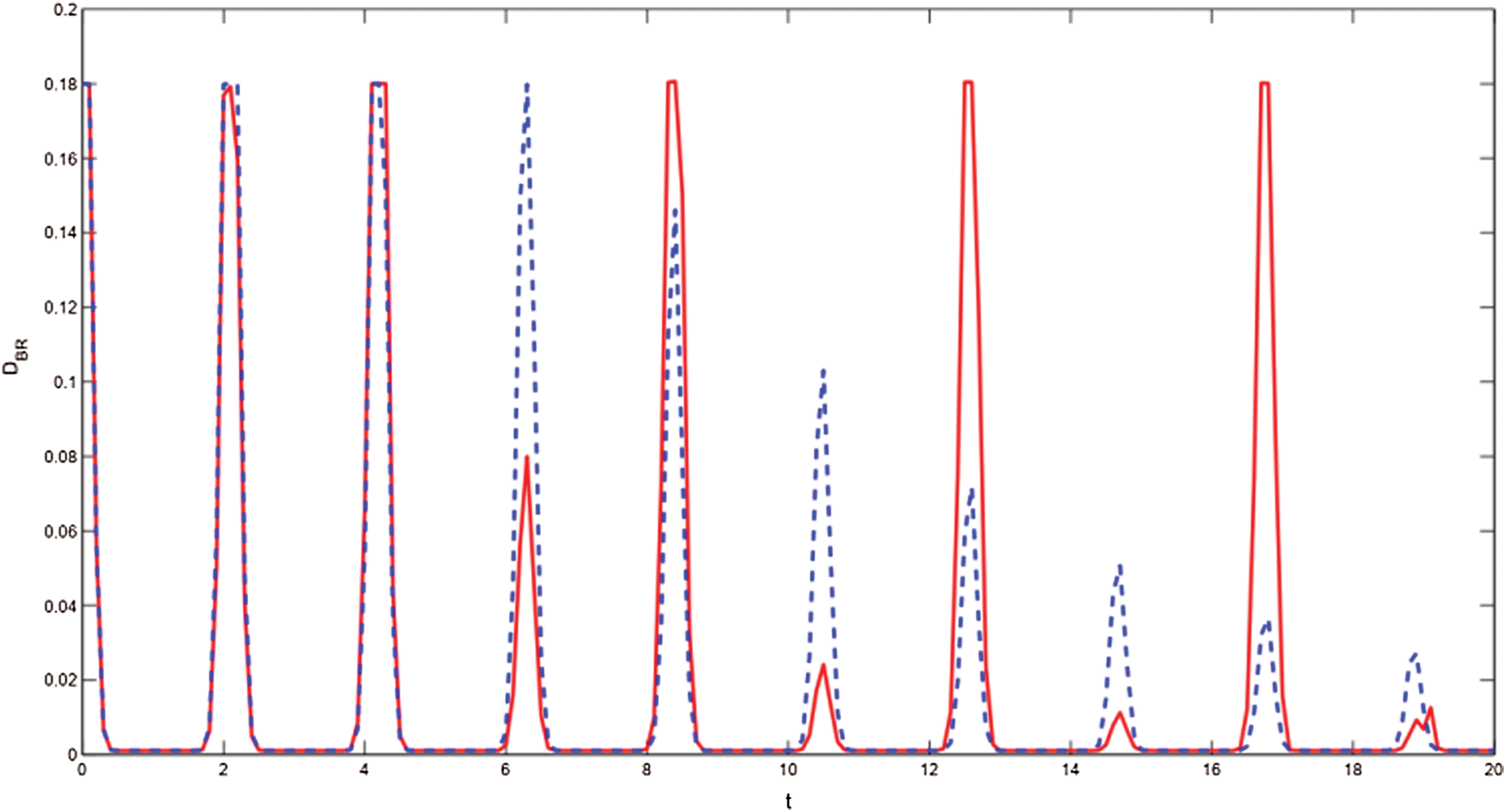
Figure 6: Under the condition of inconsistent Bures distance, the freezing phenomenon of X initial states changes with time t. The red solid line displays the changing behaviors of quantum correlation for jump function q12(t) and q23(t), satisfying q12(t) = q23(t) = 0 for 
, otherwise q12(t) = q23(t) = 50 ps−1. The blue dash line displays the changing behaviors of quantum correlation for q12(t) = q23(t) = 10 ps−1. Other parameters are the same as Fig. 1
In Fig. 7, the controllability of the freezing phenomenon is shown by using the outfield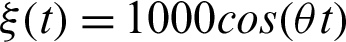 
. Determined from Figs. 7a–7c, 
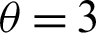gives the most stable freezing platform (see Fig. 7b) when the external field oscillation frequency is equal to the oscillation frequency of quantum correlation (see Fig. 6). This unique property stems from the sum values of the external field 
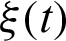pulsing 
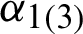in the time period of emergence of freezing phenomenon, and the freezing phenomenon is strengthened for an upper bound (about 800 ps−1) of the sum value. For 
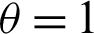(see Fig. 7a), there exists a longer time horizon for the sum value over upper bound at 6.5, 13, 19.5 s which comes from the slower change of the external field, showing a longer time freezing phenomenon platform. But the in conformity between 
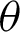and the oscillation frequency of quantum correlation arouses the decrease of the sum value at some time horizon. Finally, this unevenly frozen platform appears in Fig. 7a. Conversely, Fig. 7c shows the vibration and unstable freezing platform for 
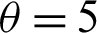arising from the faster change of the external field. Therefore, the additional field comes from control action, inner interaction of environments.
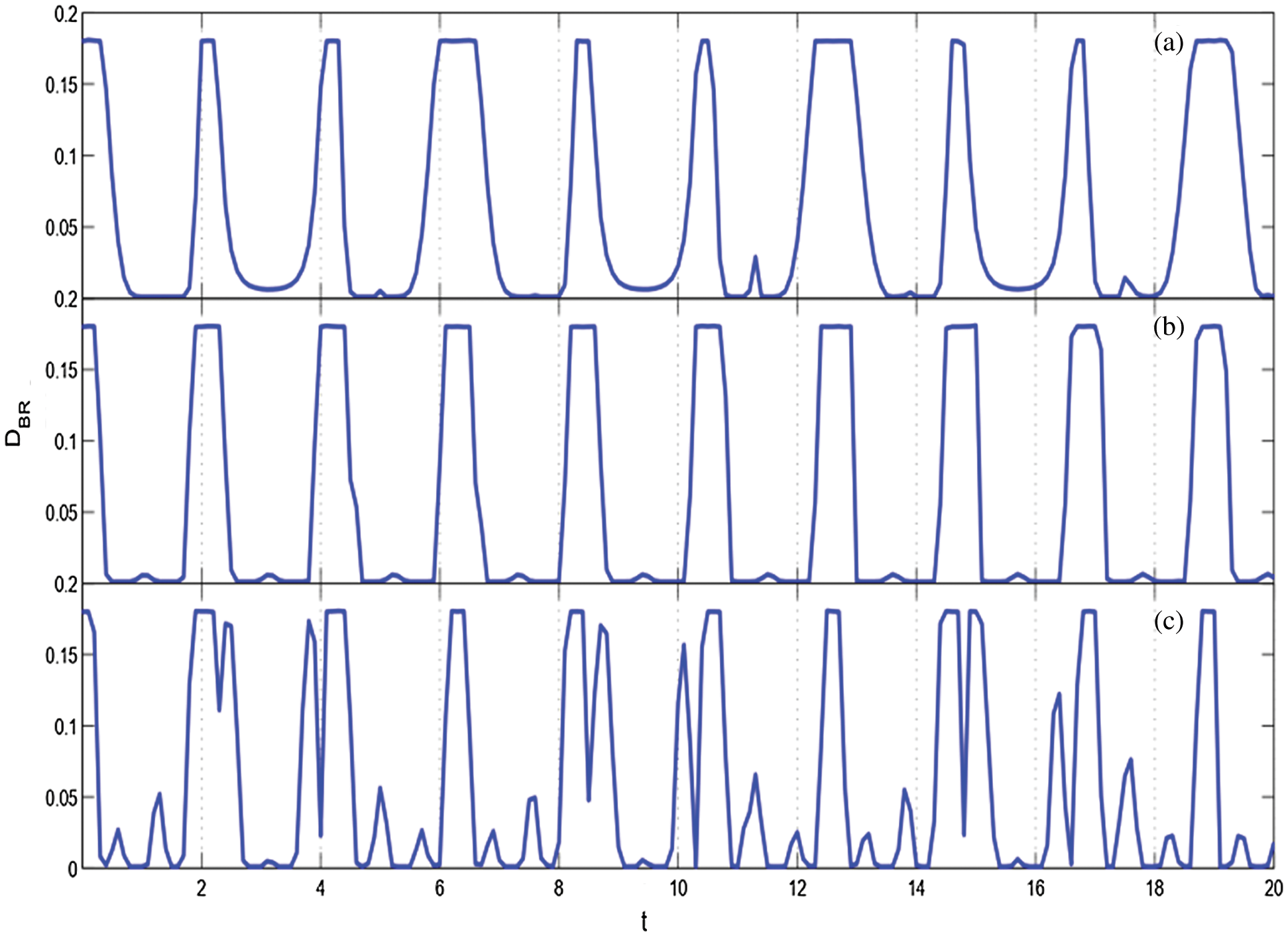
Figure 7: The freezing phenomenon is shown as a function of time t for X initial states under Bures distance discord when a field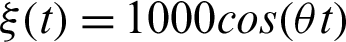 
is applied
5.2 The Steady of Freezing Platform
In this section, it is shown how two different situations affect quantum correlation and the feasibility of the controllability of quantum correlation by parameters q(t) and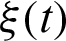 
. Meanwhile, there are some worthwhile open problems for the different external fields, such as different forms of 
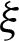(t) along x-axis and y-axis.
Figs. 7a–7c show the properties for the different frequencies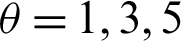 
, respectively. The parameters 
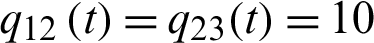ps−1. The other parameters are the same as Fig. 1.
According to the characteristics of the information flow between the system and the environment, since environment 2 provides a new information transmission channel, the system information feedback from environment 1 and environment 3 affect each other. Therefore, by considering the random fluctuations of the parameters q12(t) and q23(t), the stability of the frozen platform caused by the random fluctuations of this new information transmission channel [22] is discussed. Here, Gaussian noise is added to this channel to arouse the stochastic fluctuation of q12(t) and q23(t), and the stability of the freezing platform 
for X initial states and Bures distance is defined as:
where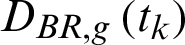 
and D′BR, g(tk) denote the quantum correlation for absence and presence of Gaussian noise condition at time tk, respectively. The number g is the recalculation time of the statistical average. Note that the time tk is only selected during the time interval during which freezing occurs.
In Fig. 8, the stability of the frozen platform under different Gaussian noise intensity is shown. The frozen platform appears at the time interval of 4s and collapses at the next time interval of 6 s. The stability of the frozen platform shows a flipping behavior at a Gaussian noise intensity of 35. This flipping behavior stems from two aspects: (1) In Sections 2–4, it is shown that the stable freezing platform for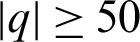 
ps−1, corresponding to the sum of q12(t) and q23(t) and the amplitude of the noise which is different from the noise intensity can be negative. (2) For the Gaussian distribution of noise, the probability of |q| < 50 increases with noise. Nevertheless, the Gaussian distribution is flatter with the increase of noise, the probability of |q| < 50 decreases when the noise intensity excesses a threshold 35 with the parameters of Fig. 8.
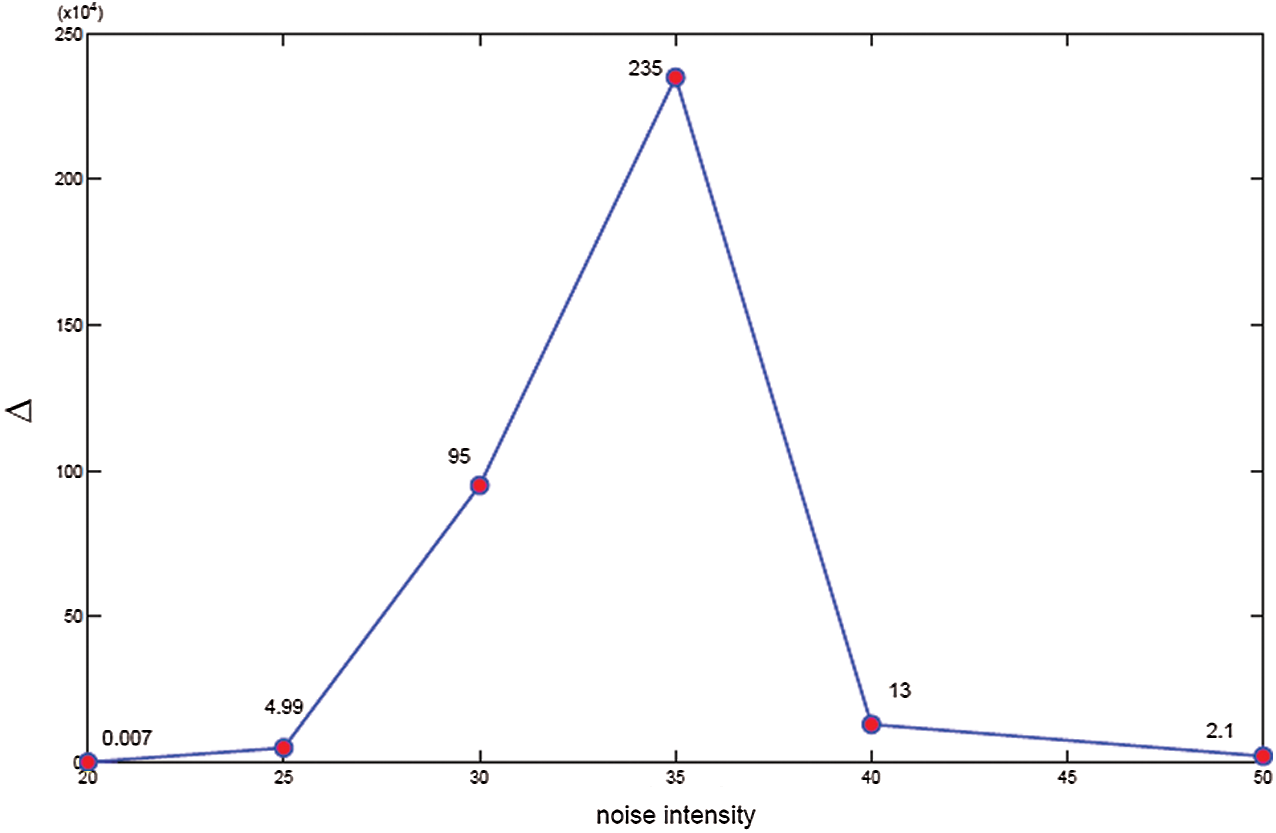
Figure 8: (Color online) The stability of the freezing platform for X initial states under Bures distance discord when a Gaussian noise applied on the information exchange channels between the environments which are described by the q12(23)(t). Whilst, k = 50, t = [1,3], q23(t) = q23(t) is equal to 50 ps−1. The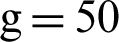 
times and the other parameters are the same as Fig. 1
The quantum correlation of a novel time-dependent three environments open system model has been discussed by using several common quantification methods of quantum correlation. Although all quantitative methods show the revival behavior for X and SCI initial states, the freezing phenomenon had been only displayed for some quantitative methods. Particularly, the freezing phenomenon of the SCI initial state gives a powerful proof of the fact that it is not a mathematical accident. Meanwhile, DHS shows the worst properties among the mentioned discords for quantification of quantum correlation, as supported by the previous literature. According to the general properties of revival and freezing phenomenon, we put forward two different methods to show the controllability of quantum correlation, especially the controllability of freezing phenomenon. It provides an effective way to control quantum correlation and design nanospintronic devices. The present results put forward a worthy study for open problems, especially the role of a multi-environment quantum system in quantum information.
Funding Statement: This work was supported by Scientific Research Starting Project of SWPU [Zheng, D., No. 0202002131604]; Major Science and Technology Project of Sichuan Province [Zheng, D., No. 8ZDZX0143]; Ministry of Education Collaborative Education Project of China [Zheng, D., No. 952]; Fundamental Research Project [Zheng, D., Nos. 549, 550].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1 M. A. Nielsen and I. L. Chuang. (2010). “General applications of the quantum Fourier transform,” in Quantum Computation and Quantum Information. England: Cambridge University Press, pp. 234–242. [Google Scholar]
2 K. Modi, A. Brodutch, H. Cable, T. Paterek and V. Vedral. (2012). “The classical-quantum boundary for correlations: Discord and related measures,” Review of Modern Physics, vol. 84, no. 4, pp. 1655. [Google Scholar]
3 H. Ollivier and W. H. Zurek. (2001). “Quantum discord: A measure of the quantumness of correlations,” Physical Review Letters, vol. 88, no. 1, pp. 17901. [Google Scholar]
4 L. Henderson and V. Vedral. (2001). “Classical, quantum and total correlations,” Journal of Physics A: Mathematical and General, vol. 34, no. 35, pp. 6899. [Google Scholar]
5 M. Cianciaruso, T. R. Bromley, W. Roga, R. Lo Franco and G. Adesso. (2015). “Universal freezing of quantum correlations within the geometric approach,” Scientific Reports, vol. 5, no. 1, pp. 10177. [Google Scholar]
6 D. F. V. James, P. G. Kwiat, W. J. Munro and A. G. White. (2001). “Measurement of qubits,” Physical Review A, vol. 64, no. 5, pp. 52312. [Google Scholar]
7 B. Dakic, V. Vedral and C. Brukner. (2010). “Necessary and sufficient condition for non-zero quantum discord,” Physical Review Letters, vol. 105, no. 19, pp. 190502. [Google Scholar]
8 A. Benjamin, R. Lo Franco, C. Giuseppe and A. Gerardo. (2013). “Hierarchy and dynamics of trace distance correlations,” New Journal of Physics, vol. 15, no. 9, pp. 93022. [Google Scholar]
9 C. C. Ding, Q. S. Zhu, S. Y. Wu and W. Lai. (2017). “The effect of the multi-environment for quantum correlation: Geometry discord vs. quantum discord,” Annalen Der Physik, vol. 529, pp. 1700014. [Google Scholar]
10 B. Mario, P. S. Kaushik and M. W. Mark. (2015). “Rényi generalizations of the conditional quantum mutual information,” Journal of Mathematical Physics, vol. 56, no. 2, pp. 22205. [Google Scholar]
11 V. Inés de and A. Daniel. (2017). “Dynamics of non-Markovian open quantum systems,” Review of Modern Physics, vol. 89, no. 1, pp. 15001. [Google Scholar]
12 Q. S. Zhu, C. C. Ding, S. Y. Wu and W. Lai. (2015). “The role of correlated environments on non-Markovianity and correlations of a two-qubit system,” European Physical Journal D, vol. 69, pp. 231. [Google Scholar]
13 K. B. Daniel, F. Paolo, G. Vittorio, N. Hiromichi, P. Saverio. (2014). et al., “Exponential rise of dynamical complexity in quantum computing through projections,” Nature Communications, vol. 5, pp. 5173. [Google Scholar]
14 Q. S. Zhu, C. C. Ding, S. Wu and W. Lai. (2016). “Geometric measure of quantum correlation: The influence of the asymmetry environments,” Physica A, vol. 458, pp. 67. [Google Scholar]
15 X. Y. Li, Q. S. Zhu, M. Z. Zhu, H. Wu, S. Y. Wu. (2019). et al., “The freezing Rényi quantum discord,” Scientific Reports, vol. 9, pp. 14739. [Google Scholar]
16 M. Piani. (2012). “Problem with geometric discord,” Physical Review A, vol. 86, no. 3, pp. 34101. [Google Scholar]
17 L. Chang and S. Luo. (2013). “Remedying the local ancilla problem with geometric discord,” Physical Review A, vol. 87, no. 6, pp. 62303. [Google Scholar]
18 I. Rajibul, M. Ruichao, M. P. Philipp, M. T. Eric, L. Alexander. (2015). et al., “Measuring entanglement entropy through the interference of quantum many body twins,” Nature, vol. 528, no. 7580, pp. 77. [Google Scholar]
19 M. Avijit, B. Anindya, K. P. Arun, S. D. Aditi and S. Ujjwal. (2015). “Quantum correlation with sandwiched relative entropies: Advantageous as order parameter in quantum phase transitions,” Physical Review E, vol. 91, no. 5, pp. 52125. [Google Scholar]
20 C. Cervetti, A. Rettori, M. G. Pini, A. Cornia, A. Repollés. (2016). et al., “The classical and quantum dynamics of molecular spins on graphene,” Nature Materials, vol. 15, no. 2, pp. 164. [Google Scholar]
21 T. Chanda, A. K. Pal, A. Biswas, A. SenDe and U. Sen. (2015). “Freezing of quantum correlations under local decoherence,” Physical Review A, vol. 91, no. 6, pp. 62119. [Google Scholar]
22 Z. G. Qu, S. Y. Wu, W. J. Liu and X. J. Wang. (2019). “Analysis and improvement of steganography protocol based on Bell states in noise environment,” Computers, Materials & Continua, vol. 59, no. 2, pp. 607–624. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |
and 