DOI:10.32604/cmc.2021.013228
| Computers, Materials & Continua DOI:10.32604/cmc.2021.013228 | |
| Article |
Artificial Neural Networks for Prediction of COVID-19 in Saudi Arabia
1Department of Basic Sciences, College of Science and Theoretical Studies, Saudi Electronic University, Riyadh, 11673, Saudi Arabia
2Department of Mechanical Engineering, College of Engineering, Prince Mohammad Bin Fahd University, Al Khobar, 31952, Saudi Arabia
3Department of Mathematics and Natural Sciences, College of Sciences & Human Studies, Prince Mohammad Bin Fahd University, Al Khobar, 31952, Saudi Arabia
4College of Computing and Informatics, Saudi Electronic University, Riyadh, 11673, Saudi Arabia
5Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, 72915, Vietnam
6King Abdullah University Hospital, University of Science and Technology, Irbid, 22110, Jordan
*Corresponding Author: Ilyas Khan. Email: ilyaskhan@tdtu.edu.vn
Received: 30 July 2020; Accepted: 13 September 2020
Abstract: In this study, we have proposed an artificial neural network (ANN) model to estimate and forecast the number of confirmed and recovered cases of COVID-19 in the upcoming days until September 17, 2020. The proposed model is based on the existing data (training data) published in the Saudi Arabia Coronavirus disease (COVID-19) situation—Demographics. The Prey-Predator algorithm is employed for the training. Multilayer perceptron neural network (MLPNN) is used in this study. To improve the performance of MLPNN, we determined the parameters of MLPNN using the prey-predator algorithm (PPA). The proposed model is called the MLPNN–PPA. The performance of the proposed model has been analyzed by the root mean squared error (RMSE) function, and correlation coefficient (R). Furthermore, we tested the proposed model using other existing data recorded in Saudi Arabia (testing data). It is demonstrated that the MLPNN-PPA model has the highest performance in predicting the number of infected and recovering in Saudi Arabia. The results reveal that the number of infected persons will increase in the coming days and become a minimum of 9789. The number of recoveries will be 2000 to 4000 per day.
Keywords: COVID-19; ANN modeling; multilayer perceptron neural network; prey-predator algorithm
The history of coronavirus (CoV) is not new in this world and has appeared with different names like Middle East Respiratory Syndrome Coronavirus (MERS-CoV), Severe Acute Respiratory Syndrome (SARS-CoV), etc. The first one was transmitted from civet cats to humans in 2002 in China, and the second virus was transmitted from dromedary camels to humans in 2012 in the Kingdom of Saudi Arabia (KSA) [1,2]. Any virus can cause illness, starting from the common cold and reaches to more severe diseases. These viruses were not found as risky as the newly discovered COVID-19 in Wuhan City in December 2019 [3]. After that, COVID-19 became an international outbreak, and this virus spread out almost all over the world. It was named as an acute respiratory syndrome coronavirus 2 (SARS-CoV-2) by the International Committee on Taxonomy of Viruses. In the second week of February 2020, it was identified as the causative virus by Chinese authorities [4–6]. A common belief of COVID-19 origination is from the animals and seafood, as witnessed in the Wuhan city market. As this virus (COVID-19) transmits from an infected person to another healthy person through close contact without proper protection (human-to-human interaction). The primary source of COVID-2019 was the traveling of the public from city to city and country to country [7,8]. In KSA, the first case of COVID-19 was registered on March 2, 2020. The second COVID-19 case was reported a day after the first case, and then on March 5, three new cases were identified. All these five COVID-19 patients traveled from Iran to KSA via different routes. After that, the new cases were boosted exponentially. Several researchers from various fields, such as mathematics, physics, chemistry, economics, statistics, computer, geophysics, medical, etc. are working on COVID-19. However, nobody came up with the final decision. In addition, the symptoms of this disease are changing continuously. The initial symptoms of COVID-19 include cough, fever, and shortness of breath (breathing difficulties). In the next steps, the infection can cause pneumonia, severe acute respiratory syndrome, kidney failure, heart failure, and even death. In mathematics, the researchers working on biomathematics are mainly interested in studying the mathematical/physical aspects of this disease. However, due to the complex nature of the COVID-19 virus itself, the known information about this virus is fewer compared to the unknown data. It is also not easy to count all the infected people due to several reasons. Some of the basic ideas are: (i) The infected people afraid to go for a test and then to get admission in the hospital. (ii) A low number of screenings, mainly on “suspect” cases or those presenting significant symptoms, does not give a precise idea of the number of people who could potentially become infected without knowing them. This gap between the day of infection and the day of diagnosis can have severe consequences for the spread of the epidemic, etc. [9].
Recently, several studies on COVID-19 have already been published on computational, mathematical, and statistical aspects of different viruses. On the mathematical side, different models are used to study the dynamics of COVID-19. One of the most used models for the dynamics of various diseases is Susceptible-Infectious-Recovered (SIR) model. This model provides the epidemic growth through a system of time-dependent differential equations. The SIR model and its various modified versions have been used extensively by researchers to Ebola and AIDS diseases [10,11]. Quite recently, such models were used to model the coronavirus epidemic spreading. Berger et al. [12] used the SEIR infectious disease model with testing and conditional quarantine. Iwata et al. [13] examined the potential secondary spread of Novel Coronavirus in an exported country using a stochastic epidemic SEIR model. Godio et al. [14] utilized an SEIR epidemiological model to study the recent SARS-CoV-2 outbreak with a particular focus on Italy. They applied the useful application of a stochastic approach in fitting the model parameters using a Particle Swarm Optimization (PSO) solver, to improve the reliability of predictions in the medium term (30 days). They compared their results with the data and forecasts of Spain and South Korea. Baleanu et al. [15] used a fractional differential equation model for the COVID-19 transmission by using the Caputo–Fabrizio derivative. Few other exciting studies on COVID-19 are also available in [16,17].
The real number of COVID-19 data represents a series of observations, where methods used for time-series prediction are native to the statistics field, such as Machine learning-based methods (such as artificial neural networks), Meta-predictors, and Structure-based methods [18,19]. ANNs are frequently employed for time series forecasting [20]. One of the main advantages of ANN-based techniques over machine learning techniques is that it can be fueled with raw data and automatically find the required feature representation [21]. Based on several factors like performance, accuracy, latency, speed, convergence, and size, ANN provides reliable results. It is important to note that this study is based on ANNs for the prediction of a time series problem to investigate the status of COVID-19 in KSA [22]. Additionally, we used the prey-predator algorithm (PPA), which is a metaheuristic algorithm, to improve model performance by specifying the optimum value for model parameters [23,24].
Multilayer perceptron neural network (MLPNN) is a feed-forward neural network with three types of layers (input layer, hidden layers, and output layer), as shown in Fig. 1 [25,26]. In this study, we have used one hidden layer with ten hidden neurons, and the hidden activation function (sigmoid function), that is defined in the following equation.
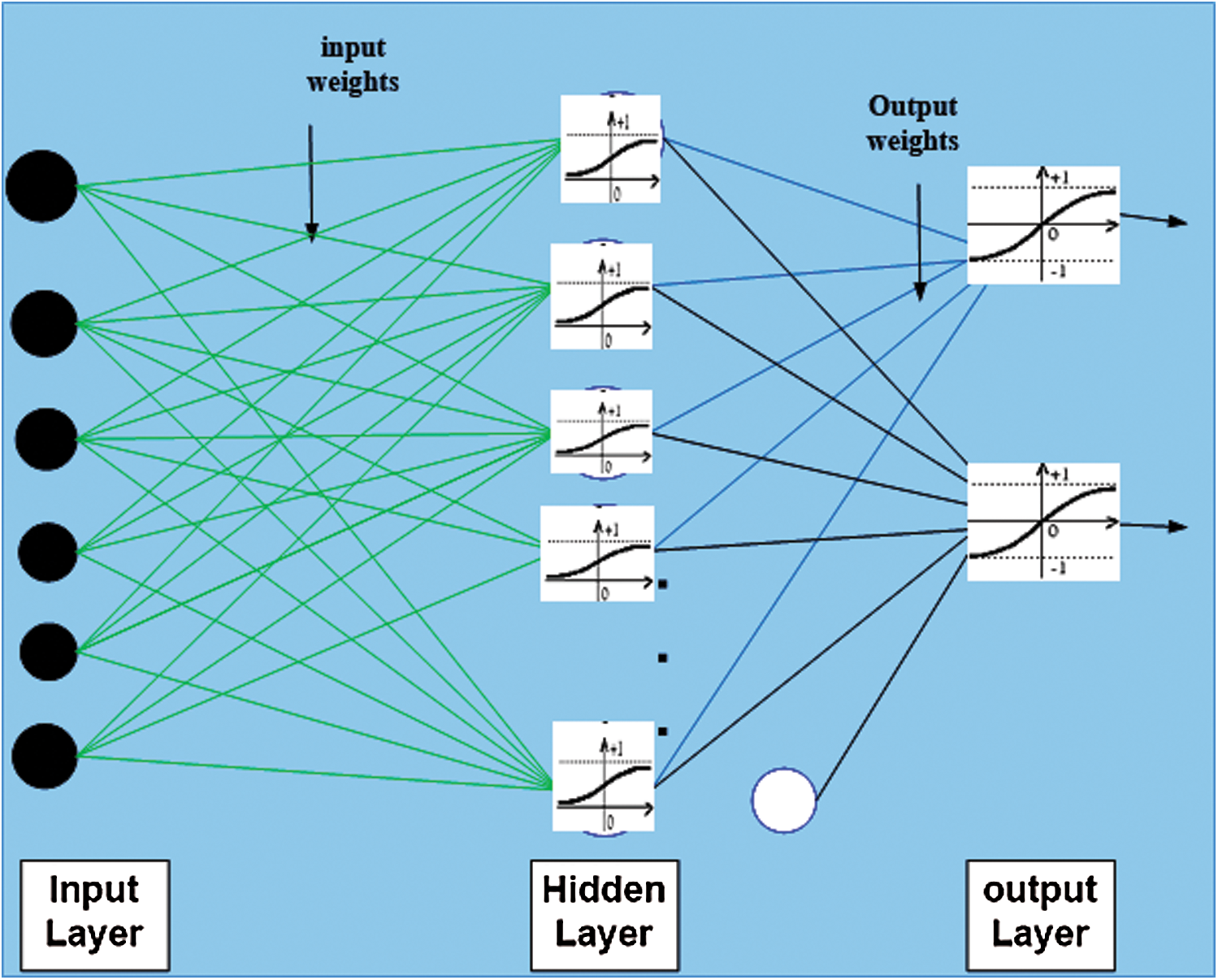
Figure 1: Structure of a multilayer perceptron neural network
where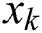 
is the value of input neuron i, 
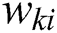is the input weight and 
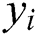is the value of the hidden neuron i.
In the output layer, we have two input neurons that represent the infected and recovered number of persons. Also, we have a hyperbolic tangent transfer function that has an output ranging from –1 to +1 Eq. (2).
where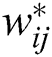 
is the value of output weight between the hidden neuron i and the output neuron j, and 
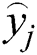is the value of the output neuron j.
The supervised learning method of ANNs is the best technique using to determine the optimal values of all ANN parameters, which are the “input weights” and “output weights.” Therefore, finding the values of the parameters of an ANN leads to becoming an ANN model. This phase is known as the training ANNs via observed values (training data), and optimization algorithm (see Fig. 2). The root means squared error (RMSE) function that is currently used as a fitness function for testing the performance of the ANNs, whereas the correlation coefficient (R) is used to enhance the performance. Following [27,28], these functions can be written as
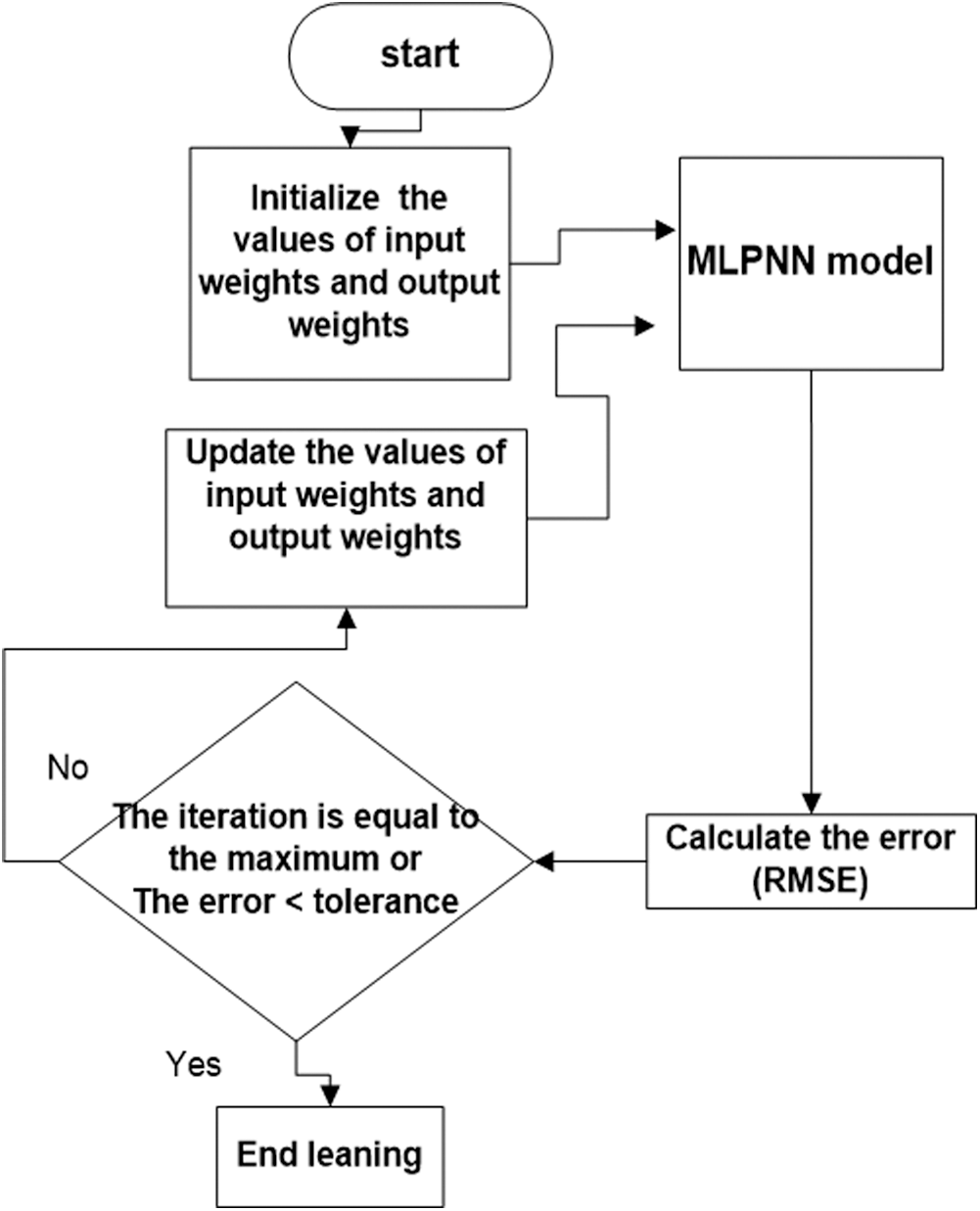
Figure 2: The training process of MLPNNs
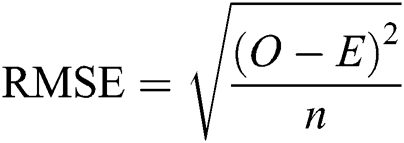
where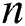 
is the number of cases; 
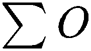is the sum of all observed cases; 
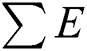is the sum of all expected values; 
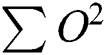is the sum of all squared observed values; 
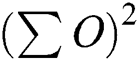is the square of the sum of all observed values; 
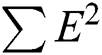is the sum of all squared expected values; 
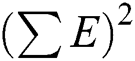is the square of the sum of all expected values.
Several algorithms have been used for the training to find the optimal values of the parameters, such as metaheuristic optimization algorithms [23,29–33]. In this study, PPA is used for training because it is one of the most effective metaheuristic optimization algorithms [25]. The principle of PPA work came from the idea of inspired by prey-predator interaction of animals [24]. The algorithm simulates how a predator works and chases its prey as each prey tries to stay inside a region (a feasible region) and find a place to hide (optimal solution). Therefore, the solutions of PPA are called prey and Predator. Note that, Predator is the solution (survival value) with the smallest performance value in terms of RMSE function. The best performance (highest survival value) is called the best prey. Note that in each iteration. The Predator searches for weak prey while the prey escapes to a suitable location and try to follow other prey. These explorations are based upon the direction and the step length. The aim of each solution can be determined as follows:
where v is an algorithm parameter.
Setting different values of v will affect the size of the jump for the solution xi. Moreover, the best direction is chosen from the paths generated to set the global solution. Step length is another problem with updating solutions. The second issue related to updating the solution is the step length for exploration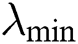 
and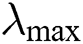 
(
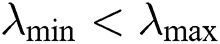). The procedure movement of the prey and the Predator can be summarized as follows [24,25,34].
Movement of a common prey:
i) If follow up probability is met,
If the follow-up probability does not meet the criteria, then
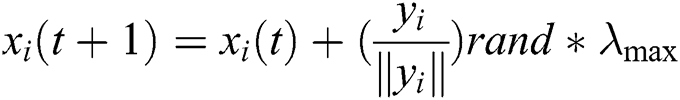
Movement of the best prey:
Movement of Predator:
In this study, we have proposed an ANN model to predict and to offer a quantitative overview of the Status of COVID 19 in KSA during the period (June 22 to September 17, 2020). Note that using artificial inelegance is a new technique in the field of epidemiological studies. The observed data (infected and recovered) during the period (March 12 to June 16, 2020) trains the ANN model, as shown in Fig. 3. The structure of the ANN model has one input neuron—ten hidden neurons—two output neurons. Note that the input value is “the requested date,” and the two output neurons; one represents the infected numbers (cases), and the second output neuron represents “recovered numbers.”
We have used PPA for the training to determine the optimal values of the ANN model parameters (input weights and output weights). We have trained the ANN model in 20 trials, while the number of the iterations in PPA has been set for 1000, the number of population is equal 50, and the number of predators 8, local search directions 1, and the number of best prey 4, and then the best the values are reported.
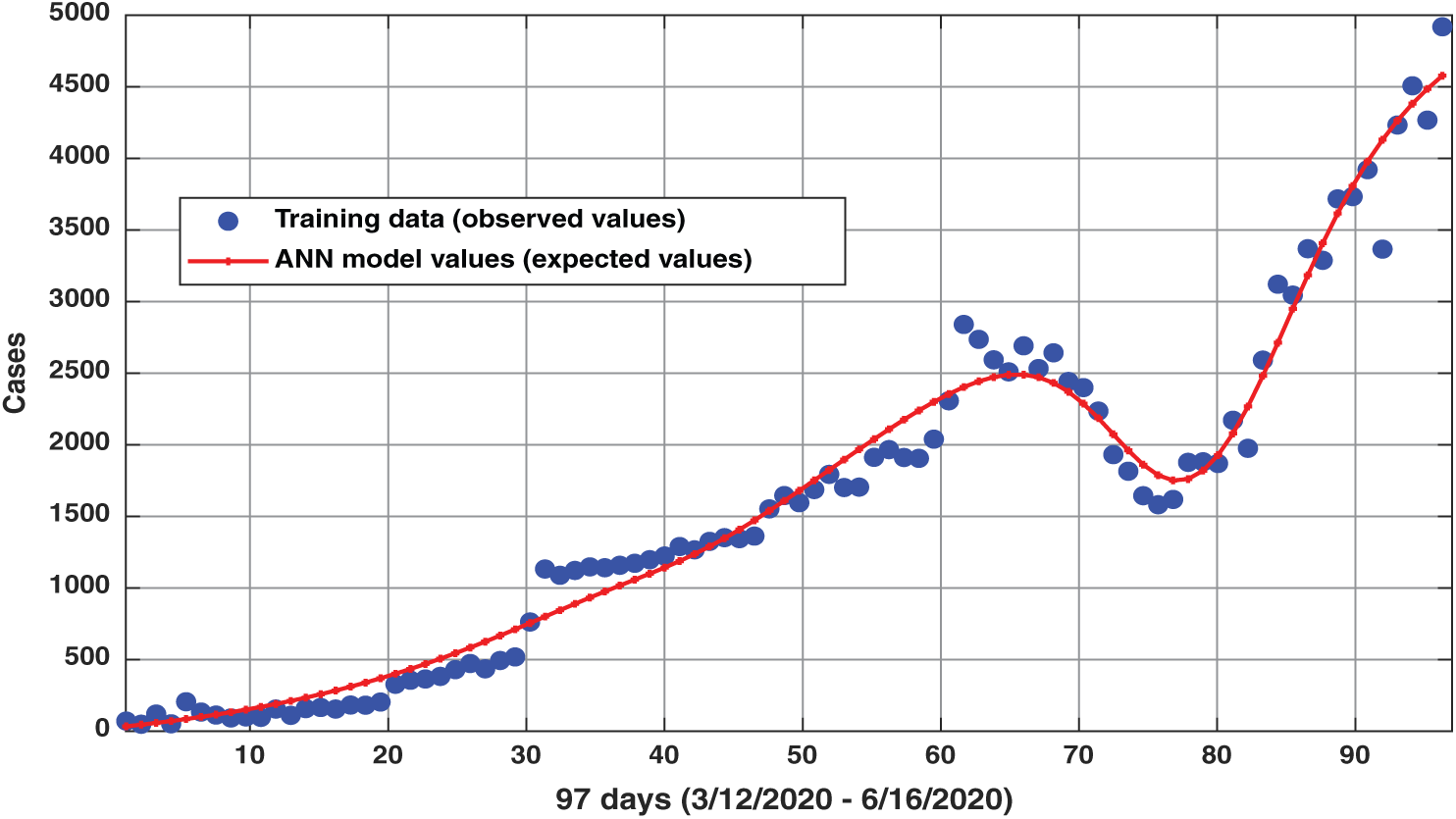
Figure 3: The observed values, which have used for training and the corresponding values, which determine by ANN model
With a minimal value of RMSE (13%) and correlation coefficient R (93%), represents the values of the training data and the expected data of “infected.” Fig. 4 represents all ANN model values from March 12 to September 17, 2020 (red color). Because of the (RMSE = 13%), the range of the expected values of “infected” will be bounded by 1.13* ANN model values (Purple color), and 0.87* ANN model values (green color). The blue color represents the testing data from June 17 to June 21, 2020. Where the study indicates that the minimum number of “infected” at the beginning (June 22, 2020) is closed to 4,000 (see Fig. 5), moreover, the minimum number of expected daily “infected” after 87 from June 22 to September 17, 2020, will approach 10,000 (see Fig. 5).
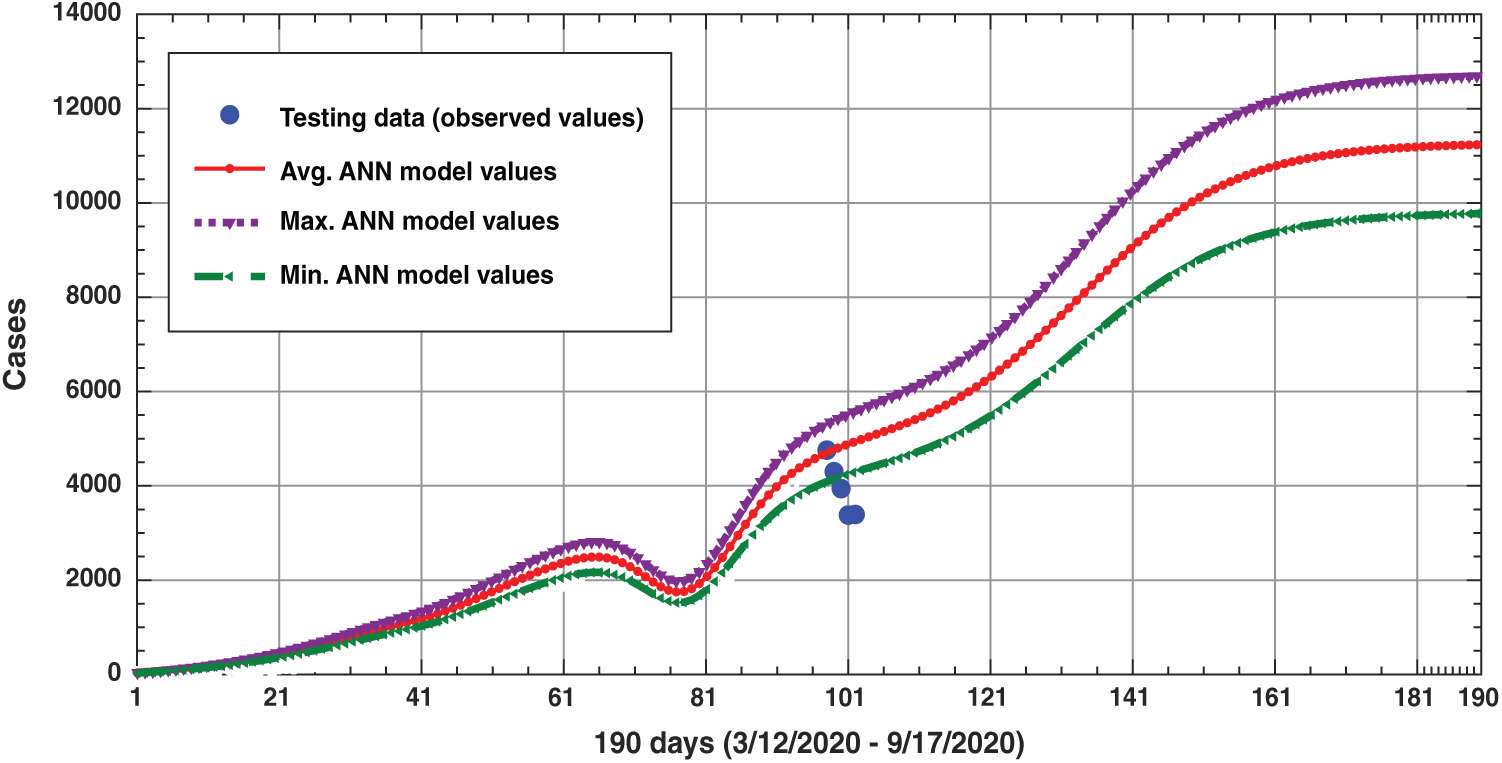
Figure 4: ANN model results for 190 days (from March 12 to September 17, 2020), and the observed values (testing values) from June 17 to June 21, 2020
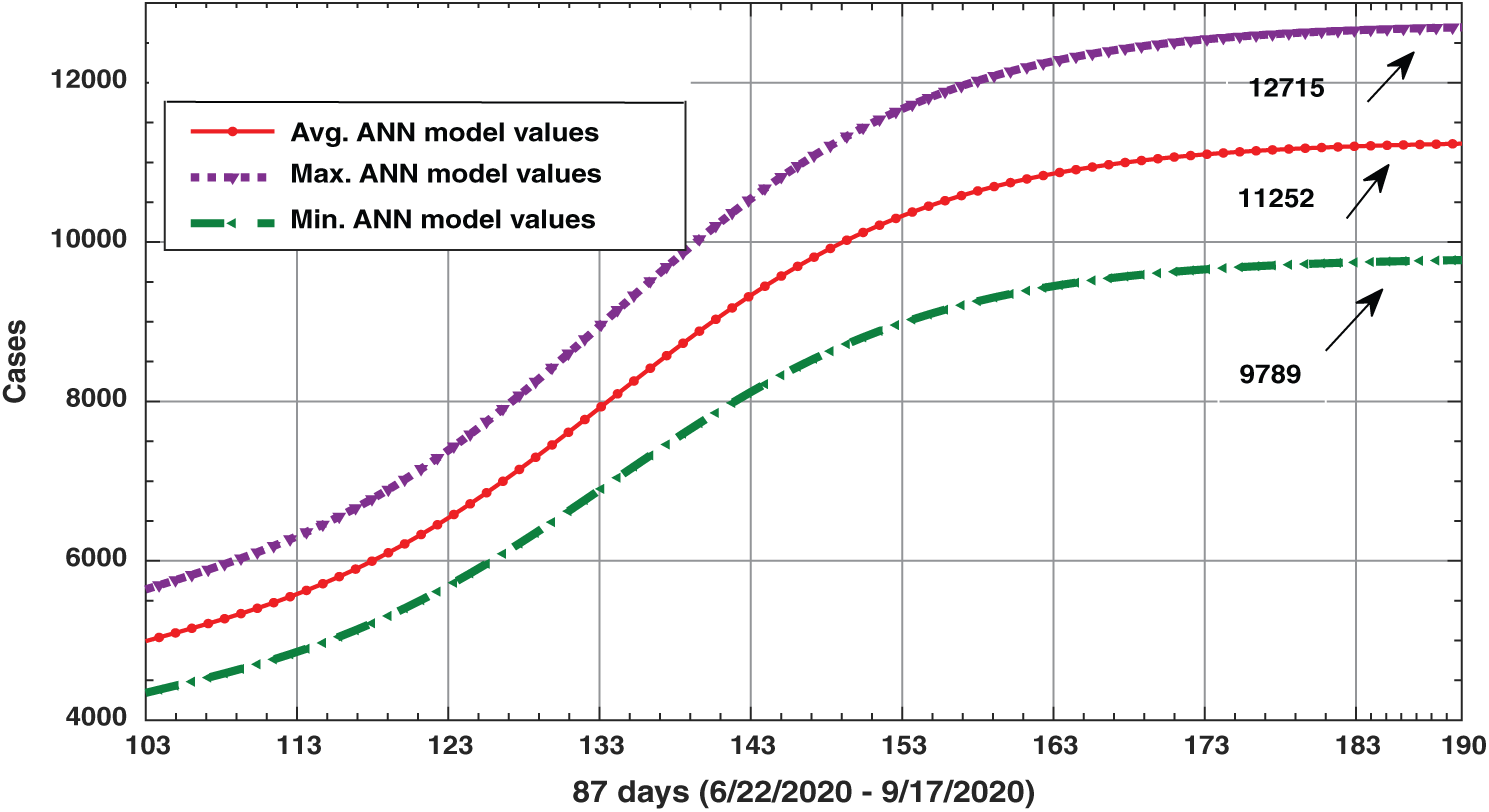
Figure 5: ANN model results for 87 days (from June 22 to September 17, 2020)
On the other hand, to propose the ANN model for the number of recovered persons per day, we have used the observed data (training data) of “recovered” from June 22 to September 17, 2020. The best ANN model that we have proposed has RMSE = 35% and correlation coefficient R =93.6% (see Fig. 6).
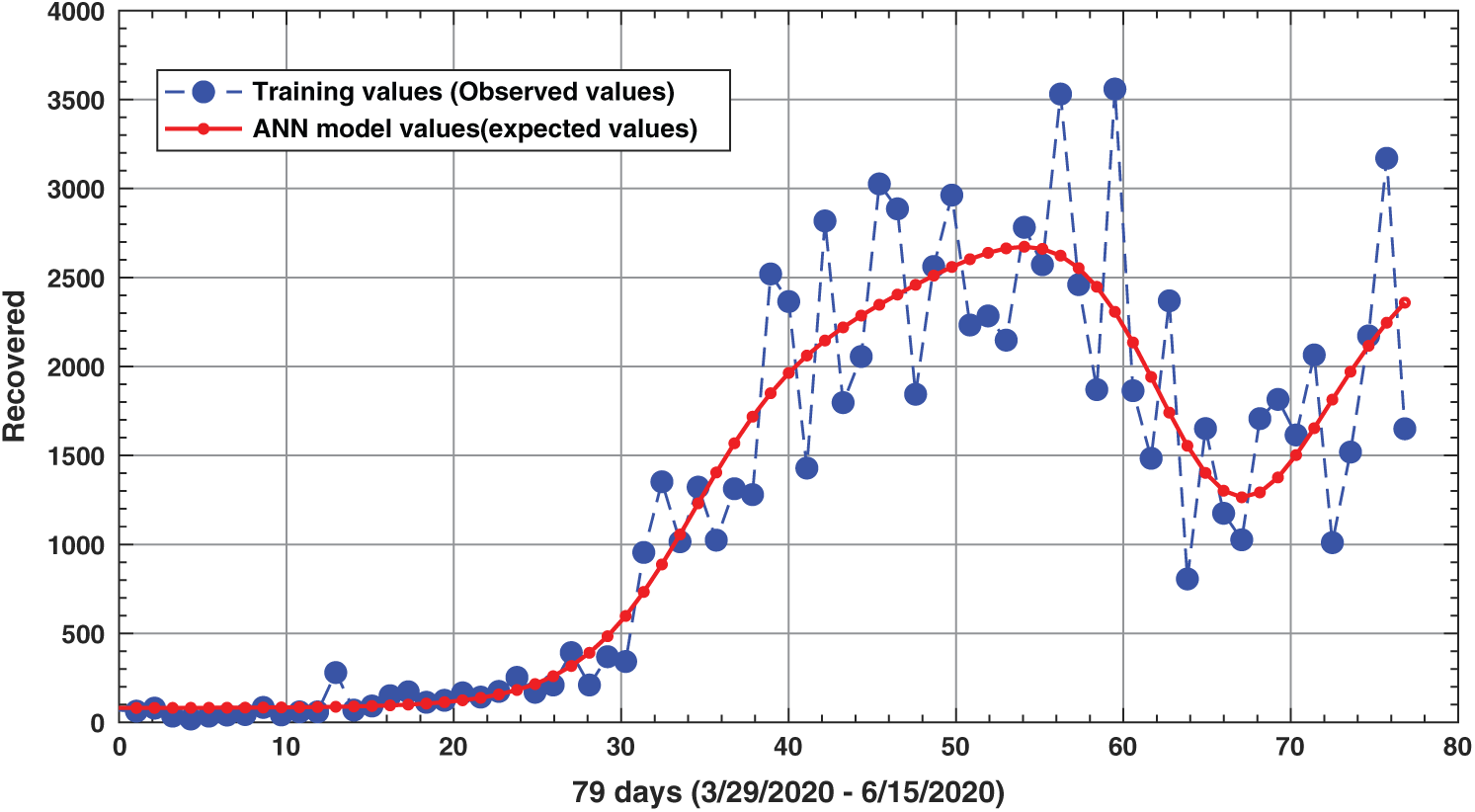
Figure 6: The observed values of “Recovered” which have used for training, and the corresponding values which determine by ANN model
Fig. 7 represents all ANN model values from March 29 to September 17, 2020 (red color). Because of the (RMSE = 35%), the range of the expected values of “Recovered” will be bounded by 1.35* ANN model values (brown color), and 0.75* ANN model values (green color). The blue color represents the testing data from June 16 to June 21, 2020. Where the study indicates that the minimum number of “Recovered” at the beginning (6/22/2020) is closed to 1800 (see Fig. 7), moreover, the minimum number of expected daily “Recovered” after 87 from June 22 to September 17, 2020, will approach 2100 see Fig. 8. The maximum number of expected daily “Recovered” will be more than 4000 per day.
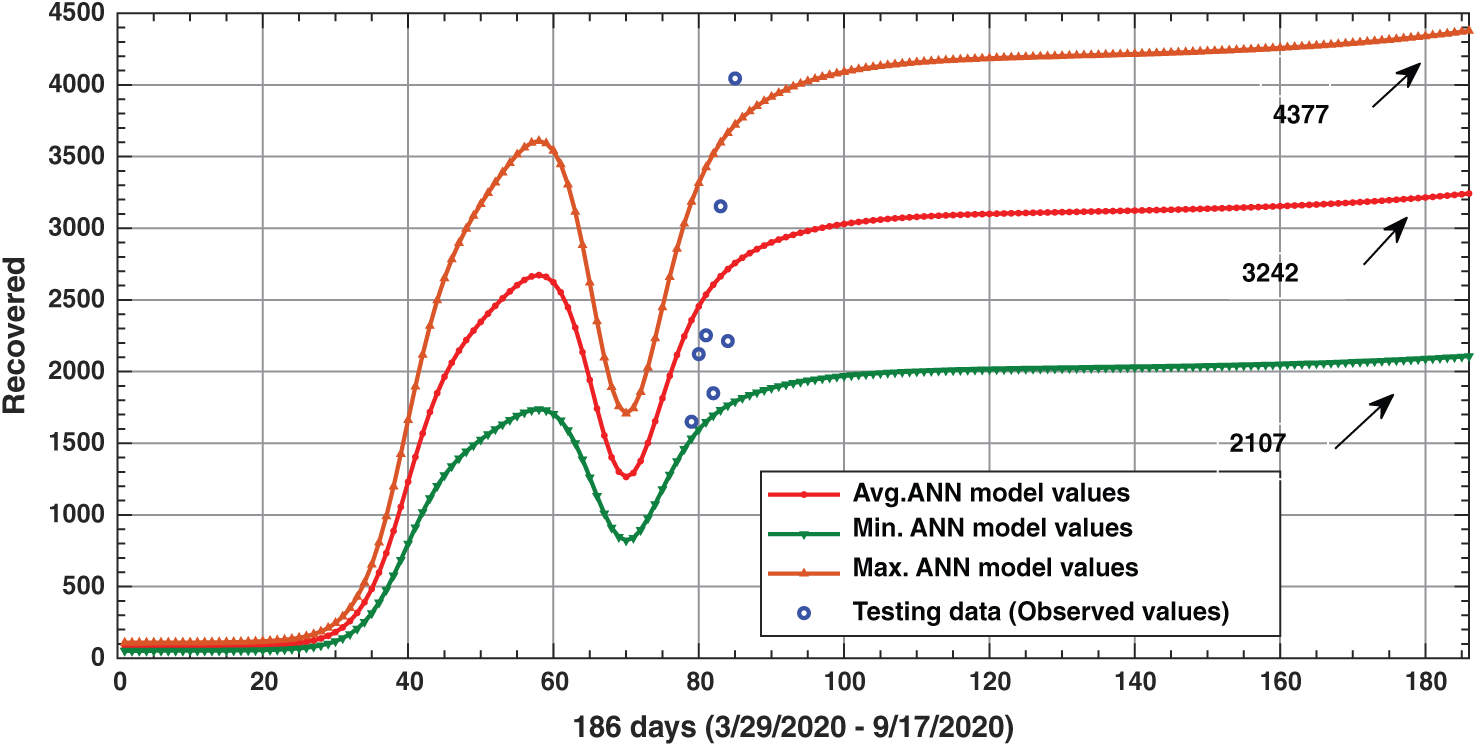
Figure 7: ANN model results for 186 days (from March 29 to September 17, 2020), and the observed values (testing values) from June 16 to June 22, 2020
Figure 8: ANN model results of “recovered” for 87 days (from June 22 to September 17, 2020)
In this study, we have proposed an artificial neural network (ANN) prediction model using a multilayer perceptron neural network (MLPNN) and a prey-predator algorithm (PPA). This model, called hybrid MLPNN-PPA, is applied as an artificial inelegance forecasting technique for COVID-19 in Saudi Arabia. PPA is used to improve the performance of the model by determining the optimal values for the model parameters. The proposed model has a high performance in predicting the number of infected (cases), and the number of recovered in terms of root means squared error and correlation coefficient.
The proposed model has a high performance in predicting the number of infected and recovered persons within 87 days (from June 22 to September 17, 2020). According to the promising results obtained by the MLPNN-PPA model, the number of infected persons will increase in the coming days and become a minimum of 9789. The number of recoveries will be 2000 to 4000 per day.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Usaini, A. S. Hassan, S. M. Garba and J. S. Lubuma. (2019). “Modeling the transmission dynamics of the Middle East Respiratory Syndrome Coronavirus (MERS-CoV) with latent immigrants,” Journal of Interdisciplinary Mathematics, vol. 22, no. 6, pp. 903–930. [Google Scholar]
2. M. Tahir, S. Shah, G. Zaman and T. Khan. (2018). “Prevention strategies for mathematical model MERS-corona virus with stability analysis and optimal control,” Journal of Nanoscience and Nanotechnology, vol. 2, pp. 1–11. [Google Scholar]
3. T. M. Chen, J. Rui, Q. P. Wang, Z. Y. Zhao, J. A. Cui et al. (2020). , “A mathematical model for simulating the phase-based transmissibility of a novel coronavirus,” Infectious Diseases of Poverty, vol. 9, no. 1, pp. 1–8. [Google Scholar]
4. L. Peng, W. Yang, D. Zhang, C. Zhuge and L. Hong. (2002). “Epidemic analysis of COVID-19 in China by dynamical modeling, vol. 2, pp. 1–11. [Google Scholar]
5. Q. Li, X. Guan, P. Wu, X. Wang, L. Zhou et al. (2020). , “Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia,” New England Journal of Medicine, vol. 382, no. 13, pp. 1199–1207.
6. Z. J. Cheng and J. Shan. (2020). “Novel coronavirus: Where we are and what we know,” Infection, vol. 48, no. 2, pp. 155–163. [Google Scholar]
7. P. P. Sainaghi. (2020). “Fatality rate and predictors of mortality in a large Italian cohort of hospitalized COVID-19 patients,” Preprint from Research Square, vol. 1, pp. 1–19. [Google Scholar]
8. Y. Chen, J. Cheng, Y. Jiang and K. Liu. (2020). “A time delay dynamic system with external source for the local outbreak of 2019-nCoV,” Applicable Analysis, vol. 33, pp. 1–12. [Google Scholar]
9. Ojo O. A., Ojo A. B., Taiwo O. A. and Oluba O. M. (2020). “Novel Coronavirus (SARS-CoV-2) main protease: Molecular docking of Puerarin as a Potential inhibitor,” Preprint from Research Square, vol. 1, pp. 1–14. [Google Scholar]
10. O. Zakary, A. Larrache, M. Rachik and I. Elmouki. (2016). “Effect of awareness programs and travel-blocking operations in the control of HIV/AIDS outbreaks: A multi-domains SIR model,” Advances in Difference Equations, vol. 2016, no. 1, pp. 1–17. [Google Scholar]
11. A. Khaleque and P. Sen. (2017). “An empirical analysis of the Ebola outbreak in West Africa,” Scientific Reports, vol. 7, no. 1, pp. 1–8. [Google Scholar]
12. D. W. Berger, K. F. Herkenhoff and S. Mongey. (2020). “An SEIR infectious disease model with testing and conditional quarantine,” National Bureau of Economic Research, pp. 1–29. [Google Scholar]
13. K. Iwata and C. Miyakoshi. (2020). “A simulation on potential secondary spread of novel coronavirus in an exported country using a stochastic epidemic SEIR model,” Journal of Clinical Medicine, vol. 9, no. 4, pp. 944. [Google Scholar]
14. A. Godio, F. Pace and A. Vergnano. (2020). “SEIR modeling of the Italian epidemic of SARS-CoV-2 using computational swarm intelligence,” International Journal of Environmental Research and Public Health, vol. 17, no. 10, pp. 3535. [Google Scholar]
15. D. Baleanu, H. Mohammadi and S. Rezapour. (2020). “A fractional differential equation model for the COVID-19 transmission by using the Caputo−Fabrizio derivative,” Advances in Difference Equations, vol. 2020, no. 1, pp. 1–27, , 2020. [Google Scholar]
16. E. Bonyah. (2020). “Fractional conformable and fractal-fractional power-law modeling of Coronavirus,” Mathematics in Engineering, Science and Aerospace, vol. 11, no. 3, pp. 1–20. [Google Scholar]
17. A. Atangana. (2020). “Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination?,” Chaos, Solitons & Fractals, vol. 136, pp. 109860. [Google Scholar]
18. F. Meng, V. N. Uversky and L. Kurgan. (2017). “Comprehensive review of methods for prediction of intrinsic disorder and its molecular functions,” Cellular and Molecular Life Sciences, vol. 74, no. 17, pp. 3069–3090. [Google Scholar]
19. M. A. A. Al-qaness, A. A. Ewees, H. Fan and M. Abd El Aziz. (2020). “Optimization method for forecasting confirmed cases of COVID-19 in China,” Journal of Clinical Medicine, vol. 9, no. 3, pp. 674. [Google Scholar]
20. L. Wang, Z. Wang, H. Qu and S. Liu. (2018). “Optimal forecast combination based on neural networks for time series forecasting,” Applied Soft Computing, vol. 66, pp. 1–17. [Google Scholar]
21. T. A. Eriksson, H. Bülow and A. Leven. (2017). “Applying neural networks in optical communication systems: Possible pitfalls,” IEEE Photonics Technology Letters, vol. 29, no. 23, pp. 2091–2094. [Google Scholar]
22. KAPSARC. (2020). “Saudi Arabia Coronavirus disease (COVID-19) situation—Demographics,” . [Online]. Available: https://datasource.kapsarc.org/explore/dataset/saudi-arabia-coronavirus-disease-covid-19-situation-demographics/information/. [Google Scholar]
23. N. N. Hamadneh, W. S. Khan and W. A. Khan. (2019). “Prediction of thermal conductivities of polyacrylonitrile electrospun nanocomposite fibers using artificial neural network and prey predator algorithm,” Journal of King Saud University−Science, vol. 31, no. 4, pp. 618–627. [Google Scholar]
24. S. L. Tilahun and H. C. Ong. (2016). “Prey-predator algorithm: A new metaheuristic algorithm for optimization problems,” International Journal of Information Technology & Decision Making, vol. 14, no. 6, pp. 1331–1352. [Google Scholar]
25. N. Hamadneh, W. Khan and S. Tilahun. (2018). “Optimization of microchannel heat sinks using prey-predator algorithm and artificial neural networks,” Machines, vol. 6, no. 2, pp. 26. [Google Scholar]
26. N. Hamadneh. (2020). “Dead sea water levels analysis using artificial neural networks and firefly algorithm,” International Journal of Swarm Intelligence Research, vol. 11, no. 3, pp. 19–29. [Google Scholar]
27. S. Mefoued. (2013). “Assistance of knee movements using an actuated orthosis through subject’s intention based on MLPNN approximators,” in The 2013 International Joint Conference on Neural Networks, pp. 1–6. [Google Scholar]
28. M. F. Triola, W. M. Goodman, R. Law and G. Labute. (2006). Elementary Statistics. Reading, MA: Pearson/Addison-Wesley. [Google Scholar]
29. S. L. Tilahun, J. M. T. Ngnotchouye and N. N. Hamadneh. (2019). “Continuous versions of firefly algorithm: A review,” Artificial Intelligence Review, vol. 51, no. 3, pp. 445–492. [Google Scholar]
30. W. S. Khan, N. N. Hamadneh and W. A. Khan. (2017). “Prediction of thermal conductivity of polyvinylpyrrolidone (PVP) electrospun nanocomposite fibers using artificial neural network and prey-predator algorithm,” PLoS One, vol. 12, no. 9, pp. e0183920.
31. L. Zhang, L. Liu, X. S. Yang and Y. Dai. (2016). “A novel hybrid firefly algorithm for global optimization,” PloS One, vol. 11, no. 9, pp. 1–17.
32. X. S. Yang. (2010). Nature-Inspired Metaheuristic Algorithms. United Kingdom: Luniver Press.
33. N. N. Hamadneh, W. A. Khan, I. Khan and A. S. Alsagri. (2019). “Modeling and optimization of gaseous thermal slip flow in rectangular microducts using a particle swarm optimization algorithm,” Symmetry, vol. 11, no. 4, pp. 488. [Google Scholar]
34. H. C. Ong, S. L. Tilahun, W. S. Lee and J. M. T. Ngnotchouye. (2017). “Comparative study of prey predator algorithm and firefly algorithm,” Intelligent Automation & Soft Computing, pp. 1–8. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |