DOI:10.32604/cmc.2021.013395
| Computers, Materials & Continua DOI:10.32604/cmc.2021.013395 | |
| Article |
Synchronization Phenomena Investigation of a New Nonlinear Dynamical System 4D by Gardano’s and Lyapunov’s Methods
1School of Mathematics, Madurai Kamaraj University, Madurai, 625021, India
2Specialty of Mathematics, Gifted School of Nineveh, Mosul, Iraq
3Al-Nahrain University, Baghdad, 70030, Iraq
4Institute of Research and Development, Duy Tan University, Danang, 550000, Vietnam
5Faculty of Information Technology, Duy Tan University, Danang, 550000, Vietnam
*Corresponding Author: Dac-Nhuong Le. Email: ledacnhuong@duytan.edu.vn
Received: 05 August 2020; Accepted: 07 September 2020
Abstract: Synchronization is one of the most important characteristics of dynamic systems. For this paper, the authors obtained results for the nonlinear systems controller for the custom Synchronization of two 4D systems. The findings have allowed authors to develop two analytical approaches using the second Lyapunov (Lyp) method and the Gardano method. Since the Gardano method does not involve the development of special positive Lyp functions, it is very efficient and convenient to achieve excessive system SYCR phenomena. Error is overcome by using Gardano and overcoming some problems in Lyp. Thus we get a great investigation into the convergence of error dynamics, the authors in this paper are interested in giving numerical simulations of the proposed model to clarify the results and check them, an important aspect that will be studied is Synchronization Complete hybrid SYCR and anti-Synchronization, by making use of the Lyapunov expansion analysis, a proposed control method is developed to determine the actual. The basic idea in the proposed way is to receive the evolution of between two methods. Finally, the present model has been applied and showing in a new attractor, and the obtained results are compared with other approximate results, and the nearly good coincidence was obtained.
Keywords: Chaos; Lu model; anti-synchronization; hybrid synchronization; Gardano’s method; nonlinear dynamical system
Chaotic systems with real state variables are boing found and studied with increased attention in several aspects of nonlinear dynamical systems, the first physical and mathematical model of a chaotic system is the system of Lorenz, which only includes real variables discovered in 1963 and opens the way to other chaos systems such as the system of Chen, Lu’s system (2002), Liu’s system (2004), and the system of the Pan system (2009). Each system has a 3-D of differential equations and just one positive Lyapunov exponent [1–5].
Exponent Lyapunov and nonlinear dynamic systems attractor play an important and actively involved role in classifying these systems and have attracted increasing interest in engineering application and different scientific research as, encrypting [6–9], engineering [10–13], and nonlinear circuits [14]. One important application in the field of engineering is secure communication i.e., messages crazy by simple chaotic processes like these are not always secure. The suggestion is that the higher dimensional hyperchaotic systems can be used to solve this problem, thereby the randomness and unpredictability [15–20].
Rössler performed the first 4-D hyperchaotic system with real variables in 1979 with two positive exponents of Lyapunov and discovered a further 4-D and 5-D hyperchaotic system with three positive exponents of Lyapunov [21–25] and some other systems. In contrast to low dimensions, dynamic systems with higher dimensions are effective and interesting [17–19].
Several papers on the subject today are dedicated to studying the new hyperchaotic systems in higher dimensions (Dimension 5) [16]. But most of these research focuses on 4-D and 5-D systems only, while a few kinds of researches are available in 6 dimensional nonlinear dynamical systems [17–20]. The 4D system consists of ten-term operators with four parameters and different features which include the Lyapunov exponents of balances and stability. The thrilling attractor is one of the latest dynamic systems classifications, with recent research separating attractors into self-enthusiastic or secret ones. Within the following paragraphs, the results of this work are summarized.
• The synchronization of similar 4-D hyperchaotic systems are studied and is then theoretically introduced as an Engineering application to detect error dynamics between each and its stable communication.
• Non-linear stability-based control methods in Lyapunov, Gardano approach design the various controllers of synchronization phenomena.
• By comparing the results of the Lyapunov method with the Gardano method, the best fitting controllers are found.
2 The Description of the Problem and Our Solution
We use the second Lyapunov method and the methods of Gardano, where we infer that Lyapunov functions as a certain constructive tool as:
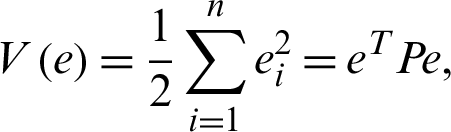
There P is a regular function and the Lyapunov function derivatives
Be certainly negative, i.e., Q is a positive, square matrix. Nevertheless, if the Q matrix is defined as a negative, we will change the P matrix to ensure that a given Q matrix is obtained.
While in Gardano [1–4], the distinguishing formula of Eq. (3) is considered in the 4D hyperchaotic method
Let
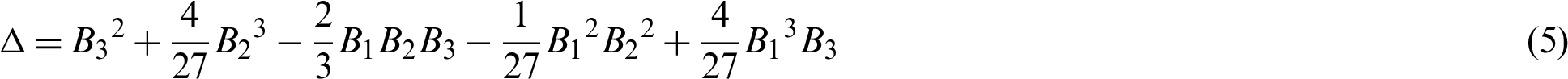
This approach allows one to find the roots of the cubic equation (Eq (3)) on the basis of 
as:
• If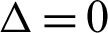 
, then there are three roots in the second term of Eq. (3), but one is multiple:
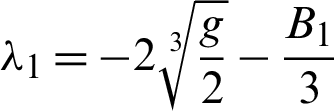
• When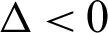 
, then three separate root terms have been described by the second term (3):
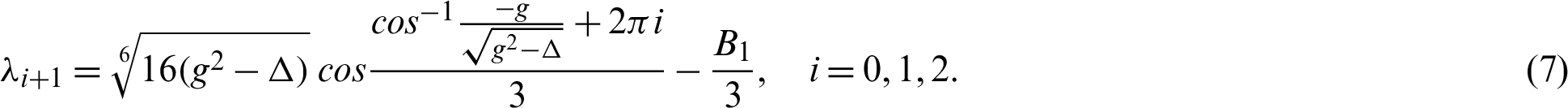
• When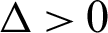 
, then the second term of Eq. (3) has one real root and two complexes conjugate roots with imaginary sections which do not vanish:
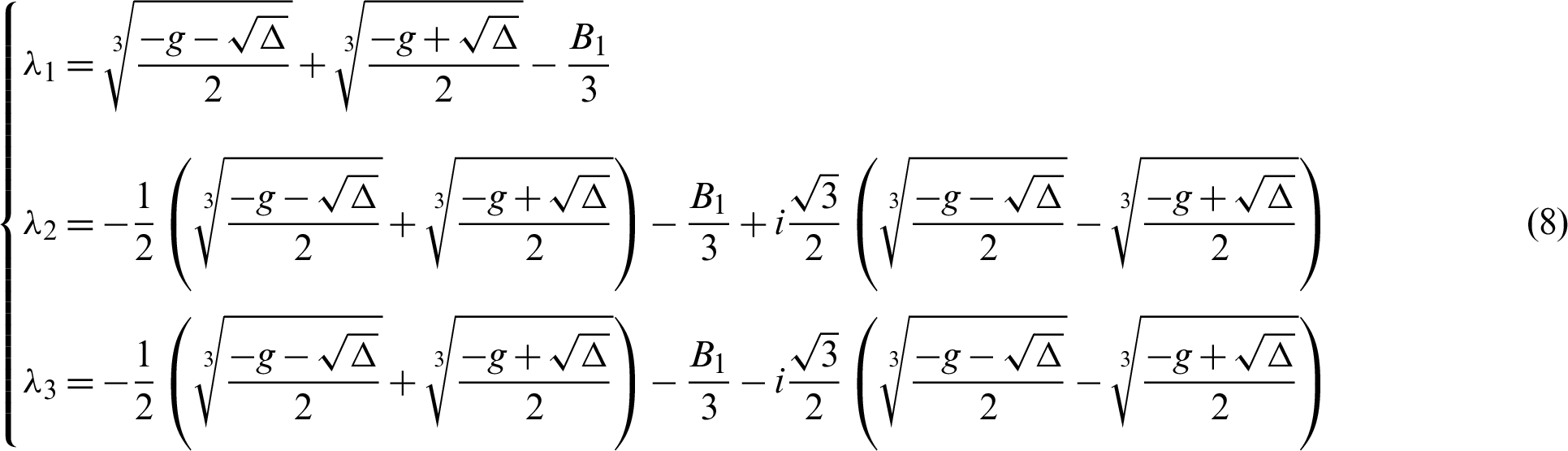
Here, to construct all roots with negative real parts, not choosing an appropriate nonlinear controller U like the Lyapunov method is essential.
Briefly, this final point poses three fundamental questions. First, does the Lyapunov method always succeed? Second, is the Gardano method better? Thirdly, how can these two approaches be distinguished? This paper starts with two ways of answering these questions.
The Lorenz system was one of the most commonly studied 3-D chaotic systems. By adding a linear feedback controller, the original design was changed into a 4-D and 5-D hyperchaotic design. The new 4-D hyperchaotic system that contains is designed three positive Lyapunov Exponents LE1 = 0.94613, LE2 = 0.28714, LE3 = 0.0047625, and one negative Lyapunov Exponents LE4 = −12.4021. The 4-D system which is described by the following mathematical form:
where the real state variables are x1, x2, x3, x4, and a, b, c, h, the all positive real parameters are equal (10, 8/3, 34, 2.5), and this system is rich of dynamical properties. Figs. 1a and 1b show the 3-D attractor of the system (9), while Figs. 2a and 2b display the 2-D attractor of the structure (9).
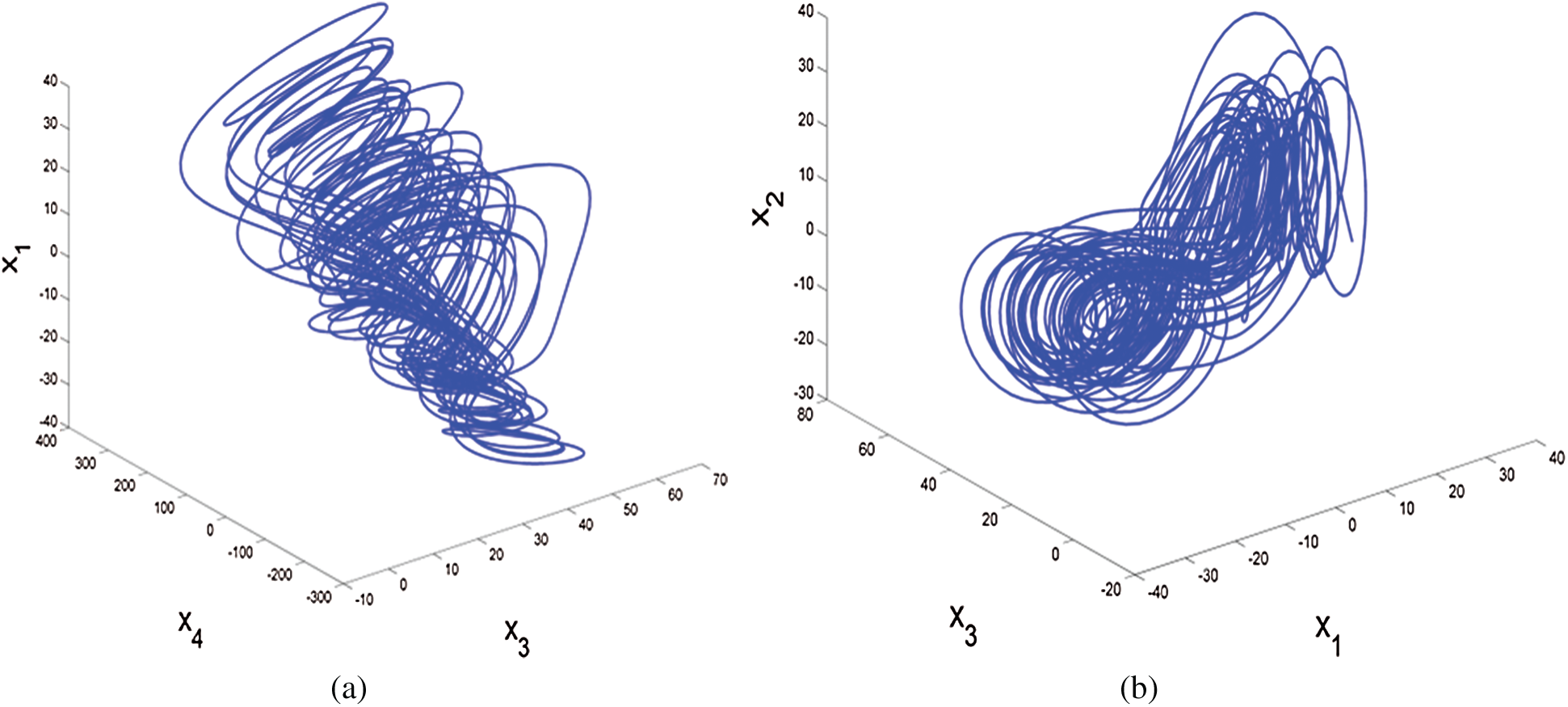
Figure 1: 3-D attractor of the system (9) in the (a) 
space; (b) 
space
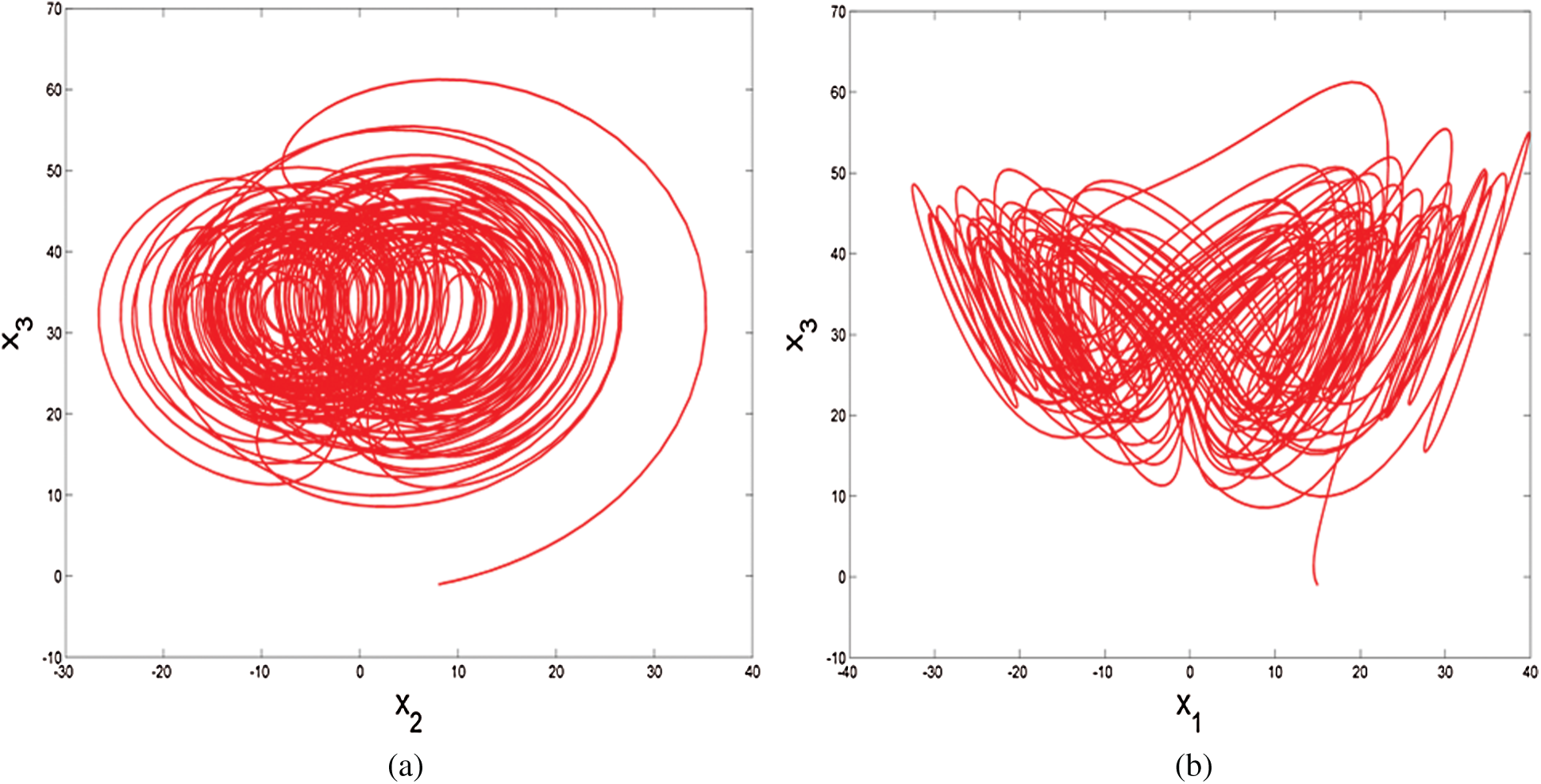
Figure 2: 2-D attractor of the system (9) in the (a)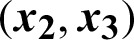 
plane; (b) 
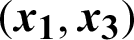plane
3.1 Lyapunov Exponents and Dimensions
The numerical simulation of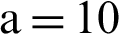 
, 
, 
, 
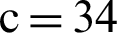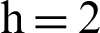, 5 was performed based on Wolf Algorithm and MATLAB software. The initial value (15, 8, −1, −2) of the system (9) was hyperchaotic, with three positive exponents of Lyapunov, i.e., LE1 = 0.94613, LE2 = 0.28714, LE3 = 0.0047625.
The exponents of the plot of Lyapunov are shown in Fig. 3.
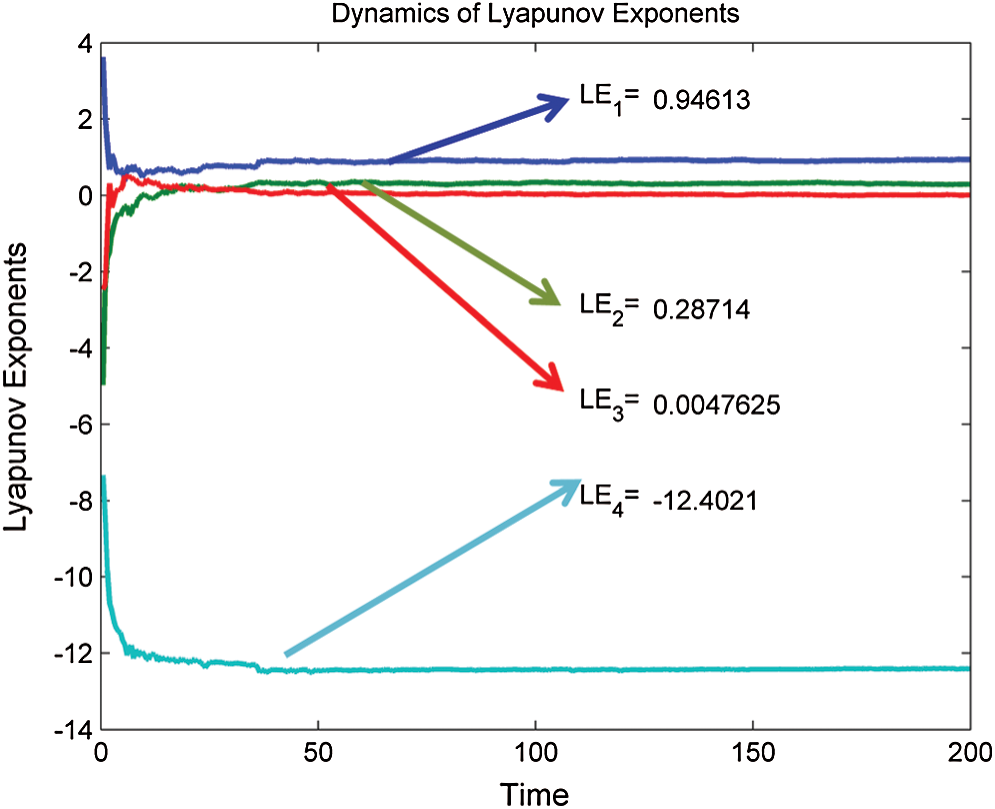
Figure 3: 4-D hyperchaotic system exponents of Lyapunov
Dimensions of Lyapunov are found as:
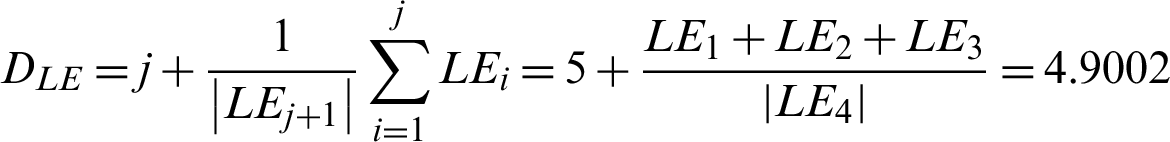
4.1 The New Lorenz 4-D Hyperchaotic Systems are Synchronized
In this section one of the main applications of secure communication engineering is considered theoretical studies and numerical simulations. Therefore, the first system (called drive system) represents the image or message information to be transmitted and, while the second system represents noise following this information, it ensures that it is not penetrated. The second system (called response system) assumes the machine (9) is a drive mechanism and is writable as,
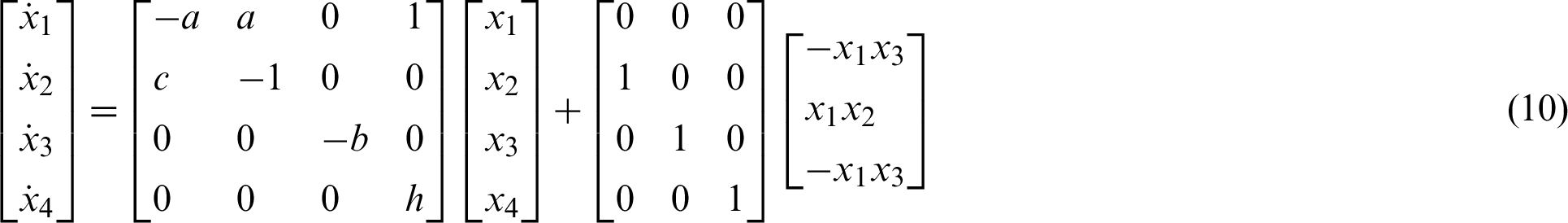
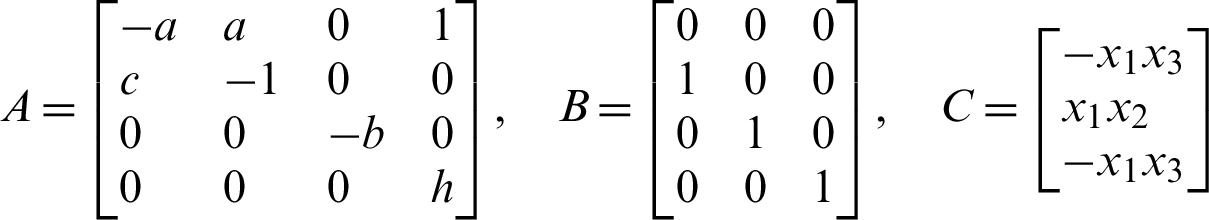
A and BC represents parameters matrix and nonlinear part of the system (9) respectively.
While the response system is as follows:
and let U = [u1, u2, u3, u4]T is the nonlinear controller to be designed.
The synchronization error dynamics between the 4-D hyperchaotic system (10) and system (11) is defined as ei = yi − xi, i = 1, 2, 3, 4 and satisfied that, 
.
The dynamics of the error are defined as follows:
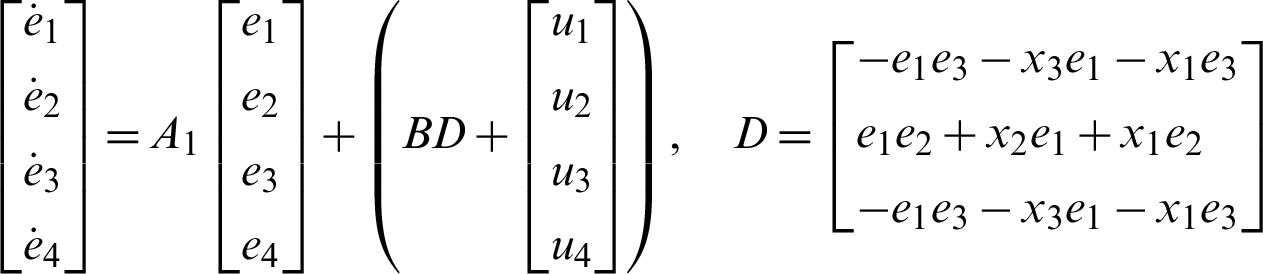
i.e.,
The matrix A1 equal to A, i.e., A1 = A for identical systems. But, in non-identical systems (different) the matrix 
.
Now, by designing several controllers based on Lyapunov and Gardano methods we will try to control the error system (12), and compare them. Here arises the problem of the two methods, which is the better method? Our questions are answered in the following theorems.
Theorem 1. If the regulator U of structure (12) is scheme as the following:
The system (11) can then be tracked with two methods by system (10).
Proof. Replace the error dynamics (12) mechanism over control, we receive:
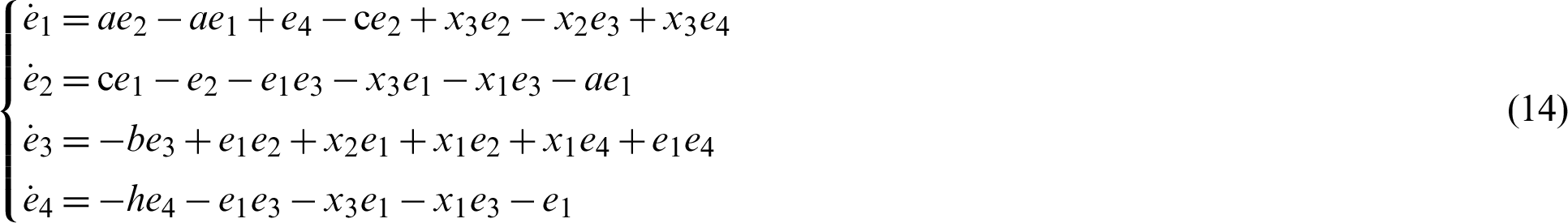
We are now building a positively defined Lyapunov candidate, based on the Lyapunov method,
where P defines as in Eq. (1), Lyapunov’s derivative V(e) function is time-related as:
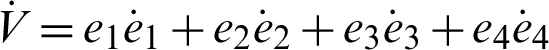
where Q = diag(a, 1, b, h), so Q > 0. Consequently,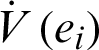 
is negative definite on R4. The nonlinear controller is suitable and the complete synchronization is achieved.
The characteristic equation between system (12) and control (13) is defined in Gardano method, and according to Eq. (3),
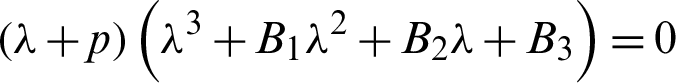
where
For simplified, we substitute the value of constants as a = 10, b = 8/3, c = 34, h = 2.5, in the above equation can be rewritten as:
Therefore, we have g = −1117,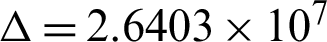 
. Since 
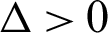than the roots are calculate according to Eq. (8) as:
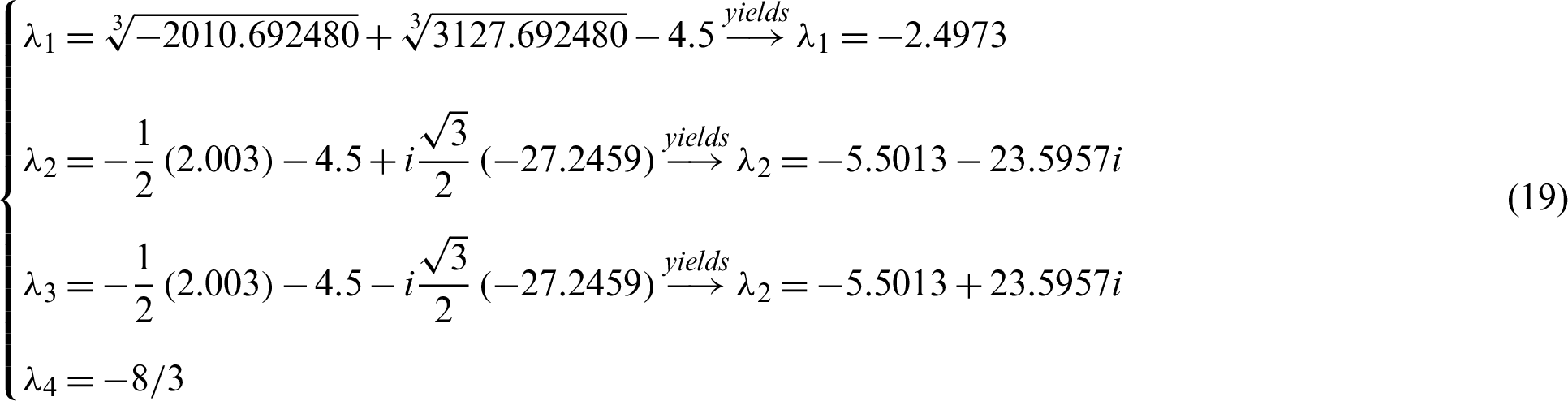
Of course, all roots with negative actual parts are successfully synced with system (11) and system (10), therefore the Gardano method is efficient. The evidence is complete. Such tests are numerically checked in Figs. 4 and 5. Where we take the drive system and the response system’s initial values are (15, 8, −1, −2) and ( −15, −10, 16, 8) respectively.
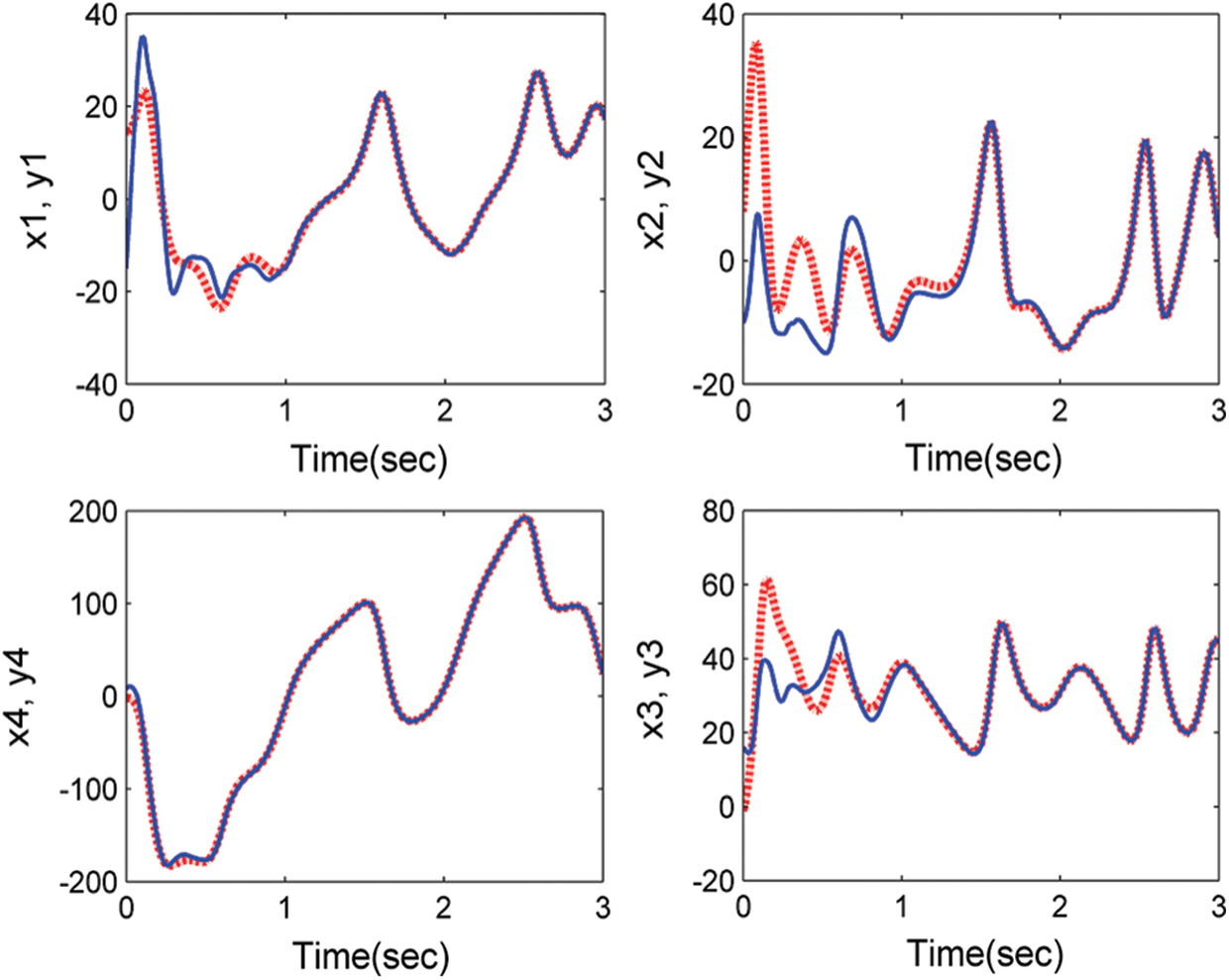
Figure 4: Anti-synchronization between systems (11) and (10) with control (13)
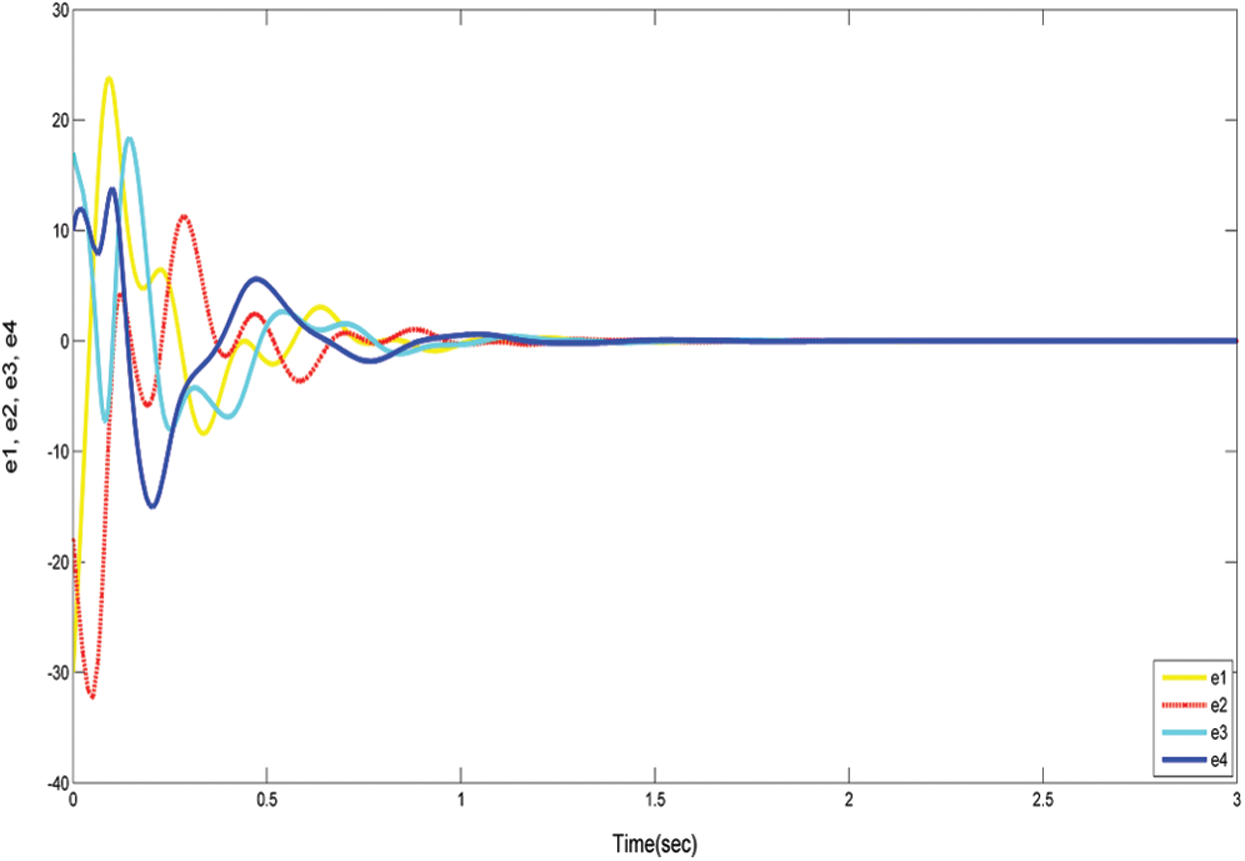
Figure 5: The convergence of system (12) with controllers (13)
The non-linear control approach, which uses two theoretical methods, offers an anti-synchronization between two related highly hyperchaotic systems. To stop collisions, it involves two systems; the first (called drive systems) reflects the first, and the second (called the responses system). This mechanism is the second train, which is used to ensure that there is no collision with the first train. The second is used to prevent collisions. The first train will have a second system. Suppose that the system (10) is the drive system and the reaction system (11).
The 4D hyperchaotic system (10) and system (11) are described as anti-synchronization error dynamics as ei = yi + xi, i = 1, 2, 3, 4 and satisfied that,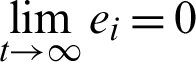 
.
The error dynamics is calculated as the following:
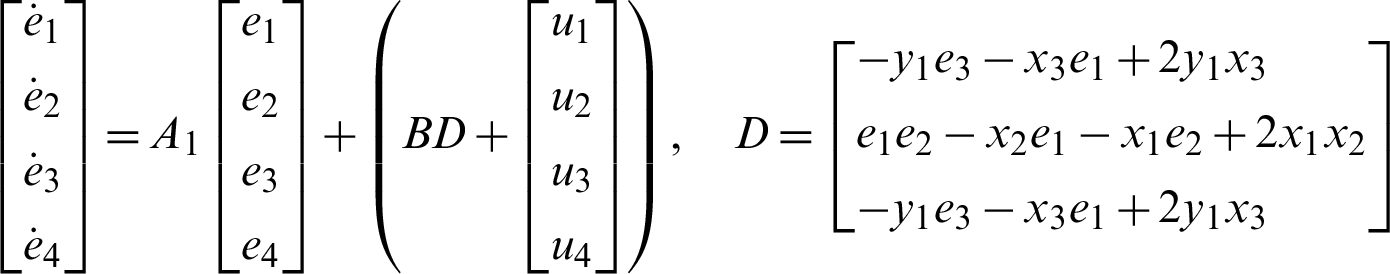
i.e.,
Theorem 2. For system (15) with nonlinear control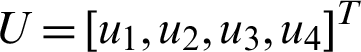 
such that
Proof. From the above control (21) with the error system (20), we get:
Now, based on the Lyapunov method:
The derivative of the Lyapunov function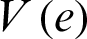 
with respect to time is
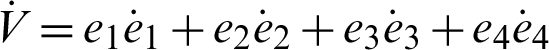
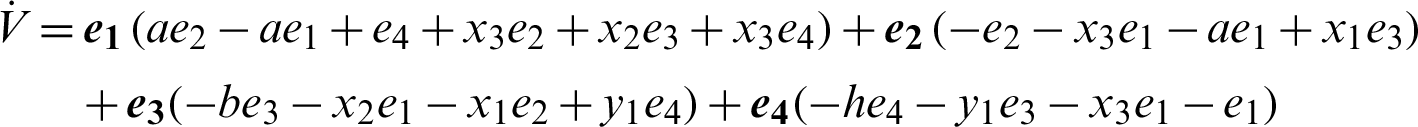
where Q = diag(a, 1, b, h) , so Q > 0. Consequently,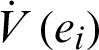 
is negative definite on R4. The nonlinear controller is suitable and the anti-synchronization is achieved.
In Gardano method
After substituting the values of the constants (a,b,c,h), we get
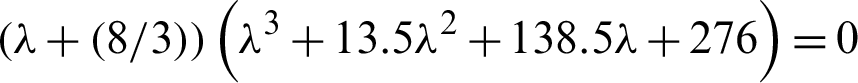
Therefore, we have g = −165,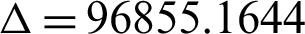 
. Since 
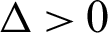than the roots are calculate according to Eq. (8) as:
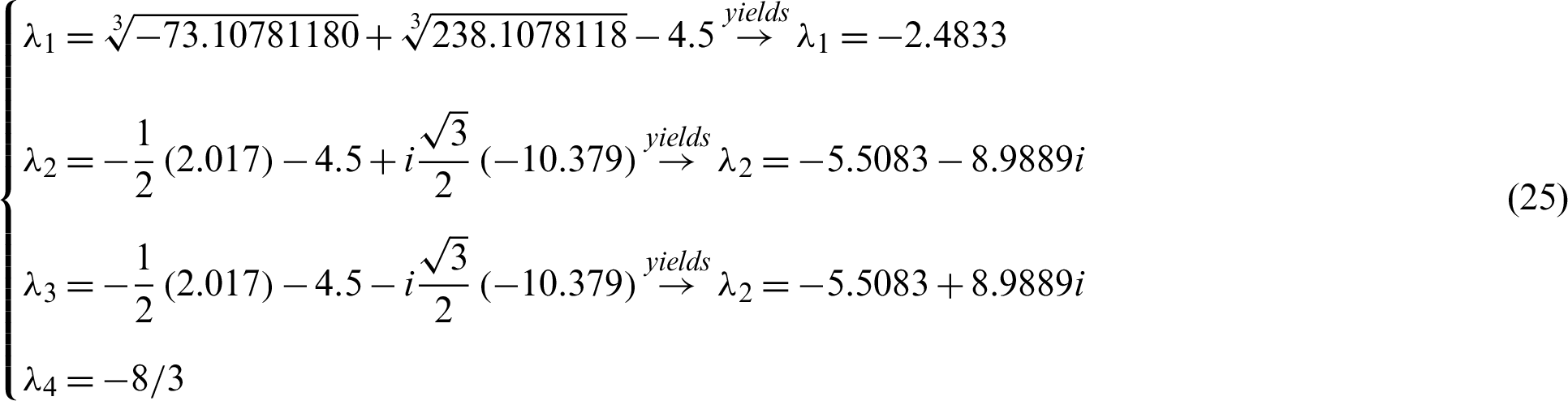
Of course, all roots with negative actual parts are successfully synced with the system (11) and system (10), therefore the Gardano method is efficient. The evidence is complete. These results are numerically checked in Figs. 6 and 7. Where the drive system and the response system initial values are used (15, 8, −1, −2) and ( −15, −10, 16, 8) respectively.
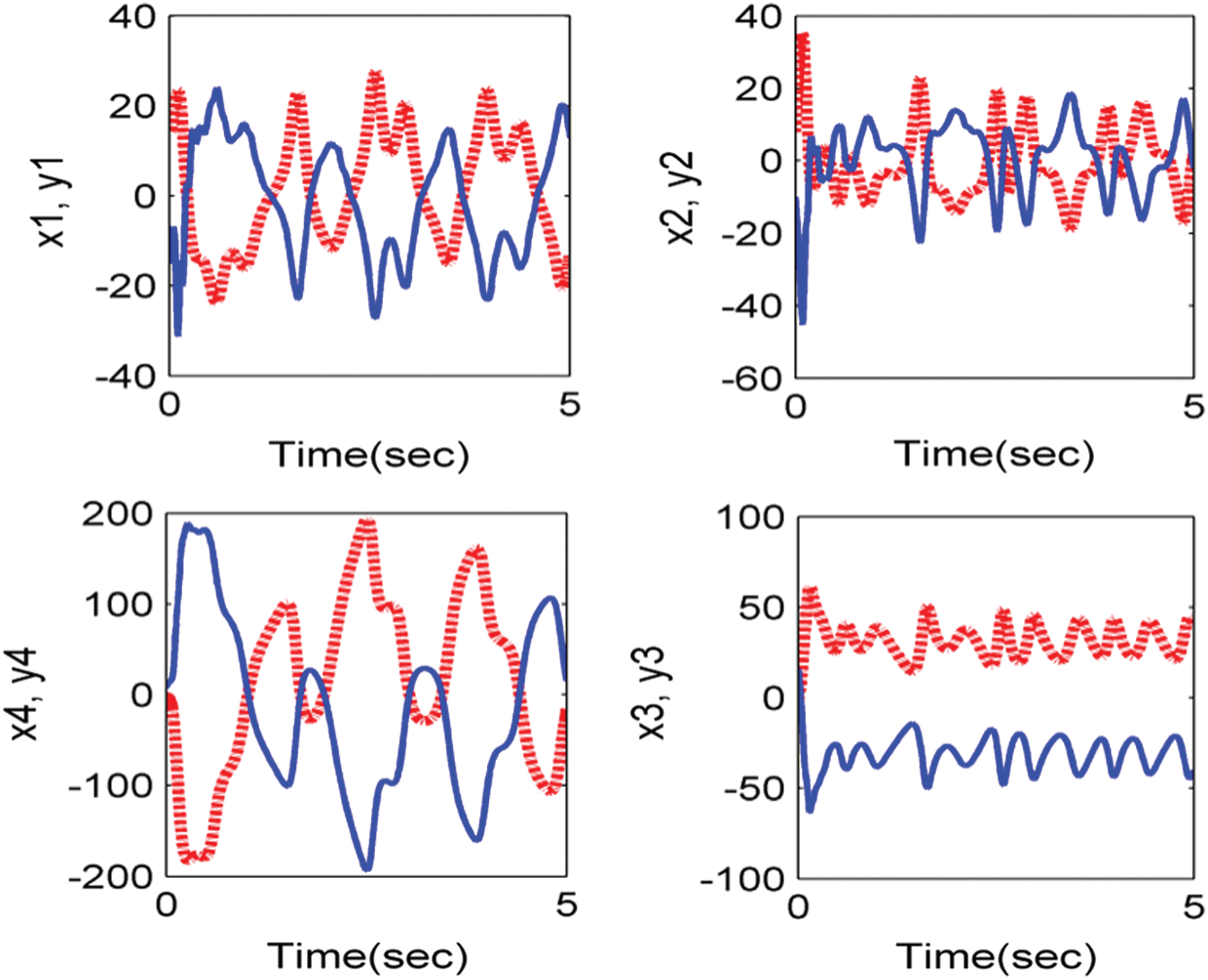
Figure 6: Anti-synchronization between systems (11) and (10) with control (13)
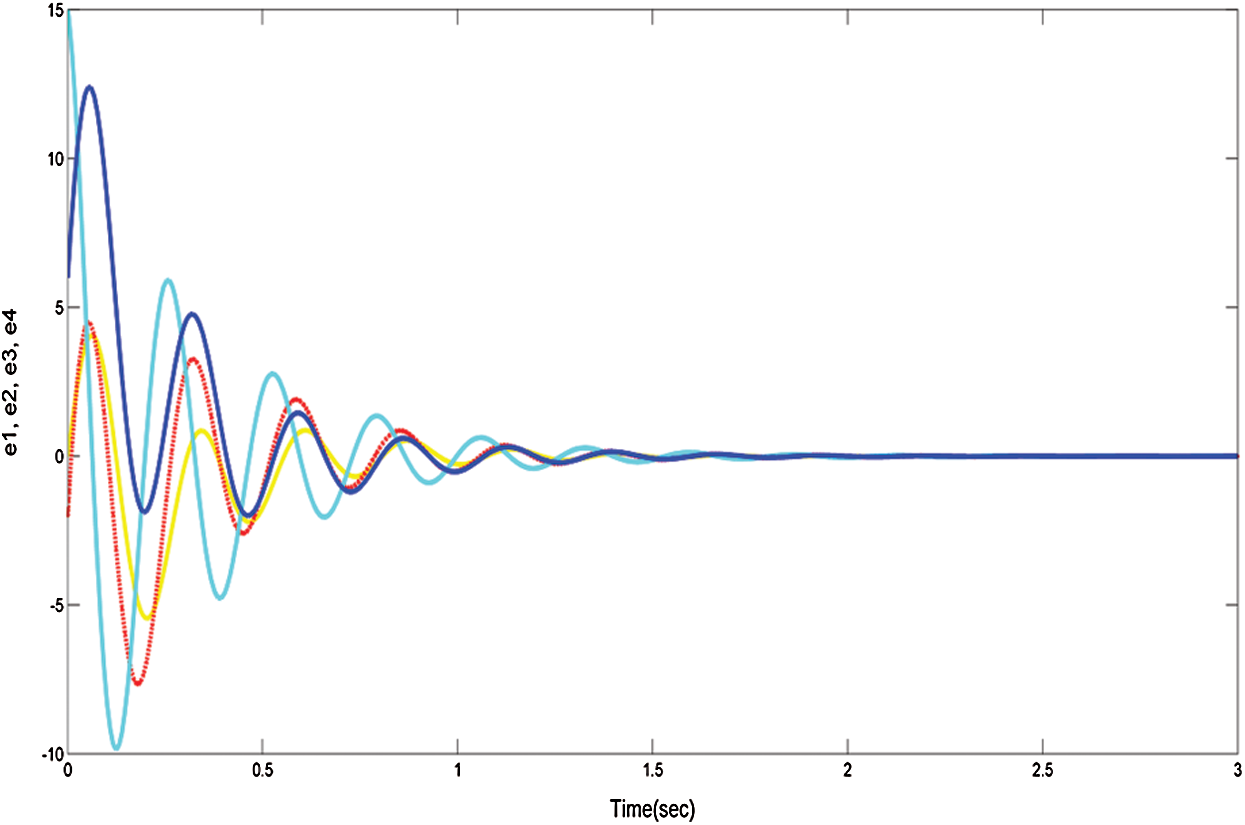
Figure 7: The convergence of system (20) with controllers (21)
Hybrid synchronization is a mixture of the previous two phenomena (Complete synchronization and Anti-synchronization). There are thus two appropriate systems, one system (Called drive system), the other system (Called response system). There are two systems. Assume that the drive system is (10) and the reaction system is (11):
The hybrid synchronization error dynamics is defined as ei = yi − xi, ej = yj + xj, i = 1, 3; j = 2, 4, and satisfied that ,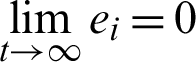 
.
The error dynamics is calculated as the following:
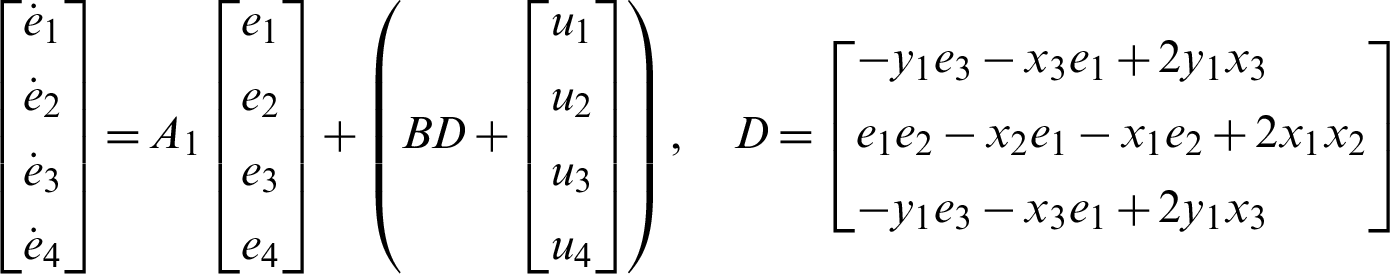
i.e.,
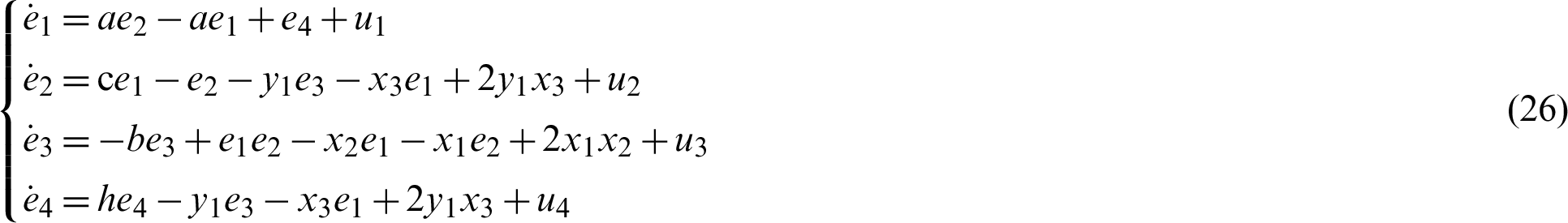
Theorem 3. If the nonlinear control U of error dynamical system (6) is designed as the following:
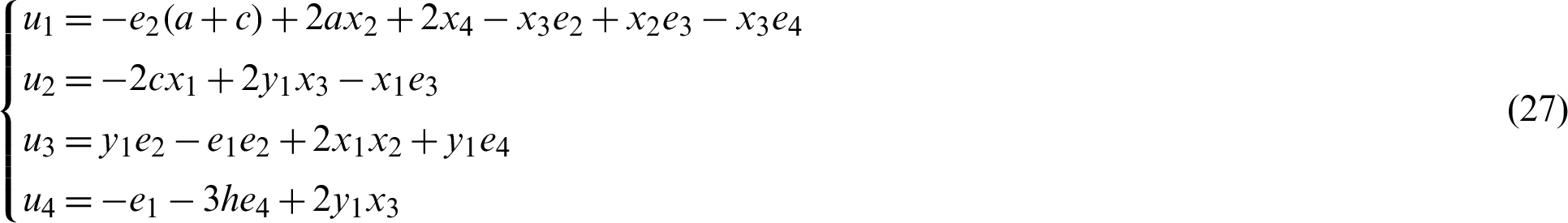
Proof. Rewrite system (26) with control (27) as follows:
Now, based on the Lyapunov method:
The derivative of the Lyapunov function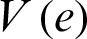 
with respect to time is
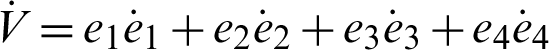
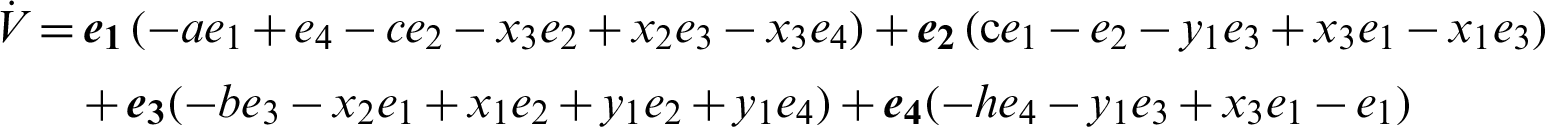
where Q = diag(a, 1, b, h), so Q > 0. Consequently,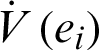 
is negative definite on R4. The nonlinear controller is suitable and the anti-synchronization is achieved.
In Gardano method:
After substituting the values of the constants (a, b, c, h), we get
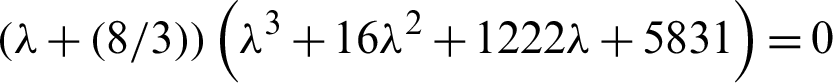
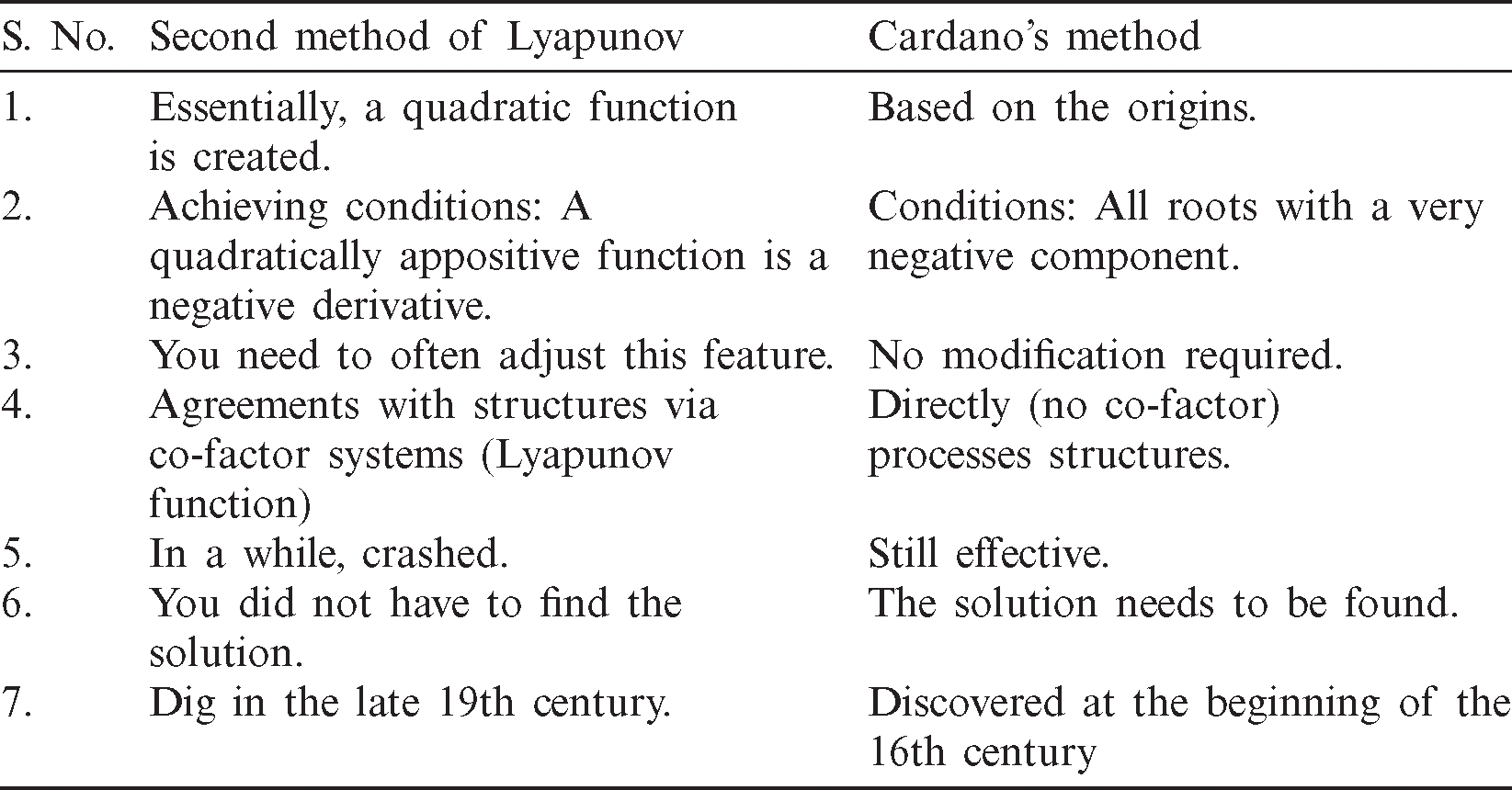
Tab.1 shows the variance amongst second method of Lyapunov and Cardano’s method.
Table 1: The variance amongst second method of Lyapunov and Cardano’s method
The structure of the subject of synchronization phenomena in two methods is shown in Fig. 10.
Therefore, we have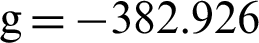 
, 
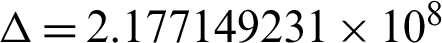. Since 
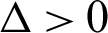than the roots are calculate according to Eq. (8) as:
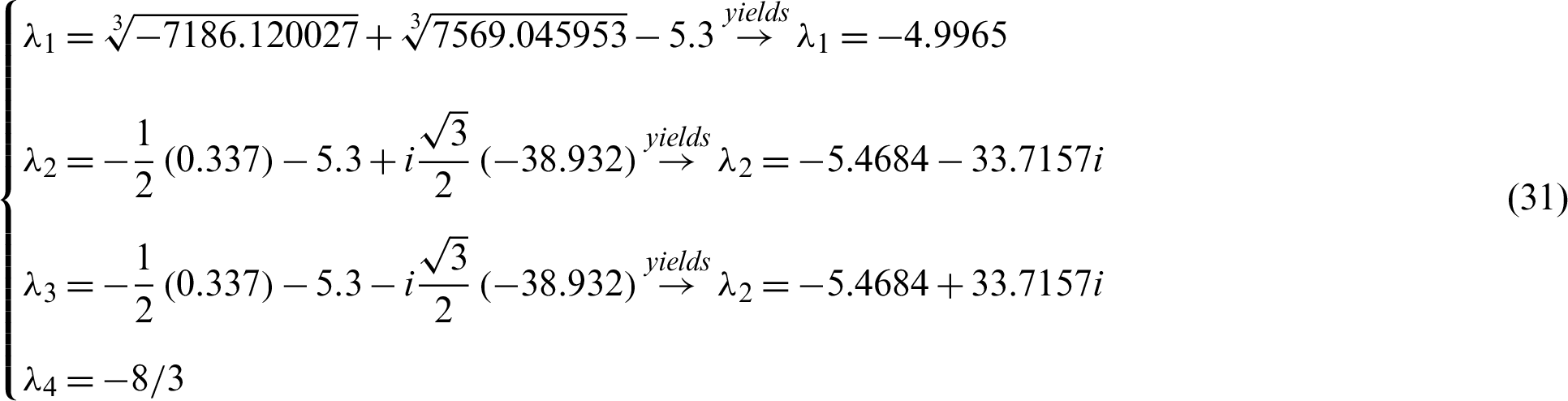
In addition, all roots with negative actual parts are successfully synced with system (11) and system (10), therefore the Gardano method is efficient. The evidence is complete. Such tests are numerically checked in Figs. 8 and 9. Where the drive system and the response system initial values are used (15, 8, −1, −2) and ( −15, −10, 16, 8) respectively.
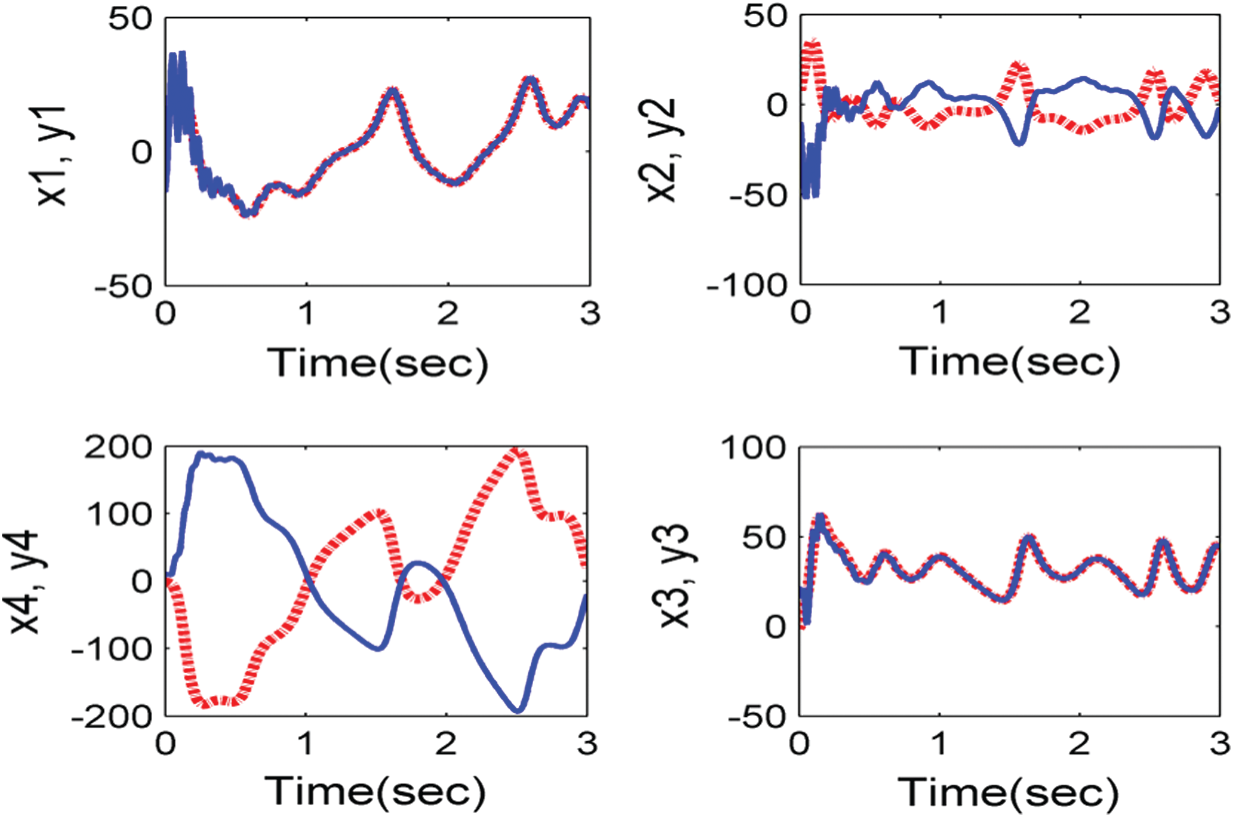
Figure 8: Anti-synchronization between systems (11) and (10) with control (13)
Figure 9: The convergence of system (26) with controllers (27)
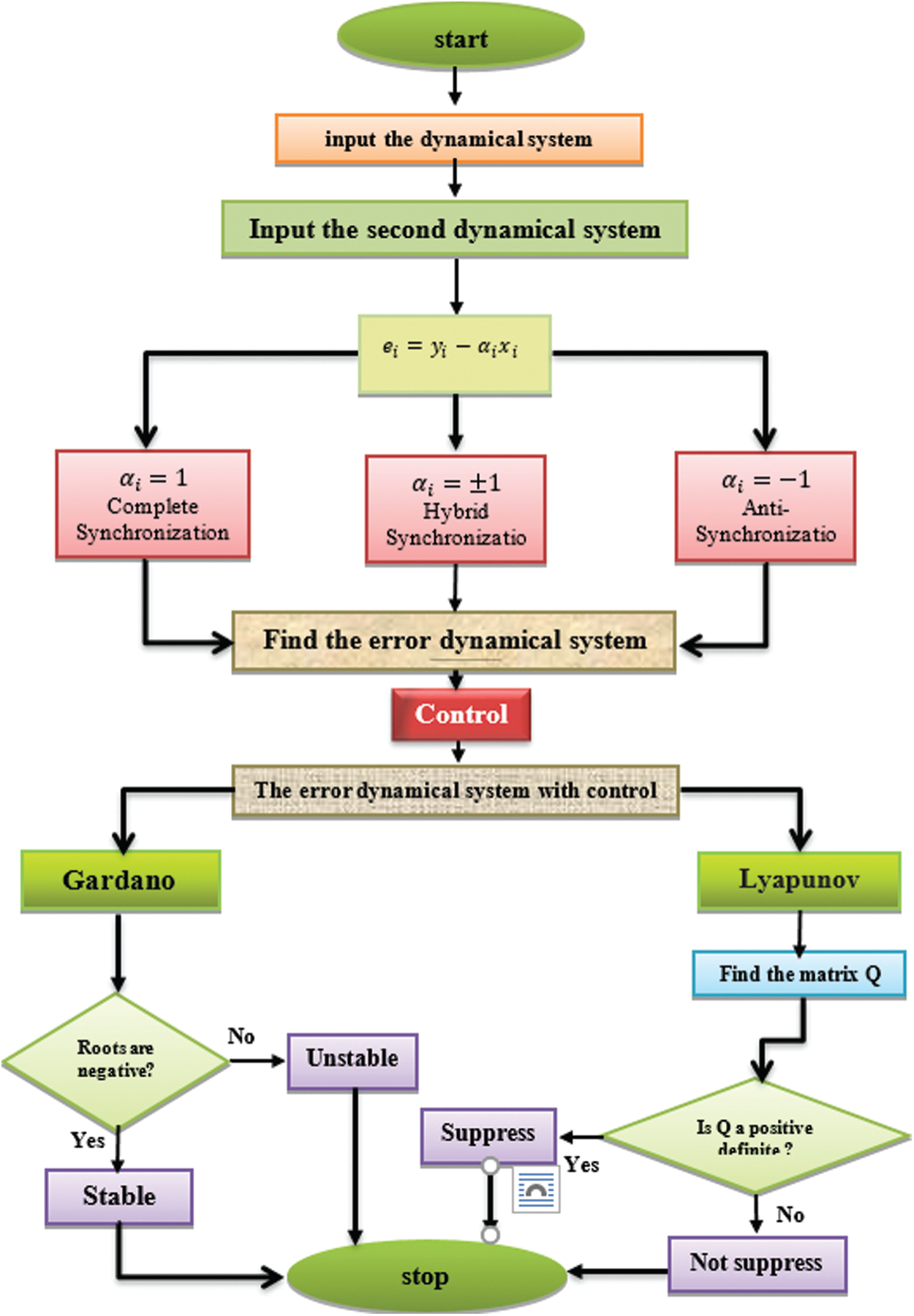
Figure 10: A diagram showing the structure of the subject of synchronization phenomena in two methods
Thus, all questions in this section are answered in these theorems, and the following table indicates that the Cardano method is stronger than the Lyapunova method.
The second method Lyapunov and the Cardano method are based on nonlinear models and two theoretical approaches. We have been trying to grasp the discrepancies in each process and how to achieve synchronization? Within this article, two identical 4D hyperchaotic systems deal with the synchronization phenomena. What is the best method? This paper, therefore, answers all these questions in the Cardano method and makes notice that a supporting function, like the Lyapunov method, should not be created or modified. The Cardano process is better than the Lyapunov procedure. The computational simulation was used to describe the same findings.
The following scheme shows the topics of research:
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1 S. F. AL-Azzawi. (2012). “Stability and bifurcation of pan chaotic system by using Routh-Hurwitz and Gardan methods,” Applied Mathematics and Computation, vol. 219, no. 3, pp. 1144–1152. [Google Scholar]
2 S. F. Al-Azzawi and M. M. Aziz. (2018). “Chaos synchronization of nonlinear dynamical systems via a novel analytical approach,” Alexandria Engineering Journal, vol. 57, no. 4, pp. 3493–3500.
3 S. F. Al-Azzawi, L. Patria Mujiarto, A. Sambas and W. S. M. Sanjaya. (2020). “Stability of Lorenz system at the second equilibria point based on Gardano’s method,” Journal of Physics: Conference Series, vol. 1477, no. 2, 22009.
4 Z. N. Al-Kateeb and M. F. Jader. (2020). “Encryption and hiding text using DNA coding and hyperchaotic system,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 19, no. 2, pp. 766– 774. [Google Scholar]
5 Z. N. Al-Kateeb and S. J. Mohammed. (2020). “Encrypting an audio file based on integer wavelet transform and hand geometry,” TELKOMNIKA Telecommunication, Computing, Electronics and Control, vol. 18, no. 4, pp. 2012–2017. [Google Scholar]
6 Z. N. Al-Kateeb and S. J. Mohammed. (2020). “A novel approach for audio file encryption using hand geometry,” Multimedia Tools and Applications, vol. 79, no. 27–28, pp. 19615–19628. [Google Scholar]
7 K. A. Abed and A. A. Ahmad. (2020). “The best parameters selection using PSO algorithm to solving for ITO system by new iterative technique,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 18, no. 3, pp. 1638–1645.
8 A. A. Ahmad. (2020). “By using a new iterative method to the generalized system Zakharov–Kuznetsov and estimate the best parameters via applied the PSO algorithm,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 19, no. 2, pp. 1055–1061.
9 O. I. Khalaf, G. M. Abdulsahib, H. D. Kasmaei and K. A. A. Ogudo. (2020). “A new algorithm on blockchain technology application in live stream video transmissions and telecommunications,” International Journal of e-Collaboration, vol. 16, no. 1, pp. 16–32. [Google Scholar]
10 M. L. Thivagar, A. A. Hamad and S. G. Ahmed. (2020). “Conforming dynamics in the metric spaces,” Journal of Information Science and Engineering, vol. 36, no. 2, pp. 279–291. [Google Scholar]
11 M. L. Thivagar, M. A. Ahmed, V. Ramesh and A. A. Hamad. (2020). “Impact of nonlinear electronic circuits and switch of chaotic dynamics,” Periodicals of Engineering and Natural Sciences, vol. 7, no. 4, pp. 2070–2091.
12 S. Al-Obeidi and S. F. Al-Azzawi. (2018). “Complete synchronization of a novel 6-D hyperchaotic Lorenz system with known parameters,” International Journal of Engineering & Technology (UAE), vol. 7, no. 4, pp. 5345–5349.
13 S. Al-Obeidi and S. F. Al-Azzawi. (2020). “Chaos synchronization in a 6-D hyperchaotic system with self-excited attractor,” TELKOMNIKA Telecommunication, Computing, Electronics and Control, vol. 18, no. 3, pp. 1483–1490. [Google Scholar]
14 A. S. Al-Obeidi and S. F. Al-Azzawi. (2019). “Chaos synchronization of a class 6-D hyperchaotic Lorenz system,” Modelling Measurement and Control B, vol. 88, no. 1, pp. 17–22. [Google Scholar]
15 A. S. Al-Obeidi and S. F. Al-Azzawi. (2019). “Projective synchronization for a class of 6-D hyperchaotic Lorenz system,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 16, no. 2, pp. 692–700. [Google Scholar]
16 S. F. Al-Azzawi and M. M. Aziz. (2019). “Strategies of linear feedback control and its classification,” TELKOMNIKA Telecommunication Computing Electronics and Control, vol. 17, no. 4, pp. 1931– 1940. [Google Scholar]
17 M. M. Aziz and S. F. Al-Azzawi. (2016). “Control and synchronization with known and unknown parameters,” Applied Mathematics, vol. 7, no. 3, pp. 292–303. [Google Scholar]
18 M. M. Aziz and S. F. Al-Azzawi. (2016). “Complete synchronization, anti-synchronization and hybrid synchronization between two different 4D nonlinear dynamical systems,” Mathematics Letters, vol. 2, no. 5, pp. 36–41.
19 S. Y. Al-hayali and S. F. AL-Azzawi. (2020). “An optimal control for complete synchronization of 4D Rabinovich hyperchaotic systems,” TELKOMNIKA Telecommunication Computing Electronics and Control, vol. 18, no. 2, pp. 994–1000. [Google Scholar]
20 S. Y. Al-hayali and S. F. Al-Azzawi. (2020). “An optimal nonlinear control for anti-synchronization of Rabinovich hyperchaotic system,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 19, no. 1, pp. 379–386. [Google Scholar]
21 Z. Sh. Al-Talib and S. F. Al-Azzawi. (2020). “Projective and hybrid projective synchronization of 4-D hyperchaotic system via nonlinear controller strategy,” TELKOMNIKA Telecommunication Computing Electronics and Control, vol. 18, no. 2, pp. 1012–1020. [Google Scholar]
22 Z. Sh. Al-Talib and S. F. Al-Azzawi. (2020). “Projective synchronization for 4D hyperchaotic system based on adaptive nonlinear control strategy,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 19, no. 2, pp. 715–722.
23 G. Srivastava, R. Gupta, R. Kumar and D. N. Le. (2019). “Space-time code design using quaternions, octonions and other non-associative structures,” International Journal of Electrical and Computer Engineering Systems, vol. 10, no. 2, pp. 91–95.
24 S. F. Al-Azzawi, M. A. Mohamed, H. Rubiani, M. Mamat, J. Titaley et al. (2020). “Chaotic Lorenz system and it’s suppressed,” Journal of Advanced Research in Dynamical and Control Systems, vol. 12, no. 2, pp. 548–555.
25 A. Sambas, S. Vaidyanathan, S. Zhang, M. A. Mohamed, Y. Zeng et al. (2020). “A new 4-D chaotic hyperjerk system with coexisting attractors, its active backstepping control, and circuit realization,” in Backstepping Control of Nonlinear Dynamical Systems, Academic Press, Elsevier, pp. 73–94. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |