DOI:10.32604/cmc.2021.014442

| Computers, Materials & Continua DOI:10.32604/cmc.2021.014442 |  |
| Article |
Non-Associative Algebra Redesigning Block Cipher with Color Image Encryption
1Department of Mathematics, Quaid-i-Azam University, Islamabad, 44000, Pakistan
2Department of Computer Science, Quaid-i-Azam University, Islamabad, 44000, Pakistan
*Corresponding Author: Nazli Sanam. Email: nazli.sanam@iiu.edu.pk
Received: 21 September 2020; Accepted: 23 October 2020
Abstract: The substitution box (S-box) is a fundamentally important component of symmetric key cryptosystem. An S-box is a primary source of non-linearity in modern block ciphers, and it resists the linear attack. Various approaches have been adopted to construct S-boxes. S-boxes are commonly constructed over commutative and associative algebraic structures including Galois fields, unitary commutative rings and cyclic and non-cyclic finite groups. In this paper, first a non-associative ring of order 512 is obtained by using computational techniques, and then by this ring a triplet of  S-boxes is designed. The motivation behind the designing of these S-boxes is to upsurge the robustness and broaden the key space due to non-associative and non-commutative behavior of the algebraic structure under consideration. A novel color image encryption application is anticipated in which initially these 3 S-boxes are being used to produce confusion in three layers of a standard RGB image. However, for the sake of diffusion 3D Arnold chaotic map is used in the proposed encryption scheme. A comparison with some of existing chaos and S-box dependent color image encryption schemes specs the performance results of the anticipated RGB image encryption and observed as approaching the standard prime level.
S-boxes is designed. The motivation behind the designing of these S-boxes is to upsurge the robustness and broaden the key space due to non-associative and non-commutative behavior of the algebraic structure under consideration. A novel color image encryption application is anticipated in which initially these 3 S-boxes are being used to produce confusion in three layers of a standard RGB image. However, for the sake of diffusion 3D Arnold chaotic map is used in the proposed encryption scheme. A comparison with some of existing chaos and S-box dependent color image encryption schemes specs the performance results of the anticipated RGB image encryption and observed as approaching the standard prime level.
Keywords: Block cipher; s-box; nonlinearity; color image encryption; 3D chaotic map
Cryptology is the science dealing with storage and data communication in secure and typically secret form. There are two further subdivisions of cryptology viz; cryptography and cryptanalysis. Cryptography is the method of keeping the information confidentiality using mathematical tools. Cryptanalysis is the art of cracking encrypted information by the means of mathematical and computational devices. It is powerful enough to breach the cryptographic security systems, without accessing the cryptographic key, and it obtains permissions to the content of encrypted communications. Although, both cryptography and cryptanalysis aim at the same target, however the methods and techniques for cryptanalysis have been modified radically throughout the history of cryptography. Among several the Differential cryptanalysis is frequently used for block ciphers. It is based on the analysis of the concern of specific difference in plaintext pairs on the difference of the consequent cipher text pairs. These differences are used to allocate probabilities to the practicable keys and to find the virtually all possible keys [1].
A repetitive arrangement from the concept of single output Boolean function is the extension of that idea to multiple output Boolean functions, along with denoted as a substitution box (S-box) [2]. The linking between the input and output bits in standings of dimension and exclusivity gives upsurge to several S-boxes. A  S-box is a mapping
S-box is a mapping  from k input to l output binary bits, whereas, there are 2k and 2l number of inputs and outputs, respectively. Formerly, an S-box is just a set of m single output Boolean functions combined in a static order. The dimension of an S-box has an outcome on the exclusiveness of the output and the input, which might disturb the characteristics of S-box. If there is an S-box with dimension
from k input to l output binary bits, whereas, there are 2k and 2l number of inputs and outputs, respectively. Formerly, an S-box is just a set of m single output Boolean functions combined in a static order. The dimension of an S-box has an outcome on the exclusiveness of the output and the input, which might disturb the characteristics of S-box. If there is an S-box with dimension  , l < k such that the number of input bits is greater than output bits, then certain entries in the S-box unquestionably be repeated; where, an
, l < k such that the number of input bits is greater than output bits, then certain entries in the S-box unquestionably be repeated; where, an  S-box might whichever contain different entries, where each input is mapped to dissimilar output, or replication of several entries of the S-box. Bijective S-boxes are the ones which are both injective and surjective and they are reversible [3,4]. S-box is the backbone of almost all the cryptosystems, which makes the system nonlinear. In the improvement of symmetric cryptosystems, which are constructed as substitution-permutation networks (DES and AES-like systems), most of the nonlinearity is found in the S-boxes portion of the algorithm. Modest softness in the S-boxes might hence lead to cryptosystems, which are just cracked. S-boxes are used as an exasperating scheme to allow the strength of cryptographic algorithms. So, the design of S-boxes must be cryptographically sound in order to acquire secure cryptosystems [2,3,5]. In contemporary cryptography, the S-boxes are commonly constructed over finite Galois fields
S-box might whichever contain different entries, where each input is mapped to dissimilar output, or replication of several entries of the S-box. Bijective S-boxes are the ones which are both injective and surjective and they are reversible [3,4]. S-box is the backbone of almost all the cryptosystems, which makes the system nonlinear. In the improvement of symmetric cryptosystems, which are constructed as substitution-permutation networks (DES and AES-like systems), most of the nonlinearity is found in the S-boxes portion of the algorithm. Modest softness in the S-boxes might hence lead to cryptosystems, which are just cracked. S-boxes are used as an exasperating scheme to allow the strength of cryptographic algorithms. So, the design of S-boxes must be cryptographically sound in order to acquire secure cryptosystems [2,3,5]. In contemporary cryptography, the S-boxes are commonly constructed over finite Galois fields  . For instance S-boxes; AES, Residue Prime [6], Gray [7], APA [8], S8 AES, Skipjack [9], and Xyi [10].
. For instance S-boxes; AES, Residue Prime [6], Gray [7], APA [8], S8 AES, Skipjack [9], and Xyi [10].
It is concluded from the literature review that differential attack is the only attack which applies on such S-boxes that are constructed by finite Galois field extension of binary field  . The S-boxes are typically constructed over Galois field and some other commutative and associative structures. In [11], a novel design of S-boxes is introduced over the elements of inverse property loop and the attractive features of the structure are; it is non-associativity and the existence of the inverse of zero elements. These properties increase the availability of the number of structures of IP-Loops. This motivated us to initiate this study to size
. The S-boxes are typically constructed over Galois field and some other commutative and associative structures. In [11], a novel design of S-boxes is introduced over the elements of inverse property loop and the attractive features of the structure are; it is non-associativity and the existence of the inverse of zero elements. These properties increase the availability of the number of structures of IP-Loops. This motivated us to initiate this study to size  S-boxes through a non-commutative and non-associative ring of order 512. The purpose of these S-boxes is to increase the robustness due to non-associative and non-commutative behavior of the ring structure under consideration and increase 65,536 times the key space. Thus, the obtained S-boxes having significant level of resistance against existing crypt analyses attack.
S-boxes through a non-commutative and non-associative ring of order 512. The purpose of these S-boxes is to increase the robustness due to non-associative and non-commutative behavior of the ring structure under consideration and increase 65,536 times the key space. Thus, the obtained S-boxes having significant level of resistance against existing crypt analyses attack.
In last two decades, the notion of chaos has found several applications in various scientific. In Cryptography  S-boxes are also been produced by using chaotic maps [12,13]. Because of its low non-linearity, they do not get much significance like S-boxes constructed through algebraic structures. Cryptography, which might be supposed to be a branch of arithmetic and technology, has clutched a tremendous deal of consideration and an oversize variety of analysis work, is devoted to the experience of chaos-based cryptologic algorithms [13,14]. The qualities of chaotic maps stand after their use within the smartness of such algorithms. These main options comprise highly sensitive dependence on initial conditions and controlling parameter, ergodicity, randomness, mixing, etc., that are alike the confusion and diffusion properties of Claude Shannon [15]. Precisely, the random-like behavior of the outputs of chaotic maps brands them suitable bases to be used in cryptographs. A lot of image encryption algorithms are built on chaotic systems, for instance [16–18]. Whereas Liu et al. [19], anticipated a chaos-based color image block encryption scheme using S-box. A novel color image encryption application is foreseen in which primarily newly obtained 3 S-boxes are being castoff to crop confusion in three layers of a standard RGB image. Though, for diffusion 3D Arnold chaotic map is used in the proposed encryption scheme. A comparison with some of current chaos and S-box reliant color image encryption schemes spectacles the performance results of the estimated RGB image encryption and pragmatic as approaching the standard principal level.
S-boxes are also been produced by using chaotic maps [12,13]. Because of its low non-linearity, they do not get much significance like S-boxes constructed through algebraic structures. Cryptography, which might be supposed to be a branch of arithmetic and technology, has clutched a tremendous deal of consideration and an oversize variety of analysis work, is devoted to the experience of chaos-based cryptologic algorithms [13,14]. The qualities of chaotic maps stand after their use within the smartness of such algorithms. These main options comprise highly sensitive dependence on initial conditions and controlling parameter, ergodicity, randomness, mixing, etc., that are alike the confusion and diffusion properties of Claude Shannon [15]. Precisely, the random-like behavior of the outputs of chaotic maps brands them suitable bases to be used in cryptographs. A lot of image encryption algorithms are built on chaotic systems, for instance [16–18]. Whereas Liu et al. [19], anticipated a chaos-based color image block encryption scheme using S-box. A novel color image encryption application is foreseen in which primarily newly obtained 3 S-boxes are being castoff to crop confusion in three layers of a standard RGB image. Though, for diffusion 3D Arnold chaotic map is used in the proposed encryption scheme. A comparison with some of current chaos and S-box reliant color image encryption schemes spectacles the performance results of the estimated RGB image encryption and pragmatic as approaching the standard principal level.
2 Fundamentals on Order 512 Non-Associative Algebraic Structure
A left almost semigroup (LA-semigroup) (or AG-groupoid) is a groupoid S satisfying the left invertive law; (ab)c = (cb)a for all, a, b, c in S [20]. It is a structure mid-way amongst a groupoid and a semigroup and it is a generalization of a commutative semigroup. The extended notion of LA-semigroup to LA-group or AG-group is given in [21]. An LA-group is an LA-semigroup with a left identity e in S, such that ea = a, for all a in S; and for each a in S, its inverse exists, i.e., there exists a−1 such that aa−1 = a−1a = e. In case of an additive LA-group the left identity would be called left zero element. Accordingly, the notion of a non-associative structure with respect to the two binary operations ‘+’ of LA-group and ‘ ’ of LA-semigroup was the natural consequence. Therefore, an LA-ring is a non-empty set R with at least two elements such that (R,+) is an LA-group and
’ of LA-semigroup was the natural consequence. Therefore, an LA-ring is a non-empty set R with at least two elements such that (R,+) is an LA-group and  is an LA-semigroup and both left, and right distributive laws hold. Fundamental properties are given in [22], while in [23] the existence of non-associative LA-rings is documented and a special case of LA-ring is launched.
is an LA-semigroup and both left, and right distributive laws hold. Fundamental properties are given in [22], while in [23] the existence of non-associative LA-rings is documented and a special case of LA-ring is launched.
Using a special LA-ring Rn of order n, a set  can be constructed where m is a positive integer and um+1 = 0. There are nm+1 elements in R of the form
can be constructed where m is a positive integer and um+1 = 0. There are nm+1 elements in R of the form 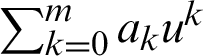 , where all ak belong to Rn. R is a special LA-ring. The operations in
, where all ak belong to Rn. R is a special LA-ring. The operations in  follow from the operations in Rn are defined as:
follow from the operations in Rn are defined as:  and
and  . In R,
. In R,  ,
,  ,
,  .
. 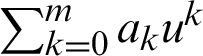 is a unit in R if and only if a0 is unit in Rn.
is a unit in R if and only if a0 is unit in Rn.
3 For S-Boxes Pairs Generating Algorithm
Take LA-ring  with identity. Addition and multiplication are defined in Tab. 1.
with identity. Addition and multiplication are defined in Tab. 1.

Here the element 0 is 2 and the left identity element is 4. Units in R8 are: 0, 1, 3, and 4. The set R = R8 +uR8 +u2R8 (with u3 = 0) is a special LA-ring with 512 elements. The left identity element in R is 422. An element a + bu + cu2 is a unit in R = R8 +uR8 +u2R8 if and only if a is a unit in R8. So, there are 256 units in R = R8 +uR8 +u2R8. The scheme of the S-boxes triplets is based on two substructures of the special LA-ring R. One of the substructures is the sub LA-module  of LA-ring R, which is decimal equivalent to
of LA-ring R, which is decimal equivalent to  and the second is the multiplicative group
and the second is the multiplicative group  of unit elements of the ring R which is decimal equivalent to
of unit elements of the ring R which is decimal equivalent to  . The first one has two operations; addition and scalar multiplication, the last one holds only multiplication. Actions of group PGL(2, GF(28)) to the Galois field GF(28) yield the ultimate S-boxes.
. The first one has two operations; addition and scalar multiplication, the last one holds only multiplication. Actions of group PGL(2, GF(28)) to the Galois field GF(28) yield the ultimate S-boxes.
3.1 Case I: Generating S-Boxes Over Sub LA-Module of R-LA-Module R
As M is R-sub LA-module of R-module R, we can define an affine mapping 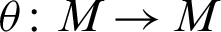 ,
,  where r = 342 and m = 653 are fixed elements in U(R) and M respectively. As the elements of M are 9 binary bits representation, so we define a bijection
where r = 342 and m = 653 are fixed elements in U(R) and M respectively. As the elements of M are 9 binary bits representation, so we define a bijection  by
by

Finally, the linear fractional transformation is given as;  defined as:
defined as:  where a = 158, b = 54, c = 20, d = 92 in GF(28) such that
where a = 158, b = 54, c = 20, d = 92 in GF(28) such that  For the construction of this S-box, the algorithm begins with the sub LA-module M of a special LA-ring R and use of
For the construction of this S-box, the algorithm begins with the sub LA-module M of a special LA-ring R and use of 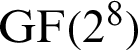 . Eventually, the function. purposes the S-box with the action of PGL(2, GF(28) on GF(28). The newly constructed S-box, using the suggested algorithm is given in Tab. 2. This is a
. Eventually, the function. purposes the S-box with the action of PGL(2, GF(28) on GF(28). The newly constructed S-box, using the suggested algorithm is given in Tab. 2. This is a  look up table and it can be used to process eight binary bits of data.
look up table and it can be used to process eight binary bits of data.
Table 2: S-Box 1 designed over LA-sub-module of LA-ring R

3.2 Case II: Generating S-Boxes over 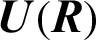
We define the inverse and affine linear mappings  ,
,  by
by  and
and  , where r′ = 436 and m′ = 275 are fixed elements in U(R) and
, where r′ = 436 and m′ = 275 are fixed elements in U(R) and  respectively. Accordingly, the composition
respectively. Accordingly, the composition  of mappings is defined by
of mappings is defined by  1. As the elements of U(R) are 9 binary bits representation, so we define a bijection
1. As the elements of U(R) are 9 binary bits representation, so we define a bijection  by
by

Rm is the remainder when divided by 256. So, in the end, the linear fractional transformation is given as;  ,
,  , where a′ = 210, b′ = 17, c′ = 84, d′ = 60 in GF(28) such that
, where a′ = 210, b′ = 17, c′ = 84, d′ = 60 in GF(28) such that  For the construction of this S-box, the algorithm activates with the LA-group U(R) of unit elements in the special LA-ring R and use of Galois field GF(28). Ultimately, the function
For the construction of this S-box, the algorithm activates with the LA-group U(R) of unit elements in the special LA-ring R and use of Galois field GF(28). Ultimately, the function  designs the S-box with the action of PGL(2, GF(28)) on GF(28). Tab. 3 shows the new S-box constructed through the proposed algorithm, a
designs the S-box with the action of PGL(2, GF(28)) on GF(28). Tab. 3 shows the new S-box constructed through the proposed algorithm, a  look up table that can be used to process eight binary bits of data.
look up table that can be used to process eight binary bits of data.
Table 3: S-Box 2 designed over LA-group of units in LA-ring R

To synthesize another S-box, we take the composition of above generated S-boxes. The S-box obtained by the composition is given by Tab. 4. Fig. 1 illustrates the flow chart for S-boxes pairs generation over the special LA-ring  .
.
Table 4: S-Box 3 obtained by composition of S-boxes 1,2


Figure 1: Flow chart for S-boxes pairs generation over the non-associative ring 
In case when we consider the special LA-ring R = R8 +uR8 +u2R8, the affine map  such that g(x) = ax + b for all x in U(R) results 256 possible choices of the fixed unit element a in U(R) and 256 choices of the element b in M. Hence, we obtained
such that g(x) = ax + b for all x in U(R) results 256 possible choices of the fixed unit element a in U(R) and 256 choices of the element b in M. Hence, we obtained 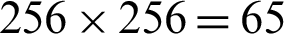 ,536 possible affine mappings. Accordingly, we get 65,536 number of
,536 possible affine mappings. Accordingly, we get 65,536 number of  pseudo S-boxes of dimension
pseudo S-boxes of dimension  . These
. These  pseudo S-boxes are transforming into byte based 65,536 vague random sequences by using the bijective maps
pseudo S-boxes are transforming into byte based 65,536 vague random sequences by using the bijective maps  . Thus we are able to get a huge number of
. Thus we are able to get a huge number of  S-boxes with their diversified strength.
S-boxes with their diversified strength.
The key space is the total number of unlike keys cast-off in the encryption or decryption process. For an efficient cryptosystem, the key space must be sufficiently large to repel brute-force attacks. In the first case of proposed algorithm 256! Number of choices for affine function and from the action of PGL(2, GF(28)) on 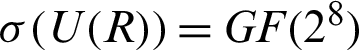 , we could design 16776960 number of S-boxes [24]. Though due to step 2 of the algorithm 256 choices for Affine functions could be considered and thus
, we could design 16776960 number of S-boxes [24]. Though due to step 2 of the algorithm 256 choices for Affine functions could be considered and thus 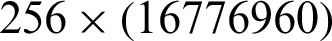 will be the possible choices in computing
will be the possible choices in computing  S-boxes. Consequently, combining all possibilities, we have large enough key space to armor contrary to brute force attack.
S-boxes. Consequently, combining all possibilities, we have large enough key space to armor contrary to brute force attack.
5 Performance Analyses of S-Boxes
An efficient S-box should satisfy some specific cryptographic criteria; bijectiveness, nonlinearity, outputs bit independence, strict avalanche and linear approximation probability. We device diverse analyses to test their strong suit and standing with respect to few other well-known S-boxes.
The distance between the Boolean function f and the set of all affine linear functions is said to be nonlinearity of f. This means the nonlinearity of a Boolean function f represents the number of bits which changed in the truth table of f to touch the nearby affine function. The upper bound of nonlinearity (NL) is  [10], thus, for n = 8, the maximum value of nonlinearity is 120. Followed Tab. 5 that average nonlinearity of S-boxes 1and 2 are 103.25 and 104.75, and better than Prime S-box.
[10], thus, for n = 8, the maximum value of nonlinearity is 120. Followed Tab. 5 that average nonlinearity of S-boxes 1and 2 are 103.25 and 104.75, and better than Prime S-box.
Table 5: Performance Indexes for proposed S-Box
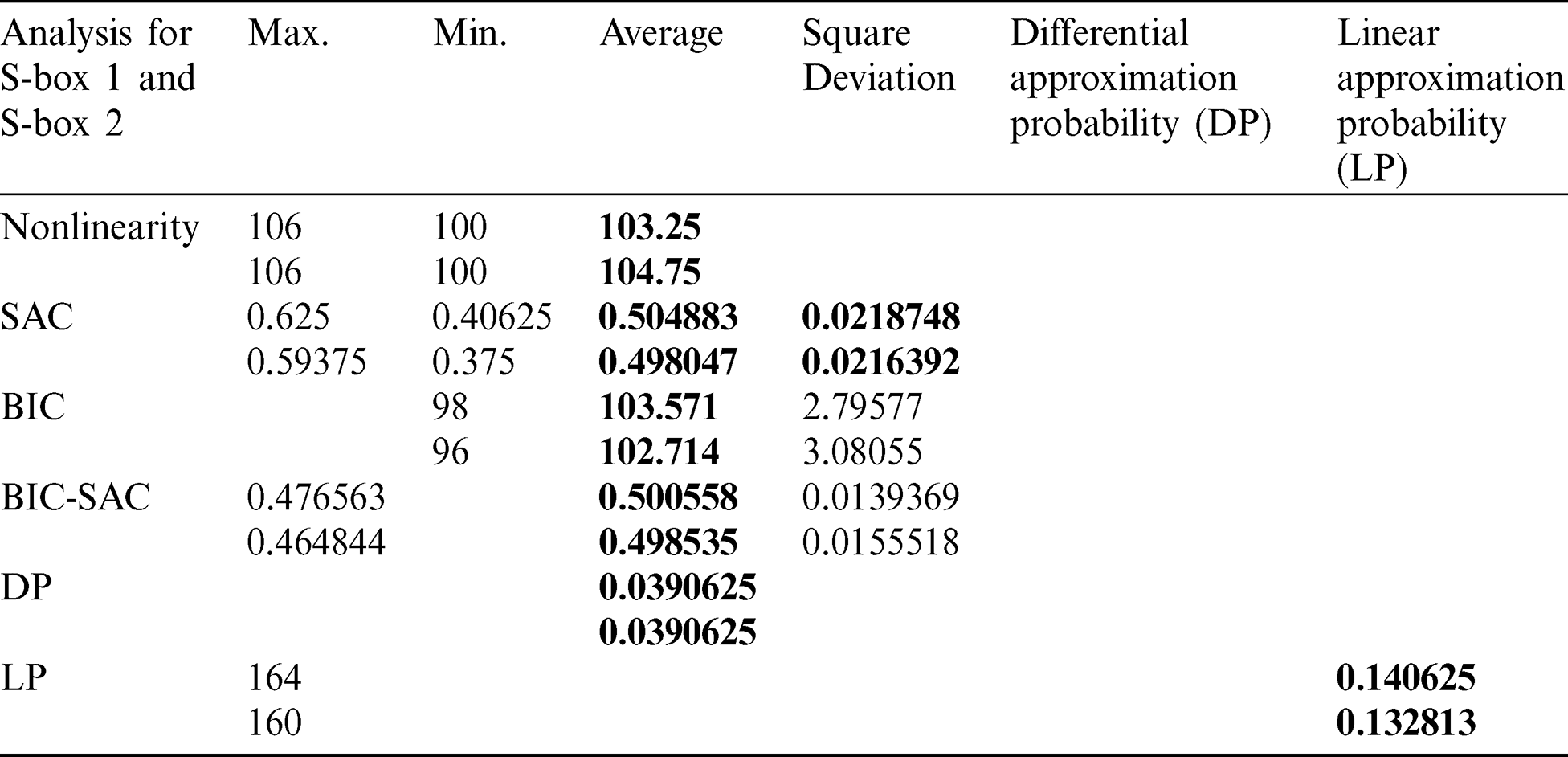
The SAC was first familiarized in 1895 by Webster et al. [2]. The SAC constructs on the notions of completeness and avalanche. It is satisfied if, whenever a single bit of input changed, each of the output bits changes with a 0.5 probability that is, while one bit of input is altered, half of its corresponding output bits will change. Tab. 5 shows that the proposed S-box successfully satisfied SAC.
The BIC was also first introduced in [2] which is another required property for any cryptographic methods. Tab. 5 shows the results of BIC analysis of proposed S-box and in the sense of encryption strength; the BIC of the proposed S-box is adequate. Tab. 5 shows that the rank of designed S-box is comparable with S-boxes in literature and its BIC is adequate.
5.4 Linear Approximation Probability
The maximum value of the imbalance of an event is said to be the linear approximation probability. The parity of the input bits selected by the mask Gx is equal to the parity of the output bits selected by the mask Gy. By [25], LP of a given S-box is defined as:  and Gy is input and output covers, respectively, “X” the set of all possible inputs; and 2n is the number of elements of X. From Tab. 5, we see that the average value of LP of the proposed S-boxes is 0.132813 and it is appropriate against linear attacks and better from Xyi S-box and S-box on residue of prime numbers.
and Gy is input and output covers, respectively, “X” the set of all possible inputs; and 2n is the number of elements of X. From Tab. 5, we see that the average value of LP of the proposed S-boxes is 0.132813 and it is appropriate against linear attacks and better from Xyi S-box and S-box on residue of prime numbers.
5.5 Differential Approximation Probability
The differential approximation probability (DP) of S-box is a measure for differential uniformity and is defined as: 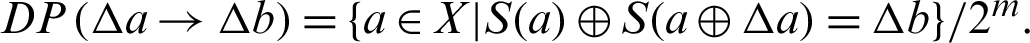 This implies, an input differential
This implies, an input differential  , should uniquely map to an output differential
, should uniquely map to an output differential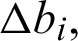 thus ensuring a uniform mapping probability for each i. The average value of differential approximation probability for proposed S-boxes are 0.140625 and (see Tab. 5), whereas the Tab. 6 shows the comparison of differential approximation probability of new S-box with AES, APA, Gray, S8 AES, Skipjack, Xyi and residue prime S-boxes and we observed that the results of DP of proposed box are relatively better from skip jack, Xyi, prime and Lui S-boxes. As there are
thus ensuring a uniform mapping probability for each i. The average value of differential approximation probability for proposed S-boxes are 0.140625 and (see Tab. 5), whereas the Tab. 6 shows the comparison of differential approximation probability of new S-box with AES, APA, Gray, S8 AES, Skipjack, Xyi and residue prime S-boxes and we observed that the results of DP of proposed box are relatively better from skip jack, Xyi, prime and Lui S-boxes. As there are  possible S-boxes depending on the choice of defined parameters, so after variety of options one can obtain the best S-boxes having optimal strength against statistical attacks.
possible S-boxes depending on the choice of defined parameters, so after variety of options one can obtain the best S-boxes having optimal strength against statistical attacks.
Table 6: Comparison of performance indexes of proposed S-Box

The Arnold map is one the most important 2D Chaotic map [26,27], specifically in image encryption algorithms. The following equation signifies the 2D Arnold cat map. For xi, yi in the interval [0,1),

The determinant of the matrix 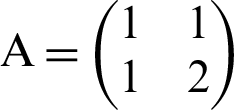 is 1. Thus, the map is area preserving. The Eigen values
is 1. Thus, the map is area preserving. The Eigen values  2 and
2 and 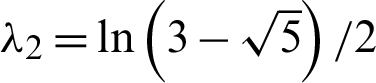 of the matrix A represents the two Lyapunov exponents. The positive Lyapunov exponent spectacles the chaotic behavior in Eq. (1) hence its exponential sensitivity to its initial conditions is observed. In [26], the generalized form of Eq. (1) is given as
of the matrix A represents the two Lyapunov exponents. The positive Lyapunov exponent spectacles the chaotic behavior in Eq. (1) hence its exponential sensitivity to its initial conditions is observed. In [26], the generalized form of Eq. (1) is given as

Furthermore, the map of Eq. (2) is transformed to a 3D cat map described as

where the matrix A is answerable for producing chaotic behavior, here 
The general form of matrix A is

In matrix A all ax, ay, az, bx, by, bz are considered to be the positive integers. It is trivial to verify that matrix A is area preserving, that is  . The Eigen values of A are
. The Eigen values of A are  and
and  .1466. As the larger Eigen value is greater than 1, so Eq. (3) shows chaotic behavior and thus holds all the characteristics of chaos. To generate the chaotic sequence Xi+1, the initial values used in this work are
.1466. As the larger Eigen value is greater than 1, so Eq. (3) shows chaotic behavior and thus holds all the characteristics of chaos. To generate the chaotic sequence Xi+1, the initial values used in this work are  ,
, 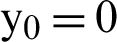 .3494 and
.3494 and 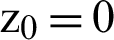 .6789.
.6789.
S-boxes are considered as a main part of a block cipher, the only component of a cipher that produces non-linearity and hence surety the resistance against linear and differential attacks. Currently, advancement in techniques of cryptanalysis and in computer technology, which enhances correspondingly support, generating S-boxes of good quality is the subject of core attention. Due to uncertainty in communication and in storage of RGB images, a need for the encryption is preferred. One of the aims of this article is to encrypt RGB images using 3 S-boxes originated by a non-associative structure of LA-ring. For the need of the RGB image encryption each layer is passed through the different  S-box. In the subsequent step, the 3D Arnold cat map is functional not to correlate the adjacent pixel of the image.The image encryption scheme is illustrated below. Following are the steps for encrypting the image: Substitute the S-boxes S1, S2 and S3 in Red, Green and Blue channels of the color image. Thus, instead of a single S-box used for encryption our proposed scheme provides three different S-boxes S1, S2and S3. Use the 3D Arnold cat map to produce non-correlated behavior between adjacent pixels of the image.
S-box. In the subsequent step, the 3D Arnold cat map is functional not to correlate the adjacent pixel of the image.The image encryption scheme is illustrated below. Following are the steps for encrypting the image: Substitute the S-boxes S1, S2 and S3 in Red, Green and Blue channels of the color image. Thus, instead of a single S-box used for encryption our proposed scheme provides three different S-boxes S1, S2and S3. Use the 3D Arnold cat map to produce non-correlated behavior between adjacent pixels of the image.
7 Texture Analysis of Image Encryption
Texture is one of the further most significant parameters of a material that enlightens the physical appearance of a material surface except its chromatic character. Texture may be analyzed in diverse approaches but Fourier methodology among these techniques is the most operative. A fascinating analysis, however, is intriguing as it relates to how the human visual system realizes the texture, the first line of the texture, and is extensively used in the segmentation of photograph. Over and done with this method we can calculate 5 diverse characteristics of image which are: Contrast, Homogeneity, Correlation, Energy and Entropy to elucidate texture.
Through energy analysis we can measure the energy of an encrypted image which discards the gray-level co-occurrence matrix (GLCM). The energy is defined as the sum of squared components in GLCM and is given as  where m and n are the image pixels and p(m, n) gives the number of gray-level co-occurrence matrices. Remark that for constant image the energy value is unity.
where m and n are the image pixels and p(m, n) gives the number of gray-level co-occurrence matrices. Remark that for constant image the energy value is unity.
The entropy is the measure of level of disorder and randomness in a system. The maximal level of randomness makes the image difficult to recognize and the randomness of an image can be amplified by considering its non-linear components which is defined as  where x i defines the Histogram calculations.
where x i defines the Histogram calculations.
To differentiate the objects of an image the observer has to contrast it is used. Owed to image encryption process, a robust encryption can be realized from the high level of contrast. This factor is directly linked to the confusion created by the S-box. Mathematically, the contrast is obtained by the formula: 
In Homogeneity analysis, the closeness of distributed pixels of Gray Level Co-occurrence Matrix (GLCM) to GLCM is tested. Mathematical equation is 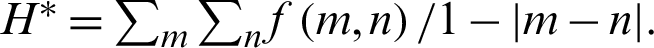
To analyse the adjacent pixel correlation of an image, correlation analysis is performed. Normally, three different types of correlation are performed to ensure the strength of the encrypted image. These are: the horizontal, the vertical, and the diagonal correlation. The following equation shows how to calculate the correlation:  For a healthier correlation value we need to achieve the number 1 or −1. Whereas uncorrelated data this figure is round about 0. Tab. 7 realizes that the new encryption algorithm has robust upright cryptographic properties, and succeeds for encryption.
For a healthier correlation value we need to achieve the number 1 or −1. Whereas uncorrelated data this figure is round about 0. Tab. 7 realizes that the new encryption algorithm has robust upright cryptographic properties, and succeeds for encryption.
Table 7: Second order texture analyses for plain and encrypted Lena image

Tab. 8 signifies the entropy of Lena color image. Obviously, the proposed encryption procedure displays opposition to all the well-known attacks. Analyses reveal that the entropy score of our proposed scheme is close to the optimal values. In analogy, the comparison with chaos-based encryption scheme is also provided. Entropy of the proposed scheme is nicer than the rest. In Tab. 9, the result for correlation coefficient of Lena  color image is presented. Results ensure the potency of the proposed encryption technique. It is apparent from analyses that the correlation results are up to the mark and can be matched with other chaos-based encryption techniques. Information images transmitting via digital communicating media has great similarity amongst their neighboring pixels. For an incredibly well-connected image the estimated correlation coefficient is
color image is presented. Results ensure the potency of the proposed encryption technique. It is apparent from analyses that the correlation results are up to the mark and can be matched with other chaos-based encryption techniques. Information images transmitting via digital communicating media has great similarity amongst their neighboring pixels. For an incredibly well-connected image the estimated correlation coefficient is 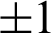 , while for an extra ordinary non-correlated image its values move toward 0. The pixels correlation among original and encrypted Lena image is displayed in Tab. 9. The correlation score shows that the pixels are good non-correlated as its value are more equally 0. Hence, the proposed algorithm gives extra ordinarily de connections the nearby pixels of the encrypted image and meet on hopes of an effective encryption structure.
, while for an extra ordinary non-correlated image its values move toward 0. The pixels correlation among original and encrypted Lena image is displayed in Tab. 9. The correlation score shows that the pixels are good non-correlated as its value are more equally 0. Hence, the proposed algorithm gives extra ordinarily de connections the nearby pixels of the encrypted image and meet on hopes of an effective encryption structure.
Table 8: Comparing entropy for Lena (256  256) image
256) image
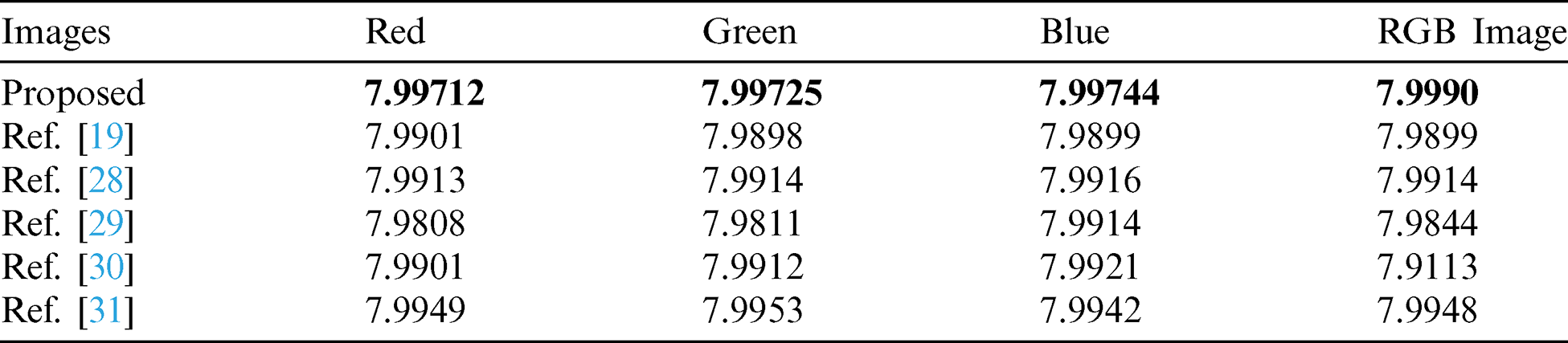
Table 9: Horizontal, vertical and diagonal correlations between different layers of original and encrypted images

Figs. 4–9 show the correlation distribution of horizontally, vertically and diagonally adjacent pixels of a color image. Figs. 4, 6, 8 (a, b, c) signifies the correlation of the adjacent pixels of Lena original image whereas Figs. 5, 7, 9 (a, b, c) looks from the nearby pixels of encrypted image. It is clear from the figure that there is a great dispassion between nearby pixels of the encrypted image. The approving correlation coefficient is computed for Lena encrypted image and are shown in Tab. 9.
8 Analyses of Experimental Work
Experimental analyses of the image encryption technique are given here. A standard Lena image of size  is chosen for encryption as shown in Fig. 2. Where Fig. 3, represents the encrypted Lena image. Histogram of RGB layers of the original and encrypted image are also shown in parallel. Tab. 8 enlists the image quality measures of the encrypted and original image using one round encryption by 3 S-boxes and AC 3D map. The performance of the proposed notion is shown in Tab. 9.
is chosen for encryption as shown in Fig. 2. Where Fig. 3, represents the encrypted Lena image. Histogram of RGB layers of the original and encrypted image are also shown in parallel. Tab. 8 enlists the image quality measures of the encrypted and original image using one round encryption by 3 S-boxes and AC 3D map. The performance of the proposed notion is shown in Tab. 9.

Figure 2: (a) represents Lena original image. (b), (c) and (d) represent the histogram of red(R) green(G) and blue(B) layer of (a)
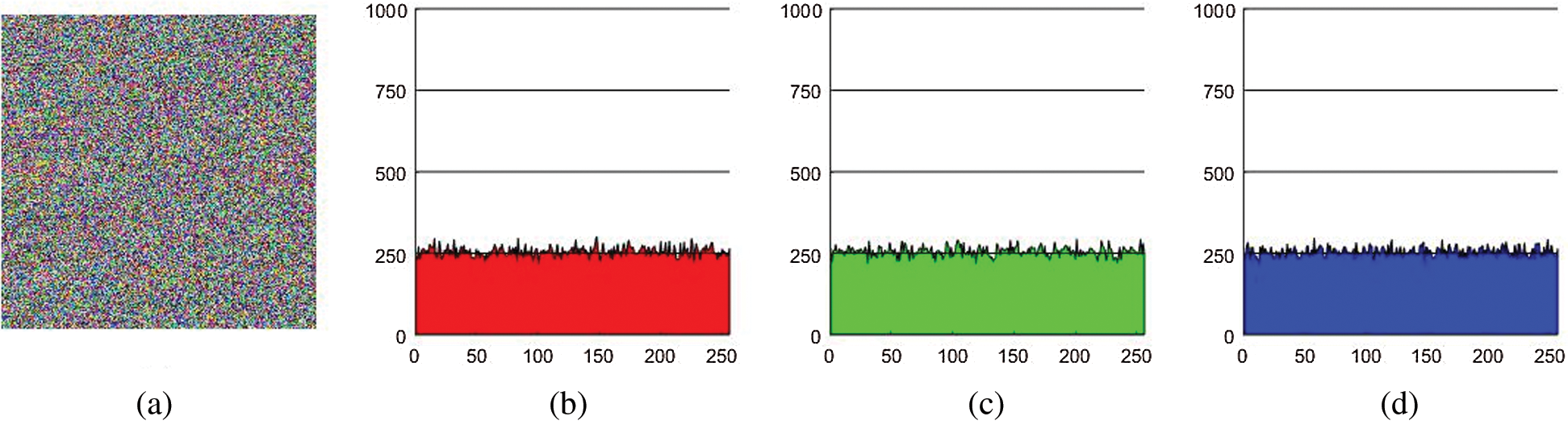
Figure 3: (a) Encrypted Lena image. (b), (c) and (d) show the histogram layers of R, G and B channel of the encrypted image (a)

Figure 4: (a–c): represent horizontal correlation pixels for R, G and B layers of original  Lena image respectively
Lena image respectively

Figure 5: (a–c): Shows the horizontal Correlation pixels for R, G and B channel of encrypted Lena image

Figure 6: (a–c): represent vertical correlation pixels for R, G and B layers of original 256  256 Lena image respectively
256 Lena image respectively

Figure 7: (a–c): shows the vertical correlation pixels for R, G and B channel of encrypted Lena image

Figure 8: (a–c): represent diagonal correlation pixels for R, G and B layers of original 256  256 Lena image respectively
256 Lena image respectively

Figure 9: (a–c): shows the diagonal correlation pixels for R, G and B channel of encrypted Lena image
In statistics, the mean square error (MSE) or mean square deviation (MSD) of an image measures the common of the squares of the errors. This means the arithmetic mean square distinction between the calculable values and what’s estimated. MSE is a risk function, comparable to the mean of the squared error loss. Followed [26], it judges quality of an encrypted image. It is calculated as  where
where 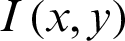 is the plain image,
is the plain image, 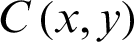 is the ciphered version and M, N are the dimensions of the images, respectively. A higher value for MSE can be understood as the better first-rate.
is the ciphered version and M, N are the dimensions of the images, respectively. A higher value for MSE can be understood as the better first-rate.
8.2 Peak Signal-To-Noise Ratio (PSNR)
Signal representation dependability may be affected by corrupting noise [32]. Thus the ratio defined amongst the power of a signal and the power of corrupting noise is designated as Peak signal-to-noise ratio (PSNR). It is expressed in terms of the logarithmic decibel gauge due to the diverse dynamic range of signals. Occasionally, the PSNR is used for to evaluate the quality of restoration of the encrypted image. In this study, signal is characterized by plain image and noise is the distortion created by encryption. The PSNR value is directly proportional to the rate of rebuilding of an image. It is defined as  .
.
8.3 Normalized Cross-Correlation (NK)
The correlation function also gives the idea that how much two digital images are closed to each other as shown in [33]. The normalized cross-correlation (NK) measures the resemblance amongst two images and is calculated by as:  where
where 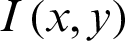 is the plain image,
is the plain image,  is the ciphered version and M, N are respectively the dimensions of the images.
is the ciphered version and M, N are respectively the dimensions of the images.
The difference between reference signal and test image is given the name of Average difference (AD) [32]. AD is calculated by the formula:  where
where  is original,
is original,  is the encrypted version and M, N are the dimensions of the images.
is the encrypted version and M, N are the dimensions of the images.
One of the correlation based measure is the structural content (SC) [32] and it measures the resemblance among two images. SC is premeditated as  where
where  is the plain image,
is the plain image,  is the encrypted version and M, N are respectively the dimensions of the images.
is the encrypted version and M, N are respectively the dimensions of the images.
Scheming maximum of the error signals gives what we call maximum difference (MD) (difference between the test image and reference signal) (see [34]) and it is attained by  , where
, where  is the plain image,
is the plain image, 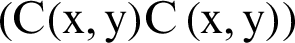 is the encrypted version and M, N are respectively the dimensions of the images.
is the encrypted version and M, N are respectively the dimensions of the images.
By [31], the Normalized absolute error between the plain and ciphered image is calculated as  where
where  is the plain image,
is the plain image,  is the encrypted version and M, N are the dimensions of the images.
is the encrypted version and M, N are the dimensions of the images.
8.8 Root Mean Square Error (RMSE)
It is the square root of the mean of the square of all the errors [31]. RMSE is a regularly times used method to measure the variations between original image and the cipher image.  , where
, where  represents the plain image,
represents the plain image,  is the encrypted version and M, N are respectively the dimensions of the images.
is the encrypted version and M, N are respectively the dimensions of the images.
8.9 Universal Quality Index (UQI)
According to [35], the UQI breaks the comparison between original and distorted image into three comparisons: Contrast, luminance and structural comparisons. The UQI for original image “O” and encrypted image “E” might be defined as  where
where  represents the mean values of plain and distorted images and
represents the mean values of plain and distorted images and  denote the standard deviation of plain and distorted images.
denote the standard deviation of plain and distorted images.
To obtain the amount of information from encrypted image for the agreeing plain image is termed as MI given in [35]. The MI of two images “O” and “E” can be defined as  where p(x, y) is the joint probability function of
where p(x, y) is the joint probability function of  and C, further p(x) and p(y) are the marginal probability distribution functions of O and E respectively.
and C, further p(x) and p(y) are the marginal probability distribution functions of O and E respectively.
8.11 Structural Similarity (SSIM)
By [36], the structural similarity index is an enhanced edition of the universal quality index. Through this technique we determine the similarity between two images. The structural similarity index is calculated on various frames of an image. The measure between two frames  and
and  of common size
of common size  is
is 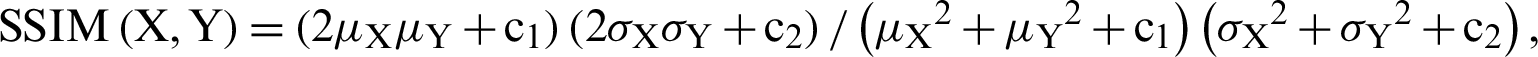 where average of
where average of  and
and  is represented by
is represented by  and
and  the variance of
the variance of  and
and 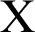 by
by  and
and  respectively. Whereas
respectively. Whereas  is the covariance of
is the covariance of  and
and  ,
,  and
and  are the variables to soothe the division with weak denominator. L
are the variables to soothe the division with weak denominator. L 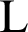 is the range of the pixel values and
is the range of the pixel values and  by default. The SSIM index lies between −1 and 1. For similar images this value is 1. Tab. 10 shows that through our proposed RGB image encryption scheme the optimal values of Image Quality Measures can be achieved.
by default. The SSIM index lies between −1 and 1. For similar images this value is 1. Tab. 10 shows that through our proposed RGB image encryption scheme the optimal values of Image Quality Measures can be achieved.
Table 10: Image quality measures for proposed RGB image encryption of Lena image

A uniform histogram for an image is the calmest and supreme approach to measure the security strength of an encryption procedure against various attacks. Here, we analyze an RGB Lena image of size  The histogram of the three channels of ciphered image under the proposed scheme is likewise matching though for plain Lena image they are dissimilar. Figs. 2 and 3 show histogram of different layers of plain image and encrypted image. A perfect encrypted image comprises of uniform histogram trickles to sphere the opposing of separating any supportive data from the rocky histogram. Subsequently, no statistical attack can die out this proposed encryption scheme.
The histogram of the three channels of ciphered image under the proposed scheme is likewise matching though for plain Lena image they are dissimilar. Figs. 2 and 3 show histogram of different layers of plain image and encrypted image. A perfect encrypted image comprises of uniform histogram trickles to sphere the opposing of separating any supportive data from the rocky histogram. Subsequently, no statistical attack can die out this proposed encryption scheme.
To exploit the strong suit of differential analyses on an image encryption arrangement the NPCR (Number of Pixels Change Rate) and UACI (unified average changing intensity) analyses are implemented. It measures the normal power of contrast between the two images, i.e., original and encrypted image. To compare the encrypted images cryptanalysts realize the bond among the plain image and ciphered image. Attack of this kind is famous for differential attack.The NPCR and UACI are the two typically used tests to ensure the strength of the encrypted scheme against differential analysis. For more details, see [35]–[37].
9.2.1 Number of Pixels Change Rate (NPCR)
By [36], the impact of one-pixel change on the whole image ciphered by the suggested scheme has been verified by NPCR. The number of pixels change rate of encrypted image when one pixel of original image is changed is measured by NPCR. Take an encrypted image “ ” of dimension
” of dimension  , whose corresponding original image “Img2” has only one-pixel difference.
, whose corresponding original image “Img2” has only one-pixel difference. 
9.2.2 Unified Average Changing Intensity (UACI)
By [36], the unified average changing intensity of the given two (plain and ciphered) images measures the average intensity of the images. Take two encrypted images  and
and  of dimension
of dimension  .
. 
Tab. 11 gives the NPCR and UACI measures of different channels of the color Lena encrypted image. The comparison is taken with encryption schemes based on Chaos and S-box. It verifies the strength of the proposed Image encryption scheme via S-boxes 1, 2 and 3. Clearly, analyses show that the NPCR and UACI values of our novel encryption technique give optimal values.
Table 11: A comparison of differential analyses 256  256 Lena image
256 Lena image

10 Randomness of Test for Cipher
Uniform distribution, Long period and high complexity of the output are the main properties to observe the security strength of a cryptosystem. By a definite end objective to attain these prerequisites, we used NIST SP 800–22 [39] for testing the randomness of digital images. A part of these tests involve copious subclasses. The distorted Lena digital image is cast-off to clasp all NIST tests. The ciphered data is produced by the proposed RGB image encryption scheme of a colored Lena plain image of dimension  and 3D a chaotic map. Tab. 12, shows the outcomes of the tests.
and 3D a chaotic map. Tab. 12, shows the outcomes of the tests.
Table 12: NIST test results for proposed encrypted image

Noticeably our proposed digital image encryption tool proficiently passes the NIST tests. Thus, due to the proficient outcomes, the designed random cryptosystem used for RGB Image Encryption constructed via S-boxes from a non-commutative and non-associative finite ring and 3D chaotic map might be professed that are very irregular in its crop.
In this paper we constructed S-boxes through non-associative and non-commutative structures of rings having order 512. The main resolution of these S-boxes designing was to produce 256 times more  S-boxes created through linear fractional transformations having excellent robustness. This study provides
S-boxes created through linear fractional transformations having excellent robustness. This study provides  choices in constructing
choices in constructing  S-boxes of diverse strength. Thus, combining all possibilities, we have a large enough key space to defend brute force attack. As a futuristic perspective, a successful development in constructing 256 elements LA-field will be more helpful in designing
S-boxes of diverse strength. Thus, combining all possibilities, we have a large enough key space to defend brute force attack. As a futuristic perspective, a successful development in constructing 256 elements LA-field will be more helpful in designing  S-boxes over it. A new color image encryption usage is estimated in which firstly these 3 S-boxes were used in producing confusion in each layer of a standard RGB color image. Nevertheless, for the purpose of diffusion 3D Arnold chaotic map is utilized in the newly introduced encryption scheme. A comparison with some of existing chaos and S-box dependent color image encryption schemes were given and the performance outcomes of the estimated RGB image encryption and noted as approaching the standard main level.
S-boxes over it. A new color image encryption usage is estimated in which firstly these 3 S-boxes were used in producing confusion in each layer of a standard RGB color image. Nevertheless, for the purpose of diffusion 3D Arnold chaotic map is utilized in the newly introduced encryption scheme. A comparison with some of existing chaos and S-box dependent color image encryption schemes were given and the performance outcomes of the estimated RGB image encryption and noted as approaching the standard main level.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. E. Biham and A. Shamir. (1991). “Differential cryptanalysis of DES like cryptosystems,” Journal of Cryptology, vol. 4, no. 1, pp. 3–72.
2. A. F. Webster and S. Tavares. (1986). “On the design of S-boxes,” in Advanced Cryptology: Proc. CRYPTO-85. Lecture Notes in Computer Science, Berlin, Heidelberg: Springer, pp. 523–534.
3. C. Adams and S. E. Tavares. (1989). “Good S-boxes are easy to find,” in Advanced Cryptology: Proc. CRYPTO-89. Lecture Notes in Computer Science, NY, USA: Springer, pp. 612–615.
4. I. Hussain and T. Shah. (2013). “Literature survey on nonlinear components and chaotic nonlinear components of block cipher,” Nonlinear Dynamics, vol. 74, no. 4, pp. 869–904.
5. I. Hussain, T. Shah and H. Mahmood. (2012). “A group theoretic approach to construct cryptographically strong substitution boxes,” Neural Computing and Applications, vol. 23, no. 1, pp. 97–104.
6. I. Hussain, T. Shah, H. Mahmood, M. A. Gondal and U. Y. Bhatti. (2011). “Some analysis of S-box based on residue of prime number,” Proceedings of the Pakistan Academy of Sciences, vol. 48, no. 2, pp. 111–115.
7. M. T. Tran, D. K. Bui and A. D. Doung. (2008). “Gray S-box for advanced encryption standard,” in Int. Conf. on Computational Intelligence and Security, Suzhou, China, pp. 253–256.
8. L. Cui and Y. Cao. (2007). “A new S-box structure named affine-power-affine,” International Journal of Innovative Computing, Information and Control, vol. 3, no. 3, pp. 45–53.
9. J. Kim and R. C. W. Phan. (2009). “Advanced differential-style cryptanalysis of the NSA’s skipjack block cipher,” Cryptologia, vol. 33, no. 3, pp. 246–270.
10. X. Yi, S. X. Cheng, X. H. You and K. Y. Lam. (1997). “A method for obtaining cryptographically strong S-boxes,” in IEEE GLOBECOM 97. Conf. Record, Phoenix, AZ, USA, pp. 689–693. [Google Scholar]
11. Y. Naseer, T. Shah, S. Hussain and A. Ali. (2019). “Steps towards redesigning cryptosystems by a non-associative algebra of IP-loops,” Wireless Personal Communications, vol. 108, pp. 1–14. [Google Scholar]
12. I. Hussain, T. Shah, M. A. Gondal and H. Mahmood. (2013). “An efficient approach for the construction of LFT S-boxes using chaotic logistic map,” Nonlinear Dynamics, vol. 71, no. 1, pp. 133–140. [Google Scholar]
13. M. Khan, T. Shah, H. Mahmood and M. A. Gondal. (2013). “An efficient method for the construction of block cipher with multi-chaotic systems,” Nonlinear Dynamics, vol. 71, no. 3, pp. 489–492. [Google Scholar]
14. G. Jakimoski and L. Kocarev. (2001). “Chaos and cryptography: Block encryption ciphers based on chaotic maps,” IEEE Transactions on Circuits and Systems I: Fundament Theory and Applications, vol. 48, no. 2, pp. 163–169. [Google Scholar]
15. C. Shannon. (1949). “Communication theory of secrecy systems,” Bell System Technical Journal, vol. 28, no. 4, pp. 656–715. [Google Scholar]
16. I. Hussain, T. Shah and M. A. Gondal. (2012). “A novel approach for designing substitution-boxes based on nonlinear chaotic algorithm,” Nonlinear Dynamics, vol. 70, no. 3, pp. 1791–1794. [Google Scholar]
17. X. Wang and Q. Wang. (2014). “A novel image encryption algorithm based on dynamic S-boxes constructed by chaos,” Nonlinear Dynamics, vol. 75, no. 3, pp. 567–576. [Google Scholar]
18. A. K. Farhan, N. M. G. Al-Saidi, A. T. Maolood and F. Nazarimehr. (2019). “Entropy analysis and image encryption application based on a new chaotic system crossing a cylinder,” Entropy, vol. 21, no. 10, pp. 958. [Google Scholar]
19. H. Liu, A. Kadir and Y. Niu. (2014). “Chaos-based color image block encryption scheme using S-box,” AEU International Journal of Electronics and Communications, vol. 68, no. 7, pp. 676–686. [Google Scholar]
20. M. A. Kazim and M. Naseerudin. (1972). “On almost semigroups,” Aligarh Bulletin of Mathematics, vol. 2, pp. 1–7. [Google Scholar]
21. M. S. Kamran. (1993). “Conditions for LA-semigroups to resemble associative structures,” Ph.D. dissertation, Quaid-i-Azam University, Islamabad, Pakistan. [Google Scholar]
22. T. Shah and I. Rehman. (2010). “On LA-rings of finitely non-zero functions,” International Journal of Contemporary Mathematical Sciences, vol. 5, no. 5, pp. 209–222. [Google Scholar]
23. I. Rehman, M. Shah, T. Shah and A. Razzaque. (2013). “On existence of non-associative LA-rings,” Analele Universitatii Ovidus Costanta. Seria Matematic, vol. 21, no. 3, pp. 223–228. [Google Scholar]
24. A. Altaleb, S. M. Saeed, I. Hussain and M. Aslam. (2017). “An algorithm for the construction of substitution boxes for block ciphers based on projective general linear group,” AIP Advances, vol. 7, no. 3, pp. 035116. [Google Scholar]
25. M. Matsui. (1993). “Linear cryptanalysis method for DES cipher,” in Advances in Cryptology–-EUROCRYPT’93. Lecture Notes in Computer Science, T. Helleseth, vol. 765. Berlin, Heidelberg: Springer, pp. 386–397. [Google Scholar]
26. G. Chen, Y. Mao and C. Chui. (2004). “A symmetric image encryption scheme based on 3D chaotic cat maps,” Chaos Solitons and Fractals, vol. 21, no. 3, pp. 749–761. [Google Scholar]
27. G. Chen and X. Dong. (1998). “From chaos to order: Methodologies, perspectives and applications,” Singapore: World Scientific. [Google Scholar]
28. H. Liu, A. Kadir, X. Sun and Y. Li. (2018). “Chaos based adaptive double-image encryption scheme using hash function and S-boxes,” Multimedia Tools and Applications, vol. 77, no. 1, pp. 1391–1407. [Google Scholar]
29. H. Liu, A. Kadir and P. Gong. (2015). “A fast color image encryption scheme using one-time s-Boxes based on complex chaotic system and random noise,” Optics Communications, vol. 338, pp. 340–347. [Google Scholar]
30. J. H. Wu, X. F. Liao and B. Yang. (2017). “Color image encryption based on chaotic systems and elliptic curve ElGamal scheme,” Signal Processing, vol. 141, pp. 109–124. [Google Scholar]
31. M. A. Murillo-Escobar, C. Cruz-Hernández, F. Abundiz-Pérez, R. M. López-Gutiérrez and O. A. Del Campo. (2015). “A RGB image encryption algorithm based on total plain image characteristics and chaos,” Signal Processing, vol. 109, pp. 119–131. [Google Scholar]
32. Q. Huynh-Thu and M. Ghanbari. (2008). “Scope of validity of PSNR in image/video quality assessment,” Electronic Letters, vol. 44, no. 13, pp. 800–801. [Google Scholar]
33. Z. Wang. (2002). “A universal image quality index,” IEEE Signal Processing Letters, vol. 9, no. 3, pp. 81–84. [Google Scholar]
34. M. E. Ahmet and S. F. Paul. (1995). “Image quality measures and their performance,” IEEE Transactions on Communications, vol. 43, no. 12, pp. 2959–2965. [Google Scholar]
35. Z. Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli. (2004). “Image quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–612. [Google Scholar]
36. Y. Wu, J. P. Noonan and S. Agaian. (2011). “NPCR and UACI randomness tests for image encryption,” Cyber Journals: Multidisciplinary Journals in Science and Technology, Journal of Selected Areas in Telecommunications, April Edition, pp. 31–38. [Google Scholar]
37. I. Hussain, T. Shah and M. A. Gondal. (2012). “Image encryption algorithm based on PGL (2, GF (28)) S-boxes and TD-ERCS chaotic sequence,” Nonlinear Dynamics, vol. 70, no. 1, pp. 181–187. [Google Scholar]
38. I. Hussain and M. A. Gondal. (2014). “An extended image encryption using chaotic coupled map and S-box transformation,” Nonlinear Dynamics, vol. 76, no. 2, pp. 1355–1363. [Google Scholar]
39. F. Pareschi, R. Rovatti and G. Setti. (2012). “On statistical tests for randomness included in the NIST SP800-22 test suite and based on the binomial distribution,” IEEE Transactions on Information Forensics and Security, vol. 7, no. 2, pp. 491–505. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |