DOI:10.32604/cmc.2021.013196
| Computers, Materials & Continua DOI:10.32604/cmc.2021.013196 | |
| Article |
Diabetes Type 2: Poincaré Data Preprocessing for Quantum Machine Learning
1Department of Computer Science and Engineering, University of Louisville, Louisville, KY, USA
2Apolo Scientific Computing Center, Universidad EAFIT, Medellín, Colombia
3eVida Research Group, University of Deusto, Bilbao, Spain
*Corresponding Author: Daniel Sierra-Sosa. Email: desier01@louisville.edu
Received: 17 July 2020; Accepted: 07 December 2020
Abstract: Quantum Machine Learning (QML) techniques have been recently attracting massive interest. However reported applications usually employ synthetic or well-known datasets. One of these techniques based on using a hybrid approach combining quantum and classic devices is the Variational Quantum Classifier (VQC), which development seems promising. Albeit being largely studied, VQC implementations for “real-world” datasets are still challenging on Noisy Intermediate Scale Quantum devices (NISQ). In this paper we propose a preprocessing pipeline based on Stokes parameters for data mapping. This pipeline enhances the prediction rates when applying VQC techniques, improving the feasibility of solving classification problems using NISQ devices. By including feature selection techniques and geometrical transformations, enhanced quantum state preparation is achieved. Also, a representation based on the Stokes parameters in the Poincaré Sphere is possible for visualizing the data. Our results show that by using the proposed techniques we improve the classification score for the incidence of acute comorbid diseases in Type 2 Diabetes Mellitus patients. We used the implemented version of VQC available on IBM’s framework Qiskit, and obtained with two and three qubits an accuracy of 70% and 72% respectively.
Keywords: Quantum machine learning; data preprocessing; stokes parameters; Poincare sphere
Several efforts have been made in recent time to advance quantum software capable of exploiting the power of the available Noisy Intermediate Scale Quantum (NISQ) devices. These devices are being developed on a variety of hardware platforms and technologies with a number of qubits ranging from fifty to a few hundred [1]. Despite the limitations in the number of qubits and their susceptibility to noise, these devices are leading to the development of more powerful quantum technologies for the future [2]. Each successful application is an important step in the development of Quantum Computing. One of these applications lies in the advance of Machine Learning (ML) techniques, a technology that is widely used in a multitude of real-world applications [3] motivated by the advances achieved in different knowledge fields and the derivative commercial applications.
Quantum Machine Learning (QML) is one of the most encouraging applications, being actively studied by several research groups [4]. In general, looking forward to developing new techniques able to exploit Quantum Computing advantages to improve machine learning [5]. Supervised learning is a specific QML task recently emerging with massive interest from academy and industry. There are several contributions in this field, including approaches with quantum inspired neural networks and their applications [6–8], hybridized low-depth Variational Quantum Circuits (VQC) [9], optimization algorithms [10] with simple error-mitigation [11], preprocessing techniques like PCA showing exponential improvements [12], and experiments for classification [13,14]. Also, multiple implementations of linear regression [15,16] in Quantum Computers have been propose.
Several approaches to encode classical data into quantum states have been presented. These describe advantages including the experimental overhead reduction in terms of resources and the introduction of non-linearities in the data [14,17], enabling the use of linear classifiers and kernel-based methods [18,19] on near-term quantum processors, with an exponential speed-up when compared to classical algorithms [20]. In references [21,22] independent authors described the advantages from the usage of quantum algorithms in machine learning methods, being one example the polynomial reduction from query complexity in nearest–neighbor classification when compared to classical algorithms [23].
Multiple examples from the usage of quantum computing techniques in machine learning applications for well-known datasets have been presented. Datasets such as MNIST, Wine, Cancer and Iris are of common use to test these approaches [13,18,24,25]. Nonetheless, real-world applications are scarce, a handful of applications including a Reactor Coolant Pump (RCP) state classification at a Nuclear Power Plan [26], Wine recognition [8], Dementia prediction [27] and the partial dynamics of a complex 10-spin system [28] have been explored. There is a need for explore real applications using quantum machine learning, that motivate further research in this area, using quantum properties in real-world applications. It should be noted that quantum machine learning algorithms may not yield to an advantage when compared with their classical counterparts, but understanding their scope and limitations is critical in the development of current quantum technologies.
In this paper we present a real case study of Type 2 Diabetes Mellitus (T2DM), this disease is the fourth cause of mortality, with rising prevalence this disease is a major public health problem [29]. There are 415 million people with diagnosed diabetes and it is estimated that around 193 million people suffer the disease without diagnosis, in both cases it could lead to micro and macrovascular complications, causing major distress to both patients and caregivers [30]. We introduce a preprocessing technique to map the data into quantum states to perform quantum classification. In particular, this technique is based on a data representation using the Stokes parameters, enhancing data encoding techniques proposed by [3], improving on average a 20% the classification score of a Quantum Variational Classifier implemented using IBM’s framework Qiskit [31]. We conducted three different experiments using VQC over the same data features and parameters. In the first experiment, we normalized the data with zero standard deviation, in the second we add to this normalization an Ellipsoidal coordinate transform and finally in the third we found the Stokes parameters from data.
This paper is organized as follows: First, we present the proposed pipeline to pre-process data describing each of the stages developed: Feature Scaling and selection, ellipsoidal coordinate mapping and Stokes parameters data representation, then we describe the employed quantum classifier and the experiments performed to classify acute comorbidities incidence in Type 2 Diabetes Mellitus (T2DM) patients. Finally, we present the obtained results and a discussion about these results and conclusions.
The current limitations of NISQ devices impose restrictions on Quantum Machine Learning techniques [1]. Currently, many proposed QML applications rely on using well-known datasets, where the preprocessing techniques are now standard [13,18,24]. When using real-world datasets these techniques are not always suitable to adequate the data to be processed by Quantum Classification models. We proposed a data preprocessing pipeline presented in Fig. 1, to transform datasets before applying current kernel techniques for VQC algorithms. Each of the components of this pipeline are described.
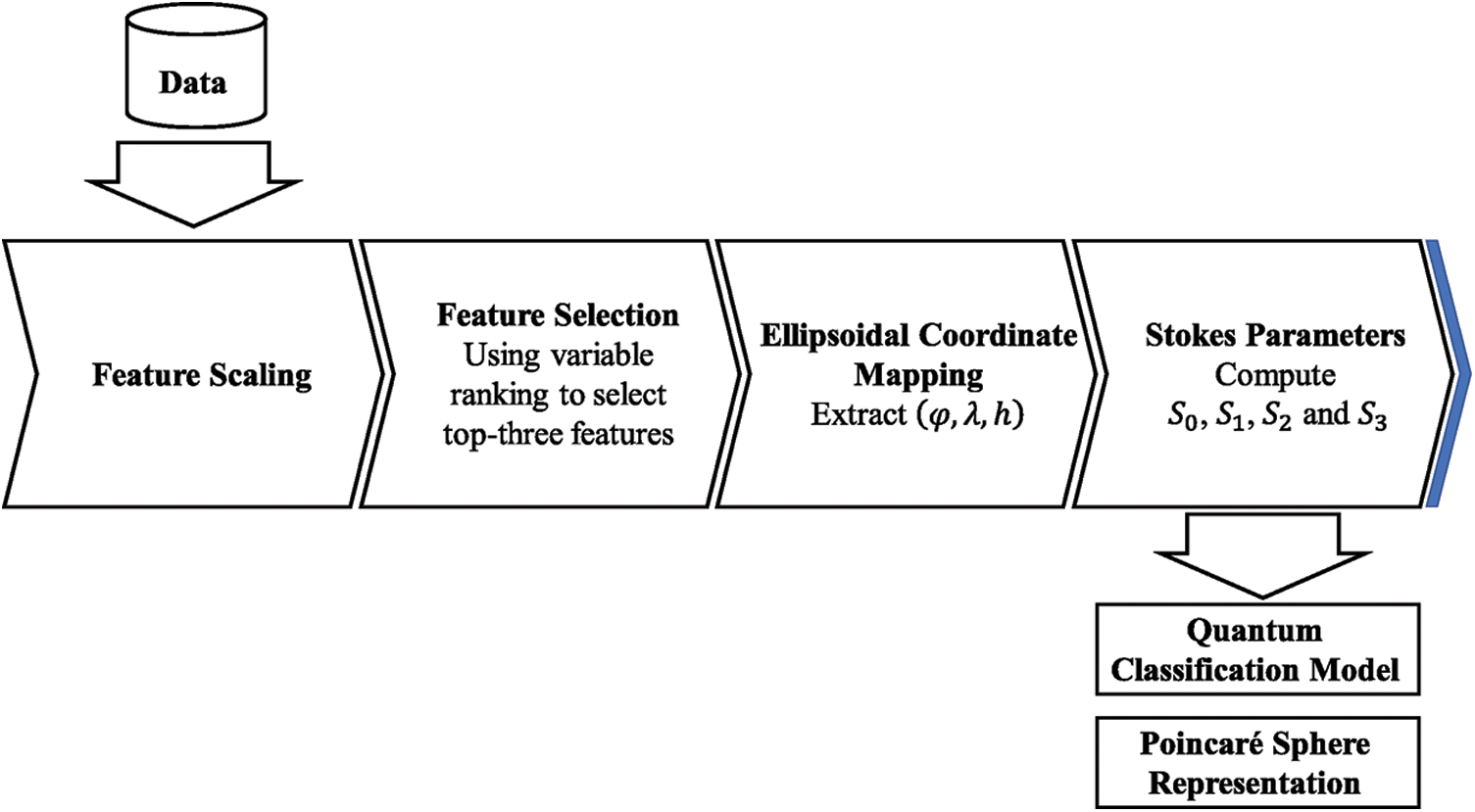
Figure 1: Proposed preprocessing pipeline
This step ensures same scaling for the numerical inputs in the model, enhancing the accuracy and speed of optimization methods during training. In general, this is a required step in the data preprocessing pipeline for most of the classical Machine Learning techniques [32]. For QML implementations, this is a fundamental step due to data constraints when representing it as quantum states. These restrictions result from quantum mechanics properties, in this sense, we standardized the data to zero mean deviation and unit variance. Then, each feature vector was scaled to a range of [ −1, +1].
Feature selection techniques are based on the idea of identifying and removing less relevant or redundant features, providing faster and more cost-effective predictors [33]. These techniques are relevant when processing medical datasets where features could induce noise in the models, making the classification process more difficult during training. Algorithms like Principal Component Analysis (PCA) have proven to be proficient to perform data preparation, even in QML applications and processing [12,34]. However, using this kind of algorithms make data interpretation unfeasible, therefore, avoiding artificial transformations enables feature interpretation before using them for the model.
In this sense, we based our methodology in variable ranking, calculating the mean value from the scores obtained using the feature importance of four different classical classification methods. Our main goal was to find a subset of features from our dataset that give us the best performance in classification, using the minimum number of features considering the encoding transformation to define quantum states, and the current quantum devices limitations in terms of quantum volume. Therefore, we selected the top three features of the calculated score, this dimensionality constrained is imposed by the ellipsoidal coordinate mapping. Our chosen classification methods were Gradient Boosting [35], Random forest, K-Best and Extra Trees that minimizes overfitting the data.
2.3 Ellipsoidal Coordinate Mapping
The selected features were transformed into a coordinate space where it can be easily represented using the Poincaré sphere. We use an iterative method based on [36] to transform those features from a Cartesian coordinate space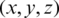 
to an ellipsoidal coordinate space 
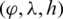, following Eqs. (1)–(3).
where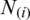 
is defined as:
The constant p is:
and e is based on the semi-major axis a, the semi-minor axis b.
We executed the method specifying a dispersion error of 10−5 for each data point.
2.4 Stokes Parameters: Poincaré Sphere Representation
A convenient geometrical representation of the Quantum States is obtained when using the Bloch Sphere, also known as Poincaré Sphere, it has been used to describe polarization states by using the Stokes parameters. By defining the data in terms of ellipsoids, these definitions are mathematically analogous to Stokes parameters to describe polarization, however, they have no physical relation with them. The ellipses parameters are represented by:
where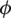 
is the azimuth angle between the semi-major axis of the ellipse and the x-axis, and 
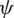is the elliptic angle, defined by the inverse tangent of the relation between the length of the semi-axes of the ellipse (Fig. 2a). A simple geometric representation of these parameters is obtained when defining a spherical surface of unit radius:
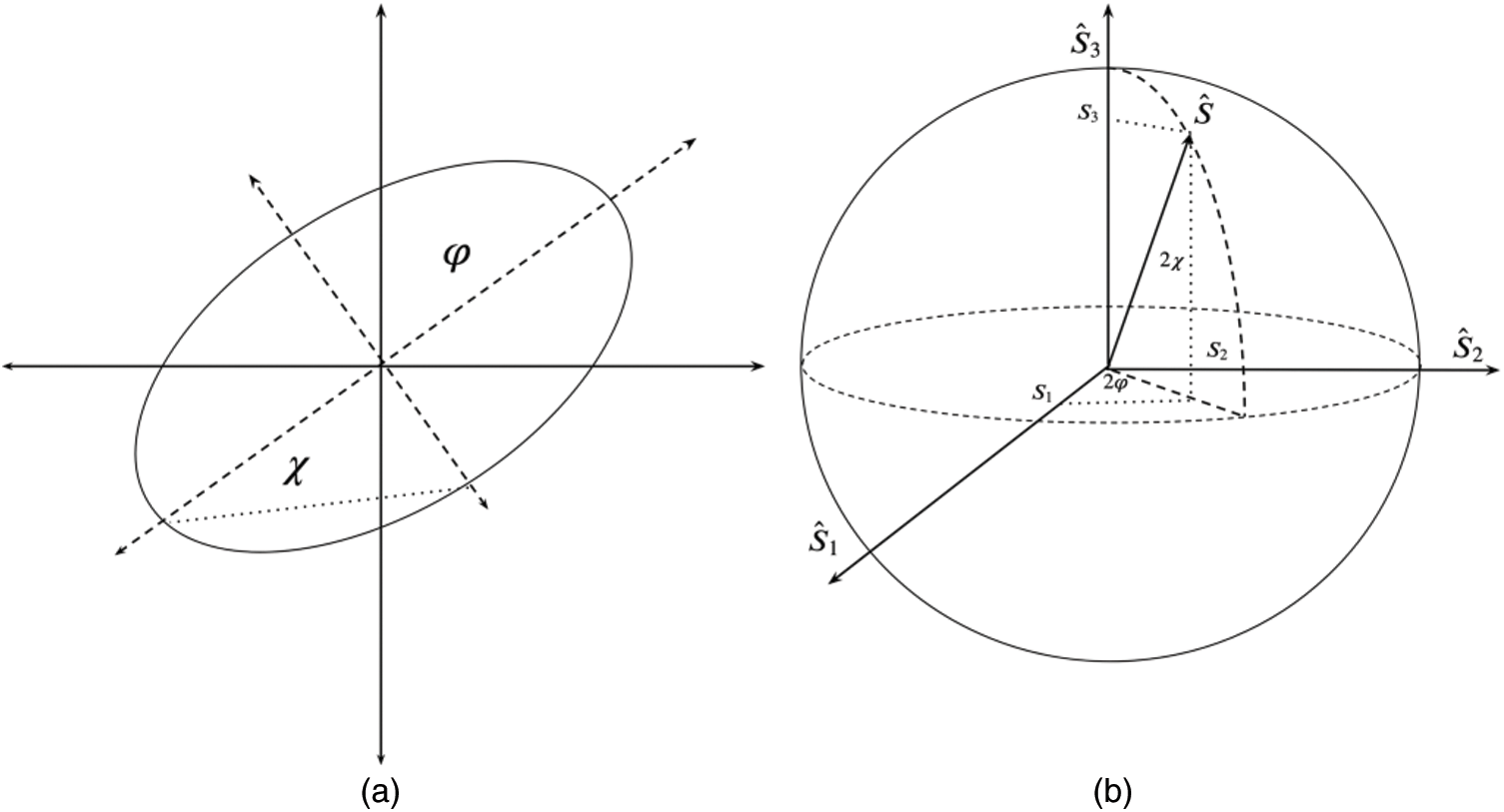
Figure 2: In (a) semi-axes of the ellipse, in (b) Stokes parameters represented over Poincaré sphere
Fig. 2b depicts these coordinates representation in the Poincaré sphere. In this, the variables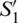 
, 
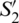and 
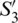can be considered as the Cartesian coordinates of the point 
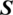on the surface of the unitary radius sphere, being 
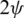and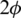 
the angular coordinates of this point.
2.5 Variational Quantum Classifier
The Variational Quantum Classifier (VQC) is a quantum method for supervised learning that allows performing classification problems in current NISQ devices. Based on a method proposed by Havlíček et al. [3] this algorithm allows to obtain experimental results in NISQ devices without the need to perform additional error-correction techniques. The calculation of the cost function based on the iterative measurements from the device serve as error mitigation, by including noisy measurements into optimization calculations. Also, it has been showed that mapping features to quantum states using amplitude encoding, is a suitable option to preprocess data when using VQC, provided that data is low dimensional or its structure allows for efficient approximate preparation [14,18,37]. This method is a hybrid approach where the parameters are optimized and updated in a classical computer, making the optimization process without increasing the coherence times needed [3,28].
One of the key components from this method is the feature map definition, which maps data into a potentially vastly higher-dimensional Hilbert space of a quantum system [14] allowing to perform efficient computations over non-linear basic functions on a possibly intractably large space, the feature space. A similar implementation known as kernel-trick has been explored using classical machine learning [38]. Nonetheless, using classical devices to perform these operations could take exponential resources, therefore quantum computing allows for creating more complex models that could predict with higher precision [28].
Havlíček et al. [3] proposed a VQC with two main elements presented in Fig. 3. First, a feature map that works as a fixed black-box encoding classical data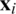 
into a quantum states 
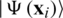, by applying transformations to the ground state 
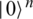using products of single and two-qubits unitary phase-gates. In specific, the experimental implementation of the authors results in a unitary gate 
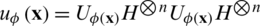where H represent the Hadamard gate and 
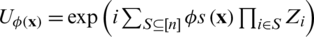, is a diagonal gate in the Pauli-Z basis. Second, a short depth unitary 
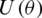circuit with l layers of 
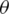-parameters, optimized during training by minimizing a cost function in a classical device, and tuning 
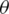iteratively. Using parameterized quantum circuits known as quantum circuit learning QCL, implies the usage of an exponential number of functions with respect to the number of qubits from the parameterized circuit, this is intractable on classical computers, therefore, allows to represent more complex functions than the classical counterparts [28].
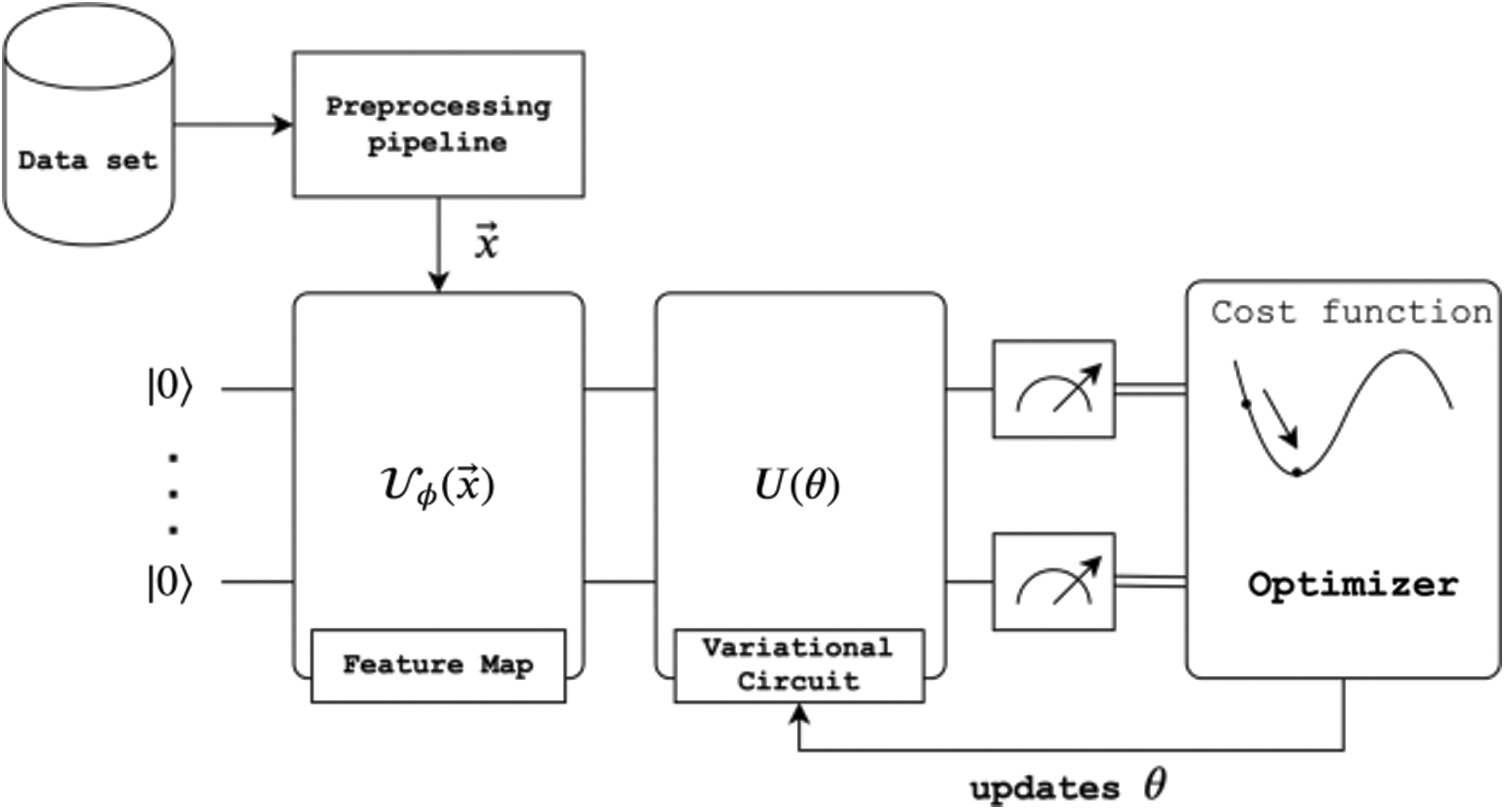
Figure 3: Schematic view of VQC algorithm [27]
3 Case Study: Incidence of Acute Diseases in Diabetic Patient
Diabetes Type 2 is a rising public health problem [29]. The patients with Diabetes Type 2 represent over 90% of the total of patients with any type of diabetes and is the seventh cause of death worldwide [29,39]. This disease leads to a number of micro and macrovascular events [40], which represent short and long-term complications such as cardiovascular disease, nephropathy, retinopathy, peripheral neural disease, limb amputation, erectile dysfunction, depression, among others. Given its close relation with lifestyle and obesity, the numbers of people suffering from this condition and its complications keep increasing [30]. The steady increment in the number of people suffering from Type 2 Diabetes Mellitus results in a huge burden on the health-care system increasing the healthcare costs [30,41,42]. Provided the wide range of complications and disabilities that come along, this disease has a major impact on the patients’ life and on healthcare system supporting them.
Several T2DM related complications have been studied through different classical Machine learning, Deep Learning and Data Mining techniques [43,44]. The risk factor identification associated with these complications is of great value to the clinical management of individuals with diabetes. Due to the high level of disability and incremental costs of the disease, it is necessary to investigate the causes involved in the genesis of complications. In order to address them in the future and apply the medical knowledge not only from a healing perspective but also on a preventive one, saving suffering to the patient and money to the health care system.
A dataset containing clinical information from patients diagnosed with Type 2 Diabetes Mellitus has been used. For each subject a successive 12-month time period was defined, during this period, a patient is considered diagnosed with T2DM if the disease onset date was prior to the established cut-off point. By following these criteria, the total study population was 149,015 filtered from a larger database containing Electronic Health Records (EHR) from Osakidetza (Basque Health Service) in Bilbao, Spain. This dataset includes clinical variables such as LDL-Cholesterol, Body Mass Index and glycated hemoglobin (A1C). Also, demographic variables including age, gender and socioeconomic status position were considered.
The study protocol was approved by the Clinical Research Ethics Committee of Euskadi (PI2014074), Spain. Informed consent was not obtained because patient health records were made anonymous and de-identified prior to analysis.
In particular, our concern is the prediction acute conditions, we studied the incidence of acute myocardial infarction, major amputation or avoidable hospitalizations. Following the methodology discussed in Section 2.2 for feature selection we used gender, cholesterol LDL and Johns Hopkins’ Aggregated Diagnosis Groups (ADG). These features were contained in the higher scores when gradient boosting, random forest, k-best and tree-based techniques were applied as feature selectors.
Furthermore, the included features are relevant for the diabetes patients care, there is a strong correlation between diabetes and cholesterol [45], ADG has been used in the past to assess diabetic patients’ mortality [46], and we included gender as one of the selected features because it provides a differential characteristic, meaning that could enhance separability due to non-direct correlation with the output. This could be explained by the difference in hormones, fatty tissue distribution or simply differences in the lifestyles.
Then we randomly selected a balanced set of 250 samples for the data. These were split into two subsets, 200 for train and 50 for testing. After preprocessing the data, it is possible to represent the data points using the Poincare Sphere as depicted in Fig. 4, where the red dots represent patients with acute conditions and blue dots without. Albeit this step is not needed to process the information, it provides a good visual representation of the data distribution.
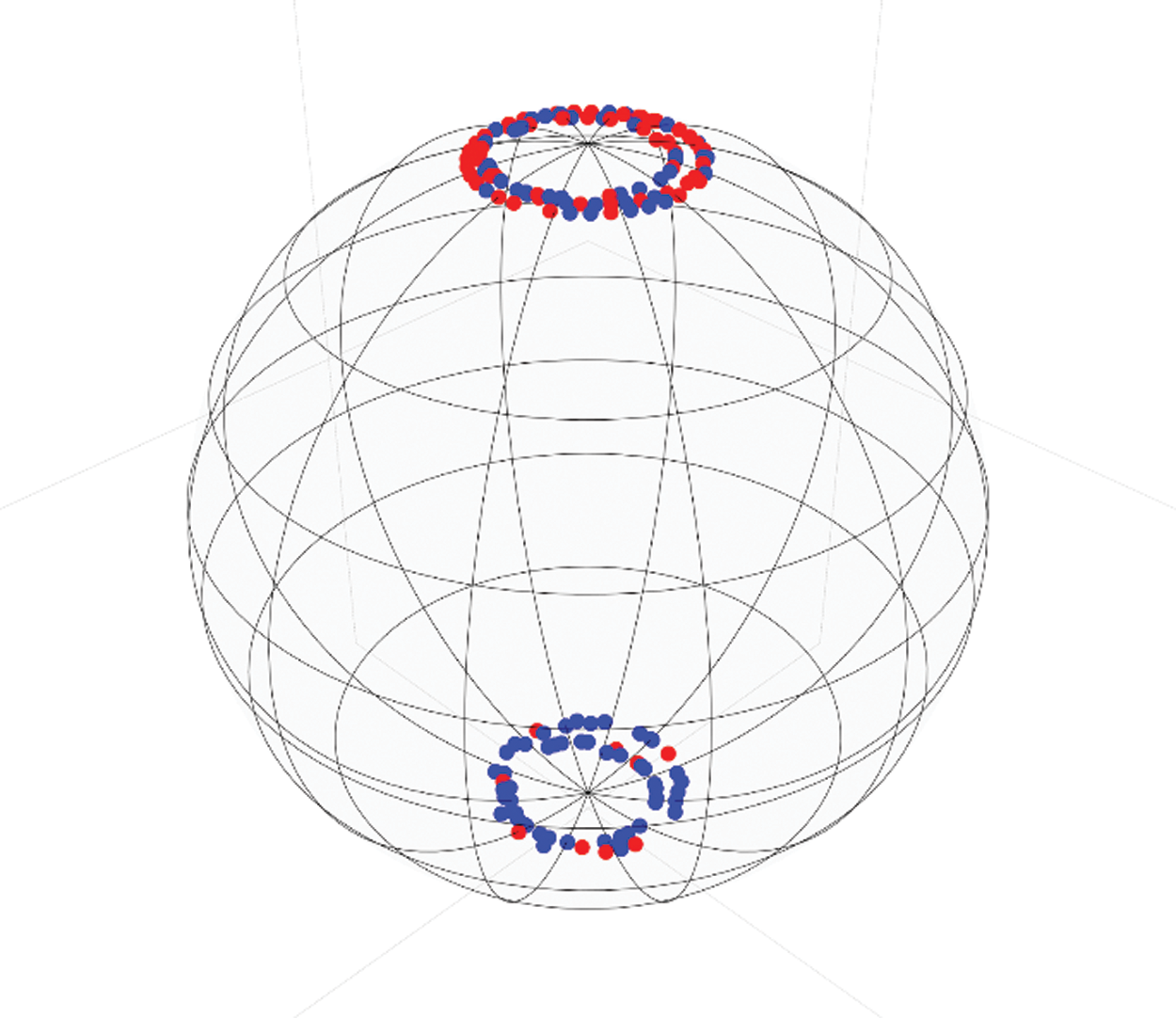
Figure 4: Poincaré geometrical data representation
Data classification was performed by using the implemented version of VQC in IBM’s framework Qiskit version 0.11.1 and executed in the provided simulator Aer version 0.2.3 [31]. Every combination of the experiments was executed with 1024 shots, using the implemented version of the COBYLA optimizer [47] through the same framework. We conducted tests with two and three qubits, in each case we compared the accuracy, precision, recall and F1-Score when applying data normalization between −1 and 1 with zero standard deviation, adding to this normalization the ellipsoidal coordinate transform, and finally adding the Stokes parameter representation, the results from these experiments are summarized in Tab. 1.
Table 1: VQC results for acute disease prediction in Diabetes patients
To show the advantage of using the proposed pipeline and its elements we performed three experiments using VQC over the T2DM dataset. In the first experiment we normalized the data using zero standard deviation before passing to the model. In addition to the normalization, in the second experiment we also transformed the data to Ellipsoidal coordinates. Finally, in the third experiment we calculated the Stokes parameters additional to all the previous steps, giving the possibility to visualize the data points using a Poincaré sphere. By including all the data preprocessing elements, we obtained a pipeline that enhance data preparation for VQC application. The results of these experiments are presented in Fig. 5, using accuracy, precision, recall and F1-score as metrics to evaluate the model’s performance. In these figures it can be seen that using the proposed pipeline to transform data, induce significant improvements in the classification performance in particular in the 2 qubits case. Moreover, by using the proposed technique, the model results when employing 2 qubits resemble those obtained when 3 qubits were used, enhancing the classification results even if fewer resources are available.
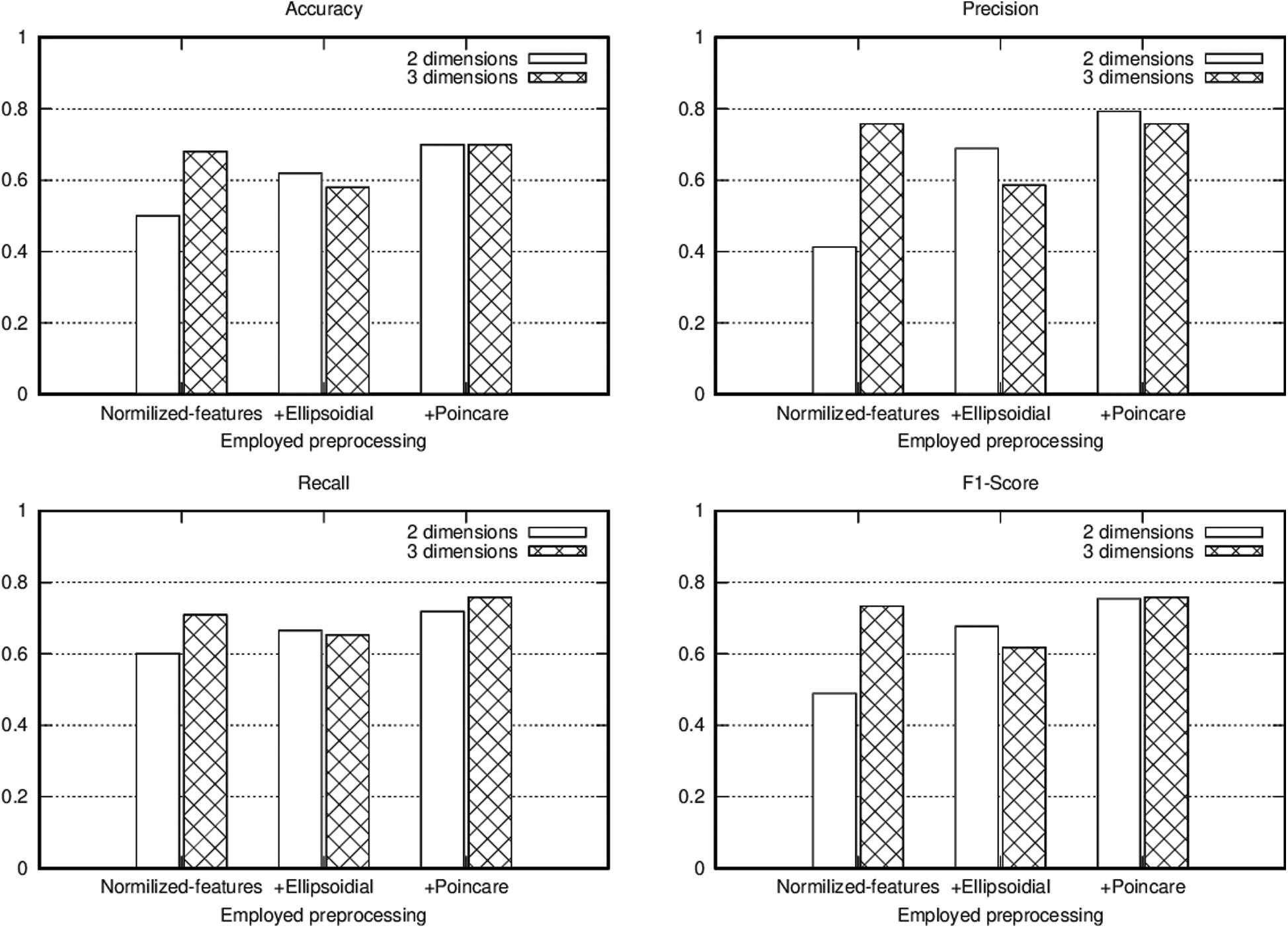
Figure 5: T2DM acute disease classification metrics for the conducted experiments
Research on Quantum Machine Learning applications is advancing the uses of current state quantum computers, given the wide range of applications and the industry interest in machine learning techniques to solve practical problems. We consider that this work contributes in the usage of new techniques for the exploitation of NISQ devices in “real-world” applications of QML.
A milestone to pursue is to achieve quantum advantages for commercial applications. Machine learning is an area of computer science where statistics, data processing and analytics converge, given the relevance of data across the different fields and the breadth of applications. In particular, Quantum Machine Learning is being actively investigated by several research groups, as the exploit of quantum computing advantages could improve and expand the range of real-world machine learning applications.
In this paper we propose a pipeline to transform and preprocess data, making it feasible to be classified using Quantum Machine Learning techniques. By using this pipeline, we enhanced the quantum state preparation for VQC algorithm. Our results showed that by using the proposed techniques we obtained similar results when classifying the incidence of acute diseases in diabetes patients using a Variational Quantum Classifier with two and three qubits, with 70% and 72% accuracy respectively. We are currently studying and developing unsupervised and supervised machine learning techniques suitable for NISQ devices, given the current limitations on coherence times and qubits available on current devices. In particular, conducting further research on the application of the proposed pre-processing pipeline to improve the data suitability for different QML techniques such as Quantum Support Vector Machine. We are also evaluating the execution advantages of applying the proposed technique in different environments.
Acknowledgement: This work was supported by Osakidetza that provided the database. The study protocol was approved by the Clinical Research Ethics Committee of Euskadi (PI2014074), Spain. Informed consent was not obtained because patient health records were made anonymous and de-identified prior to analysis.
Funding Statement: This project was partially funded by eVIDA Research group IT-905-16 from Basque Government.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. J. Preskill. (2018). “Quantum computing in the NISQ era and beyond,” Quantum, vol. 2, pp. 79. [Google Scholar]
2. M. A. Nielsen and I. L. Chuang. (2011). Quantum computation and quantum information. 10th ed., New York, USA: Cambridge University Press. [Google Scholar]
3. V. Havlıček, A. Córcoles, K. Temme, A. Harrow, A. Kandala et al. (2019). , “Supervised learning with quantum-enhanced feature spaces,” Nature, vol. 567, no. 7747, pp. 209–212. [Google Scholar]
4. M. Benedetti, E. Lloyd, S. Sack and M. Fiorentini. (2019). “Parameterized quantum circuits as machine learning models,” Quantum Science and Technology, vol. 4, no. 4, pp. 43001. [Google Scholar]
5. A. Perdomo-Ortiz, M. Benedetti, J. Realpe-Gómez and R. Biswas. (2018). “Opportunities and challenges for quantum-assisted machine learning in near-term quantum computers,” Quantum Science and Technology, vol. 3, pp. 30502. [Google Scholar]
6. J. M. Arrazola, T. R. Bromley, J. Izaac, C. R. Myers, K. Brádler et al. (2019). , “Machine learning method for state preparation and gate synthesis on photonic quantum computers,” Quantum Science and Technology, vol. 4, pp. 24004. [Google Scholar]
7. J. Li. (2015). “Quantum-inspired neural networks with application,” Open Journal of Applied Sciences, vol. 5, no. 6, pp. 233–239. [Google Scholar]
8. E. Farhi and H. Neven. (2018). “Classification with quantum neural networks on near term processors.” arXiv preprint arXiv: 1802.06002. [Google Scholar]
9. M. Ostaszewski, E. Grant and M. Benedetti. (2019). “Quantum circuit structure learning,” arXiv preprint arXiv: 1905.09692. [Google Scholar]
10. G. G. Guerreschi and M. Smelyanskiy. (2017). “Practical optimization for hybrid quantum-classical algorithms,” arXiv preprint arXiv: 1701.01450. [Google Scholar]
11. N. Moll, P. Barkoutsos, L. S. Bishop, J. M. Chow, A. Cross et al. (2018). , “Quantum optimization using variational algorithms on near-term quantum devices,” Quantum Science and Technology vol. 3, pp. 30503. [Google Scholar]
12. S. Lloyd, M. Mohseni and P. Rebentrost. (2014). “Quantum principal component analysis,” Nature Physics, vol. 10, no. 9, pp. 631–633. [Google Scholar]
13. M. Schuld, M. Fingerhuth and F. Petruccione. (2017). “Implementing a distance-based classifier with a quantum interference circuit,” Europhysics Letters, vol. 119, pp. 60002. [Google Scholar]
14. M. Schuld and N. Killoran. (2019). “Quantum machine learning in feature Hilbert spaces,” Physical Review Letters, vol. 122, pp. 40504. [Google Scholar]
15. Z. Zhao, J. K. Fitzsimons and J. F. Fitzsimons. (2019). “Quantum-assisted Gaussian process regression,” Physical Review A, vol. 99, pp. 052331. [Google Scholar]
16. M. Schuld, I. Sinayskiy and F. Petruccione. (2016). “Prediction by linear regression on a quantum computer,” Physical Review A, vol. 94, pp. 022342. [Google Scholar]
17. J. Romero, J. P. Olson and A. Aspuru-Guzik. (2017). “Quantum autoencoders for efficient compression of quantum data,” Quantum Science and Technology, vol. 2, pp. 45001. [Google Scholar]
18. M. Schuld, A. Bocharov, K. Svore and N. Wiebe. (2020). “Circuit-centric quantum classifiers,” Physical Review A, vol. 101, no. 3, pp. 32308. [Google Scholar]
19. G. Verdon, M. Broughton and J. Biamonte. (2017). “A quantum algorithm to train neural networks using low-depth circuits. arXiv preprint arXiv: 1712.05304. [Google Scholar]
20. P. Rebentrost, M. Mohseni and S. Lloyd. (2013). “Quantum support vector machine for big data classification,” Physical Review Letters, vol. 113, pp. 130503. [Google Scholar]
21. N. Wiebe, A. Kapoor and K. Svore. (2014). “Quantum algorithms for nearest-neighbor methods for supervised and unsupervised learning. arXiv preprint arXiv: 1401. 2142. [Google Scholar]
22. S. Lloyd, M. Mohseni and P. Rebentrost. (2013). “Quantum algorithms for supervised and unsupervised machine learning,” arXiv preprint arXiv: 1307.0411. [Google Scholar]
23. Y. Ruan, X. Xue, H. Liu, J. Tan and X. Li. (2017). “Quantum algorithm for k-nearest neighbors classification based on the metric of hamming distance,” International Journal of Theoretical Physics, vol. 56, no. 11, pp. 3496–3507. [Google Scholar]
24. I. Kerenidis and A. Luongo. (2018). “Quantum classification of the MNIST dataset via slow feature analysis,” Physical Review A, vol. 10.1103, pp. 101.062327. [Google Scholar]
25. M. Schuld, I. Sinayskiy and F. Petruccione. (2014). “Quantum computing for pattern classification,” in PRICAI 2014: Trends in Artificial Intelligence, D.-N. Pham and S.-B. Park, Cham: Springer, pp. 208–220. [Google Scholar]
26. M. Zidan, A.-H. Abdel-Aty, M. El-shafei, M. Feraig, Y. Al-Sbou et al. (2019). , “Quantum classification algorithm based on competitive learning neural network and entanglement measure,” Applied Sciences, vol. 9, no. 7, pp. 1277. [Google Scholar]
27. D. Sierra-Sosa, J. Arcila-Moreno, B. Garcia-Zapirain, C. Castillo-Olea and A. Elmaghraby. (2020). “Dementia prediction applying variational quantum classifier,” arXiv preprint arXiv: 2007.08653. [Google Scholar]
28. K. Mitarai, M. Negoro, M. Kitagawa and K. Fujii. (2018). “Quantum circuit learning,” Physical Review A, vol. 98, pp. 32309. [Google Scholar]
29. G.-l Du, Y.-x Su, H. Yao, J. Zhu, Q. Ma et al. (2016). , “Metabolic risk factors of type 2 diabetes mellitus and correlated glycemic control/complications: A cross-sectional study between rural and urban uygur residents in xinjiang uygur autonomous region,” PLOS ONE, vol. 11, pp. 1–18. [Google Scholar]
30. C. Bommer, E. Heesemann, V. Sagalova, J. Manne-Goehler, R. Atun et al. (2017). , “The global economic burden of diabetes in adults aged 20–79 years: A cost-of-illness study,” Lancet Diabetes Endocrinology, vol. 5, pp. 423–430. [Google Scholar]
31. H. Abraham, I. Y. Akhalwaya, G. Aleksandrowicz, T. Alexander, G. Alexandrowics et al. (2019). , “Qiskit: An open-source framework for quantum computing,”. [Google Scholar]
32. A. Gron. (2017). Hands-on machine learning with Scikit-Learn and TensorFlow: Concepts, tools, and techniques to build intelligent systems, ch. 2, 1st ed., USA: O’Reilly Media, Inc., pp. 65. [Google Scholar]
33. H. Liu and R. Setiono. (1998). “Some issues on scalable feature selection,” Expert Systems with Applications, vol. 15, no. 3, pp. 333–339. [Google Scholar]
34. C.-H. Yu, F. Gao, S. Lin and J. Wang. (2019). “Quantum data compression by principal component analysis,” Quantum Information Processing, vol. 18, pp. 249. [Google Scholar]
35. Z. Xu, G. Huang, K. Q. Weinberger and A. X. Zheng. (2014). “Gradient boosted feature selection,” in Proc. of the 20th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, KDD ’14, ACM, New York, USA, pp. 522–531. [Google Scholar]
36. J. S. Subirana, J. M. Zornoza and M. Hernández-Pajares. (2016). “Ellipsoidal and cartesian coordinates conversion,” . https://gssc.esa.int/navipedia/index.php/Ellipsoidal_and_Cartesian_Coordinates_Conversion. [Google Scholar]
37. I. F. Araujo, D. K. Park, F. Petruccione and A. J. da Silva. (2020). “A divide-and-conquer algorithm for quantum state preparation,” arXiv preprint arXiv: 2008.01511. [Google Scholar]
38. C. M. Bishop. (2006). Pattern recognition and machine learning (Information Science and Statistics). Berlin, Heidelberg: Springer-Verlag. [Google Scholar]
39. Global Health Observatory (GHO) data. (2020). “Top 10 causes of death,” . Available: https://www.who.int/gho/mortality_burden_disease/causes_death/top_10/en/. [Google Scholar]
40. E. Gregg, N. Sattar and M. Ali. (2016). “The changing face of diabetes complications,” Lancet Diabetes Endocrinology, vol. 4, no. 6, pp. 537–547. [Google Scholar]
41. M. L. Alva, A. Gray, B. Mihaylova, J. Leal and R. Holman. (2014). “The impact of diabetes related complications on healthcare costs: New results from the ukpds (ukpds 84),” Diabetic Medicine, vol. 32, no. 4, pp. 459–466. [Google Scholar]
42. J. Lopez-Bastida, M. Boronat, J. Oliva-Moreno and W. Schurer. (2013). “Costs, outcomes and challenges for diabetes care in spain,” Globalization and Health, vol. 9, pp. 17. [Google Scholar]
43. V. Lagani, F. Chiarugi, S. Thomson, J. Fursse, E. Lakasing et al. (2015). , “Development and validation of risk assessment models for diabetes-related complications based on the dcct/edic data,” Journal of Diabetes and Its Complications, vol. 29, no. 4, pp. 479–487. [Google Scholar]
44. D. Sierra-Sosa, B. Garcia-Zapirain, C. Castillo, I. Oleagordia, R. Nuño-Solinis et al. (2019). , “Scalable healthcare assessment for diabetic patients using deep learning on multiple GPUS,” IEEE Transactions on Industrial Informatics, vol. 15, no. 10, pp. 5682–5689. [Google Scholar]
45. A. L. Kennedy, T. R. Lappin, T. D. Lavery, D. R. Hadden, J. A. Weaver et al. (1978). , “Relation of high-density lipoprotein cholesterol concentration to type of diabetes and its control,” BMJ, vol. 2, no. 6146, pp. 1191–1194. [Google Scholar]
46. P. C. Austin, B. R. Shah, A. Newman and G. M. Anderson. (2012). “Using the Johns Hopkins’ aggregated diagnosis groups (ADGS) to predict 1-year mortality in population-based cohorts of patients with diabetes in Ontario, Canada,” Diabetic Medicine, vol. 29, no. 9, pp. 1134–1141. [Google Scholar]
47. M. Powell. (1994). “A direct search optimization method that models the objective and constraint functions by linear interpolation,” Advances in Optimization and Numerical Analysis, vol. 275, pp. 51–67. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |