DOI:10.32604/cmc.2021.014255
| Computers, Materials & Continua DOI:10.32604/cmc.2021.014255 | |
| Article |
Rayleigh Waves Propagation in an Infinite Rotating Thermoelastic Cylinder
1Department of Physics, Faculty of Science, Jazan University, Jazan, Saudi Arabia
2Department of Physics, Faculty of Science, Zagazig University, Zagazig, Egypt
*Corresponding Author: A. M. Farhan. Email: afarhan_afarhan@yahoo.com
Received: 09 September 2020; Accepted: 11 October 2020
Abstract: In this paper, we investigated the inuence of rotating half-space on the propagation of Rayleigh waves in a homogeneous isotropic, generalized thermo-elastic body, subject to the boundary conditions that the surface is traction free. In addition, it is subject to insulating thermal conduction. A general solution is obtained by using Lame’ potential’s and Hankel transform. The dispersion equations has been derived separately for two types of Rayleigh wave propagation properties by solving the equations of motion with appropriate boundary conditions. It is observed that the rotation, frequency and r exert some influence in the homogeneous isotropic medium due to propagation of Rayleigh waves. The frequency equation has been derived of homogeneous properties by solving the equations of motion with appropriate boundary conditions. It has been found that the frequency equation of waves contains a term involving the rotating. Therefore, the phase velocity of Rayleigh waves changes with respect to this rotating. When the rotating vanishes, the derived frequency equation reduces to that obtained in classical generalized thermo-elastic case which includes the relaxation time of heat conduction. In order to illustrate the analytical development, the numerical solution is carried out and computer simulated results in respect of Rayleigh wave velocity and attenuation coefficient are presented graphysically. A comparative and remarkable study has been carried out through various graphs to deliberate the consequences of different parameter on the frequency equation. The obtained results can be very useful in the design and optimization of Rayleigh wave.
Keywords: Rayleigh waves; wave propagation; generalized thermoelasticity; thermal stress; rotation
There are many previous studies on generalized thermoelastic waves. Abd-Alla [1] found the phase velocity of propagation of Rayleigh waves in an elastic half-space of orthotropic material. Abd-Alla et al. [2] studied the effect of initial stress, gravity field, and rotation on the propagation of Rayleigh waves in an orthotropic material elastic half-space. Bagri et al. [3] discussed a unified generalized thermoelasticity solution for cylinders and spheres. El-Naggar et al. [4] investigated the effect of initial stress on the generalized thermoelastic problem in an infinite circular cylinder. Singh et al. [5] discussed the effect of rotation on the propagation of Rayleigh waves in an incompressible orthotropic elastic solid half-space with impedance boundary conditions. Singh [6] studied the Rayleigh waves in an incompressible fiber-reinforced elastic solid with impedance boundary conditions. Green et al. [7] introduced the theory of thermoelasticity. Lebon [8] introduced the generalized theory of thermoelasticity. Lord et al. [9] solved the dynamical theory of generalized thermoelasticity to take into account the time needed for the acceleration of the heat flow. Singh et al. [10] investigated the generalized thermoelastic waves in a transversely isotropic media. The generalized thermoelastic waves are discussed by Sharma et al. [11]. Sharma et al. [12] studied the effect of magnetic field on Rayleigh–Lamb waves in a thermoelastic homogeneous isotropic plate. Misra et al. [13] discussed the thermo-viscoelastic waves in an infinite aeolotropic body with a cylindrical cavity. Sharma [14] studied the Rayleigh waves at the surface of a general anisotropic poroelastic medium. Othman [15] investigated the effects of rotation on plane waves in generalized thermo-elasticity with two relaxation times. Othman [16] investigated the effect of rotation and relaxation time on the thermal shock problem for a half-space in generalized thermo-viscoelasticity. Sinha et al. [17] found the eigenvalue approach to study the effect of rotation and relaxation time in generalized thermoelasticity. Schoenberg et al. [18] studied the effect of rotation on propagation waves in an elastic media. Tanaka et al. [19] studied the application of the boundary element method to 3D problems of coupled thermoelasticity. Nowaki [20] introduced thermoelasticity.
This paper brings out the analytical study of generalized thermoelastic medium subjected to rotation. The generalized thermoelastic cylinder is assumed under the influence of rotation and the relaxation time. The main aim of the paper is to investigate the effects of involved parameters on the Rayleigh wave velocity and attenuation coefficient of the wave. Numerical computation has been accomplished to manifest the effect of rotation and relaxation time on the Rayleigh wave velocity and attenuation coefficient of the wave for different types of parameters. The numerical results have been obtained and presented graphically.
2 Formulations of the Problem and Boundary Conditions
Let us consider a homogeneous isotropic elastic solid with an infinite circular cylinder under initial temperature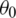 
. The elastic medium is rotating uniformly with an angular velocity 
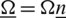, where 
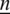is a unit vector representing the direction of the axis of rotation. The displacement equation of motion in the rotating frame has two additional terms, centripetal acceleration, 
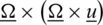due to time-varying motion only where 
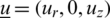is the displacement vector, and 
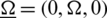. All quantities considered will be functions of the time variable t and the coordinates r and z.
The dynamic equation of motion is given by Sharma et al. [12] as follows:
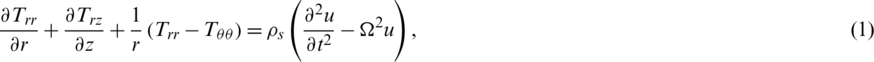
The heat conduction equation is given by [4]:
Where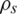 
is the density of the material, k is thermal conductivity, cv is the specific heat of the material per unit mass, Trr, 
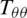, Tzz, and Trz are the stresses components, u and w are the displacement components, and 
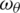is the rotating component.
The stress–strain relations are given by Abd-Alla [12]:
where,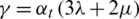 
, 
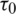and 
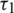are thermal relaxation time.
The strain components and the rotation are given by Bagri et al. [13] as follows:
Using Eqs. (4)–(9) into Eqs. (1) and (2), the following can be written as:
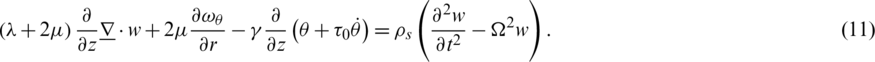
By Helmholtz’s theorem [14], the displacement vector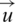 
can be written in the following form:
Where the scalar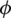 
and the vector 
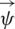represent irrational and rotational parts of the displacement 
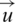. The component of the vector 
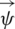to be non-zero, as
From Eqs. (12a) and (12b), we obtain
Substituting from (12a)–(12c) into Eqs. (3), (10), and (11), we get two equations for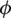 
and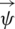 
as follows:
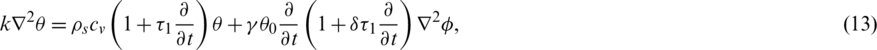
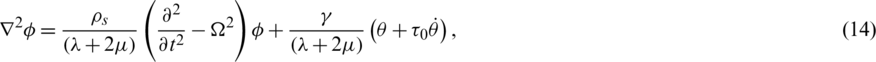
Where,
Eq. (14) represents the longitudinal wave in the direction of r with velocity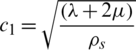 
and Eq. (15) represents the velocity of the shear wave in the direction of r with velocity 
.
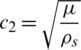Let us consider a homogeneous and isotropic elastic solid with an infinite cylinder of the radius a. The axis of the cylinder is taken along the z direction, subjected to the boundary conditions are given as follows:
The thermal boundary condition is
Assume that the temperature and potential functions of solid satisfy
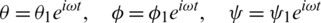
Eqs. (13)–(15) yield a set of differential equations:
where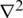 
is the Laplace operator. 
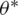can be eliminated from Eq. (20) by substituting it in Eq. (19), giving
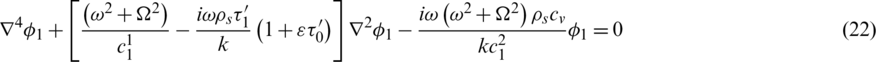
Where
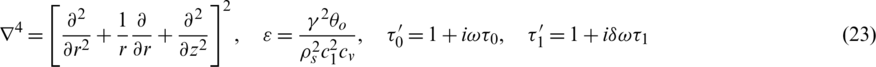
The general solution of Eqs. (21) and (22) can be found. If we introduce the inversion of the Hankel transform which is defined by
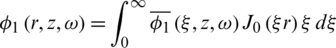
We obtain
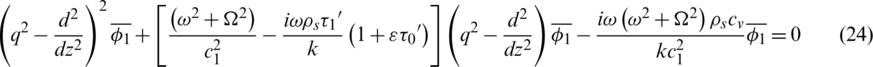
By putting 
, the indicial equation governing (24) is
where 
are the roots of Eq. (24) and 
, j = 1, 2.
If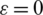 
, then the roots of Eq. (25) become
The above roots correspond to the case in which the elastic wave and generalized heat condition equations are not coupled. For small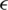 
, i.e., only the first order is taken. The roots of Eq. (25) take the form
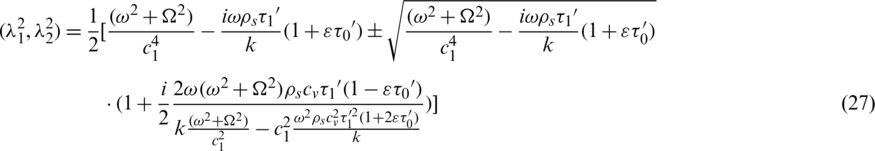
Then the solution of Eq. (24) is
which leads to
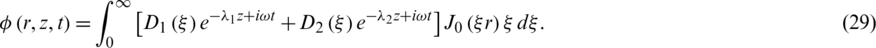
The solution of Eq. (21) is
Where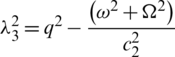 
and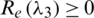 
.
Substituting Eq. (29) into Eq. (20) yields
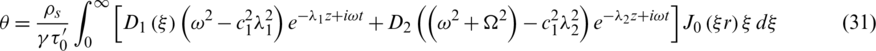
The stress components Trr and Trz are given by
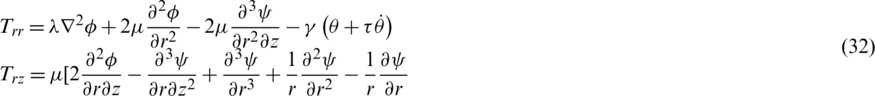
Substituting Eqs. (29)–(31) into Eqs. (12c) and (32), we get
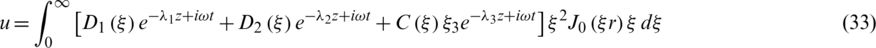
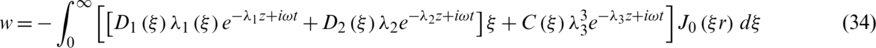
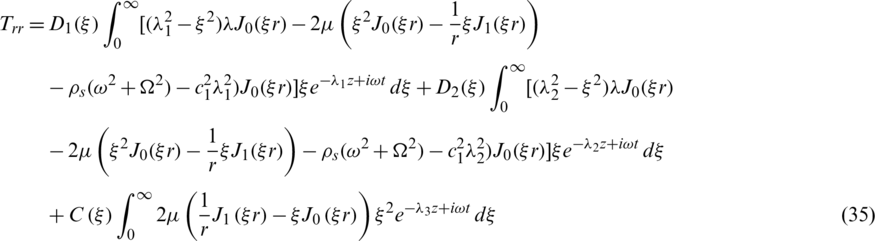
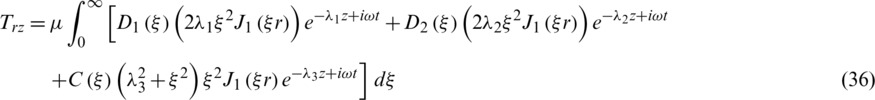
In this section, we are going to obtain the frequency equation for the boundary conditions which specify that the outer surface of the cylinder is traction free and the thermal boundary conditions are illustrated. Substituting Eqs. (31) and (32) into the boundary conditions (17) and (18), we get
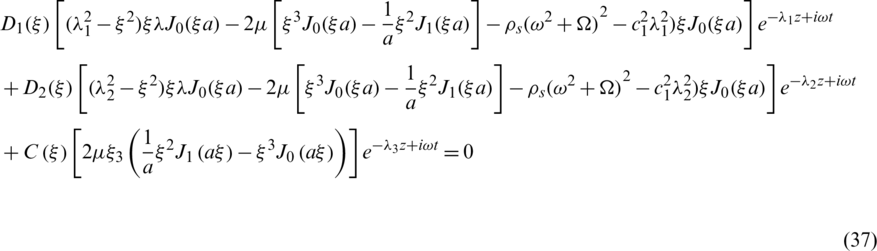
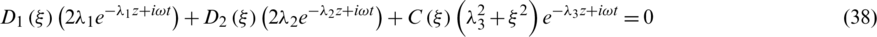
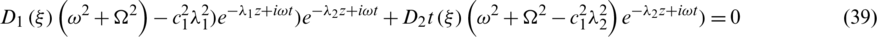
By eliminating constraints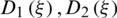 
and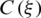 
, the frequency equation is given in a form of third order determinant as follows:
where
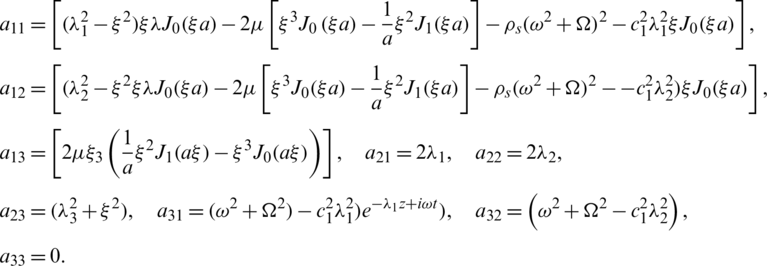
The frequency Eq. (40) has a complex root. The real part (Re) gives the velocity of Rayleigh waves and the imaginary part (I’m) gives the attenuation coefficient.
6 Numerical Results and Discussion
The numerical calculation was carried out of the Rayleigh waves velocity and attenuation coefficient. To illustrate the theoretical results obtained in the preceding section, we now present some numerical results. The material chosen for this purpose was carbon steel, the physical data for which are given below [16]:
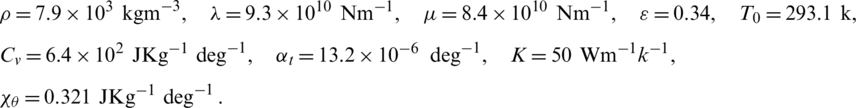
Fig. 1 shows the variations of Rayleigh waves velocity and attenuation coefficient with respect to frequency 
for different values of rotation 
for the Lord-Schulman theory. The Rayleigh wave velocity decreases with the increase of rotation and frequency, while the attenuation coefficient increases with the increase of rotation and frequency.
Figure 1: Variations of Rayleigh waves velocity and attenuation coefficient with respect to frequency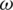 
for different values of 
at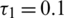 
, r = 2
Fig. 2 shows the variations of Rayleigh wave velocity and attenuation coefficient with respect to frequency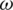 
for different values of relaxation time 
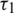for the Lord-Schulman theory. The Rayleigh wave velocity decreases with the increase of relaxation time and frequency, while the attenuation coefficient increases with the increase of relaxation time and frequency.
Figure 2: Variations of Rayleigh waves velocity and attenuation coefficient with respect to frequency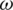 
for different values of relaxation time of 
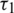at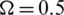 
, and r = 2
(II) GL-model (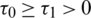
, 
), 
.
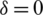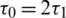Fig. 3 shows the variations of Rayleigh wave velocity and attenuation coefficient with respect to frequency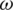 
for different values of rotation 
for the Green-Linsay theory. The Rayleigh wave velocity decreases with the increase of rotation and frequency, while the attenuation coefficient increases with the increase of rotation and frequency; the attenuation coefficient shifts from positive to negative in the range of frequency.
Figure 3: Variations of Rayleigh wave velocity and attenuation coefficient with respect to frequency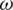 
for different values of rotation 
, at 
, 
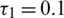
Fig. 4 shows the variations of Rayleigh wave velocity and attenuation coefficient with respect to frequency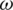 
for different values of relaxation time 
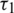for the Lord-Schulman theory. The Rayleigh wave velocity decreases with the increase of relaxation time and frequency, while the attenuation coefficient increases with the increase of relaxation time and frequency.
Figure 4: Variations of Rayleigh waves velocity and attenuation coefficient with respect to frequency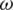 
for different values of relaxation time 
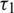at 
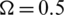and 
The governing field equations for linear homogeneous and isotropic thermoelastic materials with rotation are solved to work out appropriate surface wave solutions in an infinite cylinder. The frequency equation for the Rayleigh surface wave is obtained. The numerical results are illustrated graphically against frequency for different values of rotation and relaxation time. Some concluding remarks are given as follows
1. The rotation and relaxation time significantly influence the variations of the Rayleigh wave.
2. Analysis of Rayleigh wave developed into a body due to rotation and relaxation time.
3. The rotation and relaxation time of an infinite cylinder give the same effect in the problem as mentioned above in the results.
4. The present theoretical results may provide interesting information for experimental scientists, researchers, and seismologists working on this subject.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author declares that there are no conflicts of interest to report regarding the present study.
1. A. M. Abd-Alla. (1999). “Propagation of Rayleigh waves in an elastic half-space of orthotropic material,” Applied Mathematics and Computation, vol. 99, pp. 61–69. [Google Scholar]
2. A. M. Abd-Alla, S. M. Abo-Dahab and T. A. Al-Thamali. (2012). “Propagation of Rayleigh waves in a rotating orthotropic material elastic half-space under initial stress and gravity,” Journal of Mechanical Science and Technology, vol. 26, no. 9, pp. 2815–2823. [Google Scholar]
3. A. Bagri and M. R. Eslami. (2007). “A unified generalized thermoelasticity: Solution for cylinders and spheres,” International Journal of Mechanical Sciences, vol. 49, no. 12, pp. 1325–1335. [Google Scholar]
4. A. M. El-Naggar and A. M. Abed-Allah. (1987). “Generalized thermoelastic problem in an infinite circular cylinder under initial stress,” Earth, Moon and Planets, vol. 34, no. 3, pp. 213–225. [Google Scholar]
5. B. Singh and B. Kaur. (2017). “Propagation of Rayleigh waves in an incompressible rotating orthotropic elastic solid half-space with impedance boundary conditions,” Journal of the Mechanical Behavior of Materials, vol. 26, no. 3–4, pp. 73–78. [Google Scholar]
6. B. Singh. (2015). “Rayleigh waves in an incompressible fibre-reinforced elastic solid with impedance boundary conditions,” Journal of the Mechanical Behavior of Materials, vol. 24, no. 5–6, pp. 183–186. [Google Scholar]
7. E. Green and A. Lindsay. (1972). “Thermoelasticity,” Journal of Elasticity, vol. 2, no. 1, pp. 1–7. [Google Scholar]
8. G. A. Lebon. (1982). “A generalized theory of thermoelasticity,” Technical Physics, vol. 23, pp. 37–46. [Google Scholar]
9. H. W. Lord and Y. Shulman. (1967). “A generalized dynamical theory of thermoelasticity,” Journal of the Mechanics and Physics of Solids, vol. 7, pp. 71–75. [Google Scholar]
10. H. Singh and J. N. Sharma. (1985). “Generalized thermoelastic waves in transversely isotropic media,” Journal of the Acoustical Society of America, vol. 77, no. 3, pp. 1046–1053. [Google Scholar]
11. J. N. Sharma and H. Singh. (1989). “Generalized thermoelastic waves in anisotropic media,” Journal of the Acoustical Society of America, vol. 85, no. 4, pp. 1407–1413. [Google Scholar]
12. J. N. Sharma and P. Mohinder. (2004). “Rayleigh–Lamb waves in magneto-thermoelastic homogeneous isotropic plate,” International Journal of Engineering Science, vol. 42, no. 2, pp. 137–155. [Google Scholar]
13. J. C. Misra, N. C. Chatopadhyay and S. C. Samanta. (1994). “Thermo-viscoelastic waves in an infinite aeolotropic body with a cylindrical cavity, A study under the review of generalized theory of thermoelasticity,” Composite Structure, vol. 52, no. 4, pp. 705–717. [Google Scholar]
14. M. D. Sharma. (2018). “Rayleigh wave at the surface of a general anisotropic poroelastic medium: Derivation of real secular equation,” Proceedings of the London Mathematical Society A, vol. 474, no. 2211, pp. 1–12. [Google Scholar]
15. M. I. A. Othman. (2004). “Effects of rotation on plane waves in generalized thermo-elasticity with two relaxation times,” International Journal of Solids and Structures, vol. 41, no. 11–12, pp. 2939–2956. [Google Scholar]
16. M. I. A. Othman. (2005). “Effect of rotation and relaxation time on thermal shock problem for a half-space in generalized thermo-viscoelasticity,” Acta Mechanica, vol. 174, no. 3–4, pp. 129–143. [Google Scholar]
17. M. Sinha and R. K. Bera. (2003). “Eigenvalue approach to study the effect of rotation and relaxation time in generalized thermoelasticity,” Computers & Mathematics with Applications, vol. 46, no. 5–6, pp. 783–792. [Google Scholar]
18. M. Schoenberg and D. Censor. (1973). “Elastic waves in rotating media,” Quarterly of Applied Mathematics, vol. 31, no. 1, pp. 115–125. [Google Scholar]
19. M. Tanaka, M. Matsumoto and M. Moradi. (1995). “Application of the boundary element method to 3-D problems of coupled thermoelasticity,” Engineering Analysis with Boundary Elements, vol. 16, no. 4, pp. 297–303. [Google Scholar]
20. W. Nowaki. (1986). Thermoelasticity. London: Addison Publishing Company, Inc. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |