DOI:10.32604/cmc.2021.014875
| Computers, Materials & Continua DOI:10.32604/cmc.2021.014875 | |
| Article |
Estimation Performance for the Cubature Particle Filter under Nonlinear/Non-Gaussian Environments
1Department of Communications, Navigation and Control Engineering, National Taiwan Ocean University, Keelung, 202301, Taiwan
2National Center for High-Performance Computing, National Applied Research Laboratories, Hsinchu, 30076, Taiwan
*Corresponding Author: Dah-Jing Jwo. Email: djjwo@mail.ntou.edu.tw
Received: 23 October 2020; Accepted: 12 December 2020
Abstract: This paper evaluates the state estimation performance for processing nonlinear/non-Gaussian systems using the cubature particle filter (CPF), which is an estimation algorithm that combines the cubature Kalman filter (CKF) and the particle filter (PF). The CPF is essentially a realization of PF where the third-degree cubature rule based on numerical integration method is adopted to approximate the proposal distribution. It is beneficial where the CKF is used to generate the importance density function in the PF framework for effectively resolving the nonlinear/non-Gaussian problems. Based on the spherical-radial transformation to generate an even number of equally weighted cubature points, the CKF uses cubature points with the same weights through the spherical-radial integration rule and employs an analytical probability density function (pdf) to capture the mean and covariance of the posterior distribution using the total probability theorem and subsequently uses the measurement to update with Bayes’ rule. It is capable of acquiring a maximum a posteriori probability estimate of the nonlinear system, and thus the importance density function can be used to approximate the true posterior density distribution. In Bayesian filtering, the nonlinear filter performs well when all conditional densities are assumed Gaussian. When applied to the nonlinear/non-Gaussian distribution systems, the CPF algorithm can remarkably improve the estimation accuracy as compared to the other particle filter-based approaches, such as the extended particle filter (EPF), and unscented particle filter (UPF), and also the Kalman filter (KF)-type approaches, such as the extended Kalman filter (EKF), unscented Kalman filter (UKF) and CKF. Two illustrative examples are presented showing that the CPF achieves better performance as compared to the other approaches.
Keywords: Nonlinear estimation; non-Gaussian; Kalman filter; unscented Kalman filter; cubature particle filter
State estimation for the dynamic system [1] using a sequence of noisy observations made on the system has been an important issue in engineering science, statistical signal processing, and econometrics. The estimation problem is to sequentially estimate the state of the dynamic system using noisy observations of the system made up to that time. Linear states estimation deals with the dynamic system of linear process and measurement models. General methods to optimal nonlinear filtering can be interpreted in a unified way using the recursive Bayesian estimation. One difficulty of the application of the Bayesian estimation theory in practical applications is that the realistic dynamic systems are often nonlinear and/or non-Gaussian [2].
The nonlinear state-space method is convenient for handing multivariate data and nonlinear/non-Gaussian processes, and it provides a significant advantage over time-series approach for state estimation problems [3], where some examples illustrating the applications of nonlinear/non-Gaussian state space models are given. The Bayesian method provides a rigorous framework for dynamic state estimation. For the Bayesian filtering, the posterior probability density function (pdf) of the state space of a dynamic system is constructed based on all the available information. For the linear Gaussian models, the value of the pdf remains Gaussian and the state equations propagate and update the mean and covariance of the distribution. In general, for nonlinear and/or non-Gaussian models, there is no simple way to proceed for the required pdf.
One example of the several approximate methods that have been proposed is the extended Kamlan filter (EKF) [1,2], which assumes a Gaussian posterior density and relies on the first order linearization of the system model to provide local approximation of the mean and covariance of the state. EKF is sensitive to system nonlinearity in the measurements, and is likely to yield poor performance if the measurements involve non-Gaussian distributed noises. In practice, the EKF may diverge where the state equations are highly nonlinear and the posterior density is non Gaussian. The unscented Kalman filter (UKF) [4–10] was first proposed by Julier et al. to address nonlinear state estimation problems, which uses a finite number of sigma points to propagate the probability of state distribution through the nonlinear dynamics of system. Unlike the EKF where the linearization process is involved, the UKF performs a Gaussian approximation with a limited number of points (sigma points) using the unscented transform (UT), which is a method for calculating the statistics of a random variable which undergoes a nonlinear transformation. The sigma points are propagated through the true nonlinear system to capture the posterior mean and covariance of transformed distribution. It is based on the principle that it is easier to approximate a Gaussian distribution than to approximate an arbitrary nonlinear function. The possible negative weights can be avoided through tuning the parameters with flexibility [5].
Nevertheless, the UKF-calculated estimation covariance matrix is not always guaranteed to be positive definite, and thus decomposition of the covariance matrix is sometimes unavailable. The UKF is likely to become unstable due to the possible negative weights on the center point for high-dimensional nonlinear systems. To overcome these limitations, a nonlinear filter based on the Bayesian framework, commonly referred to as the cubature Kalman filter (CKF) proposed by Arasaratnam et al. [11], is potentially useful [10–18]. As a general approach to approximating the Bayesian solution, the CKF has gained increasing interest in the development of nonlinear Bayesian filters. The spherical-radial cubature rule employed in CKF is a special case of the quadrature rules involved in UKF. The CKF is in general considered to be more accurate and stable than the UKF without additional tuning on parameters in nonlinear filtering realization and has been used in many engineering applications [10,15]. The standard CKF utilizes a third-degree spherical-radial cubature rule to solve the integration in Bayesian filtering problem for numerically computing the multivariate moment integrals encountered in the nonlinear filtering framework. It is based on the spherical-radial transformation and generates an even number of equally weighted cubature points. In the spherical-radial cubature rule, the desired integral is composed of spherical and radial integrals, where the spherical integral is approximated using spherical cubature rule and the radial integral is approximated using the Gauss-Laguerre quadrature rule, respectively. CKE can be furtherly extended using numerical approximation methods providing a higher-order approximation to the spherical and radial integrals [16–18].
When the non-linearity and non-Gaussianity are highly prominent, the Kalman filter (KF)-type approaches (e.g., EKF, UKF and CKF discussed in this paper) assume the noise to be Gaussian distribution, which does not provide a good approximation to the posterior distribution. Proposed to approximate the posterior distribution of states through sequential importance sampling (SIS), the particle filter (PF) is a non-parametric filter and hence can easily deal with nonlinear and/or non-Gaussian state estimation [19–27]. However, the PF suffers from two problems: sample degeneracy and impoverishment. Since the traditional PF adopts the state transition prior distribution function which is lack of measurement information as an importance density function to approximate the posterior density function. There is a great deviation between the samples from the importance of sampling density and the true posterior probability density, which can lead to degeneracy phenomenon and possibly filter divergence [21,23]. To solve the degeneracy problem, one strategy is to choose the proper proposal distribution that can approximate the posterior distribution reasonably well. The particle filter-based approaches, including the extended particle filter (EPF) and unscented particle filter (UPF) were proposed for which the EKF and UKF, respectively, were used to generate the proposal distributions. Their combination has demonstrated improved performance in terms of accuracy and robustness. However, it suffers from the computational load and numerical instability. For improving the estimation accuracy and filtering performance, a novel version of PF, referred to as the cubature particle filter (CPF) was proposed. In the CPF, the CKF is used to generate the proposal distribution for acquiring a maximum a posteriori probability estimate of the nonlinear system, and the importance density function can approximate the true posterior density distribution. The use of the importance proposal distribution integrates the latest observation into system state transition density, so as to properly match the posteriori density. Performance comparison for the CPF, UPF, and EPF approaches had been presented in the literatures, e.g., [28–30].
This paper is organized as follows. In Section 2, preliminary background on the Kalman filter-type approaches is briefly reviewed and successively presents the Bayesian solution for nonlinear/non-Gaussian state estimation problems. The various types of particle filters including the EPF, UPF and CPF are discussed in Section 3. In Section 4, two illustrative examples are presented for assessment of nonlinear/non-Gaussian state estimation capabilities using the CPF algorithm in comparison to those by to the relatively conventional approaches. Conclusions are given in Section 5.
2 The Kalman Filter-Type Approaches
The well-known KF is an optimal closed-form solution in linear systems with Gaussian process and measurement noises. In nonlinear systems, the optimal estimation solution to the recursive Bayesian filtering problem is infinite dimensional and computationally intractable. The most widely used approximate nonlinear filter is the EKF.
The nonlinear system governed by the stochastic difference equations can be written as:
where the state vector 
, process noise vector 
, measurement vector 
, and measurement noise vector 
. The vectors 
and 
are zero mean Gaussian white sequences having zero cross-correlation with each other:
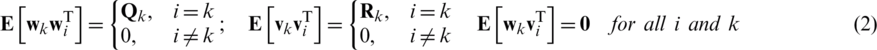
where 
is the process noise covariance matrix, 
is the measurement noise covariance matrix.
From the Bayesian perspective, the state estimation problem is required to construct the probability density function 
, given the measurement 
up to time k. Then, the 
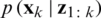may be obtained recursively in two steps, namely, (1) time update based on Eqs. (3a); and (2) measurement update based on Eq. (3b).
These equations can be derived using the Markov property and Bayes’ rule from probability theory.
2.1 The Extended Kaman Filter and Unscented Kalman Filter
The EKF is an approximate nonlinear filter which linearizes the dynamic system and measurement equations about a single sample point with the assumption that the a priori distributions are Gaussian. The state distribution of the EKF is approximated by a Gaussian random variable (GRV), which is then propagated analytically through the linearization of the nonlinear system. The EKF might suffer from the performance degradation and divergence problem due to the linearization process for the system nonlinearity. To better treat the nonlinearity, other filters such as the UKF were proposed. Unlike the EKF with first-order accuracy where the linearization process using the Jacobian matrices is involved, the UKF employs a minimal set of sigma points (weighted samples) by deterministic sampling approach and at least the second order accuracy of the posterior mean and covariance can be captured.
Consider an n dimensional random variable 
, having the mean 
and covariance 
, and suppose that it propagates through an arbitrary nonlinear function 
. The UT creates 2n + 1 sigma vectors 
(a capital letter) and weighted points W, given by
where 
is the i th row of the matrix square root. 
can be obtained from the lower-triangular matrix of the Cholesky factorization; 
is a scaling parameter; 
determines the spread of the sigma points around 
; 
is a secondly scaling parameter; 
is used to incorporate prior knowledge of the distribution of 
. 
is the weight for the mean associated with the ith point; and 
is the weigh for the covariance associated with the ith point, as follows:
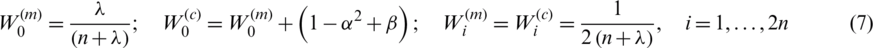
The first step in the UKF is to sample the prior state distribution by generating the sigma points through the UT. A set of weighted samples (sigma points) are deterministically chosen to adequately capture the true mean and covariance of the random variable. The basic premise is that to approximate a probability distribution is easier than to approximate an arbitrary nonlinear transformation. The samples are propagated through true nonlinear equations, and the linearization of the model is not required. The UKF requires less computational cost due to deterministic sampling of the sigma points as opposed to the randomly generated particles in the particle filter. Appendix A provides the algorithm for implementation of the UKF.
Not guaranteed always to be positive definite, the decomposition of the covariance matrix in the UKF is sometimes unavailable. Proposed by Arasaratnam et al. [11], the CKF is a general approach to approximate the Bayesian solution. The CKF is another type of nonlinear filtering approach without linearization of the nonlinear model. To develop the CKF, it is assumed that the predictive density of the joint state-measurement random variable is Gaussian. The CKF uses cubature points with the same weights through spherical-radial criterion, which employs analytical probability density function to capture the mean and covariance of the posterior distribution using the total probability theorem and subsequently uses the measurement to update with Bayes’ rule.
From the perspective of numerical analysis, the third-degree spherical-radial cubature rule can be viewed as an UT of special form with better numerical stability. The CKF is known as the approximate filter in the sense of completely preserving second-order information due to the maximum entropy principle and thus provides an efficient solution even for high-dimensional nonlinear filtering problems. For improving numerical accuracy in nonlinear system, the CKF is reformulated to propagate the square roots of the error-covariance matrices, and hence it avoids computing numerically sensitive matrix calculations. In contrast to UKF, the CKF follows directly from the cubature rule for numerically computing Gaussian-weighted integrals whose important property is that it does not entail any free parameters, whereas the UKF introduces a nonzero scaling parameter.
The CKF algorithm involves the following stages: Firstly, it approximates the mean and variance of the probability distribution through a set of 2n (where n is the dimension of the system model) cubature points with the same weight, propagates the cubature points through the nonlinear functions, and then calculates the mean and variance of the current approximate Gaussian distribution by the propagated cubature points. A set of 2n cubature points are given by 
, where 
is the ith cubature point and wi is the corresponding weight:
where 
denotes the ith column vector of the identity matrix 
.
The CKF also involves a two stage procedure comprising of prediction step and update step. Under the assumption that the posterior density at time k −1 is known, the steps involved in the time and measurement updates of the CKF are summarized in Appendix B. Although the CKF solves the nonlinear approximation issue in a different way from UKF and EKF, it does not sufficiently provide tolerance to the non-Gaussian estimation problem. Development of robust demand for non-Gaussian Bayesian filtering framework is sometimes required.
3 The Particle Filter-Based Approaches
In contrast to KF-type approaches, the PF was presented for handling multimodal probability density functions and solving nonlinear non-Gaussian problems [24,25]. It is a sequential importance sampling method based on Monte Carlo simulation and Bayesian estimation theory. The Monte Carlo simulation technique is employed to approximate the non-Gaussian probability distribution through a set of weighted samples called particles around the mean and covariance of Gaussian random variable. Three important steps are involved for implementation of the PF: (1) Sampling current value of each particle; (2) Evaluation of the recursive important weights and (3) Resampling. The simulated particles are propagated through the nonlinear system model yielding the prior probabilistic density which works as an importance density function. Thereafter, the observation probability density function obtained from the predicted particles through the nonlinear observation model is used to update the importance density particles. Finally, a resampling step is applied to remove the samples with low weights and the posterior probability is redistributed according to the new selected weights.
3.1 The Generic Particle Filter
The sequential importance sampling (SIS) is one of the methods which enable the Bayesian estimation by Monte Carlo simulation. The principle of SIS uses the samples with weights to approximate the posterior 
. When the number of samples is infinite, the approximation approaches the true posterior density. The basic idea is to represent the required posterior density function by a set of random samples with associated weights and to compute estimates based on these samples and weights.
Let 
denote a random measure that characterizes the joint posterior pdf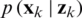 
. Here 
is the particles with weights 
, which are normalized such that 
. At time step k, the posterior density can be approximated as
The recursive estimate for the importance weights of particle i can be derived through:
where 
is the likelihood function of the measurements 
, 
is the prior and 
is the importance density. After normalizing the importance weights:
the estimated state vector can then be approximated by
In general, the PF relies on the sequential importance sampling and requires the design of proposal distributions used to approximate the posterior distribution reasonably well. As can be seen from Eqs. (10) and (11), PF involves recursive propagation of the weights and support points as each measurement is received sequentially. Degeneracy problem is a common problem which may degrade the accuracy of state estimation in the generic PF. One of the strategies to avoid the degeneracy phenomenon of the particles is to increase the number of samples (i.e., particles) at the expense of larger computational burden devoted. Furthermore, it is difficult to determine the best number of particles. As an effective way to suppress degeneracy, the resampling process is added on the basis of importance sampling to eliminate the particle with low weight and remain the particle with high weight.
3.2 The Extended Particle Filter and Unscented Particle Filter
The importance density function is used in the SIS scheme, where the transition prior does not take into consideration the most recent measurement data 
. Consequently, deficiency may arise in particle filters, especially when there is little overlap between the importance density function and the posterior pdf 
. To avoid this problem that may arise from using the transition prior as the importance density function, the filter needs to incorporate the latest measurement data into it. As for the resampling scheme, there are several selections currently employed, such as multinomial resampling, residual resampling and systematic resampling. In the systematic resampling method, the importance weights of the particles will be updated through resampling. In the classical resampling framework, the particles can be generated by EKF or UKF, respectively, for proposal distribution generation within a particle filter framework, referred to as the EPF and UPF, respectively. The basic idea is to use a separate EKF/UKF to generate and propagate a Gaussian importance distribution for each particle:
where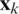 
and 
are estimates of the mean and covariance computed by EKF or UKF at time k using measurement 
. The UKF-based importance density tends to move the particles 
towards the high-likelihood regions by producing new particles 
with included knowledge about the latest observation.
It should be noticed that the EKF tends to underestimates the true covariance of the state in highly nonlinear systems. This violates the distribution support requirement for the proposal distribution and may lead to poor performance and even filter divergence. It provides a good alternative for propagating the mean and covariance of the Gaussian approximation to the state distribution.
3.3 The Cubature Particle Filter
The CPF introduces the CKF into the PF framework for generating the importance density function, so as to closely match the true posterior density by integrating the latest observation information. In other words, the CPF considers the recent measurement, such as the recent capacity degradation data, to iteratively update the weights of the random particles used in the PF framework.
To construct the proposed distribution function of the PF, the CPF uses the current measurement information and cubature points to calculate the mean and the variance of the nonlinear random function directly by setting a defined group of sample points and corresponding weights. Theoretically, The CPF requires fewer cubature points than the UPF when generating the importance proposal distribution, thus requires less computational overheads. Furthermore, the CPF uses the square root of the error covariance for iterating and possesses better stability and accuracy performance. Implementation algorithm for the PF-based approaches: EPF, UPF, and CPF, is provided in Appendix C.
4 Performance Evaluation and Discussion
To assess the efficiency of the state estimation using the CPF algorithm in comparison with those of UPF, EPF and KF-type approaches, two illustrative examples are adopted for demonstrating the effectiveness under nonlinear/non-Gaussian environments. The two examples presented includes the univariate nonstationary growth model (UNGM) and the ballistic target tracking. Both have significant nonlinearity and have been extensively investigated in the literature as the benchmark problems [7,8,10,26]. The root-mean-square error (RMSE) metrics is used to perform the performance comparison of KF-type approaches and PF-based approaches.
4.1 Example 1-Univariate Nonstationary Growth Model
The UNGM is important in econometrics and has been used as a benchmark for validating and comparing nonlinear filters. Its high nonlinearity and bimodality makes filtering a difficult task. The UNGM dynamic process model is given by
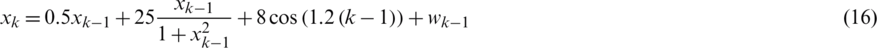
and the measurement equation is
where the process noise wk −1 is a zero mean Gaussian random variable with variance 
. The likelihood 
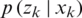has bimodal nature when zk > 0 and unimodal when zk < 0. The bimodality makes the problem more difficult to address using traditional methods. Then, vk is the zero-mean random error that represents the probability density function (pdf) 
. It is assumed that the measurement noise follows a Gaussian mixture distribution with pdf of the form
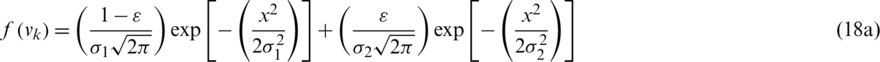
or equivalently,
where 
and 
are the standard deviations of the individual Gaussian distributions, and 
is a perturbing parameter that represents error model contamination. In order to demonstrate the validity of the performance of the nonlinear filtering based methods in non-Gaussian distributions, the perturbed conditions 
(i.e., with 70% contamination), and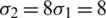 
have been used. The initial conditions were 
, 
. The parameters utilized are 
, 
, 
in the UKF. The reference data were generated using x0 = 0.1 and the total number of measurements N = 500, the total number of Monte Carlo simulation runs is 60. Fig. 1 shows the two Gaussian pdf’s employed to generate the measurement errors for Example 1.
Figure 1: The two Gaussian pdf’s employed to generate the Gaussian mixture model used in the measurement errors—Example 1
Fig. 2 provides the absolute error based on EKF, UKF, and CKF, respectively, for Example 1. Fig. 3 shows the RMSE of KF-type approaches across each of the 60 Monte Carlo runs. As can be seen, the CKF outperforms the other two filters, because the third-degree spherical-radial cubature rule provides stability against deviations from Gaussian distribution assumption. The estimation accuracy of the CKF depends on what third-degree cubature rule is used based on numerical integration method to approximate the proposal distribution. The estimation errors of the KF-type approaches in term of nonlinear/non-Gaussian state estimation is summarized in the ascending order: 
.
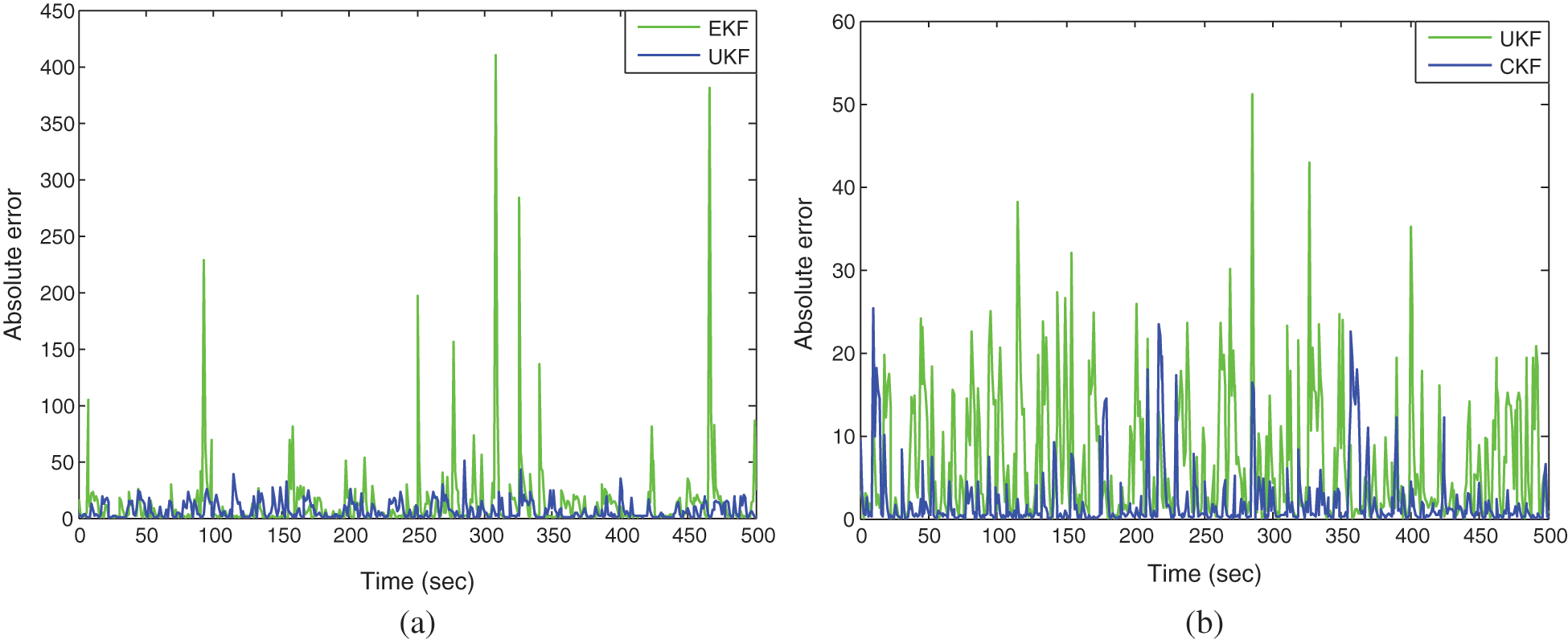
Figure 2: Estimation errors for the Kalman type-approaches, EKF, UKF, and CKF for Example 1: (a) EKF vs. UKF; (b) UKF vs. CKF
Figure 3: RMSE of the Kalman filter-type approaches across 60 random runs
Due to the errors induced by arithmetic operations performed on finite word-length computers, the basic properties of an error covariance matrix of UT, i.e., symmetry and positive definiteness, are not always guaranteed to hold. However, the cubature-based nonlinear filter essentially propagates the square-root of the predictive and posterior error covariance, which possesses the ability to preserve symmetry and positive definite, and thereby improves the numerical accuracy and stability. The result shows that the performance of CPF is superior to UPF solutions when same numbers of particles are used, since the proposal distribution based on CKF taken into approximate the true posterior distribution is more precise than UKF. The CKF is developed using the spherical-radial rule, which is more accurate than the Gaussian quadrature rule involved in UT.
4.2 Example 2: The Ballistic Target Re-Entry Problem
In the second example, application of the nonlinear filters to the target tracking problem using the range measurement is performed. The altitude, velocity and constant ballistic coefficient of a vertically falling body are estimated. The geometry for the ballistic target tracking using ground radar for the benchmark problem is illustrated in Fig. 4. The altitude of the body is measured at discrete-time instants using radar capable of measuring range contaminated by non-Gaussian noise.
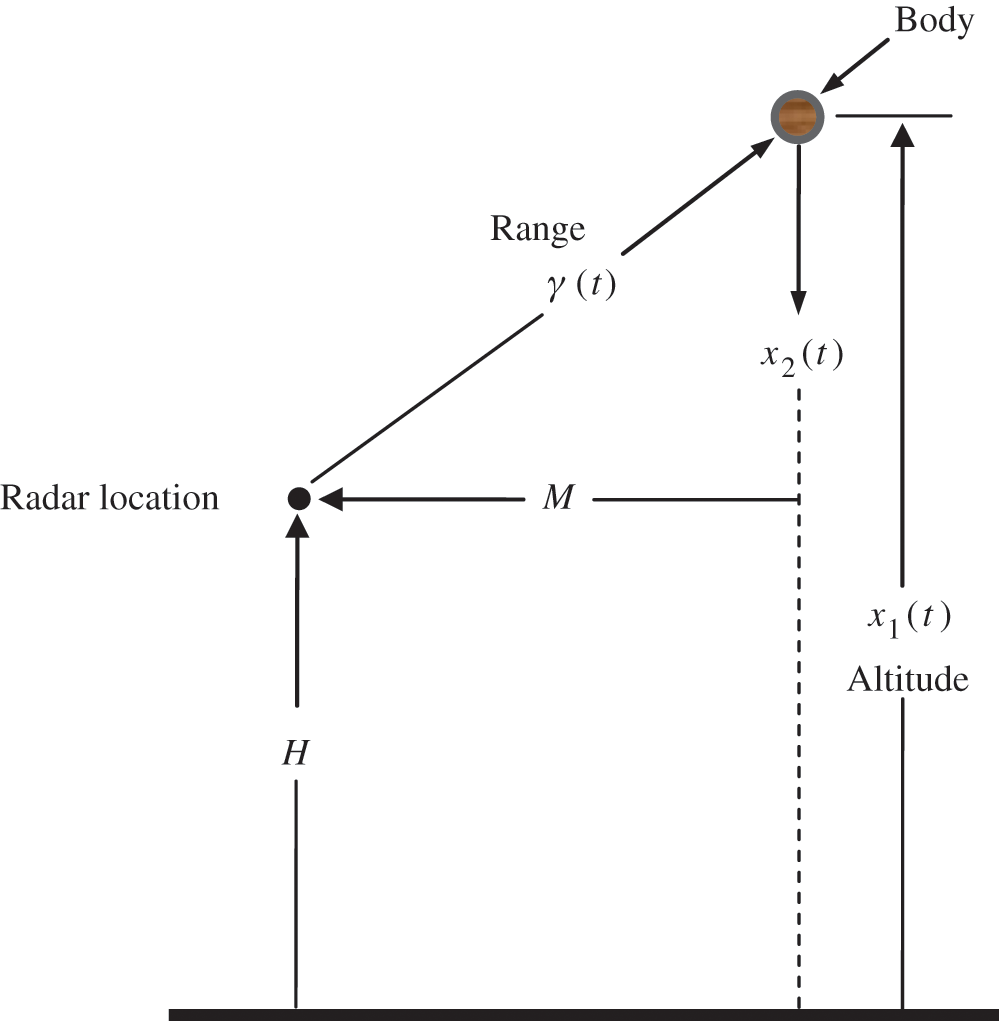
Figure 4: The geometry for ballistic target tracking using ground radar
The dynamic process model of this nonlinear system is given by
where the sequence 
is white and Gaussian with associated process noise covariance and 
relates the air density with altitude. The range measurement from the radar is given as
where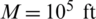 
is the horizontal range between the vertical body and radar and 
is the altitude of the radar. The measurement noise 
is assumed to follow a Gaussian mixture distribution of the form as in Eq (18). The parameters utilized are 
, 
, 
in the UKF. Fig. 5 shows the two Gaussian pdf’s employed to generate the Gaussian mixture model used in the measurement errors for Example 2. The true state at the initial time 
of the system was 
and the initial estimate is 
with covariance matrix.
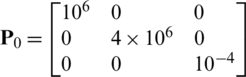
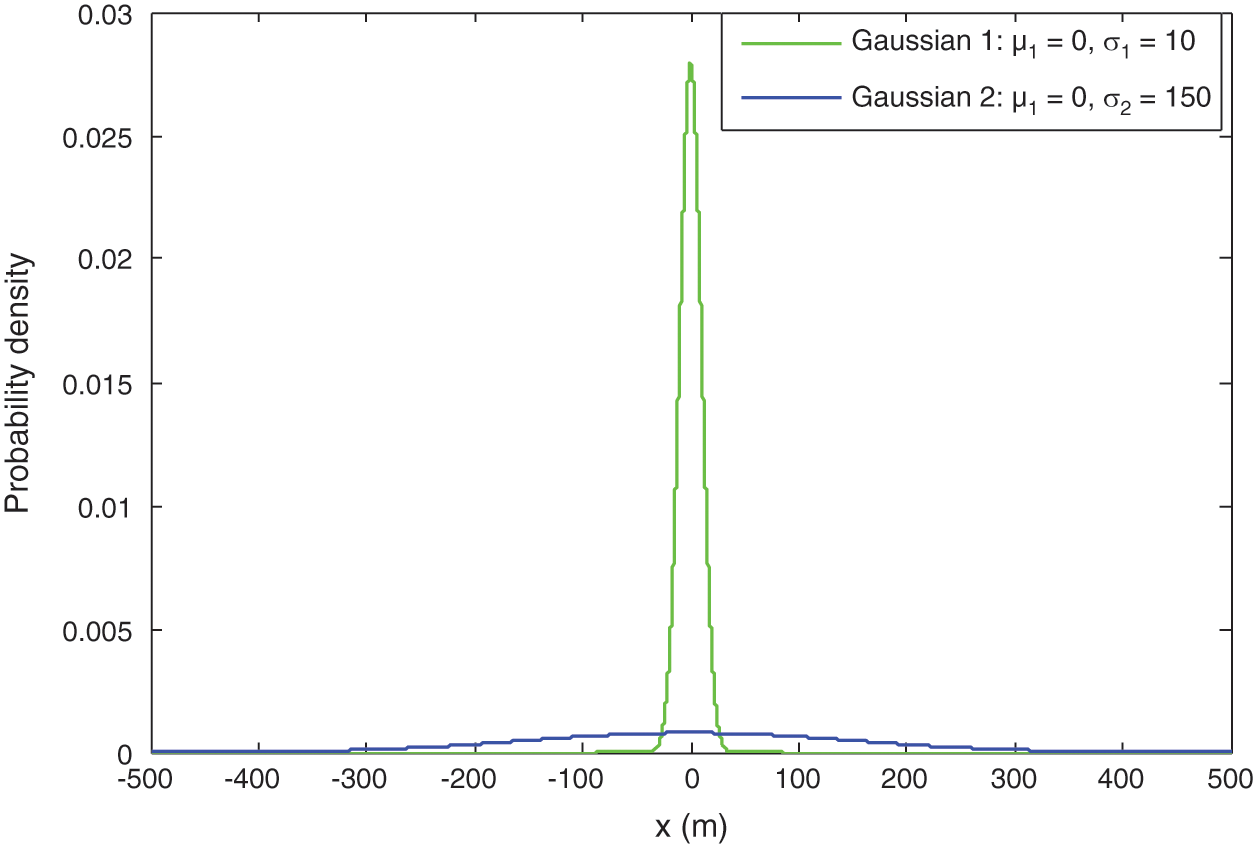
Figure 5: The two Gaussian pdf’s employed to generate the Gaussian mixture model used in the measurement errors—Example 2
The results are shown from Figs. 6 to 9. Prior to incorporation of the PF framework, the results for EKF, UKF and CKF are presented, shown in Fig. 6. The estimation accuracies based on the conventional nonlinear approaches: EKF, UKF and CKF are presented, shown as in Fig. 6, where the merits of the CKF have been shown. For all the three PF-based approaches, 100 particles were used. Fig. 7 shows the absolute error based on PF-based approaches. The CPF utilizes the 100 particles generated by the CKF employed for generating and propagating an importance density function. It can be seen that estimation accuracy was noticeably improved by using the PF-based approaches, i.e., the EPF, UPF and CPF. The results presented in the Fig. 7 indicate that the performance of the CPF algorithm is superior to the UPF and EPF in case that the same numbers of particles were used. This is due to the fact that the proposal distribution based on CKF possesses better accuracy than the UKF and EKF methods. Meanwhile, the square root of the variance for iterating in the CKF provides the merit of improved stability and accuracy.
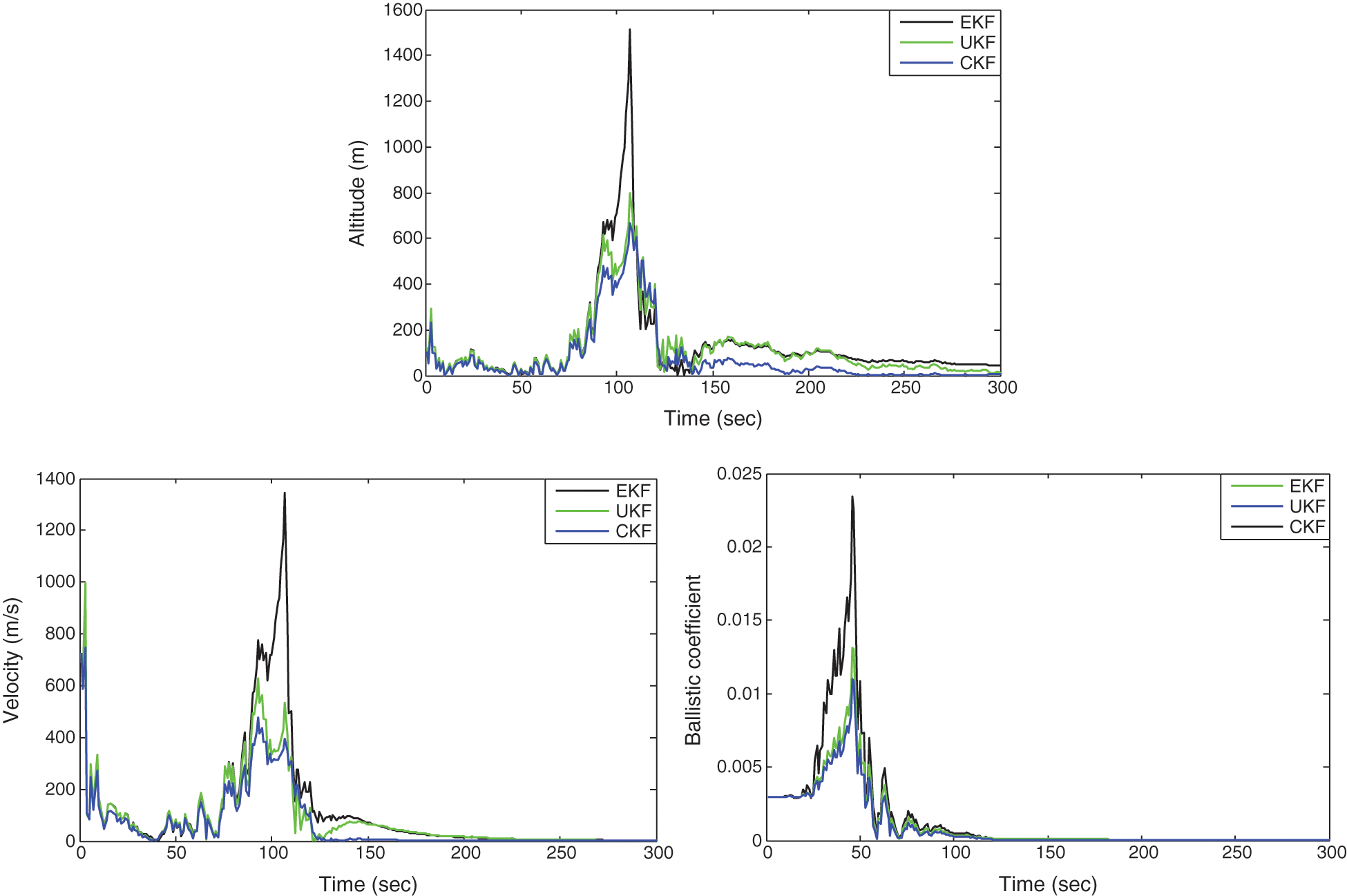
Figure 6: Estimation errors for the three KF-type approaches: EKF, UKF, and CKF
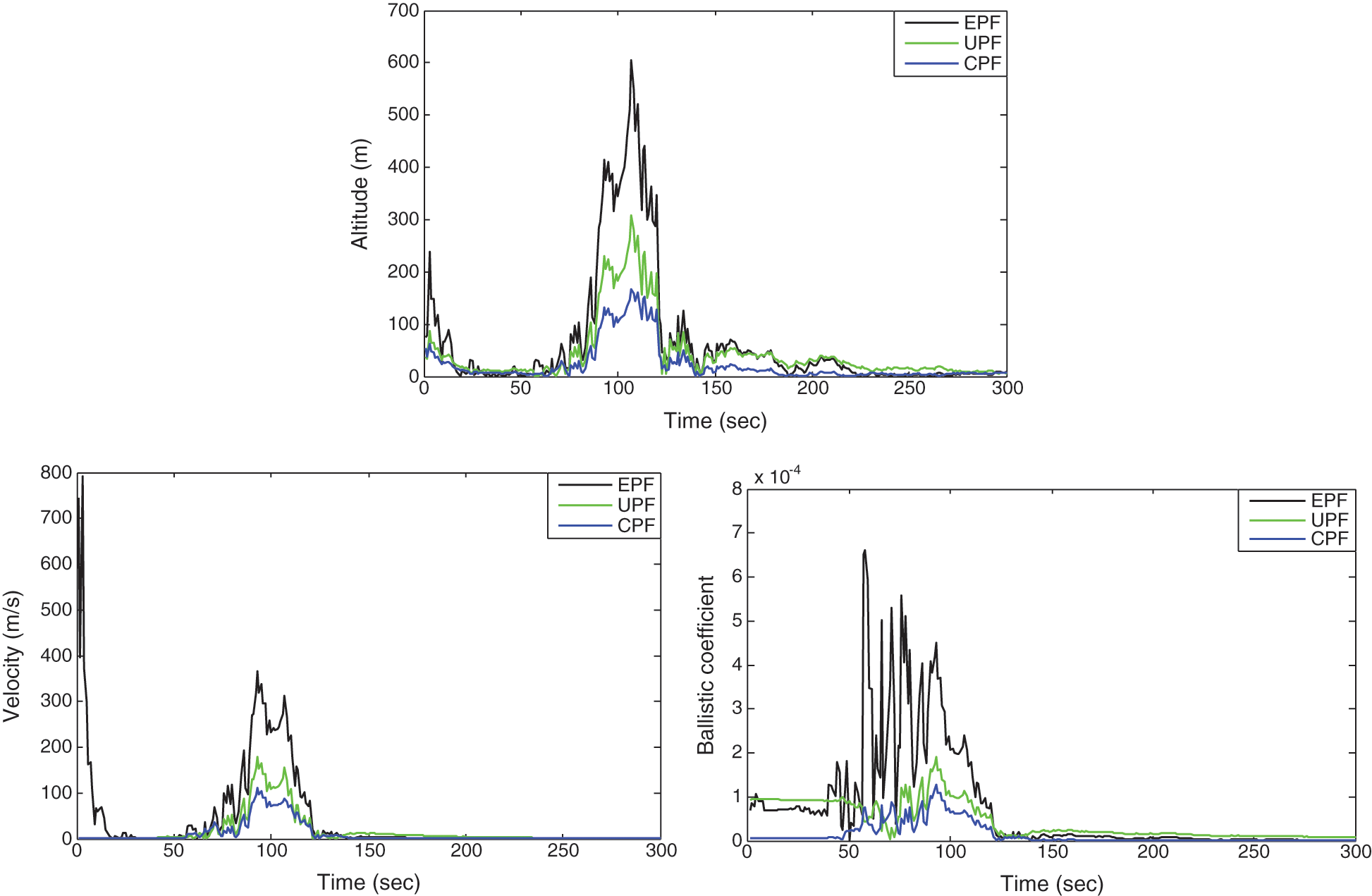
Figure 7: Estimation errors for the three PF-based approaches: EPF, UPF, and CPF
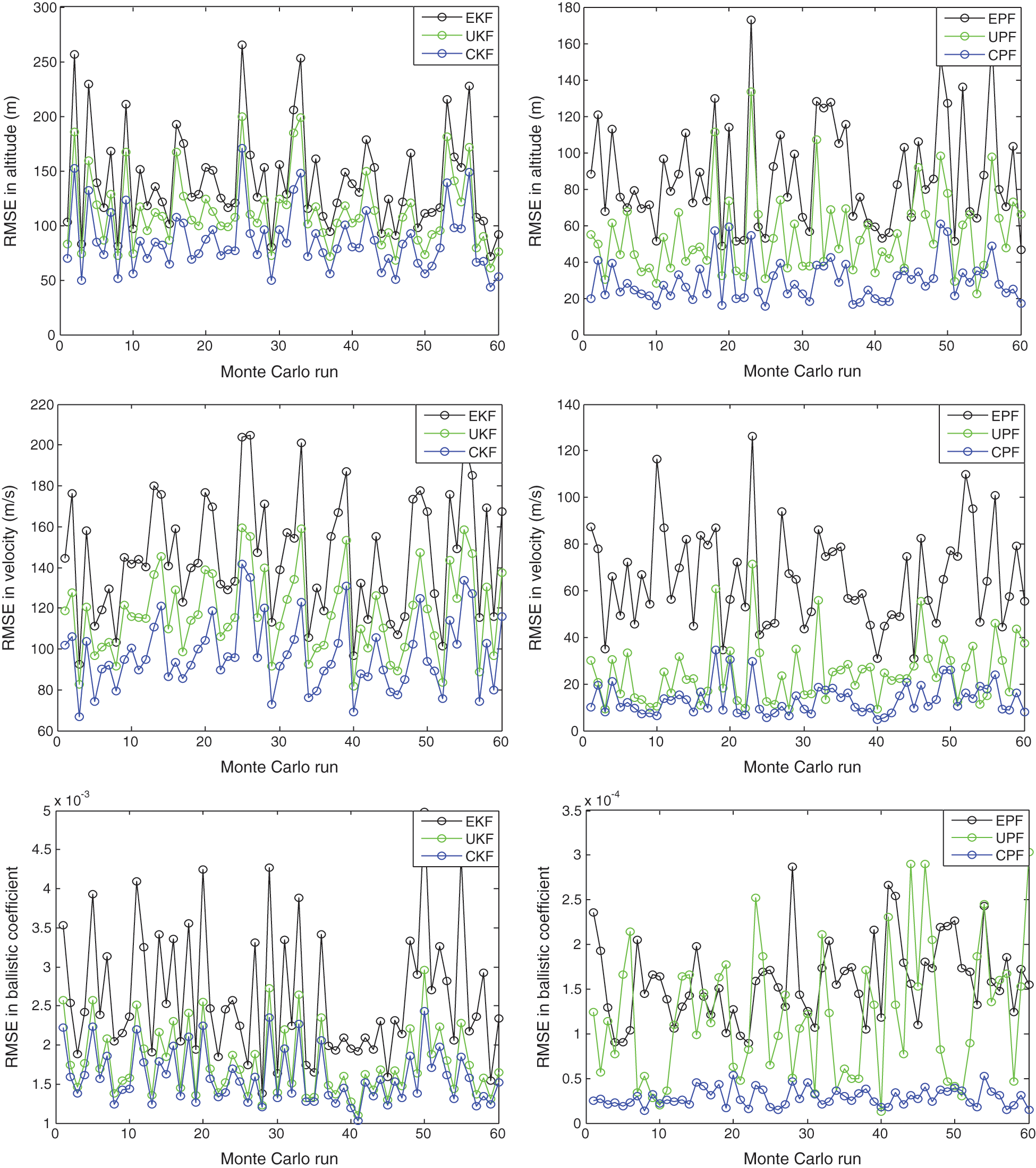
Figure 8: RMSEs for the two groups of filters across 60 random runs: KF-type approaches (3 subplots on the left side); PF-based approaches (3 subplots on the right side)
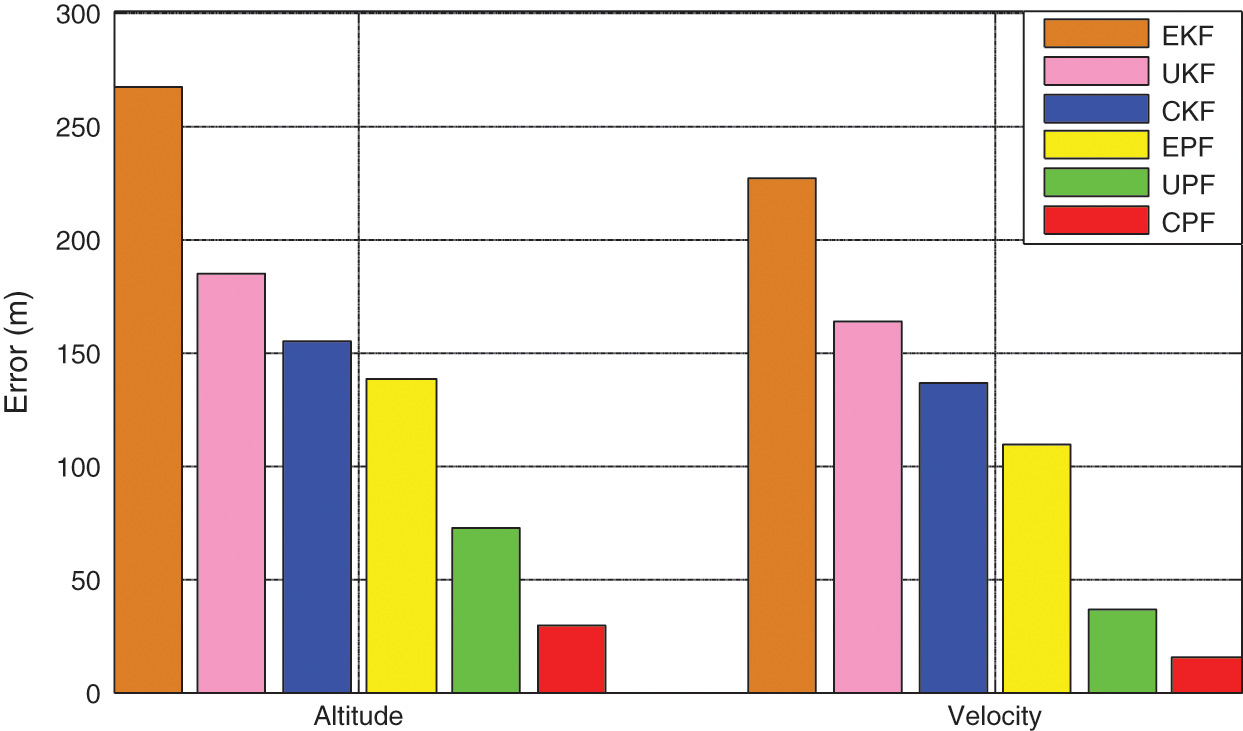
Figure 9: Comparison of altitude and velocity RMSE (in units of m and m/s, respectively) among filters
Fig. 8 presents the RMSE for the two groups of estimators across 60 Monte Carlo simulation runs. For constructing importance density function, the CPF algorithm takes the nonlinear/non-Gaussian state estimates of updated measurement as a reference and optimizes the proposed distribution to increase the diversity of effective particles through CKF-involved method. In general, using more particles produce better approximation to the true posterior distribution. A large number of particles are required to sample the high dimensional state space effectively, which increases the computational load, leading to poor real-time performance. The CPF algorithm used less cubature points than the UPF, and has less computational overheads. Tab. 1 summarizes the execution time of various approaches.
Table 1: Comparison of execution times for various filtering approaches
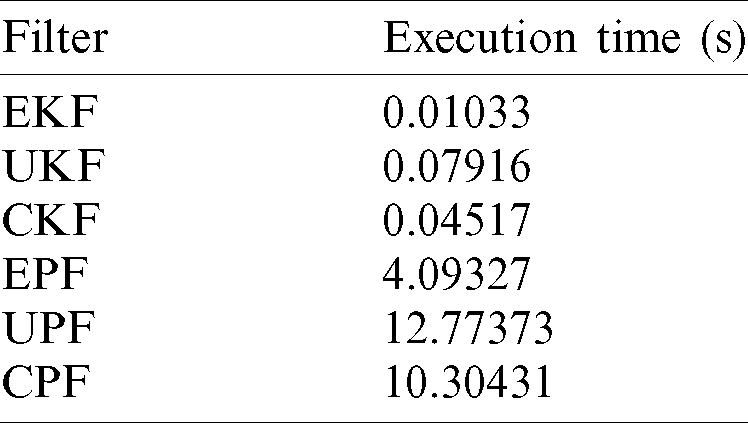
The CKF demonstrates noticeable improvement over the EKF and UKF while the EPF slightly outperforms the CKF. The particles degeneracy can be attributed to the measurement of highly non-Gaussian noise. The measurement noise should have a relatively heavy tail so that it is insensitive to the outliers. To determine the number of particles are important for the sequential importance sampling, which depends on the importance distribution of particles. Therefore, an importance density tuned for a particular problem will yield an appropriate trade-off between the number of particles and the estimation accuracy.
The UKF introduces a non-zero scaling parameter, which defines the non-zero center point and is often associated with a set of weighted samples higher than that of the minimal set of sigma points. The CKF follows directly from the spherical-radial cubature rule for numerically computing Gaussian-weighted integrals with the property without entailing free parameters. Although additional tuning on parameters in UKF provides flexibility, one can fix them as their default values or just exclude the center point and the CKF is automatically obtained, if bothering to tune them. The CKF in this work is based on the third-degree spherical-radial cubature rule to propagate the cubature points through the nonlinear functions, so as to solve the integration in Bayesian filtering problem for numerically computing the multivariate moment integrals, which are numerically computed by the spherical cubature rule and the Gaussian quadrature rule, respectively.
The filtering performance of the PF-based approaches (namely CPF, UPF and EPF) outperforms the KF-type approaches (namely CKF, UKF, and EKF) due to consideration of the latest observations. Fig. 9 presents comparisons of altitude and velocity RMSE among six filters, showing that the corresponding estimation errors are in the following ascending order: 
. The CPF algorithm outperforms the other nonlinear filters. The result shows that when the measurements are contaminated with non-Gaussian errors, the CKF can adequately capture the non-Gaussianity and demonstrate noticeably better performance. The performance of CPF is in general superior to UPF solutions when same numbers of particles used, since the proposal distribution based on CKF taken into approximate the true posterior distribution is more precise than UKF, without additional tuning on parameters. The results are based on numerical simulation and can be served as a general guide. These profound insights will be helpful for choosing the appropriate nonlinear filters in specific applications when certain trade-off is necessary.
This paper provides profound insight into the estimation performance of CPF for nonlinear/non-Gaussian processes. Assessment of the nonlinear filtering approaches to the nonlinear/non-Gaussian state estimation performance has been carried out. The CPF algorithm possesses the merits of the PF framework to handle non-Gaussian errors and the CKF can deal with the nonlinearity with better numerical stability to improve the estimation accuracy. In a CPF, the CKF is used to generate the importance proposal distribution of the PF. The CKF employs third-degree spherical-radial cubature rule to solve the integration in Bayesian filtering problem for numerically computing the multivariate moment integrals encountered. By integrating the latest observation information and approximating the posterior distribution, the CKF performance is improved. Furthermore, the CKF will facilitate selection of importance sampling in practice that is useful to effectively alleviate the degeneracy and impoverishment problems in the PF.
To improve the stability of the nonlinear filter, the CKF can effectively avoid round-off errors of numerical computation, and possesses better stability than the UKF and EKF. The spherical-radial cubature rule employed in CKF is a special case of the quadrature rules involved in UKF. Namely, if the parameters of the UPF are well-tuned, the estimation performance of the UPF and the CPF will be similar or identical. Although the CKF can be treated as a special case of the UKF, CKF is, in general, considered to be more accurate and stable than the UKF in nonlinear filtering realization without additional tuning on parameters as in the UKF. The result shows that the performance of CPF is superior to UPF solutions when same numbers of particles are used, since the proposal distribution based on CKF taken into approximate the true posterior distribution is more precise than UKF.
To assess the performance of various estimation algorithms, two illustrative examples are presented, especially for the cases under nonlinear/non-Gaussian environments. Performance comparisons on the KF-type approaches: EKF, UKF, CKF and PF-based approaches: EPF, UPF, CPF have been presented. Simulation results show that the CPF algorithm possesses superior performance than the KF-type approaches and other PF-based approaches, among which the CPF algorithm shows superior estimation accuracy with less computational cost than the UPF. The performance in terms of estimation accuracy, numerical stability and computational costs can be improved. Developed to deal with nonlinear and/or non-Gaussian distribution assumptions, the CPF algorithm possesses good potential as the alternative for the nonlinear and/or non-Gaussian state estimation.
Funding Statement: This work has been partially supported by the Ministry of Science and Technology, Taiwan [Grant No. MOST 108-2221-E-019-013].
Conflicts of Interest: The authors declare that they have no conflict of interest to report regarding the present study.
1. D. Simon. (2006). Optimal State Estimation: Kalman, H∞, and Nonlinear Approaches. Hoboken, NJ, USA: John Wiley & Sons Inc. [Google Scholar]
2. F. Daum. (2005). “Nonlinear filters: Beyond the Kalman filter,” IEEE Aerospace and Electronic Systems Magazine, vol. 20, no. 8, pp. 57–69. [Google Scholar]
3. G. Kitagawa and W. Gersch. (1996). Smoothness Priors Analysis of Time Series. New York, NY, USA: Springer-Verlag. [Google Scholar]
4. S. J. Julier, J. K. Uhlmann and H. F. Durrant-whyte. (1995). “A new approach for filtering nonlinear system,” in Proc. of the American Control Conf., Seattle, WA, USA, pp. 1628–1632. [Google Scholar]
5. S. J. Julier, J. K. Uhlmann and H. F. Durrant-whyte. (2000). “A new method for the nonlinear transformation of means and covariances in filters and estimators,” IEEE Transactions on Automatic Control, vol. 5, no. 3, pp. 477–482. [Google Scholar]
6. E. A. Wan and R. van der Merwe. (2001). “Chapter 7: The unscented Kalman filter,” in Kalman Filtering and Neural Networks, Simon Haykin (Ed.New York, NY, USA: John Wiley & Sons Inc. [Google Scholar]
7. Y. Zhou, C. Zhang, Y. Zhang and J. Zhang. (2015). “A new adaptive square-root unscented Kalman filter for nonlinear systems with additive noise,” International Journal of Aerospace Engineering, vol. 2015, no. 5, pp. 1–9. [Google Scholar]
8. B. Leela Kumari and K. Padma Raju. (2013). “Performance evaluation of unscented Kalman filter for Gaussian/non-Gaussian tracking application,” International Journal of Electrical and Computer Engineering, vol. 3, no. 1, pp. 93–101. [Google Scholar]
9. T. Zhou, B. Lian, S. Yang, Y. Zhang and Y. Liu. (2018). “Improved GNSS cooperation positioning algorithm for indoor localization,” Computers, Materials & Continua, vol. 56, no. 2, pp. 225–245. [Google Scholar]
10. Z. Ding and B. Balaji. (2012). “Comparison of the unscented and cubature Kalman filters for radar tracking applications,” in Proc. of the IET Int. Conf. on Radar Systems, Glasgow, UK, pp. 1–5. [Google Scholar]
11. I. Arasaratnam and S. Haykin. (2009). “Cubature Kalman Filters,” IEEE Transactions on Automatic Control, vol. 54, no. 6, pp. 1254–1269. [Google Scholar]
12. I. Arasaratnam, S. Haykin and T. R. Hurd. (2010). “Cubature Kalman filtering for continuous-discrete systems: Theory and simulations,” IEEE Transactions on Signal Processing, vol. 58, no. 10, pp. 4977–4993. [Google Scholar]
13. P. H. Leong, S. Arulampalam, T. A. Lamahewa and T. D. Abhayapala. (2013). “A Gaussian-sum based cubature Kalman filter for bearings-only tracking,” IEEE Transactions on Aerospace and Electronic Systems, vol. 49, no. 2, pp. 1161–1176. [Google Scholar]
14. X. C. Zhang and Y. L. Teng. (2014). “A new derivation of the cubature Kalman filters,” Asian Journal of Control, vol. 16, no. 5, pp. 1501–1510. [Google Scholar]
15. W. Li and Y. Jia. (2012). “Location of mobile station with maneuvers using an IMM-based cubature Kalman filter,” IEEE Transactions on Industrial Electronics, vol. 59, no. 11, pp. 4338–4348. [Google Scholar]
16. B. Jia, M. Xin and Y. Cheng. (2012). “The high-degree cubature Kalman filter,” in Proc. of the 51st IEEE Conf. on Decision and Control, Maui, HI, USA, pp. 4095–4100. [Google Scholar]
17. A. Singh. (2020). “Szego quadrature kalman filter for oscillatory systems,” IEEE Access, vol. 8, pp. 194700–194708. [Google Scholar]
18. Y. Nie and T. Zhang. (2018). “Some relations between unscented and cubature Kalman filters,” in Proc. of the 30th Chinese Control and Decision Conf., Glasgow, UK, pp. 6120–6124. [Google Scholar]
19. A. Doucet, S. J. Godsill and C. Andrieu. (2000). “On sequential Monte Carlo sampling methods for Bayesian filtering,” Statistics and Computing, vol. 10, no. 3, pp. 197–208. [Google Scholar]
20. N. J. Gordon, D. J. Salmond and A. F. M. Smith. (1993). “Novel approach to nonlinear/non-Gaussian Bayesian state estimation,” IEE Proceedings F-Radar and Signal Processing, vol. 140, no. 2, pp. 107–113. [Google Scholar]
21. S. Y. Cheng and J. Y. Zhang. (2008). “Review on particle filters,” Journal of Astronautics, vol. 29, no. 4, pp. 1099–1111. [Google Scholar]
22. N. Gordon, B. Ristic and S. Arulampalam. (2004). Beyond the Kalman Filter: Particle Filter for Tracking Applications. Boston, MA, USA: Artech House. [Google Scholar]
23. T. Li, S. Sun, T. P. Sattar and J. M. Corchado. (2014). “Fight sample degeneracy and impoverishment in particle filters: A review of intelligent approaches,” Expert Systems with Applications, vol. 41, no. 8, pp. 3944–3954. [Google Scholar]
24. J. Wang, Y. Jin, D. Dai, H. Dong and T. Quan. (2007). “Particle filter initialization in non-linear non-Gaussian radar target tracking,” Journal of Systems Engineering and Electronics, vol. 18, no. 3, pp. 491–496. [Google Scholar]
25. T. Schon, F. Gustafsson and P. J. Nordlund. (2005). “Marginalized particle filters for mixed linear/nonlinear state-space models,” IEEE Transactions on Signal Processing, vol. 53, no. 7, pp. 2279–2289. [Google Scholar]
26. M. S. Arulampalam, S. Maksell, N. Gordon and T. Clapp. (2002). “A tutorial of particle filters for online nonlinear/non-Gaussian Bayesian tracking,” IEEE Transactions on Signal Processing, vol. 50, no. 2, pp. 174–188. [Google Scholar]
27. J. H. Kotecha and P. M. Djuric. (2003). “Gaussian particle filtering,” IEEE Transactions on Signal Processing, vol. 51, no. 10, pp. 2592–2601. [Google Scholar]
28. G. Shan, H. Chen, B. Ji and K. Zhang. (2013). “Cubature Kalman particle filters,” in Proc. of the 2nd Int. Conf. on Computer Science and Electronics Engineering, Hangzhou, China, pp. 456–460. [Google Scholar]
29. J. Mu and Y. Cai. (2016). “Cubature particle filter with MCMC and applications to re-entry ballistic target tracking,” IACSIT International Journal of Engineering and Technology, vol. 8, no. 1, pp. 65–69. [Google Scholar]
30. B. Xia, Z. Sun, R. Zhang, D. Cui, Z. Lao et al. (2017). , “A comparative study of three improved algorithms based on particle filter algorithms in SOC estimation of Lithium ion batteries,” Energies, vol. 10, pp. 1149. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |