DOI:10.32604/cmc.2021.015565
| Computers, Materials & Continua DOI:10.32604/cmc.2021.015565 | |
| Article |
A New Metaheuristic Optimization Algorithms for Brushless Direct Current Wheel Motor Design Problem
1Department of Electrical and Electronics Engineering, GMR Institute of Technology, Rajam, 532127, India
2Department of Electrical and Electronics Engineering, National Institute of Technology, Tiruchirappalli, 620015, India
3Rajasthan Rajya Vidyut Prasaran Nigam, Sikar, 305001, India
4Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Aldawaser, 11991, Saudi Arabia
5Systems Engineering Department, King Fahd University of Petroleum & Minerals, Dhahran, Saudi Arabia
*Corresponding Author: Kottakkaran Sooppy Nisar. Email: n.sooppy@psau.edu.sa
Received: 08 November 2020; Accepted: 18 December 2020
Abstract: The Equilibrium Optimizer (EO), Grey Wolf Optimizer (GWO), and Whale Optimizer (WO) algorithms are being recently developed for engineering optimization problems. In this paper, the EO, GWO, and WO algorithms are applied individually for a brushless direct current (BLDC) design optimization problem. The EO algorithm is inspired by the models utilized to find the system’s dynamic state and equilibrium state. The GWO and WO algorithms are inspired by the hunting behavior of the wolf and the whale, respectively. The primary purpose of any optimization technique is to find the optimal configuration by maximizing motor efficiency and/or minimizing the total mass. Therefore, two objective functions are being used to achieve these objectives. The first refers to a design with high power output and efficiency. The second is a constraint imposed by the reality that the motor is built into the wheel of the vehicle and, therefore, a lightweight is needed. The EO, GWO, and WOA algorithms are then utilized to optimize the BLDC motor’s design variables to minimize the motor’s total mass or maximize the motor efficiency by simultaneously satisfying the six inequality constraints. The simulation is carried out using MATLAB simulation software, and the simulation results prove the dominance of the proposed algorithms. This paper also suggests an efficient method from the proposed three methods for the BLDC motor design optimization problem.
Keywords: BLDC motor; constrained; equilibrium optimizer; single-objective optimization
A DC motor is an electrical machine that transforms direct current electrical energy into mechanical energy. The popular forms depend on the magnetic field forces that produce. The BLDC motors have been implemented for practical applications due to their features, such as more efficient, less noisy operation, and more output power. An integrated inverter or switching power supply is used to power the BLDC motors with a DC electric source, which generates AC power to power the motor. In real-time applications, such as computers, automotive applications, and electronics, they have been used successfully [1,2]. They are more powerful and lighter than conventional motors with equal power output, and they also need low maintenance because the carbon brushes are not required. Furthermore, due to their capacity in the torque and speed field [3,4], they are more flexible. A wheel motor that propels a solar vehicle during a race is the motor presented in this paper. The cost during production and the materials is unnecessary, while the main points are motor mass and efficiency [5]. In this paper, a BLDC motor analytical model is utilized as a benchmark consisting mainly of 78 non-linear equations, and it has been applied with six limitations of inequality and five design variables [5]. In other words, five parameters are calculated by the design process to minimize the total mass or to maximize efficiency and meet six inequality constraints simultaneously. Therefore, a more sophisticated optimization algorithm is necessary to accomplish these artifacts.
The Lagrange multipliers and the Lagrangian function could be used in an improved manner to optimization problems that have equality constraints. It allows you to find the maximum or minimum of a multi-objective function whenever the input parameters are constrained. The reality that Lagrange multiplier approaches are not always complex enables numerical optimization difficult. This can be dealt with by measuring the gradient magnitude since the magnitude zeros must be local minima. The downside of this method is however that it falsely expands the problem’s dimension [6]. To handle this difficulty, constrained optimization problems are also solved without Lagrange multipliers. The authors of [7] presented few asymptotic techniques for the discrete solutions of nonlinear fractional differential equations and nonlinear differential-difference equations. The approaches, such as ancient Chinese mathematics, Yang–Fourier transform, Yang–Laplace transform, parameter-expansion method, and the Hamiltonian are considered to solve the constrained optimization problems. However, to deal with the real-world constraint multi-objective optimization problems, a sophisticated optimization technique is required.
Recently, evolutionary optimization techniques have been used extensively in real-world engineering optimization problems, including mechanical engineering, electrical engineering, thermal engineering, etc. [8–11]. The reason for this popularity is because of two essential features of these evolutionary algorithms. The evolutionary algorithms start with the random initial results, and the initial solution is enhanced to obtain the optimal solutions. For instance, differential evolutionary (DE) [12], particle swarm optimization (PSO) [13], genetic algorithm [14], teaching-learning algorithm [15], etc., are the important evolutionary techniques that are widely used in the electromagnetic fields. The operators of these algorithms and few modifications in the basic version are presented to improve the solution accuracy, and these modified versions are claiming superior performance than their basic versions. For instance, modified PSO [16], adaptive DE [17], Krill herd algorithm [18], imperialist competitive algorithm, etc., are some of the modified versions. To solve multi-target optimization problems, it can also be expanded [19–22]. The optimal solutions for multi-target optimization problems are a group of non-dominated solutions by best convergence between two or three objective functions situated in a curve known as the Pareto front. In recent years, bio-inspired or nature-inspired algorithms, such as Grey Wolf Optimizer (GWO), Whale Optimizer (WO), Equilibrium Optimizer (EO), salp swarm optimization, flower pollination, Ant Colony Optimization (ACO), artificial bee colony optimization algorithm, Bat Algorithm (BA), etc. are reported in various literature to solve real-world engineering problems [23]. However, GWO, WO, EO algorithms are not utilized to solve the BLDC motor design optimization problem due to its freshness. Five design variables should be adjusted for the BLDC motor optimization problem to achieve an acceptable trade-off between efficiency and total motor mass.
In this paper, the optimized values of the motor’s design variables, which satisfies the design settings, can be achieved by a recent single-objective algorithm and applied to the empirical model of BLDC motors. There are two main objectives for the design optimization problem of the BLDC motor: minimization of total mass and maximization of efficiency. To deal with these multi-objective problems, multi-objective algorithms are required; however, a single-objective algorithm is used due to its computation complexity and implementation complexity. But the objective functions are handled separately to discover the optimal variables of the BLDC motor.
The remainder of the paper is organized as follows. Section 2 presents the problem formulation of the BLDC motor design optimization problem. Section 3 discusses the basic versions of EO, GWO, and WO and their application in the BLDC motor optimization problem. The simulation results are discussed in Section 4, and finally, Section 5 concludes the paper.
The BLDC motors are beneficial to conventional DC motors because they are highly powerful and need low maintenance because they do not have any brushes to carry the current. They are also more flexible, primarily due to their torque and speed capabilities. Built on the compact kit of BLDC motors, they are used in various computer and automotive applications [24]. The BLDC motors are the typical and commonly tested application and have many findings to compare in this context. Few researchers discuss the shape optimization through the surface response method [25] or the multi-target increase in torque and reduction in cogging torque as aims through a genetic algorithm [26] or Equivalent Circuit Network Method [27].
The MATLAB model is required that can be selected from [28] for analysis when 78 non-linear equations with five design variables subjected to six inequality constraints are introduced for optimization in single-objective, or with 5 constraints in multiple objectives. The mathematical model of this problem can be seen in [5]. From [5], a benchmark for the BLDC wheel motor was accessible, and the MATLAB source code is also publicly accessible for computing the objective function, as discussed. The BLDC wheel motor’s design problems have an objective, such as minimizing total mass and maximizing efficiency with five decision/design variables: airgap magnetic induction, Be, stator bore diameter, Ds, both teeth magnetic induction, Bd, and stator back iron induction, Bcs, and conductor’s current density,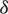 
. And, there are six inequality constraints, such as external diameter, 
, internal diameter, 
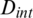, total mass, 
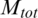, temperature, Ta, the maximum magnetizing current, 
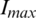, and lastly, Discr is a determinant utilized in slot height calculation, and this is depending on five design variables. The total mass of the motor should not outdo 15 kg, the external diameter must be less than 340 mm, such that the motor fits into the wheel rim, the internal diameter should be greater than 76 mm, the magnets must be assisted without demagnetization by a current of 125 A, and the magnet temperature must be less than 120
C. Fig. 1 illustrates the geometry of the BLDC wheel motor. Tab. 1 displays the design variables, definitions, and ranges. The six inequality constraints and their description, linked to operational, technical, and motor considerations, are presented in Tab. 2.
Figure 1: Structure of the BLDC wheel motor [5]
Table 1: Design variables and their boundaries
Table 2: Six inequality constraints
Two objective functions for the BLDC motor design problem is given as follows.
Therefore, the objective of the function f1 is to optimize the motor’s efficiency, which is the same as minimizing the power losses, and the objective of the function f2 is to minimize the total mass of the motor.
3 Recent Meta-Heuristic Methods Based BLDC Wheel Motor Design Problem
A brief description of implemented meta-heuristic algorithms, such as GWO, WOA, and EO, is discussed in this section of the paper. These algorithms were chosen because they were not previously applied to the BLDC motor design optimization problem.
3.1 Grey Wolf Optimizer (GWO) Algorithm
The GWO was introduced in 2014 and employs the hunting behavior and leadership skill of grey wolves [29]. The hierarchy of the grey wolf is alpha (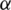
), beta (
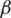), delta (
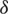), and omega (
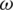), respectively, in which 
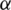is the leader, and it has responsibilities of hunting, place to sleep, and so on. The 
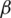and 
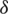are the second and third hierarchy level, and 
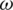is the last level of the hierarchy. The hunting has three stages: find, chase, and approach the victim, encircle and harass the target, and attack in the prey direction. During hunting, the wolves encircle the prey, and it is mathematically represented as follows.
where the current iteration is denoted as t, coefficient vectors are represented as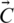 
and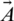 
. The position of the prey is denoted as 
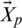and the wolf position is denoted as 
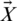. The vector coefficients are represented as follows, in which, 
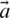is reduces from 2 to 0 linearly, and the random vectors are denoted as r1 and r2.
The hunting activity of grey wolves is simulated mathematically because the alpha, beta, and delta know the prey’s possible better position. The first top three results generated so far are therefore saved, and the other search agents (including omegas) are forced to update their positions as per the location of the best search agents. In this regard, the following formulas are proposed.
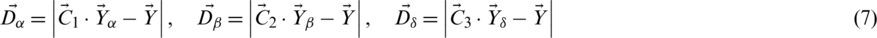
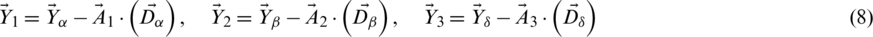
By attacking the prey when it stops moving, the grey wolves end the chase., as described above. The value of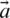 
is reduced in order to mathematically model the approach of the prey by the grey wolves and the 
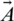is dominated by 
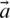as well. To explore the search space, the random parameters A and C support candidate solutions.
3.2 Whale Optimization (WO) Algorithm
The WO algorithm was introduced in 2016 has become one of the intelligent meta-heuristic algorithms and is inspired by the hunting mechanism of a humpback whale [30]. In hunting, these whales are superior, and hunting actions can be considered to overcome the non-linear engineering optimization problem. The whale’s hunting system is called a bubble-net feed. The trivial fishes near the surface tend to hunt these whales. The steps to be taken are to encircle the target, bubble-net feed movement, and hunt for targets in the search area. The search agent determines the target location and surrounds the prey. For the algorithm, the initial search space location is uncertain, and it assumes that the target prey is the best solution at present. The algorithm chooses the best agent with this assumption while the other is updating its best position. The search agents swim around the target within the shrinking circle, and the best position is updated simultaneously. The whale’s hunting activity is modeled as follows.
where the current iteration is defined by m,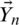 
is the position vector of the search agents, 
is the best current vector position and modified when each iteration has a successful solution, and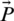 
, 
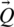and 
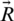are the vector coefficients. n is a random number [0, 1] and b is a random number [ −1, 1]. The vector coefficients, such as 
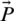and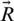 
are given as follows.
where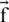 
in both the search space decreases from 2 to 0 over the iteration and the random variables 
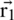and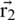 
between [0, 1].
3.3 Equilibrium Optimizer (EO) Algorithm
The idea behind the single-objective Equilibrium Optimizer was introduced in 2020 [31]. On a control volume, where it uses a mass balance equation, EO is based on a dynamic mass balance. The mass balance equation checks the mass amount in a control volume entering, leaving, and producing. The equation of mass balance seeks the system’s equilibrium state. In order to be eligible as a well-performing algorithm, EO has many benefits. These attributes include the ability to maintain a balance between discovery and exploitation, the ability to execute them quickly, and the ability to retain flexibility between individual solutions. As a result, addressing several single-objective optimizations, real-world problems have begun to gain popularity. In the following three steps, the mathematical model of the single-objective EO algorithm is clarified.
During initialization, EO uses a particle group, in which each particle describes the vector of concentration that includes the solution to the problem. The initial concentration vector is arbitrarily developed using the following formula in the search space.
where,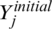 
denotes the vector concentration of the jth particle, ub and lb are upper and lower limits of each variable, 
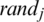is a random number [0, 1], and n denotes the number of particles. The EO algorithm chases for the system’s equilibrium state. While obtaining the equilibrium state, EO achieves the near-optimal solution. EO doesn’t understand the amount of concentrations that achieve the equilibrium state. Therefore, it assigns equilibrium candidates to the best four particles in the population, plus another one containing the average of the best four particles. In the exploitation and exploration processes, these five equilibrium candidates support EO. The first four candidates seek better exploration, while the fifth candidate with an average value is seeking change in exploitation. These five candidates possess a vector called the equilibrium pool.
The update of the concentration allows EO to balance exploration and exploitation fairly.
where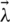 
is a random vector supposed to differ between 0 and 1, allowing turnover rate fluctuations over a period of time, and t is reduced as the iteration count increases as per Eq. (17).
It and Max_it are respectively, the current and the maximum number of iterations, and a2 is a constant to control the capacity to exploit. Another variable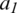 
, is used to improve both exploration and exploitation and is defined as follows.
The rate of generation is referred to as G, which improves exploitation and is described as follows.
where,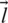 
is a random vector (0, 1), and the initial generation rate called 
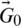is formulated as follows.
where the random numbers are denoted as r1 and r2 and varies between 0 and 1. The vector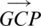 
is the parameter which controls the generation rate that controls whether the generation rate is applied to the updating stage or not. Lastly, EO is updated using Eq. (22).
The value of V is equal to 1. Readers are advised to refer [3] to the EO process for a more comprehensive description.
The implementation procedure of the BLDC motor parameter design process for all selected algorithms is discussed as follows.
a) The initialization is the first step in optimization problems.
b) For position Yi, the problem dimension D is equal to five.
c) 
, and the values of Yi1, Yi2, Yi3, Yi4, and Yi5 are within the range as specified in Tab. 1.
d) Initialize other parameters for all selected algorithms and adjust the parameters to get the required performance.
e) Two objective functions, such as f1 and f2, are handled separately in this paper.
f) Evaluate the search agent’s position and look for the best position, and the position is updated using Eqs. (9), (11), (22) for GWO, WO, and EO algorithms, respectively.
g) The iteration count is updated by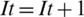 
for all algorithms.
If It is less than Max_it, return to Step 6, else evaluate the current positions Y, and the algorithm is terminated and gives the optimal output.
4 Simulation Results and Discussions
The selected algorithms, such as GWO, WO, and EO, are tested for all the benchmark test functions and few real-world problems. However, none of these algorithms are tested for BLDC wheel motor design problems. Therefore, all the selected algorithms are applied directly to solve this design problem and optimize the design variables by minimizing the motor’s total mass or maximizing the motor’s efficiency. All the algorithms run 10 times for both the objective functions and the control parameters of all algorithms are listed in Tab. 3. The control parameters are selected based on several trial runs and literature studies.
Table 3: Control parameters of all algorithms
All the selected algorithms proved their capability in handling real-world engineering problems. The design of the BLDC motor mentioned in Section 2 is added to test the effectiveness of all algorithms further. For two objective problems, all algorithms also run 10 times, as stated earlier. Two different case studies, such as minimizing the mass and maximizing efficiency, are studied, and simulation is carried out.
Case 1: Maximizing the Motor Efficiency - In this case study, the BLDC motor design variables are optimized by considering the objective function 1 given in Eq. (1). The selected algorithms, such as GWO, WO, and EO algorithms are directly applied to the objective function 1, and the optimized design variables for all 10 individual runs are listed in Tabs. 4–6. The bold letters in each table display the best results for 10 runs. Tab. 4 shows that the best motor efficiency is achieved by GWO during the 8th run and is equal to 95.3105%. From Tab. 5, it is observed that the best motor efficiency is achieved by WO during the 9th run and is equal to 95.1545%. Tab. 6 shows that the best motor efficiency is achieved by EO during the 8th run and is equal to 95.3177%, and also observed from Tab. 6 that the EO algorithm is giving consistent results during all the runs. The convergence curve for all selected algorithms is illustrated in Fig. 2.
Table 4: Optimized variables for objective function 1 by GWO for all 10 runs
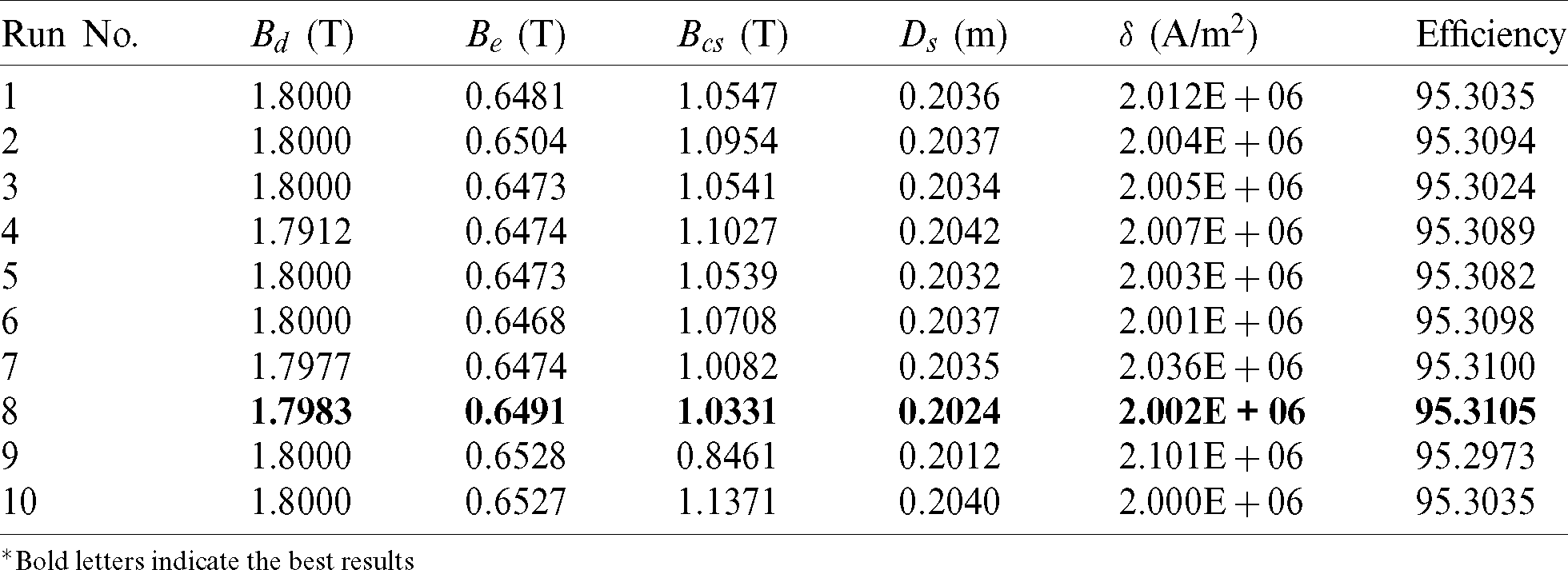
*Bold letters indicate the best results
Table 5: Optimized variables for objective function 1 by WO for all 10 runs
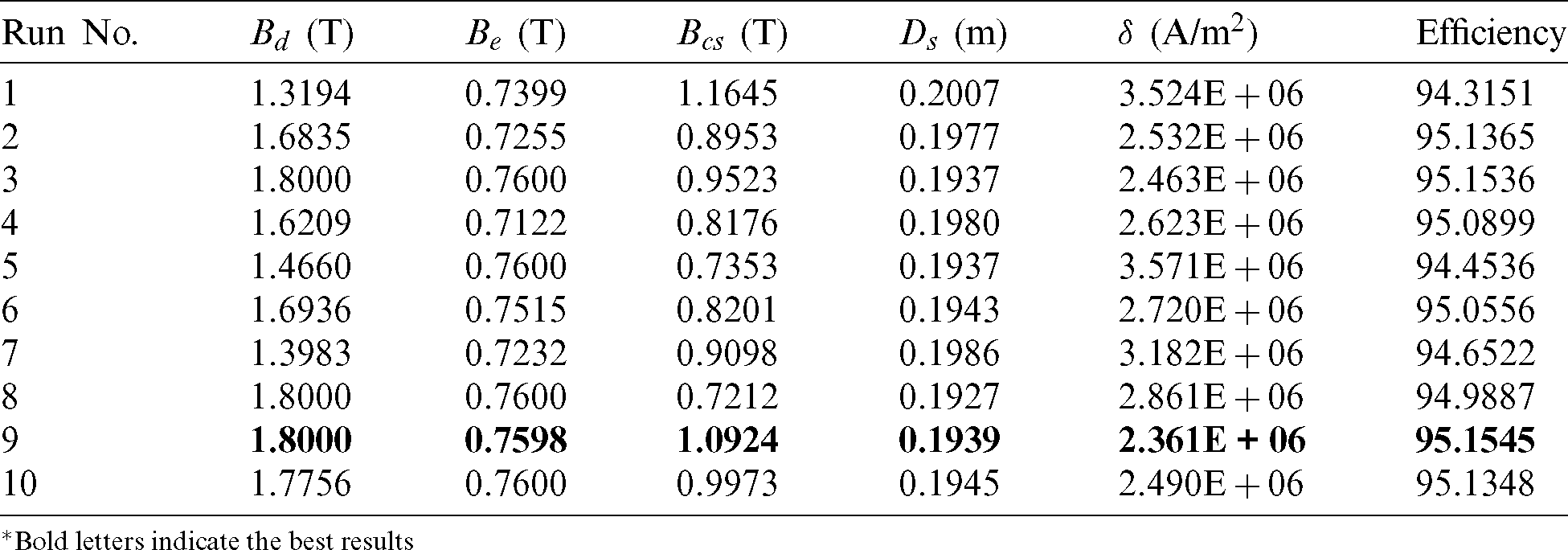
*Bold letters indicate the best results
Table 6: Optimized variables for objective function 1 by EO for all 10 runs
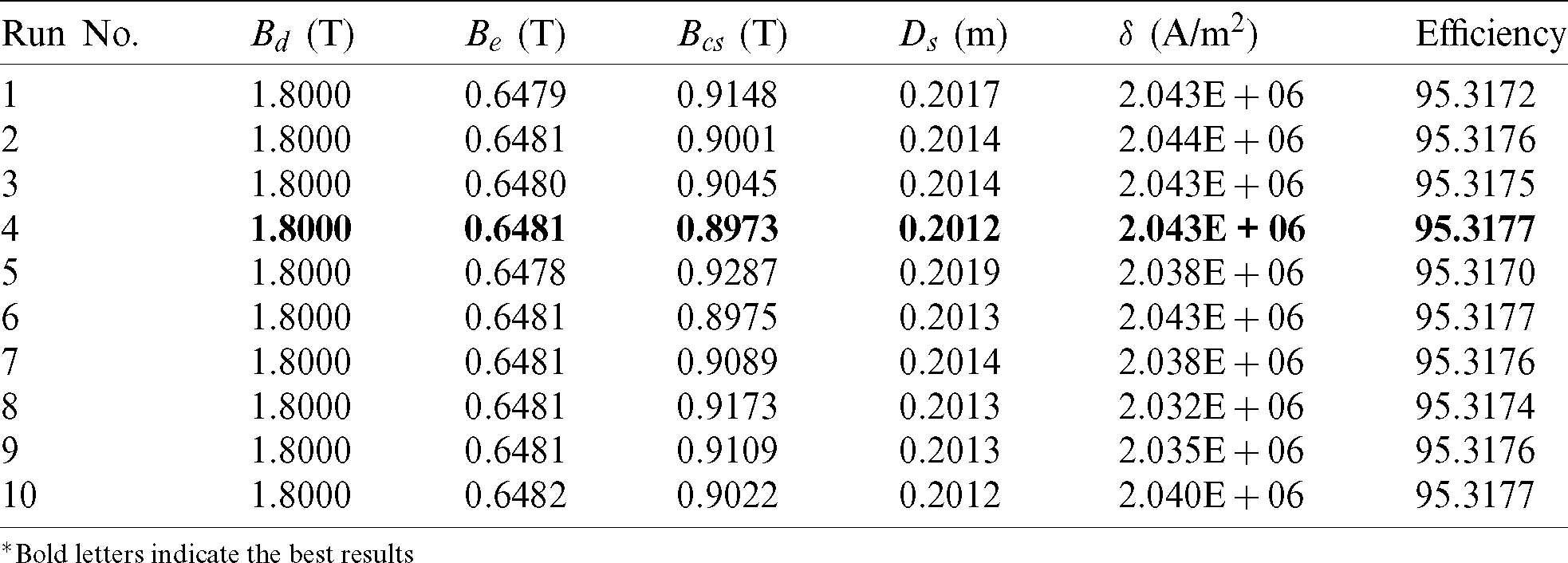
*Bold letters indicate the best results
Figure 2: Convergence curve for objective function 1; (a) GWO, (b) WO, (c) EO
From Fig. 2, it is observed that the EO algorithm converges to the maximum efficiency very quickly than the GWO and WO algorithms. Therefore, it is concluded that the EO algorithm is performing better in handling objective function 1 of the BLDC motor design problem.
Case 2: Minimizing the Motor Mass - In this case study, the BLDC motor design variables are optimized by considering the objective function 2 as given in Eq. 2. As similar to the previous case study, the selected algorithms, such as GWO, WO, and EO algorithms, are directly applied to objective function 2, and the optimized design variables for all 10 individual runs are listed in Tabs. 7–9. The bold letters in each table display the best results for 10 runs. Tab. 6 shows that the best motor mass is achieved by GWO during the 1st run and is equal to 10.5770 kg. From Tab. 8, it is observed that the best motor mass is achieved by WO during the 3rd run and is equal to 10.6286 kg. From Tab. 9, it is observed that the best motor mass is achieved by EO during the 8th run and is equal to 10.5690 kg, and also observed from Tab. 9 that the EO algorithm is giving consistent results during all the runs. The convergence curve for all selected algorithms is illustrated in Fig. 3.
Table 7: Optimized variables for objective function 2 by GWO for all 10 runs
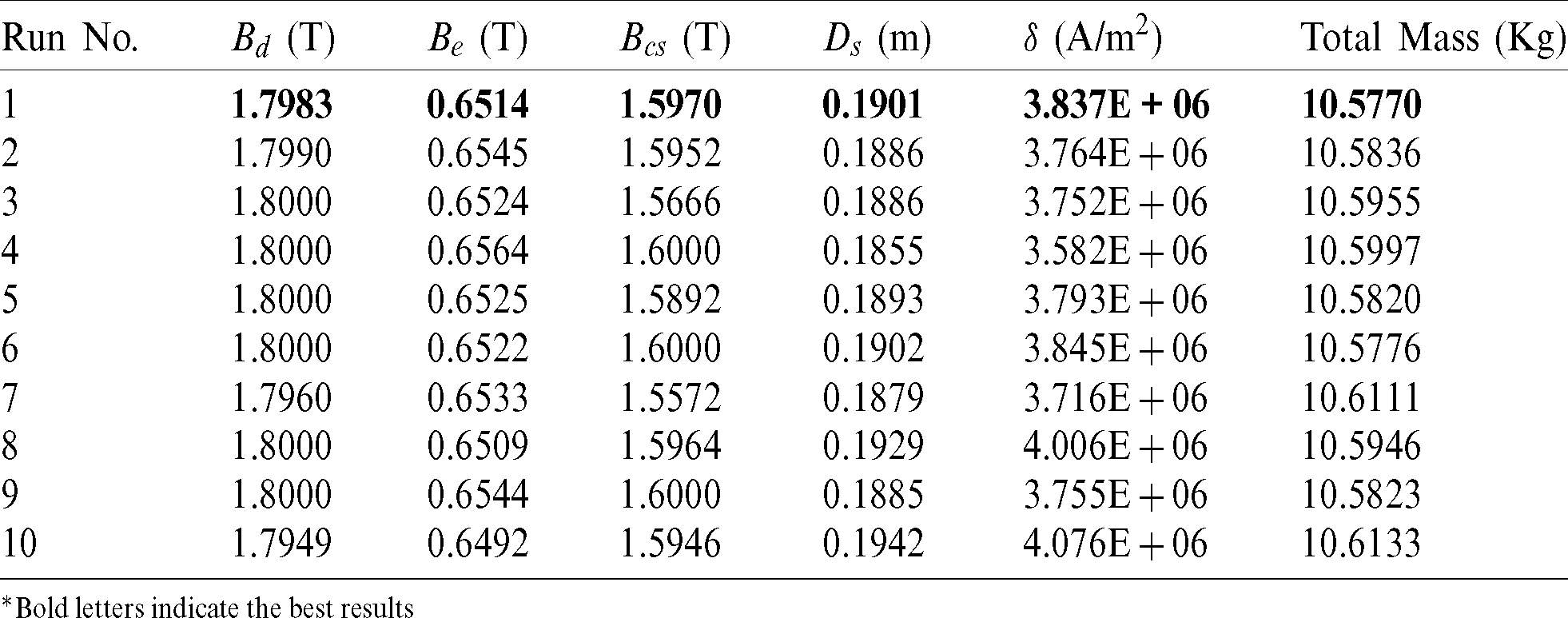
*Bold letters indicate the best results
Table 8: Optimized variables for objective function 2 by WO for all 10 runs
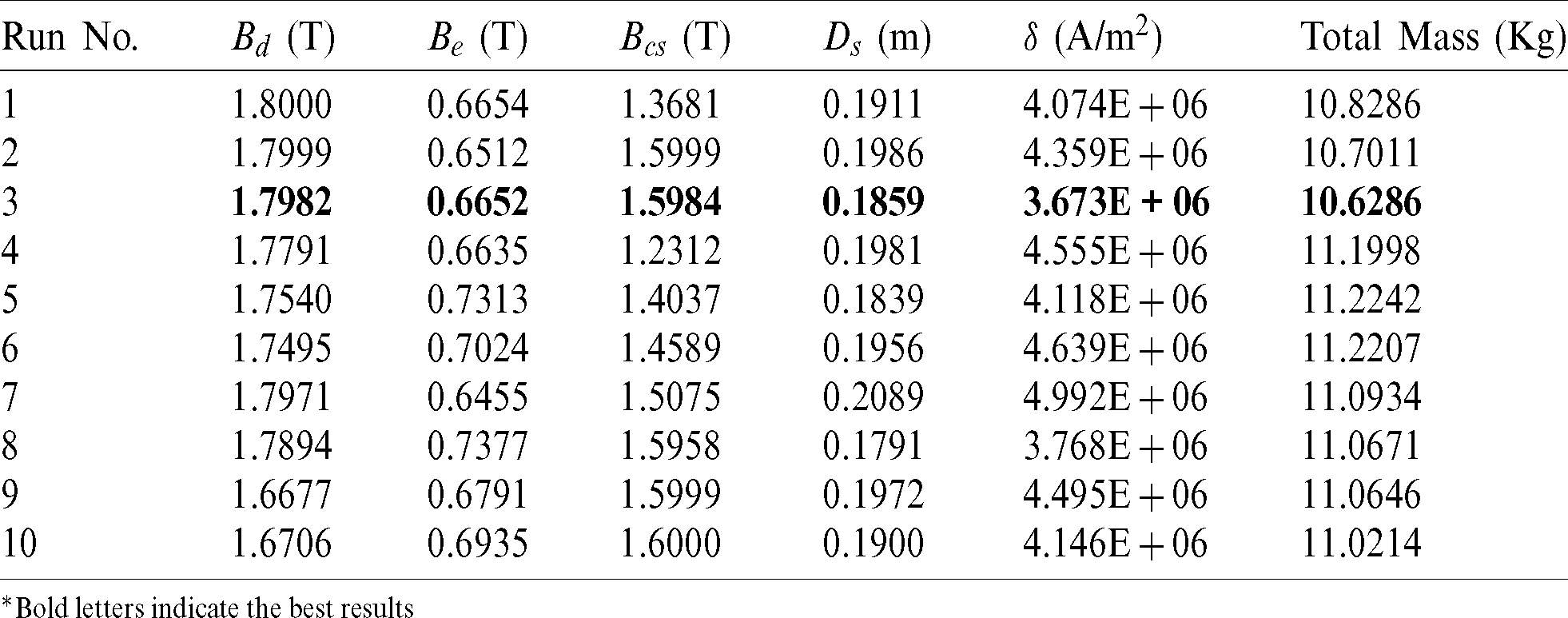
*Bold letters indicate the best results
Table 9: Optimized variables for objective function 2 by EO for all 10 runs
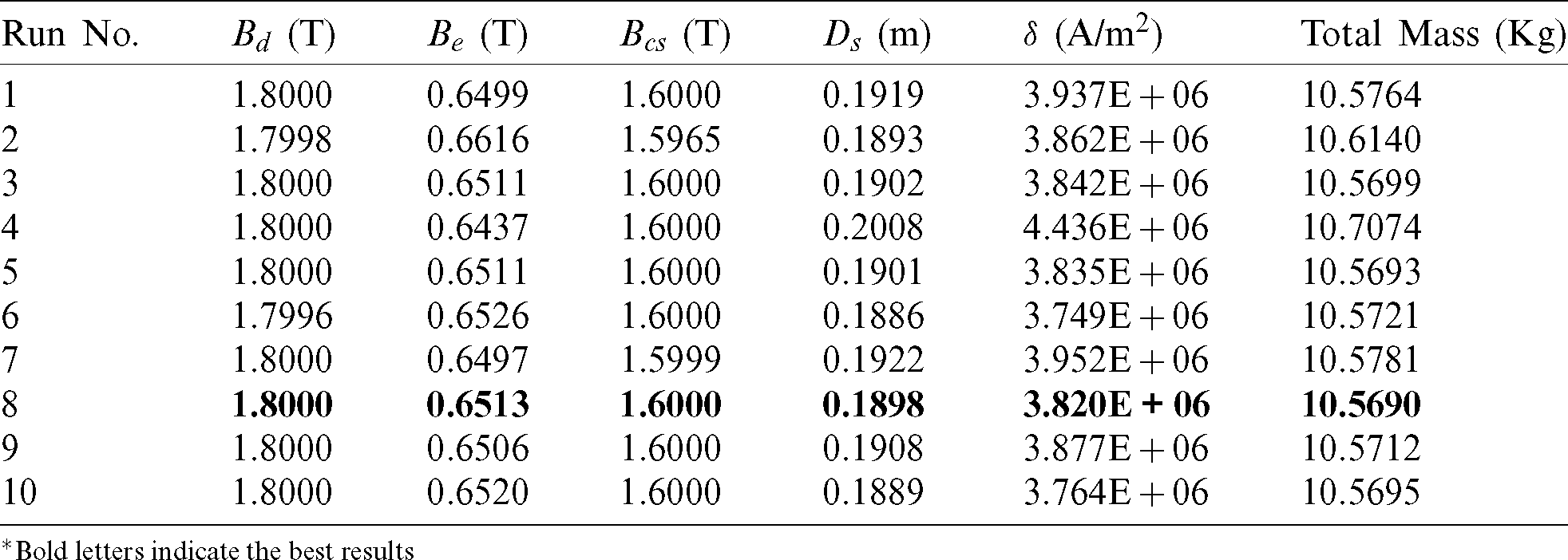
*Bold letters indicate the best results
Figure 3: Convergence curve for objective function 2; (a) GWO, (b) WO, (c) EO
From Fig. 3, it is observed that the EO algorithm converges to the minimum mass very quickly than the GWO and WO algorithms. Therefore, it is concluded that the EO algorithm is performing better in handling objective function 2 of the BLDC motor design problem.
The performance of the selected algorithms, such as GWO, WO, and EO, are compared with other metaheuristic algorithms, such as PSO, ACO, and BA. The optimized design variables for both objective functions of the BLDC motor by all algorithms are listed in Tabs. 10 and 11. All algorithms run 10 times to check the reliability, and the best results are listed.
Table 10: Performance results of objective function 1 for maximizing efficiency
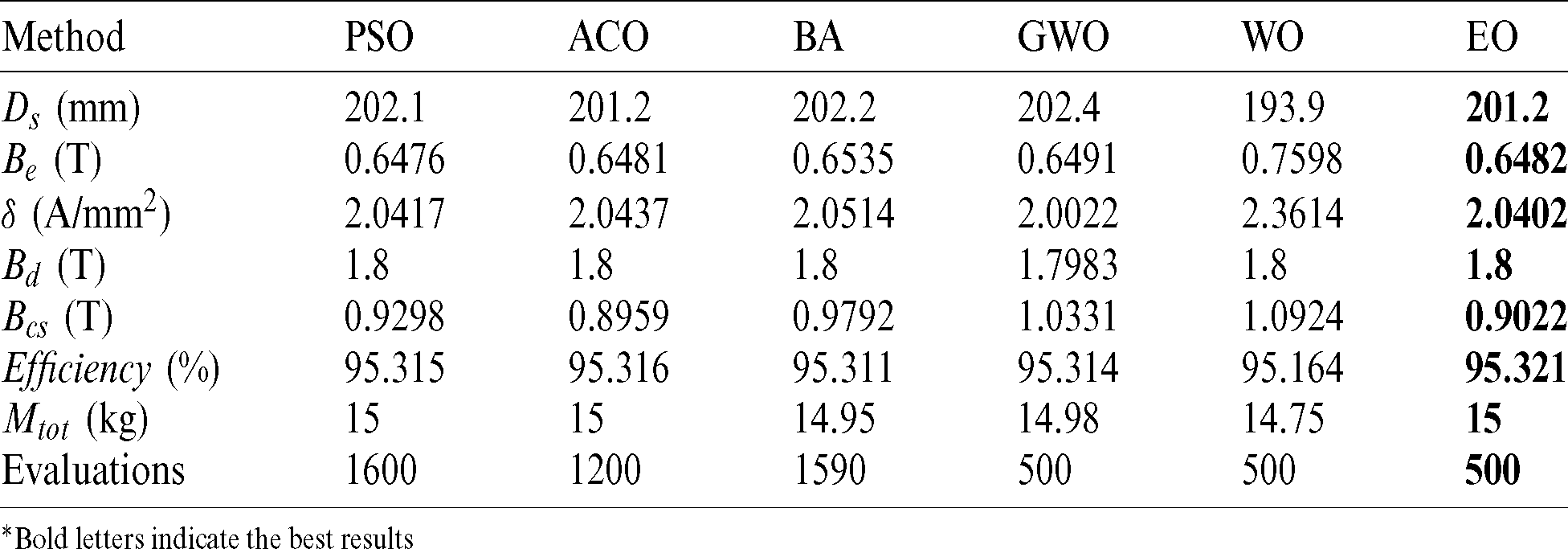
*Bold letters indicate the best results
Table 11: Performance Results of objective function 2 for minimizing the mass
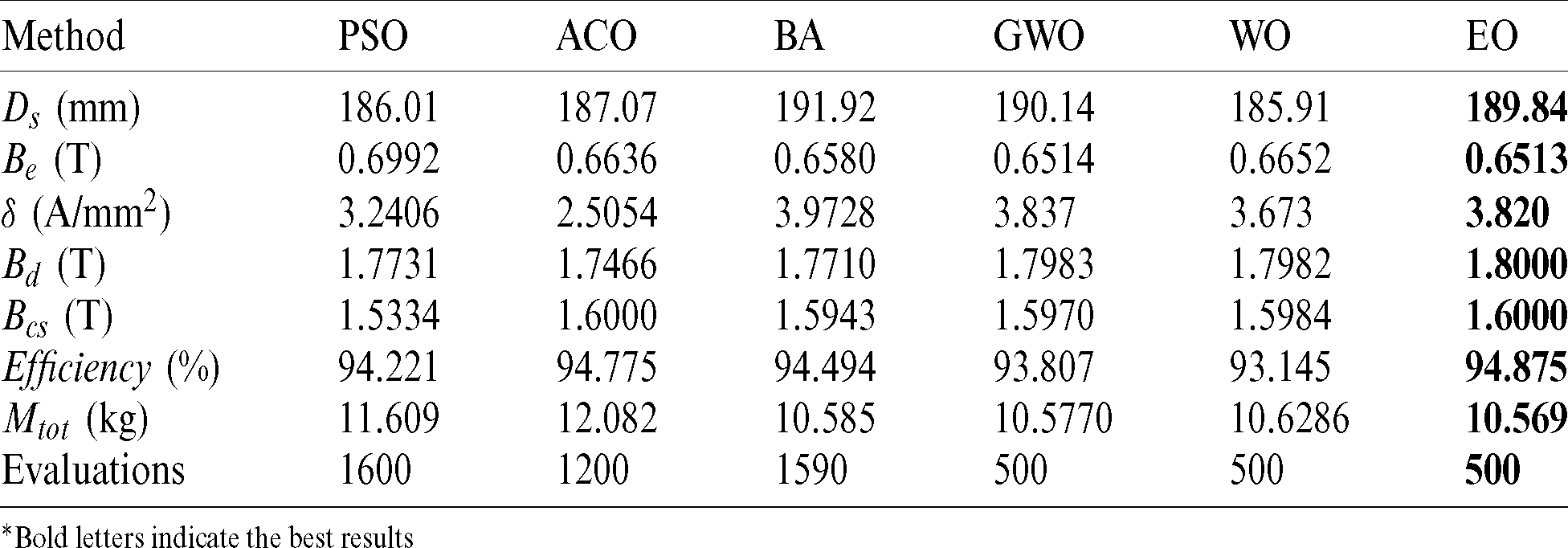
*Bold letters indicate the best results
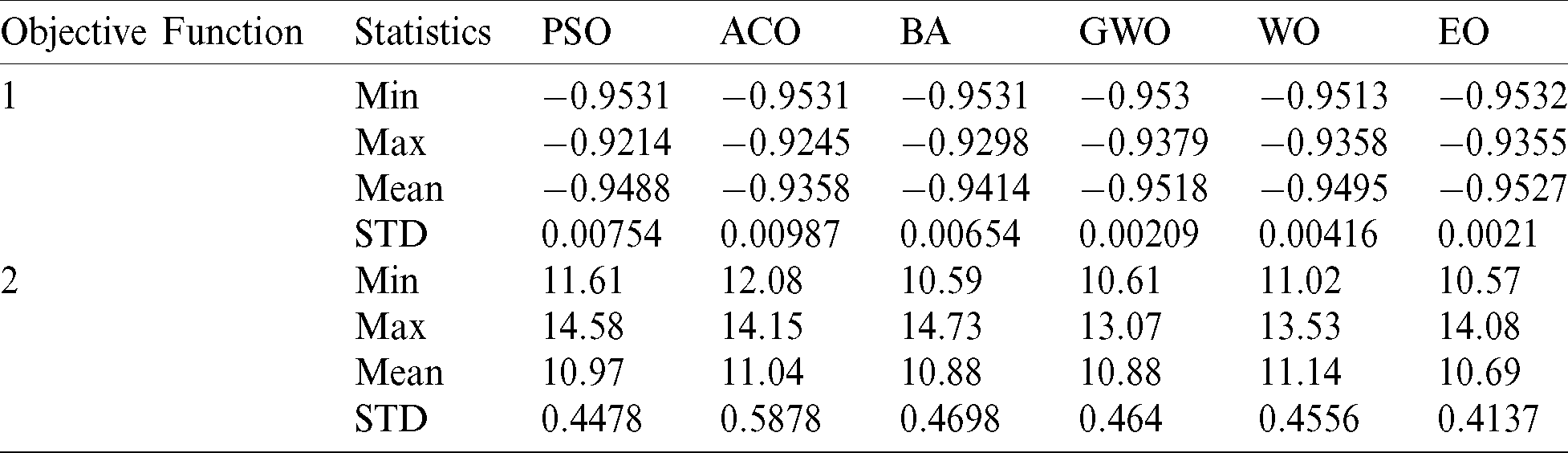
It is observed from Tabs. 10 and 11 that the EO algorithm is performing better than any of the algorithms, and the results produced by the EO algorithm are consistent, and the reliability of the EO is comparatively higher than the other algorithms. The statistical results, such as Min, Max, Mean, and standard deviation (STD) of all algorithms, are listed in Tab. 12. The superiority of the EO over PSO, ACO, BA, GWO, and WO in the above-mentioned indicators can be concluded. The design parameters achieved by the proposed EO algorithm, when the efficiency is maximum or when the total mass is minimal, are shown in Tab. 12.
Table 12: Statistical summary of all algorithms
This paper deals with the optimal design of a brushless DC wheel motor, and the main aim of the optimization technique is to maximize the efficiency of the machine or minimize its total mass. An analytical model discussed in the literature was considered to accomplish this purpose, and numerous optimization techniques, such as GWO, WO, and EO, were applied. Two different objective functions are formulated and utilized to optimize the design variable of the BLDC motor. The results obtained from the selected algorithms are compared with the other metaheuristic algorithms, such as PSO, ACO, and BA, and show that the EO algorithm can give optimized and best results for both the objective functions. Also, in terms of Min, Max, Mean, and STD, the EO algorithm can give the lowest values than the other algorithms. It can thus be inferred that the EO algorithm is an effective algorithm to be applied to the problem of BLDC wheel motor design.
For future research, the authors have planned to investigate both the objective functions simultaneously to get the optimal trade-off between the motor mass and motor efficiency by applying the multi-objective versions of GWO, WO, and EO. In addition, the multi-objective versions can also be investigated to handle different uncertainties during the optimization process.
Acknowledgement: We extend our thankfulness to GMR Institute of Technology, Rajam, Andhra Pradesh, India, for providing the facility and allowing us to validate the performance of the algorithms at the laboratory.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. Premkumar, J. S. V. Sivakumar, R. Vijaya Krishna and R. Sowmya. (2018). “Design, analysis and fabrication of solar PV powered BLDC hub motor driven electric car,” International Journal of Mechanical and Production Engineering Research and Development, vol. 8, no. 1, pp. 1255–1270. [Google Scholar]
2. A. Dadashnialehi, A. Bab-Hadiashar, Z. Cao and A. Kapoor. (2014). “Intelligent sensorless antilock braking system for brushless in-wheel electric vehicles,” IEEE Transaction on Industrial Electronics, vol. 62, no. 3, pp. 1629–1638. [Google Scholar]
3. S. M. J. Shiadeh, M. Ardebili and P. Moamaei. (2015). “Three-dimensional finite-element-model investigation of axial-flux PM BLDC machines with similar pole and slot combination for electric vehicles,” in Proc. of Power and Energy Conference, Illinois, USA, pp. 1–4. [Google Scholar]
4. P. Yadav, R. Kumar and S. K. Panda. (2010). “Improved harmony search algorithm based optimal design of the brushless DC wheel motor,” in Proc. of IEEE Int. Conf. on Sustainable Energy Technologies, Kandy, Sri Lanka, pp. 1–6. [Google Scholar]
5. S. Brisset and P. Brochet. (2005). “Analytical model for the optimal design of a brushless DC wheel motor,” COMPEL International Journal for Computation and Mathematics in Electrical and Electronic Engineering, vol. 24, no. 3, pp. 829–848. [Google Scholar]
6. J. H. He. (2019). “Lagrange crisis and generalized variational principle for 3D unsteady flow,” International Journal of Numerical Methods for Heat & Fluid Flow, vol. 30, no. 3, pp. 1189–1196. [Google Scholar]
7. J. H. He. (2012). “Asymptotic methods for solitary solutions and compactons,” Abstract and Applied Analysis, vol. 2012, pp. 916793. [Google Scholar]
8. W. Kang-Jia, H. Chu-Xia and L. Yan-Hong. (2020). “Thermal optimization of a 3-D integrated circuit,” Thermal Science, vol. 24, no. 4, pp. 2615–2620. [Google Scholar]
9. P. Jangir, S. A. Parmar, I. N. Trivedi and R. H. Bhesdadiya. (2017). “A novel hybrid particle swarm optimizer with multi verse optimizer for global numerical optimization and optimal reactive power dispatch problem,” Engineering Science and Technology: An International Journal, vol. 20, no. 2, pp. 570–586. [Google Scholar]
10. M. Bhoye, M. H. Pandya, S. Valvi, I. N. Trivedi, P. Jangir et al. (2016). , “An emission constraint economic load dispatch problem solution with microgrid using JAYA algorithm,” in Proc. of the Int. Conf. on Energy Efficient Technologies for Sustainability, Nagercoil, Tamil Nadu, India, pp. 497–502. [Google Scholar]
11. I. N. Trivedi, P. Jangir, A. Kumar, N. Jangir, R. H. Bhesdadiya et al. (2018). , “A novel hybrid PSO-DA algorithm for global numerical optimization,” in Networking Communication and Data Knowledge Engineering-Lecture Notes on Data Engineering and Communications Technologies. vol. 3. Germany: Springer, pp. 85–92. [Google Scholar]
12. H. K. Kim, J. K. Chong, K. Y. Park and D. A. Lowther. (2007). “Differential evolution strategy for constrained global optimization and application to practical engineering problems,” IEEE Transaction on Magnetics, vol. 43, no. 4, pp. 1565–1568. [Google Scholar]
13. L. Dos Santos Coelho, L. Z. Barbosa and L. Lebensztajn. (2010). “Multiobjective particle swarm approach for the design of a brushless DC wheel motor,” IEEE Transactions on Magnetics, vol. 46, no. 8, pp. 2994–2997. [Google Scholar]
14. A. Rahideh, T. Korakianitis, P. Ruiz, T. Keeble and M. T. Rothman. (2010). “Optimal brushless DC motor design using genetic algorithms,” Journal of Magnetism and Magnetic Materials, vol. 322, no. 22, pp. 3680–3687. [Google Scholar]
15. P. Sharma and R. Gupta. (2014). “Tuning of PID controller for a linear BLDC motor using TLBO technique,” in Proc. of the Int. Conf. on Computational Intelligence and Communication Networks, Bhopal, India, pp. 1224–1228. [Google Scholar]
16. P. Qi. (2012). “An improved PSO-based optimum design of speed controller for BLDC motor,” in Proc. of the Int. Conf. on Automatic Control and Artificial Intelligence, Xiamen, China, pp. 453–456. [Google Scholar]
17. I. Elomary, A. Abbou, L. Idoumghar and B. Kassame. (2018). “Optimization design of the BLDC motor using success-history based adaptive differential evolution algorithm,” in Proc. of the Int. Conf. on Electronics, Control, Optimization and Computer Science, Kenitra, Morocco, pp. 1–5. [Google Scholar]
18. H. V. H. Ayala, E. H. V. Segundo, V. C. Mariani and L. Dos Santos Coelho. (2016). “Multiobjective krill herd algorithm for electromagnetic optimization,” IEEE Transactions on Magnetics, vol. 52, no. 3, pp. 1–4. [Google Scholar]
19. M. A. Sharifi and H. Mojallali. (2019). “Multi-objective modified imperialist competitive algorithm for brushless DC motor optimization,” IETE Journal of Research, vol. 65, no. 1, pp. 96–103. [Google Scholar]
20. C. R. Raquel and P. C. Naval. (2005). “An effective use of crowding distance in multiobjective particle swarm optimization,” in Proc. of the Genetic Evolutionary Computation Conference, Washington, DC, USA, pp. 257–264. [Google Scholar]
21. K. Deb, A. Pratap, S. Agarwal and T. Meyarivan. (2002). “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transaction on Evolutionary Computation, vol. 6, no. 2, pp. 182–197. [Google Scholar]
22. S. Mirjalili, P. Jangir and S. Saremi. (2017). “Multi-objective ant lion optimizer: A multi-objective optimization algorithm for solving engineering problems,” Applied Intelligence, vol. 46, no. 1, pp. 79–95. [Google Scholar]
23. A. Darwish. (2018). “Bio-inspired computing: Algorithms review, deep analysis, and the scope of applications,” Future Computing and Informatics Journal, vol. 3, no. 2, pp. 231–246. [Google Scholar]
24. N. Umadevi, M. Balaji, V. Kamaraj and L. A. Padmanaban. (2015). “Data interpolation and design optimisation of brushless DC motor using generalized regression neural network,” Journal of Electrical Engineering & Technology, vol. 10, no. 1, pp. 188–194. [Google Scholar]
25. P. S. Shin, H. D. Kim, G. B. Chung, H. S. Yoon, G. S. Park et al. (2007). , “Shape optimization of large-scale BLDC motor using an adaptive RSM utilizing design sensitivity analysis,” IEEE Transactions on Magnetics, vol. 43, no. 4, pp. 1653–1656. [Google Scholar]
26. K. J. Han, H. S. Cho, D. H. Cho and H. K. Yung. (2006). “Optimal core shape design for cogging torque reduction of brushless DC motor using genetic algorithm,” IEEE Transactions on Magnetics, vol. 36, no. 4, pp. 1927–1931. [Google Scholar]
27. Y. D. Chun, S. Wakao, T. H. Kim, K. B. Yang and J. Lee. (2004). “Multiobjective design optimization of brushless permanent magnet motor using 3D equivalent magnetic circuit network method,” IEEE Transactions on Applied Superconductivity, vol. 14, no. 2, pp. 1910–1913. [Google Scholar]
28. Stéphane Brisset. Lille Laboratory of Electrical Engineering and Power Electronics (L2EP). (2005, Sep. 01Analytical Model, Benchmark Functions. [Online]. Available: http://l2ep.univ-lille1.fr/come/benchmark-wheel-motor/Math.htm [Accessed on August 2020]. [Google Scholar]
29. S. Mirjalili, S. M. Mirjalili and A. Lewis. (2014). “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61. [Google Scholar]
30. S. Mirjalili and A. Lewis. (2016). “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67. [Google Scholar]
31. A. Faramarzia, M. Heidarinejad, B. Stephens and S. Mirjalili. (2020). “Equilibrium optimizer: A novel optimization algorithm,” Knowledge-Based Systems, vol. 191, pp. 105190. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |