DOI:10.32604/cmc.2021.012583
| Computers, Materials & Continua DOI:10.32604/cmc.2021.012583 | |
| Article |
Model of Fractional Heat Conduction in a Thermoelastic Thin Slim Strip under Thermal Shock and Temperature-Dependent Thermal Conductivity
1Department of Mathematics and Statistics, College of Science, Taif University, Taif, 21944, Saudi Arabia
2Department of Mathematics, Faculty of Science, South Valley University, Qena, 83523, Egypt
3Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, Egypt
4Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt
5Department of Mathematics, Faculty of Science, Al-Azhar University, Giza, Egypt
*Corresponding Author: S. M. Abo-Dahab. Email: sdahb@yahoo.com
Received: 05 July 2020; Accepted: 28 August 2020
Abstract: The present paper paper, we estimate the theory of thermoelasticity a thin slim strip under the variable thermal conductivity in the fractional-order form is solved. Thermal stress theory considering the equation of heat conduction based on the time-fractional derivative of Caputo of order 
is applied to obtain a solution. We assumed that the strip surface is to be free from traction and impacted by a thermal shock. The transform of Laplace (LT) and numerical inversion techniques of Laplace were considered for solving the governing basic equations. The inverse of the LT was applied in a numerical manner considering the Fourier expansion technique. The numerical results for the physical variables were calculated numerically and displayed via graphs. The parameter of fractional order effect and variation of thermal conductivity on the displacement, stress, and temperature were investigated and compared with the results of previous studies. The results indicated the strong effect of the external parameters, especially the time-fractional derivative parameter on a thermoelastic thin slim strip phenomenon.
Keywords: Non-Fourier heat conduction; thermoelasticity; fractional derivative; variable thermal conductivity
Recently, more attention has been given to the uncoupled classical thermoelastic theory, which predicts that two phenomena have a confliction and do not agree with the physical laboratory results. While the heat conduction equation is the first phenomenon without any elastic terms, the second is the prediction of infinite propagation speed for heatwaves due to the thermal signals in the equation of heat in a parabolic type. Biot [1] is the prior who presented the coupled thermoelasticity theory between the motion equation and equation of heat to overcome and release the confliction of the first shortcoming. However, the equation of heat for the theory of coupled thermoelasticity in a parabolic form. Thus, both theories have shared and addressed the second shortcoming.
During the last five decades, more different theories developed the thermoelasticity theory to the generalized theory of thermoelasticity. Lord et al. [2] who is the first introduced the theory by the heat conduction equation based on the modified law of Fourier’s considering one relaxation time that transforms the equation of heat conduction in a parabolic form to hyperbolic form the equation of heat conduction. Green et al. (GL) [3] who modified the equation of energy and the relation of Duhamel-Neumann, taking into account two thermal relaxation times. The third was by Green et al. (GN) [4] who introduced a generalized theory of thermoelasticity. They included the ‘displacement gradient-thermal’ within the constitutive variables independence but without dissipation accommodate of the thermal energy.
The material characteristics at high temperatures, such as Poisson’s ratio, the elasticity modulus, the coefficient of thermal expansion, and the thermal conductivity are not constants any more [5]. Recently and because of scientific and technological development, the need to understand the actual actions of the material features has become actual [6]. Budaev et al. [7] discussed the dependence temperature of shear elasticity for some liquids which indicated that the increase of temperature depends on the decrease of shear modulus and is explainable by increasing the fluctuation free volume. Rishin et al. [8] employed the method of dynamic resonance to define the dependence temperature of the elasticity modulus of some materials that have plasma-sprayed. The increasing results of test temperature in a monotonic decrease in elasticity modulus. Honig et al. [9] discussed a method for the numerical inversion of the Laplace transform.
The equations of fractional derivatives and fractional differential were applied to obtain solutions to some problems in viscoelasticity, fluid mechanics, physics, engineering, biology, signal processing, mechanical engineering, systems identification, control theory, electrical engineering, finance, and fractional dynamics [10]. It describes anomalous diffusion (subdiffusion, superdiffusion, diffusion of non-Gaussian) that does not conform to the classical law of Fick in [11,12]. Numerically, the experiments show that in various one-dimensional systems that have total momentum conservation, the thermal conduction does not form in the Fourier law. Moreover, the thermal conductivity matches the size of the system in [13].
Podlubny [14] introduced an important overview of different fractional calculus applications in science, engineering, and technology. Ross [15] and Miller et al. [16] introduced a historical brief of the progress of fractional order calculus. Youssef et al. [17] discussed and made a new model for generalized thermoelasticity theory in fractional order. Sherief et al. [18] presented a fractional calculus-based thermoelasticity theory. Povstenko [19] studied axisymmetric stresses from pulses instantaneous and diffusion sources in an infinite space in a diffusion of time-fractional equation in a two-dimensional. Povstenko [20] applied Caputo time-fractional derivative technique on the thermal stresses theory based on the equation of thermal conduction to explore thermal stresses in a circular cylindrical hole an infinite body. Allam et al. [21] examined the interactions between the electromagneto-thermoelastic in a body with a spherical cavity an infinite perfectly conducting considering the GN model. The elasticity modulus is considered a linear function of temperature. Abouelregal [22] investigated the generalized thermo-piezoelectric semi-infinite under the assumption of the fractional-order with temperature-dependent and ramp-type heating. Structural continuous dependence in micropolar porous bodies is discussed in [23]. Study of heat and mass transfer in the Eyring–Powell model of peristaltically fluid propagating through a rectangular compliant channel has been discussed by Riaz et al. [24]. Some new related works have been discussed in [25–28].
In this work, we studied the thermoelasticity theory of a thin slim strip under the variable thermal conductivity in the fractional-order form is solved. Thermal stress theory considering the equation of heat conduction based on the time-fractional derivative of Caputo of order 
is applied to obtain a solution. We assumed that the strip surface is to be free from traction and impacted by a thermal shock. The transform of Laplace (LT) and numerical inversion techniques of Laplace were considered for solving the governing basic equations. The inverse of the LT was applied in a numerical manner considering the Fourier expansion technique. The numerical results for the physical variables were calculated numerically and displayed via graphs. The parameter of fractional order effect and variation of thermal conductivity on the displacement, stress, and temperature were investigated and compared with the results of previous studies. The results indicated the strong effect of the external parameters, especially the time-fractional derivative parameter on a thermoelastic thin slim strip phenomenon. The obtained results are deduced to special case if thermal conductivity and thermal shock neglect.
Considering an isotropic homogeneous thermoelastic thin slim strip, the generalized thermoelastic governing differential equations in the fractional-order form [29] consist of:
(i) The motion equations, if the body forces were neglected
(ii) The constitutive (stress-strain) equations
where 
and 
are the Lamé parameters, 
is the tensor of stress, 
, 
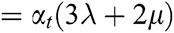is the thermal expansion coefficient, and 
is the medium density, 
are the elements of the strain tensor, 
is the temperature reference, 
is the temperature, and 
are the elements of the displacement vector.
(iii) Assuming series of Taylor of time-fractional order 
is the new fractional form in the present paper [21] presented the time-nonlocal dependence between the the heat flux vector and temperature gradient discussed concerning fractional integrals and derivatives as follows:
where 
is the heat conductivity, 
is the vector of thermal flux, 
is the fractional derivative of Caputo, and 
is the fractional-order parameter.
(iv) The equation of heat conduction as time-fractional form takes the form [29]
where 
is the unit mass specific heat.
Eq. (4) is the fractional derivatives of generalized energy equation considering the relaxation time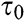 
. Some of the theories of the law of thermal conduction follow different values of 
and 
as limit cases. The theories of coupled or generalized thermoelasticity with one relaxation time and the generalized theory of thermoelasticity without energy dissipation (TWOED) adopt restricted cases according to the value of 
, 
and 
.
The temperature Eq. (4), 
and 
tends to:
this is the generalized theory that has a thermal relaxation time.
In the restricted case, when 
and 
the heat conduction Eq. (4), tends to
This is the GN generalized theory without energy dissipation.
Eq. (4) in the thermoelasticity coupled theory in the limiting case 
and 
as
Variations in mechanical properties due to an imposed temperature field are not the only ones that accompany heating. Similar variations are observed in the thermal properties characterized by such coefficients as the thermal linear expansion coefficients of 
, conductivity of thermal 
and others. An acceptable approximation in limited temperature interval is obtained by considering the thermal conductivity to depend linearly on the change of temperature.
The function of thermal conductivity formed as a linear function of temperature is given as [30]
where 
is thermal conductivity as temperature-dependent, 
is the thermal conductivity variation (usually negative experimental coefficient), 
denotes the thermal conductivity at T = T0, 
is the diffusivity, and 
is the time.
Using Eq. (4) with Eq. (8), we get
Using the mapping
where 
is the mapping function.
Differentiating with respect to the coordinates, Eq. (10) tends to
Redifferentiating concerning the coordinates axis, we obtain
Similarly, by differentiating with respect to time, the mapping is
From Eqs. (12) and (13), Eq. (9) is given as
From Eqs. (10) and (11), we have
Substituting from Eq. (11) into Eq. (1), we obtain
For the linearity governing partial differential equations, considering the condition 
, give the approximating function of the thermal conductivity 
.
Then, Eq. (16) takes the form
Using Eq. (15) and neglecting the small values of temperature, the constitutive relation reduces to
Taking into account a thin rod semi-infinite with the half-space region 
, the 
axis perpendicular to the layer, parallel to 
plane, the one-dimension displacement vector is given as
The strain components are
The heat equation is
The equation of motion is
The constitutive relation takes the form
Considering a half-space 
that primarily rests and has an initial temperature 
with zero velocity of temperature, the original conditions are
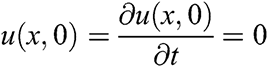
We assume that when 
, the surface becomes free from stresses and is put in sudden heating. The boundary conditions take the form
• The thermal boundary conditions:
where 
is function of Heaviside unit step
• The boundary conditions concerning mechanical stress, displacement, and temperature are
• and
To simplify the physical quantities, we put them in the following non-dimensional forms
From Eq. (26), the governing equations (eliminating the primes for convenience) take the forms
where 
and 
6 The Solution in the Laplace Transform Domain
If we apply the following LT
Applying it in Eqs. (27)–(30), and using the initial conditions in Eq. (22), we get
The boundary conditions in Eqs. (24) and (25) and the regularity condition in the LT domain take the forms
By eliminating 
, we get
By eliminating 
between Eqs. (36) and (37), we get
Also, we can show that 
satisfies
where
The solution of Eqs. (38) and (39) takes the form
where the parameters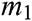 
and 
satisfy the equation
We can get the displacement using Eq. (28), such that
Thus, we obtain
The temperature increment 
is given by providing a solution to (15) to give
We utilize the problem’s boundary conditions to evaluate the 
and 
parameters. Eqs. (34) and (35) with Eqs. (40) and (41), they immediately give
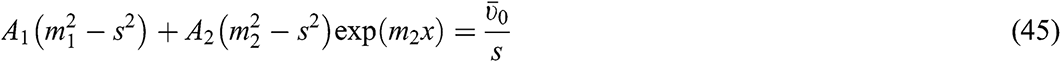
The solution of the former system of the linear equations provides the parameters 
and 
in the form
Hence,
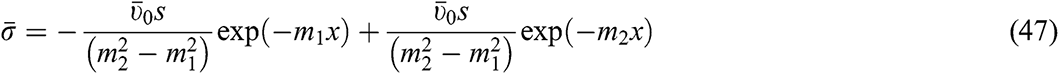
Accordingly, the problem is solved in the transformed domain completely.
7 Inversion of the Laplace Transform
It is too difficult to obtain the analytical inverse the LT of the intricate solutions to the temperature, displacement, stress, and strain in the LT domain. The method of numerical inversion is outlined to solve the problem in the physical domain. Durbin [31] obtained the approximation formula
It is worth noting that choosing the free parameters 
and 
is significant for the accurate results and applying the method’s Korrecktur and the methods of convergence acceleration. The values of the parameters in Eq. (50) are defined as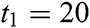 
, 
and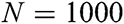 
.
To calculate the analytical procedure, we take into account a numerical physical example. The findings depict the variations of the non-dimensional values of temperature, displacement, and thermal stresses. Thus, we consider the following values material constants (Copper material and the type 316) as shown in Tab. 1.
Table 1: The constants of the material [32]
The computations for the results obtained are carried out for the time 
to obtain the displacement 
, temperature 
and stress 
. They were conducted for several 
, for different values of the parameter of fractional-order 
with a wide range of 
that contains both cases of conductivity; 
for low conductivity and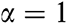 
for normal conductivity. Here, the numerical results are displayed graphically in Figs. 1–3.
Figure 1: The effect of fractional order parameter on temperature distribution
Figure 2: The effect of fractional order parameter on displacement distribution
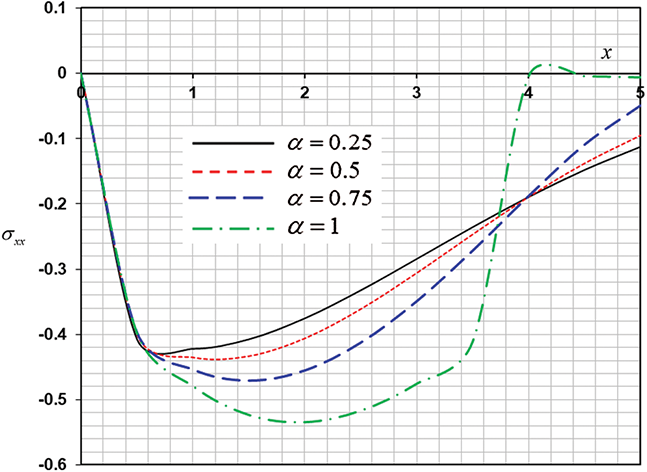
Figure 3: The effect of fractional order parameter on stress distribution
It should be pointed out that, the increasing value of 
decreases the speed of wave propagation of the stress and the temperature, whereas the displacement increases. We have noticed that the 
value has a strong effect on all distributions. From these figures, the surface stress equals zero and matches the prescribed boundary condition.
In Figs. 4–6, we presented the stress, temperature, and displacement, respectively with different values of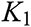 
. The thermal conductivity parameter has a significant impact on all fields. Physically, for the variable 
, the temperature is a linear function with negative values of 
, the heat conductivity decreases with the arising of the temperature, and the distance between the particles increases. The wave speed progress of all fields is slower. Thus, the values of all fields of quantities decrease.
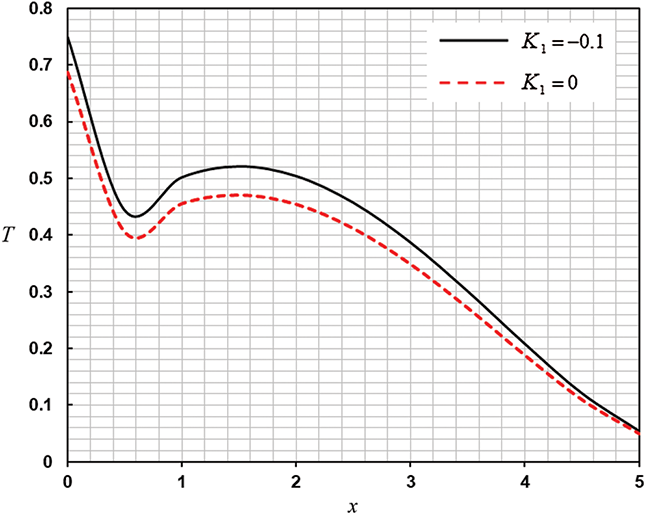
Figure 5: The effect of variation of thermal conductivity on temperature distribution
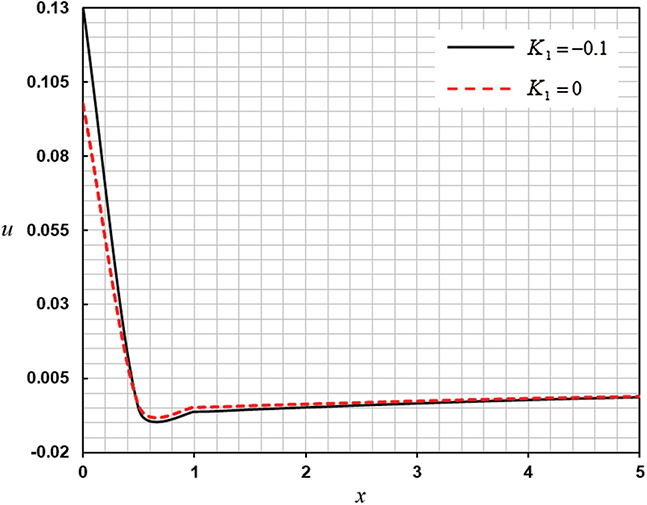
Figure 4: The effect of variation of thermal conductivity on displacement distribution
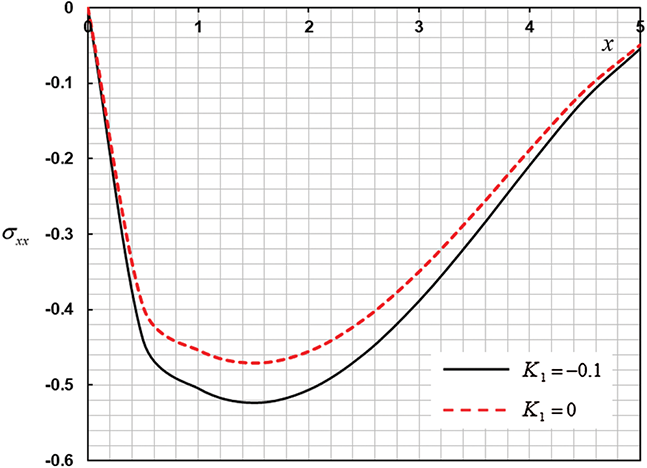
Figure 6: The effect of variation of thermal conductivity on the stress distribution
The physical field variables numerical values were calculated and presented by graphs in Figs. 7–9 respect to the axis 
to clear the variations nature of the field in the context of different thermoelastic models. The figures illustrate that all variables nearly have the same nature for the (LS), (GN), and (CD) models. Their behaviors are significantly different. The wave propagation with finite speeds is manifested in all figures for theories of (LS) and (GN). It differs for the case for considering the coupled equation of heat conduction (CD) model, in which the mechanical and thermal effects fill the entire space.
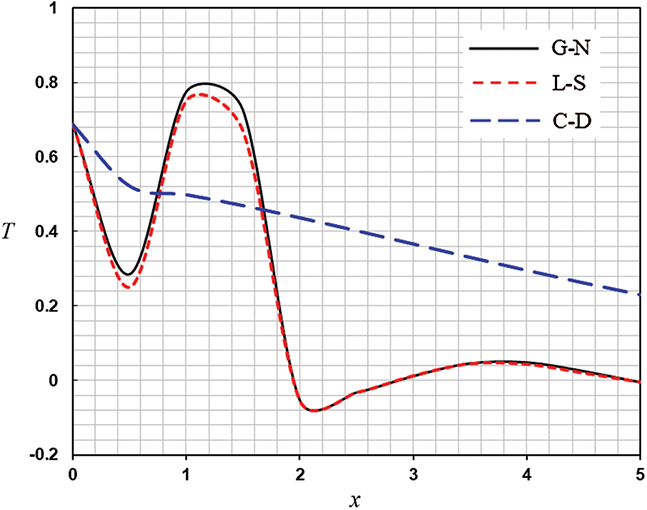
Figure 7: The temperature distribution in different theories of thermoelasticity
Figure 8: The displacement distribution in different theories of thermoelasticity
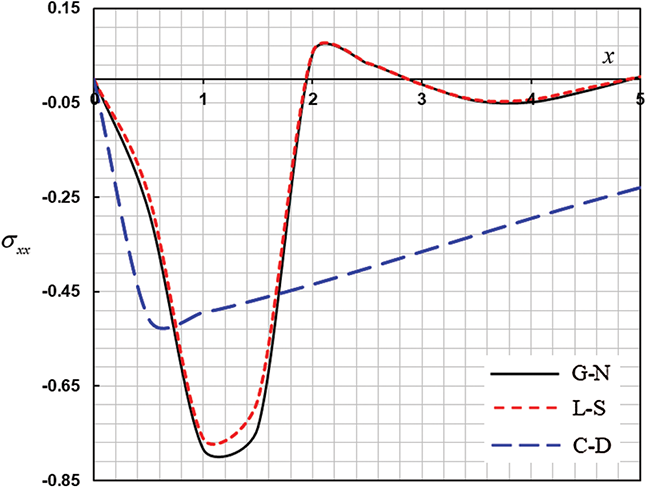
Figure 9: The stress distribution in different theories of thermoelasticity
The main observations from these figures are organized as:
• The LT technique is applied to derive the temperature, displacement, and stress due to the mechanical and thermal shock temperatures.
• The parameter 
has a strong impact on all the physical quantities.
• Considering the new models applied, we introduced a novel classification for the materials based on their fractional order parameter 
- a novel sign of ability.
• The results motivate the investigation of the conducting thermoelastic.
• The graphs illustrate the significant effect of the thermal conductivity on all the quantities fields and in different materials that we take into account in any analysis of heat conduction.
• The field quantities, displacement, temperature, stress, and do not depend only on the state and the space variables 
and 
but rely on the value of 
, as well which has a considerable role in developing all quantities.
• The different thermoelasticity theories, i.e., Lord and Shulman, GN, and classical dynamical coupled theories were compared.
• In the generalized thermoelasticity, the wave propagation with a finite speed is evident in all these figures. This is not the case of the theory of coupled thermoelasticity, where the considered function has non-vanishing values for all of 
values due to the propagation with an infinite speed of the signal thermal waves.
Acknowledgement: Taif University Researchers Supporting Project number (TURSP-2020/164), Taif University, Taif, Saudi Arabia.
Funding Statement: The author(s) received no specific funding for this study.
Conflicts of Interest: The authors declare that there is no conflicts of interest between all authors.
1. M. Biot. (1956). “Thermoelasticity and irreversible thermodynamics,” Journal of Applied Physics, vol. 127, no. 3, pp. 240–253. [Google Scholar]
2. H. W. Lord and Y. Shulman. (1967). “A generalized dynamical theory of thermoelasticity,” Journal of the Mechanics and Physics of Solids, vol. 15, no. 5, pp. 299–309. [Google Scholar]
3. A. E. Green and K. Lindsay. (1972). “Thermoelasticity,” Journal of Elasticity and the Physical Science of Solids, vol. 2, no. 1, pp. 1–7. [Google Scholar]
4. A. E. Green and P. M. Naghdi. (1993). “Thermoelasticity without energy dissipation,” Journal of Elasticity, vol. 31, no. 3, pp. 189–209. [Google Scholar]
5. V. A. Lomakin. (1976). The Theory of Elasticity of Non-Homogeneous Bodies. [in Russian], Izd. Mosk. Univ., Moscow. [Google Scholar]
6. F. Szuecs, M. Werner, R. S. Sussmann, C. S. J. Pickles and M. J. Frecht. (1999). “Temperature dependence of Young’s modulus and degradation of chemical vapor deposited diamond,” Journal of Applied Physics, vol. 86, no. 11, pp. 6010–6017. [Google Scholar]
7. O. R. Budaev, M. N. Ivanova and B. B. Damdinov. (2003). “Temperature dependence of shear elasticity of some liquids,” Advanced Colloid Interface Science, vol. 104, no. 1–3, pp. 307–310. [Google Scholar]
8. V. V. Rishin, B. A. Lyashenko, K. G. Akinin and G. N. Nadezhdin. (1973). “Temperature dependence of adhesion strength and elasticity of some heat resistant coatings,” Strength Materials, vol. 5, no. 1, pp. 123–126. [Google Scholar]
9. G. Honig and U. Hirdes. (1984). “A method for the numerical inversion of the Laplace transform,” Journal of Computation and Applied Mathematics, vol. 10, no. 1, pp. 113–132. [Google Scholar]
10. A. Carpinter and F. Mainardi. (1997). Fractals and Fractional Calculus in Continuum Mechanics. CISM International Centre for Mechanical Sciences, Springer Verlag, pp. 291–348. [Google Scholar]
11. D. A. Benson, S. W. Wheatcraft and M. M. Meerschaert. (2000). “The fractional-order governing equation of Lévy motion,” Water Resources Research, vol. 36, no. 6, pp. 1413–1423. [Google Scholar]
12. R. Metzler and J. Klafter. (2000). “The random walk’s guide to anomalous diffusion: A fractional dynamics approach,” Physics Reports, vol. 339, no. 1, pp. 1–77. [Google Scholar]
13. F. Khanna and D. Matrasulov. (2006). “Non-linear dynamics and fundamental interactions,” Series II: Mathematics, Physics and Chemistry, vol. 213, NATO Public Diplomacy Division. [Google Scholar]
14. I. Podlubny. (1999). Fractional Differential Equations. New York: Academic Press, pp. 340. [Google Scholar]
15. B. Ross. (1977). “The development of fractional calculus,” Historia Mathematica, vol. 4, no. 1, pp. 75–89. [Google Scholar]
16. K. S. Miller and B. Ross. (1993). An introduction to the fractional calculus and fractional differential equations. New York: A Wiley-Interscience Publication, John Wiley & Sons. [Google Scholar]
17. H. M. Youssef and E. A. Al-Lehaibi. (2010). “Fractional order generalized thermoelastic half-space subjected to ramp-type heating,” Mechanics Research Communications, vol. 37, no. 5, pp. 448–452. [Google Scholar]
18. H. H. Sherief, A. M. A. El-Sayed and A. M. Abd El-Latief. (2010). “Fractional order theory of thermoelasticity,” International Journal of Solids and Structures, vol. 47, no. 2, pp. 269–275. [Google Scholar]
19. Y. Z. Povstenko. (2007). “Two-dimensional axisymmetric stresses exerted by instantaneous pulses and sources of diffusion in an infinite space in a case of time-fractional diffusion equation,” International Journal of Solids and Structures, vol. 44, no. 7–8, pp. 2324–2348. [Google Scholar]
20. Y. Z. Povstenko. (2010). “Fractional radial heat conduction in an infinite medium with a cylindrical cavity and associated thermal stresses,” Mechanics Research Communications, vol. 37, no. 4, pp. 436–440. [Google Scholar]
21. M. N. Allam, K. A. Elsibai and A. E. Abouelregal. (2010). “Magneto-thermoelasticity for an infinite body with a spherical cavity and variable material properties without energy dissipation,” International Journal of Solids and Structures, vol. 47, pp. 2631–2638. [Google Scholar]
22. A. E. Abouelregal. (2011). “Fractional order generalized thermo-piezoelectric semi-infinite medium with temperature-dependent properties subjected to a ramp-type heating,” Journal of Thermal Stresses, vol. 34, no. 11, pp. 1139–1155. [Google Scholar]
23. M. Marin, A. M. Abd-Alla, D. Raducanu and S. M. Abo-Dahab. (2015). “Structural continuous dependence in micropolar porous bodies,” Computers, Materials & Continua, vol. 45, no. 2, pp. 107–125. [Google Scholar]
24. A. Riaz, R. Ellahi, M. M. Bhatti and M. Marin. (2019). “Study of heat and mass transfer in the Eyring–Powell model of fluid propagating peristaltically through a rectangular compliant channel,” Heat Transfer Research, vol. 50, no. 16, pp. 1539–1560. [Google Scholar]
25. S. M. Abo-Dahab. (2011). “Reflection of P and SV waves from stress-free surface elastic half-space under influence of magnetic field and hydrostatic initial stress without energy dissipation,” Journal of Vibration and Control, vol. 17, no. 14, pp. 2213–2221. [Google Scholar]
26. S. M. Abo-Dahab and Kh. Lotfy. (2015). “Generalized magneto-thermoelasticity with fractional derivative heat transfer for a rotation of a fibre-reinforced thermoelastic,” Journal of Computational and Theoretical Nanoscience, vol. 12, no. 8, pp. 1869–1881. [Google Scholar]
27. S. M. Abo-Dahab and A. M. Abd-Alla. (2016). “Green Lindsay model on reflection and refraction of p- and SV-waves at interface between solid-liquid media presence in magnetic field and initial stress,” Journal of Vibration and Control, vol. 22, no. 12, pp. 2885–2897. [Google Scholar]
28. M. S. Abdalla, M. Abdel-Aty and A. S. F. Obada. (2002). “Degree of entanglement for anisotropic coupled oscillators interacting with a single atom,” Journal of Optics B: Quantum and Semiclassical Optics, vol. 4, no. 6, pp. 396–401. [Google Scholar]
29. M. A. Ezzat. (2011). “Magneto-thermoelasticity with thermoelectric properties and fractional derivative heat transfer,” Physica B, vol. 406, pp. 30–35. [Google Scholar]
30. S. M. Abo-Dahab and I. A. Abbas. (2011). “LS model on thermal shock problem of generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity,” Applied Mathematical Modeling, vol. 35, pp. 3759–3768. [Google Scholar]
31. F. Durbin. (1974). “Numerical inversion of Laplace transformation: An efficient improvement to Durbin and Abate’s method,” Computer Journal, vol. 17, no. 4, pp. 371–376. [Google Scholar]
32. S. M. Abo-Dahab, A. A. El-Bary, Y. Al-Hadeethi and M. Alkashif. (2020). “Mathematical model on gravitational electro-magneto-thermoelasticity with two temperature and initial stress in the context of three theories,” Mathematics, vol. 8, pp. 1–31. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |