DOI:10.32604/cmc.2021.014746

| Computers, Materials & Continua DOI:10.32604/cmc.2021.014746 |  |
| Article |
Energy-Efficient Low-Complexity Algorithm in 5G Massive MIMO Systems
1Wireless and Radio Science Centre (WARAS), Faculty of Electrical and Electronic Engineering, Universiti Tun Hussein Onn Malaysia, Batu Pahat, Johor, 86400, Malaysia
2Faculty of Engineering Technology, Universiti Tun Hussein Onn Malaysia, Pagoh, Muar, Johor, Malaysia
3Fakulti Kejuruteraan Elektrik, Universiti Teknologi MARA Kampus Permatang Pauh Permatang Pauh, Pulau Pinang, 13500, Malaysia
*Corresponding Author: Lukman Audah. hanif@uthm.edu.my
Received: 13 October 2020; Accepted: 16 November 2020
Abstract: Energy efficiency (EE) is a critical design when taking into account circuit power consumption (CPC) in fifth-generation cellular networks. These problems arise because of the increasing number of antennas in massive multiple-input multiple-output (MIMO) systems, attributable to inter-cell interference for channel state information. Apart from that, a higher number of radio frequency (RF) chains at the base station and active users consume more power due to the processing activities in digital-to-analogue converters and power amplifiers. Therefore, antenna selection, user selection, optimal transmission power, and pilot reuse power are important aspects in improving energy efficiency in massive MIMO systems. This work aims to investigate joint antenna selection, optimal transmit power and joint user selection based on deriving the closed-form of the maximal EE, with complete knowledge of large-scale fading with maximum ratio transmission. It also accounts for channel estimation and eliminating pilot contamination as antennas  . This formulates the optimization problem of joint optimal antenna selection, transmits power allocation and joint user selection to mitigate inter-cell-interference in downlink multi-cell massive MIMO systems under minimized reuse of pilot sequences based on a novel iterative low-complexity algorithm (LCA) for Newton’s methods and Lagrange multipliers. To analyze the precise power consumption, a novel power consumption scheme is proposed for each individual antenna, based on the transmit power amplifier and CPC. Simulation results demonstrate that the maximal EE was achieved using the iterative LCA based on reasonable maximum transmit power, in the case the noise power is less than the received power pilot. The maximum EE was achieved with the desired maximum transmit power threshold by minimizing pilot reuse, in the case the transmit power allocation
. This formulates the optimization problem of joint optimal antenna selection, transmits power allocation and joint user selection to mitigate inter-cell-interference in downlink multi-cell massive MIMO systems under minimized reuse of pilot sequences based on a novel iterative low-complexity algorithm (LCA) for Newton’s methods and Lagrange multipliers. To analyze the precise power consumption, a novel power consumption scheme is proposed for each individual antenna, based on the transmit power amplifier and CPC. Simulation results demonstrate that the maximal EE was achieved using the iterative LCA based on reasonable maximum transmit power, in the case the noise power is less than the received power pilot. The maximum EE was achieved with the desired maximum transmit power threshold by minimizing pilot reuse, in the case the transmit power allocation 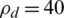 dBm, and the optimal
dBm, and the optimal  Mb/j.
Mb/j.
Keywords: Massive MIMO; energy efficiency; base station; active users; pilot contamination; low-complexity algorithm; radio frequency
Massive multiple-input multiple-output (MIMO) systems are an increasingly interesting area of study. They have become an essential technology for fifth-generation (5G) cellular networks that support big rate traffic. The 5G and beyond-5G based on cognitive radio technologies are helpful to use the available spectrum to achieve the QoS and increase the overall quality of the network [1–3]. Furthermore, massive MIMO systems are crucial when investigating power trade-off pilot sequences for channel estimation to acquire higher energy efficiencies (EEs) for green communication systems.
One of the major challenges facing massive MIMO systems is pilot contamination (PC), which arises from a large number of pilot reuse sequences (PRSs) due to non-orthogonal pilot sequences between neighboring cells. This problem requires a finite number of PRS due to the limited channel coherence intervals. The interference of active users (UEs) in neighboring cells is largely determined based on the evaluation of large-scale fading involved in the joint channel processing [4]. Predicting the mean signal strength decays is highly important in an occupation to measure the status of the channel due to the raised power created from the distance between the base station (BS) and UEs based on the large-scale fading. Additionally, the asymptotic signal-to-interference noise ratio (SINR) only relates to the large-scale fading of UEs that reuse pilot sequences. Meanwhile, the growth in the number of antenna (NoA) arrays at the BS provides more power consumption, since every antenna connects with a complex number of radio frequency (RF) chains that consume more power. Massive MIMO systems can achieve higher EE due to their active interference suppression at reasonable complexities [4,5].
In both the BS and UE, a larger number of RF chains consume more power because of the processing performance in the digital-to-analogue converter (DAC), power amplifier, multiplexer and filter. Moreover, all antennas at the BS must connect with the RF chains. It is estimated that about a third of the total electricity has been consumed, and 30 million tonnes of carbon dioxide  is emitted on a yearly basis [6] in multiple cellular systems. Recent studies report that around 80% of the energy is consumed in the cellular network at the BS. This creates the need to redesign the BS technology in order to decrease the power consumption, and in turn extend the battery life at the terminal. One important challenge that arises involves finding a way to reduce the high hardware complexity due to the consumption of the circuit power at the BS. This depends on the number of available antennas using the best performing antenna selection, optimal power allocation, and channel state information (CSI) accuracy for maximal transmission power. There is also a requirement to reduce the circuit power consumption (CPC) at the BS in order to determine consumption at the BS by determining the optimal number of RF chains when the NoAs is increased. BSs are accountable for 80% of the total energy expended in cellular systems. This significant consumption is a technical challenge that cannot be ignored [7,8]. Achieving maximal EE is a complex problem. This difficulty is compounded in massive MIMO systems because designing energy-efficient systems depends on analyzing the growth of the NoAs, distributed users, and the transmit power in each. Achieving antenna selection and optimal transmission power are crucial features for increasing EE.
is emitted on a yearly basis [6] in multiple cellular systems. Recent studies report that around 80% of the energy is consumed in the cellular network at the BS. This creates the need to redesign the BS technology in order to decrease the power consumption, and in turn extend the battery life at the terminal. One important challenge that arises involves finding a way to reduce the high hardware complexity due to the consumption of the circuit power at the BS. This depends on the number of available antennas using the best performing antenna selection, optimal power allocation, and channel state information (CSI) accuracy for maximal transmission power. There is also a requirement to reduce the circuit power consumption (CPC) at the BS in order to determine consumption at the BS by determining the optimal number of RF chains when the NoAs is increased. BSs are accountable for 80% of the total energy expended in cellular systems. This significant consumption is a technical challenge that cannot be ignored [7,8]. Achieving maximal EE is a complex problem. This difficulty is compounded in massive MIMO systems because designing energy-efficient systems depends on analyzing the growth of the NoAs, distributed users, and the transmit power in each. Achieving antenna selection and optimal transmission power are crucial features for increasing EE.
The EE metric becomes an important design when taking into account CPC. The optimal transmit power allocation highly depends on selection of the optimal antenna and of flexible users to improve the EE in the cellular system. More transmit antennas are required to serve a number of allocated UEs, in which case the RF chains and high CPC are involved in signal transmission from BS to UEs. Prior work [4,9–12] has investigated a joint PC and transmit data power allocation with respect to deriving SINR per UEs and the power transmits constraint to maximize the global EE. Additionally, the EE was maximized using joint pilot optimized power allocation and an optimal number of activated antennas. The SINR for pilot sequences improved the channel, making it possible to acquire a closed-form rate of transmitting power allocation, and a significant NoAs.
In this work, the energy-efficient massive MIMO system focused not only on joint antenna selection, optimal transmit power, and joint user selection, but also analyzed a CPC to balance the radiated EE and adjust the length of the pilot sequences to improve channel estimation as shown in Fig. 1. The new power consumption model for each antenna was proposed based on transmit power and CPC to obtain the exact power consumption. This algorithm for joint antenna selection helps in selecting an accurate number of active RF chains to reduce CPC and the PRS, in order to improve channel estimation and achieve higher data rates and EE. These primary objectives of this study are as follows:
• To investigate the lower bounds of the achievable downlink (DL) data rate and SINR based on relative channel estimation with full knowledge of large-scale fading by using PRS and performance analysis of maximum ratio transmission (MRT) to eliminate different levels of PC.
• To minimise the consumption circuit power for antenna selection and obtain a high-quality channel estimate based on correlates of the training signal with the established PRS of every UE for the linear processing MRT to mitigate interference.
• To analyse the exact power consumption based on a proposed novel power consumption model for each antenna based on the analysis of the power amplifier and CPC that enable the use of low-cost RF amplifiers that exploit antenna selection.
• To propose a novel iterative low-complexity algorithm (LCA) for optimal antenna selection, joint optimal transmit power, and joint user selection under the impact of PRS to achieve optimal EE.

Figure 1: System model for massive multi-cell MIMO
The EE metric becomes an important design criterion, because it allows operations to remain practically affordable through regulated energy consumption levels. The orthogonal pilot sequences for all UEs in the same cell prevent channel estimation from being affected by the interference of other UEs. Prior work [13,14] analysed the PC, which impacts the data rate to provide equivalent channel estimation and reduce inter-cell interference to obtain a suitable performance system and in turn achieve a high data rate. Furthermore, determining the status of the CSI requires a comparison of the received pilot from every UE with the recognised pilot signal associated with that UE. The key requirement for maximising EE is to compute the joint transmission power and optimal antenna selection under the affected pilot sequences. The number of selected antennas is crucial, because when the RF chains are connected to the selected antennas, those antennas consume more power and have a negative impact on EE. Moreover, the increased NoAs when transmitting pilot sequences to every UE estimate the M channel in the DL. The authors in [15–21] aimed to enhance the EE by using a novel power consumption model by analysing the transmit power. They also proposed that the RF chain pattern could be determined by employing antenna selection schemes to optimise the energy and cost efficiency of the 5G system shown in Tab. 1. The majority of researchers focused only on reducing RFs at the raised numbers of antennas to maximise EE, while others investigated the number of RF chains, taking into account the influence of channel estimation for large PRS when the NoAs increased. However, the authors in [22–31] investigated the maximum EE by studying the DL massive MIMO system with optimising the NoAs, a number of UEs, and CPC for transmitting power, by taking into account the channel estimation and PC. The computational power with a minimum number of RF chains and the joint antenna selection optimise EE when the transmitter was equipped with a significant NoA.
Table 1: The summary of previous related studies on related data rate and EE

Many works have investigated the progress of actual models and efficient algorithms user selection. Optimal performance EE is achieved by applying lower computational complexity by employed equal transmit power allocated to every UE. The authors in [32–35] proposed improving cell capacity by activating a large number of BSs by reducing cost with a limited number of RF chains. The combinatorial complexity of low-complexity joint antenna selection and user scheduling provide a high cell capacity by mitigating inter-cell interference. The user selection and channel estimation improved based on mitigating the inter-user interference by using a low-complexity iterative solution to obtain optimal transmit power control and user selection. Moreover, the author in [36] proposed the low-complexity iterative solution in multi-cell Non-Orthogonal Multiple Access-based 5G cellular networks to study the fairness SINR-based exploiting transmit power allocation for diverse UE. Maximised EE was studied in [37–45] to achieve data rates with low transmit power by selecting the user’s maximum transmit power and minimum rate constraints. The maximum EE achieved the minimum required power and rate constraints depends on analysing the circuit power when the transmitter was equipped with a significant NoA.
In this research, the problem arises due to the increasing NoAs in the massive MIMO system, due to inter-cell interference for CSI. Moreover, a higher number of RF chains at the BS and UEs consume more power, due to the processing activities in the DAC and power amplifier. Therefore, antenna selection, user selection, optimal transmission power, and PRS are vital aspects in improving EE. In this work, we propose channel estimation with comprehensive knowledge of large-scale fading to eliminate PC. The channel estimation was evaluated at the received signal based on the BS correlating the training signal with the recognised PRS of each UE, to achieve a high-quality channel estimate. This work also investigated the performance of a joint optimal antenna selection, optimal transmit power, and joint user selection with minimum PRS, based on proposing a novel LCA algorithm by applying Newton’s method and Lagrange multiplier. Whereas the purpose of using LCA is to improve the joint optimal antenna selection, optimal transmit power allocation and joint user selection for optimisation problems under the impact of PRS to maximise EE.
In a DL multi-cell network, every cell contains one BS. Each BS contains several transmit antennas, M, and users, K, each of which is equipped with one antenna. The BS transmits data signals simultaneously, where  . The assumed channel reciprocities are the same in the uplink and DL channels, where the channel model
. The assumed channel reciprocities are the same in the uplink and DL channels, where the channel model  is able to assign a different antenna correlation to every channel between the UEs in BS l and M in BS j. In
is able to assign a different antenna correlation to every channel between the UEs in BS l and M in BS j. In 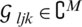 ,
, 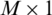 is the small-scale fading channel and
is the small-scale fading channel and  accounts for the corresponding channel correlation matrix for large-scale fading (from BS l to UE k in cell j). The channel between BS l and the
accounts for the corresponding channel correlation matrix for large-scale fading (from BS l to UE k in cell j). The channel between BS l and the  user in cell j is given by the following equation:
user in cell j is given by the following equation:

The DL assumed that the BS is working with an imperfect CSI. The received signal of the  user,
user,  inside the jth cell can be expressed as follows:
inside the jth cell can be expressed as follows:

where 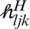 is the Hermitian transpose channel matrix, and the UEs, K, in every cell employ orthogonal pilot reuse to estimate the channel. The transmit signal vector for the BS
is the Hermitian transpose channel matrix, and the UEs, K, in every cell employ orthogonal pilot reuse to estimate the channel. The transmit signal vector for the BS  ,
,  representing the linear precoding matrix,
representing the linear precoding matrix,  is the data symbol transmitted from the BS in cell l to the UEs, and
is the data symbol transmitted from the BS in cell l to the UEs, and 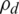 is the DL transmit power. The channels are estimated using pilot sequences transmitted by UEs. Through the uplink-training phase, K UEs in the similar cell transmit an orthogonal pilot sequence, where
is the DL transmit power. The channels are estimated using pilot sequences transmitted by UEs. Through the uplink-training phase, K UEs in the similar cell transmit an orthogonal pilot sequence, where 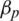 the symbol of the DL is pilot, and
the symbol of the DL is pilot, and 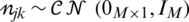 is the received noise vector. The massive MIMO worked to acquire full channel knowledge based on the minimum mean squared error (MMSE) properties employed in [10]. The distributed channel,
is the received noise vector. The massive MIMO worked to acquire full channel knowledge based on the minimum mean squared error (MMSE) properties employed in [10]. The distributed channel,  , can be estimated as follows:
, can be estimated as follows:

3.2 Suppressed Pilot Contamination in Downlink Transmission
Based on the correlated received pilot sequences and channel estimation, the interference is reduced to achieve low-complexity in channel estimation, which is expressed as follows:

where 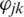 is the variance channel and
is the variance channel and  is the equivalent channel correlation matrix for large-scale fading. Channel estimation requires a limited number of PRS for channel coherence, so the received training signal is used for the same PRS to adjacent cells, and can also be used to estimate the channel as follows:
is the equivalent channel correlation matrix for large-scale fading. Channel estimation requires a limited number of PRS for channel coherence, so the received training signal is used for the same PRS to adjacent cells, and can also be used to estimate the channel as follows:

The MMSE estimate of the channel depends on 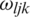 and matrix inversion, where
and matrix inversion, where  . According to the received training signal for large-scale fading,
. According to the received training signal for large-scale fading,  , the estimation channel proportional to MMSE is given as follows:
, the estimation channel proportional to MMSE is given as follows:

By substituting Eqs. (4)–(6), the channel response is estimated based on the mitigated PC using a correlated channel matrix. According to [33], the received signal is decomposed as follows:
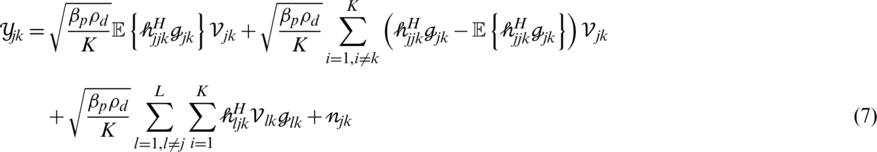
3.3 Achievable Data Rate in Downlink Transmission
The achievable data rate for transmission from BS l is obtained by considering Gaussian noise as the worst case in the uncorrelated noise channel, which can be represented as follows:

According to several studies [4,9,10,13–17,33–35], PRS is used in the average channel gain of 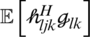 . Many antennas employ an orthogonal pilot sequence to evaluate the channel according to the number of transmit antennas, where the PRS are correlated between the channel,
. Many antennas employ an orthogonal pilot sequence to evaluate the channel according to the number of transmit antennas, where the PRS are correlated between the channel, 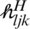 and the precoding,
and the precoding,  in a neighbouring cell. The correlation occurred between a signal’s spatial direction and the regular received signal gain
in a neighbouring cell. The correlation occurred between a signal’s spatial direction and the regular received signal gain 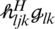 . Obtaining a high-quality channel estimation depends on when the BS correlates the training signal by the conventional PRS of every UE, and based on the training received signal for large-scale fading
. Obtaining a high-quality channel estimation depends on when the BS correlates the training signal by the conventional PRS of every UE, and based on the training received signal for large-scale fading  . The SINR was derived at the kth UEs. The conventional user selection is established according to SINR, and the desired signal for the SINR [36] can be written as follows:
. The SINR was derived at the kth UEs. The conventional user selection is established according to SINR, and the desired signal for the SINR [36] can be written as follows:

The uncorrelated noise power can be written as follows:
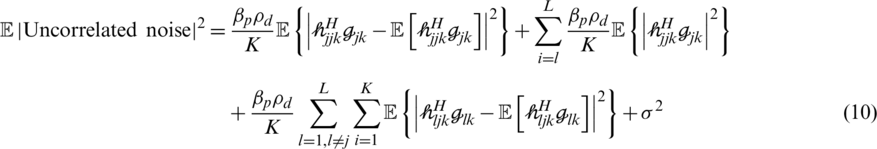
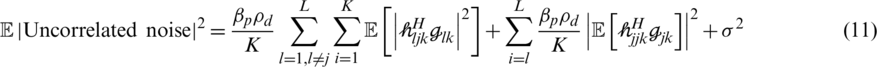
The SINR of UEs is calculated in Eq. (12) as

From the received signal in Eq. (12), the average channel is estimated and interference power in the closed-form for MRT precoding, which can be expressed as follows:

The noise variance was obtained from the large fading. The properties of the variance channels were used from [26,33]: 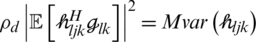 . Using Eq. (4), the row vector of the channel response estimated,
. Using Eq. (4), the row vector of the channel response estimated, 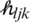 between UEs in the jth cell and the BS in the l th cell, where
between UEs in the jth cell and the BS in the l th cell, where 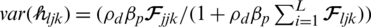 . The channel CSI was obtained for the MMSE when the covariance channel interference was small and the pilot power was reasonable. The achievable data rate in closed-form is expressed as.
. The channel CSI was obtained for the MMSE when the covariance channel interference was small and the pilot power was reasonable. The achievable data rate in closed-form is expressed as.
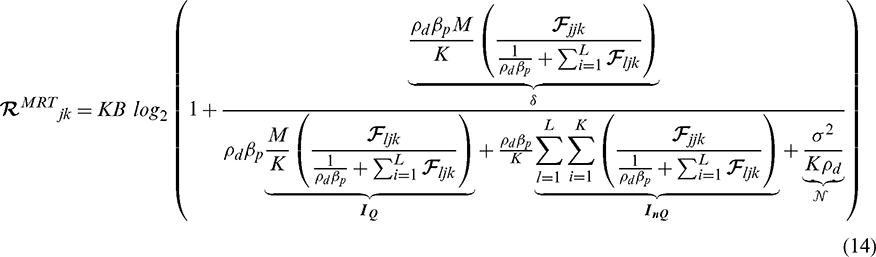
Following the asymptotic analysis by [17,26,33–36], based on Eq (14), the estimated channel accuracy was obtained based on the received average signal power for the desired signal in the numerator,

According to Eq (14), the first term in the denominator represents the inter-cell interference power affected by PC, which is limited in MRT at increased power for the coherence channel, impacted with a pilot at an increasing number of M.

The second term Eq (14) in the denominator represents the non-coherence inter-cell interference power created by signals from the interfering BSs, and was independent of the NoAs, M. Meanwhile, an increase in the NoA arrays at BS resulted in more power consumption at a higher number of RF chains, and increased the amount of the inter-cell interference for channels, as follows:

The third term Eq (14) in the denominator, where  represents additive Gaussian noise.
represents additive Gaussian noise.

From 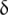 in the numerator,
in the numerator, 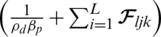 , the interference becomes limited in the DL, while
, the interference becomes limited in the DL, while 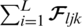 represents the sum of the square of the propagation transmitted from the BS in the jth cell to every user inside the lth cell. Each BS provided ab asymptotic data rate with MRT. Based on these substitutions from Eq. (14a) to Eqs. (14d) and (15) can be simplified as follows:
represents the sum of the square of the propagation transmitted from the BS in the jth cell to every user inside the lth cell. Each BS provided ab asymptotic data rate with MRT. Based on these substitutions from Eq. (14a) to Eqs. (14d) and (15) can be simplified as follows:

where B represents the bandwidth of the baseband signal. From Eq. (15), the inter-cell interference in the denominator can be simplified as 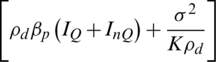 by substituting
by substituting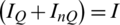 . By using a correlated received pilot matrix, the conventional (low-complexity) channel estimation is obtained by mitigating the impact of the correlation property of the pilots according to Eq. (9), to Eq (14). The interference is limited for imperfect channel estimation with MRT in multi-cell when the I > 0 and
. By using a correlated received pilot matrix, the conventional (low-complexity) channel estimation is obtained by mitigating the impact of the correlation property of the pilots according to Eq. (9), to Eq (14). The interference is limited for imperfect channel estimation with MRT in multi-cell when the I > 0 and  . This allows many orders of EE gains, because a large multiplexing gain is achieved with small power consumption. The aim is to obtain exact expressions by achieving the interesting effect of physical insights on the achievable rate of the massive MIMO system, due to inter-cell interference for CSI, CPC with the number of BS antennas, and the number of users. Furthermore, it is shown that the exact expression of (14) has remained elusive because it involves exponential integral functions and becomes more sophisticated and complicated. Therefore, it is hard to offer intuitive physical insight. To handle these disadvantages, a tractable approximate expression that could let us have intuitive insights is derived. These insights establish a compelling rationale for the massive MIMO system. According to the random matrix theory [37,40], the closed-form of the achievable data rate can be expressed as follows:
. This allows many orders of EE gains, because a large multiplexing gain is achieved with small power consumption. The aim is to obtain exact expressions by achieving the interesting effect of physical insights on the achievable rate of the massive MIMO system, due to inter-cell interference for CSI, CPC with the number of BS antennas, and the number of users. Furthermore, it is shown that the exact expression of (14) has remained elusive because it involves exponential integral functions and becomes more sophisticated and complicated. Therefore, it is hard to offer intuitive physical insight. To handle these disadvantages, a tractable approximate expression that could let us have intuitive insights is derived. These insights establish a compelling rationale for the massive MIMO system. According to the random matrix theory [37,40], the closed-form of the achievable data rate can be expressed as follows:

The improved EE based on the proposed methods for the joint antenna selection, transmit power allocation and joint user selection by utilizing LCA to reduce the CPC and power consumption.
The power consumed for DL transmission comprises the power consumed by the circuit and the power used for pilot transmission. Due to a reduction in energy consumption, a large numbers of antennas, M allow the use of low-cost RF amplifiers that exploit antenna selection for each subcarrier, including the pilot sequences and data transmission.

The peak-to-average power ratio (PAPR) followed  . The coherence interval for channel estimation involved a finite number of orthogonal pilot sequences and desired pilot signals, which provide high data power to minimise the power consumption requirements for antenna selection [38,39]. The transmit RF chain chose the performing antenna selection in the case an equal power allocation included UEs from Eq. (18). The transmit power for pilot and data transmission can be expressed as follows:
. The coherence interval for channel estimation involved a finite number of orthogonal pilot sequences and desired pilot signals, which provide high data power to minimise the power consumption requirements for antenna selection [38,39]. The transmit RF chain chose the performing antenna selection in the case an equal power allocation included UEs from Eq. (18). The transmit power for pilot and data transmission can be expressed as follows:
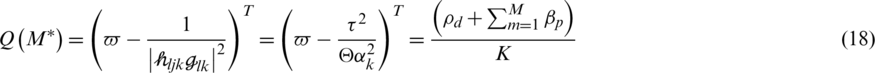
where  ,
,  , and
, and 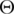 represent the path loss exponent satisfying the constraint power, noise power at receiver, and the propagation loss respectively. The diagonal matrix in data rate
represent the path loss exponent satisfying the constraint power, noise power at receiver, and the propagation loss respectively. The diagonal matrix in data rate  , contains singular values
, contains singular values  . The dynamic power consumption Qc consists of transmitting power, a proportional to the number of transmission antennas, and the circuit power of the RF chains QRF. CPC increases proportionally to the NoA, M. From the practical view of power consumption, CPC cannot be ignored when the NoA increases. Additionally, CPC Qc, represents baseband processing power, QBB, due to conversion from analogue to digital or digital-to-analogue (ADC/DAC), and QRF is the power consumption for each antenna in the RF chains, due to the noise amplifier. The possibility for RF chains to have limited functionality such as much lower transmit power, limited PAPR of the power amplifier, and low-resolution ADCs having only a few bits, potentially reduces the cost per RF frontend, where Qc = QBB + QRF. The total power consumed by the power amplifier
. The dynamic power consumption Qc consists of transmitting power, a proportional to the number of transmission antennas, and the circuit power of the RF chains QRF. CPC increases proportionally to the NoA, M. From the practical view of power consumption, CPC cannot be ignored when the NoA increases. Additionally, CPC Qc, represents baseband processing power, QBB, due to conversion from analogue to digital or digital-to-analogue (ADC/DAC), and QRF is the power consumption for each antenna in the RF chains, due to the noise amplifier. The possibility for RF chains to have limited functionality such as much lower transmit power, limited PAPR of the power amplifier, and low-resolution ADCs having only a few bits, potentially reduces the cost per RF frontend, where Qc = QBB + QRF. The total power consumed by the power amplifier  related to transmission power,
related to transmission power,  , according to [32,39]. To analyse the precise power consumption, two primary components proposed at the BS: power consumed by the power amplifier
, according to [32,39]. To analyse the precise power consumption, two primary components proposed at the BS: power consumed by the power amplifier  and power consumed by the circuit, where the CPC accounts for the energy consumption to the number of RF chains. In order to give physical insights about the radiation of RF power in massive MIMO system. It is shown that the exact expression of (19) has remained elusive because the field around an RF transmitter antenna is an energy harvesting system. Also, from the practical view of power consumption, CPC cannot be ignored when the NoA increases. The transmitted power might be increased up to the maximum power level according to NoAs, which can be expressed as follows:
and power consumed by the circuit, where the CPC accounts for the energy consumption to the number of RF chains. In order to give physical insights about the radiation of RF power in massive MIMO system. It is shown that the exact expression of (19) has remained elusive because the field around an RF transmitter antenna is an energy harvesting system. Also, from the practical view of power consumption, CPC cannot be ignored when the NoA increases. The transmitted power might be increased up to the maximum power level according to NoAs, which can be expressed as follows:

4 Low Complexity Algorithm and Problem Formulation
In this process, it is complicated to design the joint antenna selection, joint power allocation and joint user selection that maximises EE if only using the ratio of achievable data rates to overall consumed power at the BS for a significant number of transmit antennas.
4.1 Maximising Energy Efficiency
The maximum of EE depends on calculating the optimisation PRS, 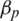 and data rate used as the index to compute system output and total power consumption. The aim is to obtain exact expressions by achieving the interesting effect of physical insights on the maximal EE of the massive MIMO system. Designing energy-efficient systems depend on analyzing the growth a higher number of RF chains at the BS and UEs consume more power, due to the processing activities in the DAC and power amplifier. Furthermore, it is shown that the exact expression of (20) has remained elusive because EE becomes a quasi-concave function with respect to the number of antennas in order to give physical insights about the radiation of RF power in massive MIMO system. To handle these disadvantages, a tractable approximated expression that could let us have intuitive insights is derived. The new model was used to perform EE by reducing the consumption power, and this had slightly affected the data rate. The maximised EE based on the channel condition achieved both high data rates and low power consumption, according Eqs. (16) and (19), as
and data rate used as the index to compute system output and total power consumption. The aim is to obtain exact expressions by achieving the interesting effect of physical insights on the maximal EE of the massive MIMO system. Designing energy-efficient systems depend on analyzing the growth a higher number of RF chains at the BS and UEs consume more power, due to the processing activities in the DAC and power amplifier. Furthermore, it is shown that the exact expression of (20) has remained elusive because EE becomes a quasi-concave function with respect to the number of antennas in order to give physical insights about the radiation of RF power in massive MIMO system. To handle these disadvantages, a tractable approximated expression that could let us have intuitive insights is derived. The new model was used to perform EE by reducing the consumption power, and this had slightly affected the data rate. The maximised EE based on the channel condition achieved both high data rates and low power consumption, according Eqs. (16) and (19), as

Energy-efficient power allocations maximise the EE by evaluating the transmit power, CPC and minimum rate constrained with imperfect channel estimation. The EE depends on distributed users in multi-cell by using a LCA for joint user selection that generates low-complexity at the BS, and improves the system performance. The conception of the data rate for joint user selection is denoted by the sum of the products between the binary association and data rate  . In order to denote the transmit power allocation and joint user selection, the user selection
. In order to denote the transmit power allocation and joint user selection, the user selection  determines whether the UEs is connected with BS to UEs. If the user k is connected with BS, the
determines whether the UEs is connected with BS to UEs. If the user k is connected with BS, the  ; otherwise,
; otherwise,  . From Eq. (20), the EE increased jointly and became quasi-concave with the increasing NoA, M, and distributed UEs in every cell K.
. From Eq. (20), the EE increased jointly and became quasi-concave with the increasing NoA, M, and distributed UEs in every cell K.
4.2 Proposed Low-Complexity Algorithm for Antenna Selection
According to the optimisation theory [36–39], joint transmit power is less than maximum transmit power, Qmax. Thus, following Eq. (20), the EE is formulated for the optimisation problem as follows.




where N is the NoA available. Constraints Eq. (20b) and Eq. (20d) are linear, while the EE is affected when transmitting 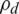 and
and  based on
based on  and becomes quasi-concave with respect to
and becomes quasi-concave with respect to 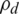 or
or 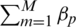 . The optimisation problem will be solved if
. The optimisation problem will be solved if 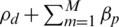 is less than Qmax. From Eq. (20), the EE decreases with circuit power, Qc when
is less than Qmax. From Eq. (20), the EE decreases with circuit power, Qc when  and
and 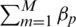 are fixed due to unavoidable interference from distributed users in the imperfect channel. The Newton method was adopted to solve the optimisation problem Eqs. (20)–(20d). A general nonlinear fractional programme can be expressed as
are fixed due to unavoidable interference from distributed users in the imperfect channel. The Newton method was adopted to solve the optimisation problem Eqs. (20)–(20d). A general nonlinear fractional programme can be expressed as

where 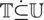 ,
, 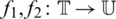 ,
, 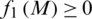 , and
, and 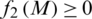 . The fractional programme in Eq. (21) was accomplished under concave-convex conditions, where
. The fractional programme in Eq. (21) was accomplished under concave-convex conditions, where 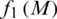 is concave and
is concave and  is convex on
is convex on  [40]; the maximum EE constraint can be expressed as:
[40]; the maximum EE constraint can be expressed as:

where 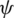 as the antenna set of the cell. However, after the calculated derivative was zero, the Newton method delays. For small values of the derivative, the Newton iteration off shoots away from the current point of repetition and can converge to a root far away from the intended domain. Obtaining the solution of the optimisation problem depends on rewriting Eq. (22) based on using the fractional programme, as follows
as the antenna set of the cell. However, after the calculated derivative was zero, the Newton method delays. For small values of the derivative, the Newton iteration off shoots away from the current point of repetition and can converge to a root far away from the intended domain. Obtaining the solution of the optimisation problem depends on rewriting Eq. (22) based on using the fractional programme, as follows

where f1 and f2 represent the concave,  is the fixed value with the concave, and
is the fixed value with the concave, and  is the peak value of the objective function in Eq. (21). Following Eq. (20), the problem of joint optimal antenna selection can be expressed as
is the peak value of the objective function in Eq. (21). Following Eq. (20), the problem of joint optimal antenna selection can be expressed as

Eq. (24) shows that the numerator of 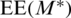 is concave, whereas the denominator is convex. A low-complexity iterative algorithm is employed to compute the optimal antenna by informing the iteration for every UE, to obtain the root of
is concave, whereas the denominator is convex. A low-complexity iterative algorithm is employed to compute the optimal antenna by informing the iteration for every UE, to obtain the root of  , which is estimated using Newton’s method to solve the root of
, which is estimated using Newton’s method to solve the root of 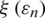 .
.

where M* is the optimal value of 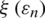 ; the function can also be represented as
; the function can also be represented as 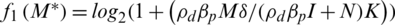 and as
and as  . Our objective is to obtain a LCA for an optimal antenna using the constrained transmit power in Eqs. (20b)–(20d). From Eq. (24), the NoA is inversely proportional Qc at a significant NoA, which in turn creates the interference for a significant number of PRS, and consumes more power in the denominator. To achieve the maximal EE, the PRS
. Our objective is to obtain a LCA for an optimal antenna using the constrained transmit power in Eqs. (20b)–(20d). From Eq. (24), the NoA is inversely proportional Qc at a significant NoA, which in turn creates the interference for a significant number of PRS, and consumes more power in the denominator. To achieve the maximal EE, the PRS 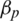 needs to be minimised when the number of
needs to be minimised when the number of 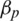 is smaller than the optimal number of available antennas. Every antenna M must transmit its pilot sequences using maximum transmit power
is smaller than the optimal number of available antennas. Every antenna M must transmit its pilot sequences using maximum transmit power 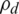 . According to Eq. (24), the near-optimal antenna selection M* was proved, which is proportional to the distributed number of users K. Moreover, the optimal antenna M* updates the iteration for every UE to obtain the optimal value of
. According to Eq. (24), the near-optimal antenna selection M* was proved, which is proportional to the distributed number of users K. Moreover, the optimal antenna M* updates the iteration for every UE to obtain the optimal value of 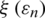 , which can be obtained using Eq. (26) when the value of Qc is small, which does not affect the value of Qc.
, which can be obtained using Eq. (26) when the value of Qc is small, which does not affect the value of Qc.

 converges to optimal values when the constraint conditions are achieved according to Eqs. (20a), (20b).
converges to optimal values when the constraint conditions are achieved according to Eqs. (20a), (20b).

:
4.3 Proposed Low-Complexity Algorithm for Transmission Power
In this process, the problem in Eq. (20) concerns the quasi-concavity of the system EE function using the achievable data rates to total power for pilot transmission. The maximum EE is evaluated based on the transmit power with PRS, 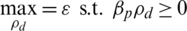 from the BS to the UE. The issue of power consumption between the UEs and BSs arising from the activity of UEs association with the BS needs to be considered. The joint optimal transmit power with a LCA is proposed to solve the optimisation problem. A maximum EE was achieved by applying the constraint user selection for data rate and transmission power, under the impact of PRS,
from the BS to the UE. The issue of power consumption between the UEs and BSs arising from the activity of UEs association with the BS needs to be considered. The joint optimal transmit power with a LCA is proposed to solve the optimisation problem. A maximum EE was achieved by applying the constraint user selection for data rate and transmission power, under the impact of PRS,  . The maximum EE was evaluated based on transmit power with PRS,
. The maximum EE was evaluated based on transmit power with PRS,  from the BS to UEs. The EE varies based on the accuracy of channel estimation for the transmitting rate, user selection and power consumption. To address this problem, these variables were relaxed and replaced Eqs. (20b)–(20d) with the following:
from the BS to UEs. The EE varies based on the accuracy of channel estimation for the transmitting rate, user selection and power consumption. To address this problem, these variables were relaxed and replaced Eqs. (20b)–(20d) with the following:

From [12,18,42] the relaxed problem Eqs. (27)–(27i) for transmission power can be expressed as follows:









where 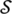 is an
is an  matrix with every element,
matrix with every element, 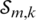 representing the allocation of distributed users,
representing the allocation of distributed users, 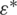 represents the maximum EE, and
represents the maximum EE, and  represents the minimum data rate transmitted to K. According to Eq. (27), the precise value of
represents the minimum data rate transmitted to K. According to Eq. (27), the precise value of  could not be achieved until the relaxed problem is solved, and the optimal
could not be achieved until the relaxed problem is solved, and the optimal 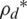 is obtained. The convergence condition for EE is achieved by updating the transmit power,
is obtained. The convergence condition for EE is achieved by updating the transmit power, 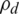 . The Eqs. (27a) and (27b) achieved the minimum data rate requirement of all users km to satisfy and guarantee the quality-of-service (QoS), a transmit signal from BS to UE. The constraints power allocation Eqs. (27c)–(27f) guarantee the upper and lower transmit power to every selection user. The Eq. (27i) shows that every UE is associated with only one BS by assigning the channel to one UE. Eqs. (27g) and (27h) represent km, the load of BS m in the cellular network, and the number of users selection with the BS. The relaxed problem shows that the EE was still quasi-concave when the total transmit power was used for the pilot,
. The Eqs. (27a) and (27b) achieved the minimum data rate requirement of all users km to satisfy and guarantee the quality-of-service (QoS), a transmit signal from BS to UE. The constraints power allocation Eqs. (27c)–(27f) guarantee the upper and lower transmit power to every selection user. The Eq. (27i) shows that every UE is associated with only one BS by assigning the channel to one UE. Eqs. (27g) and (27h) represent km, the load of BS m in the cellular network, and the number of users selection with the BS. The relaxed problem shows that the EE was still quasi-concave when the total transmit power was used for the pilot, 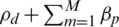 , when the transmit power is larger than the circuit power in Eqs. (27d) and (27e). Ebq. (27b) guarantees the minimal rate for every UE
, when the transmit power is larger than the circuit power in Eqs. (27d) and (27e). Ebq. (27b) guarantees the minimal rate for every UE  channel, which involves guaranteeing the transfer of the minimal rate constraint as achieved by the optimal transmit power
channel, which involves guaranteeing the transfer of the minimal rate constraint as achieved by the optimal transmit power  allocation. From [42,43], the objective function for fractional programming was equivalent to
allocation. From [42,43], the objective function for fractional programming was equivalent to 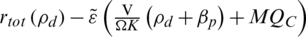 , and was used to obtain the optimal value of
, and was used to obtain the optimal value of 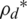 . The DL transmit power allocation is applied to achieve suitable performance in the LCA by using the Lagrange dual-decomposition method to solve the relaxed problem Eqs. (27)–(27d) as follows:
. The DL transmit power allocation is applied to achieve suitable performance in the LCA by using the Lagrange dual-decomposition method to solve the relaxed problem Eqs. (27)–(27d) as follows:
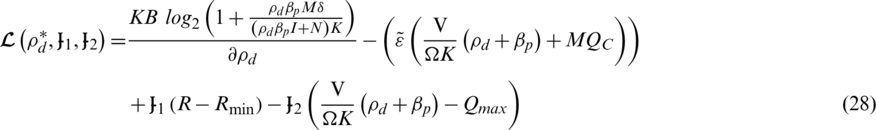
The maximum EE depends on the updated value of EE, 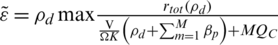 which was obtained by updating the transmit power
which was obtained by updating the transmit power . From Eqs. (27a) and (27d), it shows that
. From Eqs. (27a) and (27d), it shows that  , and the problem formulated in Eq. (27d) became a convex optimisation of transmission power to all UEs. Furthermore, the affected EE was due to a high pilot, which required optimisation of the PRS in the high SINR regime. The Lagrange multipliers
, and the problem formulated in Eq. (27d) became a convex optimisation of transmission power to all UEs. Furthermore, the affected EE was due to a high pilot, which required optimisation of the PRS in the high SINR regime. The Lagrange multipliers 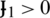 and
and  corresponded to the constraints of a data rate, which impacted interference for PRS and transmission power, which can be seen in Eqs. (27a) and (27d).
corresponded to the constraints of a data rate, which impacted interference for PRS and transmission power, which can be seen in Eqs. (27a) and (27d).
The relaxed problem Eqs. (27)–(27d) formulated in Eq. (28) was achieved for a given optimum value 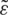 , when the relaxed problem is converted into a convex problem of distributed power allocation. The optimisation power allocation in Eq. (28) is solved by using the Karush-Kuhn-Tucker conditions to obtain the optimal value of the transmission power,
, when the relaxed problem is converted into a convex problem of distributed power allocation. The optimisation power allocation in Eq. (28) is solved by using the Karush-Kuhn-Tucker conditions to obtain the optimal value of the transmission power,  , according to [32,39]:
, according to [32,39]:
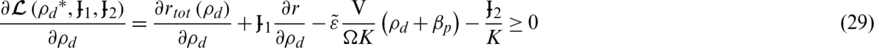
where  is the Lagrange multiplier vector corresponding to the data rate constraints with element,
is the Lagrange multiplier vector corresponding to the data rate constraints with element,  , and
, and  is the Lagrange multiplier corresponding to the transmit power constraint. From the Lagrange multiplier, the dual-decomposition method can be expressed as
is the Lagrange multiplier corresponding to the transmit power constraint. From the Lagrange multiplier, the dual-decomposition method can be expressed as

The transmit power should be allocated to every user by using a high-channel gain. From Eq. (30), the optimal transmit power obtained based on fixed and iterative Lagrange multipliers, where  :
:

where 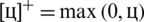 ,
,  is the maximal value of Eq. (21). Greater transmit power should be allocated to pilots to obtain reasonable channel estimation with large PRS,
is the maximal value of Eq. (21). Greater transmit power should be allocated to pilots to obtain reasonable channel estimation with large PRS,  when the NoA is fixed. The optimal power allocation,
when the NoA is fixed. The optimal power allocation,  for every UE in the DL increases with the desired pilot signals, the power to minimise the power consumption. Furthermore, when
for every UE in the DL increases with the desired pilot signals, the power to minimise the power consumption. Furthermore, when  converges to optimal values, the optimal transmit power,
converges to optimal values, the optimal transmit power, 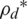 is obtained based on the power constraints in Eqs. (27a) and (27i). The EE increases initially, and then decreases due to the increased CPC for everyM, and impacted the interference for the pilot sequence when the transmitted power was increased. The optimal transmission power
is obtained based on the power constraints in Eqs. (27a) and (27i). The EE increases initially, and then decreases due to the increased CPC for everyM, and impacted the interference for the pilot sequence when the transmitted power was increased. The optimal transmission power  was derived according to the Lagrange multiplier. Consequently, the Lagrange multiplier could be updated using the gradient method.
was derived according to the Lagrange multiplier. Consequently, the Lagrange multiplier could be updated using the gradient method.


where 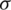 and
and  are step sizes, and
are step sizes, and 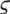 is the iteration index.
is the iteration index.

:
4.4 Proposed Low-Complexity Algorithm for Joint User Selection
In this section, the proposed low-complexity algorithm jointly realises a determined scheduled user selection. The network EE is maximised based on an investigation of the relaxed problem of transmit power allocation and joint user selection. The nonlinear problem in Eqs. (27a)–(27h) is a very challenging one, which is converted into convex optimisation by satisfying both the minimum rate and power constraints 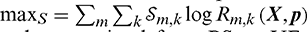 . The joint optimal user selection depends on good signal strength transmitted from BS to UE, to mitigate interference. Low-complexity transmit power and user scheduling was obtained by designing the user selection and power allocation,
. The joint optimal user selection depends on good signal strength transmitted from BS to UE, to mitigate interference. Low-complexity transmit power and user scheduling was obtained by designing the user selection and power allocation,  and
and  respectively. Notice that the BS transmits a signal to every UE if
respectively. Notice that the BS transmits a signal to every UE if  0, where every UE is able to connect with multi-cell BS. Based on the relaxed problem in Eqs. (27c), (27g), (27f) and (27i), applying the joint user selection in DL transmit power allocation achieves a good performance in the LCA by using the Lagrange dual-decomposition method to solve the relaxed problem Eqs. (27)–(27i) [37–45]. According to the relaxed problem, the study initiates auxiliary variables
0, where every UE is able to connect with multi-cell BS. Based on the relaxed problem in Eqs. (27c), (27g), (27f) and (27i), applying the joint user selection in DL transmit power allocation achieves a good performance in the LCA by using the Lagrange dual-decomposition method to solve the relaxed problem Eqs. (27)–(27i) [37–45]. According to the relaxed problem, the study initiates auxiliary variables  and defines
and defines 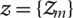 . Based on the log utility function presentation of the user rate, the relaxed problem was converted into convex optimisation as follows:
. Based on the log utility function presentation of the user rate, the relaxed problem was converted into convex optimisation as follows:



The relaxed problem was converted into a convex optimisation one by using the non-negative Lagrange dual-decomposition method for joint selection users can be expressed as follows:
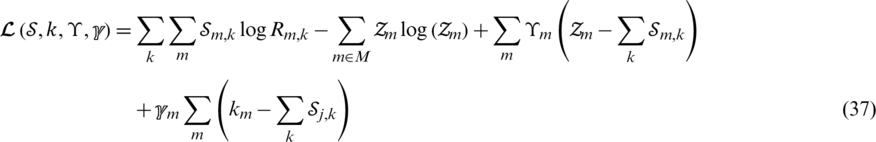
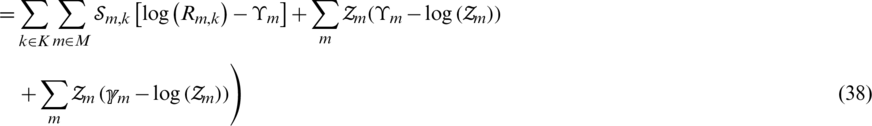
where  ,
,  are non-negative Lagrangian multipliers. User selection sets or assigns user direction to antenna arrays at the BS in multi-cell. In order to denote user selection, the convex optimisation problem with the benefit of the Lagrangian multipliers method is represented as follows:
are non-negative Lagrangian multipliers. User selection sets or assigns user direction to antenna arrays at the BS in multi-cell. In order to denote user selection, the convex optimisation problem with the benefit of the Lagrangian multipliers method is represented as follows:

The LCA is improved by assigning the user direction to antennas arrays at the BS. Every user must achieve a data rate with the smallest transmit power allocation by satisfying the minimum rate requirement, and adopting user selection 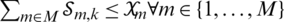 . The first term in Eq. (39), can be expressed as follows:
. The first term in Eq. (39), can be expressed as follows:



Eqs. (27h)–(27i)
The Eq. (27i) represents that every user selected with only one BS in order to reduce interference. The second term in Eq. (39) can be written as follows:


where 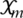 represents the users’ selection with different spatial multiplexing gain of BS antennaM in the multi-cell. The dual problem
represents the users’ selection with different spatial multiplexing gain of BS antennaM in the multi-cell. The dual problem 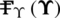 and
and  can be written as follows:
can be written as follows:

Energy-efficient user selection is enhanced to decrease the total power consumption. In order to denote the joint user selection, the user selection employs 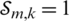 for a LCA that guarantees the optimal joint selection users
for a LCA that guarantees the optimal joint selection users 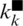 to the BS in multi-cell when
to the BS in multi-cell when  . Therefore, the equivalent transmit power mitigated the influence inter-cell interference to provide the required data rate Rm, k and selecting the optimal of joint UEs. The optimal solution is obtained by applying the Karush-Kuhn-Tucker (KKT) conditions to solve a nonlinear problem to be optimal and set the partial derivative
. Therefore, the equivalent transmit power mitigated the influence inter-cell interference to provide the required data rate Rm, k and selecting the optimal of joint UEs. The optimal solution is obtained by applying the Karush-Kuhn-Tucker (KKT) conditions to solve a nonlinear problem to be optimal and set the partial derivative 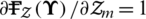 , when the user selection
, when the user selection 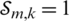 , as follows:
, as follows:

The dual problem is guaranteed with respect to conventional user selection if 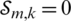 . To find joint user selection, the KKT conditions apply by deriving
. To find joint user selection, the KKT conditions apply by deriving  [30], which has exponential complexity order to produce
[30], which has exponential complexity order to produce

In this section, we apply a series of Monte Carlo simulations to evaluate the maximal EE performance of the proposed LCA. The performance presents the proposed channel model that accounts for imperfect channel estimation using MMSE. The proposed LCA are evaluated as shown in Tab. 2.
Table 2: The summary aspects LCA design

Antenna selection in a massive MIMO system was investigated from the large-scale fading for channel estimation under PRS. More antennas are equipped for relative channel estimation with complete knowledge of large-scale fading by using PRS to eliminate PC. In terms of the relationship between EE and the number of transmitting antennas from the proposed LCA, the EE values increased when the NoA increased. According to Fig. 2, the number of UEs was set as K = 20 in every cell, and the number of PRS as  . The EE showed an increasing trend with low-complexity for optimal antenna selection under minimal PRS. At low transmission powers (
. The EE showed an increasing trend with low-complexity for optimal antenna selection under minimal PRS. At low transmission powers (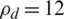 dBm), and with
dBm), and with  , the proposed LCA provided lower EE as compared to the transmission power of
, the proposed LCA provided lower EE as compared to the transmission power of 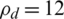 dBm, and number of users,
dBm, and number of users,  . Consequently, improvement in EE depends on the transmission of M antennas with fixed transmission power. Furthermore, optimal antenna selection occurs when the transmission power is reasonable, as demonstrated by Eqs. (20a) and (20b).
. Consequently, improvement in EE depends on the transmission of M antennas with fixed transmission power. Furthermore, optimal antenna selection occurs when the transmission power is reasonable, as demonstrated by Eqs. (20a) and (20b).

Figure 2: Performance of the proposed LCA withM under the effect of pilot sequences user
According Fig. 2, the maximal EE depends on the number of antennas that can be selected. When the number of multipath increased at number 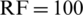 , the EE started to decrease because the switches of RF did not achieve a sufficient resolution, which limited transmission and led to exploding costs and power consumption. Consequently, to become more energy-efficient, the number of RF chains needed to be connected to only a subset of the BS antennas. Only a few RF transmissions needed to be highly promising in achieving a balance between the rate enhancement and power saving.
, the EE started to decrease because the switches of RF did not achieve a sufficient resolution, which limited transmission and led to exploding costs and power consumption. Consequently, to become more energy-efficient, the number of RF chains needed to be connected to only a subset of the BS antennas. Only a few RF transmissions needed to be highly promising in achieving a balance between the rate enhancement and power saving.
Fig. 3 shows the EE versus the minimum data rate 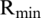 . The maximum EE was achieved with a minimum rate according to Eqs. (27a) and (27b). The minimum rate constraint depends on the guarantee minimum rate constraint for every UE. From Eq. (27b), the minimum rate was achieved with the minimum transmit power. In the scenario
. The maximum EE was achieved with a minimum rate according to Eqs. (27a) and (27b). The minimum rate constraint depends on the guarantee minimum rate constraint for every UE. From Eq. (27b), the minimum rate was achieved with the minimum transmit power. In the scenario  , the minimum
, the minimum 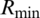 is not achieved, since the channel gains and
is not achieved, since the channel gains and 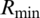 requirement affected every UE, and the optimal solution is to transmit power greater than the CPC. A significant number of UEs increase with large transmit power, but decreases with the a minimum rate
requirement affected every UE, and the optimal solution is to transmit power greater than the CPC. A significant number of UEs increase with large transmit power, but decreases with the a minimum rate  . The EE increases depending on the optimal transmit power
. The EE increases depending on the optimal transmit power 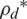 to several of the distributed UEs K. After that, the EE decreases with increasing high data rate, because of large transmit power to UEs according to Eq. (27b). The EE decreases with an increase in a high data rate and a weak channel, as well as the effect of PRS. According to Fig. 3, when the number of UEs
to several of the distributed UEs K. After that, the EE decreases with increasing high data rate, because of large transmit power to UEs according to Eq. (27b). The EE decreases with an increase in a high data rate and a weak channel, as well as the effect of PRS. According to Fig. 3, when the number of UEs  and
and 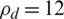 dBm, the maximal
dBm, the maximal  Mbits/J, and the minimum rate
Mbits/J, and the minimum rate 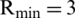 (bits/s). However, when the number of UEs is decreased K = 15 and
(bits/s). However, when the number of UEs is decreased K = 15 and 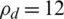 dBm the maximal
dBm the maximal 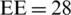 Mbits/J and the minimum rate
Mbits/J and the minimum rate  (bits/s). Meanwhile, when the number of users K = 10 and
(bits/s). Meanwhile, when the number of users K = 10 and 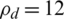 dBm, the maximal
dBm, the maximal 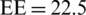 Mbits/J, and the minimum rate
Mbits/J, and the minimum rate 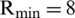 (bits/s). However, the proposed low-complexity algorithm offers a large value of EE when the transmission power is high (
(bits/s). However, the proposed low-complexity algorithm offers a large value of EE when the transmission power is high ( dBm) and the number of distributed UEs is large (
dBm) and the number of distributed UEs is large ( ). The EE improved with optimal transmit power and better channel gains to provide minimum rate requirements.
). The EE improved with optimal transmit power and better channel gains to provide minimum rate requirements.

Figure 3: Performance of the proposed low-complexity algorithm with minimum rate 
From Fig. 4, the proposed LCA results in improved EE based on the transmit power with PRS. Fig. 4 shows that, after obtaining a high maximum value, the EE starts to decrease due to an increase in the transmission power and the number of distributed users inside the cells, which depends on the transmission power and power of the PRS. The EE was quasi-concave when the transmission power exceeded the CPC, as well as under optimal transmit powers that satisfied the constraint in the relaxed problem Eqs. (27)–(27d). From Fig. 4, when the maximal  Mbits/J, the transmit power,
Mbits/J, the transmit power,  dBm with (K, M) = (20, 100). However, when the NoA is small (K, M) = (15, 60), the transmit power,
dBm with (K, M) = (20, 100). However, when the NoA is small (K, M) = (15, 60), the transmit power,  dBm, and the maximal
dBm, and the maximal 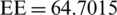 Mbits/J. Furthermore, in the case the NoA decreases to (K, M) = (10, 30), the transmit power,
Mbits/J. Furthermore, in the case the NoA decreases to (K, M) = (10, 30), the transmit power, 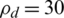 dBm, and the maximum
dBm, and the maximum  Mbits/J. This shows that the maximum EE was achieved with the desired maximum transmit power and minimum PRS. The reason for this is because more antennas must be activated for satisfying the data rate requirement. However, as the maximum transmit power allowance
Mbits/J. This shows that the maximum EE was achieved with the desired maximum transmit power and minimum PRS. The reason for this is because more antennas must be activated for satisfying the data rate requirement. However, as the maximum transmit power allowance 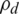 increases, the proposed LCA gradually approaches a constant power consumption, since further increasing the transmit power does not activate more antennas.
increases, the proposed LCA gradually approaches a constant power consumption, since further increasing the transmit power does not activate more antennas.

Figure 4: Performance of the proposed LCA with transmission power
According to Fig. 4, note the EE for all curves changes in a nonlinear manner to the transmit power. Hence, it requires selecting the optimal transmit power according to Eq. (31). It can be observed that the maximum EE of the proposed LCA starts to decreases in the high transmit power regime. This is because the proposed LCA clips the transmit power at the BS, in order to maximize the system EE according to Eqs. (27a) and (27f). In the high transmit power regime, the data rate requirement is satisfied because of the high transmit power and because the LCA tends to use the minimum number of antennas based on Eqs. (27a) and (27h). This demonstrates the effectiveness of the proposed power allocation, especially in the larger power constraint region.
Fig. 5 shows the EE versus the number of RF chains. The maximal EE decreases faster with the NoA, M, taking into account the non-coherence inter-cell interference power, 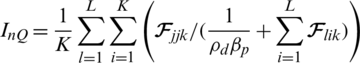 in the denominator in the second term in Eq (14). Based on the estimation channel, the non-coherence inter-cell interference with the optimal transmit power increases with more antennas. The optimal number of transmit antennas maximises EE with MRT. The proposed LCA results in a maximum EE by choosing the optimal activated antenna for RF chains with sufficient power allocation. The optimal number of RF chains could be selected when the NoA selection is
in the denominator in the second term in Eq (14). Based on the estimation channel, the non-coherence inter-cell interference with the optimal transmit power increases with more antennas. The optimal number of transmit antennas maximises EE with MRT. The proposed LCA results in a maximum EE by choosing the optimal activated antenna for RF chains with sufficient power allocation. The optimal number of RF chains could be selected when the NoA selection is 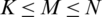 , comparable with all available transmit antennas, and based on the knowledge of good CSI for every UE according to Eq. (20a). From Fig. 5, the maximal
, comparable with all available transmit antennas, and based on the knowledge of good CSI for every UE according to Eq. (20a). From Fig. 5, the maximal 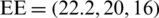 Mbits/J, when the number of RF
Mbits/J, when the number of RF 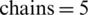 . However, when the number of RF chains
. However, when the number of RF chains 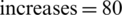 , the EE faster decreases
, the EE faster decreases 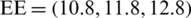 Mbits/J.
Mbits/J.
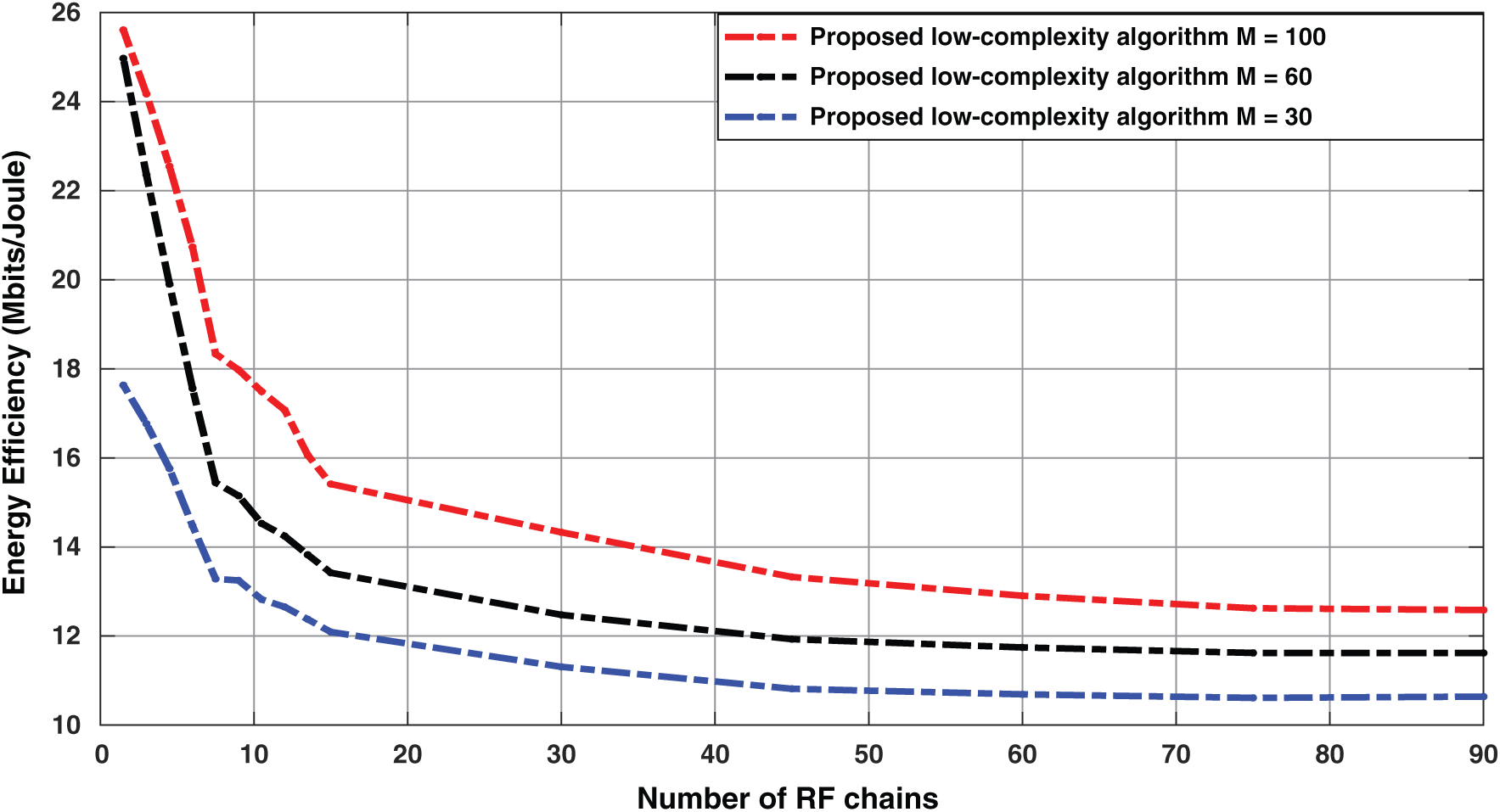
Figure 5: Effect of the proposed LCA with the number of RF chains
Fig. 6 shows optimal values for the EE versus the number of UEs. The power is consumed in the circuit at the BS, primarily due to transmitting signals to every UE. The low-complexity for user scheduling shows that the EE first increases when the number of UEs is small, and then decreases when the increase in the number of UEs in every cell depends on the number of propagation channels. It also minimises PRS due to the limitation of coherence length interval for channels which require mitigating inter-cell interference. Consequently, a fixed number of UEs in every cell provides the maximal EE, depending on the NoA and the optimal number of UEs in every cell. The EE increased monotonically, and started to decrease due to the high transmit power that employed more RF chains. The maximal EE provided (37.552, 40.384, 44.776) Mbits/J. The maximal EE is obtained for the corresponding number of users, K = 70, 78, and 80, when the NoA, M = 30, 60 and 100 respectively. The proposed LCA aims to offer maximum EE, depending on the movement of UEs, but random users cannot guarantee energy-efficient performance.

Figure 6: Maximal EE with a distributed number of users
In this work, to maximise the EE, a novel iterative low complexity algorithm was proposed for joint optimal antenna selection, optimal transmit power allocation and joint user selection under minimised PRS. Our simulation results demonstrate that the proposed iterative low complexity algorithm was used to maximise the EE based on a reasonable maximum transmit power in the case the noise power is less than the power of the received pilot sequence. The optimal antenna selection occurs when the transmission power is practical. The EE is affected by the use of minimised PRS at high SINRs. The proposed LCA prevented repeated searching for joint optimal antenna selection, optimal transmission power and joint user selection, in order to reduce the complexity caused by the increasing NoA. The hybrid precoding technique meets the anticipate emerging as key solutions and growth of traffic demands for high-data-rate multimedia of millimetre wave frequency-based for 5G and beyond-5G. This technique of hybrid precoding equipped with fully-connected and partially-connected structures that are able to reduce hardware complexity and energy consumption for high-frequency designs.
Funding Statement: The authors would like to thank the Universiti Tun Hussein Onn Malaysia for the generous financial support under the Multi-Disciplinary Research (MDR) Grant (H470), and the Ministry of Higher Education Malaysia under the Fundamental Research Grant Scheme (FRGS/1/2019/TK04/UTHM/02/8).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Yu, M. K. Afzal, Y. B. Zikria, A. Rachedi and F. H. Fitzek. (2020). “Tactile internet: Technologies, test platforms, trials, and applications,” Future Generation Computer Systems, vol. 106, pp. 685–688. [Google Scholar]
2. H. Yu and Y. B. Zikria. (2020). “Cognitive radio networks for internet of things and wireless sensor networks,” Sensors, vol. 5288, pp. 1–6. [Google Scholar]
3. Q. Y. Ahmad, A. Nauman, Y. B. Zikria, A. V. Vasilakos and S. W. Kim. (2020). “The future of healthcare internet of things: A survey of emerging technologies,” IEEE Communications Surveys & Tutorials, vol. 22, no. 2, pp. 1121–1167. [Google Scholar]
4. Y. Zhang, W. P. Zhu and J. Ouyang. (2016). “Energy efficient pilot and data power allocation in multi-cell multi-user massive MIMO systems,” in IEEE 84th Vehicular Technology Conf., Montreal, QC, Canada, pp. 1–5. [Google Scholar]
5. R. Zi, X. Ge, J. Thompson, C. X. Wang, H. Wang et al. (2016). , “Energy efficiency optimization of 5G radio frequency chain systems,” IEEE Journal on Selected Areas in Communication, vol. 34, no. 4, pp. 758–771. [Google Scholar]
6. B. M. Lee, J. Choi, J. Bang and B. C. Kang. (2013). “An energy efficient antenna selection for large scale green MIMO systems,” in IEEE Int. Sym. on Circuits and Systems, Beijing, China, pp. 950–953. [Google Scholar]
7. K. Qian, W. Q. Wang and H. Shao. (2014). “Low-complexity transmit antenna selection and beamforming for large-scale MIMO,” International Journal Antennas and Propagation, vol. 2014, pp. 1–11. [Google Scholar]
8. P. Kou, X. Li and Y. Hei. (2015). “Joint antenna selection and power optimization for energy efficient MIMO systems,” in Electronics, Communications and Networks IV: Proc. of the 4th Int. Conf. on Electronics, Communications and Networks, Beijing, China, pp. 173–178. [Google Scholar]
9. H. Q. Ngo, E. G. Larsson and T. L. Marzetta. (2013). “Energy and spectral efficiency of very large multiuser MIMO systems,” IEEE Transaction Communication, vol. 61, no. 4, pp. 1436–1449. [Google Scholar]
10. F. A. Figueiredo, F. A. Cardoso, I. Moerman and G. Fraidenraich. (2018). “Channel estimation for massive MIMO TDD systems assuming pilot contamination and flat fading,” EURASIP Journal Wireless Communication Network, vol. 1, pp. 2–10. [Google Scholar]
11. S. Dong, Y. Wang, L. Jiang and Y. Chen. (2016). “Energy efficiency analysis with circuit power consumption in downlink large-scale multiple antenna systems,” in IEEE 83rd Vehicular Technology Conf., Nanjing, China, pp. 1–5. [Google Scholar]
12. T. M. Nguyen, V. N. Ha and L. B. Le. (2015). “Resource allocation optimization in multi-user multi-cell massive MIMO networks considering pilot contamination,” IEEE Access, vol. 3, pp. 1272–1287. [Google Scholar]
13. W. Zhaocheng, C. Qian, L. Dai, J. Chen, C. Sun et al. (2015). , “Location-based channel estimation and pilot assignment for massive MIMO systems,” in IEEE Int. Conf. on Communication Workshop, London, UK, pp. 1264–1268. [Google Scholar]
14. D. Ha, K. Lee and J. Kang. (2013). “Energy efficiency analysis with circuit power consumption in massive MIMO systems,” in IEEE 24th Annual Int. Sym. on Personal, Indoor, and Mobile Radio Communications, London, UK, pp. 938–942. [Google Scholar]
15. T. H. Tai, W. H. Chung and T. S. Lee. (2015). “A low complexity antenna selection algorithm for energy efficiency in massive MIMO systems,” in IEEE Int. Conf. on Data Science and Data Intensive Systems, Sydney, NSW, Australia, pp. 284–289. [Google Scholar]
16. X. Wenjun, S. Li, S. Wang, Z. Feng, J. Lin et al. (2016). , “Joint parameter selection for massive MIMO: An energy-efficient perspective,” IEEE Access, vol. 4, pp. 3719–3731. [Google Scholar]
17. W. Liu, S. Han and C. Yang. (2015). “Is massive MIMO energy efficient?,” arXiv preprint arXiv:1505.07187. [Google Scholar]
18. K. K. Mensah, R. Chai, D. Bilibashi and F. Gao. (2016). “Energy efficiency based joint cell selection and power allocation scheme for HetNets,” Digital Communication Network, vol. 12, no. 4, pp. 184–190. [Google Scholar]
19. X. Ge, Y. Sun, H. Gharavi and J. Thompson. (2018). “Joint optimization of computation and communication power in multi-user massive MIMO systems,” IEEE Transaction on Wireless Communication, vol. 17, no. 6, pp. 4051–4063. [Google Scholar]
20. E. Björnson, L. Sanguinetti, J. Hoydis and M. Debbah. (2015). “Optimal design of energy-efficient multi-user MIMO systems: Is massive MIMO the answer?,” IEEE Transactions on Wireless Communications, vol. 14, no. 6, pp. 3059–3075. [Google Scholar]
21. H. Q. Ngo, L. N. Tran, T. Q. Duong, M. Matthaiou and E. G. Larsson. (2017). “On the total energy efficiency of cell-free massive MIMO,” IEEE Transactions on Green Communication and Networking, vol. 2, no. 1, pp. 25–39. [Google Scholar]
22. H. Li, J. Cheng, Z. Wang and H. Wang. (2018). “Joint antenna selection and power allocation for an energy-efficient massive MIMO system,” IEEE Wireless Communications Letters, vol. 8, no. 1, pp. 257–260. [Google Scholar]
23. S. He, Y. Huang, L. Yang, B. Ottersten and W. Hong. (2015). “Energy efficient coordinated beamforming for multi-cell system: Duality-based algorithm design and massive MIMO transition,” IEEE Transactions on Communications, vol. 63, no. 12, pp. 4920–4935. [Google Scholar]
24. N. P. Le and F. Safaei. (2015). “Antenna selection strategies for MIMO-OFDM wireless systems: An energy efficiency perspective,” IEEE Transactions on Vehicular Technology, vol. 65, no. 4, pp. 2048–2062. [Google Scholar]
25. Z. Liu, J. Li and D. Sun. (2017). “Circuit power consumption-unaware energy efficiency optimization for massive MIMO systems,” IEEE Wireless Communications Letters, vol. 6, no. 3, pp. 370–373. [Google Scholar]
26. W. Liu, S. Han and C. Yang. (2016). “Energy efficiency scaling law of massive MIMO systems,” IEEE Transactions on Communications, vol. 65, no. 1, pp. 107–121. [Google Scholar]
27. F. Tan, T. Lv and S. Yang. (2017). “Power allocation optimization for energy-efficient massive MIMO aided multi-pair decode-and-forward relay systems,” IEEE Transactions on Communication, vol. 65, no. 6, pp. 2368–2381. [Google Scholar]
28. S. Maimaiti, G. Chuai, W. Gao, K. Zhang, X. Liu et al. (2019). , “A low-complexity algorithm for the joint antenna selection and user scheduling in multi-cell multi-user downlink massive MIMO systems,” EURASIP Journal on Wireless Communications and Networking, vol. 2019, no. 1, pp. 1–4. [Google Scholar]
29. J. Choi, N. Lee, S. N. Hong and G. Caire. (2019). “Joint user selection, power allocation, and precoding design with imperfect CSIT for multi-cell mu-MIMO downlink systems,” IEEE Transactions on Wireless Communications, vol. 19, no. 1, pp. 162–176. [Google Scholar]
30. M. W. Baidas, Z. Bahbahani and E. Alsusa. (2019). “User association and channel assignment in downlink multi-cell NOMA networks: A matching-theoretic approach,” EURASIP Journal on Wireless Communications and Networking, vol. 2019, no. 1, pp. 1–21. [Google Scholar]
31. Y. Lin, Y. Wang, C. Li, Y. Huang and L. Yang. (2017). “Joint design of user association and power allocation with proportional fairness in massive MIMO HetNets,” IEEE Access, vol. 5, pp. 6560–6569. [Google Scholar]
32. H. Pervaiz, L. Musavian and Q. Ni. (2013). “Joint user association and energy-efficient resource allocation with minimum-rate constraints in two-tier HetNets,” in IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications, London, UK, pp. 1634–1639. [Google Scholar]
33. J. Hoydis, S. T. Brink and M. Debbah. (2013). “Massive MIMO in the UL/DL of cellular networks: How many antennas do we need?,” IEEE Journal Selection Areas Communication, vol. 31, no. 2, pp. 160–171. [Google Scholar]
34. P. Liu, S. Jin, T. Jiang, Q. Zhang and M. Matthaiou. (2017). “Pilot power allocation through user grouping in multi-cell massive MIMO systems,” IEEE Transactions on Communication, vol. 65, no. 4, pp. 1561–1574. [Google Scholar]
35. T. Van Chien, E. Björnson and E. G. Larsson. (2016). “Joint power allocation and user association optimization for massive MIMO systems,” IEEE Transactions on Wireless Communication, vol. 15, no. 9, pp. 6384–6399. [Google Scholar]
36. A. Salh, L. Audah, N. S. Shah and S. A. Hamzah. (2020). “Mitigating pilot contamination for channel estimation in multi-cell massive MIMO systems,” Wireless Personal Communication, vol. 112, no. 3, pp. 1643–1658. [Google Scholar]
37. R. Couillet and M. Debbah. (2011). Random Matrix Methods for Wireless Communications. New York: Cambridge University Press, pp. 10–65. [Google Scholar]
38. Z. Xu, C. Yang, G. Y. Li, S. Zhang, Y. Chen et al. (2011). , “Energy-efficient power allocation between pilots and data symbols in downlink OFDMA systems,” in IEEE Global Telecommunication Conf. (GLOBECOMKathmandu, Nepal, pp. 1–6. [Google Scholar]
39. J. Xu, L. Qiu and C. Yu. (2011). “Improving energy efficiency through multimode transmission in the downlink MIMO systems,” EURASIP Journal on Wireless Communications and Networking, vol. 1, pp. 1–12. [Google Scholar]
40. S. Boyd and L. Vandenberghe. (2004). Convex Optimization, Cambridge: Cambridge University Press. [Google Scholar]
41. L. Zhao, H. Zhao, F. Hu, K. Zheng and J. Zhang. (2013). “Energy efficient power allocation algorithm for downlink massive MIMO with MRT precoding,” in IEEE Vehicular Technology Conf., Las Vegas, NV, USA, pp. 1–5. [Google Scholar]
42. D. W. K. Ng, E. S. Lo and R. Schober. (2012). “Energy efficient resource allocation for secure OFDMA systems,” IEEE Transactions on Vehicular Technology, vol. 61, no. 6, pp. 2572–2585. [Google Scholar]
43. K. K. Mensah, R. Chai, D. Bilibashi and F. Gao. (2016). “Energy efficiency based joint cell selection and power allocation scheme for HetNets,” Digital Communications and Networks, vol. 2, no. 4, pp. 184–190. [Google Scholar]
44. A. Salh, N. S. Shah, L. Audah, Q. Abdullah, W. A. Jabbar et al. (2020). , “Energy efficient power allocation and joint user association in multiuser-downlink massive MIMO system,” IEEE Access, vol. 8, pp. 1314–1326. [Google Scholar]
45. D. Fooladivanda and C. Rosenberg. (2012). “Joint resource allocation and user association for heterogeneous wireless cellular networks,” IEEE Transaction Wireless Communication, vol. 12, no. 1, pp. 248–257. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |